1 Introduction

The International Terrestrial Reference System (ITRS) is fundamental for many Earth Science applications. Users access this system by means of the coordinates of fundamental stations distributed on the Earth’s surface that materialize the International Terrestrial Reference Frame (ITRF). The time evolution of those station positions is described by a functional kinematic (or trajectory) model. This model has historically been composed of piece-wise linear functions describing linear displacements such as those due to continental drift and glacial isostatic adjustment, but also offsets due, for instance, to equipment changes or co-seismic displacements. It was extended with exponential and logarithmic functions in ITRF2014 to account for post-seismic displacements (Altamimi et al. 2016), then with annual and semiannual sine waves in ITRF2020 to account for the seasonal deformation of the Earth (Altamimi et al. 2022).

However, part of the Earth’s surface deformation is not captured by those deterministic functions, such as interannual hydrological loading deformation (e.g., Wu et al. 2006; Nahmani et al. 2012; Tiwari et al. 2014), high-frequency atmospheric loading deformation (e.g., vanDam et al. 1994; Martens et al. 2020), slow slip events (e.g., Schwartz and Rokosky 2007; Vergnolle et al. 2010; Wallace 2020) or the Earth’s response to recent ice melting (e.g., Velicogna and Wahr 2006; Métivier et al. 2012, 2020a, b). To account for such aperiodic (i.e., nonlinear and non-seasonal) displacements in a long-term terrestrial reference frame which would thus better describe the shape variations of the Earth, Dong et al. (1998) and Wu et al. (2015) proposed to represent the time evolution of station positions not by deterministic functions, but instead by time series of regularly sampled (e.g., weekly) positions. This idea was put into practice with JTRF2014 (Abbondanza et al. 2017), the first combined terrestrial reference frame published in the form of a time series. Note that although JTRF2014 is published as a time series, the time evolution of station positions is described, within its computation, by deterministic functions (like in the ITRF), plus a stochastic component aiming at capturing the nonlinear, non-seasonal deformation of the Earth (not present in the ITRF).

In the ITRF computation, the station coordinates of the different space geodetic techniques (DORIS, GNSS, SLR, VLBI) need to be tied into a common frame. For the linear part of station coordinates, this is achieved by means of appropriately weighted terrestrial local ties and co-velocity constraints within co-location sites. In the ITRF2020 computation, weighted co-seasonal-motion constraints were additionally applied in order to tie the seasonal displacements of the different techniques into a common frame, with special care taken of the inconsistencies observed at several co-location sites (Collilieux et al. 2018).

In the same way, taking into account aperiodic displacements in a terrestrial reference frame would require aperiodic motions of the different space geodetic techniques to be tied in a common frame by means of co-motion constraints (Altamimi et al. 2019). The assumption underlying these co-motion constraints is that co-located stations should in principle be subject to the same nonlinear, non-seasonal displacements.

However, station position time series of the four techniques are known to contain random and systematic errors of various natures and amplitudes (e.g., Williams and Willis 2006; Ray et al. 2013; Lovell et al. 2013; Luceri et al. 2019), as well as unexplained variations [e.g., flicker noise in GNSS time series (Zhang et al. 1997; Mao et al. 1999; Williams 2003; Santamaría-Gómez et al. 2011)]. Thus, even if the stations of the different techniques are subject to common geophysical aperiodic displacements within co-location sites, these displacements may be masked by technique-specific errors. It is therefore not guaranteed that co-motion constraints applied to measured aperiodic displacements would actually tie real nonlinear, non-seasonal displacements, rather than mix technique errors.

In this study, we investigate whether common aperiodic displacements (other than post-seismic deformation) can actually be detected at the ITRF co-location sites given current technique errors. For that purpose, we compare station position time series extracted from the DORIS, GNSS, SLR and VLBI solutions provided for ITRF2014. Station position time series from the four space geodetic techniques were already compared in previous studies, but those were generally focused on long-term velocities (Tornatore et al. 2016), annual signals (Tesmer et al. 2009) or on the estimation of the technique precisions (Feissel-Vernier et al. 2007; Abbondanza et al. 2015). To our knowledge, only Collilieux et al. (2007) previously attempted to estimate correlations between the nonlinear, non-seasonal vertical displacements sensed by GNSS, SLR and VLBI, and found significant positive correlations for only a few (mostly GNSS-VLBI) co-located station pairs. A re-evaluation of the consistency of the aperiodic displacements sensed by the four techniques, in all three components, based on recent reprocessed data, therefore seems necessary.

The rest of this paper is organized as follows. Section 2 introduces the data used and their preprocessing, in particular the careful alignment procedure used to bring station position time series from the different techniques to a common frame, while preserving potential common aperiodic displacements. Section 3 describes how the aligned time series were then modeled and filtered for trends, offsets, post-seismic displacements and periodic signals (due to both the seasonal deformation of the Earth and technique-specific errors), in order to retain aperiodic variations only. In Sect. 4, the filtered time series of co-located stations are confronted with each other, and the impact of non-tidal loading corrections on the observed correlations is also assessed. Section 5 finally discusses the obtained results and their implications for the use of co-aperiodic-motion constraints in the formation of a terrestrial reference frame.

2 Data and preprocessing

This study uses 21-year long station position time series over the period 1994.0–2015.0. Those time series are derived from the solutions provided by the IAG space geodetic technique services for the ITRF2014 computation (Altamimi et al. 2016). Each of these solutions contains the estimated coordinates of a network of geodetic stations together with their variance/covariance information—or equivalently a normal equation system. The DORIS (Moreaux et al. 2016) and SLR (Luceri and Pavlis 2016) products are provided on a weekly basis. For consistency, we use the weekly GNSS solutions provided by the International GNSS Service (IGS; Rebischung et al. 2016). Finally, the VLBI products (Bachmann et al. 2016) are delivered by observation sessions, but VLBI station position time series will also be re-sampled at weekly intervals later on. Note that not all VLBI solutions provided for ITRF2014 are used in this study, but only those with at least four stations and a station network whose convex hull has a volume larger than \(10^{19} \mathrm {m^3}\).

To compare the station position time series provided by the four space geodetic techniques, they first need to be expressed with respect to a common reference frame. However, aligning weekly or session-wise technique solutions to a long-term linear frame such as the ITRF2014 is known to affect seasonal signals (Collilieux et al. 2007, 2009). Likewise, because of the different geometries of the technique station networks, the nonlinear, non-seasonal displacements sensed by the different techniques could be affected differently by such an alignment, i.e., each technique could be affected by a different “network effect,” which could jeopardize the detection of possible common aperiodic displacements across techniques.

We therefore use another alignment approach. Namely, all DORIS, SLR and VLBI solutions are aligned to the GNSS solution of the same week. With such an alignment of instantaneous solutions to other instantaneous solutions, the network effect due to nonlinear deformation of the Earth should cancel, and possible common nonlinear displacements across techniques should be retained.

The next sections detail this alignment procedure. Section 2.1 describes the pseudo-local ties that are used to align the DORIS, SLR and VLBI solutions to the GNSS solutions. Section 2.2 then details the manipulations performed on the technique solutions (or normal equations).

2.1 Pseudo-local ties

To align each DORIS, SLR or VLBI solution to the GNSS solution of the same week, a reference solution has to be derived from the GNSS solution, in which vectors tying GNSS stations to the co-located DORIS, SLR or VLBI stations are applied to the GNSS station positions. We do not use actual surveyed local ties for that purpose, because they are not available at every co-location site, and because they show various levels of inconsistency with the space geodetic observations, as evidenced by the ITRF combination residuals (Altamimi et al. 2016). Pseudo-local ties are used instead.

To derive these pseudo-local ties, we start by forming a long-term, homogeneous, multi-technique solution. We use as inputs the same four technique-specific long-term solutions as used for the ITRF2014 computation. But instead of combining them together with local ties, we align them to ITRF2014 via the 14-parameter Helmert transformations estimated during the ITRF2014 inter-technique combination. In this way, the technique-specific solutions are not distorted by the conflicting local ties, but retain their intrinsic shapes. Let us denote the long-term, homogeneous, multi-technique solution thus obtained as ITRF2014A.

To determine pseudo-local ties from GNSS to a specific technique, e.g., SLR, on a specific week, the ITRF2014A coordinates are first propagated to the middle of the week. We then compute, from the propagated ITRF2014A solution, all vectors between GNSS stations available in the weekly GNSS solution and co-located SLR stations available in the weekly SLR solution, which form our pseudo-local ties. In case more than one pseudo-local tie is available at the same co-location site, we select and use only the one between the stations whose ITRF2014 residual time series have the smallest weighted root mean square (WRMS).

2.2 Alignment

The weekly solutions provided by the IGS for ITRF2014 were aligned to the IGb08 reference frame (IGSMAIL-6663Footnote 1). Our first step is thus to align them to ITRF2014A. For that purpose, each weekly GNSS solution is first compared with ITRF2014A via a 7-parameter Helmert transformation. Possible inconsistent station coordinates are iteratively removed from the comparison in order to obtain a clean list of reference stations. Then, the constraints reported in the weekly GNSS SINEX file are removed. No-net-rotation (NNR) and no-net-translation (NNT) with respect to ITRF2014A via the selected reference stations are added instead, and the normal equation is re-inverted.

The next step is to align the weekly DORIS, weekly SLR and session-wise VLBI solutions to the weekly GNSS solutions. For each of these alignments, a reference solution is first formed by adding the pseudo-local ties obtained in Sect. 2.1 to the weekly GNSS solution. The solution to be aligned is then compared with the reference solution via a 7-parameter Helmert transformation, and possible outlying stations are iteratively removed from the reference solution. Then, in case of SLR or DORIS, a reference frame-free normal equation is obtained from the weekly solution using Equation B.22 of Rebischung (2014). In case of VLBI, the same equation is used, but to remove only the scale information from the provided normal equation (which already has six rotation and translation singularities). Finally, NNR, NNT and no-net-scale (NNS) constraints with respect to the clean reference solution are added to the reference frame-free normal equation. A DORIS, SLR or VLBI solution is thus obtained which is aligned in orientation, origin and scale to the GNSS solution of the week via the pseudo-local ties.

3 Time series modeling

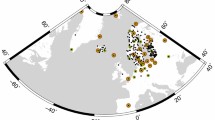
Thanks to the alignment methodology described in Sect. 2, DORIS, SLR, VLBI and GNSS solutions aligned to a common reference frame were obtained. Station position time series were extracted from those solutions, and the VLBI station position estimates were averaged over weekly bins to match the weekly sampling of the other techniques. In the following, only stations that are part of ITRF2014, whose position time series contain at least 200 weeks, and are at least 50% complete, are considered. Figure 1 shows the distribution of this station selection. It includes 109 DORIS stations, 771 GNSS stations, 27 SLR stations and 11 VLBI stations.

Fig. 1
figure 1

ITRF2014 stations used for time series analysis

Full size image

The station position time series thus obtained exhibit linear trends, offsets, post-seismic displacements and periodic variations, on top of aperiodic variations commonly referred to as background noise. Our objective is to compare the aperiodic variations observed by the different techniques at co-location sites; therefore, all the other components need to be removed from the series. For that purpose, we start by adjusting to each time series the same kinematic model as used in ITRF2014, which includes a piece-wise linear part accounting for linear trends and offsets, plus exponential and/or logarithmic functions accounting for post-seismic deformation where necessary. Note that, when adjusting these models, outliers are iteratively removed from the series. Also note that the amplitudes and relaxation times of the exponential and logarithmic functions are held fixed to their ITRF2014 values.

The residuals from these initial models still include periodic signals, such as seasonal variations or the well-known GPS draconitic errors (Ray et al. 2008), which still need to be filtered out in order to compare aperiodic variations only. For that purpose, we have to identify all significant periodic variations in the time series of each technique, and augment our initial kinematic models accordingly (Sect. 3.1). Section 3.2 summarizes the significant periods detected during this process.

3.1 Spectral analysis

In order to analyze the spectral content of the residual station position time series, to test for the significance of potential periodic signals, and to account for the most significant ones in our kinematic models, we employ the least square harmonic estimation (LSHE) method (Amiri-Simkooei et al. 2007). This method tests the logarithm of the likelihood ratio between a null model and alternative models, each of which includes one additional sine wave at a given frequency. Under the null hypothesis, the logarithm of the likelihood ratio follows a \(\chi ^2\) distribution with two degrees of freedom. For a given series, if the null model is adequate, the LSHE test statistic, represented as a function of the frequency, is thus expected to be “flat” and centered around 2. On the other hand, if a significant periodic signal is unaccounted for by the kinematic model, the LSHE test statistic will show a peak around the corresponding frequency. However, if the noise model of the series is inadequate, then the LSHE test statistic will also depart from flatness, though continuously in frequency. Testing for the significance of potential periodic signals using the LSHE method therefore requires that the noise in the time series is adequately modeled.

The background noise in GNSS station position time series is well described by the combination of variable white noise and power-law noise (Zhang et al. 1997; Mao et al. 1999; Williams 2003; Santamaría-Gómez et al. 2011; Gobron et al. 2021), where the variable white noise is an uncorrelated process whose standard deviations are proportional to formal errors. The literature about the background noise in the station position time series of the other techniques is scarcer and less conclusive (Williams and Willis 2006; Feissel-Vernier et al. 2007; Ray et al. 2008; Klos et al. 2018). Nevertheless, the stacked Lomb-Scargle periodograms presented by Abbondanza et al. (2015) suggest that a white plus power-law noise model could also be appropriate for DORIS, SLR and VLBI time series. (The appropriateness of this noise model, in average, for DORIS, SLR and VLBI time series will actually be confirmed by the flatness of the stacked LSHE test statistics presented later on.) We thus adjust variable white plus power-law noise models to our time series, simultaneously with their deterministic models. The noise model parameters are estimated by restricted maximum likelihood, an unbiased alternative to classical maximum likelihood estimation (Patterson and Thompson 1971; Harville 1977; Gobron et al. 2022). Thus accounting for the characteristics of the background noise in the series, the LSHE method can now be used to test for the significance of potential periodic signals in the time series, and iteratively refine our kinematic models accordingly.

We start this iterative process by considering the ITRF2014 kinematic models, which include no periodic signals, and compute the LSHE test statistic for every station and every East, North, Up component, over a common set of evenly spaced frequencies. In order both to increase the power of the LSHE test, and to identify significant periodic signals per technique rather than per station, we sum, for every technique, the LSHE test statistics over all stations and components. Note that only stations with time series longer than 1/f contribute to the stacked LSHE test statistic at frequency f. The obtained stacked LSHE test statistics are shown by the light curves in Fig. 2. Assuming independence across stations and components and the null hypothesis (no significant harmonic signal at frequency f), they follow \(\chi ^2\) distributions with \(2\times n\times 3\) degrees of freedom, where n is the number of contributing stations and 3 is the number of components.

For each technique, we then perform a first automatic, iterative detection of significant periodic signals. At each iteration, we look for the frequency with maximal stacked LSHE test statistic. If this maximum statistic exceeds a certain quantile of the \(\chi ^2\) distribution with \(2\times n\times 3\) degrees of freedom, we add sine waves at the corresponding frequency in the kinematic models of all stations of the technique, and iterate. Otherwise, we stop iterations. Note that the noise parameters are re-estimated at every iteration, simultaneously with the kinematic models. For DORIS, SLR and VLBI, we use the 99.9999% quantile as threshold. For GNSS, in order to avoid an over-detection of periodic signals, we found necessary to use a higher, arbitrary threshold. This is probably related to the fact that the background noise in GNSS time series is spatially correlated (Williams et al. 2004; Amiri-Simkooei 2009; Amiri-Simkooei et al. 2017; Benoist et al. 2020); hence, the assumption of independence across stations is not met in practice.

This first automatic detection highlighted a number of periodic signals previously observed in geodetic station position time series (i.e., seasonal signals, draconitic signals, tidal aliases—see Sect. 3.2). However, the periods attributed by our automatic detection procedure to these known signals were in some cases slightly shifted from their theoretical periods. Besides, this first automatic detection led in some cases to the inclusion of several sine waves with nearby frequencies in the kinematic models. This could be expected from the fact that the amplitudes and phases of certain periodic signals in geodetic station position time series are not constant. This is, for instance, known to be the case with seasonal signals (Davis et al. 2012; Chen et al. 2013; Klos et al. 2017) and GPS draconitic signals (Rebischung et al. 2021). However, having several sine waves with uncontrolled nearby frequencies in the kinematic models can turn out problematic, particularly for short time series. Hence, we will prefer another way of accounting for time-variable periodic signals in the following.

To deal with the aforementioned issues, a second automatic, iterative refinement of our kinematic models is carried out. Our starting points are the ITRF2014 kinematic models complemented with sine waves at all the known periods highlighted during the first detection (i.e., seasonal harmonics, draconitic harmonics and tidal aliases). We use the theoretical periods of these signals, not those retrieved from the first detection. Then, the same iterative procedure as above is used to refine these initial models, with just one difference: at each iteration, we look for the sine wave already present in the kinematic models whose frequency \(f_s\) is the closest to the frequency \(f_m\) of the maximal stacked LSHE test statistic. If both frequencies differ by less than 0.0003 cycle-per-day (cpd), then we do not add a new sine wave at frequency \(f_m\) into the models, but instead “complexify” the one already present at frequency \(f_s\). Namely, if the sine wave currently present in the kinematic models at frequency \(f_s\) is still a simple time-invariant sine wave, it is replaced by a “degree-1 variable” sine wave; while if the sine wave currently present in the kinematic models at frequency \(f_s\) is already a “degree-d variable” sine wave, it is replaced by a “degree-\(d+1\) variable” sine wave. A “degree-d variable” sine wave is here defined as a sine wave whose sine and cosine coefficients are degree-d polynomials of time:

$$\begin{aligned} S(t) = \left( \sum _{i = 0}^{d}a_it^{i}\right) \cos (2\pi ft) + \left( \sum _{i = 0}^{d} b_it^{i}\right) \sin (2 \pi ft) \end{aligned}$$
(1)

where the coefficients \((a_i, b_i)_{0\le i\le d}\) are to be estimated. To ensure that no significant periodic signals are missed, but no over-detection occurs either, we manually choose the stopping iteration for each technique, based on a visual inspection of the stacked LSHE test statistics (see Fig. 2).

Fig. 2
figure 2

Light plain curves: stacked LSHE test statistics obtained with the initial ITRF2014 kinematic models. Dark plain curves: stacked LSHE test statistics obtained with the final kinematic models. Dashed curves: Expected values of stacked LSHE test statistics under null hypothesis (see text). The vertical lines indicate the frequencies of the (time-variable) sine waves included in the final kinematic models

Full size image

The kinematic models obtained at the end of this second iterative procedure are our final models. The stacked LSHE test statistics obtained with these final models are shown by the dark curves in Fig. 2. They are flat except at the lowest frequencies, where less and less stations contribute to the stacked LSHE test statistics. Figure 2 also shows the expected values of the stacked LSHE test statistics under the null hypothesis, i.e., no significant periodic signal missing in the kinematic models (dashed curves). The agreement between the stacked LSHE statistics and their expected values under the null hypothesis is an indication of the appropriateness of the employed white plus power-law noise model, in average, for the time series of the four techniques.

Figure 3 provides statistics on the estimated levels of noise. It represents the distribution of the estimated noise standard deviations over all stations for each technique and each component. As the variance of power-law noise depends on the length of the time series, following the example of Gobron et al. (2021), we computed the scatter of equivalent 10-year long time series from the estimated parameters of the power-law noise models. In this figure, we can observe that the level of white noise is much lower for GNSS than for the other techniques, especially in the horizontal components. This difference is less marked for power-law noise, but it is still noticeable that the estimated level of power-law noise depends on the technique. This implies that the power-law noise present in station position time series does not only reflect Earth’s surface deformation, but also includes technique-specific errors.

Fig. 3
figure 3

Distributions of estimated white noise and power-law noise standard deviations for each technique and component (see the convention for the definition of power-law noise standard deviation in the text)

Full size image

3.2 Detected periods

The two iterative procedures described in Sect. 3.1 led to the detection of significant periodic signals in the station position time series of the different techniques, and to the inclusion of time-invariant or time-variable sine waves into our kinematic models. The frequencies of those sine waves are indicated by the vertical lines in Fig. 2. A list of their periods and degrees of variability can additionally be found in “Appendix A.” The detected periodic signals fall into four different categories: seasonal signals, draconitic signals, tidal aliases and other periodic signals of unknown origins. These four categories are discussed in the next paragraphs.

Annual and semiannual signals have long been evidenced in station position time series of the different techniques and consist of a superposition of various physical phenomena and systematic errors (Dong et al. 2002; Collilieux et al. 2007). (Time-variable) sine waves with periods of 365.25 and 182.63 days have consistently been detected and included in our kinematic models for all four techniques. Our analysis also evidenced significant ter-annual signals (with periods of 121.75 days) in DORIS and GNSS station position time series, consistently with the analyses of Williams and Willis (2006) and Klos et al. (2018) for DORIS; Gobron et al. (2021) and Rebischung et al. (2021) for GNSS.

Draconitic signals were evidenced in our analysis for all three satellite techniques (DORIS, GNSS and SLR). Frequencies close to the first eight harmonics of the GPS draconitic year (\(\approx \)351.6 days; Ray et al. 2008; Amiri-Simkooei 2013) were found during our first automatic analysis of the GNSS time series. Sine waves at the first eight GPS draconitic harmonics are thus included in our final kinematic models of the GNSS time series, which are all time-variable sine waves, consistently with the non-stationarity of GPS draconitic signals pointed out by Rebischung et al. (2021). As regards DORIS, significant periodic signals close to the first four harmonics of the TOPEX/Poseidon/Jason-1/Jason-2 draconitic period (117.56 daysFootnote 2) were evidenced, consistently with the observations of Williams and Willis (2006) and Klos et al. (2018). These draconitic signals are accounted for by time-variable sine waves in our final kinematic models of the DORIS time series. For SLR finally, periodic signals close to the draconitic periods of both LAGEOS satellites (559.29 and 222.63 days\(^{2}\)) were evidenced, consistently with the observations of Luceri et al. (2019) in time series of range bias estimates. Signals at the second harmonic of the LAGEOS-1 draconitic period (279.65 days) were additionally detected, which have recently been observed in SLR geocenter motion times series also (Yu et al. 2021). These draconitic signals are accounted for by time-invariant or time-variable sine waves in our final kinematic models of the SLR time series.

Station position time series from the satellite techniques are also known to include spurious signals due the aliasing of tide model errors via the sampling of the time series and/or the ground repeat periods of the satellites (Penna and Stewart 2003). For DORIS, significant periodic signals close to the alias periods of the \(O_1\) and \(M_2\) tides via the weekly sampling of the DORIS time series (14.19 and 14.77 days, respectively) were found. The same \(O_1\) aliasing period was also detected in SLR time series. For GNSS, finally, a single tide-related period was detected at 14.39 days, which can be explained by a two-step aliasing process: (1) aliasing of \(M_2\) tide model errors to a period of 13.62 days via the ground repeat period of the GPS satellites, as described by Penna and Stewart (2003) and observed by, e.g., Rebischung et al. (2021; 2) aliasing of the 13.62-day signals present in the daily IGS solutions via the weekly averaging of those solutions. All the detected tidal aliases are accounted for by time-invariant or time-variable sine waves in our final kinematic models.

We finally detected several unexplained, significant periodic signals in the DORIS and SLR time series. Two such periods were found for DORIS at 20.22 and 25.99 days. While \(\approx \)26-day signals have to our knowledge never been reported before, \(\approx \)20.2-day signals were previously observed in DORIS time series by Williams and Willis (2006) and Klos et al. (2018), but remain unexplained. For SLR, a cluster of \(\approx \)30-day periods was detected (28.60, 30.09 and 30.47 days), of which we found no trace in the literature, except for a mention of 28-day signals in SLR geocenter time series by Yu et al. (2021). Although these periodic signals are unexplained, they clearly stand out from the background noise in DORIS and SLR time series (see Fig. 2). They are therefore included in our final kinematic models as time-invariant sine waves in order not to affect the comparison of aperiodic variations observed by the different techniques presented in the next section.

4 Comparison of residual time series

The residual position time series computed in Sect. 3 reflect the aperiodic variations (or background noise) in the station position time series from the four space geodetic techniques. They include actual noise, systematic errors and common aperiodic displacements across techniques. In the present section, we compare the obtained residual time series within the ITRF co-location sites, with the purpose of assessing these possible common aperiodic displacements. Figure 4 shows as examples the residual time series obtained at two co-location sites: Ny-Ålesund (Svalbard, Norway) and Hartebeesthoek (South Africa). It clearly illustrates the different levels of noise between techniques and components. Besides, common variations across techniques can clearly be observed in some cases, like in the vertical component at the Ny-Ålesund site.

It is worth mentioning that the residual time series used in this section were obtained from an adjustment of the final kinematic models using a variable-white-noise-only stochastic model. Indeed, we noticed that the residuals computed with variable white plus power-law noise models exhibited in many cases small trends and/or offsets. This can be explained by the fact that the residuals from least-squares adjustments tend to mimic the specified noise model and may make use of the trends and/or offsets present in the series for that purpose. On the other hand, we observed that trends and offsets were effectively absorbed in the adjusted kinematic models when using a variable-white-noise-only stochastic model.

Fig. 4
figure 4

Residual position time series at the Ny-Ålesund (left) and Hartebeesthoek (right) co-location sites. Within each subfigure, the top subplot shows the residual position time series of all stations available at the site, shifted by multiples of 20 mm for clarity. The bottom subplot is the superposition of all Vondrák-filtered residuals with a 2 cpy cutoff frequency (Vondrák 1969). Each technique is shown with a different color: blue for GNSS, orange for VLBI, pink for DORIS and turquoise for SLR

Full size image

Section 4.1 describes the results from the comparison of residual time series between each pair of techniques available at each co-location site. Then, Sect. 4.2 investigates which part of the coherence between the aperiodic displacements sensed by the different techniques is attributable to loading deformation. In the following, we only consider co-located station pairs that share at least 200 weeks of common data. The selected stations are depicted in Fig. 5.

Fig. 5
figure 5

Selected co-located stations

Full size image

4.1 Concordance correlation coefficients

Lin (1989) introduces the concordance correlation coefficient to compare two measurements of the same variable. The concordance correlation coefficient of two time series a and b with zero means is defined as:

$$\begin{aligned} c=\frac{2\sigma _{ab}}{\sigma _a^2 + \sigma _b^2} \end{aligned}$$
(2)

where \(\sigma _{a}^2\) and \(\sigma _{b}^2\) are the sample variances of the time series and \(\sigma _{ab}\) is their sample covariance. This coefficient measures the proportion of the total variance of the two series which can be explained by a common signal. We prefer Lin’s concordance correlation coefficient over Pearson’s ordinary correlation coefficient as the latter measures the strength of a linear relationship between two variables, whichever the proportionality coefficient, i.e., how close the scatter plot of b against a falls close to some straight line. Lin’s concordance correlation coefficient measures how close the scatter plot of b against a falls close to a \(45^{\circ }\) straight line, i.e., whether the two series contain a common signal with the same amplitude, as it should be the case with possible common aperiodic ground deformation.

The concordance correlation coefficients between the residual time series of the selected GNSS stations and of the co-located stations of the other techniques are represented in Fig. 6. When several pairs of stations of the same techniques are available at a given co-location site, only the highest concordance correlation coefficient is displayed. The green boxplots in Fig. 7 show the distributions of those concordance correlation coefficients for each technique and component. To get an idea of what concordance correlation coefficients concretely represent, it is helpful to consider Fig. 4 again. At the Ny-Ålesund co-location site, in the vertical component where common aperiodic variations across techniques can be observed, the concordances between GNSS and the other techniques are all larger than 0.4. On the other hand, they are all less or equal than 0.2 at the Hartebeesthoek co-location site.

In order to assess the significance of the concordance correlation coefficient computed for each given station pair and component, we simulated 10,000 pairs of white noise time series with the same number of points as the number of common weeks between both stations, and the same theoretical concordance correlation coefficient as the one actually computed for that station pair and component. We then computed the empirical concordances of the 10,000 pairs of simulated time series and the 2.5% and 97.5% quantiles of their distribution to obtain a 95% confidence interval. Figures showing the concordance correlation coefficients obtained for each technique pair, together with their 95% confidence intervals, are available in “Appendix B.” The sizes of these intervals vary with the number of common points between each pair of time series, as well as on the value of their concordance. Nevertheless, they are all equal or lower than 0.25. Hence, if a concordance value is equal to or greater than 0.13, zero is not contained in its confidence interval and the concordance value can be considered significantly different from zero. On the other hand, the significance of any concordance value lower than 0.13 must be verified on a case-by-case basis because it depends on the size of its confidence interval.

Fig. 6
figure 6

Concordance correlation coefficients between residual coordinate time series of selected GNSS stations and of co-located stations of the other techniques

Full size image
Fig. 7
figure 7

Distributions of the concordance correlation coefficients between residual coordinate time series of selected GNSS stations and of co-located stations of the other techniques, with (pink) and without (green) non-tidal loading corrections applied

Full size image

It can clearly be observed in Fig. 6 and “Appendix B” that the concordance correlation coefficients obtained for the horizontal components of the GNSS-SLR and GNSS-DORIS station pairs are generally very low and not significantly different from zero. Their medians are 0.01 for both technique pairs. The concordance correlation coefficients obtained for the horizontal components of the GNSS-VLBI station pairs are somewhat higher, particularly in the East component, where their median reaches 0.15. These results may be put in perspective with the levels of noise observed in Fig. 3. It would thus seem that, although VLBI observations are intermittent, the observation noise of VLBI is low enough to allow detecting some common aperiodic horizontal displacements with GNSS. On the other hand, possible common aperiodic horizontal displacements between GNSS and SLR/DORIS are likely hidden by the higher observation noise of the latter techniques. Note that SLR observations are also discontinuous due in particular to weather contingency.

In vertical, the concordance correlation coefficients between GNSS and the three other techniques are significantly different from zero for most station pairs. Their medians are 0.19 for GNSS-VLBI station pairs, 0.16 for GNSS-SLR station pairs and 0.13 for GNSS-DORIS station pairs. It appears that thanks to higher signal-to-noise ratios than in horizontal, common aperiodic vertical displacements are detected between GNSS and the three other techniques.

4.2 Impact of non-tidal loading corrections

In order to investigate to which extent loading deformation may explain the concordances obtained in Sect. 4.1 between the residual time series of the four techniques, we repeated the whole analysis starting from weekly or session-wise technique solutions from which the non-tidal loading deformation model provided by Boy (2021) was removed. Note that the loading displacements were averaged separately for each station over the observing period of the station within each solution. Also note that loading corrections were applied at the normal equation level rather than directly to station position estimates.

Figure 8 compares, for the vertical component, the concordance correlation coefficients obtained with and without loading corrections. Similar maps are not shown for the horizontal components, as the impact of loading corrections was found to be marginal. All figures in “Appendix B” nevertheless show the concordances obtained from both raw and loading-corrected residual time series.

Fig. 8
figure 8

Concordance correlation coefficients between vertical residual time series of selected GNSS stations and of co-located stations of the other techniques without (left) and with (middle) loading corrections. The difference between both sets of concordances is shown on the right

Full size image

It can be observed that the vertical concordances partially decrease with loading corrections. However, most of the vertical concordances between loading-corrected residual time series are actually still significantly different from zero according to their individual 95% confidence levels. The medians of the loading-corrected vertical concordances are 0.10 for GNSS-VLBI station pairs, 0.10 for GNSS-DORIS station pairs and 0.09 for GNSS-SLR station pairs. The observed partial reduction indicates that the common aperiodic vertical displacements detectable across techniques are partly attributable to loading deformation, but not entirely. The remaining common aperiodic vertical displacements may be explained by a combination of other non-loading deformation sources (e.g., thermoelastic or poroelastic deformation) and missing contributions in the loading model.

In case of GNSS-DORIS pairs, sites at which the vertical concordances are most reduced by the loading corrections tend to be located in areas where non-tidal atmospheric loading corrections are also most effective in reducing the non-seasonal scatter in GNSS time series (Rebischung et al. 2021). Unfortunately, further conclusions can hardly be drawn due to the small number and poor distribution of co-located station pairs, particularly for SLR and VLBI.

5 Summary and discussion

The aim of this study is to assess the coherence of nonlinear, non-periodic station motions at ITRF co-location sites. For that purpose, we used station position time series extracted from the solutions provided by the four space geodetic technique services for ITRF2014, sampled on a weekly basis. To make them comparable, they were first aligned to a common reference frame, while paying attention to minimize technique-specific network effects (Sect. 2). Then, to isolate aperiodic variations, the significant periodic components present in the time series were identified and removed (Sect. 3). During this analysis, previously known periodic signals were identified (seasonal signals, draconitic signals, tidal aliases), but several additional unexplained signals were also detected: at periods of 20.22 and 25.99 days for DORIS and at a cluster of \(\approx \)30-day periods for SLR.

After removing the kinematic models obtained in Sect. 3, the residual aperiodic time series were compared in Sect. 4 within ITRF co-location sites, by means of Lin (1989)’s concordance correlation coefficient. The absence of common aperiodic horizontal displacements between GNSS and SLR/DORIS was thus evidenced, while modest concordances were noticed for GNSS/VLBI station pairs in horizontal. In fact, common aperiodic displacements were detected mostly in the vertical component, which are only partly explained by Boy (2021)’s non-tidal loading deformation model. The remaining common aperiodic vertical displacements may be explained by a combination of other non-loading deformation sources and missing contributions in the loading model. Yet, in light of the calculated concordances, common displacements explain only a minor part of the aperiodic variations present in the vertical station position time series. Most of the aperiodic variations in the station position time series therefore appear to be explained by technique-specific errors and random noise, both in horizontal and vertical.

As discussed by Altamimi et al. (2019), accounting for aperiodic ground motion in a terrestrial reference frame would require that the nonlinear, non-seasonal displacements of the different techniques can be tied into a common frame in order, e.g., to bring aperiodic GNSS station displacements to the instantaneous SLR origin. This would require that the aperiodic displacements measured by the different techniques are equated within co-location sites by means of co-motion constraints.

However, the results of this study indicate that technique errors dominate the aperiodic displacements sensed by the different techniques, particularly in the horizontal components. The pertinence of co-motion constraints equating them, and their impact, can therefore be questioned. One may wonder, for instance, about the outcome of a combination in which co-motion constraints would be applied, despite little or no common aperiodic displacements being present in the time series of the different techniques.

Firstly, as GNSS station position time series are less scattered than those of the other techniques, they usually get more weight in inter-technique combinations. As a consequence, the combined aperiodic displacements can be expected to follow more or less the GNSS aperiodic displacements. This comes down to trusting the aperiodic variations in GNSS time series, whereas they show little to no similarity with those of the other techniques, and whereas the flicker noise in GNSS time series does likely reflect ground deformation only to a minor extent. Indeed, Rebischung et al. (2017) and Gobron et al. (2021) found that, after non-tidal loading corrections, 40% or less of the flicker noise present in GNSS time series is spatially correlated. The remaining spatially uncorrelated \(\approx \)60% are likely explained by station-specific errors (including monument motions), which is corroborated by the observation of flicker noise in short GNSS baselines (King and Williams 2009; Hill et al. 2009). As for the spatially correlated 40%, it is currently unknown which fraction represents real ground deformation and which fraction may be due to spatially correlated GNSS errors (e.g., orbit errors). Thus, equating the aperiodic displacements of the different techniques likely means forcing the other techniques to follow GNSS errors more than real ground deformation.

A second potential issue with such a combination would concern the Helmert transformation parameters estimated between the aperiodic displacements of the different techniques. Their precision and accuracy would depend on the level of random and systematic errors in the technique-specific aperiodic displacements, as well as on the number and distribution of co-located stations available every week. Given that technique errors dominate over common aperiodic signals, particularly in horizontal, and given the poor distribution of, e.g., SLR and VLBI co-located stations available on a given week, one can wonder whether the resulting errors in the estimated Helmert parameters would not be larger than the actual aperiodic ground deformation at most sites. For instance, even assuming that the aperiodic variations in GNSS time series reflect real ground deformation, it could still be that the aperiodic GNSS variations translated to the instantaneous SLR origin become contaminated by errors in the GNSS-SLR translation estimates.

Table 1 Periodic signals detected in station position time series
Full size table

The observed dissimilarity between the aperiodic displacements sensed by the different techniques thus raises questions regarding the application of co-aperiodic-motion constraints in the formation of a terrestrial reference frame. However, the results of this study do not allow drawing a firm conclusion yet. In future work, we will perform an actual combination of the aperiodic displacements sensed by the different techniques, in order to evaluate the precision of the reference frame transfer between them and the statistical significance of the combined aperiodic displacements. Complementary simulations will be carried out, in which the levels of technique errors, as well as the number and distribution of co-located stations will be varied, in order to evaluate the impact of those factors on the precision of the reference frame transfer and combined aperiodic displacements. Using additional data (from 2014 to 2022) will also help to improve the distribution of co-location sites as new stations have been installed since 2014. Furthermore, while this study has so far evaluated the broadband consistency between the aperiodic displacements sensed by the different techniques, we will later investigate how this consistency may vary across different frequency bands. (Are interannual variations, for instance, more consistent across techniques than sub-seasonal variations?) Finally, as already advocated by Altamimi et al. (2019), we would like to encourage research toward a better understanding and characterization of the technique errors, as this is the key for the establishment of terrestrial reference frames that would reliably account for nonlinear and non-seasonal displacements.