Newtonian (moving mass) calibration of tilt and gravity meters and the investigation of some factors influencing its accuracy

Abstract

The idea of moving mass calibration (MMC) of relative gravity meters dates back to the seventies of the last century. Probably the MMC apparatus built in the underground Mátyáshegy Gravity and Geodynamics Laboratory Budapest has been used most extensively and several spring type instruments (LaCoste and Romberg and Scintrex) have been investigated and calibrated by it. Its test mass is a cylindrical ring having a weight of 3 tons. Its main advantage is simplicity in terms of metrology. The same principle and technology can be used to test compact tilt sensors having nanoradian resolution capability. Up to now rigorous testing methods below microradian range were not available in practice. The analysis of the so-called off-axis variation of the gravitational vector generated by the vertical movement of the cylindrical ring mass of the Mátyáshegy MMC device, however, showed that a sufficiently accurate reference signal having (15 ± 0.02) nrad peak-to-peak amplitude can be provided for calibration. It is just in the range of tilt induced by earth tide effect, which is a “standard” signal component in the time series recorded in observatory environment. In the first part of the paper, a discussion of the proposed methodology of tilt meter calibration is given. Then the analysis of the effect of volumetric discretization of the cylindrical ring on the accuracy of calibration is provided. Finally, possible material inhomogeneities of the ring mass and their gravitational effects are investigated by forward simulations and inversion. For this purpose the results of 300 gravimeter calibration experiments, analysed and published earlier, were utilized.

1 A short introduction to the history of MMC and its recent application

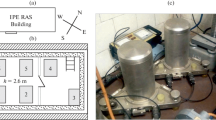
The birth of the idea of moving mass calibration probably coincides with the time of invention of gravity meters, however, the first publication of the application of a device using a spherical test mass is given by Warburton et al. (1975). Thereafter the feasibility of test mass geometries different from the sphere (e.g. toroidal mass) were investigated (e.g. Bartha et al. 1986) and some devices were constructed applying e.g. cylindrical ring (Achilli et al. 1995). The Mátyáshegy MMC device, operated by Mining and Geological Survey of Hungary, was built in 1990 based on the ideas of Péter Varga and used extensively by the scientific community (Varga et al. 1995, personal communications of B. Meurers and P. Varga). The primary aim was to provide reliable scale factors (at 0.1–0.2% level) for gravity meters used in the earth tide research (Csapó and Varga 1991). Due to size constraints, only LaCoste and Romberg gravity meters (both G and D types) could be tested at that time. Just recently Koppán et al. (2020) have tested successfully Scintrex CG-5 instruments too. It has to be mentioned that ring masses (as perturbing gravitational sources) have also been used for the laboratory determination of the universal gravitational constant G (e.g. Schwarz et al. 1998; Rothleitner and Francis 2014), which is a kind of “inverse” problem. For gravimeter calibration, the value of G has to be known in order to calculate the disturbing gravitational effect of the ring mass and then compare it to the one observed by the instrument being calibrated. For G determination, only the mass and geometry of the ring mass have to be known, the value of G can be derived from the exact measurements of the trajectory perturbations of a free falling test mass. Koppán et al. (2020) showed that the Mátyáshegy device is excellent for gravimeter testing at real sub microGal ($1 {\upmu \mathrm{Gal}}=10\,\, \mathrm{nm}/{\mathrm{s}}^{2}$) level since the careful and complex analysis of the accuracy of the reference signal generated by the cylindrical mass provided a maximum uncertainty of $\pm 3\,\,\mathrm{ nm}/{\mathrm{s}}^{2}$ in absolute sense. This analysis, however, could not be a complete study. Therefore, it did not include either the modelling of possible material inhomogeneities inside the cylindrical ring mass or the investigation of its effect on the uncertainty of the calibrating signal. Moreover, it did not discuss the numerical approximation aspects of the off-axis computation of mass attraction components (axis means the vertical/rotation axis of the cylindrical ring), which is unavoidable for ensuring the necessary precision in gravimeter calibration. In fact, the investigation of this latter problem led to the idea of Newtonian tilt meter calibration, since nonzero horizontal mass attraction components can be generated by the cylindrical ring of the MMC device only in off-axis (eccentric) position of the sensor.

Consequently, the first part of this recent paper gives an overview on both the traditional way of tilt meter (spirit level) calibration and the theoretical foundation of a new method based on the Newtonian approach. Its second part is dedicated to those practical and numerical considerations which have been missing from the related previous studies. Therefore, it systematically compares two possible ways of discretization (prisms and polyhedrons) of the cylindrical ring mass in terms of accuracy and computational efficiency and investigates the effect of mass inhomogeneites utilizing both forward and inverse gravitational modelling tools. The results will be summed up and concluded at the end of the paper. Certain details referring to numerical aspects of the investigations are discussed in the Appendix to help the reader to keep the focus on the main achievements and save time for non-specialists.

2 Two in one - feasibility of the MMC device to calibrate compact tilt sensors

2.1 Limits of the application of traditional mechanical spirit level balances

The ancestors of modern electronic tilt sensors were the spirit (bubble) levels used to set horizontal or vertical position of elements of surveying instruments, parts of machines, mounting platforms, etc. The most accurate tubular spirit levels providing a few tenth of 4.85 µrad (1 arcsec) sensitivity were used in geodesy and astronomy where angle measurements required very fine alignment of the mechanical axes connected to the divided reading circles. These levels were extensively tested in so-called level balances (or mechanical tilt platforms). A level balance consists of a firm and heavy base construction supporting a hinge (or a horizontal axis) of a rigid arm and a vertical micrometre screw threaded very finely. The screw can lift or sink the end of the arm by turning it, respectively, so the tilt of the arm can be changed precisely. Depending on the length of the arm and the pitch of the micrometre screw (i.e. the number of threads per millimetre) reference tilts can be applied on the tested levels with sufficient resolution (usually around 0.484 µrad). Theoretically, the resolution can be improved by increasing either the length of the arm and/or the pitch. Both possibilities have their own limits due to structural and elaboration (finishing) constraints so the supply of accurate angles smaller than 0.5 µrad is not a common task at all for calibration. Moreover, the measuring method can be applied only in a restricted range of tilts due to the approximation of the circular movement (i.e. rotation of the balance arm) by a linear (tangential) one implicitly applied in the mechanical construction.

The new tilt sensors, however, provide angle resolution either with four orders of magnitude higher so new methods have to be applied if one wants to check their capabilities and characteristics below µrad level.

2.2 Testing of Lippmann-type pendulum tilt sensors by a traditional level balance

In the past, the predecessor of the Institute of Earth Physics and Space Science (EPSS), the Geodetic and Geophysical Research Institute of the Hungarian Academy of Sciences, as an independent, non-profit oriented national laboratory, had strong professional relations to the Hungarian Optical Works (Magyar Optikai Művek/MOM). MOM had a more than 100-year-old history in the development of optics and fine mechanics applied to different surveying and measuring instruments and devices until its reorganization in the 1990s. So EPSS still has a well-maintained level balance which was used extensively in the 1960s, 1970s and 1980s to provide small vertical angles for the investigation of surveying instruments and levels. Its native resolution capability is 2.42 µrad (0.5 arcsec) but it could be increased by one order of magnitude according to the needs. Although the resolution of the Lippmann-type tilt sensors (LTS HRTM series) is much better than this, some experiments were done only to check the general characteristics of the HRTM series in their whole measuring range (about ± 1.9 mrad). One should note that LTS is a biaxial sensor so it provides a 2D vector quantity ${\varvec{\tau}}=\left({\tau }_{x},{\tau }_{y}\right)$ in its own coordinate frame marked by Ch#1 and Ch#2 ($x\left\| {{\text{Ch}}} \right.\# {\text{1}},{\text{y}}\left\| {{\text{Ch}}} \right.\# {\text{2}}$). In a specific case when any of the axes of LTS is parallel with the direction of tilt defined by, e.g. the structure of the level balance

$${\tau }_{x}=0\vee {\tau }_{y}=0$$

(1)

holds. In the following, $\tau$ means the nonzero component of the tilt for the sake of simplicity. Equation 1 can be provided by the proper orientation of the sensor during the measurements.

Three sensors (named SOP1, SOP2 and HRTM1) were tested using the balance. In these tests steps of 24.2 µrad (5 arcsec) were applied to go through gradually the measuring range which is equal to ± 800 micrometer unit (1 micrometer unit (m.u.) = 1 dial unit = 0.5 arcsec). The measured tilt data were recorded at 1 Hz sampling rate and 20 readings were used to provide an average tilt in each position of the balance arm. Although the old and new tests were made at different places (SOP1/2015: Sopronbánfalva Geodynamical Observatory, SOP2/HRTM1/2021: the laboratory of EPSS in the town of Sopron) having very different background noise the results (Figs. 1, 2, 3 and 4) show basically the same characteristics for all the three sensors in the measuring range:

• 1) Beyond ± 400 m.u. the residual tilt

  $$\delta \tau =\tau -\widehat{\tau }=\tau -{(s\tau }_{\mathrm{dial}}+{\tau }_{0}),$$

  (2)

  where $\tau$ is the observed tilt in any of the examined coordinate direction Ch#1 or Ch#2, $\widehat{\tau }$ is a proper reference model, ${\tau }_{dial}$ is the dial reading (i.e. the applied tilt regarded as reference) of the level balance, $s$ is the scale factor and ${\tau }_{0}$ is the constant parameter of the regression model, indicates slight nonlinear characteristics.

• 2) Between –400 and + 400 m.u. the scale factors between the reference tilt provided by the level balance and the tilt observed by any LTS seem to be mainly constant. In this interval, neglecting the periodicity of $\delta \tau$, the relation between $\delta \tau$ and ${\tau }_{dial}$ is considerably linear.

• 3) The so-called periodical error of the micrometre screw with the period of 360 m.u. (1 full dial rotation) can be identified by applying a higher (e.g. 3rd) degree regression model in Eq. 2 even if the background noise observed in 2021 was higher than in 2015, due to different locations of the experiments.

• 4) The scale factors derived from the corresponding linear regression computations (Table 1) processed by L2 norm adjustment (Mikhail and Ackermann 1976) are very close to the nominal value of the level balance (2424 nrad/m.u.). The deviation is around 2% for any of the sensors.

Fig. 1

The results of the level balance experiments with LTS SOP1 tilt sensor. The left vertical axes refer to the measured tilt values (magenta/dark grey points), right vertical axes scale the tilt residuals (green/light grey points) after removing the linear trend (Eq. 2). Location: SOPGO; year: 2015

Fig. 2

The results of the level balance experiments with LTS SOP1 tilt sensor. The left vertical axes refer to the measured tilt values (magenta/dark grey points), right vertical axes scale the tilt residuals (green/light grey points) after removing the linear trend (Eq. 2). Location: EPSS, year: 2021

Fig. 3

The results of the level balance experiments with LTS SOP1 tilt sensor. The left vertical axes refer to the measured tilt values (magenta/dark grey points), right vertical axes indicate the tilt residuals (green/light grey points) after removing the linear trend (Eq. 2). Location: EPSS, year: 2021

Fig. 4

The $\delta \tau$ residuals (green/light grey points) after the removal of a 3rd degree polynomial model from the observations and their error bars (grey Ι-shaped markers). a LTS SOP1 sensor, b LTS HRTM1 sensor

Table 1 The results of the determinations of the scale factor $s$ and its reliability (variance) ${\mu }_{s}$. Data are provided by the L2 norm adjustment of tilt observations (Eq. 2) obtained from level balance tests of HRTM1, SOP2 and SOP1 Lippmann-type tilt sensors

There can be a few reasons of the nonlinearity of the residual tilts. First, there is a trigonometric approximation applied in the mechanical construction of the level balance:

$${\text{arc}}\left(\alpha \right)\approx \mathrm{tan}\left(\alpha \right),$$

(3)

where $\alpha$ is the tilt of the balance arm (Fig. 5a). Whereas the dial of the micrometre screw, the rotation of which moves the end of the arm of the balance up and down, displays angles on a divided circle the screw itself moves linearly. So the measure of this tangential displacement is approximated by the length of the arc, which is assumed to be equal to $\alpha$ given in radians. The difference

$$\Delta \alpha =\mathrm{tan}\left(\alpha \right)-{\text{arc}}(\alpha )$$

(4)

between them monotonically increases (Fig. 5b).

Fig. 5

a The LTS SOP1 sensor on the level balance of EPSS operated at SOPGO in 2015. The red disc on the left side of the device is the micrometre dial with 360 divisions (1 div. = 1 m.u.). b The difference between the arc length and the tangent belonging to the same central angle $\alpha$ in the half measuring range of LTS instruments. Nominally 1 m.u. = 2.425 μrad = 0.5 arcsec. Left and right scales are given in nrad and milliarcsec (mas), respectively

Figure 5b, however, shows that the calculated $\Delta \alpha$ is definitely smaller by almost four orders of magnitude than the observed residuals $\delta \tau$ displayed in Figs. 1, 2, 3 and 4. Therefore, the systematic components of the residuals, except the periodical signal, are resulted by the transfer characteristics of the capacitive transducer built in the tilt sensor.

The periodical component of the residuals indicates the uneven pitch of the thread of the micrometre screw. This is a consequence of the precision limits of manufacturing of fine threads. Until the recent experiments its exact measure could not be determined because the amplitude of this error signal ($\sim 0.2\,\mathrm{arcsec}\approx 1\,{ \mu rad}$) is well below of the resolution and reading capabilities of the traditional spirit levels.

2.3 A possibility to generate gravitational tilt at nrad level by the MMC device

The off-axis computations (Koppán et al. 2020) of the gravitational effect ($\widetilde{{\varvec{g}}}=({\widetilde{g}}_{x},{\widetilde{g}}_{y,}{\widetilde{g}}_{z})$) of the cylindrical ring of Mátyáshegy MMC device defined by parameters ${r}_{1}=160\,\, \text{mm, }{r}_{2}=385\,\,\, {\text{mm}} \,\,{\text{and}}\,\,\, L=1030$ mm (Fig. 6) showed that near to its inner mantle, a significant change of horizontal mass attraction ${\widetilde{g}}_{xy}=\sqrt{{\left({\widetilde{g}}_{x}\right)}^{2}+{\left({\widetilde{g}}_{y}\right)}^{2}}$ can be observed during the vertical movement of the mass. Following the notation of the paper (see Fig. 2a, Koppán et al. 2020) the height of the mass is marked by $l$ (0 mm $\le l \le$ 1300 mm). The height $l=0$ mm refers to the start position of the lifting process, when the top face of the cylindrical ring is below the sensor. The height $l=$ 1300 mm is the highest position when its bottom face is above that (see the horizontal dashed lines on Fig. 6b). By definition, in case of homogenous mass density, the horizontal mass attraction is zero (${\widetilde{g}}_{x}={\widetilde{g}}_{y}=0$) in the axis of symmetry of the cylindrical ring due to the circular symmetry of the mass distribution therefore

$${\varvec{g}}=(\mathrm{0,0},\mathrm{grad}W+{\widetilde{g}}_{z})$$

(5)

defined as a sum of the gradient of the gravity potential $W$ of the Earth and the vertical attraction component ${\widetilde{g}}_{z}$ generated by the cylindrical mass. In an eccentric position, when $d>0$ (Fig. 6) the nonzero horizontal components, however, deflect the local gravity vector given by (5)

$${\varvec{g}}=\left({\widetilde{g}}_{x},{\widetilde{g}}_{y},\mathrm{grad}W+{\widetilde{g}}_{z}\right),$$

(6)

by angle $\tau$ from its along axis (i.e. vertical) direction which results in gravitational (Newtonian) tilt ${\tau }_{N}$ (Meurers et al. 2021). ${\tau }_{N}$, as a function of the height $z$ (Fig. 6), changes between well-defined extrema and increases (in absolute sense) as the distance $d$ of the computation point from the axis of symmetry increases. One should note that axis $z$ is fixed to the cylindrical ring (that is $z=0$ at its lower horizontal plane). The gravitational components discussed in this paper are always computed at a point moving along or parallel to this coordinate axis. The other vertical axis $l$, however, indicates the instantaneous vertical position of the upper horizontal plane of the cylinder during its movement. When $l=0$ the cylindrical ring mass rests on the floor and the sensor of either the gravity or the tilt meter is above the upper horizontal plane of the cylinder by about 15 cm (Fig. 2a, Koppán et al. 2020). A simple vertical shift can be applied to transform the vertical positions from one system to the other one (Fig. 6).

Fig. 6

a Explanation of off-axis (eccentric) position of a test point and the change ${\widetilde{g}}_{xy}$ of the gravitational vector $g$ as it is shifted by distance $d$ away from the axis of rotation, where $d=0$. ${\tau =\tau }_{N}$ is the gravitational (Newtonian) tilt caused by the horizontal force ${\widetilde{g}}_{xy}$. b The change of tilt ${\tau }_{N}$ along the vertical in function of $z$ and the eccentricity $d$. Green (light grey): $d=$ 100 mm, magenta (dashed dark grey): $d=$ 120 mm, black: $d=$ 140 mm) inside the ring ($d<160 {\text{mm}}$). The geometrical parameters of the cylindrical ring: ${r}_{1}=160\,\, \text{mm, }{r}_{2}=385 \,\,{\text{mm}}$ and the height of the cylinder $L=1030\,\, {\text{mm}}$ (for further details see Koppán et al. 2020). The computations were performed in the coordinate system fixed to the cylindrical ring. The thick horizontal black lines represent the vertical positions of its bottom and top faces along the $z$ axis. The horizontal dashed lines define the range of mass movement

Eventually, if all the physical and geometrical parameters of the cylindrical ring are fixed then

$${\tau }_{N}={{\mathrm{cos}}^{-1}\left({\varvec{g}}(z,\mathrm{d})\cdot {\varvec{g}}(z,0)/\left|{\varvec{g}}(z,\mathrm{d})\right|/\left|{\varvec{g}}(z,0)\right|\right)=\tau }_{N}\left(z,\mathrm{d}\right),$$

(7)

where

$${\tau }_{N}=\left|{{\varvec{\tau}}}_{{\varvec{N}}}\right|$$

(8)

$$\begin{aligned} {{{\varvec{\tau}}}_{{\varvec{N}}}} & =\left({{{\tau }_{{N}_{x}}}},{{{\tau }_{{N}_{y}}}}\right)\\ & =\left({\mathrm{tan}}^{-1}\left(\frac{{\widetilde{g}}_{x}}{\mathrm{grad}W+{\widetilde{g}}_{z}}\right),{\mathrm{tan}}^{-1}\left(\frac{{\widetilde{g}}_{y}}{\mathrm{grad}W+{\widetilde{g}}_{z}}\right)\right).\end{aligned} $$

(9)

The peak-to-peak change of ${\tau }_{N}$ generated by the MMC device in Mátyáshegy Observatory, Budapest is about 15 nrad (Fig. 6b) when the upper or the lower face of the cylindrical ring is just close ($l \le 0.35$ m or $l \ge$ 0.95 m) to the vertical position of the test point (i.e. the reference point of the sensor) and $d=120\,\,\, {\text{mm}}$. In case of the compact (ca. 80 mm x 60 mm x 120 mm) Lippmann-type tilt sensors (LTS) this is a maximum radial distance (eccentricity) which can be applied since the inner radius of the ring ${r}_{1}$ is 160 mm. It, however, is sufficient because the theoretical amplitudes ${\theta }_{f}$ of the main diurnal ($f\approx 1\,\, {\text{day}}$) and semidiurnal ($f\approx 0.5\,\, {\text{day}}$) tidal constituents in N-S and E-W directions are $3.1\,\, {\text{nrad}}\le {\theta }_{f}^{N-S}\le 38.2\,\, {\text{nrad}}$ and $6.5\,\, {\text{nrad}}\le {\theta }_{f}^{E-W}\le 51.4\,\, {\text{nrad}}$, respectively, according to both the Dehant body tide model (see, e.g. Meurers et al. 2021) and the in situ tidal tilt time series recorded, e.g. at the Conrad Observatory, Austria by LTS SOP2 sensor (Fig. 7).

Fig. 7

One month long time series of N-S (magenta/dark grey) and E-W (green/light grey) tidal tilt components recorded by a Lippmann-type pendulum tilt sensor (LTS SOP2) at the Conrad Observatory, Austria. The data are low pass filtered and decimated from 1 s samples to 1 min samples. The linear trend has been removed

Further details on the off-axis computations of the gradients (${\widetilde{g}}_{x},{\widetilde{g}}_{y,}{\widetilde{g}}_{z}$) of the gravitational potential $\widetilde{V}$ generated by the cylindrical ring can be found in Sect. 3 of the paper.

2.4 Disturbing effects: ground loading and tidal tilt

The pillar, on which the investigated instruments are set up, is not perfectly immobile during the calibration process. The vertical movement of the cylindrical ring generates slightly varying ground loading ($gl$) effect which results in some ground deformation tilt ${{\varvec{\tau}}}_{gl}$ because of the coupling between the ground and the support frame of the lifting apparatus. For the description of the device and its geological environment, see Koppán et al. (2020).

The observed tilt ${\varvec{\tau}}$ generally consists of some other effects too:

$${\varvec{\tau}}={{\varvec{\tau}}}_{gl}+{{\varvec{\tau}}}_{N}+{{\varvec{\tau}}}_{\theta }+{{\varvec{\tau}}}_{\mathrm{drift}}+{\varvec{e}},$$

(10)

where ${{\varvec{\tau}}}_{\theta }$ is the tide induced tilt, ${{\varvec{\tau}}}_{\mathrm{drift}}$ is the apparent tilt induced by instrumental drift and ${\varvec{e}}$ is the measurement noise (e.g. microseisms, city noise, the noise generated by the lifting device).

Assuming that in a specific case

$${{\varvec{\tau}}}_{\theta }+{{\varvec{\tau}}}_{\mathrm{drift}}+{\varvec{e}}=0$$

(11)

holds and the steel pillar is sufficiently rigid, its motion (i.e. tilt) during the experiments is uniform for all of its points. Consequently ${{\varvec{\tau}}}_{gl}$ can be accurately determined if the tilt sensors investigated are centred to the axis of symmetry of the cylindrical ring. In this position, the horizontal gravitational effect

$$ \tilde{g}_{{xy}} = 0 \Rightarrow \tau _{N} = 0, $$

(12)

so the detected tilt signal in Eq. 10 is purely deformation

$${\varvec{\tau}}={{\varvec{\tau}}}_{gl} .$$

(13)

Since the same signal ${{\varvec{\tau}}}_{gl}$ is expected during the calibration of the tilt sensor positioned off-axis ($d>0$) the residual $\Delta{\varvec{\tau}}(z,d)$ is

$$\Delta{\varvec{\tau}}\left(z,d\right)={{\varvec{\tau}}\left(z,d\right)-{\varvec{\tau}}}_{gl}\left(z,d\right)={{\varvec{\tau}}}_{N}\left(z,d\right),$$

(14)

eventually.

Recalling that the Lippmann-type tilt sensors are biaxial so they provide two independent (perpendicular) components (Ch#1 and Ch#2) of the full horizontal tilt vector:

$${\varvec{\tau}}={{\varvec{\tau}}}_{gl}+{{\varvec{\tau}}}_{N}=\langle {\tau }_{{gl}_{x}},{\tau }_{{gl}_{y}} \rangle +\langle {\tau }_{{N}_{x}},{\tau }_{{N}_{y}} \rangle ,$$

(15)

if $x\parallel {\text{Ch}}\#1$ and $y\parallel {\text{Ch}}\#2$, for instance. With a proper testing configuration, when the investigated component (x or y) is aligned in any radius of the inner circle of the ring mass Eq. 15 is reduced to:

$$\begin{aligned} & {\varvec{\tau}}={{\varvec{\tau}}}_{gl}+{{\varvec{\tau}}}_{N}=\langle {\tau }_{{gl}_{x}},0 \rangle +\langle {\tau }_{{N}_{x}},0 \rangle\,\mathrm{or}\\ & {\varvec{\tau}}={{\varvec{\tau}}}_{gl}+{{\varvec{\tau}}}_{N}=\langle 0,{\tau }_{{gl}_{y}} \rangle +\langle 0,{\tau }_{{N}_{y}}\rangle \end{aligned} $$

(16)

provided that ${{\varvec{\tau}}}_{gl}\parallel {{\varvec{\tau}}}_{N}$. This condition can be easily fulfilled if the corresponding sensor axis (x or y) always aligned in the same radius vector regardless the sensor is placed in the axis of symmetry of the ring mass or in off-axis position (Fig. 8a).

Fig. 8

a The proper alignment of the investigated sensor (here axis x) for the determination of tilts generated purely by the ground load ${{\varvec{\tau}}}_{gl}$ and the Newtonian mass attraction ${{\varvec{\tau}}}_{N}$. In this alignment ${\tau }_{{N}_{y}}=0$ anywhere along the ray starting at point O (dotted line). ${r}_{1}$ is the inner radius of the ring. b The orientation of the coordinate system $XY$ in which the instrumental tilts of the gravity meters calibrated by Koppán et al. (2020) were recorded. The medium grey ring and the dark hatched circle represent the cylindrical ring and the instrument pier, respectively

During the experiments described by Koppán et al. (2020) the tilt of the gravimeters placed on the instrument pillar (Fig. 8b) was also recorded continuously as the built in electronic levels ($X$/cross, $Y$/long) of the LCR gravity meters measured that. These time series, however, can only give a rough estimate on the size and characteristics of geometric tilts since no detailed information is available about their resolution capabilities and reliability. The sensitivity of the levels (i.e. the scale factors for both directions $X$/cross and $Y$/long in arcsec/mV unit) indicating the actual tilts in mV unit were determined a priori to the moving mass experiment using the level balance of EPSS. Although these levels are not designed to measure tilts below microradian range some general tendencies can be outlined from the average ${\overline{{\varvec{\tau}}} }_{gl}(z,0)$ observations

$${\left({\overline{\tau }}_{{gl}_{X}}\right)}_{i}=\sum_{j=1}^{{N}_{i}}{\left({\tau }_{{gl}_{X}}\right)}_{ij}/{N}_{i},{\left({\overline{\tau }}_{{gl}_{Y}}\right)}_{i}=\sum_{j=1}^{{N}_{i}}{\left({\tau }_{{gl}_{Y}}\right)}_{ij}/{N}_{i},$$

(17)

where ${\left({\tau }_{{gl}_{X}}\right)}_{ij}$ and ${\left({\tau }_{{gl}_{Y}}\right)}_{ij}$ are the $i{\text{th}}$ tilt observation at the height position ${l}_{i} (i={l}_{i})$ given in (mm) in the $j{\text{th}}$ testing series and ${N}_{i}$ is the number of the available observations at the $i{\text{th}}$ height position as Fig. 9 shows:

• (1) ${\overline{{\varvec{\tau}}} }_{gl}\left(z,0\right)$ is neither constant nor linear in the investigated height range (0 mm ≤ $l$  ≤ 400 mm), and their amplitudes are higher by one order of magnitude then that of ${{\varvec{\tau}}}_{N}(z,d)$. One should note that the height range defined above corresponds to the length of the interval containing two consecutive extrema (a maximum and a minimum). So the investigations can be restricted to this specific interval (see Fig. 6b) regarding the viewpoints of calibration.

• (2) The scatter of the ${{\varvec{\tau}}}_{gl}(z,0)$ curves from one mass lifting to the next one is not negligible as the green (light grey) curves show.

• (3) The scatter strongly depends on the direction. In the $X$ direction (actually it is the so called cross-level direction of the LCR gravity meters), it is significantly larger than in the $Y$ direction (so-called long-level direction).

Fig. 9

a–c X/cross and Y/long-level instrumental tilts assumed to be identical to ${\tau }_{gl}\left(z,0\right)$ of the LCR G949 gravity meter in function of the lifting height $l$ as it was indicated by the electronic levels of the instrument during the calibration in years a 2014, b 2016 and c 2017. The green (light grey) curves show the tilt time series recorded one by one whereas the magenta (dark grey) curves are defined by Eq. 17 as the interval average of the tilts. $l=0\equiv z=-145$ mm. d The short periodic part of the spectra of $X$ tilt (green/light grey) and $Y$ tilt (magenta/dark grey) recorded during the calibration of LCR G949 gravity meter in 2014 by the Mátyáshegy MMC device. The discrete peaks show the ${T}_{gravimeter\_heating}=\text{13 sec}$ cycle time and its harmonics. 0.1 mV = 1018 nrad

The scatter of ${{\varvec{\tau}}}_{gl}(z,0)$ curves probably depends on the change of ambient temperature in the room of the MMC device (Fig. 10). Although it is an underground laboratory facility operated in a natural cave system, consequently, the daily thermal stability is better than 0.1 C°/day, the operation of the lifting device consisting of an electromotor and a winch system provides extra heat, which rises temporarily the temperature by even (0.4–0.5) C° during the experiments. One, however, must consider that whereas the sampling rate of gravity and tilt signals was 1 sample/sec that of the temperature, humidity and air pressure was only 1 sample/min. Moreover, the measured values of the gravimeter tilts are affected by the heating process of the gravimeter sensor which keeps the sensor at a stable working temperature. Unfortunately, its on–off state modulates the output voltage of the electronic levels periodically (Fig. 9b) according to a square function. So, taking into account also the low resolution (0.1 °C) of the recorded temperature, these auxiliary data are certainly insufficient to investigate such a relation in detail.

Fig. 10

The relationship between temperature and a $X/cross$ and b $Y/long$ tilts after the last experiments of measurement days (actually during night time) in 2014 (23th of April–30th of April)

The scatter of ${{\varvec{\tau}}}_{gl}(z,0)$ curves depends also on the direction, which comes probably from the structure of the lifting apparatus (see the figures and images in the papers by Varga et al. 1995; Csapó and Szatmári 1995). The cross-level ($X$ direction) of the gravimeter was always oriented to the direction of the winch system pulling/lifting the heavy mass by a pulley system. Since the winch is fixed to the floor and the top of the support frame where the pulling direction turns to vertical is at about 2.5 m high, the horizontal component of the rope force certainly bends the whole support frame towards the winch. Therefore ${{\varvec{\tau}}}_{{gl}_{X}}$ is certainly more influenced and disturbed by the lifting process than ${{\varvec{\tau}}}_{{gl}_{Y}}$. It means that rather the $Y$ direction, which is eventually perpendicular to the plain defined by the rope force and the direction of the vertical (Fig. 8b) can be used for calibration.

In case of gravimeter calibration the time duration of lifting or sinking of the test mass of the MMC device is around 15 min. Although it is not long time a proper measuring strategy based on the methodology given by Koppán et al. (2020) is needed to minimize the tilt effect of the earth tide ${{\varvec{\tau}}}_{\uptheta }$. One can easily justify from Fig. 7 that the most suitable observation periods are defined by the condition $\frac{\partial {{\varvec{\tau}}}_{\uptheta }}{\partial t}\approx \text{const.}$ where the change of ${{\varvec{\tau}}}_{\uptheta }$ is sufficiently linear. In practice it means that time intervals around the inflexion points as well as local extrema of the tidal curves (Fig. 7) are suitable for testing. In these intervals both the tidal effects and the instrumental drift can be modelled by a single linear component ${\widehat{{\varvec{\tau}}}}_{\theta ,\mathrm{drift}}$ (Koppán et al. 2020) since the variation is linear either we formulate the connection in time $t$ or lifting height $l$:

$${{\widehat{{\varvec{\tau}}}}_{\theta ,\mathrm{drift}}\left(l\right)={\varvec{\tau}}}_{\theta }\left(l\right)+{{\varvec{\tau}}}_{\mathrm{drift}}\left(l\right),$$

(18)

where $l=vt$ and the lifting speed $v={\text{const}}$. This way Eq. 11 can be rewritten:

$${\varvec{\tau}}\left(l\right)={{\varvec{\tau}}}_{gl}\left(l\right)+{{\varvec{\tau}}}_{N}\left(l\right)+{\widehat{{\varvec{\tau}}}}_{\theta ,\mathrm{drift}}\left(l\right)+{\varvec{e}}.$$

(19)

Eventually, the tilt effect (Newtonian tilt) of the gravitational change ${{\varvec{\tau}}}_{N}\left(l\right)$ generated by the vertical movement of the cylindrical ring is obtained:

$${{\varvec{\tau}}}_{N}\left(l\right)+{\varvec{e}}={\varvec{\tau}}\left(l\right)-{{\varvec{\tau}}}_{gl}\left(l\right)-{\widehat{{\varvec{\tau}}}}_{\theta ,\mathrm{drift}}\left(l\right).$$

(20)

Applying the proper instrument orientation required fulfilling the conditions of Eq. 17 and considering the anisotropy of ${{\varvec{\tau}}}_{gl}$ discussed above, the $x$ (Ch#1) and $y$ (Ch#2) sensors of LTS can be calibrated separately (cf. Fig. 8b):

$$ {\tau _{{{N}_{x}}} \left( l \right) + {e_{x} }} = {\tau _{x}} \left( l \right) - {\tau _{{{gl}_{y}}}} \left( l \right) - {\hat{\tau }_{{{\theta ,drift}_{x}}}} (l),{\text{where}}{\mkern 1mu} {\mkern 1mu} x\left\| Y \right.,{\text{consequently}}\,{\tau _{{{N}_{y}}}} \left( l \right) = 0 $$

(21)

and

$$ {\tau _{{{N}_{y}}}} \left( l \right) + {e_{y}} = \tau _{y} \left( l \right) - {\tau _{{gl}_{Y}}} \left( l \right) - \hat{\tau }_{{\theta ,{drift}_{x}}} (l),{\text{where}}{\mkern 1mu} {\mkern 1mu} y\left\| Y \right.,{\text{consequently}}\,\tau _{{{N}_{x}}} \left( l \right) = 0. $$

(22)

3 Computation of the gravitational attraction of the cylindrical mass in off-axis (eccentric) positions

As the previous sections demonstrated, the accurate computation of the components of the gravitational acceleration generated by the test mass $\widetilde{{\varvec{g}}}=({\widetilde{g}}_{x},{\widetilde{g}}_{y,}{\widetilde{g}}_{z})$ in any point inside the cylindrical ring ($d<{r}_{1}$) is crucial. The calculated tilt effects are hardly larger by one order of magnitude than the nominal resolution capability of the tilt sensors so some further investigation is needed to complete the results already provided by Koppán et al. (2020).

The gravitational potential $\widetilde{V}$ and its first and higher order derivatives (e.g. ${\widetilde{g}}_{x}=\frac{\partial \widetilde{V}}{\partial x},{\widetilde{g}}_{y}=\frac{\partial \widetilde{V}}{\partial y},{\widetilde{g}}_{z}= \frac{\partial \widetilde{V}}{\partial z},\frac{{\partial }^{2}\widetilde{V}}{\partial {x}^{2}},\dots$) of the cylindrical ring can analytically be described only in points of the axis of symmetry. At an off-axis (i.e. eccentric) point, however, these parameters can be evaluated either numerically (Sung Ho Na et al. 2015; Singh 1977; Nagy 1966; Nabighian 1962), or by the application of an approximate mass model consisting of volume elements having analytically described gravitational potential (Koppán et al. 2020).

Based on the theory of superposition one can compute the gravitational field of the cylindrical ring with arbitrary accuracy by increasing the resolution of its approximate model. For a given geometrical resolution, an algorithm developed by the authors builds up the model with optimal number of elements constrained by the base geometry of the elementary volume element. The right rectangular geometry of the prism, however, is less optimal for modelling of cylindrical bodies than that of the general polyhedron so the application of the latter is discussed in the following as well.

3.1 Volumetric approximation of the cylinder by polyhedrons and prisms

The homogeneous cylindrical ring mass (${r}_{1}=0.160\,\, {\text{m}}$, ${r}_{2}=0.385\,\, {\text{m}}$, $H=1.03 \,\,{\text{m}}$, $mass_{{MMC}} = 3.103765 \cdot 10^{3} \,\,{\text{kg}} \Leftrightarrow \rho {\text{ = 7822}}{\text{.0883 kg/m}}^{3}$) described in the paper by Csapó and Szatmári (1995) is approximated by a set of special polyhedral volume elements (right triangular prisms). Each element has the same height as that of the cylindrical ring (see Fig. 8/b, Csapó and Szatmári 1995). The bases of the right triangular prisms are similar in both size and shape. The prisms extend vertically from the lower to the upper base of the cylindrical ring. The total number of these elementary volume elements was successively increased using equal angular division $\beta$ of the circular base of the cylinder providing $n$ sectors, each containing three triangles. $n$ is called “model resolution” of the polyhedron model ${\left({M}_{ph}\right)}_{ij}^{n}$ in the following discussion. For each n four models, notated by indices $ij\in \{\mathrm{00,01,10,11}\}$ were generated where digits 0 and 1 refer to the modality of approximation of the circular arc. Digit 0 stands for the case of approaching by the adherent chord and 1 for the case of approaching by the corresponding tangent segment (Fig. 11). The row order of digits indicates which mantle of the ring is approximated by the chord or tangent. The first and second digits stand for the inner and outer mantles, respectively. Obviously, the discretization of the curved surface of the mantles (inner and outer) of the cylindrical ring (${M}_{cr}$) results in a geometrical misfit defined as

$${\left(\epsilon \right)}^{n}=\mathop{\mathrm{max}}\limits_{{i,j\in} \{{\mathrm{0,1}}\}} \left\{ {\mathrm{dist}} \{{M}_{cr}; {\left({M}_{ph}\right)}_{ij}^{n}\}\right\}. $$

(23)

Fig. 11

The scheme of the sectorial division of the cylindrical ring by angle $\beta$ ($n\beta =$ 360°) and the further division of the sectors by three triangles (dashed lines). The Fig. also explains the way of the approximation of the circular arcs by secants and tangential segments. The cases are marked by 0 (chord) and 1 (tangent). The first and second positions of these numbers indicate their location on the outer and the inner mantle of the cylindrical ring, respectively

The influence of the increasing model resolution on the differences between 1) the volumes ${\left(\nu \right)}_{ij}^{n}$ and ${\nu }_{cr}$ and 2) the mantles of the cylindrical ring and its approximations ${\left({M}_{ph}\right)}_{ij}^{n}$, respectively, can be seen in Table 2.

Although the idea of modelling of a cylinder by a set of joining right rectangular parallelepipeds seems nonsense from geometrical point of view it is yet worth to demonstrate its inefficiency in this special case, especially compared to the application of polyhedrons. The smallest volume element generated by the algorithm developed to fill the cylinder by prisms has

$$2{r}_{2}/{2}^{m} \times 2{r}_{2}/{2}^{m} \times H$$

(24)

dimension, where ${r}_{2}$ and $H$ are the outer radius and the height of the cylindrical ring, respectively. The computations were performed for $m = 8,\dots , 13$, where the model discretization (quad-tree) parameter $m$ is the number of predefined quartering steps eventually. For a detailed description of the methodology, see Appendix.

3.2 The effect of sensor eccentricity on the vertical component of gradV

The computation of mass attraction effects were performed in a coordinate system the z axis of which is situated in the axis of symmetry of the cylindrical ring and the origin ($x=y=z=0$) located on its bottom face (Fig. 6/b). Based on the definition of maximum norm $\Vert \Vert$ the accuracy estimates (gravitational misfits)

$${\delta \left({g}_{z}\right)}_{ij}^{n}=\left\Vert {\widetilde{g}}_{z}-{\left({\widetilde{g}}_{z}\right)}_{ij}^{n}\right\Vert $$

(25)

and

$$\delta {\overline{\left({g}_{z}\right)}}^{n}=\left\Vert {\widetilde{g}}_{z}-\frac{{\left({\widetilde{g}}_{z}\right)}_{00}^{n}+{\left({\widetilde{g}}_{z}\right)}_{11}^{n}}{2}\right\Vert $$

(26)

of the first derivatives of the gravitational potential generated by approximate polyhedron models ${\left({M}_{ph}\right)}_{ij}^{n}$ were investigated as a function of $n$ (Table 3) in points P of the computation domains detailed in Fig. 16.

Figure 17a shows the vertical variation of ${\left({\widetilde{g}}_{z}\right)}_{ij}^{n}$ generated in-axis by different approximate polyhedron models. Based on the data given in Table 3 the model ${\left({M}_{ph}\right)}_{ij}^{n=7200}$ provides a gravitational misfit better than ± 0.1 pm/s² in all of the investigated domains, which is orders of magnitude smaller than the limits of achievable measurement accuracy in gravimetry: $\mu _{g} \approx 10{\mkern 1mu} {\mkern 1mu} {\text{nm/s}}^{2} \,\,{\text{and}}\,\,\mu _{{\Delta g}} \approx 0.1\,\,{\text{nm/s}}^{2}$ for free-fall absolute and superconducting relative gravity meters, respectively. Consequently the ring can be approximated sufficiently by the polyhedron model ${\left({M}_{ph}\right)}_{ij}^{n=450}$ because it already provides a gravitational misfit ${\delta \left({g}_{z}\right)}_{ij}^{n}\le 0.01 \text{nm/}{\text{s}}^{2}$ in all the investigated domains for $ij\in \{\mathrm{00,01,10,11}\}$.

The same models were used to simulate the gravitational tilts ${\left({\widetilde{\tau }}_{N}\right)}_{ij}^{n}$ which were referenced to ${\left({\widetilde{\tau }}_{N}\right)}_{ij}^{n=36000}$ tilts generated by ${\left({M}_{ph}\right)}_{ij}^{n=36000}$ at $d=120$ mm eccentricity. Figure 17b shows that the accuracy of ${\left(\widetilde{\tau }\right)}_{ij}^{n=450}$ is also sufficient because its application limits the errors far below the sensitivity of the sensors, below 0.1 picorad (prad).

4 The gravitational effect of mass inhomogeneity of the cylindrical ring material

Although the mass of the MMC device is made of multiple milled iron plates, some inhomogeneity of its material cannot be excluded. For the estimation of the effect of mass inhomogeneity on ${\widetilde{g}}_{z}$ both a polyhedron ${\left({\widehat{M}}_{ph}\right)}_{00}^{n=450}$ and a prism ${\left({\widehat{M}}_{p}\right)}^{m=8}$ models were used. In order to obtain ${\left({\widehat{M}}_{ph}\right)}_{00}^{n=450}$ the volume elements of ${\left({M}_{ph}\right)}_{00}^{n=450}$ were divided further vertically so finally the number of elements was 135,000 having a vertical resolution of ≈ 10 mm. This model provides an accuracy better than 0.004 nm/s.² for in-axis (domain a) simulations of ${\widetilde{g}}_{z}$ (Table 3). ${\left({\widehat{M}}_{p}\right)}^{m=8}$ contains 258,176 adaptive volume elements applying a modification of (24)

$$\frac{{r}_{2}}{{2}^{\mathrm{m}}}\times \frac{{r}_{2}}{{2}^{\mathrm{m}}}\times \frac{H}{{2}^{\mathrm{m}}}.$$

(27)

Based on the technical data given by Csapó and Szatmári (1995), highly overestimated but still realistic (see, e.g. Wilzer et al. 2013) density variations with normal

$$\Delta {\rho }_{i}=N(0{;}10\,\mathrm{kg}/\mathrm{m}^3)$$

(28)

and uniform

$$\Delta {\rho }_{i}=U(0{;}17\;\mathrm{kg}/\mathrm{m}^3)$$

(29)

distribution were applied to assign various density values to each elementary polyhedral and prism volume element. From the mass determination of the cylindrical ring, the uncertainty of the total mass was 0.021 kg (Csapó and Szatmári 1995). So the estimated uncertainty of the mass density is only ${\sigma }_{{\rho }_{MMC}}=$ 0.055 kg/m³.

Even if the assumed density uncertainties (Eqs. 28 and 29) are 100 times larger than the value of ${\sigma }_{{\rho }_{MMC}}$ the maximum gravitational difference ($\delta \left({\widetilde{g}}_{z}\right)$) along the axis of symmetry generated by the mass inhomogeneity $\Delta \rho$ (Fig. 12/a) satisfies

$$\mathrm{max}\left(\left|\delta \left({\widetilde{g}}_{z}\right)\right|\right)={\text{max}}\left(\left|{\widetilde{g}}_{z}\left(\Delta \rho \right)\right|\right)<0.05 \,\text{nm/}{\text{s}}^{2}$$

(30)

where

$${\widetilde{g}}_{z}\left(\Delta \rho \right)=f\left({\left({\widehat{M}}_{ph}\right)}_{00}^{n=450}\right)\vee {\widetilde{g}}_{z}\left(\Delta \rho \right)=f\left({\left({\widehat{M}}_{p}\right)}^{m=8}\right).$$

(31)

Fig. 12

a The effect $\delta \left({\widetilde{g}}_{z}\right)$ of density inhomogeneity $\Delta \rho$ along the axis of symmetry of cylindrical ring. Applied models: magenta/dark grey-${\left({\widehat{M}}_{ph}\right)}_{00}^{n=450},\Delta \rho \in N(0;10\,\mathrm{ kg}/{\mathrm{m}}^{3})$, green /light grey-${\left({\widehat{M}}_{p}\right)}^{m=8}, \Delta \rho \in U(0;17\mathrm{ kg}/{\mathrm{m}}^{3})$ and dashed green/dashed light grey-${\left({\widehat{M}}_{p}\right)}^{m=8}, \Delta \rho \in N(0;10\,\mathrm{ kg}/{\mathrm{m}}^{3})$. b The density inhomogeneities (dashed thin magenta/dark grey: Eq. 32, dashed thick magenta/dark grey: Eq. 33) and their gravitational effects (solid thin and thick magenta/dark grey lines respectively). The same line styles are used for the gravitational effects as for the corresponding density contrast models

The $\delta \left({\widetilde{g}}_{z}\right)$ curves, interestingly, show non-random features (Fig. 12). Koppán et al. (2020) indicated also non-random residual signals provided by the least squares adjustment of the gravitational change observed by LCR gravity meters related to the theoretical calibrating signal (see Fig. 15, Koppán et al. 2020). They concluded that it is linked to the speed of vertical gravity change $\partial {g}_{z}/\partial z$ reflecting the elasto-mechanical rheology of the spring sensors. Now this conclusion is supported because the amplitude of adjustment residuals is about 10 nm/s² which is more than two order of magnitude higher than what is obtained from the recent simulations of $\delta \left({\widetilde{g}}_{z}\right)$ from density inhomogeneities.

In order to study the effect of systematic $\Delta \rho$ vertical density inhomogeneites height dependent density contrast functions in forms of first- and second-order polynomials (Fig. 12/b) were used:

$$\Delta {\rho }_{1}\left(z\right)=34.7z-17.87\,\,\mathrm{ kg}/{\mathrm{m}}^{3}$$

(32)

$$\Delta {\rho }_{2}\left(z\right)=125.0{z}^{2}-128.75z+22.1\,\,\,\mathrm{ kg}/{\mathrm{m}}^{3}$$

(33)

satisfying the conditions

$$\int_{z=0}^{z=1.03}\Delta \rho \left(z\right)=0$$

(34)

$$-20\,\,\, \text{kg/}{\text{m}}^{3}\le \Delta {\rho }_{1}\left(z\right), \Delta {\rho }_{2}\left(z\right)\le +20\,\,\mathrm{ kg}/{\mathrm{m}}^{3}.$$

(35)

Based on metallurgic investigations (e.g. Wilzer et al. 2013), the range of density perturbations defined by Eq. 35 is realistic. Figure 12b shows that the gravitational effect ${\widetilde{g}}_{z}\left(\Delta \rho \right)$ of such systematic density perturbations (i.e. inhomogeneities) is typically less than 1.0 nm/s² along the axis of symmetry of the cylindrical ring.

Another systematic but discrete density distribution model was applied using the trial and error method to simulate the amplitude (~ 20 nm/s² peak-to-peak) of the residual signal presented by Koppán et al. (2020) and discussed above. For this, the whole cylinder was divided vertically into three segments (Fig. 13a) with the following geometrical parameters: ${z}_{1}-{z}_{0}=0.4 \,\,{\text{m}}$, ${z}_{2}-{z}_{1}=0.38\,\, {\text{m}}$, ${z}_{3}-{z}_{2}=0.25 \,\,{\text{m}}$ ($H=\sum_{i=1}^{3}{z}_{i}-{z}_{i-1}=1030\,\, {\text{mm}}$). As Fig. 13b shows an adequate anomalous density distribution:

$${\Delta \rho }_{1} = -60\,\, \text{kg/}{\text{m}}^{3}, {\Delta \rho }_{2} = 220\,\, \text{kg/}{\text{m}}^{3},\Delta {\rho }_{3} = -160 \,\,\text{kg/}{\text{m}}^{3}$$

(36)

can produce a systematic (signal like) vertical gravitational anomaly $\delta \left({\widetilde{g}}_{z}\right)$ having an amplitude around 10 nm/s² whereas (34) holds. This specific density model, however, represents so big density inhomogeneities the existence of which is excluded by the modern technology of steel metallurgy (Wilzer et al. 2013).

Fig. 13

a The sketch of the simple anomalous mass model (Eq. 36) of the cylindrical ring. b The black continuous curve shows the anomalous gravitational signal of it. Different colours/shades of grey indicate both the constituting cylindrical ring segments (coloured/dashed grey squares) and their single gravitational effects. Green/medium grey dashed line: ${\Delta \rho }_{1}$, violet/strong grey dashed line: ${\Delta \rho }_{2}$ and yellow/light grey dashed line: ${\Delta \rho }_{3}$

The effect of the mass inhomogeneities (Eqs. 28, 32, 33 and 36) on ${\tau }_{N}$ was also calculated (Fig. 14). The results show that the tilt signals generated by realistic models (Eqs. 28, 32 and 33) is much less than 100 prad (0.1 nrad) in the off-axis position $d=$ 120 mm.

Fig. 14

The effect of a random like and b, c, d systematic density inhomogeneities defined by Eqs. 28 and 32, 33, 36 on ${\tau }_{N}$, respectively. The bottom and top scales on a refers to ${\tau }_{N}$ defined by ${\left({\widehat{M}}_{ph}\right)}_{00}^{n=450},\Delta \rho \in N(0;10\,\,\,\mathrm{ kg}/{\mathrm{m}}^{3})$ and ${\left({\widehat{M}}_{p}\right)}^{m=8}, \Delta \rho \in N(0;10\,\,\,\mathrm{ kg}/{\mathrm{m}}^{3})$, respectively. Off-axis positions: $d=120$  mm (solid line), $d=150$ mm (dashed line). Applied models: magenta/dark grey-${\left({\widehat{M}}_{ph}\right)}_{00}^{n=450},\Delta \rho \in N(0;10\,\,\,\mathrm{ kg}/{\mathrm{m}}^{3})$ and green/light grey-${\left({\widehat{M}}_{p}\right)}^{m=8}, \Delta \rho \in N(0;10\,\,\,\mathrm{ kg}/{\mathrm{m}}^{3})$

5 Inversion of the residual gravity signals obtained from gravimeter calibration using the MMC device

The results presented in Koppán et al. (2020) show that the observation residuals provided by Full-Fit adjustment process (as described by Eqs. 6 and 7, Koppán et al. 2020) is not random exclusively. It still contains a systematic constituent with amplitude of (10–20) nms⁻², which correlates well with the second vertical derivative of the calibrating signal, as it is indicated by a previous study (Eq. 8, Koppán et al. 2020). The most probable reason of the systematic residuals (see Fig. 15, Koppán et al. 2020) determined by the Full-Fit method is the response characteristics (rheology) of the spring type sensors. Based on the discussion in Sect. 4, it seems that a realistic, either random or systematic, density inhomogeneity of the cylindrical ring cannot explain the residual signal at all. This guess, however, can be justified using the gravity inversion method.

Fig. 15

a Average residual gravity signals (plot symbols) provided by the Full-fit mehod (Koppán et al. 2020) and averaged on $\Delta l=10$ mm height intervals and the responses (solid lines) of the respective discrete density inhomogeneity models containing 6 sections (A,B,C,D,E,F) fitted to the averages given by Eq. 40. b The sketch of the density model (left panel) and the adjusted density inhomogoneities (right panel). The colours (grey shades) indicate different years of the calibration of LCR G949 gravity meter. The thin vertical grey stripe on the right panel shows the range of realistic density inhomogeneities of $\pm \text{20 kg/}{\text{m}}^{3}$(e.g. Wilzer et al. 2013)

If the cylinder consists of m vertical sections (${z}_{0}=0, {z}_{1},\dots , {z}_{m}=H=1030\, {\text{mm}}$) a discrete, vertically anomalous density distribution of the cylindrical ring can be described by a series of (${\rho }_{1},{z}_{2}-{z}_{1}$),…., (${\rho }_{m},{z}_{m}-{z}_{m-1}$) parameter couples, where

$${\rho }_{j}=\overline{\rho }+\Delta {\rho }_{j} (j=\text{1,m})$$

(37)

and $\overline{\rho }$ = 7822.0883 kg/m³ is the density of the homogeneous cylindrical ring determined by the right hand side of Eq. 13 given in the paper by Koppán et al. (2020) and $\Delta {\rho }_{j}$ denotes the density inhomogeneity of the jth section.

Introducing the new unknown parameters ${\Delta \rho }_{j}$ ($j=1,m$) the observation equation (Eq. 6, Koppán et al. 2020) can be modified to:

$$\delta {\left({\widetilde{g}}_{z}\right)}_{i}={e}_{i}=\widetilde{g}\left({\Delta \rho }_{1}, ...,{\Delta \rho }_{m},{h}_{0}-{l}_{i},{g}_{0}\right),$$

(38)

where ${e}_{i}$ is the correction of the ith observation obtained from a previous adjustment providing the scale factor of the investigated gravimeter (Koppán et al. 2020) and ${l}_{i}$ is the height of the top face of the cylindrical ring. This way the $\delta {\left({\widetilde{g}}_{z}\right)}_{i}$ residuals are exclusively determined by the density inhomogeneities discretized by a set of joining cylindrical rings and the two additive parameters ${h}_{0}$ and ${g}_{0}$. These latter quantities are practically provided by the previous adjustment of the observations therefore Eq. 38 can be further simplified to:

$$\delta {\left({\widetilde{g}}_{z}\right)}_{i}={e}_{i}=\widetilde{g}\left({\Delta \rho }_{1}, ...,{\Delta \rho }_{m}\right).$$

(39)

Since the density distribution and consequently the density inhomogeneity of the cylindrical ring is time invariant, $\delta {\left({\widetilde{g}}_{z}\right)}_{i}$ in Eq. 39 can be replaced by data averaged from the observation series recorded by the gravimeter at $\Delta l=10$ mm height intervals along the total lifting height range of 1300 mm

$$\delta {\left({\overline{g} }_{z}\right)}_{j}^{a}=\frac{1}{{K}_{a}}\sum_{k=1}^{{K}_{a}}{\delta \left({\widetilde{g}}_{z}\left({l}_{i}\right)\right)}_{k} ,i=1,N;j=1,\dots ,130,$$

(40)

where $N$ is the number of observations in a specific calibration experiment (typically $N=900,\dots ,1000$), ${K}_{a}$ is the number of experiments in a given year $a$ (${K}_{2014}=106, {K}_{2016}=100, {K}_{2017}=124$) meanwhile

$$\left(j-1\right)\Delta l\le {l}_{i}<j\Delta l$$

sorting rule is followed.

This way three sets ($\delta {\left({\overline{g} }_{z}\right)}_{j}^{2014}, \delta {\left({\overline{g} }_{z}\right)}_{j}^{2016}, \delta {\left({\overline{g} }_{z}\right)}_{j}^{2017}$) were computed for LCR G949 gravity meter and used as observables (Fig. 15/a) to solve Eq. 39 for six unknown density inhomogeneities (${\Delta \rho }_{1}, ...,{\Delta \rho }_{6}$) the result of which can be seen in Fig. 15/b. It shows that the residual signal can be modelled only by the application of unrealistic density inhomogeneities.

6 Discussion and conclusions

Based on thorough investigations Koppán et al. (2020) stated that the MMC device is an excellent tool to test and calibrate local area scale of both LCR’s and Scintrex’s spring type gravity meters at a few nm/s² accuracy level. This recent paper absolutely confirms their conclusions extending the accuracy analysis of the method to the investigation of 1) some numerical problems related to the discretization of the cylindrical ring mass and 2) the gravitational effect of possible density inhomogeneities of the material of the cylindrical ring.

The discretization of the ring mass is unavoidable due to the rigorous calculations required to determine the effect of off-axis position of the gravity sensor during the calibration experiments. The exact position of the effective point of the sensor of an LCR gravity meter, however, is not known because of the complexity of its sensor mechanics. Therefore, one should give a worst-case estimation to quantify the limit on the largest possible effect of sensor eccentricity related to the axis of symmetry of the cylindrical test mass. Analytical expression for off-axis computation of its gravitational attraction is, however, not available, so the division of the mass to simple volume elements having closed gravitational formula is also unavoidable. Rectangular prisms and polyhedrons possessing triangular base were applied to fill (i.e. discretize/approximate) the volume of the cylindrical ring and a kind of convergence analysis was performed to see the effect of the increasing spatial resolution of the respective models. Based on in-axis investigations which let the comparison of gravitational effects obtained by exact (analytical) and approximate (analytically generated by the discrete model) computations possible a polyhedron model ${\left({M}_{ph}\right)}_{00}^{n=7200}$ was selected as reference. It was shown that with this grade of discretization an accuracy of ${\widetilde{g}}_{z}$ better then 10^–4 nm/s² can be achieved for both in- and off-axis computations. Table 4 proves that on one hand any of the applied and tested prism models (e.g. ${\left({M}_{p}\right)}^{m=12}$ containing 23,852 prisms) can provide only much lower accuracy (~ 1 nm/s²) and on the other, even for the generation of such a model ($m >$ 10) needs much higher computational efforts related to polyhedron modelling. This accuracy, however, is already provided by a very low resolution polyhedron model ${\left({M}_{ph}\right)}_{00}^{n=60}$ containing 180 volume elements which proves its efficiency against prisms.

The possibility of the presence of density inhomogeneities inside the mass of cylindrical ring could not be considered by Koppán et al. (2020) in details so it left an open question regarding its effect on the absolute accuracy of the MMC device. In this paper, an extensive and detailed analysis of the problem was also given. It was shown that realistic density inhomogeneities ($\pm 20\,\, \text{kg/}{\text{m}}^{3}$) proved by metallurgic investigations (Wilzer et al. 2013) cannot modify the calibrating signal significantly. Its contribution is less than $0.05\,\, \text{nm/}{\text{s}}^{2}$ and $1 \,\,\,\text{nm/}{\text{s}}^{2}$ in terms of gravity acceleration, 20 prad and 100 prad in terms of tilt in case of random like and systematic distributions of density inhomogeneities, respectively.

In order to explain the residual gravity signal provided by the least squares adjustment of the gravity variation recorded during MMC experiment, as it is described by Koppán et al. (2020), both direct and inverse gravitational computations were performed. This signal has a 20 nm/s² peak-to-peak amplitude showing systematic characteristics. In the direct computations, fictive density contrasts (related to $\overline{\rho }$ = 7822.0883 kg/m³) were applied in the form of segmented cylindrical ring. Based on the characteristics of the residual signal a model consisting of 3 joining segments supplied with high and different density contrast ($\Delta \rho \text{=(-60, 220, -160) kg/}{\mathrm{m}}^{3}$) was selected. Indeed, such a model can generate a gravitational signal having an amplitude similar to that of the residual signal indicated by Koppán et al. (2020). The size of these density inhomogeneities are, however, unrealistic based on both the error estimate on the total mass of the cylindrical ring given by Csapó and Szatmári (1995) and the data obtained from metallurgic investigations (Wilzer et al. 2013). The L2 norm inversion of the residual signal solved for 6 joining cylindrical rings results in also very high (i.e. unrealistic) density variations along the vertical providing excellent fit (2014: $\pm \text{3.5}$ nm/s², 2016: $\pm \text{3.4}$ nm/s², 2017: $\pm \text{2.5}$ nm/s²) between the observables and the gravitational effect of the 6 cylinder model. Consequently, the residual signal cannot be interpreted as the gravitational effect of the mass inhomogeneities of the cylindrical ring.

Based on the achievements described in Sect. 3 the theoretical feasibility of the MMC device to test and calibrate high (nrad) resolution compact tilt meters is also demonstrated. To the knowledge and experience of the authors, this has been a quite challenging and unsolved technical problem because the traditional mechanical level balances could have been used only in the range above µrad. Now, however, a Newtonian method to generate tilt signals in the order of magnitude of the solid earth tidal effect is grounded and its accuracy analysis is also presented in Sect. 4. It shows that the discretization of the volume/mass of the cylindrical ring by ${\left({M}_{ph}\right)}_{00}^{n=450}$ provides a model resolution sufficient to calculate gravitational tilts with 0.1 prad accuracy. The maximum contribution of realistic density inhomogeneities to its error budget is probably larger but still below 0.1 nrad because rather random than systematic density variations are expected in the steel material of the cylindrical ring. One should consider the segmented structure of the MMC device (Csapó and Szatmári 1995) and the method how the uniform segments were weighted one by one before those were put together to form a single cylindrical ring. This excludes the existence of significant systematic, either vertical or horizontal density inhomogeneities. The practical feasibility of the MMC device to test high resolution tilt sensors, however, needs further investigations and experiments.

As Koppán et al. (2020) concluded the accuracy of the MMC device could be further improved if a new device was built. Beyond its favourable metrological aspects, it would have a double benefit. Due to the increased diameters and mass proposed for the cylindrical ring the device could be used to test GWR iGrav (R. Warburton personal communication) superconducting and Muquans (B. Desruelle personal communication) absolute quantum gravity meters. Beyond this it would also increase the peak-to-peak amplitude of the reference tilt signal to 30 nrad in off-axis positions near to the inner mantle of the ring.

Appendix

1.1 A1 Volumetric approximation of the cylinder by polyhedrons

See Table 2.

Table 2 The geometrical misfit ${\left(\epsilon \right)}^{n}$ defined by Eq. 23 and the differences of volumes provided by approximate models ${\left(\nu \right)}_{ij}^{n}$ and the exact volume of the cylindrical ring (${\nu }_{cr}=$ 0.396794933121 m³). The index 0 denotes the approximation of arc by the secant belonging to the arc whereas index 1 denotes the approximation by the tangential segment (Fig. 11)

1.2 A2 The effect of sensor eccentricity on the vertical component of gradV

See Figs. 16, 17 and Table 3.

Fig. 16

Domains of simulations of horizontal (${\widetilde{g}}_{x}$,${\widetilde{g}}_{y}$) and vertical (${\widetilde{g}}_{z}$) gravitational accelerations generated by the mass of cylindrical ring are marked by medium grey hatched areas. The concentric rings show the top view of the cylindrical ring (dark grey areas). a $d=$ 0 mm (in-axis), $\Delta z=$ 135 mm, b $d\le$ 80 mm, $\Delta z=$ 135 mm, c $d\le 150$ mm, $\Delta z=485$ mm and d $d\le 1000$ mm, $\Delta z=$ 135 mm

Fig. 17

a The difference of gravity vector components ${\left({\widetilde{g}}_{z}\right)}_{ij}^{n}$ and ${\widetilde{g}}_{z}$ generated by two polyhedron models ${\left({M}_{ph}\right)}_{ij}^{n=450}$ and ${\left({M}_{ph}\right)}_{ij}^{n=7200}$ ($ij\in \left\{\mathrm{00,01,10,11}\right\}$) and the cylindrical ring along the axis of symmetry ($d=0$), respectively. b The difference between tilts ${\left({\widetilde{\tau }}_{N}\right)}_{ij}^{n}$ generated by the same polyhedron models (n = 450, n = 7200) and reference ${\left({\widetilde{\tau }}_{N}\right)}_{ij}^{n=36000}$ in off-axis position ($d=120$ mm). The solid and dotted lines represent the tilt differences ${\delta \left({\widetilde{\tau }}_{N}\right)}_{ij}^{n=450}$ and ${\delta \left({\widetilde{\tau }}_{N}\right)}_{ij}^{n=7200}$, respectively. Horizontal thick black lines indicate the positions of the top and bottom faces of the cylindrical ring at $z=0\, {\text{m}}$ and at $z=1.03\, {\text{m}}$, respectively. The horizontal dashed black lines define the range of mass movement indicated by axis $l$

Table 3 The accuracy estimates (gravitational misfits) of the first vertical derivative of the potential ${\left({\widetilde{g}}_{z}\right)}_{ij}^{n}$ generated by approximate polyhedron models as function of 1) model resolution $n$ and 2) different ways of approximation of the inner and outer arcs of the cylindrical ring $ij\in \{\mathrm{00,01,10,11}\}$. The table refers to different domains explained in Fig. 16. The estimates were derived by Eqs. 25 and 26. ${\widetilde{g}}_{z}$ and ${\left({\widetilde{g}}_{z}\right)}_{00}^{n=7200}$ were used as reference for in-axis (Fig. 16a) and off-axis (Fig. 16b,c,d) computations, respectively. All the data in the table are given in nm/s² unit

1.3 A3 Volumetric approximation of the cylinder by prisms

See Figs. 18, 19 and Table 4.

Fig. 18

Graphical presentation of two results of adaptive prism model generation using a m = 8 (1512 prism elements) b m = 11 (12,004 prism elements). For more details see Table 4

Fig. 19

The gravitational misfits $\delta {\left({g}_{z}\right)}^{m}$ defined by Eq. 44 in function of $m$ (model resolution) and $d$ (eccentricity) in domain defined in Fig. 16d. The coordinate axes define a radial cross section (actually a vertical plane) of the cylindrical ring the axis of symmetry of which is located at $d=0$. The rectangles marked by black lines indicate the vertical half-section of the cylindrical ring and its position in $(d,z)$ coordinate system. a $m=8$, contour interval is 0.5 nm/s², b $m=11$, contour interval is 0.1 nm/s² and c $m=13$, contour interval is 0.05 nm/s²

Table 4 contains the model characteristics (number of volume elements, volume deficiency) and the influence of the value of $m$ on error of vertical gravitational acceleration ${\left({\widetilde{g}}_{z}\right)}^{m}$ generated by the approximate prism model ${\left({M}_{p}\right)}^{m}$. In order to obtain descriptive statistics its value is referenced to ${\left({\widetilde{g}}_{z}\right)}_{00}^{n=7200}$ for any of the domains of computations investigated. In each consecutive step of the construction of ${\left({M}_{p}\right)}^{m}$ the algorithm generates uniform square base prisms $(2{r}_{2} \times 2{r}_{2}\times H, 2{r}_{2}/2 \times 2{r}_{2}/2 \times H, \dots , 2{r}_{2}/{2}^{k} \times 2{r}_{2}/{2}^{k} \times H, \dots , 2{r}_{2}/{2}^{m} \times 2{r}_{2}/{2}^{m} \times H$) halving the edges defined in the previous step. Any prism satisfying the conditions

$$2{r}_{2}/{2}^{k} \times 2{r}_{2}/{2}^{k}\times H\subset \mathrm{cylindrical\, ring}$$

(41)

and

$$2{r}_{2}/{2}^{k} \times 2{r}_{2}/{2}^{k}\times H\notin 2{r}_{2}/{2}^{l} \times 2{r}_{2}/{2}^{l}\times H (l<k)$$

(42)

is identified as a building element of the model. If Eqs. 41 and 42 are false and true, respectively, the investigated prism is sorted for further processing (i.e. quartering) in the next step $k=k+1$. Based on this scheme this adaptive algorithm fills the remaining space between the mantle of the cylindrical ring and its cubic approximation step by step by smaller and smaller prisms until $k=m$. Eventually the process defines a set of vertically joining prisms having the same height as that of the cylindrical ring. The sizes of their bases are different but strictly defined by Eq. 24. All the square bases of these prisms, however, are fully involved in the area determined by the base of the ring (Fig. 18). The geometrical misfit

$${\left(\epsilon \right)}^{m}=2{r}_{2}/{2}^{m}$$

(43)

of the prism model is characterized by the smallest prism dimension (Table 4). For example $m=8$ gives 256 uniform divisions of edges resulting in ${\left(\epsilon \right)}^{8}=2{r}_{2}/{2}^{8}=3\, {\text{mm}}$ (${r}_{2}= 0.385\, {\text{m}}$). Figure 18 shows the results of adaptive prism model generation using $m = 8\, \mathrm{and}\, m =11$.

It is obvious that the volume deficiency and the geometrical misfit of polyhedron model belonging to $n = 600$ are more than two orders of magnitude smaller compared to those of the prism model belonging to m = 13 (c.f. Tables 2 and 4). It means that in this specific case the efficiency of polyhedron modelling is superior related to prism modelling because much less number of polyhedron volume elements gives much better approximation in terms of both modelled volume and geometrical misfit than what is provided by prisms. It also has its benefits regarding the computational aspects, especially the memory usage and runtime. Moreover in domain b (Fig. 16b) the gravitational misfit

$$\delta {\left({g}_{z}\right)}^{m}=\left\Vert {\left({\widetilde{g}}_{z}\right)}_{00}^{n=7200}-{\left({\widetilde{g}}_{z}\right)}^{m}\right\Vert $$

(44)

obtained from the comparison of comparison of ${\left({\widetilde{g}}_{z}\right)}^{m=13}$ and ${\left({\widetilde{g}}_{z}\right)}_{00}^{n=7200}$ is two orders of magnitude larger than that of obtained from the comparison of the first vertical derivatives of gravity potential ${\left({\widetilde{g}}_{z}\right)}_{00}^{n=600}$ and ${\left({\widetilde{g}}_{z}\right)}_{00}^{n=7200}$(c.f. Tables 3 and 4):

$$\delta {\left({g}_{z}\right)}^{m=13}\approx 100 {\left({\delta \left(g\right)}_{z}\right)}_{00}^{n=600}.$$

(45)

Extrapolating the results one can easily realize that $m= 20$ has to be applied in order to achieve the same accuracy (~ 0.005 nm/s²) provided by the solution by $n=600$ in terms of gravitational attraction. The number (actually $\sim 5.7\cdot {10}^{6}$ adaptive prisms) of volume elements necessary for that is 4.5 orders of magnitude greater than the number of necessary polyhedrons (1800 right triangular prisms). The average accuracy of ${\left({\widetilde{g}}_{z}\right)}^{m=12}$ solution based on 23,852 adaptive volume elements is around 1 nm/s² in domain (b) (Fig. 16b). However, as one can see from Table 3, the same accuracy can be achieved by only 180 polyhedrons ($n=$ 60). Figure 19 shows the distributions of $\delta {\left({g}_{z}\right)}^{m} (m = 8,\,11,\,13)$ defined by Eq. 44 in domain $d\le 1$ m (Fig. 16d).

Table 4 The characteristics of the prism models investigated. The reference volume of the cylindrical ring ${\nu }_{cr}=$ 0.396794933121 m³. The domain of computations of the vertical accelerations ${\left({\widetilde{g}}_{z}\right)}_{00}^{n=7200}$ and ${\left({\widetilde{g}}_{z}\right)}^{m}$ generated by the reference polyhedron model ${\left({M}_{ph}\right)}_{00}^{n=7200}$ and the approximate prism model ${\left({M}_{p}\right)}^{m}$, respectively, is defined by Fig. 16d. The geometrical ${\left(\epsilon \right)}^{m}$ and gravitational $\delta {\left({g}_{z}\right)}^{m}$ misfits are defined by Eqs. 43 and 44, respectively. The value of m denotes the model discretization parameter as defined by Eq. 24