Characterization and stabilization of the downward continuation problem for airborne gravity data

Abstract

In this study, we compare six commonly used methods for the downward continuation of airborne gravity data. We consider exact and noisy simulated data on grids and along flight trajectories and real data from the GRAV-D airborne campaign. We use simulated and real surface gravity data for validation. The methods comprise spherical harmonic analysis, least-squares collocation, residual least-squares collocation, least-squares radial basis functions, the inverse Poisson method and Moritz’s analytical downward continuation method. We show that all the methods perform similar in terms of surface gravity values. For real data, the downward continued airborne gravity values are used to compute a geoid model using a Stokes-integral-based approach. The quality of the computed geoid model is validated using high-quality GSVS17 GPS-levelling data. We show that the geoid model quality is similar for all the methods. However, the least-squares collocation approach appears to be more flexible and easier to use than the other methods provided that the optimal covariance function is found. We recommend it for the downward continuation of GRAV-D data, and other methods for second check.

1 Introduction

The Gravity for the Redefinition of the American Vertical Datum (GRAV-D) project aims to cover the US territory with airborne gravity measurements while extending about 100 km into Canada and Mexico. It is the largest airborne gravimetric campaign ever undertaken in the world. The project is to develop a geoid-based vertical datum at the precision of 2 cm for much of the country. The flight heights range from 4 to 11 km with a nominal height of about 6 km to achieve a minimum spatial resolution of 20 km (GRAV-D Team 2017a, b; Li et al. 2016). The GRAV-D data need to be reduced onto the Earth’s surface or geoid when being combined with terrestrial gravity data by the Stokes method to determine a gravimetric geoid model. This reduction step has been termed as the downward continuation (DC). One intermediate question is: which method is most suitable for the DC of airborne gravity data, in particular the high-altitude GRAV-D data? The answer is not yet evident despite studies and the development of DC methods for many decades.

The DC problem (DCP) is an ill-posed problem (Schwarz 1978; Rummel et al. 1979; Jekeli 1981a, b). Schwarz (1978) summarizes numerical features of the ill-posed problem as follows:

• (a) The solution does not continuously depend on the given data, i.e., small changes in the data may cause large changes in the solution.

• (b) The matrices resulting from the discretization of the problem will be ill-conditioned, i.e., the condition numbers will be large enough to severely amplify data noise.

• (c) The accuracy of the solution does not increase with the grid density, i.e., as the grid size becomes smaller, the solution error will increase in any norm.

As Milbert (1999) stated, one is faced with the “dilemma of downward continuation”. If one uses a coarse grid, the geoid omission error may be dominant; if one uses a fine grid, the geoid commission error may be dominant, mainly due to noise amplification during downward continuation. He showed numerically that 1 mGal zero-mean white Gaussian noise may be amplified to 47.5 mGal when downward-continued from an altitude of 4000 m without regularization.

There has been a long history of studies dealing with DCP of airborne gravity data in the context of (quasi-) geoid modeling (e.g., Forsberg 1986, 1987; Novák and Heck 2002, Novák et al. 2003). There are three classical methods for the DC of gravity data: i) inverse Poisson, which solves Poisson’s integral equation (e.g., Heiskanen and Moritz 1967; Vaníček et al. 1996; Martinec 1996); ii) Moritz’s analytical DC (1980); and iii) Least-Squares Collocation (LSC) (Moritz 1980, 2002; Forsberg 1987, 2002; Tscherning 2013; Hwang et al. 2007). In recent decades, Radial Basis Functions (RBF) have become popular in local (quasi-) geoid modeling, but can also be used straightforwardly for gravity DC (e.g., Schmidt et al., 2007; Klees et al. 2008; Lieb et al. 2016; Li 2018a; Liu et al. 2020). Furthermore, the Spherical Harmonic Analysis (SHA) method has been adapted for DC of GRAV-D data (Smith et al. 2013; Holmes 2016). Recently, the Residual LSC (RLSC) has been developed and applied to GRAV-D data (Willberg et al. 2019; 2020). A question naturally arises: do all these methods perform equally?

This paper characterizes the DCP, assesses stability and equivalence of the six DC methods, and finds suitable DC methods for DC of airborne gravity data. Section 2 reviews the DC methods. In Sect. 3 and 4, we apply the DC methods to simulated and real data, respectively. Section 5 concludes this study.

2 Downward continuation

2.1 Overview of downward continuation methods

There are six methods of downward continuation (DC) considered in this study. The first one is the spherical harmonic analysis approach currently used at the National Geodetic Survey (Smith et al. 2013). The basic idea is to convert the local data into global data by padding zeros outside of the study area with tapering near the border area to have a gradual transition from nonzero values to zero values. Appendix A1 provides more information about this method.

The second method is Least Squares Collocation (LSC). The standard LSC was originally derived for stationary processes and, later, extended to weakly stationary processes (Darbeheshti and Featherstone 2010). The quality of an LSC solution depends on the correctness of the covariance function. In the context of gravity field modeling, there are many previous studies on how to build covariance functions (e.g., Kaula 1959; Krarup 1969; Moritz 1972; Tscherning and Rapp 1974; Forsberg 1987; and Jekeli 2010). The covariance function that is most commonly used for airborne gravity data is the one by Forsberg (1987), see Appendix A2. This study also includes the newly developed Residual Least Squares Collocation method (RLSC) (Wilberg et al. 2019; 2020), see Appendix A3 for more information.

The fourth method is least-squares radial basis function (RBF) approximation (e.g., Schmidt et al. 2007; Klees et al. 2008). This method has become popular in regional gravity field modeling due to the quasi-localizing properties of the RBFs and the advantages of least-squares techniques (e.g., Schmidt et al., 2007; Klees et al. 2008; Slobbe 2013; Lieb et al. 2016; Slobbe et al. 2019; Liu et al. 2020). Once an RBF model has been fitted to the data, it can also be used for downward continuation. The detailed formulation is given in Appendix A4.

The fifth method is based on Poisson’s integral and numerically solves a Fredholm’s integral equation of the first-kind (e.g., Heiskanen and Moritz 1967; Vaníček et al. 1996; Martinec 1996; Milbert 1999; Novák and Heck 2002; Alberts and Klees 2004). Several different regularization strategies of this ill-posed problem can be found in previous studies (see e.g., Alberts and Klees 2004; Jiang et al 2011; Liu et al 2016; Zhao et al 2018). More comprehensive discussions of regularization can be found in, e.g., Xu (1992), Xu and Rummel (1994), Kusche and Klees (2002), Kern (2003), and Cai et al (2004). In this study, the integral equation is discretized and solved numerically using the method of Huang (2002). The detailed formulation is given in Appendix A5.

The sixth method included in this study is the Analytical Downward Continuation (ADC), which was formulated for the Molodensky boundary value problem by Moritz (1980). The detailed formulation is given in Appendix A6.

2.2 Noise amplification by downward continuation

It is a standard procedure in gravity field modeling to decompose the gravity field into a reference (normal) field and an anomalous (disturbing) field. Then, the data are reduced for the contribution of the reference field and the disturbing field is estimated from the reduced (residual) data. Well-known functionals of the anomalous field are gravity anomalies (representing residual surface gravity data) and gravity disturbances (representing residual airborne gravity data). Using spherical harmonics, they may be written as

$$ \Delta g\left( {r ,\phi ,\lambda } \right) = \mathop \sum \limits_{n = 0}^{\infty } \left( \frac{R}{r} \right)^{n + 2} \Delta g_{n} \left( {\phi ,\lambda } \right) $$

(1)

And

$$ {{\updelta }}g\left( {r~,\phi ~,\lambda ~} \right) = \mathop \sum \limits_{{n = 0}}^{\infty } \left( {\frac{R}{r}} \right)^{{n + 2}} {{\updelta }}g_{n} \left( {\phi ~,\lambda ~} \right) $$

(2)

respectively (Heiskanen and Moritz 1967). The triplet $\left(r ,\phi ,\lambda \right)$ represents spherical coordinates (radius, latitude, longitude); $R$ the radius of the geoid in spherical approximation; and ${\Delta g}_{n}$ and ${\updelta g}_{n}$ are the Laplace surface harmonics for gravity anomaly and gravity disturbance, respectively. Let $r=R+\mathrm{HC}$, and $\mathrm{HC}$ is a constant height, then we can express the gravity disturbance at the constant height of $\mathrm{HC}$ into the surface spherical harmonics

$$ {\updelta }g\left( {R + {\text{HC}} ,\phi ,\lambda } \right) = \mathop \sum \limits_{n = 0}^{\infty } {\updelta }g_{n}^{{{\text{HC}}}} \left( {\phi ,\lambda } \right) $$

(3)

where

$$ {\updelta }g_{n}^{{{\text{HC}}}} \left( {\phi ,\lambda } \right) = \left( {\frac{R}{{R + {\text{HC}}}}} \right)^{n + 2} {\updelta }g_{n} \left( {\phi ,\lambda } \right) $$

(4)

or

$$ {\updelta }g_{n} \left( {\phi ,\lambda } \right) = \left( {\frac{{R + {\text{HC}}}}{R}} \right)^{n + 2} {\updelta }g_{n}^{{{\text{HC}}}} \left( {\phi ,\lambda } \right) $$

(5)

Substituting Eq. (5) into Eq. (2), and let $r = R$, we obtain the gravity disturbance on the geoid as

$$ {\updelta }g\left( {R ,\phi ,\lambda } \right) = \mathop \sum \limits_{n = 0}^{\infty } \left( {\frac{{R + {\text{HC}}}}{R}} \right)^{n + 2} {\updelta }g_{n}^{{{\text{HC}}}} \left( {\phi ,\lambda } \right) $$

(6)

It can be seen that the gravity disturbance component of degree n at the height of $HC$ is amplified by a factor of ${\left(\frac{R+\mathrm{HC}}{R}\right)}^{n+2}$ when it is continued downward to the geoid. For $\mathrm{HC}=6$ km and $n=\mathrm{2,160}$ (corresponding to a 5’ spatial resolution), the amplification factor is about 8. When $n=\mathrm{10,800}$ (corresponding to a 1’ spatial resolution), the amplification factor is about 26,000. The same amplification factors also apply for the error components rendering the DC unstable. A filtering or regularization method must be used to control noise amplification at the cost of introducing a bias into the estimated signal. An effective DC method makes a tradeoff between noise amplification and bias.

There are three basic methods to compress the errors of DC: spatial filtering, LSC and the least-squares regularization. The first method spectrally filters out errors in gravity data to stabilize DC (e.g., Jekeli 1981a, b), while the second and third methods compress the errors by regularization (see e.g., Rummel et al. 1979). As an example of spectral filtering, SHA acts as a low-pass filter up to the maximum degree of SHA to avoid the high-degree noise.

3 Numerical experiments using simulated data

3.1 Setup of the simulations

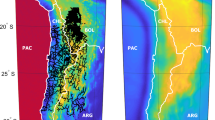
Two simulation scenarios were considered. The first one used simulated gridded data at a constant altitude (see Fig. 1); the second one used simulated data along real flight trajectories. For each scenario, three datasets were generated, which differ in the superimposed noise: noise-free, zero-mean white Gaussian noise with a standard deviation (SD) of 1 mGal, and AR(1) colored noise with autoregressive parameter 0.9, driven by zero-mean white Gaussian noise with a SD of 0.44 mGal (Brockwell and Davis 1991). The latter ensures a noise SD of 1 mGal. The Power Spectral Density (PSD) of the two noise processes, shown in Fig. 2, indicates that the AR(1) noise process has more power at frequencies below 0.035 [cycles/km] compared to the white Gaussian noise process.

Fig. 1

Simulated gravity disturbances from EGM2008 at an altitude of 6200 m

Fig. 2

One-Sided Welch periodogram of (bandlimited) white noise and colored noise realizations, respectively. The noise standard deviation is 1 mGal in both cases. The noise realizations were used to generate two noisy gravity datasets

For the simulation using gridded data, a 1’ × 1’ grid of gravity disturbances was synthesized from EGM2008 (Pavlis et al. 2012) in an area of 5° × 9° [34°–39°N; 250°–259°E] at 6200 m altitude (the mean flight height of the MS05 GRAV-D block over the area of Colorado) (Fig. 1). A reference model, xGeoid16refA, truncated at different SH degrees was used in the Remove-Compute-Restore (RCR) method. xGeoid16refA was developed at NGS, and is a combination of EGM2008 and GOCO05s. The model is complete to degree and order 2159 with some additional coefficients up to degree 2190, similar to EGM2008. Downward continuation errors were assessed at several grids of different altitudes ranging from 6000 m down to the surface of the reference ellipsoid.

For the simulation using real flight trajectories, we generated gravity disturbances along the flight trajectories of the GRAV-D's MS05 campaign in Colorado (cf. Fig. 3) from EGM2008. The flight altitudes range from 5200 to 7900 m. Note the data gaps in the survey. Different from the gridded case, the reference field is a combination of the XGM18 model complete to spherical harmonic degree 760 (which corresponds to an ellipsoidal harmonic degree of 719) and the Earth2014 model (Rexer et al. 2016) for ellipsoidal harmonic degrees 720–2190. Downward continuation errors were assessed at the location of the 31,358 NGS surface gravity points, as shown in Fig. 4. The control dataset exhibits strong signal variations in the mountainous regions in the west, and relatively little variations in the flat eastern part. The mean value is − 6.4 mGal and the standard deviation is 30.9 mGal (cf. Fig. 4).

Fig. 3

Simulated EGM2008 gravity disturbances along real flight trajectories (left panel is for flight altitudes; right panel is for the simulated gravity disturbances from EGM2008. The mean value is 5.76mGal. The standard deviation is 29.10 mGal. The range is from − 46.71 mGal to 118.96 mGal)

Fig. 4

Simulated gravity disturbances at 31,358 points on the topography, which were used as control dataset (mean = − 6.38mGal; standard deviation = 30.89mGal; min = − 72.73mGal; max = 152.74mGal)

3.2 Numerical results using gridded data

3.2.1 LSC

The first step of LSC is building the covariance functions as defined by Eq. (24). Figure 5 shows the empirical covariance functions as well as the corresponding best fits to residuals with respect to the reference fields of different maximum degrees by choosing appropriate high-frequency attenuation depth parameter D, and low-frequency attenuation depth parameter T. The most important part of the fitting is the part up to the half-power point (or sometimes the zero crossing). What happens to larger lags, as shown by the sinusoidal oscillations in the figure, is less relevant for determination of the covariance function, as the DC effects are primarily affected by the correlation length of the input signal.

Fig. 5

The empirical covariance functions (red) and the fitted model covariances (green) for different simulated noise-free datasets (red curves are computed from the data; green curves are the model fits)

Once a suitable set of covariance parameters are found, the LSC prediction is carried out to continue the input grids from 6200 m altitude to lower altitudes, at which the predicted values are compared with the corresponding values synthesized from EGM2008. To speed up the computation, OpenMP and fully parallelized matrix inversion and multiplication subroutines are added to the original GRAVSOFT program (Forsberg and Tscherning 2014). Due to RAM limitations, the input grid is 2’ × 2’ that is extracted from 1’ × 1’ data, while the prediction output is a 1’ × 1’ grid to be identical to the outputs from other methods. The 2’ × 2’ spacing is still sufficient for this simulation because the true resolution of simulation input is 5’ × 5’. The RMS of the differences are shown in Fig. 6.

Fig. 6

LSC DC errors as function of altitude for various reference fields of different maximum spherical harmonic degree (color red, green, and blue are used for cases of error free, white noise, and colored noise, respectively)

The first thing that needs to be pointed out is that LSC works well for the full field for noise free and noisy datasets. The DC errors for the noisy datasets is less than 1.5 times of the DC errors for the noise free dataset. This is explained by the regularizing effect of the noise covariance matrix (e.g., Rummel et al., 1979). The DC errors are larger for the colored noise dataset for both the full field and the residual field solution (reference field complete to degree 690).

We want to mention that LSC applied to the noise-free dataset provides a meaningless solution unless an artificial diagonal noise covariance matrix is added to stabilize the solution (cf. Eq. (26)).

3.2.2 SHA

Figure 7 shows the degree amplitudes of the (residual) gravity disturbances after fitting the data over the simulation area into SHA by using the procedures described in Appendix A1.

Fig. 7

Degree amplitudes of the SHA models from the simulation input data after removing xGeoid16refA truncated at various spherical harmonic degrees (color red, green, and blue are used for cases of error free, white noise, and colored noise, respectively. Black curves are the true values directly computed from the models. Dashed green curves are the differences between white noise and noise free data. Dashed blue curves are the differences between colored noise and noise free data)

We observe that the power of this local field after global zero padding is completely different from the power of the global field. For the full field signal (first row, first column), the peak of the degree variance for the full field data locates around spherical harmonic degree 55, which is about a wavelength of 730 km approximating the dimension of the entire study area. Then the power decreases more or less according to Kaula’s rule (${n}^{-\alpha }$ with $n$ being degree and $\alpha$ a positive number) toward the higher degrees as expected. There are obvious spectral components in the low degrees because of the use of the global function for a representation of space-limited data. The noise effects are relatively small. The white noise is more evenly distributed than the colored one in the spectral domain as expected. Due to the strong signal-to-noise ratios, they are not being mistakenly taken into the models so much as to smear the signal. The noisy spectrum becomes more and more significant when removing a higher degree reference field, the signal to noise ratio reduces as there is less signal power in the residual field.

For the residual fields, the corresponding degree amplitudes plots in Fig. 7 show the location of the maximum degrees removed. They also show the power due to the GOCO05s updates to EGM2008, especially when a reference field complete to degree 2190 is used.

Figure 8 shows the DC errors for the SHA method. This method models the gravity field with an inherent lowpass filtering process, which effectively stabilizes DCP. It manifests a direct way to compress the large DC errors of high-frequency so that the SHA DC errors are at the comparable magnitude between the noise free and two types of noise input data. The colored noise results show larger errors than the white noise ones because of the differences in their spectral distribution of noise (see Fig. 2). Interestingly, this method “works well” even when the “local” coefficients do not match the “global” coefficients. For example, for the case when the reference field is complete to degree 2190, the RMS value of the DC error from 6200 m to the ellipsoid is 0.0189 mGal, much smaller than the RMS of the original residual gravity disturbances (i.e., the differences between the full field EGM2008 and xGeoid16refA), which is 0.298mGal. Because we know the differences between EGM2008 and xGeoid16refA range from degree 2 to 280, the residual coefficients higher than degree 280 are due to the space-limitation of the data. If the residual coefficients are only used up to degree 280 in the restore step, the RMS mismatch increases from 0.0189 mGal to 0.0431 mGal (red vs red dash lines in the bottom-right graph of Fig. 8). Though the RMS values in this case are very small, we know that the “residual coefficients” are not spectrally ‘real’ in a global sense.

Fig. 8

SHA downward continuation errors as function of altitude for various reference fields and input datasets (color red, green, and blue are used for cases of error free, white noise, and colored noise, respectively. Dashed red line is for the case of using coefficients just up to degree 280)

3.2.3 Inverse Poisson

The Poisson DC has been performed using the three sets of simulation input data with the threshold RMS values at 0.001 mGal and 1.0 mGal. These thresholds represent the accuracy of input data without and with noise, respectively. The iterative solutions are convergent for the noise free case regardless the small grid size of 1’ and the large altitude of 6200 m. When the 1 mGal white and colored noise are included, the iterative solutions do not converge with the threshold RMS values of 0.001 mGal when the maximum number of iterations is 1000. The noise level is amplified by a factor of 2 and 3 in magnitude when the maximum iterations are set equal to 100 and 1000, respectively. This reflects the ill-conditioning of the inverse Poisson problem for the chosen set-up. Setting the threshold value to 1.0 mGal makes the solutions convergent leading to an error level which is one order of magnitude higher than the input noise level. The resulting DC errors from 6200 m to lower altitudes are evaluated and shown in Fig. 9 with the maximum number of iterations set to 100. DC errors have been estimated with both the full simulation field shown in Fig. 1 and the residual fields with respect to xGeoid16refA truncated at different degree.

Fig. 9

Inverse Poisson downward continuation errors as function of altitude for different reference fields and input datasets (color red, green, and blue are used for cases of error free, white noise, and colored noise, respectively. Solid curves use threshold 0.001mGal. Dashed curves use threshold 1mGal)

In the case of noise free input data and a threshold of 0.001 mGal, the DC errors shown as red lines are smaller than 1 mGal for the full field DC, and smaller than 0.1 mGal for the residual fields. When a threshold of 1 mGal is set with the noise free input, the errors shown as red dash lines increase to several mGal suggesting that the signal of omission below the level of 1 mGal is significantly amplified in the DC solutions. In the case of white and colored noise input data with the threshold of 0.001 mGal, the noise levels are amplified more than 100 times in the DC results. This suggests that filtering high-frequency noise is essential before the DC is applied; otherwise, it may fail. The threshold of 1 mGal effectively reduces the DC errors to a few mGal, though this is still large. Again, it points out the necessity of filtering noisy input data before DC when using the inverse Poisson method (see e.g., Alberts and Klees 2004). It is noticeable that the white noise causes larger DC errors than the colored noise. This can be explained by the fact that the PSD of white noise is much larger than that of the AR(1) noise at higher frequencies (cf. Fig. 2). There are a few sharp turning patterns in the error curves when using a 0.001 mGal threshold, which are due to numerical round-off errors.

3.2.4 Moritz’s ADC

DC errors for Moritz’s ADC have been estimated for the 5th order approximation. The results are shown in Fig. 10. In the case of noise free data, the DC errors are at the mGal level. However, in the case of noisy input data, the DC errors are 10 to 100 times larger than the input noise level. Similar to the Inverse Poisson, the white noise causes much larger DC errors than the colored noise. There is no effective way to control the amplification of noise by the method itself other than truncating the ADC series ${G}_{n}$ to a lower order, and a pre-filtering process is necessary before ADC is used.

Fig. 10

ADC downward continuation errors as function of altitude for different reference fields and input datasets (color red, green, and blue are used for cases of error free, white noise, and colored noise, respectively)

3.2.5 Least-squares RBF

We only examine the extreme case, which is DC from 6200 to 0 m, and study the amplification pattern of DC errors. Input data are the gravity disturbance residuals with respect to the reference model, xGeoid16refA, truncated at degree 190. RBFs band-limited to degrees 190–2190 were fitted using ordinary least-squares to the noise-free, white-noise and colored-noise datasets, respectively. We used Tikhonov regularization with unit regularization matrix. The regularization parameter was determined using method B in (Xu 1992), which minimizes the trace of the mean square error matrix. For error-free data, the DC errors range from − 5 to 5 mGal with a standard deviation of 1 mGal. Figure 11 shows the DC errors for the white noise and colored noise datasets, respectively. The magnitude of DC errors is significantly lower than those of the Inverse Poisson and Moritz’s ADC. We also tested Poisson wavelets of order 3 (Holschneider and Iglewska-Nowak 2007) located on a Fibonacci grid with an average distance between the RBF centers of 7.0 km at a depth of 50 km below the Earth’s surface, which yields similar results.

Fig. 11

RBF downward continuation errors without (left column) and with (right column) regularization applied. Top row: white noise input dataset; bottom row: colored noise input dataset

3.2.6 Remarks

The statistics of DC errors for the simulation using xGeoid16refA complete to degree 190 and DC to the surface of the reference ellipsoid are shown in Table 1. It is worth pointing out that these numerical experiments with the gridded data are more on characterizing and stabilizing DCP rather than ranking theories on which these methods are based. On the one hand, the inverse Poisson and Moritz’s methods clearly show how the noise input led to the divergent DC results because of the ill-posed nature of DCP. On the other hand, LSC uses the noise variance-covariance matrix and the least-squares RBF uses the band-limited fitting and Tikhonov regularization, to give stable DC results, while SHA effectively constrains the amplification of DC errors by limiting the maximum degree of the SH expansion. In principle, the least-squares regularization can be applied to the inverse Poisson method as well. However, it is not as computationally efficient and feasible compared to LSC and RBF because the resulting large linear system of equations poses a numerical challenge to form and solve for (e.g., Huang 2002). Note that RLSC has not been used for the gridded data experiment because of the numerical complexity. Instead, it is used for the following case of experiments along real flight trajectories (Sect. 3.3) for which the covariance matrices were calculated for an earlier study (Willberg et al. 2020).

Table 1 Simulated gridded data: statistics of DC errors from 6200 m altitude to the surface of the reference ellipsoid. The reference gravity field is xGeoid16refA complete to degree 190

3.3 Numerical results using data along real flight trajectories

The simulation data in sub-Sect. 3.1 are used in this case simulation. Both simulated airborne and surface gravity disturbances have the same spectral content as EGM2008, with the data at the flight level being smoother than the surface data, as a natural consequence of the attenuation of gravity field variations with altitude.

SHA, inverse Poisson, and ADC require gridded data. Here we constructed a 1' × 1' grid of flight altitudes, with the node altitudes obtained by interpolation from the altitudes of the nearest flight trajectory data points by LSC. To allow for a fair comparison with the other methods, the signal covariance function used in least-squares interpolation was estimated from the flight track data. It should be noted that the inverse Poisson and ADC results were computed in two steps. First, the gridded residual gravity disturbances were downward continued to the surface of the reference ellipsoid. Then, residual gravity disturbances at the surface points were computed by the forward Poisson method. The SHA results were computed in a different two-step procedure. First, a spherical harmonic gravitational model was developed, and then the results were synthesized from the model. LSC, RLSC, and RBF directly operate on the flight line data without interpolation to the nodes of a grid.

The error statistics are shown in Table 2. For noise free data, the error standard deviations range from 0.13 mGal (RBF) to 0.69 mGal (LSC + ADC). Note that using LSC on the full signal gives a worse standard deviation of 0.96 mGal. The spatial distribution of the errors is heterogeneous with largest errors in mountainous regions. The RLSC solution did not perform better than the LSC solution, though the method was developed to improve over LSC (Willberg et al. 2019). For the SHA method, truncating the coefficients below degree 300, where the global model should be dominating the spectrum, almost doubles the DC error (0.35–to 0.63 mGal) in the error free case because of the space-limited data.

Table 2 Simulated data along flight trajectories: statistics of DC errors at the 31,358 surface gravity points (unit: mGal)

For white noise data, LSC, RLSC, and RBF provide comparable results (0.93–1.01 mGal DC error standard deviation). The other three methods have error standard deviations which are 30–50% larger. Unlike the simulation case with the gridded data, the inverse Poisson and ADC solutions are affected by the white noise only at a moderate level demonstrating that the LSC gridding before downward continuation has a stabilizing effect. This is in line with the findings in Alberts and Klees (2004).

For colored noise data, Moritz’s ADC with the LSC gridding provides the smallest error standard deviation (1.59 mGal); the error standard deviations for the other methods range from 1.91 mGal (LSC, LSC + SHA, LSC + inverse Poisson) to 2.13 mGal (RLSC). The solutions based on colored noise data have significantly larger error standard deviations than the solutions based on white noise data. We explain this by the fact that the noise power at the long wavelengths is significantly above the white noise power. The LSC DC errors for the three scenarios of input error (error-free, white noise and colored noise) are shown here in Fig. 12 to illustrate the distribution of DC errors.

Fig. 12

LSC downward continuation errors for various input datasets. From top to bottom: noise-free, white noise, and colored noise

A common feature of the DC errors for these methods is the correlation with the spatial variation of the gravity field itself. The stronger horizontal gravity gradient the field is, the larger the DC errors. One explanation is that the attenuation of gravity signals at the high flight levels leads to the loss of detail at altitude, which is magnified along with instrumental noise in the DC process. We speculate that less loss may be achieved by the use of RCR (Remove-Compute-Restore; see appendix A3) scheme with high-quality and extra-high degree EGM models, which regain more details in the restore step. This appears to be the case for the LSC method as shown in Table 1, Fig. 12 (top panel) demonstrates for the case of noise free input. It is clear that the LSC method only “breaks down” in several rare spots where the observations have gaps.

4 Numerical experiments using real data

We further evaluate the performance of the various DC methods using the airborne data set used in the Colorado 1 cm geoid experiment project (Wang et al. 2021; Sanchez et al. 2021). The Colorado GRAV-D airborne data are decimated to every 8 s, which result in 35,587 airborne data. The same combination of XGM18 and Earth 2014 model as used in the flight-trajectory simulation of Sect. 3.1 was used as the reference field and subtracted from the airborne gravity disturbances to generate gravity disturbance residuals. It is worth noting that the spectral band of the airborne data is limited (Li 2009, 2011). If their spectral content is different from the spectral content of the control surface gravity data, all the methods will be subject to the same errors. The NGS shared surface gravity data in the Colorado experiment project are used as control data set. Note that all the duplicated surface points in that study are removed. A combination of XGM18 and Earth 2014 were removed from the surface data so that the residuals are comparable with the downward continued residuals of the GRAV-D data.

Prior to the comparison with the downward-continued airborne gravity data, the surface gravity control dataset was corrected for the high-frequency contribution of topography using the RTM method (Forsberg 1984). The surface gravity anomalies are converted into gravity disturbances by using EGM2008 geoid values. In general, this evaluation is the same as the simulation in sub-Sect. 3.3 except for that the datasets are real and are identical to those in Willberg (2020).

The DC errors are summarized in Table 3 for all the six methods. Strictly speaking, the GRAV-D data are not directly comparable with the surface gravity data because the former are band-limited due to the high altitude and along-track filtering applied while the latter are surface point observations. In the case of errors negligible in observation and computation, the difference between them largely reflects the omission error of GRAV-D data. Otherwise, the residuals comprise the omission error, observational error, and computational error. Again, only the LSC results are illustrated here in Fig. 13. As it can be seen, large errors are mostly associated with higher topography in the region of study where the omission error tends to dominate.

Table 3 Real data experiment: statistics (mean and standard deviation, SD) of the differences between the downward continued airborne data and control surface gravity data before and after RTM and harmonic correction applied to the control surface gravity data (units: mGal)

Fig. 13

Differences between LSC downward continued residual airborne data and residual surface gravity data. No RTM correction applied

Table 3 shows the statistics of the differences between the downward-continued airborne gravity data and the control surface gravity data. The standard deviations range from 11.4 to 11.9 mGal depending on the method used. This large standard deviation cannot be explained by the downward continuation errors as the results in Sect. 3.2 have shown. A significant error source is the omission error of the airborne data compared to the control surface gravity data. A more realistic estimate of the downward continuation error could be obtained when applying topographic reductions (e.g., provided by the RTM method) to both datasets. For airborne gravity data this would require information about the lowpass filter used in the gap-free airborne gravity data pre-processing. This information is, however, not accessible to the authors of this study. In an attempt to reduce the spectral gap between the control surface gravity datasets and the airborne gravity dataset, we applied various RTM corrections to the former. By varying the smoothness of the RTM surface, we generated a whole bunch of RTM corrected control surface gravity data. Finally, we chosen the RTM surface which provided the smallest RMS difference to the downward-continued airborne data. Figure 14 shows the RMS differences as function of the spherical harmonic degree of the RTM surface. The smallest RMS difference is in the band between spherical harmonic degrees 2500 and 3000. After applying the RTM correction (and harmonic correction whenever the surface points were located below the RTM surface) to the control surface gravity data, the standard deviation of the differences to the downward-continued airborne gravity data reduced to 5.4–5.8 mGal, depending on the method (cf. Figure 14 and Table 3).

Fig. 14

RMS of the differences between the downward continued airborne data and the RTM-reduced control surface gravity data as function of the spherical harmonic degree of the RTM surface. Note that airborne gravity and control surface gravity data were already reduced from the effect of the XGM2108 and Earth2014 models

What we are interested in is the computational error of DC caused by each method. As the residual results from all the methods are subject to the same omission error and observational error, a lower level of residuals indicates a better agreement with the surface gravity data. The residuals shown in Table 3 are similar among all six methods, and the differences are not significant enough to tell which method is the best when taking in consideration the observational errors from the GRAV-D and surface data, which are estimated to be typically 1–2 mGal for each source.

However, LSC has an advantage because it combines regularization and DC into one step through a 3D covariance function and provide comparable results with the other methods. Unlike LSC, RLSC is built upon covariance matrices computed from the reference GGM. RBF is also attractive because it is a local method and can directly operate on scattered data; only in case of larger data gaps, interpolation may be necessary to obtain optimal results. An effective check to the LSC DC is the combination of LSC gridding and Poisson DC to detect systematic biases by LSC alone. Though the Inverse Poisson can start from scattered points too, it has been shown that it is better to start from gridded data (Alberts and Klees, 2004). For the SHA method, truncating the coefficients below degree 300 increases the SHA DC error.

The geoid models were computed from the gravity disturbances downward-continued to the surface of the reference ellipsoid as (see Appendix B)

$$ N\left( {\Omega } \right) = \zeta_{0} \left( {\Omega } \right) + \zeta_{1} \left( {\Omega } \right) + \zeta_{{{\text{Ref}}}} \left( {\Omega } \right) + d\zeta \left( {\Omega } \right) + C_{{\text{T}}} \left( {\Omega } \right) $$

(7)

where $\zeta_{0}$ and $\zeta_{1}$ are the degree-0 and degree-1 terms, respectively (Sánchez et al. 2021; Wang et al. 2021); $\zeta_{{{\text{Ref}}}}$ is the height anomaly on the reference ellipsoid (GRS80), which is synthesized from XGM18 and the synthetic topographic geopotential model predicted from Earth2014; and

$$ \begin{aligned} d\zeta \left( \Omega \right) &= \frac{R}{4\pi \gamma \left( \Omega \right)}\int_{{\sigma_{0} }} {S_{{{\text{MDB}}}} \left( \psi \right)}\\ & \times {\left[ {\Delta g_{{{\text{Airborne}}}} \left( {\Omega^{^{\prime}} } \right) - \Delta g_{{{\text{Ref}}}} \left( {\Omega^{^{\prime}} } \right)} \right]d\sigma } \end{aligned}$$

(8)

where $\gamma \left( {\Omega } \right)$ is the normal gravity on the reference ellipsoid; $S_{{{\text{MDB}}}}$ a modified degree-banded Stokes kernel function which spans from spherical harmonic degree 210 to 2160 with transitional bands of 60 and 120 degrees at the low and high ends, respectively (Huang and Véronneau 2013). $\Delta g_{{{\text{Ref}}}}$ is the gravity anomaly on the reference ellipsoid synthesized from XGM18 and the synthetic topographic geopotential model predicted from Earth2014 too. The full airborne gravity disturbance continued onto the reference ellipsoid is transformed into the gravity anomaly by

$$ \Delta g_{{{\text{Airborne}}}} \left( {\Omega } \right) = \delta g_{{{\text{Airborne}}}} \left( {\Omega } \right) - 0.3086N_{{{\text{CGG2013}}}} \left( {\Omega } \right) $$

(9)

The term ${C}_{\text{T}}$ transforms the height anomaly evaluated on the reference ellipsoid into the geoid height.

The resulting geoid models are validated using the GSVS17 GPS-levelling data in the region of study (van Westrum et al. 2021). The results are shown in Fig. 15. As it can be seen that all the methods have a similar performance except for two cases. The case of Poisson1 gives a slightly poor agreement, in which the DC threshold value is set as 1 mGal to reflect the data error. The other case is for SHA300, in which the spherical harmonic model is truncated to degree 300. These geoid validation results are consistent with the gravity ones shown in Table 3.

Fig. 15

Geoid model differences (model-GNSS/Leveling) with respect to the GSVS17 validation data

The bias of ~ 62 cm originates from two sources. One is NAVD88, which is defined at the tide gage in Rimouski, Québec on the lower St. Lawrence River. NAVD88 has a tilt ranging from − 0.199 m to 1.328 m (Li 2018b). The GSVS17 levelling line is constrained to one bench mark of NAVD88. The other is the choice of equipotential surface. This study selects the equipotential surface defined by ${W}_{0}^{NA}=62 636 856{m}^{2}{s}^{-2}$, which represents the best fit of mean sea level for the North American region (Véronneau and Huang 2016; Huang et al. 2019; and Huang and Véronneau 2005). This equipotential surface is about 0.26 m lower than the IAG-endorsed surface, which is defined by ${W}_{0}^{IHRS}=62 636 853.4{m}^{2}{s}^{-2}$. Like the GPS ellipsoidal heights for GSVS17, the geoid models in this study refer to the reference ellipsoid is GRS80 (Moritz 1980). All of the related quantities (Amin et al 2019) are shown in Fig. 16.

Fig. 16

The origin of the bias in the GNSS/Leveling comparison

From Eq. (2–181) of Heiskanen and Moritz (1967), we have:

$$ N = - \frac{{\left( {W_{0}^{{{\text{NA}}}} - U_{0}^{{{\text{GRS80}}}} } \right)}}{\gamma } + \frac{{T_{{{\text{gravity}}}} }}{\gamma } $$

(10)

From Fig. 16, we have:

$$ N = - \frac{{W_{0}^{Rimouski} + tilt - U_{0}^{GRS80} }}{\gamma } + \frac{{T_{GPSLeveling}^{{}} }}{\gamma } $$

(11)

Equation (10) minus Eq. (11) gives:

$$ {\text{dN}} = \frac{{W_{0}^{{{\text{Rimouski}}}} + {\text{tilt}} - W_{0}^{{{\text{NA}}}} }}{\gamma } + \frac{{T_{{{\text{gravity}}}} - T_{{{\text{GPSLeveling}}}} }}{\gamma } $$

(12)

The first term in Eq. (12) gives the bias term. The second term gives the de-biased geoid model residuals.

5 Summary and conclusions

Downward continuing airborne gravity data from flight heights onto the surface of the Earth or a level surface, from scattered points into regular sampled grids, enables the direct use of the classical geoid procedures that is based on Stokes’s integrals. However, this downward continuation procedure is not a trivial task due to the instability of this procedure. Four classical DC methods and two relatively newer approaches have been tested using both simulated data and real data.

For the simulation tests, both regular sampled grids and scattered points are used in two scenarios of noise. If the data are regularly sampled and noise free, all methods perform reasonably well, except for an artificial noise term which needs to be added to LSC to reduce the impact of the ill-conditioned signal covariance matrix on the downward-continued gravity data. These ideal data sets are used to verify the correctness of the developed software that can be shared on request. For the SHA approach, all of the spectrum of the real gravity field is distorted. The reason is that when fitting an SH model to a space-limited dataset, the power in the signal is distributed over all frequency (i.e., over the SH coefficients) providing a power spectrum which differs completely from the power spectrum of the global dataset. The least-squares constraint does not control the spectrum when minimizing the residuals. This casts a heavy doubt on any method that tries to directly combine a global gravity field and local gravity field in the spherical harmonic domain.

In the white noise and colored noise cases, the performances of all methods are degraded; the inverse Poisson becomes unstable, while Moritz’s ADC diverges. However, the covariance matrix in LSC and the linear solver in SHA can still control the noise effects to reasonable magnitudes. For the LSC, an accurate estimation of the noise level is equally important as the estimation of the covariance functions. The tests on the gridded data prove that there are no major problems in the developed software, i.e., no bugs in the codes.

For the simulated tests on scattered points, the RBF gives the best results in the error free case. Even in the white and colored noise cases, RBF still performs reasonably well if the data is band-limited. Further improvements are expected when using a more careful RBF network design and a better regularized weighted least-squares estimator instead of the ordinary least-squares estimator (e.g., Slobbe 2013; Slobbe et al. 2019).

In the real data tests, the residual gravity disturbances are not band-limited in the spectral range after removing the GGM and Earth2014. This is a typical situation in airborne data applications, where the goal is to exactly detect problems in medium-wavelength gravity field variations. In the Colorado case, the different methods gave similar results, mainly due to the unavoidable errors in airborne data, and the relatively high flight level.

We note that due to the lack of band-limited data, the current implementation of RBF cannot efficiently distinguish signal from noise, which is also true for inverse Poisson. The afore-mentioned improvements may provide a significantly better RBF solution. We also note that both the simulated tests and the real tests do not show significant numerical improvement from LSC to RLSC, though the latter has some theoretical advantages, but also requires more intense computational effort to establish the complicated covariance matrices. This casts a doubt on the practical application of this improved LSC method for airborne gravity data.

The geoid models are computed from the DC results from all the methods, and are validated by the GSVS GPS-levelling data. They show a similar agreement around 3 cm r.m.s., with LSC performing marginally better than the other methods. Giving the rough topography in the Colorado areas this is a good result, but also highlights the limits of high-level airborne gravity data in terms on reaching a 1 cm-geoid as a stand-alone data source without supplementary surface gravimetry data.

Appendices

Appendix A

1.1 The derivation of the equations of downward continuation of airborne gravity data using various approaches

1.1.1 Spherical harmonic analysis (SHA)

In spherical approximation, band-limited (full/residual) gravity disturbances from airborne gravimetry can be modelled as

$$ \begin{aligned} & \delta g\left( {r~,\phi ~,\lambda ~} \right) \approx - \frac{{\partial T}}{{\partial r}} \\ & \quad = \frac{{{\text{GM}}}}{{R^{2} }}\mathop \sum \limits_{{n = n1}}^{{n2}} \left( {\frac{R}{{r~}}} \right)^{{n + 2}} \left( {n + 1} \right)\\ &\quad \times \mathop \sum \limits_{{m = 0}}^{n} \left( {\bar{c}_{{{\text{nm}}}} ~\cos \left( {m\lambda } \right) + \bar{s}_{{{\text{nm}}}} ~\sin \left( {m\lambda } \right)} \right)\bar{p}_{{{\text{nm}}}} ~\left( {\sin \phi } \right) \\ \end{aligned} $$

(13)

where $T$ is the gravity disturbing potential; ${\text{GM}}$ is the product of the Universal gravitational constant and the assigned reference mass; $R$ is the mean Earth’s radius; $\overline{p}_{{{\text{nm}}}}$ are the fully normalized associated Legendre functions of degree $n$ and order $m$; $\left\{ {\overline{c}_{{{\text{nm}}}} ,\overline{s}_{{{\text{nm}}}} } \right\}$ are the Stokes’s coefficients to be solved from the airborne gravity disturbances ${\updelta }g$; and the limits of $n1$ to $n2$ define the bandwidth of the airborne gravity disturbances.

However, solving for all coefficients $\left\{ {\overline{c}_{{{\text{nm}}}} ,\overline{s}_{{{\text{nm}}}} } \right\}$ from airborne data given inside a local area is not possible; in fact, there are infinitely many solutions to this problem. To foster one particular solution, one may assume zero gravity data outside the local area.

This treatment will definitely reduce the power in the spherical harmonic coefficients because of applying the global function for a representation of space-limited data. This set of coefficients are no longer representing the true gravity field of the Earth, especially outside the study region (Jekeli 2016). An intuitive explanation is that all the data of the world implies that $\left\{ {\overline{c}_{{{\text{nm}}}} ,\overline{s}_{{{\text{nm}}}} } \right\}$ are zeros, except only a small amount of regional data says they are not zeros. Note that the spherical harmonic functions, $\overline{p}_{{{\text{nm}}}} \left( {\sin \phi } \right)\cos \left( {m\lambda } \right)$ and $\overline{p}_{{{\text{nm}}}} \left( {\sin \phi } \right)\sin \left( {m\lambda } \right)$, are global functions; using regional data, it is impossible to estimate all spherical harmonic coefficients.

In addition to the theoretical shortcomings of using SHA to downward continue airborne data, numerically, Eq. (13) cannot be established directly on the original airborne survey point $i\left( {r_{i} ,\phi_{i} ,\lambda_{i} } \right)$ in order to utilize the EGM208 block diagonal engine to quickly solve the 4 –million spherical harmonic coefficients. In practice, the point airborne data has to be reduced from the flight altitude onto a grid on the surface of a larger (in terms of semi-major axis) reference ellipsoid that is located in the mean flight height in order to solve the spheroidal harmonic coefficients quickly by using the well-known block diagonal method (Pavlis 1998), which are then transformed into spherical harmonics by using Jekeli’s method (1988). Finally, the spherical harmonic coefficients are scaled back to the desired system. The details of spheroidal harmonic analysis and their transformations to the spherical harmonic are well-known and will not be repeated here.

In the GRAV-D airborne gravity data, the flight heights can vary by several thousand meters in a typical survey campaign. The real flights are not on a mean flight height as assumed by some algorithms. A novel iterative scheme (Smith et al. 2013) described by the following steps was developed to downward continue the real data from varying flight heights on to an inflated ellipsoid whose mean radius is $R^{{{\text{big}}}}$, and its surface is located at the numerical mean flight height. Then the spherical harmonic coefficients are scaled back by using the ratio between $R^{{{\text{big}}}}$ and $R_{{}}^{{}}$.

• (1) First, let’s assume the residual airborne gravity disturbances are given on the surface of an inflated ellipsoid and solve the spherical harmonic coefficients:

  $$ \begin{aligned}& \left\{ {\overline{c}_{{{\text{nm}}}}^{T0} ,\overline{s}_{{{\text{nm}}}}^{T0} } \right\}\\ &\quad= {\mathcal{F}}_{0}^{ - 1} \left\{ {{\updelta }\underline {g}_{0} \left( {r_{i} - h,\phi_{i} ,\lambda_{i} } \right) = {\updelta }\underline {g} \left( {r_{i} ,\phi_{i} ,\lambda_{i} } \right)} \right\}, \end{aligned}$$

  (14)

  where ${\updelta }\underline {g}_{0} \left( {r_{i} - h_{i} ,\phi_{i} ,\lambda_{i} } \right)$ are the pseudo gravity disturbances on the reference ellipsoid; ${\mathcal{F}}_{0}^{ - 1} \left\{ \cdot \right\}$ represent spherical harmonic analysis operator for the block diagonal method (for simplicity of description the steps to transform the ellipsoid harmonics into spherical harmonics are neglected, but it is applied in the computation);

• (2) Then, the following two terms are generated for the next iteration.

The first term is called the misclosure:

$$ {\updelta }\underline {g}^{M1} = {\mathcal{F}}_{0}^{{\left( {r_{i} ,\phi_{i} ,\lambda_{i} } \right)}} \left\{ {\overline{c}_{{{\text{nm}}}}^{T0} ,\overline{s}_{nm}^{T0} } \right\} - {\updelta }\underline {g} , $$

(15)

where ${\mathcal{F}}_{0}^{{}} \left\{ \cdot \right\}$ is the spherical harmonic synthesis operator (SHS) at the original airborne survey points at the real altitudes based on $\left\{ {\overline{c}_{{{\text{nm}}}}^{T0} ,\overline{s}_{{{\text{nm}}}}^{T0} } \right\}$. Basically, this term shows the errors in the spherical harmonic coefficients due to the assumption made in step (1).

The second term is the DC term:

$$ {\updelta }\underline {g}^{{{\text{DC1}}}} = {\mathcal{F}}_{0}^{{\left( {r_{i} ,\phi_{i} ,\lambda_{i} } \right)}} \left\{ {\overline{c}_{{{\text{nm}}}}^{T0} ,\overline{s}_{{{\text{nm}}}}^{T0} } \right\} - {\mathcal{F}}_{0}^{{\left( {r_{i} - h_{i} ,\phi_{i} ,\lambda_{i} } \right)}} \left\{ {\overline{c}_{{{\text{nm}}}}^{\delta 0} ,\overline{s}_{{{\text{nm}}}}^{\delta 0} } \right\} $$

(16)

• (3) Based on the DC term, a new observation as shown in Eq. (17) is assumed to be given on the surface of the bigger ellipsoidal surface for the next round of SHA as shown in Eq. (18).

  $$ {\updelta }\underline {g}_{1} \left( {r_{i} - h_{i} ,\phi_{i} ,\lambda_{i} } \right) = {\updelta }\underline {g} \left( {r_{i} ,\phi_{i} ,\lambda_{i} } \right) - {\updelta }\underline {g}^{{{\text{DC1}}}} , $$

  (17)
  $$ \left\{ {\overline{c}_{{{\text{nm}}}}^{T1} ,\overline{s}_{{{\text{nm}}}}^{T1} } \right\} = {\mathcal{F}}_{1}^{ - 1} \left\{ {{\updelta }\underline {g}_{1} \left( {r_{i} - h,\phi_{i} ,\lambda_{i} } \right)} \right\}, $$

  (18)

Another misclosure term is obtained by:

$$ {\updelta }\underline {g}^{M2} = {\mathcal{F}}_{1}^{{\left( {r_{i} ,\phi_{i} ,\lambda_{i} } \right)}} \left\{ {\overline{c}_{{{\text{nm}}}}^{T1} ,\overline{s}_{{{\text{nm}}}}^{T1} } \right\} - {\updelta }\underline {g} , $$

(19)

• (4) In this step, the DC term of the misclosure term is computed according to:

  $$ \left\{ {\overline{c}_{{{\text{nm}}}}^{T2} ,\overline{s}_{{{\text{nm}}}}^{T2} } \right\} = {\mathcal{F}}_{2}^{ - 1} \left\{ {{\updelta }\underline {g}^{M2} } \right\}, $$

  (20)
  $$\begin{aligned} {\updelta }\underline{\Delta g}^{{{\text{DC2}}}}& = {\mathcal{F}}_{2}^{{\left( {r_{i} ,\phi_{i} ,\lambda_{i} } \right)}} \left\{ {\overline{c}_{{{\text{nm}}}}^{T2} ,\overline{s}_{{{\text{nm}}}}^{T2} } \right\} \\& \quad - {\mathcal{F}}_{2}^{{\left( {r_{i} - h_{i} ,\phi_{i} ,\lambda_{i} } \right)}} \left\{ {\overline{c}_{{{\text{nm}}}}^{T2} ,\overline{s}_{{{\text{nm}}}}^{T2} } \right\}, \end{aligned}$$

  (21)

• (5) Finally, the original airborne gravity is reduced from the flight trajectories onto the surface of the inflated ellipsoid by:

  $$ {\updelta }\underline {g}_{3} \left( {r_{i} - h_{i} ,\phi_{i} ,\lambda_{i} } \right) = {\updelta }\underline {g}_{1} - \left( {{\updelta }\underline {g}^{M2} - {\updelta }\underline {g}^{{{\text{DC2}}}} } \right), $$

  (22)

Finally, the spherical harmonic coefficients for the original airborne data are given as

$$ \left\{ {\overline{c}_{{{\text{nm}}}}^{T} ,\overline{s}_{{{\text{nm}}}}^{T} } \right\} = {\mathcal{F}}_{3}^{ - 1} \left\{ {{\updelta }\underline {g}_{3} } \right\}, $$

(23)

Note that a gridding step is still needed to interpolate the scattered airborne gravity data onto the nodes of a grid (one data grid and one DEM grid) to start the iterations described above.

1.1.2 Least squares collocation (LSC) method

Forsberg’s (1987) covariance model is based on a power spectral model for a planar residual gravity field, matching the Kaula rule up in the main band frequency band up to a “depth” parameter D (equivalent to the use of a Bjerhammar sphere, but twice the magnitude). This gives rise to a gravity covariance function ${C}_{\delta g,\delta g}$ of shape − log(z + r), where z = z₁ + z₂ + D is a height parameter, and r the slant range between the two covariance points. To avoid singularities in the geoid terms for a fully self-consistent model, several log-terms are needed to be combined through a deeper “compensation depth” T, giving a relatively complicated expression of form

$$ \begin{aligned} & C_{{\delta g,\delta g}} \left\{ {P\left( {\phi _{i} ,\lambda _{i} ,h_{i} } \right),Q\left( {\phi _{j} ,\lambda _{j} ,h_{j} } \right)} \right\}\\ &\quad = \frac{{\sigma ^{2} }}{{3\log \left( {D + T} \right) - 3\log \left( {D + 2T} \right) + \log \left( {D + 3T} \right) - \log \left( D \right)}}\\ &\qquad \times \left\{ \begin{gathered} 3\log \left( {D + T + h_{i} + h_{j} + \sqrt {s + \left( {D + T + h_{i} + h_{j} } \right)^{2} } } \right) \hfill \\ - 3\log \left( {D + 2T + h_{i} + h_{j} + \sqrt {s + \left( {D + 2T + h_{i} + h_{j} } \right)^{2} } } \right) \hfill \\ + \log \left( {D + 3T + h_{i} + h_{j} + \sqrt {s + \left( {D + 3T + h_{i} + h_{j} } \right)^{2} } } \right) \hfill \\ - \log \left( {D + h_{i} + h_{j} + \sqrt {s + \left( {D + h_{i} + h_{j} } \right)^{2} } } \right) \hfill \\ \end{gathered} \right\} \end{aligned} $$

(24)

where $\sigma_{{}}^{2}$ is the data variance; $D$ is the depth to the high frequency attenuation layer; $T$ is the thickness to bottom layer, low frequency attenuation; and $s = \sqrt {x_{{}}^{2} + y_{{}}^{2} }$ the planar distance (approximated here with $x = 111.11{\text{km}} \times \left( {\lambda_{i} - \lambda_{j} } \right)\cos \overline{\phi }$ and $y = 111.11{\text{km}} \times \left( {\phi_{i} - \phi_{j} } \right)\cos \overline{\phi }$; $h_{i}^{{}}$ and $h_{j}^{{}}$ are the flight height in km).

The covariance between gravity disturbance, $\delta g,$ and height anomaly, ${\upzeta }$, based on the covariance model of gravity anomalies is (Forsberg, 1987):

$$ \begin{gathered} C_{\delta g,\zeta } \left\{ {P\left( {\phi_{i} ,\lambda_{i} ,h_{i} } \right),Q\left( {\phi_{j} ,\lambda_{j} ,h_{j} } \right)} \right\} = - \frac{1}{\gamma }\frac{{\sigma^{2} }}{{3\log \left( {D + T} \right) - 3\log \left( {D + 2T} \right) + \log \left( {D + 3T} \right) - \log \left( D \right)}} \hfill \\ \quad \times\left\{ \begin{gathered} \left( {\sqrt {s + \left( {D + h_{i} + h_{j} } \right)^{2} } - \left( {D + h_{i} + h_{j}^{{}} } \right)\log \left( {D + h_{i} + h_{j} + \sqrt {s + \left( {D + h_{i} + h_{j} } \right)^{2} } } \right)} \right) \hfill \\ - 3\left( {\sqrt {s + \left( {D + T + h_{i} + h_{j} } \right)^{2} } - \left( {D + T + h_{i} + h_{j} } \right)\log \left( {D + T + h_{i} + h_{j} + \sqrt {s + \left( {D + T + h_{i} + h_{j} } \right)^{2} } } \right)} \right) \hfill \\ + 3\left( {\sqrt {s + \left( {D + 2T + h_{i} + h_{j} } \right)^{2} } - \left( {D + 2T + h_{i} + h_{j} } \right)\log \left( {D + 2T + h_{i} + h_{j} + \sqrt {s + \left( {D + 2T + h_{i} + h_{j} } \right)^{2} } } \right)} \right) \hfill \\ - \left( {\sqrt {s + \left( {D + 3T + h_{i} + h_{j} } \right)^{2} } - \left( {D + 3T + h_{i} + h_{j} } \right)\log \left( {D + 3T + h_{i} + h_{j} + \sqrt {s + \left( {D + 3T + h_{i} + h_{j} } \right)^{2} } } \right)} \right) \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered} $$

(25)

Given the covariance function, the prediction of gravity anomalies and height anomalies including error variances using LSC can be implemented by the well-known collocation equations:

$$ \widehat{\delta g}^{{{\text{pred}}}} = C_{{\delta g^{{{\text{pred}}}} ,\delta g^{{{\text{obs}}}} }} \left( {C_{{\delta g^{{{\text{obs}}}} ,\delta g^{{{\text{obs}}}} }} + D_{n,n} } \right)^{ - 1} \left[ {\begin{array}{*{20}c} {\delta g_{1}^{{{\text{obs}}}} } \\ {\begin{array}{*{20}c} {\delta g_{2}^{{{\text{obs}}}} } \\ \vdots \\ \vdots \\ \end{array} } \\ {\delta g_{n}^{{{\text{obs}}}} } \\ \end{array} } \right], $$

(26)

$$ \begin{aligned} D\{ \widehat{\delta g}^{{{\text{pred}}}} \} &= C_{{\delta g,\underline{\delta g} }} - C_{{\delta g^{{{\text{pred}}}} ,\delta g^{{{\text{obs}}}} }} \left( {C_{{\delta g^{{{\text{obs}}}} ,\delta g^{{{\text{obs}}}} }} + D_{n,n} } \right)^{ - 1}\\ & \quad C_{{\delta g^{{{\text{pred}}}} ,\underline{\delta g}^{{{\text{obs}}}} }}^{T} ,\end{aligned} $$

(27)

$$ {\hat{\zeta }}^{{{\text{pred}}}} = C_{{{\upzeta }^{{{\text{pred}}}} ,\underline{\delta g}^{{{\text{obs}}}} }} \left( {C_{{\delta g^{{{\text{obs}}}} ,\delta g^{{{\text{obs}}}} }} + D_{n,n} } \right)^{ - 1} \left[ {\begin{array}{*{20}c} {\delta g_{1}^{{{\text{obs}}}} } \\ {\begin{array}{*{20}c} {\delta g_{2}^{{{\text{obs}}}} } \\ \vdots \\ \vdots \\ \end{array} } \\ {\delta g_{n}^{{{\text{obs}}}} } \\ \end{array} } \right], $$

(28)

$$ \begin{aligned} D\{ {\hat{\zeta }}^{{{\text{pred}}}} \} &= C_{{{\upzeta },{\upzeta }}} - C_{{{\upzeta }^{{{\text{pred}}}} ,\underline{\delta g}^{{{\text{obs}}}} }} \left( {C_{{\underline{\delta g}^{{{\text{obs}}}} ,\underline{\delta g}^{{{\text{obs}}}} }} + D_{n,n} } \right)^{ - 1} \\& \quad C_{{{\upzeta }_{{}}^{{{\text{pred}}}} ,\underline{\delta g}^{{{\text{obs}}}} }}^{T} ,\end{aligned} $$

(29)

where $C_{{{\upzeta },{\upzeta }}} = \frac{1}{{\gamma^{2} }}\left[ {\frac{3}{4}zr + \left( {\frac{1}{4}r^{2} - \frac{3}{4}z^{2} } \right)\log \left( {z + r} \right)} \right].$

In the planar approximation, the covariance model is described only by three parameters, i.e., gravity variance $\sigma_{{}}^{2}$, high-frequency attenuation depth parameter $D$, and low-frequency attenuation depth parameter $T$. Due to its simplicity, it is widely used in processing airborne gravity data (Forsberg et al. 1996, 1999, 2000, 2003). However, the simplified covariance function cannot always yield a good fit of the data in the remove-compute-restore scenario, especially for the geoid part, as the covariance functions have difficulties to approximate the negative covariances coming from removing a reference field (which again is a consequence of the planar approximation).

1.1.3 A.3 Residual LSC

Residual least-squares collocation is a modified form of LSC (Willberg et al. 2019) in the context of remove-compute-restore (RCR). In RLSC, the covariance modeling is taken from the global gravity field modeling (GGM) and forward topographic modeling instead of empirical parameterization. The general form of RLSC reads as (Willberg et al. 2019):

$$ {\mathbf{s}} = \left( {{\mathbf{C}}_{{\hat{s}\hat{l}}}^{m} + {\mathbf{C}}_{{\hat{s}\hat{l}}}^{t} } \right)\left( {{\mathbf{C}}_{ll} + {\mathbf{C}}_{{\hat{l}\hat{l}}}^{m} + {\mathbf{C}}_{{\hat{l}\hat{l}}}^{t} } \right)^{ - 1} \left( {{\mathbf{l}} - {\hat{\mathbf{l}}}^{m} - {\hat{\mathbf{l}}}^{t} } \right) + {\hat{\mathbf{s}}}^{m} + {\hat{\mathbf{s}}}^{t} , $$

(30)

where ${\mathbf{s}}$ is the signal, ${\mathbf{l}}$ is the observable, and the super-scripts $m$ and $t$ are representing information from GGM and topography, respectively. The circumflexes indicates the corresponding quantities are a-priori estimates from GGM and topographic modeling. ${\hat{\mathbf{l}}}^{m} , {\hat{\mathbf{l}}}^{t}$ are linked to the remove step, ${\hat{\mathbf{s}}}^{m} ,{\hat{\mathbf{s}}}^{t}$ are linked to the restore step.

From Eq. (30), we can see that RLSC uses separated error covariance matrices ${\mathbf{C}}$ to describe signal correlations from every input source. In particular, ${\mathbf{C}}_{{\widehat{ \cdot }\widehat{ \cdot }}}^{m}$ includes the full covariance information from a high-resolution GGM, which is not included in LSC. Accordingly, it considers accuracies and correlations of the high-resolution GGM and models the gravity field of the Earth as anisotropic and location-dependent (up to the maximum degree of the GGM). This more realistic representation of the gravity field should generally improve the quality of a regional gravity field model.

A more detailed differentiation between LSC and RLSC is explained in Willberg et al. (2019), which also highlights corresponding similarities to specific realizations of LSC that already include accuracy information from a GGM in different forms (e.g., Haagmans & van Gelderen, 1991; Pail et al. 2010).

1.1.4 Radial basis function (RBF)

The (residual) gravity disturbing potential is written as

$$ \begin{aligned}\delta T\left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right)& = \frac{{{\text{GM}}}}{{R_{{}}^{{}} }}\mathop \sum \limits_{q = 1}^{{Q_{L} }} \alpha_{q} \mathop \sum \limits_{n = n1}^{n2} \left( {\frac{R}{{r_{p} }}} \right)^{n + 1}\\ & \quad \times b_{n} \sqrt {2n + 1} \overline{p}_{n} \left( {\frac{{\vec{r}_{p} \cdot \vec{r}_{q} }}{{\left| {\vec{r}_{p} } \right|\left| {\vec{r}_{q} } \right|}}} \right)\end{aligned} $$

(31)

where $b_{n}$ is a set of parameters that control the type of RBF (Schmidt et al. 2007), which determine the spectrum of the RBF, $\vec{r}_{q}$ denotes the location of the center of the RBF,$\overline{p}_{n}$ is the $4\pi$-normalized Legendre polynomial of degree n, and $\alpha_{q}^{{}}$ are the parameters to be estimated from the data, and $Q_{L}$ is the total number of coefficients. Then, in spherical approximation, the residual gravity disturbance is given by:

$$\begin{aligned} &\delta \delta g\left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right) = - \frac{\partial \delta T}{{\partial r_{p} }} = \frac{{{\text{GM}}}}{{R^{2} }}\mathop \sum \limits_{q = 1}^{{Q_{L} }} \alpha_{q} \\& \quad \times\mathop \sum \limits_{n = n1}^{n2} \left( {\frac{R}{{r_{p} }}} \right)^{n + 2} b_{n} \left( {n + 1} \right)\sqrt[{}]{2n + 1}\overline{p}_{n} \left( {\frac{{\vec{r}_{p} \cdot \vec{r}_{q} }}{{\left| {\vec{r}_{p} } \right|\left| {\vec{r}_{q} } \right|}}} \right),\end{aligned} $$

(32)

Eq. (32) provides the functional model for the estimation of the RBF parameters using ordinary least-squares techniques. Note that the computation of residual gravity disturbances at the Earth’s surface requires an extra synthesis step once the RBF parameters have been computed. Conceptually, using least-squares to estimate the RBF parameters allows the use of the original data along the flight directory without any spatial interpolation prior to the estimation of the RBF coefficients. This convenience avoids all of the complicated data pre-processing needed in steps (1) to (5) in A.1. Furthermore, the spatial concentration of a RBF allows for a parameterization of a regional gravity field requiring much less coefficients compared to the use of spherical harmonics (e.g., Klees et al. 2008; Lieb et al. 2016; Li 2018a).

The performance of the RBF least-squares approach critically depends on the definition of the RBF network, i.e., the location, including the depth (for some types of RBFs), and distribution of the RBFs. There are many ways to find a suitable RBF network (e.g., Schmidt et al. 2007, Klees et al. 2008, Eicker et al. 2013, Naeimi 2013, Lin et al. 2019, Foroghi et al. 2018). In this study, we use the nodes of a Reuter grid to position the RBFs horizontally (Eicker et al. 2013, Naeimi 2013, Lieb et al. 2016, Klees et al. 2018, Klees et al. 2019).

After setting up the system, the observation equations can be written as a Gauss-Markov Model (Schaffrin 2006):

$$ {\mathbf{E}}\left( {\mathbf{y}} \right) = A{\varvec{\xi}}, D\left( y \right) = \sigma_{0}^{2} P^{ - 1} , $$

(33)

where ${\mathbf{y}}$ is a $m \times 1$ column vector that contains the residual gravity disturbances, $A$ is a $m \times k$ design matrix with $k = Q_{L}^{{}}$ number of basis functions used, and ${\varvec{\xi}}$ is a $k \times 1$ vector comprising the RBF parameters. The regularized ordinary least-squares solution is given by (Eq. 78 Schmidt et al. 2007):

$$ \hat{\user2{\xi }} = \left( {A^{T} PA + {{\varvec{\upkappa}}}^{{{\mathbf{om}}}} {\mathbf{I}}} \right)^{ - 1} (A^{T} {\mathbf{Py}}), $$

(34)

where the optimal regularization parameter ${{\varvec{\upkappa}}}_{{{\mathbf{om}}}}$ is computed using Algorithm B in (Xu 1992) and

$$ {\varvec{D}}\{ \widehat{{{\varvec{\xi}}\} }} = \sigma_{y}^{2} \left( {A^{T} A + {{\varvec{\upkappa}}}_{{{\mathbf{om}}}} {\mathbf{I}}} \right)^{ - 1} \left( {A^{T} A} \right)\left( {A^{T} A + {{\varvec{\upkappa}}}_{{{\mathbf{om}}}} {\mathbf{I}}} \right)^{ - 1} , $$

(35)

The downward continued gravity disturbance is simply given by:

$$ {\hat{\mathbf{y}}} = A^{dc} \hat{\user2{\xi }};\user2{ }D\left\{ {{\hat{\mathbf{y}}}} \right\} = A^{dc} D\left\{ {\hat{\user2{\xi }}} \right\}A^{dcT} , $$

(36)

1.1.5 Inverse Poisson method

The formula for the upward continuation of a harmonic function $r_{p} {\updelta }g\left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right)$ at flight altitude P ($r_{p} ,\phi_{p} ,\lambda_{p}$) from a spherical surface ($\sigma_{R}^{{}} \left( {Q_{{}}^{^{\prime}} } \right)$) is given by the Poisson integral as (e.g., Alberts and Klees 2004):

$$\begin{aligned} &r_{p} {\updelta }g\left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right) = \frac{1}{{4\pi R^{2} }}\iint\limits_{{\sigma_{R}^{{}} }} {R{\updelta }g\left( {r_{q}^{^{\prime}} ,\phi_{q}^{^{\prime}} ,\lambda_{q}^{^{\prime}} } \right)}\\ & \quad {\wp \left( {R,\frac{{\vec{r}_{p} \cdot \vec{r}_{q}^{^{\prime}} }}{{\left| {\vec{r}_{p} } \right|\left| {\vec{r}_{q}^{^{\prime}} } \right|}},r_{p} } \right)d\sigma_{R} \left( {Q^{^{\prime}} } \right),} \end{aligned}$$

(37)

where $\wp \left( {R,\frac{{\vec{r}_{p} \cdot \vec{r}_{q}^{^{\prime}} }}{{\left| {\vec{r}_{p} } \right|\left| {\vec{r}_{q}^{^{\prime}} } \right|}},r_{p} } \right)$ is the Poisson kernel given by

$$ \begin{aligned}&\wp \left( {R,\frac{{\vec{r}_{p} \cdot \vec{r}_{q}^{^{\prime}} }}{{\left| {\vec{r}_{p} } \right|\left| {\vec{r}_{q}^{^{\prime}} } \right|}},r_{p} } \right) = \mathop \sum \limits_{n = 0}^{\infty } \left( {\frac{R}{{r_{p} }}} \right)^{n + 1} \sqrt {2n + 1} \overline{p}_{n} \left( {\frac{{\vec{r}_{p} \cdot \vec{r}_{q}^{^{\prime}} }}{{\left| {\vec{r}_{p} } \right|\left| {\vec{r}_{q}^{^{\prime}} } \right|}}} \right) \\&\quad = \mathop \sum \limits_{n = 0}^{\infty } 2n + 1\left( {\frac{R}{{r_{p} }}} \right)^{n + 1} P_{n} \left( {\frac{{\vec{r}_{p} \cdot \vec{r}_{q}^{^{\prime}} }}{{\left| {\vec{r}_{p} } \right|\left| {\vec{r}_{q}^{^{\prime}} } \right|}}} \right) = R\frac{{r_{p}^{2} - R^{2} }}{{l^{3} }}, \end{aligned}$$

(38)

The distances between $P\left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right)$ and $Q^{\prime}\left( {r_{q}^{^{\prime}} ,\phi_{q}^{^{\prime}} ,\lambda_{q}^{^{\prime}} } \right)$ is

$$ l = \sqrt {r_{p}^{2} + R^{2} - 2rR\frac{{\vec{r}_{p} \cdot \vec{r}_{q}^{^{\prime}} }}{{\left| {\vec{r}_{p} } \right|\left| {\vec{r}_{q}^{^{\prime}} } \right|}}} = \sqrt {r_{p}^{2} + R^{2} - 2\vec{r}_{p}^{{}} \cdot \vec{r}_{q}^{^{\prime}} } $$

(39)

Thus, the relationship between the observed gravity disturbances at altitude and the counterparts on the geoid in a spherical approximation is given by:

$${{\updelta }}g\left( P \right) = \frac{{R^{2} }}{{4\pi r_{p} }}\iint\limits_{{\sigma _{R} }} {{{\updelta }}g\left( {Q^{'} } \right)\frac{{r_{p}^{2} - R^{2} }}{{l^{3} }}{\rm{d\sigma }}_{R} \left( {Q^{'} } \right)}$$

(40)

Solving $\updelta g\left({Q}^{^{\prime}}\right)$ from $\updelta g\left(P\right)$ is called the DC of the gravity disturbance or the inverse Poisson problem. In general, it belongs to the Fredholm integral equation of the first kind in mathematics, which is ill-posed due to the amplification of noise when dealing with a high-resolution field. It is essential to stabilize the Poisson DC using regularization or smoothing (see e. g. Martinec 1996).

For the DC of airborne data, the inversion is done for a regional area using a regional dataset. It is well-known that the missing data outside the data area (the far-zone) has limited impact on the solution over the area of interest if the data are reduced for the contribution of a global gravity model. Hence, it is not necessary to modify the Poisson kernel in the case of the remove-compute-restore (RCR) scheme. In the case of RCR, a one-degree cap has been shown to be sufficient (Huang 2002).

After selecting an inner zone cap size, it remains to discretize the integral and solve the linear system of equations. The inner zone ($\psi <{\psi }_{0}$) contribution of the (residual) gravity disturbance at point $p$ can be expressed by numerical discretization of the integral in Eq. (40) as.

$$ {\updelta }g_{i}^{p} = \mathop \sum \limits_{j = 1}^{M} B_{ij} {\updelta }g_{j}^{q^{\prime}} $$

(41)

where

$$ \begin{aligned} & B_{ij} \\ & = \left\{ {\begin{array}{ll} {\frac{R}{{4\pi r_{i} }}\sigma_{j} \wp \left( {R,{{\cos}}(\psi_{ij} ),r_{p} } \right)} & {{\text{if}} \psi_{ij} \le \psi_{0} ;{\text{and}} i \ne j} \\ {\frac{R}{r}d^{l} \left( {r_{p} ,\psi_{0} ,R} \right) - \mathop \sum \limits_{j = 1,j \ne i}^{K} B_{ij} } & {{\text{if}} \psi_{ij} \le \psi_{0} ;{\text{and }}i = j} \\ 0 & {{\text{if}}\; \psi_{ij} > \psi_{0} } \\ \end{array} } \right.\end{aligned} $$

(42)

$$ d^{l} \left( {r_{p} ,\psi_{0} ,R} \right) = \frac{1}{2}\left[ {\frac{r + R}{r}\left( {1 - \frac{r - R}{l}} \right)} \right] $$

(43)

and the integral area on a unit sphere is ${\sigma }_{j}={\Delta }_{\phi }{\Delta }_{\lambda }\mathrm{cos}(\phi )$.

Eq. (40) can be expressed in a matrix representation as $={\varvec{g}}$, which is then solved by direct computations, or the following iterations (Huang 2002):

$$ {\varvec{f}} = A{\varvec{f}} + {\varvec{g}} $$

(44)

where $A=I-B$, I being an identity matrix. Eq. (44) shows the sums of the observed downward continued gravity disturbances and correction terms. The iteration in Eq. (44) can start from

$$ {\varvec{f}}_{{}}^{0} = {\varvec{g}} $$

(45)

Followed by, ${{\varvec{f}}}^{1}={\varvec{A}}{{\varvec{f}}}^{0}+{\varvec{g}}$, ${{\varvec{f}}}^{2}={\varvec{A}}{{\varvec{f}}}^{1}+{\varvec{g}}$,…,${{\varvec{f}}}^{{\varvec{i}}}={\varvec{A}}{{\varvec{f}}}^{{\varvec{i}}-1}+{\varvec{g}}$, and ${{\varvec{f}}}^{{\varvec{i}}+1}={\varvec{A}}{{\varvec{f}}}^{{\varvec{i}}}+{\varvec{g}}$.

The dimension of the linear system in Eq. (44) depends on the discretization step and data coverage, and can become very large. In order to avoid solving a huge system of linear equations, a block-wise approach is adopted to solve the DC for a block of 1° × 1° at a time without overlapping. No tile pattern is found in the DC results. Each side of the block is extended at least 1° in spherical distance to avoid edge effects. The iteration stops when the RMS differences between two consecutive solutions are smaller than a specified threshold value. The RMS differences correspond to the solution residuals of the previous iteration, as shown by Kingdon and Vaníček (2011). In this study, the threshold RMS difference and residual are set to 0.001 and 1.0 mGal, respectively, for the convergence of the inverse Poisson method.

1.1.6 Moritz’s analytical downward continuation

Moritz’s ADC method (Moritz 1980, Sect. 45) was originally derived to continue the gravity anomaly from the telluroid to the point level for the determination of the height anomaly by Molodensky’s theory. The DC correction is expressed as the sum of a series of terms. The G1 term represents the first order approximation, i.e., a linear gradient DC correction. When the DC of the data is well-posed, the higher-order terms attenuate rapidly to lead to a convergent correction. Otherwise the series becomes numerically divergent when the DC problem is numerically ill-posed, and must be truncated empirically to produce an approximate result.

In this study, we apply it to the DC of airborne gravity disturbance. The computational equations (Huang 2002, Sect. 5.2) are shown below.

$$ \delta g\left( {r_{g} ,\phi_{p} ,\lambda_{p} } \right) = \mathop \sum \limits_{n = 0}^{\infty } G_{n} $$

(46)

$$ G_{0} \left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right) = \delta g\left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right) $$

(47)

$$ G_{n} \left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right) = - \mathop \sum \limits_{r = 1}^{n} H^{r} L_{r} \left( {G_{n - r} \left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right)} \right) $$

(48)

where the $L$ operator is given by:

$$\begin{aligned}& L\left( {G\left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right)} \right) = \frac{{R^{2} }}{2\pi }\iint\limits_{{\sigma_{R}^{{}} }} {\frac{G\left( Q \right) - G\left( P \right)}{{(2R\sin \left( {\frac{\psi }{2}} \right))^{3} }}d\sigma_{R} \left( Q \right)} \\ & \quad {- \frac{1}{R}G\left( {r_{p} ,\phi_{p} ,\lambda_{p} } \right)} \end{aligned}$$

(49)

Empirically the DC is truncated to order 5 so that a potential divergence manifest itself, and can be controlled numerically for an ill-posed case.

Appendix B

2.1 Method for computing a geoid model from band-limited downward continued airborne gravity data

Using the remove-compute-restore (RCR) Stokes–Helmert scheme, a geoid model is computed from the gravity disturbances given on the surface of the reference ellipsoid by (Huang and Véronneau 2013):

$$ N\left( {\Omega } \right) = N_{0} \left( {\Omega } \right) + N_{1} \left( {\Omega } \right) + N_{{\text{H}}} \left( {\Omega } \right) + \delta N_{{{\text{PITE}}}} \left( {\Omega } \right) $$

(50)

where ${N}_{0}\left(\Omega \right) \mathrm{and} {N}_{1}\left(\Omega \right)$ are degree-0 and -1 terms; the last term stands for the primary indirect topographical effect on the geoid, and the Helmert co-geoid components above degree-1 can be expressed as

$$ N_{{\text{H}}} \left( {\Omega } \right) = N_{{{\text{HRef}}}} \left( {\Omega } \right) + dN\left( {\Omega } \right) $$

(51)

$$ N_{{{\text{HRef}}}} \left( {\Omega } \right) = \zeta_{{{\text{Ref}}}} \left( {\Omega } \right) - \delta N_{{{\text{DTE}}}} \left( {\Omega } \right) $$

(52)

$$ dN\left( {\Omega } \right) = \frac{R}{{4\pi \gamma \left( {\Omega } \right)}}\int\limits_{{{\upsigma }_{{0}} }} {S_{{{\text{MDB}}}} \left( \psi \right)dg_{{\text{H}}} \left( {{\Omega }^{^{\prime}} } \right)d\sigma } $$

(53)

When the residual geoid height is determined to the same spectral band as the reference field, the direct topographical effect (DTE) on the airborne data are computed to the same band as the reference field. Then we have

$$\begin{aligned} dg_{{\text{H}}} \left( {\Omega } \right) &= \left[ {\Delta g_{{{\text{Airborne}}}} \left( {\Omega } \right) - \delta \Delta g_{{{\text{DTE}}}} \left( {\Omega } \right)} \right] \\&- \left[ {\Delta g_{{{\text{Ref}}}} \left( {\Omega } \right) - \Delta g_{{{\text{DTE}}}} \left( {\Omega } \right)} \right] \end{aligned}$$

(54)

or

$$ dg_{{\text{H}}} \left( {\Omega } \right) = \Delta g_{{{\text{Airborne}}}} \left( {\Omega } \right) - \Delta g_{{{\text{Ref}}}} \left( {\Omega } \right) $$

(55)

Therefore, Eq.(53) can be re-written as

$$ \begin{aligned} dN\left( {\Omega } \right) &= d\zeta \left( {\Omega } \right) = \frac{R}{{4\pi \gamma \left( {\Omega } \right)}}\int\limits_{{{\upsigma }_{0} }} {S_{{{\text{MDB}}}} \left( \psi \right)}\\ & \quad{ \times \left[ {\Delta g_{{{\text{Airborne}}}} \left( {\Omega } \right) - \Delta g_{{{\text{Ref}}}} \left( {\Omega } \right)} \right]d\sigma } \end{aligned}$$

(56)

Considering Eq. (51–56) and the degree-0 and degree-1 terms for the geoid height are equal to the same terms for the height anomaly on these reference ellipsoid, Eq. (50) can be re-written as

$$ N\left( {\Omega } \right) = \zeta_{0} \left( {\Omega } \right) + \zeta_{1} \left( {\Omega } \right) + \zeta_{{{\text{Ref}}}} \left( {\Omega } \right) + d\zeta \left( {\Omega } \right) + C_{{\text{T}}} \left( {\Omega } \right) $$

(57)

where

$$ C_{{\text{T}}} \left( {\Omega } \right) = - \delta N_{{{\text{DTE}}}} \left( {\Omega } \right) + \delta N_{{{\text{PITE}}}} \left( {\Omega } \right) $$

(58)

The ${C}_{\text{T}}\left(\Omega \right)$ term is given in (Huang and Véronneau 2015, equations A9–10), which converts the height anomaly evaluated on the reference ellipsoid to the geoid height. Note that Sjöberg (Eq. 23, 2007) derived an equivalent equation to (10) to the 3rd order approximation, and named it the topographic bias with a negative sign.