A new global grid model for the determination of atmospheric weighted mean temperature in GPS precipitable water vapor

Abstract

In ground-based global positioning system (GPS) meteorology, atmospheric weighted mean temperature, $T_\mathrm{m}$, plays a very important role in the progress of retrieving precipitable water vapor (PWV) from the zenith wet delay of the GPS. Generally, most of the existing $T_\mathrm{m}$ models only take either latitude or altitude into account in modeling. However, a great number of studies have shown that $T_\mathrm{m}$ is highly correlated with both latitude and altitude. In this study, a new global grid empirical $T_\mathrm{m}$ model, named as GGTm, was established by a sliding window algorithm using global gridded $T_\mathrm{m}$ data over an 8-year period from 2007 to 2014 provided by TU Vienna, where both latitude and altitude variations are considered in modeling. And the performance of GGTm was assessed by comparing with the Bevis formula and the GPT2w model, where the high-precision global gridded $T_\mathrm{m}$ data as provided by TU Vienna and the radiosonde data from 2015 are used as reference values. The results show the significant performance of the new GGTm model against other models when compared with gridded $T_\mathrm{m}$ data and radiosonde data, especially in the areas with great undulating terrain. Additionally, GGTm has the global mean $\hbox {RMS}_{\mathrm{PWV}}$ and $\hbox {RMS}_{\mathrm{PWV}} /\hbox {PWV}$ values of 0.26 mm and 1.28%, respectively. The GGTm model, fed only by the day of the year and the station coordinates, could provide a reliable and accurate $T_\mathrm{m}$ value, which shows the possible potential application in real-time GPS meteorology, especially for the application of low-latitude areas and western China.

1 Introduction

Water vapor, an important component of the Earth’s atmosphere, plays a key role in global atmospheric radiation, water cycling and energy balance (Wang et al. 2007; Wang and Zhang 2009; Jin and Luo 2009). Understanding the spatial and temporal distribution of water vapor in the atmosphere is of great scientific and practical significance in weather forecasting and climate prediction. Traditional techniques for detecting water vapor mainly include water vapor radiometers, radiosondes and remote sensing. These methods are unable to meet the increasing demands of modern meteorological development, primarily due to the expensive devices, heavy workload and low spatiotemporal resolution.

A global positioning system (GPS) technique has advantages of all-weather conditions, high precision and wide coverage and has been fully operational since 1994. The GPS signal path through the Earth’s atmosphere is influenced by troposphere refraction, resulting in a GPS signal delay, i.e., a tropospheric delay. The tropospheric delay can be expressed as zenith total delay (ZTD) multiplied by the tropospheric mapping function. Meanwhile, the ZTD consists of two parts: zenith hydrostatic delay (ZHD) and zenith wet delay (ZWD). Precipitable water vapor (PWV) is the total precipitation of the vapor content in a unit area cylinder from the ground to the outer layer of the atmosphere (Chen et al. 2014). Bevis et al. (1992) first proposed the concept of GPS meteorology and developed an approach to calculate the crucial parameter, weighted mean temperature ($T_\mathrm{m} )$, for retrieving the PWV from the ZWD of GPS. The ZTD can be calculated precisely using GPS measurements, and the ZHD can also be determined using a tropospheric empirical model. Then, ZWD can be computed by subtracting ZHD from ZTD. Therefore, the GPS technique becomes a powerful method to detect atmospheric water vapor with advantages of high precision, real time and high spatiotemporal resolution. The relationship between ZWD and PWV can be expressed as follows (Askne and Nordius 1987; Bevis et al. 1994; Ross and Rosenfeld 1997):

$$\begin{aligned} \hbox {PWV}={\Pi }\cdot \hbox {ZWD} \end{aligned}$$

(1)

where ${\Pi }$ is a conversion factor, with an expression as follows:

$$\begin{aligned} {\Pi }=\frac{10^{6}}{\rho _\mathrm{w} R_\mathrm{v} \left( {\frac{k_3 }{T_\mathrm{m} }+k_2^{\prime } } \right) } \end{aligned}$$

(2)

where $R_\mathrm{v}$ is the specific gas constant for water vapor; $\rho _\mathrm{w}$ is the density of water; $k_{2}^{\prime }$ and $k_{3}$ are the atmospheric refractivity constants given in Bevis et al. (1994); and $T_\mathrm{m}$ is the weighted mean temperature and the key variable to determine the conversion factor $\Pi$ (Bevis et al. 1992). According to the law of error propagation, the precision of calculated PWV is mainly affected by the error sources of $T_\mathrm{m}$ and ZWD based on Eqs. (1) and (2). Equations (3) and (4) could provide an explanation of how the errors from $T_\mathrm{m}$ and ZWD affect PWV.

$$\begin{aligned} \sigma _{\mathrm{PWV}}= & {} {\Pi }\cdot \sigma _{\mathrm{ZWD}} +\hbox {ZWD}\cdot \sigma _{\Pi } \end{aligned}$$

(3)

$$\begin{aligned} \sigma _{\Pi }= & {} \frac{10^{6}k_3 }{\rho _\mathrm{w} R_\mathrm{v} \left( {k_3 +k_2^{\prime } T_\mathrm{m} } \right) ^{2}}\sigma _{T_\mathrm{m} } \end{aligned}$$

(4)

where $\sigma _{\mathrm{PWV}}$, $\sigma _{\mathrm{ZWD}}$, $\sigma _{T_\mathrm{m}}$ and $\sigma _{\Pi }$ are errors from PWV, ZWD, $T_\mathrm{m}$ and ${\Pi }$, respectively. Currently, the precision of the ZTD product provided by the International GNSS Service (IGS) is better than 5 mm (Byun and Bar-Sever 2009). The ZHD can be accurately estimated using surface pressure measurements or numerical weather models (Hobiger et al. 2008a; Lu et al. 2016; Zhang et al. 2017), while for the application of real-time/near real-time mode, one can use a short-range forecast from a weather model (e.g., the forecast VMF1) to derive ZHD (Hobiger et al. 2008b; Lu et al. 2017). Thus, the ZWD can achieve a remarkable accuracy. If the ZWD has an error of 1 cm, the error of calculated PWV caused by ZWD error is approximately 1.5 mm (Yao et al. 2014a), and the accuracy of $T_\mathrm{m}$ is considered one of the largest error sources in PWV estimation. Bevis et al. (1994) indicated that the relative error of ${\Pi }$ is basically equal to that of $T_\mathrm{m}$. Precisely estimating $T_\mathrm{m}$, therefore, is the key to improving the accuracy of PWV calculation.

Generally, in post-processing mode the $T_\mathrm{m}$ can be exactly determined using atmospheric profiles (such as water vapor pressure and temperature) based on integration, while in real-time/near real-time mode the $T_\mathrm{m}$ can also be derived using fairly accurate atmospheric profiles from numerical weather models (Lu et al. 2017). However, to enhance the efficiency of $T_\mathrm{m}$ calculation and provide convenience for users, an accurate $T_\mathrm{m}$ empirical model is needed to meet such demands. Bevis et al. (1992) conducted an analysis of the correlation between surface temperature ($T_\mathrm{s} )$ and $T_\mathrm{m}$ using 8718 radiosonde profiles in North America, and they found that $T_\mathrm{m}$ and $T_\mathrm{s}$ have a good linear correlation; thus, the Bevis formula, $T_\mathrm{m} =a+bT_\mathrm{s}$, is a commonly used model to estimate $T_\mathrm{m}$. In the Bevis formula, the coefficients of a and b are largely season- and location-dependent and should be estimated using meteorological measurements from specific areas and seasons (Bevis et al. 1992; Ross and Rosenfeld 1997; Emardson et al. 1998; Emardson and Derks 2000; Wang et al. 2011). Some regional linear functions of $T_\mathrm{m}$ and $T_\mathrm{s}$ were established in China (Li et al. 1999; Wang et al. 2011), and the coefficients of these functions were re-estimated using local radiosonde profiles with higher precision than that of the Bevis formula for local use. Similarly, Yao et al. (2014a) analyzed the correlation of $T_\mathrm{m}$ and $T_\mathrm{s}$ around the globe and established a global latitude-related linear regression model based on the gridded $T_\mathrm{m}$ data as provided by TU Vienna (abbreviated as gridded $T_\mathrm{m}$ data) and the European center for medium-range weather forecasts (ECMWF) $T_\mathrm{s}$ data, and the new model can obtain excellent results around the globe. Yao et al. (2014b) studied the relation between $T_\mathrm{m}$ and $T_\mathrm{s}$, water vapor pressure ($e_\mathrm{s} )$ and surface pressure ($P_\mathrm{s} )$ and then developed one/multi-parameter $T_\mathrm{m}$ models that consider seasonal and geographic variations. The two models show better performance around the globe. The regression models can achieve great results if in situ meteorological measurements are available. Unfortunately, meteorological sensors are not installed at most GPS stations, and the linear regression models of $T_\mathrm{m}$ and $T_\mathrm{s}$ become invalid in real-time application of GPS meteorology because the in situ $T_\mathrm{s}$ measurements are unavailable.

In recent years, the PWV retrieved from GPS signal is widely used for the analysis or nowcasting of severe weather conditions such as heavy rainfall, flood, deep convective and typhoon events (Sapucci et al. 2016; Huelsing et al. 2017; Adams et al. 2013; Zhao et al. 2018), because of its high accuracy, high temporal resolution and all-weather conditions. An accurate real-time GPS-PWV estimation is helpful to improve weather for- and now casting. Thus, an empirical model is needed to provide a real-time $T_\mathrm{m}$ value for retrieving real-time GPS-PWV. Emardson and Derks (2000) developed an empirical $T_\mathrm{m}$ model in Europe that considers the latitude and annual variations of $T_\mathrm{m}$, and it could be used largely in real-time GPS meteorology as it is without any meteorological parameters for input. Yao et al. (2015a) established an improved atmospheric conversion factor model in low-latitude China by considering the height variation in the model of Emardson and Derks (2000). Zhang et al. (2017) established two enhanced $T_\mathrm{m}$ models, GM-$T_\mathrm{m}$ (a mixed-grid model) and GH-$T_\mathrm{m}$, using ERA-Interim data sets over China. These two models both show a high accuracy over China. To improve the global applicability of the model, extensive researches have been conducted for global $T_\mathrm{m}$ modeling. Yao et al. (2012) developed the Global Weighted Mean Temperature (GWMT) model based on radiosonde data of 135 global sites, but due to the uneven distribution of the global radiosonde sites (no radiosonde sites in oceanic areas), it cannot obtain sufficient accuracy in the southern Pacific Ocean. To overcome these problems, however, an improved model, GTm-II, was proposed by re-estimating the coefficients using $T_\mathrm{m}$ from the Bevis formula over oceanic areas (Yao et al. 2013), where $T_\mathrm{s}$ is calculated from the global pressure and temperature (GPT) model (Böhm et al. 2007). Chen et al. (2014) proposed an improved $T_\mathrm{m}$ model, GTm_N, using the America National Centers for Prediction (NCEP) reanalysis data, which takes the influence of annual and semi-annual periodicity of $T_\mathrm{m}$ into account. Similarly, Yao et al. (2015b) developed the GWMT-G model by improving the GTm-II using gridded $T_\mathrm{m}$ data. The GTm-II model was further improved (taking semi-annual and diurnal variations into account) into GTm-III (Yao et al. 2014c). Because the lapse rate of $T_\mathrm{m}$, in most cases, is neglected in some empirical models, He et al. (2017) developed an empirical grid $T_\mathrm{m}$ model, GWMT-D, based on the annual, semi-annual and diurnal variations in $T_\mathrm{m}$. Because it takes the lapse rate of $T_\mathrm{m}$ into account, the new model shows excellent performance at different altitudes all over the globe. In addition, the newly released empirical tropospheric delay models, such as the GPT2w model (Böhm et al. 2015) and ITG model (Yao et al. 2015c), also provide a precise $T_\mathrm{m}$ product.

The purpose of this study is to develop a global $T_\mathrm{m}$ empirical model for providing accurate real-time $T_\mathrm{m}$ value to derive an accurate real-time PWV estimate. As previously analyzed, $T_\mathrm{m}$ shows apparent season and location dependence over the globe, and also it presents a high correlation with both latitude and altitude. The model equations of the existing $T_\mathrm{m}$ models, as mentioned, only take one spatial factor into account, i.e., either latitude or altitude. In this study, both latitude and altitude variations are considered in modeling, and a new global grid $T_\mathrm{m}$ model, GGTm, will be developed based on the sliding window algorithm using gridded $T_\mathrm{m}$ data and global ellipsoidal height grid data.

2 Methods for calculating $T_\mathrm{m}$

Two data sets are used to estimate $T_\mathrm{m}$: gridded $T_\mathrm{m}$ data and radiosonde profiles. Gridded $T_\mathrm{m}$ data from 2007–2014 are used to establish the new GGTm model, while both gridded $T_\mathrm{m}$ data and radiosonde profiles in 2015 are used to evaluate the GGTm model as well as the Bevis formula and GPT2w model.

2.1 Computing $T_\mathrm{m}$ based on radiosonde profiles

The radiosonde technique is one of the most common methods to measure meteorological parameters. The radiosonde data mainly contain surface parameters (such as $T_\mathrm{s}$, $P_\mathrm{s}$ and PWV) and pressure level parameters (such as geopotential height H, relative humidity RH and absolute temperature T at every pressure level) at UTC 00:00 and 12:00 every day. Currently, there are in total more than 1500 radiosonde sites distributed over the globe. The radiosonde profiles can be retrieved free from the upper-air archive at the websites of the University of Wyoming (http://weather.uwyo.edu/upperair/sounding.html) or the Integrated Global Radiosonde Archive (IGRA) (http://www.ncdc.noaa.gov/oa/climate/igra/). The $T_\mathrm{m}$ values are obtained through numerical integration using geopotential height, absolute temperature and relative humidity measurements at every pressure level along the zenith direction. The formula to calculate $T_\mathrm{m}$ can be expressed as follows:

$$\begin{aligned} T_\mathrm{m} =\frac{\int \left( {e/T} \right) \hbox {d}H}{\int \left( {e/T^{2}} \right) \hbox {d}H} \end{aligned}$$

(5)

where T is the absolute temperature (K) and e is the water vapor pressure (hPa), as radiosonde profiles provide the relative humidity RH and absolute temperature T (K), which can be used to calculate the e (hPa) in the following formula (Bolton 1980; Wang et al. 2016):

$$\begin{aligned} e= & {} \frac{\text {RH}\cdot e_\mathrm{s} }{100} \end{aligned}$$

(6)

$$\begin{aligned} e_\mathrm{s}= & {} 6.11\times 10^{\left( {\frac{7.5\times T_\mathrm{d} }{237.3+T_\mathrm{d} }} \right) } \end{aligned}$$

(7)

where $e_\mathrm{s}$ is the saturated vapor pressure and $T_\mathrm{d}$ is the atmospheric temperature in Celsius ($T=T_\mathrm{d} +273.15)$. In practice, Eq. (5) will be discretized using the following integral formula:

$$\begin{aligned} T_\mathrm{m} =\frac{\int \left( {e/T} \right) \hbox {d}H}{\int \left( {e/T^{2}} \right) \hbox {d}H}=\frac{\sum _1^n \psi \left( {e_i ,T_i } \right) \Delta h_i }{\sum _1^n \phi \left( {e_i ,T_i } \right) \Delta h_i } \end{aligned}$$

(8)

where $\psi \left( {e_i ,T_i } \right) =\frac{e_i }{T_i }$, $\phi \left( {e_i ,T_i } \right) =\frac{e_i }{T_i^2 }$; $\Delta h_i$ indicates the thickness of the atmosphere at the ith layer (m), n is the number of layers; and $T_i$ and $e_i$ indicate the average temperature and water vapor pressure at the ith layer of the atmosphere, respectively.

2.2 Computing $T_\mathrm{m}$ based on the linear regression formula

Several researchers have noted that the relationship between $T_\mathrm{m}$ and $T_\mathrm{s}$ has a strong linear correlation over the globe (Bevis et al. 1992; Yao et al. 2014a); thus, $T_\mathrm{m}$ can be estimated using a linear function of $T_\mathrm{s}$ for a specific area. Bevis et al. (1994) developed the Bevis $T_\mathrm{m} -T_\mathrm{s}$ relationship using 2 years of radiosonde profiles from 13 radiosonde sites distributed in the United States, and the formula is as follows:

$$\begin{aligned} T_\mathrm{m} =70.2+0.72T_\mathrm{s}. \end{aligned}$$

(9)

According to Eq. (9), $T_\mathrm{m}$ can easily be calculated from $T_\mathrm{s}$, making it the most widely used $T_\mathrm{m}$ model. The relationship between $T_\mathrm{m}$ and $T_\mathrm{s}$ varies with season and location (Emardson and Derks 2000; Wang et al. 2005; Yao et al. 2014a), and the coefficients of the formula are estimated from radiosonde measurements in North America, while its accuracy would be affected when applied globally. Additionally, few GPS stations are equipped with meteorological sensors for measuring $T_\mathrm{s}$, thus limiting its application in real-time GPS meteorology.

2.3 $T_\mathrm{m}$ derived from the GPT2w model

When modeling tropospheric delay or atmospheric weighted mean temperature, the resolution and accuracy of a model will be improved if the model parameters are stored in the form of a grid. Global pressure and temperature 2 wet (GPT2w), an empirical troposphere delay model, was developed by Böhm et al. (2015) using ERA-Interim data sets (the newest products of ECMWF). This empirical model, an improved model for GPT, can provide several tropospheric parameters, such as $T_\mathrm{m}$, pressure, temperature and water vapor pressure with two horizontal resolutions of $1^{{\circ }}\times 1^{{\circ }}$ and $5^{{\circ }}\times 5^{{\circ }}$. $T_\mathrm{m}$ is calculated by the following equation:

$$\begin{aligned} T_\mathrm{m}^{\mathrm{GPT}2\hbox {w}}= & {} A_0 +A_1 \cos \left( {\frac{\hbox {doy}}{365.25}2\pi } \right) \nonumber \\&+B_1 \sin \left( {\frac{\hbox {doy}}{365.25}2\pi } \right) + A_2 \cos \left( {\frac{\hbox {doy}}{365.25}4\pi } \right) \nonumber \\&+B_2 \sin \left( {\frac{\hbox {doy}}{365.25}4\pi } \right) \end{aligned}$$

(10)

where doy is the day of year, and the other coefficients in this equation are determined based on a regular grid of $1^{{\circ }}\times 1^{{\circ }}$ and $5^{{\circ }}\times 5^{{\circ }}$. Thus far, GPT2w is one of the newest released models, which has excellent performance in the computation of tropospheric parameters against other models.

3 Construction of a new global grid $T_\mathrm{m}$ model: GGTm

Extensive studies, as mentioned in Sect. 1, have focused on establishing a regional $T_\mathrm{m}$ model using local radiosonde measurements, which undoubtedly can yield a better performance for local use but is not suitable globally. In recent years, several empirical global $T_\mathrm{m}$ models have been developed, and the parameters of these models are mainly expressed by spherical harmonics or are stored in the form of a grid. A fitting error of the model parameters will be introduced if using the spherical harmonics for global $T_\mathrm{m}$ modeling. For global grid models, i.e., models with the parameters stored in the form of a grid, the realization of the $T_\mathrm{m}$ calculation is usually accomplished by adopting bilinear interpolation after achieving four gridded coefficients around the site. These types of models generally have good results over the globe. As we know, a regional $T_\mathrm{m}$ model should be the recommended model in a specific area due to its superior performance, but how can one realize a regional $T_\mathrm{m}$ model for global application? Greater efforts were made here to derive a new approach.

Fig. 1

The realization process of the sliding window algorithm over the globe (The figure is drawn using Microsoft Visio 2010)

3.1 Introduction of the sliding window algorithm

In this study, a new approach, the sliding window algorithm, will be introduced to solve the aforementioned problems or shortages. Yao et al. (2014a) conducted an analysis of the correlation between $T_\mathrm{m}$ and $T_\mathrm{s}$ over the globe using a sliding window algorithm. On a global scale, it can be divided into numerous regular areas (i.e., each area denotes one sliding window) of the same size by employing the sliding window algorithm.

In the sliding window algorithm, there are two key steps that need to be employed. The first step requires dividing the globe into a grid. In this work, the global gridded $T_\mathrm{m}$ data with a horizontal resolution of $2.5^{\circ }\times 2^{\circ } \left( {\hbox {lon}. \times \hbox {lat}.} \right)$ are employed to compute the new model parameters. Hence, the globe can be divided into regular grids with the same quantities and horizontal resolution of gridded $T_\mathrm{m}$ data. The second step requires determining the size of the sliding window. The determination of window size is dependent on several factors, such as guaranteeing that the quantity of windows over the globe is an integer, maintaining continuity between windows and ensuring the computability of model parameters in each window. Considering these factors, we take the size of the sliding window as $5^{\circ }\times 4^{\circ } \left( {\hbox {lon}. \times \hbox {lat}.} \right)$, as an example, to describe the realization process of the sliding window algorithm, as shown in Fig. 1. For each window, data at the $3\times 3$ grid points in the sliding window are used to estimate model parameters, which will then be taken as results of the center point of the sliding window. First, calculate the model parameters of the sliding window $N_{1}$ at the upper-left corner as the results of the center point of window $N_{1}$ (the red rectangle denotes the size of the sliding window, and the red dot denotes the center point of each window, as shown in Fig. 1); then, moving the sliding window by two points along the latitude, calculate the model parameters of the sliding window $N_{2}$ as the results of the center point of window $N_{2}$, continuing until the last sliding window $N_{k}$ of this latitude. Moving the sliding window by two points along the longitude, and then calculate the model parameters of all sliding windows at this latitude according to the methods as previously mentioned, continuing until the model parameters of all sliding windows over the globe are calculated. Finally, a new global grid with a resolution of $5^{\circ }\times 4^{\circ } \left( {\hbox {lon}. \times \hbox {lat}.} \right)$, which consists of red dots and blue dashed lines as shown in Fig. 1, will be created.

3.2 Expression of GGTm

There have been extensive studies conducted on the spatiotemporal characteristic of $T_\mathrm{m}$, and the empirical $T_\mathrm{m}$ model was developed based on its characteristics. The characteristics of the time series of $T_\mathrm{m}$ mainly show annual and semi-annual variations (Wang et al. 2005; Chen et al. 2014; Böhm et al. 2015). While the diurnal variation in $T_\mathrm{m}$ is generally small, with mean amplitudes of 0.5–1.5 K over most land areas and less than 0.5 K over most oceans (Wang et al. 2005), it is also season- and location-dependent and is difficult to model precisely using simple trigonometric functions (He et al. 2017). For the spatial characteristic of $T_\mathrm{m}$, the model equations of the existing $T_\mathrm{m}$ models, as mentioned in Sect. 1, only take one spatial factor into account (i.e., either latitude or altitude); in addition, $T_\mathrm{m}$ is slightly affected by longitude (Yao et al. 2014b). As previously discussed, the GGTm considers annual and semi-annual variations and takes both latitude and altitude variations into account in the model expression of each window. The model expression of each window is as follows:

$$\begin{aligned} T_\mathrm{m} \left( {\varphi _U ,\lambda _U ,h,\text {doy}} \right)= & {} \alpha _1 \left( {\varphi _i ,\lambda _i } \right) \nonumber \\&+\alpha _2 \left( {\varphi _i ,\lambda _i } \right) \cdot \varphi _U +\alpha _3 \left( {\varphi _i ,\lambda _i } \right) \cdot h\nonumber \\&+\alpha _4 \left( {\varphi _i ,\lambda _i } \right) \cdot \cos \left( {2\pi \frac{\text {doy}}{365.25}} \right) \nonumber \\&+\alpha _5 \left( {\varphi _i ,\lambda _i } \right) \cdot \sin \left( {2\pi \frac{\text {doy}}{365.25}} \right) \nonumber \\&+\alpha _6 \left( {\varphi _i ,\lambda _i } \right) \cdot \cos \left( {4\pi \frac{\text {doy}}{365.25}} \right) \nonumber \\&+\alpha _7 \left( {\varphi _i ,\lambda _i } \right) \cdot \sin \left( {4\pi \frac{\text {doy}}{365.25}} \right) \nonumber \\ \end{aligned}$$

(11)

where doy is the day of the year; $\left( {\varphi _i ,\lambda _i } \right)$ are the latitude (in degree) and longitude (in degree) of the center point of the ith window, respectively; $\varphi _U , \lambda _U$, and h are the latitude (in degree), longitude (in degree) and height (in meter) of the target location, respectively; $\alpha _1$ is the average value of $T_\mathrm{m}$; $\alpha _2$ is the latitude correction; $\alpha _3$ is the height correction; and ($\alpha _4$, $\alpha _5 )$ and ($\alpha _6$, $\alpha _7$) are the amplitudes of annual and semi-annual periodicity, respectively. As shown in Eq. (11), these coefficients can be estimated by using the least square adjustment based on at least seven grid-point-specific data sets of each window. According to the factors determining window size as described in Sect. 3.1, in this work, we finally chose the size of the window as $5^{\circ }\times 4^{\circ } \left( {\hbox {lon}. \times \hbox {lat}.} \right)$. The coefficients of GGTm, hence, are also expressed in the form of a $5^{\circ }\times 4^{\circ } \left( {\hbox {lon}. \times \hbox {lat}.} \right)$ grid. Thus, we can divide the globe into 3240 regular windows (grid points).

Here, we introduce the use of GGTm. Users only need to provide the doy and target position and then find the nearest grid point between the target position and grid points of the model parameters based on the latitude and longitude of the target location. The $T_\mathrm{m}$ values at the target position can be calculated using the nearest gridded coefficients and Eq. (11).

3.3 Data source for establishing GGTm

The website of global geodetic observing system (GGOS) Atmosphere (a server at TU Vienna) can provide global atmospheric delay grid data (such as ZHD, ZWD and $T_\mathrm{m} )$ at a spatial resolution of $2.5^{\circ }\times 2^{\circ } \left( {\hbox {lon}.\times \hbox {lat}.} \right)$ and with a temporal resolution of 6 h (at UTC 00:00, 06:00, 12:00 and 18:00) (http://ggosatm.hg.tuwien.ac.at). These global surface grid products are calculated from ECMWF reanalysis data and all correspond to the ellipsoidal heights; the global ellipsoidal height grid data are also provided by GGOS Atmosphere with a spatial resolution of $2.5^{\circ }\times 2^{\circ } \left( {\hbox {lon}. \times \hbox {lat}.} \right)$. Yao et al. (2014c) conducted an accuracy test for gridded $T_\mathrm{m}$ data using 341 globally distributed radiosonde sites; the results suggest that the gridded $T_\mathrm{m}$ data are highly reliable and precise and can be used as a data source for establishing the GGTm. In this work, the GGTm model parameters are estimated using gridded $T_\mathrm{m}$ data from 2007 to 2014 and global ellipsoidal height grid data based on the least square method. The parameters of GGTm are all stored in the form of a $5^{\circ }\times 4^{\circ } \left( {\hbox {lon}. \times \hbox {lat}.} \right)$ grid over the globe.

4 Validation of GGTm

To assess the performance of the new GGTm model, we compared it to the widely used Bevis formula ($T_\mathrm{m} =70.2+0.72T_\mathrm{s} )$ and the newest release of the GPT2w model using the same reference $T_\mathrm{m}$ values derived from gridded $T_\mathrm{m}$ data and radiosonde profiles. The GPT2w model has two horizontal resolutions of $1^{{\circ }}\times 1^{{\circ }}$ and $5^{{\circ }}\times 5^{{\circ }}$. To describe them conveniently, we defined these two resolutions as GPT2w-1 and GPT2w-5, respectively. In this work, bias and root mean square error (RMS) were considered as the criteria for accuracy assessment and are calculated by the following equations:

$$\begin{aligned}&\hbox {bias}=\frac{1}{N}\sum _{i=1}^N \left( {T_\mathrm{m}^{M_i } -T_\mathrm{m}^{R_i } } \right) \end{aligned}$$

(12)

$$\begin{aligned}&\hbox {RMS}=\sqrt{\frac{1}{N}\sum _{i=1}^N \left( {T_\mathrm{m}^{M_i } -T_\mathrm{m}^{R_i } } \right) ^{2}} \end{aligned}$$

(13)

where $T_\mathrm{m}^{M_i }$ is the $T_\mathrm{m}$ value calculated by the model, $T_\mathrm{m}^{R_i }$ is the reference $T_\mathrm{m}$ value derived from gridded $T_\mathrm{m}$ data or radiosonde profiles, and N is the number of samples.

4.1 Comparison to gridded $T_\mathrm{m}$ data

In this section, for the global gridded $T_\mathrm{m}$ data from 2015, there are a total of 13,195 $T_\mathrm{m}$ grids, and these are used as the reference values to assess the four models. The global gridded $T_\mathrm{m}$ data with a temporal resolution of 6 h (at UTC 00:00, 06:00, 12:00 and 18:00) and the $T_\mathrm{m}$ of each grid point at the same time are calculated using the GGTm, GPT2w-1, GPT2w-5 and Bevis models; thus, the daily bias and RMS can be obtained for these models. For the Bevis formula ($T_\mathrm{m} =70.2+0.72T_\mathrm{s} )$, the $T_\mathrm{s}$ measurements are unavailable in oceanic areas. The $T_\mathrm{s}$ value can thus be derived from empirical GPT series models (Böhm et al. 2007, 2015). Here, we regard the gridded $T_\mathrm{m}$ data from 2015 as the reference values to analyze the impact of $T_\mathrm{s}$ values calculated from the GPT, GPT2w-5 and GPT2w-1 models on the Bevis formula. The statistical results of the bias and RMS of different models in 2015 are shown in Table 1.

Table 1 Statistical results of the impact of $T_\mathrm{s}$ derived from the GPT, GPT2w-5 and GPT2w-1 models on Bevis formula calculation using gridded $T_\mathrm{m}$ data from 2015

Table 1 shows that both the bias and RMS of $T_\mathrm{m}$ derived from Bevis&GPT2w-1 are the smallest; thus, GPT2w-1 can provide the most precise $T_\mathrm{s}$ value for the Bevis formula compared to that of the other two models. Therefore, we chose the $T_\mathrm{s}$ derived from GPT2w-1 for the calculation of the Bevis formula. As previously described, the estimated $T_\mathrm{m}$ values from these models are compared to the gridded $T_\mathrm{m}$ data. The statistical results of the bias and RMS of the different models tested by gridded $T_\mathrm{m}$ data in 2015 are shown in Table 2 and Fig. 2.

Table 2 shows that for GGTm, the bias is − 0.05 K and ranges from − 2.24 to 3.48 K; the RMS is 2.89 K and ranges from 0.86 to 5.67 K. In terms of RMS, GGTm performs an approximately 0.5 K (16%) and 0.4 K (12%) improvement against GPT2w-5 and GPT2w-1 over the globe, respectively; GPT2w-1 shows slightly better than GPT2w-5, while the Bevis formula shows the largest RMS value. Figure 2 reflects larger errors in parts of western China, the Himalayas, Antarctic areas, Chile, Peru and Greenland for the GPT2w-5. Relative to GPT2w-5, GPT2w-1 improves the spatial resolution of the model parameters, larger errors are still observed in parts of Greenland, Chile, western China and the Antarctic, which are mainly affected by the complex topography because GPT2w does not take the height variation of $T_\mathrm{m}$ into account. While the GGTm shows stable and accurate results in $T_\mathrm{m}$ estimation over the globe. Therefore, GGTm significantly outperforms GPT2w in these areas with great undulating terrain. For the Bevis formula, it shows strong negative bias in low latitudes and positive bias in the Antarctic regions; similarly, a larger RMS exists in parts of Greenland and western China, especially south of $60^{\circ }\hbox {S}$ latitude toward the Antarctic region and parts of the oceanic areas. The Bevis formula only uses radiosonde profiles in North America for modeling. In addition, the Bevis formula does not consider the vertical lapse of $T_\mathrm{m}$, which results in a worse performance when used in these areas. In all, GGTm shows significant superiority against other models and is without large error in estimating $T_\mathrm{m}$ on a global scale.

Table 2 Statistical results of different models validated by using gridded $T_\mathrm{m}$ data from 2015

To analyze the stability and accuracy of different models on different days of the year (DOY), the daily bias and RMS at all grids of each model were statistically analyzed, and the results varied with DOY as shown in Fig. 3.

From Fig. 3, the Bevis formula shows significant positive bias all year, larger bias and RMS values are observed during both the spring and autumn months, and it has the largest bias and RMS among all the models. The other three models show obvious negative bias during both spring and winter days and positive bias during summer days, while for the RMS, these three models are without obvious seasonal variation. In all, the GGTm shows the best accuracy (in terms of RMS) during the whole year-long period.

Fig. 2

Global distribution of bias and RMS in different models tested by using gridded $T_\mathrm{m}$ data from 2015

Fig. 3

Results of different models tested by gridded $T_\mathrm{m}$ data during different days of the year

4.2 Comparison to radiosonde data

A total of 412 globally distributed radiosonde stations are selected. The distribution of the selected radiosonde stations is shown in Fig. 4. There are more radiosonde stations distributed in the Northern Hemisphere than there are in the Southern Hemisphere. As described in Sect. 2.1, the $T_\mathrm{m}$ values computed from radiosonde profiles using the integration method at UTC 00:00 and 12:00 every day in 2015 are treated as the reference values to validate the new GGTm, GPT2w-5, GPT2w-1 and Bevis $T_\mathrm{m} -T_\mathrm{s}$ formula ($T_\mathrm{s}$ is in situ surface temperature derived from the radiosonde site). All the 412 selected radiosonde stations contain available data of over half of the year (the abnormal radiosonde profiles are removed) to ensure the reliability of validation. The statistical results of bias and RMS of the different models are shown in Table 3 and Fig. 5.

Fig. 4

Global distribution of selected 412 radiosonde stations for the validation of GGTm

Table 3 Statistical results of different models validated using radiosonde data from 2015

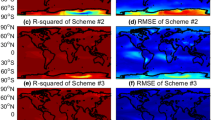
From Table 3, the Bevis formula has the largest RMS of 4.10 K and the smallest absolute bias of 0.02 K. The RMS is 4.03 K for GPT2w-5 and 3.82 K for GPT2w-1. Both the largest negative bias and RMS are observed for GPT2w-5, meaning that GPT2w-1 shows relative stable values than those of GPT2w-5 through improving the spatial resolution of the model. GGTm has the smallest RMS of 3.54 K and ranges from 1.14 to 6.90 K, which performs an approximately 0.5 K (12%) and 0.3 K (8%) improvement against both GPT2w-5 and GPT2w-1 over the globe, respectively. Therefore, GGTm shows excellent performance against other models over the globe. Figure 5 shows that all of these models can achieve relatively high accuracy (in terms of RMS) over low latitude areas; the reasons for this will be analyzed later. The Bevis formula shows an obvious cold bias in low latitudes and a warm bias in Russia as well as western areas of China, but it presents relatively high accuracy in North American areas, where the radiosonde sites are more involved in the Bevis modeling. For GPT2w-5, both larger bias and RMS are observed in parts of Northwest China and Chile. In addition, both GPT2w-5 and GPT2w-1 show larger cold bias in parts of Northwest China and western North America; relative to GGTm, GPT2w-1 still shows larger RMS values in parts of Northwest China and Northwest South America. While for GGTm, both bias and RMS are small and stable on a global scale. Additionally, the results of bias and RMS at all selected radiosonde sites of each model were further statistically analyzed, and the error distribution and statistics of the different models are shown in Figs. 6 and 7.

Fig. 5

Global distribution of bias and RMS of different models tested using radiosonde data from 2015

Fig. 6

Histogram of bias of different models tested by using radiosonde data from 2015

Figure 6 shows that the bias of GGTm is highly concentrated around zero; although the bias of the Bevis formula is relatively concentrated around zero, the number of strong negative biases is approximately equal to the number of positive biases, resulting in a small mean bias, while the biases of both GPT2w-5 and GPT2w-1 are relatively scattered (most are negative biases), which indicates that the $T_\mathrm{m}$ derived from the GPT2w model has few systematic deviations compared to those of the radiosonde data. From Fig. 7, we can see more intuitively that the RMS of the Bevis formula comprises 77% below 5 K and only 21% below 3 K, and it has a large proportion (7%) over 6 K. For GPT2w-5, the RMS comprises 78% (83% for GPT2w-1) below 5 K and only 26% (28% for GPT2w-1) below 3 K, and the proportion over 6 K is higher than that of GPT2w-1, but the proportion below 2 K is slightly greater than that of GPT2w-1, while the RMS of GGTm accounts for the both the largest proportion of below 5 K (90%) and below 3 K (32%) among the four models. For the proportion of below 5 K, that of GGTm increased by 12 and 7% over GPT2w-5 and GPT2w-1, respectively, while for the proportion of below 3 K, that of GGTm increased by 6 and 4% over GPT2w-5 and GPT2w-1, respectively. In addition, GGTm has the smallest proportion over 6 K (2%) and the largest proportion below 2 K (11%). For the proportion of over 6 K, that of GGTm decreased by 5 and 2% over GPT2w-5 and GPT2w-1, respectively, while for the proportion of below 2 K, that of GGTm increased by 3 and 5% over GPT2w-5 and GPT2w-1, respectively. Therefore, it further illustrated that the GGTm model performs excellent performance against other models over the globe.

Fig. 7

Proportional distribution of RMS values of different models tested using radiosonde data from 2015

To analyze the bias and RMS of the seasonal variations in different models, the daily results at all selected stations of each model were statistically analyzed, and the bias and RMS values of different models varying with DOY are shown in Fig. 8.

Fig. 8

Results of different models tested using radiosonde data during different days of the year

From Fig. 8, the biases of GGTm are generally the smallest and without obvious seasonal variation. Both GPT2w-5 and GPT2w-1 show negative bias during most DOY, and relatively strong negative bias existed during spring and winter days, further indicating that the $T_\mathrm{m}$ calculated from the GPT2w model has some systematic errors, while the Bevis formula shows obvious positive bias during the spring and negative bias during the summer. In terms of RMS, all of these models have obvious seasonal variations, which show relative larger RMS values during the spring and winter and smaller RMS values during summer days. Because most of the selected radiosonde stations are in the middle and high latitudes of the Northern Hemisphere, $T_\mathrm{m}$ changes are small during the summer and larger during the winter. The GGTm shows the highest accuracy and stability during the whole year period. For the other models, however, the stability and accuracy of the models vary at different DOY. To further illustrate the performance of the GGTm model in terms of the seasonal variation, the results of the monthly bias and RMS in different models are shown in Fig. 9.

From Fig. 9a, one can see that both GPT2w-5 and GPT2w-1 present larger negative monthly bias among 12 months, while GGTm shows a stable and smaller monthly bias. From January to June as well as October to December, GGTm performs significant advantages against both GPT2w-5 and GPT2w-1 in terms of monthly bias. Figure 9b shows that the GGTm still has excellent performance against other models in terms of monthly RMS. GGTm performs an approximately 0.5 and 0.3 K improvement over the GPT2w-5 and GPT2w-1, respectively. Therefore, GGTm performs excellent performance over other models in terms of the monthly or seasonal variation.

Fig. 9

Monthly performance of different models tested using radiosonde data

The $T_\mathrm{m}$ has strong correlations with both altitude and latitude. To investigate the relations between altitude and the bias and RMS, 412 radiosonde stations were sorted into six categories based on altitude, i.e., lower than 500, 500–1000, 1000–1500, 1500–2000, 2000–2500, and above 2500 m. The results of the bias and RMS in each altitude range are shown in Fig. 10.

Figure 10 shows that in general, both the bias and RMS increase with increasing altitude in the Bevis formula; although those of both GPT2w-5 and GPT2w-1 are not obvious, larger bias and RMS still existed in high-altitude areas for GPT2w-5 and GPT2w-1. The GGTm significantly outperforms all the other models in high-altitude areas, especially in the areas with altitude of above 2500 m, which performs an approximately 2.5, 1.3 and 1.2 K improvement (in terms of RMS) over the Bevis formula, GPT2w-5 and GPT2w-1, respectively. In contrast, the GGTm has both the smallest bias and RMS in each altitude range and small differences among them at different altitude ranges, verifying excellent performance of the GGTm as compared to that of the other three models.

Fig. 10

Results of bias and RMS of the different models at different altitude ranges

Furthermore, the relations between latitude and the bias and RMS values in different models were analyzed. To visualize the variation in the bias and RMS, 412 radiosonde stations were sorted in terms of latitude in 15$^{\circ }$ intervals. The results are shown in Fig. 11.

From Fig. 11, one can see that the Bevis formula has both relatively larger bias and RMS at most of the latitude ranges, and the bias of the Bevis formula increases with increasing latitude in the Northern Hemisphere. In addition, the Bevis formula, GPT2w-5 and GPT2w-1 show obvious negative biases at low and middle latitudes, especially in the high-latitude areas of the Southern Hemisphere, where larger bias and RMS were observed for Bevis formula and GPT2w-5. The accuracy (in terms of RMS) of the Bevis formula at middle latitudes ($30^{\circ }\hbox {N}{-} 60^{\circ }\hbox {N})$ in the Northern Hemisphere is slightly higher than that of both GPT2w-5 and GPT2w-1. These results reflect the advantage of the Bevis formula in those regions where the radiosonde data are involved in the modeling. The best performance of all models is obtained at low latitudes ($30^{\circ }\hbox {S}{-} 30^{\circ }\hbox {N})$, where the amplitudes of $T_\mathrm{m}$ are much smaller than those at high latitudes (Yao et al. 2014b). However, the GGTm performs excellent performance against other models in the areas with the latitude range from $15^{\circ }\hbox {S}$ to $45^{\circ }\hbox {N}$. In all, GGTm shows best accuracy and stability over other models.

Fig. 11

Results of bias and RMS of different models at different latitude ranges

Fig. 12

The theoretical RMS of PWV resulting from different models using radiosonde data from 2015

Fig. 13

The theoretical relative error of PWV resulting from different models using radiosonde data from 2015

4.3 Impact of $T_\mathrm{m}$ on GPS-PWV

In GPS meteorology, the goal of determining $T_\mathrm{m}$ is to map the ZWD onto GPS-PWV. Most of the GPS stations are not equipped with meteorological sensors as the initial purpose of these was mainly for space geodetic studies. In addition, the GPS stations and radiosonde stations are not co-located, and thus, it is difficult to make a comprehensive and global assessment of the impact of $T_\mathrm{m}$ on GPS-PWV. Several investigations have been conducted to analyze the impact of $T_\mathrm{m}$ on its resultant GPS-PWV in terms of theoretical function (Wang et al. 2005, 2016; He et al. 2017). In this paper, a similar method is employed to analyze the impact of $T_\mathrm{m}$ on GPS-PWV, and the commonly used relationship of the RMS between $T_\mathrm{m}$ and PWV can be calculated using the following:

$$\begin{aligned} \frac{\hbox {RMS}_{\mathrm{PWV}} }{\hbox {PWV}}= & {} \frac{\hbox {RMS}_{\Pi } }{{\Pi }}=\frac{k_3 \hbox {RMS}_{T _\mathrm{m} } }{\left( {\frac{k_3 }{T_\mathrm{m} }+k_2^{\prime } } \right) T_\mathrm{m}^2 }\nonumber \\= & {} \frac{k_3 }{\left( {\frac{k_3 }{T_\mathrm{m} }+k_2^{\prime } } \right) T_\mathrm{m} }\cdot \frac{\hbox {RMS}_{T _\mathrm{m} } }{T_\mathrm{m} } \end{aligned}$$

(14)

where $\hbox {RMS}_{\mathrm{PWV}}$ is the error in PWV, $\hbox {RMS}_{T _\mathrm{m} }$ is the error in $T_\mathrm{m}$ achieved from Sect. 4.2, PWV and $T_\mathrm{m}$ are set to annual mean values and are also obtained from Sect. 4.2, $\hbox {RMS}_{\mathrm{PWV}} /\hbox {PWV}$ is defined as the relative error of PWV, and $\hbox {RMS}_{\mathrm{PWV}}$ and $\hbox {RMS}_{\mathrm{PWV}} /\hbox {PWV}$ are used to evaluate the impact of the errors in $T_\mathrm{m}$ on its resultant GPS-PWV. Some radiosonde stations with insufficient PWV data have been removed; finally, the 403 globally distributed radiosonde stations are selected. The global distributions of the theoretical results of $\hbox {RMS}_{\mathrm{PWV}}$ and $\hbox {RMS}_{\mathrm{PWV}} /\hbox {PWV}$ in different models are shown in Figs. 12 and 13 and Table 4.

Figure 12 shows the global distribution of $\hbox {RMS}_{\mathrm{PWV}}$ in 2015. The four models all show smaller $\hbox {RMS}_{\mathrm{PWV}}$ in both the Antarctic and Arctic regions, where the annual mean values of PWV are only approximately 3.0 and 8.0 mm in our experiment, respectively. According to Eq. (14), smaller annual mean $\hbox {RMS}_{\mathrm{PWV}}$ values can be achieved, although the smaller annual mean values of $T_\mathrm{m}$ are also observed in these regions (approximately 255 and 260 K, respectively). For the Bevis and GPT2w-5 models, the larger $\hbox {RMS}_{\mathrm{PWV}}$ values are observed at low latitudes ($30^{\circ }\hbox {S}{-} 30^{\circ }\hbox {N})$, especially in parts of Southern Asia for the Bevis formula, where it has the largest $\hbox {RMS}_{\mathrm{PWV}}$ value of approximately 1.0 mm. At these low latitudes, both the largest annual mean PWV and $T_\mathrm{m}$ values of approximately 37.3 mm and 286 K occur for those two models in our experiment, respectively; similarly, though the smaller annual mean RMS values of $T_\mathrm{m}$ are obtained (described in Sect. 4.2) in these areas, there still resulting in larger annual mean $\hbox {RMS}_{\mathrm{PWV}}$ values as a contribution of larger PWV values. In contrast, for the GPT2w-1 and GGTm models, which show relatively smaller annual mean $\hbox {RMS}_{\mathrm{PWV}}$ values. From Fig. 13, one can see that the GGTm, GPT2w-5 and GPT2w-1 models all show smaller $\hbox {RMS}_{\mathrm{PWV}} /\hbox {PWV}$ at low latitudes, especially from south of $15^{\circ }$ latitude to the north of $15^{\circ }$ latitude, where the Bevis formula shows relatively larger $\hbox {RMS}_{\mathrm{PWV}} /\hbox {PWV}$ than that of the other three models. The smallest RMS of $T_\mathrm{m}$ and the largest $T_\mathrm{m}$ values are obtained in these regions, resulting in the smaller annual mean $\hbox {RMS}_{\mathrm{PWV}} /\hbox {PWV}$ values. For the Bevis formula, GPT2w-5 and GPT2w-1, relatively larger $\hbox {RMS}_{\mathrm{PWV}} /\hbox {PWV}$ values are still observed in parts of western China, while GGTm shows relative stable performance over the globe. From Table 4, the $\hbox {RMS}_{\mathrm{PWV}}$ values of the GGTm are less than 0.65 mm and with a global mean $\hbox {RMS}_{\mathrm{PWV}}$ value of 0.26 mm; in terms of $\hbox {RMS}_{\mathrm{PWV}} /\hbox {PWV}$, GGTm has a global mean value of 1.28% and ranges from 0.40 to 2.53%. As the GGTm is an empirical global model, which can provide an accurate Tm values for retrieving accurate real-time PWV. Thus, GGTm has possible potential applications in the real-time analysis or nowcasting of severe weather conditions such as heavy rainfall, flood, and typhoon events, especially for the application of low-latitude areas and western China.

Table 4 Statistical results of theoretical RMS and relative error of PWV resulting from different models validated by using radiosonde data from 2015

5 Conclusions

$T_\mathrm{m}$ is a crucial parameter for detecting GPS-PWV. A reliable and accurate $T_\mathrm{m}$ empirical model is needed for the application of real-time PWV sounding, especially when in situ meteorological observations are unavailable. $T_\mathrm{m}$ shows significant season and location dependence on a global scale. The existing $T_\mathrm{m}$ empirical models do not completely account for variations in both altitude and latitude. In this research, both latitude and altitude variations were considered in the modeling, and a new global grid $T_\mathrm{m}$ model, namely GGTm, was developed based on a sliding window algorithm using global gridded $T_\mathrm{m}$ data and global ellipsoidal height grid data.

The accuracy and stability of the GGTm were validated using global gridded $T_\mathrm{m}$ data and globally distributed radiosonde station data from 2015, and detailed comparisons to the Bevis, GPT2w-5 and GPT2w-1 models were also conducted. GGTm shows significant accuracy and stability among the four models over the globe when compared using global gridded $T_\mathrm{m}$ data, especially in the areas with highly undulating terrain, while the Bevis formula shows the worst results and obvious systematic bias. When compared using radiosonde data, GGTm still maintained excellent performance against other models, with an annual mean bias and RMS of 0.03 and 3.54 K, respectively. GPT2w-1 showed slightly better performance than GPT2w-5, but both models had significant systematic bias, especially in high-altitude areas due to the GPT2w does not take the height variation of $T_\mathrm{m}$ into account, while the Bevis formula still presented the worst result. Additionally, the impact of $T_\mathrm{m}$ on GPS-PWV was analyzed, showing that the global mean values of $\hbox {RMS}_{\mathrm{PWV}}$ and $\hbox {RMS}_{\mathrm{PWV}} /\hbox {PWV}$ are 0.26 mm and 1.28% for GGTm, respectively.

In this experiment, the Bevis formula and GPT2w models show a relatively poorer ability to calculate the $T_\mathrm{m}$ in high-altitude areas, as both models do not consider the altitude variation in modeling; GPT2w-1, to a certain extent, can mitigate this effect by improving the spatial resolution of model parameters, but larger errors are still existed in the areas with the altitude of above 2500 m. GGTm has the ability to provide excellent accurate and reliable $T_\mathrm{m}$ value over the globe and requires no in situ meteorological parameters as inputs, making the GGTm model more powerful and practical for calculating $T_\mathrm{m}$, and it will have wide applicability in real-time GPS-PWV sounding, especially for the application of low-latitude areas and western China. In future work, we will mainly focus on considering diurnal variation in the model, analyzing the impact of the window size on the model, and combining multi-source data in the modeling.