The impact of common versus separate estimation of orbit parameters on GRACE gravity field solutions

Abstract

Gravity field parameters are usually determined from observations of the GRACE satellite mission together with arc-specific parameters in a generalized orbit determination process. When separating the estimation of gravity field parameters from the determination of the satellites’ orbits, correlations between orbit parameters and gravity field coefficients are ignored and the latter parameters are biased towards the a priori force model. We are thus confronted with a kind of hidden regularization. To decipher the underlying mechanisms, the Celestial Mechanics Approach is complemented by tools to modify the impact of the pseudo-stochastic arc-specific parameters on the normal equations level and to efficiently generate ensembles of solutions. By introducing a time variable a priori model and solving for hourly pseudo-stochastic accelerations, a significant reduction of noisy striping in the monthly solutions can be achieved. Setting up more frequent pseudo-stochastic parameters results in a further reduction of the noise, but also in a notable damping of the observed geophysical signals. To quantify the effect of the a priori model on the monthly solutions, the process of fixing the orbit parameters is replaced by an equivalent introduction of special pseudo-observations, i.e., by explicit regularization. The contribution of the thereby introduced a priori information is determined by a contribution analysis. The presented mechanism is valid universally. It may be used to separate any subset of parameters by pseudo-observations of a special design and to quantify the damage imposed on the solution.

1 Introduction

Gravity models of the Earth at monthly or even sub-monthly intervals, which monitor the slowly varying gravity signal of the cryosphere and of hydrological or other geophysical origin, are the major result of the Gravity Recovery And Climate Experiment (GRACE, Tapley et al. 2004). Such models are provided by the official processing centers, namely the German Research Centre for Geosciences (GFZ, Dahle et al. 2012) and the Center for Space Research (CSR, Bettadpur 2012). The Jet Propulsion Laboratory (JPL, Watkins and Yuan 2012) serves as a backup and computes models for validation. Models of different time spans are also provided by a number of alternative sources, e.g., the Department for Theoretical Geodesy of the University of Bonn (ITG, Kurtenbach et al. 2009), the Groupe de Recherche de Geodesie Spatiale (GRGS, Bruinsma et al. 2010), the Delft Institute for Earth-oriented Space Research (DEOS, Liu et al. 2010), and the Astronomical Institute of the University of Bern (AIUB, Meyer et al. 2012).

The estimation of gravity field parameters from observations of the GRACE satellite mission is a non-linear parameter estimation process. The classical approach solves it as a generalized orbit determination problem. Arc-specific orbit parameters and general model parameters, e.g., the spherical harmonic coefficients of the gravity field are solved simultaneously in one parameter estimation process.

The quality of the gravity field models is not necessarily characterized by their spatial resolution, which is limited by the density of the ground track pattern during the corresponding time intervals (Weigelt et al. 2013), but by the error and signal content of the spherical harmonic coefficients (in the spectral domain), or equivalently, the grid values of geoid heights or quantities derived therefrom (in the spatial domain).

The attempt can be made to suppress the noise in a post-processing step by filtering (in the spectral or in the spatial domain). Numerous papers dedicated to advanced filtering methods were published since and even prior to the availability of GRACE data (e.g., Wahr et al. 1998; Han et al. 2005; Swenson and Wahr 2006; Davis et al. 2008). The critical point of filtering is, however, how much signal is accidentally damaged by the filtering process. More recent publications on the topic (Kusche 2007; Klees et al. 2008) make use of approximations of the signal covariance to protect the signal during the filtering process.

On the other hand, the estimation process can be stabilized and the noise suppressed by regularization, i.e., by the introduction of a priori knowledge via pseudo-observations of the model parameters (Tikhonov and Arsenin 1977). The a priori knowledge is weighted relative to the original observations and the optimal balance between a priori and observed signal content may be found, e.g., by variance components (Koch and Kusche 2002). For the estimation of monthly gravity models from GRACE data regularization has been applied, e.g., during phases of orbit resonance resulting in sparse ground track coverage.¹

But there exists another way to suppress noise in the monthly solutions that has been applied by GFZ in their original RL05. The signal to noise ratio of the monthly gravity fields profits from the separate estimation of orbit and gravity field parameters in combination with the introduction of a time variable a priori model. It has already been noted by Zhao et al. (2010) that a separate estimation of the K-band instrument parameters leads to a reduction of low frequency noise, compared to a common estimation of instrument parameters and gravity field coefficients. Zhao et al. (2010) also showed in a simulation study that time variable signal in the gravity field solution is absorbed in case of separate estimation of K-band instrument parameters and gravity field coefficients. Note that all experiments of Zhao et al. (2010) were based on static a priori models of the gravity field. In this study, we do not estimate K-band instrument parameters at all, but focus on the empirical orbit parameters. We also consider time variable a priori models. We describe the mechanism of hidden regularization taking place when the estimation of gravity coefficients is separated from that of the orbit parameters. We detail the effects on the monthly fields and quantify the impact of the a priori model on the solutions.

Meanwhile, a number of high-resolution static gravity field models with deterministically modeled time variable coefficients (trend, once-per-year and twice-per-year variations) were published [EIGEN-GRGS,² EIGEN-6S/C,³ AIUB-GRACE03S (see footnote 3)]. For the GFZ-RL05 monthly gravity models (Dahle et al. 2012), EIGEN-6C was used in the a priori force model. Arc- and instrument-specific parameters were then determined in a first step and the resulting orbits were kept fixed, while in a second step corrections to the a priori gravity field parameters were estimated. Thus, correlations between gravity field and arc/instrument specific parameters were ignored. The signal absorbed by the accelerometer biases was irrevocably lost for the resulting monthly gravity models (Meyer et al. 2015). When comparing trend estimates derived from the original GFZ-RL05 with results from other time series (see Fig. 1) one finds significant differences. We interpret these differences as the result of a hidden regularization. When this problem became obvious, GFZ replaced its entire RL05 product suite by the RL05a⁴ product suite which avoided the problems described before.⁵

Fig. 1

Monthly geoid variations (in equivalent water heights) and fitted trends near the East coast of Greenland

The frequent accelerometer biases set up for GFZ-RL05 may be considered as pseudo-stochastic orbit parameters that are the key element of the Celestial Mechanics Approach (CMA, Beutler et al. 2010a, b). The CMA represents a dynamic approach (e.g., Tapley 1973) that unifies deterministic and stochastic elements. It was adapted to reproduce the processing scheme of GFZ. Experiments were performed to illustrate the mechanism of the hidden regularization process. The piecewise constant accelerations set up by both, the GFZ and AIUB, turned out to be of critical importance. If these arc-specific parameters are determined in a first step using a given a priori force model and are introduced as fixed in a consecutive step to determine the parameters of the gravity model, the resulting gravity field coefficients heavily depend on the used a priori force model.

This is illustrated strikingly by $C_{20}$ which is not well determined from GRACE data (e.g., Meyer et al. 2010). For the experiment, these a priori values were either taken from AIUB-GRACE03S (known to contain a $C_{20}$-estimate of reduced quality) or derived from satellite laser ranging (SLR) analysis (Sośnica 2014). While in a common estimation the monthly $C_{20}$-values, independently of their a priori value, show a “wild” but identical scatter, they closely follow the a priori model in the case of fixing the orbit parameters (see Fig. 2). The same is true for the arbitrarily chosen coefficient $C_{44}$ (see Fig. 3) which is well determined by GRACE and is correctly recovered, independently of the a priori model, as long as orbit and model parameters are estimated together. As soon as the orbit is fixed, the a priori values are closely reproduced (even if they were artificially degraded for the sake of the experiment). In both cases, the signal in contradiction to the a priori model is to a large extent absorbed by the arc-specific parameters as soon as the orbits are fixed and consequently lost for the gravity field recovery in the second step. The same happened in original GFZ-RL05, where the a priori model for $C_{20}$, derived from SLR, was reproduced by the monthly estimates, as already noted by Chambers and Bonin (2012).

Fig. 2

Impact of the a priori gravity field model on the estimation of the spherical harmonic coefficient $C_{20}$ (ill determined by K-band) when either estimating orbit and gravity parameters together or separating the gravity field estimation step by first fixing the orbit parameters

Fig. 3

Impact of the a priori gravity field model on the estimation of the spherical harmonic coefficient $C_{44}$ (well determined by GRACE) when either estimating orbit and gravity parameters together or separating the gravity field estimation step by first fixing the orbit parameters

Several sets of monthly models were computed, differing by the a priori gravity model used, by the empirical parameterization of the orbits and by the solution strategy applied (common versus separate estimation of orbit and gravity model). The resulting monthly models are analyzed spectrally and spatially. Finally, a formalism is derived to equivalently replace the indirect regularization, resulting from the suppression of correlations in the case of separate estimation, by the introduction of pseudo-observations, i.e., by explicit regularization. The influence of the a priori information on the resulting gravity models can then be determined via contribution analysis (Sneeuw 2000).

The paper is structured as follows: Sect. 2 provides an introduction to the CMA and the classical processing scheme at AIUB. Section 3 explains how the quality of the resulting gravity fields is evaluated. In Sect. 4, the formalism of fixing the orbit parameters is detailed in the framework of the CMA and its effect on the gravity model parameters is illustrated with several experiments. In Sect. 5, the estimation process is reformulated as explicit regularization and the contributions of the real and the pseudo-observations to the resulting monthly gravity models are determined. In Sect. 6, finally the relevance of the findings for the practice of gravity model estimation from low Earth orbiting satellites (LEOs) is discussed.

2 Orbit and gravity field determination with the CMA

The CMA is based on a generalized orbit improvement process starting from an a priori gravity model as the main part of the force model. In the course of the orbit adjustment, arc-specific parameters as well as corrections to the a priori force model are simultaneously estimated by a least-squares adjustment process. The kinematic satellite positions (including covariance information) resulting from a GPS single point positioning procedure are used as observations (Jäggi et al. 2011b). The K-band range-rates (KRR) derived from the ranges which are observed with micrometer accuracy by the inter-satellite link between the GRACE satellites (Dunn et al. 2003) are also used as observations. Both observation types are combined on the level of daily normal equations (NEQs).

A key feature of the CMA is the extensive use of pseudo-stochastic orbit parameters ${x_o}$, i.e., piecewise constant accelerations at constant time intervals, set up in the course of the orbit determination to absorb deficiencies of the a priori force model (Jäggi et al. 2006). As long as the orbit is in the center of interest, the gravity model parameters are normally not solved for and their correlations with the pseudo-stochastic parameters do not play a role. When the interest is on the spherical harmonic coefficients (SHC) of the gravity model, care has to be taken not to absorb gravity signal by the pseudo-stochastic parameters. This may be achieved to a wide extent by limiting the absolute size of and the variability between these parameters by absolute and relative constraints. The constraining is realized via pseudo-observations

$$\begin{aligned} {x_o}={0} \end{aligned}$$

(1)

for absolute constraints or

$$\begin{aligned} \Delta {x_o}={0} \end{aligned}$$

(2)

for relative constraints. All orbit and force model parameters are set up together in one common parameter estimation process.

The CMA processing strategy for GRACE is detailed in Jäggi et al. (2011a). Pseudo-stochastic accelerations in radial, cross-track and quasi along-track direction are set up at 15-min time intervals. For numerical reasons, the corresponding arc-specific parameters of GRACE A and B are transformed to their mean values and half their differences (Beutler et al. 2010a). The mean values, mainly determined by the GPS observable, are typically constrained to zero at the level of $3\times 10^{-9}$ m/s$^2$. The differences, mainly determined by the ultra-precise K-band observable, are constrained even tighter by a factor of 100 (both values were determined empirically). The arc-specific parameters are of no special interest and are pre-eliminated (implicitly solved) from the combined GPS$+$K-band daily NEQs. Unless a back-substitution process is performed, they are not further available, while the correlations to the SHC are implicitly kept in the NEQ system. The resulting reduced daily NEQs are accumulated to monthly NEQs and inverted to result in monthly estimates of the Earth’s gravity field.

The choice of the a priori gravity model deserves a few remarks. In the case of the determination of a static model to high degree and order, the result is virtually independent of the a priori model, as long as the model is solved at least up to the same degree and order as the a priori model and the range of linearity is not left. Due to the pseudo-stochastic parameters of the CMA the danger to leave the range of linearity is rather small and all the static gravity models generated at AIUB so far (Jäggi et al. 2010, 2011a) were computed starting from EGM96. As soon as monthly models are determined, the resolution of the solved for SHC needs to be limited to a lower degree of, e.g., 60 (due to the reduced ground track coverage of the globe) while the observations are still sensitive to a much higher degree. In order not to bias the solved for SHC, a good a priori model thus has to be used (at least for the SHC not determined in the estimation process).

The first time series computed at AIUB applying the strategy outlined above was published as AIUB-RL01 (Meyer et al. 2012). The release of revised GRACE observation data and updated background models made a re-processing necessary. The new time series is based on:

• GRACE L1B-RL02 data,

• a priori gravity model AIUB-GRACE03S up to 160$^{\circ }$ including time variations up to 30$^{\circ }$,

• ocean tide model EOT11A (Savcenko and Bosch 2011) up to 100$^{\circ }$ including admittances (Mayer-Gürr, personal communication), and

• atmosphere and ocean de-aliasing products AOD1B-RL05 (Flechtner and Dobslaw 2013) up to 100$^{\circ }$.

Monthly models to full degree and order 90 (labeled “AIUB-RL02p”) were computed for comparison with GFZ-RL05. For analyses in this article, different sets of solutions were set up to a reduced degree and order of 60 [the reduced models derived analogously to AIUB-RL02p are labeled “AIUB-RL02p(60)”].

3 Methods for comparison of monthly gravity fields

The signal content and the noise are measures of the quality of the monthly gravity models. To assess the noise, we study areas where little time variable signal is expected. We compute monthly geoid heights at $3^{\circ }$-grid points all over the globe and subtract a static mean geoid. Because most of the signal observed by GRACE is confined to the continents (hydrology, ice mass change), we cut out the continents. To further avoid leakage from the continental signal, we significantly shrink the oceans by $9^{\circ }$ (three grid points) along all coasts. Then, we derive monthly standard deviations (STD) from all remaining ocean grid points, weighted by the cosine of the latitude. Finally, we estimate and subtract seasonal variations. Note that the resulting measure for the noise nevertheless is a pessimistic one, because all other variations of oceanic origin are treated as noise.

Figure 4 shows the noise levels derived in this manner from AIUB-RL01 and RL02p, GFZ-RL04 and the original RL05. The quality gain from GFZ-RL04 to RL05 and from AIUB-RL01 to RL02p is clearly visible. All shown results are unfiltered, AIUB-RL02p and GFZ-RL05 were truncated at 60$^{\circ }$ to correspond to GFZ-RL04, for AIUB-RL01 (the original maximum order is 45) a special version to full degree and order 60 was used. Despite the re-processing, the noise level of the original GFZ-RL05 could not be reached by AIUB-RL02p. This fact originally motivated the studies presented in this article.

Fig. 4

Weighted STD over the oceans of different releases of monthly gravity field models

To assess the signal content in the monthly models, we select regions where strong variations are expected. One of our test locations is situated in the center of South America near the Amazon basin ($\phi =-16.5^\circ$ and $\varLambda =304.5^\circ$), the other near the East coast of Greenland ($\phi =73.5^\circ$ and $\varLambda =322.5^\circ$). To keep things simple, we do not evaluate river basins or ice sheets but simply calculate the mean around the chosen location, weighted by a Gaussian bell curve with a half-width radius of 300 km. Because the variations are predominantly related to the hydrological cycle (in the Amazon) or the ice mass change (in Greenland), we express them in equivalent water heights (Wahr et al. 1998).

Finally, one may calculate difference degree variances between monthly solutions and a static or time variable reference gravity model. In this way, the consistency between the models is visualized degree wise. Note that a gain in consistency is not necessarily also a gain in quality, since the difference degree variances also include residual gravitational variations. Moreover, with the classical degree variances no statement related to spherical harmonic order is possible. Nevertheless, they are very helpful to visualize regularization effects (where artificially the consistency with an a priori gravity model is enforced via pseudo-observations).

4 Separate estimation of orbit and gravity model parameters

The observation equations for the parameter estimation problem including orbit ${x_o}$ and gravity model parameter ${x_g}$ may be written as follows

$$\begin{aligned} \left[ \begin{array}{c} {l}\\ {p} \end{array} \right] = \left[ \begin{array}{l@{\quad }l} {A_{lo}}&{}{A_{lg}}\\ {A_{po}}&{}{A_{pg}} \end{array} \right] \left[ \begin{array}{c} {x_o}\\ {x_g} \end{array} \right] + {\epsilon } \end{aligned}$$

(3)

with observations ${l}$ (kinematic orbits, K-band), pseudo-observations ${p}$ (constraints) and noise ${\epsilon }$. The design matrix ${A}$ consists of four sub-matrices containing the partial derivatives of the observations (subscript $l$) or pseudo-observations (subscript $p$) w.r.t. the orbit (subscript $o$) or gravity model (subscript $g$) parameters. The constraining is done according to Eq. (1). In the original CMA, the gravity model parameters are not constrained and consequently ${A_{pg}}={0}$. The set of orbit parameters ${x_o}$ consists of the initial state of the satellites (the regular arc-length is 24 h) and the stochastic accelerations. Note that the initial state is not constrained either. The formalism used throughout Sects. 4 and 5 is nevertheless valid, if we simply choose the weights of the corresponding pseudo-observations $x_o=0$ to be zero (this is assumed without further notice whenever the constraining of orbit parameters is concerned).

The normal equations take the form

$$\begin{aligned} \left[ \begin{array}{l@{\quad }l} {N_{oo}}&{}{N_{og}}\\ {N_{og}}^\mathrm{T}&{}{N_{gg}} \end{array} \right] \left[ \begin{array}{c} {x_o}\\ {x_g} \end{array} \right] = \left[ \begin{array}{c} {b_o}\\ {b_g} \end{array} \right] , \end{aligned}$$

(4)

where the normal matrix ${N}$ consists of four sub-matrices, related either to orbit or gravity model parameters or to both parameter types. The right-hand sides ${b_o}$ and ${b_g}$ contain the products of the sub-matrices of the design matrix with the corresponding weighted observations.

In the case of pre-elimination of the arc-specific parameters, as normally done in the CMA approach, the first line of Eq. (4) is solved for ${x_o}$ and inserted into the second line, leading to

$$\begin{aligned} ({N_{gg}} - {N_{og}}^\mathrm{T}{N_{oo}}^{-1}{N_{og}}) {x_g} = {b_g} - {N_{og}}^\mathrm{T}({N_{oo}}^{-1}{b_o}). \end{aligned}$$

(5)

The dimension of the resulting NEQs is decreased by the number of arc-specific parameters ${x_o}$, while the impact of these parameters is correctly taken into account when solving for the gravity field model parameters.

Let us now break with the processing scheme described in Sect. 2 and fix the orbit parameters to previously determined values while estimating corrections to the parameters of the force model. This may be done easily by explicitly solving for the arc-specific parameters using the a priori force model and consequently deleting them from the NEQ system [instead of the implicit solution described by Eq. (5)]. The subsystem

$$\begin{aligned} {N_{oo}}{x'_o} = {b_o} \end{aligned}$$

(6)

is solved independently from the remaining part of Eq. (4) and the parameters ${x'_o}$ are introduced in the following as known. Note that in this case the correlations between orbit and gravity model parameters are ignored and that ${x'_o}$ strongly depend on the a priori gravity model. The remaining NEQ system

$$\begin{aligned} {N_{gg}}{x'_g} = {b_g} - {N_{og}}^\mathrm{T}{x'_o} = {b_g} - {N_{og}}^\mathrm{T}({N_{oo}}^{-1}{b_o}) \end{aligned}$$

(7)

necessarily leads to different solutions ${x'_g}$ for the gravity model parameters than the solution ${x_g}$ of Eq. (5). The right-hand side of Eq. (7), however, is identical to Eq. (5).

To study the effect of different stochastic orbit parameterizations on the solution, one may reduce the sampling of the piecewise constant accelerations on NEQ level. This transformation may be performed efficiently by stacking of consecutive accelerations.

Table 1 Overview over the different experiments and their labels in Figs. 5 and 6, the treatment of the orbit parameters (common/separate estimation), the sampling of the pseudo-stochastic accelerations, the a priori model used (AIUB-GRACE03S static part only or including time variations) and the corresponding subplot in Fig. 7

Fig. 5

Weighted STD over the oceans of monthly gravity field models. In the case of fixed orbit parameters the sampling of the pseudo-stochastic accelerations is noted in the legend (15 min/60 min). The attributes static/timvar. refer to the a priori gravity model used

Fig. 6

Time variable signal in monthly gravity field models in central South America

Fig. 7

Equivalent water heights of a monthly solution with 15-min pseudo-stochastic accelerations (top); stoch. acc. stacked to 60 min and fixed (second row); 15 min stoch. acc. fixed (third row); a priori model (bottom). All figures were Gauss-filtered with 300 km half-width radius. The numeric values give the weighted STD over the oceans and the max. difference to the a priori model over land for the first three plots

The influence of fixing the orbit on the gravity model parameters is remarkable. Figure 5 illustrates the results of a number of experiments in terms of the noisiness of the resulting monthly models. All sets of solutions were set up to a maximum degree and order of 60, the different experiments and corresponding labels are summarized in Table 1. Starting from the daily gravity field NEQs [corresponding to the solution denoted “AIUB-RL02p(60)” in all figures], which still include the 15-min pseudo-stochastic accelerations, monthly solutions were computed where the orbit parameters were fixed (denoted “15 min timevar.” in Figs. 5, 6). In another series of monthly solutions, the pseudo-stochastic accelerations were stacked to 60 min prior to fixing (denoted “60 min timevar.”). To study the role of the a priori gravity model in the case of fixed pseudo-stochastic orbit parameters, the latter experiment was repeated on the basis of the static part of AIUB-GRACE03S only (denoted “60 min static”).

All series of solutions with fixed orbit parameters show a significant reduction of the noise over the oceans. In Sect. 5, the process of fixing the orbit parameters is reformulated as explicit regularization which explains the observed “de-noising”. But regularization has the side effect of damping all signals not contained in the a priori knowledge. We therefore show in Fig. 6 the corresponding signal strength at our example location in South America. The effect of fixing the orbit to the static a priori gravity field is clearly visible. Obviously, part of the signal is absorbed by the pseudo-stochastic orbit parameters. In contrast, not much damping can be observed when the time variable part of AIUB-GRACE03S is introduced a priori and the pseudo-stochastic parameters are stacked to 60 min. In the case of 15-min pseudo-stochastic accelerations, the damping effect starts to become more prominent even when the time variable a priori model is used.

Figure 7 gives a visual impression of the de-noising effect of fixing the orbit parameters. It shows the equivalent water heights for an example month (March 2008), chosen because of the generally low noise of GRACE monthly models in the mid of the mission period and the absence of data artifacts (gaps, outliers, etc.) which may influence the solution. The figure on top shows our standard solution “AIUB-RL02p(60)”. Below, the corresponding solutions with fixed pseudo-stochastic accelerations at 60- and 15-min intervals (both with time variations included in the a priori gravity field model) are provided. Finally, the deterministic a priori time variations of AIUB-GRACE03S are shown for comparison. To quantify the de-noising effect, the weighted STD over the oceans is given below the first three figures. To illustrate the damping of signal the maximum difference to the a priori model over the continents is provided as well. It is obvious that with even denser stochastic parameterizations than 15-min accelerations the signal will be perfectly reduced to the time variations included in the a priori model.

By fixing the orbit parameters, the subsequently estimated gravity model parameters are less noisy, but the signal content may be significantly dampened depending on the chosen orbit parameterization. The relevant factors governing the process of de-noising and signal damping are

• the rate of solved for pseudo-stochastic orbit parameters and

• the quality of the a priori model.

They have to be chosen carefully when aiming at separating the gravity field estimation from the orbit determination process.

5 Regularization and contribution analysis

The implicit regularization, obviously taking place when orbit and gravity model determination is separated, does not allow quantifying the influence of the a priori information on the determined SHC. A quantification is possible, however, by adopting a contribution analysis (Sneeuw 2000) for all types of explicit observations and pseudo-observations. We therefore reformulate the process of fixing the orbit parameters by introduction of pseudo-observations and demonstrate that it is equivalent to an explicit regularization.

In the classic CMA approach, the pseudo-stochastic orbit parameters are constrained via pseudo-observations of the orbit parameters

$$\begin{aligned} {p}={A_{po}}{x_o}+{\epsilon }, \end{aligned}$$

(8)

where ${p}={0}$ and ${A_{po}}$ for absolute constraining reads as

$$\begin{aligned} {A_{po}}={I} \end{aligned}$$

(9)

with identity matrix ${I}$; weight matrix ${P_{oo}}$ in this case is a diagonal matrix with elements

$$\begin{aligned} P_{oo}=\sigma _0^2/\sigma _p^2, \end{aligned}$$

(10)

where $\sigma _0$ is the mean error a priori and $\sigma _p$ is the imposed standard deviation of the pseudo-observations that represents the level of constraining. The resulting contribution to the normal equation matrix consists only of diagonal terms $\sigma _0^2/\sigma _p^2$. It is superimposed to the normal equation matrix related to the orbit parameters

$$\begin{aligned} {N^{*}_{oo}}={N_{oo}}+{P_{oo}}. \end{aligned}$$

(11)

In the case of separate estimation of orbit and gravity model parameters, we require that the gravity field coefficients can be determined independently of the orbit parameters that have been solved beforehand, i.e.,

$$\begin{aligned} {N_{og}}{x_g}={0}. \end{aligned}$$

(12)

We set up a new condition equation

$$\begin{aligned} {A_{pg}}{x_g}={0}, \end{aligned}$$

(13)

where ${A_{pg}}$ is defined according to Eq. (12) by

$$\begin{aligned} {A_{pg}}={N_{og}}. \end{aligned}$$

(14)

Equation (13) is nothing else but a set of more general pseudo-observations that constrain the gravity field parameters ${x_g}$. The number of these new pseudo-observations equals the number of orbit parameters ${x_o}$. In analogy to Eq. (8), they are equal to $0$ and only alter ${N_{gg}}$ on the left-hand side of Eq. (4):

$$\begin{aligned} {N^{*}_{gg}}={N_{gg}}+{N_{og}}^\mathrm{T}{P_{oo}}{N_{og}}. \end{aligned}$$

(15)

If we define the weight matrix ${P_{oo}}$ of the new pseudo-observations as

$$\begin{aligned} {P_{oo}}={N_{oo}}^{-1} \end{aligned}$$

(16)

and subsequently pre-eliminate the orbit parameters according to Eq. (5):

$$\begin{aligned} ({N^{*}_{gg}}-{N_{og}}^\mathrm{T}{N_{oo}}^{-1}{N_{og}}){x_g}'={b_g}-{N_{og}}^\mathrm{T}({N_{oo}}^{-1}{b_o}), \end{aligned}$$

(17)

the constraint from Eq. (15) on ${N^{*}_{gg}}$ balances the corrective term $-{N_{og}}^\mathrm{T}{N_{oo}}^{-1}{N_{og}}$ to the left-hand side of Eq. (17) caused by the pre-elimination. The resulting equation

$$\begin{aligned} {N_{gg}}{x_g}'={b_g}-{N_{og}}^\mathrm{T}({N_{oo}}^{-1}{b_o}) \end{aligned}$$

(18)

is identical to Eq. (7). The right-hand sides of Eqs. (5) and (18) look similar, but they differ by the important fact, that in the latter case [and in Eq. (7)] the corrective term to ${b_g}$ solely depends on a priori information. The newly introduced pseudo-observations do not truly de-correlate orbit ${x_o}$ and model parameters ${x_g}$. The solutions ${x_g}$ and ${x_g}'$ will differ.

While for the separation of orbit and model parameters it is in principle not necessary to introduce both types of pseudo-observations (for orbit or model parameters) simultaneously, it turns out, that for practical reasons (for the sake of invertibility of ${N_{oo}}$) this may be necessary. Note that the level of constraining in the case of orbit parameters may be adapted (by adapting $\sigma _p$), while for orbit fixing the weight matrix ${P_{oo}}$ of the pseudo-observations for gravity model parameters is fixed. This reflects the fact that one cannot fix the orbit parameters just slightly.

The contribution of an observation type to the estimated unknown parameters is measured by the so-called contribution numbers (Sneeuw 2000), which assume values between 0 (no contribution) and 1 (the parameter is solely determined by the observation type under question). The contribution numbers for observation type $j$ are the diagonal elements of the resolution matrix ${R_j}$:

$$\begin{aligned} {R_j}={N}^{-1}{N_j}. \end{aligned}$$

(19)

In our case, $j$ is replaced either by observations $l$ [e.g., kinematic orbits (subscript GPS) and/or KRR] or by pseudo-observations $p$ (related to orbit and/or force model parameters). The normal matrix ${N}$ consists of the sum of the observation type-specific contributions ${N_j}$:

$$\begin{aligned} {N}=\sum _j{N_j} \end{aligned}$$

(20)

If the individual ${N_j}$ are scaled relative to each other, then the scaling factors have to be applied in both Eqs. (19) and (20).

Let us first compute the relative contribution of the kinematic orbits versus KRR observations in a standard monthly solution (with 15-min pseudo-stochastic accelerations). We are solely interested in the contribution of observations to the gravity parameters ${x_g}$. But because it is not possible to pre-eliminate the orbit parameters from ${N_{\mathrm{KRR}}}$ due to singularities (KRR is only sensitive to the differences in the orbit parameters of GRACE A and B, see Sect. 2), we have to keep the orbit parameters in the NEQ system and explicitly solve for them after combination with ${N_{\mathrm{GPS}}}$ (sensitive to the orbit parameters). Kinematic orbits are usually down-weighted relative to KRR in the standard CMA solutions by a factor of $10^{-10}$ (determined empirically), the combined NEQ system thus is computed by ${N}=1\times 10^{-10}\ {N_{\mathrm{GPS}}}+{N_{\mathrm{KRR}}}$. We again select March 2008 as an example (the observations do not enter the contribution analysis, but the orbit geometry is taken into account).

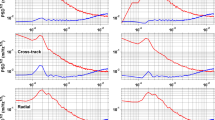
Figure 8 shows the well-known pattern of sensitivity of the GPS observable (i.e., the kinematic orbits) for sectorial SHC (see Beutler et al. 2010b) and for orders related to orbit resonance (15, 31, 46). Consequently, the contribution of KRR (Fig. 9) to these coefficients is reduced. The sensitivity of the kinematic orbits for resonant orders is only visible, as long as we heavily constrain the pseudo-stochastic accelerations. If we loosen the constraints, the orbits will be essentially decomposed into 15-min short-arcs (without loosing continuity in orbital position and velocity) and the relation to orbit resonance is lost (not shown).

Fig. 8

Coefficient wise contribution of the kinematic orbits to SHC of a combined GPS/KRR monthly solution, left part of the triangle the SIN, right the COS coefficients

Fig. 9

Contribution of KRR to a combined GPS/KRR monthly solution (pseudo-stochastic accelerations constrained to ${\pm }3\times 10^{-9}$ m/s$^2$)

Let us now fix the orbit by the introduction of pseudo-observations [Eq. (13)]. We are facing several practical problems: First, the part of the normal matrix related to orbit parameters ${N_{oo}}$ is singular. This problem is home-made, because the pseudo-stochastic accelerations are set up at constant time intervals regardless of data gaps. We cure the problem by the introduction of very loose constraints on the orbit parameters (to a level of ${\pm }3\times 10^{-6}$ m/s$^2$). At this point, we meet the second problem. As mentioned above in the case of fixing the orbits the orbit parameters depend mainly on the a priori force model. This is also true, if we realize the orbit fixing via pseudo-observations. As opposed to the approach in the classical CMA we therefore have to constrain the orbit parameters not to zero, but to the a priori values estimated in the first a priori orbit determination based on the a priori force model.

The last hurdle is encountered when adding the contribution of the pseudo-observations to ${N_{gg}}$ according to Eq. (15). The resulting normal matrix is singular by construction, because the frequencies of the pseudo-stochastic accelerations in ${N_{og}}^\mathrm{T}{N_{oo}}^{-1}{N_{og}}$ overlap the spectrum of the SHC in ${N_{gg}}$ (the pseudo-stochastic accelerations cannot be separated from the corresponding SHC). The same problem is met in the case of daily pre-elimination of the orbit parameters, but is aggravated here, because we have to handle the parameters of the entire month at once. Again, constraining the pseudo-stochastic accelerations helps and again the level of ${\pm }3\times 10^{-6}$ m/s$^2$ turned out to be sufficient for a stable solution.

Figure 10 shows the contribution of the a priori information, entering the system via the pseudo-observations of $x_g$. Obviously, the coefficients related to low frequencies, i.e., the low harmonic SHC and the sectorial ones, which are also sensed at low frequencies by near polar orbiting satellites, are affected most. For these coefficients, the contribution of the a priori model is about $50\,\%$. Repeating the experiment with fewer pseudo-stochastic accelerations (at 60 instead of 15-min intervals) the contribution of the a priori model (see Fig. 11) is reduced to fewer coefficients (related to even lower frequencies).

Fig. 10

Contribution of a priori model to a regularized monthly solution (pseudo-stochastic orbit parameters set up at 15-min intervals and fixed)

Fig. 11

Contribution of a priori model to a regularized monthly solution (pseudo-stochastic orbit parameters set up at 60-min intervals and fixed)

To verify the validity of our regularization approach, we compute the actual solutions (not necessary for the contribution analysis). We show the results in terms of difference degree variances w.r.t. AIUB-GRACE03S, evaluated at the epoch of our example month, and compare them to the results achieved with separate estimation of orbit and gravity model. Figure 12 shows the degree variances of the standard solution as well as of the two solutions with fixed orbit parameters and time variable a priori model (with 15- or 60-min pseudo-stochastic accelerations). For both solutions with fixed orbits, the gain in consistency is clearly visible throughout all degrees. The degree variances do not tell whether this gain is due to a noise reduction or a signal damping.

Fig. 12

Difference degree variances of monthly gravity field models (March 2008) relative to AIUB-GRACE03S (including time variable terms up to 30$^{\circ }$)

Replacing the step of fixing the orbit parameters by the explicit regularization of the gravity model parameters (as detailed above), we end up with very similar results. The small differences may be explained by the extra regularization of the pseudo-stochastic accelerations we had to apply to invert the NEQs.

Actually, in the differences between a monthly gravity field obtained with fixed orbit parameters versus one obtained by a common solution, many more SHC are affected than predicted by our contribution analysis (Fig. 13). Most of the observed differences in Fig. 13 may be attributed to observation noise that is not taken into account by the contribution analysis. The coefficients beyond order 45 are effectively dominated by noise (Meyer et al. 2012). The differences in the low degree and sectorial SHC predicted by Fig. 10 are also visible in Fig. 13, so in this point the predictions of our contribution analysis are verified.

Fig. 13

Differences per SHC between standard solution and fixed orbit solution (March 2008), pseudo-stochastic parameters set up at 15-min intervals (color scale logarithmic)

The vertical stripes, prominent near resonant orders 15, 31 and 46, can be observed whenever comparing gravity models computed with different processing strategies. Seo et al. (2008) explain them by aliasing of non-tidal geophysical model errors. But in fact the linear dependence between coefficients of different degree at near resonant orders predicted by first-order perturbation theory (e.g., Gooding and King-Hele 1989) and the signal absorption on the same frequencies by the stochastic orbit parameters that is discussed in Meyer et al. (2015) for the case of circular orbits could also play a role.

6 Discussion

Having detailed the effect of fixing the arc-specific parameters during the gravity estimation step, either explicitly ignoring the correlations with the gravity model parameters (Sect. 4), or indirectly via the introduction of pseudo-observations (Sect. 5), we still have to answer the question, whether this regularization is justified.

The noise reduction certainly is welcome, the damping of signal content certainly is not. The situation is aggravated, because, as revealed by the contribution analysis, signals are dampened in particular at low frequencies, where according to the sensitivity analyses (e.g., Wahr et al. 1998) most time variable signal has to be expected.

The regularization effect on the gravity parameters when fixing the orbit parameters is hidden and difficult to assess. As shown in Sect. 5, it can be replaced by an explicit regularization by the introduction of pseudo-observations of a special design, but even in this case the regularization cannot be controlled, because the weighting of the pseudo-observations is given and may not be chosen freely.

The contribution analysis applied in Sect. 5 is a pre-mission analysis tool showing the sensitivity of the SHC to certain observation types. It does not take into account the observation noise or aliasing by model errors. Moreover, our analysis is based on the assumption that ${N_{gg}}$ is not impaired by the effect of orbit resonance. The validity of this assumption is not guaranteed and more coefficients than predicted may be affected by the hidden regularization.

In any case, the consequences of a regularization, hidden or not, for the estimated monthly models are obvious. Any gravity signal not contained in the a priori model is dampened. Singular events like an exceptional flood or drought are not reproduced by the monthly estimates to their full extent. An accelerating ice mass loss in Greenland may become invisible. As long as the gravity field is in the center of interest, we therefore strongly advise against a separate estimation of dynamic orbits and force model parameters.