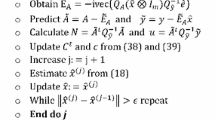1 Introduction

The well-known least-squares (LS) has been widely used for adjusting the Gauss–Markov model (GMM) in geodesy and related fields. The usual prerequisite for applying this linear LS technique within the GMM is that the coefficient matrix is error free. However, this assumption is not always satisfied in many cases, for example, in regression problems (e.g., Schaffrin and Wieser 2008; Grafarend and Awange 2012; Amiri-Simkooei et al. 2014) as well as in geodetic transformations (e.g., Teunissen 1988; Schaffrin and Felus 2008; Cai and Grafarend 2009). In mathematics, if the coefficient matrix is affected by random errors, this nonlinear LS estimation within the GMM containing such a coefficient matrix is called total least-squares (TLS) within the errors-in-variables (EIV) model (see Golub and Van Loan 1980; Van Huffel and Vandewalle 1991). It is acknowledged that in Teunissen (1988) it is the first time that an EIV or TLS problem was formulated and solved in the geodetic literature. Moreover, the solution given was an exact, non-iterative, analytical solution with an outstanding example of the planar similarity transformation. From a geodetic point of view, this is in fact (Teunissen 1988) as well as Teunissen (1985) reformulated the EIV model to the standard nonlinear Gauss–Markov model, and therefore they have the advantage that all available knowledge (numerical and statistical) of solving nonlinear observation equations by least-squares can be directly applied. Of course, the EIV model can be also handled as a nonlinear Gauss–Helmert model (GHM) (see Neitzel 2010), and equivalently transformed to condition equations containing an uncertain coefficient matrix (see Schaffrin and Wieser 2011).

Recently a large number of iterative algorithms were investigated which attempted to solve the weighted TLS (WTLS) problem (see Schaffrin and Wieser 2008; Neitzel 2010; Amiri-Simkooei and Jazaeri 2012, 2013; Mahboub 2012; Snow 2012; Xu et al. 2012; Amiri-Simkooei 2013; Jazaeri et al. 2014; Xu and Liu 2014). These algorithms were individually developed using different approaches, but all of them were based on the first derivative of the WTLS objective function. Fang (2011) and Fang (2013) proposed an iterative Newton method based on the second-order approximation of the WTLS objective function. This Newton approach presented its local quadratic convergence rate (e.g., Teunissen 1990) and can treat the WTLS problem with an arbitrary positive definite cofactor matrix.

It is quite common to introduce constraints of unknown parameters in a system of equations. As far as we know, incorporating equality constraints frequently avoid a trivial solution, introduce the prior knowledge, guarantee the stability of estimates and mitigate bias. The biases are namely due to the nonlinearities involved. By making use of differential geometric concepts, the bias of the nonlinear least-squares estimators of the similarity transformation has been determined in Teunissen (1989a). The bias results in Teunissen (1989a) are also given in the textbook by Borre and Strang (2012), p. 186. The same consideration to introduce the constraints arises in the EIV model. The constrained TLS (CTLS) problem has been discussed primarily in mathematics and geodesy. (Van Huffel and Vandewalle (1991), p. 275) and Dowling et al. (1992) proposed a closed form solution for the TLS problem with linear constraints. Schaffrin and Felus (2005) and Schaffrin (2006) presented an iterative CTLS solution with the fixed and stochastic right-hand-side vector in linear constraint equations, respectively. In quadratic constraints, Golub et al. (1999) and Sima et al. (2004) and Beck and Ben-Tal (2006) established the CTLS algorithms that dealt with a quadratic constraint in the context of regularization. In this case, where linear and quadratic constraints are considered simultaneously, Schaffrin and Felus (2009) proposed a solution to treat the mixed constrained TLS problem, which also could be extended to the fairly weighted case, according to Schaffrin and Wieser (2008). The mixed constrained TLS solution is obtained iteratively by solving the Lagrange multiplier associated with the quadratic constraint within a deduced quadratic equation. Recently, Mahboub and Sharifi (2013) extended the mixed constrained TLS solution to the mixed constrained WTLS (CWTLS) solution and presented its regularization effects. This estimator is capable of solving the constrained WTLS problem in a weighted case, where the structure of the weighted matrix of the coefficient matrix is not limited. Quite recently, Fang (2014a) generalized the CWTLS to a fully populated covariance matrix, including cross-correlations between the coefficient matrix and the traditional observation vector. One should not underestimate the significance in the differences of weights, as they represent different levels of generality in admission of weights into the EIV model. Regarding the importance and progression of weighting schemes within the EIV model, we refer to Snow (2012) discussion for the WTLS, which is also valid in the constrained WTLS environment. Furthermore, De Moor (1990), Zhang et al. (2013) and Fang (2014b) investigated the TLS or WTLS problem with linear inequality constraints.

The types and the number of the constraints, however, have still been limited until now. For example, existing methods only allow linear constraints and a maximum of one quadratic constraint to be considered. In addition, Schaffrin and Felus (2009) admitted that the exact convergence behavior of their algorithm is still to be determined, which is also the case for Mahboub and Sharifi (2013) and Fang (2014a). These algorithms might be inefficient, especially in a case with large perturbations, see Example 2 in Schaffrin and Felus (2009). It is also mentioned in Schaffrin and Felus that the CTLS solution should be examined in real geodetic applications. Furthermore, the statistical analysis of the constrained WTLS solution have not received due attention.

In this contribution, a WTLS problem with arbitrary types and numbers of applicable constraints (defined in the next section) is investigated. Based on sequential quadratic programming (SQP), the algorithm is designed, which is then presented to be directly applicable to affine, similarity and rigid transformation in the two- and three-dimensional space. The quality description of the CWTLS solution is given. Applications are then employed to demonstrate the use of the algorithm in the geodetic problems.

2 CWTLS problem and its nonlinear normal equations

2.1 CWTLS problem

Let the constrained EIV model be defined by the functional model and constraints:

$$\begin{aligned}&{\mathbf {y}}-{\mathbf {e}}_{\mathbf {y}} =( {{\mathbf {A}}-{\mathbf {E}}_{\mathbf {A}} }){\mathbf {\xi }} \nonumber \\&\mathrm{subject} \, \mathrm{to} \, {\mathbf {c}}( {\mathbf {\xi }})={\mathbf {0}} \end{aligned}$$
(1)

and the stochastic model representing properties of random errors

$$\begin{aligned} {\mathbf {e}}\!:=\!\left[ {{\begin{array}{cc} {\mathrm{vec}( {{\mathbf {E}}_{\mathbf {A}} })} \\ {{\mathbf {e}}_{\mathbf {y}} } \\ \end{array} }} \right] =\left[ {{\begin{array}{cc} {{\mathbf {e}}_{\mathbf {A}} } \\ {{\mathbf {e}}_{\mathbf {y}} } \\ \end{array} }} \right] \sim \left( {\left[ {{\begin{array}{cc} {\mathbf {0}} \\ {\mathbf {0}} \\ \end{array} }} \right] ,\sigma _0^2 {\mathbf {Q}}_{{\mathbf {ll}}} \!=\!\sigma _0^2 {\mathbf {P}}^{-1}}\right) \end{aligned}$$
(2)

In the above constrained EIV model \({\mathbf {y}}\) and \({\mathbf {e}}_{\mathbf {y}} \) are the \(n\times 1\) observation vector and the corresponding random error vector, respectively. Matrices \({\mathbf {A}}\) and \({\mathbf {E}}_{\mathbf {A}} \) are the full column-rank \(n\times u\) stochastic model matrix and the corresponding random error matrix, respectively. Vector \({\mathbf {\xi }}\) is the unknown parameter vector with dimension \(u\times 1\). \({\mathbf {e}}\) is the extended random error vector, where \({\mathbf {e}}_{\mathbf {A}} =\mathrm{vec}({{\mathbf {E}}_{\mathbf {A}} })\) (‘vec‘ denotes the operator that stacks one column of a matrix underneath the previous one, see Schaffrin and Felus 2008). The symbol \(\sigma _0^2 \) denotes the unknown variance component. Matrices \({\mathbf {Q}}_{{\mathbf {ll}}} \) and \({\mathbf {P}}\) are the cofactor matrix and the weight matrix of the extended observation vector \({\mathbf {l}}:=\mathrm{vec}( {\left[ {{\mathbf {A}},{\mathbf {y}}} \right] })\). The applicable constraints \({\mathbf {c}}( {\mathbf {\xi }})={\mathbf {0}}\) with dimension \(m\times 1\) denote a compact formulation of constraints. ‘Applicable’ refers to 1) that the constraints \({\mathbf {c}}( {\mathbf {\xi }})\) are assumed to be twice differentiable; 2) that the number of constraints must be smaller than the number of unknown parameters, i.e., \(m<u\); and 3) that the Jacobian matrix of the constraints with respect to the unknown parameter vector has full row-rank. Except for the three constraint properties mentioned above, the types and the number of the constraint functions can be arbitrary.

The cofactor matrix is segmented in further detail (see Fang 2011) as

$$\begin{aligned}&{\mathbf {Q}}_{{\mathbf {ll}}} =\left[ {{\begin{array}{cc} {{\mathbf {Q}}_{{\mathbf {AA}}} } &{} {{\mathbf {Q}}_{{\mathbf {Ay}}}} \\ {{\mathbf {Q}}_{{\mathbf {yA}}} } &{} {{\mathbf {Q}}_{\mathbf {y}}{\mathbf {y}} } \\ \end{array} }} \right] =\left[ {{\begin{array}{*{20}c} {{\mathbf {Q}}_1 } \\ \ldots \\ {{\mathbf {Q}}_k } \\ \ldots \\ {{\mathbf {Q}}_{u+1} } \\ \end{array} }} \right] \nonumber \\&\qquad \quad =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {{\mathbf {Q}}_{11} } &{} \ldots &{} {{\mathbf {Q}}_{1j} }&{} \ldots &{} {{\mathbf {Q}}_{1( {u+1})} } \\ {...} &{} &{} {...} &{} &{} {...} \\ {{\mathbf {Q}}_{k1} } &{} {...} &{} {{\mathbf {Q}}_{kj} } &{} {...} &{} {{\mathbf {Q}}_{k( {u+1})} } \\ {...} &{} &{} {...} &{} &{} {...} \\ {{\mathbf {Q}}_{( {u+1})1} } &{} {...} &{} {{\mathbf {Q}}_{({u+1})j} } &{} {...} &{} {{\mathbf {Q}}_{( {u+1})( {u+1})} } \\ \end{array} }} \right] ,\nonumber \\ \end{aligned}$$
(3)

where \({\mathbf {Q}}_{{\mathbf {AA}}} \), \({\mathbf {Q}}_{{\mathbf {Ay}}} \), \({\mathbf {Q}}_{{\mathbf {yA}}} \) and \({\mathbf {Q}}_{\mathbf {y}}{\mathbf {y}} \) are the block cofactor matrices with dimension \(nu\times nu\), \(nu\times n\), \(n\times nu\) and \(n\times n\), respectively. Matrix \({\mathbf {Q}}_{k}\) is an \(n\times n({u+1})\) cofactor matrix and \({\mathbf {Q}}_{kj}\) is an \(n\times {n}\) cofactor matrix, both being certain blocks of whole cofactor matrix \({\mathbf {Q}}_{{\mathbf {ll}}} \).

2.2 Constrained normal equation through using the Lagrange approach

A CWTLS problem can be formulated by a WTLS target function subject to Eq. (1) as

$$\begin{aligned} \begin{array}{l} \min {\mathbf {e}}^\mathrm{T}{\mathbf {Pe}} \\ \mathrm{subject}\,\mathrm{to}\,{\mathbf {y}}-{\mathbf {A\xi }}+{\mathbf {E}}_{\mathbf {A}} {\mathbf {\xi }}-{\mathbf {e}}_{\mathbf {y}} ={\mathbf {0}} \\ \text{ and } {\mathbf {c}}( {\mathbf {\xi }})={\mathbf {0}}. \\ \end{array} \end{aligned}$$
(4)

According to the traditional Lagrange approach, the CWTLS target function is formed as follows:

$$\begin{aligned}&\Phi ( {{\mathbf {e}},{\mathbf {\lambda }},{\mathbf {\xi }},{\mathbf {\mu }}})={\mathbf {e}}^\mathrm{T}{\mathbf {Pe}}+2{\mathbf {\lambda }}^\mathrm{T}( {{\mathbf {y}}-{\mathbf {A\xi }}+{\mathbf {E}}_{\mathbf {A}} {\mathbf {\xi }}-{\mathbf {e}}_{\mathbf {y}} })+2{\mathbf {\mu }}^\mathrm{T}{\mathbf {c}}( {\mathbf {\xi }}) \nonumber \\&\quad ={\mathbf {e}}^\mathrm{T}{\mathbf {Pe}}+2{\mathbf {\lambda }}^\mathrm{T}( {{\mathbf {y}}-{\mathbf {A\xi }}+{\mathbf {Be}}})+2{\mathbf {\mu }}^\mathrm{T}{\mathbf {c}}( {\mathbf {\xi }}), \end{aligned}$$
(5)

where the vectors \({\mathbf {\lambda }}\) and \({\mathbf {\mu }}\) are the Lagrange multipliers vectors associated with the functional model and the constraint functions, respectively. The full row-rank matrix \({\mathbf {B}}_{n\times n( {u+1})} \) is defined by \(\left[ {{\mathbf {\xi }}^\mathrm{T}\otimes {\mathbf {I}}_n ,-{\mathbf {I}}_n } \right] \) where \(\otimes \) is the Kronecker product. \({\mathbf {I}}_n \) is identity matrix with dimension \(n\times n\).

Setting the partial derivatives of the target function with respect to vectors \({\mathbf {\xi }},{\mathbf {e}},{\mathbf {\lambda }}\) and \({\mathbf {\mu }}\) each equal to zero, gives the necessary conditions as

$$\begin{aligned} \frac{1}{2}\frac{\partial \Phi }{\partial {\mathbf {\xi }}}\left| {_{{\hat{\mathbf {\xi }}},{\tilde{\mathbf {e}}},{\hat{\mathbf {\lambda }}},{\hat{\mathbf {\mu }}}}}\right. =-{\mathbf {A}}^\mathrm{T}{\hat{\mathbf {\lambda }}}+{\tilde{\mathbf {E}}}_{\mathbf {A}}^\mathrm{T}{\hat{\mathbf {\lambda }}}+{\hat{\mathbf {C}}}^\mathrm{T}{\hat{\mathbf {\mu }}=0}, \end{aligned}$$
(6)
$$\begin{aligned} \frac{1}{2}\frac{\partial \Phi }{\partial {\mathbf {e}}}\left| {_{{\hat{\mathbf {\xi }}},{\tilde{\mathbf {e}}},{\hat{\mathbf {\lambda }}}} } \right. ={\mathbf {P}\tilde{\mathbf {e}}}+{\hat{\mathbf {B}}}^\mathrm{T}{\hat{\mathbf {\lambda }}=0}, \end{aligned}$$
(7)
$$\begin{aligned} \frac{1}{2}\frac{\partial \Phi }{\partial {\mathbf {\lambda }}}\left| {_{{\hat{\mathbf {\xi }}},{\tilde{\mathbf {e}}}} } \right. ={\mathbf {y}}-{{{A} {\hat{\mathbf {\xi }}}}}+{\hat{{\mathbf {B}}}\tilde{\mathbf {e}}}={\mathbf {0}}, \end{aligned}$$
(8)
$$\begin{aligned} \frac{1}{2}\frac{\partial \Phi }{\partial {\mathbf {\mu }}}\left| {_{{\hat{\mathbf {\xi }}}} }\right. ={\mathbf {c}}( {\hat{\mathbf {\xi }}})={\mathbf {0}} \end{aligned}$$
(9)

with \({\mathbf {C}}={\mathbf {C}}( {\mathbf {\xi }}):={\partial {\mathbf {c}}( {\mathbf {\xi }})}/{\partial {\mathbf {\xi }}^\mathrm{T}}\). From Eq. (7) the random error vector is predicted as

$$\begin{aligned} {\tilde{\mathbf {e}}}=-{\mathbf {Q}}_{{\mathbf {ll}}} {\hat{\mathbf {B}}}^\mathrm{T}{\hat{\mathbf {\lambda }}}. \end{aligned}$$
(10)

Using Eq. (10) in Eq. (8) \({\hat{\mathbf {\lambda }}}\) can be estimated by

$$\begin{aligned} {\hat{\mathbf {\lambda }}}=( {{\hat{{\mathbf {B}}\mathbf {Q}}}_{{\mathbf {ll}}} {\hat{\mathbf {B}}}^\mathrm{T}})^{-1}( {{\mathbf {y}}-{\mathbf {A}\hat{{\mathbf {\xi }}}}}). \end{aligned}$$
(11)

Then by reinserting Eq. (11) into Eq. (10), the predicted error vector is directly formed by \({\mathbf {e}}( {{\hat{\mathbf {\xi }}}})\), a function of the estimated parameter vector:

$$\begin{aligned} {\tilde{\mathbf {e}}}={\mathbf {e}}( {\hat{\mathbf {\xi }}})=-{\mathbf {Q}}_{{\mathbf {ll}}} {\hat{\mathbf {B}}}^\mathrm{T}( {\hat{\mathbf {B}}\mathbf {Q}}_{{\mathbf {ll}}} {\hat{\mathbf {B}}}^{\mathrm{T}})^{-1}( {\mathbf {y}}-{\mathbf {A}\hat{{\mathbf {\xi }}}}). \end{aligned}$$
(12)

The above predicted error vector leads to the predicted random error matrix \({\tilde{\mathbf {E}}}_{\mathbf {A}}\) by \({\mathbf {E}}_{\mathbf {A}} ( {{\hat{\mathbf {\xi }}}})\) as:

$$\begin{aligned} {\tilde{\mathbf {E}}}_{\mathbf {A}}&= {\mathbf {E}}_{\mathbf {A}} ( {{\hat{\mathbf {\xi }}}})\nonumber \\&=-\left[ {{\mathbf {Q}}_1^ {\hat{\mathbf {B}}}T( {{\hat{\mathbf {B}}\mathbf {Q}}}_{{\mathbf {ll}}} {\hat{\mathbf {B}}}^\mathrm{T}}){-1}( {{\mathbf {y}}-{\mathbf {A}\hat{{\mathbf {\xi }} }}}), \ldots ,\right. \nonumber \\&\qquad \qquad \left. {\mathbf {Q}}_u^ {\hat{\mathbf {B}}T}( {{\hat{\mathbf {B}}\mathbf {Q}}}_{{\mathbf {ll}}} {\hat{\mathbf {B}}}^\mathrm{T}){-1}( {{\mathbf {y}}-{\mathbf {A}\hat{{\mathbf {\xi }} }}}) \right] . \end{aligned}$$
(13)

Combining Eqs. (6), (9) and (11), the constrained normal equations can be formulated by

$$\begin{aligned}&( {{\tilde{\mathbf {E}}}_{\mathbf {A}}-{\mathbf {A}}})^\mathrm{T}( {{\hat{\mathbf {B}}\mathbf {Q}}}_{{\mathbf {ll}}} {\hat{\mathbf {B}}}^\mathrm{T})^{-1}( {\mathbf {y}}-{\mathbf {A}{\hat{\mathbf {\xi }}}})+{\hat{\mathbf {C}}}^{\mathrm{T}}{\hat{\mathbf {\mu }}=0} \nonumber \\&\quad {\mathbf {c}}( {{\hat{\mathbf {\xi }}}})={\mathbf {0}}. \end{aligned}$$
(14)

The solution of the CWTLS problem is now converted to solve the constrained nonlinear normal equations (CNNE). It is well known that nonlinear equations can be solved by a Newton type method. Forming an equivalent CWTLS problem based on the knowledge presented in Fang (2013) will facilitate directly applying the Newton method.

2.3 Equivalent approach in forming the constrained normal equations

Another formulation of the CWTLS problem can be written based on the alternative WTLS objective function by Fang (2011) and Fang (2013) with the same constraint functions as follows:

$$\begin{aligned} \begin{aligned}&\min f( {\mathbf {\xi }})=\frac{1}{2}( {{\mathbf {y}}-{\mathbf {A\xi }}})^\mathrm{T}( {{\mathbf {BQ}}_{{\mathbf {ll}}} {\mathbf {B}}^\mathrm{T}})^{-1}( {{\mathbf {y}}-{\mathbf {A\xi }}}) \\&\mathrm{subject}\,\mathrm{to} {\mathbf {c}}( {\mathbf {\xi }})={\mathbf {0}}, \end{aligned} \end{aligned}$$
(15)

where \({\mathbf {B}}=\left[ {{\mathbf {\xi }}^\mathrm{T}\otimes {\mathbf {I}}_n ,-{\mathbf {I}}_n } \right] \).

The analytical form of the gradient vector \({\mathbf {g}}( {\mathbf {\xi }})\) and the Hessian matrix \({\mathbf {H}}( {\mathbf {\xi }})\) of the function \(f( {\mathbf {\xi }})\) was presented in Fang (2013), Fang (2014b) and repeated here as

$$\begin{aligned} \begin{aligned} {\mathbf {g}}( {\mathbf {\xi }})&=\frac{\partial f( {\mathbf {\xi }})}{\partial {\mathbf {\xi }}}=-( {{\mathbf {A}}+{\mathbf {A}}^*})^\mathrm{T}( {{\mathbf {BQ}}_{{\mathbf {ll}}} {\mathbf {B}}^\mathrm{T}})^{-1}( {{\mathbf {y}}-{\mathbf {A\xi }}}) \\&\quad =( {{\mathbf {E}}_{\mathbf {A}} ( {\mathbf {\xi }})-{\mathbf {A}}})^\mathrm{T}( {{\mathbf {BQ}}_{{\mathbf {ll}}} {\mathbf {B}}^\mathrm{T}})^{-1}( {{\mathbf {y}}-{\mathbf {A\xi }}}), \end{aligned} \end{aligned}$$
(16)
$$\begin{aligned} {\mathbf {H}}( {\mathbf {\xi }})&= \frac{\partial ^2f( {\mathbf {\xi }})}{\partial {\mathbf {\xi }}\partial {\mathbf {\xi }}^\mathrm{T}}=( {{\mathbf {A}}+{\mathbf {A}}^*+{\mathbf {A}}^{**}})^\mathrm{T}( {{\mathbf {BQ}}_{{\mathbf {ll}}} {\mathbf {B}}^\mathrm{T}})^{-1}\nonumber \\&\times ( {{\mathbf {A}}+{\mathbf {A}}^*+{\mathbf {A}}^{**}})-\left[ {\varpi _{kj} } \right] , \end{aligned}$$
(17)

with the auxiliary matrices \({\mathbf {A}}^*\quad {\mathbf {A}}^{**}\) and \(\left[ {\varpi _{kj} } \right] \) defined by:

$$\begin{aligned} {\mathbf {A}}^{*}&= \left[ {{\mathbf {Q}}_{1} {\mathbf {B}}^{T} \left( {{\mathbf {BQ}}_{{{\mathbf {ll}}}} {\mathbf {B}}^{T} } \right) ^{{ - 1}} \left( {{\mathbf {y}} - {\mathbf {A\xi }}} \right) ,} \ldots ,\right. \nonumber \\&\quad \left. {{\mathbf {Q}}_{u} {\mathbf {B}}^{T} \left( {{\mathbf {BQ}}_{{{\mathbf {ll}}}} {\mathbf {B}}^{T} } \right) ^{{ - 1}} \left( {{\mathbf {y}} - {\mathbf {A\xi }}} \right) } \right] , \nonumber \\ {\mathbf {A}}^{{**}}&= \left[ {{\mathbf {BQ}}_{1}^{T} \left( {{\mathbf {BQ}}_{{{\mathbf {ll}}}} {\mathbf {B}}^{T} } \right) ^{{ - 1}} \left( {{\mathbf {y}} - {\mathbf {A\xi }}} \right) ,} \ldots ,\right. \nonumber \\&\quad \left. {{\mathbf {BQ}}_{u}^{T} \left( {{\mathbf {BQ}}_{{{\mathbf {ll}}}} {\mathbf {B}}^{T} } \right) ^{{ - 1}} \left( {{\mathbf {y}} - {\mathbf {A\xi }}} \right) } \right] , \nonumber \\ \varpi _{{kj}}&= \left( {{\mathbf {y}} - {\mathbf {A\xi }}} \right) ^{T} \left( {{\mathbf {BQ}}_{{{\mathbf {ll}}}} {\mathbf {B}}^{T} } \right) ^{{ - 1}} {\mathbf {Q}}_{{kj}} \left( {{\mathbf {BQ}}_{{{\mathbf {ll}}}} {\mathbf {B}}^{T} } \right) ^{{ - 1}} \left( {{\mathbf {y}} - {\mathbf {A\xi }}} \right) .\nonumber \\ \end{aligned}$$
(18)

In order to obtain the minimum of (15), the Lagrange function is again used for this context as

$$\begin{aligned} L( {{\mathbf {\xi }},{\mathbf {\mu }}})=f( {\mathbf {\xi }})+{\mathbf {\mu }}^\mathrm{T}{\mathbf {c}}( {\mathbf {\xi }}). \end{aligned}$$
(19)

The first order necessary condition of this problem, minimization of the function \(L( {{\mathbf {\xi }},{\mathbf {\mu }}})\), can be written as a system of \(u+m\) equations including the \(u+m\) unknowns \({\mathbf {\xi }}\) and \({\mathbf {\mu }}\):

$$\begin{aligned} {\mathbf {f}}( {{\hat{\mathbf {\xi }}},{\hat{\mathbf {\mu }}}})=\left. {\frac{\partial L( {{\mathbf {\xi }},{\mathbf {\mu }}})}{\partial \left[ {{\mathbf {\xi }}^\mathrm{T},{\mathbf {\mu }}^\mathrm{T}} \right] ^\mathrm{T}}} \right| _{{\hat{\mathbf {\xi }}},{\hat{\mathbf {\mu }}}} =\left[ {{\begin{array}{*{20}c} {{\mathbf {g}}+{\mathbf {C}}^\mathrm{T}{\hat{\mathbf {\mu }}}} \\ {\mathbf {c}} \\ \end{array} }} \right] ={\mathbf {0}}. \end{aligned}$$
(20)

Note that the identity of (14) and (20) can be recognized by the formulation of the vector \({\mathbf {g}}\). For brevity of notation, we denote the estimates \({\mathbf {\xi }}\) and \({\mathbf {\mu }}\) by \({\hat{\mathbf {\xi }}}\) and \({\hat{\mathbf {\mu }}}\) but keep the notation of \({\mathbf {c}}\), \({\mathbf {g}}\), \({\mathbf {H}}\) and \({\mathbf {C}}\) to denote their estimates \({\mathbf {c}}( {{\hat{\mathbf {\xi }}}})\), \({\mathbf {g}}( {{\hat{\mathbf {\xi }}}})\), \({\mathbf {H}}( {{\hat{\mathbf {\xi }}}})\) and \({\mathbf {C}}( {{\hat{\mathbf {\xi }}}})\) in the following part, respectively.

Equation (20), the first-order derivatives \({\mathbf {f}}( {{\hat{\mathbf {\xi }}},{\hat{\mathbf {\mu }}}})={\mathbf {0}}\), are identical to the CNNE (14). This equivalence indicates that the alternative CWTLS objective function (15) yields an identical solution to the solution based on the optimization problem (4). The strict CTLS solution is further verified by the positive quadratic form of the Hessian matrix \({\mathbf {H}}\) and any feasible active direction which is determined by the constraints.

3 WTLS and CWTLS solution based on Newton iteration

As far as we know, Eq. (15) is a standard nonlinear program. Thus, the CWTLS problem (15) can be categorized as a local SQP problem (see Nocedal and Wright 2006, p. 530). One approach to solving Eq. (20) is here suggested by Newton’s method. The total Hessian matrix with respect to the augmented vector \(\left[ {{\mathbf {\xi }}^\mathrm{T},{\mathbf {\mu }}^\mathrm{T}} \right] ^\mathrm{T}\) is given by

$$\begin{aligned}&\left. {\left. {\frac{\partial ^2L( {{\mathbf {\xi }},{\mathbf {\mu }}})}{\partial \left[ {{\mathbf {\xi }}^\mathrm{T},{\mathbf {\mu }}^\mathrm{T}} \right] ^\mathrm{T}\left[ {{\mathbf {\xi }}^\mathrm{T},{\mathbf {\mu }}^\mathrm{T}} \right] }} \right| _{{\hat{\mathbf {\xi }}},{\hat{\mathbf {\mu }}}} =\frac{\partial {\mathbf {f}}( {{\hat{\mathbf {\xi }}},{\hat{\mathbf {\mu }}}})}{\partial \left[ {{\mathbf {\xi }}^\mathrm{T},{\mathbf {\mu }}^\mathrm{T}} \right] }} \right| _{{\hat{\mathbf {\xi }}},{\hat{\mathbf {\mu }}}}\nonumber \\&\quad =\left[ {{\begin{array}{*{20}c} {{\mathbf {H}}+\sum \limits _{t=1}^m {\hat{\mu }_t {\mathbf {H}}_t } } &{}\quad {{\mathbf {C}}^\mathrm{T}} \\ {\mathbf {C}} &{}\quad {\mathbf {0}} \\ \end{array} }} \right] , \end{aligned}$$
(21)

where the Hessian matrix of the tth constraint is defined as \({\mathbf {H}}_t ={\mathbf {H}}_t ( {{\hat{\mathbf {\xi }}}}){=\partial ^2c_t ( {{\hat{\mathbf {\xi }}}})} /{\partial {\mathbf {\xi }}\partial {\mathbf {\xi }}^\mathrm{T}}\), and \(\hat{\mu }_t \) is the tth component of the vector \({\hat{\mathbf {\mu }}}\) (\(t=1,...,m)\).

By combining Eqs. (20) and (21), the Newton step to compute increments of the parameter vector and the Lagrange multiplier vector is presented as

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {{\mathbf {H}}+\sum \limits _{t=1}^m {\hat{\mu }_t {\mathbf {H}}_t } } &{}\quad {{\mathbf {C}}^\mathrm{T}} \\ {\mathbf {C}} &{}\quad {\mathbf {0}} \\ \end{array} }} \right] \left[ {{\begin{array}{*{20}c} {d{\hat{\mathbf {\xi }}}} \\ {d{\hat{\mathbf {\mu }}}} \\ \end{array} }} \right] =-\left[ {{\begin{array}{*{20}c} {{\mathbf {g}}+{\mathbf {C}}^\mathrm{T}{\hat{\mathbf {\mu }}}} \\ {\mathbf {c}} \\ \end{array} }} \right] . \end{aligned}$$
(22)

By elimination of the increment of the Lagrange multipliers vector \(d{\hat{\mathbf {\mu }}}\), the estimates of the parameter increment \(d{\hat{\mathbf {\xi }}}\) and the Lagrange multipliers vector \({\hat{\mathbf {\mu }}}\) can be iteratively derived based on Eq. (22) by

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {d{\hat{\mathbf {\xi }}}} \\ {{\hat{\mathbf {\mu }}}} \\ \end{array} }} \right] =-\left[ {{\begin{array}{*{20}c} {{\mathbf {H}}+\sum \limits _{t=1}^m {\hat{\mu }_t {\mathbf {H}}_t } } &{} {{\mathbf {C}}^\mathrm{T}} \\ {\mathbf {C}} &{} {\mathbf {0}} \\ \end{array} }} \right] ^{\text{-1 }}\left[ {{\begin{array}{*{20}c} {\mathbf {g}} \\ {\mathbf {c}} \\ \end{array} }} \right] . \end{aligned}$$
(23)

This Newton iteration is well defined when the augmented Hessian matrix is nonsingular. If the regular inversion of the augmented matrix is not available, we can establish a positive definite matrix as the approximation of the original Hessian matrix.

If these constraints are not considered, the unconstrained WTLS solution can be simplified based on Eq. (23). The increment of the parameter \(d{\mathbf {\xi }}\) can be obtained by multiplying the gradient vector by the negative inverted Hessian matrix (Fang 2013):

$$\begin{aligned} \mathrm{d}{\hat{\mathbf {\xi }}}=-{\mathbf {H}}^{-1}{\mathbf {g}}. \end{aligned}$$
(24)

In summation, the algorithm of this WTLS solution with or without arbitrary applicable constraints is designed as:

figure a

Being a Newton’s type, this compact algorithm for solving the WTLS with or without constraints works efficiently, and provides a local quadratic convergence at the desired local minimum (Nocedal and Wright 2006)—bearing in mind that the convergence behavior of other CTLS algorithms is unknown. It is noted that this local behavior implies (Teunissen 1990): (1) that convergence is not guaranteed and (2) that approximate values still need to be good enough. The linear search strategy to find the step length, which satisfies the (strong) Wolfe condition, can be introduced to improve convergence behavior of the iterative TLS solution (e.g., Teunissen 1990; Fang 2014c). Furthermore, the compact form presented will be a promising tool for estimating the transformation parameters in different types of geodetic transformations.

4 Universal formula for geodetic symmetrical transformations

It is well known that attaining an estimation of the transformation parameters in the presence of two sets of (2D or 3D) coordinates for a given geodetic network is a long-standing problem in geodetic science (see Schaffrin et al. 2012; Fang 2014c). In Table 1, the adjustment of the different geodetic transformations, including affine, similarity and rigid transformations, can be interpreted as the WTLS or CWTLS problem if one perfectly describes the constraints for the corresponding 2D or 3D transformation models.

Table 1 The common functional model and stochastic model, and the different constraints represent the three transformations in the 2D and 3D cases
Full size table

In 2D case, the matrix \({\mathbf {\Xi }}_{2\times 2} =\left[ {{\begin{array}{*{20}c} {\xi _{11} } &{} {\xi _{12} } \\ {\xi _{21} } &{} {\xi _{22} } \\ \end{array} }} \right] \) contains the four synthetic parameters, and its transpose is computed using the product of the rotation matrix, the affinity matrix and the scaling matrix containing two scales for the x and y coordinates (see Mahboub 2012). It is noted that if one deals with a rotation matrix, then not only the columns are of unit length and mutually orthogonal, but also the determinant of the matrix must be +1. \({\mathbf {x}}_t \) and \({\mathbf {y}}_t \) are the random vectors of the x and y coordinates of the target system while \({\mathbf {x}}_s \) and \({\mathbf {y}}_s \) are the random vectors of the x and y coordinates of the source system. \(\left[ {{\begin{array}{*{20}c} {\Delta {x}} &{} {\Delta y} \\ \end{array} }} \right] ^\mathrm{T}\) are the translations in the x and y orientations. \({\mathbf {1}}\) is the vector of ones with the corresponding size (number of common points). The matrix \({\mathbf {F}}_{2D} =\frac{\partial \mathrm{vec}( {\mathbf {A}})}{\partial \left[ {{\begin{array}{*{20}c} {{\mathbf {x}}_t^\mathrm{T} } &{} {{\mathbf {y}}_t^\mathrm{T} } \\ \end{array} }} \right] }\) represents the relationship between the vectorized coefficient matrix and the coordinates of the target system.

In 3D case, the parameter matrix \({\mathbf {\Xi }}_{3\times 3} =\left[ {{\begin{array}{*{20}c} {\xi _{11} } &{} {\xi _{12} } &{} {\xi _{13} } \\ {\xi _{21} } &{} {\xi _{22} } &{} {\xi _{23} } \\ {\xi _{31} } &{} {\xi _{32} } &{} {\xi _{33} } \\ \end{array} }} \right] \) is enlarged with a dimension of \(3\times 3\) and the translation \(\Delta z\) in the z axis is considered. The covariance matrix calculated by \({\mathbf {F}}_{3D} =\frac{\partial \mathrm{vec}( {\mathbf {A}})}{\partial \left[ {{\begin{array}{*{20}c} {{\mathbf {x}}_t^\mathrm{T} } &{} {{\mathbf {y}}_t^\mathrm{T} } &{} {{\mathbf {z}}_t^\mathrm{T} } \\ \end{array} }} \right] }\), which can be obtained as it is computed in the 2D case, is also valid for all three types of 3D transformations.

Although the matrix \({\mathbf {A}}\), the observation vector \({\mathbf {y}}\) and the parameter vector \({\mathbf {\xi }}\) in a 3D case are different from those in a 2D case, we can still use the same symbols \({\mathbf {A}}\), \({\mathbf {y}}\) and \({\mathbf {\xi }}\) to hold the formulation of the EIV model. Furthermore, the functional model (the matrix \({\mathbf {A}}\), the observation vector \({\mathbf {y}}\) and the parameter vector \({\mathbf {\xi }})\) and the stochastic model (the cofactor matrix \({\mathbf {Q}}_{{\mathbf {ll}}} )\) are common for the three kinds of transformations in the corresponding dimension.

It has been presented that affine, similarity and rigid transformations in 2D and 3D space can be interpreted as the WTLS problem with or without constraints. Hence, Algorithm 1 can be directly applicable to all of the transformations and can be referred to as a universal formula for geodetic symmetrical transformations. When some extra constraints (e.g., fixed baselines) need to be taken into consideration simultaneously (see Shen et al. 2011), our proposed algorithm is also applicable.

5 Statistical analysis of CWTLS solution

Although our algorithm has been developed for the CWTLS problem, statistical aspects of the CWTLS estimation were not investigated. Teunissen (1989b) provided general diagnostics of the first and second moments of the nonlinear LS estimate for the first time in the geodetic literature. Xu et al. (2012) applied the theory and methods by Box (1971) to work out the statistical aspects of parameter estimation in the unconstrained EIV model.

In order to obtain the quality description by using the existing knowledge, we can formulate the functional part of the TLS model as a nonlinear LS problem (Teunissen 1988):

$$\begin{aligned} \begin{array}{l} {\mathbf {y}}-{\mathbf {e}}_{\mathbf {y}} ={\bar{\mathbf {A}}\xi }=( {{\mathbf {\xi }}_T \otimes {\mathbf {I}}})( {{\mathbf {F}}_t {\mathbf {a}}_I+{\mathbf {d}}}) \\ {\mathbf {a}}_I -{\mathbf {e}}_{{\mathbf {A}}I} ={\bar{\mathbf {a}}}_I \\ \end{array} \end{aligned}$$

The symbol \({\bar{\mathbf {a}}}_I \) with dimension \(\text{ s }\times \text{1 }\) and \({\mathbf {e}}_{{\mathbf {A}}I} \) denotes the true vector of the independent elements within the true coefficient matrix \({\bar{\mathbf {A}}}\) and its error vector, respectively. \({\mathbf {F}}_t \) is the transformation matrix (\({\mathbf {F}}_{2D} \) or \({\mathbf {F}}_{3D} )\) to convert the vector \({\bar{\mathbf {a}}}_I \) to the vectorized (true) coefficient matrix \(\mathrm{vec}( {{\bar{\mathbf {A}}}})={\mathbf {F}}_t {\bar{\mathbf {a}}}_I +{\mathbf {d}}\).

In the case of the CWTLS model, it is usually formulated that the constraints approximately equal pseudo-equations: \({\mathbf {0}}-{\mathbf {\delta }}\approx {\mathbf {c}}( {\mathbf {\xi }})\) with \({\mathbf {\delta }}\sim ( {{\begin{array}{*{20}c} {{\mathbf {0}},} &{} {\sigma _0^2 {\mathbf {Q}}_{{\mathbf {\delta \delta }}} } \\ \end{array} }})\). However, we should note that it is numerically admissible to treat the constraints completely as the pseudo-equations (\({\mathbf {0}}-{\hat{\mathbf {\delta }}}={\mathbf {c}}( {{\hat{\mathbf {\xi }}}}))\), as the variance of the random vector \({\mathbf {\delta }}\) is sufficiently small (see Fang 2011, p. 45).

Combining the above models, a nonlinear Gauss–Markov model can be written as follows:

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {\mathbf {y}} \\ {{\mathbf {a}}_I } \\ {\mathbf {0}} \\ \end{array} }} \right] ={\mathbf {f}}( {\mathbf {x}})+{\mathbf {\varepsilon }}={\mathbf {f}}\left( {\left[ {{\begin{array}{*{20}c} {\mathbf {\xi }} \\ {{\bar{\mathbf {a}}}_I } \\ \end{array} }} \right] }\right) +\left[ {{\begin{array}{*{20}c} {{\mathbf {e}}_{\mathbf {y}} } \\ {{\mathbf {e}}_{{\mathbf {A}}I} } \\ {\mathbf {\delta }} \\ \end{array} }} \right] \end{aligned}$$

Based on the existing knowledge, the first-order approximation of the dispersion matrix and the bias vector \({\mathbf {b}}_{\mathbf {x}} \) of the CWTLS estimates of the extended unknown parameter vector \({\mathbf {x}}\) are simply given as follows:

$$\begin{aligned} D( {\mathbf {x}})=\sigma _0^2 ( {{\mathbf {F}}^\mathrm{T}{\mathbf {WF}}})^{-1} \end{aligned}$$
(25)

and

$$\begin{aligned} {\mathbf {b}}_{\mathbf {x}} =-\frac{\sigma _0^2 }{2}( {{\mathbf {F}}^\mathrm{T}{\mathbf {WF}}})^{-1}{\mathbf {F}}^\mathrm{T}{\mathbf {Wm}} \end{aligned}$$
(26)

with

$$\begin{aligned} \begin{array}{l} {\mathbf {F}}=\frac{\partial {\mathbf {f}}}{\partial {\mathbf {x}}^\mathrm{T}}=\left[ {{\begin{array}{*{20}c} {{\bar{\mathbf {A}}}} &{}\quad {( {{\mathbf {\xi }}^\mathrm{T}\otimes {\mathbf {I}}_n }){\mathbf {F}}_t } \\ {\mathbf {0}} &{}\quad {{\mathbf {I}}_s } \\ {\mathbf {C}} &{}\quad {\mathbf {0}} \\ \end{array} }} \right] {\mathbf {W}}=\left[ {{\begin{array}{*{20}c} {{\mathbf {P}}_I } &{}\quad {\mathbf {0}} \\ {\mathbf {0}} &{}\quad {{\mathbf {Q}}_{{\mathbf {\delta \delta }}}^{-1} } \\ \end{array} }} \right] \\ {\mathbf {m}}=\left[ {{\begin{array}{*{20}c} {tr( {( {{\mathbf {F}}^\mathrm{T}{\mathbf {WF}}})^{-1}{\mathbf {M}}_1 })} \\ {tr( {( {{\mathbf {F}}^\mathrm{T}{\mathbf {WF}}})^{-1}{\mathbf {M}}_2 })} \\ \vdots \\ {tr( {( {{\mathbf {F}}^\mathrm{T}{\mathbf {WF}}})^{-1}{\mathbf {M}}_{s+n+t} })} \\ \end{array} }} \right] {\mathbf {M}}_i =\frac{\partial ^2f_i }{\partial x\partial x^\mathrm{T}} \\ \end{array} \end{aligned}$$

where \(f_i \) is the ith function of \({\mathbf {f}}\), and \({\mathbf {P}}_I \) denotes the weight matrix of the independent errors.

In the case of the above nonlinear adjustment problem, we have the second partial derivatives \({\mathbf {M}}_i \) for each \(f_i \), which is given by

$$\begin{aligned} {\mathbf {M}}_i =\left\{ {{\begin{array}{*{20}c} {\left[ {{\begin{array}{*{20}c} {\mathbf {0}} &{} {( {{\mathbf {I}}_u \otimes {\mathbf {e}}_i }){\mathbf {F}}_t } \\ {{\mathbf {F}}_t^\mathrm{T} ( {{\mathbf {I}}_u \otimes {\mathbf {e}}_i^\mathrm{T} })} &{} {\mathbf {0}} \\ \end{array} }} \right] } \\ {\mathbf {0}} \\ {\left[ {{\begin{array}{*{20}c} {{\mathbf {H}}_{i-n-s} } &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {0}} \\ \end{array} }} \right] } \\ \end{array} }} \right. {\begin{array}{*{20}c} {{i=1,\ldots ,n}} \\ \\ {{i=n+1,\ldots ,n+s}} \\ {{i=n+s}+{1,\ldots ,n+s}+t} \\ \end{array} } \end{aligned}$$

The total sum of squared residual (TSSR) is easily determined from objective function \(f( {{\hat{\mathbf {\xi }}}_\mathrm{CWTLS} })\) so that a estimate of the variance component can be obtained through

$$\begin{aligned} \hat{\sigma }_0^2 =\frac{f( {{\hat{\mathbf {\xi }}}_{CWTLS} })}{n-u+t}. \end{aligned}$$
(27)

6 Case study of 2D and 3D affine, similarity and rigid transformations

In this case study, we demonstrate Algorithm 1 as the universal formula for affine, similarity and rigid transformations in 2D and 3D space, and provide the quality description for the solutions. The data for the 2D transformations, as seen in Table 2, originate from (Mikhail and Gracie (1981), p. 397–402), and was also presented in Neitzel (2010) and Schaffrin et al. (2012) for the WTLS problem.

For these problems of affine, similarity and rigid transformations in 2D, Algorithm 1 was implemented when the constraints were perfectly described, as proposed in Sect. 4. In Table 3, we present the WTLS solution for the affine transformation and the CWTLS solution for the similarity and rigid transformations. The results of the similarity transformation coincide with the iterative GHM solution presented in Neitzel (2010). The results of the affine and rigid transformation are not much different from the results of the similarity transformation since the noises of the data set are small. It is clear that the last row of Table 3 shows that the values of the objective functions become larger from the affine to similarity to rigid transformation, as more constraints are considered for the affine to similarity to rigid transformation.

Table 2 Target and source coordinates from (Mikhail and Gracie (1981), p. 397–402)
Full size table
Table 3 Estimates of the case study by Algorithm 1 for three types of 2D transformation
Full size table
Table 4 Standard deviations of the parameter estimates for three types of 2D transformation
Full size table

According to Eqs. (25) and (26), we computed the standard deviations and biases of the estimates of the 2D transformations and show them in Tables 4 and 5, respectively. The standard deviations of the parameter vector for affine, similarity and rigid are presented at the level of \(10^{-4}\) for the elements of the matrix \({\mathbf {\Xi }}_{2\times 2} \) and at the level of \(10^{-2}\) for the translations. Table 4 indicates the fact that the more constraints are considered, the smaller the standard deviation of each parameter is. The biases of the parameters are presented in the magnitude of \(10^{-6}\). The biases of the similarity can be neglected in \(10^{-6}\), whereas the biases of the affine and the rigid have opposite signs for each parameter.

Table 5 Biases of the parameter estimates for three types of 2D transformation
Full size table

A recent survey by Felus and Burtch (2009) lists a large number of methods that have been developed to compute 3D geodetic transformations between two sets of corresponding points. Here, we will use the data set presented in this paper to demonstrate the proposed solutions. In this demonstration, six control points are identified and recorded in the two coordinate systems (WGS 84 and a local datum), and those x, y and z coordinate values are given in Table 6.

Table 6 Coordinates of source system and target system from Felus and Burtch (2009)
Full size table

Algorithm 1 was used to compute the transformation parameters displayed in Tables 7, 8 and 9 for the affine, similarity and rigid transformations, respectively. The results for the similarity transformation are identical to the solution presented in Felus and Burtch. In these three transformations, the differences between the estimated translations for the similarity transformation and the estimated translations for the affine and rigid transformation are significant. This could be explained by the restricted rotation matrices and scale factor as well as the magnitude of the coordinates. Note that the estimated rotation angles for the three transformations are quite small (only at the level of seconds). The objective function for the three types of transformations demonstrates the fact that the similarity and rigid transformation includes more constraints, thus resulting in a larger objective function than the affine.

Now we calculate the standard deviations and biases of the estimated parameters, for the 3D affine, similarity and rigid transformations, and present them in Tables 10 and 11, respectively. All the standard deviations for the elements within the matrix \({\mathbf {\Xi }}_{3\times 3}\) are given in \(10^{-4}\) while the standard deviations of the translations are relatively large, in the magnitude of \(10^4\) for the affine, and in the magnitude of \(10^2\) for similarity and rigid. It needs to be pointed out, however, that the computed standard deviations of the translations depends on the datum, i.e., if we treat the real data by multiplying the idempotent matrix (e.g., Felus and Burtch 2009), the standard deviations are largely reduced. The phenomenon that the standard deviations become smaller when more constraints are available is also valid for the 3D case.

Table 7 Estimates of the case study by Algorithm 1 for the 3D affine transformation
Full size table
Table 8 Estimates of the case study by Algorithm 1 for the 3D similarity transformation
Full size table
Table 9 Estimates of the case study by Algorithm 1 for the 3D rigid transformation
Full size table
Table 10 Standard deviations of the parameter estimates for three types of 3D transformation
Full size table

Comparing the most insignificant biases of the estimated parameters for the similarity, the biases of the estimated parameters for the affine transformation are large, especially for the translations. These large biases may be explained by the significant differences between the translation estimates of the affine and similarity transformations. In full analogy in the 2D case, the biases of the affine and the rigid have opposite signs for each parameter here (see Table 11 columns 2 and 4).

Table 11 Biases of the parameter estimates for three types of 3D transformation
Full size table

7 Conclusions

This article investigated the WTLS solution with constraints, which is intuitively very appealing for a symmetrical adjustment of various geodetic transformations. Unlike other CWTLS solutions, the proposed algorithm adapts itself to arbitrarily applicable constraints. Furthermore, our method is also highly reliable and efficient from a numerical point of view due to having known quadratic convergence behavior.

Our proposed algorithm, which is referred to as the universal formula for the adjustment of transformations, was implemented to deal with various transformations in 2D and 3D space by simply changing constraints. Furthermore, the statistical analysis of the CWTLS estimates was investigated.

Along with Fang (2013, 2014b) this paper completes the WTLS framework with varying types of prior information about unknown parameters (random parameters, linear and nonlinear, equality and inequality constraints).