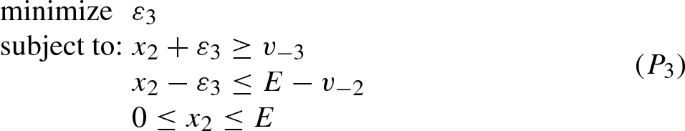Abstract
Even though aggregate monotonicity appears to be a reasonable requirement for solutions on the domain of convex games, there are well known allocations, the nucleolus for instance, that violate it. It is known that the nucleolus is aggregate monotonic on the domain of essential games with just three players. We provide a simple direct proof of this fact, obtaining an analytic formula for the nucleolus of a three-player essential game. We also show that the core-center, the center of gravity of the core, satisfies aggregate monotonicity for three-player balanced games. The core is aggregate monotonic as a set-valued solution, but this is a weak property. In fact, we show that the core-center is not aggregate monotonic on the domain of convex games with at least four players. Our analysis allows us to identify a subclass of bankruptcy games for which we can obtain analytic formulae for the nucleolus and the core-center. Moreover, on this particular subclass, aggregate monotonicity has a clear interpretation in terms of the associated bankruptcy problem and both the nucleolus and the core-center satisfy it.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Several monotonicity properties have been proposed for solutions of coalitional games. Megiddo (1974) introduces aggregate monotonicity which states that if the worth of the grand coalition increases whereas the worths of all other coalitions remain the same, then everyone’s payoff shouldn’t decrease. Among well known solution concepts, the Shapley value, the egalitarian rule, and the per-capita nucleolus are aggregate monotonic while the nucleolus is not.
Aggregate monotonicity is generally viewed as a desirable property and a natural requirement. Most of the examples presented in the literature of solutions that violate it are technical and lack a clear interpretation. But Tauman and Zapechelnyuk (2010) argue that: “Whether there is a trade-off between monotonicity and other desirable properties of a solution or not depends on the context from which a cooperative game arises. Some contexts may narrow down the class of games to a subclass where the nucleolus is monotonic. Other contexts may prove the monotonicity requirement completely unreasonable.” In fact, Tauman and Zapechelnyuk (2010) provide an example of a uniparametric family of 4-player games that highlights a class of economic situations where aggregate monotonicity is not appealing. Analogously some allocation rules are more suitable for some specific classes of games than others. So, it is interesting to know whether or not a solution satisfies aggregate monotonicity in some important subclasses of games such as the convex games. In that respect, Hokari (2000) shows that the nucleolus is not aggregate monotonic on the domain of convex games, and that this lack of monotonicity holds even if there are as few as four players. In this paper, we identify a subclass of convex games where the nucleolus is aggregate monotonic.
Housman and Clark (1998) show that for 3-player games a generalization of the nucleolus, called \(\alpha \)-prenucleolus, is coalitional monotonic (Young 1985), a stronger requirement than aggregate monotonicity. Therefore, the nucleolus is aggregate monotonic on the domain of essential games with three players. Nevertheless, Leng and Parlar (2010) obtain an analytic formula for the nucleolus of a 3-player superadditive game and claim that it is possible to find examples of 3-player games for which the nucleolus violates aggregate monotonicity. To clarify the matter, first we compute a simplified version of the formula for the nucleolus of a 3-player essential game. For balanced games we make use of the property of first agent consistency introduced for the 1-nucleolus by Estévez-Fernández et al. (2017). If a game is essential and not balanced the computation of the lexicographic center of the game is carried out by solving a sequence of linear programming problems to determine the excesses of the players following the standard method outlined by Maschler et al. (1979). Then, we give a direct proof that confirms that the nucleolus is aggregate monotonic: the coordinates of the nucleolus are piecewise linear functions of the worth of the grand coalition and then, checking if the nucleolus is aggregate monotonic is equivalent to showing that its coordinate functions are monotonically increasing.
González-Díaz and Sánchez-Rodríguez (2007) define a solution, the core-center, on the domain of games with a non-empty core, by considering that all of the core alternatives are equally preferable and then selecting the average stable payoff. That is, the core-center of a balanced game is the center of gravity (the centroid) of its core. This solution was studied on the domain of airport games by González-Díaz et al. (2015, 2016) and its relationship with other well known solutions such as the Shapley value and the nucleolus was addressed by Mirás Calvo et al. (2016). On the domain of bankruptcy games, the properties of this solution were studied by Mirás Calvo et al. (2019). The analysis of the core-center reveals some important properties of the core of the game.
The core, as a set-valued solution,Footnote 1 satisfies aggregate monotonicity on the class of games with non-empty core. Since this is a mild property, one can ask if the core-center (a “proxy” of the core) is aggregate monotonic as a single-valued solution. In this paper, we show that the core-center is not aggregate monotonic on the domain of convex games with at least four players. For balanced games with three players, we provide an analytic expression for the core-center that allows us to prove that, in this domain, it is aggregate monotonic. Again, the coordinates of the core-center are functions of the worth of the grand coalition and studying aggregate monotonicity reduces to see if these coordinates are monotonically increasing functions. Naturally, the computations are now laborious but the general idea is the same as in the case of the nucleolus.
In general, aggregate monotonicity of a solution of a bankruptcy game does not translate into a meaningful property of the corresponding rule for the associated bankruptcy problem. We identify a particular subclass of bankruptcy games for which aggregate monotonicity can be expressed in terms of the corresponding bankruptcy problem. Moreover, we can provide analytic formulae for the nucleolus and the core-center for this special bankruptcy games. Once equipped with the analytic expressions, using the same technique as in the 3-player case, we show that both the core-center and the nucleolus satisfy aggregate monotonicity on this subclass.
The structure of the paper is the following. In Sect. 2 we introduce the main concepts and properties. Section 3 is devoted to study aggregate monotonicity of the nucleolus of a 3-player essential game, while the corresponding analysis for the core-center of a 3-player balanced game is carried out in Sect. 4. We present an example in Sect. 5 that illustrates that neither the core-center nor the nucleolus are aggregate monotonic on the domain of convex games with at least four players. We give explicit formulae for the nucleolus and the core-center for a particular subclass of bankruptcy games in Sect. 6, and show that the nucleolus and the core-center are aggregate monotonic on this class. Section 7 is a summary of the findings and some additional discussion. Finally, we leave to the “Appendix” the proofs of the main results that are technical.
2 Notation and preliminaries
Let \(N=\{1,\dots ,n\}\). A coalitional game with set of players N is a function \(v:2^{N}\rightarrow {\mathbb {R}}\) such that \(v(\emptyset )=0\). Let \({\mathcal {G}}^N\) be the set of all coalitional games with player set N. A subset \(S\in 2^N\) of N is called a coalition and let |S| denote the number of players in S. Any vector \(x \in {\mathbb {R}}^n\) is called an allocation. Given \(x \in {\mathbb {R}}^n\) and \(S\in 2^N\) let \(x(S)=\sum _{{i \in S}} x_i\). An allocation \(x \in {\mathbb {R}}^n\) is said to be efficient, or a preimputation, for a game \(v \in {\mathcal {G}}^N\) if \(x(N)=v(N)\). The set of all efficient allocations for game v is the hyperplane \(H(v)=\{x\in {\mathbb {R}}^n: x(N)=v(N)\}\). Given some class of games \({\mathcal {F}}\subset {\mathcal {G}}^N\), a solution on \({\mathcal {F}}\) is a mapping \(\varphi : {\mathcal {F}} \rightarrow {\mathbb {R}}^n\) that associates with each game \(v\in {\mathcal {F}}\) a preimputation \(\varphi (v) \in H(v)\). We say that \(\varphi \) satisfies:
-
Aggregate monotonicity (Megiddo 1974) if for each \(v,w \in {\mathcal {F}}\), if \(v(N)<w(N)\) and \(v(S)=w(S)\) for all \(S\in 2^N\), \(S\not =N\), then \(\varphi _i(v)\le \varphi _i(w)\) for all \(i\in N\).
The set of imputations of a game \(v \in {\mathcal {G}}^N\) is defined as \(I(v)=\bigl \{x\in H(v) : x_{i}\ge v(\{i\}) \text { for all } i \in N\bigr \}\). A game \(v\in {\mathcal {G}}^N\) is called essential if \(I(v)\not =\emptyset \). Let \({\mathcal {E}}^N\) be the set of all essential games with player set N. Clearly, \(v\in {\mathcal {E}}^N\) if and only if \(v(N)\ge {\sum _{i\in N}} v(\{i\})\). The core of a game \(v\in {\mathcal {G}}^N\) is the set \(C(v)=\bigl \{x\in I(v): x(S) \ge v(S) \text { for all } S \in 2^N\bigr \}\). The allocations that belong to the core are called stable allocations. A game \(v\in {\mathcal {G}}^N\) is called balanced if its core is non-empty. A family \(\Sigma \) of non-empty coalitions of N is called balanced if there are positive weights \(0< \delta _{S}\le 1\), one for each \(S\in \Sigma \), such that \({\sum _{S\in \Sigma :i\in S}} \delta _S=1\) for all \(i \in N\). A balanced family \(\Sigma \) is minimal if for each balanced family \(\Sigma '\) with \(\Sigma '\subset \Sigma \) we have \(\Sigma '=\Sigma \). The Bondareva-Shapley condition establishes that a game \(v\in {\mathcal {G}}^N\) is balanced if and only if \({\sum _{S\in \Sigma }}\delta _{S}v(S)\le v(N)\) for every balanced family \(\Sigma \) with positive weights \(\{\delta _{S}:S\in \Sigma \}\). In fact, a game is balanced if and only if all balanced inequalities are satisfied for minimal balanced families. Let \({\mathcal {B}}^N\) be the set of all balanced games with player set N. If \(v\in {\mathcal {B}}^N\) then C(v) is a non-empty convex polytope of dimension at most \(n-1\). A game \(v\in {\mathcal {G}}^N\) is convex if \(v(S\cup T)+v(S \cap T)\ge v(S)+v(T)\) for all \(S,T\in 2^N\). Let \({\mathcal {C}}^N\) be the set of all convex games with player set N. It is a well known fact that \({\mathcal {C}}^N\subset {\mathcal {B}}^N\).
Let \(v\in {\mathcal {G}}^N\). The utopia value of player \(i\in N\) is \(M_i(v)=v(N)-v(N\backslash \{i\})\). The minimal right of player \(i\in N\) is defined as
Tijs and Lipperts (1982) introduce the core cover of a game \(v\in {\mathcal {G}}^N\) as the set \(CC(v)=\bigl \{x\in I(v): m_i(v) \le x_i \le M_i(v), \ i\in N\bigr \}\) and show that \(C(v)\subset CC(v)\). A game \(v\in {\mathcal {G}}^N\) is called compromise admissible if \(CC(v)\not = \emptyset \). A compromise admissible game \(v\in {\mathcal {G}}^N\) is compromise stable if \(C(v)=CC(v)\).
In general, given a convex polytope \(K \subset H(v)\) denote by \({\text {Vol}}(K)\) its \((n-1)\)-dimensional Lebesgue measure and by \(\mu (K)\) its center of gravity. The convexity of K ensures that \(\mu (K) \in K\). Also \(\mu (a+K)=a+\mu (K)\) for all \(a\in {\mathbb {R}}^n\). If \(K=\overset{s}{\sum _{i=1}{\bigcup }} K_i\) and \({\text {Vol}}\bigl (K_i \cap K_j \bigr )=0\) for all \(i\not = j\), then \(\mu (K)=\overset{s}{\sum _{i=1}} \rho _i\mu (K_i)\), where \(\rho _i=\tfrac{{\text {Vol}}(K_i)}{{\text {Vol}}(K)}\), \(i=1,\dots , s\). Let \({\text {Hull}}(P)={\text {Hull}}(\{P_1,\dots , P_s\})\) be the convex hull of the finite set of points \(P=\{P_i\}_{i=1}^s\subset {\mathbb {R}}^n\).
The core-center is a solution defined on the domain of games with a non-empty core (González-Díaz and Sánchez-Rodríguez 2007) as the mathematical expectation of the uniform distribution over the core of the game. Therefore, if \(v\in {\mathcal {B}}^N\) then the core-center of v is the center of gravity of C(v), i.e., \(\mu (v)=\mu (C(v))\).
Denote by \(\Sigma ^0=\{ S\in 2^N:S\not =\emptyset , S\not =N\}\). Given a game \(v\in {\mathcal {G}}^N\), the excess of a coalition \(S\in 2^N\) with respect to a preimputation \(x\in H(v)\) is \(e(S,x)=v(S)-x(S)\). Denote by \(\theta (x)\in {\mathbb {R}}^{2^{n}-2}\) the vector whose coordinates are the excesses e(S, x), with \(S\in \Sigma ^0\), rearranged in non-increasing order, that is, \(\theta _{\ell }(x)\ge \theta _m(x)\) for every \(1\le \ell \le m\le 2^{n}-2\). For all \(\theta , \theta ' \in {\mathbb {R}}^{2^{n}-2}\), \(\theta \) is lexicographically smaller than \(\theta '\), written as \(\theta <_L \theta '\), if \(\theta _1<\theta _1'\) or if there is \(k\ge 2\) such that \(\theta _k<\theta '_k\) and \(\theta _m<\theta '_m\) for all \(m\le k-1\). The nucleolus of \(v\in {\mathcal {G}}^N\) is defined as:
Schmeidler (1969) showed that the nucleolus of an essential game exists and is unique. Analogously, Estévez-Fernández et al. (2017) defined the 1-nucleolus as \(\eta ^1(v)=\bigl \{x\in I(v) : \theta ^1(x)\le _L\theta ^1(y)\text { for all }y\in I(v) \bigr \}\) where if \(z\in I(v)\), \(\theta ^1(z)\in {\mathbb {R}}^{2n}\) is the vector whose coordinates are the excesses e(S, z) for all coalitions \(S\in \Sigma ^0\) such that \(|S|=1\) or \(|S|=n-1\), rearranged in non-increasing order. Naturally, the 1-nucleolus of an essential game exists and is unique.
A game \(v \in {\mathcal {G}}^N\) is additive if \(v(S)={\sum _{i \in S}} v(\{i\})\) for all \(S \in 2^N\), in which case \(C(v)=I(v)=\bigl \{\bigl (v(\{i\}) \bigr )_{i\in N} \bigr \}\). Thus, an additive game \(v\in {\mathcal {G}}^N\) is characterized by the vector \(a=\bigl (v(\{i\}) \bigr )_{i\in N} \in {\mathbb {R}}^N\). To simplify the notation, we will identify by the same letter both the vector and the corresponding additive game. A game \(v \in {\mathcal {G}}^N\) is zero-normalized if \(v(\{i\})=0\) for each player \(i \in N\). Let \({\mathcal {G}}_{0}^N\) be the set of all coalitional games with player set N that are zero-normalized. Given a game \(v \in {\mathcal {G}}^N\) the zero-normalization of v is the game \(v_0\in {\mathcal {G}}_{0}^N\) defined by \(v_0(S)=v(S)-{\sum _{i\in S}} v(\{i\})\) for all \(S \in 2^N\). Clearly, a game \(v\in {\mathcal {G}}^N\) and its zero-normalization \(v_0 \in {\mathcal {G}}_{0}^N\) satisfy that \(v=a+v_0\), where \(a=\bigl (v(\{i\}) \bigr )_{i\in N}\). Let us denote \({\mathcal {E}}_0^N={\mathcal {G}}_{0}^N\cap {\mathcal {E}}^N\), \({\mathcal {B}}_{0}^N={\mathcal {G}}_{0}^N\cap {\mathcal {B}}^N\), and \({\mathcal {C}}_{0}^N={\mathcal {G}}_{0}^N\cap {\mathcal {C}}^N\) the set of zero-normalized games that are essential, balanced, and convex respectively.
A balanced game \(v \in {\mathcal {B}}^N\) is called exact if for all \(S \in 2^N\), there is \(x \in C(v)\) such that \(x(S)=v(S)\) or, equivalently, if \(v(S)=\min \{x(S): x \in C(v)\}\) for all \(S \in 2^N\). The exact envelope of a game \(v \in {\mathcal {B}}^N\) is the game \(v^e\in {\mathcal {B}}^N\) defined by \(v^e(S)=\min \{x(S): x \in C(v)\}\), for every \(S\in 2^N\). The exact envelope \(v^e \in {\mathcal {B}}^N\) is the unique exact game for which \(C(v^e)=C(v)\).
A bankruptcy problem with set of claimants N is a pair (E, d) where \(E\ge 0\) is the endowment to be divided and \(d\in {\mathbb {R}}^N\) is the vector of claims satisfying \(d_i\ge 0\) for all \(i\in N\) and \(E\le {\sum _{i\in N}} d_i\). We denote the class of bankruptcy problems with set of players N by \({\mathcal {P}}^N\). The bankruptcy game \(w\in {\mathcal {G}}^N\) associated with the bankruptcy problem \((E, d)\in {\mathcal {P}}^N\) is defined by \(w(S)=\max \bigl \{0,\ E - {\sum _{j\in N\backslash S}} d_j\bigr \}\) for all \(S \in 2^N\). The class of bankruptcy games is a proper subclass of the class of convex games. For each bankruptcy problem \((E, d)\in {\mathcal {P}}^N\), the constraint equal awards rule, \({\text {CEA}}(E,d)\) is given, for each \(i\in N\), by \({\text {CEA}}_i(E,d)=\min \{ d_i, \lambda \}\) where \(\lambda \in {\mathbb {R}}\) is chosen so that \({\sum _{i \in N}} \min \{ d_i, \lambda \} =E\). The Talmud rule, \({\text {T}}\), assigns to each bankruptcy problem \((E, d)\in {\mathcal {P}}^N\) and each \(i\in N\) the value \({\text {T}}_i(E,d)={\text {CEA}}_i(E,\tfrac{1}{2}d)\) if \(E\le \tfrac{1}{2}{\sum _{i \in N}} d_i\) and \({\text {T}}_i(E,d)=d-{\text {CEA}}_i({\sum _{i \in N}} d_i-E,\tfrac{1}{2}d)\) if \(E\ge \tfrac{1}{2}{\sum _{i \in N}} d_i\). Aumann and Maschler (1985) show that the Talmud rule of a bankruptcy problem \((E, d)\in {\mathcal {P}}^N\) is the nucleolus of the associated bankruptcy game \(w\in {\mathcal {G}}^N\), i.e., \(\eta (w)={\text {T}}(E,d)\).
3 Monotonicity of the nucleolus for 3-player essential games
For games with just two players the nucleolus and the core-center coincide. If \(N=\{1,2\}\) then \({\mathcal {E}}^N={\mathcal {B}}^N={\mathcal {C}}^N=\bigl \{ (v_{1},v_{2}, E) \in {\mathbb {R}}^{3}: v_{1}+v_{2} \le E \bigr \}\) and the core of v is the line segment with endpoints \((v_{1},E-v_{1})\) and \((E-v_{2},v_{2})\). Therefore
so, both the nucleolus and the core-center are the middle point of that segment (Fig. 1).
Proposition 3.1
On the domain of essential games with just two players the core-center and the nucleolus are aggregate monotonic.
Proof
Let \(N=\{1,2\}\), \((v_{1},v_{2} )\in {\mathbb {R}}^2\) and \(i\in N\). The coordinate function \(\mu _i :[v_{1}+v_{2},\infty ) \rightarrow {\mathbb {R}}\) that assigns to each \(E\in [v_{1}+v_{2},\infty )\) the value \(\mu _i((v_{1},v_{2},E))\) is a monotonically increasing linear function. Therefore, \(\mu \) satisfies aggregate monotonicity on \({\mathcal {E}}^N\). Recall that \(\eta (v)=\mu (v)\) for all \(v\in {\mathcal {E}}^N\). \(\square \)
Let us recall some properties of the nucleolus of an essential game with a general player set \(N=\{1, \dots , n\}\) before turning to the particular case when \(N=\{1,2,3\}\). It is well known that if \(v\in {\mathcal {E}}^N\), \(a=\bigl ( v(\{i\}) \bigr )_{i\in N}\), and \(v_0\in {\mathcal {E}}_0^N\) is the zero-normalization of v then \(\eta (v)=a+\eta (v_0)\). Let \({\mathscr {B}}\) be a non-empty collection of proper coalitions and \(b\ge 1\) its cardinality. Following Reijnierse and Potters (1998), we define the excess map \(E_{{\mathscr {B}}}:I(v) \rightarrow {\mathbb {R}}^{{\mathscr {B}}}\) by \(E_{{\mathscr {B}}}(x)_S=e(S,x)\) for all \(x\in I(v)\) and \(S\in E_{{\mathscr {B}}}\). The coordinate ordering map \(\theta _{E_{{\mathscr {B}}}} :{\mathbb {R}}^{E_{{\mathscr {B}}}} \rightarrow {\mathbb {R}}^b\) orders the coordinates of a vector in \({\mathbb {R}}^{E_{{\mathscr {B}}}}\) in decreasing order. Let \(\le _L\) be the lexicographic order on \({\mathbb {R}}^b\). The \({\mathscr {B}}\)-nucleolus of v is defined by
The \({\mathscr {B}}\)-nucleolus is a non-empty subset of I(v) that, in general, may consist of more than one point. Naturally, \(\eta (v)=\eta (\Sigma ^0,v)\). We say that a collection \({\mathscr {B}}\) determines the nucleolus of v if \(\eta (v)=\eta ({\mathscr {B}},v)\). Reijnierse and Potters (1998) show that if \(v\in {\mathcal {G}}_{0}^N\) then \({\mathscr {B}}=\{S\in \Sigma ^0: v(S)\ge 0\}\) determines the nucleolus of v. As a consequence, changing negative coalition values into zero does not change the nucleolus of a zero-normalized game. Given \(v\in {\mathcal {E}}^N\) let \(v^+\in {\mathcal {E}}^N\) be the game defined by \(v^+(S)=\max \{ 0, v(S) \}\) for all \(S\in 2^N\).
Lemma 3.2
Let \(v\in {\mathcal {E}}^N\), \(a=\bigl ( v(\{i\}) \bigr )_{i\in N}\), and \(v_0\in {\mathcal {E}}_0^N\) the zero-normalization of v. Then \(\eta (v)=a+\eta (v_0^+)\).
Proof
We know that \(\eta (v)=a+\eta (v_0)\). Since \({\mathscr {B}}=\{S\in \Sigma ^0: v_0(S)\ge 0\}\) determines the nucleolus of the zero-normalized game \(v_0\in {\mathcal {E}}^N\), we have that \(\eta ({\mathscr {B}},v_0)=\eta (v_0)\). For each \(\varepsilon >0\) let \(v_0^{\varepsilon }(S)=v_0(S)\) if \(S\in {\mathscr {B}}\cup N\) and \(v_0^{\varepsilon }(S)=\varepsilon v_0(S)\) otherwise. Clearly, \(v_0^{\varepsilon } \in {\mathcal {E}}^N\) and \({\mathscr {B}}\) determines the nucleolus of \(v_0^{\varepsilon }\). Then, \(\eta (v_0^{\varepsilon })=\eta ({\mathscr {B}},v_0^{\varepsilon })=\eta ({\mathscr {B}},v_0)=\eta (v_0)\). Since the nucleolus is a continuous function and \(v_0^+={\sum _{\varepsilon \rightarrow 0}{\lim }} v_0^{\varepsilon }\) we conclude that \(\eta (v_0^*)=\eta (v_0)\). \(\square \)
Another important property satisfied by the nucleolus is anonymity. The nucleolus is independent of the names given to the players, i.e., if \(\pi :N \rightarrow N\) is a permutation of N then for each \(v\in {\mathcal {E}}^N\), \(\pi (\eta (v))=\eta (w)\) where \(w(S)=v(\pi (S))\) for all \(S\in 2^N\).
Now, we consider games with just three players, so let \(N=\{1,2,3\}\). According to Lemma 3.2, in order to find a formula to compute the nucleolus we can restrict our attention to games that belong to \({\mathcal {E}}_{0^+}^N\), that is, the zero-normalized essential games for which the values of the characteristic function are non-negative. Given \(v\in {\mathcal {E}}_{0^+}^N\) denote \(v_{-3}=v(\{1,2\})\), \(v_{-2}=v(\{1,3\})\), \(v_{-1}=v(\{2,3\})\), and \(E=v(\{1,2,3\})\). Since the nucleolus satisfies anonymity, we can assume that the players are ordered so that \(0\le v_{-3}\le v_{-2} \le v_{-1}\). Then, as \(v(\{1\})=v(\{2\})=v(\{3\})=0\), the class \({\mathcal {E}}_{0^+}^N\) can be identified with the set \({\mathcal {E}}_{0^+}^N=\bigl \{(v_{-3},v_{-2}, v_{-1}, E) \in {\mathbb {R}}^4: 0\le v_{-3}\le v_{-2} \le v_{-1}, \ E\ge 0 \bigr \}\). Now, we give an analytic formula for the nucleolus of a game that belongs to \({\mathcal {E}}_{0^+}^N\), the details of the proof are presented in the “Appendix”.
Proposition 3.3
Let \(N=\{1,2,3\}\) and \(v=(v_{-3},v_{-2},v_{-1},E)\in {\mathcal {E}}_{0^+}^N\).
-
1.
If \(v_{-1}<v_{-2}+v_{-3}\) then
$$\begin{aligned} \eta _1(v)&= {\left\{ \begin{array}{ll} 0 &{} \text {if } E\le 2v_{-1}-v_{-2}-v_{-3}\\ {\vspace{3pt}} \tfrac{1}{3}\bigl ( E+v_{-3}+v_{-2}-2v_{-1} \bigr ) &{} \text {if } 2v_{-1}-v_{-2}-v_{-3} \le E \le 2(v_{-2}+v_{-3})-v_{-1}\\ {\vspace{3pt}} \tfrac{1}{2}\bigl ( E-v_{-1} \bigr ) &{} \text {if } 2(v_{-2}+v_{-3})-v_{-1} \le E \le 3v_{-1}\\ {\vspace{3pt}} \tfrac{1}{3}E &{} \text {if } 3v_{-1}\le E \end{array}\right. } \\ \eta _2(v)&= {\left\{ \begin{array}{ll} 0 &{} \text {if } E\le v_{-2}-v_{-3}\\ {\vspace{3pt}} \tfrac{1}{2}\bigl ( E+v_{-3}-v_{-2} \bigr ) &{} \text {if } v_{-2}-v_{-3}<E\le 2v_{-1}-v_{-2}-v_{-3}\\ {\vspace{3pt}} \tfrac{1}{3}\bigl ( E+v_{-3}-2v_{-2}+v_{-1}\bigr ) &{} \text {if } 2v_{-1}-v_{-2}-v_{-3} \le E \le 2(v_{-2}+v_{-3})-v_{-1}\\ {\vspace{3pt}} \tfrac{1}{4}\bigl ( E+2v_{-3} -2v_{-2}+v_{-1}\bigr ) &{} \text {if } 2(v_{-2}+v_{-3})-v_{-1} \le E \le v_{-1}+2v_{-3}\\ {\vspace{3pt}} \tfrac{1}{2}\bigl ( E-v_{-2} \bigr ) &{} \text {if } v_{-1}+2v_{-3} \le E\le v_{-1}+2v_{-2} \\ {\vspace{3pt}} \tfrac{1}{4}\bigl ( E+v_{-1} \bigr ) &{} \text {if } v_{-1}+2v_{-2} \le E\le 3v_{-1}\\ {\vspace{3pt}} \tfrac{1}{3}E &{} \text {if } 3v_{-1}\le E \end{array}\right. } \\ \eta _3(v)&= {\left\{ \begin{array}{ll} E &{} \text {if } E\le v_{-2}-v_{-3}\\ {\vspace{3pt}} \tfrac{1}{2}\bigl ( E-v_{-3}+v_{-2} \bigr ) &{} \text {if } v_{-2}-v_{-3}<E\le 2v_{-1}-v_{-2}-v_{-3}\\ {\vspace{3pt}} \tfrac{1}{3}\bigl ( E-2v_{-3}+v_{-2}+v_{-1} \bigr ) &{} \text {if } 2v_{-1}-v_{-2}-v_{-3} \le E \le 2(v_{-2}+v_{-3})-v_{-1}\\ {\vspace{3pt}} \tfrac{1}{4}\bigl ( E-2v_{-3} +2v_{-2}+v_{-1}\bigr ) &{} \text {if } 2(v_{-2}+v_{-3})-v_{-1} \le E \le v_{-1}+2v_{-3} \\ {\vspace{3pt}} \tfrac{1}{2}\bigl ( v_{-2}+v_{-1} \bigr ) &{} \text {if } v_{-1}+2v_{-3} \le E\le v_{-1}+2v_{-2} \\ {\vspace{3pt}} \tfrac{1}{4}\bigl ( E+v_{-1} \bigr ) &{} \text {if } v_{-1}+2v_{-2} \le E\le 3v_{-1}\\ {\vspace{5pt}} \tfrac{1}{3}E &{} \text {if } 3v_{-1}\le E \end{array}\right. } \end{aligned}$$ -
2.
If \(v_{-1}\ge v_{-2}+v_{-3}\) then
$$\begin{aligned} \eta _1(v)&= {\left\{ \begin{array}{ll} 0 &{} \qquad \text {if } E\le v_{-1}\\ {\vspace{3pt}} \tfrac{1}{2}\bigl ( E-v_{-1} \bigr ) &{}\qquad \text {if } v_{-1}< E \le 3v_{-1}\\ {\vspace{3pt}} \tfrac{1}{3}E &{}\qquad \text {if } 3v_{-1}\le E \end{array}\right. } \\ \eta _2(v)&= {\left\{ \begin{array}{ll} 0 &{} \text {if } E\le v_{-2}-v_{-3}\\ \tfrac{1}{2}\bigl ( E+v_{-3}-v_{-2} \bigr ) &{} \text {if } v_{-2}-v_{-3}<E\le v_{-1}\\ {\vspace{3pt}} \tfrac{1}{4}\bigl ( E+2v_{-3} -2v_{-2}+v_{-1}\bigr ) &{} \text {if } v_{-1}< E \le v_{-1}+2v_{-3}\\ {\vspace{3pt}} \tfrac{1}{2}\bigl ( E-v_{-2} \bigr ) &{} \text {if } v_{-1}+2v_{-3} \le E\le v_{-1}+2v_{-2} \\ {\vspace{3pt}} \tfrac{1}{4}\bigl ( E+v_{-1} \bigr ) &{} \text {if } v_{-1}+2v_{-2} \le E\le 3v_{-1}\\ {\vspace{3pt}} \tfrac{1}{3}E &{} \text {if } 3v_{-1}\le E \end{array}\right. } \\ \eta _3(v)&= {\left\{ \begin{array}{ll} E &{} \text {if } E\le v_{-2}-v_{-3}\\ {\vspace{3pt}} \tfrac{1}{2}\bigl ( E-v_{-3}+v_{-2} \bigr ) &{} \text {if } v_{-2}-v_{-3}<E\le v_{-1}\\ {\vspace{3pt}} \tfrac{1}{4}\bigl ( E-2v_{-3} +2v_{-2}+v_{-1}\bigr ) &{} \text {if }v_{-1} \le E \le v_{-1}+2v_{-3} \\ {\vspace{3pt}} \tfrac{1}{2}\bigl ( v_{-2}+v_{-1} \bigr ) &{} \text {if } v_{-1}+2v_{-3} \le E\le v_{-1}+2v_{-2} \\ {\vspace{3pt}} \tfrac{1}{4}\bigl ( E+v_{-1} \bigr ) &{} \text {if } v_{-1}+2v_{-2} \le E\le 3v_{-1}\\ {\vspace{3pt}} \tfrac{1}{3}E &{} \text {if } 3v_{-1}\le E \end{array}\right. } \end{aligned}$$
Leng and Parlar (2010) provide an analytic formula for the nucleolus of a 3-player superadditive game. Proposition 3.3 not only presents a simplified version of that result but also allows us to compute the nucleolus of an arbitrary 3-player essential game. Certainly, if \(N=\{1,2,3\}\) and \(w\in {\mathcal {E}}^N\) then \(\eta (w)\) can be obtained following the steps:
-
1.
Compute \(w_0\in {\mathcal {E}}_0^N\), the zero-normalization of game w. Let \(a=\bigl ( w(\{i\}) \bigr )_{i\in N}\).
-
2.
Compute the game \(w_0^+\in {\mathcal {E}}_{0^+}^N\) given by \(w_0^+(S)=\max \{0,w_0(S)\}\) for all \(S\in 2^N\).
-
3.
Find a permutation \(\pi :N \rightarrow N\) such that the game \(v=w_0^+\circ \pi \), given by \(v(S)=w_0^+(\pi (S))\) for all \(S\in 2^N\), satisfies that \(v_{-3}\le v_{-2}\le v_{-1}\), where \(v_{-i}=v(N\backslash \{i\})\), \(i\in N\).
-
4.
Compute the nucleolus of \(v\in {\mathcal {E}}_{0^+}^N\) according to the analytic expressions given in Proposition 3.3.
-
5.
Compute the nucleolus of \(w_0\) as \(\eta (w_0)=\eta (w_0^+)=\pi ^{-1}(\eta (v))\).
-
6.
Compute the nucleolus of w as \(\eta (w)=a+\eta (w_0)\).
Let \(\alpha =(\alpha _1, \dots , \alpha _{n-1})\) be a vector consisting of positive real numbers. Define the \(\alpha \)-excess of a coalition S with respect to \(x\in {\mathbb {R}}^n\) to be \(e_{\alpha }(S,x)=\alpha _{|S|}(v(S)-x(S))\). Housman and Clark (1998) present a generalization of the nucleolus (and the per-capita nucleolus) called the \(\alpha \)-prenucleolus: the allocation that lexicographically minimizes the \(\alpha \)-excesses. The nucleolus is obtained when \(\alpha _k=1\) for all \(k\in N\). If \(|N|=3\), they show that the \(\alpha \)-prenucleoli satisfying \(\alpha _1\ge \alpha _2>0\) are coalitional monotonic. Coalitional monotonicity, introduced by Young (1985), is a stronger requirement than aggregate monotonicity: if the worth of a given coalition increases whereas the worths of all other coalitions remain the same then no member of that coalition is worse off. Then, as a corollary of the result in Housman and Clark (1998), the nucleolus is aggregate monotonic on the domain of essential games with three players. Here, we present a direct proof of this fact.
Theorem 3.4
If \(|N|=3\), the nucleolus satisfies aggregate monotonicity on \({\mathcal {E}}^N\).
Proof
It suffices to prove that the nucleolus is aggregate monotonic on \({\mathcal {E}}_{0^+}^N\). Fix a vector \((v_{-3},v_{-2},v_{-1})\in {\mathbb {R}}^N\) such that \(0\le v_{-3}\le v_{-2}\le v_{-1}\). If \(E\ge 0\) then \(v_E=(v_{-3},v_{-2},v_{-1},E)\in {\mathcal {E}}_{0^+}^N\). Now, for each \(i\in N\), consider the function \(\eta _i:[0,+\infty ) \rightarrow {\mathbb {R}}\) that assigns to each \(E\in [0,+\infty )\) the value \(\eta _i(E)=\eta _i(v_E)\). It is clear that \(\eta \) satisfies aggregate monotonicity on \({\mathcal {E}}_{0^+}^N\) if and only if \(\eta _i\) is monotonically increasing over \([0,+\infty )\) for all \(i\in N\). But, as a direct consequence of Proposition 3.3, each coordinate of the nucleolus, \(\eta _i\), \(i\in N\), is a monotonically increasing continuous piecewise linear function. \(\square \)
Remark 3.5
Leng and Parlar (2010) claim that if \(v_{-1}+2v_{-2}\le E \le 3v_{-1}\) and considering the game \(v'=(v_{-3},v_{-2}, v_{-1}, E')\in {\mathcal {B}}_{0}^N\) with \(E' \ge E\) sufficiently large so that \(E'\ge 3v_{-1}\) then one or two players may be worse off with the nucleolus. Naturally, this claim contradicts Theorem 3.4 and the aforementioned result in Housman and Clark (1998). Observe that the game \(v=(2,3,5,12)\in {\mathcal {B}}_{0}^N\) satisfies the required conditions and \(\eta (v)=(3.5, 4.25 , 4.25)\). But if \(v'=(2,3,5,E')\) with \(E'\ge 15\) then \(\eta (v')=\bigl (\tfrac{E'}{3},\tfrac{E'}{3},\tfrac{E'}{3}\bigl )\) and, certainly, \(\eta _i(v)\le 5\le \tfrac{E'}{3}=\eta _i(v')\) for all \(i\in \{1,2,3\}\).
4 Monotonicity of the core-center for 3-player balanced games
We start the section by providing an analytic formula for the core-center of a 3-player balanced game. Let \(N=\{1,2,3\}\). Recall that if \(v\in {\mathcal {B}}^N\) and \(v_0\in {\mathcal {B}}^N_0\) is its zero-normalization then \(\mu (v)=a+\mu (v_0)\) where \(a=\bigl ( v(\{i\}) \bigr )_{i\in N}\). Therefore, we restrict our attention to zero-normalized balanced games. As the core-center satisfies anonymity, as in the previous section, we will represent a zero-normalized game v as a vector \((v_{-3},v_{-2}, v_{-1}, E) \in {\mathbb {R}}^4\) such that \(v_{-3}\le v_{-2} \le v_{-1}\). Now, a game is balanced if and only if it satisfies the Bondareva-Shapley conditions. There are just five minimal balanced families for three players: \(\bigl \{ \{1\},\{2\},\{3\}\bigr \}\) with weights \(\delta _{\{1\}}= \delta _{\{2\}}= \delta _{\{3\}}=1\); \(\bigl \{ \{1\},\{2,3\}\bigr \}\) with weights \(\delta _{\{1\}}=\delta _{\{2,3\}}= 1\); \(\bigl \{ \{2\},\{1,3\}\bigr \}\) with weights \(\delta _{\{2\}}=\delta _{\{1,3\}}= 1\); \(\bigl \{ \{3\},\{1,2\}\bigr \}\) with weights \(\delta _{\{3\}}=\delta _{\{1,2\}}= 1\); and \(\bigl \{ \{1,2\},\{1,3\},\{2,3\}\bigr \}\) with weights \(\delta _{\{1,2\}}=\delta _{\{1,3\}}=\delta _{\{2,3\}}= \tfrac{1}{2}\). So, the balanced inequalities corresponding to the minimal balanced families are: \(0\le E\), \(v_{-1}\le E\), \(v_{-2}\le E\), \(v_{-3}\le E\), and \(\tfrac{1}{2}\bigl ( v_{-3}+v_{-2}+v_{-1}\bigr ) \le E\). If we denote \(\alpha =\max \bigl \{0, v_{-1}, \tfrac{1}{2}( v_{-1}+v_{-2}+v_{-3}) \bigr \}\), the class \({\mathcal {B}}_0^N\) can be represented by the set
Given \(v=(v_{-3},v_{-2}, v_{-1}, E) \in \mathcal {MB}^N\), if we define the vector of claims \(d=(d_1,d_2,d_3)\) by \(d_i=E-v_{-i}\) for \(i\in N\), then (E, d) is a bankruptcy problem. Let \(w\in {\mathcal {C}}^N\) be the bankruptcy game associated with \((E,d)\in {\mathcal {P}}^N\). Since w is a convex game (and then exact) it must be the exact envelope of v, i.e, \(w=v^e\). As a consequence, \(C(v)=C(w)\) and \(\mu (v)=\mu (w)\). Therefore, we may focus on the games that belong to \(\mathcal {MB}^N\) that are convex. Now, the convexity inequalities applied to a game \(v\in \mathcal {MB}^N\) imply that \(v_{-i}\ge 0\), \(E\ge v_{-i}\), and \(E\ge v_{-i}+v_{-j}\) for all \(i,j\in N\), \(i\not =j\). Then, the domain of zero-normalized convex games with three players can be represented by the set:
The imputation set of a 3-player zero-normalized convex game can be expressed as the union of the core of the game and up to three equilateral triangles. Moreover, the intersection of any two pieces of this decomposition will have null measure. Therefore, the center of gravity of the imputation set is the weighted average of the center of gravity of the decomposition triangles and the core-center of the game. The corresponding weights are the percentage of imputations that belong to each piece of the decomposition (Fig. 2).
Let \(v\in \mathcal {MC}^N\). The imputation set I(v) is the equilateral triangle with vertices \(a^1=(E,0,0)\), \(a^2=(0,E,0)\), and \(a^3=(0,0,E)\). Moreover, \({\text {Vol}}(I(v)) =\tfrac{\sqrt{3}}{2}E^{2}\) and \(\mu (I(v)) =(\tfrac{E}{3},\tfrac{E}{3},\tfrac{E}{3})\). The core C(v) is the non-empty convex polytope given by:
The core has (at most) 6 vertices: \(m^{3,2}=(0,v_{-3},E-v_{-3})\), \(m^{2,3}=(0,E-v_{-2},v_{-2})\), \(m^{3,1}=(v_{-3},0,E-v_{-3})\), \(m^{1,3}=(E-v_{-1},0,v_{-1})\), \(m^{2,1}=(v_{-2},E-v_{-2},0)\), and \(m^{1,2}=(E-v_{-1},v_{-1},0)\). Consider the three equilateral triangles: \(T^1={\text {Hull}}(\{m^{1,2},m^{1,3},a^1\})\), \(T^2={\text {Hull}}(\{m^{2,1},m^{2,3},a^2\})\), and \(T^3={\text {Hull}}(\{m^{3,1},m^{3,2},a^3\})\).
Proposition 4.1
Let \(N=\{1,2,3\}\) and \(v=(v_{-3},v_{-2},v_{-1}, E) \in \mathcal {MC}^N\).
-
1.
\(I(v)=T^1\cup T^2\cup T^3 \cup C(v)\). Moreover \({\text {Vol}}(T^i \cap T^j)=0\) and \({\text {Vol}}(T^i \cap C(v))=0\) for all \(i,j\in N\), \(i\not =j\).
-
2.
\(\mu (v)=(0,\tfrac{E}{2},\tfrac{E}{2})\) if \(v_{-3}=v_{-2}=0\) and \(E=v_{-1}\). Otherwise:
$$\begin{aligned} \mu _1(v)&=\tfrac{E^3-3Ev_{-1}^2+2v_{-1}^3-v_{-3}^3-v_{-2}^3 }{ 3\left( E^2-(v_{-3}^2+v_{-2}^2+v_{-1}^2)\right) },\, \mu _2(v)=\tfrac{E^3-3Ev_{-2}^2+2v_{-2}^3-v_{-3}^3-v_{-1}^3}{3\left( E^2-(v_{-3}^2+v_{-2}^2+v_{-1}^2)\right) }, \\ \mu _3(v)&=\tfrac{E^3-3Ev_{-3}^2+2v_{-3}^3-v_{-2}^3-v_{-1}^3}{3\left( E^2-(v_{-3}^2+v_{-2}^2+v_{-1}^2)\right) }. \end{aligned}$$ -
3.
\(\mu _1(v) \le \mu _2(v) \le \mu _3(v)\).
Proof
It is easy to check that \(I(v)=T^1\cup T^2\cup T^3 \cup C(v)\) and that \(T^1\), \(T^2\), \(T^3\), and C(v) have negligible intersections. Moreover, \({\text {Vol}}(T^1) =\tfrac{\sqrt{3}}{2}v_{-1}^{2}\), \({\text {Vol}}(T^2) =\tfrac{\sqrt{3}}{2}v_{-2}^{2}\), \({\text {Vol}}(T^3) =\tfrac{\sqrt{3}}{2}v_{-3}^{2}\), \(\mu (T^1) =(\tfrac{3E-2v_{-1}}{3},\tfrac{v_{-1}}{3},\tfrac{v_{-1}}{3})\), \(\mu (T^2) =(\tfrac{v_{-2}}{3},\tfrac{3E-2v_{-2}}{3},\tfrac{v_{-2}}{3})\), and \(\mu (T^3) =(\tfrac{v_{-3}}{3},\tfrac{v_{-3}}{3},\tfrac{3E-2v_{-3}}{3})\). Therefore \({\text {Vol}}(C(v))=\tfrac{\sqrt{3}}{2}\bigl ( E^2-v_{-1}^{2}-v_{-2}^{2}-v_{-3}^{2}\bigl )\). Obviously, \({\text {Vol}}(C(v))=0\) if and only if \(v_{-3}=v_{-2}=0\) and \(E=v_{-1}\). In fact, if \({\text {Vol}}(C(v))=0\) then either \(C(v)={\text {Hull}}(\{ a^2,a^3\})\), when \(E>0\), or \(C(v)=I(v)=\{(0,0,0)\}\), when \(E=0\). In both cases \(\mu (v)=(0,\tfrac{E}{2},\tfrac{E}{2})\). If \({\text {Vol}}(C(v))>0\), we have that \( \mu (I(v))=\sum _{i=1}^3 \frac{{\text {Vol}}(T^i)}{{\text {Vol}}(I(v))} \mu (T^i) + \frac{{\text {Vol}}(C(v))}{{\text {Vol}}(I(v))} \mu (v). \) From this equality the formula of \(\mu (v)\) is easily obtained. The inequalities \(\mu _1(v) \le \mu _2(v) \le \mu _3(v)\) are straightforward. \(\square \)
Let \(N=\{1,2,3\}\) and \(w\in {\mathcal {B}}^N\). In order to compute the core-center \(\mu (w)\) we have to follow the steps:
-
1.
Compute \(w_0\in \mathcal {MB}^N\), the zero-normalization of game w. Let \(a=\bigl ( w(\{i\}) \bigr )_{i\in N}\).
-
2.
Compute \(w^e\in {\mathcal {C}}^N\) the exact envelope of game \(w_0\).
-
3.
Compute \(w^e_0\in \mathcal {MC}^N\) the zero-normalization of game \(w^e\). Let \(b=\bigl ( w^e(\{i\}) \bigr )_{i\in N}\).
-
4.
Find a permutation \(\pi :N \rightarrow N\) such that the game \(v=w^e_0\circ \pi \), given by \(v(S)=w^e_0(\pi (S))\) for all \(S\in 2^N\), satisfies that \(v_{-3}\le v_{-2}\le v_{-1}\), where \(v_{-i}=v(N\backslash \{i\})\), \(i\in N\).
-
5.
Compute the core-center of \(v\in \mathcal {MC}^N\) according to the analytic expressions given in Proposition 4.1.
-
6.
Compute the core-center of \(w^e_0\) as \(\mu (w^e_0)=\pi ^{-1}(\mu (v))\).
-
7.
Compute the core-center of w as \(\mu (w)=a+\mu (w_0)=a+\mu (w^e)=a+b+\mu (w^e_0)\).
In the “Appendix”, we apply this procedure to derive an analytic formula for the core-center of an arbitrary zero-normalized 3-player balanced game.
Proposition 4.2
Let \(N=\{1,2,3\}\), \(v=(v_{-3},v_{-2}, v_{-1}, E) \in \mathcal {MB}^N\) and \(\alpha =\max \bigl \{0, v_{-1}, \tfrac{1}{2}( v_{-1}+v_{-2}+v_{-3}) \bigr \}\). Then:
-
1.
If \(v_{-k}\ge 0\), for all \(k \in N\),
$$\begin{aligned} \mu _1(v)&= {\left\{ \begin{array}{ll} \frac{1}{3}(E+v_{-3}+v_{-2}-2v_{-1}) &{}\text {if } E\in [\alpha ,v_{-3}+v_{-2}] \\ \frac{(E-v_{-1})(5E-3(v_{-2}+v_{-3})-2v_{-1})}{3(3E-2v_{-3}-2v_{-2}-v_{-1})}&{}\text {if } E\in (v_{-3}+v_{-2},v_{-3}+v_{-1}] \\ \frac{3E^3 - 3(2v_{-1} +v_{-2})E^2 + 3(v_{-1}^2 + 2v_{-2} v_{-1})E - v_{-3}^3 - 3 v_{-2} v_{-1}^2}{3(2 E^2 - 2E(v_{-1}+v_{-2}) +2 v_{-2} v_{-1} - v_{-3}^2)}&{}\text {if } E\in (v_{-3}+v_{-1},v_{-2}+v_{-1}] \\ \tfrac{E^3-3Ev_{-1}^2+2v_{-1}^3-v_{-3}^3-v_{-2}^3 }{ 3( E^2-(v_{-3}^2+v_{-2}^2+v_{-1}^2)) }&{} \text {if } E\in [v_{-2}+v_{-1}, +\infty ) \end{array}\right. }\\ \mu _2(v)&= {\left\{ \begin{array}{ll} \frac{1}{3}(E+v_{-3}+v_{-1}-2v_{-2}) &{}\text {if } E\in [\alpha ,v_{-3}+v_{-2}] \\ \frac{2E^2 + (3v_{-3} - 6v_{-2} + 2v_{-1})E - 3v_{-3}^2 - 3v_{-3}v_{-1} + 3v_{-2}^2 - v_{-1}^2}{3(3E - 2v_{-3} - 2v_{-2} - v_{-1})}&{}\text {if } E\in (v_{-3}+v_{-2},v_{-3}+v_{-1}] \\ \frac{3E^3 - 3(2v_{-2} + v_{-1}) E^2 + 3( v_{-2}^2 + 2 v_{-1} v_{-2})E - v_{-3}^3 - 3 v_{-1} v_{-2}^2}{3(2 E^2 - 2E(v_{-1}+v_{-2}) +2 v_{-2} v_{-1} - v_{-3}^2)}&{}\text {if } E\in (v_{-3}+v_{-1},v_{-2}+v_{-1}] \\ \frac{E^3-3Ev_{-2}^2+2v_{-2}^3-v_{-3}^3-v_{-1}^3}{3( E^2-(v_{-3}^2+v_{-2}^2+v_{-1}^2))}&{} \text {if } E\in [v_{-2}+v_{-1}, +\infty ) \end{array}\right. } \end{aligned}$$$$\begin{aligned} \mu _3(v)&= {\left\{ \begin{array}{ll} \frac{1}{3}(E+v_{-2}+v_{-1}-2v_{-3}) &{}\text {if } E\in [\alpha ,v_{-3}+v_{-2}] \\ \frac{2E^2 + (3v_{-2} - 6v_{-3} + 2v_{-1})E + 3v_{-3}^2 - 3v_{-2}^2 - 3v_{-2} v_{-1} - v_{-1}^2}{3(3E - 2v_{-3} - 2v_{-2} - v_{-1})}&{}\text {if } E\in (v_{-3}+v_{-2},v_{-3}+v_{-1}] \\ \frac{3(v_{-2} +v_{-1})E^2 - 3(v_{-3}^2 +v_{-2}^2 +2v_{-2} v_{-1} +v_{-1}^2)E + 2v_{-3}^3 + 3 v_{-2}^2 v_{-1} + 3v_{-2} v_{-1}^2}{3(2 E^2 - 2E(v_{-1}+v_{-2}) +2 v_{-2} v_{-1} - v_{-3}^2)}&{}\text {if } E\in (v_{-3}+v_{-1},v_{-2}+v_{-1}] \\ \tfrac{E^3-3Ev_{-3}^2+2v_{-3}^3-v_{-2}^3-v_{-1}^3}{3( E^2-(v_{-3}^2+v_{-2}^2+v_{-1}^2))} &{} \text {if } E\in [v_{-2}+v_{-1}, +\infty ) \end{array}\right. } \end{aligned}$$ -
2.
There is \(k \in N\) such that \(v_{-k}\le 0\).
-
If \(v_{-1}\le 0\) then \(\mu (v)=\bigl ( \tfrac{E}{3}, \tfrac{E}{3}, \tfrac{E}{3}\bigr )\) for \(E\in [0,+\infty )\).
-
If \(v_{-2}\le 0 \le v_{-1}\) then \(\mu (v)=\bigl ( \tfrac{E}{3}-\tfrac{2v_{-1}^2}{3(E+v_{-1})}, \tfrac{E}{3}+\tfrac{v_{-1}^2}{3(E+v_{-1})} ,\tfrac{E}{3}+\tfrac{v_{-1}^2}{3(E+v_{-1})}\bigr )\) for \(E\in [v_{-1},+\infty )\).
-
If \(v_{-3}\le 0 \le v_{-2}\) then

-
Moreover, \(\mu _1(v) \le \mu _2(v) \le \mu _3(v)\).
Once equipped with a formula for the core-center of a 3-player balanced game, we can establish that it is aggregate monotonic.
Theorem 4.3
If \(|N|=3\) then the core-center satisfies aggregate monotonicity on \({\mathcal {B}}^N\).
Proof
First note that it suffices to prove that the core-center is aggregate monotonic on \(\mathcal {MB}^N\). Now, fix a vector \((v_{-3},v_{-2}, v_{-1}) \in {\mathbb {R}}^3\) such that \(v_{-3}\le v_{-2} \le v_{-1}\) and let \(\alpha =\max \bigl \{0, v_{-1}, \tfrac{1}{2}( v_{-1}+v_{-2}+v_{-3}) \bigr \}\). Then \(v_E=(v_{-3},v_{-2}, v_{-1},E) \in \mathcal {MB}^N\) if \(E\in [\alpha ,+\infty )\). For each \(i\in N\) consider the function \(\mu _i: [\alpha ,+\infty )\rightarrow {\mathbb {R}}\) that assigns to each \(E\in [\alpha ,+\infty )\) the value \(\mu _i(E)=\mu _i(v_E)\). We already know, as a consequence of the general properties of the core-center proven by González-Díaz and Sánchez-Rodríguez (2007), that \(\mu _i\) is continuous for all \(i\in N\). We show in the “Appendix” that \(\mu _i\) is a differentiable function for all \(i\in N\) and that the derivatives \(\frac{d \mu _i}{d E}\) are non-negative. Therefore, \(\mu _i\) is monotonically increasing over \([\alpha ,+\infty )\) for all \(i\in N\) which implies that the core-center is aggregate monotonic on \(\mathcal {MB}^N\). \(\square \)
Example 4.4
Let \(N=\{1,2,3\}\) and consider the vector \((v_{-3},v_{-2},v_{-1})=(3,5,6)\). For each \(E\in [0,\infty )\) the game \(v_E=(3,5,6,E)\in {\mathcal {E}}_{0^+}^N\). The three coordinates of the nucleolus \(\eta (v_E)\) are depicted in Fig. 3 left. Note that the three coordinates preserve the ordering of the players, are piecewise linear, and monotonically increasing. Since \(\alpha = \max \{0,v_{-1},\tfrac{1}{2}(v_{-3}+v_{-2}+v_{-1})\}=\max \{0,6,7\}=7\), we know that \(v_E=(3,5,6,E)\in \mathcal {MB}^N\) for all \(E\in [7,+\infty )\). The game \(v_E\) is convex whenever \(E\ge 11\). The graphs of \(\mu _i(v_E)\), for \(i\in N\), are depicted in Fig. 3 right. Observe that the three paths preserve the ordering of the players, are smooth, and monotonically increasing.
5 Convex games with at least four players
Hokari (2000) shows that the nucleolus is not aggregate monotonic on the domain of convex games, and that this lack of monotonicity holds even if there are as few as four players.
We present an example that shows that the core-center is not aggregate monotonic on \({\mathcal {C}}^N\) when \(|N|>3\).
Theorem 5.1
On the domain of convex games with at least four players, the core-center is not aggregate monotonic.
Proof
Let \(N=\{1,2,3,4\}\). Consider the convex games \(v,w \in {\mathcal {C}}^N\) given by \(v(N)=1.5\), \(w(N)=1.6\); \(v(S)=w(S)=0.5\) if \(S=\{1,4\}\), \(S=\{2,4\}\) or \(S=\{3,4\}\); \(v(S)=w(S)=1\) if \(S=\{1,2,4\}\), \(S=\{1,3,4\}\) or \(S=\{2,3,4\}\); \(v(S)=w(S)=0\) otherwise.Footnote 2 The transformations \(g_v, g_w :{\mathbb {R}}^{3} \rightarrow {\mathbb {R}}^4\), \(g_v(x_1,x_2, x_{3})=(x_1,x_2,x_3, 1.5-x_1-x_2 - x_{3})\), \(g_w(x_1,x_2, x_{3})=(x_1,x_2,x_3, 1.6-x_1-x_2 - x_{3})\), define coordinate systems for C(v) and C(w) respectively, so that \({\hat{C}}(v)=g_v^{-1}(C(v))\) and \({\hat{C}}(w)=g_w^{-1}(C(w))\) are the projections of C(v) and C(w) onto \({\mathbb {R}}^{3}\) that simply “drop” the forth coordinate. Consequently, for all \(i=1,2,3\), \(\mu _i(v) = \mu _i({\hat{C}}(v))\) and \(\mu _i(w) = \mu _i({\hat{C}}(w))\). Now, the vertices of C(v) are: (0, 0, 0, 1.5), (0, 0, 0.5, 1), (0, 0.5, 0, 1), (0, 0.5, 0.5, 0.5), (0.5, 0, 0, 1), (0.5, 0, 0.5, 0.5), (0.5, 0.5, 0, 0.5), and (0.5, 0.5, 0.5, 0). So, \({\hat{C}}(v)\) is a cube with edge length \(\tfrac{1}{2}\), shown in Fig. 4 (left), and \(\mu (v)=(\tfrac{1}{4},\tfrac{1}{4},\tfrac{1}{4},\tfrac{3}{4})\). On the other hand, the core projection \({\hat{C}}(w)\), depicted in Fig. 4 (right), is a convex polytope with vertices: \(a_i=g_w^{-1}(A_i)\), \(i=1, \dots , 13\), where \(A_1=(0, 0, 0, 1.6)\), \(A_2=(0, 0, 0.6, 1)\), \(A_3=( 0, 0.6, 0, 1)\), \(A_4=( 0, 0.5, 0.6, 0.5)\), \(A_5=( 0, 0.6, 0.5, 0.5)\), \(A_6=( 0.6, 0, 0, 1)\), \(A_7=( 0.5, 0, 0.6, 0.5)\), \(A_8=( 0.6, 0, 0.5, 0.5)\), \(A_9=( 0.5, 0.6, 0, 0.5)\), \(A_{10}=( 0.6, 0.5, 0, 0.5)\), \(A_{11}=( 0.5, 0.5, 0.6, 0)\), \(A_{12}=( 0.5, 0.6, 0.5, 0)\), and \(A_{13}=( 0.6, 0.5, 0.5, 0)\). Consider the points
Clearly \(B={\text {Hull}}( \{a_1, a_2, a_3, a_6, b_1,b_2,b_3,b_4\})\) is a cube with edge length \(\tfrac{3}{5}\). Let us also consider the three right triangular prisms: \(P^1={\text {Hull}}(\{a_9,a_{10},b_1, a_{12}, a_{13},b_5\})\), \(P^2={\text {Hull}}(\{a_7,a_{8},b_2, a_{11}, a_{13},b_6\})\), and \(P^3={\text {Hull}}(\{a_4,a_{5},b_3, a_{11}, a_{12},b_7\})\). Finally, let \(Q={\text {Hull}}(\{a_{11},a_{12},a_{13},b_4\})\). Then \(B={\hat{C}}(w) \cup P^1 \cup P^2 \cup P^3 \cup Q\) and the intersection of any two pieces of the decomposition has volume zero. Moreover,  Then, \({\text {Vol}}\bigl ({\hat{C}}(w)\bigr )=\tfrac{623}{3000}\) and
Then, \({\text {Vol}}\bigl ({\hat{C}}(w)\bigr )=\tfrac{623}{3000}\) and
Finally, \(\mu (w)=g_w\bigl ( \mu \bigl ({\hat{C}}(w) \bigr ) \bigr )= (\tfrac{647}{2207},\tfrac{647}{2207},\tfrac{647}{2207},\tfrac{2029}{2816})\). Now, \(\mu _i(v)<\mu _i(w)\) if \(i=1,2,3\) but \(\mu _4(v)>\mu _4(w)\), then the core-center violates aggregate monotonicity. \(\square \)
Let \(v\in \mathcal {MC}^N\) be the game defined in Theorem 5.1. For each \(E\in [1.5,2]\) consider the game \(v_E\in {\mathcal {G}}^N\) given by \(v_E(S)=v(S)\) for all \(S\in 2^N\), \(S\not =N\), and \(v_E(N)=E\). It is easy to check that \(v_E\in {\mathcal {C}}^N\) for all \(E\in [1.5,2]\). The graph of the function \(\mu _4(E)=\mu _4(v_E)\) is depicted in Fig. 5. Clearly \(\mu _4\) is not monotonically increasing.
Remark 5.2
It has already being stated, see Hokari (2000), that the nucleolus is not aggregate monotonic on the domain of convex games with at least four players. Observe that being \(N=\{1,2,3,4\}\) and \(v,w \in {\mathcal {C}}^N\) the convex games given in Theorem 5.1, one has that \(\eta (v)=(0.25,0.25,0.25,0.75)\) and \(\eta (w)=(0.3,0.3,0.3,0.7)\) so \(\eta _i(v)<\eta _i(w)\) if \(i=1,2,3\) but \(\eta _4(v)>\eta _4(w)\).
6 Aggregate monotonicity on a subclass of bankruptcy games
Even though the nucleolus and the core-center are not aggregate monotonic in the class of convex games with at least four players, we can find subclasses of convex games in which both solutions satisfy the property. Our goal is to extend the class \(\mathcal {MC}^N\), defined in Sect. 4 when \(|N|=3\), to an arbitrary number of players and to exploit the connection of these games with bankruptcy problems.
We say that a game \(v\in {\mathcal {G}}^N\) belongs to the class \({\mathcal {M}}^N\) if \(v(S)=0\) whenever \(|S|<n-1\). To simplify the notation we write \(v_{-i}=v(N\backslash \{i\})\) for \(i\in N\), \(E=v(N)\), and assume, without loss of generality, that the players are ordered so that \(v_{-n}\le \dots \le v_{-1}\). Therefore, we can write \({\mathcal {M}}^N=\bigl \{ (v_{-1},\dots ,v_{-n}, E) \in {\mathbb {R}}^{n+1}: v_{-n}\le \dots \le v_{-1}\bigr \}\). Let \(\mathcal {MB}^N={\mathcal {M}}^N \cap {\mathcal {B}}^N\) and \(\mathcal {MC}^N={\mathcal {M}}^N \cap {\mathcal {C}}^N\) be the subclasses of games that belong to \({\mathcal {M}}^N\) that are balanced and convex respectively. Let us assume that \(|N|\ge 3\). Applying the Bondareva-Shapley conditions for balancedness and the definition of convexity, we deduce that:
Each game in \(\mathcal {MB}^N\) can be identified with a bankruptcy problem. Let \(v=(v_{-n},\dots ,v_{-1}, E)\in \mathcal {MB}^N\) and define the vector of claims \(d=\bigl (d_i\bigr )_{i\in N}=\bigl ( E-v_{-i}\bigr )_{i\in N}\). Then \((E,d) \in {\mathcal {P}}^N\) is a bankruptcy problem such that \(d_1\le \dots \le d_n\). Conversely, if \((E,d) \in {\mathcal {P}}^N\) with \(d_1\le \dots \le d_n\) then \(v=(E-d_n, \dots ,E-d_1,E) \in \mathcal {MB}^N\).
Proposition 6.1
Let \(|N|\ge 3\), \(v=(v_{-n},\dots ,v_{-1}, E) \in \mathcal {MB}^N\) and \(d=\bigl (d_i\bigr )_{i\in N}=\bigl ( E-v_{-i}\bigr )_{i\in N}\). If \(w\in {\mathcal {C}}^N\) is the bankruptcy game associated with the bankruptcy problem \((E,d) \in {\mathcal {P}}^N\), then:
-
1.
\(m_i(v)=w(\{i\})=m_i(w)\) and \(M_i(v)=d_i\) for all \(i\in N\).
-
2.
\(C(v)=C(w)\), \(w=v^e\) and \(\mu (v)=\mu (w)\).
-
3.
v is compromise stable and \(\eta (v)=\eta ^1(v)={\text {T}}(E,d)=\eta (w)\).
Proof
Since \(w\in {\mathcal {C}}^N\) is the bankruptcy game associated with the bankruptcy problem (E, d) we know, see Quant et al. (2005), that \(m_i(w)=w(\{i\})=\max \bigl \{0,\ E - {\sum _{j\not = i}} d_j\bigr \}\) and \(M_i(w)=\min \{E,d_i\}\) for all \(i\in N\). Let \(v=(v_{-n},\dots ,v_{-1}, E)\in \mathcal {MB}^N\). Then \(M_i(v)=E-v_{-i}=d_i\) for all \(i\in N\). Now, fix \(i\in N\) and take \(S\subset N\backslash \{i\}\).
-
If \(|S|\le n-3\) then \(v(S\cup \{ i\})=0\) and \(v(S\cup \{ i \} )-{\sum _{j\in S}} M_j(v)=-{\sum _{j\in S}} d_j\le 0\), being this value 0 for \(S=\emptyset \).
-
If \(S=N\backslash \{i,k\}\) with \(k\not =i\), then \(v(S\cup \{ i \} )-{\sum _{j\in S}} M_j(v)=v_{-k}-{\sum _{j\not = i,k}} d_j=E - {\sum _{j\not = i}} d_j\).
-
If \(S=N\backslash \{i\}\) then \(v(S\cup \{ i \} )-{\sum _{j\in S}} M_j(v)=v_{N}-{\sum _{j\not = i}} d_j=E - {\sum _{j\not = i}} d_j\).
Therefore, \(m_i(v)=\underset{S\subset N\backslash \{ i \} }{\max } \Bigl \{ v(S\cup \{ i \} )-{\sum _{j\in S}} M_j(v)\Bigr \}=\max \bigl \{0,\ E - {\sum _{j\not = i}} d_j\bigr \}=w(\{i\})\).
The game w is compromise stable so its core is:
Clearly, \(C(v)=\bigl \{x \in H(v): 0 \le x_i \le d_i \text {, for all }i \in N \bigr \}\). Since \(H(w)=H(v)\) we have that \(C(w)\subset C(v)\). In order to prove that \(C(v)\subset C(w)\) we have to check that if \(x\in C(v)\) then \(w(\{ i\}) \le x_i \le \min \{E,d_i\}\) for all \(i\in N\). Since \(x\in H(v)\) then for each \(i\in N\), \(x_i=E-{\sum _{j\not = i}} x_j\). Now \(x_i \le d_i\) and \(x_j\ge 0\) for all \(j\not =i\) so \(x_i=E-{\sum _{j\not = i}} x_j\le E\) and, consequently, \(x_i\le \min \{E,d_i\}\). On the other hand, since \(|N|\ge 3\) we have that \(x_i\ge 0\) and \(x_j\le d_j\) for all \(j\not =i\) so \(x_i=E-{\sum _{j\not = i}} x_j\ge E-{\sum _{j\not = i}} d_j\). Then, \(x_i\ge \max \{ 0, E-{\sum _{j\not = i}} d_j\}=w(\{i\})\) and \(C(v)=C(w)\). As w is a convex game, and therefore exact, and \(C(v)=C(w)\), we can conclude that w is the exact envelope of game v, i.e., \(w=v^e\). Obviously, \(\mu (v)=\mu (C(v))=\mu (C(w))=\mu (w)\).
Showing that \(CC(v)=\bigl \{x \in H(v): m_i(v) \le x_i \le M_i(v) \text {, for all }i \in N \bigr \} \subset C(v)\) is trivial. As \(C(v)\subset CC(v)\), v is compromise stable. Moreover, for all \(i\in N\), \(m_i(v)-v(\{i\})=m_i(v)=m_i(w)\). Then, applying property i) of Theorem 5.3 in Estévez-Fernández et al. (2017), \(\eta (v)=\eta ^1(v)={\text {T}}(E,d)\). Finally, \({\text {T}}(E,d)=\eta (w)\) because the Talmud rule of a bankruptcy problem \((E, d)\in {\mathcal {P}}^N\) is the nucleolus of its associated bankruptcy game \(w\in {\mathcal {G}}^N\). \(\square \)
For each bankruptcy problem \((E,d)\in {\mathcal {P}}^N\) we associate two different coalitional games: the bankruptcy game \(w \in {\mathcal {C}}^N\), which is always convex, and the balanced game \(v=(E-d_n,\dots , E-d_1, E)\in \mathcal {MB}^N\). Even though both games are different, in fact the bankruptcy game w is the exact envelope of v, their nucleolus and core-center coincide. Now, we want to identify the subclass of bankruptcy problems for which these two games coincide. Let \(\mathcal {PC}^N=\{(E,d)\in {\mathcal {P}}^N: d_1\le \dots \le d_n,\ d_n \le E \le d_1+d_2\}\) be the subclass of bankruptcy problems for which the endowment is bigger than the claims but less than the sum of any two of them.
Proposition 6.2
If \((E,d) \in \mathcal {PC}^N\), \(w\in {\mathcal {C}}^N\) is its associated bankruptcy game, and \(v=(E-d_n,\dots , E-d_1, E)\in \mathcal {MB}^N\) then \(v=w\in \mathcal {MC}^N\). Conversely, if \(v=(v_{-n},\dots ,v_{-1}, E) \in \mathcal {MC}^N\) and \(d=\bigl (d_i\bigr )_{i\in N}=\bigl ( E-v_{-i}\bigr )_{i\in N}\) then \((E,d) \in \mathcal {PC}^N\) and v is its associated bankruptcy game.
Proof
Let \((E,d) \in \mathcal {PC}^N\) and \(w\in {\mathcal {C}}^N\) is associated bankruptcy game. If \(S\in 2^N\) such that \(|S|<n-1\) then \(|N\backslash S|\ge 2\). Since \(E \le d_i+d_j\) for all \(\{i,j\}\subset N\) we conclude that
Then \(w=v=(E-d_n,\dots , E-d_1, E)\in \mathcal {MC}^N\). The proof of the other part is analogous. \(\square \)
Monotonicity requirements on rules have played an important role in the analysis of bankruptcy problems. Thomson (2019) provides a comprehensive survey of the rules and their relevant properties. For instance, a rule satisfies endowment monotonicity whenever the amount to divide increases then each claimant receives at least as much as he did initially.Footnote 3 Observe that the aggregate monotonicity of a solution for bankruptcy games is not equivalent to endowment monotonicity of the corresponding bankruptcy rule. In fact, aggregate monotonicity is a property that can not be expressed in terms of bankruptcy problems. Nevertheless, aggregate monotonicity on \(\mathcal {MC}^N\) has a translation to a meaningful requirement on \(\mathcal {PC}^N\). We say that a rule R on \({\mathcal {P}}^N\) satisfies:
-
Equal endowment and claims increment monotonicity if for each \((E,d)\in {\mathcal {P}}^N\) and each \((E',d')\in {\mathcal {P}}^N\) such that \(E'-E=d'_i-d_i>0\) for all \(i\in N\) then \(R(E,d) \le R(E',d')\).
A rule satisfies endowment and claims increment monotonicity whenever the endowment to be divided and all the claims increase by the same amount, then each claimant receives at least as much as he did initially. Naturally, any solution \(\varphi \) on \(\mathcal {MC}^N\) defines a rule on \(\mathcal {PC}^N\) that associates to a bankruptcy problem \((E,d)\in \mathcal {PC}^N\) the division between the claimants \(\varphi (E,d)=\varphi (v)\) where \(v=(E-d_n, \dots ,E-d_1,E)\in \mathcal {MC}^N\).
Proposition 6.3
Let \(\varphi \) be a solution that satisfies aggregate monotonicity on \(\mathcal {MC}^N\). Then \(\varphi \) satisfies equal endowment and claims increment monotonicity on \(\mathcal {PC}^N\).
Our goal is to prove that both the core-center and the nucleolus are aggregate monotonic on \(\mathcal {MC}^N\). In Sect. 4, in order to prove that the core-center is aggregate monotonic on the domain of convex games with three players, we rely on an analytic formula for the core-center derived from a decomposition of the imputation set as the union of the core of the game and several equilateral triangles. If, for an n-player game, its imputation set is the union of its core and several regular simplices that have negligible intersections, then we can provide an analytic formula for the core-center and, therefore, examine its monotonicity properties. For the class \(\mathcal {MC}^N\) such a decomposition exists.
If \(v=(v_{-n},\dots ,v_{-1}, E) \in \mathcal {MC}^N\), the imputation set I(v) is the regular simplex spanned by the n points \(a^i=(a^i_1, \dots , a^i_n)\in {\mathbb {R}}^n\), \(i\in N\), where \(a^i_i=E\) and \(a^i_j=0\) if \(i\not =j\). Moreover, \({\text {Vol}}(I(v)) =\tfrac{\sqrt{n}}{(n-1)!}E^{n-1}\) and \(\mu _i (I(v)) =\tfrac{E}{n}\) for \(i \in N\). The core is a non-empty convex polytope with at most \(n(n-1)\) vertices. In fact,
where \(m^{i,j}=(m^{i,j}_1, \dots ,m^{i,j}_n)\in {\mathbb {R}}^n\) is given by \(m^{i,j}_i=E-v_{-i}\), \(m^{i,j}_j=v_{-i}\), and \(m^{i,j}_k=0\) otherwise. For each \(i\in N\), let \(v_{\{i\}} \in {\mathcal {G}}^N\) be the game: \(v_{\{i\}} (N)=E\), \(v_{\{i\}} (S)=E-v_{-i}\) if \(S\not =N\) and \(i\in S\), and \(v_{\{i\}} (S)=0\) otherwise.
Proposition 6.4
Let \(|N|\ge 3\) and \(v=(v_{-n},\dots ,v_{-1}, E) \in \mathcal {MC}^N\).
-
1.
\(I(v)= C(v) \cup \Bigl ( \underset{i\in N}{\bigcup } C(v_{\{i\}}) \Bigr )\). Moreover, for all \(i,j\in N\), \(i\not =j\), the sets \(C(v_{\{i\}}) \cap C(v_{\{j\}})\) and \(C(v_{\{i\}}) \cap C(v)\) have null \((n-1)\)-measure.
-
2.
\(\mu (v)=(0,\tfrac{E}{n-1},\dots ,\tfrac{E}{n-1})\) if \(E=v_{-1}\) and \(v_{-i}=0\) for all \(i\in N\backslash \{1\}\). Otherwise, for each \(i\in N\):
$$\begin{aligned} \mu _i(v)=\frac{1}{n} \frac{E^{n}-nEv_{-i}^{n-1}+K_i}{E^{n-1}-L}, \end{aligned}$$where \(L=\overset{n}{\sum _{j=1}} v_{-j}^{n-1}\) and \(K_i=(n-1)v_{-i}^n- {\sum _{k\not =i}} v_{-k}^{n}\).
-
3.
\(\mu _i(v) \le \mu _j(v)\) for all \(i,j \in N\), \(i<j\).
Proof
For each \(i\in N\), consider the game \(w_{\{i\}} \in G^N\) given by \(w_{\{i\}}(N)=v_{-i}\) and \(w_{\{i\}} (S)=0\) otherwise. Clearly, \(C(w_{\{i\}})=I(w_{\{i\}})\). Then \(C(w_{\{i\}})\) is a regular simplex such that \({\text {Vol}}(C(w_{\{i\}} ))=\tfrac{\sqrt{n}}{(n-1)!} v_{-i}^{n-1}\) and \(\mu _j(C(w_{\{i\}})) = \tfrac{v_{-i}}{n}\) for all \(j\in N\). Now, \(v_{\{i\}} =e^i + w_{\{i\}}\) where \(e^i=(e^i_1, \dots , e^i_n)\in {\mathbb {R}}^n\) is given by \(e^i_i=E-v_{-i}\) and \(e^i_j=0\) for \(j\not = i\). As a consequence, \(C(v_{\{i\}})=e^i+ C(w_{\{i\}})\) and \(\mu (C(v_{\{i\}}) = e^i + \mu (C(w_{\{i\}})\) for all \(i\in N\). The decomposition of the imputation set and the fact that any two pieces have negligible intersection follow immediately. Clearly, \({\text {Vol}}(C(v))=0\) if \(E=v_{-1}\) and \(v_{-i}=0\) for all \(i>1\). In fact, if \({\text {Vol}}(C(v))=0\) then either \(C(v)={\text {Hull}}(\{a^2,\dots ,a^n\})\) when \(E>0\), or \(C(v)=I(v)=\{(0,\dots ,0)\}\) when \(E=0\). In both cases \(\mu (v)=(0,\tfrac{E}{n-1},\dots ,\tfrac{E}{n-1})\). If \({\text {Vol}}(C(v))>0\), we have that \(\mu (I(v))= \tfrac{{\text {Vol}}(C(v))}{{\text {Vol}}(I(v))}\mu (v) + \sum \nolimits _{i\in N} \tfrac{{\text {Vol}}( C(v_{\{i\}}) )}{{\text {Vol}}(I(v))} \mu (v_{\{i\}})\). From this equality, the expression for the core-center follows at once. Finally, a small manipulation shows that \(\mu _i(v) \le \mu _j(v)\) whenever \(i<j\). \(\square \)
Theorem 6.5
The core-center satisfies aggregate monotonicity on \(\mathcal {MC}^N\).
Proof
When \(|N|=2\) or \(|N|=3\) the result is a particular case of Proposition 3.1 and Theorem 4.3 respectively. The proof when \(|N|\ge 4\) mirrors that of Theorem 4.3 (details are in the “Appendix”). \(\square \)
Now, we want to establish that the nucleolus is aggregate monotonic on \(\mathcal {MC}^N\). The analysis is based on the property of first agent consistency.
Let \(|N|\ge 4\). For each \(v\in {\mathcal {B}}^N\) let \(v_{1,\eta _1(v)} \in {\mathcal {M}}^{N\backslash \{1\}}\) be the game defined, for all \(S\in 2^{N\backslash \{1\}}\), by
Estévez-Fernández et al. (2017) show that the 1-nucleolus satisfies the property of first agent consistency,Footnote 4 that is, if \(v\in {\mathcal {B}}^N\) and \(v_{1,\eta ^1_1(v)}\in {\mathcal {B}}^N\) then \(\eta ^1_i(v)=\eta ^1_i(v_{1,\eta ^1_1(v)})\) for all \(i\in N\backslash \{1\}\). Our next result, whose proof is left to the “Appendix”, adapts this property to the class \(\mathcal {MB}^N\).
Proposition 6.6
If \(v\in \mathcal {MB}^N\) then \(v_{1,\eta _1(v)} \in \mathcal {MB}^{N\backslash \{1\}}\) and \(\eta _i(v)=\eta _i(v_{1,\eta _1(v)})\) for all \(i\in N\backslash \{1\}\).
Proof
Let \(v=(v_{-n}, \dots , v_{-1}, E) \in \mathcal {MB}^N\). First, we prove that \(v_{1,\eta _1(v)} \in \mathcal {MB}^{N\backslash \{1\}}\). Denote \(w=v_{1,\eta _1(v)} \in {\mathcal {M}}^{N\backslash \{1\}}\). Obviously \(w(N\backslash \{1\})=E-\eta _1(v)\ge 0\), \(w_{-j}=w(N\backslash \{1,j\})=v_{-j}-\eta _1(v)\) for all \(j\in N\backslash \{1\}\) and \(w(N\backslash \{1\})\ge w_{-2}\). Therefore, \(w_{-n}\le \dots \le w_{-2}\le w(N\backslash \{1\})\). It remains to be proved that \((n-2)w(N\backslash \{1\})\ge {\sum _{j=2}{^{n}}} w_{-j}\) or, equivalently, \(\eta _1(v) \ge {\sum _{j=2}{^{n}}} v_{-j}-(n-2)E\).
Case 1: If \((n-2) E\ge {\sum _{i \in N}} v_{-i} =v_{-1}+ {\sum _{j=2}{^{n}}} v_{-j}\) then \({\sum _{j=2}{^{n}}} v_{-j}-(n-2)E\le -v_{-1}\). Clearly \({\sum _{j=2}{^{n}}} v_{-j}-(n-2)E\le -v_{-1}\le 0 \le \eta _1(v)\) when \(v_{-1}\ge 0\). But if \(v_{-1}<0\) then \(v_{-j}<0\) for all \(j\in N\backslash \{1\}\) and, since \(E\ge 0\), we have that \({\sum _{j=2}{^{n}}} v_{-j}-(n-2)E\le 0 \le \eta _1(v)\).
Case 2: Assume that \((n-2) E< {\sum _{i \in N}} v_{-i}\). Then
Now, simple calculations show that \(\frac{E+(1-n)v_{-1}+{\sum _{j=2}{^{n}}} v_{-j}}{n} \ge {\sum _{j=2}{^{n}}} v_{-j}-(n-2)E\) if and only if \((n-1)E \ge {\sum _{i \in N}} v_{-i}\). But the last inequality holds because \(v\in \mathcal {MB}^N\) so \(\eta _1(v)\ge {\sum _{j=2}{^{n}}} v_{-j}-(n-2)E\).
The second part of the result is a direct consequence of Proposition 6.1 and the fact that the 1-nucleolus satisfies first agent consistency. \(\square \)
Our next step is to compute the first coordinate of the nucleolus for a game in \(\mathcal {MB}^N\), that is to say, the first coordinate for the nucleolus of a bankruptcy game. The calculations are left to the “Appendix”
Proposition 6.7
Let \(v=(v_{-n}, \dots , v_{-1}, E)\in \mathcal {MB}^N\) and \(\alpha =\max \big \{ v_{-1}, \tfrac{1}{n-1} {\sum _{i\in N}} v_{-i} \big \}\). Then
Now, we focus our attention on the class \(\mathcal {MC}^N\) when \(|N|\ge 4\). Let \(v=(v_{-n}, \dots , v_{-1}, E) \in \mathcal {MC}^N\) and denote \(w=v_{1,\eta _1(v)} \in \mathcal {MB}^{N\backslash \{1\}}\). We will see that convexity of v implies that \((n-2)E\ge {\sum _{i\in N}} v_{-i}\) and so the formula for \(\eta _1(v)\) is simplified. One can not guarantee that \(w_{-2}=w(N\backslash \{1,2\})=v_{-2}-\eta _1(v)\ge 0\) so, in general, w is not convex. Nevertheless, we can compute \(\eta _1(v)\) and apply first agent consistency to obtain \(\eta _j(v)\) for \(j>1\). The calculations are made in the “Appendix”.
Proposition 6.8
Let \(|N|\ge 4\) and \(v=(v_{-n}, \dots , v_{-1}, E) \in \mathcal {MC}^N\). Then,
and, for all \(j \in N\backslash \{1\}\),
Now that we have an expression for the nucleolus of games that belong to \(\mathcal {MC}^N\), aggregate monotonicity follows immediately.
Theorem 6.9
The nucleolus satisfies aggregate monotonicity on \(\mathcal {MC}^N\).
Proof
When \(|N|=2\) or \(|N|=3\) the result is a particular case of Proposition 3.1 and Theorem 3.4 respectively. Assume that \(|N|\ge 4\). Fix a vector \((v_{-n},\dots , v_{-1}) \in {\mathbb {R}}^n\) such that \(0\le v_{-n}\le \dots \le v_{-1}\). For each \(i\in N\) consider the function \(\eta _i: [\alpha ,+\infty )\rightarrow {\mathbb {R}}\) that assigns to each \(E\in [\alpha ,+\infty )\) the value \(\eta _i(E)=\eta _i(v_E)\), where \(v_E=(v_{-n},\dots , v_{-1},E) \in \mathcal {MB}^N\). Proposition 6.8 shows that \(\eta _i\) is a continuous piecewise linear function such that \(\frac{d \eta _j}{d E} \ge 0\) on each piece. Therefore, \(\eta _j\) is monotonically increasing over \([\alpha ,+\infty )\) for each \(j\in N\), and, consequently \(\eta \) is aggregate monotonic on \(\mathcal {MC}^N\). \(\square \)
Remark 6.10
As a consequence of Proposition 6.3, Theorems 6.5 and 6.9, we conclude that the nucleolus and the core-center satisfy equal endowment and claims increment monotonicity on the subclass of bankruptcy problems \(\mathcal {PC}^N\).
7 Summary and discussion
In this paper we have analyzed whether or not the nucleolus and the core-center satisfy aggregate monotonicity on several classes of coalitional games. Some of the results were already known in the literature, and suitable references are given throughout the text, but all of these instances were revisited in the paper using new approaches. Here we provide a summary of the findings:
-
If \(|N|=3\).
-
If \(|N|>3\).
-
For all \(N=\{1, \dots , n\}\).
Moreover, the analytic formula for the coordinates of the nucleolus of a 3-player zero-normalized supperadditive game given by Leng and Parlar (2010) is extended in Proposition 3.3 in a simplified framework for any 3-player essential game. We also provide analytic expressions for the core-center of a 3-player zero-normalized balanced game (Proposition 4.2). We obtain generalizations of all these formulae to the class \(\mathcal {MC}^N\): for the nucleolus in Proposition 6.8 and for the core-center in Proposition 6.4.
The procedure developed to compute the core-center rule for bankruptcy problems in \(\mathcal {PC}^N\) can be extended for any given bankruptcy problem. For a bankruptcy game, Mirás Calvo et al. (2020) show that the set of imputations that are not stable can be partitioned through cores of particular bankruptcy games. This decomposition provides a backwards recurrence algorithm to compute the core-center rule. These findings for bankruptcy games could be the basis for a general method for convex or balanced games: one needs to find a decomposition of the imputation set as the union of the core of the game and some other pieces, preferably cores of games, with a simple structure. We would like to point out that the computation of the center of gravity of a general convex polyhedron is a specially challenging task. Since the center of gravity is a relevant point in problems arising in many different fields, finding instances where an analytic formula, or even an algorithm, is available for its computation is always valuable. Also bear in mind that the core-center is just the center of gravity (the centroid) of a particular type of convex polyhedron (the core). Therefore, the analytic formula for the core-center derived in this paper could be applied to computing the centroid of any core-like polyhedron of the class described.
Although, as Thomson (2019) remarks, many of the properties for bankruptcy rules consider changes in only one parameter at a time, there are situations in which several of them could change simultaneously. For instance, the dual property of order preservation under claims variations says that if an agent’s claim and the endowment increase by equal amounts then for any two other claimants the smaller one should gain as much as as the larger one. This property, in which two parameters change, is a weaker version of equal endowment and claims increment monotonicity. It will be worth examining the behavior of the central bankruptcy rules with respect to these two particular properties and, in general, when multiple parameters change simultaneously.
Young (1985) and Housman and Clark (1998) showed that if a rule always selects an allocation in the core then it violates coalitional monotonicity when the number of players is greater than three. Nevertheless, core selection and coalitional monotonicity are compatible on the domain of convex games: the Shapley value is such a rule. Zhou (1991) formulates a condition of weak coalitional monotonicity that the nucleolus satisfies: if the worth of a given coalition increases whereas the worths of all other coalitions remain the same, then the sum of the payoffs of the members of that coalition shouldn’t decrease. González-Díaz and Sánchez-Rodríguez (2007) prove that the core-center satisfies weak coalitional monotonicity. Obviously, coalitional monotonicity implies weak coalitional monotonicity. As a corollary of the results about the nucleolus, the core-center and aggregate monotonicity, it is clear that neither the nucleolus nor the core-center satisfy coalitional monotonicity on the domain of convex games with at least four players. So, similar questions to the ones we have responded in this paper could be raised concerning coalitional monotonicity. We conjecture that the core-center is coalitional monotonic on the domain of 3-player balanced games. Likely, in some subclasses of convex games, for instance \(\mathcal {MC}^N\), the nucleolus or the core-center could be coalitional monotonic.
Notes
A set-valued solution is said to be aggregate monotonic if it possesses a single-valued selection that is aggregate monotonic.
For \(n > 4\), this example can be adapted by adding dummy players.
A rule R satisfies endowment monotonicity if for each \((E,d)\in {\mathcal {P}}^N\) and each \(E'> E\) then \(R(E,d) \le R(E',d)\).
Notice that the definition of the game \(v_{1,\eta _1(v)}\) has been readjusted so that the value of the single player coalitions are positive, otherwise first agent consistency breaks down.
The general result is valid for any player set N.
References
Aumann RJ, Maschler M (1985) Game theoretic analysis of a bankruptcy problem from the Talmud. J Econ Theory 36:195–213
Estévez-Fernández A, Borm P, Fiestras-Janeiro MG, Mosquera MA, Sánchez-Rodríguez E (2017) On the 1-nucleolus. Math Methods Oper Res 86:309–329
González-Díaz J, Sánchez-Rodríguez E (2007) A natural selection from the core of a TU game: the core-center. Int J Game Theory 36:27–46
González-Díaz J, Mirás Calvo MA, Quinteiro Sandomingo C, Sánchez Rodríguez E (2015) Monotonicity of the core-center of the airport game. TOP 23:773–798
González-Díaz J, Mirás Calvo MA, Quinteiro Sandomingo C, Sánchez Rodríguez E (2016) Airport games: the core and its center. Math Soc Sci 82:105–115
Hokari T (2000) The nucleolus is not aggregate-monotonic on the domain of convex games. Int J Game Theory 29:133–137
Housman D, Clark L (1998) Core and monotonic allocation methods. Int J Game Theory 27:611–616
Leng M, Parlar M (2010) Analytic solution for the nucleolus of a three-player cooperative game. Naval Res Log 57:667–672
Maschler M, Peleg B, Shapley LS (1979) Geometric properties of the kernel, nucleolus, and related solution concepts. Math Oper Res 4:303–338
Megiddo N (1974) On the monotonicity of the bargaining set, the kernel and the nucleolus of a game. SIAM J Appl Math 27(2):355–358
Mirás Calvo MA, Quinteiro Sandomingo C, Sánchez Rodríguez E (2019) The core-center rule for the bankruptcy problem (preprint)
Mirás Calvo MA, Quinteiro Sandomingo C, Sánchez Rodríguez E (2016) Monotonicity implications to the ranking of rules for airport problems. Int J Econ Theory 12:379–400
Mirás Calvo M-A, Núñez Lugilde I, Quinteiro Sandomingo C, Sánchez Rodríguez E (2020). An algorithm to compute the core center rule of a claims problem with an application to the allocation of CO2 emissions (preprint)
Quant M, Borm P, Reijnierse H, van Velzen B (2005) The core cover in relation to the nucleolus and the Weber set. Int J Game Theory 33:491–503
Reijnierse H, Potters J (1998) The \({\cal{B}}\)-nucleolus of TU-games. Games Econ Behav 24:77–96
Schmeidler D (1969) The nucleolus of a characteristic function game. SIAM J Appl Math 17:1163–1170
Tauman Y, Zapechelnyuk A (2010) On (non-) monotonicity of cooperative solutions. Int J Game Theory 39:171–175
Thomson W (2019) How to divide when there isn’t enough. From Aristotle, the Talmud, and Maimonides to the axiomatics of resource allocation. Cambridge University Press, Cambridge
Tijs SH, Lipperts F (1982) The hypercube and the core cover of the n-person cooperative games. Cahiers Centre d’Études Recherche Opérationnelle 24:27–37
Young HP (1985) Monotonic solutions of cooperative games. Int J Game Theory 14:65–72
Zhou L (1991) A weak monotonicity property of the nucleolus. Int J Game Theory 19:407–411
Acknowledgements
This work was supported by FEDER/Ministerio de Ciencia, Innovación y Universidades. Agencia Estatal de Investigación/MTM2017-87197-C3-2-P and PID2019-106281GB-I00 (AEI/FEDER,UE).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of Proposition 3.3
Let \(N=\{1,2,3\}\) and \(v=(v_{-3},v_{-2}, v_{-1}, E) \in {\mathcal {E}}_{0^+}^N\) so that \(0\le v_{-3}\le v_{-2} \le v_{-1}\) and \(E\ge 0\). First, let us assume that v is a balanced game, that is, \(E\ge \alpha =\max \bigl \{v_{-1}, \tfrac{1}{2}( v_{-1}+v_{-2}+v_{-3}) \bigr \}\). Clearly, for 3-player balanced games the 1-nucleolus and the nucleolus coincide, so \(\eta (v)=\eta ^1(v)\). Estévez-Fernández et al. (2017) proveFootnote 5 that if \(v\in \mathcal {MB}^N\) and we define the vector \(d=(d_1,d_2,d_3)\) as \(d_i=E-v_{-i}\) for all \(i\in N\) then \((E,d)\in \mathcal {P^N}\) and the 1-nucleolus of v coincides with the Talmud rule of (E, d), i.e., \(\eta ^1(v)=T(E,d)\). Then, the formula for \(\eta _1(v)\) is straightforward. Moreover, Estévez-Fernández et al. (2017) show that the 1-nucleolus satisfies first agent consistency:
-
If \(v\in {\mathcal {B}}^N\) and we consider the game \(v_{1,\eta _1(v)} \in {\mathcal {B}}^{\{2,3\}}\) defined, for all \(S\subset \{2,3\}\), by:
$$\begin{aligned} v_{1,\eta _1(v)}(S)= {\left\{ \begin{array}{ll} 0 &{} \text {if } S=\emptyset \\ \max \bigl \{ 0, v(S \cup \{1\})-\eta _1(v) \bigr \} &{} \text {if } |S|=1\\ v(N)-\eta _1(v) &{} \text {if } S=\{2,3\} \end{array}\right. } \end{aligned}$$then \(\eta _i(v)=\eta _i(v_{1,\eta _1(v)})\) for \(i\in \{2,3\}\).
Applying first agent consistency it is easy to deduce the expressions for \(\eta _2(v)\) and \(\eta _3(v)\). In fact,
Next, we compute the nucleolus of an essential zero-normalized game that is not balanced. So, let \(v\in {\mathcal {E}}_{0^+}^N\) such that \(v\not \in {\mathcal {B}}^N\), that is, \(\max \bigl \{ v_{-1}-E, v_{-3}+v_{-2}+v_{-1}-2E \bigr \}>0\). Maschler et al. (1979) present a method of finding the nucleolus that requires to solve a sequence of minimization linear programming problems. In the first step, the procedure finds all the imputations \(x\in I(v)\) whose maximal excess \(\theta _1(x)\) is as small as possible. So, let \(\varepsilon _1(v)=\underset{x\in I(v)}{\min }\ \underset{S\in \Sigma ^0}{\max }\ e(x,S)\). Clearly \(\varepsilon _1(v)>0\) since \(C(v)=\emptyset \) so \(\varepsilon _1(v)\) is the optimum value of the mathematical programming problem:

Denote by \(X^1=\{ x \in I(v): e(S,x)\le \varepsilon _1(v) \text { for all } S\in 2^N \}\) the set of imputations at which the minimum of the excesses is attained. Let \(\Sigma _1=\{ S\in \Sigma ^0: e(S,x)=\varepsilon _1(v) \text { for all } x\in X^1\}\) be the set of all coalitions at which the maximal excess \(\varepsilon _1(v)\) is attained at all \(x\in X^1\), and let \(\Sigma ^1=\{ S\in \Sigma ^0: S\not \in \Sigma _1\}=\Sigma ^0\backslash \Sigma _1\). Denote \(\varepsilon ^*=\max \bigl \{v_{-1}-E, \tfrac{1}{3} (v_{-3}+v_{-2}+v_{-1}-2E) \bigr \}\). Since \(v\not \in {\mathcal {B}}^N\) we have that \(\varepsilon ^*>0\). Now, if \((x_1,x_2,\varepsilon _1)\) is a feasible solution of (\(P_1\)) then \(0\le \varepsilon _1 +E-v_{-1}\), \(0\le \varepsilon _1 +E-v_{-2}\) and \( v_{-3}-\varepsilon _1\le E\) so \(\varepsilon _1\ge v_{-1}-E\ge v_{-2}-E\ge v_{-3}-E\). Moreover, \(x_1+x_2\le 2\varepsilon _1+2E-v_{-1}-v_{-2}\) and then \(v_{-3}-\varepsilon _1\le 2\varepsilon _1+2E-v_{-1}-v_{-2}\) which implies that \(\varepsilon _1\ge \tfrac{1}{3}\bigl (v_{-3}+v_{-2}+v_{-1}-2E \bigr )\). As a consequence \(\varepsilon _1(v)\ge \varepsilon ^*\).
Suppose that \(\varepsilon ^*=\tfrac{1}{3} (v_{-3}+v_{-2}+v_{-1}-2E)\). Then \((x^*_1,x^*_2,\varepsilon _1^*)=\tfrac{1}{3}\bigl (E+v_{-3}+v_{-2}-2v_{-1}, E+v_{-3}-2v_{-2}+v_{-1},v_{-3}+v_{-2}+v_{-1}-2E\bigr )\) is a feasible solution of (\(P_1\)), so \(\varepsilon _1(v)=\tfrac{1}{3} (v_{-3}+v_{-2}+v_{-1}-2E)\). But \((x^*_1,x^*_2,\varepsilon _1^*)\) is the only feasible solution at which the minimum \(\varepsilon _1^*\) is attained, so \(X^1=\{ (x_1^*,x_2^*,E-x_1^*-x_2^*) \}\). Therefore, if \(\varepsilon ^*=\tfrac{1}{3} (v_{-3}+v_{-2}+v_{-1}-2E)\) we have that \(\eta (v)=(x_1^*,x_2^*,E-x_1^*-x_2^*)\).
Now, \(\varepsilon ^*=v_{-1}-E\) if and only if \(E\le 2v_{-1}-v_{-2}-v_{-3}\). If this condition holds, we distinguish three cases:
-
1.
If \(E<v_{-1}-v_{-2}\le v_{-1}-v_{-3}\) then \((0,x_2,\varepsilon _1^*)\) is a feasible solution of (\(P_1\)) for all \(0\le x_2 \le E\). Therefore, \(\varepsilon _1(v)=v_{-1}-E\), \(X^1=\{(0,x_2,E-x_2):0\le x_2 \le E\}\), and \(\Sigma _1=\{ \{2,3\} \}\).
-
2.
If \(v_{-1}-v_{-2}\le E\le v_{-1}-v_{-3}\) then \((0,x_2,\varepsilon _1^*)\) is a feasible solution of (\(P_1\)) for all \(0\le x_2 \le v_{-1}-v_{-2}\). Therefore, \(\varepsilon _1(v)=v_{-1}-E\), \(X^1=\{(0,x_2,E-x_2):0\le x_2 \le v_{-1}-v_{-2}\}\), and \(\Sigma _1=\{ \{2,3\} \}\).
-
3.
If \(v_{-1}-v_{-2}\le v_{-1}-v_{-3}\le E\) then \((0,x_2,\varepsilon _1^*)\) is a feasible solution of (\(P_1\)) for all \(E-(v_{-1}-v_{-3} )\le x_2 \le v_{-1}-v_{-2}\). Therefore, \(\varepsilon _1(v)=v_{-1}-E\), \(X^1=\{(0,x_2,E-x_2):E-v_{-1}+v_{-3}\le x_2 \le v_{-1}-v_{-2}\}\), and \(\Sigma _1=\{ \{2,3\} \}\).
Therefore, if \(\varepsilon ^*=v_{-1}-E\), we have to proceed with the second step in the method described in Maschler et al. (1979), that is, we must find the minimum second-largest excess. Let \(\varepsilon _2(v)=\underset{x\in X^1}{\min }\ \underset{S\in \Sigma ^1}{\max }\ e(x,S)\). Denote \(X^2=\{ x \in X^1: e(S,x)\le \varepsilon _2(v) \text { for all } S\in \Sigma ^1 \}\), \(\Sigma _2=\{ S\in \Sigma ^1: e(S,x)=\varepsilon _2(v) \text { for all } x\in X^2\}\), and \(\Sigma ^2=\{ S\in \Sigma ^1: S\not \in \Sigma _2\}=\Sigma ^1\backslash \Sigma _2\). Then, \(\varepsilon _2(v)\) is the value of the following linear program:
But if \(x=(x_1,x_2,x_3)\in X^1\) then \(x_1=0\). Since \(\{1\}\not \in \Sigma _1\) and \(e(\{1\},x)=0\), we have that \(\varepsilon _2(v)\ge 0\). As a consequence, \(\varepsilon _2(v)\) is the solution of the reduced linear program with unkowns \(x_2,\varepsilon _2\):

If \((x_2,\varepsilon _2)\) is a feasible solution of (\(P_2\)) then \(v_{-3}- \varepsilon _2 \le E-v_{-2}+\varepsilon _2\), that is, \(\varepsilon _2 \ge \tfrac{1}{2}(v_{-3}+v_{-2}-E)\). So \(\varepsilon _2(v) \ge \varepsilon _2^*=\max \{ 0, \tfrac{1}{2}(v_{-3}+v_{-2}-E)\}\). The intersection of the straight lines \(x_2+\varepsilon _2= v_{-3}\) and \(x_2-\varepsilon _2= E-v_{-2}\) is the point \(({\hat{x}}_2,{\hat{\varepsilon }}_2)=\bigl ((\tfrac{1}{2}(E+v_{-3}-v_{-2}),\tfrac{1}{2}(v_{-3}+v_{-2}-E)\bigr )\). Clearly \({\hat{x}}_2\ge 0\) if and only if \(E\ge v_{-2}-v_{-3}\) and \({\hat{\varepsilon }}_2\ge 0\) whenever \(E\le v_{-2}+v_{-3}\). Therefore, we distinguish three cases:
-
1.
If \(0\le E\le v_{-2}-v_{-3}\) then the constraint set is \(\{(x_2,\varepsilon _2)\in {\mathbb {R}}^2: 0\le x_2\le E, x_2-\varepsilon _2\le E-v_{-2}\}\) and has two extreme points: \((0,v_{-2}-E)\) and \((E,v_{-2})\). So the optimum feasible solution of (\(P_2\)) is \((x_2^*,\varepsilon _2^*)=(0,v_{-2}-E)\). Therefore \(\varepsilon _2(v)=v_{-2}-E\ge 0\) and \(\eta (v)=(0,0,E)\).
-
2.
If \(v_{-2}-v_{-3}\le E\le v_{-2}+v_{-3}\) then the constraint set has three extreme points: \((0,v_{-3})\), \((E,v_{-2})\), and \(({\hat{x}}_2,{\hat{\varepsilon }}_2)\). Clearly, \(({\hat{x}}_2,{\hat{\varepsilon }}_2)\) is the optimum feasible solution of (\(P_2\)). Therefore \(\varepsilon _2(v)=\tfrac{1}{2}(v_{-3}+v_{-2}-E)\) and \(\eta (v)=\bigl (0,\tfrac{E+v_{-3}-v_{-2}}{2}, \tfrac{E-v_{-3}+v_{-2}}{2}\bigr )\).
-
3.
If \(E> v_{-3}+v_{-2}\) then \(\varepsilon _2^*=0\). So \((x_2,0)\) is a feasible solution of (\(P_2\)) for all \(v_{-3}\le x_2 \le E-v_{-2}\). Therefore, \(\varepsilon _2(v)=0\), \(X^2=\{(0,x_2,E-x_2):v_{-3}\le x_2 \le E-v_{-2}\}\), and \(\Sigma _2=\{ \{1\} \}\). Let \(\varepsilon _3(v)=\underset{x\in X^2}{\min }\ \underset{S\in \Sigma ^2}{\max }\ e(x,S)\) be the minimum third-largest excess. Then, \(\varepsilon _3(v)\) is the solution of the linear program with unkowns \(x_2,\varepsilon _3\):
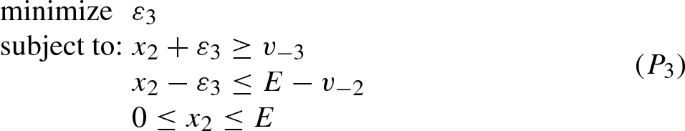
Observe that the only difference between the linear programs (\(P_2\)) and (\(P_3\)) is the positivity constraint \(\varepsilon \ge 0\). Then, the constraint set of (\(P_3\)) has three extreme points: \((0,v_{-3})\), \((E,v_{-2})\), and \(({\hat{x}}_2,{\hat{\varepsilon }}_2)\). Since \(\tfrac{1}{2}(v_{-3}+v_{-2}-E)<0\), the optimal feasible solution is \(({\hat{x}}_2,{\hat{\varepsilon }}_2)\). Therefore \(\varepsilon _3(v)=\tfrac{1}{2}(v_{-3}+v_{-2}-E)\) and \(\eta (v)=\bigl (0,\tfrac{E+v_{-3}-v_{-2}}{2}, \tfrac{E-v_{-3}+v_{-2}}{2}\bigr )\).
1.2 Proof of Proposition 4.2
Let \(N=\{1,2,3\}\) and \(v=(v_{-3},v_{-2},v_{-1},E)\in \mathcal {MB}^N\) such that \(v_{-3}\le v_{-2} \le v_{-1}\) and \(\alpha =\max \bigl \{0, v_{-1}, \tfrac{1}{2}( v_{-1}+v_{-2}+v_{-3}) \bigr \}\le E\). Let \(w\in {\mathcal {C}}^N\) be the exact envelope of v, i.e., \(w=v^e\), so \(C(v)=C(w)\) and \(\mu (v)=\mu (w)\). We identify the convex game \(w\in {\mathcal {C}}^N\) with the vector
Let \(a=\bigl (w(\{i\}) \bigr )_{i\in N}\) and \(w^0=(w^0_{-3},w^0_{-2},w^0_{-1},w^0(N)) \in \mathcal {MC}^N\) be the zero-normalization of w so that \(w=a+w^0\). Since \(w_0\in \mathcal {MC}^N\), from the analytic formula given in Proposition 4.1, we can obtain \(\mu (w^0)\). But having into account that \(\mu (v)=\mu (w)=a+\mu (w^0)\), we can derived the following expressions for \(\mu (v)\):
-
1.
\(v_{-k}\ge 0\) for all \(k \in N\).
-
If \(E\in [\alpha ,v_{-3}+v_{-2}]\) then \(w=(v_{-3}+v_{-2}-E,v_{-3}+v_{-1}-E,v_{-2}+v_{-1}-E,v_{-3},v_{-2},v_{-1},E)\in {\mathcal {C}}^N\) and \(w^0=\bigl (2E- {\sum _{i\in N}} v_{-i} , 2E- \underset{i\in N}{\sum } v_{-i} , 2E- {\sum _{i\in N}} v_{-i} ,2(2E- {\sum _{i\in N}} v_{-i} )\bigr )\in \mathcal {MC}^N\). Therefore \(\mu _i(v)=\mu _i(w)= \mu _i(w_0)+{\sum _{k\ne i}} v_{-k}-E\) for all \(i\in N\). Moreover, \(\mu _1(v) \le \mu _2(v) \le \mu _3(v)\).
-
If \(E\in [v_{-3}+v_{-2},v_{-3}+v_{-1}]\) then \(w=(0,v_{-3}+v_{-1}-E,v_{-2}+v_{-1}-E,v_{-3},v_{-2},v_{-1},E) \in {\mathcal {C}}^N\) and \(w^0=\bigl (E-v_{-1}, E-v_{-1}, 2E-{\sum _{i\in N}} v_{-i} ,3E-v_{-3}-v_{-2}-2v_{-1}\bigr )\in \mathcal {MC}^N\). In this case, \(\mu _1(v)=\mu _1(w)= \mu _1(w_0)\), \(\mu _2(v)=\mu _2(w)= \mu _2(w_0)+v_{-3}+v_{-1}-E\) and \(\mu _3(v)=\mu _3(w)= \mu _3(w_0)+v_{-2}+v_{-1}-E\). We have that \(\mu _1(v) \le \mu _2(v) \le \mu _3(v)\).
-
If \(E\in [v_{-3}+v_{-1},v_{-2}+v_{-1}]\) then \(w=(0,0,v_{-2}+v_{-1}-E,v_{-3},v_{-2},v_{-1},E) \in {\mathcal {C}}^N\) and \(w^0=\bigl (v_{-3}, E-v_{-1}, E-v_{-2},2E-v_{-2}-v_{-1}\bigr )\in \mathcal {MC}^N\). Now, \(\mu _1(v)=\mu _1(w)= \mu _1(w_0)\), \(\mu _2(v)=\mu _2(w)= \mu _2(w_0)\) and \(\mu _3(v)=\mu _3(w)= \mu _3(w_0)+v_{-2}+v_{-1}-E\). Again, \(\mu _1(v) \le \mu _2(v) \le \mu _3(v)\).
-
If \(E\in [v_{-2}+v_{-1},+\infty )\) then \(w^0=w\), and \(\mu (v)=\mu (w)=\mu (w^0)\).
-
-
2.
There is \(k \in N\) such that \(v_{-k}\le 0\).
-
If \(v_{-1}\le 0\) then \(w=w^0=\bigl (0,0,0,E \bigr )\) and \(\mu _i (v)=\mu _i (w_0)=\frac{E}{3}\) for all \(i \in N\).
-
If \(v_{-2}\le 0 \le v_{-1}\) then \(w=w^0=\bigl (0,0, v_{-1},E \bigr )\) and \(\mu _1 (v)=\tfrac{E^3-3Ev_{-1}^2+2v_{-1}^3}{3(E^2-v_{-1}^2)} =\tfrac{E^2+Ev_{-1}-2v_{-1}^2}{3(E+v_{-1})}=\tfrac{E}{3}-\tfrac{2v_{-1}^2}{3(E+v_{-1})}\), \(\mu _2 (v) =\mu _3(v)=\tfrac{E^3-v_{-1}^3}{3(E^2-v_{-1}^2)} =\tfrac{(E-v_{-1})(E^2+Ev_{-1}+v_{-1}^2)}{3(E-v_{-1})(E+v_{-1})}=\tfrac{E^2+Ev_{-1}+v_{-1}^2}{3(E+v_{-1})}=\tfrac{E}{3}+\tfrac{v_{-1}^2}{3(E+v_{-1})}\).
-
If \(v_{-3}\le 0 \le v_{-2}\) and \(E\le v_{-2}+v_{-1}\) then \(w=(0,0,v_{-2}+v_{-1}-E,0,v_{-2},v_{-1},E)\) and \(w_0= \bigl (0,E-v_{-1},E-v_{-2},2E-v_{-2}-v_{-1} \bigr )\). Therefore, \(\mu _1 (v)=\mu _1 (w_0)=\tfrac{E-v_{-1}}{2}\), \(\mu _2 (v)=\mu _2 (w_0)=\tfrac{E-v_{-2}}{2}\), and \(\mu _3 (v)=\mu _3 (w_0)+v_{-2}+v_{-1}-E=\tfrac{v_{-2}+v_{-1}}{2}\).
-
If \(v_{-3}\le 0 \le v_{-2}\) and \(v_{-2}+v_{-1}\le E\), then \(w=w^0=\bigl (0,v_{-2}, v_{-1},E \bigr )\). As a consequence \(\mu _1 (v)=\tfrac{E^3 - 3Ev_{-1}^2 - v_{-2}^3 + 2 v_{-1}^3}{3( E^2 -v_{-2}^2- v_{-1}^2)}\), \(\mu _2 (v)=\tfrac{E^3 - 3Ev_{-2}^2 - v_{-1}^3 + 2 v_{-2}^3}{3( E^2 -v_{-2}^2- v_{-1}^2)}\), and \(\mu _3 (v)=\tfrac{E^3 -v_{-2}^3- v_{-1}^3}{3( E^2 -v_{-2}^2- v_{-1}^2)}\).
Note that in all the cases we have that \(\mu _1(v)\le \mu _2(v) \le \mu _3(v)\).
-
1.3 Proof of Theorem 4.3
Fix a vector \((v_{-3},v_{-2}, v_{-1}) \in {\mathbb {R}}^3\) such that \(v_{-3}\le v_{-2} \le v_{-1}\) and let \(\alpha =\max \bigl \{0, v_{-1}, \tfrac{1}{2}( v_{-1}+v_{-2}+v_{-3}) \bigr \}\). For each \(i\in N\) consider the function \(\mu _i: [\alpha ,+\infty )\rightarrow {\mathbb {R}}\) that assigns to each \(E\in [\alpha ,+\infty )\) the value \(\mu _i(E)=\mu _i(v_E)\), where \(v_E=(v_{-3},v_{-2}, v_{-1},E) \in \mathcal {MB}^N\). It is known (González-Díaz and Sánchez-Rodríguez 2007) that \(\mu _i\) is continuous for all \(i\in N\). We claim that \(\mu _i\) is a differentiable function for all \(i\in N\) and that \(\frac{d \mu _i}{d E} (v_E) \ge 0\) for all \(E\in [\alpha ,+\infty )\) and all \(i\in N\). For each \(i\in N\), it is evident from Proposition 4.2 that \(\mu _i\) is a piecewise function. On each piece, \(\mu _i\) is either constant, linear or a rational function and therefore it is differentiable in the corresponding open interval. Now, applying the basic rules for differentiation we compute the derivative \(\frac{d \mu _i}{d E}\) on each piece and show that it is non-negative.
-
1.
\(v_{-k}\ge 0\) for all \(k \in N\).
-
It is clear that \(\frac{d \mu _i}{d E} (v)=\frac{1}{3} > 0\) for all \(i \in N\), when \(E\in (\alpha ,v_{-3}+v_{-2})\).
-
If \(E\in (v_{-3}+v_{-2},v_{-3}+v_{-1})\) then \( \tfrac{d \mu _1}{d E} (v) \!=\! \tfrac{15E^2 -\alpha _1 E \!+\! \alpha _0}{3\delta ^2}\), \(\tfrac{d \mu _2}{d E} (v)\!=\!\tfrac{d \mu _3}{d E} (v)=\tfrac{6E^2 - \beta _1 E + \beta _0}{3\delta ^2}\), where \(\delta =3E -2v_{-3} - 2v_{-2} - v_{-1}\) and
$$\begin{aligned} \begin{array}{llll} \alpha _1&{}=20v_{-3} +20v_{-2} +10v_{-1} &{}\qquad \alpha _0=6v_{-3}^2 + 12v_{-3}v_{-2}\\ &{}&{}\qquad \quad + 8v_{-3}v_{-1} + 6v_{-2}^2 + 8v_{-2}v_{-1} + v_{-1}^2 \\ \beta _1&{}=8v_{-3} +8v_{-2} +4v_{-1} &{}\qquad \beta _0= 3v_{-3}^2 + 6v_{-3}v_{-2} + 2v_{-3}v_{-1}\\ &{}&{}\qquad \quad + 3v_{-2}^2 + 2v_{-2}v_{-1} + v_{-1}^2. \end{array} \end{aligned}$$Observe that \(\frac{d \mu _2}{d E} (v)\ge 0\) because \(f(E)=6E^2-\beta _1E+\beta _0\) is a convex quadratic function that has its minimum point, \((\frac{2 v_{-3} + 2v_{-2} +v_{-1}}{3},\frac{(v_{-3} + v_{-2} - v_{-1})^2}{3})\), above the x axis. Moreover, \( \tfrac{d \mu _1}{d E} (v)-\tfrac{d \mu _2}{d E} (v)=\tfrac{(v_{-3}+ v_{-2}-E)(v_{-3}+ v_{-2} + 2v_{-1} - 3E )}{\delta ^2}. \) Since \(v_{-3}+ v_{-2}- E \le 0\) and \(v_{-3} + v_{-2} + 2v_{-1}- 3E\le 0\) when \(E\in (v_{-3}+v_{-2},v_{-3}+v_{-1})\), we have that \(\frac{d \mu _1}{d E} (v)-\frac{d \mu _2}{d E} (v)\ge 0\). Then \(\frac{d \mu _1}{d E} (v)\ge \frac{d \mu _2}{d E} (v)=\frac{d \mu _3}{d E} (v)\ge 0\).
-
If \(E\in (v_{-3}+v_{-1},v_{-2}+v_{-1})\) then we obtain \( \tfrac{d \mu _1}{d E} (v) = \tfrac{2E^4 -4(v_{-2}+v_{-1}) E^3 + \varepsilon _2 E^2+\varepsilon _1E+\varepsilon _0}{3\rho ^2}\), \(\tfrac{d \mu _2}{d E} (v) = \tfrac{6E^4 -12(v_{-2}+v_{-1}) E^3 + \gamma _2 E^2+\gamma _1E+\gamma _0}{3\rho ^2}\), and \(\tfrac{d \mu _3}{d E} (v) = \tfrac{v_{-3}^2 (6E^2 - \lambda _1E+\lambda _0)}{3\rho ^2}\), where \(\rho = 2Ev_{-2} + 2Ev_{-1} - 2v_{-2}v_{-1} - 2E^2 + v_{-3}^2\) and
$$\begin{aligned} \varepsilon _2&= 2v_{-2}^2 + 8v_{-2}v_{-1} + 2v_{-1}^2 - 3v_{-3}^2\\ \gamma _2&= -9v_{-3}^2+6v_{-2}^2+24v_{-2}v_{-1}+6v_{-1}^2 \\ \varepsilon _1&= \tfrac{4}{3}v_{-3}^3 + 2v_{-3}^2v_{-2} + 4v_{-3}^2v_{-1} - 4v_{-2}^2v_{-1} - 4v_{-2}v_{-1}^2 \\ \varepsilon _0&= \tfrac{2}{3}v_{-3}^3v_{-2} - \tfrac{2}{3}v_{-3}^3v_{-1} - 2v_{-3}^2v_{-2}v_{-1} - v_{-3}^2v_{-1}^2 + 2v_{-2}^2v_{-1}^2 \\ \gamma _1&= 4v_{-3}^3+12v_{-3}^2v_{-2}+6v_{-3}^2v_{-1}-12v_{-2}^2v_{-1}-12v_{-2}v_{-1}^2 \\ \gamma _0&=-2v_{-3}^3v_{-2}-2v_{-3}^3v_{-1}-3v_{-3}^2v_{-2}^2-6v_{-3}^2v_{-2}v_{-1}+6v_{-2}^2v_{-1}^2 \\ \lambda _1&= 8v_{-3}+6v_{-2} +6v_{-1} \\ \lambda _0&= 3v_{-3}^2 + 4v_{-3}v_{-2} + 4v_{-3}v_{-1} + 3v_{-2}^2 + 3v_{-1}^2. \end{aligned}$$Again, \(\frac{d \mu _3}{d E} (v)\ge 0\) because \(g(E)=6E^2-\lambda _1E+\lambda _0\) is a convex quadratic function that has its minimum point, \((\tfrac{4v_{-3}+3v_{-2}+3v_{-1}}{6},\tfrac{2v_{-3}^2+9(v_{-2}-v_{-1})^2}{6})\), above the x axis. But, since \(v_{-2} - v_{-1}\le 0\) and \(v_{-2}+ v_{-1} - 2E\le 0\) whenever \(E\in (v_{-3}+v_{-1},v_{-2}+v_{-1})\) we have that \( \tfrac{d \mu _1}{d E} (v)-\tfrac{d \mu _2}{d E} (v)=\tfrac{v_{-3}^2(v_{-2} - v_{-1})(v_{-2}+ v_{-1} - 2E )}{\rho ^2}\ge 0 \). On the other hand, \( \tfrac{d \mu _2}{d E} (v)-\tfrac{d \mu _3}{d E} (v)= \tfrac{(E-v_{-3} - v_{-1}) (2E^3+\theta _2E^2+\theta _1E+\theta _0)}{\rho ^2} \) being \(\theta _2=2v_{-3} - 4v_{-2} - 2v_{-1}\), \(\theta _1= - 3v_{-3}^2 - 4v_{-3}v_{-2} + 2v_{-2}^2 + 4v_{-1}v_{-2}\), and \(\theta _0= v_{-3}^3 + 2v_{-3}^2v_{-2} + v_{-1}v_{-3}^2 + 2v_{-3}v_{-2}^2 - 2v_{-1}v_{-2}^2\). We claim that \(h(E)=2E^3+\eta _2E^2+\eta _1E+\eta _0\ge 0\), because h is monotonically increasing over the interval \((v_{-3}+v_{-1},v_{-2}+v_{-1})\) and \(h(v_{-3}+v_{-1})=2v_{-3}(v_{-3}(3v_{-1}-3v_{-2}+v_{-3})+2(v_{-1}-v_{-2})^2) \ge 0\). Indeed, consider the convex quadratic function \(h'(E)=6E^2+4(v_{-3}-2v_{-2}-v_{-1})E+(2v_{-2}^2+4v_{-2} v_{-1} -3 v_{-3}^2-4 v_{-3} v_{-1})\). Clearly, \(h'(v_{-3}+v_{-1})=7v_{-3}^2 + 12v_{-3}(v_{-1}-v_{-2})+ 2(v_{-1}-v_{-2})^2 \ge 0\). But, \(h'\) has its minimum point at \(\frac{2v_{-2}+v_{-1}-v_{-3}}{3}\) such that \(\frac{2v_{-2}+v_{-1}-v_{-3}}{3}\le v_{-3} +v_{-1}\). Therefore, \(h'(E)\ge 0\) for all \(E\in (v_{-3}+v_{-1},v_{-2}+v_{-1})\) and h is monotonically increasing over that interval. Since \(\frac{d \mu _2}{d E} (v)\ge 0\), \(\frac{d \mu _1}{d E} (v)-\frac{d \mu _2}{d E} (v)\ge 0\) and \(\frac{d \mu _2}{d E} (v)-\frac{d \mu _3}{d E} (v)\ge 0\), we have that \(\frac{d \mu _1}{d E} (v)\ge \frac{d \mu _2}{d E} (v)=\frac{d \mu _3}{d E} (v)\ge 0\).
-
If \(E\in (v_{-2}+v_{-1},+\infty )\) then \(\tfrac{d \mu _3}{d E} (v) = \tfrac{E^4-3(v_{-2}^2+v_{-1}^2)E^2+2(v_{-2}^3+v_{-1}^3-2v_{-3}^3)E+3Cv_{-3}^2}{3(E^2-C)^2}\), where \(C=v_{-3}^2+v_{-2}^2+v_{-1}^2\ge 0\). Consider the function \(N(x)=x^4-3(v_{-2}^2+v_{-1}^2)x^2+2(v_{-2}^3+v_{-1}^3-2v_{-3}^3)x+3Cv_{-3}^2\). We claim that \(N(x) \ge 0\) for all \(x\in [v_{-2}+v_{-1},+\infty )\), in which case \(\frac{d \mu _3}{d E}(v) \ge 0\). Indeed, we will show that \(N(v_{-2}+v_{-1})\ge 0\) and that \(N'(x) \ge 0\) for all \(x \ge v_{-2}+v_{-1}\). First \( N(v_{-2}+v_{-1})=v_{-3}^2 \bigl ( 3v_{-3}^2-4(v_{-2}+v_{-1})v_{-3}+3(v_{-2}^2+v_{-1}^2)\bigr )\ge 0 \), because the quadratic function \(f(x)=3x^2-4(v_{-2}+v_{-1})x+3(v_{-2}^2+v_{-1}^2)\ge 0\) for all \(x\in {\mathbb {R}}\). On the other hand \(N'(x)=4x^3-6(v_{-2}^2+v_{-1}^2)x+2(v_{-2}^3+v_{-1}^3-2v_{-3}^3)\) and \(N''(x)=12x^2-6(v_{-2}^2+v_{-1}^2)\). Since the positive root of the quadratic equation \(N''(x)=0\) is \(x_1=\sqrt{\tfrac{v_{-2}^2+v_{-1}^2}{2}}\) and \(v_{-2}+v_{-1} \ge \sqrt{(v_{-2}+v_{-1})^2-2v_{-2}v_{-1}}=\sqrt{v_{-2}^2+v_{-1}^2} \ge x_1\), we conclude that \(N''(x) \ge 0\) for all \(x \ge v_{-2}+v_{-1}\), that is, \(N'\) is monotonically increasing over the interval \([v_{-2}+v_{-1},+\infty )\). Moreover, \(N'(v_{-2}+v_{-1})=6v_{-2}^2v_{-1}+6v_{-1}^2v_{-2}-4v_{-3}^3 \ge 12v_{-3}^3-4v_{-3}^3\ge 0\). Then, certainly, \(N'(x) \ge 0\) for all \(x \ge v_{-2}+v_{-1}\). Now, differentiating \(\mu _1\) and \(\mu _2\) with respect to E, we have that \(\tfrac{d \mu _1}{d E}(v) = \tfrac{E^4-3(v_{-3}^2+v_{-2}^2)E^2+2(v_{-3}^3+v_{-2}^3-2v_{-1}^3)E+3Cv_{-1}^2}{3(E^2-C)^2}\) and \(\tfrac{d \mu _2}{d E} (v) = \tfrac{E^4-3(v_{-3}^2+v_{-1}^2)E^2+2(v_{-3}^3+v_{-1}^3-2v_{-2}^3)E+3Cv_{-2}^2}{3(E^2-C)^2}\). It is straightforward to check that \(\frac{d \mu _1}{d E} \ge \frac{d \mu _2}{d E}\) if and only if \((v_{-1}^2-v_{-2}^2)E^2-2(v_{-1}^3 -v_{-2}^3)E+C(v_{-1}^2-v_{-2}^2) \ge 0\). But, the quadratic function \(f(x)=(v_{-1}^2-v_{-2}^2)x^2-2(v_{-1}^3 -v_{-2}^3)x+C(v_{-1}^2-v_{-2}^2) >0\) for all \(x\ge v_{-2}+v_{-1}\), because f attains its minimum at \(x^*=\tfrac{v_{-1}^3-v_{-2}^3}{v_{-1}^2-v_{-2}^2}\), \(v_{-2}+v_{-1}\ge x^*\), and \(f(v_{-2}+v_{-1})=v_{-3}^2(v_{-1}^2-v_{-2}^2)\ge 0\). Similarly, \(\frac{d \mu _2}{d E} \ge \frac{d \mu _3}{d E}\) if and only if \((v_{-2}^2-v_{-3}^2)E^2-2(v_{-2}^3 -v_{-3}^3)E+C(v_{-2}^2-v_{-3}^2) \ge 0\) which follows directly from the properties of the quadratic function \(g(x)=(v_{-2}^2-v_{-3}^2)x^2-2(v_{-2}^3 -v_{-3}^3)x+C(v_{-2}^2-v_{-3}^2)\).
-
-
2.
There is \(k \in N\) such that \(v_{-k}\le 0\).
-
If \(v_{-1}\le 0\) then \(\frac{d \mu _i}{d E} (v)=\frac{1}{3}\ge 0, \text { for all } i \in N\).
-
If \(v_{-2}\le 0 \le v_{-1}\) then \(\frac{d \mu _1}{d E} (v)=\tfrac{1}{3}+\tfrac{2v_{-1}^2}{3(E+v_{-1})^2}>0\) because \(v_{-1}\ge 0\) and \(\frac{d \mu _i}{d E} (v)=\frac{1}{3}\bigl ( 1- \bigl (\tfrac{v_{-1}}{E+v_{-1}}\bigr )^2 \bigr ) >0\) for \(i \in \{2,3\}\).
-
If \(v_{-3}\le 0 \le v_{-2}\) and \(v_{-2}+v_{-1}\ge E\) then \(\frac{d \mu _i}{d E} (v)=\tfrac{1}{2}\) for all \(i \in \{1,2\}\) and \(\frac{d \mu _3}{d E} (v)=0\).
-
If \(v_{-3}\le 0 \le v_{-2}\) and \(v_{-2}+v_{-1}\le E\), then \(\mu (v)=\mu (w)\) where \(w=(0,v_{-2},v_{-1},E)\). Then applying the last item of case 1 we have directly that \(\frac{d \mu _i}{d E} (v)\ge 0\) for all \(i \in \ N\).
-
Given \(i\in N\), we have seen that \(\mu _i\) is a piecewise continuously differentiable function. It remains to be established that \(\mu _i\) is differentiable at the points between the pieces. This is easily done by checking that the one-sided limits of the derivative function \(\frac{d \mu _i}{d E}\) at these points are equal.
1.4 Proof of Theorem 6.5
Fix a vector \((v_{-n},\dots , v_{-1}) \in {\mathbb {R}}^n\) such that \(0\le v_{-n}\le \dots \le v_{-1}\). For each \(i\in N\) consider the function \(\mu _i: [v_{-2}+v_{-1},+\infty )\rightarrow {\mathbb {R}}\) that assigns to each \(E\in [v_{-2}+v_{-1},+\infty )\) the value \(\mu _i(E)=\mu _i(v_E)\), where \(v_E=(v_{-n},\dots , v_{-1},E) \in \mathcal {MC}^N\). It is known (González-Díaz and Sánchez-Rodríguez 2007) that \(\mu _i\) is continuous on \([v_{-2}+v_{-1},+\infty )\). But \(\mu _i\) is differentiable on \((v_{-2}+v_{-1},+\infty )\) because \(\mu _i\) is the rational function given in Proposition 6.4. Therefore, the core-center is aggregate monotonic on \(\mathcal {MC}^N\) if and only if \(\frac{d \mu _i}{d E}(v_E) \ge 0\) for all \(E\in (v_{-2}+v_{-1},+\infty )\) and all \(i\in N\). Now, applying the quotient rule for differentiation,
Then, \(\tfrac{d \mu _i}{d E}(v_E) - \tfrac{d \mu _{i+1}}{d E}(v_E) = \tfrac{F(E)}{n(E^{n-1}-L)^2}\), if \(i<n\), where F is the polynomial function
But \(F'(x)=n(n-1)(n-2)x^{n-3}\Bigl ( \bigl ( v_{-i}^{n-1} -v_{-(i+1)}^{n-1} \bigr ) x- \bigl ( v_{-i}^{n} -v_{-(i+1)}^{n} \bigr )\Bigr )\). Therefore, F is monotonically increasing over the interval \(J=\bigl [ \frac{v_{-i}^{n} -v_{-(i+1)}^{n} }{v_{-i}^{n-1} -v_{-(i+1)}^{n-1} }, +\infty \bigr )\). Since, \(F(v_{-i}+v_{-(i+1)} )\ge 0\) and \(v_{-i}+v_{-(i+1)}\in J\), we have that \(F(x)\ge 0\) for all \(x\ge v_{-i}+v_{-(i+1)}\). Now, \(E\ge v_{-1}+v_{-2}\ge v_{-i}+v_{-(i+1)}\), so \(F(E) \ge 0\) and, as a consequence, \(\frac{d \mu _i}{d E}(v_E) \ge \frac{d \mu _{i+1}}{d E}(v_E)\). Then it suffices to prove that \(\frac{d \mu _n}{d E}(v_E) \ge 0\) for all \(E\in (v_{-2}+v_{-1},+\infty )\) . But \(\frac{d \mu _n}{d E}(v_E) =\frac{G(E)}{n(E^{n-1}-L)^2}\) where \(G(x)=x^{2(n-1)}-n(L-(n-2)v_{-n}^{n-1})x^{n-1}-(n-1)K_nx^{n-2}+nLv_{-n}^{n-1}\) is a polynomial function. Then \(G'(x)=(n-1)x^{n-3}\bigl ( 2x^n+n( (n-2)v_{-n}^{n-1}-L)x-(n-2)K_n\bigr )\). We claim that \(G'(x)\ge 0\) for all \(x\in I=[v_{-1}+v_{-2},+\infty )\) and that \(G(v_{-1}+v_{-2})\ge 0\). In that case, \(G(x)\ge 0\) for all \(x\in I\), in particular, \(G(E)\ge 0\) because \(E > v_{-1}+v_{-2}\) and the proof concludes.
Proof that \(G'(x)\ge 0\) for all \(x\in I\): Note that \(G'(x) \ge 0\) for all \(x\in I\) if an only if \(H(x)=2x^n+n\bigl ((n-2)v_{-n}^{n-1}-L \bigr )x-(n-2)K_n \ge 0\) for all \(x\in I\). Then, it suffices to prove that \(H(v_{-1}+v_{-2})\ge 0\) and \(H'(x)\ge 0\) for all \(x\in I\). First, we show that \(H(v_{-1}+v_{-2})\ge 0\). Observe that \(H(v_{-1}+v_{-2}) =A-B\) where
Then, we have that
On the other hand
But \(v_{-i} \le v_{-j}\) whenever \(i>j\). Then, clearly, \(n(n-2)v_{-n}^{n-1}(v_{-1}+v_{-2}) \ge (n-1)(n-2)v_{-n}^n\). Moreover, since \(\left( {\begin{array}{c}n\\ k\end{array}}\right) \ge n\) for all \(1\le k \le n-1\),
Therefore \(A\ge B\) and \(H(v_{-1}+v_{-2})\ge 0\).
Let us show that \(H'(x) \ge 0\) for all \(x\in I\). Obviously \(H'(x)=2nx^{n-1}+n((n-2)v_{-n}^{n-1}-L)\) and \(L-(n-2)v_{-n}^{n-1}\ge 0\). We distinguish two cases:
n is even: H has a unique extreme point, a minimum, at \(x^*=\root n-1 \of {\frac{L-(n-2)v_{-n}^{n-1}}{2}}\). Then H is monotonically increasing over the interval \([x^*,+\infty )\), so \(H'(x)\ge 0\) for all \(x\ge x^*\). But,
Then \(I\subset [x^*,+\infty )\) and, as a consequence, \(H'(x)\ge 0\) for all \(x\in I\).
n is odd: H has two extreme points, a minimum at \(x_2^*=\root n-1 \of {\frac{L-(n-2)v_{-n}^{n-1}}{2}}\) and a maximum at \(x^*_1=-x^*_2\). Therefore, H is monotonically increasing over the interval \([x^*_2,+\infty )\), so \(H'(x)\ge 0\) for all \(x\ge x^*_2\). Similarly as above, we can prove that \(x^*_2 \le v_{-1}+v_{-2}\). Then \(I\subset [x^*_2,+\infty )\) and, as a consequence, \(H'(x)\ge 0\) for all \(x\in I\).
Proof that \(G(v_{-1}+v_{-2})\ge 0\): Easy computations lead to \(G(v_{-1}+v_{-2})=(v_{-1}+v_{-2})^{n-2}(A-B)+nLv_{-n}^{n-1}\), where \(A,B\ge 0\) are given by:
We distinguish three cases:
Case \(n\ge 5\): For all \(2\le k\le n-2\) it holds that \(\left( {\begin{array}{c}n\\ k\end{array}}\right) v_{-1}^{n-k}v_{-2}^k \ge v_{-k}^{n-1}v_{-1}+ v_{-k}^{n-1}v_{-2}\), because \(\left( {\begin{array}{c}n\\ k\end{array}}\right) \ge 2n\) and \(v_{-k}\le v_{-2}\le v_{-1}\). Moreover, \(n(n-3)v_{-n}^{n-1}(v_{-1}+v_{-2}) \ge 2n(n-3) v_{-n}^n \ge (n-1)^2v_{-n}^n\). Then \(A\ge B\) and \(G(v_{-1}+v_{-2})\ge 0\).
Case \(n=3\): \(A-B=-4v_{-3}^3\le 0\) but \(G(v_{-1}+v_{-2})=-4v_{-3}^3(v_{-1}+v_{-2})+3(v_{-1}^2+v_{-2}^2+v_{-3}^2)v_{-3}^2=v_{-3}^2\bigl (3v_{-3}^2-4(v_{-1}+v_{-2})v_{-3}+3(v_{-1}+v_{-2}) \bigr )\ge 0\), because the quadratic function \(f(x)=3x^2-4(v_{-1}+v_{-2})x+3(v_{-1}^2+v_{-2}^2)\ge 0\) for all \(x\in {\mathbb {R}}\) (see the proof of Theorem 4.3, case 1, when \(E>v_{-2}+v_{-1}\)).
Case \(n=4\): \(G( v_{-1}+v_{-2})=(v_{-1}+v_{-2})^2(6v_{-1}^2v_{-2}^2+4v_{-4}^3v_{-1}+4v_{-4}^3v_{-2}+3v_{-3}^4-4v_{-3}^3v_{-1}-4v_{-3}^3v_{-2}-9v_{-4}^4)+4v_{-4}^3(v_{-1}^3+v_{-2}^3+v_{-3}^3+v_{-4}^3)\). Consider the polynomial function \( f(x)=4x^6-9(v_{-1}+v_{-2})^2x^4+4\alpha x^3+\beta , \) where \(\alpha =(v_{-1}+v_{-2})^3+v_{-1}^3+v_{-2}^3+v_{-3}^3\) and \(\beta =(v_{-1}+v_{-2})^2\bigl (3v_{-3}^4+6v_{-1}^2v_{-2}^2-4v_{-1}v_{-3}^3-4v_{-2}v_{-3}^3 \bigr )\). Clearly, \(f(v_{-4})=G(v_{-1}+v_{-2})\). We claim that: f is monotonically increasing over the interval \([0,v_{-3}]\) and \(f(0)=\beta \ge 0\). First, let us see that \(f'(x)\ge 0\) if \(x\in [0,v_{-3}]\). But, \(f'(x)=12x^2g(x)\), being \(g(x)=2x^3-3(v_{-1}+v_{-2})^2x+\alpha \). Now, \(g'(x)=6x^2-3(v_{-1}+v_{-2})^2\le 0\) if \(x \in J=[-\frac{v_{-1}+v_{-2}}{\sqrt{2}},\frac{v_{-1}+v_{-2}}{\sqrt{2}}]\). Since \([0,v_{-2}]\subset J\) we conclude that g is monotonically decreasing over the interval \([0,v_{-2}]\). But \(g(v_{-2})\ge 0\). Indeed, \(g(v_{-2})=v_{-2}^3+2v_{-1}^3+v_{-3}^3-3v_{-1}v_{-2}^2\). Since \(P(x)=x^3-3v_{-1}x^2+2v_{-1}^3+v_{-3}^3\) is monotonically decreasing over \([0,2v_{-1}]\) we have that \(g(v_{-2})=P(v_{-2})\ge P(v_{-1})=v_{-3}^3\ge 0\). So, finally, if \(x\in [0,v_{-3}]\) we have that \(g(x)\ge g(v_{-3}) \ge g(v_{-2}) \ge 0\) or, equivalently, \(f'(x)\ge 0\) if \(x\in [0,v_{-3}]\).
Secondly, \(\beta \ge 0\) if and only if \(h(v_{-3})\ge 0\) where \(h(x)=3x^4-4(v_{-1}+v_{-2})x^3+6v_{-1}^2v_{-2}^2\). Since \(h'(x)=12x^2(x-(v_{-1}+v_{-2}))\), h is monotonically decreasing over the interval \((-\infty ,v_{-1}+v_{-2}]\). But \(h(v_{-2})=6v_{-1}^2v_{-2}^2- 4v_{-1}v_{-2}^3-v_{-2}^4\ge 0\) so \(h(x)\ge 0\) for all \(x\le v_{-2}\), in particular, \(h(v_{-3})\ge 0\).
1.5 Proof of Proposition 6.7
Let \(v=(v_{-n}, \dots , v_{-1}, E) \in \mathcal {MB}^N\). According to Lemma 3.2 we can assume that \(v_{-i}\ge 0\) for all \(i\in N\). Take the claims vector \(d=\bigl (d_i\bigr )_{i\in N}=\bigl ( E-v_{-i}\bigr )_{i\in N}\) so that \((E,d) \in {\mathcal {P}}^N\). Then, \((n-2) E \ge {\sum _{i \in N}} v_{-i}\) if and only if \(E\le \tfrac{1}{2} {\sum _{i \in N}} d_{i}\) and, by Proposition 6.1,
where \(A=E-v_{-1}-\tfrac{1}{n}\bigl ( (n-1)E-{\sum _{i \in N}} v_{-i} \bigr ) \) and \(B=E-v_{-1}-\tfrac{1}{2} (E-v_{-1})=\tfrac{1}{2} (E-v_{-1})\). Since \(A-B=\tfrac{1}{2n} \Bigl ( 2{\sum _{i \in N}} v_{-i}-(n-2)E-nv_{-1} \Bigr )\) we have that if \((n-2)E\le {\sum _{i \in N}} v_{-i} \) then
On the other hand, if \((n-2)E\ge {\sum _{i \in N}} v_{-i}\), we have that
because \(\tfrac{1}{n}E \ge \tfrac{1}{2}(E-v_{-1})\) if and only if \(\tfrac{n}{n-2}v_{-1}\le E\).
1.6 Proof of Proposition 6.8
First, observe that if \(v\in \mathcal {MB}^N\) then \({\sum _{i\in N}} v_{-i}=v_{-1}+v_{-2}+{\sum _{i=3}{^{n}}} v_{-i}\le 2v_{-1}+(n-2)v_{-2}\). Now, since \(n\ge 4\) and \(E\ge v_{-1}+v_{-2}\) we can write \({\sum _{i\in N}} v_{-i} \le (n-2) (v_{-1}+v_{-2} ) \le (n-2)E\). Therefore, if \(v\in \mathcal {MC}^N\) the formula of \(\eta _1(v)\) is a direct consequence of Proposition 6.7.
Denote \(w=v_{1,\eta _1(v)} \in \mathcal {MB}^{N\backslash \{1\}}\). Now, \(\tfrac{n-1}{n-3}w_{-2}\le w(N\backslash \{1\})\) if and only if \(E-\eta _1(v)-\tfrac{n-1}{n-3}(v_{-2}-\eta _1(v))\ge 0\) or, equivalently, \(\tfrac{1}{2} (E+v_{-1})-\tfrac{n-1}{n-3}(v_{-2}-\eta _1(v))\ge 0\). But, since \(E\ge v_{-1}+v_{-2}\) we have that
Therefore, \(\tfrac{n-1}{n-3}w_{-2}\le w(N\backslash \{1\})\) if and only if \((n-3)(E+v_{-1})-(n-1)(E-v_{-1})\ge 0\), that is, whenever \((n-2)v_{-1}\ge E\). We have two possibilities:
Case 1: if \(\tfrac{1}{n-2} \bigl ( {\sum _{i\in N}} v_{-i} \bigr ) \le E \le \tfrac{n}{n-2}v_{-1}\) then \(\eta _1(v)=\tfrac{1}{2}(E-v_{-1})\) and \(v_{-1}\ge \tfrac{n-2}{n}E\). But \(\tfrac{n-2}{n}E\ge \tfrac{1}{n-2}E\) if and only if \(n^2-5n+4\ge 0\) which holds because \(n\ge 4\). Therefore, \(\tfrac{n-1}{n-3}w_{-2}\le w(N\backslash \{1\})\) and according to Proposition 6.7, \( \eta _2(w)=\tfrac{1}{n-1}w(N\backslash \{1\})=\tfrac{1}{n-1}(E-\eta _1(v))=\tfrac{1}{n-1}\bigl (E- \tfrac{1}{2}(E-v_{-1}) \bigr )=\tfrac{1}{2(n-1)}(E+v_{-1}). \) Obviously, since \(\tfrac{n-1}{n-3}w_{-2}\le w(N\backslash \{1\})\), \(\eta _j(w)=\eta _2(w)\) for all \(j\in N\), \(j\ge 3\). From Theorem 6.6 it follows that \(\eta _j(v)=\eta _2(w)\) for all \(j\in N\backslash \{1\}\).
Case 2: if \(\tfrac{n}{n-2}v_{-1}\le E\) then \(\eta _j(v)=\eta _1(v)=\tfrac{1}{n} E\) for all \(j\in N\backslash \{1\}\).
Rights and permissions
About this article
Cite this article
Mirás Calvo, M.Á., Quinteiro Sandomingo, C. & Sánchez-Rodríguez, E. Considerations on the aggregate monotonicity of the nucleolus and the core-center. Math Meth Oper Res 93, 291–325 (2021). https://doi.org/10.1007/s00186-020-00733-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00186-020-00733-7