1 Introduction

When analysing the association between two categorical variables that form a contingency table, there are typically two important aspects that one should consider. Firstly, the analyst can identify the strength of the association between the variables. This may be conducted by considering standard statistical tests such as Pearson’s chi-squared test of independence. Secondly, where a statistically significant association is detected, one may determine those categories within and between the variables that are similar or different in terms of the conditional distribution of the cell counts. Graphical summaries provide a very simple and intuitive way to view these two characteristics. However different types of graphical summaries used to visualise this association (or lack of it) can lead to different conclusions about the way in which the variables are related.

There are many relatively sophisticated ways to visualise the association in two-way contingency tables. Some of the more popular approaches include using various types of biplots. One may consider, for example, the relatively recent extensive discussions of biplots by Gower et al. (2011) and Greenacre (2010a). One may also construct plots from any one of the many members of the correspondence analysis family; see Beh and Lombardo (2012, 2014) and Nishisato (2007) for an extensive and diverse list of such members.

In this paper, a simple algebraic generalisation is proposed that incorporates, as special cases, many aspects of correspondence analysis. Specifically, the generalisation involves decomposing the matrix of standardised residuals, but can also be extended to decompose other residuals and to incorporate other measures of association including the tau index of Goodman and Kruskal (1954) and the Freeman–Tukey statistic of Freeman and Tukey (1950). The most popular method of decomposition used is singular value decomposition (SVD) and it is this method of decomposition that is considered in this paper. However, there are others that can be incorporated into the proposed algebraic generalisation including the bivariate moment decomposition (BMD) used for graphically depicting the association between ordinal categorical variables; see Beh (1997, 1998), Best (1995), Best et al. (1999, 2000), Lombardo et al. (2007, 2016). Another type of decomposition is the hybrid of SVD and BMD discussed by Beh (2001) which Beh (2008) used to graphically analyse nominal-ordinal two-way contingency tables.

Irrespective of the method of decomposition used, the purpose of decomposing the residuals is to provide a mechanism for selecting a sub-set of dimensions from the optimal number required to visualise the relationship between the variables. This is achieved while maximising the association structure between the variables. Generally one, two or at most three dimensions are enough for a simple visualisation of the association structure. For a two-dimensional view of multi-dimensional data, many graphical procedures can be used, including Andrew’s Curve Andrews (1972), Chernoff’s face Chernoff (1973), cobweb diagrams (Upton 2000, 2016) and the mosaic display (Friendly 1994, 1999). One may also consider methods of constructing elliptical regions for simple correspondence analysis that can include information contained in dimensions higher than the second; see Beh (2010). Alternatively, bootstrap techniques can be used for constructing such regions (Linting et al. 2007; Lombardo and Ringrose 2012; Markus 1994; Ringrose 2012).

We must point out that discussing generalisatons in the context of correspondence analysis are not new. For example, one may consider Choulakian (1988), De Leeuw (1993), Lorenzo-Seva et al. (2009), Velden and Kiers (2005) and Yanai (1986) as examples of such generalisations. What makes these contributions to the correspondence analysis literature different from what is described in this paper is that, in the past, generalisations have focused on showing how viewing correspondence analysis from a variety of perspectives leads to similar row/column scoring solutions. Our approach provides a broad, yet relatively simple, algebraic generalisation that incorporates, as special cases, the growing diversity of mathematical and graphical perspectives that have been developed over the past few decades.

To derive the simple algebraic generalisation of visualising categorical variables, this paper is divided into seven further sections. Section 2 defines the notation used throughout the paper and describes the application of SVD on the matrix of standardised residuals, yielding the classic approach to correspondence analysis. An unbalanced generalised framework for the analysis of two-way contingency tables is given in Sect. 3 and special cases of these are described in Sect. 4. A balanced generalised framework is discussed in Sect. 5 and special cases of it are looked at in Sect. 6. Section 8 provides some further insight into how these generalisations may be implemented. Some concluding remarks are made in Sect. 9.

2 Simple correspondence analysis

To begin our algebraic generalisation, we shall first briefly highlight some of the key features of the correspondence analysis of a two-way contingency table. There are a number of variations of correspondence analysis that can be considered, and our generalisation incorporates some of the commonly used approaches.

For a \( r \times c\) two-way contingency table \(\mathbf{N}\), denote its grand total by n. Also, denote the matrix of joint proportions by \(\mathbf{P}\) so that \(\mathbf{P} = \mathbf{N}/n\). Let \(\mathbf{r}\) be the vector of row marginal proportions and \(\mathbf{c}\) be the vector of column marginal proportions. Denote \(\mathbf{D}_r\) as the diagonal matrix of row marginal proportions such that \(\mathbf{D}_r = \text {diag}\left( \mathbf{r} \right) \). Similarly, let \(\mathbf{D}_c = \text {diag}\left( \mathbf{c} \right) \).

Consider the decomposition of Pearson’s matrix of standardised residuals

$$\begin{aligned} \mathbf{Z} = \mathbf{D}_r^{-1/2} \left( \mathbf{P}- \mathbf{r} \mathbf{c}' \right) \mathbf{D}_c^{-1/2} = D^* \left( \mathbf{D}_ {\lambda },\, \mathbf{U},\, \mathbf{V} \right) . \end{aligned}$$
(1)

The right hand side of (1), \(D^*\left( \bullet \right) \), denotes the type of decomposition used. For this paper we will focus on the case where \(D^*\left( \bullet \right) \) is the SVD of \(\mathbf{Z}\), however other decomposition methods may be considered. Two such alternatives are the Bivariate Moment Decomposition (BMD) commonly used for two ordinal variable or the Hybrid Decomposition (HD) for a singly ordered two-way contingency table that combines specific features of SVD and BMD into a single decomposition. When the standardised residuals are considered, the total variation in the table can be quantified by

$$\begin{aligned} X^2 = n \; \text {trace}\left[ \mathbf{Z}\, \mathbf{Z}' \right] = n \; \text {trace}\left[ \mathbf{Z}' \mathbf{Z} \right] \end{aligned}$$
(2)

and has a chi-squared distribution with \(\left( r-1\right) \left( c-1 \right) \) degrees of freedom. Note that, for (1), \(\mathbf{P} - \mathbf{r}{} \mathbf{c}'\) is the difference between the observed proportions, \(\mathbf{P}\), and its expected value under complete independence.

It is well known that the chi-squared statistic is proportional to the sample size. That is, even if the association structure between the row and column variables remains unchanged, the chi-squared statistic increases as the sample size increases. Therefore, correspondence analysis focuses on \(X^2/n\) as a measure of the strength of association between the variables and refers to it as the total inertia of the contingency table.

To determine the subspace needed to visually represent the association between the row and column variables, correspondence analysis is undertaken by applying SVD to the matrix of standardised residuals such that

$$\begin{aligned} D^* \left( \mathbf{D}_ {\lambda },\,\,\, \mathbf{U},\, \mathbf{V} \right) = \mathbf{U} \mathbf{D}_{\lambda } \mathbf{V}'. \end{aligned}$$
(3)

Here \(\mathbf{U}\) is a \(r \times M\) matrix and \(\mathbf{V}\) is a \(c \times M\) matrix where \(M=\min \left( r,\,c \right) -1\). These matrices contain column vectors which are row and column generalised basic vectors, respectively, and have the property

$$\begin{aligned} \mathbf{U}'\,\mathbf{U}=\mathbf{I}_M \quad \quad \mathbf{V}' \, \mathbf{V} = \mathbf{I}_M \end{aligned}$$
(4)

where \(\mathbf{I}_M\) is an \(M\times M\) identity matrix. The matrix \(\mathbf{D}_{\lambda }\) is a \(M\times M\) diagonal matrix with elements \(\lambda _1, \, \ldots \,,\, \lambda _{M}\) that are real and positive. They are the first M singular values of \(\mathbf{Z}\) and are arranged in descending order so that

$$\begin{aligned} 1 \; \ge \; \lambda _1 \; \ge \; \lambda _2 \; \ge \; \cdots \; \ge \; \;\lambda _{M} \; > \; 0. \end{aligned}$$

To obtain a graphical summary of the association using simple correspondence analysis, the variation between the row and column categories can be made by considering the matrix of coordinates

$$\begin{aligned} \mathbf{F} = \mathbf{D}_r ^{-1/2} \mathbf{U} \mathbf{D}_\lambda \mathbf{G} = \mathbf{D}_c ^{-1/2} \mathbf{V} \mathbf{D}_\lambda \end{aligned}$$

such that

$$\begin{aligned} \frac{X^2}{n} = \text {trace} \left( \mathbf{F}' \mathbf{D}_r \mathbf{F} \right) = \text {trace} \left( \mathbf{G}' \mathbf{D}_c \mathbf{G} \right) = \text {trace} \left( \mathbf{D}_\lambda ^2 \right) . \end{aligned}$$

Therefore row and column coordinates situated at some distance from the origin will coincide with large singular values, and hence a large total inertia. Similarly, a small total inertia will mean that the row and column coordinates will lie close to the centroid of the graphical display. This finding is consistent with all special cases considered in this paper.

Other types of graphical procedures may be considered, including the variety of different biplots that are available to the analyst. The following section provides a generalised framework whereby this approach to correspondence analysis, non-symmetrical correspondence analysis and biplot analysis are special cases.

3 The unbalanced generalisation

3.1 The decomposition

The graphical representation of the association between the row and column responses in a low dimensional space is of interest here. Therefore we shall denote the \(r \times M\) matrix of the row coordinates by \(\mathbf{F}\) (as we did above). Similarly, denote the \(c \times M\) matrix of column coordinates by \(\mathbf{G}\). We can generalise the decomposition (1) by noting that \(D^*\) can be alternatively expressed in terms of these coordinates such that

$$\begin{aligned} \mathbf{Z} = D \left( \mathbf{D}_\lambda , \mathbf{F}, \, \mathbf{G};\, \alpha ,\,\beta \right) = \mathbf{W}_r^{-1} \mathbf{F} \, \mathbf{D}_\lambda ^{1-(\alpha +\beta )} \mathbf{G}' \mathbf{W}_c^{-1} \end{aligned}$$
(5)

for some value of \(\alpha \), and \(\beta \) where \(\mathbf{F}\) and \(\mathbf{G}\) may be expressed by

$$\begin{aligned} \mathbf{F}= & {} \mathbf{W}_r \, \mathbf{U} \, \mathbf{D}_\lambda ^{\alpha }\,, \end{aligned}$$
(6)
$$\begin{aligned} \mathbf{G}= & {} \mathbf{W}_c \, \mathbf{V} \, \mathbf{D}_\lambda ^{\beta } \end{aligned}$$
(7)

respectively. For (5), \(\mathbf{W}_r\) is a \(r \times r\) diagonal matrix of row weights and, depending on the analysis under consideration, may be specified as, for example, \(\mathbf{D}_r^{-1/2}\) or by the identity matrix \(\mathbf{I}_r\). Similarly \(\mathbf{W}_c\) is a \(c \times c\) diagonal matrix. The assignment of \(\alpha \) and \(\beta \) can be chosen to be any value, or have any relationship, for example, \(\alpha +\beta =1\). Although \(\alpha \) and \(\beta \) typically will be chosen so that \(0\le \alpha \le 1\) and \(0\le \beta \le 1\). As we shall see, typically, \(\alpha \) (say) will be chosen to be either 0, 0.5 or 1 since the graphical display from such specifications will yield interpretable distances between row and column points.

By rearranging (6) and (7) and substituting them into (3) \(\mathbf{Z}\) can be expressed in terms of \(\mathbf{F}\), or \(\mathbf{G}\), such that

$$\begin{aligned} \mathbf{Z} = \mathbf{W}_r^{-1} \mathbf{F} \mathbf{D}_\lambda ^{1-\alpha } \mathbf{V}' = \mathbf{U} \mathbf{D}_\lambda ^{1-\beta } \mathbf{G}' \mathbf{W}_c^{-1}. \end{aligned}$$
(8)

Therefore, using (2) and (8), the total inertia is expressed in terms of \(\mathbf{F}\) and \(\mathbf{G}\) by

$$\begin{aligned} \frac{X^2}{n}= & {} \text {trace}\left[ \mathbf{D}_\lambda ^{1-\alpha } \mathbf{F}' \mathbf{W}_r^{-2} \mathbf{F} \mathbf{D}_\lambda ^{1-\alpha } \right] \end{aligned}$$
(9)
$$\begin{aligned}= & {} \text {trace}\left[ \mathbf{D}_\lambda ^{1-\beta } \mathbf{G}' \mathbf{W}_c^{-2} \mathbf{G} \mathbf{D}_\lambda ^{1-\beta }\right] . \end{aligned}$$
(10)

In fact, by substituting \(\mathbf{F}\) and \(\mathbf{G}\), as defined by (6) and (7), back into (9) and (10), we can see that

$$\begin{aligned} \frac{X^2}{n} = \text {trace} \left( \mathbf{D}_\lambda ^2 \right) . \end{aligned}$$

That is, the total inertia of the contingency table is measured as the sum of squares of the singular values obtained from the SVD of the matrix of standardised residuals, \(\mathbf{Z}\). This result also shows that, irrespective of the choice of \(\alpha \), \(\beta , \mathbf{W}_r\) and \(\mathbf{W}_c\), the mth principal axis of the graphical display will account for \(100 \times \left( \lambda _m^2/\frac{X^2}{n}\right) \%\) of the variation that exists in the contingency table. So from a descriptive point of view the interpretation of the axes will be identical, but the relative position, and configuration, of the row and column coordinates will depend on the choice of \(\alpha , \beta , \mathbf{W}_r\) and \(\mathbf{W}_c\).

Consider the matrix of row coordinates, \(\mathbf{F}\), given by (6). We can express \(\mathbf{U}\) in terms of this matrix such that

$$\begin{aligned} \mathbf{U} = \mathbf{W}_r^{-1} \mathbf{F} \mathbf{D}_\lambda ^{-\alpha } \end{aligned}$$

so that, from its orthogonality property, we obtain the result

$$\begin{aligned} \mathbf{D}_\lambda ^{2\alpha } = \mathbf{F}' \mathbf{W}_r^{-2} \mathbf{F} . \end{aligned}$$
(11)

Therefore, since the right hand side of (11) is diagonal, the total inertia may be expressed in terms of \(\mathbf{F}\) by

$$\begin{aligned} \frac{X^2}{n} = \text {trace}\left[ \left( \mathbf{F}' \mathbf{W}_r^{-2} \mathbf{F} \right) ^{1/\alpha } \right] \end{aligned}$$
(12)

for \(\alpha = 1\). When the total inertia of the contingency table remains unchanged, and keeping \(\mathbf{W}_r\) constant, if \(\alpha \) increases then (12) shows that the configuration of row coordinates in the low-dimensional space will be situated some distance from the centre of the display, called the centroid. If, on the other hand, \(\alpha \) is relatively small (close to zero, say) then the row coordinates will be drawn towards the centroid. Similarly, when \(\beta = 1\), by using the orthogonality property of \(\mathbf{V}\), the total inertia can be expressed in terms of the column coordinates \(\mathbf{G}\) by

$$\begin{aligned} \frac{X^2}{n} = \text {trace}\left[ \left( \mathbf{G}' \mathbf{W}_c^{-2} \mathbf{G} \right) ^{1/\beta } \right] \end{aligned}$$

and so the configuration of column coordinates relative to the centroid will depend on the choice of \(\beta \).

3.2 Reconstituting \(\mathbf{P}\)

An important feature of the generalisation (5) is that the matrix of joint proportions, \(\mathbf{P}\) can be reconstituted from the row and column coordinates, the generalised basic vectors and the singular values.

If the matrices \(\mathbf{U}, \mathbf{V}\) and \(\mathbf{D}_\lambda \) are of full rank, then the values of \(\mathbf{P}\) can be reconstituted exactly by

$$\begin{aligned} \mathbf{P} = \mathbf{r} \mathbf{c}' + \mathbf{D}_r^{1/2} \mathbf{Z} \mathbf{D}_c^{1/2}. \end{aligned}$$

This is termed the saturated reconstitution formula and can be alternatively expressed in terms of the matrices of row and column coordinates, \(\mathbf{F}\) and \(\mathbf{G}\), by

$$\begin{aligned} \mathbf{P} = \mathbf{r}{} \mathbf{c}' + \tilde{\mathbf{W}}_r \mathbf{F} \,\mathbf{D}_\lambda ^{1-(\alpha +\beta )} \mathbf{G}' \tilde{\mathbf{W}}_c \end{aligned}$$
(13)

where \(\tilde{\mathbf{W}}_r = \mathbf{D}_r^{1/2} \mathbf{W}_r^{-1}\) and \(\tilde{\mathbf{W}}_c = \mathbf{W}_c^{-1} \mathbf{D}_c^{1/2}\). Therefore \(\tilde{\mathbf{W}}_r \mathbf{F} \, \mathbf{D}_\lambda ^ {1- (\alpha +\beta )} \mathbf{G}' \tilde{\mathbf{W}}_c\) measures the deviation from complete independence of the cell proportions. Complete independence between the two categorical variables will result when all \(\lambda _m=0\) regardless of the choice of \(\alpha \) or \(\beta \). When this is the case, by (11), the row coordinates will be situated at the centroid. Similarly, the column coordinates will also exist at the centroid.

The advantage of the reconstitution formula is that, even if a subset of axes are selected to graphically depict the association, the joint proportions in \(\mathbf{P}\) can be approximately reconstituted. This is helpful when a test of the number of dimensions needed to construct the plot is required. For example, Escoufier (1988) looks at this issue using a special case of (13) for correspondence analysis; see Sect. 6.3

Suppose \(\mathbf{F}_{\left( k \right) }\) and \(\mathbf{G}_{\left( k\right) }\) contain the first k column vectors of \(\mathbf{F}\) and \(\mathbf{G}\), respectively, so that they are the row and column coordinates for the first \(k < M\) dimensions of a joint plot. Also suppose that \(\mathbf{D}_{\lambda (k)}\) is the \(k \times k\) diagonal matrix of the first k singular values. Then \(\mathbf{P}\) can be approximated by the unsaturated reconstitution model

$$\begin{aligned} \mathbf{P} \approx \mathbf{P}_{\left( k\right) } = \mathbf{r} \mathbf{c}' + \tilde{\mathbf{W}}_r \mathbf{F}_{\left( k\right) } \, \mathbf{D}_{\lambda (k)}^{1-\left( \alpha +\beta \right) } \mathbf{G}_ {(k)}' \tilde{\mathbf{W}}_c \, . \end{aligned}$$
(14)

3.3 Transition formula

Another special property of the general decomposition (5) is that one can obtain the row coordinates from the column coordinates, denoted by \(\mathbf{G} \rightarrow \mathbf{F}\), and vice versa, that is \(\mathbf{F} \rightarrow \mathbf{G}\). Formulae which describe such transitions are called transition formulae.

By rearranging (6) and (7), the transition formula for \(\mathbf{G} \rightarrow \mathbf{F}\) is

$$\begin{aligned} \mathbf{F} = \mathbf{W}_r \mathbf{Z} \mathbf{W}_c^{-1} \mathbf{G} \mathbf{D}_\lambda ^{\alpha - \beta -1} \end{aligned}$$

while the formula for \(\mathbf{F} \rightarrow \mathbf{G}\) is

$$\begin{aligned} \mathbf{G} = \mathbf{W}_c \mathbf{Z}' \mathbf{W}_r^{-1} \mathbf{F} \mathbf{D}_\lambda ^{\beta - \alpha - 1}. \end{aligned}$$

As a result of these formulae, cells with a large standardised residual will result in the row and column responses that cross-classify that cell to be at close proximity to one another.

Let’s consider some popular coordinate systems that are specific cases of these generalisations.

4 Special unbalanced cases

4.1 \(\mathbf{W}_r = \mathbf{I}_r, \mathbf{W}_c = \mathbf{I}_c\) and \(\alpha +\beta =1\)

With this specification of \(\mathbf{W}_r, \mathbf{W}_c, \alpha \) and \(\beta \) we obtain the matrix of residuals

$$\begin{aligned} \mathbf{Z} = \mathbf{F} \,\mathbf{G}' \end{aligned}$$

which is the factorisation, for categorical data, used for the construction of the biplot; see Gabriel (1971). Thus, the row and column coordinates are

$$\begin{aligned} \mathbf{F}= & {} \mathbf{U} \mathbf{D}_\lambda ^{\alpha } \\ \mathbf{G}= & {} \mathbf{V} \mathbf{D}_\lambda ^{1-\alpha }\,. \end{aligned}$$

Coordinates of this form were described by, for example, Aitchison and Greenacre (2002) and Goodman (1996, pp. 422–424). Different values of \(\alpha \) will produce different coordinates. The choice of \(\alpha \), and therefore \(\beta \), is made depending on the variable of interest. This is an important issue when meaningful interpretations are required and depend on the variable of interest. For example, for the analysis of quantitative variables (Gabriel 1971, p. 458) describes three sets coordinates which coincide with \(\alpha =1/2, \alpha =1\) and \(\alpha =0\) so that \(\beta =1/2\), \(\beta =0\) and \(\beta =1\) respectively. In the case of categorical variables, the assignment of these values have also been described as symmetric, row isometric and column isometric factorisations, respectively; refer to Lombardo et al. (1996). The case where \(\alpha =0\) and \(\beta =1\) was discussed by Grassi and Visentin (1994) who refer to their graphical displays using these sets of coordinates as “a symmetric \(\beta \)-plots”.

Special characteristics of this analysis include expressing the total inertia by

$$\begin{aligned} \frac{X^2}{n} = \text {trace}\left[ \mathbf{D}_\lambda ^{1-\alpha } \mathbf{F}' \mathbf{F} \mathbf{D}_\lambda ^{1-\alpha } \right] = \text {trace}\left[ \mathbf{D}_\lambda ^{\alpha } \mathbf{G}' \mathbf{G} \mathbf{D}_\lambda ^{\alpha }\right] \,. \end{aligned}$$

Also, the matrix of joint probabilities \(\mathbf{P}\) can be reconstituted by

$$\begin{aligned} \mathbf{P} = \mathbf{r}{} \mathbf{c}' + \mathbf{D}_r^{-1/2} \mathbf{F} \, \mathbf{G}' \mathbf{D}_c^{-1/2} \end{aligned}$$
(15)

while the transition formulae are

$$\begin{aligned} \mathbf{F}= & {} \mathbf{D}_r^{-1/2} \mathbf{P} \mathbf{D}_c^{-1/2} \mathbf{G} \mathbf{D}_\lambda ^{2(\alpha -1)}\\ \mathbf{G}= & {} \mathbf{D}_c^{-1/2} \mathbf{P}' \mathbf{D}_r^{-1/2} \mathbf{F} \mathbf{D}_\lambda ^{-2\alpha } \,. \end{aligned}$$

Thus, for the row isometric factorisation \(\mathbf{F} = \mathbf{D}_r^{-1/2} \mathbf{P} \mathbf{D}_c^{-1/2} \mathbf{G}\) and, for the column isometric factorisation, \(\mathbf{G} = \mathbf{D}_r^{-1/2} \mathbf{P}' \mathbf{D}_r^{-1/2} \mathbf{F}\).

If we considered instead the specification \(\mathbf{W}_r = \mathbf{D}_r^{-1/2}\) and \(\mathbf{W}_c = \mathbf{D}_c^{-1/2}\), then the row and column principal coordinates are defined as

$$\begin{aligned} \mathbf{F}= & {} \mathbf{D}_r^{-1/2} \mathbf{U} \mathbf{D}_\lambda ^\alpha \\ \mathbf{G}= & {} \mathbf{D}_c^{-1/2} \mathbf{V} \mathbf{D}_\lambda ^{1-\alpha } \end{aligned}$$

and have been the subject of much discussion in the correspondence analysis literature. These coordinates are described by Lorenzo-Seva et al. (2009) and Velden and Kiers (2005) where their focus was on the rotation of the configuration of points to yield the most interpretable display. Just as others have done in similar situations, Lorenzo-Seva et al. (2009) and Velden and Kiers (2005) described the advantages of considering specific values of \(\alpha \); those being \(\alpha = 0, \alpha = 1\) and \(\alpha = 1/2\). Such a generalisation (irrespective of the choice of \(\alpha \)) leads to the same type of biplots described above and so the reader is invited to consider these articles for a more indepth discussion of the issue. For a general discussion of the role of biplots in correspondence analysis one may refer to Greenacre (1993), Gower et al. (2011, 2014). See also Section 4.5.3 of Beh and Lombardo (2014) for an overview of a variety of biplot displays for correspondence analysis.

4.2 \(\mathbf{W_r} = n^{-1/2} \mathbf{D}_r^{-1/2}, \mathbf{W}_c = \mathbf{D}_c^{1/2}, \alpha =1\) and \(\beta =0\)

For this combination of values, the row and column coordinates are

$$\begin{aligned} \mathbf{F}= & {} n^{-1/2} \mathbf{D}_r^{-1/2} \, \mathbf{U} \, \mathbf{D}_\lambda \end{aligned}$$
(16)
$$\begin{aligned} \mathbf{G}= & {} \mathbf{D}_c^{1/2} \mathbf{V} \ \end{aligned}$$
(17)

which is the coordinate system used for the column metric preserving (CMP) biplot for categorical variables; see Gabriel and Orodoff (1990, p. 483). In this case, the matrix of standardised residuals may be expressed in terms of \(\mathbf{F}\) and \(\mathbf{G}\) by

$$\begin{aligned} \mathbf{Z} = n^{-1/2} \mathbf{D}_r^{1/2} \mathbf{F} \mathbf{G}' \mathbf{D}_c^{-1/2} \end{aligned}$$

which leads to the singular value decomposition of the centred row profiles \(\mathbf{D}_r^{-1} \mathbf{P} - \mathbf{1}{} \mathbf{c}'\). For a CMP analysis, the saturated reconstitution formula is

$$\begin{aligned} \mathbf{P} = \mathbf{r} \mathbf{c}' + n^{-1/2} \mathbf{D}_r \mathbf{F} \mathbf{G}' \end{aligned}$$

and the transition formulae \(\mathbf{G} \rightarrow \mathbf{F}\) and \(\mathbf{F} \rightarrow \mathbf{G}\) are

$$\begin{aligned} \mathbf{F}= & {} n^{-1/2} \mathbf{D}_r^{-1} \mathbf{P} \mathbf{D}_c^{-1} \mathbf{G} \\ \mathbf{G}= & {} n^{1/2} \mathbf{P}' \mathbf{F} \mathbf{D}_\lambda ^{-2} \end{aligned}$$

respectively. Note that, for \(\mathbf{F} \rightarrow \mathbf{G}, \mathbf{D}_r^{-1} \mathbf{P} \mathbf{D}_c^{-1}\) is just the matrix of Pearson ratio’s; see Beh (2004), Beh and Lombardo (2014) and Goodman (1996). For such ratio’s, complete independence between the row and column variables will arise when all the elements of \(\mathbf{D}_r^{-1} \mathbf{P} \mathbf{D}_c^{-1}\) are equal to 1. Therefore in this case we get, under complete independence, \(\mathbf{P} = \mathbf{r}{} \mathbf{c}'\), as expected.

5 A balanced generalisation

A generalisation that leads to other popular approaches is when, for (5), \(\alpha =\beta \). Since, for our general framework, only the matrix of row and column coordinates, \(\mathbf{F}\) and \(\mathbf{G}\), involve \(\alpha \) and \(\beta \), such a result means that the association that exists between the variables forming a contingency table is being represented equally by the row and column categories. Therefore one may consider such a framework to be balanced. The nature of the representation of the row and column coordinates may be considered through the specification of \(\mathbf{W}_r\) and \(\mathbf{W}_c\). A balanced analysis may further be considered by specifying these matrices such that \(\mathbf{W}_r = \mathbf{D}_r\) and \(\mathbf{W}_c = \mathbf{D}_c\), or \(\mathbf{W}_r = \mathbf{I}_r\) and \(\mathbf{W}_c = \mathbf{I}_c\), say.

By imposing the constraint \(\alpha =\beta \), the matrix of standardised residuals, \(\mathbf{Z}\), can be expressed by

$$\begin{aligned} \mathbf{Z} = D \left( \mathbf{D}_\lambda , \mathbf{F}, \, \mathbf{G};\, \alpha \right) = \mathbf{W}_r^{-1} \mathbf{F} \, \mathbf{D}_\lambda ^{1-2\alpha } \mathbf{G}' \mathbf{W}_c^{-1} \end{aligned}$$
(18)

for \(0\le \alpha \le 1\), so that the row and column coordinates are

$$\begin{aligned} \mathbf{F}= & {} \mathbf{W}_r \, \mathbf{U} \, \mathbf{D}_\lambda ^{\alpha } \end{aligned}$$
(19)
$$\begin{aligned} \mathbf{G}= & {} \mathbf{W}_c \, \mathbf{V} \, \mathbf{D}_\lambda ^{\alpha } \end{aligned}$$
(20)

respectively. Using these results, the total inertia can be expressed by

$$\begin{aligned} \frac{X^2}{n}= & {} \text {trace}\left[ \mathbf{D}_\lambda ^{1-\alpha } \mathbf{F}' \mathbf{W}_r^{-2} \mathbf{F} \mathbf{D}_\lambda ^{1-\alpha } \right] \nonumber \\= & {} \text {trace}\left[ \mathbf{D}_\lambda ^{1-\alpha } \mathbf{G}' \mathbf{W}_c^{-2} \mathbf{G} \mathbf{D}_\lambda ^{1-\alpha }\right] \nonumber \\= & {} \text {trace} \left( \mathbf{D}_\lambda ^2 \right) \,. \end{aligned}$$
(21)

For the balanced generalisation the reconstitution of \(\mathbf{P}\) can be made so that

$$\begin{aligned} \mathbf{P} = \mathbf{r}{} \mathbf{c}' + \tilde{\mathbf{W}}_r \mathbf{F} \, \mathbf{D}_\lambda ^{1-2\alpha } \mathbf{G}' \tilde{\mathbf{W}}_c \end{aligned}$$

and the transition formulae for \(\mathbf{G} \rightarrow \mathbf{F}\) and \(\mathbf{F} \rightarrow \mathbf{G}\) are

$$\begin{aligned} \mathbf{F}= & {} \mathbf{W}_r \mathbf{Z} \mathbf{W}_c^{-1} \mathbf{G} \mathbf{D}_\lambda ^{ -1} \\ \mathbf{G}= & {} \mathbf{W}_c \mathbf{Z}' \mathbf{W}_r^{-1} \mathbf{F} \mathbf{D}_\lambda ^{- 1} \end{aligned}$$

respectively. Thus, for the balanced generalisation, the transition formulae do not depend on the value of \(\alpha \), but only rely on the choice of \(\mathbf{W}_r\) and \(\mathbf{W}_c\).

6 Special balanced cases

6.1 \(\mathbf{W}_r = \mathbf{D}_r^{-1/2}, \mathbf{W}_c = \mathbf{D}_c^{-1/2}, \alpha =0\)

One of the most simple coordinate system that we can use is when \(\mathbf{W}_r = \mathbf{D}_r^{-1/2}, \mathbf{W}_c = \mathbf{D}_c^{-1/2}\) and \(\alpha =0\). The matrix of standardised residuals is

$$\begin{aligned} \mathbf{Z} = \mathbf{D}_r^{1/2} \mathbf{F}\, \mathbf{D}_\lambda \mathbf{G}' \mathbf{D}_c^{1/2} \end{aligned}$$

where the row and column coordinates are

$$\begin{aligned} \mathbf{F}= & {} \mathbf{D}_r^{-1/2} \mathbf{U} \\ \mathbf{G}= & {} \mathbf{D}_c^{-1/2} \mathbf{V} \end{aligned}$$

respectively. These coordinates are commonly referred to as standard coordinates since each of the axes that are used to construct the plot have an equal weight of 1; see, for example, Beh and Lombardo (2014) and Greenacre (1984). This is evident since, by setting \(\alpha =0\) in (11),

$$\begin{aligned} \mathbf{D}_\lambda ^{2\alpha } = \mathbf{F}' \mathbf{D}_r \mathbf{F} = \mathbf{U}' \mathbf{U} = \mathbf{I}_M. \end{aligned}$$

In this case the saturated reconstitution formulae is

$$\begin{aligned} \mathbf{P}= & {} \mathbf{r}{} \mathbf{c}' + \mathbf{D}_r \mathbf{F} \, \mathbf{D}_\lambda \mathbf{G}' \mathbf{D}_c\\= & {} \mathbf{r}{} \mathbf{c}' \left( \mathbf{1} + \mathbf{F} \, \mathbf{D}_\lambda \mathbf{G}' \right) \end{aligned}$$

where here 1 is an \(r \times c\) matrix of 1’s.

6.2 \(\mathbf{W}_r = \mathbf{D}_r^{-1/2}, \mathbf{W}_c = \mathbf{D}_c^{-1/2}\) and \(\alpha =1\)

For this combination of \(\mathbf{W}_r, \mathbf{W}_c\) and \(\alpha \), the matrix of residuals may be decomposed so that

$$\begin{aligned} \mathbf{Z} = \mathbf{D}_r^{1/2} \mathbf{F} \mathbf{D}_\lambda ^{-1} \mathbf{G}' \mathbf{D}_c^{1/2} \end{aligned}$$

where the row and column coordinates can be expressed by

$$\begin{aligned} \mathbf{F}= & {} \mathbf{D}_r^{-1/2} \, \mathbf{U} \, \mathbf{D}_\lambda \\ \mathbf{G}= & {} \mathbf{D}_c^{-1/2} \, \mathbf{V} \, \mathbf{D}_\lambda \end{aligned}$$

respectively. These coordinates are those obtained from the classical version of the simple correspondence analysis of a two-way contingency table; see, for example, Beh (2004), Beh and Lombardo (2014), Greenacre (1984) and Greenacre (2010b). Therefore, the total inertia can be expressed in terms of \(\mathbf{F}\) and \(\mathbf{G}\) such that

$$\begin{aligned} \frac{X^2}{n} = \text {trace}\left[ \mathbf{F}' \mathbf{D}_r \mathbf{F} \right] = \text {trace}\left[ \mathbf{G}' \mathbf{D}_c \mathbf{G}\right] \end{aligned}$$

which is the trace of the simple weighted Euclidean distances between the row coordinates (and column coordinates). The reconstitution formula is, as it is for simple correspondence analysis,

$$\begin{aligned} \mathbf{P}= & {} \mathbf{r}{} \mathbf{c}' + \mathbf{D}_r \mathbf{F} \mathbf{D}_\lambda ^{-1} \mathbf{G}' \mathbf{D}_c \end{aligned}$$
(22)
$$\begin{aligned}= & {} \mathbf{r}{} \mathbf{c}' \left( \mathbf{1} + \mathbf{F} \mathbf{D}_\lambda ^{-1} \mathbf{G}' \right) \end{aligned}$$
(23)

and is also referred to as correspondence model by Goodman (1986) and Greenacre (1984). It was pointed out by Gilula et al. (1988) that there are important differences between the interpretation of the elements of \(\mathbf{D}_\lambda \) for the correspondence model and the Goodman RC model. Refer to these authors for more details. This highlights that careful interpretation of the configuration of points is needed when looking at different choices of weights in (5) and (18).

Using this combination of \(\alpha , \mathbf{W}_r\) and \(\mathbf{W}_c\) leads to the transition formulae

$$\begin{aligned} \mathbf{F}= & {} \mathbf{D}_r^{-1} \mathbf{P} \mathbf{G} \mathbf{D}_\lambda ^{-1} \\ \mathbf{G}= & {} \mathbf{D}_c^{-1} \mathbf{P}' \mathbf{F} \mathbf{D}_\lambda ^{-1} \,. \end{aligned}$$

Note that this approach to performing simple correspondence analysis is equivalent to considering Pearson’s contingencies \(\mathbf{D}_r^{-1} \mathbf{P} \mathbf{D}_c^{-1} - \mathbf{1}\); see Goodman (1996). However, in this case \(\mathbf{W}_r = \mathbf{D}_r^{-1/2}, \mathbf{W}_c = \mathbf{D}_c^{-1/2}\) and \(\alpha =1/2\).

6.3 \(\mathbf{W}_r = \mathbf{I}_r, \mathbf{W}_c = \mathbf{I}_c, \alpha =1/2\)

When \(\mathbf{W}_r = \mathbf{I}_r, \mathbf{W}_c = \mathbf{I}_c, \alpha =1/2\), the decomposition of the matrix of standardised residual takes the form

$$\begin{aligned} \mathbf{Z} = \mathbf{F} \mathbf{G}' \end{aligned}$$

and is a special case of the biplot generalisation of (5) where \(\alpha =\beta =1/2\) so that \(\alpha +\beta =1\). Therefore row and column coordinates

$$\begin{aligned} \mathbf{F}= & {} \mathbf{U} \, \mathbf{D}_\lambda ^{1/2} \\ \mathbf{G}= & {} \mathbf{V} \, \mathbf{D}_\lambda ^{1/2} \end{aligned}$$

are balanced factorisations of the matrix of residual, while the saturated reconstitution formulae is given by (15). These coordinates can be confirmed by substituting \(\alpha =1/2\) into (19) and (20). For this case the total inertia may be expressed in terms of the row and column coordinates by

$$\begin{aligned} \frac{X^2}{n} = \text {trace} \left[ \mathbf{D}_\lambda \mathbf{G}' \mathbf{G} \right] = \text {trace} \left[ \mathbf{D}_\lambda \mathbf{F}' \mathbf{F} \right] \end{aligned}$$

Also the matrix of singular values can be expressed as

$$\begin{aligned} \mathbf{D}_\lambda = \mathbf{F}'{} \mathbf{F} = \mathbf{G}' \mathbf{G} \end{aligned}$$

so that (21) is verified. For this specification of \(\mathbf{W}_r, \mathbf{W}_c\) and \(\alpha \), the transition formulae are

$$\begin{aligned} \mathbf{F}= & {} \mathbf{D}_r^{-1/2} \mathbf{P} \mathbf{G} \\ \mathbf{G}= & {} \mathbf{D}_r^{-1/2} \mathbf{P}' \mathbf{F}\,. \end{aligned}$$

Therefore, a relatively large cell value will mean that the row and column categories that share this cell will be drawn close together in the display.

7 Simple demonstration

7.1 The data

We now consider a simple demonstration of the generalisation using the data summarised in the two-way contingency table given by Table 1. These data were used as a motivating example in the exploration of correspondence analysis by Beh and Lombardo (2014). It cross-classifies 1117 insulation workers in metropolitan New York by the number of years they have been exposed to asbestos and the severity of asbestosis they were diagnosed with. This contingency table appears in Beh and Smith (2011) but is from a more comprehensive study of the the impact of asbestos on health by Selikoff (1981). We note that Beh and Lombardo (2014) did not examine the association between the two variables of Table 1 in the context of any generalised form of correspondence analysis. Therefore, we compare the results of the analysis of Table 1 under the following two special cases:

  • Unbalanced case \(\mathbf{W}_r = \mathbf{I}_r, \mathbf{W}_c = \mathbf{I}_c, \alpha = 0.9\) and \(\beta = 0.1\), which coincides with the special unbalanced case outlined in Sect. 4.1 (for a specific value of \(\alpha \) and \(\beta \) where \(\alpha + \beta = 1\))

  • Balanced case \(\mathbf{W}_r = \mathbf{D}_r^{-1/2}, \mathbf{W}_c = \mathbf{D}_c^{-1/2}\) and \(\alpha = 1\), which coincides with the special balanced case outlined in Sect. 4.2.

Table 1 Selikoff’s data for 1117 New York workers with occupational exposure to asbestos
Full size table

Any of the other special cases could also have been considered but we restrict our attention to these two cases for the sake of brevity. The two analyses performed here is made using the R function gensimpleca() given in the electronic supplementary material that accompanies this paper. Before we consider the application of the generalisation outlined above, we briefly examine the association between the variables. For Table 1, the chi-squared statistic, \(X^2\) is 648.812 and has a p-value that is less than 0.0001. Therefore, there is a statistically significant association between the number of years of occupational exposure to asbestos and the severity of asbestosis that a worker contracts. From a correspondence analysis perspective, the total inertia is \(648.812/1117 = 0.581\). The nature of the association can be explored using the traditional approach to simple correspondence analysis. Although we shall instead consider here the two special cases of the generalisation presented above, where the second case is equivalent to simple correspondence analysis. To visualise the association between the row and column categories of Table 1, the optimal number of dimensions from the generalisation is \(\min \left( 5,\, 4 \right) - 1 = 3\) and so the total inertia can be partitioned to yield a contribution that each axis makes. We shall show that, from a practical perspective using the two cases described above, both yield identical numerical summaries of the total inertia and principal inertia values and many other features.

7.2 Unbalanced case: \(\mathbf{W}_r = \mathbf{I}_r, \mathbf{W}_c = \mathbf{I}_c, \alpha = 0.9\) and \(\beta = 0.1\)

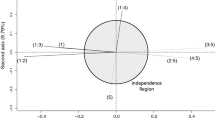
For this specification of parameters, the two-dimensional display is given by Fig. 1. This plot suggests that workers who were exposed to asbestos for no more than 10 years are likely to not be diagnosed with any form of asbestosis, while those with more than 40 years of exposure are linked to the highest levels of severity.

Fig. 1
figure 1

A two-dimensional display of the association between the variables of Table 1 where \(\mathbf{W}_r = \mathbf{I}_r, \mathbf{W}_c = \mathbf{I}, \alpha = 0.9\) and \(\beta = 0.1\)

Full size image

From a numerical perspective, the overall association can be quantified by the total inertia of the contingency table using (12). Doing so gives \(X^2/n = 0.581\) which is equivalent to the total inertia calculated in Sect. 7.1; see also the numerical output summarised in the Appendix.

For each axis of the optimal three-dimensional plot, Table 2 provides a summary of the principal inertia values, their percentage contribution to the total inertia and the cummulative inertia. It shows that a three-dimensional plot, defined by specifying the above combination of \(\mathbf{W}_r, \mathbf{W}_c\), \(\alpha \) and \(\beta \), visually represents 100% of the association between the variables- this should be of no surprise. It also shows that the two-dimensional plot of Fig. 1 accounts for 99.567% of this association - which makes it a very good quality visual summary of the association. We can also reconstitute the cell frequencies of the contingency table using the reconstitution formula (14), where \(k = 2\). Doing so gives expected cell frequencies summarised in Table 3.

Table 2 Summary of the principal inertia, its percentage contribution to the total inertia and the cummulative percentage contribution to the total inertia
Full size table
Table 3 Two-dimensional reconstitution of Table 1
Full size table

7.3 Balanced case: \(\mathbf{W}_r = \mathbf{D}_r^{-1/2}, \mathbf{W}_c = \mathbf{D}_c^{-1/2}\) and \(\alpha = 1\)

Suppose we now consider the specification of parameters described in Sect. 4.2. That is, substitute \(\mathbf{W}_r = \mathbf{D}_r^{-1/2}\), \(\mathbf{W}_c = \mathbf{D}_c^{-1/2}\) and \(\alpha = 1\) into (18)–(20). In doing so we obtain the same total inertia value and principal inertia values calculated in Sect. 7.2. Therefore, the two special cases yield identical percentage contributions to the total inertia for each of the three axes; see Table 2 for these summaries. While these numerical summaries are equivalent to those given in Sect. 7.2, this specification of parameters yields the same two-dimensional reconstituted cell frequencies that appear in Table 3. However, since the scaling of the row and column points are different (due to the different specification of \(\mathbf{W}_r, \mathbf{W}_c\) and \(\alpha \)) the two-dimensional visual display provides a slightly different configuration of points when compared with Fig. 1; Fig. 2 provides a two-dimensional display that is just the traditional two-dimensional correspondence plot obtained from performing simple correspondence analysis on Table 1.

Fig. 2
figure 2

A two-dimensional display of the association between the variables of Table 1 where \(\mathbf{W}_r = \mathbf{D}_r^{-1/2}, \mathbf{W}_c = \mathbf{D}_c^{-1/2}\) and \(\alpha = 1\)

Full size image

8 Other issues

8.1 Non-symmetrical correspondence analysis

Further generalisations can be made by considering other residuals or decompositions of \(\mathbf{Z}\). For example, they can be modified to include as a special case non-symmetrical correspondence analysis (NSCA); see, for example, D’Ambra and Lauro (1989, 1992) and Kroonenberg and Lombardo (1998). In the case where the column categories are treated as responses to an explanatory variable and the row categories comprising of the response variable, the matrix of standardised residuals, (1), can be modified to consider NSCA by considering

$$\begin{aligned} \tilde{\mathbf{Z}}= \left( \mathbf{P} - \mathbf{r}{} \mathbf{c}' \right) \mathbf{D}_c^{-1/2} = \mathbf{U} \mathbf{D}_\lambda \mathbf{V}'\,. \end{aligned}$$

As a result, \(N_\tau = n\,\text {trace}\left[ \tilde{\mathbf{Z}}' \tilde{\mathbf{Z}} \right] \) is the numerator of the Goodman-Kruskal tau index, Goodman and Kruskal (1954), and represents the absolute increase in predictability of a row response given the knowledge of a column category. Therefore, NSCA can be viewed as an example of the column isometric factorisation of \(\tilde{\mathbf{Z}}\) (where \(\mathbf{W}_r = \mathbf{I}_r, \mathbf{W}_c = \mathbf{I}_c, \alpha = 0\) and \(\beta = 1\)) so that \(\mathbf{F} = \mathbf{U}\) and \(\mathbf{G} = \mathbf{V} \mathbf{D}_\lambda \) and \(N_\tau = \text {trace}\left[ \mathbf{D}_\lambda ^2 \right] = \text {trace}\left[ \mathbf{G}' \mathbf{G} \right] \); see also Sect. 4.1. This suggests that a further generalisation may be considered by replacing \(\mathbf{Z}\) with \(\bar{\mathbf{Z}}\) in (1) where

$$\begin{aligned} \bar{\mathbf{Z}} = \mathbf{D}_r^{-\phi /2} \left( \mathbf{P} - \mathbf{r}{} \mathbf{c}'\right) \mathbf{D}_c^{-\psi /2}\,. \end{aligned}$$
(24)

Therefore, if we let \(\hat{\mathbf{Z}} = \hat{\mathbf{Z}}_{\left( \phi ,\, \psi \right) }\) the general total inertia of the contingency table may be expressed as \(\text {trace}\left( \hat{\mathbf{Z}}_{\left( \phi ,\, \psi \right) }' \hat{\mathbf{Z}}_{\left( \phi ,\, \psi \right) } \right) \). The value of the inertia depends on the analysis conducted and therefore depends on the specification of \(\phi \) and \(\psi \). For example, the following specifications of \(\phi \) and \(\psi \) lead to the following types of analyses

  • \(\phi = 1\) and \(\psi = 1\) - the correspondence analysis, or biplot analysis, of the matrix of standardised residuals,

  • \(\phi = 0\) and \(\psi = 1\) - the NSCA of a contigency table where the rows are response categories and the columns are explanatory categories,

  • \(\phi = 1\) and \(\psi = 0\) - the NSCA of a contingency table where the rows are explanatory categories and the columns are response categories.

The way in which the graphical depiction of association is represented may be obtained using those specifications of \(\mathbf{W}_r, \mathbf{W}_c, \alpha \) and \(\beta \) given above.

8.2 Analysis of adjusted residuals

As we have discussed throughout this paper, typically, the graphical display of association using methods akin to correspondence analysis and biplots, involves the SVD of Pearson’s standardised residuals; see (1). However, Agresti (2002, p. 81) points out that the asymptotic variance of the residuals are less than 1, and Haberman (1973) notes that the variance of the \(\left( i,\,j \right) \)th cell of \(n^{-1/2}{} \mathbf{Z}\) is \(\left( 1 - p_{i \bullet } \right) \left( 1 - p_{\bullet j} \right) \) where \(p_{i \bullet }\) and \(p_{\bullet j}\) are the \(\left( i,\,i \right) \)th and \(\left( j,\,j \right) \)th element of \(\mathbf{D}_r\) and \(\mathbf{D}_c\) respectively. Therefore, one may consider the matrix of adjusted residuals

$$\begin{aligned} \hat{\mathbf{Z}} = \mathbf{D}_r^{-1/2} \left( \mathbf{I}_r - \mathbf{D}_r \right) ^{-1/2} \left( \mathbf{P} - \mathbf{r}{} \mathbf{c}' \right) \left( \mathbf{I}_c - \mathbf{D}_c \right) ^{-1/2} \mathbf{D}_c^{-1/2} \end{aligned}$$

which can also be incorporated into the generalisation. Recently, Beh (2012) considered the application of correspondence using adjusted residuals. Therefore, such an adaptation of correspondence analysis may be incorporated into the general framework discussed here by considering the SVD of the adjusted residuals a special case of

$$\begin{aligned} \hat{\mathbf{Z}} = \mathbf{D}_r^{-\phi /2} \left( \mathbf{I}_r - \mathbf{D}_r \right) ^{-\gamma /2} \left( \mathbf{P} - \mathbf{r}{} \mathbf{c}' \right) \left( \mathbf{I}_c - \mathbf{D}_c \right) ^{-\delta /2} \mathbf{D}_c^{-\psi /2} \end{aligned}$$
(25)

where \(\phi = \psi = \gamma = \delta = 1\). Decompositions akin to (5) and (18) may therefore be adopted by considering \(\hat{\mathbf{Z}}\) instead of \(\mathbf{Z}\). One may note that if \(\gamma =\delta =0\), then (25) is just the matrix of residuals given by (24).

8.3 Freeman–Tukey residual

Yet another generalisation of our approach is that, rather than considering the standardised residual, or its adjusted version, correspondence analysis can be performed through the SVD of the Freeman–Tukey residual. The matrix of Freeman–Tukey residuals is of the form

$$\begin{aligned} {\breve{\mathbf{Z}}} = 2\left( \mathbf{P}^{1/2} - \left( \mathbf{r}\mathbf{c}'\right) ^{1/2} \right) \end{aligned}$$

so that the total inertia using the Freeman–Tukey statistic (Freeman and Tukey 1950) is

$$\begin{aligned} \frac{T^2}{n} = \text {trace}\left[ {\breve{\mathbf{Z}}}' {\breve{\mathbf{Z}}}\right] = \text {trace}\left[ {\breve{\mathbf{Z}}} {\breve{\mathbf{Z}}}'\right] \,. \end{aligned}$$

The role of this statistic in correspondence analysis was briefly described by Beh and Lombardo (2014, Section 9.3). So, the residual \({\breve{\mathbf{Z}}}\) can be built into the general residual of (25) by

$$\begin{aligned} \hat{\mathbf{Z}}= & {} 2^{\theta - 1}\left[ \mathbf{D}_r^{-\phi /2} \left( \mathbf{I}_r - \mathbf{D}_r \right) ^{-\gamma /2}\right] ^{\theta -1} \left( \mathbf{P}^{\theta /2} - \left( \mathbf{r}{} \mathbf{c}'\right) ^{\theta /2} \right) \\&\times \left[ \left( \mathbf{I}_c - \mathbf{D}_c \right) ^{-\delta /2} \mathbf{D}_c^{-\psi /2} \right] ^{\theta -1}\,. \end{aligned}$$

When \(\theta = 2\) this expression reduces to (25) while the matrix of Freeman–Tukey residuals when \(\theta = 1\).

8.4 Multiple correspondence analysis

The algebraic generalisations given in this paper have been described with the analysis of two categorical variables in mind. However, the same generalisations can also be applied to the analysis of multiple categorical variables in certain cases. These cases are when the traditional approach to multiple correspondence analysis is performed and this arises when the multi-way contingency table is converted to either its indicator matrix form or Burt matrix form, then simple correspondence analysis is applied to these matrices. For more information on multiple correspondence analysis, see, for example, Beh and Lombardo (2014), Greenacre (1984, 1990) and Greenacre and Blasius (2006).

9 Discussion

This paper presents a simple algebraic generalisation that unifies the growing number of variations and features of the correspondence analysis of a two-way contingency table. These approaches are reflected by the unbalanced equation (5) and its balanced version (18). By considering (25), the association structure of the row and column categories may be investigated by considering the departure from complete independence via the more general result

$$\begin{aligned} \mathbf{P} = \mathbf{r}{} \mathbf{c}' + \bar{\mathbf{W}}_r \mathbf{F} \mathbf{D}_\lambda ^{1 - \left( \alpha +\beta \right) } \mathbf{G}' \bar{\mathbf{W}}_c' \end{aligned}$$

where

$$\begin{aligned} \bar{\mathbf{W}}_r= & {} \mathbf{D}_r^{\phi /2}\left( \mathbf{I}_r - \mathbf{D}_r \right) ^{\gamma /2} \mathbf{W}_r^{-1}\\ \bar{\mathbf{W}}_c= & {} \mathbf{D}_r^{\psi /2}\left( \mathbf{I}_c - \mathbf{D}_c \right) ^{\delta /2} \mathbf{W}_c^{-1}\,. \end{aligned}$$

For such a specification, the row and column categories may be graphically represented by considering their matrix of coordinates

$$\begin{aligned} \mathbf{F}= & {} \mathbf{W}_r \mathbf{U} \mathbf{D}_\lambda ^\alpha \,,\\ \mathbf{G}= & {} \mathbf{W}_c \mathbf{V} \mathbf{D}_\lambda ^\beta \end{aligned}$$

respectively.

A key issue of this framework then is to decide on the specification of \(\alpha , \beta , \gamma , \delta , \phi , \psi , \mathbf{W}_r\) and \(\mathbf{W}_c\). By considering specific quantifications of these, one can undertake a variety of known analyses that fall within the correspondence analysis (and related biplot) family of techniques. One may consider, for example, any one of the special cases described above. The framework described in this paper also opens up the possibility of considering previously unexplored options such as implementing NSCA using an adaptation of adjusted residuals (although the benefits of doing so will not be investigated here).

Our generalisation, and much of the literature that discusses the construction, choice and interpretation of biplots, focuses on specific values of \(\alpha \) and \(\beta \); namely, for \(\alpha \), \(\alpha = 0\) and \(\alpha = 1\). These values of \(\alpha \) lead to interpretations of these asymmetric biplots that are relatively simple. This is because the categories of one variable are depicted using the traditional principal coordinates while the other variable is depicted using standard coordinates. Such specifications of \(\alpha \) allow for row/column distances to be meaningful and, through the principal coordinates, for the reconstruction of the total inertia of the contingency table. However, there is no reason why alternative specifications of \(\alpha \) (and \(\beta \)) can not be made, although in such cases the total inertia may well be an unknown measure of association. We, therefore, leave further investigations of this topic for future consideration.

The generalisation described above are not confined to the implementation of SVD. Other methods of decomposition can be considered as long as the properties associated with \(\mathbf{U}\) and \(\mathbf{V}\) are preserved. For example, Bivariate Moment Decomposition (BMD), which is especially applicable for ordinal categories, may be considered in the correspondence analysis of a two-way contingency table; see, for example, Beh (1997, 1998) and Lombardo et al. (2007). Alteratively, a Hybrid Decomposition (HD) utilising features of SVD and BMD may be considered; Beh (2001, 2008) and Lombardo et al. (2011).