Entry with two correlated signals: the case of industrial espionage and its positive competitive effects

Abstract

Recent advances in information and communication technologies have increased the incentives for firms to acquire information about rivals. These advances may have major implications for market entry because they make it easier for potential entrants to gather valuable information about, for example, an incumbent’s cost structure. However, little theoretical research has actually analyzed this question. This paper advances the literature by extending a one-sided asymmetric information version of Milgrom and Roberts’ (1982) limit pricing model. Here, the entrant is allowed access to an intelligence system (IS) of a certain precision that generates a noisy signal on the incumbent’s cost structure. The entrant thus decides whether to enter the market based on two signals: the price charged by the incumbent and the signal sent by the IS. Crucially, for intermediate values of IS precision, the set of pooling equilibria with ex-ante profitable market entry is non-empty. Moreover, the probability of ex-ante non-profitable entry is strictly positive. In classical limit pricing models, an entrant never enters in a pooling equilibrium, so this result suggests that the use of an IS may potentially increase competition.

1 Introduction

Information is a valuable resource for all firms because it allows them to improve the quality of their decisions. Of particular importance is information about other firms with which interaction occurs both directly and indirectly. Key information aspects include other firms’ infrastructures, technologies, manufacturing processes, cost structures, product pipelines, and strategies. When this information is deemed crucial but is difficult to find through public sources (“open sources”), firms sometimes push the limits of competitive intelligence, resorting to industrial espionage (Roche 2016).¹ For example, Roche (2006) reported that “when General Motors learned that a competitor had purchased property to construct a very large factory, but did not know for what purpose, it set up a ‘spy center’ to determine what its competitor was doing” (Roche 2006, p. 61).²

In recent years, industrial espionage has become even more important (Bhatti and Alymenko 2017). Initially, this rise in importance might have occurred because thousands of professionals in information gathering were seeking employment in the private sector after the end of the Cold War (Solberg 2016). However, the real driver has been the recent advances in information and communication technologies. These advances have increased the incentive for firms to engage in this illegal information gathering. Not only have they meant that a huge amount of firms’ information is electronically stored and that information systems are connected to the Internet, but they have also made cyber espionage activities “far safer and less risky” (Solberg 2016, p. 52). Many tools can be used in modern cyber industrial espionage to collect other firms’ confidential information. Trojan horses, adware, and cookies are just some examples. These instruments can provide unauthorized access and remote control of devices (“Botnets”), which enables the extraction of the desired information (Bederna and Szadeczky 2020).

Just as in the past, companies today are poor at detecting and preventing espionage and prefer to hide such cases, considering them negative publicity. As stated by Solberg (2016, p. 52), “there is always a fear that admission of breach may lead to loss of confidence and lower share price. So the stories seldom become public, if they are not leaked by state intelligence organizations or spread as anecdotes by retired executives at cocktail parties.”³ Accordingly, reliable knowledge about real espionage cases is scarce (Bhatti and Alymenko 2017). Moreover, when information about an industrial espionage case is obtained for research purposes, a restrictive confidentiality agreement must typically be signed, meaning that the real names of the implicated companies are not revealed and that the narrative is one-sided (Solberg 2016).

This situation is unfortunate because theoretical work in the field cannot be inspired or tested with real-life examples. Nevertheless, a few recent cases have become public. For instance, in 2015, it was discovered that cyber espionage tools had been employed some years ago to extract confidential information slowly and methodically from two U.S. tech companies, Avago and Skywords. The objective of the attackers was to collect relevant data to start their own business in the industry. The extracted information included recipes, product designs, equipment and facilities specifications, project plans, and performance data (Securonix 2015).

One of the most crucial business decisions is whether to start operating in a certain industry. As the previous case of industrial cyber espionage shows, there is a huge incentive to gather valuable confidential information, including performance data, from incumbents in the target industry before making an entry decision. In fact, incomplete information about incumbents’ cost structures is considered an important aspect in the theoretical explanation of market entry behavior. Milgrom and Roberts (1982) initiated this strand of research in the theoretical literature on market entry,⁴ but little theoretical research has analyzed the implications of a potential entrant’s attempts to reduce such an information disadvantage.

The goal of this paper is to advance in this direction by considering these potential entrant’s attempts in the context of modern cyber espionage. This paper extends a one-sided asymmetric information version of Milgrom and Roberts’ (1982) model. In this extended version, the entrant has access to an intelligence system (IS) of a certain precision. This IS, which consists of some of the cyber espionage instruments discussed earlier, is then employed to better detect the cost structure of an incumbent monopolist before deciding whether to enter the market (as in the case study discussed by Securonix 2015).⁵ The IS generates a noisy signal on the incumbent’s cost structure. The entrant thus decides whether to enter the market based on two signals: the price charged by the incumbent and the signal sent by the IS.

It is assumed that the precision of the IS is exogenously given. This assumption is consistent with the fact that the entrant already had access to the spying technology before considering whether to enter the market. Under this assumption, we show that gathering information about the cost structure of the incumbent produces two results: (1) for intermediate values of IS precision, the set of pooling equilibria with ex-ante profitable market entry is non-empty and (2) there exist pooling equilibria in which the probability of ex-ante non-profitable entry is strictly positive.

A body of theoretical literature explores the role of incomplete information about an incumbent’s cost structure as a crucial aspect in explaining market entry behavior. This literature stems from the long-standing question in industrial organization regarding whether an incumbent firm can set prices to deter entry that would otherwise be profitable. Bain (1949) provided an early argument that an incumbent could deter entry by limit pricing. Subsequent analysis, however, suggested that early economists exaggerated the entry-deterring effects of incumbent pricing. As Needham (1976) argued, the incumbent’s pre-entry behavior deters entry only if some link exists between this behavior and the potential entrant’s expected post-entry profit. This would be the case if the incumbent could commit to maintaining its pre-entry price in the event of entry, but such an assumption seems implausible.

Later research used game-theoretic models to reconsider whether limit pricing can deter entry. Several studies have proposed an information link between the incumbent’s pre-entry behavior and the entrant’s expected post-entry profit. In a classic paper by Milgrom and Roberts (1982), the authors (referred to as MR hereafter) assumed that the incumbent has private information about its costs of production and thus endogenously generates an interdependence between the pre-entry output rate and the potential entrant’s expected post-entry profits and entry decision. MR showed that a separating equilibrium may exist, in which the incumbent sets a below monopoly price (limit price) and thereby signals that its costs are low. The potential entrant then infers the incumbent’s cost type and enters exactly when entry would be profitable under complete information. Pooling equilibria only exist when entry is not profitable because profitable entry cannot be deterred. Therefore, in the setting considered by MR, there exists no pooling equilibrium in which the potential entrant enters the market with positive probability.

Bagwell and Ramey (1988) extended the MR model to allow the incumbent to have two signals: price and advertising.⁶ In their model, the incumbent is privately informed as to whether its costs are high or low, the potential entrant’s costs are commonly known, and entry is profitable if and only if the incumbent has high costs. In a refined separating equilibrium, the low-cost incumbent engages in “cost-reducing distortion,” meaning that it adopts the same price and advertising selection as it hypothetically would in an uncontested monopoly with even lower costs. The low-cost incumbent thus limits prices and distorts its demand-enhancing advertising upward. Once again, due to signaling, profitable entry is not deterred. However, once pooling equilibria are considered, Bagwell and Ramey (1988) showed that for some parameters, refined pooling equilibria exist in which the high-cost incumbent uses limit pricing and an upward distortion in advertising to deter entry that would be profitable under complete information. The MR result is in the benchmark model of Bagwell (2007), where both prices and advertising expenditure are signals of the incumbent monopolist’s costs. Bagwell (2007) extended the benchmark game to include two dimensions of private information. Specifically, the incumbent is privately informed of its cost type and its level of patience and selects price and advertising in the pre-entry period. Bagwell (2007) finds pooling equilibrium (satisfying the intuitive criterion) associated with the behavior of the patient high-cost incumbent, which pools with the impatient low-cost incumbent.

In this paper, we consider a monopolist engaged in R&D activity with the aim of reducing its cost of production. The outcome of the R&D project is private information belonging to the incumbent. A potential entrant assigns a certain probability that the monopolist fails to reduce its cost of production. If the project fails and the entrant enters, it will have a positive profit. If the project succeeds and the entrant enters, it will not be able to cover the entry costs. As already mentioned, we consider the case in which the entrant has access to an IS, which consists of some of the modern cyber espionage tools discussed above. This IS is used to collect (noisy) information about the incumbent’s cost structure before deciding whether to enter the market. The IS sends out one of two signals. Signal $h$ indicates that the investment was not successful, in which case we refer to the incumbent as having high cost (type H), whereas signal $l$ indicates that the investment was successful and the incumbent reduces its cost of production (type L).

Consistent with the entrant having access to the spying device (e.g., having the ability to plant one or several cyber espionage instruments in the information system of the incumbent firm) before considering whether to enter the market, we assume that the precision of the IS is exogenously given. The entrant decides whether to enter the market based on a pair of signals: the price charged by the incumbent for its product and the signal sent by the IS. If the entrant enters the market, it competes with the incumbent (under Cournot competition, Bertrand competition, or any other mode of competition).

The interaction between the entrant and the monopolist is described as a three-stage game. In the first stage, the incumbent, which knows the outcome of the R&D project, sets a price, and the IS sends a signal. Based on this pair of signals, the entrant decides whether to enter the market in the second stage. If it enters, it will be engaged in a certain mode of competition with the incumbent in the third stage of the game. The game is of incomplete information. Following Harsanyi (1967, 1968), we analyze it as a three-player game, where the players are the two types of incumbent and the entrant. We analyze the sequential equilibria of this game. The case where the IS precision is ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ (not informative) is the limit pricing model of MR for the case where the entrant’s cost is common knowledge.

We distinguish between two cases. The first is the case with separating equilibrium where the two types of incumbent charge different prices; the second is the case with pooling equilibrium where both types charge the same price.

The analysis provides several interesting findings. First, the entrant’s best response entails two different threshold entry prices, one for each IS signal. That is, for each signal, there is a threshold price such that the entrant enters if and only if the observed price is higher than the signal-related threshold price. The threshold price associated with signal $l$ (i.e., when the incumbent is of type L) is higher than the one associated with the other signal (signal $h$). This result means that the entrant will stay out for a higher range of prices when $l$ is observed than when $h$ is observed. Second, the analysis supports the separating equilibria in MR and Bagwell and Ramey (1988). Namely, the low-cost incumbent separates itself from the high-cost type, and separation is achieved through a cost-reducing distortion if the cost difference is not too far apart. In other words, at any separating equilibrium, the low-cost incumbent limits prices. This behavior enables the potential entrant to infer the incumbent’s cost so that profitable entry is not deterred. We show that the separating equilibria of our model coincide with those of MR and Bagwell and Ramey (1988), and the IS makes no difference for either the entrant or the incumbent. This result is unsurprising because the entrant in a separating equilibrium identifies the incumbent’s type with or without the use of the IS. The only difference between our separating equilibria and those of the aforementioned papers is in the behavior of the entrant when observing prices off the equilibrium path.

Third, we show that the IS plays an important role in pooling equilibria. As already mentioned, a classical game-theoretical result is that limit pricing cannot deter profitable entry. Thus, the set of pooling equilibria when the entrant’s expected profits are positive is empty. The same result is obtained in our model if the IS precision is sufficiently low to affect the entrant’s decision. In the other extreme, if the IS precision is very accurate (close to 1), then, contrary to the MR model, no pooling equilibrium exists, even when entry is not profitable ex-ante. In this case, the entrant identifies the incumbent’s type with high probability and enters the market if the IS sends signal $h$ but stays out if the signal is $l$. The high-cost monopolist, which knows that its type is detected with high probability, benefits from a deviation to its monopoly price, upsetting a pooling equilibrium.

However, the results change for intermediate values of the IS precision (i.e., when the precision of the IS is bounded away from 1 and from ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$). We show that the set of pooling equilibria is non-empty, even under ex-ante profitable entry. The entrant’s decision is to follow the signal, entering if the signal is h and staying out if the signal is $l$. Thus, when the IS precision is bounded away from 1, the high-cost monopolist knows with a high probability that the entrant will obtain the wrong signal and will stay out. Hence, it has a positive probability of succeeding in “fooling” the entrant about its type.

To compare this result with the result obtained in the MR model, let us first suppose that, prior to the completion of the R&D project, the expected payoff of E from entering the market is positive. Then no pooling equilibrium exists in the MR model. Moreover, the entrant never enters in a pooling equilibrium when the expected profit of entry is negative. Contrary to the MR model, the entrant in our model enters the market with positive probability (when the IS signal is $h$), even if its ex-ante expected profit is negative. This scenario suggests the positive competitive effects of industrial espionage in contrast to the negative ones that would emerge when a non-spied incumbent operated in more than one market (Pires and Jorge 2012). Moreover, an IS with intermediate values of precision allows for pooling equilibria with ex-ante profitable entry.

In our model, the incumbent only signals its costs by price; the other signal is generated by the IS operated by the entrant. In contrast, in the model of Bagwell and Ramey (1988), the incumbent signals its costs with both price and advertisement. Bagwell (2007) found an (intuitive) pooling equilibrium, where the incumbent has two dimensions of private information: costs and level of patience. In contrast, our model also shows the existence of pooling equilibria under ex-ante profitable entry even with only one dimension of private information by the incumbent. Nevertheless, there are two IS signals correlated with price. These signals provide additional (probabilistic) information to the entrant about the incumbent’s type and help the entrant to smooth the best response. The entrant’s best response is completely smooth in Matthews and Mirman (1983) in a limit pricing model where demand is stochastic. Accordingly, prices reveal only statistical information about the incumbent’s private information. Their (separating) equilibrium differs from standard signaling equilibria in that it can be unique, it depends on prior beliefs, and it is rich in comparative statics.

This paper is also closely related to a recent strand in the theoretical literature (Barrachina et al. 2014; Barrachina 2019) that analyzes the effects of gathering noisy information (through an IS like the one considered in this paper) in the context of entry deterrence. Barrachina et al. (2014) elaborated on the general game-theoretic framework to analyze espionage games, as suggested by Solan and Yariv (2004). They considered the case in which a potential entrant can gather noisy information about the incumbent’s decision regarding capacity expansion. As in the present paper, their results suggest that market competition is likely to increase under the entrant’s industrial espionage. Alternatively, Barrachina (2019) considered the case in which the owner of the IS is the incumbent. He identified the conditions under which communicating that the entrant’s strength can be detected is an effective entry deterrence strategy. As in the present paper, Barrachina (2019) considered espionage in the context of asymmetric information, much like Perea and Swinkels (1999) and Ho (2008). However, in the model of Perea and Swinkels (1999) and Ho (2008), the espionage was carried out by a decision maker who could act strategically.

This theoretical literature on espionage in an economic and industrial context is somewhat sparse. In a recent paper, Barrachina and Forner-Carreras (2020) also considered a market entry context but focused on the interaction of one country’s noiseless espionage with another country’s counter-espionage. The analysis shows that the optimal counter-espionage effort, concerned with social welfare in the target market, is always positive but decreases with the level of competition in that market. Counter-espionage has also been analyzed by Whitney and Gaisford (1999), Grabiszewski and Minor (2019), and Fan et al. (2019).

The expected increase in the level of market competition showed in the research by Barrachina et al. (2014) and in the present paper is likely to improve social welfare. The theoretical studies by Sakai (1985), Billand et al. (2016), and Kozlovskaya (2018) are more focused on the effect of industrial information gathering on social welfare. As in our paper, Sakai (1985) analyzed two firms and information gathering to ascertain the cost structure of the opponent firm. However, unlike us, Sakai (1985) considered two firms already competing in the market that knew neither the costs of their opponent nor their own costs.

The remainder of the paper is organized as follows. Section 2 presents the model. The entrant’s strategy is described in Sect. 3. Section 4 presents the pooling equilibria, and Sect. 5 analyzes the separating equilibria of the game. Section 6 concludes the paper. Most of the proofs are presented in the Appendix.

2 The model

We consider a monopolist M and a potential entrant E. The monopolist M is engaged in R&D activity to reduce its cost of production from $C_{H} \left( q \right)$ to $C_{L} \left( q \right)$, where $q$ is the production level. The outcome of the R&D project is information that is the private property of M. The potential entrant, E, assigns a certain probability $\mu > 0$ that M fails to reduce its cost, with probability $1 - \mu > 0$ indicating that the project was successful. Therefore, the cost function of M is private information that can be of one of two types: L (low cost) or H (high cost). The potential entrant, E, assigns the probability $\mu$ that M is of type H. If the project fails and E enters, it obtains positive profit. If the project succeeds and E enters, it will not be able to cover its entry cost and will end up with a negative profit.

The entrant has access to an IS that allows it to gather (noisy) information about the cost structure of M. The IS sends out one of two signals. Signal $h$ indicates that the investment was not successful, in which case we refer to M as having type H, whereas signal $l$ indicates that the investment was successful, so M is of type L. The precision of the IS is $\alpha$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} \le \alpha \le 1$. That is, the signal sent by the IS is correct with probability $\alpha$. The case where $\alpha = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ is equivalent to the case where E does not use an IS. The case where $\alpha = 1$ is the case where E knows the exact outcome of the project. It is assumed that the precision $\alpha$ of the IS is exogenously given.

The interaction between E and M is described as a three-stage game $G\left( \alpha \right)$. In the first stage, M chooses a price as a function of its type. The entrant decides whether to enter based on a pair of signals: the price, $p$, that M charges for its product and the signal, $s$ ($h$ or $l$), sent by the IS. If E enters, it will incur an entry cost, $K$, and compete with M (whether it is Cournot competition, Bertrand competition, or any other mode of competition). The form of competition (Cournot, Bertrand, or otherwise) is commonly known, and once E enters, the outcome of the competition is assumed to be uniquely determined. It is assumed that the above information is commonly known (including the precision, $\alpha$, of the IS).

The game $G\left( \alpha \right)$ is a game of incomplete information. Using Harsanyi’s approach, we analyze it as a three-player game where the players are the two types, H and L, of the monopolist, M, and the entrant, E. The case where $\alpha = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$, namely where the IS has no value (and may therefore be ignored), is exactly the limit pricing model MR when the entrant only has an entry cost type. Therefore, our model is an extension of the MR model where the entrant has access to an intelligence system with precision ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < 1$.

Let $Q\left( p \right)$ be the demand function and $C_{t} \left( q \right)$ be the cost function of the t-type monopoly. Let $D_{H}$ and $D_{L}$ be the duopoly profits of the H-type and the L-type monopolists, respectively. For short, we denote the H-type and the L-type monopolists by H and L, respectively. Let $\Pi_{H} \left( p \right)$ be the profit of H and let $\Pi_{L} \left( p \right)$ be the profit of L when the price is set at $p$ and when E does not enter. We denote by $D_{E} \left( H \right)$ and $D_{E} \left( L \right)$ the duopoly profits of E when E competes with H and L, respectively. We denote by $p_{H}^{M}$ and $p_{L}^{M}$ the monopoly prices of H and L, respectively (and by $q_{H}^{M}$ and $q_{L}^{M}$ the monopoly quantities). The following assumptions are standard in the literature.

Assumptions

• 1. $D_{E} \left( L \right) - K \equiv \Delta_{E} \left( L \right) < 0$ and $D_{E} \left( H \right) - K \equiv \Delta_{E} \left( H \right) > 0$.

• 2. $\Pi_{t} \left( p \right)$, $t \in \left\{ {H,L} \right\}$, is increasing in $p$ whenever $p \le p_{t}^{M}$ and is decreasing in $p$ whenever $p \ge p_{t}^{M}$.

• 3. $\Pi_{L} \left( {p_{L}^{M} } \right) - D_{L} > \Pi_{H} \left( {p_{H}^{M} } \right) - D_{H}$. Namely, L loses from entry more than H.

• 4. The cost functions $C_{t} \left( x \right)$, $t \in \left\{ {H,L} \right\}$, are differentiable, $C^{\prime}_{H} \left( q \right) > C^{\prime}_{L} \left( q \right)$ and $C_{H} \left( 0 \right) \ge C_{L} \left( 0 \right)$.

• 5. $Q\left( p \right)$ is differentiable and $Q^{\prime}\left( p \right) < 0$ for all $p \ge 0$.

• 6. All parameters of the model and the above five assumptions are commonly known.

Let $\hat{p}$ be the price for H and let $p_{0}$ be the price for L that yields the duopoly profits for H and L respectively, i.e.,

$\Pi_{H} \left( {\hat{p}} \right) = D_{H}$ and $\hat{p} < p_{H}^{M}$.

and

$\Pi_{L} \left( {p_{0} } \right) = D_{L}$ and $p_{0} < p_{L}^{M}$.

Lemma 1. (i) $\Pi_{L} \left( p \right) - \Pi_{H} \left( p \right)$ is decreasing in $p$.

(ii) $p_{H}^{M} > p_{L}^{M}$.

(iii) $\hat{p} > p_{0}$.

Proof: See Appendix.

We restrict our study to sequential equilibria of $G\left( \alpha \right)$. A sequential equilibrium is a combination of strategies and beliefs such that strategies are sequentially rational given the players’ beliefs, and beliefs are consistent in all information sets.

A strategy for the entrant E is an entry rule, $\sigma_{E} :\left\{ {h,l} \right\} \times R \to \left\{ {0,1} \right\}$. After observing a first period price $p \in {\mathbb{R}}_{ + }$ and a signal $s \in \left\{ {h,l} \right\}$, E enters if $\sigma_{E} \left( {s,p} \right) = 1$ and does not enter if $\sigma_{E} \left( {s,p} \right) = 0$. A strategy for firm M is a pricing rule, $p:\left\{ {H,L} \right\} \to R$ that specifies a price $p_{t}$, $t = \left\{ {H,L} \right\}$.

Given $\alpha$, for every pair of signals $\left( {s,p} \right)$, $s \in \left\{ {h,l} \right\}$ and $p \in {\mathbb{R}}_{ + }$, let $Prob\left( {H\left| {s,p} \right.} \right)$ and $Prob\left( {L\left| {s,p} \right.} \right) = 1 - Prob\left( {H\left| {s,p} \right.} \right)$ be the conditional probability that E assigns to the event that M is of type H and of type L, respectively.

It is assumed that, conditional on the type of M, the signals are mutually independent. Namely, M chooses price $p$ independently of the choice of the IS. Nevertheless, the signals $p$ and $s$ are correlated. If E observes a very high price, it will be more likely to observe signal $h$. If, however, E observes a low price, it will be more likely to observe signal $l$. The Bayesian posterior belief that E assigns to the types of M is

$$Prob\left( {H\left| {h,p} \right.} \right) = \frac{{Prob\left( {h,p\left| H \right.} \right)Prob\left( H \right)}}{{Prob\left( {h,p\left| H \right.} \right)Prob\left( H \right) + Prob\left( {h,p\left| L \right.} \right)Prob\left( L \right)}}$$

$$= \frac{{Prob\left( {h\left| H \right.} \right)Prob\left( {p\left| H \right.} \right)Prob\left( H \right)}}{{Prob\left( {h\left| H \right.} \right)Prob\left( {p\left| H \right.} \right)Prob\left( H \right) + Prob\left( {h\left| L \right.} \right)Prob\left( {p\left| L \right.} \right)Prob\left( L \right)}}$$

Equivalently,

$$Prob\left( {H\left| {h,p} \right.} \right) = \frac{{\mu \alpha f\left( {p\left| H \right.} \right)}}{{\mu \alpha f\left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f\left( {p\left| L \right.} \right)}}$$

(1)

Similarly,

$$Prob\left( {H\left| {l,p} \right.} \right) = \frac{{\mu \left( {1 - \alpha } \right)f\left( {p\left| H \right.} \right)}}{{\mu \left( {1 - \alpha } \right)f\left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\alpha f\left( {p\left| L \right.} \right)}}$$

(2)

where $f\left( {p\left| t \right.} \right)$ is the (density) probability that E assigns to the event that M of type $t$, $t \in \left\{ {H,L} \right\}$, sends the signal $p$.

In a pure strategy equilibrium, if H assigns probability 1 to the event that $p = p_{H}$, then $f\left( {p_{H} \left| H \right.} \right) = 1$ and $f\left( {p\left| H \right.} \right) = 0$ if $p \ne p_{H}$. In this case, $f\left( {p\left| H \right.} \right)$ is identified with the probability that H selects $p$. Similarly, $f\left( {p_{L} \left| L \right.} \right) = 1$ and $f\left( {p\left| L \right.} \right) = 0$, $\forall p \ne p_{L}$. Hence, for $p \ne p_{H}$ and $p \ne p_{L}$, (1) and (2) are not well defined (the numerators and denominators are zero). To apply the sequential equilibrium concept, we need to consistently define beliefs for any observed $p$. Therefore, off the equilibrium path, we approach $f\left( {p\left| t \right.} \right)$ by a sequence $\left( {f_{n} \left( {p\left| t \right.} \right)} \right)_{n = 1}^{\infty }$, such that $f_{n} \left( {p\left| t \right.} \right) > 0$ and $\mathop {\lim }\limits_{n \to \infty } f_{n} \left( {p\left| t \right.} \right) = f\left( {p\left| t \right.} \right)$ for all $p \in {\mathbb{R}}_{ + }$. Let

$$Prob_{n} \left( {H\left| {h,p} \right.} \right) \equiv \frac{{\mu \alpha f_{n} \left( {p\left| H \right.} \right)}}{{\mu \alpha f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}}$$

(3)

$$Prob_{n} \left( {H\left| {l,p} \right.} \right) \equiv \frac{{\mu \left( {1 - \alpha } \right)f_{n} \left( {p\left| H \right.} \right)}}{{\mu \left( {1 - \alpha } \right)f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\alpha f_{n} \left( {p\left| L \right.} \right)}}$$

(4)

Now $Prob_{n} \left( {H\left| {h,p} \right.} \right)$ is well defined for all $p \in {\mathbb{R}}_{ + }$, and (1) can be modified to be

$$Prob\left( {H\left| {h,p} \right.} \right) \equiv \mathop {\lim }\limits_{n \to \infty } \frac{{\mu \alpha f_{n} \left( {p\left| H \right.} \right)}}{{\mu \alpha f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}}$$

We modify (2) in the same way. Note that different sequences of $\left( {f_{n} \left( {p\left| t \right.} \right)} \right)_{n = 1}^{\infty }$ generate different conditional probabilities $Prob\left( {t\left| {s,p} \right.} \right)$, $t \in \left\{ {H,L} \right\}$, $s \in \left\{ {h,l} \right\}$,$p \in {\mathbb{R}}_{ + }$.

Let $\Pi_{E} \left( {s,p} \right)$ be the expected payoff of E given its on- and off-equilibrium beliefs, namely

$$\Pi_{E} \left( {s,p} \right) \equiv Prob\left( {H\left| {s,p} \right.} \right)\Delta_{E} \left( H \right) + Prob\left( {L\left| {s,p} \right.} \right)\Delta_{E} \left( L \right)$$

(5)

In a sequential equilibrium, if $\Pi_{E} \left( {s,p} \right) < 0$, E does not enter the market, and if $\Pi_{E} \left( {s,p} \right) > 0$, E enters. To simplify the analysis, we assume that E also stays out when $\Pi_{E} \left( {s,p} \right) = 0$. Namely, E stays out if and only if it observes $\left( {s,p} \right)$ such that

$$\Pi_{E} \left( {s,p} \right) \equiv Prob\left( {H\left| {s,p} \right.} \right)\Delta_{E} \left( H \right) + Prob\left( {L\left| {s,p} \right.} \right)\Delta_{E} \left( L \right) \le 0$$

3 Conditions for limit pricing: the entry rule

For firm M to engage in limit pricing, entry should be more likely when prices are high rather than when they are low for any observed signal. This is the case if $\sigma_{E} \left( {s,p} \right)$ specifies entry if and only if for each signal $s$ the observed price exceeds the entry price. The following assumptions help ensure that $\sigma_{E} \left( {s,p} \right)$ is of this form for any $p$ and for each $s \in \left\{ {h,l} \right\}$.

Assumption 7

• (1) For each $t \in \left\{ {H,L} \right\}$ and each $n$, $f_{n} \left( {p\left| t \right.} \right)$ is differentiable in $p$ for all $p \ge 0$.

• (2) Let

  $$g_{n} \left( p \right) = {{f_{n} \left( {p\left| H \right.} \right)} \mathord{\left/ {\vphantom {{f_{n} \left( {p\left| H \right.} \right)} {f_{n} \left( {p\left| L \right.} \right)}}} \right. \kern-\nulldelimiterspace} {f_{n} \left( {p\left| L \right.} \right)}}$$

  Then $g_{n} \left( p \right)$ is increasing in $n$ for each $p$, and is increasing in $p$ for each $n$. Furthermore, for every $n$, $\mathop {\lim }\limits_{p \to 0} g_{n} \left( p \right) = 0$ and $\mathop {\lim }\limits_{p \to \infty } g_{n} \left( p \right) = \infty$.

• (3) Let $g\left( p \right) = \mathop {\lim }\limits_{n \to \infty } g_{n} \left( p \right)$. Then $g\left( p \right)$ is continuous in $p$.

Note that, ${{f\left( {p\left| H \right.} \right)} \mathord{\left/ {\vphantom {{f\left( {p\left| H \right.} \right)} {f\left( {p\left| L \right.} \right)}}} \right. \kern-\nulldelimiterspace} {f\left( {p\left| L \right.} \right)}}$ is the likelihood ratio. To be increasing in $p$ or, equivalently, to satisfy the Monotone Likelihood Ratio Property in $p$ (MLRP, Milgrom 1981) implies that a high price is more likely to come from H than from L. Most of the common densities such as the uniform, normal, and exponential satisfy the MLRP. Assumption 7 guarantees continuity and monotonicity of the conditional probability $Prob\left( {t\left| {s,p} \right.} \right)$, $t \in \left\{ {H,L} \right\}$, $s \in \left\{ {h,l} \right\}$, $p \in {\mathbb{R}}_{ + }$. The next lemma shows the continuity and monotonicity of such conditional probabilities. The proof is given in the Appendix.

Lemma 2. (i) For each $s \in \left\{ {h,l} \right\}$ and $t \in \left\{ {H,L} \right\}$, $Prob\left( {t\left| {s,p} \right.} \right)$ is continuous in $p$ and $Prob\left( {H\left| {s,p} \right.} \right)$ is non-decreasing in $p$, $p \ge 0$.

(ii) For every $p \ge 0$, $Prob\left( {H\left| {h,p} \right.} \right) > Prob\left( {H\left| {l,p} \right.} \right)$.

By the above lemma, $\Pi_{E} \left( {s,p} \right)$ is continuous and non-decreasing in $p$. This result follows from the fact that $Prob\left( {H\left| {s,p} \right.} \right)$ is continuous and non-decreasing in $p$, $\Delta_{E} \left( H \right) > 0$, $Prob\left( {L\left| {s,p} \right.} \right) = 1 - Prob\left( {H\left| {s,p} \right.} \right)$ and $\Delta_{E} \left( L \right) < 0$. Moreover,

Lemma 3. Let $J_{s} = \left\{ {\left. {p \ge 0} \right|\Pi_{E} \left( {s,p} \right) \le 0} \right\}$. Then $J_{s}$ and ${\mathbb{R}}_{ + } \backslash J_{s}$ are both non-empty sets. In other words, $\Pi_{E} \left( {s,p} \right) < 0$ for sufficiently small $p$, and $\Pi_{E} \left( {s,p} \right) > 0$ when $p$ is sufficiently large.

Proof: See Appendix.

Recall that by Assumption 1, $D_{E} \left( L \right) - K \equiv \Delta_{E} \left( L \right) < 0$,$D_{E} \left( H \right) - K \equiv \Delta_{E} \left( H \right) > 0$.

Proposition 1. Suppose that Assumption 1 holds. Then any beliefs of E that satisfy Assumption 7 imply that $\Pi_{E} \left( {s,p} \right)$ is continuous and non-decreasing in $p$ and uniquely determines $p_{h}$ and $p_{l}$. In every sequential equilibrium with these beliefs, $p_{h} < p_{l}$ and E enters the market if and only if it observes signal $\left( {h,p} \right)$ with $p > p_{h}$ or signal $\left( {l,p} \right)$ with $p > p_{l}$.

Proof: See Appendix.

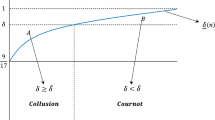
Because $p_{l} > p_{h}$, the best response entry rule of E when it observes the pair of signals $\left( {s,p} \right)$ is given by Fig. 1 below.

Fig. 1

The entry rule

The correlation between signals and prices gives rise to the ordering of the threshold prices associated with signals. Accordingly, the threshold price associated with signal $l$ is higher than the threshold price associated with signal $h$. Thus, for instance, the entrant will stay out for a higher range of prices when observing $l$ than when observing $h$. This conclusion is intuitive because the signal sent by the IS is informative (albeit noisy), and E will be more inclined to enter the market when receiving signal $h$ than when receiving signal $l$.

Our next goal is to characterize the sequential equilibrium of $G\left( \alpha \right)$ given the above decision rule of E.

4 Conditions for entry deterrence: pooling equilibria

We first analyze the existence of sequential pooling equilibria, which is our main contribution. We claim that the set of pooling equilibria with ex-ante profitable market entry is non-empty and that the probability of ex-ante non-profitable entry is strictly positive (specifically, when the IS signal is $h$) if the cost function of H is not substantially higher than that of L and the IS precision belongs to some intermediate level. This result is observed in our model, in which the incumbent only has one dimension of private information, because the entrant receives one of the two IS signals correlated with price. This signal provides the entrant with additional (probabilistic) information about the incumbent’s type. This result also offers support to the predictions of the earlier literature, where Bain (1949) describes the condition under which limit pricing may deter entry.

4.1 The conditional-to-signal entry rule

Pooling equilibria refer to triples of the form $\left( {\sigma_{E} ,p_{H} ,p_{L} } \right)$, where $\sigma_{E}$ is the strategy of E and $p_{H} = p_{L} \equiv p^{*}$.

We first calculate the entrant’s expected payoff conditional on receiving a signal from the IS and observing price $p^{*}$. Recall that, by Assumption 1, $D_{E} \left( L \right) - K \equiv \Delta_{E} \left( L \right) < 0$ and $D_{E} \left( H \right) - K \equiv \Delta_{E} \left( H \right) > 0$, where $D_{E} \left( H \right)$ and $D_{E} \left( L \right)$ denote the duopoly profits of E when it competes with H and L, respectively.

Given signal $l$ of the IS, the expected payoff of E conditional on receiving such a signal is

$$\Pi_{E} \left( {\left. l \right|\alpha } \right) \equiv Prob\left( {H\left| l \right.} \right)\Delta_{E} \left( H \right) + Prob\left( {L\left| l \right.} \right)\Delta_{E} \left( L \right)$$

Equivalently,

$$\Pi_{E} \left( {\left. l \right|\alpha } \right) = \frac{{\mu \left( {1 - \alpha } \right)}}{{\mu \left( {1 - \alpha } \right) + \left( {1 - \mu } \right)\alpha }}\Delta_{E} \left( H \right) + \frac{{\left( {1 - \mu } \right)\alpha }}{{\mu \left( {1 - \alpha } \right) + \left( {1 - \mu } \right)\alpha }}\Delta_{E} \left( L \right)$$

Hence, if the IS sends signal $l$, E does not enter the market when observing price $p^{*}$ if and only if $\Pi_{E} \left( {\left. l \right|\alpha } \right) \le 0$.

Let

$$\overline{\alpha }_{l} = \frac{{\mu \Delta_{E} \left( H \right)}}{{\mu \Delta_{E} \left( H \right) - \left( {1 - \mu } \right)\Delta_{E} \left( L \right)}}$$

(6)

Therefore, suppose that the entrant’s expected profits conditional on receiving signal l are non-positive. Then the entrant does not enter when observing price $p^{*}$ if and only if the IS precision is sufficiently high (i.e., $\alpha \ge \overline{\alpha }_{l}$).

Since, in our model, $1/2 < \alpha < 1$, and $0 < \overline{\alpha }_{l} < 1$, we wish to know when $\overline{\alpha }_{l} < 1/2$. From (6) and recalling that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right)$ is the entrant’s expected profit without the IS, then $\overline{\alpha }_{l} < 1/2$ if and only if

$$\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$$

(7)

Therefore, E does not enter when receiving signal $l$ if and only if the entrant’s unconditional expected payoffs are negative (i.e., (7) is satisfied).

Next, suppose that the IS sends signal $h$. Then the expected payoff of E conditional on receiving $h$ is

$$\Pi_{E} \left( {\left. h \right|\alpha } \right) \equiv Prob\left( {H\left| h \right.} \right)\Delta_{E} \left( H \right) + Prob\left( {L\left| h \right.} \right)\Delta_{E} \left( L \right)$$

Equivalently,

$$\Pi_{E} \left( {\left. h \right|\alpha } \right) = \frac{\mu \alpha }{{\mu \alpha + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}\Delta_{E} \left( H \right) + \frac{{\left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}{{\mu \alpha + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}\Delta_{E} \left( L \right)$$

Hence, if the IS sends signal $h$, E does not enter the market when observing price $p^{*}$ if and only if $\Pi_{E} \left( {\left. h \right|\alpha } \right) \le 0$.

Let

$$\overline{\alpha }_{h} = \frac{{ - \left( {1 - \mu } \right)\Delta_{E} \left( L \right)}}{{\mu \Delta_{E} \left( H \right) - \left( {1 - \mu } \right)\Delta_{E} \left( L \right)}}$$

(8)

Note that $\Pi_{E} \left( {\left. h \right|\alpha } \right) \le 0$ if and only if the IS precision is sufficiently low (i.e., $\alpha \le \overline{\alpha }_{h}$).

As above, $0 < \overline{\alpha }_{h} < 1$ and, from (8), $\overline{\alpha }_{h} > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ if and only if (7) is satisfied (i.e., the entrant’s expected profit without signals is negative).

Corollary 1. Suppose that ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < 1$ and

$$\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$$

Then E stays out if and only if it observes signal $l$ or receives signal $h$ and the IS precision is low enough (i.e., $\alpha \le \overline{\alpha }_{h}$).

Alternatively, when the entrant’s expected profit without signals is negative, E enters the market if and only if it receives signal $h$ and the IS precision is sufficiently high (i. e., $\alpha > \overline{\alpha }_{h}$).

When $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$, then $\overline{\alpha }_{h} < 1/2 < \overline{\alpha }_{l} < 1$. Hence, $\alpha > \overline{\alpha }_{h}$ $\forall \alpha$, $1/2 < \alpha < 1$. Namely, if the IS sends signal $h$, E enters the market when price $p^{*}$ is observed, irrespective of the precision $\alpha$ of the IS. Also, $\overline{\alpha }_{l} > 1/2$, so we may have $1/2 < \alpha < \overline{\alpha }_{l}$ or $\overline{\alpha }_{l} \le \alpha < 1$. In the former case, E enters the market when price $p^{*}$ is observed, irrespective of the signal sent by the IS. In the latter, when price $p^{*}$ is observed, E enters the market if the IS sends signal $h$ but does not enter if the IS sends signal $l$. Therefore,

Corollary 2. Suppose that $1/2 < \alpha < 1$ and

$$\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$$

Then the entrant stays out if and only if it observes signal $l$ and the IS precision is high enough (i.e., $\alpha \ge \overline{\alpha }_{l}$).

Alternatively, when the entrant’s expected profit without signals is positive, then it enters the market when price $p^{*}$ is observed if and only if it observes signal $h$ or an imprecise signal $l$ (i.e., $\alpha < \overline{\alpha }_{l}$).

In the classical threshold price model, pooling equilibria entail a pooling price smaller than or equal to such a threshold. Here, however, by the entry rule, there are two threshold prices, $p_{h}$ and $p_{l}$, such that E enters the market if and only if it observes signal $\left( {h,p} \right)$ with $p > p_{h}$ or signal $\left( {l,p} \right)$ with $p > p_{l}$. Moreover, a key factor for entry is the sign of the entrant’s expected payoff conditional on receiving signal $s \in \left\{ {h,l} \right\}$. By Corollary 1, this sign depends on the entrant’s expected profit without signals and IS precision.

Proposition 2 below characterizes the set of pooling equilibria of the game $G\left( \alpha \right)$. The proof is long and tedious because the incentive compatibility conditions must account for the entrant’s positive and negative expected payoffs, the different bounds on $\alpha$, the differences of the incumbent’s cost technology, and the different orderings of the entrant’s threshold prices $p_{h}$ and $p_{l}$ with respect to the monopoly and duopoly prices. Therefore, most of it is shown in the Appendix. Nevertheless, we first motivate the approach, show some general results, and provide some notation.

We describe next some useful properties and the incentive compatibility conditions of the monopolist types that any pooling equilibrium of $G\left( \alpha \right)$ must satisfy.

4.2 Properties of pooling equilibria

Let $A_{l} = \left\{ {\alpha \left| {\Pi_{E} \left( {\left. l \right|\alpha } \right) \le 0} \right.} \right\}$ and $A_{h} = \left\{ {\alpha \left| {\Pi_{E} \left( {\left. h \right|\alpha } \right) \le 0} \right.} \right\}$. First, suppose that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$. In this case, $\overline{\alpha }_{l} < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \overline{\alpha }_{h} < 1$. Hence, $\alpha > \overline{\alpha }_{l}$ and $\alpha \in A_{l}$$\forall \alpha$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < 1$. Namely, if the IS sends signal $l$, E does not enter the market when price $p^{*}$ is observed, irrespective of the precision $\alpha$ of the IS. This case is split into two subcases: a) ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$ and b) $\overline{\alpha }_{h} < \alpha < 1$.

(a) We start with the subcase ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$. Here, $\alpha \in A_{l} \cap A_{h}$. That is, E does not enter the market when price $p^{*}$ is observed, irrespective of the signal sent by the IS. Hence, belief consistency (see Proposition 1) implies that $p^{*} \le p_{h}$. The following lemma, proven in the Appendix, establishes a useful result.

Lemma 4. Suppose that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$. Then, in every pooling equilibrium, $p_{H}^{M} > p_{L}^{M} \ge p_{h}$.

Using Lemma 4, we now offer the incentive compatibility conditions of the two types of incumbent for low values of IS precision.

4.3 The incentive compatibility condition of H ($ICC_{H}$) when ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$.

By belief consistency, $p^{*} \le p_{h}$, and by Lemma 4, $p_{H}^{M} > p_{h}$. Thus, it suffices for the $ICC_{H}$ to consider only deviations to $p > p_{h}$. In this case, when observing such a $p$, E may enter the market with some probability, and H may be better off choosing $p_{H}^{M}$. Conditional on the monopolist of type H and for any $p \in \left( {p_{h} ,p_{l} } \right]$, E receives signal $h$ with probability $\alpha$ and enters yet receives signal $l$ with probability $\left( {1 - \alpha } \right)$ and does not enter. If $p > p_{l}$, then E always enters.

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right)$ be the only $p$ whose profits are equal to the expected profits of H when E enters with probability $\alpha$. That is, $\alpha$, i.e.,

$$\Pi_{H} \left( p \right) = \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right) = D_{H} + \left( {1 - \alpha } \right)\left( {\Pi_{H} \left( {p_{H}^{M} } \right) - D_{H} } \right) > D_{H}$$

And let $\tilde{p}_{H} \left( \alpha \right)$ be the (unique) solution for $p$ of the following equation

$$\Pi_{H} \left( p \right) = \alpha \Pi_{H} \left( {p_{H}^{M} } \right) + \left( {1 - \alpha } \right)D_{H} > D_{H}$$

In other words, $\tilde{p}_{H} \left( \alpha \right)$ is the unique $p$ whose profits are equal to the expected profits of H when E enters with probability $\left( {1 - \alpha } \right)$. Note that $\tilde{p}_{H} \left( \alpha \right) > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right) > \hat{p}$.

Both $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right)$ and $\tilde{p}_{H} \left( \alpha \right)$ play a key role in the relevant $ICC_{H}$ when ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$, summarized by the following lemma.

Lemma 5. If $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$, then the $ICC_{H}$ requires that at any pooling equilibrium $p^{*}$.

(1) $p_{H}^{M} > p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right)$ if $p_{h} < p_{H}^{M} \le p_{l}$;

(2) $p_{H}^{M} > p^{*} \ge \hat{p}$ if $p_{H}^{M} > p_{l}$, with $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$.

Proof: See Appendix.

The incentive compatibility conditions for H state that for $p^{*}$ to be a pooling equilibrium price, it should provide profits that are greater than or equal to those from E entering with probability $\alpha$ when $p_{h} < p_{H}^{M} \le p_{l}$ (part (1) of Lemma 5) and greater than or equal to those of the duopoly profits when $p_{H}^{M} > p_{l}$, provided that $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$ (part (2) of Lemma 5).

The role of $\tilde{p}_{H} \left( \alpha \right)$ is the following. For any value of IS precision $\alpha \in \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2},\overline{\alpha }_{h} } \right]$, the second-period expected profits after a first-period pooling are the monopoly profits. Those following a deviation to $p_{l}$ are a linear combination of the duopoly and monopoly expected profits, weighted by probability $\alpha$. Therefore, a pooling $p^{*} \ge \hat{p}$ avoids a deviation to $p_{l}$ whenever, for example, first-period profits from $p^{*} = \hat{p}$ plus the difference between second-period expected profits from the pooling and those from the deviation are greater than or equal to the profits from $p_{l}$. Hence, $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$.

4.4 The incentive compatibility condition of L ($ICC_{L}$) when ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$.

For the specification of the relevant $ICC_{L}$ when ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$, it must again be considered that, by Lemma 4, $p_{L}^{M} \ge p_{h}$. Hence, when $p_{L}^{M} = p_{h}$, the only possible pooling equilibrium price that satisfies belief consistency is $p^{*} = p_{L}^{M}$, and L would have no incentive to deviate. When $p_{L}^{M} > p_{h}$, L may consider deviations to $p_{L}^{M}$. Note that, conditional on having the monopolist of type L and for any $p \in \left( {p_{h} ,p_{l} } \right]$, E receives signal $l$ with probability $\alpha$ and does not enter yet receives signal $h$ with probability $\left( {1 - \alpha } \right)$ and enters. Also, for any $p > p_{l}$, E always enters.

Define $\tilde{p}_{L} \left( \alpha \right)$ as the unique price solving

$$\Pi_{L} \left( p \right) = \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} = D_{L} + \alpha \left( {\Pi_{L} \left( {p_{L}^{M} } \right) - D_{L} } \right) > D_{L}$$

In other words, $\tilde{p}_{L} \left( \alpha \right)$ is the only $p$ whose profits are equal to the expected profits of L when E enters with probability $\left( {1 - \alpha } \right)$. Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ be the unique price solving

$$\Pi_{L} \left( p \right) = \alpha D_{L} + \left( {1 - \alpha } \right)\Pi_{L} \left( {p_{L}^{M} } \right) > D_{L}$$

That is, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ is the only $p$ whose profits are equal to the expected profits of L when E enters with probability $\alpha$. Note that $\tilde{p}_{L} \left( \alpha \right) > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right) > p_{0}$.

Both $\tilde{p}_{L} \left( \alpha \right)$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ play a key role in the relevant $ICC_{L}$ when ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$, as specified in the following lemma.

Lemma 6. If $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$, then the $ICC_{L}$ requires that at any pooling equilibrium $p^{*}$.

(1) $p_{L}^{M} > p^{*} \ge \tilde{p}_{L} \left( \alpha \right)$ if $p_{h} < p_{L}^{M} \le p_{l}$;

(2) $p_{L}^{M} > p^{*} \ge p_{0}$ if $p_{L}^{M} > p_{l}$, with $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right) \ge p_{l}$.

Proof: See Appendix.

Similarly to $ICC_{H}$ in Lemma 5, the incentive compatibility conditions for L indicate that for $p^{*}$ to be a pooling equilibrium price, it should give profits that are greater than or equal to those from when E enters with probability $\left( {1 - \alpha } \right)$ when $p_{h} < p_{L}^{M} \le p_{l}$ (part (1) of Lemma 6) and greater than or equal to those of the duopoly profits when $p_{L}^{M} > p_{l}$, provided that $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right) \ge p_{l}$ (part (1) of Lemma 6).

Notice that part (2) in Lemmas 5 and 6 imply that $p_{h}$ and $p_{l}$ have to be sufficiently close to each other.

(b) We now analyze the incentive compatibility conditions of the two types of incumbent for high values of IS precision. Let us consider that $\overline{\alpha }_{h} < \alpha < 1$. In this case $\alpha \in A_{l} \backslash \overline{A}_{h}$. Thus, when price $p^{*}$ is observed, E enters the market if the IS sends signal $h$ and does not enter if the IS sends signal $l$. Hence, by belief consistency (see Proposition 1), $p_{h} < p^{*} \le p_{l}$. There are some useful properties of the pooling equilibria in this case. First, a useful result is established by the following lemma. The proof is provided in the Appendix.

Lemma 7. If $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\overline{\alpha }_{h} < \alpha < 1$, then at any $p^{*}$, $p_{H}^{M} > p_{L}^{M} \ge p_{l}$.

The above lemma allows us to present the incentive compatibility conditions for the two types of incumbent when IS precision is high.

4.5 The incentive compatibility condition of H ($ICC_{H}$) when $\overline{\alpha }_{h} < \alpha < 1$

By Lemma 7, $p_{H}^{M} > p_{l}$. This result, together with the fact that $\overline{\alpha }_{h} < \alpha < 1$ and hence that E enters if it observes signal $h$, is behind the $ICC_{H}$ summarized in Lemma 8. Further details are given in the proof of this lemma in the Appendix.

Lemma 8. If $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\overline{\alpha }_{h} < \alpha < 1$, then the $ICC_{H}$ requires that at any pooling equilibrium $p^{*}$, $p^{*} \ge \tilde{p}_{H} \left( \alpha \right) > \hat{p}$ and $\hat{p} \ge p_{h}$.

The intuition of this lemma is that at any pooling $p^{*} \in \left( {p_{h} ,p_{l} } \right]$ ${\mathrm{p}}^{*}\in$, by Proposition 1, the entrant will enter with positive probability when signal $h$ is received, and the second-period expected profits for H are

$$\alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right) = \Pi_{H} \left( {p_{H}^{M} } \right) - \alpha \left( {\Pi_{H} \left( {p_{H}^{M} } \right) - D_{H} } \right)$$

where $\alpha = Prob\left( {s = h/H} \right)$ or the entry probability when the monopoly is of type H.

In other words, for any value of IS precision $\alpha \in \left( {\overline{\alpha }_{h} ,1} \right)$, the second-period expected profits after a first-period pooling are the monopoly profits minus the probability of entry times the difference between the monopoly and duopoly profits. By Lemma 7,$p_{H}^{M} > p_{l}$, so any pooling $p^{*} \in \left( {p_{h} ,p_{l} } \right]$ requires that the inequality

$$\Pi_{H} \left( {p^{*} } \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{H}^{M} } \right) + D_{H}$$

is satisfied, which is equivalent to satisfying

$$\Pi_{H} \left( {p^{*} } \right) \ge D_{H} + \alpha \left( {\Pi_{H} \left( {p_{H}^{M} } \right) - D_{H} } \right)$$

Thus, the profits from the first-period pooling must compensate for the second-period expected loss from entry, which, for the H-type monopoly, implies that $p^{*} \ge \tilde{p}_{H} \left( \alpha \right)$, as shown above.

Also, the pooling profits must be higher than the duopoly profits. This condition is met whenever $p^{*} \ge \tilde{p}_{H} \left( \alpha \right) > \hat{p}$ with $\hat{p} \ge p_{h}$, where $\hat{p}$ is the price for H that yields the duopoly profits.

4.6 The incentive compatibility condition of L ($ICC_{L}$) when $\overline{\alpha }_{h} < \alpha < 1$

By Lemma 7, $p_{L}^{M} \ge p_{l}$. Hence, when $p_{L}^{M} = p_{l}$, the only possible pooling equilibrium price satisfying belief consistency is $p^{*} = p_{L}^{M}$, and L would have no incentive to deviate. Consequently, the relevant $ICC_{L}$ is specified in Lemma 9 (proven in the Appendix).

Lemma 9. If $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\overline{\alpha }_{h} < \alpha < 1$, then the $ICC_{L}$ requires that at any pooling equilibrium $p_{L}^{M} > p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ and $p_{0} \ge p_{h}$.

The intuition of Lemma 9 is similar to that of Lemma 8 but for the monopoly of type L. Specifically, the second-period expected profits for the L-type monopoly after the pooling $p^{*}$, for any value of IS precision $\alpha \in \left( {\overline{\alpha }_{h} ,1} \right)$ are

$$\alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} = \Pi_{L} \left( {p_{L}^{M} } \right) - \left( {1 - \alpha } \right)\left( {\Pi_{L} \left( {p_{L}^{M} } \right) - D_{L} } \right)$$

where $\left( {1 - \alpha } \right) = Prob\left( {s = h/L} \right)$ or the probability of market entry when the monopoly is of type L. By Lemma 7 $p_{L}^{M} \ge p_{l}$. Thus, any pooling $p^{*} \in \left( {p_{h} ,p_{l} } \right]$ requires

$$\Pi_{L} \left( {p^{*} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} \ge \Pi_{L} \left( {p_{L}^{M} } \right) + D_{L}$$

to be satisfied, which is equivalent to satisfying

$$\Pi_{L} \left( {p^{*} } \right) \ge \alpha D_{L} + \left( {1 - \alpha } \right)\Pi_{L} \left( {p_{L}^{M} } \right) = D_{L} + \left( {1 - \alpha } \right)\left( {\Pi_{L} \left( {p_{L}^{M} } \right) - D_{L} } \right)$$

Thus, again, the profits from the first-period pooling must compensate for the second-period expected loss from entry. The above implies that $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ for the L-type monopoly. Additionally, the pooling profits must be higher than the duopoly profits. This condition is met whenever $p_{L}^{M} > p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ with $p_{0} \ge p_{h}$, where $p_{0}$ is the price for L that yields the duopoly profits.

We now consider the case in which the entrant’s expected profit without signals is positive, such that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$. By Corollary 2, the relevant threshold for E to assess the precision of the IS and hence the entry decision is $\overline{\alpha }_{l}$. It is easy to show that the properties and incentive compatibility conditions that must be satisfied in every pooling equilibrium here are equivalent to those analyzed for the case in which $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$. Further details are offered in the Appendix.

We now present the pooling equilibria of $G\left( \alpha \right)$. Essentially, given the entrant’s entry rule, the two incentive compatibility conditions must be compatible and sequentially rational at equilibrium, and the entry rule must be consistent with equilibrium prices. Let $\delta = {{\left( {\Pi_{H} \left( {p_{L}^{M} } \right) - D_{H} } \right)} \mathord{\left/ {\vphantom {{\left( {\Pi_{H} \left( {p_{L}^{M} } \right) - D_{H} } \right)} {\left( {\Pi_{H} \left( {p_{H}^{M} } \right) - D_{H} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\Pi_{H} \left( {p_{H}^{M} } \right) - D_{H} } \right)}}$ be a threshold to bound the IS precision by above.

Proposition 2. Consider the game $G\left( \alpha \right)$, where ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < 1$. Let $SPEP$ be the set of all sequential pooling equilibrium prices and $SPE$ the set of all sequential pooling equilibria of $G\left( \alpha \right)$.

• (1) Suppose that expected profits (not conditioned on the IS signals) from entry are negative, such that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$. Then

  • (i) If $p_{L}^{M} < \hat{p}$ (the cost technology is quite far apart), then $SPE = \emptyset$,

  • (ii) If $p_{L}^{M} = \hat{p}$ and $\alpha \le \overline{\alpha }_{h}$, then $SPEP = \left\{ {p_{L}^{M} } \right\}$. If $\alpha > \overline{\alpha }_{h}$, then $SPE = \emptyset$,

  • (iii) If $p_{L}^{M} > \hat{p}$ (intermediate cost technology) then

• (iii.1) For $\alpha \le \overline{\alpha }_{h}$, in every equilibrium in $SPE$, E stays out, irrespective of the signal $s$, and $SPEP = \left[ {\hat{p},p_{L}^{M} } \right]$.

• (iii.2) If $\overline{\alpha }_{h} < \delta$, then, for all $\alpha$, $\overline{\alpha }_{h} < \alpha \le \delta$, E enters if and only if $s = h$, $SPE \ne \emptyset$, and $SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$.

• (iii.3) For $\alpha > \delta$, $SPE = \emptyset$.

• (2) Suppose that expected profits (not conditioned on the IS signals) from entry are positive, such that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$. Then,

  • (i) If $p_{L}^{M} \le \hat{p}$ (the cost technology is quite far apart), then $SPE = \emptyset$,

  • (ii) If $p_{L}^{M} > \hat{p}$ (intermediate cost technology) then

• (ii.1) For $\alpha < \overline{\alpha }_{l}$, $SPE = \emptyset$.

• (ii.2) (If $\overline{\alpha }_{l} \le \delta$, then, for all $\alpha$, $\overline{\alpha }_{l} \le \alpha \le \delta$, E enters if and only if $s = h$, $SPE \ne \emptyset$, and $SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$.

• (ii.3) (For $\alpha > \delta$, $SPE = \emptyset$.

• (3) Suppose that $\delta < \max \left( {\overline{\alpha }_{l} ,\overline{\alpha }_{h} } \right) = \overline{\alpha }_{l}$, then $SPE = \emptyset$. Suppose that $\delta < \max \left( {\overline{\alpha }_{l} ,\overline{\alpha }_{h} } \right) = \overline{\alpha }_{h}$, then $SPE = \emptyset$ whenever $\alpha > \overline{\alpha }_{h}$.⁷

Proof: See Appendix.

Proposition 2 asserts that a sequential pooling equilibrium does not exist if either $p_{L}^{M} < \hat{p}$ or if $\alpha > \delta$. The first condition, $p_{L}^{M} < \hat{p}$, implies that the cost function of H is substantially higher than that of L. Even the duopoly price $\hat{p}$ when H competes with E is above the monopoly price of L. In this case, it is too costly for H to mimic L and to “fool” E about its type. The other condition, $\alpha > \delta$, means that the IS is sufficiently accurate so that when E observes signal $h$, it has a high probability of knowing that the true type of M is H and is better off entering the market. In this case, H, which knows that there is a high probability that its type is detected, has no reason to pool and is better off charging the monopoly price $p_{H}^{M}$, upsetting the pooling equilibrium.

When the cost technology is not too far apart and for intermediate values of $\alpha$ (i.e., $\overline{\alpha }_{h} < \alpha \le \delta$ or $\overline{\alpha }_{l} \le \alpha \le \delta$), the set of pooling equilibria is non-empty, even under profitable entry. The decision of E is to enter the market if and only if the signal sent by the IS is $h$. In this case, M of type H knows that $\alpha$ is sufficiently low, and therefore, E has a high probability $(1 - \alpha )$ of obtaining the wrong signal $l$ and will stay out.

The meaning of set $SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$ is the following. As already explained, $p^{*} \ge \tilde{p}_{H} \left( \alpha \right)$ gives H the first-period profits from pooling that compensate for the second-period expected loss from entry. Similarly, $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ plays the same role for L. Therefore any pooling $p^{*} \in \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$ satisfies the ICCs of the two types of monopoly and sequential rationality with the entry rule.

Proposition 2 also asserts that for $p_{L}^{M} > \hat{p}$ (intermediate cost technology), the existence of these pooling equilibria with a positive likelihood of market entry requires a not too low precision $\alpha$ of the IS. If $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ (in which case $\overline{\alpha }_{h} < 1/2 < \overline{\alpha }_{l}$) and if $\alpha$ is relatively small ($\alpha < \overline{\alpha }_{l}$), then $SPE = \emptyset$. In other words, no pooling equilibrium exists because E enters the market, irrespective of the signal s, and both types of M are better off deviating to their monopoly price. In contrast, when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\alpha$ is relatively small ($\alpha \le \overline{\alpha }_{h}$), then $SPE \ne \emptyset$. More precisely, $SPEP = \left[ {\hat{p},p_{L}^{M} } \right]$. However E stays out irrespective of the signal s. This result is so because the IS is not accurate enough for the entrant to trust signal $h$, but the pooling prevents the entrant from guessing the true type of M, and M of type H mimics type L.

Nevertheless, the incumbent can deter profitable entry with a high probability for intermediate values of the IS precision. Namely, for $\overline{\alpha }_{l} \le \alpha \le \delta$, $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$, entry will be deterred if the signal sent by the IS is l. This probability is $\alpha > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$ when M is of type L and $\left( {1 - \alpha } \right)$ when M is of type H.

Remark 1. Note that when $\alpha = \delta$, then $\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) = \tilde{p}_{H} \left( \alpha \right) = p_{L}^{M}$ and $SPEP = \left\{ {p_{L}^{M} } \right\}$. Also note that the relationship between $\delta$ and $\overline{\alpha }_{s}$, where $s \in \left\{ {h,l} \right\}$, in game $G\left( \alpha \right)$ is not obvious and is generally complex.

Remark 2. This relationship between $\delta$ and $\overline{\alpha }_{s}$, and therefore the existence of pooling equilibria in which there is a positive likelihood of market entry, is highly sensitive not only to the entrant’s beliefs about the success of the incumbent’s R&D project (determined by $\mu$), but also to the characteristics of the market demand, the firms’ cost structures, and the mode of competition if the entrant enters the market. This situation is illustrated in the following example.

Example: This example is used to study the statement in Remark 2 under Cournot and Bertrand competition in a market with linear demand and linear cost functions. Suppose that $p = a - Q$ is the total demand function and suppose that the cost functions are given by,

$C_{L} \left( q \right) = C_{E} \left( q \right) = c_{L} q$, $C_{H} \left( q \right) = c_{H} q$, where $c_{L} < c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} = {{\left( {a + c_{L} } \right)} \mathord{\left/ {\vphantom {{\left( {a + c_{L} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}$.

In this linear model,

$p_{L}^{M} = \frac{{a + c_{L} }}{2}$, $p_{H}^{M} = \frac{{a + c_{H} }}{2}$ and $\Pi_{L} \left( {p_{L}^{M} } \right) = \left( {\frac{{a - c_{L} }}{2}} \right)^{2}$, $\Pi_{H} \left( {p_{H}^{M} } \right) = \left( {\frac{{a - c_{H} }}{2}} \right)^{2}$.

We characterize the existence of pooling equilibria in which there is a positive likelihood of market entry in this linear version of $G\left( \alpha \right)$ under Cournot and Bertrand competition. More specific details can be found in the Appendix.

4.6.1 Cournot competition

Let us focus on the case in which $c_{H} < \tilde{c}_{H}$, where ${{\tilde{c}_{H} = \left( {5a + \left( {3\sqrt {14} - 4} \right)c_{L} } \right)} \mathord{\left/ {\vphantom {{\tilde{c}_{H} = \left( {5a + \left( {3\sqrt {14} - 4} \right)c_{L} } \right)} {\left( {1 + 3\sqrt {14} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 + 3\sqrt {14} } \right)}} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$. Let $\tilde{K}_{1}$ be the solution to $\delta = \overline{\alpha }_{l}$ and let $\tilde{K}_{2}$ be the solution to $\delta = \overline{\alpha }_{h}$, where $\tilde{K}_{1} > {{\left( {a - c_{L} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - c_{L} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$ and $\tilde{K}_{2} < {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$ since $c_{L} < c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$. Moreover,

$$\tilde{K}_{1} < \mu {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9} + \left( {1 - \mu } \right){{\left( {a - c_{L} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - c_{L} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9} < \tilde{K}_{2}$$

since $c_{H} < \tilde{c}_{H}$. Therefore, in terms of the entry cost $K$, there are two interesting cases in which there is a positive likelihood of market entry under pooling equilibrium.

Case 1: $\tilde{K}_{1} \le K < \mu {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9} + \left( {1 - \mu } \right){{\left( {a - c_{L} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - c_{L} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$ (intermediate-low entry cost). Note that in this case $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ and $\delta \ge \overline{\alpha }_{l} > 1/2$. Therefore, there exists some $\alpha$ such that $\overline{\alpha }_{l} \le \alpha \le \delta$ for which E enters if and only if $s = h$ (i.e., with probability $\alpha$ if M is of type H). Then, $SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$. These pooling equilibria do not exist when the entry cost is too low, more specifically when $0 < K < \tilde{K}_{1}$ because, in this case, $\delta < \overline{\alpha }_{l}$.

Case 2: $\mu {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9} + \left( {1 - \mu } \right){{\left( {a - c_{L} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - c_{L} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9} < K < \tilde{K}_{2}$ (intermediate-high entry cost). Note that, in this case, $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\delta > \overline{\alpha }_{h} > 1/2$. Therefore, there exists some $\alpha$ such that $\overline{\alpha }_{h} < \alpha \le \delta$ for which E enters if and only if $s = h$ (i.e., with probability $\alpha$ if M is of type H). Again, $SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$. These pooling equilibria do not exist when the entry cost is too high, more specifically when $\tilde{K}_{2} \le K < {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$ because, in that case, $\delta \le \overline{\alpha }_{h}$.

4.6.2 Bertrand competition

Let us focus on the case in which $c_{H} < \overline{c}_{H}$, where $\overline{c}_{H} = {{\left( {a + \sqrt 2 c_{L} } \right)} \mathord{\left/ {\vphantom {{\left( {a + \sqrt 2 c_{L} } \right)} {\left( {1 + \sqrt 2 } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 + \sqrt 2 } \right)}} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$. Let $\overline{K}_{1}$ be the solution to $\delta = \overline{\alpha }_{l}$ and let $\overline{K}_{2}$ be the solution to $\delta = \overline{\alpha }_{h}$, where $\overline{K}_{1} > 0$ and $\overline{K}_{2} < \left( {c_{H} - c_{L} } \right)\left( {a - c_{H} } \right)$ since $c_{L} < c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$. Moreover, $\overline{K}_{1} < \mu \left( {c_{H} - c_{L} } \right)\left( {a - c_{H} } \right) < \overline{K}_{2}$ since $c_{H} < \overline{c}_{H}$. Therefore, in terms of the entry cost, $K$_, there are two interesting cases in which there is a positive likelihood of market entry under pooling equilibrium.

Case 1: $\overline{K}_{1} \le K < \mu \left( {c_{H} - c_{L} } \right)\left( {a - c_{H} } \right)$ (intermediate-low entry cost). Note that, in this case, $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ and $\delta \ge \overline{\alpha }_{l} > 1/2$. Therefore, there exists some $\alpha$ such that $\overline{\alpha }_{l} \le \alpha \le \delta$ for which E enters if and only if $s = h$ (i.e., with probability $\alpha$ if M is of type H). Then, $SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$. These pooling equilibria do not exist when the entry cost is too low, more specifically when $0 < K < \overline{K}_{1}$ because, in this case, $\delta < \overline{\alpha }_{l}$.

Case 2: $\mu \left( {c_{H} - c_{L} } \right)\left( {a - c_{H} } \right) < K < \overline{K}_{2}$ (intermediate-high entry cost). Note that, in this case, $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\delta > \overline{\alpha }_{h} > 1/2$. Therefore, there exists some $\alpha$ such that $\overline{\alpha }_{h} < \alpha \le \delta$ for which E enters if and only if $s = h$ (i.e., with probability $\alpha$ if M is of type H), and again $SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$. These pooling equilibria do not exist when the entry cost is too high, more specifically when $\overline{K}_{2} \le K < \left( {c_{H} - c_{L} } \right)\left( {a - c_{H} } \right)$ because, in that case, $\delta \le \overline{\alpha }_{h}$.

This example illustrates the statement in Remark 2. For instance, in this example, pooling equilibria in which there is a positive likelihood of market entry do not exist if $\tilde{c}_{H} \le c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$ when the mode of competition is à la Cournot and if $\overline{c}_{H} \le c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$ when the mode of competition is à la Bertrand. Hence, the mode of competition directly determines the characteristics of the market demand and the firms’ cost structures for which there exist pooling equilibria in which espionage is likely to increase market competition.

4.7 Comparison with the case in which the IS is not informative ($\alpha = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$)

A natural benchmark of comparison is when the IS precision is $\alpha = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}$. This situation is a modification of the MR set up, when the entrant only has a cost type and does not have access to an IS on M. This game is denoted by $G_{MR}$. Recall that $\hat{p}$ is the price for H and that $p_{0}$ is the price for L yielding the duopoly profits for H and L, respectively. In this game, the entrant’s strategy, $\sigma_{E} \left( p \right)$, is a threshold strategy,

$$\sigma_{E} \left( p \right) = \left\{ \begin{gathered} Stay\,out,\,\,\,\,\,p \le \overline{p} \hfill \\ Enter,\,\,\,\,\,\,\,\,\,\,p > \overline{p} \hfill \\ \end{gathered} \right.$$

where the threshold $\overline{p}$ is the choice by E, given E’s beliefs $Prob\left( {H\left| p \right.} \right)$ and $Prob\left( {L\left| p \right.} \right)$ for any $p$. Trivially, for $\alpha = 1/2$, $p_{l} = p_{h} = \overline{p}$. Therefore, for any $\alpha > 1/2$.

$\Pi_{E} \left( {l,p_{l} } \right) = \Pi_{E} \left( {h,p_{h} } \right) = \Pi_{E} \left( {\overline{p} } \right) > \Pi_{E} \left( {l,p_{h} } \right)$,

which implies that $\Pi_{E} \left( {l,p_{l} } \right) > \Pi_{E} \left( {l,p_{h} } \right)$, $\Pi_{E} \left( {h,p_{h} } \right) > \Pi_{E} \left( {l,p_{h} } \right)$, and hence that $\overline{p} = p_{h} < p_{l}$.

Therefore, when $\alpha = 1/2$, the game $G\left( \alpha \right)$ collapses to $G_{MR}$, and the entrant’s expected profit is now $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right)$. We provide the pooling equilibria of $G_{MR}$.

Proposition 3. Consider the game $G_{MR}$. Let $SPEP_{MR}$ be the set of all sequential pooling equilibrium prices and $SPE_{MR}$ the set of all sequential pooling equilibria of $G_{MR}$. Then,

(1) When $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < \, 0$.

(i) $SPEP_{MR} = \left\{ {p_{H} = p_{L} = p^{*} = \overline{p}} \right\}$, and

(ii) $\hat{p} \le p^{*} \le p_{L}^{M}$.

(2) When $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > \, 0$, the set of all sequential pooling equilibria in $G_{MR}$ is the empty set: $SPE_{MR} = \emptyset$.

Proposition 3 shows that, in $G_{MR}$, there exists no pooling equilibrium in which the potential entrant enters the market with positive probability. Moreover, when the entrant’s expected profit is positive, such that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right)$ > 0, the entrant will enter when it observes price $p^{*}$. Hence, both types, H and L, of monopolist should select their monopoly prices $p_{H}^{M}$ and $p_{L}^{M}$, respectively, destroying the pooling equilibria. Therefore, profitable entry is never deterred. This result holds even when the incumbent monopolist does not know the entry costs of the entrant (see MR). It also holds in the benchmark model of Bagwell and Ramey (1988), where prices and advertising are both signals for the incumbent monopolist. Bagwell (2007) extended the benchmark game to include two dimensions of private information. Specifically, the incumbent is privately informed as to its cost type and its level of patience and selects price and advertising in the pre-entry period. Bagwell (2007) found an (intuitive) pooling equilibrium associated with the behavior of the patient high-cost incumbent, who pools with the impatient low-cost incumbent.

In contrast, our model also offers the existence of pooling equilibria under ex-ante profitable entry with only one dimension of private information by the incumbent but with two IS signals correlated with price. These signals provide additional (probabilistic) information about the incumbent’s type. In fact, by Proposition 2, when the cost technology is intermediate, the entrant’s expected profits without the IS are positive, and the IS is of intermediate accuracy, pooling equilibria with a positive likelihood of market entry exist. More precisely, when the entrant receives signal h. Moreover, entry may also occur when, under the same technology, the entrant’s expected profits without the IS are negative, and the IS is accurate enough for the entrant to trust signal $h$.

However, by comparing the pooling equilibria of game $G\left( \alpha \right)$ with those of $G_{MR}$, the use of a relatively inaccurate but informative IS has no impact on either entry or entry deterrence. Thus, for intermediate cost technology, positive expected profits without the IS of the entrant, and an uninformative or relatively small $\alpha$, $SPE = \emptyset$ in both games. In other words, no pooling equilibrium exists because E will enter the market and both types of M are better off deviating to their monopoly price. Similarly, if, for the same technology, the expected profits without the IS of the entrant are negative and the IS is uninformative or is informative but relatively inaccurate, then $SPE \ne \emptyset$ in both games but E always stays out. Finally, as discussed earlier, the existence of pooling equilibria requires the IS precision to be not so high that type-H of M, knowing that there is a high probability that it has been detected, is better off deviating and upsetting the pooling equilibrium.

5 Separating equilibrium

The analysis in this section captures the central theme of the classic limit pricing paper by MR in that limit pricing occurs and yet profitable entry is never deterred. Bagwell and Ramey (1988) presented a related model but assumed that the probability of entry jumps from 0 to 1 once the belief rises above a critical value. In our model, signals help the entrant smooth the best response. Nevertheless, the difference between our sequential separating equilibria and those of MR and Bagwell and Ramey (1988) is only in the behavior of the entrant for prices off the equilibrium path.

A separating equilibrium consists of a pair of prices $(p_{H} ,p_{L} )$ with $p_{H} \ne p_{L}$, and an entry rule, $\sigma_{E} \left( {s,p} \right)$, which is sequentially rational given consistent beliefs $Prob\left( {H\left| {h,p} \right.} \right)$ and $Prob\left( {H\left| {l,p} \right.} \right)$ for any pair $(s,p)$. In this equilibrium, E identifies the type of M with probability 1. Hence, E enters the market when observing the price $p_{H}$, irrespective of the signal of the IS, and E stays out when observing $p_{L}$, again irrespective of $s$. Therefore, by the entrant’s strategy $p_{H} > p_{l}$ and $p_{L} \le p_{h}$.

The following proposition characterizes the sequential separating equilibrium prices of $G\left( \alpha \right)$. The proof is also quite long. Because the results are not too different from those in the literature, we offer only a sketch in the Appendix.⁸

Proposition 4. Consider the game $G\left( \alpha \right)$ for ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}} < \alpha < 1$ and let $SSE$ be the set of all sequential separating equilibrium points of $G\left( \alpha \right)$. Let $SSE_{t}$ be the set of all equilibrium prices of the $t$-type monopolist in $SSE$. Then, given consistent beliefs $Prob\left( {H\left| {h,p} \right.} \right)$ and $Prob\left( {H\left| {l,p} \right.} \right)$, for any $p$ and $s$,

• (1) $SSE_{L} = \left\{ {p_{L} \left| {p_{0} \le p_{L} \le \min \left( {p_{L}^{M} ,\hat{p}} \right)} \right.} \right\}$ and $SSE_{H} = \left\{ {p_{H}^{M} } \right\}$.

• (2) Let $p_{L} \in SSE_{L}$. If $p_{L} < p_{L}^{M}$, then $p_{L} = p_{h}$. If $p_{L} = p_{L}^{M}$, then $p_{L}^{M} \le p_{h}$.

Note that when the cost functions are not too far apart (i.e. $\hat{p} < p_{L}^{M}$), all the separating equilibria limit price: $p_{0} \le p_{L} < p_{L}^{M}$. By contrast, when the cost function of H is substantially higher than that of L in the sense that $p_{L}^{M} \le \hat{p}$, then $p_{L} \le p_{L}^{M}$. Therefore limit pricing is more likely in sequential separating equilibria when the cost technology is not too far apart because, in this case, L needs a reduction of its monopoly price $p_{L}^{M}$ to separate from H. When the cost function of H is substantially higher than that of L in the sense that $p_{L}^{M} \le \hat{p}$, limit pricing will only occur when the monopoly price $p_{L}^{M}$ is not too low in the sense that either $p_{h} < p_{l} < p_{L}^{M}$ or $p_{h} < p_{L}^{M} < p_{l}$.

One crucial question is whether some of these separating equilibria exist in the same parameter region as some of the pooling equilibria with a positive likelihood of market entry (characterized in Proposition 2 in the previous section) and dominate them. As stated above, in a separating equilibrium, E identifies with probability 1 the type of M. Knowing that E will enter the market when price $p_{H}$ is observed, the H-type monopoly is better off choosing its monopoly price. Therefore, $SSE_{H} = \left\{ {p_{H}^{M} } \right\}$, as stated in Proposition 4. The fact that $p_{H} = p_{H}^{M} > p_{l}$ implies that, in every possible separating equilibrium, $p_{h} < \hat{p}$ and $p_{l} < \tilde{p}_{H} \left( \alpha \right)$ must hold. Otherwise, H might have incentives to deviate to $p_{h}$ or $p_{l}$, respectively. The key implication of this last constraint, $p_{l} < \tilde{p}_{H} \left( \alpha \right)$, is that pooling equilibrium prices for intermediate values of $\alpha$, where $\overline{\alpha }_{h} < \alpha \le \delta$ if $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\overline{\alpha }_{l} \le \alpha \le \delta$ if $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$, ensure that no separating equilibrium exists in the same parameter region, which leads to the following important result.

Corollary 3. No pooling equilibrium price of the form $\tilde{p}_{H} \left( \alpha \right) < p^{*} = p_{l} \le p_{L}^{M}$ can be dominated by any separating equilibrium. Therefore, the existence of pooling equilibrium with a positive likelihood of market entry is ensured.

We characterize the separating equilibria in $G_{MR}$ in the following proposition to compare them with those of game $G(\alpha )$.

Proposition 5. Consider the game $G_{MR}$ and let $SSE^{MR}$ be the set of all sequential separating equilibrium points of $G_{MR}$. Then, given consistent beliefs $Prob\left( {H\left| {h,p} \right.} \right)$ and $Prob\left( {H\left| {l,p} \right.} \right)$, for any $p$,

• (1) $SSE_{L}^{MR} = \left\{ {p_{L} \left| {p_{0} \le p_{L} \le \min \left( {p_{L}^{M} ,\hat{p}} \right)} \right.} \right\}$ and $SSE_{H}^{MR} = \left\{ {p_{H}^{M} } \right\}$.

• (2) Let $p_{L} \in SSE_{L}^{MR}$. If $p_{L} < p_{L}^{M}$, then $p_{L} = \overline{p}$. If $p_{L} = p_{L}^{M}$, then $p_{L}^{M} \le \overline{p}$.

Remark 3. By Lemma 1,$\hat{p} > p_{0}$, and $SSE_{MR}$ is non-empty.

The combination of Proposition 5 and Proposition 4 enables comparison of the separating equilibria of both $G_{MR}$ and $G(\alpha )$. This comparison is summarized in the following corollary.

Corollary 4. (1) The set $SSE$ coincides with $SSE_{MR}$, the set of all sequential separating equilibrium points of $G_{MR}$.

(2) Let $p_{L} \in SSE_{L}$ and suppose that $p_{L} < p_{L}^{M}$. Let $p_{h}$ and $\overline{p}$ be the equilibrium cutoff price for entry when in $G\left( \alpha \right)$ (when $s = h$) and in $G_{MR}$, respectively. Then, $\overline{p} = p_{h}$.

(3) Let $p_{L} \in SSE_{L}$ and suppose that $p_{L} < p_{L}^{M}$. Then the equilibrium strategy of E in $G\left( \alpha \right)$ coincides with the equilibrium strategy of E in $G_{MR}$ for all $p_{L} \notin \left( {p_{h} ,p_{l} } \right]$. If $p_{L} \in \left( {p_{h} ,p_{l} } \right]$, then E enters the market in $G\left( \alpha \right)$ with positive probability, which is $\alpha$ if M is of type H and ($1 - \alpha$) if M is of type L, and always enters the market in $G_{MR}$.

Part (3) of the corollary asserts that E is less inclined to enter the market in $G\left( \alpha \right)$. For all prices below $\overline{p} = p_{h}$, E stays out of the market in both games $G_{MR}$ and $G\left( \alpha \right)$. For prices above $p_{l}$, E always enters in both games. However, for prices $p$, $p_{h} < p \le p_{l}$, E enters the market in game $G\left( \alpha \right)$ if and only if the signal sent by the IS is $h$. In contrast, in this region, E always enters the market in game $G_{MR}$. The difference between $G\left( \alpha \right)$ and $G_{MR}$ with regard to sequential separating equilibria is only in the behavior of E off the equilibrium path. Therefore, for prices off the equilibrium path, the monopolist is better off with an entrant with access to an IS of commonly known precision.

6 Conclusions

Recent advances in information and communication technologies have increased the incentive for firms to acquire information about rivals by pushing the limits of competitive intelligence and engaging in industrial espionage. This situation may have important implications for market entry because potential market entrants can find it easier to gather valuable information about incumbents in the target market. From a theoretical point of view, incomplete information about incumbents’ cost structures has been cited as a relevant aspect in explaining market entry behavior. However, little theoretical research has analyzed situations in which a potential entrant attempts to reduce such an information disadvantage.

This paper advances in this direction by studying a potential entrant’s activities in the context of modern cyber espionage. Specifically, it extends a one-sided asymmetric information version of Milgrom and Roberts’ (1982) model, considering that a potential market entrant, E, does not observe the outcome of an R&D project by an incumbent monopolist aimed at reducing its cost of production. The potential entrant develops an intelligence system (IS) of precision $\alpha$ that allows it to gather noisy information about the cost structure of M. Based on this information and the price that M charges for its product, E decides whether to enter the market. We assume that $\alpha$ is exogenously given and is known by both firms.

Our main contribution, considering only one dimension of private information belonging to the incumbent, is twofold. First, we show the pooling equilibria, even under ex-ante profitable entry. Second, we show the positive likelihood of market entry, even in pooling equilibria under ex-ante non-profitable entry. These pooling equilibria exist for intermediate values of IS precision, where E enters the market if the IS indicates that the cost of M is high. Thus, there is a high probability that spying on incumbent firms increases market competition. If the precision $\alpha$ of the IS is sufficiently low to affect the entrant’s decision to stay out, then no pooling equilibrium exists. Likewise, no pooling equilibrium exists when $\alpha$ is very accurate.

Finally, the separating equilibria of our model are not affected by espionage by E. This finding is unsurprising because, in a separating equilibrium, E identifies the type of M with or without the use of an IS.

Appendix

Proof of Lemma 1

(i)

$$\Pi_{L} \left( p \right) - \Pi_{H} \left( p \right) = C_{H} \left( {Q\left( p \right)} \right) - C_{L} \left( {Q\left( p \right)} \right)$$

$$\frac{\partial }{\partial p}\left[ {\Pi_{L} \left( p \right) - \Pi_{H} \left( p \right)} \right] = Q^{\prime}\left( p \right)\left[ {C^{\prime}_{H} \left( {Q\left( p \right)} \right) - C^{\prime}_{L} \left( {Q\left( p \right)} \right)} \right]$$

By Assumptions 4 and 5, the right-hand side of the above expression is negative.

(ii)

$$\begin{gathered} p_{L}^{M} q_{L}^{M} - C_{L} \left( {q_{L}^{M} } \right) \ge p_{H}^{M} q_{H}^{M} - C_{L} \left( {q_{H}^{M} } \right) \hfill \\ p_{H}^{M} q_{H}^{M} - C_{H} \left( {q_{H}^{M} } \right) \ge p_{L}^{M} q_{L}^{M} - C_{H} \left( {q_{L}^{M} } \right) \hfill \\ \end{gathered}$$

Adding the two inequalities gives

$$C_{H} \left( {q_{L}^{M} } \right) - C_{L} \left( {q_{L}^{M} } \right) \ge C_{H} \left( {q_{H}^{M} } \right) - C_{L} \left( {q_{H}^{M} } \right)$$

By Assumption 4, we have that $q_{L}^{M} \ge q_{H}^{M}$ and hence $p_{L}^{M} \le p_{H}^{M}$.

Let us show that $p_{L}^{M} < p_{H}^{M}$. If not, then $p_{L}^{M} = p_{H}^{M}$. Since the first-order condition (FOC) for M of type $t$ is

$$\frac{{\partial \Pi_{t} }}{\partial p}\left( {Q\left( p \right)} \right) = 0 \leftrightarrow C^{\prime}_{t} \left( {Q\left( p \right)} \right) = p + \frac{Q\left( p \right)}{{Q^{\prime}\left( p \right)}}$$

the solution does not depend on $t$, namely $C^{\prime}_{L} \left( {Q\left( {p_{L}^{M} } \right)} \right) = C^{\prime}_{H} \left( {Q\left( {p_{L}^{M} } \right)} \right)$. However, this contradicts Assumption 4.

(iii) By Assumption 3,

$$\Pi_{L} \left( {p_{L}^{M} } \right) - D_{L} > \Pi_{H} \left( {p_{H}^{M} } \right) - D_{H}$$

Note that $D_{L} = \prod_{L} \left( {p_{0} } \right)$ and $D_{H} = \prod_{H} \left( {\hat{p}} \right)$. Hence, this inequality can be written as

$$\Pi_{L} \left( {p_{L}^{M} } \right) - \Pi_{L} \left( {p_{0} } \right) > \Pi_{H} \left( {p_{H}^{M} } \right) - \Pi_{H} \left( {\hat{p}} \right)$$

Thus,

$$\Pi_{L} \left( {p_{L}^{M} } \right) - \Pi_{H} \left( {p_{L}^{M} } \right) + \underbrace {{\Pi_{H} \left( {p_{L}^{M} } \right) - \Pi_{H} \left( {p_{H}^{M} } \right)}}_{ < 0} > \Pi_{L} \left( {p_{0} } \right) - \Pi_{H} \left( {\hat{p}} \right)$$

Hence,

$$\Pi_{L} \left( {p_{L}^{M} } \right) - \Pi_{H} \left( {p_{L}^{M} } \right) > \Pi_{L} \left( {p_{0} } \right) - \Pi_{H} \left( {\hat{p}} \right)$$

(A1)

Since $p_{0} \le p_{L}^{M}$, we have by section (i) of Lemma 1

$$\Pi_{L} \left( {p_{0} } \right) - \Pi_{H} \left( {p_{0} } \right) > \Pi_{L} \left( {p_{L}^{M} } \right) - \Pi_{H} \left( {p_{L}^{M} } \right)$$

Together with (A1), this implies that

$$\Pi_{H} \left( {\hat{p}} \right) > \Pi_{H} \left( {p_{0} } \right)$$

But $p_{0} < p_{H}^{M}$ and $\hat{p} < p_{H}^{M}$ and by Assumption 2 $p_{0} < \hat{p}$.

Proof of Lemma 2

(i) By (3) in the main text,

$$Prob_{n} \left( {H\left| {h,p} \right.} \right) = \frac{{\mu \alpha \frac{{f_{n} \left( {p\left| H \right.} \right)}}{{f_{n} \left( {p\left| L \right.} \right)}}}}{{\mu \alpha \frac{{f_{n} \left( {p\left| H \right.} \right)}}{{f_{n} \left( {p\left| L \right.} \right)}} + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}$$

Hence,

$$Prob\left( {H\left| {h,p} \right.} \right) = \frac{\mu \alpha g\left( p \right)}{{\mu \alpha g\left( p \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}$$

(A2)

and by Assumption 7, $Prob\left( {H\left| {h,p} \right.} \right)$ is continuous in $p$.

The proof that $Prob\left( {H\left| {l,p} \right.} \right)$ is continuous is similarly derived from (4) in the main text.

Since $Prob\left( {L\left| {s,p} \right.} \right) = 1 - Prob\left( {H\left| {s,p} \right.} \right)$, then $Prob\left( {L\left| {s,p} \right.} \right)$ is also continuous.

Next, note that $g\left( p \right)$ is non-decreasing in $p$ since $g_{n} \left( p \right)$ is increasing in $p$ for all $n$. Therefore, Theorem 1 in Milgrom (1981) implies that if $p_{1} > p_{2}$, the posterior $Prob\left( {H\left| {s,p_{1} } \right.} \right)$ dominates $Prob\left( {H\left| {s,p_{2} } \right.} \right)$, $s = \left\{ {h,l} \right\}$, in the sense of first-order stochastic dominance. In fact, it is easy to verify by (A2) that $\frac{\partial }{\partial p}Prob\left( {H\left| {h,p} \right.} \right) \ge 0$ if and only if $g^{\prime}\left( p \right) \ge 0$ and thus $Prob\left( {H\left| {h,p} \right.} \right)$ is non-decreasing in $p$. The proof that $Prob\left( {H\left| {l,p} \right.} \right)$ is non-decreasing is similar.

(ii) Let

$$x_{n} \left( p \right) = \frac{{Prob_{n} \left( {H\left| {h,p} \right.} \right)}}{{Prob_{n} \left( {H\left| {l,p} \right.} \right)}}$$

By (3) and (4) in the main text,

$$\begin{gathered} x_{n} \left( p \right) - 1 = \frac{{\frac{\alpha }{1 - \alpha }\left[ {\mu \left( {1 - \alpha } \right)f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\alpha f_{n} \left( {p\left| L \right.} \right)} \right]}}{{\mu \alpha f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}} - 1 \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\left( {1 - \mu } \right)\frac{{\alpha^{2} }}{1 - \alpha }f_{n} \left( {p\left| L \right.} \right) - \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}}{{\mu \alpha f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\left( {1 - \mu } \right)f_{n} \left( {p\left| L \right.} \right)\left( {2\alpha - 1} \right)}}{{\left( {1 - \alpha } \right)\left[ {\mu \alpha f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)} \right]}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\left( {1 - \mu } \right)\left( {2\alpha - 1} \right)}}{{\left( {1 - \alpha } \right)\left[ {\mu \alpha g_{n} \left( p \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)} \right]}} \hfill \\ \end{gathered}$$

Hence,

$$\mathop {\lim }\limits_{n \to \infty } \left[ {x_{n} \left( p \right) - 1} \right] = \frac{{\left( {1 - \mu } \right)\left( {2\alpha - 1} \right)}}{{\left( {1 - \alpha } \right)\left[ {\mu \alpha g\left( p \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)} \right]}}\, > 0$$

Hence $\mathop {\lim }\limits_{n \to \infty } x_{n} \left( p \right)\, > 1$ and, consequently, for every $p \ge 0$,

$$Prob\left( {H\left| {h,p} \right.} \right) > Prob\left( {H\left| {l,p} \right.} \right)$$

Proof of Lemma 3. By (5) in the main text,

$$\begin{gathered} \Pi_{E} \left( {s,p} \right) = Prob\left( {H\left| {s,p} \right.} \right)\Delta_{E} \left( H \right) + Prob\left( {L\left| {s,p} \right.} \right)\Delta_{E} \left( L \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = Prob\left( {L\left| {s,p} \right.} \right)\left[ {\frac{{Prob\left( {H\left| {s,p} \right.} \right)}}{{Prob\left( {L\left| {s,p} \right.} \right)}}\Delta_{E} \left( H \right) + \Delta_{E} \left( L \right)} \right] \hfill \\ \end{gathered}$$

(A3)

Let $s = h$. For every $p$,

$$\frac{{Prob\left( {H\left| {h,p} \right.} \right)}}{{Prob\left( {L\left| {h,p} \right.} \right)}} = \mathop {\lim }\limits_{n \to \infty } \frac{{\mu \alpha f_{n} \left( {p\left| H \right.} \right)}}{{\left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}} = \frac{\mu \alpha }{{\left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}g\left( p \right)$$

We claim that $g\left( p \right) \to 0$ as $p \to 0$. This follows from Dini’s theorem, as $g_{n} \left( p \right)$ is increasing in $n$, $g_{n} \left( p \right)$ is continuous in $p$, and $g\left( p \right)$ is also continuous. Hence, for every $\gamma > 0$, $\mathop {\lim }\limits_{n \to \infty } g_{n} \left( p \right) = g\left( p \right)$ uniformly on $\left[ {0,\gamma } \right]$. Since, for every $n$, $g_{n} \left( p \right) \to 0$ as $p \to 0$, we have $g\left( p \right) \to 0$ as $p \to 0$. Consequently,

$\mathop {\lim }\limits_{p} \frac{{Prob\left( {H\left| {h,p} \right.} \right)}}{{Prob\left( {L\left| {h,p} \right.} \right)}} = 0$, as $p \to 0$ (A4).

Inequality (A4) also holds when $h$ is replaced by $l$ (the proof is similar).

Next, let us show that $Prob\left( {L\left| {h,p} \right.} \right) > 0$ for small $p$.

$$\begin{gathered} Prob_{n} \left( {L\left| {h,p} \right.} \right) = \frac{{\left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}}{{\mu \alpha f_{n} \left( {p\left| H \right.} \right) + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)f_{n} \left( {p\left| L \right.} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{{1 + \frac{{\mu \alpha g_{n} \left( p \right)}}{{\left( {1 - \mu } \right)\left( {1 - \alpha } \right)}}}} \hfill \\ \end{gathered}$$

(A5)

Again, since $g_{n} \left( p \right) \to g\left( p \right)$ as $n \to \infty$ uniformly in any interval $\left[ {0,\gamma } \right]$, $\gamma > 0$, and since $g\left( p \right) \to 0$ as $p \to 0$,

$Prob\left( {L\left| {h,p} \right.} \right) = \mathop {\lim }\limits_{n} Prob_{n} \left( {L\left| {h,p} \right.} \right) \to 1$, as $p \to 0$.

In particular, $Prob\left( {L\left| {h,p} \right.} \right) > 0$ for $p$ sufficiently small. Similarly, we can prove that $Prob\left( {L\left| {l,p} \right.} \right) > 0$ for $p$ sufficiently small.

Now, (A3), (A4), and the fact that $\Delta_{E} \left( L \right) < 0$ and $Prob\left( {L\left| {s,p} \right.} \right) > 0$ for small $p$, imply that for sufficiently small $p$, $\Pi_{E} \left( {s,p} \right) < 0$ and $J_{s} \ne \emptyset$.

Let us show that for $p$ sufficiently large, $\Pi_{E} \left( {s,p} \right) > 0$. We use the following claim.

Claim 1. $\mathop {\lim }\limits_{p} Prob\left( {L\left| {s,p} \right.} \right) = 0$ as $p \to \infty$.

Proof: Let $n = 1$ and $s = h$. By Assumption 7.2, $\lim \frac{{f_{1} \left( {p\left| H \right.} \right)}}{{f_{1} \left( {p\left| L \right.} \right)}} = \infty$. By (A5),

$Prob_{1} \left( {L\left| {h,p} \right.} \right) \to 0$ as $p \to \infty$.

Hence, for every $\varepsilon > 0$, there exists $P$ such that for all $p > P$,

$$Prob_{1} \left( {L\left| {h,p} \right.} \right) < \varepsilon$$

By (3) in the main text,

$$Prob_{n} \left( {H\left| {h,p} \right.} \right) = \frac{\mu \alpha }{{\mu \alpha + \left( {1 - \mu } \right)\left( {1 - \alpha } \right)\frac{{f_{n} \left( {p\left| L \right.} \right)}}{{f_{n} \left( {p\left| H \right.} \right)}}}}$$

By Assumption 7.2, $Prob_{n} \left( {H\left| {h,p} \right.} \right)$ is increasing in $n$ and, hence, $Prob_{n} \left( {L\left| {h,p} \right.} \right)$ is decreasing in $n$ for every $p$. Thus, for all $p > P$,

$$Prob_{n} \left( {L\left| {h,p} \right.} \right) < Prob_{1} \left( {L\left| {h,p} \right.} \right) < \varepsilon$$

Hence, for every $\varepsilon > 0$ and for all $p > P$,

$$Prob\left( {L\left| {h,p} \right.} \right) = \mathop {\lim }\limits_{n \to \infty } Prob_{n} \left( {L\left| {h,p} \right.} \right) \le \varepsilon$$

implying that

$$\mathop {\lim }\limits_{p \to \infty } Prob\left( {L\left| {h,p} \right.} \right) = 0$$

The proof that $\mathop {Prob}\limits_{p} \left( {L\left| {l,p} \right.} \right) = 0$, as $p \to \infty$ is similarly derived.

Claim 1 together with (5), in the main text, imply that for $p$ sufficiently large, $\Pi_{E} \left( {s,p} \right) > 0$, and the proof of Lemma 3 is completed.

Proof of Proposition 1. By part (i) of Lemma 2 and by (5), $\Pi_{E} \left( {s,p} \right)$ is continuous and non-decreasing in $p$. This follows from the fact that $Prob\left( {H\left| {s,p} \right.} \right)$ is continuous and non-decreasing in $p$, $\Delta_{E} \left( H \right) > 0$, $Prob\left( {L\left| {s,p} \right.} \right) = 1 - Prob\left( {H\left| {s,p} \right.} \right)$ and $\Delta_{E} \left( L \right) < 0$.

By Lemma 3, $\Pi_{E} \left( {s,p} \right) < 0$ for small $p$ and $\Pi_{E} \left( {s,p} \right) > 0$ for sufficiently large $p$.

Let

$$p_{h} = \max \left\{ {p \ge 0\left| {\Pi_{E} \left( {h,p} \right) \le 0} \right.} \right\}$$

$$p_{l} = \max \left\{ {p \ge 0\left| {\Pi_{E} \left( {l,p} \right) \le 0} \right.} \right\}$$

By the continuity of $\Pi_{E} \left( {s,p} \right)$ in $p$,

$$\Pi_{E} \left( {h,p_{h} } \right) = \Pi_{E} \left( {l,p_{l} } \right) = 0$$

(A6)

and E enters the market if and only if it observes either $\left( {h,p} \right)$ such that $p > p_{h}$ or $\left( {l,p} \right)$ such that $p > p_{l}$.

By part (ii) of Lemma 2, it is easy to verify that

$$\Pi_{E} \left( {h,p} \right) > \Pi_{E} \left( {l,p} \right)$$

(A7)

By (A6) and (A7)

$$\Pi_{E} \left( {l,p_{l} } \right) = \Pi_{E} \left( {h,p_{h} } \right) > \Pi_{E} \left( {l,p_{h} } \right)$$

and since $\Pi_{E} \left( {s,p} \right)$ is non-decreasing in $p$, we have $p_{l} > p_{h}$.

Proof of Lemma 4. First, suppose that $p_{H}^{M} \le p_{h}$. Then also $p_{L}^{M} < p_{h}$ and, according to Proposition 1, E stays out whether it observes $p_{L}^{M}$ or $p_{H}^{M}$. Hence, both types of M will set their (different) monopoly prices, giving a contradiction.

Next, suppose that $p_{L}^{M} < p_{h}$ and $p_{H}^{M} > p_{h}$. Since $\alpha \le \overline{\alpha }_{h}$, E stays out and $p^{*} \le p_{h}$. Therefore, $p^{*} = p_{L}^{M}$. In this case, H is better off by deviating to $p_{h}$ since

$$\Pi_{H} \left( {p_{L}^{M} } \right) + \Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{h} } \right) + \Pi_{H} \left( {p_{H}^{M} } \right)$$

implies that $p_{L}^{M} \ge p_{h}$, which is a contradiction.

The incentive compatibility condition when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$ .

Proof of Lemma 5 ($ICC_{H}$). Considering the discussion about the relevant $ICC_{H}$ in the main text, for $p^{*}$ to be a pooling equilibrium price of H, the following should hold,

$$\Pi_{H} \left( {p^{*} } \right) + \Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{H}^{M} } \right) + \left\{ \begin{gathered} \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right),\,\,\,if\,p_{h} < p_{H}^{M} \le p_{l} \hfill \\ D_{H} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,p_{H}^{M} > p_{l} \hfill \\ \end{gathered} \right.$$

The first inequality implies that

$$\Pi_{H} \left( {p^{*} } \right) \ge \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right)$$

Recalling that $D_{H} = \Pi_{H} \left( {\hat{p}} \right)$ and the definition of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right)$ in the main text, $\Pi_{H} \left( {p^{*} } \right) \ge \Pi_{H} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right)} \right)$ implies that $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right)$.

The second inequality requires that $\Pi_{H} \left( {p^{*} } \right) \ge D_{H}$ or that $p^{*} \ge \hat{p}$.

Additionally, another potential deviation is the following. When $p_{H}^{M} > p_{l}$ H may deviate to $p_{l}$, where E enters with probability $\alpha$. To avoid this deviation,

$$\Pi_{H} \left( {p^{*} } \right) + \Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{l} } \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right)$$

Since $p_{H}^{M} > p_{l}$ and, by above, $p^{*} \ge \hat{p}$, take without loss of generality $p^{*} = \hat{p}$. Then

$$D_{H} + \Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{l} } \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right)$$

(A8)

Recalling the definition of $\tilde{p}_{H} \left( \alpha \right)$ in the main text, inequality (A8) is satisfied whenever $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$.

Proof of Lemma 6 ($ICC_{L}$). Considering the discussion about the relevant $ICC_{L}$ in the main text, to avoid deviations, and, therefore, for $p^{*}$ be a pooling equilibrium price of L, the following should hold,

$$\Pi_{L} \left( {p^{*} } \right) + \Pi_{L} \left( {p_{L}^{M} } \right) \ge \Pi_{L} \left( {p_{L}^{M} } \right) + \left\{ \begin{gathered} \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} ,\,\,\,\,\,if\,p_{h} < p_{L}^{M} \le p_{l} \hfill \\ D_{L} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,p_{L}^{M} > p_{l} \hfill \\ \end{gathered} \right.$$

Recall that $D_{L} = \Pi_{L} \left( {p_{0} } \right)$ and the definition of $\tilde{p}_{L} \left( \alpha \right)$ in the main text. Then the first inequality above is satisfied whenever $p_{L}^{M} > p^{*} \ge \tilde{p}_{L} \left( \alpha \right)$.

For the second inequality, it suffices that $p^{*} \ge p_{0}$. To deter deviation to $p_{l}$, when $p_{L}^{M} > p_{l}$, take $p^{*} = p_{0}$, then

$$D_{L} + \Pi_{L} \left( {p_{L}^{M} } \right) \ge \Pi_{L} \left( {p_{l} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L}$$

(A9)

Therefore, a pooling $p^{*} \ge p_{0}$ avoids a deviation to $p_{l}$ whenever, for example, first-period profits from $p^{*} = p_{0}$, plus the difference between second-period expected profits from the pooling and those from the deviation are greater than or equal to the profits from $p_{l}$. Taking into account the definition of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ in the main text, this implies that (A9) is satisfied whenever $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right) \ge p_{l}$.

Proof of Lemma 7. Suppose first that $p_{H}^{M} \le p_{h}$. Then also $p_{L}^{M} < p_{h}$ and both L and H are better off deviating to their monopoly prices. Hence $p_{H}^{M} > p_{h}$.

Now suppose that $p_{L}^{M} = p_{h}$, then for any $p^{*} \in \left( {p_{h} ,p_{l} } \right]$,

$$\Pi_{L} \left( {p^{*} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} \ge \Pi_{L} \left( {p_{L}^{M} } \right) + \Pi_{L} \left( {p_{L}^{M} } \right)$$

which is a contradiction. Consider that $p_{l} > p_{L}^{M} > p_{h}$ and $p_{H}^{M} \le p_{l}$, then for any $p^{*}$,

$$\Pi_{L} \left( {p^{*} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} \ge \Pi_{L} \left( {p_{L}^{M} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L}$$

The above is impossible unless $p^{*} = p_{L}^{M}$. Therefore, L will deviate to $p_{L}^{M}$. This is similarly true for H, which will deviate to $p_{H}^{M}$.

Finally, consider that $p_{h} < p_{L}^{M} < p_{l}$ and $p_{H}^{M} > p_{l}$, then L will deviate to $p_{L}^{M}$, and H will be better off deviating to $p_{l}$. Therefore, $p_{L}^{M} \ge p_{l}$, and Lemma 7 follows.

The incentive compatibility condition when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\overline{\alpha }_{h} < \alpha < 1$ .

Proof of Lemma 8 ($ICC_{H}$). We have that $\overline{\alpha }_{h} < \alpha < 1$ and hence that E enters if it observes signal $h$. Also, $p_{H}^{M} > p_{l}$ (according to Lemma 7). Then, for H not to deviate to $p_{H}^{M}$ at a pooling $p^{*} \in \left( {p_{h} ,p_{l} } \right]$,

$$\Pi_{H} \left( {p^{*} } \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{H}^{M} } \right) + D_{H}$$

or

$$\Pi_{H} \left( {p^{*} } \right) \ge \alpha \Pi_{H} \left( {p_{H}^{M} } \right) + \left( {1 - \alpha } \right)D_{H} = \Pi_{H} \left( {\tilde{p}_{H} \left( \alpha \right)} \right)$$

where $\tilde{p}_{H} \left( \alpha \right)$ is defined in the main text. Then, $p^{*} \ge \tilde{p}_{H} \left( \alpha \right)$.

Notice that H might have incentives to deviate to $p_{h}$. To deter this deviation, let us assume that $p^{*} = \tilde{p}_{H} \left( \alpha \right)$. Then

$$\Pi_{H} \left( {\tilde{p}_{H} \left( \alpha \right)} \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{h} } \right) + \Pi_{H} \left( {p_{H}^{M} } \right)$$

By the definition of $\tilde{p}_{H} \left( \alpha \right)$ in the main text, the above inequality is equivalent to $D_{H} \ge \Pi_{H} \left( {p_{h} } \right)$ or $\hat{p} \ge p_{h}$. The result of Lemma 8 follows.

Proof of Lemma 9 ($ICC_{L}$). To deter deviations by L to $p_{L}^{M}$ when $p_{L}^{M} > p_{l}$, a pooling price has to satisfy,

$$\Pi_{L} \left( {p^{*} } \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} \ge \Pi_{L} \left( {p_{L}^{M} } \right) + D_{L}$$

or

$$\Pi_{L} \left( {p^{*} } \right) \ge \left( {1 - \alpha } \right)\Pi_{L} \left( {p_{L}^{M} } \right) + \alpha D_{L} = \Pi_{L} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right)$$

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ is defined in the main text. Then, $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$.

To avoid a deviation to $p_{h}$, consider that $p^{*} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$. Then,

$$\Pi_{L} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) + \alpha \Pi_{L} \left( {p_{L}^{M} } \right) + \left( {1 - \alpha } \right)D_{L} \ge \Pi_{L} \left( {p_{h} } \right) + \Pi_{L} \left( {p_{L}^{M} } \right)$$

By the definition of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ in the main text, the above inequality implies $D_{L} \ge \Pi_{L} \left( {p_{h} } \right)$ or $p_{0} \ge p_{h}$ and Lemma 9 follows.

The incentive compatibility condition when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$.

By the discussion before Corollary 2 in the main text, $\overline{\alpha }_{h} < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \overline{\alpha }_{l} < 1$. Hence $\alpha > \overline{\alpha }_{h}$ and $\alpha \notin A_{h}$, $\forall \alpha$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < 1$. Namely, if the IS sends signal $h$, E enters the market when price $p^{*}$ is observed, irrespective of the precision $\alpha$ of the IS. This case is also split into two subcases: 1) ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < \overline{\alpha }_{l}$ and 2) $\overline{\alpha }_{l} \le \alpha < 1$.

(1) Consider that ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < \overline{\alpha }_{l}$. In this case $\alpha \notin A_{l} \cup A_{h}$. Namely, E enters the market when price $p^{*}$ is observed, irrespective of the signal sent by the IS. Therefore, both H and L should select the prices $p_{H}^{M}$ and $p_{L}^{M}$, respectively. Together with $p_{L}^{M} < p_{H}^{M}$, this leads to the following corollary:

Corollary A1. No pooling equilibrium exists when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < \overline{\alpha }_{l}$.

(2) Suppose now that $\overline{\alpha }_{l} \le \alpha < 1$. In this case $\alpha \in A_{l} \backslash \overline{A}_{h}$. Namely, similarly to the case (b) in the main text, E enters the market when price $p^{*}$ is observed if the IS sends the signal $h$ and does not enter if the IS sends signal $l$. Hence,

Corollary A2. The properties of the pooling equilibria and the incentive compatibility conditions of H and L when $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ and $\overline{\alpha }_{l} \le \alpha < 1$ are the same as in the case in which $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\overline{\alpha }_{h} < \alpha < 1$, but the relevant threshold for $\alpha$ is $\overline{\alpha }_{l}$, not $\overline{\alpha }_{h}$.

Proof of Proposition 2. Let us consider the four cases analyzed in the main text.

(a) Recall that in this case $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$.

First, consider that $p_{L}^{M} < \hat{p}$. The next lemma proves part 1.(i) of Proposition 1 when ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$.

Lemma A1. If $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$,${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$ and $p_{L}^{M} < \hat{p}$, then $SPE = \emptyset$.

Proof: As stated in the main text, in every possible pooling equilibrium satisfying belief consistency $p^{*} \le p_{h}$. Together with Lemma 4, this implies that $p_{L}^{M} \ge p_{h} \ge p^{*}$, which is incompatible with the $ICC_{H}$, since either $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right) > \hat{p}$ (see Lemma 5 (1)) or $p^{*} \ge \hat{p}$ (see Lemma 5 (2)). Hence $p_{L}^{M} \ge p^{*} = p_{h} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right) > \hat{p} > p_{L}^{M}$, giving a contradiction.

The next lemma proves the first part of case 1.(ii) of Proposition 1.

Lemma A2. Suppose that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$ and $p_{L}^{M} = \hat{p}$. Then if $p^{*} \in SPEP$, $p^{*} = \left\{ {p_{L}^{M} } \right\}$.

Proof: First we prove that $p_{L}^{M} \in SPEP$. By Lemma 4 $p_{L}^{M} \ge p_{h}$. Suppose that $p_{h} = p_{L}^{M} < p_{l} < p_{H}^{M}$. On the one hand, as stated in the main text, the only possible pooling equilibrium price satisfying belief consistency in this case is $p^{*} = p_{L}^{M}$. On the other hand, by Lemma 5 (2) $p_{H}^{M} > p^{*} \ge \hat{p}$ and H has no incentive to deviate to $p_{H}^{M}$ in this case since $p_{L}^{M} = \hat{p}$.

To avoid deviations by H to $p_{l}$, it suffices that $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$ (see Lemma 5 (2)).

For configurations $p_{L}^{M} > p_{h}$, belief consistency requires $p^{*} = p_{h}$ which is incompatible with the $ICC_{H}$, where either $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right) > \hat{p}$ if $p_{h} < p_{H}^{M} \le p_{l}$, or $p^{*} \ge \hat{p}$ if $p_{H}^{M} > p_{l}$ (see Lemma 5 (1) and Lemma 5 (2) respectively), since $p_{L}^{M} = \hat{p}$. Hence, $SPE = \emptyset$ in these cases.

We now deal with the case $p_{L}^{M} > \hat{p}$, and prove part 1.(iii.1) of Proposition 1. Lemma A3 below proves this result. We show that $SPEP = \left\{ {p^{*} \left| {\hat{p} \le p^{*} \le p_{L}^{M} } \right.} \right\}$ for all $\alpha$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$.

Lemma A3. Suppose that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha \le \overline{\alpha }_{h}$ and $p_{L}^{M} > \hat{p}$. Then $SPEP = \left[ {\hat{p},\,p_{L}^{M} } \right]$.

Proof: First, note that the set

$$\left\{ {p^{*} \left| {\hat{p} \le p^{*} \le p_{L}^{M} } \right.} \right\} \subseteq SPEP$$

To see that this is the case, consider any configuration such that $p_{L}^{M} = p_{h}$ and $p_{H}^{M} > p_{l}$. As stated in the main text, the only possible pooling equilibrium price satisfying belief consistency in this case is $p^{*} = p_{L}^{M}$. Note that by the $ICC_{H}$, $p_{H}^{M} > p^{*} \ge \hat{p}$ (see Lemma 5.(2)), H has no incentive to deviate to $p_{H}^{M}$ in this case since $p_{L}^{M} > \hat{p}$.

To avoid deviations by H to $p_{l}$, by Lemma 5 (2) any $p^{*} > \hat{p}$ deters these deviations whenever $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$. Since $p^{*} = p_{L}^{M} > \hat{p}$, then no deviation takes place.

Next consider configurations such that $\hat{p} \le p_{h}$ and $p_{l} < p_{L}^{M} < p_{H}^{M}$. Clearly in this case (by belief consistency) $p^{*} = p_{h}$. By the $ICC_{H}$, $p^{*} \ge \hat{p}$ so that H does not deviate to $p_{H}^{M}$ (see Lemma 5 (2)) and by the $ICC_{L}$, $p^{*} \ge p_{0}$ so that L does not deviate to $p_{L}^{M}$ (see Lemma 6 (2)). Both incentive compatibility conditions are compatible since $\hat{p} > p_{0}$ (see Lemma 1).

To avoid deviations by both H and L to $p_{l}$, it suffices that, by Lemma 5 (2) $\tilde{p}_{H} \left( \alpha \right) \ge p_{l}$, and by Lemma 6 (2) $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right) \ge p_{l}$, respectively.

Hence, $\hat{p} \le p^{*} = p_{h} < p_{l} < p_{L}^{M}$ for $\min \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) \ge p_{l}$ is an incentive compatible pooling equilibrium that satisfies belief consistency.

Therefore, $\left\{ {p^{*} \left| {\hat{p} \le p^{*} \le p_{L}^{M} } \right.} \right\} \subseteq SPEP$ as claimed.

Next, we prove that $SPEP \subseteq \left[ {\hat{p},\,p_{L}^{M} } \right]$. On the one hand, for any configuration $\hat{p} \le p_{h} < p_{L}^{M}$, if a pooling exists, by belief consistency $p^{*} = p_{h}$ and therefore $p^{*} \in \left[ {\hat{p},\,p_{L}^{M} } \right]$. On the other hand, note that whenever $\hat{p} > p_{h}$ no equilibrium exists since by belief consistency $p^{*} = p_{h}$. This is not compatible with the $ICC_{H}$, $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{H} \left( \alpha \right) > \hat{p}$ (see Lemma 5 (1)) or $p^{*} \ge \hat{p}$ (see Lemma 5 (2)).

Therefore, if $p^{*} \in SPEP$, then $p^{*} \in \left[ {\hat{p},\,p_{L}^{M} } \right]$ as claimed.

(b) Recall that in this second case $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$ and $\overline{\alpha }_{h} < \alpha < 1$.

The next lemma completes the proofs of parts 1. (i) and 1.(ii) of Proposition 1.

Lemma A4. Suppose that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$, $\overline{\alpha }_{h} < \alpha < 1$ and $p_{L}^{M} \le \hat{p}$, then $SPE = \emptyset$.

Proof: As stated in the main text, in every possible pooling equilibrium satisfying belief consistency in this case, $p_{h} < p^{*} \le p_{l}$. Together with Lemma 7, this implies that $p_{L}^{M} \ge p^{*}$, which is incompatible with the $ICC_{H}$, $p^{*} \ge \tilde{p}_{H} \left( \alpha \right) > \hat{p}$ (see Lemma 8).

Now suppose that $\hat{p} < p_{L}^{M}$. Let us prove next that if $\overline{\alpha }_{h} < \alpha \le \delta$, then.

$SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$,

i.e., part 1.(iii.2) of Proposition 1.

Lemma A5. Suppose that $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) < 0$,$\overline{\alpha }_{h} < \alpha < 1$ and $\hat{p} < p_{L}^{M}$. Then

$$SPEP = \left\{ {p^{*} \left| {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) \le p^{*} \le p_{L}^{M} } \right.} \right\}$$

and this set is non-empty if $\delta > \overline{\alpha }_{h}$ for all $\alpha$, $\overline{\alpha }_{h} < \alpha \le \delta$.

Proof: First, consider the case $p_{L}^{M} = p_{l}$. As stated in the main text, the only possible pooling equilibrium price satisfying belief consistency in this case is $p^{*} = p_{L}^{M}$. Note that the $ICC_{H}$ requires that $p^{*} \ge \tilde{p}_{H} \left( \alpha \right) > \hat{p}$ (see Lemma 8), which in this case is equivalent to $p_{L}^{M} \ge \tilde{p}_{H} \left( \alpha \right) > \hat{p}$. Note that $p_{L}^{M} \ge \tilde{p}_{H} \left( \alpha \right)$ implies

$$\Pi_{H} \left( {p_{L}^{M} } \right) + \alpha D_{H} + \left( {1 - \alpha } \right)\Pi_{H} \left( {p_{H}^{M} } \right) \ge \Pi_{H} \left( {p_{H}^{M} } \right) + D_{H}$$

or that

$$\alpha \le \frac{{\Pi_{H} \left( {p_{L}^{M} } \right) - D_{H} }}{{\Pi_{H} \left( {p_{H}^{M} } \right) - D_{H} }} = \frac{{\Pi_{H} \left( {p_{L}^{M} } \right) - \Pi_{H} \left( {\hat{p}} \right)}}{{\Pi_{H} \left( {p_{H}^{M} } \right) - \Pi_{H} \left( {\hat{p}} \right)}} \equiv \delta$$

Clearly, $0 < \delta < 1$.

To avoid deviations by H and L to $p_{h}$, by Lemmas 8 and 9, it suffices that $p_{0} \ge p_{h}$ (see Lemma 1 (iii)). Hence $p^{*} = p_{L}^{M} > \hat{p}$, for $p_{0} \ge p_{h}$ and $\overline{\alpha }_{h} < \alpha \le \delta$, is an incentive compatible pooling equilibrium that satisfies belief consistency.

Notice now that if $p_{L}^{M} > p_{l}$, then, as stated in the main text, the unique pooling equilibrium guaranteeing belief consistency is $p^{*} = p_{l}$. The $ICC_{H}$ requires that $p^{*} \ge \tilde{p}_{H} \left( \alpha \right) > \hat{p}$ (see Lemma 8), and the $ICC_{L}$ requires that $p^{*} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)$ (see Lemma 9). Therefore $\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) \le p_{l} = p^{*} < p_{L}^{M}$ should hold, where $\tilde{p}_{H} \left( \alpha \right) < p_{L}^{M}$ implies $\alpha < \delta$.

To deter deviations by both H and L to $p_{h}$, the $ICC_{H}$ given by Lemma 8 and the $ICC_{L}$ given by Lemma 9 again apply. Hence $\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) \le p_{l} = p^{*} < p_{L}^{M}$, for $p_{0} \ge p_{h}$ and $\overline{\alpha }_{h} < \alpha < \delta$, is an incentive compatible pooling equilibrium that satisfies belief consistency.

Hence set $SPEP = \left[ {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right),p_{L}^{M} } \right]$ as claimed.

Notice that the above implies part 1.(iii.3) of Proposition 1, i.e., for $\alpha > \delta$, $SPE = \emptyset$.

(c) In this case $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ and ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < \overline{\alpha }_{l}$. By Corollary A1, $SPE = \emptyset$ in this case (part 2.(ii.1) of Proposition 1).

(d) In this case $\mu \Delta_{E} \left( H \right) + \left( {1 - \mu } \right)\Delta_{E} \left( L \right) > 0$ and $\overline{\alpha }_{l} \le \alpha < 1$. By Corollary A2, this case is equivalent to the case (b) above, but the relevant threshold for $\alpha$ is $\overline{\alpha }_{l}$, not $\overline{\alpha }_{h}$. Hence, if $\hat{p} < p_{L}^{M}$, then.

$SPEP = \left\{ {p^{*} \left| {\max \left( {\tilde{p}_{H} \left( \alpha \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{L} \left( \alpha \right)} \right) \le p^{*} \le p_{L}^{M} } \right.} \right\}$,

and this set is non-empty if $\delta \ge \overline{\alpha }_{l}$ and for all $\alpha$, $\overline{\alpha }_{l} \le \alpha \le \delta$. This proves part 2.(ii.2) of Proposition 1. As above, note that 2.(ii.3) of the Proposition (i.e., for $\alpha > \delta$, $SPE = \emptyset$) is satisfied.

As in the proofs of parts 1.(i) and 1.(ii) of the Proposition (see Lemmas A1 and A2 above), if $p_{L}^{M} \le \hat{p}$, then $SPE = \emptyset$, which proves part 2.(i).

Finally, note that parts 2.(ii.1) and 2.(ii.3) of the Proposition imply the first part of point (3), while parts 1.(iii.1) and 1.(iii.3) imply the second part.

1.1 Example

1.1.1 Cournot competition

The equilibrium under Cournot competition in between L and E is characterized by $p_{0} = {{\left( {a + 2c_{L} } \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c_{L} } \right)} 3}} \right. \kern-\nulldelimiterspace} 3}$ and $D_{L} = D_{E} \left( L \right) = {{\left( {a - c_{L} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - c_{L} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$; and the competition in between H and E is characterized by $\hat{p} = {{\left( {a + c_{L} + c_{H} } \right)} \mathord{\left/ {\vphantom {{\left( {a + c_{L} + c_{H} } \right)} 3}} \right. \kern-\nulldelimiterspace} 3}$, $D_{H} = {{\left( {a - 2c_{H} + c_{L} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{H} + c_{L} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$ and $D_{E} \left( H \right) = {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$. Note that $p_{L}^{M} = {{\left( {a + c_{L} } \right)} \mathord{\left/ {\vphantom {{\left( {a + c_{L} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2} > \hat{p} = {{\left( {a + c_{L} + c_{H} } \right)} \mathord{\left/ {\vphantom {{\left( {a + c_{L} + c_{H} } \right)} 3}} \right. \kern-\nulldelimiterspace} 3}$ since $c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$.

Consequently, under Cournot competition, Assumption 1, according to which $D_{E} \left( L \right) - K < 0$ and $D_{E} \left( H \right) - K > 0$, is satisfied for all $K$ such that ${{\left( {a - c_{L} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - c_{L} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9} < K < {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {a - 2c_{L} + c_{H} } \right)^{2} } 9}} \right. \kern-\nulldelimiterspace} 9}$. Moreover, Assumption 3, according to which $\Pi_{L} \left( {p_{L}^{M} } \right) - D_{L} > \Pi_{H} \left( {p_{H}^{M} } \right) - D_{H}$ is satisfied given that $c_{L} < c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$.

1.1.2 Bertrand competition

The equilibrium under Bertrand competition in between L and E is characterized by $p_{0} = c_{L}$ and $D_{L} = D_{E} \left( L \right) = 0$; and the competition in between H and E is characterized by $\hat{p} = c_{H}$, $D_{H} = 0$ and $D_{E} \left( H \right) = \left( {c_{H} - c_{L} } \right)\left( {a - c_{H} } \right)$. Note that $p_{L}^{M} = {{\left( {a + c_{L} } \right)} \mathord{\left/ {\vphantom {{\left( {a + c_{L} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2} > \hat{p} = c_{H}$ since $c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$.

Consequently, under Bertrand competition, Assumption 1, according to which $D_{E} \left( L \right) - K < 0$ and $D_{E} \left( H \right) - K > 0$, is satisfied for all $K$ such that $0 < K < \left( {c_{H} - c_{L} } \right)\left( {a - c_{H} } \right)$. Moreover, Assumption 3, according to which $\Pi_{L} \left( {p_{L}^{M} } \right) - D_{L} > \Pi_{H} \left( {p_{H}^{M} } \right) - D_{H}$ is satisfied given that $c_{L} < c_{H} < \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}$.

A sketch of the proof of Proposition 4. As stated in the main text, in this equilibrium, E identifies the type of M with probability 1. Hence, E enters the market when price $p_{H}$ is observed, irrespective of the signal of the IS, and E stays out when $p_{L}$ is observed, again irrespective of $s$. Therefore, by the entrant’s strategy, $p_{H} > p_{l}$ and $p_{L} \le p_{h}$. See Fig. 1 in the main text.

Knowing that entry will occur, the H-type monopoly is better off choosing the price $p_{H}^{M}$. Thus $SSE_{H} = \left\{ {p_{H}^{M} } \right\}$ and E enters for sure when it observes price $p_{H}^{M}$. In particular, $p_{H}^{M} > p_{l}$.

We need to prove that $SSE_{L} = \left\{ {p_{L} \left| {p_{0} \le p_{L} \le \min \left( {p_{L}^{M} ,\hat{p}} \right)} \right.} \right\}$ for all $\alpha$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < \alpha < 1$. Hence, there are two relevant cases: when $p_{L}^{M} \le \hat{p}$ and when $\hat{p} < p_{L}^{M}$.

The proof follows two steps. The first step consists of showing that $p_{L} \in \left[ {p_{0} ,\min \left( {p_{L}^{M} ,\hat{p}} \right)} \right]$ in both cases $p_{L}^{M} \le \hat{p}$ and $\hat{p} < p_{L}^{M}$.

In the first case, when $p_{L}^{M} \le \hat{p}$, $p_{L} = p_{L}^{M}$ can be supported as a separating equilibrium price (no type of M has incentives to deviate), for instance when

$$p_{L} = p_{L}^{M} \le p_{h} \le \hat{p} < p_{l} \le \tilde{p}_{H} \left( \alpha \right) < p_{H}^{M}$$

And $p_{L} \in \left[ {p_{0} ,p_{L}^{M} } \right)$ can also be supported as a separating equilibrium price, for instance when

$p_{L} = p_{h} < p_{l} < p_{L}^{M} \le \hat{p} < \tilde{p}_{H} \left( \alpha \right) < p_{H}^{M}$.

Similarly, in the second case $\hat{p} < p_{L}^{M}$ $p_{L} \in \left[ {p_{0} ,\hat{p}} \right]$ can be supported as a separating equilibrium price, for instance when

$$p_{L} = p_{h} \le \hat{p} < p_{l} < \min \left( {p_{L}^{M} ,\tilde{p}_{H} \left( \alpha \right)} \right) < p_{H}^{M}$$

The second step of the proof is to show that if $p_{L} \notin \left[ {p_{0} ,\min \left( {p_{L}^{M} ,\hat{p}} \right)} \right]$, then $p_{L} \notin SSE_{L}$, which is easy to show considering the relevant positions of $p_{h}$ and $p_{l}$.