Preserving coalitional rationality for non-balanced games

Abstract

In cooperative games, the core is one of the most popular solution concept since it ensures coalitional rationality. For non-balanced games however, the core is empty, and other solution concepts have to be found. We propose the use of general solutions, that is, to distribute the total worth of the game among groups rather than among individuals. In particular, the $k$-additive core proposed by Grabisch and Miranda is a general solution preserving coalitional rationality which distributes among coalitions of size at most $k$, and is never empty for $k\ge 2$. The extended core of Bejan and Gomez can also be viewed as a general solution, since it implies to give an amount to the grand coalition. The $k$-additive core being an unbounded set and therefore difficult to use in practice, we propose a subset of it called the minimal negotiation set. The idea is to select elements of the $k$-additive core mimimizing the total amount given to coalitions of size greater than 1. Thus the minimum negotiation set naturally reduces to the core for balanced games. We study this set, giving properties and axiomatizations, as well as its relation to the extended core of Bejan and Gomez. We give a method of computing the minimum bargaining set, and lastly indicate how to eventually get classical solutions from general ones.

1 Introduction

One of the major challenges of the theory of cooperative games with transferable utility is to propose an allocation of gains obtained by a set $N$ of players. Typically, this distribution (called a solution) is done among the individual players, and many concepts of solutions have been proposed so far, the core being one of the best known solution since it ensures coalitional rationality. However, in many real situations, the distributions of gains is not done to individuals but often to groups of individuals (associations, companies, families, etc.), which can further distribute among their members according to their own rules, which can differ from one group to another. Also, the drawbacks of the classical solutions like the core are well known. For example, the core is often empty, which obliges to take other solution concepts, often violating coalitional rationality.

A natural generalization of the classical view of solutions should be then to distribute among groups rather than among individuals. We call this a general solution, and observe that we can already find in the literature two attempts in this direction. The first one is the $k$-additive core proposed by Grabisch and Miranda (2008), Miranda and Grabisch (2010), which was also proposed earlier by Vassil’ev Vassil’ev (1978) in a publication in Russian. The extended core of Bejan and Gómez (2009) can also be viewed as a general solution,¹ since it implies to give an amount to the grand coalition. In the $k$-additive core, the distribution of $v(N)$ is done among coalitions of size at most $k$, and coalitional rationality is ensured (thus, the 1-additive core is the classical core). In the $\mathsf {G}$-extended core, the distribution is done among individuals and the grand coalition. When the core is empty, these two general solutions allocate some negative amounts (debts) to some coalitions (the grand coalition in the case of the $\mathsf {G}$-extended core).

The aim of this paper is to propose a subset of solutions of the $k$-additive core, and to relate it to the $\mathsf {G}$-extended core. Indeed, if the $k$-additive core has some remarkable features (it is never empty as soon as $k\ge 2$, and it preserves coalitional rationality), its main drawback is that it is an unbounded set for any $k\ge 2$. We call the subset of the $k$-additive core we propose the minimum negotiation set, since it is based on the following idea: the less negotiation is necessary, the better the solution. Indeed, a general solution obliges individuals belonging to a group which has received an allocation to bargain among them in order to share the amount received by the group (often a negative amount, if the core is empty). Therefore, it is desirable to focus on solutions minimizing the number of groups and the allocation given to them. This is achieved by minimizing a norm of the vector of allocations to groups. We will show that the minimum negotiation set coincides with the core when the latter is nonempty, it is a singleton for all $L_p$ norms with $p>1$, and for the $L_1$ norm, the payments given to individuals are exactly those produced by the $\mathsf {G}$-extended core.

An important feature of general solutions is that they do not define a payment to individuals like classical solutions. Hence, strictly speaking they are not solutions to the game, but rather pre-solutions, which need an additional step where payments given to coalitions (in fact, as we have shown, these are most often debts) have to be further redistributed among the members of these coalitions. The question is then: What do we (l)earn from general solutions if eventually they collapse to classical solutions? A short answer to this question would be that doing so, we main attain solutions which could have never been reached by classical mechanisms. A more refined answer is that by this two-step procedure, we control the result by imposing appropriate rationales at each step. For example, using the $k$-additive core or subsets of it, we guarantee coalitional rationality in the first step. In the second step, we can choose for each coalition in debt an appropriate sharing rule (and then we get an element of the selectope Derks et al. (2000)) or, more generally, considering this as a bankruptcy problem Thomson (2003), we can choose an appropriate division rule. Other methods can be used as well, like bargaining procedures. The main aim of the paper is not to develop this second step, which should deserve a whole study, but to focus on the first one and to study properties of general solutions and their relationship. However, we have devoted a section to the second step giving the main ideas.

The paper is organized as follows: Section 2 introduces the concept of general solution and the basic material which is needed. In particular, we present properties for general solutions, and we introduce the $k$-additive core and the $\mathsf {G}$-extended core. Section 3 focusses on the main achievement of the paper, the minimum negotiation set. It studies its properties, and two particular cases of norms ($L_1$ and $L_p$ for $p>1$), and gives axiomatizations. Also, the notion of autonomous coalition is introduced, as well as a method to find them. Section 4 addresses the problem of computing the minimum negotiation set, and lastly we give a brief account on how to derive a classical payoff vector from a general one in Sect. 5, and finishes the paper with concluding remarks.

2 General payoff vectors and solutions

2.1 Basic definitions and notations

We start by fixing the notation and introducing basic definitions. Let $N=\{1,\ldots ,n\}\subset \mathbb {N}$ be a finite and nonempty set of agents or players. Coalitions of players are subsets of $N$, denoted by capital letters $S, T$, and so on. Whenever possible, we will omit braces for singletons and pairs, denoting $\{i\},\{i,j\}$ by $i,ij$ respectively, in order to avoid a heavy notation. A transferable utility (TU) game on $N$ is a pair $(N,v)$ where $v$ is a mapping $v : 2^N \rightarrow \mathbb {R}$ satisfying $v(\emptyset )=0$. We will denote by $\mathcal {G}(N)$ the set of all games over $N$. For any coalition $S, v(S)$ represents the worth of $S$, i.e., what coalition $S$ could earn regardless of other players.

To every game $v\in \mathcal {G}(N)$ we associate its Möbius transform Rota (1964) (also known as Harsanyi dividends Harsanyi (1963)) $m^v:2^N\rightarrow {\mathbb R}$, defined by

$$\begin{aligned} m^{v}(S):= \sum _{T \subseteq S} (-1)^{|S\setminus T|} v(T), \quad \forall S \subseteq N, \end{aligned}$$

(1)

and $m^v(\emptyset )=0$. Conversely, $v$ can be recovered from $m^v$ by the inverse transform

$$\begin{aligned} v(S) = \sum _{T\subseteq S} m^v(T),\quad \forall S\subseteq N. \end{aligned}$$

(2)

Hence the Möbius transform is a linear bijection on $\mathcal {G}(N)$. Note in particular that $m^v(\{i\})=v(\{i\})$ for all $i\in N$, implying that $m^v(S)=0$ if $|S|>1$ whenever $v$ is additive. We recall also that the Möbius transform gives the coordinates of a game into the $(2^n-1)$-dimensional basis of unanimity games $\{u_S\}_{S\subseteq N, S\ne \emptyset }$, with $u_S(T)=1$ if $T\supseteq S$, and 0 otherwise.

A payoff vector is a vector $x\in \mathbb {R}^n$ that assigns agent $i$ the payoff $x_i$. Given $x\in \mathbb {R}^n$, and $S\subseteq N$, denote by $x(S)$ the sum $\displaystyle {\sum _{i\in S}x_i}$ with the convention that $x(\emptyset )=0$. A payoff vector is efficient for game $v$ if $x(N)=v(N)$. We will call preimputation of $v$ each efficient payoff vector of $v$ and we denote by $PI(v)$ the set of preimputations of $v$.

Coalition $S$ is able to improve upon payoff $x$ if $x(S)< v(S)$. The core $\mathsf {C}(v)$ of a game $v$ is the set of efficient payoffs that cannot be improved upon by any coalition, i.e.,

$$\begin{aligned} \mathsf {C}(v)=\{x\in \mathbb {R}^n \mid \forall S \subsetneq N, x(S)\ge v(S), \text { and } x(N)=v(N)\}. \end{aligned}$$

A game with a nonempty core is said to be balanced. Whenever convenient, we consider the core as a correspondence $\mathsf {C}:\mathcal {G}(N)\rightrightarrows {\mathbb R}^n$.

A general payoff vector is a vector $x\in \mathbb {R}^{2^N\setminus \emptyset }$ that assigns to a coalition $S\subseteq N$ a payoff $x_S$. Also, $1_S$ with $S\subseteq N$ indicates the vector with coordinate 1 for $S$ and 0 otherwise.

The notion of efficiency easily generalizes: as for the classical case, the sum of payoffs given to all coalitions should be equal to the total available amount, that is, $v(N)$. Formally, a general payoff vector is said to be efficient for $v$ if ${\sum _{\emptyset \ne S\subseteq N}x_S=v(N)}$.

Example 1

A payoff vector $x\in {\mathbb R}^n$ defines a general payoff vector by considering $x_S=0$ for all $S\subseteq N$ such that $|S|\ge 2$. Hence, any element of the core induces a general efficient payoff vector.

Example 2

A less trivial example of general payoff vector, which will be central in our study, is the Möbius transform $m^v$ of a game $v$. Note that by (2) $m^v$ is efficient for $v$.

A solution on the set of games $\mathcal {G}(N)$ is a correspondence $\sigma :\mathcal {G}(N)\rightrightarrows {\mathbb R}^n$, i.e., it assigns to any game $v\in \mathcal {G}(N)$ a set of payoff vectors, with the additional property that they are all efficient for $v$. Analogously, a general solution assigns to every game $v$ in $\mathcal {G}(N)$ a set of general payoff vectors efficient for $v$.

The core is a well-known solution for games. A trivial example of general solution is the Möbius transform $m$ (see Example 2). Although the notion of general solution is not explicitely considered in the literature, there are two recent remarkable examples of general solutions. The first one is the $k$-additive core Miranda and Grabisch (2010), where a payoff is given to each coalition of size at most $k$, while the second example is the extended core Bejan and Gómez (2009), which can be viewed as a general solution. In the extended core, apart from giving a payoff to each player, a payoff is also (virtually) given to the grand coalition $N$. We will study this concept in Sect. 2.4. Our paper mainly focusses on the $k$-additive core, which is presented in Sect. 2.3. Before that, we introduce some properties for general solutions.

2.2 Properties of general solutions

We propose several properties for general solutions, some of them being direct generalization of classical properties of solutions. Let $\sigma$ be a general solution on $\mathcal {G}(N)$. We say that $\sigma$

• is covariant under strategic equivalence (COV) if $\forall v \in \mathcal {G}(N), \forall \alpha > 0,$ for all additive game $\beta$, we have:

  $$\begin{aligned} \sigma (\alpha v + \beta )=\alpha \sigma (v)+m^{\beta }. \end{aligned}$$

• is an idempotent solution (IDEM) if

  $$\begin{aligned} \sigma (m^{-1}\circ \sigma )=\sigma . \end{aligned}$$

  The property means that applying the same solution concept to the set of solutions found (after transforming them into games by $m^{-1}$) does not give more solutions.

• is symmetric (SYM) if $\forall v \in \mathcal {G}(N)$, for all permutations $\pi$ on $N$ such that $v(\pi (S))=v(S)$ holds for all $S\subseteq N$:

  $$\begin{aligned} (\sigma (v))_{\pi (S)}=(\sigma (v))_S,\quad \forall \emptyset \ne S\subseteq N, \end{aligned}$$

  where $\pi (S)=\{\pi (i),i\in S\}$. The property says that if a permutation leaves the game invariant (e.g., $i$ and $j$ can be permuted), then the same permutation leaves the general payoff vectors in the solution invariant too (e.g., $S\cup i$ and $S\cup j$ receive the same payoff for all $S\not \ni i,j$).

• is coalitionally rational (CR) if $\forall v \in \mathcal {G}(N), \forall S \subseteq N, \forall x \in \sigma (v)$,

  $$\begin{aligned} \sum _{T\subseteq S}x_T \ge v(S). \end{aligned}$$

  As in the case of efficiency, this is a direct extension of the classical definition. Indeed, the total amount given to coalition $S$ (that is, to all its individuals and all subcoalitions) is precisely $\sum _{T\subseteq S}x_T$, which should be at least equal to the worth that $S$ can achieve by itself, that is, $v(S)$.

• gives a preimputation (PI) if $\forall v \in \mathcal {G}(N), \forall S \subseteq N$ such that $|S|\ge 2$ we have:

  $$\begin{aligned} \forall x \in \sigma (v), \, x_S=0. \end{aligned}$$

  Only classical solutions, like the core or the Shapley value, satisfy (PI).

• satisfies the dummy player property (DPP) if for any dummy player $i$, we have:

  $$\begin{aligned} \forall x\in \sigma (v),\, x_i=v(i), \end{aligned}$$

  where as usual a player $i$ is dummy if $v(S\cup i)=v(S)+v(i)$ for every $S\subseteq N\setminus i$.

• is a minimization of the global debt (MGD) if for all nonnegative games $v$, for all $x\in \sigma (v)$,

  $$\begin{aligned} \sum _{\begin{array}{c} S\subseteq N\\ |S|\ge 2 \end{array}}{\min (x_S,0)}=-\bar{t}(v), \end{aligned}$$

  where $\bar{t}(v)=\min \{t\ge 0\mid \mathsf {C}(v^t)\ne \emptyset \}$, with $v^t$ the game defined by $v^t(N)=v(N)+t$, and $v^t(S)=v(S)$ otherwise (see Sect. 2.4). This axiom can be explained as follows. By definition, $\bar{t}(v)$ is the minimal amount given to the grand coalition so that coalitional rationality with classical payoff vectors is ensured. However, the players in $N$ are in debt of the amount $\bar{t}(v)$. In terms of general payoff vectors, this means that $N$ has to pay the debt, or more generally, it can be spread among coalitions. The axiom says that the total debt should not exceed the minimal amount $\bar{t}(v)$, and since it cannot be less without losing coalitional rationality,² equality follows.

The set of general solutions is a partially ordered set with the relation $\preccurlyeq$ defined by:

$$\begin{aligned} \sigma _1 \preccurlyeq \sigma _2 \Longleftrightarrow \forall v \in \mathcal {G}(N), \, \sigma _1(v)\subseteq \sigma _2(v). \end{aligned}$$

For any set $A$ of general solutions, whenever it exists we denote by $\displaystyle {\top (A)}$ the top element of $A$ for the relation $\preccurlyeq$, that is, the element satisfying $\sigma \preccurlyeq \top (A)$ for all $\sigma \in A$.

For example, if we denote by $PICR$ the set of general solutions which satisfy (PI) and (CR), then

$$\begin{aligned} \mathsf {C}=\top (PICR). \end{aligned}$$

2.3 The $k$-additive core

A game $v\in \mathcal {G}(N)$ is said to be $k$ -additiveGrabisch (1997) if its Möbius transform $m^v$ vanishes for subsets of more than $k$ players: $m^v(S)=0$ if $|S|>k$, and there exists $K\subseteq N, |K|=k$, such that $m^v(K)\ne 0$. Note that a 1-additive game is an additive game in the usual sense. A game $v$ is said to be at most $k$ -additive if it is $q$-additive for some $q\in \{1,\ldots ,k\}$. We denote by $\mathcal {G}^k(N)$ the set of all at most $k$-additive games.

The $k$-additive core, introduced by Grabisch and Miranda Grabisch and Li (2011), Grabisch and Miranda (2008), Miranda and Grabisch (2010), and also by Vassil’ev Vassil’ev (1978), is the set of efficient and coalitionally rational general payoff vectors, with the restriction that payoffs are limited to coalitions of at most size $k$.

Definition 1

Let $v$ be a game. The $k$ -additive core ³ of $v$, denoted by $\mathsf {C}^k(v)$, is given by

$$\begin{aligned} \mathsf {C}^k(v)&= \Big \{x\in {\mathbb R}^{2^N\setminus \emptyset }\mid \sum _{T\subseteq S}x_T\ge v(S), \forall S\subseteq N, \, \sum _{T\subseteq N}x_T\\&\qquad =v(N), x_T=0, \forall T\subseteq N,|T|>k\Big \}. \end{aligned}$$

As before we may consider the $k$-additive core as a correspondence $\mathsf {C}^k:\mathcal {G}(N)\rightrightarrows {\mathbb R}^{2^N\setminus \emptyset }$.

Example 3

We consider a game $v$ on $N=\{1,2,3\}$ defined by:

$$\begin{aligned} \begin{array}{|l|ccccccr|} \hline S &{} 1 &{} 2 &{} 3 &{} 12 &{} 13 &{} 23 &{} 123 \\ \hline v(S) &{} 1 &{} 1 &{} 1 &{} 1.5 &{} 1.5 &{} 1.5 &{} 2 \\ \hline \end{array} \end{aligned}$$

Let a general payoff vector $x$ be defined by

$$\begin{aligned} \begin{array}{|l|ccccccr|} \hline S &{} 1 &{} 2 &{} 3 &{} 12 &{} 13 &{} 23 &{} 123 \\ \hline x_S &{} 2 &{} 2 &{} 3 &{} -1 &{} -2 &{} -2 &{} 0 \\ \hline \end{array} \end{aligned}$$

It is easy to check that $x$ satisfies coalitional rationality and efficiency. Moreover, $x_{123}=0$, hence $x\in \mathsf {C}^2(v)$. The corresponding 2-additive game $\phi$ can be computed through the inverse Möbius transform (Eq. (2)):

$$\begin{aligned} \begin{array}{|l|ccccccr|} \hline S &{} 1 &{} 2 &{} 3 &{} 12 &{} 13 &{} 23 &{} 123 \\ \hline \phi (S) &{} 2 &{} 2 &{} 3 &{} 3 &{} 3 &{} 3 &{} 2 \\ \hline \end{array} \end{aligned}$$

Theorem 1

Miranda and Grabisch (2010) The $k$-additive core is a convex polyhedron, nonempty for $k\ge 2$.

$$\begin{aligned} \mathsf {C}^k(v)\ne \emptyset , \quad \forall v\in \mathcal {G}(N),\forall k \ge 2. \end{aligned}$$

Unlike the core, the $k$-additive core is always nonempty. However, it is an unbounded set, as shown by the next proposition.

Theorem 2

For all $k \ge 2$, the $k$-additive core is unbounded and pointed.⁴ Moreover, for $k=2$, its extremal rays are of the form $1_i-1_{ij}$, for all $i\ne j\in N$.

Proof

Since for any game $v$, the inclusion $\mathsf {C}^2(v)\subseteq \mathsf {C}^k(v)$ holds for any $k\ge 2$, it suffices to show that the 2-additive core is unbounded.

From standard results in polyhedra, studying the unboundedness of the 2-additive core amounts to studying its recession cone, i.e., the set of inequalities where the right member is replaced by 0 (see, e.g., (Fujishige (2005), Ch. 1)). If the recession cone is a pointed cone not reduced to $\{0\}$, then the corresponding polyhedron has vertices and rays. i.e., it is unbounded. We denote naturally by $\mathsf {C}^2(0)$ the recession cone of $\mathsf {C}^2(v)$.

The system of inequalities defining $x\in \mathsf {C}^2(0)$ reads:

$$\begin{aligned} x_i&\ge 0,\quad \forall i\in N\\ x_i + x_j + x_{\{i,j\}}&\ge 0,\quad \forall i,j\in N, i\ne j\\ \sum _{i\in S}x_i + \sum _{\{i,j\}\subseteq S}x_{\{i,j\}}&\ge 0,\quad \forall S\subseteq N, 2<|S|<n\\ \sum _{i\in N} x_i + \sum _{\{i,j\}\subseteq N}x_{\{i,j\}}&= 0. \end{aligned}$$

We claim that any vector of the form $r=1_i-1_{\{i,j\}}$, i.e., having value 1 for coordinate $i, -1$ for coordinate $\{i,j\}$, and 0 otherwise, is an extremal ray. Indeed, the vector $\alpha r$ satisfies the above system for any $\alpha >0$, and it cannot be expressed as the sum of other rays since any ray must have at least 2 nonzero coordinates. Note also that there is no other extremal ray.

As a conclusion, the 2-additive core is unbounded.

Let us show that the $k$-additive core is pointed. This amounts to finding in the system of equalities $\sum _{\begin{array}{c} T\subseteq S\\ |T|\le k \end{array}}x_T= 0, S\subseteq N$, a subsystem of exactly $n+\left( {\begin{array}{c}n\\ 2\end{array}}\right) +\cdots +\left( {\begin{array}{c}n\\ k\end{array}}\right)$ equations whose unique solution is the zero vector. For this, it suffices to take those corresponding to all $S$ such that $|S|\le k$.$\square$

Proposition 1

For all $k\in \{1,\ldots , n\}, \mathsf {C}^k$ satisfies (COV), (IDEM), (SYM), and (CR). Moreover, if we denote by $CR$ the set of general solutions which satisfies (CR), we have:

$$\begin{aligned} \mathsf {C}^n=\top (CR). \end{aligned}$$

Proof

We prove only (IDEM), the rest being clear. For clarity, we introduce the notation $\mathsf {c}^k=m^{-1}(\mathsf {C}^k)$. Then, it amounts to prove $\mathsf {c}^k\circ \mathsf {c}^k=\mathsf {c}^k$. Let $v$ be a game on $N$. Take any $\phi \in \mathsf {c}^k(v)$. Then $\phi \in \mathsf {c}^k(\phi )$, therefore $\phi \in \mathsf {c}^k(\mathsf {c}^k(v))$

Conversely, if $\phi \in \mathsf {c}^k(\mathsf {c}^k(v))$, then $\exists \psi \in \mathsf {c}^k(v)$ such that $\phi \in \mathsf {c}^k(\psi )$. We have $\phi (S) \ge \psi (S) \ge v(S) \quad \forall S\subseteq N$ and $\phi (N) = \psi (N) = v(N)$. Since $\phi$ is $k\text {-additive}$ we have $\phi \in \mathsf {c}^k(v)$.$\square$

2.4 The $\mathsf {G}$-extended core

In this section we introduce a new general solution based on the principle of the extended core $\mathsf {EC}(v)$ of Bejan and Gomez. Given a game $v$ and $t\ge 0$, define its $t$ -expansion $v^t$ by $v^t(S):=v(S)$ for all $S\subset N$, and $v^t(N):=v(N)+t$. Now, to any game $v$ we assign $\bar{t}(v):=\min \{t\ge 0 \mid \mathsf {C}(v^t)\ne \emptyset \}$, the minimum amount to be given to the grand coalition in order to ensure balancedness. Given $v$ a game and $x$ a preimputation, we introduce the real number $t(v,x):=\min \{l(N)\mid l\in \mathbb {R}^n_+ \text { and } (x+l)(S)\ge v(S), \, \forall S \subseteq N\}$.

Bejan and Gómez (2009) have introduced the concept of extended core of $v$ as follows:

$$\begin{aligned} \mathsf {EC}(v):= \{x\in PI(v) \mid t(v,x)=\bar{t}(v)\}. \end{aligned}$$

The extended core of $v$ coincides with the core whenever $\mathsf {C}(v)\ne \emptyset$. It is the set of preimputations $x$ for which there exists $l^x\in \mathbb {R}^n_+$ such that $(x+l^x)(S)\ge v(S),\quad \forall S\subseteq N$ and $\displaystyle {\sum _{i\in N}l^x_i=\bar{t}(v)}$. In other words, the extended core is the set of those preimputations that require a minimal subsidy to the grand coalition.

Since the extended core is a set of preimputations, it is not a general solution as announced in the introduction. However, a general solution is inherent in the way Bejan and Gomez use the extended core: given a tax rule, take any vector in the core of $v^{\bar{t}(v)}$ (where precisely the amount $\bar{t}(v)$ has been given to the grand coalition) and tax every player according to the chosen rule, where the tax is $\bar{t}(v)$. In what follows, we propose a rewriting of the extended core as a general solution, which we call the $\mathsf {G}$-extended core.

Consider $z\in \mathsf {EC}(v)$ and its associated vector $l^z\in \mathbb {R}^n_+$ as above. We build from $z$ a general payoff vector $x^z$ defined as follows:

$$\begin{aligned} x^z_S = {\left\{ \begin{array}{ll} z_i+l_i^z, &{} \text { if } S=\{i\}\\ -\bar{t}(v), &{} \text { if } S=N\\ 0 , &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

Based on this, we define the $\mathsf {G}$-extended core of $v$ as follows.

Definition 2

Let $v$ be a game. Its $\mathsf {G}$-extended core is the set defined by

$$\begin{aligned} \mathsf {GEC}(v):=\{x^z\in {\mathbb R}^{2^N\setminus \emptyset } \mid z\in \mathsf {EC}(v)\}, \end{aligned}$$

or equivalently

$$\begin{aligned} \mathsf {GEC}(v) = \{x\in \mathbb {R}^{2^N\setminus \emptyset }\mid (x_i)_{i\in N}\in \mathsf {C}(v^{\bar{t}(v)}), \quad x_N=-\bar{t}(v), \quad x_S=0 \text { otherwise}\}. \end{aligned}$$

Proposition 2

The following properties hold for $\mathsf {GEC}$.

• (i) $\mathsf {GEC}(v)$ is a nonempty convex and compact polyhedral set for all $v\in \mathcal {G}(N)$. It is equal to the core⁵ if the latter is nonempty.

• (ii) $\mathsf {GEC}$ satisfies (CR). Hence, $\mathsf {GEC}(v)\subseteq \mathsf {C}^n(v)$.

• (iii) $\mathsf {GEC}$ satisfies (IDEM), (COV), (SYM) and (MGD).

Proof

Most of the properties are clear by definition. We detail only (IDEM). As before, we use the shorthand $\mathsf {c}$ for $m^{-1}(\mathsf {C})$, as well as $\mathsf {gec}=m^{-1}\circ \mathsf {GEC}$. We suppose first that $v$ is balanced. Therefore, $\mathsf {gec}(v)=\mathsf {c}(v)$ and the property holds since $\mathsf {c}\circ \mathsf {c}=\mathsf {c}$.

Suppose then that $v$ is not balanced. Take any $\phi \in \mathsf {gec}(v)$ and let us prove that $\phi \in \mathsf {gec}(\phi )$. Since $\phi \ge v$ and $\phi (N)=v(N)$, we have $\bar{t}(\phi )\ge \bar{t}(v)$. We have $(\phi _i)_{i\in N}\in \mathsf {c}(\phi ^{\bar{t}(v)})$, since for all $S\ne N, \sum _{i\in S}\phi _i\ge \phi (S)$, and $\sum _{i\in N}\phi _i=v(N)+\bar{t}(v)= \phi (N)+\bar{t}(v)$. This proves that $\bar{t}(\phi )=\bar{t}(v)$, and consequently $\phi \in \mathsf {gec}(\phi )$. In conclusion, $\mathsf {gec}(v)\subseteq \mathsf {gec}\circ \mathsf {gec}(v)$.

Conversely, let $\phi \in \mathsf {gec}\circ \mathsf {gec}(v)$. Then there exists $\psi \in \mathsf {gec}(v)$ such that $\phi \in \mathsf {gec}(\psi )$. Reasoning as above, we find that $\bar{t}(\psi )=\bar{t}(v)$. Then for any $S\ne N$ we have $\sum _{i\in S}\phi _i\ge \psi (S)\ge v(S)$, and $\sum _{i\in N}\phi _i=\psi (N)+\bar{t}(v) = v(N)+\bar{t}(v)$. Lastly, $m^\phi (N)=-\bar{t}(v)$, which proves that $\phi \in \mathsf {gec}(v)$.$\square$

We observe that although the global amount of debt is minimal, it is concentrated only on the grand coalition and therefore does not necessarily optimally express how far it is possible to tax each coalition. By contrast, in the $k$-additive core, the smallest coalitions are in charge of distributing the debt.

3 The minimum negotiation set

The principle of the $k$-additive core is: if a payment $x_S$ is given to coalitions $S$ up to size $k$, that is, if each player accepts to pool a part of his gain with the other players, it is possible to preserve coalitional rationality. However, we can note two important problems of the $k$-additive core: First, for $k\ge 2$, the $k$-additive core is unbounded, secondly, there could be a conflict between the agents of a coalition $S$ on how the payment $x_S$ made by the $k$-additive core will be allocated to each player. Two situations can occur: either the payment is positive (a benefit has to be shared), or it is negative (a debt has to be shared). Sharing implies that each player in the coalition receives a nonnegative amount in case of benefit, and has to pay a nonnegative amount in case of debt.⁶ The more there are coalitions $S$ with high amounts $|x_S|$, the more the solution $x$ involves negotiation among the agents in $N$. The idea of the minimum negotiation set is to select those solutions in the $k$-additive core which involve the “fewest” negotation. Here, “fewest” is defined through a norm of the vector of payments made to coalitions of size at least 2. Taking the family of $L_p$ norms, we may consider the three usual cases: the $L_1$ norm (the negotiation level is the sum of absolute values of the payments), the $L_2$ norm (sum of squares of payments: high payments are over-weighted), and the $L_\infty$ norm (the maximal payment is the negotiation level).

Another view of the minimal negotiation set is that it is the set of solutions minimizing the distance (defined through the norm) to the set of preimputations. Hence the negotiation level of a payoff of the $k$-additive core can be seen as a kind of measure of its deviation from additivity.

3.1 The set $\mathsf {I}^k(v)$ of minimal negotiation

Let $2\le k\le n$ be fixed and $\Vert \cdot \Vert$ be a symetric norm on $\mathbb {R}^{2^n}$.

We consider the following nonlinear program:

$$\begin{aligned} \text {Minimize }&B_{\Vert \cdot \Vert }(x):=\Vert (x_S)_{\begin{array}{c} S\subseteq N\\ |S|\ge 2 \end{array}}\Vert \\ \text {subject to }&x \in \mathsf {C}^k(v). \end{aligned}$$

We call $B_{\Vert \cdot \Vert }(x)$ the negotiation level of $x$. For a game $v\in \mathcal {G}(N)$ and $\epsilon \ge 0$, we define the set $\mathsf {C}_{\epsilon }^k(v)$ by

$$\begin{aligned} \mathsf {C}_{\epsilon }^k(v):=\{x \in \mathsf {C}^k(v), \, B_{\Vert \cdot \Vert }(x) \le \epsilon \} \end{aligned}$$

and the set $\mathsf {I}^k(v)$ by

$$\begin{aligned} \mathsf {I}^k(v):=\bigcap _{\begin{array}{c} \epsilon \ge 0 \\ \mathsf {C}^k_{\epsilon }(v) \ne \emptyset \end{array}}\mathsf {C}^k_{\epsilon }(v). \end{aligned}$$

$\mathsf {I}^k(v)$ is nonempty for all games in $\mathcal {G}(N)$ because $\mathsf {C}^k(v)\ne \emptyset$ implies that there exists $\epsilon _0$ such that $\mathsf {C}^k_{\epsilon _0}(v)\ne \emptyset$. Moreover, $\mathsf {I}^k(v)$ is the set of optimal solutions of the above nonlinear program.

Theorem 3

Let $v\in \mathcal {G}(N), 2\le k\le n$, and $\epsilon \ge 0$. The following statements hold:

• (i) $\forall \epsilon \ge 0, \, \mathsf {C}^k_{\epsilon }(v)$ is a convex and compact set which is equal⁷ to $\mathsf {C}(v)$ if $\epsilon = 0$.

• (ii) $\mathsf {I}^k(v)$ is a nonempty convex and compact set, equal to $\mathsf {C}(v)$ if $\mathsf {C}(v)\ne \emptyset$, otherwise $\exists \epsilon ^* > 0$ such that $\mathsf {I}^k(v)=\mathsf {C}^k_{\epsilon ^*}(v)$.

Proof

• (i) It is obvious that $\mathsf {C}^k_{0}(v)=\mathsf {C}(v)$. Also, $\mathsf {C}^k_{\epsilon }(v)$ is closed $\forall \epsilon \ge 0$, and if $0 \le \epsilon _1 \le \epsilon _2$, then $\mathsf {C}^k_{\epsilon _1}(v)\subseteq \mathsf {C}^k_{\epsilon _2}(v)$. Let us prove convexity. If $a$ and $b$ are in $\mathsf {C}^k_{\epsilon }(v)$ then $\forall t \in [0,1]$, the payoff vector $t a+(1-t) b$ is in $\mathsf {C}^k(v)$ because $\mathsf {C}^k(v)$ is convex. Furthermore, by convexity of $x \mapsto \Vert x\Vert$,

  $$\begin{aligned} \Vert (ta_S+(1-t)b_S)_{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}\Vert \le t \underbrace{\Vert (a_S)_{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}\Vert }_{\le \epsilon } + (1-t)\underbrace{\Vert (b_S)_{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}\Vert }_{\le \epsilon }, \end{aligned}$$

  from which we deduce that $\mathsf {C}^k_{\epsilon }(v)$ is convex. It remains to prove compactness. Suppose $a\in \mathsf {C}^k_{\epsilon }(v)$. By definition,

  $$\begin{aligned} \Vert (a_S)_{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}\Vert \le \epsilon , \end{aligned}$$

  which implies that each component $a_S, |S|\ge 2$, is bounded, and so is $\sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}a_S$. Now we have:

  $$\begin{aligned} v(N)=\sum _{i\in N}a_i+\sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}a_S , \end{aligned}$$

  which implies that $\sum _{i\in N}a_i$ is bounded. Since $a\in \mathsf {C}^k(v)$, we have $a_i \ge v(i)$ for all $i\in N$. Hence, each $a_i$ is bounded. It follows that each coordinate $a_S$ is bounded, therefore $\mathsf {C}^k_{\epsilon }(v)$ is compact.

• (ii) $\mathsf {I}^k(v)$ is an intersection of compact, convex and nonempty nested sets, therefore $\mathsf {I}^k(v)$ is a compact, convex and nonempty set. It is easy to see that if $\mathsf {C}(v)$ is nonempty then $\mathsf {I}^k(v)=\mathsf {C}(v)$. Let us define

  $$\begin{aligned} \epsilon ^{*}=\sup \{\epsilon \ge 0 \text { such that } \mathsf {C}^k_{\epsilon }(v)=\emptyset \} \end{aligned}$$

  with the convention $\sup (\emptyset )=0$. It is easily verified that $\mathsf {C}^k_{\epsilon ^{*}}(v)\subseteq \mathsf {I}^k(v)$ and, $\forall n\in \mathbb {N}$, the set $\mathsf {I}^k(v)$ satisfies $\mathsf {I}^k(v)\subseteq \mathsf {C}^k_{\epsilon ^{*}+\frac{1}{n}}(v)$. Therefore

  $$\begin{aligned} \mathsf {I}^k(v)\subseteq \bigcap _{n\in \mathbb {N}^{*}}\mathsf {C}^k_{\epsilon ^{*}+\frac{1}{n}}(v)=\mathsf {C}^k_{\epsilon ^{*}}(v). \end{aligned}$$

  Hence $\exists \epsilon ^* \ge 0$ such that $\mathsf {I}^k(v)=\mathsf {C}^k_{\epsilon ^{*}}(v)$ and $\forall x \in \mathsf {I}^k(v)$, we have $B_{\Vert \cdot \Vert }(x)=\epsilon ^*$.

The next proposition gathers properties of elements of $\mathsf {I}^k(v)$.$\square$

Proposition 3

Let $2\le k\le n$ be fixed, $\Vert \cdot \Vert$ be a given norm which is strictly increasing in each coordinate,⁸ and $v\in \mathcal {G}(N)$. For any element $x\in \mathsf {I}^k(v)$, it holds:

• (i) $x_S\le 0, \forall S\subseteq N \text { such that } |S|\ge 2$.

• (ii) The corresponding $k$-additive game $\phi =m^{-1}(x)$ is concave.

• (iii) The vector $(x_i)_{i\in N}$ belongs to $\mathsf {C}(v^{B_{\Vert \cdot \Vert _1}(x)})$, where $\Vert \cdot \Vert _1$ is the $L_1$ norm.

• (iv) $\displaystyle \Big |\sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}x_S\Big | \ge \bar{t}(v)$.

Proof

• (i) Let $x \in \mathsf {I}^k(v)$. Suppose that $x_S>0$ for some $S$ with $|S|\ge 2$, then the general payoff vector $x^{eq}$ defined by :

  $$\begin{aligned} \left\{ \begin{array}{lll} x^{eq}_i&{}=x_i + \frac{1}{|S|} x_S, &{} \quad \forall i \in S\\ x^{eq}_S&{}=0 &{} \\ x^{eq}_T&{}=x_T &{} \quad \text { otherwise,} \end{array}\right. \end{aligned}$$

  belongs to $\mathsf {C}^k(v)$, satisfies $x^{eq}_S=0$ and $B_{\Vert \cdot \Vert }(x^{eq})<B_{\Vert \cdot \Vert }(x)$ since $\Vert \cdot \Vert$ is strictly increasing, which contradicts $x\in \mathsf {I}^k(v)$.

• (ii) It is known Chateauneuf and Jaffray (1989) that concavity of $\phi$ is equivalent to $\sum _{S|A\subseteq S\subseteq B}m^\phi (S)\le 0$ for every $A,B$ such that $|A|=2$ and $B\supseteq A$, which holds by (i) since $m^\phi (S)=x_S$.

• (iii) Let $x \in \mathsf {I}^k(v)$. By (i), $x_S\le 0$ for all $S$ such that $|S|\ge 2$. Then, $\sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}x_S=-B_{\Vert \cdot \Vert _1}(x)$ and the vector $(x_i)_{i\in N}$ satisfies

  $$\begin{aligned} \sum _{i\in S}x_i \ge&\sum _{i\in S}x_i+\underbrace{\sum _{\begin{array}{c} T\subseteq S \\ |T|\ge 2 \end{array}}x_T}_{\le 0} \ge v(S)=v^{B_{\Vert \cdot \Vert _1}(x)}(S),\quad S\ne N, |S|\ge 2 \\ \sum _{i\in N}x_i =&v(N)-\underbrace{\sum _{\begin{array}{c} T\subseteq N \\ |T|\ge 2 \end{array}}x_T}_{=-B_{\Vert \cdot \Vert _1}(x)} =v^{B_{\Vert \cdot \Vert _1}(x)}(N). \end{aligned}$$

• (iv) By (iii), $\mathsf {C}(v^{B_{\Vert \cdot \Vert _1}(x)})$ is nonempty. Hence by definition of $\bar{t}(v)$, we have $\bar{t}(v)\le B_{\Vert \cdot \Vert _1}(x)$. By (i), $B_{\Vert \cdot \Vert _1}(x) = \Big |\sum \limits _{\begin{array}{c} S\subseteq N\\ |S|\ge 2 \end{array}}x_S\Big |$, hence the result. $\square$

We comment on these results. (i) shows that only negative or zero payments are given to coalitions. Hence, if the game is non-balanced, the debts implied by the satisfaction of coalitional rationality are to be paid by groups, not individuals, and (iii) shows the exact nature of the payment given to individuals. (iv) shows that the total amount of debts may exceed the minimal amount $\bar{t}(v)$, hence axiom (MGD) may be not satisfied. We will prove later that for the $L_1$ norm, (MGD) is always satisfied.

3.2 The minimum negotiation set as a general solution

$\mathsf {I}^k(v)$ being a subset of the $k$-additive core $\mathsf {C}^k(v)$, it is a general solution, preserving the desirable properties of the $k$-additive core without having its drawbacks. Indeed, it preserves coalitional rationality, it is never empty and coincides with the core when the latter is nonempty as shown in Theorem 3, and unlike the $k$-additive core, it is bounded, and can even be reduced to a singleton when the $L_p$ norm with $p>1$ is used, as it will be shown in Sect. 3.5.

In this section and the subsequent ones, we will investigate the properties of this general solution. The next proposition shows that the minimum negotiation set satisfies all properties of general solutions satisfied by the $k$-additive core.

Proposition 4

$\mathsf {I}^k$ satisfies (CR), (COV), (SYM) and (IDEM) for any norm.

Proof

(CR): Clear.

(COV): $\mathsf {I}^k$ satisfies (COV) if and only if $\forall v \in \mathcal {G}(N), \forall \alpha > 0, \forall \beta \in \mathbb {R}^{2^n-1}$ we have:

$$\begin{aligned} \mathsf {I}^k(\alpha v + \beta )=\alpha \mathsf {I}^k(v)+ \beta . \end{aligned}$$

Since $\mathsf {C}^k(v)$ satisfies (COV),

$$\begin{aligned} \text {Minimize }&B_{\Vert \cdot \Vert }(x):=\Vert (x_S)_{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}\Vert \\ \text {subject to }&x \in \mathsf {C}^k(\alpha v+\beta ) \end{aligned}$$

is equivalent to

$$\begin{aligned} \text {Minimize }&B_{\Vert \cdot \Vert }(x):=\Vert (x_S)_{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}\Vert \\ \text {subject to }&x \in \alpha \mathsf {C}^k(v)+\beta . \end{aligned}$$

(SYM): Similarly, since $\mathsf {C}^k(v)$ satisfies (SYM), we have that for all permutations $\pi$ such that $v(\pi (S))=v(S)$ for all $S\subseteq N$,

$$\begin{aligned} \text {Minimize }&B_{\Vert \cdot \Vert }(x):=\Vert (x_S)_{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}\Vert \\ \text {subject to }&x \in \mathsf {C}^k(v) \end{aligned}$$

is equivalent to

$$\begin{aligned} \text {Minimize }&B_{\Vert \cdot \Vert }(x):=\Vert (x_S)_{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}\Vert \\ \text {subject to }&x \in \mathsf {C}^k(v\circ \pi ). \end{aligned}$$

(IDEM): Here also we use the shorthand $\mathsf {c}=m^{-1}(\mathsf {C})$, and $\mathsf {i}=m^{-1}(\mathsf {i})$. We have to show that $\mathsf {i}^k\circ \mathsf {i}^k=\mathsf {i}^k$. First, if $\mathsf {i}^k(v)=\mathsf {c}(v)$, then for each $x\in \mathsf {c}(v)$, considering $x$ as an additive game, we have $\mathsf {i}^k(x)=\{x\}$. Therefore $\mathsf {i}^k(\mathsf {c}(v))=\mathsf {c}(v).$

Now, suppose $\mathsf {c}(v)=\emptyset$ and take any $\phi \in \mathsf {i}^k(v)$. Since $\phi \in \mathsf {c}^k(v)$, it follows that $\mathsf {c}^k(\phi )\subseteq \mathsf {c}^k(v)$. Therefore, since $\phi$ minimizes the negotiation level over $\mathsf {c}^k(v), \phi$ minimizes the negotiation level over $\mathsf {c}^k(\phi )$, which implies $\phi \in \mathsf {i}^k(\phi )$ and

$$\begin{aligned} \mathsf {i}^k(v)\subseteq \mathsf {i}^k(\mathsf {i}^k(v)). \end{aligned}$$

Let $\phi \in \mathsf {i}^k(\mathsf {i}^k(v))$. Then there exists $\psi \in \mathsf {i}^k(v)$ such that $\phi \in \mathsf {i}^k(\psi )$. Observe that $\psi \in \mathsf {c}^k(\psi )\subseteq \mathsf {c}^k(v)$. Since $\psi$ minimizes the negotiation level over $\mathsf {c}^k(v)$ and $\phi$ minimizes the negotiation level over $\mathsf {c}^k(\psi )$, it follows that these negotiation levels are equal. Moreover, $\phi$ is a $k$-additive game which satisfies $\phi (S)\ge v(S)$ for all $S\subset N$ and $\phi (N)=v(N)$. Therefore $\phi \in \mathsf {i}^k(v)$ and

$$\begin{aligned} \mathsf {i}^k(\mathsf {i}^k(v))\subseteq \mathsf {i}^k(v). \end{aligned}$$

$\square$

3.3 Properties of $\mathsf {I}_1^n$

In this section, $\Vert \cdot \Vert$ is the $L_1$ norm. We denote by $\mathsf {I}_1^k$ the solution $\mathsf {I}^k$ for the $L_1$ norm.

By Proposition 4, we know that $\mathsf {I}_1^k$ satisfies (CR), (COV), (SYM) and (IDEM). In addition, we show that $\mathsf {I}_1^n$ satisfies (DPP) and (MGD).

Proposition 5

$\mathsf {I}_1^n$ satisfies (DPP) and (MGD).

Proof

(i) We prove (MGD) first. Let $v$ be a game in $\mathcal {G}(N)$, and $x\in \mathsf {C}(v^{\bar{t}(v)})$. It is clear that the general payoff vector $y$ defined by

$$\begin{aligned} \left\{ \begin{array}{lll} y_i&{}=x_i, &{} \forall i \in N\\ y_S&{}=0, &{} \forall S \subseteq N, S\ne N \text { and } |S|\ge 2 \\ y_N&{}= -\bar{t}(v) &{} \end{array} \right. \end{aligned}$$

belongs to $\mathsf {C}^n(v)$. We have

$$\begin{aligned} B_{\Vert \cdot \Vert _1}=\sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}|y_S| = \bar{t}(v). \end{aligned}$$

Therefore $\forall z \in \mathsf {I}_1^n(v)$, we have

$$\begin{aligned} \sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}|z_S|= B_{\Vert \cdot \Vert _1} \le B_{\Vert \cdot \Vert _1} = \bar{t}(v). \end{aligned}$$

By Proposition 3 (i),

$$\begin{aligned} \sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}|z_S|= |\sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}z_S| \end{aligned}$$

and by Proposition 3 (iv),

$$\begin{aligned} \Big |\sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}z_S\Big | \ge \bar{t}(v). \end{aligned}$$

Therefore, $\mathsf {I}_1^n$ satisfies (MGD).

(ii) We prove now (DPP). By (MGD) and Proposition 3 (i) the negotiation level is equal to $\bar{t}(v)$, and by Proposition 3 (iii), we deduce that for all $y\in \mathsf {I}_1^n(v)$, we have $(y_i)_{i\in N}\in \mathsf {C}(v^{\bar{t}(v)})$.

Suppose $i$ is dummy for $v$ and take $x\in \mathsf {C}(v^{\bar{t}(v)})$. Then the vector $x^* \in {\mathbb R}^n$ defined by: $x^*_i=v(i)$ and $x^*_j=x_j$ for $j\in N\setminus i$ satisfies:

$$\begin{aligned}&x^{*}(N)\le x(N)\\&x^*(S) = x(S) \ge v(S), \quad \text {if } i\notin S\\&x^*(S) = x(S\setminus i)+v(i)\ge v(S\setminus i)+v(i)=v(S),\quad \text {if } i\in S. \end{aligned}$$

Therefore $x^*(N)=x(N)$, which entails $x_i=x^*_i=v(i)$, proving that $\mathsf {I}_1^n$ satisfies (DPP).$\square$

The next theorem is a characterization of $\mathsf {I}_1^n$.

Theorem 4

Let $MGDCR$ be the set of general solutions satisfying (MGD) and (CR). Then $\mathsf {I}_1^n=\top (MGDCR)$.

In words, $\mathsf {I}_1^n$ is the largest general solution satisfying coalitional rationality and minimizing the amount of the global debt.

Proof

We already know that $\mathsf {I}_1^n$ satisfies (CR), and by Proposition 5, we know that $\mathsf {I}_1^n$ satisfies (MGD).

Conversely, let $\sigma$ be a general solution which satisfies (CR) and (MGD). Let $x\in \sigma (v)$. Since $\sigma$ satisfies (CR), $x\in \mathsf {C}^n(v)$ because $\displaystyle {\mathsf {C}^n(v)=\top (CR)}$. Moreover, since $\sigma$ satisfies (MGD), the negotiation level of $x$ is equal to the negotiation level of each element of $\mathsf {I}_1^n(v)$. Therefore $x$ minimizes the negotiation level over $\mathsf {C}^n(v)$.

We conclude that $x\in \mathsf {I}_1^n(v)$ and $\forall v\in \mathcal {G}(N), \sigma (v)\subseteq \mathsf {I}_1^n(v)$.$\square$

Remark 1

We have seen that $\mathsf {GEC}$ satisfies (MGD) and (CR). Therefore we have the following inclusions:

$$\begin{aligned} \mathsf {C}(v)\subseteq \mathsf {GEC}(v) \subseteq \mathsf {I}_1^n(v) \subseteq \mathsf {C}^n(v), \end{aligned}$$

for all games $v$. It follows that $\mathsf {GEC}$ inherits the properties of $\mathsf {I}_1^n$.

From the above results, we notice the following important fact.

Corollary 1

Let $v\in \mathcal {G}(N)$. We have:

$$\begin{aligned} \{(x_i)_{i\in N} \mid x \in \mathsf {I}_1^n(v)\}=\mathsf {C}(v^{\bar{t}(v)})=\{(x_i)_{i\in N}\mid x\in \mathsf {GEC}(v)\}. \end{aligned}$$

Proof

We prove the first equality. From the proof of Proposition 5, we see that for all $x\in \mathsf {I}_1^n(v)$, it holds $(x_i)_{i\in N}\in \mathsf {C}(v^{\bar{t}(v)})$. The reverse inclusion holds by Remark 1.

Now, the second equality holds by definition of $\mathsf {GEC}$.$\square$

These two last results elucidate the nature of $\mathsf {I}_1^n(v)$ and its relation to previously introduced notions like the extended core. In a sense, we may say that elements of $\mathsf {GEC}(v)$ and $\mathsf {I}_1^n(v)$ implement or realize elements of $\mathsf {C}(v^{\bar{t}(v)})$, which are not solutions of the game $v$. Indeed, by $\mathsf {GEC}(v)$, an element $x$ of $\mathsf {C}(v^{\bar{t}(v)})$ becomes realizable by putting a debt $\bar{t}(v)$ on the grand coalition $N$. Now, $\mathsf {I}_1^n(v)$, by allowing to putting debts on any coalition of size at least 2, gives the possibility of a negociation in any coalition.

Proposition 6

$\mathsf {I}_1^n$ is an upper hemicontinuous correspondence.

Proof

We set $\mathsf {i}_1^n=m^{-1}\circ \mathsf {I}_1^n$ and prove upper hemicontinuity of $\mathsf {i}_1^n$. It is sufficient to prove that $\mathsf {i}_1^n$ is a closed and bounded correspondence (see, e.g., (Peleg and Sudhölter (2003), Ch. 9)).

$$\begin{aligned} Gr(\mathsf {i}_1^n)&= \{(v,\phi )\in \mathcal {G}(N)^2, \, \phi (N)=v(N), \phi (S)\ge v(S), \, \forall S \subseteq N, \\&m^\phi _S\le 0 \, \forall S \subseteq N, \, |S|\ge 2, \text {and } \sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}m^{\phi }(S)=-\bar{t}(v)\} \end{aligned}$$

is a closed subset of $\mathcal {G}(N)^2$. Let $B$ be a compact subset of $\mathcal {G}(N)$. We define $w_1$ and $w_2$ two games such that

$$\begin{aligned} w_1(S)=\inf _{v\in B}v(S) \text { and } w_2(S)=\sup _{v\in B}v(S). \end{aligned}$$

Let $\phi \in \mathsf {i}_1^n(B)=\cup _{v\in B}\mathsf {i}_1^n(v)$. Obviously, for all $S\subseteq N$, we have

$$\begin{aligned} w_1(S)\le \phi (S). \end{aligned}$$

We prove now that for all $S\subseteq N, \phi (S)\le n \max _{S\subseteq N}w_2(S)$. Let $\psi$ be an additive game defined by

$$\begin{aligned} \psi (i)=\max _{S\subseteq N}w_2(S) \qquad \forall i\in N. \end{aligned}$$

Clearly, $\forall v\in B, v(S)\le \sum _{i\in S}\psi (i)$, hence, $\forall v\in B$,

$$\begin{aligned} v(N)+\bar{t}(v)\le \sum _{i\in N}\psi (i)\le n \max _{S\subseteq N}w_2(S). \end{aligned}$$

Suppose there exists $S\subseteq N$ such that $n \max _{S\subseteq N}w_2(S)<\phi (S)$. Then there exists $v\in B$ such that

$$\begin{aligned} n \max _{S\subseteq N}w_2(S)<\phi (S)\le \sum _{i\in N}\phi (i)=v(N)+\bar{t}(v)\le n \max _{S\subseteq N}w_2(S), \end{aligned}$$

a contradiction.$\square$

3.4 Autonomous coalitions

We introduce now the concept of autonomous coalition. Consider a game $v$ and the core $\mathsf {C}(v^{\bar{t}(v)})$ of its t-expansion. Suppose it exists a coalition $T\ne N$ such that, for any payoff $x\in \mathsf {C}(v^{\bar{t}(v)}), x(T)=v(T)$. It means that the coalition can never receive more than its worth $v(T)$. Moreover, if the game is not balanced, the debt $\bar{t}(v)>0$ has to be paid anyway by the players, so that it is likely that the members of $T$ will eventually receive in total strictly less than $v(T)$. Such a game is unstable, because $S$ has nothing to gain from cooperation (and in case $v$ is not balanced, $S$ may even have incentive to leave), and therefore can remain independent of the grand coalition. In this sense, we say that $S$ is autonomous.

In what follows, first we show that there always exists an autonomous coalition when the game is not balanced, and second, we show how to characterize them, and how it is possible to find them in a very easy way by $\mathsf {I}_1^n(v)$. We think that it is an important issue to detect autonomous coalitions since they are the source of instability of the game.

Definition 3

We say that a coalition $T\subset N$ is autonomous if for any payoff vector $x$ of $\mathsf {C}(v^{\bar{t}(v)})$, it holds $x(T) = v(T)$.

For any coalition $T\subset N$, we denote by $v_T$ the restriction of $v$ to the coalition $T$. As an immediate consequence of the definition, we remark that $\mathsf {C}(v_{T})$ is nonempty whenever $T$ is autonomous. Indeed, any element $x$ of $\mathsf {C}(v^{\bar{t}(v)})$ is such that $(x_i)_{i\in T}\in \mathsf {C}(v_T)$.

Proposition 7

Any non-balanced game $v$ has an autonomous coalition $T\subset N$.

Proof

Suppose that $v$ is not balanced, and that $\forall T \subset N, \exists x\in \mathsf {C}(v^{\bar{t}(v)})$ such that $x(T)>v(T)$. Then, the convexity of $\mathsf {C}(v^{\bar{t}(v)})$ implies that there exists $x'$ such that $\forall T\subset N, x'(T)>v(T)$. Let $\displaystyle {T'\in \arg \min _{T\subseteq N}(x'(T)-v(T))}$. The vector $\tilde{x}$ defined by:

$$\begin{aligned} \tilde{x}_i= {\left\{ \begin{array}{ll} x'_i-\frac{x(T')-v(T')}{|T|}, &{} \text { if } i \in T' \\ x'_i, &{} \text { otherwise} \end{array}\right. } \end{aligned}$$

satisfies

$$\begin{aligned} \tilde{x}(S)\ge v(S), \, \forall S\subset N \end{aligned}$$

and

$$\begin{aligned} \tilde{x}(N) < x(N) = v(N)+\bar{t}(v). \end{aligned}$$

This is not possible by definition of $\bar{t}(v)$.$\square$

It is easy to find all autonomous coalitions. It suffices to compute the coordinates $(\bar{x}_i)_{i\in N}$ of the barycenter of $\mathsf {GEC}(v)$ (or equivalently of the barycenter of $\mathsf {I}_1^n(v)$). By Corollary 1, it is plain that $T\ne N$ is autonomous if and only if $\sum _{i\in T}\bar{x}_i=v(T)$.

The next theorem gives another way to detect the greatest autonomous coalitions.

Theorem 5

Let $v$ be a game on $N$, and $S$ be a coalition of $N$ such that $|S|\ge 2$. The following properties are equivalent:

• (i) There exists $T\supseteq S$ such that $T$ is autonomous.

• (ii) $\forall x \in \mathsf {I}_1^n(v), x_S=0$.

(see proof in the appendix)

The above result says that the greatest (in the sense of inclusion) autonomous coalitions correspond to coalitions $T$ such that $x_T=0$ for all $x\in \mathsf {I}_1^n(v)$, and any superset of $T$ does not satisfy this property. Combining this with the fact for all $x\in \mathsf {I}_1^n(v), x_S\le 0$ for all $S, |S|\ge 2$ (Proposition 3 (i)), the barycenter $\bar{x}$ of $\mathsf {I}_1^n(v)$ permits to detect autonomous coalitions as follows: $T$ is autonomous if $\bar{x}_T=0$ and $\bar{x}_{T\cup i}<0$ for all $i\in N\setminus T$.

3.5 Properties of $\mathsf {I}_p^k$ with $p\in ]1,+\infty [$

In this section, $\Vert \cdot \Vert$ is the $L_p$ norm, with $p>1$:

$$\begin{aligned} \Vert x\Vert _p = \Big (\sum _{i=1}^n |x_i|^p\Big )^{\frac{1}{p}}. \end{aligned}$$

We denote by $\mathsf {I}_p^k$ the general solution $\mathsf {I}^k$ for the norm $L_p$.

Theorem 6

Let $p> 1$. Then $\mathsf {I}_p^k(v)=\mathsf {C}(v)$ if $\mathsf {C}(v)\ne \emptyset$, otherwise $\mathsf {I}_p^k(v)$ reduces to the unique element of $\mathsf {C}^k(v)$ which minimizes the negotiation level.

Proof

Let $a$ and $b$ be two different payoff vectors in $\mathsf {I}_p^k(v)$. From Theorem 3 (ii), there exists $\epsilon ^* \ge 0$ such that $\mathsf {I}_p^k(v)=\mathsf {C}^k_{\epsilon ^{*}}(v)$, and, for $t \in ]0,1[$, the payoff vector $ta+(1-t)b$ belongs to $\mathsf {I}_p^k(v)$ by convexity, so in particular for $t=\frac{1}{2}$. If $\epsilon ^* = 0$ then $\mathsf {I}_p^k=\mathsf {C}(v)$, otherwise we have, by Proposition 3 (i) :

$$\begin{aligned} (B_{\Vert \cdot \Vert }(a))^p= \sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}(-a_S)^p&=(\epsilon ^*)^p\\ (B_{\Vert \cdot \Vert }(b))^p= \sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}(-b_S)^p&=(\epsilon ^*)^p\\ \Big (B_{\Vert \cdot \Vert }\Big (\frac{a+b}{2}\Big )\Big )^p=\sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}\Big (-\frac{1}{2} a_S-\frac{1}{2} b_S\Big )^p&=(\epsilon ^*)^p. \end{aligned}$$

Now, if $\epsilon ^*\ne 0$ and $a \ne b$, we have by strict convexity of $x\mapsto x^p$ on $[0,+\infty )$:

$$\begin{aligned} (\epsilon ^*)^p=\sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}\Big (-\frac{1}{2}a_S-\frac{1}{2}b_S\Big )^p < \frac{1}{2}\sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}(-a_S)^p+ \frac{1}{2} \sum _{\begin{array}{c} S\subseteq N \\ |S|\ge 2 \end{array}}(-b_S)^p=(\epsilon ^*)^p, \end{aligned}$$

a contradiction. Therefore $\epsilon ^*=0$ or $a=b$.

To conclude, if $\epsilon ^*=0$ then $\mathsf {I}_p^k(v)=\mathsf {C}(v)$, otherwise $a=b$ and $\mathsf {I}_p^k(v)=\{a\}$.$\square$

Unlike $\mathsf {I}_1^n$, the general solution $\mathsf {I}_p^k$ does not satisfy (MGD), as shown by the following example with $p=2$.

Example 4

We suppose that $k=2$, and consider a game $v$ on $N=\{1,2,3\}$ defined by:

$$\begin{aligned} \begin{array}{|l|ccccccr|} \hline S &{} 1 &{} 2 &{} 3 &{} 12 &{} 13 &{} 23 &{} 123 \\ \hline v(S) &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 1-\epsilon \\ \hline \end{array} \end{aligned}$$

Clearly, $\bar{t}(v)=\epsilon$ and $\mathsf {I}_2^2(v)$ reduces to a singleton. If (MGD) holds, the minimum negotiation level is $\epsilon$, hence by Proposition 3 (iii), $((\mathsf {I}_2^2(v))_i)_{i\in N}$ belongs to $\mathsf {C}(v^\epsilon )=\{(1,0,0)\}$. This implies in turn

$$\begin{aligned} \left\{ \begin{array}{lll} 1+(\mathsf {I}_2^2(v))_{12} \ge 1 &{} \Rightarrow &{} (\mathsf {I}_2^2(v))_{12}\ge 0 \\ 1+(\mathsf {I}_2^2(v))_{13} \ge 1 &{} \Rightarrow &{} (\mathsf {I}_2^2(v))_{13}\ge 0 \\ (\mathsf {I}_2^2(v))_{23} \ge 0. &{} &{} \end{array}\right. \end{aligned}$$

This is impossible because by Proposition 3 (i), $(\mathsf {I}_2^2(v))_{ij}\le 0$ for all $\{i,j\}\subseteq N$, and by MGD, $(\mathsf {I}_2^2(v))_{12}+(\mathsf {I}_2^2(v))_{13}+(\mathsf {I}_2^2(v))_{23}=-\epsilon$.

4 Computation of the minimum negotiation set

In general the minimum negotiation set $\mathsf {I}^k(v)$ is difficult to compute because it is a general nonlinear optimization problem. However, in the case of the $L_1$ norm, the optimization problem reduces to a linear program. We have also some partial result for the case of the $L_2$ norm.

4.1 Computation of $\mathsf {I}_1^k$

Proposition 8

The set $\mathsf {I}_1^k(v)$ is the solution of the linear program:

$$\begin{aligned} maximize \sum _{\begin{array}{c} S\subseteq N\\ 2\le |S|\le k \end{array}}x_S \end{aligned}$$

under the conditions:

$$\begin{aligned} \begin{array}{llclrr} (i) &{} \displaystyle {\sum _{S\subseteq N}x_S} &{} = &{} v(N) &{} &{} \\ (ii) &{} \displaystyle {\sum _{S\subseteq T}x_S} &{} \ge &{} v(T) &{} \quad \forall T\subseteq N &{}\\ (iii) &{} x_S &{} \le &{} 0 &{} \quad \forall S\subseteq N &{}\text { such that } |S|\ge 2. \\ (iv) &{} x_S &{} = &{} 0 &{} \quad \forall S\subseteq N &{}\text { such that } |S|> k. \end{array} \end{aligned}$$

Proof

Each $x\in \mathsf {I}_1^k(v)\subseteq \mathsf {C}^k(v)$ is such that $x$ satisfies $(i), (ii)$, and $(iv)$. Furthermore Proposition 3 (i) implies that $x_S\le 0$ $\forall S\subseteq N, |S|\ge 2$, which is $(iii)$. Lastly, minimizing ${\sum _{\begin{array}{c} S\subseteq N\\ 2\le |S|\le k \end{array}}|y_S|}$ for $y \in \mathsf {C}^k(v)$ is equivalent to maximize ${\sum _{\begin{array}{c} S\subseteq N\\ 2\le |S|\le k \end{array}}y_S}$ under the conditions $y \in \mathsf {C}^k(v)$ and $y_S\le 0, \quad \forall |S|\ge 2$.

Example 5

We consider a game $v$ on $N=\{1,2,3\}$ defined by:

$$\begin{aligned} \begin{array}{|l|ccccccr|} \hline S &{} 1 &{} 2 &{} 3 &{} 12 &{} 13 &{} 23 &{} 123 \\ \hline v(S) &{} 20 &{} 40 &{} 30 &{} 40 &{} 40 &{} 40 &{} 50 \\ \hline \end{array} \end{aligned}$$

We have $\mathsf {C}(v)=\emptyset$, and $\forall t \in [0,1]$, the payoff vector $x$ defined by:

$$\begin{aligned} \begin{array}{|l|ccccccr|} \hline S &{} 1 &{} 2 &{} 3 &{} 12 &{} 13 &{} 23 &{} 123 \\ \hline x_S &{} 20 &{} 40 &{} 30 &{} -20t &{} -10t &{} -10t &{} -40(1-t) \\ \hline \end{array} \end{aligned}$$

belongs to $\mathsf {I}_1^n(v)$, and we observe that the optimal value of the objective function is $-\bar{t}(v)=-40$.

4.2 Computation of $\mathsf {I}_2^k$

Giving an exact expression of $\mathsf {I}_2^k$ in the general case is quite difficult because it is necessary to solve a quadratic program. However, we can obtain an exact expression of $\mathsf {I}_2^2$ in the case of a symmetric⁹ and subadditive game.

Proposition 9

If $v$ is a nonnegative, symmetric and subadditive game on $N$ then:

$$\begin{aligned} (\mathsf {I}_2^2(v))_i&=\max _{k\in \{1,\ldots ,n-1\}}\left\{ \frac{n-1}{k(n-k)}v_k-\frac{k-1}{n(n-k)}v_n \right\} , \, \forall i \in N\\ (\mathsf {I}_2^2(v))_{ij}&=\frac{2}{n(n-1)}\left( v(N)-n(\mathsf {I}_2(v))_1\right) , \, \forall i,j \in N \end{aligned}$$

where $v_k:=v(K), |K|=k$.

Proof

Subadditivity of $v$ implies $\mathsf {C}(v)=\emptyset$ or reduced to a singleton. Therefore $\mathsf {I}_2^2(v)$ is a singleton.

Now, symmetry of $v$ implies by definition of $\mathsf {I}_2^2$ that $\forall i \in N, (\mathsf {I}_2^2(v))_{i}=(\mathsf {I}_2^2(v))_{1}$ and $\forall i,j \in N, (\mathsf {I}_2^2(v))_{ij}=(\mathsf {I}_2^2(v))_{12}$.

Denote by $\alpha$ the value of $(\mathsf {I}_2^2(v))_{1}$ and by $\beta$ the value of $(\mathsf {I}_2^2(v))_{12}$. $\mathsf {I}_2^2(v)\subseteq \mathsf {C}^2(v)$ therefore, $\forall k \in \{1,\ldots ,n-1\}$,

$$\begin{aligned} \frac{k(k-1)}{2}\beta + k\alpha \ge v_k \end{aligned}$$

and

$$\begin{aligned} \frac{n(n-1)}{2}\beta + n\alpha = v_n. \end{aligned}$$

These two expressions are equivalent to:

$$\begin{aligned} \beta =2\left( \frac{v_n-n\alpha }{n(n-1)}\right) \, (*) \end{aligned}$$

and $\forall k\ne n$ and $n\ne 1$

$$\begin{aligned} \alpha \ge \frac{n-1}{k(n-k)}v_k-\frac{k-1}{n(n-k)}v_n \, (**) \end{aligned}$$

Furthermore, $v$ is symmetric, therefore, the minimization of $B_{\Vert \cdot \Vert }(x)$ under the condition $x \in \mathsf {C}^2(v)$ is equivalent to the minimization of $(\beta )^2$ under the conditions $(*)$ and $(**)$, i.e., the maximization of $\beta$ since $\beta \le 0$ by Proposition 3 (i). This amounts to the maximization of $v_n-n\alpha$, hence the minization of $\alpha$. The minimum is reached for $\alpha =\max _{k\in \{1,\ldots ,n-1\}}\left\{ \frac{n-1}{k(n-k)}v_k-\frac{k-1}{n(n-k)}v_n \right\}$ and $\beta =2\left( \frac{v_n+n(n-2)\alpha }{n(n-1)}\right) .$

$\square$

Example 6

We consider a symmetric subadditive game $v$ on $N=\{1,2,3\}$ defined by:

$$\begin{aligned} \begin{array}{|l|ccccccr|} \hline S &{} 1 &{} 2 &{} 3 &{} 12 &{} 13 &{} 23 &{} 123 \\ \hline v(S) &{} 1 &{} 1 &{} 1 &{} 1.5 &{} 1.5 &{} 1.5 &{} 2 \\ \hline \end{array} \end{aligned}$$

We have $\mathsf {C}(v)=\emptyset$. Using the above result, we get:

5 From general payoff vectors to classical payoff vectors

As explained in the introduction, the ultimate step when using a general solution is to transform selected general payoff vectors into classical payoff vectors, i.e., sharing among individual players.

A first way to deal with this problem is to consider the selectope Derks et al. (2000) of the game corresponding to a general payoff vector. Let us first recall some material on the selectope. We consider the set of sharing functions given by:

$$\begin{aligned} \mathcal {Q}(N)&:= \{q:2^N\setminus \{\emptyset \}\times N\rightarrow [0,1]\mid q(S,i)\\&= 0 \text { if } i \notin S, \sum _{i\in S}q(S,i)=1,\forall S\subseteq N,S\ne \emptyset \}. \end{aligned}$$

For each subset $S$ and each player $i$ in $S$, the sharing function specifies the proportion of a good (assigned to $S$) which should be given to $i$, noting that nothing is given to players outside $S$. Each sharing function $q$ induces a sharing value $x^q$ defined by:

$$\begin{aligned} x^q:\mathcal {G}(N)\rightarrow \mathbb {R}^n \text { such that } x_i^q(v):=\sum _{S\ni i}q(S,i)m^v(S), \text { } i\in N. \end{aligned}$$

Thus, the sharing value shares among players the dividends (Möbius transform) $m^v(S), S\subseteq N$, according to the sharing rule $q$. The selectope Derks et al. (2000) of a game $v\in \mathcal {G}(N)$, denoted by $\mathsf {S}(v)$, is defined as the set of all preimputations which can be obtained by sharing functions applied on $m^v$:

$$\begin{aligned} \mathsf {S}(v):= \{x^q(v), q\in \mathcal {Q}(N)\}. \end{aligned}$$

Let us come back to our concern and consider a game $v$ and a general payoff vector $x$ belonging for example to the $k$-additive core $\mathsf {C}^k(v)$ or any other general solution of $v$. The simplest way to transform $x$ into a classical payoff vector is to share each component $x_S$ for $|S|>1$ among the members of $S$ using some sharing rule $q\in \mathcal {Q}(N)$. In other words, recalling that general payoff vectors can be seen as games through the Möbius transform, the set of all possible (classical) payoff vectors which can be derived from $x$ is the selectope of the game $m^{-1}(x)$.

As before, we use as a shorthand $\mathsf {c}^k=m^{-1}(\mathsf {C}^k), \mathsf {i}_1^n=m^{-1}(\mathsf {I}_1^n), \mathsf {gec}=m^{-1}(\mathsf {GEC})$, etc. The following result shows that any preimputation can be attained from the $k$-additive core by a sharing function.

Theorem 7

(Grabisch and Li (2011)) For any $x^q, \, q \in \mathcal {Q}(N)$ such that $q(K,i)>0$ for all $K\subseteq N$ and $i\in K$, for any $v \in \mathcal {G}(N)$, for any $k\in \{2,\ldots ,n\}$, we have

$$\begin{aligned} x^q(\mathsf {c}^k)(v)=PI(v). \end{aligned}$$

where $PI(v)$ is the set of preimputations.

More interestingly, restricting to the minimum negotiation set, we obtain by using all sharing functions the extended core of Bejan and Gomez.

Theorem 8

The selectope of $\mathsf {i}_1^n(v)$ is given by:

$$\begin{aligned} \mathsf {S}(\mathsf {i}_1^n(v))=\mathsf {S}(\mathsf {gec}(v))=\mathsf {C}(v^{\bar{t}(v)})-\bar{t}(v)\Delta ^n=\mathsf {EC}(v) \end{aligned}$$

where $\Delta ^n:=\{\eta \in [0,1]^n \mid \displaystyle {\sum _{i\in \{1,\ldots , n\}}\eta _i}=1\}$.

Proof

Take $\phi \in \mathsf {i}_1^n(v)$. Since $\mathsf {I}_1^n$ satisfies (MGD), and by Proposition 3 (i), we have $(\phi (1),\ldots ,\phi (n))\in \mathsf {C}(v^{\bar{t}(v)})$. Therefore $\mathsf {S}(\phi )\subseteq \mathsf {C}(v^{\bar{t}(v)})-\bar{t}(v)\Delta ^n$.

Conversely, since $\mathsf {GEC}(v)\subseteq \mathsf {I}_1^n(v)$ by Remark 1, we have $\mathsf {S}(\mathsf {gec}(v))\subseteq \mathsf {S}(\mathsf {i}_1^n(v))$. Furthermore, we have immediatly $\mathsf {S}(\mathsf {gec}(v)) = \mathsf {C}(v^{\bar{t}(v)})-\bar{t}(v)\Delta ^n$.

In summary, we have shown

$$\begin{aligned} \mathsf {C}(v^{\bar{t}(v)})-\bar{t}(v)\Delta ^n=\mathsf {S}(\mathsf {gec}(v))\subseteq \mathsf {S}(\mathsf {i}_1^n(v))\subseteq \mathsf {C}(v^{\bar{t}(v)})-\bar{t}(v)\Delta ^n \end{aligned}$$

so that equality holds throughout.$\square$

It is well known that the Shapley value can be obtained as a sharing and therefore always belongs to the selectope of the game (it corresponds to the equal sharing). However, observe that, in general, the Shapley value does not belong to the selectope of $\mathsf {I}_1^n(v)$, as shown by the following example.

Example 7

We consider a game $v$ on $N=\{1,2,3\}$ defined by:

Clearly, $\bar{t}(v)=\frac{1}{10}$ and $\mathsf {C}(v^{\bar{t}(v)})=\{(1,0,0)\}$.

Therefore the selectope of $\mathsf {I}_1^n(v)$ is:

$$\begin{aligned} \mathsf {S}(\mathsf {I}_1^n(v))=\left\{ (1-\eta _1,-\eta _2,-\eta _3), \, \eta _i\ge 0 \, \forall i \in N, \text { and } \eta _1+\eta _2+\eta _3=\frac{1}{10} \right\} \end{aligned}$$

and the Shapley value of $v$ is

$$\begin{aligned} Sh(v)=\left( \frac{19}{30},\frac{4}{30},\frac{4}{30})\not \in \mathsf {S}(\mathsf {I}_1^n(v)\right) . \end{aligned}$$

A more general way to make a sharing of the amounts given to coalitions is to put the problem into a bankruptcy or tax problem. This was also considered by Bejan and Gómez (2009), however in their case the problem was simpler since only the grand coalition has debt. We limit ourselves to giving the main ideas, a complete treatment of this topic would deserve a whole study.

Consider some payoff $x\in \mathsf {I}^k(v)$, and the list of coalitions $S_1,\ldots ,S_p$ with $|S|>1$ such that $x_S<0$, ordered in a way which is compatible with inclusion (i.e., $S_i\subset S_j$ cannot occur for $i>j$). Take $S_1$ and define the following bankruptcy problem: the set of agents is $S_1$, the estate is $\phi (S_1)$, where $\phi =m^{-1}(x)$ is the game version of $x$, and the claims of the agents are simply their individual payoff $x_i, i\in S_1$. This is a bankruptcy problem because the estate is strictly less than the sum of demands:

$$\begin{aligned} \phi (S_1) = \sum _{T\subseteq S_1}x_T = \sum _{i\in S_1}x_i + x_S<\sum _{i\in S_1}x_i \end{aligned}$$

by the ordering on the $S_i$’s and since $x_S<0$. Taking some division rule (equal award rule Thomson (2003), Talmud rule Aumann and Maschler (1985), etc.), one ends up with a payment vector $(x'_1,\ldots , x'_n)$. Also, we modify the game $\phi$ since the debt $x_{S_1}$ has been paid, as follows: $\phi '(S) = \sum _{T\subseteq S, T\ne S_1}x_S$, and we set $x'_j=x_i$ for all $i\not \in S_1$. Note that $x'\le x$ and $\phi '\ge \phi$.

We take now the next set $S_2$ in the list and define a new bankruptcy problem with estate $\phi '(S_2)$ and claims $x'_i, i\in S_2$. Since $x'\le x$ and $\phi '\ge \phi$, it may happen that the estate is sufficient to pay the claims. If not, we have again a bankruptcy problem, and proceed as above. This leads to vector $x''$ and we update the game $\phi '$ as follows: $\phi ''(S) = \sum _{T\subseteq S, T\ne S_1,S_2}x_S$. We continue the procedure till $S_p$.

Clearly, this way of sharing is more general since the underlying sharing function depends in particular on $x$. We think for this reason that it is better suited to the problem, although more complicated. Its full study is left for further research.

6 Concluding remarks

We summarize the main findings of the paper and indicate research perspectives.

• (i) We have proposed the idea of general payoff vectors and general solutions, based on previous works like the $k$-additive core of Grabisch and Miranda, and the extended core of Bejan and Gomez, which can be seen as a general solution (called here the $\mathsf {G}$-extended core ($\mathsf {GEC}$)).

• (ii) We have proposed the minimum negotiation set, as the subset of the $k$-additive core minimizing the distance to classical preimputations. There are many advantages considering this solution: it is compact and convex, never empty, it coincides with the core if the latter is nonempty, guarantees coalitional rationality while minimizing the amounts given to coalitions of size larger than 2. Properties of the minimum negotiation set have been thoroughly investigated.

• (iii) If the $L_1$ norm is chosen for the minimum negotiation set, then one obtains a set of general payoffs which includes $\mathsf {GEC}$, and whose payments to individuals coincide with the core elements of the $t$-expansion of the game (i.e., elements of $\mathsf {C}(v^{\bar{t}(v)})$). Moreover, it is guaranteed that the total debt to be paid by coalitions is minimal. If the $L_2$ norm is chosen or any $L_p$ norm with $p>1$, the advantage is to get a single-valued solution, like the nucleolus. Further study is needed to investigate the properties of this solution.

• (iv) Ultimately, one should derive classical payoff vector(s) from the general payoff vector chosen by the solution. A simple way to do this is to consider fixed sharing functions, in order to share the debts on coalitions among its members. Taking all possible sharing functions (the selectope) for $\mathsf {I}_1^n$ or $\mathsf {GEC}$ shows that we recover exactly the extended core of Bejan and Gomez. A more clever way, although more complicated, is to consider the payment of a debt by a coalition as a bankruptcy problem, and use appropriate division rules. The latter proposition seems to be promising and deserves further research.

Appendices

Appendix

Proof of Theorem 5

First we need the following result.

Proposition 10

Let $v$ be a game on $N$. Suppose it exists $S\subset N, |S|\ge 2$, such that for all $x \in \mathsf {I}_1^n(v), x_S=0$. Then the following holds.

• (i) For all $x \in \mathsf {I}_1^n(v)$, for all $T\subseteq S, |T|\ge 2$, we have $x_T=0$.

• (ii) There exists $T\supseteq S, T\ne N$, such that $\mathsf {C}(v_T)\ne \emptyset$.

Proof

• (i) Suppose there exists $x \in \mathsf {I}_1^n(v)$ and $T\subseteq S$ such that $x_S=0$ and $x_T<0$. Then the payoff $x'$ defined by

  

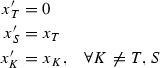
  belongs to $\mathsf {I}_1^n(v)$, which contradicts the definition of $S$.

• (ii) Take $S\subset N, |S|\ge 2$, such that for all $x \in \mathsf {I}_1^n(v), x_S=0$. We prove that if $\forall T\supseteq S, T\ne N$, we have $\mathsf {C}(v_T) = \emptyset$, then there exists $x\in \mathsf {I}_1^n(v)$ such that $x_S<0$.

Let $\tilde{x}\in \mathsf {GEC}(v)\subseteq \mathsf {I}_1^n(v)$. We put

$$\begin{aligned} t=\min _{T \supseteq S,T\ne N}\{\sum _{K\subseteq T}\tilde{x}_K-v(T)\}. \end{aligned}$$

Observe that $t>0$. Indeed, $t=0$ would imply that for some $T\supseteq S, T\ne N, \sum _{K\subseteq T}\tilde{x}_K=v(T)$. Since $\tilde{x}\in \mathsf {GEC}$, its coordinates are 0 for all nonsingleton subsets of $T$. Therefore, $\sum _{i\in T'}\tilde{x}_i\ge v(T')$ for all $T'\subset T$, and $\sum _{i\in T}\tilde{x}_i= v(T)$. It follows that the vector $(\tilde{x}_i)_{i\in N}$ is an element of the core $\mathsf {C}(v_T)$, a contradiction.

Then the general payoff vector $x$ defined by

$$\begin{aligned} x_K=&\tilde{x}_K,\quad \forall K\subset N, \quad K\ne S \\ x_S=&-t \\ x_N=&-\bar{t}(v)+t \end{aligned}$$

belongs to $\mathsf {I}_1^n(v)$.$\square$

(of Theorem 5) (i) $\Rightarrow$ (ii). Let $x\in \mathsf {I}_1^n(v)$. By Corollary 1, we have $(x_1,\ldots ,x_n)\in \mathsf {C}(v^{\bar{t}(v)})$, which yields $\sum _{i\in T}x_i=v(T)$. Therefore if $x_S<0$, we would have $\sum _{S\subseteq T}x_T<v(T)$, which contradicts $x\in \mathsf {I}_1^n(v)$.

(ii) $\Rightarrow$ (i). Define $T$ as a maximal element (in the sense of inclusion) of $\{L \supseteq S, \, x_L=0, \, \forall x\in \mathsf {I}_1^n(v)\}$. Suppose $T=N$. Then for all $x\in \mathsf {I}_1^n(v), x_N=0$, which implies that $\bar{t}(v)=0$ since $\mathsf {GEC}(v)\subseteq \mathsf {I}_1^n(v)$. Therefore $\mathsf {C}(v)\ne \emptyset$, and (i) holds for $T=N$.

We assume now that $T\ne N$. Due to Proposition 10 (i) and the definition of $T$, for any set $L\subseteq T, |L|\ge 2$, we have $x_L=0$ for all $x\in \mathsf {I}_1^n(v)$, and for all $L\supset T, x_L\ne 0$ for at least one $x\in \mathsf {I}_1^n(v)$. It follows that

$$\begin{aligned} \sum _{i\in T}x_i=\sum _{K\subseteq T}x_K, \quad \forall x \in \mathsf {I}_1^n(v). \end{aligned}$$

For the rest of the proof, we introduce the shorthand $\phi ^x$ for $m^{-1}(x)$, where $x$ is a general payoff vector. From the above equation and Corollary 1, it suffices to show that $\phi ^x(T)=v(T)$ for all $x\in \mathsf {I}_1^n(v)$ in order to prove that $y(T)=v(T)$ for all $y\in \mathsf {C}(v^{\bar{t}(v)})$. Suppose then that there exists $x_0\in \mathsf {I}_1^n(v)$ such that $\phi ^{x_0}(T)>v(T)$. We distinguish two cases.

Suppose first that $T=N\setminus i$. Suppose there exists $x\in \mathsf {I}_1^n(v)$ such that $\phi ^x(N\setminus i)>v(N\setminus i)$. Take $x'\in \mathsf {I}_1^n(v)$ such that $x'_N<0$ (necessarily exists otherwise $T=N$), and build the payoff vector $x''=\frac{1}{2}(x+x')$. Define $\tilde{x}$ by

$$\begin{aligned} \tilde{x}_K = {\left\{ \begin{array}{ll} \max (v(N\setminus i) - \phi ^{x''}(N\setminus i),x''_N)<0, &{} \text { if } K=N\setminus i\\ x''_N - \tilde{x}_{N\setminus i}, &{} \text { if } K=N\\ x''_K, &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$

Then $\tilde{x}\in \mathsf {I}_1^n(v)$, although $\tilde{x}_{N\setminus i}<0$, a contradiction.

Suppose next that $T$ is not of the form $N\setminus i$. We know that for all $T'\supset T, T'\ne N$, there exists $x^{T'}\in \mathsf {I}_1^n(v)$ such that $x^{T'}_{T'}<0$. Define $\tilde{x}=\sum _{T'\supset T, T'\ne N}\alpha _{T'}x^{T'}$, with $\alpha _{T'}\in (0,1), \sum _{T'\supset T,T'\ne N}\alpha _{T'}=1$. Then by convexity of $\mathsf {I}_1^n(v)$, it follows that $\tilde{x}\in \mathsf {I}_1^n(v)$, and we have $\tilde{x}_{T'}<0$, for all $T'\supset T, T\ne N$. Consider the payoff vector $x'=\frac{1}{2}(x_0+\tilde{x})$, which belongs to $\mathsf {I}_1^n(v)$ by convexity, and put

$$\begin{aligned} \epsilon = \min (\phi ^{x'}(T)-v(T),\min _{T\subset K\subset N}(-x'_K))>0, \end{aligned}$$

and choose $\tilde{K}$ which realizes the minimum of $\min _{T\subset K\subset N}(-x'_K)$. Build $x^*$ as follows:

$$\begin{aligned} x^*_K = {\left\{ \begin{array}{ll} -\epsilon , &{} \text { if } K=T\\ x'_{\tilde{K}}+\epsilon , &{} \text { if } K=\tilde{K}\\ x'_K, &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$

We claim that $x^*\in \mathsf {I}_1^n(v)$, which contradicts the hypothesis $x_T=0$ for all $x\in \mathsf {I}_1^n(v)$. Indeed, it suffices to verify coalitional rationality:

• (i) If $K\supseteq \tilde{K}$, we have $\phi ^{x^*}(K)=\phi ^{x'}(K)\ge v(K)$.

• (ii) If $K\supseteq T$ and $K\not \supseteq \tilde{K}$, then

  $$\begin{aligned} \phi ^{x^*}(K)=\phi ^{x'}(K)-\epsilon \ge \phi ^{x'}(K) - (\phi ^{x'}(K)-v(K))=v(K). \end{aligned}$$

• (iii) If otherwise $K\subseteq T$, then $\phi ^{x^*}(K)=\phi ^{x'}(K)\ge v(K)$. $\square$