An alternative single parameter functional form for Lorenz curve

Abstract

This paper proposes a single parameter functional form for the Lorenz curve and compares its performance with the existing single parameter functional forms using Australian income data for 10 years. The proposed parametric functional form performs better than the existing Lorenz functional specifications based on mean-squared error and information accuracy measure. The Gini based on the proposed functional form turns out to be second best closely behind Aggarwal’s Lorenz curve specification in each year.

1 Introduction

The Lorenz curves play an important role in the measurement and comparison of income inequality, tax progressivity and redistributive effects of government taxes/benefits on incomes. Atkinson (1970) shows that the ranking of distributions according to the Lorenz curve criterion is identical to the ranking implied by the social welfare function, provided the Lorenz curves do not intersect. Kakwani (1977a, b) shows applications of Lorenz curve in several economic issues including tax progressivity and redistributive policies. Shorrocks (1983) compares income distributions based on generalized Lorenz curves when the distributions differ in terms of mean income.

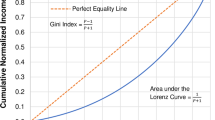
The Lorenz curve represents a graphical relationship between the cumulative proportion of population and the cumulative proportion of income. World Institute of Development Economics Research (WIDER) and World Bank publish data on income shares by decile or quintile groups of population for a large number of countries. Based on group data, Lorenz curve can be constructed (i) by interpolation techniques (Gastwirth and Glauberman 1976), (ii) by assuming a statistical distribution of income and deriving the Lorenz curve (McDonald 1984) or (iii) by specifying a parametric functional form for the Lorenz curve. The interpolation techniques assume the homogeneity of incomes within subgroups, thereby leading to a downward bias in Gini estimate. The existing income distribution functions are known to be poorly fitting the Lorenz curve and resulting in inaccurate inequality estimates.¹

The parametric Lorenz functional forms are directly estimated with the group data without assuming homogeneity of incomes within subgroups and thus are not downwardly biased. Various authors have suggested a variety of parametric functional forms to directly estimate Lorenz curve (Aggarwal 1984; Basmann et al. 1990; Chotikapanich 1993; Gupta 1984; Helene 2010; Holm 1993; Kakwani and Podder 1973; Ogwang and Rao 1996, 2000; Ortega et al. 1991; Pakes 1986; Rohde 2009; Ryu and Slottje 1996; Sarabia 1997; Sarabia and Pascual 2002; Sarabia et al. 1999, 2001, 2005, 2010, 2015, 2017; Wang and Smyth 2015).

This paper proposes an alternative single parameter Lorenz functional form and compares its performance with the existing single parametric functional forms using Australian data for 10 years, 2001–2010. It is always useful and interesting to determine which functional form performs best. This is particularly important when the aim is to construct inequality measures based on Lorenz functional form. In addition, the choice of the functional form for the Lorenz curve is mainly guided by the research objective. In certain applications, single parameter functional form has the advantage (for example, see Thistle and Formby 1987) that the estimated Lorenz curves do not intersect. For example, policy makers may be interested in looking at the effect of changes in taxes in redistributing income. In such cases, a single parameter functional form can be used to simulate the redistributive effects of linear income tax, ignoring the need to check for intersecting Lorenz curves.

In a recent paper, Sordo et al. (2014) have shown that a number of parametric Lorenz curves can be derived by distorting an original Lorenz curve. The single parameter Lorenz curve that we propose in this paper is an original Lorenz curve and has not been obtained by distorting any other baseline Lorenz curve.

2 Alternative functional forms for the Lorenz curve

2.1 Functional form and properties

If p(x) is the proportion of individuals that receive an income up to x and $\eta$ is the proportion of total income received by the same units, then the Lorenz curve is defined as

$$\begin{aligned} \eta = L(p(\mathrm{{x}})) \end{aligned}$$

(1)

The regularity conditions for the function L(p) to describe the Lorenz curve are as follows:

$$\begin{aligned} (\mathrm{{i}})\;L\left( 0 \right) \mathrm{{ }} = \mathrm{{ }}0,(\mathrm{{ii}})\;L\left( 1 \right) \mathrm{{ }} = \mathrm{{ }}1,\;\mathrm{{and \; (iii)}}\;\frac{{\hbox {d}L}}{{\hbox {d}p}}\mathrm{{ }} \ge \mathrm{{ }}0\;\mathrm{{and \; (iv)}}\;\frac{{{\hbox {d}^2}L}}{{\hbox {d}{p^2}}}\mathrm{{ }} > \mathrm{{ }}0 \end{aligned}$$

(2)

Note that (i) and (ii) imply that the Lorenz curve is defined over the domain $\mathrm{{0}} \le \mathrm{{p}} \le \mathrm{{1}}$ and (iii) and (iv) suggest that the slope of Lorenz curve is non-negative and monotonically increasing.

We propose the following functional form for the Lorenz curve

$$\begin{aligned} L\left( {p,\gamma } \right) = p\left[ {\frac{{{e^{ - \gamma \left( {1 - {e^p}} \right) }} - 1}}{{{e^{ - \gamma \left( {1 - e} \right) }} - 1}}} \right] ,\;\mathrm{{where}}\;\gamma > 0 \end{aligned}$$

(3)

It is easy to verify that Eq. (3) passes through the coordinate points (0, 0) and (1, 1) and that the first and second derivatives are greater than zero. That is, $L({0,\gamma }) = 0$, $L({1,\gamma }) = 1$ and

$$\begin{aligned}&L'\left( {p,\gamma } \right) \mathrm{{ = }}\left[ {\frac{{{e^{ - \gamma \left( {1 - {e^p}} \right) }} - 1}}{{{e^{ - \gamma \left( {1 - e} \right) }} - 1}}} \right] + p\gamma \frac{{{e^{ - \gamma \left( {1 - {e^p}} \right) + p}}}}{{{e^{ - \gamma \left( {1 - e} \right) }} - 1}}\;\; \ge 0 \end{aligned}$$

(4)

$$\begin{aligned}&L''\left( {p,\gamma } \right) = 2\gamma \frac{{{e^{ - \gamma \left( {1 - {e^p}} \right) + p}}}}{{{e^{ - \gamma \left( {1 - e} \right) }} - 1}} + p\gamma \left( {\gamma {e^p} + 1} \right) \frac{{{e^{ - \gamma \left( {1 - {e^p}} \right) + p}}}}{{{e^{ - \gamma \left( {1 - e} \right) }} - 1}}> 0\mathrm{{;}}\mathrm{{ }}\gamma \mathrm{{ > }}0,\;0 \le p \le 1\mathrm{{ }}\nonumber \\ \end{aligned}$$

(5)

This functional form is compared with the existing widely used single parameter functional forms proposed by Kakwani and Podder (1973), Chotikapanich (1993) and Aggarwal (1984)² and a form implied by Pareto distribution.

$$\begin{aligned}&\mathrm{{Pareto{:}}}\;L\left( {p,\alpha } \right) = 1 - {\left( {1 - p} \right) ^{\frac{1}{\alpha }}},\;\alpha > 1 \end{aligned}$$

(6)

$$\begin{aligned}&\mathrm{{Kakwani-Podder{:}}}\;L\left( {p,\delta } \right) = p{e^{ - \delta \left( {1 - p} \right) }},\;\delta > 0 \end{aligned}$$

(7)

$$\begin{aligned}&\mathrm{{Chotikapanich{:}}}\;L\left( {p,\kappa } \right) = \frac{{{e^{\kappa p}} - 1}}{{{e^\kappa } - 1}},\;\kappa > 0 \end{aligned}$$

(8)

$$\begin{aligned}&\mathrm{{Aggarwal{:}}}\;L\left( {p,\theta } \right) = \frac{{{{\left( {1 - \theta } \right) }^2}p}}{{{{\left( {1 + \theta } \right) }^2} - 4\theta p}},\;0< \theta < 1 \end{aligned}$$

(9)

The main motivation for fitting a Lorenz curve is to facilitate the estimation of inequality measures such as the Gini coefficient. This widely used index is defined as one minus twice the area under the Lorenz curve. Based on the proposed (new) and existing functional forms, Gini coefficients³ are expressed as follows:

$$\begin{aligned} \mathrm{{Proposed{:}}}\;G= & {} 1 - 2\int _0^1 {p\left[ {\frac{{{e^{ - \gamma \left( {1 - {e^p}} \right) }} - 1}}{{{e^{ - \gamma \left( {1 - e} \right) }} - 1}}} \right] \hbox {d}p} \end{aligned}$$

(10)

$$\begin{aligned} \mathrm{{Pareto{:}}}\;G= & {} 1 - 2\int _0^1 {\left[ {1 - {{\left( {1 - p} \right) }^{\frac{1}{\alpha }}}} \right] \hbox {d}p} \end{aligned}$$

(11)

$$\begin{aligned} \mathrm{{Kakwani-Podder{:}}}\;G= & {} 1 - 2\int _0^1 {p{e^{ - \delta \left( {1 - p} \right) }}\hbox {d}p} \end{aligned}$$

(12)

$$\begin{aligned} \mathrm {Chotikapanich{:}}\;G= & {} \frac{{(\kappa - 2){e^\kappa } + (\kappa + 2)}}{{\kappa ({e^\kappa } - 1)}} \end{aligned}$$

(13)

$$\begin{aligned} \mathrm{{Aggarwal{:}}}\;G= & {} \frac{{{{(1 + \theta )}^2}}}{{2\theta }}\left[ {\frac{{{{(1 - \theta )}^2}}}{{4\theta }}\ln {{\left( {\frac{{1 - \theta }}{{1 + \theta }}} \right) }^2} + 1} \right] - 1 \end{aligned}$$

(14)

2.2 Estimation

For the functional form proposed in this paper, closed-form expression for distribution cannot be obtained. Gomez-Deniz (2016)⁴ suggests that when the distribution function (population function) of a given Lorenz curve is unknown, estimation based on the use of the Dirichlet distribution is adequate for comparing different models. Further, in the Lorenz curve literature, a parametric functional form is usually estimated by nonlinear least-squares estimation method assuming that the errors are independently and normally distributed. However, this assumption regarding the errors is not true in the context of Lorenz curve estimation as observation on cumulative proportions, or their logarithms will neither be independent nor normally distributed. Therefore, nonlinear least-squares estimator does not provide valid inference about Lorenz curve parameters and inequality measure derived from them. Hence, in this the paper we provide maximum likelihood estimates (see Chotikapanich and Griffiths 2002, for details) of Lorenz curve assuming that the income proportions have Dirichlet joint distribution.

The maximum likelihood estimates (see Eq. (9) on p. 291 in Chotikapanich and Griffiths 2002) for parameter of interest $\theta$ can be found by maximizing the log-likelihood function,

$$\begin{aligned} \log \left[ {f\left( {q\left| \theta \right. } \right) } \right]= & {} \log \varGamma \left( \lambda \right) + \sum \limits _{i = 1}^{10} {\left( {\lambda \left[ {L\left( {{p_i},\theta } \right) - L\left( {{p_{i - 1}},\theta } \right) } \right] - 1} \right) \times \log {q_i}} \nonumber \\&- \sum \limits _{i = 1}^{10} \log {\varGamma \left( {\lambda \left[ {L\left( {{p_i},\theta } \right) - L\left( {{p_{i - 1}},\theta } \right) } \right] } \right) } \end{aligned}$$

(15)

where $\lambda$ is an additional unknown parameter, $q = \left( {{q_1},{q_2}, \ldots ,{q_{10}}} \right)$ and ${q_i}$ is the income share of ith decile group.

Table 1 Actual income shares by decile groups, 2001–2010

3 Performance of alternative functional forms of Lorenz curve

Table 1 presents the Australian income data by decile groups for 2001–2010.⁵ Based on these data, the proposed and other four functional forms of Lorenz curve (Eqs. 3 and 6 to 9) are estimated using maximum likelihood estimator. All the parameter estimates are statistically significant at the 1% level (Table 2). A comparison of these estimated functional forms is done based on two statistics.

(i) Information Inaccuracy Measure (I) = $\sum \nolimits _{i = 1}^N {{q_i}\ln ({q_i}/{{{\hat{q}}}_i})}$

Table 2 Estimates of Lorenz parameters (2001–2010)

Table 3 Information inaccuracy measure

Table 4 Mean-squared errors (MSE)

Table 5 Estimates of Gini (2001–2010)

where ${q_i}$ and ${{\hat{q}}_i}$ denote actual and predicted income shares and N represents the number of observations on the cumulative proportions. The estimated function with smaller value of I is better than those with larger values.

(ii) Mean-Squared Error (MSE) = $\frac{1}{N}\sum \nolimits _{i = 1}^N {{{\left[ {{\eta _i} - L\left( {{p_i},{{\hat{\theta }}} } \right) } \right] }^2}}$

It is always non-negative, and values closer to zero are better. Both the statistics are measures of goodness of fit. In terms of measures I and MSE, the proposed functional form performs best followed by Kakwani–Podder, Chotikapanich, Aggarwal and Pareto, respectively, in each year (Tables 3 and 4).

The true Ginis and the estimated Ginis based on alternative functional forms of Lorenz curve are statistically significant at the 1% level (Table 5). For each year, the Gini based on Aggarwal Lorenz curve specification is closest to true Gini. The Gini based on the proposed functional form is second closest to true Gini. The Ginis based on the Kakwani–Podder, Chotikapanich and Pareto Lorenz curve functional forms rank, respectively, third, fourth and fifth in terms of their closeness to true Gini.

4 Conclusion

The Australian data show the superiority of the proposed Lorenz curve functional form over other functional forms. In terms of information inaccuracy measure and MSE, the proposed form outperforms all the four functional forms in all the 10 years. The Gini based on the proposed functional form turns out to be second best closely behind Aggarwal’s Lorenz curve specification in each year.

Appendix

The standard error for Gini coefficient is calculated using the asymptotic approximation: ${\mathrm{var}} ({\hat{G}}) = {\left( {\frac{{\hbox {d}G}}{{\hbox {d}\theta }}} \right) ^2}{V_\theta }$, where ${V_\theta }$ is the asymptotic variance of the single parameter $\theta$ estimated using nonlinear least-squares for the various functional forms of Lorenz curve.

$$\begin{aligned}&\mathrm{{Chotikapanich{:}\, Var}}\left( {{\widehat{G}}} \right) = {\left[ {\frac{{2\left( {{e^{{{\widehat{\kappa }}} }}\left( {{e^2} - {{{{\widehat{\kappa }}} }^2} - 2} \right) + 1} \right) }}{{{{\left( {{{\widehat{\kappa }}} \left( {{e^{{{\widehat{\kappa }}} }} - 1} \right) } \right) }^2}}}} \right] ^2}\mathrm{{Var}}\left( {{{\widehat{\kappa }}} } \right) \\&\mathrm{{Aggarwal{:}\, Var}}\left( {{\widehat{G}}} \right) = {\left( {\frac{{\hbox {d}G}}{{\hbox {d}\theta }}} \right) ^2}\mathrm{{Var}}\left( {{{\widehat{\theta }}} } \right) \;\mathrm{{where}}\\&\frac{{\hbox {d}G}}{{\hbox {d}\theta }} = \frac{{{\theta ^2} - 1}}{{{\theta ^2}}}\left[ {\frac{{1 + {\theta ^2}}}{{2\theta }}\ln \left( {\frac{{1 - \theta }}{{1 + \theta }}} \right) + 1} \right] \\&\mathrm{{Kakwani-Podder{:}\, Var}}\left( {{\widehat{G}}} \right) = {\left( {\frac{{\hbox {d}G}}{{\hbox {d}\delta }}} \right) ^2}\mathrm{{Var}}\left( {{{\widehat{\delta }}} } \right) \;\\&\mathrm{{where}}\;\frac{{\hbox {d}G}}{{\hbox {d}\delta }} = 2\int _0^1 {p\left( {1 - p} \right) {e^{ - \delta \left( {1 - p} \right) }}\hbox {d}p} \\&\mathrm{{Pareto{:}\, Var}}\left( {{\widehat{G}}} \right) = {\left( {\frac{{\hbox {d}G}}{{\hbox {d}\alpha }}} \right) ^2}\mathrm{{Var}}\left( {{{\widehat{\alpha }}} } \right) \;\mathrm{{where}}\\&\frac{{\hbox {d}G}}{{\hbox {d}\alpha }} = - 2\int _0^1 {\frac{1}{{{\alpha ^2}}}\ln \left( {1 - p} \right) {{\left( {1 - p} \right) }^{\frac{1}{\alpha }}}\hbox {d}p} \\&\mathrm{{Proposed{:}\, Var}}\left( {{\widehat{G}}} \right) = {\left( {\frac{{\hbox {d}G}}{{\hbox {d}\gamma }}} \right) ^2}\mathrm{{Var}}\left( {{{\widehat{\gamma }}} } \right) \\&\mathrm{{where}}\;\;\frac{{\hbox {d}G}}{{\hbox {d}\gamma }} = 2\int _0^1 {\left( { - \frac{{1 - {e^p}}}{{1 - {e^{\gamma \left( {1 - {e^p}} \right) }}}} + \frac{{1 - e}}{{1 - {e^{\gamma \left( {1 - e} \right) }}}}} \right) \left( {p\left[ {\frac{{{e^{ - \gamma \left( {1 - {e^p}} \right) }} - 1}}{{{e^{ - \gamma \left( {1 - e} \right) }} - 1}}} \right] } \right) \hbox {d}p} \end{aligned}$$