Trend of high dimensional time series estimation using low-rank matrix factorization: heuristics and numerical experiments via the TrendTM package

Abstract

This article focuses on the practical issue of a recent theoretical method proposed for trend estimation in high dimensional time series. This method falls within the scope of the low-rank matrix factorization methods in which the temporal structure is taken into account. It consists of minimizing a penalized criterion, theoretically efficient but which depends on two constants to be chosen in practice. We propose a two-step strategy to solve this question based on two different known heuristics. The performance and a comparison of the strategies are studied through an important simulation study in various scenarios. In order to make the estimation method with the best strategy available to the community, we implemented the method in an R package TrendTM which is presented and used here. Finally, we give a geometric interpretation of the results by linking it to PCA and use the results to solve a high-dimensional curve clustering problem. The package is available on CRAN.

1 Introduction

Since the 1970’s, it is usual to model a one-dimensional time series by a process $(X_t)_{t\in \mathbb Z}$ satisfying

$$\begin{aligned} F_{\theta }(X_{t + q},\dots ,X_{t - q},\eta _{t + p},\dots ,\eta _{t - p}) = 0 \text { ; } t\in \mathbb Z, \end{aligned}$$

(1)

where $p,q\in \mathbb N$, $\eta = (\eta _t)_{t\in \mathbb Z}$ is a second order stationary process, often a white noise, and $\mathcal F = (F_{\theta })_{\theta \in \Theta }$ is a family of continuous maps from $\mathbb R^{2(p + q + 1)}$ into $\mathbb R$ indexed in a set $\Theta$. For instance, ARMA models, GARCH models, and all their extensions are defined this way. An advantage of Model (1) is that $\mathcal F$ can be chosen in order to take into account properties known on the dynamics of the modeled phenomenon regardless to the data. However, except in simple cases, Model (1) is difficult to extend to the high-dimensional framework. For instance, the vector autoregressive (VAR) and vector autoregressive moving average (VARMA) models have been intensively investigated on the theoretical side and in applications (see Lütkepohl 2005). However, in the high-dimensional framework, these models cannot be applied directly. Indeed, as mentioned in Gao and Tsay (2022), VARMA models often suffer the difficulties of over-parametrization and lack of identifiability. To bypass such difficulties, some authors have studied extensions of the VAR models: the LASSO regularization of the VAR models (see Shojaie and Michailidis 2010), the sparse VAR models (see Davis et al. 2016), the VAR models with low-rank transition matrix (see Alquier et al. 2020), the factor models (see Lam and Yao 2012a, Gao and Tsay 2022, etc.). Note that the VAR models and their extensions are tailor-maid to take into account a (linear) relationship between the $X_t$’s, but not a sophisticated high-dimensional trend component as in Model (2) presented below and considered throughout our paper. Finally, note that it is also difficult to bypass the stationary condition on $\eta$ (for a good reference on the classic time series models, see Gourieroux and Monfort 1997).

Independently, for almost two decades, in particular thanks to the Netflix challenge on movies recommendations, the low rank matrix factorization for the denoising (also for the completion) of high-dimensional matrices with i.i.d. entries has been deeply investigated on the theoretical side (see Cai and Zhang 2015; Klopp et al. 2017, 2019; Koltchinskii et al. 2011; Moridomi et al. 2018). Indeed, high-dimensional time series often have strong correlation, and it is thus natural to assume that the matrix that contains such a series is low rank (exactly, or approximately). Let denote by $\textbf{X}$ the observed $d\times n$ matrix which rows are d time series with length n and assume that both d and n are high. Matrix factorization consists in approximating $\textbf{X}$ by a matrix $\textbf{M}$ of low rank $k\in \mathbb N^*$ (i.e. $k\ll d\wedge n$), which can therefore be written as the product $\textbf{U} \textbf{V}$ of two matrix $\textbf{U}\in \mathcal M_{d,k}(\mathbb R)$ and $\textbf{V}\in \mathcal {M}_{k,n}(\mathbb R)$ where $\mathcal M_{d,k}(\mathbb R)$ is the set of the matrices of size $d \times k$ with coefficients in $\mathbb {R}$. Formally, let us consider the model

$$\begin{aligned} \textbf{X} =\textbf{M} +\varepsilon \end{aligned}$$

(2)

The matrix ${\textbf {M}}$ is usually estimated by using a contrast minimization approach, the most popular being the least squares contrast associated to the Frobenius norm: the best rank-k approximation of $\textbf{X}$ is

$$\begin{aligned} \widehat{\textbf{M}}_{k}\in \arg \min _{\textbf{U}\in \mathcal M_{d,k}, \textbf{V}\in \mathcal M_{k,n}(\mathbb R) } \Vert \textbf{X} -\textbf{U} \textbf{V} \Vert _{\mathcal F}^{2}, \end{aligned}$$

(3)

where $\Vert .\Vert _\mathcal {F}$ is the Frobenius norm (for a matrix $\textbf{A}$, $\Vert \textbf{A}\Vert _\mathcal {F}:= \textrm{trace}(\textbf{A} \textbf{A}^*)^{1/2}$). Then, the choice of the rank k can be viewed as a model selection issue. In the matrix factorization framework, several approaches have been proposed in the literature (see for instance Candes et al. 2013; Ulfarsson and Solo 2008; Lam and Yao 2012b for criteria based on the estimated eigenvalue study, Seghouane and Cichocki (2007); Lopes and West (2004) for the classical BIC criterion or dos S. Dias, C. T. and Krzanowski, W. J. (2003) for a cross-validation strategy).

When dealing with time series, the matrix $\textbf{X}$, besides being of low rank, can have a temporal structure, a structure in time, as periodicity, smoothness, etc. It is likely that the temporal properties of the data can be exploited to obtain an accurate factorization. Recently, Alquier and Marie (2019) has extended the latter factorization method in order to take into account the time series trends properties. To this aim, they assume that the matrix $\textbf{M}$ is structured as follows:

$$\begin{aligned} \textbf{M} =\underline{\textbf{M}}{\varvec{\Lambda }}, \end{aligned}$$

(4)

where $\underline{\textbf{M}}$ is a $d\times \tau$ matrix of low rank k (thus with $\tau >k$) and ${\varvec{\Lambda }}$ is a known $\tau \times n$ full rank matrix reflecting the temporal structure of the data. To estimate $\textbf{M}$, they developed a penalized least squares criterion (based on the Frobenius norm) and shown that, on the theoretical side, to take into account trends properties in the definition of the denoising estimator allowed to improve existing risk bounds. The penalization aims to choose two parameters: the rank k of the matrix and the parameter $\tau$ related to the temporal structure. This penalty function depends also on the noise structure and involves an unknown constant.

In practice, this joint model selection issue is not standard. In addition to a penalty constant to be chosen, parameters from the distribution of the noise need to be estimated in advance. In this paper, we propose an automatic way to deal with these two problems. First, the parameters of the noise distribution are combined with the penalty constant to get a penalty function involving a single constant. This avoids having to estimate the parameters beforehand. Then, we propose a two-stage strategy, as in Devijver et al. (2017); Collilieux et al. (2019), combined with the use of a heuristic for the constant calibration problem. Several heuristics have been considered here, now well-known for the penalty constant calibration in model selection frameworks (Lavielle 2005; Birgé and Massart 2001). We demonstrate the performances of our procedure and compare the considered heuristics in the case of independent Gaussian noises through simulation experiments. The robustness to an autoregressive noise and a nonnormality distribution are also studied.

The method has been implemented in the R package TrendTM, for Trend of High-Dimensional Time Series Matrix Estimation, which is available on the CRAN and presented here. When the factorization problem is solved using the Singular Value Decomposition (svd) method, we can make a link to the Principal Component Analysis (PCA) and give an geometrical interpretation of the factorization results. Moreover, we show that, based on this interpretation, a simple clustering method of multiple time series can be derived. It is illustrated on a benchmark dataset of such statistical purpose (see the review and the comparison in Jacques and Preda 2014).

The paper is organized as follows. Section 2 recalls the estimation procedure proposed in Alquier and Marie (2019). Section 3 presents the proposed two-stage heuristic for the joint selection of the rank and the trend parameter whose performances are studied in Sect. 4 on simulated data. Section 5 gives some details and guidelines on the proposed method in the TrendTM package and shows an application on real data. In Sect. 6, we give a geometrical interpretation of our results and present the clustering method we proposed.

2 Recall of the trend estimation method proposed by Alquier and Marie (2019)

In this section, we present the method they proposed for estimating $\textbf{M}$ in model (3) when $\textbf{M}:=\underline{\textbf{M}}{\varvec{\Lambda }}$ (see (4)) and when the noise $\varepsilon$ has Gaussian i.i.d. rows of covariance matrix ${\varvec{\Sigma }}_{\varepsilon }$. The general idea of the proposed inference is to estimate first $\underline{\textbf{M}}$ from the data $\underline{\textbf{X}}$ (with $\textbf{X}:=\underline{\textbf{X}}{\varvec{\Lambda }}$) by solving the optimization problem (3) on this new dataset and then to come back to the estimation of $\textbf{M}$.

First, the two temporal structures they considered are the following:

• periodicity: if the trend of $\textbf{X}$ is $\tau$-periodic, then $\mathbf \Lambda = (\textbf{I}_{\tau } \mid \cdots \mid \textbf{I}_{\tau })$ where $\textbf{I}_{\tau }$ is the identity matrix in $\mathcal M_{\tau ,\tau }(\mathbb {R})$,

• smoothness: if the form of the trend is $t\in \{1,\dots ,n\}\mapsto f(t/n)$ with $f\in \mathbb L^2([0,1];\mathbb R^d)$, then

  $$\begin{aligned} {\varvec{\Lambda }} = \left( \varphi _\ell \left( \frac{t}{n}\right) \right) _{(\ell ,t)\in \{1,\dots ,\tau \}\times \{1,\dots ,n\}}, \end{aligned}$$

  where $\tau$ is odd and $(\varphi _1,\dots ,\varphi _{\tau })$ is the $\tau$-dimensional trigonometric basis defined by

  $$\begin{aligned} \varphi _\ell (x):= \left\{ \begin{array}{lcl} 1 &{} {\textrm{if}} &{} \ell = 1\\ \sqrt{2}\cos (2\pi m x) &{} {\textrm{if}} &{} \ell = 2m\\ \sqrt{2}\sin (2\pi m x) &{} {\textrm{if}} &{} \ell = 2m + 1 \end{array}\right. \end{aligned}$$

  for every $x\in [0,1]$ and $m\in \{1,\dots , (\tau - 1)/2\}$.

So, the estimation procedure consists in two steps:

• Step 1: Estimation of $\textbf{M}$ for k and $\tau$ being fixed. They define the following auxiliary model

  $$\begin{aligned} \underline{\textbf{X}} =\underline{\textbf{M}} +\underline{\varepsilon }, \end{aligned}$$

  (5)

  where $\underline{\textbf{X}}:=\textbf{X}{\varvec{\Lambda }}^+$, $\underline{\varepsilon }:=\varepsilon {\varvec{\Lambda }}^+$ and ${\varvec{\Lambda }}^+ ={\varvec{\Lambda }}^*({\varvec{\Lambda }}{\varvec{\Lambda }}^*)^{-1}$ is the Moore-Penrose inverse of ${\varvec{\Lambda }}$. This model doesn’t embed some trend’s property anymore. The least squares estimator of the matrix $\underline{\textbf{M}}$ is thus classical:

  $$\begin{aligned} \widehat{\underline{\textbf{M}}}_{k,\tau }\in \arg \min _{\textbf{A}\in \mathcal S_{k,\tau }}\Vert \underline{\textbf{X}} -\textbf{A}\Vert _\mathcal {F}^{2}, \end{aligned}$$

  (6)

  where $\mathcal S_{k,\tau }=\{\textbf{U}{} \textbf{V}\text { ; } \textbf{U}\in \mathcal M_{d,k}(\mathbb R)\text { and } \textbf{V}\in \mathcal M_{k,\tau }(\mathbb R)\}$. So, a natural estimator of $\textbf{M}$ is given by

  $$\begin{aligned} \widehat{\textbf{M}}_{k,\tau }:=\widehat{\underline{\textbf{M}}}_{k,\tau }{\varvec{\Lambda }}. \end{aligned}$$

• Step 2: Choice of k and $\tau$. For a fixed $s > 0$, the final estimator of $\textbf{M}$ is $\widehat{\textbf{M}}_s:=\widehat{\textbf{M}}_{\widehat{k}(s),\widehat{\tau }(s)}$ where

  $$\begin{aligned} (\widehat{k}(s),\widehat{\tau }(s))\in \arg \min _{(k,\tau )\in \mathcal K\times \mathcal T} \{\Vert \textbf{X} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}^{2} + \textrm{pen}_{s}(k,\tau )\} \end{aligned}$$

  with $\mathcal K=\{1,\dots ,d\wedge n\}$, $\mathcal T=\{1,\dots ,n\}$, and

  $$\begin{aligned} \textrm{pen}_s(k,\tau ) := \mathfrak c_\textrm{pen}\Vert {\varvec{\Sigma }}_{\varepsilon }\Vert _\textrm{op}k(d +\tau + s) \text { ;} \forall (k,\tau )\in \mathcal K\times \mathcal T, \end{aligned}$$

  (7)

  where $\mathfrak c_\textrm{pen} > 0$ is a deterministic constant and $\Vert .\Vert _\textrm{op}$ is the operator norm on $\mathcal M_{n,n}(\mathbb R)$ ($\Vert \textbf{A}\Vert _\textrm{op}:=\sup _{\Vert x\Vert =1}\Vert \textbf{Ax}\Vert$ with $\Vert .\Vert$ the Euclidean norm on $\mathbb R^n$). They establish an oracle-type inequality on the resulting estimator (see Alquier and Marie 2019 (Theorem 4.1)): for every $\theta \in (0,1)$, with probability larger than $1 - 2e^{-s}$,

  $$\begin{aligned} \Vert \widehat{\textbf{M}}_s -\textbf{M}\Vert _\mathcal {F}^{2}\leqslant & {} \min _{(k,\tau )\in \mathcal K\times \mathcal T} \min _{\textbf{A}\in \mathcal S_{k,\tau }} \left\{ \left( \frac{1 +\theta }{1 -\theta }\right) ^2 \Vert \textbf{A}{\varvec{\Lambda }} -\textbf{M}\Vert _\mathcal {F}^{2}\right. \nonumber \\{} & {} \hspace{5cm}\left. + \frac{4}{\theta (1 -\theta )^2} \textrm{pen}_s(k,\tau ) \right\} . \end{aligned}$$

  (8)

The parameter s in the penalty is linked to the confidence level in the risk bound for a fixed k and $\tau$. Making the penalty depend on s is necessary to establish a risk bound on the adaptive estimator. This is a technical condition in fact, which we could also get rid of if we only selected $\tau$ for a fixed k (see Theorem 4.1 and Remark 4.2 in Alquier and Marie (2019)). The penalty is also proportional to the number of series d as in multiple serie estimation framework (see for example Collilieux et al. 2019) since the estimation cost increases naturally with d.

Finally, note that through the penalty defined by (7), the right-hand side of inequality (8) depends on $\Vert \Sigma _{\varepsilon }\Vert _\textrm{op}$ because of the concentration inequality for random matrices with i.i.d. (sub-)Gaussian rows (see Vershynin 2012, Theorem 5.39 and Remark 5.40.(2)) used to control the variance term in the proof of Alquier and Marie 2019, Theorem 3.2 (and then Theorem 4.1). This is one of the reasons why we consider the quadratic loss and why the second order moment $\Sigma _{\varepsilon }$ of the rows of $\varepsilon$ appears in the risk bound (8).

3 The proposed two-stage heuristic for the model selection issue in practice

Discussion on the penalty function. The penalty function given by (7) depends of some constants s and $\mathfrak c_\textrm{pen}$ that must be chosen or calibrated in practice. It also depends on the parameters of the noise distribution through $\Vert {\varvec{\Sigma }}_{\varepsilon }\Vert _\textrm{op}$ that must be estimated thus in advance: we explicit just below this norm in two cases that are considered in the simulation study (Sect. 4):

• when the errors are uncorrelated ($\textrm{cov}(\varepsilon _{1,t},\varepsilon _{1,t'}) =\sigma ^2\mathbb 1_{t \ne t'}$), then

  $$\begin{aligned} \Vert {\varvec{\Sigma }}_{\varepsilon }\Vert _\textrm{op} =\sigma ^2, \end{aligned}$$

• when $(\varepsilon _{1,t})_t$ is a zero-mean stationary AR(1) Gaussian process (defined as the solution of $\varepsilon _{1,t} =\rho \varepsilon _{1,t - 1} +\eta _{1,t}$ where $\rho \in (-1,1)$ and $(\eta _{1,t})_t$ is a white noise of standard deviation $\sigma$), we can show that

  $$\begin{aligned} \Vert {\varvec{\Sigma }}_{\varepsilon }\Vert _\textrm{op}\geqslant \sigma ^2(1 +\rho ) =: f(\rho ). \end{aligned}$$

  (9)

  Indeed, the covariance matrix of a row noise $(\varepsilon _0,\dots ,\varepsilon _{n - 1})$ is

  $$\begin{aligned} {\varvec{\Sigma }}_{\varepsilon }:= (\sigma ^2\rho ^{|i - j |})_{i,j}. \end{aligned}$$

  Then, for every $x\in \mathbb R^n$ such that $\Vert x\Vert = 1$,

  $$\begin{aligned} x^*{\varvec{\Sigma }}_{\varepsilon }x= & {} \sum _{i,j = 1}^{n}x_ix_j[{\varvec{\Sigma }}_{\varepsilon }]_{i,j} = \sigma ^2\left( \Vert x\Vert ^{2} + \sum _{i\ne j}x_i x_j\rho ^{|i - j |}\right) \\= & {} \sigma ^2\left( 1 + 2\sum _{i > j}x_ix_j\rho ^{i - j}\right) . \end{aligned}$$

  Since ${\varvec{\Sigma }}_{\varepsilon }$ is a symmetric matrix,

  $$\begin{aligned} \Vert {\varvec{\Sigma }}_{\varepsilon }\Vert _\textrm{op}= & {} \sup _{\Vert x\Vert = 1}|x^*{\varvec{\Sigma }}_{\varepsilon }x|\geqslant |\textbf{x}^*{\varvec{\Sigma }}_{\varepsilon }\textbf{x}|\quad \textrm{with}\quad \textbf{x}=\frac{1}{\sqrt{2}}(1,1,0,\dots ,0)\\\geqslant & {} \textbf{x}^*\mathbf \Sigma _{\varepsilon }\textbf{x}= \sigma ^2\left( 1 + 2\cdot \frac{1}{\sqrt{2}}\cdot \frac{1}{\sqrt{2}}\cdot \rho ^{2 - 1}\right) = \sigma ^2(1 +\rho ). \end{aligned}$$

Two-stage heursitic. We set $\mathfrak c_\textrm{cal}= \mathfrak c_\textrm{pen}\Vert {\varvec{\Sigma }}_{\varepsilon }\Vert _\textrm{op}$, representing a global penalty constant that we propose to calibrate using the data. So, this allows us to avoid the estimation of the noise distribution parameters, which turns out to be a difficult task. The penalty function is thus reduced to

$$\begin{aligned} \textrm{pen}(k,\tau ):=\mathfrak c_\textrm{cal}k(d +\tau + s) \text {;} \forall (k,\tau )\in \mathcal K\times \mathcal T, \end{aligned}$$

and the resulting adaptive estimator is denoted by $\widehat{\textbf{M}}_s:=\widehat{\textbf{M}}_{\widehat{k},\widehat{\tau }}$.

If the constant s can be easily chosen, this is not the case for the penalty constant $\mathfrak c_\textrm{cal}$. Several heuristics have been proposed in the literature for this purpose in model selection frameworks, but for a one-dimensional parameter only (see Lavielle 2005; Birgé and Massart 2001). First, in practice, we could take $s = -\log ((1 -\alpha )/2)$ with $\alpha$ fixed to $99\%$, $95\%$ or $90\%$. Here we choose to fix $s = 4$. Then, for the selection of both k and $\tau$, we follow the same strategy than in Devijver et al. (2017), that is a two-stage heuristic. We first recall some heuristics for the selection of one parameter, and then we present the two-stage heuristic for the joint selection of $(k,\tau )$.

Up to our knowledge, there exit the three following heuristics dedicated to the constant calibration question in the model selection frameworks of one parameter:

• the one proposed in Lavielle (2005), denoted here ML, that involves a threshold S which is fixed to $S = 0.75$ as suggested by the author, and

• the two proposed in Birgé and Massart (2001) (see the more recent version of Arlot and Massart (2009) and the huge survey paper of Arlot (2019)) that are two versions of the well-known slope heuristic: the ’dimension jump’ and the ’slope’, denoted here BJ and Slope respectively. The both heuristics have been implemented in the R package capushe described in Baudry et al. (2012).

A brief description of these heuristics is given in Appendix 8. For the joint selection of $(k,\tau )$, the two-stage heuristic is the following: first, we choose the best $\tau$ for each $k\in \mathcal K$ via the criterion

$$\begin{aligned} \widehat{\tau }(k) \in \arg \min _{\tau \in \mathcal T} \{\Vert \textbf{X} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}^{2} + \mathfrak c_\mathrm{cal,\tau }k(d +\tau + s)\}, \end{aligned}$$

where the penalty constant $\mathfrak c_\mathrm{cal,\tau }$ is calibrated using one of the previous heuristics, and then we select the best k among them via the criterion

$$\begin{aligned} \widehat{k}\in \arg \min _{k\in \mathcal K} \{\Vert \textbf{X} -\widehat{\textbf{M}}_{k,\widehat{\tau }(k)}\Vert _{\mathcal F}^{2} +\mathfrak c_{\text {cal},k}k (d +\widehat{\tau }(k) + s)\}, \end{aligned}$$

where the penalty constant $\mathfrak c_{\text {cal},k}$ is calibrated using the same heuristic to be consistant, and $\widehat{\tau }=\widehat{\tau }(\widehat{k})$.

Note that in practice $\mathcal K=\{1,\ldots ,k_{\max }\}$ and $\mathcal T=\{k+1,\ldots ,\tau _{\max }\}$, where $k_{\max }$ is the maximal rank and $\tau _{\max }$ is the maximal value of $\tau$. These two quantities need to be specified. Moreover, we propose this strategy and not the opposite because on the one hand $k < \tau$ theoretically and on the other hand the slope heuristic requires having a minimum point. Using the proposed strategy allows to visit clearly more dimensions $(k,\tau )$.

4 Simulation study

In this study, we conduct different simulations studies to both evaluate the performance of the proposed method and compare the three different heuristics:

• Study 1: we consider the model selection issue for k and $\tau$ separatly,

• Study 2: we illustrate the importance to take into account the trend in the estimation procedure when it exits,

• Study 3: we consider the model selection issue for both k and $\tau$.

We also performed additional separate simulations:

• Study 4: we assume that for each series there exists a temporal dependency which is modelled through an AR process,

• Study 5: we study the robustness of the proposed method to nonnormality errors.

4.1 Simulation design and quality criteria

4.1.1 Simulation design

We’ve simulated datasets with $d=100$ and $n=600$ as follows:

• (1) we generate a matrix $\underline{\textbf{M}} =\textbf{U}\textbf{V}$ by simulating $\textbf{U} \in \mathcal M_{d,k}(\mathbb R)$ and $\textbf{V}\in \mathcal M_{k,\tau }(\mathbb R)$ for which the entries of $\textbf{U}$ and $\textbf{V}$ are assumed to be i.i.d. and follows a centered Gaussian distribution with same standard deviation $\sigma _{uv}$ fixed to 0.5;

• (2) two cases are considered according to the presence or not of a trend in the simulated series: if there is no trend, then $\tau = n$ and $\textbf{M} =\underline{\textbf{M}}$, and otherwise $\textbf{M} =\underline{\textbf{M}}{\varvec{\Lambda }}$ with the matrix ${\varvec{\Lambda }}$ of the smooth case. To distinguish between these two cases in the sequel, we call them dataset$_{\text {NoTrend}}$ and dataset$_{\text {Trend}}$ respectively;

• (3) the rows of the error matrix $\varepsilon$ are assumed to be i.i.d. and follow a centered Gaussian distribution of variance $\sigma ^2$ (i.e. ${\varvec{\Sigma }}_{\varepsilon }=\sigma ^2\textbf{I}_n$) for Studies 1, 2 and 3; the rows of the error matrix $\varepsilon$ are assumed to be i.i.d. stationary AR(1) Gaussian processes with a white noise of standard deviation $\sigma > 0$ and an autocorrelation parameter $\rho \in (-1,1)$ for Study 4.

We take $k = 3$ and $\tau = 25$. We consider different values for the residual standard deviation $\sigma$ in order to have different levels of difficulty for the estimation problem. First, according to the previous considerations, $\textrm{var}(\textbf{M}_{ij}) = k \sigma _{uv}^{4}$ for dataset$_{\text {NoTrend}}$ and $\textrm{var}(\textbf{M}_{ij}) =\tau k\sigma _{uv}^{4}$ for dataset$_{\text {Trend}}$. For Studies 1, 2 and 3, let us consider $s_v\in \{0.1,0.5,1.5,2\}$. In order to have the same estimation difficulty (same ratio between $\sigma$ and the standard deviation of $\textbf{M}_{ij}$) for the two datasets, we set $\sigma = s_v$ for dataset$_{\text {NoTrend}}$ and $\sigma =\sqrt{\tau }s_v$ for dataset$_{\text {Trend}}$. The obtained four cases are judged as ‘Easy’, ‘Medium’, ‘Difficult’ and ‘Hard’ respectively. Study 4 is the same as Study 3 but with a noise modeled by an autoregressive process. More precisely, we consider two values for the standard deviation of the noise $s_v\in \{0.1,1.5\}$ and an autocorrelation parameter $\rho \in \{-0.8,-0.3,0,0.3,0.8\}$. For each combination of parameters, we’ve simulated 200 datasets.

Let us precise that when the trend is not considered in the estimation procedure, the resulting estimator is

$$\begin{aligned} \widehat{\textbf{M}}_{k \ \text {or} \ \widehat{k},n} \text {(if }k \text { is selected or not), } \end{aligned}$$

and when it is considered the resulting estimator is

$$\begin{aligned} {\widehat{\textbf{M}}_{k \ \text {or} \ \widehat{k},\tau \ \text {or} \ \widehat{\tau }} \text { (if both }k \text { and }\tau \text { are selected or one of them or none). }} \end{aligned}$$

For Study 5, we consider the same simulation design as in Study 3 but by considering a heavy-tailed distribution for the errors $\{\varepsilon _t\}_t$, namely, a Student distribution with degrees of freedom $\nu = {50, 10, 3}$ ($\nu = 50$ being the closest Gaussian case).

4.1.2 Quality criteria

The performance of our procedure is assessed via:

• the estimated k and/or $\tau$; and

• the squared Frobenius distance between $\textbf{M}$ and its estimate $\widehat{\textbf{M}}_{\widehat{k},\widehat{\tau }}$.

Moreover, we also consider the Frobenius distance between $\textbf{M}$ and

• the estimator of $\textbf{M}$ for the true k and/or $\tau$, that is $\widehat{\textbf{M}}_{k,\tau }$; and

• the trajectorial oracle, that is $\widehat{\textbf{M}}_{\widetilde{k},\widetilde{\tau }}$ where

  $$\begin{aligned} (\widetilde{k},\widetilde{\tau }) = \arg \min _{(k,\tau )\in \mathcal K\times \mathcal T} \Vert \textbf{M} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}^{2} \end{aligned}$$

  when both k and $\tau$ are selected, $\widehat{\textbf{M}}_{k,\widetilde{\tau }}$ where

  $$\begin{aligned} \widetilde{\tau }= \arg \min _{\tau \in \mathcal T} \Vert \textbf{M} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}^{2} \end{aligned}$$

  when k is fixed, and $\widehat{\textbf{M}}_{\widetilde{k},n}$ where

  $$\begin{aligned} \widetilde{k} = \arg \min _{k\in \mathcal K} \Vert \textbf{M} -\widehat{\textbf{M}}_{k,n}\Vert _\mathcal {F}^{2} \end{aligned}$$

  when no trend is considered.

4.2 Study 1: behavior of the three heuristics for the selection of k or $\tau$

We first study the selection of k for dataset$_\textrm{NoTrend}$ when no trend is considered in the estimation procedure. We consider two different values of the maximal rank $k_{\max }\in \{15,35\}$. The results are presented in Fig. 1. When the noise is small, i.e. the estimation problem is easy (cases ‘Easy’ and ‘Medium’), all the heuristics recover the true rank, and therefore the obtained estimators perform as well as $\widehat{\textbf{M}}_{k,n}$ (the estimator of $\textbf{M}$ for k fixed to its true value). When the estimation problem gets more difficult (cases ‘Difficult’ and ‘Hard’), the heuristics tend to underestimate the rank. This underestimation behavior seems to be logical and even desirable in the particular ‘Hard’ case. Indeed, we observe that in terms of Frobenius norm, the obtained estimators perform better compared to the one with the true rank. Moreover, they have performance close to the oracle. Comparing the three heuristics, the Slope heuristic shows better performances compared to the two other heuristics. This is particularly marked for the ‘Medium’ case and $k_\textrm{max} = 15$. We can note that the behavior of the three heuristics can be affected by the choice of $k_\textrm{max}$. This problem is well-known for both the BJ and Slope heuristics (see Arlot 2019 for more explanations in the case univariate series analysis).

Then, we study the selection of $\tau$ for dataset$_\textrm{Trend}$ for k fixed to the true value. We fix $\tau _{\max } = 55$. The results are presented in Fig. 2. Except with BJ that is more unstable, the heuristics retrieve the true value of $\tau$ whatever the estimation difficulty with same performance as the oracle.

From this study, we choose the Slope heuristic for the model selection issue for both k and $\tau$ in the sequel and in the developed package.

Fig. 1

Comparison of the three heuristics for the selection of k for dataset$_\textrm{NoTrend}$ (Study 1). Left: boxplot of estimated number of the rank k. Right: boxplot of $\Vert \textbf{M} -\widehat{\textbf{M}}_{\widehat{k},n} \Vert _\mathcal {F}$ for two values of $k_{\max } = 15$ (first line) and $k_{\max } = 35$ (second line), and different values of $\sigma$. On each graph and for each value of $\sigma$, from left to right, we have the result from ML, BJ, Slope ($\widehat{k}$), the true rank (k) and the oracle ($\widetilde{k}$)

Fig. 2

Comparison of the three heuristics for the selection of $\tau$ for dataset$_\textrm{Trend}$ when k is fixed to the truth ($k = 3$) for different values of $\sigma$ (Study 1). Left: boxplot of estimated $\tau$. Right: boxplot of $\Vert \textbf{M} -\widehat{\textbf{M}}_{k,\widehat{\tau }}\Vert _\mathcal {F}$. In each graph and each value of $\sigma$, from left to right, we have the result from ML, BJ, Slope ($\widehat{\tau }$), the true value ($\tau$) and the oracle ($\widetilde{\tau }$)

4.3 Study 2: accounting for the smooth structure in the trend

We compare the performance of the procedure on the dataset$_\textrm{Trend}$ when the trend is considered ($\tau =\widehat{\tau }$) or not ($\tau = n$) for k fixed to the true value. We choose $\tau _{\max } = 55$. The results are represented in Fig. 3. Whatever the difficulty of the estimation problem (different values of $\sigma$), accounting for the trend increases the precision of the estimation. This is more marked for high values of $\sigma$. Note that, similarly as Study 1, the estimation naturally degrades with the increasing of $\sigma$.

Fig. 3

Boxplot of $\Vert \textbf{M} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}$ with $\tau =\widehat{\tau }$ ($\text {select\_{tau}}$) and $\tau = n$ ($\text {tau = n}$) for different values of $\sigma$ (Study 2)

4.4 Study 3: selection of k and $\tau$

Table 1 shows that the joint heuristic retrieves the true values of k and $\tau$ whatever the difficulty of the estimation problem, except very few times. Thus, the performance of the estimator of $\textbf{M}$ is comparable to the one of the estimator $\textbf{M}_{k,\tau }$ and moreover it has performance close to the oracle (see Fig. 4). Compared to Study 1 where $\tau = n$, here for difficult estimation problems, k is not underestimated.

Table 1 Estimated k and $\tau$, $(\hat{k},\hat{\tau })$, and the oracle $(\tilde{k},\tilde{\tau })$ for different values of $\sigma$ (Study 3)

Fig. 4

Boxplot of $\Vert \textbf{M} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}$ with $(k,\tau ) = (\widehat{k},\widehat{\tau })$ the selected k and $\tau$, $(k,\tau ) = (k,\tau )$ the true values and $(k,\tau ) = (\widetilde{k},\widetilde{\tau })$ the oracle for different values of $\sigma$ (Study 3)

4.5 Study 4: robustness to autocorrelated noise

Whatever the dependence and the noise variance, the joint heuristic retrieves the true values of k and $\tau$ (see Tables 2 and 3), except for a large variance ($s_v = 1.5$) and a high positive autocorrelation ($\rho = 0.8$) where it underestimates k and the selection of $\tau$ is more variable. For all noise cases, the method leads to estimators that have close performance compared to the oracle (see Figs. 5 and 6) and with better performance than the one with the true values for the excepted case.

Moreover, we can observe that the more the autocorrelation parameter $\rho$ increases (from $-1$ to 1), the more $\Vert \textbf{M} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}$ increases also with a noticeable gap between $\rho = 0.3$ and $\rho = 0.8$ for both values of $s_v$. First, the estimation is better with high and negative autocorrelation. Then, the observed phenomenon on the norm can be explained. The variance term in the risk bound of the estimator $\widehat{\textbf{M}}_{\widehat{k},\widehat{\tau }}$ (i.e. the penalty, see (8)) depends on $\Vert {\varvec{\Sigma }}_{\varepsilon }\Vert _\textrm{op}$ (see (7)). Using (9), we can show that this term is lower-bounded by

$$\begin{aligned} f(\rho )\frac{k(d +\tau )}{dT} \end{aligned}$$

up to a multiplicative constant where f is increasing and nonnegative on $[-1,1]$.

Table 2 Estimated k and $\tau$, $(\hat{k},\hat{\tau })$, and the oracle $(\tilde{k},\tilde{\tau })$ for different values of $\rho$ and for the standard deviation $s_v = 0.1$ (Study 4)

Table 3 Estimated k and $\tau$, $(\hat{k},\hat{\tau })$, and the oracle $(\tilde{k},\tilde{\tau })$ for different values of $\rho$ and for the standard deviation $s_v = 1.5$ (Study 4)

Fig. 5

Boxplot of $\Vert \textbf{M} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}$ with $(k,\tau ) = (\widehat{k},\widehat{\tau })$ the selected k and $\tau$, $(k,\tau ) = (k,\tau )$ the true values and $(k,\tau ) = (\widetilde{k},\widetilde{\tau })$ the oracle for different values of $\rho$ and for the standard deviation $s_v = 0.1$ (Study 4)

Fig. 6

Boxplot of $\Vert \textbf{M} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}$ with $(k,\tau ) = (\widehat{k},\widehat{\tau })$ the selected k and $\tau$, $(k,\tau ) = (k,\tau )$ the true values and $(k,\tau ) = (\widetilde{k},\widetilde{\tau })$ the oracle for different values of $\rho$ and for the standard deviation $s_v = 1.5$ (Study 4)

4.6 Study 5: robustness to nonnormality of the errors

Figure 7 and Table 4 display the results of the Student simulation. The joint heuristic retrieves the true values of k and $\tau$ in average, but with a slight overestimation of k for the extreme case ($\nu =3$). However, we observe a slight degradation in the quality of the estimation of $\textbf{M}$, which is more marked as we move away from the Gaussian hypothesis.

Fig. 7

Boxplot of $\Vert \textbf{M} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}$ with $(k,\tau ) = (\widehat{k},\widehat{\tau })$ the selected k and $\tau$, $(k,\tau ) = (k,\tau )$ the true values and $(k,\tau ) = (\widetilde{k},\widetilde{\tau })$ the oracle for different values of $\nu$ (Study 5)

Table 4 Estimated k and $\tau$, $(\hat{k},\hat{\tau })$, and the oracle $(\tilde{k},\tilde{\tau })$ for different values of $\nu$ (Study 5)

5 Using the TrendTM package

The version of the package is 2.0.19.

5.1 Comments on the package

The package is organized around the main function TrendTM. In this section, we present the arguments used in a call of this function to a dataset named Data$\_$Series

This function returns a list containing six elements:

• k_est, the estimated k or the true k when no selection is chosen;

• tau_est, the estimated $\tau$ or the true $\tau$ when no selection is chosen;

• M_est, the estimation of $\textbf{M}$ (M_est = U_estV_est if no temporal structure is considered and M_est = U_estV_est ${\varvec{\Lambda }}$ if a temporal structure is considered);

• U_est, the component U of the decomposition of $\widehat{\textbf{M}}$;

• V_est, the component V of the decomposition of $\widehat{\textbf{M}}$;

• contrast, the squared Frobenius norm of Data_Series - M_est. If k and $\tau$ are fixed, the contrast is an unique value; if k is selected and $\tau$ is fixed or if $\tau$ is selected and k is fixed, the contrast is a vector containing the norms for each visiting values of k or $\tau$ respectively; and if k and $\tau$ are selected, the contrast is a matrix with $k_\textrm{max}$ rows and $\tau _\textrm{max}$ columns such that $\text {contrast}_{k,\tau } =\Vert \mathbf{{Data\_Series}} -\widehat{\textbf{M}}_{k,\tau }\Vert _\mathcal {F}^{2}$.

5.1.1 Model selection

The selection of k or/and $\tau$ is requested using the options k_select or/and tau_select that are booleans. When there is no selection, the option is set to FALSE and k_max = k or/and tau_max =$\tau$. Note that if no trend is considered in the estimation procedure, $\tau = n$, otherwise tau_max must be a smaller than n and larger than $\texttt {k\_max} + 2$ in order to ensure that the rank of $\textbf{M}$ is k.

5.1.2 Taking the trend into account

Let us give more details about the different arguments of TrendTM that need to be specified when accounting for a temporal structure in the estimation procedure.

Two temporal structures are considered: periodic trend and smooth trend. This can be specified using the option struct_temp, struct_temp=“periodic” or struct_temp=“smooth” respectively. Recall that the selection of $\tau$ is only possible when a smooth trend is considered. Thus, when

• struct_temp=“periodic”, then tau_select=FALSE and tau_max$=\tau$. In this case, $\tau$ must be such that n is a multiple of $\tau$;

• struct_temp=“smooth”, then tau_select is either FALSE or TRUE. Whatever this choice, tau_max must be an odd number.

When no trend is taken into account, struct_temp=“none” and $\texttt {tau\_max} = n$.

5.1.3 Estimation of $\textbf{M}$, k and $\tau$ being fixed (Step 1)

The least squares estimator $\widehat{\textbf{M}}_{k,\tau }$ of $\textbf{M}$, given by (6), is obtained by using the softImpute function from the R package of the same name developed for matrix completion by Hastie and Mazumder (2015). In this package, two algorithms are implemented: ‘svd’ and ‘als’. In a simulation study, we observed that they have both provided the same accuracy of the estimator (results not shown). We decide to use the ‘als’ algorithm (als for Alternating Least Squares) by default but the choice is left free to the user in our package TrendTM. In this package, this choice is specified using the option type_soft.

5.1.4 The slope heuristic

Let us now focus on the selection problem of the rank k, and write the penalty as $\textrm{pen}(k)= \mathfrak c_{\textrm{cal},k}\varphi (k)$. The Slope heuristic, proposed by Birgé and Massart (2001), consists in estimating the slope $\widehat{s}$ of the contrast $\Vert \textbf{X} -\widehat{\textbf{M}}_{k,n}\Vert _\mathcal {F}^{2}$ as a function of $\varphi (k)$ with k ‘large enough’ and defining $\mathfrak c_{\textrm{cal},k} =-2 \widehat{s}$. The implementation of this heuristic requires the choice of the dimensions on which to perform the regression, that can be difficult in practice. To deal with this problem, Baudry et al. (2012) proposed to make robust regressions for dimensions between k and $k_{\max }$ for $k = 1,2,\dots$, resulting in different selected $\widehat{k}$. The choice of the final dimension is the maximal value $\widehat{k}$ such that the length of successive same $\widehat{k}$ is greater than the option point of the function DDSE of their R package capushe. In order to avoid some implementation problems as such condition is not reached and no k is selected, we decide to take the value $\widehat{k}$ associated to the maximal length of successive same $\widehat{k}$.

5.2 Application to pollution dataset

Let us use the package on a real dataset.¹ The dataset contains:

• The date in the (DD/MM/YYYY) format,

• The time in the (HH.MM.SS) format,

• The hourly average concentration of 10 toxic gases in the air: CO, PT08.S1, NMHC, C6H6, PT08.S2, NOx, PT08.S3, NO2, PT08.S4 and PT08.S5,

• The temperature in $^{\circ }\hbox {C}$,

• The relative humidity (RH) in %,

• The absolute humidity (AH).

The concentration of the 10 toxic gases, the temperature and the relative and absolute humidity have been recorded $n = 9357$ times during one year. We do a first step of data imputation using the function complete of the package softImpute since missing values (coded with $-200$) exist in this dataset (see Alquier et al. 2022 for more details on high-dimensional time series completion).

Our procedure selects $\widehat{k} = 7$ and $\widehat{\tau }= 13$. Figure 8 shows the obtained trend estimation for the 13 toxic gases. The denoising process seems to have been well applied to the data.

Fig. 8

Data (in grey) and trend estimation (in red) for the 13 toxic gases (red)

6 Link to PCA and clustering

In this section, we give a geometrical interpretation of the results when the factorization problem is solved via a svd using the link to PCA. We also propose a simple method for the clustering of high-dimensional time series based on their projections on the resulting subspace. This method is compared to different existing methods described and compared in Jacques and Preda (2014) on the benchmark ECG dataset.

The ECG dataset. The ECG dataset (taken from the UCR Time Series Classification and Clustering website) consists in 200 electrocardiograms from 2 groups of patients sampled at 96 time instants in which 133 are classified as normal and 67 as abnormal based on medical considerations. The time series are plotted in Fig. 9.

Fig. 9

The ECG dataset (black: normal, red: abnormal)

Geometrical interpretation of the factorization results. Recall that the PCA problem is solved using a svd (Singular Value Decomposition) leading to a matrix factorization. The svd solution is unique and generates orthogonal factors allowing graphical representations. Our framework without considering the temporal trend ($\mathbf \Lambda =\textbf{I}$) and by solving the optimization problem (3) with svd is thus equivalent to a PCA, up to a centering of the matrix $\textbf{X}$. The rank-k svd solution provides $\widehat{\textbf{U}}_k$ and $\widehat{\textbf{V}}_k$ such that $\widehat{\textbf{U}}_k=\textbf{X} \widehat{\textbf{V}}_{k}^{*}$ where $\widehat{\textbf{V}}_k^*$ is an othogonal matrix and the estimator of $\textbf{M}$ with rank k, i.e. the solution of (3), is $\widehat{\textbf{M}}_{k}=\widehat{\textbf{U}}_k \widehat{\textbf{V}}_k$. Consequently, the d lines of the matrix $\widehat{\textbf{U}}_k$ contains the coordinates of the projection of the d series on the first k axes, i.e. in the basis given by the k lines of the matrix $\widehat{\textbf{V}}_k$. When a temporal structure is taken into account, as for example a $\tau$-periodic, $\textbf{M}$ is estimated via the estimation of $\underline{{\textbf{M}}}$ resulting from a PCA on the transformed data $\underline{\textbf{X}}=\textbf{X} \mathbf \Lambda ^+$. Indeed, the estimator of $\textbf{M}$ is $\widehat{\textbf{M}}_{k,\tau } =\underline{\widehat{\textbf{M}}}_{k,\tau }{\varvec{\Lambda }}$ where $\underline{\widehat{\textbf{M}}}_{k,\tau }=\widehat{\textbf{U}}_k\widehat{\textbf{V}}_{k,\tau }{\varvec{\Lambda }}$ is the solution of (6) and thus the lines of $\widehat{\textbf{U}}_k$ contains the coordinates of the transformed time series ($\underline{\textbf{X}}$) in the basis defined by the lines of $\widehat{\textbf{V}}_{k,\tau }$.

Some remarks:

• this interpretation is only possible if the factorization is solved by svd. For example, this is no longer the case when the other classical NMF (Non Negativ Matrix Factorization) method is used;

• our work provides a criterion, theoretically performant, for the choice of the rank k, i.e. for the number of axes in PCA, usually chosen using empirical criteria;

• the svd requires the calculation of eigenvalues of a matrix which is numerically tedious when the dimension of the problem is very large as in our framework. In this case, the svd is performed using the R package softImpute;

• in a simple PCA, two projected time series are close if they share globally the same trend’s property. However, in a high-dimensional space (n high), the euclidean distance used in PCA can lose its meaning and a local trend similarity could be preferred as by using the temporal structure of the series.

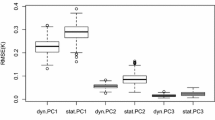
To illustrate the effect of the trend reduction (using ${\varvec{\Lambda }}^+$ on a period with length $\tau$), the PCA on the raw ECGs series and on the transformed ECGs series are represented in Fig. 10, respectively. The representation is given only on the two first axes (thus with $k=2$) and the series are colored according to the normal (black) and abnormal (red) status. For the transformed data, we considered that the temporal trend is periodic with period $\tau = 32$. The PCA on the raw data, called the raw PCA, is very structured with respect to the time. Let us consider the 28th and the 121th time series. These series are represented in Fig. 11 on the left in their raw version and after the temporal transformation on the right (called the transformed PCA). As we can observed, the raw series differ quite strongly at the beginning and at the end of time, which explains why they are quite far away on the principal components of the raw PCA. This difference is largely attenuated by the smoothing carried out by the transformation and they are close in the transformed PCA. We also compared to a Sparse PCA using the function SPC of the R package PMA (see Fig. 10). The projection is different from the transformed PCA and in particular the two previous series are no longer close or as far away as in the raw PCA.

Fig. 10

Top: PCA on $\textbf{X}$. Middle: PCA on $\underline{\textbf{X}}$ with a periodic trend ($\tau = 32$). Bottom: Sparse PCA for the ECGs series

Fig. 11

The 28th (dotted line) and the 121th (solid line) time series. Left: the raw series. Right: the transformed series with a periodic trend ($\tau =32$)

Clustering of the d times series.When dealing with high-dimensional data, a large category of methods proposed in the literature proceed in two steps: first we reduce the dimension of the data and second we perform the clustering (see Jacques and Preda 2014 for a review). Following this line, we propose here a very simple method which consists in applying a classical clustering method (that is here the well-known Hierarchical Agglomerative Clustering with the Ward’s linkage) to the projected series, i.e. on the rows of $\widehat{\textbf{U}}_k$. We apply this strategy on the ECG dataset for a fixed number of groups to 2 since we want to compare our results to those given in Jacques and Preda (2014) with different considerations: (1) with and without taking into account for a trend (here a periodic trend with $\tau =32$) and (2) for $k=2$ and for a selected number k.

The Correct Classification Rates (CCR), that is the quality criterion used by the authors, according to the known partitions are given in Table 5. We also report the CCR obtained for the best method among those tested in Jacques and Preda (2014). In addition, we indicate the time taken by the different methods on a laptop 1.6 GHz CPU. We observe that accounting for the trend improves significantly the clustering performances, which are the same compared to the best clustering method. However, our proposed strategy is clearly much more faster. We apply also the clustering on the sparse PCA result and obtained a CCR of 71 that is lower compared to both the raw and the transformed PCA.

Table 5 Correct classification rates (CCR) in percentage accounting or not for a trend on the ECG dataset and with a selection or not for k

Note that for the ECG dataset, when a trend is considered with $\tau =32$ and $\widehat{k}=6$, 3 groups is prefered according to the NbClust R package (chosen by the majority of model selection methods included in this package). Note that, in Fig. 12, the series of the ECG dataset are plotted on the left and their projections, colored according to the 3 groups, are provided on the right.

Fig. 12

Clustering of the ECG series with a periodic trend with $\tau =32$, $\widehat{k}=6$ and 3 groups. Left: the series and right: the PCA result, colored according to the groups

7 Conclusion

The penalized criterion developed in Alquier and Marie (2019) for high-dimensional time series analysis consists in selecting both the rank k of the matrix and the parameter $\tau$ related to the temporal structure. The penalty function involves a constant to be calibrated and depends on the temporal structure through its associated parameters to be estimated. For such minimization contrast estimation context, it is well-known in the literature that despite the selection of both parameters issue that is not standard, the calibration of penalty constant is not an easy task and many heuristics have been proposed to this aim. We proposed in this paper a two-stage strategy based on a popular heuristic: the slope heuristic proposed by Birgé and Massart (2001) and used in many statistical problems. We conducted a large simulation study to compare different heuristics as well as to study the performance of the method. In particular, through these simulations, we show that the joint heuristic performs well: the true values of k and $\tau$ are retrieved or underestimated when the estimation problem is more difficult, but with good reasons (the estimation is better than with the true values in this case). Moreover, whatever all the tested cases, the performance of the final estimator is comparable to that of the oracle. The method has been implemented in the R package TrendTM yet available on the CRAN and which is detailed in this paper. We also give a geometrical interpretation of the factorization results in the case of using a svd method for solving the optimization problem and propose a simple clustering method of multiple curves. On a benchmark dataset, we observed that this simple method works as well as the best ones proposed in the literature but is computationally much faster. Moreover, we show that accounting for the tendency in this dataset improve the clustering.

Our model assumes that the time series are independent. In some applications, this assumption is not realistic and a perpective of this work will be to take into account a between-series dependence.

Appendix

We give here details on the heuristics for the calibration of the penalty constant. Let us consider the model selection problem of selecting a parameter k in the set $\{1,\ldots ,k_{\text {max}}\}$ by minimizing a general penalized contrast:

$$\begin{aligned} \hat{k}(\beta ) \in \arg \min _{k} C(k) + \beta \ \textrm{pen}(k), \end{aligned}$$

where $\beta$ is the unknown penalty constant, C and $\textrm{pen}$ are the contrast and penalty function, respectively. The two well known heuristics for the calibration of one penalty constant are the following:

• the one proposed by Lavielle (2005), called ML in our paper. The idea of this heuristic is to select the dimension for which the curve C(k) w.r.t. $\textrm{pen}(k)$ ceases to decrease significantly, i.e. to look of a break in the slope of this curve. The author thus proposed the following automatic procedure:

  $$\begin{aligned} \hat{k}=\max _{k} \{k \in \{1,\ldots ,k_{\text {max}}\} \ \vert \ D(k)<S \} \end{aligned}$$

  where D(k) is the second derivative of the previous curve and S is a threshold to be fixed.

• the ‘slope heuristic’ proposed by Birgé and Massart (2001). The idea of this heuristic is based on two theoretical facts: first there exists a minimal penalty such that when the penalty is smaller then $\hat{k}$ is huge leading to overfitting, but when the penalty is larger then $\hat{k}$ is reasonable. Two data-driven algorithms have been proposed to search for this minimal penalty (see the huge paper dedicated to this heuristic Arlot and Massart 2009):

  • Slope: this heuristic consists in estimating the slope $\beta _s$ of C(k) as a function of $\textrm{pen}(k)$ for ‘large’ k and to consider $\hat{k}(\hat{\beta })$ where $\hat{\beta }=-2 \beta _s$.

  • Biggest Jump (BJ): this heursitic consists in taking the constant $\beta _{bg}$ associated to the biggest jump in the curve $\beta \mapsto \hat{k}(\beta )$ and to consider $\hat{k}(\hat{\beta })$ where $\hat{\beta }=2 \beta _{bg}$.