1 Introduction

Statistical quality control involves applying statistical methods to monitor and control processes, with the primary objective of ensuring consistency and compliance with predefined criteria. This underscores the critical importance of count data modeling in ensuring the accuracy and effectiveness of quality control measures. The serial dependence inherent in count data enables the effective use of integer-valued autoregressive time series models. Consequently, there is a growing recognition of the necessity for more flexible discrete models.

Time series models serve as indispensable tools for capturing distinct data features, especially when dealing with count data over time. The first-order integer-valued autoregressive (INAR(1)) process is a significant statistical model for studying autocorrelated count data, excelling in accurately representing counts when compared to Poisson and negative binomial models. Consequently, Al-Osh and Alzaid (1987) introduced the INAR(1) process with binomial thinning having Poisson marginals. Subsequently, other variations, such as the INAR(1) process with Poisson-transmuted exponential innovations proposed by Altun and Khan (2022), INAR(1) process with Poisson-extended exponential innovations presented by Maya et al. (2022), and INAR(1) process with new discrete Bilal innovations discussed by Ahsan-ul Haq et al. (2023), have emerged. Researchers are exploring these INAR(1) models to enhance their ability to fit real datasets optimally. This diverse collection of INAR(1) models has garnered substantial interest among researchers, undergoing in-depth exploration and contributing to the evolving landscape of time series modeling, particularly in fields like quality control.

Statistical quality control primarily focuses on count data, and the introduction of control charts has revolutionized this field, making them the primary method for process monitoring. Control charts are designed to maintain process stability and swiftly detect parameter shifts, classifying a process as “in control” if it adheres to a specified model. Consequently, efficient monitoring is essential to identify shifts in the mean promptly. The cumulative sum (CUSUM) and exponentially weighted moving average (EWMA) control charts are recognized for their ability to retain information over time and detect these changes. The frequently used conventional control charts often assume independent observations, a premise that may not consistently align with real-world scenarios. This necessitates the utilization of control charts in integer-valued time series models. As a result, Weiß and Testik (2011) proposed a CUSUM chart for monitoring the mean of the INAR(1) process with Poisson marginals. Some of the notable works include Li et al. (2022), Kim and Lee (2017) and Rakitzis et al. (2017). To enhance monitoring capabilities, EWMA charts have been introduced and compared with CUSUM charts. Following the CUSUM chart, Weiß (2011) discussed the corresponding EWMA chart. Some other works include Li et al. (2016, 2019) and Zhang et al. (2014).

Building on this foundation, our study delves into assessing the effectiveness of control charts in monitoring an INAR(1) process. Within this context, the associated discrete distributions are crucial in modeling the data. Although count data modeling has traditionally relied on Poisson and negative binomial distributions, the widespread occurrence of over-dispersion and notable skewness or kurtosis in real-world datasets has emphasized the necessity to create new models. Hence, we introduce a new discrete distribution and its associated INAR(1) process, incorporating it as innovations. Researchers have responded by introducing innovative discrete distributions through various methodologies. Here, we utilize survival discretization technique, and for a random variable (rv) X having a survival function \({\bar{F}}(x)=P(X>x)\), the corresponding probability mass function (pmf) is given by,

$$\begin{aligned} P(X=x)={\bar{F}}(x)-{\bar{F}}(x+1),\ x=0,1,2,3,\ldots . \end{aligned}$$
(1.1)

This method retains the shape of the hazard rate function (hrf) of the base model. Some of the works based on the above model include Krishna and Pundir (2009), El-Morshedy et al. (2020) and Altun et al. (2022).

Motivated by the aforementioned works, this study introduces a novel discrete mixture exponential (DME) distribution by utilizing survival discretization technique to the mixture exponential (ME) distribution proposed by Mirhossaini and Dolati (2008). The distribution’s statistical characteristics are examined, and the performance of parameter estimation approaches is assessed through a simulation study. The superior performance of the DME distribution in real data analysis allows us to explore the INAR(1) process with DME distributed innovation, denoted as the INAR(1)DME process. The superior performance of the INAR(1)DME process in real data analysis further enables us to utilize it in the field of quality control

In the context of quality control, to monitor the mean of the INAR(1)DME process, CUSUM and EWMA control charts are developed, and their statistical design and performance in detecting increasing shifts in process mean levels are investigated. The analysis encompasses the evaluation of control chart properties, particularly their average run length (ARL), which indicates their sensitivity in detecting mean changes within the process. A comparative assessment of both monitoring approaches is also undertaken, providing insights into their performance. The effectiveness of the control chart under the INAR(1)DME process in detecting shifts in the process mean is assessed by utilizing real data.

The paper is structured as follows: Sect. 2 provides an overview of the construction and characteristics of the DME distribution. Section 3 introduces the associated statistical properties, including the moment generating function (mgf), moments, skewness, and kurtosis. Section 4 delves into the discussion of parameter estimation methods and assessing their performance using a Monte Carlo simulation study. Section 5 evaluates the performance of the proposed distribution using a real data set. Section 6 introduces the INAR(1) process with DME innovations and discusses its properties, including estimation, simulation, and real data analysis. Section 7 focuses on the statistical process control procedure for INAR(1)DME processes, utilizing the CUSUM and EWMA approaches to detect mean increases, accompanied by numerical simulation and real data analysis. The study is concluded in Sect. 8.

2 The discrete mixture exponential distribution

Let X be a rv following the ME distribution. The probability density function and cumulative distribution function (cdf) of the ME distribution are given by,

$$\begin{aligned} g(x; \alpha , \theta )=\theta e^{-\theta x}\left\{ 1+\alpha \left( 2 e^{-\theta x}-1\right) \right\} , \quad x>0, \end{aligned}$$

and

$$\begin{aligned} G(x; \alpha , \theta )=\left( 1-e^{-\theta x}\right) \left( 1+\alpha e^{-\theta x}\right) , \quad x>0, \end{aligned}$$
(2.1)

where \(\theta >0,\ -1 \le \alpha \le 1\).

Applying (1.1) to (2.1), along with the reparameterization \(\lambda = e^{-\theta }\), yields the DME distribution, as outlined in the following proposition.

Proposition 2.1

Let \(X\sim \mathrm{DME}(\alpha ,\lambda )\), then the pmf is given by,

$$\begin{aligned} P(X=x)= \lambda ^x\ (1-\lambda )\ (1-\alpha ) +\alpha \ \lambda ^{2x}\ (1-\lambda ^2),\ x=0,1,2,..., \end{aligned}$$
(2.2)

where \(0<\lambda <1\) and \(-1\le \alpha \le 1\).

The corresponding cdf is given by,

$$\begin{aligned} F(x)= \left( 1-\lambda ^{(1+x)}\right) \left( 1+\alpha \lambda ^{(1+x)}\right) . \end{aligned}$$
Fig. 1
figure 1

Pmfs of the DME distribution for different parameter values

Full size image

The pmf of the DME distribution always decreases for \(-0.3<\alpha <1\) since,

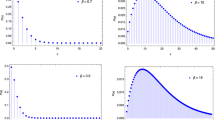
$$\begin{aligned} p^{'}(x)=(1 - \alpha )\ (1 - \lambda )\ \lambda ^x\ \log (\lambda ) + 2\ \alpha \ \lambda ^{2 x}\ (1 - \lambda ^2)\ \log (\lambda )<0. \end{aligned}$$

Figure 1 displays the pmf plots of the DME distribution. It can be seen that the DME distribution is rightly skewed and unimodal.

3 Statistical properties

This section discusses the DME distribution’s hrf, mgf, moments, skewness, and kurtosis. The hrf of the DME distribution is obtained as,

$$\begin{aligned} h(x)=\frac{(1 - \lambda ) (1 + \alpha (\lambda ^x + \lambda ^{( 1 + x)}-1))}{\lambda - \alpha \lambda + \alpha \lambda ^{( 2 + x)}}. \end{aligned}$$
Fig. 2
figure 2

Hazard rate function of the DME distribution for different parameter values

Full size image

Figure 2 showcases the DME distribution’s hrf, illustrating its ability to exhibit increasing \((-1\le \alpha <0)\), decreasing \((0<\alpha <1)\) and constant (\(\alpha =0\)) behaviors.

The mgf of the DME distribution is given by,

$$\begin{aligned} M_X(t)& {}= \sum _{x=0}^{\infty } e^{tx}\ \{\lambda ^x (1-\lambda )(1-\alpha ) +\alpha \lambda ^{2x} (1-\lambda ^2)\}\\& {}= \frac{(1-\lambda )(1-\alpha )}{1-\lambda e^t}+\frac{\alpha (1-\lambda ^2)}{1-\lambda ^2 e^t}\\& {}= \frac{(1 - \lambda ) (( e^t-1 ) \alpha \lambda + e^t \lambda ^2-1 )}{((1 - e^t \lambda ) ( e^t \lambda ^2-1 ))},\ \lambda e^t <1. \end{aligned}$$

The \(r\)th moment about the origin of X is given by,

$$\begin{aligned} \mu _r^{'}=\sum _{x=0}^{\infty }x^r\lambda ^x (1-\lambda )(1-\alpha ) +\alpha \lambda ^{2x} (1-\lambda ^2),\ r=1,2,3,.. \end{aligned}$$

Then, the mean and variance of the DME distribution are given by,

$$\begin{aligned} E(X)=\frac{\lambda (1 - \alpha + \lambda ) }{(1 - \lambda ^2)}\ \mathrm{and}\ Var(X)= \frac{\lambda ( (1 + \lambda )^2-\alpha ^2 \lambda - \alpha (1 + \lambda ^2))}{(1 -\lambda ^2)^2 }. \end{aligned}$$
(3.1)

Using (3.1), the dispersion index (DI) of the DME distribution, which quantifies variability, is given by,

$$\begin{aligned} DI(X)=\frac{Var(X)}{E(X)}=\frac{\alpha ^2 \lambda - (1 + \lambda )^2 + \alpha (1 + \ \lambda ^2)}{( \lambda -1 ) (1 + \lambda ) (1 - \alpha + \ \lambda )}. \end{aligned}$$

The shape and characteristics of the DME distribution are analyzed using the moment measures of skewness and kurtosis, which are given by,

$$\begin{aligned} S(X)&= \frac{\left[ E\left( X-E(X)\right) ^3\right] ^2}{\left[ Var(X)\right] ^3}\\&= \frac{((1 + \lambda )^3 (-1 - 3 \lambda + 4 \lambda ^2) + \alpha ^2 \lambda (1 + 6 \lambda + 11 \lambda ^2) + \alpha (1 + 4 \lambda + 2 \lambda ^2 - 16 \lambda ^3 - 9 \lambda ^4))^2}{\lambda ( (1 + \ \lambda )^2-\alpha ^2 \lambda - \alpha (1 + \lambda ^2))^3}, \\ K(X)&= \frac{E\left( X-E(X)\right) ^4}{\left[ Var(X)\right] ^2} \\&=\frac{ (1 + \lambda )^4 (1 + 7 \lambda + \lambda ^2) -3 \alpha ^4 \lambda ^3 - 6 \alpha ^3 (\lambda ^2 + \lambda ^4) - 2 \alpha ^2 \lambda (2 + 3 \lambda + 14 \lambda ^2 + 3 \lambda ^3 + 2 \lambda ^4)}{\lambda (\alpha ^2 \ \lambda - (1 + \lambda )^2 + \alpha (1 + \lambda ^2))^2} \\&\quad -\frac{\alpha (1 + 6 \lambda + 23 \lambda ^2 + 12 \lambda ^3 + 23 \lambda ^4 + 6 \lambda ^5 + \lambda ^6)}{\lambda (\alpha ^2 \ \lambda - (1 + \lambda )^2 + \alpha (1 + \lambda ^2))^2}. \end{aligned}$$

See “Appendix” for more details.

Fig. 3
figure 3

DI of the DME distribution for different parameter values

Full size image

From the 3D plot of DI given in Fig. 3, it is clear that DI is greater than 1. The 3D plots in Fig. 4 illustrate the graphical representation of skewness and kurtosis, indicating the right-skewed leptokurtic behavior of the DME distribution. Table 1 illustrates the variation in mean, variance, DI, skewness, and kurtosis with respect to the values of \(\alpha\) and \(\lambda\). The mean, variance and DI consistently increase, while skewness and kurtosis decrease with the rise in \(\lambda\) for a fixed \(\alpha \in [-1,1]\) and \(\alpha \in (-0.3,1]\), respectively.

Fig. 4
figure 4

Skewness (a) and kurtosis (b) of the DME distribution for different parameter values

Full size image
Table 1 The mean, variance, DI, skewness and kurtosis of the DME distribution
Full size table

4 Estimation

This section discusses the maximum likelihood (ML) and least squares (LS) parameter estimation for the DME distribution.

4.1 Maximum likelihood estimation

Let \(x=(x_1,x_2,...,x_n)\) be a sample of size n from the DME distribution. Then, the log-likelihood function is given by,

$$\begin{aligned} \log L(\alpha ,\lambda )= \sum _{i=1}^{n} \log\{\lambda ^{x_i} (1-\lambda )(1-\alpha ) + \alpha \lambda ^{2x_i}(1-\lambda ^2)\}. \end{aligned}$$
(4.1)

Since \(\frac{ \partial \log L(\alpha ,\lambda )}{\partial \alpha } = 0\) and \(\frac{ \partial \log L(\alpha ,\lambda )}{\partial \lambda } = 0\) failed to give explicit solutions, the maximum likelihood estimates (MLEs) \({\hat{\alpha }}\) and \({\hat{\lambda }}\) of \(\alpha\) and \(\lambda\) are obtained by direct maximization of (4.1) using numerical methods. To this end, one can use the optim function in R software.

The observed Fisher information matrix of \({\hat{\alpha }}\) and \({\hat{\lambda }}\) is given by,

$$\begin{aligned} {\hat{J}}_n=-\left. \begin{bmatrix} \frac{\partial ^2 \log L(\alpha ,\lambda )}{\partial \alpha ^2}&{}\frac{\partial ^2 \log L(\alpha ,\lambda )}{\partial \alpha \partial \lambda }\\ \frac{\partial ^2 \log L(\alpha ,\lambda )}{\partial \lambda \partial \alpha }&{}\frac{\partial ^2 \log L(\alpha ,\lambda )}{\partial \lambda ^2} \end{bmatrix}\right| _{(\alpha ,\lambda )=({\hat{\alpha }},{\hat{\lambda }})} \end{aligned}$$

Hence, the variance-covariance matrix is obtained as

$$\begin{aligned} \Sigma = {{\hat{J}}_n}^{-1}. \end{aligned}$$

4.2 Least squares estimation

Let \(x_{i:n}\) be the ith order statistic of the sample \(x=(x_1,x_2,..,x_n)\). The  LS estimates (LSEs) of the parameters are obtained by minimizing the following equation:

$$\begin{aligned} LSE(\alpha ,\lambda )=\sum _{i=1}^n\left[ \{(1-\lambda ^{(1+x_{i:n})})(1+\alpha \lambda ^{(1+x_{i:n})})\}-\frac{i}{n+1}\right] ^2. \end{aligned}$$

To this end, one can use the optim function in R software.

Table 2 Simulation results of the DME distribution
Full size table

 

4.3 Simulation

The performance of the estimation methods is assessed through a simulation study. The simulation is conducted with \(N=1000\) replications for sample sizes n of 100, 200, 300, 400, and 500, encompassing various parameter values. The following quantities are computed.

  1. 1.

    Average bias (Bias), Bias(\({\hat{a}}\))=\(\frac{1}{N}\sum \nolimits _{i=1}^{N}({\hat{a}}_{i}-a),\) where \({\hat{a}}_{i}\) is the \(i\)th estimate of the parameter a, \(a\ \in \{\alpha ,\ \lambda \}\), for \(i=1,2,\ldots ,N\).

  2. 2.

    Root mean square error (RMSE), RMSE\(({\hat{a}})=\sqrt{\frac{1}{N}\sum \nolimits _{i=1}^{N}({{\hat{a}}}_{i}-a)^{2}}.\)

Table 2 lists the Bias and RMSE for the MLEs and LSEs of the parameters \(\alpha\) and \(\lambda\). As n increases, both Bias and RMSE decrease for the ML and LS methods. Additionally, a significant decrease in both Bias and RMSE is observed when comparing the ML method to the LS. Thus, ML estimation performs very well and is appropriate for small and large sample sizes.

5 Data analysis

The corn-borer data comprises 120 observations of European corn-borer larvae (Pyrausta) numbers in the field (Bodhisuwan and Sangpoom 2016), is considered to to evaluate how well the DME distribution fits the data. The Poisson distribution, the discrete Burr (DB) distribution (Krishna and Pundir 2009), the discrete Gumbel (DG) distribution (Chakraborty and Chakravarty 2014), the discrete log-logistic (DLL) distribution (Para and Jan 2016), the discrete Bilal (DBL) distribution (Altun et al. 2022), the discrete Pareto (DPR) distribution (Krishna and Pundir 2009), and the discrete Rayleigh (DR) distribution (Roy 2004), are chosen for comparison.

Table 3 MLEs with SEs and 95% CI, information criteria and goodness-of-fit measures for the various distributions for corn-borer data
Full size table
Fig. 5
figure 5

Observed and expected frequencies of the corn-borer data under various distributions

Full size image

The unknown parameters are obtained using the ML method, along with the standard error (SE) and 95% confidence interval (CI) for the considered models. Model performance is assessed using some widely accepted information criteria and goodness-of-fit statistics. Smaller values of the Akaike information criterion (AIC) and Bayesian information criterion (BIC), as well as larger log-likelihood (logL) values, indicate the adequacy of the model. Furthermore, the goodness-of-fit for each fitted distribution is assessed using the chi-square test, where a small \(\chi ^2\) value and a large p-value indicate a good fit.

Table 3 makes it abundantly clear that the DME distribution is the best of the competitive models under consideration because it has the lowest AIC and BIC, the highest logL, and p-value, respectively.

The observed and expected frequencies of corn-borer data under various distributions are displayed in Fig. 5. The expected frequencies align more closely with the theoretical values under the DME distribution than the other considered distributions. Hence, the DME distribution performs better than the considered alternatives in modeling the data.

6 INAR(1) process with discrete mixture exponential innovations

In this section, the INAR(1) process with innovations following the DME distribution is developed. For this purpose, the INAR(1) model with a binomial thinning operator that employs independent Bernoulli counting series rvs is utilized.

Definition 6.1

The binomial thinning operator is defined as,

$$\begin{aligned} p \circ X= \sum _{i=1}^{X} B_i,\ p \in (0,1), \end{aligned}$$

where X is a non-negative integer-valued rv and \(\{B_i\}\) is a sequence of independent and identically distributed (iid) rvs with Bernoulli (p) distribution and is independent of X.

6.1 INAR(1)DME process

The INAR(1)DME process is given by,

$$\begin{aligned} X_t= p \circ X_{t-1}+\epsilon _t,\ t\ge 2, \end{aligned}$$

where “\(\circ\)” is the binomial thinning operator, \(\{\epsilon _t\}\) is a sequence of iid rvs from DME(\(\alpha ,\lambda\)) and \(\epsilon _t\) is independent of Bernoulli counting process \(\{B_i\}\) and \(X_m\) for all \(m \le t\).

The one-step transition probability of the INAR(1) process is given by,

$$\begin{aligned} P\left( X_t=k \mid X_{t-1}=l\right) =\sum _{i=0}^{\min (k,l)} \ \left( {\begin{array}{c}l\\ i\end{array}}\right) p^i(1-p)^{l-i} P\left( \epsilon _t=k-i\right) , \quad k, l \ge 0. \end{aligned}$$

Then, the one-step transition probability of the INAR(1)DME process is given by,

$$\begin{aligned} P\left( X_t=k \mid X_{t-1}=l\right) =\sum _{i=0}^{\min (k-l)} \ \left( {\begin{array}{c}l\\ i\end{array}}\right) p^i(1-p)^{l-i}\ \{\lambda ^{k-i} (1-\lambda )(1-\alpha ) +\alpha \lambda ^{2k-i} (1-\lambda ^2)\}. \end{aligned}$$
(6.1)

Also, the stationary marginal density of \(\{X_t\}\) is given by,

$$\begin{aligned} P\left( X_t=k\right)&= \sum _{l=0}^{\infty } P\left( X_t=k \mid X_{t-1}=l\right) P\left( X_{t-1}=l\right) \nonumber \\&= \sum _{l=0}^{\infty }\sum _{i=0}^{\min (k-l)} \ \left( {\begin{array}{c}l\\ i\end{array}}\right) p^i(1-p)^{l-i}\ \{\lambda ^{k-i} (1-\lambda )(1-\alpha ) +\alpha \lambda ^{2k-i} (1-\lambda ^2)\}. \end{aligned}$$
(6.2)

From Weiß (2018), the mean and variance of \(\{X_t\}\) can be computed using (3.1) as,

$$\begin{aligned} E(X_t)& {}= \mu _X= \frac{(1 - \alpha + \lambda ) \lambda }{(1 - \lambda ^2) (1-p)}, \end{aligned}$$
(6.3)
$$\begin{aligned} Var(X_t)& {}= \frac{\lambda ([ (1 + p (1 - \lambda )) (1 + \lambda )^2] -\alpha ^2 \lambda - \alpha (1 + p + \lambda ^2 - p \ \lambda ^2))}{(1 - p^2) (1 - \lambda ^2)^2}. \end{aligned}$$
(6.4)

Then, the DI of \(\{X_t\}\) is given by,

$$\begin{aligned} {\text{DI}}({{{X}}_{{t}}})= \frac{ [(1 + p (1 - \lambda )) (1 + \ \lambda )^2] -\alpha ^2 \lambda - \alpha (1 + p + \lambda ^2 - p \ \lambda ^2)}{(1 + p) (1 - \lambda ^2) (1 - \ \alpha + \lambda )}. \end{aligned}$$
(6.5)
Table 4 DI of \(\{X_t\}\) for various parameter values
Full size table

Table 4 provides the DI of \(\{X_t\}\) across different parameter configurations, indicating the model’s ability to accommodate over-dispersed data. The one-step-ahead conditional mean and variance of the INAR(1)DME process are given by,

$$\begin{aligned} E(X_t|X_{t-1})& {}\,=\, p\ X_{t-1}+\frac{(1 - \alpha + \lambda ) \lambda }{(1 - \lambda ^2)}, \end{aligned}$$
(6.6)
$$\begin{aligned} Var(X_t|X_{t-1})& {}\,=\, p\ (1-p)\ X_{t-1}+ \frac{\lambda ( (1 + \lambda )^2-\alpha ^2 \lambda - \alpha (1 + \lambda ^2))}{(1 -\lambda ^2)^2 }. \end{aligned}$$
(6.7)
Table 5 Simulation results of INAR(1)DME process
Full size table

6.2 Estimation

This section discusses the conditional maximum likelihood (CML) and conditional least squares (CLS) parameter estimation for the INAR(1)DME process.

6.2.1 Conditional maximum likelihood

The knowledge of the transition probabilities is sufficient for the creation of the likelihood function in the CML technique. For a given sample \(x_1, x_2,..., x_n\) from the INAR(1)DME process, the conditional log-likelihood function is given by,

$$\begin{aligned} l(p,\alpha ,\lambda )=\sum _{t=2}^{n}\log[ P\left( X_t=x_t \mid X_{t-1}=x_{t-1}\right)] , \end{aligned}$$
(6.8)

where \(x_1\) is fixed, and \(P\left( X_t=x_t \mid X_{t-1}=x_{t-1}\right)\) is given by (6.1). The CML estimates (CMLEs) of the parameters p, \(\alpha \ \mathrm{and}\ \lambda\) are obtained by maximizing (6.8) using the optim function in R software.

6.2.2 Conditional least squares estimation

The CLS estimates (CLSEs) of parameters p, \(\alpha \ \mathrm{and}\ \lambda\) are obtained by minimizing the following equation,

$$\begin{aligned} L(p,\alpha ,\lambda )=\sum _{t=2}^{n}(x_t-E(X_t|X_{t-1}=x_{t-1}))^2. \end{aligned}$$

To this end, one can use the optim function in R software.

6.3 Simulation

A simulation study was performed to assess the performance of the CML and CLS estimation methods under the INAR(1)DME process. The simulation is carried out by taking \(N=\) 1000 replications for samples of sizes n = 50, 100, 150, 200, and 250 with different parameter values. The Bias and RMSE are computed accordingly.

Table 5 shows that as n increases, Bias and RMSE decrease for both methods. The CMLEs exhibit lower Bias and RMSE compared to the CLSEs. Hence, the CML estimation method performs very well and is suitable for both small and large sample sizes.

6.4 Empirical study

Here, an example is presented to demonstrate the application of the INAR(1)DME process in fitting a real-world data set.

6.4.1 Methodology

Utilizing model adequacy criteria, the introduced INAR(1)DME process is compared with some existing models. To that end, the existing INAR(1) process with some well-known discrete innovations are used. The following are considered:

  • INAR(1) process with Poisson marginals, (Al-Osh and Alzaid 1987) (INARP(1))

  • INAR(1) process with negative binomial marginals, (McKenzie 1986) (INARNB(1))

  • quasi-binomial INAR(1) process with generalized Poisson marginals, (Alzaid and Al-Osh 1993) ( QINARGP(1))

  • random coefficient INAR(1) process with negative binomial marginals, (Weiß 2008) (RCINARNB(1))

  • iterated INAR(1) process with negative binomial marginals, (Al-Osh and Aly 1992) (IINARNB(1))

  • negative binomial thinning-based INAR(1) process with geometric marginals, (Ristić et al. 2009) (NBINARG(1))

  • INAR(1) process with geometric marginals, (Alzaid and Al-Osh 1988) (INARG(1))

  • dependent counting INAR(1) process with geometric marginals, (Ristić et al. 2013) (DCINARG(1))

  • INAR(1) process with zero-inflated Poisson innovations, (Jazi et al. 2012b) (INAR(1)ZP)

  • INAR(1) process with geometric innovations, (Jazi et al. 2012a) (INAR(1)G)

  • INAR(1) process with Katz family innovations, (Kim and Lee 2017) (INAR(1)KF)

The CML method is employed for parameter estimation. Subsequently, logL, AIC, BIC, and RMSE\(^*\) for all the models described above are computed.. The RMSE\(^*\) measures the differences between true values and one-step conditional expectation and is given by,

$$\begin{aligned} \mathrm {RMSE^*} =\sqrt{\frac{1}{N} \sum _{n=1}^N\left( x_n-{\hat{x}}_n\right) ^2}, \end{aligned}$$

where \({\hat{x}}_n,\ n = 1, 2,\ldots , N,\) is the predicted value, which is the realization of \({\hat{X}}_t\) and are given by,

$$\begin{aligned} {\hat{X}}_1& {}\,=\, E\left( X_t\right) _{\hat{\theta }_{\mathrm{CML}}}, \\ {\hat{X}}_t& {}\,=\, E\left( X_t \mid X_{t-1}\right) _{\hat{\theta }_{\mathrm{CML}}},\ t=2, \ldots , n, \end{aligned}$$

where \(\hat{\theta }_{\mathrm{CML}}\) is the CMLE of the parameter vector \((p,\alpha ,\lambda )\). A model exhibiting a large logL along with small AIC and BIC values offers the optimal fit to the data. Additionally, it holds the potential for good forecasts if its RMSE\(^*\) is the minimum among the models under consideration.

Further, the standardized Pearson residuals are used to check whether the INAR(1)DME process is a good fit for the data set. They are calculated using the following formula:

$$\begin{aligned} r_t=\frac{x_t-E\left( x_t \mid X_{t-1}=x_{t-1}\right) }{V\left( x_t \mid X_{t-1}=x_{t-1}\right) ^{1 / 2}}, \end{aligned}$$

where \(E(X_t|X_{t-1})\) and \(Var(X_t|X_{t-1})\) are given in (6.6) and (6.7), respectively. If the INAR(1) process is well-fitted, then the Pearson residuals are uncorrelated and have zero mean and unit variance (Harvey and Fernandes 1989). The residuals autocorrelation function (ACF) is plotted to see if they are uncorrelated.

6.4.2 Burglary data set

The burglary data from the Forecasting Principles site

(http://www.forecastingprinciples.com), which was used to fit the INAR(1)KF process introduced by Kim and Lee (2017) is considered here for demonstrating the capability of the introduced model. The data set contains 144 observations from January 1990 to December 2001, and it provides monthly counts of burglaries in the 65th police car beat in Pittsburgh. The mean and variance of this data set are 5.9583 and 17.8304, respectively.

Fig. 6
figure 6

The time series plot of the burglary data set

Full size image
Fig. 7
figure 7

The ACF (a) and PACF (b) plot for the burglary data set

Full size image

Figure 6 depicts the burglary data set’s time series plot. The ACF and partial ACF (PACF) plots are displayed in Fig. 7. Here, only the first lag is significant in the PACF plot, and the ACF plot displays an exponential decay, facilitating to model the data as an INAR(1) process.

Table 6 The CMLEs, logL, AIC, BIC and RMSE\(^*\) of the considered processes for the burglary data set
Full size table

Table 6 lists the CMLEs, logL, AIC, BIC and RMSE\(^*\), for different processes. The maximum value of logL and minimum values of AIC and BIC for the INAR(1)DME process prove that it provides a better fit than the contending models. Also, it can provide a good forecast since the RMSE\(^*\) value is the lowest among the considered models. Hence, it is convincing that the INAR(1)DME process effectively explains the data set’s characteristics.

To check whether the fitted INAR(1)DME process is statistically accurate, residual analysis is done with the Pearson residuals. The ACF of the Pearson residuals is displayed in Fig. 8, showing no autocorrelation for the Pearson residuals. To ensure this, the Ljung-Box test for the presence of autocorrelation is done with degrees of freedom 10 and has the p-value = 0.0771 > 0.05. It indicates that the residuals are uncorrelated. Also, the mean and variance of Pearson residuals are 0.00183 and 1.1235, close to the preferred values 0 and 1, respectively, validating a good fit. Hence, the INAR(1)DME process fits the burglary data set.

Fig. 8
figure 8

The ACF plot of the Pearson residuals

Full size image

The INAR(1)DME model for the burglary data set is given by,

$$\begin{aligned} X_t= 0.2551\, {\circ}\,X_{t-1}+ \epsilon _t,\ t\ge 2, \end{aligned}$$

where \(\epsilon _t\sim\) DME(\(-\)0.9999, 0.7368).

The predicted values can be obtained by

$$\begin{aligned} {\hat{x}}_1& {}= 5.9223.\\ {\hat{x}}_t& {}= \ 0.2551\ {\hat{x}}_{t-1} + 4.4118,\ t=2,3,\ldots , 144. \end{aligned}$$

7 Control charts for monitoring mean of the INAR(1)DME process

This section explores an efficient control chart for monitoring the mean of the INAR(1)DME process. In INAR(1) processes, upward shifts in the process mean indicate a collective rise in associated factors for entities, such as unemployment rate, defect percentage, and disease spread. Identification and timely reporting of such shifts are typically vital. Therefore, focusing on practical applications, this session investigates the mean upward shift within the INAR(1)DME process.

Here, the upper-sided control chart is constructed by exclusively focusing on detecting upward shifts in \(\mu _X\), as they are directly linked to process deterioration. The primary purpose is to detect quickly and accurately a change in the \(\mu _X\). It is more intuitive to directly monitor the process \(\{X_t\}\) while accounting for the impact of autocorrelation. A process is considered in control when it adheres to a specified model. Conversely, a process is deemed out of control when the parameters within the model change rather than the model itself changing. When the process is in control, the parameter values of the INAR(1)DME process will be denoted as \(p_0\), \(\alpha _0\), and \(\lambda _0\). An increasing shift in \(\mu _X\) may occur if one of the parameters p, \(\alpha\) and \(\lambda\) have changed appropriately.

Table 7 Mean of \(\{X_t\}\) of INAR(1)DME process
Full size table

It is clearly seen in Table 7 that \(\mu _X\) is affected by variations in the parameters within the INAR(1)DME process. Also, with a rise in p and \(\lambda\), there is an increase in the value of \(\mu _X\), and with a rise in \(\alpha\) in the intervals \([-0.9, -0.1]\) and [0.1, 0.9], there is a decrease in the values of \(\mu _X\). So, to effectively monitor INAR(1) processes, CUSUM and EWMA control charts are employed and their efficiency is assessed.

7.1 The CUSUM chart

Initially proposed by Page (1961), the CUSUM chart operates on the fundamental principle of the sequential probability ratio test. Its primary objective is to gather and accumulate information from sample data, thus magnifying the impact of minor process deviations. Numerous studies have extensively demonstrated the effectiveness of the CUSUM chart in monitoring time series comprising integer values, including Poisson INAR(1) by Weiß and Testik (2009) and Weiß and Testik (2011), geometrically inflated Poisson INAR(1) by Li et al. (2022), and zero-inflated Poisson INAR(1) by Rakitzis et al. (2017).

Here, the CUSUM control chart is devised due to their sensitivity in detecting small shifts. Furthermore, CUSUM charts also have known optimality properties when detecting a sustained shift from a known in control distribution to a specified out of control distribution (Weiß and Testik 2009).

From Weiß and Testik (2009), let \(C_0 = c_0,\ c_0 \in N_0\). A CUSUM statistic with reference value k is obtained as,

$$\begin{aligned} C_t = max(0, X_t - k + C_{t-1}),\ t = 1, 2, \ldots \end{aligned}$$

Here \(c_o \ge 0\) is the starting value. For \(\mu _X<k<h\), the monitoring statistics \(\{C_t\}\) are plotted on a CUSUM chart with control region [0, h], where h is the upper control limit. The INAR(1)DME process is considered as being in control unless \(C_t > h\). The reference value k prevents the chart from drifting towards control limits during in control processes and offers the ability to fine-tune chart sensitivity to specific shifts in the process mean.

7.2 The EWMA chart

Initially proposed by Roberts (2000), the EWMA chart operates on the fundamental principle of giving the highest weight to the nearest samples in the time series while previous samples contribute minimally. The EWMA chart is useful for detecting persistent shifts for INAR processes (Weiß 2009).

From Weiß (2011), let \(Q_0 = q_0,\ q_0\in \{0,1,...,u-1\}\) and \(\theta \in (0,1]\). An EWMA statistic of the INAR(1) process is given by,

$$\begin{aligned} Q_t = round (\theta \ X_t + (1 - \theta )\ Q_{t-1}),\ t \in N_0, \end{aligned}$$

where \(round (x) = z\) if and only if the integer \(z \in (x - 1/2, x + 1/2]\). Let \(u \in N\) with \(u>1\). The statistics \(Q_t\) are plotted on an EWMA chart with control region [1, u], where u is the upper control limit. The process is considered in control unless an out of control signal \(Q_t \ge u\) is triggered.

7.3 Performance of the INAR(1)DME control charts

The ARL is a commonly used measure to evaluate the effectiveness of a control chart in statistical process control. It represents the expected number of data points plotted on the control chart before it signals an out of control condition. Two specific types of ARL are considered: ARL\(_0\), also known as in control ARL, measures the number of data points plotted from the beginning of monitoring until a false alarm is triggered. On the other hand, ARL\(_1\), referred to as out of control ARL, quantifies the number of data points plotted from the start of a process shift until the chart detects that shift. To have an effective control chart, a high ARL\(_0\) combined with a small ARL\(_1\) is essential.

7.3.1 ARL of CUSUM chart

For a given \(C_0=c_0\), the values of (k, h) are chosen to ensure that the ARL\(_0\) closely matches a specified value. As \(\{X_t,\ C_t\}\) of the INAR(1)DME process forms a bivariate Markov chain, the Markov chain approach introduced in Weiß and Testik (2009) is used here for computing ARL. To offer a comprehensive overview, the computational approach is briefly outlined as follows.

Let us consider the case where \(h,\ k,\ c_0\ \in N_0\). Whenever \(X_t > k+h\), it leads to an out of control signal since \(C_t\) exceeds h if and only if \(X_t - k + C_{t-1} \ge h\). Hence, the attainable in control range of \((X_t,\ C_t)\) needs to be restricted. From Weiß and Testik (2009), under the CUSUM chart, the set of attainable in control values for the bivariate Markov process \(\{X_t,\ C_t\}\) is given by,

$$\begin{aligned} \mathcal{C}\mathcal{R}=\{(x, i)\ |\ 0 \le \ i\ \le h- 1,\ max(0,i+k-h+1)\le \ x\ \le i+k\}, \end{aligned}$$

which is of size

$$\begin{aligned} |\mathcal{C}\mathcal{R}|=\frac{1}{2}(h-k)(h+k+1)+h k. \end{aligned}$$
(7.1)

The above arguments can also be extended if \(h,\ k\) and \(c_0\) are permitted to assume values from the set \(\{r/s | r \in \mathbb {N}_0\}\), where the common denominator \(s \in \mathbb {N}, s > 1\).

From Li et al. (2022), the transition probability matrix of \((X_t,\ C_t)\) is expressed as,

$$\begin{aligned} Q^\top \triangleq (p(n, j|m, i))_{(n,j),(m,i)\ \in \ \mathcal{C}\mathcal{R}}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} p(n, j \mid m, i)&\triangleq P\left( X_t=n, C_t=j \mid X_{t-1}=m, C_{t-1}=i\right) \\&=P\left( C_t=j \mid X_t=n, X_{t-1}=m, C_{t-1}=i\right) \ P\left( X_t=n \mid X_{t-1}=m, C_{t-1}=i\right) \\&=\delta _{j, \max (0, n-k+i)}\ P\left( X_t=n \mid X_{t-1}=m\right) . \end{aligned} \end{aligned}$$

The initial probabilities are,

$$\begin{aligned} \begin{aligned} p\left( m, i \mid c_0\right)&\triangleq P\left( X_1=m, C_1=i \mid C_0=c_0\right) \\&=P\left( C_1=i \mid X_1=m, C_0=c_0\right) \ P\left( X_1=m \mid C_0=c_0\right) \\&=\delta _{i, \max \left( 0, m-k+c_0\right) }\ P\left( X_1=m\right) , \end{aligned} \end{aligned}$$

where \(\delta _{x,y}\) denotes the Kronecker delta, \(P\left( X_t=i \mid X_{t-1}=j\right)\) and \(P\left( X_1=m\right)\) are given by (6.1) and (6.2) respectively.

Also, the conditional probability that the run length of \(\left\{ X_t, Q_t\right\}\) equals r is given by,

$$\begin{aligned} p_{m,i}(r) \triangleq P\left( \left( X_{r+1}, C_{r+1}\right) \notin \mathcal{C}\mathcal{R},\left( X_r, C_r\right) , \ldots ,\left( X_2, C_2\right) \in \mathcal{C}\mathcal{R} \mid \left( X_1, C_1\right) =(m,i)\right) , \end{aligned}$$

where \((m,i) \in \mathcal{C}\mathcal{R}\).

Let the vector \(\mu _{(l)}\) denote the \(l\)th factorial moments, given by,

$$\begin{aligned} \mu _{{(l)}_{m,i}} \triangleq \sum _{r=1}^{\infty } r \cdots (r-l+1)\ p_{m,i}(r),\ l \ge 1, \end{aligned}$$

where,

$$\begin{aligned} \begin{aligned} p_{m,i}(r)&=\sum _{(n,j) \in \mathcal{C}\mathcal{R}} p_{n,j}(r-1) \ p(n,j \mid m,i). \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} \begin{aligned} \mu _{{(1)}_{m,i}}&=1+\sum _{(n,j) \in \mathcal{C}\mathcal{R}} p(n,j \mid m,i) \ \mu _{{(1)}_{n,j}}. \end{aligned} \end{aligned}$$

That is, \(\mu _{(1)}\) is the solution of the linear equation \((I-Q)\mu _{(1)}=1\). The dimension of Q and \(\mu\) is determined by (7.1). Hence, the ARL depending on the initial choice \(C_0=c_0\), is defined as,

$$\begin{aligned} ARL\left( c_0\right) =1+\sum _{(m,i) \in \mathcal{C}\mathcal{R}} \mu _{(1)_{m,i}} \ p\left( m,i \mid c_0\right) . \end{aligned}$$

7.3.2 ARL of EWMA chart

For a given \(Q_0=q_0\), the values of \((\theta ,\ u)\) are chosen to ensure that the ARL\(_0\) closely matches a specified value. Subsequently, the ARL values are calculated using the model parameters and EWMA chart designs. As \(\{X_t,\ Q_t\}\) of the INAR(1)DME process forms a bivariate Markov chain, the Markov chain approach introduced in Weiß (2011) is used here for computing ARL. To offer a comprehensive overview, the computational approach is briefly outlined as follows.

Let [x] denote the smallest integer value greater than or equal to x. From Weiß (2011), under the EWMA chart, the set of attainable in control values for the bivariate Markov process \(\{X_t,\ Q_t\}\) is given by,

$$\begin{aligned} \begin{aligned} \mathcal {I}(u, \theta )=&\left\{ (n, q) \in \left\{ 0, \ldots ,\left[ \frac{1}{\theta }\left( u-\frac{1}{2}\right) -1\right] \right\} \times \{0, \ldots , u-1\} \mid \right. \\&{\left. \left[ \frac{1}{\theta }\left( q-\frac{1}{2}-(1-\theta )(u-1)\right) \right] \le n \le \left[ \frac{1}{\theta }\left( q+\frac{1}{2}\right) -1\right] \right\} }. \end{aligned} \end{aligned}$$
(7.2)

The transition probabilities of \(\{X_t,\ Q_t\}\) is given by,

$$\begin{aligned} Q^\top \triangleq (p(n, j|m, i))_{(n,j),(m,i)\ \in \ \mathcal {I}(u, \theta )}\, \end{aligned}$$
(7.3)

where

$$\begin{aligned} \begin{aligned} p(n, j \mid m, i)&\triangleq P\left( X_t=n, Q_t=j \mid X_{t-1}=m, Q_{t-1}=i\right) \\&=\textbf{I}_{[j-1 / 2; j+1 / 2)}\ (\theta \ n +(1-\theta )\ i)\ P\left( X_t=n \mid X_{t-1}=m\right) . \end{aligned} \end{aligned}$$

The initial probabilities are,

$$\begin{aligned} \begin{aligned} p\left( m, i \mid q_0\right)&\triangleq P\left( X_1=m, Q_1=i \mid Q_0=q_0\right) \\&=\textbf{I}_{[j-1 / 2; j+1 / 2)}\ (\theta \ n +(1-\theta )\ q_0)\ P\left( X_1=m\right) , \end{aligned} \end{aligned}$$

where \(\textbf{I}_A\) denote the indicator function.

Also, the conditional probability that the run length of \(\left\{ X_t, Q_t\right\}\) equals r is given by,

$$\begin{aligned} p_{m,i}(r) \triangleq P\left( \left( X_{r+1}, Q_{r+1}\right) \notin \mathcal {I}(u, \theta ),\left( X_r, Q_r\right) , \ldots ,\left( X_2, Q_2\right) \in \mathcal {I}(u, \theta ) \mid \left( X_1, Q_1\right) =(m,i)\right) , \end{aligned}$$

where \((m,i) \in \mathcal {I}(u, \theta )\).

Then, the \(l\)th factorial moment is given by,

$$\begin{aligned} \mu _{{(l)}_{m,i}} \triangleq \sum _{r=1}^{\infty } r \cdots (r-l+1)\ p_{m,i}(r),\ l \ge 1, \end{aligned}$$
(7.4)

where

$$\begin{aligned} \begin{aligned} p_{m, i}(r)=\sum _{(n, j)\ \in \mathcal {I}(u, \theta )} p_{n, j}(r-1) \ p(n, j \mid m, i). \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} \begin{aligned} \mu _{(1)_{m, i}}=1+\sum _{(n, j) \in \mathcal {I}(u, \theta )} p(n, j \mid m, i) \ \mu _{(1)_{n, j}}. \end{aligned} \end{aligned}$$

That is, \(\mu _{(1)}\) is the solution of the linear equation \((I-Q)\mu _{(1)}=1\).

Hence, the ARL depending on the initial choice \(Q_0=q_0\), is defined as,

$$\begin{aligned} A R L\left( q_0\right) =1+\sum _{(m, i) \in \mathcal {I}(u, \theta ) } \mu _{(1)_{m, i}} \ p\left( m, i \mid q_0\right) . \end{aligned}$$
Table 8 Deviations of mean of INAR(1)DME process with in control values of \(\alpha\)
Full size table

7.4 Numerical simulation

Here, the performance of both CUSUM and EWMA in detecting changes in the process mean is assessed by employing a simulation study. The primary objective is to recognize the effect of parameters leading to changes in \(\mu _X\). Table 8 presents a comprehensive depiction of the variability observed in \(\mu _X\) across various values of the parameter \(\alpha\) with respect to \(\alpha _0\) = \(-\)0.1 and 0.9.

The deviations are calculated according to,

$$\begin{aligned} dev_\mu ^{\%} =100\%\ \times \frac{(\mu _X - \mu _0)}{\mu _0}, \end{aligned}$$

where \(\mu _0\) is the mean associated with the parameters \(p_0,\ \alpha _0\ \mathrm{and}\ \lambda _0\).

Table 8 shows that if the value of \(\alpha\) is decreased by 0.2, there is more than a 10% increase in \(\mu _X\) under the considered \(\alpha _0\).

The control chart designs are determined in such a way that the desired in control ARL value, ARL\(_0\), is 300. Due to the complexity of (6.2), the marginal probabilities are empirically obtained through a simulated process of desirable size at given \((p,\ \alpha ,\ \lambda )\). Besides ARL as a performance measure for the control charts, the usual relative deviation (RD) of the ARL from Weiß and Testik (2011) is also incorporated to assess and evaluate the efficacy and performance of the chart. It is given by,

$$\begin{aligned} \mathrm{RD} =100\%\ \times \frac{(\mathrm{ARL} - \mathrm{ARL}_0)}{\mathrm{ARL}_0}. \end{aligned}$$

Under the CUSUM chart, for a given \(C_0=c_0\), the focus revolves around possible integer h and k pairs, such that the desired in control ARL is close to ARL\(_0\). For the EWMA chart, the design parameters are obtained as follows:

  • Choose \(u \in N\) such that a corresponding one-sided C chart would have an in control ARL below the desired value ARL\(_0\).

  • Decrease \(\theta \in (0,1]\) to adjust the in control ARL close to the desired value ARL\(_0\). Subsequently, \(l=0\) in the combined EWMA chart is calculated accordingly as \(l= \Big \lfloor \frac{1}{2\theta } \Big \rfloor\), to keep an upper-sided design minimal.

  • Use \(q_0 \in \{0,...,u-1\}\) for a fine-tuning of the in control ARL.

Subsequently, the ARL values are calculated using the model parameters and chart designs.

Table 9 ARL with deviation (in parenthesis) for the CUSUM charts with \(p_0=0.4\) and \(\alpha _0= -0.1\)
Full size table

In Tables 9 and 10, the performance of ARL under CUSUM chart is examined with \(\alpha _0= (-0.1,\ 0.9)\) with various values of \(\alpha\) respectively. The results show the high efficacy of the CUSUM chart in detecting upward shifts in \(\mu _X\). For example, with a 13.36% and 39.92% increase in \(\mu _X\) (\(\lambda _0=0.4\)), the ARL decreases by approximately around 37.80% and 64.87%, respectively, signifying a notable decline as \(\mu _X\) rises. Furthermore, it is important to note that the decline in ARL is significantly greater than the corresponding rise in the magnitude of the shift in \(\mu _X\). Hence, it can be concluded that the CUSUM control chart demonstrates effective performance when applied to the INAR(1)DME process. The chart’s ability to efficiently detect upward shifts in \(\mu _X\) makes it a suitable and beneficial tool for monitoring and controlling the INAR(1)DME process.

Table 10 ARL with deviation (in parenthesis) for the CUSUM charts with \(p_0=0.4\) and \(\alpha _0= 0.9\)
Full size table
Table 11 ARL with deviation (in parenthesis) for the EWMA charts with \(p_0=0.4\) and \(\alpha _0= -0.1\) having C chart with u = (7,14)
Full size table

In Tables 11 and 12, the performance of ARL under EWMA chart is examined with

\(\alpha _0= (-0.1, 0.9)\) against various values of \(\alpha\), respectively. The results show the high efficacy of the EWMA chart in detecting upward shifts in \(\mu _X\). For example, with a 13.36% and 39.92% increase in \(\mu _X\) (\(\lambda _0=0.4\)), the ARL decreases by approximately 26.05% and 63.11%, respectively, signifying a notable decline as \(\mu _X\) rises. Furthermore, it is important to note that the decline in ARL is significantly greater than the corresponding rise in the magnitude of the shift in \(\mu _X\). Hence, it can be concluded that the EWMA control chart demonstrates effective performance when applied to the INAR(1)DME process. The chart’s ability to efficiently detect upward shifts in \(\mu _X\) makes it a suitable and beneficial tool for monitoring and controlling the INAR(1)DME process.

Table 12 ARL with deviation (in parenthesis) for the EWMA charts with \(p_0=0.4\) and \(\alpha _0= 0.9\) having C chart with u = (4, 8)
Full size table
Table 13 ARL of CUSUM and EWMA charts
Full size table

Table 13 provides a comparative analysis of CUSUM and EWMA charts within the context of the INAR(1)DME process, considering specific values of \(\alpha _0\). Bolded entries indicate instances where the RD is maximized between the two charts sharing the same model parameters. It becomes evident that both charts exhibit a more significant reduction in ARL as \(\mu _x\) increases. When comparing the RD between CUSUM and EWMA charts (e.g., (\(-\)38.48%, \(-\)34.29%), (\(-\)39.50%, \(-\)35.83%)), CUSUM exhibits approximately a 5% higher value than EWMA. Hence, when monitoring data from the INAR(1)DME process and accounting for various shift sizes, the CUSUM chart is the preferred choice for maintaining process control.

7.5 Real data analysis

The applicability of the CUSUM control chart is demonstrated by utilizing the disorderly conduct data set obtained from the 44th police car beat in Pittsburgh, (http://www.forecastingprinciples.com) which was used to fit the INAR(1)KF process introduced by Kim and Lee (2017), comprising of monthly observations from 1990 to 2001. It was used to monitor the mean under the INAR(1)KF process by Kim and Lee (2017). Initially, the data from 1990 to 1996 is used to fit the INAR(1)DME process. Subsequently, the CUSUM control chart is applied to the data from 1997 to detect the presence of any significant mean increase.

Fig. 9
figure 9

The time series plot of the disorderly conduct data set

Full size image

Figure 9 displays the time series plot of the disorderly conduct data set (the dashed line denotes December 1996). Based on the plot, detecting the mean shift after the dashed line is challenging. For the data from 1990 to 1996 (phase I data), the sample mean and variance are obtained as 3.9643 and 5.3602, respectively. Figure 10 displays the ACF and PACF plots for the phase I data. Here, only the first lag is significant in the PACF plot, and the ACF plot displays an exponential decay, facilitating to model the data as an INAR(1) process. Hence, the data is modeled using the INAR(1)DME model and other competing models on the phase I data.

Fig. 10
figure 10

The ACF (a) and PACF (b) plot of the phase I data set

Full size image

Table 14 lists the CMLEs, logL, AIC, BIC, and RMSE\(^*\) for different processes. The maximum logL and minimum AIC and BIC values for the INAR(1)DME process show that it fits better than the contending models.

To check whether the fitted INAR(1)DME process is statistically accurate, residual analysis is done with the Pearson residuals. The ACF of the Pearson residuals is displayed in Fig. 11, showing no autocorrelation for the Pearson residuals. To ensure this, the Ljung-Box test for the presence of autocorrelation is done with degrees of freedom 10 and has the p-value = 0.957 > 0.05. It indicates that they are uncorrelated. Also, the mean and variance of Pearson residuals are 0.00228 and 0.83, close to the preferred values of 0 and 1, respectively, validating a good fit. Hence, the INAR(1)DME process fits the phase I data well.

The INAR(1)DME model for the phase I data is given by,

$$\begin{aligned} X_t= 0.3789\, {\circ}\, X_{t-1}+ \epsilon _t, \ t\ge 2,\end{aligned}$$
(7.5)

where \(\epsilon _t\sim\) DME(\(-\)0.9999, 0.5957).

The predicted values can be obtained by,

$$\begin{aligned} {\hat{x}}_1& {}\,=\, 3.8585,\\ {\hat{x}}_t& {}\,=\, 0.3789\ {\hat{x}}_{t-1} + 2.3963,\ t=2,3,\ldots , 84. \end{aligned}$$
Table 14 The CMLEs, logL, AIC, BIC and RMSE* of the considered processes for the phase I data set
Full size table
Fig. 11
figure 11

The ACF plot of the Pearson residuals of the phase I data set

Full size image

Now, the CUSUM chart with reference value \(k=4\) (Kim and Lee 2017) is considered based on the INAR(1)DME process with parameters (\(p=0.3789,\ \alpha =-0.9999, \ \lambda = 0.5957\)) and a suitable limit value h is chosen.

Table 15 ARL values of CUSUM chart for disorderly conduct data with k = 4 under the considered models
Full size table

Table 15 provides the ARL values of CUSUM chart with respect to INAR(1)DME, INAR(1)KF and INARP(1) processes for \(k = 4\) and \(c_0=0\), respectively. Here, the ARL values with respect to the INAR(1)DME process are lower than those of the INAR(1)KF and INARP(1) processes. The lower ARL values indicate quicker identification of process deviation, leading to the conclusion that the CUSUM chart based on the INAR(1)DME process outperforms the others. Taking \(ARL_0=200\), the upper control limit CUSUM chart under the INAR(1)DME process is obtained as \(h = 38\).

The CUSUM chart for disorderly conduct data under INAR(1)DME process is given in Fig. 12, where the red horizontal dashed and vertical dashed lines respectively stand for \(h=38\) and December 1996.

Fig. 12
figure 12

The CUSUM plot of the monthly counts of disorderly conduct data

Full size image

From the plot, it is clearly seen that \(C_t\ge \ h\) occurred in May 2000. The sample mean of the data from January 1997 to May 2000 is 4.7073, which is greater than that of the past observations. Identifying this phenomenon is challenging unless the CUSUM control scheme has been implemented.

8 Conclusion

This paper presents a novel discrete analog of the mixture exponential distribution, namely the DME distribution, by utilizing the survival discretization technique. The statistical properties of the DME distribution are discussed, and the simulation study suggests that ML estimation outperforms LS methods. The performance of the DME distribution in modeling real data enables further exploration of its application in the field of time series. Consequently, an associated INAR(1) process with DME innovations is introduced, accompanied by a comprehensive investigation into its statistical characteristics and performance through extensive simulation studies. The work also extends to the domain of process monitoring, where custom control charts are developed to track the process mean. In this context, CUSUM and EWMA control charts are developed to monitor the mean of the INAR(1)DME process, and their effectiveness in detecting shifts is meticulously analyzed, providing valuable insights through comparative assessments. Additionally, the practical applicability of the INAR(1)DME process is confirmed through its use with real-world data under the CUSUM chart, showcasing its relevance in both statistical theory and real-world process monitoring and control applications.