A pth-order random coefficients mixed binomial autoregressive process with explanatory variables

Abstract

To capture the higher-order autocorrelation structure for finite-range integer-valued time series of counts, and to consider the driving effect of covariates on the underlying process, this paper introduces a pth-order random coefficients mixed binomial autoregressive process with explanatory variables. The basic probabilistic and statistical properties of the model are discussed. Conditional least squares and conditional maximum likelihood estimators, as well as their asymptotic properties of the estimators are obtained. Moreover, the existence test of explanatory variables are well addressed using a Wald-type test. Forecasting problem is also considered. Finally, some numerical results of the estimators and a real data example are presented to show the performance of the proposed model.

1 Introduction

As an important branch of time series analysis, integer-valued time series has attracted more and more attention in recent years. This kind of data is widely used in various fields of our daily life. For example, the annual counts of world major earthquakes (Wang et al. 2014; Yang et al. 2018), the monthly number of cases of an infectious disease (Pedeli et al. 2015; Yang et al. 2022), and the number of areas in which an infectious disease occurs per week (Ristić et al. 2016; Chen et al. 2019), among others. According to the different value ranges of the observed data, such data can be divided into two categories. The first category is integer-valued time series data that take values on the set of natural numbers $\mathbb {N}_0=\{0,1,2,\ldots \}$. The well-known integer-valued autoregressive (INAR) model (Al-Osh and Alzaid 1987) is a typical representative on modelling such data. The second category is integer-valued time series with a finite-range support, say $\mathbb {S}=\{0,1,\ldots ,N\}$. To model finite-range integer-valued time series of counts (McKenzie 1985) proposed the first-order integer-valued binomial autoregressive (BAR(1)) model, which is defined as follows:

$$\begin{aligned} X_{t}=\alpha \circ X_{t-1}+\beta \circ (N-X_{t-1}), \end{aligned}$$

where $\alpha ,\beta \in (0,1)$, “ο” is the binomial thinning operator proposed by Steutel and van Harn (1979). Let X be an integer-valued random variable and $\alpha \in (0,1)$, the binomial thinning is defined as

$$\begin{aligned} \alpha \circ X:= {\left\{ \begin{array}{ll} \sum _{i=1}^X B_i, &\quad \text{if } X>0,\\ 0,&\quad \text{if } X=0, \end{array}\right. } \end{aligned}$$

(1.1)

where $\{B_i\}$ is a sequence of independent and identically distributed (i.i.d.) Bernoulli random variables satisfying $P(B_i=1)=1-P(B_i=0)=\alpha$, which is also independent of X. All thinnings are performed independently for the BAR(1) model.

Since the seminal work by McKenzie (1985), modelling and inference for finite-range time series of counts have received considerable attention. Brännäs and Nordström (2006) generalized the BAR(1) model by replacing N with $N_t$ to present an econometric model to account for the tourism accommodation impact of arranging festivals or special events in many cities. Weiß (2009b) generalized the BAR(1) model to pth-order and develop a BAR(p) model. Weiß and Pollett (2014) proposed a binomial autoregressive process with density dependent thinning. Möller et al. (2016) developed a self-exciting threshold binomial autoregressive (SET-BAR(1)) process. Yang et al. (2018) contributed the empirical likelihood inference for the SET-BAR(1) model, and addressed the problem of estimating the threshold parameter of the SET-BAR(1) model. Zhang et al. (2020) proposed a multinomial autoregressive model for finite-range integer-valued time series with more than two states. Nik and Weiß (2021) developed a binomial smooth-transition autoregressive models for time series of bounded counts. For recent achievements and applications of binomial autoregressive models, we refer the readers to Weiß (2009a), Scotto et al. (2014), Chen et al. (2020), Kang et al. (2021), Zhang et al. (2022) and among others.

Researchers found that regression models for time series of counts are becoming increasingly often applied (Brännäs 1995). However, the binomial autoregressive models mentioned above ignore the effect of exogenous variables on the observed data. To address this problem in the area of infinite-range time series of counts, scholars have made different attempts. To make the analyzed models more applicable, Freeland and McCabe (2004a) introduced explanatory variables into the parameters of first-order INAR model via two different kinds of link functions. Enciso-Mora et al. (2009) proposed an INAR(p) process with explanatory variables both in the autoregressive coefficients and the expectation of innovation. Ding and Wang (2016), and Wang (2020) successively studied the empirical likelihood inferences and variable selection problems for first-order Poisson integer-valued autoregressive model with covariables. Yang et al. (2021) confirmed the existence of a nonlinear relationship of climate covariates on crime cases, and further suggested a random coefficients integer-valued threshold autoregressive processes driven by logistic regression. This research further expands the study of the INAR model with covariables and enhances the applicability of the model.

To capture the impact of covariates on the finite-range time series of counts, Wang et al. (2021) developed a first-order covariates-driven binomial AR (CDBAR(1)) process. Zhang and Wang (2023)) developed a binomial AR(1) process with autoregressive coefficient driven by a bivariate dependent autoregressive process with covariables. However, the two models are both first-order models. To the best of our knowledge, there is no literature discussing the high-order modelling for finite-range integer-valued time series of counts with explanatory variables. In fact, a high-order model for time series of counts is indeed very important, which is recognized by many scholars (see, e.g., Zhu and Joe (2006), Weiß (2009b), Yang et al. (2023) and among others). In this study, we aim to make a contribution towards this direction.

The remainder of the paper is organized as follows. In Sect. 2, we introduce the definition and basic properties of the pth-order random coefficients mixed binomial autoregressive process with explanatory variables, and denote the proposed model as RCMBAR(p)-X process. In Sect. 3, we discuss the parameter estimation problem via two different methods, the asymptotic properties of the estimators are also provided. In Sect. 4, we develop a Wald-type test to address the testing problem for the existence of explanatory variables. In Sect. 5, forecasting problem for the proposed model is addressed. In Sect. 6, we conduct some simulation studies to show the performances of the proposed methods. In Sect. 7, we apply the proposed method to the weekly rainfall data set in Germany. Some concluding remarks are given in Sect. 8. All proofs are postponed to the Appendixes.

2 Definition and basic properties of the RCMBAR(p)-X process

In this section, we first introduce the definition of the pth-order random coefficients mixed binomial autoregressive process with explanatory variables, and then give some important properties of it. The definition of RCMBAR(p)-X process is given as follows:

Definition 1

A sequence of integer-valued random observations $\{{X}_t\}_{t \in \mathbb {Z}}$ is said to follow a pth-order random coefficients mixed integer-valued binomial autoregressive process with explanatory variables, if $X_t$ satisfies the recursion

$$\begin{aligned} X_{t}=\left\{ \begin{array}{lcl} \alpha _t\circ X_{t-1} + \beta _{t} \circ (N-X_{t-1}), &{}&{} w.p.~\phi _1,\\ \alpha _t\circ X_{t-2} + \beta _{t} \circ (N-X_{t-2}), &{}&{} w.p.~\phi _2,\\ \ldots \\ \alpha _t\circ X_{t-p} + \beta _{t} \circ (N-X_{t-p}), &{}&{} w.p.~\phi _p, \end{array}\right. \end{aligned}$$

(2.2)

where “ο” is the binomial thinning operator defined in (1.1), $N \in \mathbb {N}$ is a predetermined upper limit of the range, the weights $\phi _1,\phi _2,\ldots ,\phi _p \in (0,1)$, $\sum _{i=1}^p \phi _i=1$, “w.p." stands for with probability, $\alpha _t, \beta _t \in (0,1)$ are the autoregressive coefficients satisfying

$$\begin{aligned} \log \left( \frac{\alpha _t}{1-\alpha _t} \right) =\varvec{Z}_t^{\top } \varvec{\delta }_1,~\log \left( \frac{\beta _t}{1-\beta _t} \right) =\varvec{Z}_t^{\top } \varvec{\delta }_2, \end{aligned}$$

(2.3)

where $\varvec{\delta }_i:=(\delta _{i,0},\delta _{i,1},\ldots ,\delta _{i,q})^{\top }$, $i=1,2$, are the regression coefficients, $\{\varvec{Z}_t:=(1,Z_{1,t},\ldots ,Z_{q,t})^{\top }\}$ is a sequence of explanatory variables with constant mean vector and covariance matrix. For a fixed $\varvec{Z}_t$, the thinning operations at time t are performed independently of each other.

As is seen in Definition 1, the RCMBAR(p)-X process is actually a mixture integer-valued autoregressive model with fixed weights. $X_t$ equals $\alpha _t\circ X_{t-i}$ + $\beta _t\circ (N-X_{t-i})$ with probability $\phi _i$, $i=1,2,\ldots ,p$. Furthermore, the autoregressive coefficients $\alpha _t$ and $\beta _t$ shared the randomness and flexibility via a logistic structure with covariates. Obviously, Definition 1 includes the covariates-driven binomial AR(1) process of Wang et al. (2021) as a special case when $p = 1$. The RCMBAR(p)-X model reduces to the binomial AR(p) model of Weiß (2009b) when $\delta _{i,j}=0$ for $i=1,2$ and $j=1,2,\ldots ,q$.

Denote by $\{\varvec{D}_t\}$ a sequence of i.i.d. multinomial random variables with parameters $\phi _1,\ldots ,\phi _p$, i.e., $\varvec{D}_t=(D_{t,1},D_{t,2},\ldots ,D_{t,p})^{\top }\sim MULT(1; \phi _1,\ldots ,\phi _p)$, then model (2.2) can be equivalently rewritten in the following form:

$$\begin{aligned} X_t=\sum _{i=1}^p D_{t,i} ( \alpha _t\circ X_{t-i}+\beta _t\circ (N-X_{t-i}) ), \end{aligned}$$

(2.4)

where $\varvec{D}_t$ is independent of all $X_s$, $\alpha _t\circ X_{t-s}$ and $\beta _t\circ (N-X_{t-s})$ with $s<t$,

$$\begin{aligned} \alpha _t=\frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}{1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)},~ \beta _t =\frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}{1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}, \end{aligned}$$

(2.5)

are implied by (2.3). It follows by the expression (2.4) that the conditional probability of $X_t$ conditional on $X_{t-i}$ $(i=1,2,\ldots ,p)$ and $\varvec{Z}_t$ fixed is given by

$$\begin{aligned}&P(X_{t}=x_t|X_{t-1}=x_{t-1},\ldots ,X_{t-p}=x_{t-p},\varvec{Z}_t)\nonumber \\&\quad =\sum _{i=1}^p\phi _i\sum _{m=a}^{b} \left( {\begin{array}{c}x_{t-i}\\ m\end{array}}\right) \left( {\begin{array}{c}N-x_{t-i}\\ x_t-m\end{array}}\right) \alpha _{t}^{m}(1-\alpha _{t})^{x_{t-i}-m}\beta _{t}^{x_t-m}(1-\beta _{t})^{N-x_{t-i}-x_t+m}\nonumber \\&\quad =\sum _{i=1}^p\phi _i\sum _{m=a}^{b} \left( {\begin{array}{c}x_{t-i}\\ m\end{array}}\right) \left( {\begin{array}{c}N-x_{t-i}\\ x_t-m\end{array}}\right) \frac{\exp (m \varvec{Z}_t^{\top }\varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top }\varvec{\delta }_1))^{x_{t-i}}} \frac{\exp ((x_t-m)\varvec{Z}_t^{\top }\varvec{\delta }_2)}{(1+\exp (\varvec{Z}_t^{\top }\varvec{\delta }_2))^{N-x_{t-i}}}, \end{aligned}$$

(2.6)

where $a=\max \left\{ 0,x_t+x_{t-i}-N\right\}$, $b=\min \left\{ x_t,x_{t-i}\right\}$. The above conditional probability can be used to derive the conditional likelihood for the RCMBAR(p)-X process. Furthermore, the conditional expectation and conditional variance are given by

$$\begin{aligned} E(X_t|X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t)=\sum _{i=1}^p \phi _i \left( \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}{1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}X_{t-i}+ \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}{1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}(N-X_{t-i})\right) , \end{aligned}$$

and

$$\begin{aligned}&\textrm{Var}(X_t|X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t)\\&\quad =\sum _{i=1}^p \phi _i \left( \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1))^2} X_{t-i} + \frac{\exp (2\varvec{Z}_t^{\top } \varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1))^2} X_{t-i}^2 +\frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2))^2} (N-X_{t-i}) \right. \\&\quad \left. +\frac{\exp (2\varvec{Z}_t^{\top } \varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1))^2} (N-X_{t-i})^2 +2\prod _{i=1}^2 \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_i)}{ 1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_i)} X_{t-i}(N-X_{t-i}) \right) \\&\quad -\left( \sum _{i=1}^p \phi _i \left( \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}{1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}X_{t-i}+ \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}{1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}(N-X_{t-i})\right) \right) ^2. \end{aligned}$$

For the detailed derivations, please see "Appendix A". Moreover, one may also interest in the autocovariance function of the RCMBAR(p)-X process. However, the derivation is complex even in the case of constant coefficients in Weiß (2009b). In this study, we rewrite the RCMBAR(p)-X process in a multivariable form, and further derive the autocovariance function. The details are given in "Appendix C".

In the following proposition, we state the strict stationary and ergodic properties of the RCMBAR(p)-X process.

Proposition 2.1

Let $\{X_t \}_{t\in \mathbb {Z}}$ be the process defined in (2.2). If the explanatory variable sequences $\{Z_{j,t}\}$ $(j=1,2,\ldots ,q)$ are all stationary sequences, then $\{X_t \}_{t\in \mathbb {Z}}$ is an irreducible, aperiodic and positive recurrent (and hence ergodic) Markov chain on state space $\mathbb {S}:=\left\{ 0, 1, \ldots , N\right\}$. Furthermore, there exists a strictly stationary process satisfying (2.2).

The proof of Proposition 2.1 is given in "Appendix B".

3 Parameters estimation

In this section, we consider the parameter estimation problem based on a series of realizations $\{X_t\}_{t=1}^n$ from the RCMBAR(p)-X process, $\{\varvec{Z}_t\}_{t=1}^n$ are the corresponding covariates. Denote by $\varvec{\theta }:=(\varvec{\delta }^{\top }_1,\varvec{\delta }^{\top }_2,\varvec{\phi }^{\top })^{\top }$ the parameter of interest, where $\varvec{\phi }=(\phi _1,\ldots \phi _{p-1})^{\top }$. The parameter vector takes values in the following parameter space

$$\begin{aligned} \Theta :=\left\{ \varvec{\theta }\in \mathbb {R}^{q+1} \times \mathbb {R}^{q+1} \times (0,1)^{p-1}\right\} . \end{aligned}$$

In the following, we study the conditional least squares (CLS) and conditional maximum likelihood (CML) estimation methods for $\varvec{\theta }$.

3.1 CLS estimation for $\varvec{\theta }$

Let

$$\begin{aligned} Q(\varvec{\theta })=\sum _{t=1}^n(X_{t}-g(\varvec{\theta },X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t))^{2}=\sum _{t=1}^nU_{t}(\varvec{\theta }), \end{aligned}$$

(3.7)

be the CLS criterion function, where $g(\varvec{\theta },X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t):=E(X_{t}|X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t)$, and $U_{t}(\varvec{\theta })=(X_{t}-g(\varvec{\theta },X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t))^{2}$. Then, the CLS-estimator $\hat{\varvec{\theta }}_{CLS}:=(\hat{\varvec{\delta }}_{1,CLS}^{\top },\hat{\varvec{\delta }}_{2,CLS}^{\top },\hat{\varvec{\phi }}_{CLS})^{\top }$ is obtained by minimizing (3.7) with respect to $\varvec{\theta }$, and giving

$$\begin{aligned} \hat{\varvec{\theta }}_{CLS}:=\arg \min _{\varvec{\theta }\in \Theta }Q(\varvec{\theta }). \end{aligned}$$

(3.8)

Since the RCMBAR(p)-X process is stationary and ergodic by Proposition 2.1, it follows by Theorems 3.1 and 3.2 in Klimko and Nelson (1978) that the CLS-estimators $\hat{\varvec{\theta }}_{CLS}$ are strongly consistent and asymptotically normally distributed. We state this property in the following theorem. The proof of this theorem is postponed to Appendix B.

Theorem 3.1

Under the conditions of Proposition 2.1 and $E \Vert \varvec{Z}_t\Vert ^3 <\infty$, the CLS-estimators $\hat{\varvec{\theta }}_{CLS}$ are strongly consistent and asymptotically normal,

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\theta }}_{CLS}-\varvec{\theta }_0) {\mathop {\longrightarrow }\limits ^{L}} N(\varvec{0},\varvec{V}^{-1}\varvec{W}\varvec{V}^{-1}), \end{aligned}$$

(3.9)

where $\varvec{\theta }_0$ is the true value of $\varvec{\theta }$, $\varvec{V}:=E_{\varvec{\theta }_0}\left( \frac{\partial }{\partial \varvec{\theta }} g(\varvec{\theta },X_{0},\ldots ,X_{1-p},\varvec{Z}_1) \frac{\partial }{\partial \varvec{\theta }^{\top }} g(\varvec{\theta },X_{0},\ldots ,X_{1-p},\varvec{Z}_1) \right)$, $\varvec{W}:=E_{\varvec{\theta }_0}\left( \frac{\partial }{\partial \varvec{\theta }} g(\varvec{\theta },X_{0},\ldots ,X_{1-p},\varvec{Z}_1) \frac{\partial }{\partial \varvec{\theta }^{\top }} g(\varvec{\theta },X_{0},\ldots ,X_{1-p},\varvec{Z}_1) U_1(\varvec{\theta })\right)$.

3.2 CML estimation for $\varvec{\theta }$

In this section, we consider the CML estimation for $\varvec{\theta }$. To this end, we need to derive the conditional likelihood function first. For fixed values of $x_{0}$, $x_{-1}$, $\ldots$, and $x_{1-p}$, the conditional likelihood function of RCMBAR(p)-X process can be written as

$$\begin{aligned} L(\varvec{\theta })=\prod _{t=1}^n P(X_{t}=x_t|X_{t-1}=x_{t-1},\ldots ,X_{t-p}=x_{t-p},\varvec{Z}_t). \end{aligned}$$

Thus, the CML-estimator $\varvec{\hat{\theta }}_{CML}$ can be obtained by minimizing the following conditional log likelihood function

$$\begin{aligned} \ell (\varvec{\theta })=\log L(\varvec{\theta })=\sum _{t=1}^n \log P(X_{t}=x_t|X_{t-1}=x_{t-1},\ldots ,X_{t-p}=x_{t-p},\varvec{Z}_t), \end{aligned}$$

and giving

$$\begin{aligned} \hat{\varvec{\theta }}_{CML}=\mathop {\arg \max }\ell (\varvec{\theta }). \end{aligned}$$

(3.10)

The existence of (2.5) in the conditional expectations and the conditional probabilities makes the calculations of (3.8) and (3.10) very complex. It is technically very difficult or even impossible to find closed-form expressions for CLS and CML estimators. Therefore, numerical procedures have to be employed. Fortunately, we can use computer programs to complete the optimization process.

The following results establish the strong consistency and the asymptotic normality of the CML-estimators.

Theorem 3.2

Under the conditions of Proposition 2.1, the CML-estimators $\hat{\varvec{\theta }}_{CML}$ are strongly consistent and asymptotically normal,

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\theta }}_{CML}-\varvec{\theta }_0) {\mathop {\longrightarrow }\limits ^{L}} N(\varvec{0},\varvec{I}^{-1}(\varvec{\theta }_0)), \end{aligned}$$

(3.11)

where $\varvec{\theta }_0$ is the true value of $\varvec{\theta }$, $\varvec{I}(\varvec{\theta })$ denotes the Fisher information matrix.

The proof of this theorem is given in "Appendix B".

4 Testing the existence of explanatory variables

In this section, we focus on an interesting issue, that is, to test whether the explanatory variables exist in the RCMBAR(p)-X model. For this purpose, we give the null hypothesis and the alternative hypothesis as follows:

$$\begin{aligned} \mathcal {H}_0:{\delta }_{i,j}=0~(i=1,2,j=1,\ldots ,q), \text{ v.s. } \mathcal {H}_1:\text{ At } \text{ least } \text{ one } {\delta }_{i,j}\ne 0~(i=1,2,j=1,\ldots ,q). \end{aligned}$$

(4.12)

The inference problem in (4.12) is indeed very important as it is testing a BAR(p) model against a RCMBAR(p)-X model. When the null hypothesis holds, the model will reduce to the BAR(p) model in Weiß (2009b).

Testing problem (4.12) is equivalent to the following hypothesis:

$$\begin{aligned} \mathcal {H}_0:~\varvec{D} \varvec{\zeta }=\varvec{0} ~~~\text{ vs }~~~ \mathcal {H}_1:~\varvec{D} \varvec{\zeta }\ne \varvec{0}, \end{aligned}$$

(4.13)

where $\varvec{\zeta }=(\varvec{\delta }_1^{\textsf {T}},\varvec{\delta }_2^{\textsf {T}})^{\textsf {T}}$, $\varvec{D}=\left( \begin{array}{cc} \varvec{B} &{} \varvec{0}\\ \varvec{0} &{} \varvec{B} \end{array} \right)$ is a block matrix with $\varvec{B}=(\varvec{0}_{q\times 1},\varvec{I}_{q\times q})$, $\varvec{I}_{q\times q}$ stands for a qth-order identity matrix. To address this testing problem, we develop a Wald-type test. For this purpose, we introduce some regularity conditions:

• (C1) $\{{X}_t\}$ is a stationary process.

• (C1) $\hat{\varvec{\zeta }}{:}=(\hat{\varvec{\delta }}_1^{\textsf {T}},\hat{\varvec{\delta }}_2^{\textsf {T}})^{\textsf {T}}$ is a consistent estimator of $\varvec{\zeta }$. Moreover, $\hat{\varvec{\zeta }}$ is asymptotically normally distributed around the true value $\varvec{\zeta }_0$, i.e.,

  $$\begin{aligned} \sqrt{n}(\hat{\varvec{\zeta }}-\varvec{\zeta }_0)\overset{L}{\longrightarrow }N(\varvec{0},\varvec{\Sigma }), \end{aligned}$$

  for some covariance matrix $\varvec{\Sigma }$.

Thus, we obtain the following theorem.

Theorem 4.3

Under the assumptions (C1–C2), the statistic for testing problem (4.13) is

$$\begin{aligned} S_n=n{\hat{ \varvec{\zeta }}^{\textsf {T}}} \varvec{D}^{\textsf {T}} {(\varvec{D}\hat{\varvec{\Sigma }}\varvec{D}^{\textsf {T}})}^{-1}\varvec{D} \hat{\varvec{\zeta }}, \end{aligned}$$

where $\hat{\varvec{\Sigma }}$ is a consistent estimator of ${\varvec{\Sigma }}$. Furthermore, when $\mathcal {H}_0$ is true,

$$\begin{aligned} S_n\overset{L}{\longrightarrow }\ \chi _{2q}^2,~n\rightarrow \infty , \end{aligned}$$

where $\chi _{2q}^2$ stands for a chi-square distribution with 2q degrees of freedom.

Theorem 4.3 follows easily by the properties of normal distribution and the Slutsky’s Theorem. Therefore, we omit the proof of it. We can use Theorem 4.3 to test weather the autoregressive coefficient of a RCMBAR(p)-X model is a constant. Also, it can be used to test whether a specific explanatory variable is included in the model. In this point of view, it provides a way to separate the proposed model from a consistent coefficient one. In practice, the estimator $\hat{\varvec{\zeta }}$ can be any consistent estimator of ${\varvec{\zeta }}$. In this study, we use the CML-estimator obtained in the previous section.

5 Forecasting for RCMBAR(p)-X process

In the following, we address the forecasting problem for the RCMBAR(p)-X process. A general method in time series forecasting is to use the conditional expectation, which yields forecasts with minimum the mean square error. However, this method is unsatisfactory for integer-valued time series, since it seldom produces integer-valued forecasts. An alternative way is to use the k-step-ahead conditional distribution (Freeland and McCabe 2004b). Provided that the k-step-ahead conditional distribution is available, point prediction such as the conditional expectation or conditional median results are easy to calculate. Yang et al. (2021) generalized (Freeland and McCabe 2004b)’s approach to a covariate-driven threshold INAR model.

In this study, we mainly focus on the one-step forecast, since it is usually often adopted in practice. A general version of k-step forecast can be easily obtained using (Freeland and McCabe 2004b)’s approach based on the representation of the RCMBAR(p)-X process given in (B.5). Notice that the state space of RCMBAR(p)-X process is a finite set on $\{0,1,\ldots ,N\},$ we can easily obtain the one-step forecasting conditional distribution with parameter $\varvec{\theta }$, as follows:

$$\begin{aligned} p(x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},\varvec{\theta }):=P({X}_{n+1}=x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},\varvec{\theta }),~x=0,1,\ldots ,N, \end{aligned}$$

(5.14)

where $P({X}_{n+1}=x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},\varvec{\theta })$ is defined in (2.6). Based on (5.14), we can calculate the point predictions such as the conditional expectation, conditional median, and so on.

In addition to point predictions, we are also interested in the forecasting confidence interval for each point in $\{0,1,\ldots ,N\}$. Given that we have already obtained some versions of $\hat{\varvec{\theta }}$, together with the asymptotic normality of $\hat{\varvec{\theta }}$ as

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\theta }}-\varvec{\theta }_0) {\mathop {\longrightarrow }\limits ^{L}} N(\varvec{0},\varvec{\Sigma }), \end{aligned}$$

(5.15)

where $\varvec{\theta }_0$ denotes the true value of $\varvec{\theta }$, $\varvec{\Sigma }$ is the covariance matrix. Then, we have the following theorem similar to Theorem 2 in Freeland and McCabe (2004b) which can be used to construct the confidence interval for $p(x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},\varvec{\theta })$. Obviously, the interval may be truncated outside [0, 1].

Theorem 5.4

For a fixed $x\in \{0,1,\ldots ,N\}$, if assumption (5.15) holds, the quantity $p(x|{X}_{n},\ldots$, ${X}_{n-p+1},\varvec{Z}_{n},\hat{\varvec{\theta }})$ has an asymptotically normal distribution with mean $p(x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},{\varvec{\theta }_0})$ and variance $n^{-1}\varvec{D}\varvec{\Sigma }\varvec{D}^{\top }$, i.e.,

$$\begin{aligned} \sqrt{n}(p(x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},\hat{\varvec{\theta }})-p(x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},{\varvec{\theta }_0}) ) {\mathop {\longrightarrow }\limits ^{L}} N(\varvec{0},\varvec{D}\varvec{\Sigma }\varvec{D}^{\top }), \end{aligned}$$

where $\varvec{D}=\left( \left. \frac{\partial p(x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},{\varvec{\theta }})}{\partial \varvec{\theta }}\right| _{\varvec{\theta }=\varvec{\theta }_0}\right)$, $\hat{\varvec{\theta }}$ is the consistent estimator of $\varvec{\theta }$.

The above Theorem 5.4 follows easily by (5.15) and the well-known delta method (see, e.g., van der Vaart (1998), Chapter 3). In practice, $\hat{\varvec{\theta }}$ can be chosen as the CML-estimator $\hat{\varvec{\theta }}_{CML}$ discussed in Sect. 3, and then $\varvec{\Sigma }$ be $\varvec{I}^{-1}(\varvec{\theta })$ accordingly. Moreover, based on Theorem 5.4, we can get the $100(1 - \alpha )$ confidence interval for $p(x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},{\varvec{\theta }})$ as follows:

$$\begin{aligned} C_{\varvec{\theta }}^{\alpha }=\left( p(x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},\hat{\varvec{\theta }})-\frac{\sigma }{\sqrt{n}} u_{1-\frac{\alpha }{2}}, p(x|{X}_{n},\ldots ,{X}_{n-p+1},\varvec{Z}_{n},\hat{\varvec{\theta }})+\frac{\sigma }{\sqrt{n}} u_{1-\frac{\alpha }{2}} \right) , \end{aligned}$$

where $\sigma =\sqrt{\varvec{D}\varvec{\Sigma }\varvec{D}^{\top }}$, $u_{1-\frac{\alpha }{2}}$ is the $(1-\frac{\alpha }{2})$-upper quantile of N(0, 1).

As an illustration, we draw the one-step forecasting distribution and 95% forecasting confidence intervals under a RCMBAR(2)-X model in Fig. 1. The parameters are chosen the same as Scenario A in Sect. 6, i.e., $(\delta _{1,0},\delta _{1,1}, \delta _{2,0},\delta _{2,1},\phi _1)$= (0.2, 0.4, 0.4, 0.3, 0.8) and $N=50$. In order to make the figure reproducible, we use R-code ‘set.seed(18)’ to fixed the random number. Then, we generate 200 ‘random observations’, where $X_{200}=25$ and $X_{199}=24$.

Figure 1 shows us that the forecasting distribution is an unimodal asymmetric distribution. The main probability points are concentrated between 12 and 40. The forecasting interval covers each probability mass. Meanwhile, the interval lengths in the middle part are greater than that on both sides. Figure 1 shows us more comprehensive statistical information about the next prediction, which is clearly more informative than a single point.

Fig. 2

One-step ahead forecasting distribution and the 95% forecasting confidence intervals

6 Simulation studies

6.1 Comparison of CLS and CML

In this subsection, we conduct simulation studies to report the performances of the proposed CLS and CML estimators. For this purpose, we choose the sample sizes $n = 100,~300$ and 500 for the following two models:

Scenario A.:

In this scenario, we consider a RCMBAR(2)-X model with parameters $(\delta _{1,0},\delta _{1,1}$, $\delta _{2,0},\delta _{2,1},\phi _1)$=(0.2, 0.4, 0.4, 0.3, 0.8) and $N=50$. The explanatory variable $Z_{1,t}$ is generated from an i.i.d. N(0, 1) distribution.

Scenario B.:

In this scenario, we consider a RCMBAR(3)-X model with parameters $(\delta _{1,0},\delta _{1,1}$, $\delta _{2,0},\delta _{2,1},\delta _{2,2},\phi _1,\phi _2)$=(0.4, 0.1, 0.2, 0.6, 0.4, 0.3) and $N=50$. The explanatory variable is generated from an AR(1) process, $Z_{1,t}=0.2Z_{1,t-1}+\epsilon _t$ with $\epsilon _t\sim N(0,1)$ and $Z_{1,0}=0$.

Scenario C.:

In this scenario, we consider a RCMBAR(2)-X model with parameters $(\delta _{1,0},\delta _{1,1},\delta _{1,2}$, $\delta _{2,0},\delta _{2,1},\delta _{2,2},\phi _1)$=(0.2, 0.4, 0.6, 0.1, 0.3, 0.5, 0.7) and $N=40$. There are two explanatory variables in the model, where $Z_{1,t}$ is generated from an i.i.d. N(0, 1) distribution, $Z_{2,t}$ is generated from an AR(1) process, $Z_{2,t}=0.5Z_{2,t-1}+\epsilon _t$ with $\epsilon _t\sim N(0,1)$ and $Z_{2,0}=0$.

Fig. 3

Sample path and ACF plots of Scenarios A, B and C

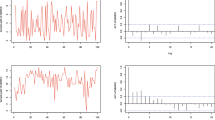
The above three scenarios consider different cases of explanatory variables. Scenarios A considers a simple independent normally distributed explanatory variable. Scenarios B considers a dependence explanatory variable of an AR(1) process. In Scenarios C, we consider two explanatory variables in the model. Firstly, we show the sample paths and autocorrelation function (ACF) plots for the two scenarios in Fig. 2. As is seen in Fig. 2 that there is no trend and seasonal characteristics in the subfigures, indicating that all series are stationary. Moreover, the three series show different autocorrelation characteristics, which implies that RCMBAR(p)-X model can describe different autocorrelation structures.

Table 1 Simulation results of Scenario A under different sample sizes

Table 2 Simulation results of Scenario B under different sample sizes

Table 3 Simulation results of Scenario C under different sample sizes

Next, we conduct simulation studies to show the performances of the proposed CLS and CML estimators. For the above three models, we calculated the estimates based on the two methods, the empirical biases (Bias), and the mean square errors (MSE). All the simulations are performed under the $\mathcal {R}$ software based on 1000 replications. The simulation results are summarized in Tables 1, 2 and 3.

It can be seen from Tables 1, 2 and 3 that the biases and MSEs are getting small with the increases of the sample size, indicating the consistency of the estimators. Generally, the CML estimates seem to be more efficient since they present smaller bias and MSE values, regardless the number and the type of explanatory variables.

6.2 Powers of the test

In this subsection, we conduct simulations to show the performances of the hypothesis test discussed in Sect. 4. To this end, we further consider the following two Scenarios:

Scenario D.:

In this scenario, we also consider a RCMBAR(2)-X model with parameters $(\delta _{1,0},\delta _{1,1}$, $\delta _{2,0},\delta _{2,1},\phi _1)$= (0.2, 0, 0.4, 0, 0.8) and $N=40$. The explanatory variable $Z_{1,t}$ is generated in the same way as Scenario A.

Scenario E.:

In this scenario, we consider a RCMBAR(3)-X model with parameters $(\delta _{1,0},\delta _{1,1}$, $\delta _{2,0},\delta _{2,1},\phi _1,\phi _2)$= (0.6, 0, 0.3, 0, 0.5, 0.3) and $N=40$. The explanatory variable $Z_{1,t}$ is generated in the same way as Scenario B.

It is clear that Scenarios D and E are cases where $\mathcal {H}_0$ is true. Firstly, we give an intuitive explanation for Theorem 4.3. For this purpose, we draw the Q-Q plots of $S_n$ under Scenarios D and E in Figs. 3 and 4, aiming to show how $S_n$ distributes when $\mathcal {H}_0$ is true. Meanwhile, we also draw the Q-Q plots of $S_n$ under Scenarios A and B in Figs. 5 and 6, aiming to investigate whether the result of chi-square distribution for $S_n$ will still hold when $\mathcal {H}_0$ is not true.

Fig. 4

Q-Q plots of $S_n$ under Scenario D based on CML method

Fig. 5

Q-Q plots of $S_n$ under Scenario E based on CML method

Fig. 6

Q-Q plots of $S_n$ under Scenario A based on CML method

Fig. 7

Q-Q plots of $S_n$ under Scenario B based on CML method

As is seen in Figs. 3 and 4 that, the sample Q-Q scatter plots getting closer to the theoretical Q-Q lines as the sample size increases. This implies the testing statistics $S_n$ gradually converges to a $\chi ^2_{2}$ distribution as expected, regardless of the order of the model. On the contrary, as is seen in Figs. 5 and 6 that the scatter plots all fall outside the confidence band areas, indicating that the $\chi ^2_{2}$ distribution is no longer valid.

Next, we show the detailed performances of testing problem (4.13) discussed in Section 4. To this end, we summary the simulation results under Scenarios A, B, D, and E using CML method in Table 4. As is seen in Table 4 that when $\mathcal {H}_0$ is true (Scenarios D and E), the empirical size is getting closer to the significance level of 0.05, which implies that the asymptotic distribution in Theorem 4.3 is correct. On the other hand, we also see that all empirical power results (Scenarios A and B) are equal to one when $\mathcal {H}_0$ is not true. This implies the proposed test statistics performs well in practice.

Table 4 Empirical power and size of test (4.13) based on CML method

7 Real data example

In this section, we will use the RCMBAR(p)-X model to fit a set of rainy days at Bremen in Germany. The data was published by the German Weather Service, and can be downloaded in the following URL: http://www.dwd.de/. The original data set records the local daily rainfall of Bremen. We choose the time period from January 2011 to December 2021. With the selected data set, we calculated the number of rainfall days per week and the corresponding rainfall. Specifically, for each week t, the value $X_t$ counts the number of rainy days, and $Z_{1,t}$ records the total rainfall of the week. Therefore, we obtain a time series of counts with a finite-range $N=7$, totally consists 574 weekly observations. Moreover, in this study, $Z_{1,t}$ is used as an explanatory variable.

Fig. 8

Time series and ACF plots of the rainfall days counts

Fig. 9

Time series plot of the covariates

For convenience, we denote $\{X_t\}_{t=0}^{573}$ and $\{Z_{1,t}\}_{t=0}^{573}$ as the sequences of observed data and explanatory variables, and further draw the time series and ACF plots of the observations in Fig. 7, draw the time series of the covariate in 8. From Fig. 7 we can see that the analyzed data set is a stationary time series. The ACF exhibits an exponential decay trend. Figure 8 also implies the sequence of covariate is stationary.

For comparison purpose, we also use the BAR(1) model  (McKenzie 1985), the BAR(p) model (Weiß 2009b) with $p=2$ and 3, and the CDBAR(1) model (Wang et al. 2021) to fit this data set, and compare different models by AIC and BIC criteria. The BAR(1) model is the original binomial autoregressive model of order one, which does not contain explanatory variables. The BAR(p) model is an extension of BAR(1) model, which is a pth-order constant coefficients binomial autoregressive model with the jth-order regime existing in the model with probability $\phi _j$ ($j=1,2,\ldots ,p$). The CDBAR(1) model is defined via introducing explanatory variables into both autoregressive coefficents of a BAR(1) model, which is also a special case of the RCMBAR(p)-X model proposed in this study. For each of the fitted model, we calculate the conditional maximum likelihood estimation (CMLE) of the model parameters, the corresponding standard errors (SE), AIC and BIC values. All the fitting results are summarized in Table 5.

Table 5 Fitting results of the rainfall days counts under different models

It can be seen from Table 4 that (i) among similar models, higher order models have better fitting effect than lower order models; and (ii) among different models, the models with explanatory variables are better than the models without explanatory variables. This shows that it is necessary to study high-order models and consider explanatory variables. Moreover, among all competition models, the RCMBAR(3)-X model has the smallest AIC and BIC values. This implies that the RCMBAR(3)-X model is a competitive model in terms of AIC and BIC, and is appropriate for fitting this data set.

In the following, we conduct the diagnostic checking for the fitted RCMBAR(3)-X model. For this purpose, we need to calculate the standardized Person residuals. As is reviewed by many authors (see, e.g., Yang et al. (2022, 2023), Zhang et al. (2022) and among others), the standardized residuals provides a relatively easy way to check whether the model fits data adequately. Specifically, if the model is correctly specified, the residuals should have no significant serial correlation. For the RCMBAR(3)-X model, the standardized residuals is defined as

$$\begin{aligned} e_{t}=\frac{X_{t}-E(X_{t}|X_{t-1},\ldots ,X_{t-3},{Z}_{1,t})}{\sqrt{\textrm{Var}(X_{t}|X_{t-1},\ldots ,X_{t-3},{Z}_{1,t})}},~t=1,2,\ldots ,n. \end{aligned}$$

(7.16)

In practice, we can substitute the CMLE results into the conditional expectation and conditional variance equations in (7.16) to calculate $\{\hat{e}_{t}\}$.

Figure 9 shows the time series plot, ACF and partial autocorrelation function (PACF) plots of the the standardized residuals under RCMBAR(3)-X model. As is shown in Fig. 9 that the residuals is a stationary series. The p-value of ADF test is smaller than 0.01, which ensures the stationarity of the residuals. Moreover, the ACF and PACF plots show that the residuals have no sequence autocorrelation. This implies $\{\hat{e}_{t}\}$ is a stationary white noise which ensures that the RCMBAR(3)-X model is correctly specified.

Fig. 10

Diagnostic checking plots in fitting RCMBAR(3)-X model with the rainfall data set. a standardized residuals; b ACF plot of the residuals; c PACF plot of the residuals

Finally, as an application, we draw the one-step ahead forecasting distribution and the forecasting confidence intervals of the corresponding points in Fig. 10. From Fig. 10 we can see that the most likely number of rainy days in the region next week are 3 - 4 days.

Fig. 11

Forecasting distribution and the 95% confidence intervals of the analyzed data sets

8 Conclusions

This article introduces a pth-order random coefficients integer-valued binomial autoregressive process with explanatory variables, which can accurately capture the higher-order dependence of integer-valued time series with bounded support, and conveniently model the relationship between observational process with covariates. The CLS and CML methods are introduced to address the parameter estimation problems for the model. The results show that the CML method has higher estimation accuracy. Moreover, we also considered the existence test of explanatory variables. Finally, a real data example is provided to show the outstanding performance of the proposed model.

Appendices

Appendix A: The derivations of moments

In the following, we derive the derivations of moments for the RCMBAR(p)-X model. With the representation of (2.4), the calculation of conditional expectation is trivial, thereby, omitted. We go on to derive the conditional variance.

Notice that (2.4) implies $D_{t,i}D_{t,j}=0$ for $i \ne j$, it follows that

$$\begin{aligned}&E(X_t^2|X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t)\\&\quad =E\left( \sum _{i=1}^p D_{t,i}^2 ( \alpha _t\circ X_{t-i}+\beta _t\circ (N-X_{t-i}) )^2|X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t \right) \\&\quad =\sum _{i=1}^p \phi _i E[(\alpha _t\circ X_{t-i})^2+2(\alpha _t\circ X_{t-i})(\beta _t\circ (N-X_{t-i}))+(\beta _t\circ (N-X_{t-i}))^2|X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t]\\&\quad =\sum _{i=1}^p \phi _i [\alpha _t(1-\alpha _t)X_{t-i}+\alpha _t^2X_{t-i}^2 + \beta _t(1-\beta _t)(N-X_{t-i}) +\beta _t^2(N-X_{t-i})^2 + 2\alpha _t\beta _tX_{t-i}(N-X_{t-i})]\\&\quad =\sum _{i=1}^p \phi _i \left( \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1))^2} X_{t-i} + \frac{\exp (2\varvec{Z}_t^{\top } \varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1))^2} X_{t-i}^2 +\frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2))^2} (N-X_{t-i}) \right. \\&~~~~~~~~~\left. +\frac{\exp (2\varvec{Z}_t^{\top } \varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1))^2} (N-X_{t-i})^2 +2\prod _{i=1}^2 \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_i)}{ 1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_i)} X_{t-i}(N-X_{t-i}) \right) . \end{aligned}$$

Therefore, the conditional variance can be derived as follows

$$\begin{aligned}&\textrm{Var}(X_t|X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t) =E(X_t^2|X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t)-E^2(X_t|X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t)\\&\quad =\sum _{i=1}^p \phi _i \left( \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1))^2} X_{t-i} + \frac{\exp (2\varvec{Z}_t^{\top } \varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1))^2} X_{t-i}^2 +\frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2))^2} (N-X_{t-i}) \right. \\&\left. +\frac{\exp (2\varvec{Z}_t^{\top } \varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1))^2} (N-X_{t-i})^2 +2\prod _{i=1}^2 \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_i)}{ 1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_i)} X_{t-i}(N-X_{t-i}) \right) \\&\quad -\left( \sum _{i=1}^p \phi _i \left( \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}{1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}X_{t-i}+ \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}{1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}(N-X_{t-i})\right) \right) ^2. \end{aligned}$$

Appendix B: The proofs of theorems

Proof of Proposition 2.1

We should first prove the RCMBAR(p)-X process defined by (2.2) is an irreducible and aperiodic Markov chain. Without loss of generality, denote by $(\Omega _j,\mathscr {A}_j,P_j)$ the probability space of $Z_{j,t}$. It follows by Definition 1 that $E|Z_{j,t}|=\int _{\Omega _j}|Z_{j,t}|\textrm{d}P_j < \infty$, which implies

$$\begin{aligned} I_{\varvec{Z}}(i,m,t):= \int _{\Omega _1}\ldots \int _{\Omega _q} \frac{\exp (m \varvec{Z}_t^{\top }\varvec{\delta }_1)}{(1+\exp (\varvec{Z}_t^{\top }\varvec{\delta }_1))^{x_{t-i}}} \frac{\exp ((x_t-m)\varvec{Z}_t^{\top }\varvec{\delta }_2)}{(1+\exp (\varvec{Z}_t^{\top }\varvec{\delta }_2))^{N-x_{t-i}}} \textrm{d} {Z}_{1,t} \ldots \textrm{d} Z_{q,t} <\infty . \end{aligned}$$

Notice that each term in (2.5) is strictly greater than zero, we obtain

$$\begin{aligned}&P(X_{t}=x_t|X_{t-1}=x_{t-1},\ldots ,X_{t-p}=x_{t-p})\nonumber \\&\quad =\int _{\Omega _1}\ldots \int _{\Omega _q} P(X_{t}=x_t|X_{t-1}=x_{t-1},\ldots ,X_{t-p}=x_{t-p},\varvec{Z}_t)\textrm{d} {Z}_{1,t} \ldots \textrm{d} Z_{q,t} \nonumber \\&\quad = \sum _{i=1}^p\phi _i\sum _{m=a}^{b} \left( {\begin{array}{c}x_{t-i}\\ m\end{array}}\right) \left( {\begin{array}{c}N-x_{t-i}\\ x_t-m\end{array}}\right) I_{\varvec{Z}}{(i,m,t)} >0. \end{aligned}$$

(A.1)

Equation (A.1) implies the process (2.2) is an irreducible and aperiodic chain. Since the state space $\mathbb {S}:=\left\{ 0, 1, \ldots , N\right\}$ has only a finite number of elements, $\{X_t\}_{t\in \mathbb {Z}}$ is also a positive recurrent Markov chain and hence ergodic. Finally, Theorem 1.3 in Karlin and Taylor (1975) guarantees the existence of the stationary distribution for $\{X_t \}$. $\square$

Proof of Theorem 3.1

In order to prove Theorem 3.1, we need to check all the regularity conditions of Theorems 3.1 and 3.2 in Klimko and Nelson (1978) hold. The regularity conditions for Theorem 3.1 in Klimko and Nelson (1978) are given as follows:

(i) $\partial g/\partial \theta _i$, $\partial ^2\,g/\partial \theta _i\partial \theta _j$, $\partial ^3\,g/\partial \theta _i\partial \theta _j\partial \theta _k$ exist and are continuous for all $\varvec{\theta }\in \Theta$, where $\theta _i$, $\theta _j$, $\theta _k$ denote the components of $\varvec{\theta }$, $i,j,k\in \{1,2, \ldots ,m\}$, g is the abbreviation for $g(\varvec{\theta },X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t)$, $m=2q+p+1$ denotes the dimension of $\varvec{\theta }$;

(ii) For $i,j \in \{1,2,\ldots ,m\}$, $E|(X_1-g)\partial g/\partial \theta _i|<\infty$, $E|(X_1-g)\partial ^2\,g/\partial \theta _i\partial \theta _j|<\infty$ and $E|\partial g/\partial \theta _i \cdot \partial g/\partial \theta _j|<\infty$, where g and its partial derivatives are evaluated at $\varvec{\theta }_0$ and the $\sigma$-filed generated by all the information before zero time;

(iii) For $i,j,k \in \{1,2,\ldots ,m\}$ there exist functions $H^{(0)}(X_0,\ldots ,X_{1-p})$, $H_i^{(1)}(X_0,\ldots ,X_{1-p})$, $H_{ij}^{(2)}(X_0,\ldots ,X_{1-p})$, $H_{ijk}^{(3)}(X_0,\ldots ,X_{1-p})$ such that

$$\begin{aligned} |g|<H^{(0)},~|\partial g/\partial \theta _i|<H_i^{(1)},~ |\partial ^2 g/\partial \theta _i\partial \theta _j|<H_{ij}^{(2)},~ |\partial ^3 g/\partial \theta _i\partial \theta _j\partial \theta _k|<H_{ijk}^{(3)}, \end{aligned}$$

(B.1)

for all $\varvec{\theta }\in \Theta$, and

$$\begin{aligned} \begin{array}{l} E|X_1\cdot H_{ijk}^{(3)}(X_0,\ldots ,X_{1-p})|<\infty ,\\ E(H^{(0)}(X_0,\ldots ,X_{1-p})\cdot H_{ijk}^{(3)}(X_0,\ldots ,X_{1-p}))<\infty ,\\ E(H_i^{(1)}(X_0,\ldots ,X_{1-p})\cdot H_{ij}^{(2)}(X_0,\ldots ,X_{1-p}))<\infty . \end{array} \end{aligned}$$

(B.2)

Recall that $g(\varvec{\theta },X_{t-1},\ldots ,X_{t-p},\varvec{Z}_t)=\sum _{i=1}^p \phi _i \left( \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}{1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_1)}X_{t-i}+ \frac{\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}{1+\exp (\varvec{Z}_t^{\top } \varvec{\delta }_2)}(N-X_{t-i})\right)$. It is easy to check that condition (i) holds. Denote by $p_k:=P(X_t=k)$, $k=0,1,\ldots ,N$. Thus, we have for any fixed $s \ge 1$,

$$\begin{aligned} E(|X_t|^s)=E(X_t^s)=\sum _{k=0}^N p_k \cdot k^s \le \sum _{k=0}^N p_k \cdot N^s =N^s <\infty . \end{aligned}$$

(B.3)

By Definition 1, $\varvec{Z}_t$ has a finite covariance matrix, which, together with (B.3) ensures that condition (ii) holds. Denote by $\varvec{x}=(x_1,\ldots ,x_n)^{\top }$ a n-dimensional vector, further denote by $\Vert \varvec{x}\Vert _1=|x_1|+|x_2|+\ldots +|x_n|$, $\Vert \varvec{x}\Vert _{\infty }=\max _{1 \le i \le n}|x_i|$. Let

$$\begin{aligned} \begin{array}{ll} H^{(0)}(X_0,\ldots ,X_{1-p})=N, &{} H_i^{(1)}(X_0,\ldots ,X_{1-p})=N \Vert \varvec{Z}_t\Vert _1,\\ H_{ij}^{(2)}(X_0,\ldots ,X_{1-p})=N \Vert \varvec{Z}_t\Vert _{\infty }^2, &{} H_{ijk}^{(3)}(X_0,\ldots ,X_{1-p})=N \Vert \varvec{Z}_t\Vert _{\infty }^3, \end{array} \end{aligned}$$

(B.4)

then for any $i,j,k \in \{1,2,\ldots ,m\}$, we can verify that (B.1) holds. Moreover, $E\Vert \varvec{Z}_t\Vert ^3 < \infty$ and (B.4) imply that (B.2) holds, which implies the $\hat{\varvec{\theta }}_{CLS}$ is a strongly consistent estimator. With the fact that $X_t-g$ is bounded by 2N, we obtain that $U_t(\varvec{\theta })$ is bounded by $4N^2$. Together with condition (ii), we have that

$$\begin{aligned} E(U_1(\varvec{\theta })|\partial g/\partial \theta _i \cdot \partial g/\partial \theta _j|)<\infty ,~i,j \in \{1,2,\ldots ,m\}. \end{aligned}$$

Therefore, the regularity conditions for Theorem 3.2 in Klimko and Nelson (1978) hold are also hold, implying the asymptotic normality for $\hat{\varvec{\theta }}_{CLS}$. $\square$

Proof of Theorem 3.2

To prove Theorem 3.2, we first give an equivalent representation of the RCMBAR(p)-X process. We begin with some notations. Let $\varvec{Y}_t:=(X_t,X_{t-1},\ldots ,X_{t-p+1})^{\top }$, $\alpha _{i,t}=D_{t,i}\alpha _t$, $\beta _{i,t}=D_{t,i}\beta _t$, $i=1,2,\ldots ,p$, and further denote two pth-order matrices $\varvec{\alpha }_t$ and $\varvec{\beta }_t$ as

$$\begin{aligned} \varvec{\alpha }_t:= \left( \begin{array}{ccccc} \alpha _{1,t} &{} \alpha _{2,t} &{} \ldots &{} \alpha _{p-1,t} &{} \alpha _{p,t}\\ 1 &{} 0 &{} \ldots &{} 0 &{} 0 \\ 0 &{} 1 &{} \ldots &{} 0 &{} 0\\ \vdots &{} \vdots &{} &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} 1 &{} 0\\ \end{array}\right)\quad \text{ and }\quad \varvec{\beta }_t:= \left( \begin{array}{ccccc} \beta _{1,t} &{} \beta _{2,t} &{} \ldots &{} \beta _{p-1,t} &{} \beta _{p,t}\\ 0 &{} 0 &{} \ldots &{} 0 &{} 0 \\ 0 &{} 0 &{} \ldots &{} 0 &{} 0\\ \vdots &{} \vdots &{} &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} 0 &{} 0\\ \end{array}\right) . \end{aligned}$$

With the fact that $0\circ X=0$ and $1\circ X=X$ (see Lemma 1 in Silva and Oliveira 2004), model (2.2) can be written in the following form:

$$\begin{aligned} \varvec{Y}_t=\varvec{\alpha }_t \circ \varvec{Y}_{t-1} + \varvec{\beta }_t \circ (\varvec{N}-\varvec{Y}_{t-1}), \end{aligned}$$

(B.5)

where $\varvec{N}^{\top } = (N,\ldots ,N)_{1\times p}$, “$\circ$” operation here denotes a matrix operation which acts as the usual matrix multiplication while replacing scaler multiplication with the binomial thinning operation. Thus, we obtain a multivariate version binomial autoregressive model with state space

$$\begin{aligned} \mathbb {S}:=\underbrace{\{0, 1, \ldots , N \} \times \{0, 1, \ldots , N \} \ldots \times \{0, 1, \ldots , N \}}_{p \text{ multiple } \text{ cartesian } \text{ product }}, \end{aligned}$$

i.e., $\mathbb {S}=\{(s_1,\ldots ,s_p)| s_j \in \{0, 1, \ldots , N\}, j=1,2, \ldots ,p\}$. Denote by $P_{t|t-1}(\varvec{\theta }):=P(\varvec{Y}_t=\varvec{y}_t|\varvec{Y}_{t-1}=\varvec{y}_{t-1})$ the transition probability of $\{\varvec{Y}_t\}$. Thus, we have

$$\begin{aligned} P_{t|t-1}(\varvec{\theta }):&\quad =P(\varvec{Y}_t=\varvec{y}_t|\varvec{Y}_{t-1}=\varvec{y}_{t-1},\varvec{Z}_t)\nonumber \\&\quad =P(X_t=x_t,\ldots ,X_{t-p+1}=x_{t-p+1}|X_{t-1}=x_{t-1},\ldots ,X_{t-p}=x_{t-p},\varvec{Z}_t)\nonumber \\&\quad =P(X_t=x_t|X_{t-1}=x_{t-1},\ldots ,X_{t-p}=x_{t-p},\varvec{Z}_t). \end{aligned}$$

(B.6)

Equations (B.6) imples models (2.2) and (B.5) have the same transition probabilities, and also have the same CML estimators accordingly. Therefore, we can use the result in Billingsley (1961) to prove Theorem 3.2. To this end, we need to verify that Condition 5.1 in Billingsley (1961) holds. Condition 5.1 of Billingsley (1961) is fulfilled provided that:

1. The set D of $(\varvec{k},\varvec{l})$ such that $P_{t|t-1}(\varvec{\theta })=P(\varvec{Y}_t=\varvec{k}|\varvec{Y}_{t-1}=\varvec{l},\varvec{Z}_t)>0$ is independent of $\varvec{\theta }$;

2. Each $P_{t|t-1}(\varvec{\theta })$ has continuous partial derivatives of third order throughout $\Theta$;

3. The $d\times r$ matrix

$$\begin{aligned} (\partial P_{t|t-1}(\varvec{\theta })/\partial \theta _{u}),~u=1,\ldots ,r, \end{aligned}$$

(B.7)

(d being the number of elements in D) has rank r throughout $\Theta$, $r:=\dim (\Theta )$.

4. For each $\varvec{\theta }\in \Theta$ there is only one ergodic set and there no transient states.

Conditions 1 and 2 are easily fulfilled by (2.6). For any $\varvec{\theta }$, we can select a r dimensional square matrix of rank r from the $d\times r$ dimensional matrix (B.7), then Condition 3 is also true. Since the state space of (B.5) is a finite set, and $P_{t|t-1}(\varvec{\theta })>0$, then Condition 4 holds. Thus, Conditions 1 to 4 are all fulfilled, which implies Condition 5.1 in Billingsley (1961) holds. Thereby, the CML-estimators $\hat{\varvec{\theta }}_{CML}$ are strongly consistent and asymptotically normal.

The proof is complete. $\square$

Appendix C: the autocovariance function

Based on model (B.5), we derive the autocovariance function in the following form. Denote by $\varvec{\gamma }(k):=\textrm{Cov}(\varvec{Y}_t,\varvec{Y}_{t-k})$. By the law of total covariance, we have

$$\begin{aligned} \varvec{\gamma }(k)&=\textrm{Cov}(E(\varvec{Y}_t|\varvec{Y}_{t-1},\ldots ),E(\varvec{Y}_{t-k}|\varvec{Y}_{t-1},\ldots ))+0\\&\quad =\textrm{Cov}(E(\varvec{\alpha }_t)\varvec{Y}_{t-1}+E(\varvec{\beta }_t)(\varvec{N}-\varvec{Y}_{t-1}),\varvec{Y}_{t-k})\\&\quad =E(\varvec{\alpha }_t)\textrm{Cov}(\varvec{Y}_{t-1},\varvec{Y}_{t-k})-E(\varvec{\beta }_t)\textrm{Cov}(\varvec{Y}_{t-1},\varvec{Y}_{t-k})\\&\quad =(E(\varvec{\alpha }_t)-E(\varvec{\beta }_t))\varvec{\gamma }(k-1)\\&\quad =\ldots \\&\quad =(E(\varvec{\alpha }_t)-E(\varvec{\beta }_t))^k \varvec{\gamma }(0). \end{aligned}$$

The above representation gives a measure of autocorrelation property of (B.5), which further gives a measure for the RCMBAR(p)-X process.