hhsmm: an R package for hidden hybrid Markov/semi-Markov models

Abstract

This paper introduces the hhsmm R package, which involves functions for initializing, fitting, and predication of hidden hybrid Markov/semi-Markov models. These models are flexible models with both Markovian and semi-Markovian states, which are applied to situations where the model involves absorbing or macro-states. The left-to-right models and the models with series/parallel networks of states are two models with Markovian and semi-Markovian states. The hhsmm also includes Markov/semi-Markov switching regression model as well as the auto-regressive HHSMM, the nonparametric estimation of the emission distribution using penalized B-splines, prediction of future states and the residual useful lifetime estimation in the predict function. The commercial modular aero-propulsion system simulation (C-MAPSS) data-set is also included in the package, which is used for illustration of the application of the package features. The application of the hhsmm package to the analysis and prediction of the Spain’s energy demand is also presented.

1 Introduction

The package hhsmm, developed in the R language (R Development Core Team 2010), involves new tools for modeling multivariate and multi-sample time series by hidden hybrid Markov/semi-Markov models, introduced by Guédon (2005). A hidden hybrid Markov/semi-Markov Model (HHSMM) is a model with both Markovian and semi-Markovian states. This package is available from the Comprehensive R Archive Network (CRAN) at https://cran.r-project.org/package=hhsmm.

The hidden hybrid Markov/semi-Markov models have many applications for the situations in which there are absorbing or macro-states in the model. These flexible models decrease the time complexity of the hidden semi-Markov models, preserving their prediction power. Another important application of the hidden hybrid Markov/semi-Markov models is in the genetics, where we aim to analysis of the DNA sequences including long interionic zones.

Several packages are available for modeling hidden Markov and semi-Markov models. Some of the packages developed in the R language are depmixS4 (Visser and Speekenbrink 2010), HiddenMarkov (Harte 2006), msm (Jackson 2007), hsmm (Bulla et al. 2010) and mhsmm (ÓConnel and Højsgaard 2011). The packages depmixS4, HiddenMarkov and msm only consider hidden Markov models (HMM), while the two packages hsmm and mhsmm focus on hidden Markov and hidden semi-Markov (HSMM) models from single and multiple sequences, respectively. These packages do not include hidden hybrid Markov/semi-Markov models, which are included in the hhsmm package. The mhsmm package has some tools for fitting the HMM and HSMM models to the multiple sequences, while the hsmm package has not such a capability. Such a capability is preserved in the hhsmm package. Furthermore, the mhsmm package is equipped with the ability to define new emission distributions, by using the mstep functions, which is also preserved for the hhsmm package. In addition to all these differences, the hhsmm package is distinguished from hsmm and mhsmm packages in the following features:

• Some initialization tools are developed for initial clustering, parameter estimation, and model initialization;

• The left-to-right models, which are the models in which the process goes from a state to the next state and never comes back to the previous state, such as the health states of a system and the states of a phoneme in speech recognition, are considered;

• The ability to initialize, fit and predict the models based on data sets containing missing values, using the EM algorithm and imputation methods, is involved;

• The regime Markov/semi-Markov switching linear and additive regression model as well as the auto-regressive HHSMM are involved;

• The nonparametric estimation of the emission distribution using penalized B-splines is added;

• The prediction of the future states is involved;

• The estimation of the residual useful lifetime (RUL), which is the remaining time to the failure of a system (the last state of the left-to-right model, considered for the health of a system), is developed for the left-to-right models used in the reliability theory applications;

• The continuous sojourn time distributions are considered in their correct form;

• The Commercial Modular Aero-Propulsion System Simulation (CMAPSS) data set is included in the package.

There are also tools for modeling HMM in other languages. For instance, the hmmlearn library in Python or hmmtrain and hmmestimate functions in Statistics and Machine Learning Toolbox of Matlab are available for modeling HMM, while none of them are not suitable for modeling HSMM or HHSMM.

The remainder of the paper is organized as follows. In Sect. 2, we introduce the hidden hybrid Markov/semi-Markov models (HHSMM), proposed by Guédon (2005). Section 3 presents a simple example of the HHSMM model and the hhsmm package. Section 4 presents special features of the hhsmm package including tools for handling missing values, initialization tools, the nonparametric mixture of B-splines for estimation of the emission distribution, regime (Markov/semi-Markov) switching regression, and auto-regressive HHSMM, prediction of the future state sequence, residual useful lifetime (RUL) estimation for reliability applications, continuous-time sojourn distributions, and some other features of the hhsmm package. Finally, the analysis of two real data sets is considered in Sect. 5, to illustrate the application of the hhsmm package.

2 Hidden hybrid Markov/semi-Markov models

Consider a sequence of observations $\{X_t\}$, which is observed for $t = 1,\ldots , T$. Assume that the distribution of $X_t$ depends on an un-observed (latent) variable $S_t$, called state. If the sequence $\{S_t\}$ is a Markov chain of order 1, and for any $t\ge 1$, $X_t$ and $X_{t+1}$ are conditionally independent, given $S_t$, then the sequence $\{(S_t, X_t)\}$ forms a hidden Markov model (HMM). A graphical representation of the dependence structure of the HMM is shown in Fig. 1.

Fig. 1

A graphical representation of the dependence structure of the HMM

The parameters of an HMM are the initial probabilities of the states, the transition probability matrix of states, and the parameters of the conditional distribution of observations given states, which is called the emission distribution.

The time spent in a state is called the sojourn time. In the HMM model, the sojourn time distribution is simply proved to be geometric distribution. The hidden semi-Markov model (HSMM) is similar to HMM, while the sojourn time distribution can be any other distribution, including discrete and continuous distributions with positive support, such as Poisson, negative binomial, logarithmic, nonparametric, gamma, Weibull, log-normal, etc.

The hidden hybrid Markov/semi-Markov model (HHSMM), introduced by Guédon (2005), is a combination of the HMM and HSMM models. It is defined, for $t=0,\ldots ,\tau -1$ and $j=1,\ldots ,J$, by the following parameters:

• 1. Initial probabilities $\pi _j = P(S_0 = j),\; \sum _{j}\pi _j = 1$,

• 2. Transition probabilities, which are

  • for a semi-Markovian state j,

    $$\begin{aligned}p_{jk} = P(S_{t+1} =k|S_{t+1} \ne j,S_t=j), \; \forall k\ne j;\; \sum _{k\ne j}p_{jk} = 1;\; p_{jj} = 0\end{aligned}$$

  • for a Markovian state j,

    $$\begin{aligned} {\tilde{p}}_{jk} = P(S_{t+1} = k|S_t = j);\; \sum _{k}{\tilde{p}}_{jk} = 1\end{aligned}$$

  By the above definition, any absorbing state, which is a state j with $p_{jj} = 1$, is Markovian. This means that if we want to conclude an absorbing state along with some semi-Markovian states in the model, we need to use the HHSMM model.

• 3. Emission distribution parameters, $\theta$, for the following distribution function

  $$\begin{aligned}f_j(x_t) = f(x_t | S_t = j; \; \theta )\end{aligned}$$

• 4. The sojourn time distribution is defined for semi-Markovian state j, as follows

  $$\begin{aligned} d_j(u)= & {} P(S_{t+u+1} \ne j,\;S_{t+u-\nu } = j, \;\nu = 0, \ldots ,u-2|S_{t+1} = j,\; S_t \ne j), \quad \\&\quad u = 1,\ldots ,M_j,\end{aligned}$$

  where $M_j$ stands for an upper bound to the time spent in state j. Also, the survival function of the sojourn time distribution is defined as $D_j(u) = \sum _{\nu \ge u}d_j(\nu )$.

For a Markovian state j, the sojourn time distribution is the geometric distribution with the following probability mass function

$$\begin{aligned}d_j(u) = (1-{\tilde{p}}_{jj}){\tilde{p}}_{jj}^{u-1},\quad u = 1,2,\cdots \end{aligned}$$

The parameter estimation of the model is performed via the EM algorithm (Dempster et al. 1977). The EM algorithm consists of two steps. In the first step, which is called the E-step, the conditional expectation of the unobserved variables (states) is computed given the observations, which are called the E-step probabilities. This step utilizes the forward-backward algorithm to calculate the E-step probabilities. The second step is the maximization step (M-step). In this step the parameters of the model are updated by maximizing the expectation of the logarithm of the joint probability density/mass function of the observed and unobserved data. A brief description of the EM and forward-backward algorithms, as well as the Viterbi algorithm, is given in the Appendix. The Viterbi algorithm obtains the most likely state sequence, for the HHSMM model.

2.1 Examples of hidden hybrid Markov/semi-Markov models

Some examples of HHSMM models are as follows:

• Models with macro-states: The macro-states are series or parallel networks of states with common emission distribution. A semi-Markovian model can not be used for macro-states and a hybrid Markov/semi-Markov model is a good choice in such situations (see Cook and Russell 1986; Durbin et al. 1998; Guédon 2005).

• Models with absorbing states: An absorbing state is Markovian by definition. Thus, a model with an absorbing state can not be fully semi-Markovian.

• Left to right models: The left-to-right models are useful tools in the reliability analysis of failure systems. Another application of these models is in speech recognition, where the feature sequence extracted from a voice is modeled by a left to right model of states. The transition matrix of a left to right model is an upper triangle matrix with its final diagonal element equal to one, since the last state of a left-to-right model is absorbing. Thus, a hidden hybrid Markov/semi-Markov model might be used in such cases, instead of a hidden fully semi-Markov model.

• Analysis of DNA sequences: It is observed that the length of some interionic zones in DNA sequences are approximately, geometrically distributed, while the length of other zones might deviate from the geometric distribution (Guédon 2005).

3 A simple example

To illustrate the application of the hhsmm package for initializing, fitting, and prediction of a hidden hybrid Markov/semi-Markov model, we first propose a simple example. We emphasize that the aim of this example is not comparing different models, while this is an example to show how can we use the flexible options of the package hhsmm for initializing and fitting different models.

To do this, we define a model, with two Markovian and one semi-Markovian state, and 2, 3, and 2 mixture components in states 1–3, respectively, as follows. The sojourn time distribution for the semi-Markovian state is considered to be the gamma distribution (see Sect. 4.8). The Boolean vector semi is used to define the Markovian and semi-Markovian states. Also, the mixture component proportions are defined using the parameter list mix.p.

Now, we simulate train and test data sets, using the simulate function. The remission argument is considered to be rmixmvnorm, which is a function for random sample generation from mixture of multivariate normal distributions. The data sets are plotted using the plot function. The plots of the train and test data sets are presented in Figs. 2 and 3, respectively. Different states are distinguished with different colors in the horizontal axis.

Fig. 2

The plots for 4 sequences of train data set

Fig. 3

The plots for 4 sequences of test data set

In order to initialize the parameters of the HHSMM model, we first obtain an initial clustering of the train data set, using the initial_cluster function. The nstate argument is set to 3, and the number of mixture components in the three states is set to c(2,2,2). The ltr and final.absorb arguments is set to FALSE, which means that the model is not left-to-right and the final element of each sequence is not in an absorbing state. Thus, the kmeans algorithm (Lloyd 1982) is used for the initial clustering.

Now, we initialize the model parameters using the initialize_model function. The initial clustering output clus is used for estimation of the parameters. The sojourn time distribution is set to "gamma" distribution. First, we use the true value of the semi vector for modeling. Thus, the initialized model is a hidden hybrid Markov/semi-Markov model.

The model is then fitted using the hhsmmfit function as follows. The initialized model initmodel1 is used as the start value.

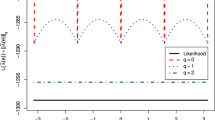
The log-likelihood trend can also be extracted and plotted as follows. This plot is presented in Fig. 4.

Fig. 4

The log-likelihood trend during the model fitting

One can observe, for instance, the estimated initial probabilities, transition matrix, and the estimated parameters of the sojourn distribution as follows.

The state sequence is now predicted using the default method "viterbi" of the predict function for the test data set. Because of the displacement property of the states, the homogeneity of the predicted states is computed using the homogeneity function for three states. Since the states are indeed clusters, the homogeneity measures, which are used for clustering, are useful for measuring the homogeneity of two sequences of state. The homogeneity of a specified cluster (state) in two sequences, is defined as the percentage of members of both sequences that are in the same cluster (state) in both sequences. The output of the homogeneity function shows the homogeneity percent of two sequences of states.

Now, we initialize and fit a fully Markovian model (HMM) by setting semi to c(FALSE,FALSE,FALSE). The same clustering output clus can be used here.

The model is again fitted using hhsmmfit function.

We can compare some of the estimated parameters of this model with those of the previous one.

Now, we predict the state sequence of the fitted model and compute its homogeneity with the true state sequence.

Finally, we initialize and fit a full semi-Markov model (HSMM) to the train data set, by setting semi to c(TRUE,TRUE,TRUE). The "gamma" distribution is considered as the sojourn time distribution for all states.

The prediction and homogeneity computation for this model is done as follows.

4 Special features of the package

The hhsmm package has several special features, which are described in the following subsections.

4.1 Handling missing values

The hhsmm package is equipped with tools for handling data sets with missing values. A special imputation algorithm is used in the initial_cluster function. This algorithm, imputes a completely missed row of the data with the average of its previous and next rows, while if some columns are missed, the predictive mean matching method of the function mice from package mice (Van Buuren and Groothuis-Oudshoorn 2011), with $m=1$, is used to initially impute the missing values. After performing the initial clustering and initial estimation of the parameters of the model, the miss_mixmvnorm_mstep function is considered, as the M-step function of the EM algorithm, for initializing and fitting the model. The function miss_mixmvnorm_mstep includes computation of the conditional means and conditional second moments of the missing values given observed values in each iteration of the EM algorithm and updating the parameters of the Gaussian mixture emission distribution, using the cov.miss.mix.wt function. Furthermore, an approximation of the mixture component weights using the observed values and conditional means of the missing values given observed values is used in each iteration. The values of the emission density function, used in the E-step of the EM algorithm are computed by replacing the missing values with their conditional means given the observed values.

Here, we provide a simple example to examine the performance of the aforementioned method. First, we define a model with three states and two variables.

Now, we simulate the complete train and test data sets.

First, we initialize and fit the model with complete data sets. To do this, we first use the initial_cluster to provide an initial clustering of the train data set.

Now, we initialize and fit the model.

Finally, we predict the state sequence of the test data set, using the predict.hhsmm function and the default "viterbi" method.

To examine the tools for modeling the data sets with missing values, we randomly select some elements of the train and test data sets and replace them with NA, as follows.

Now, we provide the initial clustering of the incomplete train data set using the initial_cluster function.

We can observe that the output of the initial_cluster function contains a flag that indicates the missingness in the data set.

Now, we initialize and fit the model for the incomplete data set.

Similarly, we predict the state sequence of the incomplete test data set, using the predict.hhsmm function.

We can observe that the homogeneity of the predictions of the complete and incomplete data sets are very close to each other.

4.2 Tools and methods for initializing model

To initialize the HHSMM model, we need to obtain an initial clustering for the train data set. For a left to right model (option ltr = TRUE of the initial_cluster function), we propose Algorithm 2, which uses Algorithm 1, for a left to right initial clustering, which are included in the function ltr_clus of the hhsmm package. These algorithms use Hotelling’s T-squared test statistic as the distance measure for clustering. The simulations and real data analysis show that the starting values obtained by the proposed algorithm perform well for a left to right model (see Sect. 5 for a real data application). If the model is not a left to right model, then the usual K-means algorithm is used for clustering. Furthermore, the K-means algorithm is used within each initial state to cluster data for mixture components. The number of mixture components can be determined automatically, using the option nmix = "auto", by analysis of the within sum of squares obtained from the kmeans function. The number of starting values of the kmeans is set to 10, for the stability of the results. The initial clustering is performed using the initial_cluster function.

After obtaining the initial clustering, the initial estimates of the parameters of the mixture of multivariate normal emission distribution are obtained. Furthermore, the parameters of the sojourn time distribution is obtained by running the method of moments estimation algorithms on the time duration observations of the initial clustering of each state. If we set sojourn = "auto" in the initialize_model function, the best sojourn time distribution is selected from the list of available sojourn time distributions, using the Chi-square goodness of fit testing on the initial cluster data of all states.

4.3 Nonparametric mixture of B-splines emission

Usually, the emission distribution belongs to a parametric family of distributions. Although the mixture of multivariate normals is shown to be a good choice in many practical situations, there are also examples in which this class of emission distribution fails to model the skewness and tail weight of the data set. Furthermore, the choice of the number of components of the mixture distribution in each state is a challenge of using mixture of multivariate normals as the emission distribution. As an alternative to parametric emission distribution, HMMs and HSMMs with non-parametric estimates of state-dependent distributions are shown to be more parsimonious in terms of the number of states, easier to interpret, and well fitted to the data (Langrock et al. 2015; Adam et al. 2019). The proposed nonparametric estimation approach of Langrock et al. (2015) and Adam et al. (2019) is based on the idea of representing the densities of the emission distributions as linear combinations of B-spline basis functions, by adding a smoothing penalty term to the quasi-log-likelihood function. In this model, the emission distribution is defined as follows

$$\begin{aligned} f_j(x) = \sum _{k=-K}^{K} a_{j,k} \phi _k(x), \quad j=1,\ldots ,J, \end{aligned}$$

(1)

where $\{\phi _{-K}(\cdot ),\ldots ,\phi _{K}(\cdot )\}$ is a sequences of B-splines and $\{a_{j,k}\}$ is the sequences of unknown coefficients to be estimated. These parameters are estimated in the M-step of the EM algorithm, by maximizing the following penalized quasi-log-likelihood function

$$\begin{aligned} \ell _P^{\mathrm{HHSMM}}(\theta ,\lambda ) = log(L^{\mathrm{HHSMM}}(\theta )) - \frac{1}{2}\sum _{j=1}^J \lambda _j \sum _{k=-K+2}^{K} (\Delta ^2 a_{j,k})^2, \end{aligned}$$

(2)

in which $L^{HHSMM}(\theta )$ the quasi-likelihood of the HHSMM model, $\theta$ is the parameters of the model, $\Delta a_k = a_k - a_{k-1}$, $\Delta ^2 a_k = \Delta (\Delta a_k)$, and $\lambda _1,\ldots ,\lambda _J$ are the smoothing parameters, which are estimated as follows (Schellhase and Kauermann 2012)

$$\begin{aligned} {\hat{\lambda }}_j = \frac{\mathrm{df}({\hat{\lambda }}_j) - p}{\sum _{k=-K+2}^{K}(\Delta ^2 {\hat{a}}_{j,k})^2}, \end{aligned}$$

where p is the dimension of the data,

$$\begin{aligned} \mathrm{df}({\hat{\lambda }}_j)=\mathrm{tr}\left( H^{-1}({\hat{a}}_j;\lambda _j = {\hat{\lambda }}_j) H({\hat{a}}_j;\lambda _j = 0)\right) , \end{aligned}$$

and $H({\hat{a}};\lambda )$ is the hessian matrix of the log-quasi-likelihood at ${\hat{a}}$ with the specified value of $\lambda$.

To illustrate the application of the hhsmm package with a nonparametric mixture of B-splines emission distribution, we present a simple simulated data example. To do this, we first simulate data from an HHSMM model with a mixture of multivariate normals as the emission distribution, as follows.

Now, we obtain an initial clustering of the data set using the initial_cluster function. Note that for a nonparametric emission distribution, we have no mixture components and we should use the option nmix = NULL.

In order to initialize a HHSMM with non-parametric estimates of the emission distribution, we use the initialize_model function with the arguments mstep = nonpar_mstep and dens.emission = dnonpar, as follows.

Now, we can use the hhsmmfit function to fit the model.

Finally, we predict the state sequence of the test data and compute the homogeneity of the predicted sequence and the reals sequence as follows.

As one can see from the output of the homogeneity function, the fitted model has a high precision for the prediction of the state sequence of the new data set.

4.4 Regime (Markov/semi-Markov) switching regression model

Kim et al. (2008) considered the following Gaussian regime-switching model

$$\begin{aligned} y_{t} = x_{t}^T \beta _{s_t} + \sigma _{s_t}\epsilon _t, \end{aligned}$$

(3)

where $y_{t}$ is the response variable, $x_{t}$ is a vector of covariates, which may include lagged values of $y_{t}$ (auto-regressive HHSMM, see the next subsection), $s_t$ is the state, and $\epsilon _t$ is the regression error, which is assumed to be distributed as standard normal distribution, for $t=1,\ldots ,T$. Model (3) can easily be extended to the case of multivariate responses and also to the case of mixture of multivariate normals. The difference between the regime-switching model (3) and the HHSMM model is that, instead of using the density of $y_{t}$ given $s_t$ in the likelihood function, we use the conditional density of $y_{t}$ given $x_{t}$ and $s_t$. A graphical representation of the regime-switching model is presented in Fig. 5. The parameters of the regime switching regression model can be estimated using the EM algorithm.

Fig. 5

Graphical representation of the regime-switching model

Langrock et al. (2018) considered an extension of the model (3) to the following additive regime-switching model

$$\begin{aligned} y_{t} = \mu _{s_t} + \sum _{j=1}^p f_{j,s_t}(x_{j,t}) + \sigma _{s_t}\epsilon _t, \end{aligned}$$

(4)

where $f_{j,s_t}(\cdot ),\; j=1,...,p$ are unknown regression functions for p covariates. They utilized the penalized B-splines for estimation of the regression functions.

The estimation of extensions of models (3) and (4) is considered in hhsmm package, using the mixlm_mstep and additive_reg_mstep functions, respectively, as the M-step estimation and dmixlm and dnorm_additive_reg functions, respectively, which define mixture of multivariate normals and multivariate normal densities, respectively, as the conditional density of the responses given the covariates. The response variables are determined using the argument resp.ind in all of these functions, with its default value equal to one, which means that the first column of the input matrix x, is the univariate response variable.

To illustrate usage of these functions in the hhsmm package, we present the following simple simulated data example. First, we simulate data using the function simulate.hhsmmspec, using the argument remission = rmixlm, covar = list(mean = 0, cov = 1). The argument covar is indeed an argument of the rmixlm function, which is either a function which generates the covariate vector or a list containing the mean vector and the variance-covariance matrix of covariates to be generated from multivariate normal distribution. The rmixlm is a function for generation of the data from mixture of linear models, for each state. The list of parameters of this emission distribution consist of the following items:

• intercept, a list of the intercepts of the regression models for each state and each mixture component,

• coefficient, a list of the coefficient vectors/matrices of the regression models for each state and each mixture component,

• csigma, a list of the conditional variances/variance-covariance matrices of the response for each state and each mixture component,

• mix.p, a list of mixture component probabilities for each state.

First, we define the model parameters and simulate the data as follows.

Now, we obtain an initial clustering of the data using initial_cluster function, with the argument regress = TRUE, which is essential for estimation the parameters of the regime switching regression models. By letting regress = TRUE and ltr = FALSE the initial_cluster function uses an algorithm similar to that of Lloyd (1982) for the K-means method, by fitting linear regression models instead of computing simple means, in each iteration of an algorithm. When using regress = TRUE and ltr = TRUE, an algorithm similar to that, described in Sect. 4.2 is used for left-to-right clustering, by using regression coefficients instead of mean vectors, and the associated Hotteling’s T-square statistic.

We initialize the model, using the initialize_model function, with arguments mstep = mixlm_mstep, which is a function for M-step estimation of the EM algorithm in the regime switching regression model, and dens.emission = dmixlm, which is a function for computation of the probability density function of the mixture Gaussian linear model, for a specified observation vector, a specified state and a specified model’s parameters. Next, we fit the model, by using the hhsmmfit function.

The plots of the clustered data as well as the estimated regime-switching regression model lines are then plotted as follows. The resulting plot is shown in Fig. 6.

Fig. 6

The regime Markov switching example

To fit the regime-switching additive regression model to the train data, we make an initial clustering of the data, using the initial_cluster function, by letting nstate = 3, nmix = NULL and regress = TRUE. Using the argument nmix = NULL is essential in this case, since the parameters of the regime switching additive regression model does not involve mixture components.

Now, we initialize the model using the function initialize_model, with arguments mstep = additive_reg_mstep and dens.emission = dnorm_additive_reg. Note that here, we only consider a full-Markovian model and thus we let semi = rep(FALSE, 3) and sojourn = NULL, while one can also consider HSMM or HHSMM models by considering different semi and sojourn arguments.

Next, we fit the model by calling the hhsmmfit function.

Again, we plot the data to add the fitted lines. The colors of the points show the true states, while the characters present the predicted states.

To obtain the predicted values of the response variable, we use the addreg_hhsmm_predict function as follows.

We add the predicted curves to the plot. The resulting plot is shown in Fig. 7.

As one can see from Fig. 7, the curves have a proper fit to the data points.

Fig. 7

The Markov regime-switching additive regression fit

4.5 Auto-regressive HHSMM

A special case of the regime-switching regression models (3) and (4) is the auto-regressive HHSMM model, in which we take $x_t = (y_{t-1},\ldots ,y_{t-\ell })$, for a specified lag $\ell \ge 1$. Here, we present a simulated data example, to illustrate this special case.

The model specification of the auto-regressive HHSMM is similar to that of the regime-switching regression model, noting that the dimension of $x_t$ is always $\ell$ times the dimension of $y_t$. So, we specify the model as follows.

To simulate the data using the simulate.hhsmm function, we have to use the argument emission.control = list(autoregress = TRUE). We, then, plot the simulated data by using plot.hhsmmdata as follows. The resulting plot is shown in Fig. 8.

Fig. 8

The ARHMM example simulated train data set

To prepare the data for fitting the regime-switching regression model, we should first construct the lagged data matrix by using the function lagdata as follows. The default of the parameter lags of this function is equal to 1, which is the number of lags to be calculated.

The resulting lagged data set is then used for obtaining the initial clustering, using the argument regress = TRUE and resp.ind = 2 in the initial_cluster function as follows.

Now, we initialize and fit the model as before. Note that we should use the argument resp.ind = 2 in place of ... in both functions (see the manual of the hhsmm package https://cran.r-project.org/web/packages/hhsmm/hhsmm.pdf)

To test the performance of the fitted model for prediction of the future time series, we need to simulate a test data set and then right-trim the test data set, using the train_test_split, and by setting train.ratio = 1, trim = TRUE and trim.ratio = 0.9, as follows. As one can see, the length of the sequences in trimmed_test$trimmed is $90\%$ of the associated lengths in test data set.

The option train.ratio = 1 means that we do not wish to split the test samples into new train and test subsets and we only need to right trim the sequences. Now, we have both trimmed sequences in trimmed object and the complete test samples in test data set, so that we can compare the true and predicted states. The object tc contains the number of trimmed items in each sequence, which has to be predicted.

Now, we use the estimated parameters of the ARHMM to predict the future values of the sequence. To do this, we predict the state sequence of the lagged trimmed test data set using the predict.hhsmm function and then we obtain the linear predictors for the future values as follows.

The resulting plot is presented in Fig. 9. The colored lines are the predicted values.

Fig. 9

Trimmed test data set and the predicted values

We try to apply the regime-switching additive regression model to fit the AR-HMM model. Again, the only difference of the initial clustering using the initial_cluster function is to set nmix = NULL.

We initialize the model using the function initialize_model by setting mstep = additive_reg_mstep and dens.emission = dnorm_additive_reg. The difference here is that we pass the parameters of these function to the initialize_model function through the argument control. In the following, we pass the response indicator and the degree of the B-splines by setting the argument control = list(resp.ind = 2, K = 7).

Now, we fit the model by calling the hhsmmfit function, as follows.

Finally, we provide the prediction plots, through the following codes.

The resulting plots are presented in Fig. 10. The colored lines are the predicted values. By comparing the Figs. 9 and 10 one can see that the regime-switching additive regression model results in more accurate prediction especially for the second sequence of the test data set.

Fig. 10

The predicted values using AR-HMM model, using the regime switching additive regression

4.6 Prediction of the future state sequence

To predict the future state sequence at times $T+1,\ldots ,T+h$, first, we use viterbi (smoothing) algorithm (see the Appendix) to estimate the probabilities of the most likely path $\alpha _j(t)$ ($L_j(t)$) for $j=1,\ldots ,J$ and $t=0,\ldots ,\tau -1$, as well as the current most likely state ${\hat{s}}_t^* =\arg \max _{1\le j\le J} \alpha _j(t)$ (${\hat{s}}_t^* =\arg \max _{1\le j\le J} L_j(t)$). Also, we might compute the probabilities

$$\begin{aligned} {\bar{\delta }}_t(j)=\frac{\alpha _{j}(t)}{\sum _{k=1}^J\alpha _{k}(t)}\quad ({\bar{\delta }}_t(j)=\frac{L_{j}(t)}{\sum _{k=1}^JL_{k}(t)}). \end{aligned}$$

(5)

Next, for $j=1,\ldots ,h$, we compute the probability of the next state, by multiplying the transition matrix by the current state probability as follows

$$\begin{aligned} {\bar{\delta }}_{next} = \Big (P\Big )^T{\bar{\delta }}_{current} \end{aligned}$$

(6)

Then, the jth future state is predicted as

$$\begin{aligned} {\hat{s}}_{next}^*=\arg \max _{1\le j \le J}{\bar{\delta }}_{next}(j) \end{aligned}$$

(7)

This process continues until the required time $T+h$. The prediction of the future state sequence is done using the function predict.hhsmm function in the hhsmm package, by determining the argument future, which is equal to zero by default. To examine this ability, we study a simple example as follows. First, we define a simple model, just like the model in section 3, and simulate train and test samples from this model, as follows.

To examine the prediction performance of the model, we split the test sample from the right, using train_test_split function and a trim ratio equal to 0.9, as follows.

As in Sect. 3, we initialize and fit an HHSMM model to the train data set, as follows.

Now, we predict the future states of each sequence of the test data set, separately, using the option future = tc[i]. Then, we print the homogeneity of real and predicted state sequences, by using the homogeneity function, as follows.

As, on can see from the above homogeneities, the predictions are quite good.

4.7 Residual useful lifetime (RUL) estimation, for reliability applications

The residual useful lifetime (RUL) is defined as the remaining lifetime of a system at a specified time point. If we analyse a reliable system with a hidden Markov or semi-Markov model, a suitable choice would be a left to right model, with the final state as the failure state. The RUL of such model is defined at time t as

$$\begin{aligned} \text{ RUL}_t = {\tilde{D}}:S_{t+{\tilde{D}}} = J, S_{t+{\tilde{D}}-1} = i;\quad 1\le i < k\le J. \end{aligned}$$

(8)

We describe a method of RUL estimation (see Cartella et al. 2015), which is used in hhsmm package. First, we should compute the probabilities in (5), using the Viterbi or smoothing algorithm.

Two different methods are used to obtain point and interval estimates of the RUL in the hhsmm package. The first method (the option confidence = "mean" in the predict function of the hhsmm package) is based on the method described in Cartella et al. (2015). This method computes the average time in the current state as follows

$$\begin{aligned} {\tilde{d}}_{avg}({\hat{s}}_t^*) = \sum _{j=1}^{J}\Big (\mu _{d_j}-{\hat{d}}_t(j)\Big ){\bar{\delta }}_t(j), \end{aligned}$$

(9)

where $\mu _{d_i}=\sum _{u=1}^{M_j} u d_i(u)$ is the expected value of the duration variable in state j, and ${\hat{d}}_t(j)$ is the estimated states duration, computed as follows (Azimi 2004)

$$\begin{aligned} {\hat{d}}_t(j) = {\hat{d}}_{t-1}(j) {\bar{\delta }}_t(j), \quad t = 2, \ldots , M_j, \quad {\hat{d}}_{1}(j)=1, \; j = 1,\ldots , J. \end{aligned}$$

In order to obtain a confidence interval for the RUL, Cartella et al. (2015) also computed the standard deviation of the duration variable in state j, $\sigma _{d_j}$, and

$$\begin{aligned}&{\tilde{d}}_{low}({\hat{s}}_t^*) = \sum _{j=1}^{J}\Big (\mu _{d_j}-{\hat{d}}_t(j)-\sigma _{d_j}\Big ){\bar{\delta }}_t(j), \end{aligned}$$

(10)

$$\begin{aligned}&{\tilde{d}}_{up}({\hat{s}}_t^*) =\sum _{j=1}^{J}\Big (\mu _{d_j}-{\hat{d}}_t(j)+\sigma _{d_j}\Big ){\bar{\delta }}_t(j) \end{aligned}$$

(11)

However, to obtain a confidence interval of the specified level $1-\gamma \in (0,1)$, we have corrected Eqs. (10) and (11) in the hhsmm package as follows

$$\begin{aligned}&{\tilde{d}}_{low}({\hat{s}}_t^*) = \sum _{j=1}^{J}\Big (\mu _{d_j}-{\hat{d}}_t(j)-z_{1-\gamma /2}\sigma _{d_j}\Big ){\bar{\delta }}_t(j), \end{aligned}$$

(12)

$$\begin{aligned}&{\tilde{d}}_{up}({\hat{s}}_t^*) =\sum _{j=1}^{J}\Big (\mu _{d_j}-{\hat{d}}_t(j)+z_{1-\gamma /2}\sigma _{d_j}\Big ){\bar{\delta }}_t(j), \end{aligned}$$

(13)

where $z_{1-\gamma /2}$ is the ${1-\gamma /2}$ quantile of the standard normal distribution.

The probability of the next state is obtained by multiplying the transition matrix by the current state probability as follows

$$\begin{aligned} {\bar{\delta }}_{next} = \Big [{\bar{\delta }}_{t+{\tilde{d}}}(j)\Big ]_{1\le j\le J}=\Big (P\Big )^T{\bar{\delta }}_t \end{aligned}$$

(14)

while the maximum a posteriori estimate of the next state is calculated as

$$\begin{aligned} {\hat{s}}_{next}^*={\hat{s}}_{t+{\tilde{d}}}^*=\arg \max _{1\le j \le J}{\bar{\delta }}_{t+{\tilde{d}}}(j) \end{aligned}$$

(15)

If ${\hat{S}}_{t+{\tilde{d}}}(j)$ coincides with the failure state J, the failure will happen after the remaining time at the current state is over and the average estimation of the failure time is ${\tilde{D}}_{avg}={\tilde{d}}_{avg}(\hat{s_t}^*)$, with the lower and upper bounds ${\tilde{D}}_{low}={\tilde{d}}_{low}(\hat{s_t}^*)$ and ${\tilde{D}}_{up}={\tilde{d}}_{up}(\hat{s_t}^*)$, respectively, otherwise, the sojourn time of the next state is calculated as

$$\begin{aligned}&{\tilde{d}}_{avg}\Big ({\hat{S}}_{t+{\tilde{d}}}^*\Big )=\sum _{j=1}^{J}\mu _{d_j}{\bar{\delta }}_{t+{\tilde{d}}}(j) \end{aligned}$$

(16)

$$\begin{aligned}&{\tilde{d}}_{low}\Big ({\hat{S}}_{t+{\tilde{d}}}^*\Big )=\sum _{j=1}^{J}\Big (\mu _{d_j}-z_{1-\gamma /2}\sigma _{d_j}\Big ){\bar{\delta }}_{t+{\tilde{d}}}(j) \end{aligned}$$

(17)

$$\begin{aligned}&{\tilde{d}}_{up}\Big ({\hat{S}}_{t+{\tilde{d}}}^*\Big )=\sum _{j=1}^{J}\Big (\mu _{d_j}+z_{1-\gamma /2}\sigma _{d_j}\Big ){\bar{\delta }}_{t+{\tilde{d}}}(j) \end{aligned}$$

(18)

This procedure is iterated until the failure state is encountered in the prediction of the next state. The estimate of the RUL is then calculated by summing all the aforementioned estimated remaining times, as follows

$$\begin{aligned} {\tilde{D}}_{avg} = \sum {\tilde{d}}_{avg}, \quad {\tilde{D}}_{low} = \sum {\tilde{d}}_{low}, \quad {\tilde{D}}_{up} = \sum {\tilde{d}}_{up} \end{aligned}$$

(19)

In the second method (the option confidence = "max" in the predict function of the hhsmm package), we relax the normal assumption and use the mode and quantiles of the sojourn time distribution, by replacing the mean $\mu _{d_j}$ with the mode $m_{d_j} = \arg \max _{1\le u \le M_j} d_j(u)$ and replacing $-z_{1-\gamma /2}\sigma _{d_j}$ with $\min \{\nu ;\; \sum _{u=1}^\nu d_j(u) \le \gamma /2\}$ and $+z_{1-\gamma /2}\sigma _{d_j}$ with $M_j - \min \{\nu ;\; \sum _{u=\nu }^{M_j} d_j(u) \le \gamma /2\}$ in Eqs. (10), (12), (13), (16), (17) and (18).

4.8 Continuous time sojourn distributions

Since the measurements of the observations are always preformed on discrete time units (assumed to be positive integers), the sojourn time probabilities of the sojourn time distribution with probability density function $g_j$, in state j, is obtained as follows

$$\begin{aligned} d_j(u)= & {} P(S_{t+u+1} \ne j,\;S_{t+u-\nu } = j, \;\nu = 0, \ldots ,u-2|S_{t+1} = j,\; S_t \ne j)\nonumber \\= & {} \int _{u-1}^{u} g_j(y) \; dy \big / \int _{0}^{M_j} g_j(y) \; dy, \quad j=1,\ldots ,J,\quad u=1,\ldots ,M_j. \end{aligned}$$

(20)

Almost all flexible continuous distributions with positive domain, which are used as the lifetime distribution, including gamma, weibull, log-normal, Birnbaum-Saunders, inverse-gamma, Fréchet, Gumbel and many other distributions, might be used as the continuous-time sojourn distribution. Some of the continuous sojourn time distributions, included in the hhsmm package, are as follows:

• Gamma sojourn: The gamma sojourn time density functions are

  $$\begin{aligned}g_j(y) = \frac{y^{\alpha _j-1}e^{-\frac{y}{\beta _j}}}{\beta _j^{\alpha _j}\Gamma (\alpha _j)}, \quad j=1,\ldots ,J,\end{aligned}$$

  which result in

  $$\begin{aligned}d_j(u) = \int _{u-1}^{u} y^{\alpha _j-1}e^{-\frac{y}{\beta _j}} \; dy \big / \int _{0}^{M_j} y^{\alpha _j-1}e^{-\frac{y}{\beta _j}} \; dy \end{aligned}$$

• Weibull sojourn: The Weibull sojourn time density functions are

  $$\begin{aligned}g_j(y) = \frac{\alpha _j}{\beta _j} \left( \frac{y}{\beta _j}\right) ^{\alpha _j-1} \exp \left\{ - \left( \frac{y}{\beta _j}\right) ^{\alpha _j}\right\} , \quad j=1,\ldots ,J,\end{aligned}$$

  which result in

  $$\begin{aligned}d_j(u) = \int _{u-1}^{u} y^{\alpha _j-1} \exp \left\{ - \left( \frac{y}{\beta _j}\right) ^{\alpha _j}\right\} \; dy \left. / \int _{0}^{M_j} y^{\alpha _j-1} \exp \left\{ - \left( \frac{y}{\beta _j}\right) ^{\alpha _j}\right\} \; dy\right. \end{aligned}$$

• log-normal sojourn: The log-normal sojourn time density functions are

  $$\begin{aligned}g_j(y) = \frac{1}{\sqrt{2\pi }\sigma _j} \exp \left\{ \frac{-1}{2\sigma _j^2}(\log y - \mu _j)^2\right\} , \quad j=1,\ldots ,J,\end{aligned}$$

  which result in

  $$\begin{aligned}d_j(u) = \int _{u-1}^{u} \exp \left\{ \frac{-1}{2\sigma _j^2}(\log y - \mu _j)^2\right\} \; dy \left. / \int _{0}^{M_j} \exp \left\{ \frac{-1}{2\sigma _j^2}(\log y - \mu _j)^2\right\} \; dy\right. \end{aligned}$$

4.9 Other features of the package

There are some other features included in the hhsmm package, which are listed below:

• dmixmvnorm: Computes the probability density function of a mixture of multivariate normals for a specified observation vector, a specified state, and a specified model’s parameters

• mixmvnorm_mstep: The M step function of the EM algorithm for the mixture of multivariate normals as the emission distribution using the observation matrix and the estimated weight vectors

• rmixmvnorm: Generates a vector of observations from mixture multivariate normal distribution in a specified state and using the parameters of a specified model

• train_test_split: Splits the data sets to train and test subsets with an option to right trim the sequences

• lagdata: Creates lagged time series of a data

• score: Computes the score (log-likelihood) of new observations using a trained model

• homogeneity: Computes maximum homogeneity of two state sequences

• hhsmmdata: Converts a matrix of data and its associated vector of sequence lengths to a data list of class "hhsmmdata"

5 Real data analysis

To examine the performance of the hhsmm package, we consider the analysis of two real data sets. The first data set is the Spain energy market data set from MSwM package and the second one is the Commercial Modular Aero-Propulsion System Simulation (CMAPSS) data set from the CMAPSS data package.

5.1 Spain energy market data set

The Spain energy market data set (Fontdecaba et al. 2009) contains the price of the energy in Spain with other economic data. The daily data is from January 1, 2002 to October 31, 2008, during working days (Monday to Friday). This data set is available in MSwM package (https://cran.r-project.org/package=MSwM), in a data-frame named energy and contains 1785 observations on 7 variables: Price (Average price of energy in Cent/kwh), Oil (Oil price in Euro/barril), Gas (Gas price in Euro/MWh), Coal (Coal price in Euro/T), EurDol (Exchange rate between Dolar-Euro in USD-Euro), Ibex35 (Ibex 35 index divided by one thousand) and Demand (Daily demand of energy in GWh). This data-set is also analysed in Fontdecaba et al. (2009), using Markov switching regression model. The objective of the analysis is to predict the response variable Price, based on the information in other variables (covariates).

In order to analyze the energy data set, we load it from MSwM package, and transform it into a "hhsmmdata" using hhsmmdata function as follows.

We consider a two-state model. Here, we consider a fully Markovian model and thus, we let semi ${\mathtt{<}}$ - rep(FALSE, J). Although an optimal value of K might be obtained by minimizing the AIC, BIC or even a cross-validation error, we set the degree of the B-splines to $K=20$ for this analysis, for the sake of briefness.

First, we make an initial clustering for the data set. Again, we point out that we should consider nmix = NULL and regress = TRUE in the initial_cluster function.

To initialize the model, we use the initialize_model function, with arguments mstep = additive_reg_mstep, dens.emission = dnorm_additive_reg and control = list(K = K).

Next, we fit the model by calling the hhsmmfit function as follows.

Now, we can obtain the response predictions using the addreg_hhsmm_predict function as follows.

To visualize the results, first, we add the predicted states to a hhsmmdata set made by the response variable. Then, we plot it using the plot.hhsmmspec function, as follows.

The resulting plot is presented in Fig. 11. The predicted states are shown by two different colors on the horizontal axis.

Fig. 11

Spain energy data and its estimated states

In the second plot, we want to show the separate predictions for the two states along with the true response values. To do this, we use the following lines of codes.

The resulting plot is presented in Fig. 12. The predictions associated with the two states’ are shown by blue and red lines.

Fig. 12

Two-state prediction of the energy price based on the other variables

To visualize the nonparametric regression curves, we consider only the covariate Oil Price, which is the second column of the energy data set. In the following, we initialize and fit the model to the data set containing only the first column as the response and the second column as the covariate.

Again, we obtain the response predictions as follows.

Now, we can plot the corresponding graph as follows.

The resulting plot is presented in Fig. 13. As one can see from Fig. 13, the two curves are well-fitted to the data points.

Fig. 13

Prediction curves for regime swithching nonparametric regression model of energy price on oil price

To compare the prediction performance of the above-mentioned model with the simple (single state) additive regression model, we can use the additive_reg_mstep function, with a weight matrix with a single column and all components equal to 1.

We compute the sum of squared errors (SSE) of the two competitive models as follows.

We plot the predictions of two competitive models by adding their SSE values to plots, as follows.

Fig. 14

Comparision with simple additive regression

The resulting plot is given in Fig. 14. As one can see from Fig. 14, the two-state regime switching additive regression model, performs much better than the simple (single state) additive regression model.

5.2 RUL estimation for the C-MAPSS data set

The turbofan engine data is from the Prognostic Center of Excellence (PCoE) of NASA Ames Research Center, which is simulated by the Commercial Modular Aero-Propulsion System Simulation (C-MAPSS). Only 14 out of 21 variables are selected, by a method mentioned by Li et al. (2019) and are included in the hhsmm package. A list of all 21 variable, as well as a description and the selected 14 variables are tabulated in Table 1. The train an test lists are of class "hhsmmdata". The original data set contains the subsets FD001-FD004, which are concatenated in the CMAPSS data set. These sets are described in Table 2. This table is presented in CMAPSS$subsets in the CMAPSS data set.

Table 1 Sensor description of the C-MAPSS data set (see Li et al. 2019)

Table 2 C-MAPSS data set overview

We load the data set and extract the train and test sets as follows.

To visualize the data set, we plot only the first sequence of the train set. To do this, this sequence is converted to a data set of class "hhsmmdata", using the function hhsmmdata as follows. The plots are presented in Fig. 15.

Initial clustering of the states and mixture components is obtained by the initial_cluster function. Since, the suitable reliability model for the CMAPSS data set is a left to right model, the option ltr = TRUE is used. Also, since the engines are failed in the final time of each sequence, the final time of each sequence is considered the absorbing state (final state of the left to right model). This assumption is given to the model by the option final.absorb = TRUE. The number of states is assumed to be 5 states, which could be one healthy state, 3 levels of damage state, and one failure state in the reliability model. The number of mixture components is computed automatically using the option nmix = "auto".

Now, we initialize the model using the initialize_model function. The sojourn time distribution is assumed to be "gamma" distribution.

Fig. 15

The time series plot of 14 variables of the first sequence of the train set for the CMAPSS data set

As a result, the initial estimates of the parameters of the sojourn time distribution and initial estimates of the transition probability matrix and the initial probability vector are obtained as follows.

Now, we fit the HHSMM model, using hhsmmfit function. The option lock.init=TRUE is a good option for a right to left model since the initial state is the first state (healthy system state in the reliability model) in such situations with probability 1. Graphical visualization of such a model is given in Fig. 16.

Fig. 16

Graphical representation of the reliability left to right model

The estimates of the transition probability matrix, the sojourn time probability matrix, the initial probability vector, and the AIC and BIC of the model, are extracted as follows.

We can plot the estimated gamma sojourn probability density functions as follows.

The resulted plot is shown in Fig. 17.

Fig. 17

The estimated gamma sojourn time density functions

Now, we obtain the estimates of the RULs, as well as the confidence intervals, by four different methods as follows. These four methods are obtained by combination of two different methods "viterbi" and "smoothing" for the prediction and two different methods "mean" and "max" for RUL estimation and confidence interval computation. The option "viterbi" uses the Viterbi algorithm to find the most likely state sequence, while the option "smoothing" uses the estimates of the state probabilities, using the emission probabilities of the test data set. On the other hand, in the "mean" method, the mean sojourn time and its standard deviation are used for estimation and confidence interval, while in the "max" method, the maximum probability sojourn time and its quantiles are used (see Sect. 4.7).

As a competitor, we fit the hidden Markov model (HMM) to the data set, which means that we consider all states to be Markovian. To de this, we try fitting the HMM to the train set, using the option semi = rep(FALSE,J) of the hhsmmfit function of the hhsmm package. We use the same initial values of the parameters, while we need to use dens.emission = dmixmvnorm in the hhsmmspec function, and set the mixture components probabilities equal to 1 (for one mixture component in each state).

For the fitted HMM model, we estimate the RULs using the aforementioned options.

Now, we use the real values of the RULs, stored in test$RUL to compute the coverage probabilities of the confidence intervals of HHSMM and HMM models.

As one can see from the above results, the HHSMM model’s coverage probabilities are much better than the HMM ones.

To visualize the results of RUL estimation, we plot the RUL estimates and RUL bounds as follows.

The resulting plots are presented in Fig. 18. From Fig. 18 and the above coverage probabilities, one can see that the “smoothing" and “max" methods perform better than other methods, in this example.

Fig. 18

RUL estimates (solid blue lines) and RUL bounds (dashed red lines) using four different methods for the CMAPSS test data set

6 Concluding remarks

This paper presents several examples of the R package hhsmm. The scope of application of this package covers simulation, initialization, fitting, and prediction of HMM, HSMM, and HHSMM models, for different types of discrete and continuous sojourn distribution, including shifted Poisson, negative binomial, logarithmic, gamma, Weibull, and log-normal. This package contains density and M-step function for estimation of the emission distribution for different types of emission distribution, including the mixture of multivariate normals and penalized B-spline estimator of the emission distribution, the mixture of linear and additive regression (conditional multivariate normal distributions of the response given the covariates; regime-switching regression models) as well as the ability to define another emission distributions by the user. As a special case of the regime-switching regression models, the auto-regressive HHSMM models can be modeled by the hhsmm package. The left to right models are considered in the hhsmm package, especially in the initialization functions. The hhsmm package uses the EM algorithm to handle the missing values when the mixture of multivariate normals is considered as the emission distribution. The ability to predict the future states, residual useful lifetime estimation for the left to right models, computation of the score of new observations, computing the homogeneity of two sequences of states, and splitting the data to train and test sequences by the ability to right-trim the test sequences, are other useful features of the hhsmm package. The current version 0.3.2 of this package is now available on CRAN (https://cran.r-project.org/package=hhsmm), while the future improvements of this package are also considered by the authors. Any report of the possible bugs of the hhsmm package are welcome through https://github.com/mortamini/hhsmm/issues and we welcome the users’ offers for any needed feature of the package in the future.

Appendix

1.1 Forward-backward algorithm for the HHSMM model

Denote the sequence $\{Y_{t},\ldots ,Y_{s}\}$ by $Y_{t:s}$ and suppose that the observation sequence $X_{0:\tau -1}$ with the corresponding hidden state sequence $S_{0:\tau -1}$ is observed. The forward-backward algorithm is an algorithm to compute the probabilities

$$\begin{aligned}L_j(t)=P(S_t=j|X_{0:{\tau -1}}=x_{0:{\tau -1}})\end{aligned}$$

within the E-step of the EM algorithm. The above probabilities are computed in the backward recursion of the forward-backward algorithm.

For a semi-Markovian state j, and $t=0,\ldots ,\tau -2$, the forward recursion computes the following probabilities (Guédon 2005),

$$\begin{aligned} F_j(t)= & P(S_{t+1}\ne j,S_t = j|X_{0:t} = x_{0:t})\nonumber \\= & \frac{f_j(x_t)}{N_t}\Biggl [\sum _{{u=1}}^{t}\Bigg \{\prod _{\nu =1}^{u-1}\frac{f_j(x_{t-\nu })}{N_{t-\nu }}\Bigg \}d_j(u)\sum _{i\ne j}p_{ij}F_i(t-u)\nonumber \\ &\qquad+\Bigg \{\prod _{\nu =1}^{t}\frac{f_j(x_{t-\nu })}{N_{t-\nu }}\Bigg \}d_j(t+1)\pi _j\Biggl ], \end{aligned}$$

(A.21)

and

$$\begin{aligned} F_j(\tau -1)= & P(S_{\tau -1} = j|X_{0:{\tau -1}} =x_{0:{\tau -1}})\nonumber \\= & \frac{f_j(x_{\tau -1})}{N_{\tau -1}}\Biggl [\sum _{u=1}^{\tau -1}\Bigg \{\prod _{\nu =1}^{u-1}\frac{f_j(x_{\tau -1-\nu })}{N_{\tau -1-\nu }}\Bigg \}D_j(u)\sum _{i\ne j}p_{ij}F_i(\tau -1-u)\nonumber \\ &\qquad+\Bigg \{\prod _{\nu =1}^{\tau -1}\frac{f_j(x_{\tau -1-\nu })}{N_{\tau -1-\nu }}\Bigg \}D_j(\tau )\pi _j\Biggl ]. \end{aligned}$$

(A.22)

where the normalizing factor $N_t$ is computed as follows

$$\begin{aligned} N_t = P(X_t = x_t|X_{0:{t-1}} = x_{0:{t-1}}) =\sum _{j}P(S_t = j,X_t = x_t|X_{0:{t-1}} = x_{0:{t-1}}) \end{aligned}$$

For a Markovian state j, and for $t = 0$,

$$\begin{aligned} {\tilde{F}}_j(0) = P(S_0 = j|X_0 = x_0)=\frac{f_j(x_0)}{N_0}\pi _j\end{aligned}$$

and for $t = 1,\ldots ,\tau -1$

$$\begin{aligned} {\tilde{F}}_j(t) = P(S_t = j|X_{0:t} = x_{0:t}) =\frac{f_j(x_t)}{N_t}\sum _{i}{\tilde{p}}_{ij}{\tilde{F}}_i(t-1) \end{aligned}$$

(A.23)

The log-likelihood of the model is then

$$\begin{aligned}\log P(X_{0:{\tau -1}} = x_{0:{\tau -1}};\theta ) = \sum _{t=0}^{\tau -1}\log N_t,\end{aligned}$$

which is used as a criteria for convergence of the EM algorithm and the evaluate the quality of the model. The backward recursion is initialized by

$$\begin{aligned}L_j(\tau -1) = P(S_{\tau -1} = j|X_{0:{\tau -1}} = x_{0:{\tau -1}}) = F_j(\tau -1) = {\tilde{F}}_j(\tau -1).\end{aligned}$$

For a semi-Markovian state j, we have

$$\begin{aligned}L_j(\tau -1) = P(S_{\tau -1} = j|X_{0:{\tau -1}} = x_{0:{\tau -1}}) = F_j(\tau -1), \end{aligned}$$

and for $t = \tau -2,\ldots ,0$,

$$\begin{aligned} L_j(t)= & {} L1_j(t) + L_j(t+1) - G_j(t+1)\sum _{i\ne j}{p}_{ij}{\tilde{F}}_i(t), \end{aligned}$$

(A.24)

where

$$\begin{aligned} L1_j(t)= & {} \sum _{k\ne j}G_k(t+1)p_{jk}F_j(t), \end{aligned}$$

(A.25)

and

$$\begin{aligned} G_j(t+1)= & {} \sum _{u=1}^{\tau -1-t}G_j(t+1,u) \end{aligned}$$

with

$$\begin{aligned} G_j(t+1,u)=\left\{ \prod _{\nu =0}^{\tau -2-t}\frac{f_j(x_{\tau -1-\nu })}{N_{\tau -1-\nu }}\right\} D_j(\tau -1-t). \end{aligned}$$

For a Markovian state j and for $t = \tau -2,\ldots ,0$

$$\begin{aligned} L_j(t)= & {} L1_j(t) \end{aligned}$$

(A.26)

Furthermore, if a mixture of multivariate normal distributions with probability density function

$$\begin{aligned} f_j(x) = \sum _{k=1}^{K_j}\lambda _{kj} {{\mathcal {N}}}_p(x; \mu _{kj}, \Sigma _{kj}),\quad j=1,\ldots ,J, \end{aligned}$$

(A.27)

is considered as the emission distribution, then the following probabilities of the mixture components are computed in the E-step of the $(s+1)$th iteration of the EM algorithm

$$\begin{aligned} \gamma _{kj}^{(s+1)}(t) = \frac{\lambda _{kj}^{(s)}{{\mathcal {N}}}_p(x_t; \mu _{kj}^{(s)}, \Sigma _{kj}^{(s)})}{f_j(x_t) }, \end{aligned}$$

(A.28)

where $\lambda _{kj}^{(s)}$, $\mu _{kj}^{(s)}$ and $\Sigma _{kj}^{(s)}$ are the sth updates of the emission parameters in the M-step of the sth iteration of the EM algorithm.

1.2 The M-step of the EM algorithm

In the M-step of the EM algorithm, the initial probabilities are updated as follows

$$\begin{aligned}\pi _j^{(s+1)} = P(S_0 = j|X_{0:{\tau -1}} = x_{0:{\tau -1}};\theta ^{(s)}) = L_j(0), \end{aligned}$$

For a semi-Markovian state i, the transition probabilities are updated as follows

$$\begin{aligned} p_{ij}^{(s+1)}= & {} \frac{\sum _{t=0}^{\tau -2}G_j(t+1)p_{ij}^{(s)}F_i(t)}{\sum _{t=0}^{\tau -2}L1_i(t)} \end{aligned}$$

(A.29)

and for a Markovian state i

$$\begin{aligned} {\tilde{p}}_{ij}^{(s+1)}= & {} \frac{\sum _{t=0}^{\tau -2}{\tilde{G}}_j(t+1){\tilde{p}}_{ij}^{(s)}{\tilde{F}}_i(t)}{\sum _{t=0}^{\tau -2}L_i(t)} \end{aligned}$$

(A.30)

If we consider the mixture of multivariate normals, with the probability density function (A.27), as the emission distribution, then its parameters are updated as follows

$$\begin{aligned}&\lambda _{kj}^{(s+1)} = \frac{\sum _{t=0}^{\tau -1}\gamma _{kj}^{(s)}(t) L_j^{(s)}(t)}{\sum _{m=1}^{K_j}\sum _{t=0}^{\tau -1}\gamma _{mj}^{(s)}(t) L_j^{(s)}(t)} = \frac{\sum _{t=0}^{\tau -1}\gamma _{kj}^{(s)}(t) L_j^{(s)}(t)}{\sum _{t=0}^{\tau -1}L_j^{(s)}(t)},\\&\mu _{kj}^{(s+1)} = \frac{\sum _{t=0}^{\tau -1}\gamma _{kj}^{(s)}(t) L_j^{(s)}(t)x_t}{\sum _{t=0}^{\tau -1}\gamma _{kj}^{(s)}(t) L_j^{(s)}(t)},\\&\Sigma _{kj}^{(s+1)} = \frac{\sum _{t=0}^{\tau -1}\gamma _{kj}^{(s)}(t) L_j^{(s)}(t)(x_t-\mu _{kj}^{(s+1)})(x_t-\mu _{kj}^{(s+1)})^T}{\sum _{t=0}^{\tau -1}\gamma _{kj}^{(s)}(t) L_j^{(s)}(t)} \end{aligned}$$

Also, the parameters of the sojourn time distribution are updated by maximization of the following quasi-log-likelihood function

$$\begin{aligned}{\tilde{Q}}_d(\{d_j(u)\}|\theta ^{(s)}) = \sum _{u=1}^{M_j}{\tilde{\eta }}_{j,u}^{(s)}\log d_j(u), \end{aligned}$$

where

$$\begin{aligned}&{\tilde{\eta }}_{j,u}=\sum _{t=0}^{\tau -2} G_j(t+1,u)\sum _{i\ne j} p_{ij} F_i(t) + A(u) d_j(u)\pi _j \prod _{v=1}^u \frac{f_j(x_{u_{\tau } - v)}}{N_{u_{\tau }-v}},\\&A(u) = \left\{ \begin{array}{lr}\frac{L_{1j}(u-1)}{F_j(u-1)},&{} u\le \tau -1\\ 1,&{} u>\tau -1,\end{array}\right. \end{aligned}$$

and $u_{\tau } = \min (u,\tau )$.

1.3 Viterbi algorithm and smoothing for the HHSMM model

The Viterbi algorithm (Viterbi 1967) is an algorithm to obtain the most likely state sequence, given the observations and the estimated parameters of the model.

For a semi-Markovian state j, and for $t=0,\ldots ,\tau -2$, the probability of the most probable state sequence is obtained by the Viterbi recursion as follows

$$\begin{aligned} \alpha _j(t)= & {} \max _{s_0,\ldots ,s_{\tau -1}}P(S_{t+1}\ne j,S_t=j,S_{0:{t-1}}=s_{0:{t-1}},X_{0:t}=x_{0:t})\nonumber \\= & {} f_j(x_t)\max \Bigg [\max _{1\le u\le t}\Bigg [\Bigg \{\prod _{\nu =1}^{u-1}f_j(x_{t-\nu })\Bigg \}d_j(u)\max _{i\ne j}\{p_{ij}\alpha _i(t-u)\}\Bigg ],\nonumber \\&\times \Bigg \{\prod _{\nu =1}^{t}f_j(x_{t-\nu })\Bigg \}d_j(t+1)\pi _j\Bigg ], \end{aligned}$$

(A.31)

and

$$\begin{aligned} \alpha _j(\tau -1)= & {} \max _{s_0,\ldots ,s_{\tau -2}} P(S_{\tau -1} =j,S_{0:{\tau -2}} =s_{0:{\tau -2}},X_{0:{\tau -1}} =x_{0:{\tau -1}})\nonumber \\= & {} f_j(x_{\tau -1})\max \Bigg [\max _{1\le u\le \tau -1}\Bigg [\Bigg \{\prod _{\nu =1}^{u-1}f_j(x_{\tau -1-\nu })\Bigg \}D_j(u)\max _{i\ne j}\{p_{ij}\alpha _i(\tau -1-u)\}\Bigg ],\nonumber \\&\times \Bigg \{\prod _{\nu }^{\tau -1}f_j(x_{\tau -1-\nu })\Bigg \}D_j(\tau )\pi _j\Bigg ], \end{aligned}$$

(A.32)

For a Markovian state j, the Viterbi recursion is initialized by

$$\begin{aligned}{\tilde{\alpha }}_j(0) = P(S_0 = j,X_0 = x_0) = f_j(x_0)\pi _j\end{aligned}$$

and for $t = 1,\ldots .\tau -1$,

$$\begin{aligned} {\tilde{\alpha }}_j(t)= & \max _{s_0,\ldots ,s_{t-1}}P(S_t = j,S_0^{t-1} = s_0^{t-1},X_{0:t} = x_{0:t})\end{aligned}$$

(A.33)

$$\begin{aligned}= & f_j(x_t)\max _i\{{\tilde{p}}_{ij}{\tilde{\alpha }}_i(t-1)\}. \end{aligned}$$

(A.34)

After obtaining the probability of the most probable state sequence, the current most likely state is obtained as ${\hat{s}}_t^* =\arg \max _{1\le j\le J} \alpha _j(t)$.

Another approach for obtaining the state sequence is the smoothing method, which uses the backward probabilities $L_j(t)$ instead of $\alpha _j(t)$.