Power comparison for propensity score methods

Abstract

We compared four propensity score (PS) methods using simulations: maximum likelihood (ML), generalized boosting models (GBM), covariate balancing propensity scores (CBPS), and generalized additive models (GAM). Although these methods have been shown to perform better than the ML in estimating causal treatment effects, no comparison has been conducted in terms of type I error and power, and the impact of treatment exposure prevalence on PS methods has not been studied. In order to fill these gaps, we considered four simulation scenarios differing by the complexity of a propensity score model and a range of exposure prevalence. Propensity score weights were estimated using the ML, CBPS and GAM of logistic regression and the GBM. We used these propensity weights to estimate the average treatment effect among treated on a binary outcome. Simulations showed that (1) the CBPS was generally superior across the four scenarios studied in terms of type I error, power and mean squared error; (2) the GBM and the GAM were less biased than the CBPS and the ML under complex models; (3) the ML performed well when treatment exposure is rare.

1 Introduction

Propensity score (PS) methods are used to estimate an average causal treatment effect (ATE) or an average treatment effect for the treated (ATT) in observational studies (Austin 2011; Brookhart et al. 2013). Typically, the ATE or ATT is estimated via inverse-probability-of-treatment-weighting (IPTW), which gives unbiased estimators under the no unmeasured confounder assumption and a correct specification of a PS model (Rosenbaum and Rubin 1983). With IPTW, researchers can avoid the challenges of specifying an outcome model correctly, which may be more difficult than correctly specifying a PS model (Brookhart et al. 2013). Therefore, the performance of IPTW estimator depends on how well a PS model is estimated.

An essential criterion to evaluate PS models is covariate balance, that is typically measured by averages of mean differences in covariates across treatment groups. There are several approaches that have been developed, which target maximizing covariate balance in PS estimation. The first approach is to use machine learning algorithms, such as generalized boosting models (GBM) used by McCaffrey et al. (2004), which requires selecting tuning parameters that optimize covariate balance. This GBM method closely follows Friedman’s gradient boosting machine (Friedman 2001). Through a simulation study, Lee et al. (2010) showed that among several tree-based methods, the GBM approach performed well and outperformed logistic regression when the true PS model includes nonlinear or nonadditive effects of covariates. This approach, however, can suffer from computational burdens in finding optimal tuning parameters when the number of covariates is huge. Imai and Ratkovic (2014) developed a covariate balance propensity score (CBPS) methodology, which solves estimating equations that optimize covariate balance. The CBPS does not require specifying tuning parameters as the GBM method. Pirracchio and Carone (2016) applied the covariate balancing principle of Imai and Ratkovic (2014) to an ensemble learner, which is called the Super Learner (a weighted linear combination of several candidate learners) and showed that bias is improved compared to the standard Super Learner and the CBPS. However, the computation for Super Learner is very demanding because it involves V-cross validation to obtain the optimal weights.

Two studies, Wyss et al. (2014) and Setodji et al. (2017), evaluated the GBM and the CBPS mainly in terms of bias and mean squared error using the same simulation scenarios with varying linearity and additivity. From an inferential point of view, however, type I error and power or bias-adjusted power are also important measures that need to be considered. As in Wyss et al. (2014) and Setodji et al. (2017), we compared these two promising PS methods, the GBM and the CBPS, with the maximum likelihood (ML) of logistic regression, which is a default method in practice. Our study is more extensive than Wyss et al. (2014) and distinct from Setodji et al. (2017) in that we evaluated the same measures used in Wyss et al. (2014) and Setodji et al. (2017) at various treatment effect sizes, and also compared type I error, power and 95% confidence intervals, and studied the effect of exposure prevalence along with PS model complexity on the performance of the methods.

We also compared these with generalized additive models (GAM) (Hastie and Tibshirani 1990). The GAM is designed to improve the prediction performance of logistic regression when covariate effects are nonlinear and has been shown to be better than the ML (Woo et al. 2008). Even though the GAM does not seek to optimize covariate balance directly as the GBM (McCaffrey et al. 2004) and the CBPS (Imai and Ratkovic 2014), it would improve covariate balance over the ML by improving prediction accuracy. We would be able to classify these PS methods into three categories as the alternatives of the ML: a method that pursues the optimal covariate balance (CBPS), a method that pursues optimal prediction (GAM), and a method that primarily pursues optimal prediction, while maintaining good covariate balance (GBM).

2 Methods

2.1 Simulation setup

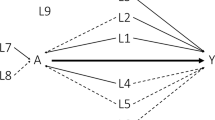
We followed the simulation design of Setoguchi et al. (2008). This simulation design was used by several articles in PS literature (Lee et al. 2010; Wyss et al. 2014; Pirracchio et al. 2015). First of all, ten covariates $X^\prime =(X_1,\ldots ,X_{10})$ were generated: $X_1, \ldots , X_4$ were confounders, $X_5, \ldots , X_7$ were correlated with only the exposure, and $X_8, \ldots , X_{10}$ were risk factors for the outcome without any associations with the exposure. Six covariates $(X_1,X_3,X_5,X_6,X_8,X_9)$ were binary, and the rest were continuous. Details about the generation of the covariates and the figure depicting the covariate relationships are in Setoguchi et al. (2008), Lee et al. (2010) and Wyss et al. (2014) respectively. For readers, we presented the figure for the simulation structure (Fig. 1), adapted from Wyss et al. (2014). The binary exposure Z was generated using a logistic regression model as a function of X. In the sequel, the binary outcome Y was generated using a logistic regression model as a function of Z and X.

Fig. 1

Data simulation structure, adapted from Wyss et al. (2014), showing causal and associational relationships between variables. There are 4 confounders ($X_1$, $X_2$, $X_3$ and $X_4$), 3 exposure predictors ($X_5$, $X_6$ and $X_7$), and 3 outcome predictors ($X_8$, $X_9$ and $X_{10}$). The arrows represent causal effects, and the arcs represent associational effects. The treatment causal effect ($A \rightarrow Y$) is controlled by an odds ratio. The number above each arc represents the correlation coefficient between the covariates

To compare the performance of different PS methods under various situations, we considered four scenarios varying the complexity of the true PS model and the prevalence of treatment exposure (Table 1).

• (A) Additive and linear PS model with moderate exposure prevalence.

• (B) Additive and linear PS model with low exposure prevalence.

• (C) Nonadditive and nonlinear PS model with moderate exposure prevalence.

• (D) Nonadditive and nonlinear PS model with low exposure prevalence.

Table 1 Description of four scenarios for data simulation

An additive and linear logistic regression model is

$$\begin{aligned} P(Z=1|X) = \frac{\exp (\beta _0 + X^\prime \beta )}{1+\exp (\beta _0 + X^\prime \beta )}. \end{aligned}$$

(1)

In scenario A, model (1) was used to generate the treatment variable with $\beta _0=0$ and

$$\begin{aligned} \beta ^\prime = (0.8,-0.25,0.6,-0.4,-0.8,-0.5,0.7,0,0,0). \end{aligned}$$

The average exposure prevalence was about 0.5. In scenario B, $\beta _0$ was set to be $-2$, and it gave the average exposure prevalence of about 0.15. In scenario C, a PS model with nonadditivity and nonlinearlity was used:

$$\begin{aligned} P(Z=1|X) = \frac{\exp (\gamma _0 + W^\prime \gamma )}{1+\exp (\gamma _0 + W^\prime \gamma )}, \end{aligned}$$

(2)

where $\gamma _0=0$ and W contains main effect terms, square terms of the continuous covariates and all pairwise interactions of $X_1,\ldots , X_7$. We used the same regression parameter values for $\gamma$ as in the scenario, used by Setoguchi et al. (2008), with a PS model with moderate nonadditivity and nonlinearlity. We did not consider the scenarios with mild nonadditivity or nonlinearlity to simplify the simulation design and to observe clear differences between the methods. In scenario D, model (2) was used, but $\gamma _0$ was set to be $-2$, which yielded the low average exposure prevalence.

As for the outcome, an additive and linear logistic regression model was considered:

$$\begin{aligned} P(Y=1|Z,X) = \frac{\exp (\theta Z + \alpha _0 + X^\prime \alpha )}{1+\exp (\theta Z + \alpha _0 + X^\prime \alpha )}, \end{aligned}$$

where $\alpha _0=-3$ and

$$\begin{aligned} \alpha ^\prime =(0.3,-0.36,-0.73,-0.2,0,0,0,0.71,-0.19,0.26,-0.4). \end{aligned}$$

The parameter of interest is $\theta$, whose exponentiated value represents the treatment effect in an odds ratio scale. To evaluate power, $1/\exp (\theta )$ varied from 0 to 3, and thus the treatment reduces the risk of the outcome if $\theta$ is non-zero. This outcome model was used to generate the outcome for all scenarios. From our simulations with the sample sizes of 1000 and 2000 under the same simulation models used in prior research (Setoguchi et al. 2008; Lee et al. 2010), we noted that the relative performance of PS methods was fairly similar across different sample sizes under each scenario. Thus, without loss of generality, we have presented results only based on a sample size of 2000, which is a typical choice for epidemiological studies (Setoguchi et al. 2008), and the common sample size used in Setoguchi et al. (2008) and Lee et al. (2010). For each scenario, we have generated 1000 data sets.

2.2 Propensity score methods

Let X be a p-dimensional covariate vector and $\pi _{\beta }(X)$ be a working PS model with a regression parameter $\beta$. The popular choice of $\pi _{\beta }(X)$ is a logistic regression model as in Eq. (1). The maximum likelihood estimator for $\beta$ is obtained by solving the score equation:

$$\begin{aligned} {\mathbb {E}}\left[ \frac{Z{{\dot{\pi }}}_{\beta }(X)}{\pi _{\beta }(X)} - \frac{(1-Z){{\dot{\pi }}}_{\beta }(X)}{1-\pi _{\beta }(X)}\right] =0, \end{aligned}$$

(3)

where ${\mathbb {E}}$ denotes sample average, and ${{\dot{\pi }}}_{\beta }(X)=\partial \pi _\beta (X)/\partial \beta ^\prime$. Therefore, the score function seeks to balance the averages of ${{\dot{\pi }}}_{\beta }(X)$ between treated and untreated groups. With a logistic regression model of $\pi _{\beta }(X)$, Eq. (3) reduces to

$$\begin{aligned} {\mathbb {E}}\left[ \{Z - \pi _{\beta }(X)\}X\right] =0, \end{aligned}$$

and thus the score funcion seeks to minimize prediction error.

The CBPS method considers solving a covariate balance estimating function. For the ATE,

$$\begin{aligned} {\mathbb {E}}\left[ \frac{Z{\tilde{X}}}{\pi _{\beta }(X)} - \frac{(1-Z){\tilde{X}}}{1-\pi _{\beta }(X)}\right] =0, \end{aligned}$$

where ${\tilde{X}}=f(X)$ is an M-dimensional vector-valued function of X for $M \ge p$. Solving this equation guarantees that the sample means of ${\tilde{X}}$ in the treatment and control groups match with the overall sample mean of ${\tilde{X}}$ if the working PS is correctly specified. For covariate balancing, a standard choice is ${\tilde{X}}=X$, which gives the just-identified CBPS model (Imai and Ratkovic 2014). The second moment of X or ${{\dot{\pi }}}_{\beta }(X)$ can be added to ${\tilde{X}}$ and this gives the over-identified CBPS model.

If the ATT is of interest, the CBPS method is implemented by solving

$$\begin{aligned} {\mathbb {E}}\left[ Z{\tilde{X}} - \frac{\pi _{\beta }(X)(1-Z){\tilde{X}}}{1-\pi _{\beta }(X)}\right] =0. \end{aligned}$$

Solving this equation ensures that the sample mean of ${\tilde{X}}$ for the control matches with that for the treated. The CBPS can be implemented using an R package called CBPS.

The GBM models a nonlinear function as a sum of trees. The GBM was effectively used for the PS analysis in McCaffrey et al. (2004), where the number of iterations were chosen to minimize the average standardized absolute mean difference (ASAM) in the covariates. This GBM algorithm that optimizes covariate balance can be implemented by the twang package, where other measures for covariate balance are available including the maximum standardized absolute mean difference. The twang package uses the gbm package (Ridgeway 2017) to run the GBM and an R’s optimize function to find the number of iterations maximizing covariate balance. Important parameters for the GBM include an amount of shrinkage, the number of iterations, the depth of covariate interactions and a stopping rule. The small size of shrinkage gives improved prediction performance, but it requires many more iterations for the model to converge. We used a shrinkage parameter of 0.01 with 10,000 iterations, a 2-way interaction depth and ASAM as a stopping rule.

The GAM was also considered for comparison. The GAM is more flexible than the logistic regression model

$$\begin{aligned} P(Z=1|X) = \frac{\exp \{\kappa + g_1(X_1) + \cdots + g_p(X_p)\}}{1+\exp \{\kappa + g_1(X_1) + \cdots + g_p(X_p)\}}, \end{aligned}$$

where each $g_j(X_j)$ is some smooth function of $X_j$. The gam package (Hastie 2016) provides local regression and smoothing splines to model $g_j(X_j)$. The backfitting algorithm is used to estimate the parameters generated by the local regression or smoothing splines (Hastie and Tibshirani 1990). We modeled the continuous covariates with the smoothing splines with a degree of freedom 4.

In summary, we compared the ML of the logistic regression with main effects, the just-identified CBPS of the logistic regression model with main effects, the GBM with 2-way interactions and the GAM of the logistic regression with the smoothing splines. In the scenario of linearity and additivity (scenarios A and B), there is no model-misspecification for the ML and the CBPS, but over-parametrization for the GAM. In the scenario of non-linearity and non-additivity (scenarios C and D), there is model-misspecification for the ML, CBPS and GAM. It is hard to describe model-misspecification and overfitting for the GBM because it is a complex data mining technique using many trees.

2.3 Performance metrics

We used IPTW to estimate the ATT using the estimated PS. The ATT is a parameter of interest in observational studies, where access to a treatment is limited (Austin 2011). As in Lee et al. (2010), to obtain the ATT estimates and correct standard error estimates, we used the R package survey (Lumley 2017) with a weighting scheme that assigns 1 to the treated subjects and $\pi _\beta (X)/\{1-\pi _\beta (X)\}$ to the untreated subjects. The following measures were used to evaluate the performance of the PS methods.

Power The percentage of rejecting the null hypothesis of no treatment effect among 1000 data sets. Let ${\hat{\theta }_j}$ be an estimate for $\theta$ from a jth data set and $t_j$ be a t-statistic for ${\hat{\theta }_j}$ calculated by the survey package. With the true parameter value $\theta$, power is defined as

$$\begin{aligned} \frac{1}{1000} \sum _{j=1}^{1000} I(|t_j| > c|\theta ), \end{aligned}$$

where $I(A|\theta )$ gives 1 if A is true with $\theta$ as a true treatment effect and 0 otherwise and c is a critical value, say 1.96, for a level of 0.05 test. The power at $\theta = 0$ gives a type I error rate.

Bias-adjusted power If there is a large bias in an estimate of treatment effect, both type I error rate and power will be inflated. In this case, comparing methods is not reliable because each method can have a different size of type I error rate. For reliable power comparison, it would be desirable to force all PS methods to have a nominal type I error rate, say 0.05. This can be achieved by adjusting a critical value, c, to make sure that all methods have a nominal type I error rate. Thus, we estimated an empirical critical value such that a type I error rate becomes 0.05. For each method and scenario, using the data sets with $\theta = 0$, we found $c^*$ satisfying

$$\begin{aligned} \frac{1}{1000} \sum _{j=1}^{1000} I(|t_j| > c^* | \theta =0) = 0.05, \end{aligned}$$

where $c^*$ is the empirical critical value. Bias-adjusted power is then defined as

$$\begin{aligned} \frac{1}{1000} \sum _{j=1}^{1000} I(|t_j| > c^*|\theta ). \end{aligned}$$

Absolute bias To reduce the effect of outliers, bias was estimated by the median of $|{\hat{\theta }_j} - \theta |$.

Root mean squared error (RMSE) To reduce the effect of outliers, the mean squared error was estimated by the sum of the square of the absolute bias and the square of the scaled median absolute deviation of ${\hat{\theta }_j}$, assuming an asymptotic normal distribution for ${\hat{\theta }_j}$.

Average standardized absolute mean difference (ASAM) A measure of covariate balance. For a particular covariate, we estimated it by the standardized difference of the mean in the treatment group and weighted mean in the control group by the standard deviation in the treatment group. Then, these standardized differences were averaged across all covariates. ASAM values of greater than 10% are considered to be of concern (Austin 2009).

Coverage rate The percentage on how many 95% confidence intervals include the true parameter value over 1000 simulated data sets.

Relationships of covariate balance with performance measures It has been noted that the c-statistic is not a good indicator of the potential for confounding adjustment by propensity scores (Westreich et al. 2011; Wyss et al. 2014). Thus, we focused on the relationships of the performance measures with covariate balance (ASAM). We aggregated all results and plotted the type I error rate, bias-adjusted power, absolute bias, RMSE, 95% confidence interval coverage rate against the ASAM in Figs. 8 and 9.

3 Results

We summarized simulation results based on 1000 data sets under scenarios A–D using the power, bias-adjusted power, absolute bias, root mean squared error, average standardized absolute mean difference and 95% confidence interval coverage rate. We considered effect sizes ranging from $1/e^\theta =1$–3. The performance of the methods with these performance measures across the effect sizes were described in Figs. 2, 3, 4, 5 and 6. We also tabulated the results for three effect sizes ($1/e^\theta =1$, 2 and 3) in Table 2. Since the ASAM does not depend on effect sizes, we separately presented the averages of the ASAM values over 1000 data sets for four scenarios, in Table 3.

Fig. 2

Power curves obtained from four PS methods under four scenarios. The x-axis indicates $1/e^\theta$, where $\theta$ moves from 0 to $\log (1/3)$. The horizontal dotted line indicates for the type I error rate to be 0.05. From left to right, and from top to bottom, scenarios A–D

Type I error and power In the scenario of linearity and additivity (scenarios A and B), the four methods had almost the same power curves and kept a nominal type I error rate of 0.05 at a null value of $\theta =0$ (Fig. 2 and Table 2). When the exposure prevalance decreased (scenario B), the power reduced for all methods. In the scenario of non-linearity and non-additivity, and moderate exposure prevalence (scenario C), the type I error rate of the ML highly inflated to be 0.088, and those of the other methods were inflated in relatively small amounts: $\hbox {CBPS} =0.063$, $\hbox {GBM}=0.068$ and $\hbox {GAM}=0.062$ (Table 2), and among these three methods the CBPS yielded the greatest power. When the exposure prevalence reduced (scenario D), the type I error rate of the ML was 0.066, the rest kept a nominal type I error: $\hbox {CBPS}=0.044$, $\hbox {GBM}=0.051$ and $\hbox {GAM}=0.053$ (Table 2), and among these three methods the CBPS was the most powerful.

Bias-adjusted power The power comparison with Fig. 2 had a problem in that the inflation of the type I error of the ML was nonignorable under the scenarios of non-linearity and non-additivity (scenarios C and D) due to its large bias (see Table 2). Comparison using the bias-adjusted power would be more reasonable because all methods were forced to have a nominal type I error under all scenarios (Fig. 3). As a result, the power curves of the ML under scenarios C and D went down toward those of the CBPS so that the two power curves almost overlapped. The ML and the CBPS had the greater bias-adjusted power than the GBM and the GAM under the complex models (scenarios C and D).

Fig. 3

Bias-adjusted power curves obtained from four PS methods under four scenarios. The x-axis indicates $1/e^\theta$, where $\theta$ moves from 0 to $\log (1/3)$. The horizontal dotted line indicates for the power to be 0.05. From left to right, and from top to bottom, scenarios A–D

Absolute bias In the scenario of linearity and additivity (scenarios A and B), the GBM yielded the largest bias, and the other methods had the similar bias (Fig. 4). In the scenario of non-linearity and non-additivity (scenarios C and D), the ML yielded huge bias compared to the other methods, the GBM tended to yield smaller bias than the CBPS when exposure prevalence is low, and GAM yielded the smallest bias.

Root mean squared error The GBM tended to have the smallest RMSE in the simple PS settings (scenarios A and B), but there was no big difference in the RMSE among the methods (Fig. 5). In the scenario of complex PS and moderate exposure prevalence (scenario C), the CBPS and GBM exhibited the lower RMSE than the ML and GAM. When the exposure prevalence reduced (scenario D), however, the ML yielded the smaller RMSE than both the GBM and GAM.

Fig. 4

Absolute bias curves obtained from four PS methods under four scenarios. The x-axis indicates $1/e^\theta$, where $\theta$ moves from 0 to $\log (1/3)$. From left to right, and from top to bottom, scenarios A–D

Fig. 5

Root mean squared error curves obtained from four PS methods under four scenarios. The x-axis indicates $1/e^\theta$, where $\theta$ moves from 0 to $\log (1/3)$. From left to right, and from top to bottom, scenarios A–D

Average standardized absolute mean difference The distributions of the ASAM for all methods were presented in Fig. 6. It was clearly shown that the CBPS method produced the best covariate balance under all scenarios. As shown by Lee et al. (2010) and Wyss et al. (2014), compared to the ML, the GBM yielded the higher ASAM in the scenario of simple PS (scenarios A and B), but, the lower ASAM in the scenario of complex PS with moderate exposure prevalence (scenario C). As exposure prevalence got lower (scenario D), however, the ML had better covariate balance than the GBM and GAM.

We have checked if the tunning parameter (number of trees) for the GBM was selected in a reasonable way within 10,000 iterations. Figure 7 shows that for one simulated data set with a shrinkage parameter of 0.01 that we used, under each scenario, the minimum value of the ASAM was achieved and a plateau happened after some iterations within 10,000 iterations. Thus, our parameter set-up for the GBM was considered to be appropriate enough to give valid ATT estimates under the simulations.

Coverage rate All methods produced the valid CR close to 0.95 ($\hbox {range} = 0.93$–0.96) except when the ML was applied to the complex PS model with moderate exposure prevalence (scenario C), but the CR values were not far from 0.95 ($\hbox {range} = 0.91$–0.94). Our results for the CR were quite different from those of Lee et al. (2010) and Pirracchio et al. (2015) showing that the coverage rates of the 95% confidence intervals for weighting estimators with logistic PS models were far below 0.95 when the true PS models were nonlinear and nonadditive. This difference may be partly from that our study looked at the treatment effect on a binary outcome while the two studies were conducted with continuous outcomes.

Relationships of covariate balance with performance measures In Fig. 8, we plotted the ASAM against the type I error rate, and bias-adjusted power. The plot for the type I error rate only considered the case when the effect size is 1 ($\theta =0$). Conversely, the plot for the bias-adjusted power excluded the case of $\theta =0$ because all methods by definition had type I error rates of 0.05 at the null treatment effect. The left-panel showed that covariate balance was almost linearly associated with the type I error rate: an increasing ASAM was associated with an increasing type I error rate. The right-panel, however, showed that there is no clear relationship between covariate balance and the bias-adjusted power.

In Fig. 9, we plotted the ASAM against the absolute bias, RMSE and CR. There were linear relationships of the ASAM with the absolute bias, and with the CR: an increasing ASAM was associated with an increasing bias, and with a decreasing CR. There was no clear linear relationship between the ASAM and the MSE.

Bias-adjusted power and RMSE as functions of bias In Figs. 10 and 11, we plotted the bias-adjusted power and RMSE against the absolute bias at fixed effect sizes: $e^{-\theta }=2$ for Fig. 10 and $e^{-\theta }=3$ for Fig. 11. Each point in figures represents the number summarized over 1000 simulations. These plots may allow one to figure out which PS methods have higher power or lower RMSEs when the biases are same or similar. The GAM had the smallest bias, but its power and RMSE were not good compared to the others. Around the bias of 0.03, the CBPS yielded the highest power and lowest RMSE. The ML tended to yield high powers, but with large biases.

Fig. 6

Distributions of average standardized absolute mean differences (ASAM) over 1000 simulated data sets in the covariates under four scenarios. From left to right, and from top to bottom, scenarios A–D

Table 2 Simulation results for $1/e^\theta =1$, 2 and 3

Table 3 The average of the ASAM values over 1000 data sets

Fig. 7

ASAM curves from the GBM as functions of the number of iterations for one simulated data set under four scenarios. From left to right, and from top to bottom, scenarios A–D

Fig. 8

Relationships of covariate balance [average standardized absolute mean difference (ASAM)] with the type I error rate in the left panel, and with the bias-adjusted power in the right panel. The plot for the type I error rate only considered the case when the effect size is 1 ($\theta =0$). The plot for the bias-adjusted power only considered the case when the treatment effect is not null ($\theta \ne 0$). The blue curve was obtained from the generalized additive model fit to each panel

Fig. 9

Relationships of covariate balance [average standardized absolute mean difference (ASAM)] with the absolute bias in the left panel, with the root mean squared error (RMSE) in the middle panel, and with the 95% confidence interval coverage rate (CR) in the right panel. These plots used all data. The blue curve was obtained from the generalized additive model fit to each panel

Fig. 10

The bias-adjusted power and RMSE as functions of the absolute bias at an effect size of $e^{-\theta }=2$

Fig. 11

The bias-adjusted power and RMSE as functions of the absolute bias at an effect size of $e^{-\theta }=3$

4 Conclusion and discussion

4.1 Summary of major findings

In summary, the ML and the CBPS are recommended for simple models with larger power and correct type I error rates. The ML should not be used for complex models except when exposure prevalence is low. The CBPS would be recommended also for complex models, but with a very large sample size, the GBM and the GAM would be recommended because of small bias. Below is the summary for each scenario.

• (A) Additivity $+$ Linearity $+$ Moderate prevalence: All methods performed similarly, but the ML and the CBPS were the least biased and GBM was the most biased.

• (B) Additivity $+$ Linearity $+$ Low prevalence: All methods performed similarly, but the ML and the CBPS was tended to be the least biased and GBM was the most biased.

• (C) Nonadditivity $+$ Nonlinearity $+$ Moderate prevalence: The CBPS was the most powerful with a little bit inflated type I error. The GAM was the least biased, but showed large variability so that its RMSE tended to be the biggest. The GBM was biased similarly to the CBPS, but its RMSE was greater than that of the CBPS, but smaller than that of the ML. The ML yielded a non-ignorable inflated type I error because of its large bias, which yielded the greatest RMSE.

• (D) Nonadditivity $+$ Nonlinearity $+$ Low prevalence: All methods showed valid type I error rates. The ML and CBPS showed the greatest power and the smallest RMSE. The GAM was the least biased, but showed the greatest RMSE. The GBM was less biased, but yielded the greater RMSE than the ML and the CBPS.

4.2 Discussion of major findings

In general, the CBPS was robust to the change in the true PS model specification in terms of a correct type I error, higher power and adjusted power, and a greater accuracy (RMSE) compared to the other methods. Previous studies (Westreich et al. 2011; Wyss et al. 2014) have revealed that rather than prediction accuracy such as the c-statistic, covariate balance is more relevant to the accuracy of the treatment effect estimates. Unlike the other methods, the CBPS estimates the model using an estimating equation that minimizes covariate imbalance directly. As a result, it exhibited superior performance in covariate balance in our simulations (Fig. 6) and other studies (Imai and Ratkovic 2014; Wyss et al. 2014; Setodji et al. 2017) in terms of the ASAM, and this might lead to the robust performance in terms of type I error, power and accuracy as pointed out by Wyss et al. (2014).

Our bias-corrected power analysis showed that the ML and the CBPS exhibited greater power than the GBM and the GAM in the scenario of nonadditivity and nonlinearity, but the CBPS kept close to a nominal type I error while the ML yielded a severe inflation of type I error rate under moderate exposure prevalence. Therefore, testing a treatment effect based on the ML may not be valid if a model-misspecification exits with moderate exposure prevalence.

In the scenario of nonadditivity and nonlinearity, the GAM showed smaller bias compared to the others. Since the GAM uses flexible methods such as the smoothing splines to model continuous covariates, in theory, it can capture nonlinear effects of continuous covariates in a PS model. Our simulations, however, showed that the GAM was also robust to the existence of nonadditivity. One disadvantage of the GAM was that it was relatively unstable and yielded large RMSE. Larger sample sizes may improve the instability of the GAM.

In our study, along with model complexity for PS, exposure prevalence also was found to be an important factor affecting the performance of methods. For example, in the scenario of nonadditivity and nonlinearity, as exposure prevalence reduced, the covariate imbalance, bias and RMSE of the ML substantially reduced. As a result, the ATT estimate from the ML had its type I error rate reduced close to a nominal one. The ATT estimates from the other methods yielded correct type I error rates in the same situation. This phenomenon might be similar to that a nonlinear model can be approximated by a linear model when outcome prevalence is low. Although Wyss et al. (2014) did not explicitly evaluate exposure prevalence in their simulations, they actually considered a real example where the exposure to one treatment is very rare with 2%. Their empirical study showed that the ML and the CBPS had better covariate balance than the two kinds of the GBM, which is consistent with our result.

We have evaluated the relationships of diverse performance measures with covariate balance. The type I error, absolute bias, and CR has strong linear relationships with the ASAM. The bias-adjusted power had no clear relationship with the ASAM, but it depended more on the PS estimation methods: parsimonious methods such as the ML and the CBPS had greater bias-adjusted power than non-parsimonious methods such as the GBM and the GAM. Our study did not show a clear linear relationship between the ASAM and the MSE as shown by Wyss et al. (2014), which considered both logistic and probit regression models to generate treatment assignment. When the logistic regression model was used, the range of the ASAM in the study of Wyss et al. (2014) and our study overlaps (0–0.10). When the probit regression model was used, however, the ASAM went up to 0.2 in the study of Wyss et al. (2014), and thus this simulation setting generated more complex model mis-specification. Thus, it might be possible to see a linear relationship between the RMSE and the ASAM if we had considered more complex treatment assignment models.

We have not considered variable selection methods, however, they should be considered to improve the estimation of treatment effects using PS especially when data is high-dimensional. Variable selection for causal inference, however, requires caution because omission of confounders or risk factors only associated with an outcome variable results in biased or inefficient estimates and including covariates only associated with a treatment variable, so called instrumental variables, reduces the efficiency of estimates (Brookhart et al. 2006). Several methods have been developed to avoid these errors, which include outcome-adaptive lasso (Shortreed and Ertefaie 2017) and group-lasso for doubly robust estimation (Koch et al. 2017). Simulation studies might be needed to assess and understand the relative performance of various variable selection methods.

We have compared various PS methods in terms of weighting, which is a convenient way to obtain the ATE or ATT. When there are outlying weights, however, weighting estimators are unstable (Lee et al. 2011). More works should be done for the comparison of PS methods using other important alternative tools such as sub-classification, regression adjustment and matching. Specially, the performance of the CBPS might be of interest in the setting of sub-classification, because the CBPS does not guarantee covariate balance within the strata.

Even though, our simulations showed that the CBPS performed favorably, it may be hard to argue that the CBPS is uniformly better than other methods such as the GBM because our study does not cover all factors such as the complexity of an outcome model. It has been recently shown that along with the relationships between treatment and covariates, those between outcome and covariates affect the performance of PS methods (Setodji et al. 2017). Prior knowledge or statistical tests for the relationships of outcome and covariates can be helpful to determine which methods should be used among the CBPS and the GBM.