Quasi-likelihood inference for self-exciting threshold integer-valued autoregressive processes

Abstract

This article redefines the self-exciting threshold integer-valued autoregressive (SETINAR(2,1)) processes under a weaker condition that the second moment is finite, and studies the quasi-likelihood inference for the new model. The ergodicity of the new processes is discussed. Quasi-likelihood estimators for the model parameters and the asymptotic properties are obtained. Confidence regions of the parameters based on the quasi-likelihood method are given. A simulation study is conducted for the evaluation of the proposed approach and an application to a real data example is provided.

1 Introduction

There has been an increasing interest in developing models for time series of (small) counts because of their wide range of applications, including epidemiology, finance, disease modeling, etc. The majority of these models are based on the thinning operators, see Al-Osh and Alzaid (1987), Du and Li (1991), Ristić et al. (2009), Zhang et al. (2010) and Li et al. (2015), among others. Weiß (2008) and Scotto et al. (2015) gave detailed reviews of the development of integer-valued time series models. Among the above models, the class of Poisson integer-valued autoregressive (INAR) moving average models (Al-Osh and Alzaid 1987, 1991, 1992; Du and Li 1991) play a central role. However, when dealing with the nonlinear time series of counts such as volatility changes in time, high threshold exceedances appearing in clusters, and the so-called piecewise phenomenon, such models will not work well.

On modelling the non-linear phenomena, especially the piecewise phenomenon, the threshold models (Tong 1978; Tong and Lim 1980) have attracted much attention and have been widely used in diverse areas. For dealing with time series of counts exhibiting piecewise-type patterns, Monteiro et al. (2012) introduced a class of SETINAR(2,1) models driven by a Poisson distribution. Wang et al. (2014) proposed a self-excited threshold Poisson autoregressive (SETPAR) model and applied it to the world major earthquakes data. Yang et al. (2017) proposed an integer-valued threshold autoregressive process based on negative binomial thinning operator (NBTINAR(1)), and compared the performances of the above threshold models. Möller and Weiß (2015) presented a brief survey of threshold models of integer-valued time series.

A drawback of SETINAR(2,1) model proposed by Monteiro et al. (2012) is the mean and variance of Poisson distribution are equal and this property is not always found in the real data. The goal of this paper is to weaken the conditions of original SETINAR(2,1) model by removing the assumption of Poisson distribution, and to present a quasi-likelihood (QL) inference for the new SETINAR(2,1) process. Quasi-likelihood method, a nonparametric inference method was initially introduced by Wedderburn (1974). QL methods are useful because (i) they can be used in cases where exact distributional information is not available, (ii) only second moment assumptions are required and, (iii) they enjoy a certain robustness of validity. Hence the proposed method allows precise estimation of the relationship between the response and the covariate variables without requiring exact distributional assumptions. QL method has been widely applied in many fields, including generalized linear models (McCullagh and Nelder 1989; Sutardhar and Rao 2001; Lu et al. 2006), stochastic volatility models (Ruiz 1994), semiparametric models (Severini and Staniswalis 1994), median regression models (Jung 1996), autoregressive models (Azrak and Mélard 1998, 2006; Ling 2007), nonstationary time series models (Kim and Park 2008; Aue and Horváth 2011), integer-valued time series models (Zheng et al. 2006a, b; Niaparast and Schwabe 2013; Christou and Fokianos 2014), among others.

The rest of this paper is organized as follows. In Sect. 2, we redefine the SETINAR(2,1) processes, and consider the quasi-likelihood inference for the unknown parameters of interest. In Sect. 3, some numerical results of the estimates are presented. In Sect. 4, we give an application of the proposed QL method to a real data set. Some concluding remarks are given in Sect. 5. All proofs are postponed to “Appendix”.

2 Main results

The SETINAR(2,1) process (originally proposed by Monteiro et al. 2012), is defined by the following recursive equation:

$$\begin{aligned} X_{t}=I_{1,t}(\alpha _{1}\circ X_{t-1})+I_{2,t}(\alpha _{2}\circ X_{t-1})+Z_t, \end{aligned}$$

(2.1)

where

• (i) $I_{1,t}:=I\{X_{t-1}\le r\}$, $I_{2,t}:=1-I_{1,t}=I\{X_{t-1}>r\}$, r is the known threshold variable;

• (ii) The thinning operator “$\circ$”, introduced in Steutel and Harn (1979), is defined as

  $$\begin{aligned} \alpha _i {\circ } X=\sum _{k=1}^X B_k^{(i)},~\alpha _i \in (0,1), \end{aligned}$$

  where $\{B_k^{(i)}\}$ is a sequence of independent and identically distributed (i.i.d.) Bernoulli random variables independent of X, satisfying $P(\alpha _i=1)=1-P(\alpha _i=0)=\alpha _i,i=1,2$;

• (iii) $\{Z_{t}\}$ is a sequence of i.i.d. random variables with $E(Z_t)=\lambda$ and $\mathrm{Var}(Z_t)=\sigma _z^2<\infty$;

• (iv) For fixed t and $i~(i=1,2)$, $Z_{t}$ is assumed to be independent of counting series in$\{\alpha _i \circ X_{t-l},~l{\ge }1\}$ and $\{X_{t-l},~l{\ge }1\}$.

Remark 2.1

In Monteiro et al. (2012), the SETINAR(2,1) process is defined with $Z_t$ follows a Poisson distribution with mean $\lambda$. In this paper, we remove the assumption of Poisson distribution (in (iii)) and use $E(Z_t) =\lambda$ and $\mathrm{Var}(Z_t)=\sigma _z^2<\infty$ instead, so that the model is more flexible.

Remark 2.2

The conditional expectation and conditional variance of the SETINAR(2,1) process are given by

• (i) $E(X_t|X_{t-1})=\alpha _1X_{t-1}I_{1,t}+\alpha _2X_{t-1}I_{2,t}+\lambda ,~t=1,2,\ldots$

• (ii) $\mathrm{Var}(X_t|X_{t-1})=\alpha _1(1-\alpha _1)X_{t-1}I_{1,t}+\alpha _2(1-\alpha _2)X_{t-1}I_{2,t}+\sigma _z^2,~t=1,2,\ldots$

Remark 2.3

Following Monteiro et al. (2012), we assume that r is known. In practice, we can use NeSS algorithm (see, e.g., Li and Tong 2016; Yang et al. 2017) to estimate r first.

The following theorem states the ergodicity of the SETINAR(2,1) process (2.1). This property will be useful in deriving the asymptotic properties of the estimators.

Proposition 2.1

The SETINAR(2,1) process $\{X_t\}_{t \in \mathbb {Z}}$ defined in (2.1) is an ergodic Markov chain.

Suppose we have a series of observations $\{X_t\}_{t=1}^n$ generated from the SETINAR(2,1) process and we want to estimate the parameter $\varvec{\beta }=(\alpha _1,\alpha _2,\lambda )^\textsf {T}$. Monteiro et al. (2012) considered the conditional least squares (CLS) estimation and the conditional maximum likelihood (CML) estimation of $\varvec{\beta }$. In what follows, we will consider the maximum quasi-likelihood (MQL) estimation of $\varvec{\beta }$ first, and then give the QL confidence regions of $\varvec{\beta }$.

Denote $\varvec{\theta }=(\theta _1,\theta _2,\sigma _z^2)^\textsf {T}$ with $\theta _i=\alpha _i(1-\alpha _i),~i=1,2$, then the variance of $X_t$ conditional on $X_{t-1}$ fixed is given by

$$\begin{aligned} {V}_{\varvec{\theta }}(X_t|X_{t-1})=\mathrm{Var}(X_t|X_{t-1})=\theta _1X_{t-1}I_{1,t}+\theta _2X_{t-1}I_{2,t}+\sigma _z^2. \end{aligned}$$

(2.2)

As discussed in Wedderburn (1974), we have the standard QL estimating equations:

$$\begin{aligned} \sum _{t=1}^n\varvec{m}_t(\varvec{\beta })=\varvec{0}, \end{aligned}$$

(2.3)

where

$$\begin{aligned} \varvec{m}_t(\varvec{\beta })= & {} (m_{1t}(\varvec{\beta }),m_{2t}(\varvec{\beta }),m_{3t}(\varvec{\beta }))^\textsf {T},~ m_{it}(\varvec{\beta })\\= & {} \frac{X_t-E(X_t|X_{t-1})}{V_{\varvec{\theta }}(X_t|X_{t-1})}\frac{\partial E(X_t|X_{t-1})}{\partial \beta _i},~i=1,2,3, \end{aligned}$$

with $\beta _1=\alpha _1$, $\beta _2=\alpha _2$, $\beta _3=\lambda$. Note that the presence of $\varvec{\theta }$ in the expression for the conditional variance makes the estimating equations (2.3) complicated and intractable in the general case. Consequently, we propose substituting a suitable consistent estimator $\hat{\varvec{\theta }}$ of $\varvec{\theta }$ obtained by other means and then solve the resulting MQL estimating equations for the primary parameters of interest. This approach leads to the following closed form estimator of $\varvec{\beta }$:

$$\begin{aligned} \hat{\varvec{\beta }}_{MQL}=\varvec{Q}_n^{-1}\varvec{q}_n, \end{aligned}$$

(2.4)

where

$$\begin{aligned} \varvec{Q}_n=\left( \begin{array}{ccc} \sum V_{\hat{\varvec{\theta }}}^{-1}(X_t|X_{t-1})I_{1,t}X_{t-1}^2 &{}\quad 0 &{}\quad \sum V_{\hat{\varvec{\theta }}}^{-1}(X_t|X_{t-1})I_{1,t}X_{t-1}\\ 0 &{}\quad \sum V_{\hat{\varvec{\theta }}}^{-1}(X_t|X_{t-1})I_{2,t}X_{t-1}^2 &{}\quad \sum V_{\hat{\varvec{\theta }}}^{-1}(X_t|X_{t-1})I_{2,t}X_{t-1}\\ \sum V_{\hat{\varvec{\theta }}}^{-1}(X_t|X_{t-1})I_{1,t}X_{t-1} &{} \quad \sum V_{\hat{\varvec{\theta }}}^{-1}(X_t|X_{t-1})I_{2,t}X_{t-1} &{}\quad \sum V_{\hat{\varvec{\theta }}}^{-1}(X_t|X_{t-1})\\ \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} \varvec{q}_n=\left( \begin{array}{c} \sum _{t=1}^n V_{\hat{\varvec{\theta }}}^{-1}(X_t|X_{t-1})I_{1,t}X_tX_{t-1}\\ \sum _{t=1}^n V_{\hat{\varvec{\theta }}}^{-1}(X_t|X_{t-1})I_{2,t}X_tX_{t-1}\\ \sum _{t=1}^n V_{\hat{\varvec{\theta }}}^{-1}(X_t|X_{t-1})X_t \end{array}\right) . \end{aligned}$$

To study the asymptotic behaviour of the estimator, we make the following assumptions:

• (C1) $\{X_t\}$ is a stationary process.

• (C2) $E|X_t|^4<\infty$.

We now state the asymptotic properties of MQL-estimators $\hat{\varvec{\beta }}_{MQL}$. Theorem 2.1 shows the MQL-estimators $\hat{\varvec{\beta }}_{MQL}$ is asymptotic normally distributed if $\varvec{\theta }$ can be estimated consistently; Theorem 2.2 constructs a consistent estimator of $\varvec{\theta }$.

Theorem 2.1

Under the assumptions (C1)–(C2), the MQL-estimators $\hat{\varvec{\beta }}_{MQL}$ is asymptotically normal,

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\beta }}_{MQL}-\varvec{\beta })~\overset{L}{\longrightarrow }~N(\varvec{0},\varvec{T}^{-1}(\varvec{\theta })), \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l} \varvec{T}(\varvec{\theta })=(T_{ij}(\varvec{\theta }))_{3\times 3},~T_{ij}(\varvec{\theta })=T_{ji}(\varvec{\theta }),~1\le i \le j \le 3;\\ T_{ii}(\varvec{\theta })=E[V_{\varvec{\theta }}^{-1}(X_1|X_0)X_0^2I_{i,1}]~(i=1,2),~T_{33}(\varvec{\theta }) =E[V_{\varvec{\theta }}^{-1}(X_1|X_0)]; \\ T_{12}(\varvec{\theta })=0,~T_{13}(\varvec{\theta })=E[V_{\varvec{\theta }}^{-1}(X_1|X_0)X_0 I_{1,1}], T_{23}(\varvec{\theta })=E[V_{\varvec{\theta }}^{-1}(X_1|X_0)X_0 I_{2,1}], \end{array} \end{aligned}$$

Furthermore, the matrix $\varvec{T}(\varvec{\theta })$ can be estimated consistently by

$$\begin{aligned} \widehat{\varvec{T}(\varvec{\theta })}=\frac{1}{n}\sum _{t=1}^n\varvec{m}_t(\hat{\varvec{\beta }}_{MQL})\varvec{m}_t(\hat{\varvec{\beta }}_{MQL})^\textsf {T}. \end{aligned}$$

(2.5)

Remark 2.4

Since the MQL-estimators $\hat{\varvec{\beta }}_{MQL}$ given in (2.4) is the result from a two-stage estimation procedure mentioned above, the true asymptotic variance is supposed to be larger than $\varvec{T}(\varvec{\theta })$ in Theorem 2.1. Fortunately, the estimator $\widehat{\varvec{T}(\varvec{\theta })}$ given in (2.5) can give a estimate of the true asymptotic variance consistently.

Note that the consistency of $\hat{\varvec{\beta }}_{MQL}$ follows readily from the above result.

Theorem 2.2

Under the assumptions (C1)–(C2), the following estimators are consistent:

$$\begin{aligned} \hat{\sigma }^2_{z}=\frac{1}{n}\sum _{t=1}^n(X_t- \hat{\alpha }_{1}X_{t-1}I_{1,t}-\hat{\alpha }_{2}X_{t-1}I_{2,t}-\hat{\lambda })^2 -\frac{1}{n}\sum _{i=1}^2\sum _{t=1}^n\hat{\alpha }_{i}(1-\hat{\alpha }_{i})X_{t-1}I_{i,t}, \end{aligned}$$

(2.6)

and

$$\begin{aligned} \hat{\varvec{\theta }}=&(\hat{\alpha }_1(1-\hat{\alpha }_1),\hat{\alpha }_2(1-\hat{\alpha }_2),\hat{\sigma }^2_{z})^\textsf {T}, \end{aligned}$$

(2.7)

where $\hat{\alpha }_i$ and $\hat{\lambda }$ are consistent estimators of $\alpha _i~(i=1,2)$ and $\lambda$. In practice, we can use the CLS-estimators of $\alpha _i~(i=1,2)$ and $\lambda$ given in Theorem 3.1 of Monteiro et al. (2012).

Theorem 2.2 gives a consistent estimator $\hat{\varvec{\theta }}$ of $\varvec{\theta }$ which depends on some consistent estimators $\hat{\alpha }_i$ ($i=1,2$) and $\hat{\lambda }$. Sometimes we may be interested in the variance of $\hat{\varvec{\theta }}$. Since the consistent estimators $\hat{\alpha }_i$ ($i=1,2$) and $\hat{\lambda }$ may have many forms, we refer to the moving block bootstrap (MBB) methods (Kreiss and Lahiri 2012) to estimate the variance of $\hat{\varvec{\theta }}$. Suppose the sample $(X_1, X_2, \ldots , X_n)$ is observed. Let $\ell$ be an integer satisfying $1<\ell <n$. We can use the following MBB method to estimate the variance of $\hat{\varvec{\theta }}$:

Step 1 :

Define the overlapping blocks $\mathbb {B}_1, \ldots ,\mathbb {B}_N$ of length $\ell$ as, $\mathbb {B}_1=(X_1,X_2, \ldots ,X_{\ell })$, $\mathbb {B}_2=(X_2, \ldots ,X_{\ell },X_{\ell +1})$, $\ldots$, $\mathbb {B}_N=(X_{n-\ell +1}, \ldots ,X_{n})$, where $N=n-\ell +1$;

Step 2 :

To generate the MBB samples, select b blocks at random with replacement from the collection $\{\mathbb {B}_1, \ldots ,\mathbb {B}_N\}$. Denote the selected MBB samples by $(X_1^{*},X_2^{*}, \ldots ,X_b^{*})$;

Step 3 :

For $j=1, \ldots ,b$, calculate the $\hat{\varvec{\theta }}_j$ by (2.6) and (2.7) with the MBB sample $X_j^{*}$;

Step 4 :

Calculate the variance of $\hat{\varvec{\theta }}$ by

$$\begin{aligned} \mathrm{Var}(\hat{\varvec{\theta }})=\frac{1}{b}\sum _{j=1}^b(\hat{\varvec{\theta }_j}-\overline{\varvec{\theta }})(\hat{\varvec{\theta }_j}-\overline{\varvec{\theta }})^{\textsf {T}}, ~\overline{\varvec{\theta }}=\sum _{j=1}^b\hat{\varvec{\theta }}_j. \end{aligned}$$

(2.8)

Next, we give the QL confidence region of $\varvec{\beta }$ based on the above theorems.

Theorem 2.3

Under the assumptions (C1)–(C2), for $0<\delta <1$, the 100 $(1-\delta )\%$ confidence region of $\varvec{\beta }$ is given by:

$$\begin{aligned} \mathcal {C}_{\beta }\{\delta \}=\{\varvec{\beta }\in \mathbb {R}^3:n(\hat{\varvec{\beta }}_{MQL}-\varvec{\beta })^\textsf {T}\widehat{\varvec{T}(\varvec{\theta })} (\hat{\varvec{\beta }}_{MQL}-\varvec{\beta })\le \chi ^2_{(3)}(\delta )\}, \end{aligned}$$

(2.9)

where $\chi _3^2(\delta )$ denotes the $\delta$-upper quantile of $\chi ^2$ distribution with degrees of freedom 3.

Equation (2.9) is called the normal approximation (NA) confidence region based on MQL method. By Theorems 3.1 and 3.3 in Monteiro et al. (2012), we can easily construct the NA confidence regions based on CLS and CML methods. In the next section, we will compare the performances of these confidence regions in terms of coverage rates.

3 Simulation studies

To report the performances of the proposed method described in the previous section, we conduct simulation studies under the following two models:

Model I. Assume that $Z_t$ follows a Poisson distribution with mean $\lambda$.

Model II. Assume that $Z_t$ follows a Geometric distribution with probability mass function (p.m.f.) given by

$$\begin{aligned} p(Z_t=z)=\frac{\lambda ^z}{(1+\lambda )^{z+1}},~z=0,1,2, \ldots \end{aligned}$$

(3.1)

It is easy to see that $E(Z_t)=\lambda ,$ $\mathrm{Var}(Z_t)=\lambda (1+\lambda ).$ These properties are different from Model I.

For all the following simulations, we generating the data with $X_0=0$. All simulation results are calculated under MATLAB software based on 1000 replications.

3.1 Performances of the MQL-estimators

In this subsection, we first show the performances of the MQL-estimators $\hat{\varvec{\beta }}_{MQL}$, then compare the performances with the CLS-estimator $\hat{\varvec{\beta }}_{CLS}$ and CML-estimators $\hat{\varvec{\beta }}_{CML}$ obtained by Monteiro et al. (2012) under Models I and II. For generating the data of Models I and II, we each consider the following three series:

• Series A. $(\alpha _1,\alpha _2,\lambda )=(0.2, 0.1, 3)$, $r=4$.

• Series B. $(\alpha _1,\alpha _2,\lambda )=(0.2, 0.1, 7)$, $r=8$.

• Series C. $(\alpha _1,\alpha _2,\lambda )=(0.8, 0.1, 7)$, $r=21$.

Remark 3.1

The parameter setting of the above three series are the same with models (A1), (B1) and (B3) in Monteiro et al. (2012). So that we can compare our simulation results with the corresponding results in Monteiro et al. (2012).

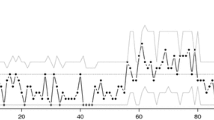
For each of the above series, the values of r was chosen such that the observations in each regime is at least 10% of the total sample size. As mentioned in Li and Tong (2016), when the proportion of observations in one regime to the whole is less than 5%, the estimate result may not be reliable. The sample paths are plotted in Fig. 1. The simulation results are summarized in Tables 1, 2, 3 and 4.

Fig. 1

Sample paths for series A–C of Model I (a–c) and Model II (d–f)

Table 1 Simulation results of MQL for Models I and II: mean bias and MSE

It is shown in Fig. 1 that the threshold r of the series A and B are relatively moderate, and the threshold r of series C (especially in Model I) is slightly larger. Compare subfigures (a)–(c) and (d)–(f) we can find that the sample paths of Model II fluctuate greatly. This is because the variance of $Z_t$ of Model II is much larger than its mean.

Table 2 Comparison of simulation results for Series A of Model I: CLS, MQL and CML

Table 3 Comparison of simulation results for Series B of Model I: CLS, MQL and CML

Table 4 Comparison of simulation results for Series C of Model I: CLS, MQL and CML

Fig. 2

Plot for SD and SE values of Model I: Series A–C

Fig. 3

Plot for SD and SE values of Model II: Series A to C

Table 1 reports the means and mean square errors (MSE) of the MQL-estimators $\hat{\varvec{\beta }}_{MQL}$. From Table 1 we can find that all the simulation results perform better as N increases, which imply that out estimators are consistent for all the parameters. Most of the biases (the means minus the corresponding true values) and MSE of Model II are bigger than those in Model I. This is because the variances of $Z_t$ in Model II are bigger than in Model I.

Figures 2 and 3 show the standard deviations (SD) of the MQL-estimators $\hat{\varvec{\beta }}_{MQL}$ across 1000 replications, and the standard errors (SE) of the MQL-estimators $\hat{\varvec{\beta }}_{MQL}$. The SE are calculated by the mean of the square roots of the asymptotic variances divided by N. From Figs. 2 and 3 we can find that the SD and SE of the $\hat{\varvec{\beta }}_{MQL}$ are very close, indicating that the MQL method converges fast. The values of SD and SE in Model II (shown in Fig. 3) are bigger than the corresponding series in Model I (shown in Fig. 2), indicating that bigger variances of $Z_t$ will result slower convergence rate of the estimate.

Table 5 Comparison of simulation results for Series D of Model I: CLS, MQL and CML

Tables 2, 3 and 4 show the simulation results based on different methods. As can be seen in Table 2 that most biases of $\hat{\varvec{\beta }}_{MQL}$ are smaller than those of CLS ones, almost all of the MSE of $\hat{\varvec{\beta }}_{MQL}$ are smaller than the $\hat{\varvec{\beta }}_{CLS}$. The CML method considered by Monteiro et al. (2012) can be used as a benchmark here. From Table 2 we can see that the MSE of the MQL and CML methods is basically the same, when the sample size is small, most of biases of MQL estimates are less than the CML estimates, which indicates that the MQL results are credible. We can obtain similar conclusions in Tables 3 and 4. In addition, when $n=50$ in Table 3, the MSE of the MQL-estimator $\hat{\varvec{\beta }}_{MQL}$ is relatively large. This may be because the QL method uses a two-step estimation. Before estimating the parameters of interest, the variance $\sigma ^2_z$ of $Z_t$ needs to be estimated. When the sample size is small, the estimator $\hat{\sigma }^2_z$ is occasionally less effective. Based on the above simulation results, we conclude that the MQL-estimators $\hat{\varvec{\beta }}_{CML}$ is better than the CLS-estimators, and the CML method is not unanimously better than the MQL method.

Considering that different samples may have some impact on the estimates, we consider another simulations based on another series of Model I, i.e., Series D: $(\alpha _1,\alpha _2,\lambda )=(0.2, 0.8, 7)$, $r=16$. In Series D, we calculate the CLS, MQL and CML estimates under the same samples. The simulation results are summarized in Table 5. As is shown in Table 5, the MQL estimates perform better than the CLS ones, and the CML estimates are not unanimously better than the MQL ones, i.e., we can get the same conclusions from Table 5 as shown in Tables 2, 3 and 4.

Table 6 Estimation the variances of $\hat{\varvec{\theta }}$ of Models I and II via the MBB method

Next we continue to show the performances of the variance of $\hat{\varvec{\theta }}$ calculated by (2.8). For generating the bootstrap samples, we choose $\ell =80\%$ of the total sample size and $b=500$. The simulation results are summarized in Table 6. We can see from Table 6 that all variances $\mathrm{Var}(\hat{\varvec{\theta }})$ convergence to zero as N increases, implying the $\hat{\varvec{\theta }}$ is consistent. Further, we can find that the variances $\mathrm{Var}(\hat{\varvec{\theta }})$ of each series of Model II are bigger than the corresponding series in Model I. This is because the true variance of Model II is much bigger than Model I. To study the sample size that can make the variance of $\hat{{\sigma }}_z^2$ in Model II close to zero, we do some additional simulations. The simulation results (not given here) show that more than 5000 samples are needed, meaning that the convergence rate of $\mathrm{Var}(\hat{{\sigma }}_z^2)$ in Model II is much slower than that of Model I.

3.2 Coverage rates of the confidence regions

In this subsection, we first consider the performances of the coverage rates of the QL confidence regions, then compare the simulation results of QL confidence regions with NA confidence regions based on CLS and CML methods in terms of overage rates.

To show the performances of QL confidence regions given in (2.9), we consider the same series of Models I and II mentioned above. Table 7 reports the coverage rates of the QL confidence regions under Models I and II based on confidence levels 0.90 and 0.95, respectively. It can be seen from Table 7 that as the sample size N increases, the coverage rates of three series (in each model) all increase. These results indicate that the QL confidence regions perform well in practice.

Figure 4 plots the QL confidence regions for Series A of Model I based on confidence level 95% with sample size $N=300$, while Fig. 5 plots the 95% QL confidence regions for Model II under the same sample size and the same series. From Figs. 4 and 5 we can see that the points which fall within the confidence regions (blue dots) are dense near the center of the confidence regions and are sparse at the edges. There are about 4% of the points (red plus) scattered outside the confidence regions, which is consistent with the confidence level 95%. Similar results are obtained for other series of Models I and II, but are not given here.

To demonstrate the robustness of the QL method, we consider the following mixed model:

Model III: Assume that $Z_t$ has the following mixed structure:

$$\begin{aligned} Z_t=\delta _tZ_{1t}+(1-\delta _t)Z_{2t}, \end{aligned}$$

(3.2)

where $Z_{1t}$ follows a Poisson distribution with mean $\lambda$, $Z_{2t}$ follows a Geometric distribution with p.m.f. given in (3.1), $\delta _t$ follows a Bernoulli distribution with p.m.f. given by $P(\delta _t = 1) = 1 - P(\delta _t = 0) = \gamma$, meaning that $Z_{1t}$ is contaminated by $Z_{2t}$ with probability $1-\gamma$. Calculate to see that $E(Z_t) = \lambda$, $\mathrm{Var}(Z_t) = \lambda ^2(1 -\gamma )+\lambda$.

Table 7 Coverage rates based on QL method for Models I and II

Fig. 4

Confidence regions for Series A of Models I with confidence level 95%

Fig. 5

Confidence regions for Series A of Models II with confidence level 95%

Table 8 Comparison of the NA confidence regions based on different methods under Model III

Table 9 The performances of $\hat{r}$ for Models I and II

For generating the data, we set the parameters setting the same as Series A, B and C mentioned above. The coefficient $\gamma$ is chosen as $\gamma =1,~0.95,~0.90$, respectively, so that we can compare the performances of NA confidence regions based on CLS, MQL and CML methods. Table 8 shows the simulation results of the coverage rates of the NA confidence regions based on different methods under contaminated samples. From Table 8 we can see that when the sample is not been contaminated ($\gamma =1$), the coverage rates of NA confidence regions based on CML method performs better than the other two methods. However, once the samples are contaminated ($\gamma =0.95,~0.90$), the results of the confidence regions based on CML method are no longer accurate, the corresponding coverage rates decrease rapidly. This shows that the CML method is not robust. The coverage accuracy of confidence regions based on CLS method is also affected (slightly) with the decrease of $\gamma$. When $\gamma$ down to 0.9, the coverage accuracy of the proposed QL method has exceeded that of the other two methods, indicating that the quasi-likelihood method is more robust than the least square method.

3.3 Performances of $\hat{r}$

In this subsection, we investigate the performances of $\hat{r}$ using the NeSS algorithm proposed by Li and Tong (2016). Yang et al. (2017) used this algorithm to estimate the threshold r in the NBTINAR(1) model. Following Li and Tong (2016), let

$$\begin{aligned} J_n(r)=\sum _{t=1}^n\left( X_t-\frac{\sum _{t=1}^n X_tX_{t-1}-\lambda \sum _{t=1}^nX_{t-1}}{\sum _{t=1}^nX_{t-1}^2}\cdot X_{t-1}-\lambda \right) ^2-S_n(r), \end{aligned}$$

where

$$\begin{aligned} S_n(r)=\sum _{t=1}^n\left( X_t-\sum _{k=1}^2\frac{\sum _{t=1}^nX_tX_{t-1}I_{k,t}(r)-\lambda \sum _{t=1}^nX_{t-1}I_{k,t}}{\sum _{t=1}^nX_{t-1}^2 I_{k,t}(r)}\cdot X_{t-1} I_{k,t}(r)-\lambda \right) ^{2}, \end{aligned}$$

with $I_{1,t}(r):=I\{X_{t-1}\le r\}$, $I_{2,t}(r):=1-I_{1,t}(r)=I\{X_{t-1}>r\}$. Then, the threshold r can be estimated by maximizing $J_n(r)$, i.e.,

$$\begin{aligned} \hat{r}=\arg \max _{r \in [\underline{r},\overline{r}]}J_n(r). \end{aligned}$$

(3.3)

For more details of the NeSS algorithm, please see Li and Tong (2016) and Yang et al. (2017). Table 9 reports the means, medians, MSE and the percentage which correctly estimate the threshold value of $\hat{r}$ across 1000 replications for Series A - C of Models I and II, respectively, under sample size $N=100,300,500$. From Table 9 we can find that all the simulation results perform better as N increases implying that the algorithm is consistent. We also find that the results of $\hat{r}$ in Model I have smaller biases, MSE and higher correct percentages than in Model II. This may be because the variance of Model II is larger than Model I for each series. Furthermore, we find that for the integer-valued r the median estimated to be better than the mean.

4 Real data example

In this section, we will use the new SETINAR(2,1) model to fit a series of criminal data, which can be downloaded from the Forecasting Principles website (http://www.forecastingprinciples.com). The analyzed data set is about the counts of drug in Pittsburgh, which consist of 144 monthly observations, starting from January 1990 to December 2001. The sample mean and sample variance are 4.181 and 10.597, respectively, showing considerable over-dispersion. Figure 6 shows the sample path and the ACF plot of the observations. From the sample path and the ACF plot shown in Fig. 6 we can see that the analyzed data set is a time series showing piecewise phenomenon with the threshold value $r = 4$. The threshold value of r is calculated by the NeSS algorithm discussed in Li and Tong (2016) and Yang et al. (2017). It also displays positive serial dependence, as can be seen in the ACF plot in Fig. 6.

Fig. 6

Sample path (left) and the ACF plot (right) of the criminal data. The blue line in the sample path estimated threshold dividing the range into two regimes

We use the following competitive counts models to fit the data set, and compare different models via the AIC criterion and BIC criterion.

• i.i.d. Poisson distribution with mean $\lambda$, denoted by i.i.d. Poisson.

• i.i.d. Geometric distribution with p.m.f. given in (3.1), denoted by i.i.d. Geometric.

• The Poisson INAR(1) model proposed by Al-Osh and Alzaid (1987), denoted by Po-INAR(1).

• The Geometric INAR(1) model proposed by Alzaid and Al-Osh (1988), denoted by Ge-INAR(1).

• SETINAR(2,1) model with innovations $Z_t$ follows a Poisson distribution with mean $\lambda$, denoted by SETINAR(2,1)-I.

• SETINAR(2,1) model with innovations $Z_t$ follows a Geometric distribution with p.m.f. given in (3.1), denoted by SETINAR(2,1)-II.

For each model, we use the CLS (if available), MQL and CML methods to estimate the parameters, and summarized the fitting results in Table 10. As can be seen from Table 10, the fitting results of the CML, CLS and MQL of SETINAR(2,1)-II are approximately the same, and the SETINAR(2,1)-II model takes the smallest AIC and BIC values. Thus, we can conclude that SETINAR(2,1)-II is appropriate for this data set. Moreover, this example also shows that it is necessary to extend the original SETINAR(2,1) model proposed by Monteiro et al. (2012).

Table 10 The fitting results of criminal data

5 Conclusions

This article extended the original SETINAR(2,1) model proposed by Monteiro et al. (2012) by removing the assumption of Poisson distribution of $Z_t$, and redefined the new SETINAR(2,1) process under the conditions of finite second moment of $Z_t$. The ergodicity of the new process is established. MQL-estimators of the model parameters and confidence regions based on QL method are derived and the asymptotic properties of the estimators are obtained. A real data example reveals that the new SETINAR(2,1) model with Geometric innovations is appropriate for the criminal data. Potential issues of future research include to test the linearity against the nonlinear model, the marginal distributions, extend the results to multivariate cases.

Appendix

Proof of Proposition 2.1

According to Theorem 3.1 of Tweedie (1975)(or Proposition 2.2 of Zheng and Basawa 2008), the sufficient condition of $\{X_t\}$ to be ergodic is that there exists a set K and a non-negative measurable function g on state space $\mathbb {N}_0$ such that

$$\begin{aligned} \int _{\mathbb {N}_0}P(x,dy)g(y)\le g(x)-1,~~x\notin K, \end{aligned}$$

(5.1)

and for some fixed B, 

$$\begin{aligned} \int _{\mathbb {N}_0}P(x,dy)g(y)=\lambda (x)\le B<\infty ,~~x\in K, \end{aligned}$$

(5.2)

where $P(x,A)=P(X_1\in A|X_0=x).$ Let $g(x)=x,$ we have

$$\begin{aligned} \int _{\mathbb {N}_0}g(y)dP(X_1=y|X_0=x_0)&=E(X_1|X_0=x_0) =\alpha _1x_0I_{0,1}+\alpha _2x_0I_{0,2}+\lambda \\&\le \alpha _{\max }x_0+\lambda , \end{aligned}$$

where $\alpha _{\max }=\max \{\alpha _1,\alpha _2\}<1.$ let $N=[\frac{1+\lambda }{1-\alpha _{\max }}]+1$, where [x] denotes the integer part of x. Then for $x_0\ge N,$ we have

$$\begin{aligned} \alpha _{\max }x_0+\lambda \le x_0-1=g(x_0)-1, \end{aligned}$$

and for $0\le x_0\le N-1,$

$$\begin{aligned} \int _{\mathbb {N}_0}g(y)dP(X_1=y|X_0=x_0)&=E(X_1|X_0=x_0) \le \alpha _{\max }x_0+\lambda \le N+\lambda <\infty . \end{aligned}$$

Let $K=\{0,1, \ldots ,N-1\},$ then (5.1) and (5.2) both hold which completes the proof. $\square$

Proof of Theorem 2.1

First, we suppose $\varvec{\theta }$ is known. Let $\mathcal {F}_t=\sigma (X_0,X_1, \ldots ,X_t)$ be the $\sigma$-field generated by $\{X_0,X_1, \ldots ,X_t\}$. For the following estimation equations:

$$\begin{aligned} S_n^{(1)}(\varvec{\theta },\varvec{\beta })=\sum _{t=1}^n V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )I_{1,t}X_{t-1}, \end{aligned}$$

we have

$$\begin{aligned}&E[V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )I_{1,t}X_{t-1}|\mathcal {F}_{t-1}]\\&\quad =V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})I_{1,t}X_{t-1}E[(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )|\mathcal {F}_{t-1}]\\&\quad =0, \end{aligned}$$

and

$$\begin{aligned}&E[S_t^{(1)}(\varvec{\theta },\varvec{\beta })|\mathcal {F}_{t-1}]\\&\quad =E[(V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )I_{1,t}X_{t-1}\\&\qquad +S_{t-1}^{(1)}(\varvec{\theta },\varvec{\beta }))|\mathcal {F}_{t-1}]\\&\quad =S_{t-1}^{(1)}(\varvec{\theta },\varvec{\beta }). \end{aligned}$$

Thus, $\{S_t^{(1)}(\varvec{\theta },\varvec{\beta }),\mathcal {F}_{t},~t\ge 0\}$ is a martingale. By (C1) and Theorem 1.1 in Billingsley (1961),

$$\begin{aligned}&\frac{1}{n}\sum _{t=1}^n V_{\varvec{\theta }}^{-2}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )^2X_{t-1}^2I_{1,t}\\&\quad \overset{a.s.}{\longrightarrow }E\left( V_{\varvec{\theta }}^{-2}(X_1|X_{0})(X_1-\alpha _1X_{0}I_{1,1}-\alpha _2X_{0}I_{2,1}-\lambda )^2X_0^2I_{1,1}\right) \\&\quad = E\left( E[V_{\varvec{\theta }}^{-2}(X_1|X_{0})(X_1-\alpha _1X_{0}I_{1,1}-\alpha _2X_{0}I_{2,1}-\lambda )^2X_0^2I_{1,1}|X_0]\right) \\&\quad = E[V_{\varvec{\theta }}^{-1}(X_1|X_0)X_0^2I_{1,1}]\\&\quad = T_{11}(\varvec{\theta }). \end{aligned}$$

Hence, by Corollary 3.2 in Hall and Heyde (1980) and the central limit theorem of martingale, we have,

$$\begin{aligned} \frac{1}{\sqrt{n}}S_n^{(1)}(\varvec{\theta },\varvec{\beta })\overset{L}{\longrightarrow }N(0,T_{11}(\varvec{\theta })). \end{aligned}$$

Similarly,

$$\begin{aligned} S_n^{(2)}(\varvec{\theta },\varvec{\beta })=\sum _{t=1}^n V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )I_{2,t}X_{t-1}, \end{aligned}$$

and

$$\begin{aligned} S_n^{(3)}(\varvec{\theta },\varvec{\beta })=\sum _{t=1}^n V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda ), \end{aligned}$$

We can verify that $\{S_t^{(i)}(\varvec{\theta },\varvec{\beta }),\mathcal {F}_{t},~t\ge 0\}$ $(i=2,3)$ are also martingales. Similar to the previous discussion, we have

$$\begin{aligned} \frac{1}{\sqrt{n}}S_n^{(i)}(\varvec{\theta },\varvec{\beta })\overset{L}{\longrightarrow }N(0,T_{ii}(\varvec{\theta })),~i=2,3. \end{aligned}$$

By Cramer-Wold device, for any $\varvec{c}^\textsf {T}=(c_1,c_2,c_3) \in \mathbb {R}^3$ and $(c_1,c_2,c_3)\ne (0,0,0)$, we have

$$\begin{aligned} \frac{\varvec{c}^\textsf {T}}{\sqrt{n}}\left( \begin{array}{c} S_n^{(1)}(\varvec{\theta },\varvec{\beta })\\ S_n^{(2)}(\varvec{\theta },\varvec{\beta })\\ S_n^{(3)}(\varvec{\theta },\varvec{\beta }) \end{array}\right)&=\frac{1}{\sqrt{n}}\sum _{i=1}^3 c_iS_n^{(i)}(\varvec{\theta },\varvec{\beta })\\&=\frac{1}{\sqrt{n}}\sum _{t=1}^n V_{\varvec{\theta }}^{-1}(X_t|X_{t-1})(X_t-\alpha _1X_{t-1}I_{1,t}-\alpha _2X_{t-1}I_{2,t}-\lambda )\\&\quad \cdot (c_1I_{1,t}X_{t-1}+c_2I_{2,t}X_{t-1}+c_3)\\&\overset{L}{\longrightarrow } N(0,E[V_{\varvec{\theta }}^{-1}(X_1|X_0)(c_1 X_{0}I_{1,1}+c_2 X_{0}I_{2,1}+c_3)^2]), \end{aligned}$$

implying

$$\begin{aligned} \frac{1}{\sqrt{n}}\left( \begin{array}{c} S_n^{(1)}(\varvec{\theta },\varvec{\beta })\\ S_n^{(2)}(\varvec{\theta },\varvec{\beta })\\ S_n^{(3)}(\varvec{\theta },\varvec{\beta }) \end{array}\right)&\overset{L}{\longrightarrow } N\left( \varvec{0},\varvec{T}(\varvec{\theta })\right) . \end{aligned}$$

Now, we replace $V_{\varvec{\theta }}(X_t|X_{t-1})$ with $V_{\hat{\varvec{\theta }}}(X_t|X_{t-1})$, where $\hat{\varvec{\theta }}$ is a consistent estimator of ${\varvec{\theta }}$. Then we want

$$\begin{aligned} \frac{1}{\sqrt{n}}\left( \begin{array}{c} S_n^{(1)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(2)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(3)}(\hat{\varvec{\theta }},\varvec{\beta }) \end{array}\right)&\overset{L}{\longrightarrow } N\left( \varvec{0},\varvec{T}(\varvec{\theta })\right) . \end{aligned}$$

(5.3)

To prove (5.3), we need to check that

$$\begin{aligned} \frac{1}{\sqrt{n}}S_n^{(i)}(\hat{\varvec{\theta }},\varvec{\beta })-\frac{1}{\sqrt{n}}S_n^{(i)}({\varvec{\theta }},\varvec{\beta })\overset{P}{\longrightarrow }0,~i=1,2,3. \end{aligned}$$

(5.4)

Let $R_n(\varvec{\theta })=(1/\sqrt{n})S_n^{(1)}(\varvec{\theta },\varvec{\beta })$. Then for any $\varepsilon >0$ and $\delta >0$, we have

$$\begin{aligned} P(|R_n(\hat{\varvec{\theta }})-R_n(\varvec{\theta })|>\varepsilon )&\le \sum _{i=1}^2P(|\hat{\theta }_i-\theta _i|>\delta )+P(|\hat{\sigma }_z^2-\sigma _z^2|>\delta )\\&\quad +P(\sup _D|R_n(\varvec{\theta }_1)-R_n(\varvec{\theta })|>\varepsilon ), \end{aligned}$$

where $\varvec{\theta }_1=(\theta _1^{1},\theta _2^{1},\sigma _1^{2})^\textsf {T}, D:=\{|\theta _1^{1}-\theta _1|<\delta ,|\theta _2^{1}-\theta _2|<\delta ,|\sigma _1^{2}-\sigma _z^2|<\delta \}.$ If $\hat{\varvec{\theta }}$ is a consistent estimator of ${\varvec{\theta }}$, then we just need to prove that

$$\begin{aligned} P\left( \sup _D|R_n(\varvec{\theta }_1)-R_n(\varvec{\theta })|>\varepsilon \right) \overset{P}{\longrightarrow }0. \end{aligned}$$

By Markov inequality,

$$\begin{aligned}&P\left( \sup _D|R_n(\varvec{\theta }_1)-R_n(\varvec{\theta })|>\varepsilon \right) \nonumber \\&\quad \le \frac{1}{\varepsilon ^2}E\left( \sup _D(R_n(\varvec{\theta }_1)-R_n(\varvec{\theta }))^2\right) \nonumber \\&\quad =\frac{1}{\varepsilon ^2}E\left( \sup _D\frac{1}{n}\sum _{t=1}^n(V_{\varvec{\theta }_1}^{-1}(X_t|X_{t-1})-V_{\varvec{\theta }}^{-1}(X_t|X_{t-1}))^2 \left( X_t-\sum _{i=1}^2\alpha _iI_{i,t}X_{t-1}-\lambda \right) ^2X_{t-1}^2I_{1,t}\right) \nonumber \\&\quad =\frac{1}{\varepsilon ^2}E\left( \sup _D(V_{\varvec{\theta }_1}^{-1}(X_1|X_{0})-V_{\varvec{\theta }}^{-1}(X_1|X_{0}))^2 \left( X_1-\sum _{i=1}^2\alpha _iI_{i,t}X_{0}-\lambda \right) ^2X_{0}^2I_{1,1}\right) \nonumber \\&\quad =\frac{1}{\varepsilon ^2}E\left( \sup _D \frac{\left( \sum _{i=1}^2\left( \theta _i-\theta _i^1\right) X_0I_{i,1}+\left( \sigma _z^2-\sigma _1^2\right) \right) ^2}{V_{\varvec{\theta }_1}^{2}(X_1|X_{0})V_{\varvec{\theta }}^{2}(X_1|X_{0})} \left( X_1-\sum _{i=1}^2\alpha _iI_{i,t}X_{0}-\lambda \right) ^2X_{0}^2I_{1,1}\right) \nonumber \\&\quad =\frac{1}{\varepsilon ^2}E\left( \sup _D \frac{\left( \sum _{i=1}^2\left( \theta _i-\theta _i^1\right) X_0I_{i,1}+\left( \sigma _z^2-\sigma _1^2\right) \right) ^2}{V_{\varvec{\theta }_1}^{2}(X_1|X_{0})V_{\varvec{\theta }}(X_1|X_{0})} X_{0}^2I_{1,1}\right) \nonumber \\&\quad \le \frac{1}{\varepsilon ^2}\sup _D \left\{ ((\theta _1-\theta _1^1)^2 m_1 +(\theta _2-\theta _2^1)^2 m_2 +(\sigma _z^2-\sigma _1^2)^2 m_3 +2m_4|\theta _1-\theta _1^2||\theta _2-\theta _2^1|\right. \nonumber \\&\quad \quad \left. +2m_5|\theta _1-\theta _1^1||\sigma _z^2-\sigma _1^2|+2m_6|\theta _2-\theta _2^1||\sigma _z^2-\sigma _1^2|) X_{0}^2I_{1,1}\right\} \nonumber \\&\quad \le \frac{C\delta ^2}{\varepsilon ^2}, \end{aligned}$$

(5.5)

where $m_i~(i=1,2, \ldots ,6)$ denote some finite moments of process $\{X_t\}$, C is a positive constant. Similar argument can be used for $1/\sqrt{n}S_n^{(i)}(\varvec{\theta },\varvec{\beta })(i=2,3)$. For any fixed $\varepsilon >0$, letting $\delta \rightarrow 0$, we get our assertion which in turn establishes (5.3).

Finally, by the ergodic theorem, we have

$$\begin{aligned} \frac{1}{n}\varvec{Q}_n\overset{P}{\longrightarrow }\varvec{T}(\varvec{\theta }). \end{aligned}$$

After some algebra, we have,

$$\begin{aligned} (\hat{\varvec{\beta }}_{MQL}-\varvec{\beta })=\varvec{Q}_n^{-1} \left( \begin{array}{c} S_n^{(1)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(2)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(3)}(\hat{\varvec{\theta }},\varvec{\beta }) \end{array}\right) , \end{aligned}$$

Therefore,

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\beta }}_{MQL}-\varvec{\beta })=\left( \frac{1}{n}\varvec{Q}_n\right) ^{-1} \frac{1}{\sqrt{n}} \left( \begin{array}{c} S_n^{(1)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(2)}(\hat{\varvec{\theta }},\varvec{\beta })\\ S_n^{(3)}(\hat{\varvec{\theta }},\varvec{\beta }) \end{array}\right) \overset{L}{\longrightarrow }N(\varvec{0},\varvec{T}^{-1}(\varvec{\theta })). \end{aligned}$$

(5.6)

The proof is complete. $\square$

Proof of Theorem 2.2

The proof follows by the ergodic theorem. $\square$

Proof of Theorem 2.3

The proof follows from Theorem 2.1. $\square$