Bayesian accelerated life testing under competing log-location-scale family of causes of failure

Abstract

This article provides Bayesian analyses of data arising from multi-stress accelerated life testing of series systems. The component log-lifetimes are assumed to independently belong to some log-concave location-scale family of distributions. The location parameters are assumed to depend on the stress variables through a linear stress translation function. Bayesian analyses and associated predictive inference of reliability characteristics at usage stresses are performed using Gibbs sampling from the joint posterior. The developed methodology is numerically illustrated by analyzing a real data set through Bayesian model averaging of the two popular cases of Weibull and log-normal, with the later getting a special focus in this article as a slightly easier example of the log-location-scale family. A detailed simulation study is also carried out to compare the performance of various Bayesian point estimators for the log-normal case.

1 Introduction

Testing modern, reliable hardware systems at normal usage condition for failures can be highly time consuming. To induce early failures, it is therefore common practice in the manufacturing and defense industry to subject the developed systems to more extreme stress levels compared to stress levels at the normal usage condition. For instance, consider the example of Class-B electrical insulation system in electric motors discussed in Nelson (1990, p. 418). The insulation system is designed to operate at a usage temperature of 403.15 K (Kelvin). Since it is extremely unlikely for the insulation systems to fail within any reasonable time at 403.15 K, they are tested at temperatures 423.15, 443.15, 463.15 and 493.15 K to produce quick breakdown data. Such tests are commonly known as Accelerated Life Tests (ALT henceforth). The observations collected on the failure times of the systems at accelerated conditions (such as the four different temperature levels mentioned above) are then used to infer about its reliability at normal usage condition (like the 403.15 K above), which is also called usage stress. Nelson (1990) provides a comprehensive account of the relevant statistical models and methods for analyzing such accelerated data.

In practice, a system often has more than one failure modes, which are the causes of system failures. For example, the insulation system mentioned above has three failure modes, called turn, phase and ground. Each of these modes of failures occurs at different parts of the insulation system, but the insulation system as a whole fails as soon as one of these causes takes place. Such systems which fail as soon as one of their causes or modes of failures occurs, are called series systems. A series system ALT data thus also consist of the causes or failure modes, along with the (observed or censored) times to system failures at the elevated stress levels. The failure modes responsible for system failures are also called components of the system and through-out this article we use these two terms interchangeably.

A number of studies in the literature has considered the maximum likelihood inference of series system ALT data with a single stress variable (see Klein and Basu 1981, 1982a, b; Nelson 1990; Kim and Bai 2002; Jiang 2011, for example). These studies exploit large-sample properties of the MLEs to infer on the component and system lifetime distributions at usage stress. However in an ALT, the available sample size is expected to be small. In such cases, Bayesian procedures are known to provide more reasonable results (see Berger 1985, p. 125). There are also situations where important prior information are available in an ALT (see Zhang and Meeker 2006). Bayesian methods allow easy and formal incorporation of such prior information into decision-making. Furthermore, as explained in the first paragraph, the goal of performing an ALT is to predict the component and system lifetime distributions at usage stress. Since the Bayesian paradigm handles the problem of prediction in a more coherent manner (see Berger 1985, pp. 67, 157), development of such Bayesian methodologies for analyzing ALT data seems imperative and important.

A considerable amount of literature exists on the Bayesian analysis of ALT data for systems with a single component (see Pathak et al. 1991; Tojeiro et al. 2004; Dorp and Mazzuchi 2004, 2005, for example). However, the literature on Bayesian analysis of accelerated data for series systems is comparatively less expansive. Bunea and Mazzuchi (2006), Tan et al. (2009) and Xu and Tang (2011) have provided Bayesian analyses of single-stress series system ALT data with independent exponential or Weibull component lives.

In these Bayesian analyses, first the Bayes’ estimates of the exponential or Weibull model parameters are obtained at each elevated stress level. The model parameters at usage stress are then estimated using the method of least squares through an assumed Stress Translation Function (STF henceforth). Thus this approach is not fully Bayesian. Roy and Mukhopadhyay (2013, 2014) have developed full Bayesian solutions to this problem assuming that the component lifetimes are independent exponentials and Weibulls with identical shape parameters (see Fan and Hsu (2014) for the non-identical Weibull case). Generalizing these analyses to a more flexible log-location-scale family, this article now presents full Bayesian analyses of fixed multi-stress ALT data of series systems.

Briefly, it is assumed that the component log-lifetimes of a series system are independent and belong to some log-concave location-scale family of distributions. The families of these distributions may be different, like some are extreme-value while the others are normal, but the location parameters of these distributions are assumed to be connected with the multiple stress variables through a linear STF. The combined choices of this log-location-scale family for the component lifetime distributions and the form of the proposed linear STF, provide a rich and comprehensive model covering all the practical and standard cases of fixed multi-stress ALT data of series systems. A detailed discussion of this model is carried out in Sect. 2.

Section 3 next discusses the issue of Bayesian analyses of such models. It is first shown that the one-dimensional conditional posterior distributions of all the model parameters given the rest are log-concave, if so are the corresponding priors. This fact is then used to Gibbs sample from the joint posterior which can be subsequently utilized for standard Bayesian predictive inference for component and system lifetime distributions at usage stresses under a fixed assumed model. Thus this approach is fully Bayesian in the sense that it takes care of the uncertainty in the model parameters through their joint posterior density, resulting in a coherent set of predictions.

Although log-normally distributed component lives is an important special case of the model introduced in Sect. 2, here the general solution can be eased (in the sense of avoiding log-concave sampling) and made more elegant through data-augmentation and choice of priors. Unlike Weibull, the other important component life distribution of the log-location-scale family, log-normal allows objective Bayesian analysis in this problem. Thus Sect. 4 is devoted to the special case of log-normal distribution demonstrating these issues and a detailed simulation study comparing different optimal (with respect to various loss functions) Bayesian point estimates.

Section 5 illustrates Bayesian analyses of the data of the example of the electrical insulation system introduced in the first paragraph. First an attempt is made to choose an “appropriate” model (among exponential, Weibull and log-normal) for the component lifetimes by computing exact Bayes’ Factor (BF henceforth) through Markov Chain Monte Carlo (MCMC henceforth). But the BF based model selections being inconclusive, the standard fixed model predictive Bayesian inference developed in Sect. 3, is further enhanced by Bayesian model averaging for obtaining appropriate Bayesian point and interval estimates of reliability characteristics at usage stress. Section 6 concludes the article by summarizing its contributions and providing a few pointers towards future research needs. The proofs are deferred to Appendix 1, and the abbreviations and notations used in the article are listed in Appendix 2.

2 Log-location-scale model with linear STF

Consider a series system with J independent causes of failure, with the jth cause having a potential lifetime $X_j$ and log-lifetime $Y_j=\log X_j$. Suppose such a system is put on an ALT with K life acceleration factors or stress variables. Let $\mathbf Z=(Z_{1},\ldots ,Z_{K})'$ denote the vector of such K stress variables acting on the system. Given $\mathbf Z=\mathbf z$, it is assumed that the $Y_j$s are mutually independent with $Y_j$ having p.d.f.

$$\begin{aligned} f_{Y_j}\left( y|\varvec{\theta }_j,\tau _j,\mathbf z\right) =\tau _jf_j\left( \tau _j\left( y-\mu _j(\varvec{\theta }_j,\mathbf z)\right) \right) , \end{aligned}$$

(1)

where $f_j(\cdot )$ is a univariate log-concave p.d.f., $\varvec{\theta }_j=\left( \theta _{1j},\ldots ,\theta _{Kj}\right) '\in \mathfrak {R}^K$ is a parameter vector of stress coefficients determining the location $\mu _j(\varvec{\theta }_j,\mathbf z)$ of the distribution of $Y_j$, and $\tau _j>0$ is a scale parameter. Thus as is standard in ALT (see Nelson 1990, p. 80, for example), Eq. (1) assumes that any change in the stresses results in just a translation or shift in location of the distribution of the component log-lifetimes (without distorting its exact shape or scaling). This is why $\mu _j(\varvec{\theta }_j,\mathbf z)$s are more commonly known as the STFs in the literature (see Klein and Basu 1981, for example). With $\overline{F}_j(t)=\int _t^\infty f_j(u)\mathrm {d}u$ and $h_j(t)=f_j(t)/\overline{F}_j(t)$, let ${\overline{F}}_{Y_j}\left( y|\varvec{\theta }_j,\tau _j,\mathbf z\right) =\overline{F}_j\left( \tau _j\left( y-\mu _j(\varvec{\theta }_j,\mathbf z)\right) \right)$ and $h_{Y_j}(y|\varvec{\theta }_j,\tau _j,\mathbf z)=\tau _jh_j\left( \tau _j\left( y-\mu _j(\varvec{\theta }_j,\mathbf z)\right) \right)$ respectively denote the s.f. and h.r. of $Y_j$ at stress $\mathbf Z=\mathbf z$.

Equation (1) as a basic model for analyzing multi-stress ALT data is very flexible in two respects. First, it gives the user a choice of component life-distributions in terms of the specification of $f_j(\cdot )$, and second, it can accommodate any multi-stress STF by an appropriate choice of $\mu _j(\varvec{\theta }_j,\mathbf z)$. Though well-known (see Meeker and Escobar 1998, p. 79, for example), for the sake of easy reference and the additional requirement of log-concavity (which is easily checked via $\frac{\mathrm {d}^2}{\mathrm {d}t^2} \log f_j(t) \le 0$ in most cases), Table 1 lists the standard life-distributions used in the literature that can be modeled by an appropriate choice of log-concave $f_j(\cdot )$, with the corresponding expressions for the location $\mu _j$ and scale $\tau _j$ in terms of the original parameters. It should be noted that for ease of recognition, Table 1 gives the names and p.d.f.s of the life-distributions in terms of that of lifetime $X_j$.

Table 1 Log-concave log-location-scale family of life distributions

Equation (1) now requires specification of the location $\mu _j$ through the STF $\mu _j(\varvec{\theta }_j,\mathbf z)$. As introduced in Roy and Mukhopadhyay (2014), here also we assume a linear STF given by:

$$\begin{aligned} \mu _{j}(\varvec{\theta }_j, \mathbf z)=\sum _{k=1}^K\theta _{kj} g_{kj}(z_k)=\sum _{k=1}^K\theta _{kj}s_{kj}={\mathbf s_{j}}'{\varvec{\theta }_{j}}, \end{aligned}$$

(2)

where $\mathbf s_{j}=\left( s_{1j},\ldots ,s_{Kj}\right) '$ with $s_{kj}=g_{kj}(z_k)$, for some real valued functions $g_{kj}(\cdot )$s.

Though already explained somewhat briefly in Roy and Mukhopadhyay (2014, 2015), the reasoning behind choosing Eq. (2) as the STF is as follows. Typically in an ALT there are several choices for stress variables such as temperature, voltage, pressure, humidity, dust, vibration, etc. and are often used in combinations. Since the final aim of an ALT requires extrapolation to usage stresses, it is imperative that the underlying models that do so, have some engineering basis (see Meeker and Escobar 1998, p. 495). In this regard there are several multi-stress models that exist in the engineering literature,¹ which express $X_j$, the time to failure (of the jth component in this case) as a non-linear function of the applied stresses. A natural way to accommodate such (non-linear) models is to let the logarithm of these functions equal the STF $\mu _j(\varvec{\theta }_j,\mathbf z)$, which in Eq. (1) is the location parameter of $Y_j=\log X_j$. Now it turns out that quite a few such standard engineering choices of STF, especially in the context of multiple stress variables, can be expressed as in Eq. (2), and are exemplified with further details in Table 2.

Table 2 Different linear stress translation functions

It needs to be remarked that as Eq. (1) allows one to assume different life distributions, Eq. (2) lets one choose different STFs for different components. This feature of the model is particularly important and attractive for the problem of multi-stress ALT of multi-component systems. This is because sometimes certain particular life distributions get associated with a specific STF for a common underlying physical or engineering reasoning of failures. For example, suppose a mechanical component of a system fails due to the “weakest link” theory leading to a Weibull, and an electrical component of the same system fails due to the “multiplicative degradation” theory leading to a log-normal, as their respective life distributions. Then with temperature as the common stress variable, while the Eyring interaction model with humidity as the second stress variable is a reasonable physical choice of STF for the Weibull component, the electromigration STF with current density as the third stress variable becomes the most natural physical choice for the log-normal component (since the same ionic movement phenomenon leads to electromigration as well as “multiplicative degradation” theory of failures in ICs). Such situations are easily accommodated by the proposed model.

Now consider modeling the lifetime of such J-component series systems. Since a series system fails as soon as one of its constituent J components fails, the system log-lifetime T at stress $\mathbf Z=\mathbf z$ is given by $\left\{ T|\mathbf {Z}=\mathbf {z}\right\} =\text{ Min }\{Y_{1}|\mathbf {Z}=\mathbf {z},\ldots ,Y_{J}|\mathbf {Z}=\mathbf {z}\}$. Now since the J components are also assumed to be independent, the system s.f. $\overline{F}_T(t|\varvec{\theta },\varvec{\tau },\mathbf {z})$ is given by

$$\begin{aligned} {\overline{F}}_T(t|\varvec{\theta },\varvec{\tau },\mathbf {z})= & {} \prod _{j=1}^J \overline{F}_j\left( \tau _j\left( t-{\mathbf s_j}'\varvec{\theta }_j\right) \right) , \end{aligned}$$

(3)

where $\varvec{\theta }=\left( \varvec{\theta }_{1}', \ldots ,\varvec{\theta }_{J}'\right) '$ and $\varvec{\tau }=\left( \tau _1,\ldots ,\tau _J\right) '$. Let the discrete random variable I, taking values in $\left\{ 1,\ldots ,J\right\}$, denote the component causing system failure. Then, clearly $I={{\mathrm{arg\,min}}}_j \left\{ Y_{j}|\mathbf Z=\mathbf z\right\}$. For a series system that has failed after being put on an ALT, one typically observes $\left( T,I\right)$. The joint p.d.f. of $\left( T,I\right)$ is given by

$$\begin{aligned} \lim _{\varDelta t \rightarrow 0}\frac{1}{\varDelta t}P\left( t\le T \le t+\varDelta t, I=j|\varvec{\theta },\varvec{\tau },\mathbf {z}\right) =p_{j}\left( t|\varvec{\theta },\varvec{\tau },\mathbf {z}\right) ,\,\,\text {say}, \end{aligned}$$

where

$$\begin{aligned} p_{j}(t|\varvec{\theta },\varvec{\tau },\mathbf {z})= & {} \tau _jh_j\left( \tau _j\left( t-{\mathbf s_j}'\varvec{\theta }_j\right) \right) \prod _{j=1}^J \overline{F}_j\left( \tau _j\left( t-{\mathbf s_j}'\varvec{\theta }_j\right) \right) . \end{aligned}$$

(4)

The complete set of model parameters is then given by $\varvec{\psi }=(\varvec{\theta }',\mathbf \tau ')'$. Also, let $\varvec{\psi }_j=({\varvec{\theta }_j}',\tau _j)'$.

3 Bayesian analysis

3.1 Likelihood function

Suppose N J-component series systems as in Sect. 2 are put on an ALT at different levels of the K stress variables. For $i=1,\ldots ,N$, let $\mathbf z^i=(z_1^i,\ldots ,z_K^i)'$ denote the value of the stress vector $\mathbf Z^i$ applied to the ith system. Let the number of systems that fail in this ALT be denoted by n. For $i=1,\ldots ,n$, let $T^i$ and $I^i$ respectively denote the log-failure time and cause of failure of ith such system. For the remaining $N-n$ systems that do not fail in the ALT, denote the future log-failure time of the rth system by $T^{n+r}$, for $r=1,\ldots ,N-n$. $(T^1,I^1),\ldots ,(T^n,I^n),T^{n+1},\ldots ,T^{N}$ are assumed to be mutually independent of each other. For $i=1,\ldots ,n$, let $t^i$ denote the observed log-failure time of the ith failed system, and for $r=1,\ldots ,N-n$, let $t^{n+r}$ denote the observed log-censoring time of the rth running system. Thus the observed data is given by

$$\begin{aligned} {\mathscr {D}}= & {} \Big \{\big (T^1=t^1,I^1,\mathbf Z^{1}=\mathbf z^{1}\big ),\ldots ,\big (T^n=t^n,I^n,\mathbf Z^{n}=\mathbf z^{n}\big ),\nonumber \\&\big (T^{n+1}>t^{n+1},\mathbf Z^{n+1}=\mathbf z^{n+1}\big ),\ldots ,\big (T^{N}>t^{N},\mathbf Z^{N}=\mathbf z^{N}\big )\Big \}. \end{aligned}$$

(5)

Now by using Eqs. (3) and (4), the likelihood function of $\varvec{\psi }$ given the observed data ${\mathscr {D}}$, is given by

$$\begin{aligned} L\left( \varvec{\psi }|{\mathscr {D}}\right)= & {} \left[ \prod _{i=1}^{n}\left\{ \frac{\tau _{I^{i}}f_{I^{i}}\left( {\tau _{I^{i}}}\left( t^{i}-{{\mathbf s_{I^{i}}^i}}'\varvec{\theta }_{I^i}\right) \right) }{\overline{F}_{I^{i}}\left( {\tau _{I^{i}}}\left( t^i-{\mathbf s_{I^{i}}^i}'\varvec{\theta }_{I^i}\right) \right) }\right\} \right] \nonumber \\&\times \left[ \prod _{i=1}^{N}\prod _{j=1}^{J}{\overline{F}_j\left( {\tau _{j}} \left( t^i-{\mathbf s_j^i}'\varvec{\theta }_j\right) \right) }\right] , \end{aligned}$$

(6)

where $\mathbf s_j^i=\left( s_{1j}^i,\ldots ,s_{Kj}^i\right) '$ with $s^i_{kj}=g_{kj}(z^i_k)$. Now it is easy to see that

$$\begin{aligned} L\left( \varvec{\psi }|{\mathscr {D}}\right) =\prod _{j=1}^J L_j\left( \varvec{\psi }_j|{\mathscr {D}}\right) \end{aligned}$$

(7)

where

$$ \begin{aligned} L_j\left( \varvec{\psi }_j|{\mathscr {D}}\right)= & {} \tau _j^{n_j} \times \displaystyle \prod _{\begin{array}{c} 1\le i \le n\\ \& \, I^i=j \end{array}} f_j\left( {\tau _j}\left( t^{i}-{\mathbf s_j^i}'\varvec{\theta }_{j}\right) \right) \times \prod _{\begin{array}{c} 1 \le i \le n\\ \& \, I^i \ne j \end{array}} \overline{F}_j\left( {\tau _{j}}\left( t^i-{\mathbf s_j^i}'\varvec{\theta }_j\right) \right) \nonumber \\&\times \prod _{i=n+1}^N \overline{F}_j\left( {\tau _{j}}\left( t^i-{\mathbf s_j^i}'\varvec{\theta }_j\right) \right) , \end{aligned}$$

(8)

and $n_j=\#\{1\le i \le n: I^i=j\}$ denotes the number of failures due to cause j so that $\sum _{j=1}^J n_j=n$.

Bayesian inference is based on $\pi \left( \varvec{\psi }|{\mathscr {D}}\right)$, the posterior p.d.f. of $\varvec{\psi }$ given ${\mathscr {D}}$, which is proportional to the product of $L\left( \varvec{\psi }|{\mathscr {D}}\right)$, the likelihood function of $\varvec{\psi }$ given in Eq. (6), and $\pi (\varvec{\psi })$, the joint prior of $\varvec{\psi }$.

3.2 Prior distribution

Equation (7) reveals a natural independence structure among the $\varvec{\psi }_j$s which is respected in the prior distribution as well, that is, $\varvec{\psi }_1,\ldots ,\varvec{\psi }_J$ are assumed to be mutually independent a priori, resulting in the joint prior p.d.f. of $\varvec{\psi }$ as

$$\begin{aligned} \pi (\varvec{\psi })=\prod _{j=1}^J\pi \left( \varvec{\psi }_j\right) , \end{aligned}$$

(9)

where $\pi \left( \varvec{\psi }_j\right)$ is the joint prior p.d.f. of $\varvec{\psi }_j=({\varvec{\theta }_j},\tau _j)'$. Furthermore, it is also assumed a priori that $\theta _{1j}, \ldots , \theta _{Kj}$ and $\tau _j$ are all mutually independent. Thus

$$\begin{aligned} \pi (\varvec{\psi }_j)= & {} \prod _{j=1}^J \left\{ \prod _{k=1}^K \pi \left( \theta _{kj}\right) \right\} \pi \left( \tau _j\right) =\pi \left( \varvec{\theta }_j\right) \pi \left( \tau _j\right) , \end{aligned}$$

(10)

where $\pi \left( \varvec{\theta }_j\right) =\prod _{k=1}^K \pi \left( \theta _{kj}\right)$ and $\pi \left( \theta _{kj}\right)$, $\pi \left( \tau _j\right)$ and $\pi \left( \varvec{\theta }_j\right)$ are the prior p.d.fs of $\theta _{kj}$, $\tau _j$ and $\varvec{\theta }_j$ respectively. In principle Bayesian computation only needs the ability of generating observations from $\pi (\psi _j|{\mathscr {D}})$. Towards that end as required in Theorem 1 below, it is further assumed that $\pi \left( \theta _{kj}\right)$ and $\pi \left( \tau _j\right)$ are log-concave functions of their respective arguments.

Under such circumstances, we propose the following simple method of choosing subjective proper priors for $\theta _{kj}$s and $\tau _j$s. First note that as defined in Sect. 2, $\theta _{kj}$s are unrestricted real numbers. Thus any log-concave density such as the $f_j(\cdot )$s listed in Table 1 with the entire real line as its support, may be chosen as a proper prior p.d.f. for $\theta _{kj}$. In case of $f_j(\cdot )$s of Table 1 (or even otherwise) as priors, their location and scale hyper-parameters may be chosen by specifying a guess-interval and one’s subjective probability of that guess-interval containing the unknown parameter value. The choice of the particular $f_j(\cdot )$s among the ones listed in Table 1 may now be used to better model one’s subjective belief, such as an additional subjective probability consistency check, both inside but more importantly outside the guess-interval. Since $\tau _j>0$, one may choose any log-concave density with $(0,\infty )$ as its support (such as gamma or Weibull with shape parameter $\ge$ 1) as a proper prior for $\tau _j$.

Along with the discussion of subjective proper priors, in Bayesian analysis it is also very important to address the issue of non-informative priors (see Berger 2006). For the location-scale regression model of Eqs. (1) and (2), a common non-informative prior is given by (see Fernández and Steel 1999, for example)

$$\begin{aligned} \pi \left( \varvec{\theta }_j,\tau _j\right) \propto \frac{1}{\tau _j}. \end{aligned}$$

(11)

Note that the above non-informative prior is improper and thus as in any other situation, care must be exercised ensuring the propriety of the resulting joint posterior before employing such improper priors. For the problem at hand, if for instance, the $X_j$s are Weibull or equivalently $Y_j$s are extreme-value, the posterior resulting from the prior in (11) may be improper (see Kim and Ibrahim 2000; Roy and Mukhopadhyay 2014).

3.3 Posterior analysis

As mentioned briefly at the end of Sect. 3.1, the joint posterior $\pi (\varvec{\psi }|{\mathscr {D}})$ is proportional to the product of $L(\varvec{\psi }|{\mathscr {D}})$ given in Eq. (6), and $\pi (\varvec{\psi })$ given in Eq. (9). But, by Eqs. (7) and (10), one gets

$$\begin{aligned} \pi (\varvec{\psi }|{\mathscr {D}})\propto \prod _{j=1}^J L_j(\varvec{\psi }_j|{\mathscr {D}})\pi (\varvec{\theta }_j) \pi (\tau _j)\propto \prod _{j=1}^J \pi (\varvec{\psi }_j|{\mathscr {D}}), \end{aligned}$$

(12)

where $\pi \left( \varvec{\psi }_j|{\mathscr {D}}\right) \propto L_j\left( \varvec{\psi }_j|{\mathscr {D}}\right) \pi (\varvec{\theta }_j) \pi (\tau _j)$ is the joint posterior p.d.f. of $\varvec{\psi }_j$ given the observed data ${\mathscr {D}}$. Thus posterior analysis of $\varvec{\psi }$ can be performed by independently drawing samples from $\pi (\varvec{\psi }_j|{\mathscr {D}})$ for $j=1,\ldots ,J$.

Now as usual, one can Gibbs sample from the joint posterior $\pi (\varvec{\psi }_j|{\mathscr {D}})$, if it is easy to generate observations from the univariate conditional posterior of each component of $\varvec{\psi }_j$, given the rest. The following theorem states why that is the case in this problem.

Theorem 1

If $f_j(\cdot )$ [in Eq. (1)], $\pi (\theta _{1j}), \ldots , \pi (\theta _{Kj})$ and $\pi (\tau _j)$ [in Eq. (10)] are log-concave, then so are the univariate conditional posteriors of $\theta _{kj}$s and $\tau _j$, given the rest, in Eq. (12).

The proof of the theorem is provided in Appendix 1. Using this result one can now employ any efficient algorithm (such as the adaptive rejection sampling technique of Gilks and Wild (1992)) to iteratively draw samples from these univariate log-concave conditional posteriors, to obtain a sample $\{\varvec{\psi }_j^{(l)}\}_{l=1}^L$ from $\pi (\psi _j|{\mathscr {D}})$ in the limit.

The main objective of performing an ALT is to infer on component and system reliability metrics at usage stress $\mathbf Z= \mathbf z_u=\left( z_{u1},\ldots ,z_{uK}\right) '$, such as MTTF, component and system s.f.s, etc. Given $\mathbf Z= \mathbf z_u$, all these are functions of $\varvec{\psi }$ and some are also of t. Let us generically denote any one of these functions by $\triangle \left( \varvec{\psi },t\right)$, for brevity.

Given a sample $\left\{ \varvec{\psi }^{(l)}=\{\varvec{\psi }_1^{(l)},\ldots ,\varvec{\psi }_J^{(l)}\}\right\} _{l=1}^L$ from the joint posterior p.d.f. $\pi \left( \varvec{\psi }|{\mathscr {D}}\right)$, the problem is to estimate $\triangle \left( \varvec{\psi },t\right)$ over a sufficiently large time interval $[0,t_{\text {max}}]$. Towards this goal, the interval $[0,t_{\text {max}}]$ is first partitioned into a grid of $(P+1)$ equispaced points given by $\left\{ 0=t_0,t_1,\ldots ,t_P=t_{\text {max}}\right\}$. Next, $\forall l=1,\ldots ,L$ and $p=0,\ldots ,P$, one computes $\triangle \left( \varvec{\psi }^{(l)},t_p\right)$ denoted by $\triangle ^{(l)}(t_p)$, yielding $\{(\triangle ^{(1)}(t_0),\ldots ,\triangle ^{(1)}(t_P)),\ldots , (\triangle ^{(L)}(t_0),\ldots ,\triangle ^{(L)}(t_P))\}$ as a sample of size L drawn from the joint posterior of $(\triangle (\varvec{\psi },t_0),\ldots ,\triangle (\varvec{\psi },t_P))$. This sample may be now used for computing the usual Bayesian point and interval estimates of $\triangle \left( \varvec{\psi },t\right)$, under J fixed models $f_1(\cdot ),\ldots ,f_J(\cdot )$ for the J component lifetimes.

4 Log-normal model

The special case of an $X_j$ having a log-normal distribution, or equivalently the corresponding $Y_j$ having a normal distribution deserves particular attention for several reasons. First, there are strong theoretical and empirical evidences for occurrence of log-normal as a life distribution in many physical failure mechanisms, such as, for example, the electromigration phenomenon mentioned in Sect. 2 (see Hauschildt et al. 2007 for a more recent account). Even otherwise also from a purely statistical perspective, it is usually required to be tested against the other popular alternative of Weibull (see Kundu and Manglick 2004; Kim and Yum 2008, for example), which require Bayesian analyses of both.

As mentioned in the Introduction, the analyses of the Weibull model through log-concave sampling as in Sect. 3.3, are available in Roy and Mukhopadhyay (2014) and Fan and Hsu (2014) (though note that the former’s model is slightly different from the one being considered here owing to the equality of the $\tau _j$s). Obviously as a special case of Eq. (1), the same can also be carried out for the log-normal distribution as in Sect. 3.3. However in this case, we propose a simple data-augmentation technique and a conjugate prior [which unlike Eq. (10) allows a priori correlation among the $\theta _{kj}$s and $\tau _j$], to circumvent the computationally expensive log-concave sampling.

4.1 Data augmentation

In the rest of this section, j is assumed to be fixed and consideration is given to the special case of $Y_j$, a given jth component log-lifetime, having a normal distribution with mean $\mu _j(\varvec{\theta }_j,\mathbf z)$ and variance $\sigma _j^2$, given $\mathbf Z=\mathbf z$. Based on the observed data ${\mathscr {D}}$ given in Eq. (5) with $\tau _j=1/\sigma _j$ (see Table 1) in Eq. (8), it then follows that

$$ \begin{aligned} L_j(\varvec{\psi }_j|{\mathscr {D}})\propto & {} \sigma _j^{-n_j} \times \displaystyle \prod _{\begin{array}{c} 1\le i \le n\\ \& \,\, I^i=j \end{array}} \phi \left( \frac{t^{i}-{\mathbf s_j^i}'\varvec{\theta }_{j}}{\sigma _j}\right) \times \prod _{\begin{array}{c} 1 \le i \le n\\ \& \,\, I^i \ne j \end{array}} \overline{\varPhi }\left( \frac{t^i-{\mathbf s_j^i}'\varvec{\theta }_j}{\sigma _j}\right) \nonumber \\&\times \prod _{i=n+1}^N \overline{\varPhi }\left( \frac{t^i-{\mathbf s_j^i}'\varvec{\theta }_j}{\sigma _j}\right) , \end{aligned}$$

(13)

where $\varvec{\psi }_j=(\varvec{\theta }_{j},\sigma _j^2)'$ and $\phi (\cdot )$ and $\overline{\varPhi }(\cdot )$ are standard normal p.d.f. and s.f. respectively. In this case, the need for log-concave sampling arises due to the presence of the $\overline{\varPhi }(\cdot )$ terms in (13), which might be thought ensuing due to incomplete information. Such situations are typically remedied by invoking a standard Bayesian tool for handling missing data called data augmentation (see Tanner and Wong 1987). Note that if needed, computations may be further accelerated using refinements such as parameter expanded data augmentation (PX-DA) algorithm (see Liu and Wu 1999, for example).

For $i=1,\ldots ,N$, let $Y^i_j$ denote the log-lifetime of the jth component of the ith system put on the ALT. Then for $i=1,\ldots ,n$, if $I^i=j$, one has $Y_j^i=t^i$ as part of ${\mathscr {D}}$, while if $I^i \ne j$, its associated $t^i$ is its survival time from cause j, and thus its $Y_j^i$, which is latent, is imputed subject to the constraint $Y_j^i>t^i$. Similarly, for $r=1,\ldots ,N-n$, all the censored $Y_j^{n+r}$ values are imputed subject to the constraint $Y_j^{n+r}>t^{n+r}$. For $i=1,\ldots ,N$, let $y^i_j$ denote this observed or imputed value of $Y^i_j$ and $\mathbf {y}_j=\left( y^1_j,\ldots ,y^N_j\right) '$. That is, the observed data set ${\mathscr {D}}$ is proposed to be augmented with an auxiliary part-latent data set ${\mathscr {Y}}_j$ to form the complete data set ${\mathscr {Y}}=\left\{ {\mathscr {D}}, {\mathscr {Y}}_j\right\}$, where ${\mathscr {Y}}_j=\left\{ Y^1_j=y^1_j,\ldots , Y^N_j=y^N_j\right\}$. It should be mentioned that this data augmentation scheme is similar to that in Mukhopadhyay and Basu (2007).

This data augmentation is done to change the problem of sample generation from $\pi \left( \varvec{\psi }_j|{\mathscr {D}}\right)$ to that from $\pi \left( \mathbf y_j,\varvec{\psi }_j|{\mathscr {D}}\right)$, since the $\varvec{\psi }_j$ values generated from $\pi (\mathbf y_j,\varvec{\psi }_j|{\mathscr {D}})$ can also be regarded as a sample from $\pi \left( \varvec{\psi }_j|{\mathscr {D}}\right)$. The later task is much easier as a Gibbs sample from $\pi (\mathbf y_j,\varvec{\psi }_j|{\mathscr {D}})$ can be generated by iteratively sampling from $\pi \left( \mathbf y_j|\varvec{\psi }_j,{\mathscr {D}}\right)$ and $\pi \left( \varvec{\psi }_j|\mathbf y_j,{\mathscr {D}}\right) =\pi \left( \varvec{\psi }_j|\mathscr {Y}\right)$ as follows.

4.2 Gibbs sampling

For $i=1,\ldots ,N$, since $Y_j^i$s are mutually independent,

$$\begin{aligned} \pi \left( \mathbf y_j|\varvec{\psi }_j,{\mathscr {D}}\right) =\prod _{i=1}^N \pi \left( y_j^i|\varvec{\psi }_j,{\mathscr {D}}\right) , \end{aligned}$$

where for $i = 1,\ldots ,n$, if $I^i = j$, $\pi \left( y_j^i|\varvec{\psi }_j,{\mathscr {D}}\right)$ is degenerate at $t^i$ and if $I^i\ne j$ and $1 \le i \le n$, or if $n < i \le N$,

$$\begin{aligned} \pi \left( y_j^{i}|\varvec{\psi }_j,{\mathscr {D}}\right) = {\left\{ \begin{array}{ll} \displaystyle \frac{\frac{1}{\sigma _j}\phi \left( \frac{y_{j}^{i}-{\mathbf s_j^i}'\varvec{\theta }_j}{\sigma _j}\right) }{\displaystyle \overline{\varPhi }\left( \frac{t^{i}-{\mathbf s_j^i}'\varvec{\theta }_j}{\sigma _j}\right) }, &{} {\text {if}}\,\,\, y_j^i>t^i \\ 0, &{} {\text {otherwise}} \end{array}\right. }. \end{aligned}$$

(14)

Thus for $i=1,\ldots ,n$, if $I^i=j$, fix $y_j^i=t^i$, otherwise for all other $1\le i \le N$, one needs to generate an $y^i_j$ according to the p.d.f. given in Eq. (14), which can be done in at least two different ways. The first is a straight-forward rejection method in which one keeps generating observations from $\text {N}\left( {\mathbf s_{j}^{i}}'\varvec{\theta }_{j},\sigma _{j}^2\right)$ until it is greater than $t^i$. The second is a univariate inversion method in which one numerically inverts the integral of $\pi (y^i_j|\varvec{\psi }_j,{\mathscr {D}})$ given in Eq. (14). The later method is numerically more efficient for large $t^i$.

This generated $\mathbf y_j$ is augmented to ${\mathscr {D}}$ to form the complete data ${\mathscr {Y}}$, so that samples may be drawn from $\pi \left( \varvec{\psi }_j|{\mathscr {Y}}\right)$, which is given by

$$\begin{aligned} \pi \left( \varvec{\psi }_j|{\mathscr {Y}}\right)\propto & {} L_j\left( \varvec{\psi }_j|{\mathscr {Y}}\right) \pi \left( \varvec{\psi }_j\right) , \end{aligned}$$

where $L_j\left( \varvec{\psi }_j|{\mathscr {Y}}\right)$ is the likelihood function of $\varvec{\psi }_j$ based on the complete data ${\mathscr {Y}}$ and $\pi (\varvec{\psi }_j)$ is the prior p.d.f. of $\varvec{\psi }_j$. By Eq. (1),

$$\begin{aligned}&L_j\left( \varvec{\psi }_j|\mathscr {Y}\right) =\prod _{i=1}^{N}\frac{1}{\sigma _j}\phi \left( \frac{y_j^i-{\mathbf s_j^i}'\varvec{\theta }_j}{\sigma _j}\right) \nonumber \\&\propto \sigma _j^{-N}\exp \left\{ -\frac{1}{2\sigma _j^2}(\mathbf y_j-\mathbf S_j\varvec{\theta }_j)'(\mathbf y_j-\mathbf S_j\varvec{\theta }_j)\right\} , \end{aligned}$$

(15)

where $\mathbf {S}_j=[{\mathbf s_j^1},\ldots ,{\mathbf s_j^N}]'$ is the $N \times K$ stress matrix corresponding to component j.

Now the prior $\pi (\varvec{\psi }_j)$ is specified as follows. It is first assumed that $\sigma _j^2 \sim \text {Inverse Gamma}\left( \alpha _j,\beta _j\right)$ a priori, i.e.,

$$\begin{aligned} \pi (\sigma _j^2)\propto (\sigma _j^2)^{-\alpha _j-1}\displaystyle \exp \left( -\frac{\beta _j}{\sigma _j^2}\right) , \,\,\,\sigma _j^2>0. \end{aligned}$$

Then it is assumed that $\varvec{\theta }_j|\sigma _j^2\sim \text {N}_{K}\left( \varvec{\zeta }_j,\sigma _j^2\mathbf P_j^{-1}\right)$ a priori, i.e.,

$$\begin{aligned} \pi \left( \varvec{\theta }_j|\sigma _j^2\right) \propto \left( \sigma _j^2\right) ^{-\frac{K}{2}}\exp \left\{ -\frac{1}{2\sigma _j^2}\left[ (\varvec{\theta }_j -\varvec{\zeta }_j)'\mathbf P_j(\varvec{\theta }_j-\varvec{\zeta }_j) \right] \right\} . \end{aligned}$$

Thus it is assumed that the joint prior p.d.f. of $\varvec{\psi }_j$ is given by

$$\begin{aligned} \pi \left( \varvec{\psi }_j\right) \propto \left( \sigma _j^2\right) ^{-\alpha _j-\frac{K}{2}-1}\exp \left\{ - \frac{1}{2\sigma _j^2} \left[ 2\beta _j+(\varvec{\theta }_j -\varvec{\zeta }_j)'\mathbf P_j(\varvec{\theta }_j-\varvec{\zeta }_j)\right] \right\} . \end{aligned}$$

(16)

Apart from conjugacy with (15), (16) also allows a user to reasonably specify his or her prior opinion about the unknown model parameters (see Gelman et al. 2013, pp. 376–378). The prior hyper-parameters may be chosen as outlined in Sect. 3.2 with the restriction of normal distribution, but here one also has an opportunity to model a priori dependence among the model parameters. With $\tau _j=(\sigma _j^2)^{-1/2}$, the non-informative prior (11) in this case [also as is standard with the likelihood in Eq. (15), see Gelman et al. (2013, p. 355)] becomes

$$\begin{aligned} \pi \left( \varvec{\psi }_j\right) \propto \frac{1}{\sigma _j^2}, \end{aligned}$$

(17)

which can be easily modeled by choosing $\alpha _j=-K/2$, $\beta _j=0$ and $\mathbf P_j=0$ in (16). Note that unlike the extreme-value case, here the posterior of $\varvec{\psi }_j$ given ${\mathscr {D}}$ with the non-informative prior in Eq. (17) is proper (i.e., $\int \pi (\varvec{\psi }_j|{\mathscr {D}})\mathrm {d}\varvec{\psi }_j < \infty$) provided (i) $n_j>K$ and (ii) the rank of ${\mathbf S}_j$ is K [this is because the $\overline{\varPhi }(\cdot )$ terms in Eq. (13) are bounded by 1 and the rest follows as in Gelman et al. (2013, p. 356)].

Now by Eqs. (15) and (16),

$$\begin{aligned} \pi \left( \varvec{\psi }_j|{\mathscr {Y}}\right) \propto \left( \sigma _j^2\right) ^{-\frac{2\alpha _j+N+K}{2}-1} \exp \Big \{-\frac{1}{2\sigma _j^2}\Big [\Big (\varvec{\theta }_j -\varvec{\eta }_j\Big )'\mathbf {V}_j \Big (\varvec{\theta }_j-\varvec{\eta }_j\Big )+C_j(\mathbf y_j)\Big ]\Big \}, \end{aligned}$$

where $\mathbf V_j=({\mathbf S_j}'\mathbf S_j+\mathbf P_j)$, $\varvec{\eta }_j= \mathbf V_j^{-1}({\mathbf S_j}'\mathbf y_j+\mathbf P_j\varvec{\zeta }_j)$ and $C_j(\mathbf y_j)= 2\beta _j+{\mathbf y_j}'\mathbf y_j+{\varvec{\zeta }_j}'\mathbf P_j\varvec{\zeta }_j-{\mathbf \eta _j}'\mathbf V_j\mathbf \eta _j$. Thus we have $\varvec{\theta }_j|\sigma _j^2, {\mathscr {Y}} \sim \text {N}_{K}(\mathbf \eta _j, \sigma _j^2 V_j^{-1})$ and $\sigma _j^2| {\mathscr {Y}} \sim$ Inverse Gamma $(\frac{2\alpha _j+N}{2}, \frac{1}{2}C_j(\mathbf y_j))$. In order to generate a $\varvec{\psi }_j$ from $\pi (\varvec{\psi }_j|{\mathscr {Y}})$, first generate a $\sigma _j^2$ from the inverse gamma distribution with parameters $(2\alpha _j+N)/2$ and $C_j(\mathbf y_j)/2$; then with that $\sigma _j^2$, generate a $\varvec{\theta }_j$ from the K-variate normal distribution with mean $\mathbf \eta _j$ and variance–covariance matrix $\sigma _j^2 V_j^{-1}$.

Implementation of Gibbs sampling involves iterative sampling from $\pi (\mathbf y_j|\varvec{\psi }_j,{\mathscr {D}})$ and $\pi (\varvec{\psi }_j|{\mathscr {Y}})$. Starting with an initial value $\varvec{\psi }_j^{(0)}$, for $l\ge 0$, one iteratively draws (i) $\mathbf y_j^{(l+1)}$ from $\pi \left( \mathbf y_j|\varvec{\psi }_j^{(l)}, {\mathscr {D}}\right)$ and (ii) $\varvec{\psi }_j^{(l+1)}$ from $\pi \left( \varvec{\psi }_j|{\mathscr {Y}}^{(l+1)}\right)$, where ${\mathscr {Y}}^{(l+1)}=\left\{ \mathbf y_j^{(l+1)},{\mathscr {D}}\right\}$. This yields a Markov chain $\left\{ \left( \mathbf y_j^{(l)},\varvec{\psi }_j^{(l)}\right) , l\ge 1\right\}$, which produces an observation from $\pi \left( \mathbf y_j,\varvec{\psi }_j|{\mathscr {D}}\right)$ in the limit. Thus generated $\{\varvec{\psi }_j^{(l)}\}_{l=1}^L$ can now be used for further Bayesian analyses as detailed in Sect. 3.3.

Since from this point on the discussion is in numerical lines, at the outset it is worth commenting on one detail regarding the collection of (Gibbs) sample from $\pi (\varvec{\psi }|{\mathscr {D}})$ or $\pi (M|{\mathscr {D}})$ (where M is a model variable). In the numerical implementations we employ a long chain strategy (of typically 1,001,000 elements) with a burn-in (of typical size 1000) and a thinning interval (of typical size 200) resulting in a Gibbs sample (of size 5000). The exact values of these parameters are determined following the MCMC convergence diagnostic tests reviewed by Cowles and Carlin (1996), which are readily available in the R-library CODA.

4.3 Simulation study

This sub-section presents a simulation study examining the performance of different Bayesian point estimates of lifetime parameters of the independent log-normal model. The basic set up of the simulation study, such as the stress variable, its levels, the number of systems allocated at each level of the stress variable in the ALT, the STF, etc. is borrowed from the electrical insulation system example of Sect. 1.

For convenience, it is assumed that the series system has two failure modes. Now suppose ($N\!\!\!=$) 40 such two-component series systems are put on an ALT at four elevated temperature levels of 423.15, 443.15, 463.15 and 493.15 K with equal number of systems allocated at each level of temperature. It is assumed that none of the ALT observations is censored, implying that the exact failure times are available for all the systems. As in the insulation system example (see Nelson 1990, p. 394), the following Arrhenius model is used as the STF for both the failure modes:

$$\begin{aligned} \mu _j\left( \theta _{1j},\theta _{2j},T_K\right) =\theta _{1j} +\theta _{2j}\left( \frac{1000}{T_K}\right) , \end{aligned}$$

(18)

where $T_K$ is temperature measured in Kelvin (K). The simulation study is carried out with two different sets of parameter values namely

• Set 1: $\theta _{11}=-24.00$, $\theta _{21}=11.00$, $\theta _{12}=-22.00$, $\theta _{22}=10.00$, $\sigma _1=1.00$ and $\sigma _2=1.00$.

• Set 2: $\theta _{11}=-20.00$, $\theta _{21}=9.00$, $\theta _{12}=-18.00$, $\theta _{22}=8.00$, $\sigma _1=1.00$ and $\sigma _2=1.00$.

Bayesian analyses are performed using six different Inverse-Gamma–Normal priors of Eq. (16) with their means, variances and correlations as listed in Table 3. The prior hyper-parameters are chosen to have the prior means fixed at the respective true values (TVs) of the parameters for priors 2, 3 and 4 (with varying degree of prior variance), and misspecified by 20 % for priors 5 and 6. For the sake of brevity, here the simulation results are discussed only for the slope parameters $\theta _{2j}$s and the scale parameters $\sigma _j$s. The findings for the intercept parameters $\theta _{1j}$s are similar to that of the slope parameters.

Table 3 Prior parameters for simulation study ($j=1,2$)

The simulation is carried out for 200 times. Tables 4, 5, 6 and 7 respectively report the average posterior mean (Avg mean), median (Avg median) and mode (Avg mode) of $\theta _{21}$, $\theta _{22}$, $\sigma _1$ and $\sigma _2$ along with their mean squared errors (MSEs) over the 200 simulations. Note that all these posterior point estimators are optimal under different symmetric loss functions. However in practice, sometimes overestimation of a lifetime parameter may be more serious than underestimation and vice versa. In such situations, one may use an asymmetric loss function like the LINEX loss function introduced by Zellner (1986). Thus Tables 4, 5, 6 and 7 also provide the average Bayes’ estimates under the LINEX loss function and the corresponding MSEs for $a=-1$ and 1, where a is as in Zellner (1986).

Table 4 Average Bayesian estimates (MSEs) of $\theta _{21}$

Table 5 Average Bayesian estimates (MSEs) of $\theta _{22}$

Table 6 Average Bayesian estimates (MSEs) of $\sigma _1$

Table 7 Average Bayesian estimates (MSEs) of $\sigma _2$

Observe that the performances of the posterior mean, median and mode of the slope parameters are almost identical under all the six priors for both sets of parameter values. When the prior means are correctly specified (i.e., for priors 2, 3 and 4), the Bayes’ estimates of the slope parameters under the LINEX loss function are clearly outperformed by the posterior mean, median and mode in all the cases. This is true even for the non-informative prior (i.e., prior 1). However, the Bayes’ estimates of the slope parameters under the LINEX loss function are clearly better than the corresponding posterior mean, median and mode, when the prior means are misspecified. When the prior means of $\theta _{21}$ and $\theta _{22}$ are over-specified as in prior 5, the Bayes’ estimates under the LINEX loss function for $a=1$ is better compared to others. This is expected since the LINEX loss function with $a=1$ penalizes overestimation more heavily than underestimation. Analogous observations may be made in case of prior 6 and $a=-1$. The biases and MSEs of all the Bayesian estimators of $\theta _{21}$ and $\theta _{22}$ are smaller under prior 3 compared to prior 2. Thus multivariate normal priors with non-zero correlation seem to perform better than independent normal priors for estimating the stress coefficients. Also as expected, the MSEs of the Bayesian estimators of $\theta _{21}$ and $\theta _{22}$ tend to go up with the increase in prior variances.

From Tables 6 and 7, it is evident that the posterior modes perform poorly compared to other point estimates of the population SDs. Unlike the slope (and intercept) parameters, curiously enough, here neither the priors nor the loss functions seem to exhibit the same expected (or even otherwise) effects on the posterior estimates.

The main purpose of performing an ALT is to predict reliability at usage stress, which is 403.15 K for the underlying example of this simulation study. Thus we also study the behavior of the posterior estimates of the mean component log-lifetimes $\mu _j$ as in (18) with $T=403.15$. The results are reported in Tables 8 and 9 from which conclusions similar to the ones for the slope parameters may be drawn. The simulation study is also repeated for $N=80$, resulting in qualitatively similar findings.

Table 8 Average Bayesian estimates (MSEs) of $\mu _1$

Table 9 Average Bayesian estimates (MSEs) of $\mu _2$

5 Data analysis

In this section, the methodologies developed in the previous two sections are illustrated by analyzing the real data set pertaining to the electrical insulation system introduced in Sect. 1. Though this system has three failure modes, due to lack of observations, like Pascual (2008, 2010) we drop the failure mode Phase and pay attention only to the remaining two failure modes Turn ($j=1$) and Ground ($j=2$). For computational ease, the system lifetimes are re-calibrated to $10^4$ hours. As in Sect. 4.3, here also the Arrhenius model given in (18) is used as the STF for both the failure modes. Now instead of assuming a particular lifetime model $f_j(\cdot )$ for the jth failure mode at the outset, since the developed methodology allows one to choose different probability distributions for different failure modes, we first attempt to resolve the issue of model selection for both Turn and Ground, based on the data ${\mathscr {D}}$.

5.1 Bayesian model selection

Though any one of the distributions of $X_j$ listed in Table 1 can serve as a possible candidate for an appropriate lifetime model for Turn or Ground, here for illustrative purpose, we consider only the three popular alternatives in the reliability literature, viz., exponential, Weibull and log-normal. Among the standard model selection methods that are currently available in the literature, two of the most popular ones are the Akaike information criterion (AIC) and the Bayes information criterion (BIC) (see Kadane and Lazar 2004, for example). Table 10 reports the maximized value of the log-likelihood, AIC and BIC for the three models for the two failure modes. Based on these preliminary numbers, though exponential can be clearly ruled out in favor of the other two, evidences for Weibull against log-normal are not so convincing. Thus the exponential model is dropped from further consideration.

Table 10 Preliminary comparison of goodness-of-fit for different models

The two criteria reported in Table 10 are “preliminary” in the sense that they have their own asymptotic interpretations for their validity as “goodness-of-fit” measures for model selection, despite possessing the attractive property of being independent of priors for the individual model parameters. The standard Bayesian criterion for assessing this is off course the BF (see Kass and Raftery 1995, for example), and thus concentration is now focused on obtaining the values of these BFs. Computation of BF has two related issues, namely the choice of priors and the integrals of the likelihoods with respect to them. While the second issue, though important, is essentially computational, the first issue of choice of prior is more critical (see Berger and Pericchi 1996, for example).

First of all the priors need to be proper. Since they also subsume the degree of knowledge about individual parameters of an underlying model, while comparing two models using a BF, it is crucial that the same level of information (be they correct or not, precise or not) is conveyed by the priors of the parameters of both the models. Towards this goal, the level of prior knowledge about a parameter value is similized to its first two prior moments. Now in order to change the level of this knowledge, the prior means and SDs of all the involved parameters (of both the models—Weibull and log-normal for both Turn and Ground) are respectively varied through the three values of their MLEs and MLEs$\pm$ SEs, and SEs and SEs$*/$2, resulting in nine different choices for the prior hyper-parameters.

Once one has the prior means and SDs of the model parameters, the prior specification now proceeds as explained in Sect. 3.2. Specifically, independent normal priors for the stress coefficients of both the Weibull and log-normal models, and gamma and inverse-gamma priors respectively for the Weibull shape ($\beta _j$) and log-normal variance ($\sigma _j^2$), are used with their respective hyper-parameters matching their first two prior moments. Thus one now needs to compute nine BFs corresponding to the nine different priors (at any given instance, the priors of all the parameters for both the models should be fixed at the same level for fair comparison as explained above).

Laplace approximations of the integrals of products of likelihoods and priors, expressed in terms of the posterior modes and the Hessian of the log-posteriors, as in equation (4) of Kass and Raftery (1995), may be readily used to compute a BF for a given set of priors. Like the AIC and BIC, this approximation is theoretically valid only for large N, but 40, its value in the present example, may not be adequate for that (with 6 unknown parameters). Currently the most popular method of computing a BF to an arbitrary degree of accuracy (limited only to time and computing resources) for any N, is the reversible jump MCMC introduced by Green (1995). In this method, if one has already developed MCMC algorithms for the individual models (as in this article), the best way to exploit them would be to use them as part of the generation of proposal samples in the Metropolis–Hastings iteration of the reversible jump MCMC (see Godsill 2001, for further details). But an easier approach, in the sense of avoiding “rejection” in the Metropolis–Hastings, is offered by Carlin and Chib (1995) (CC henceforth) through a Gibbs sampling, which also incorporates the developed MCMC algorithms for the individual models within it. However the CC approach requires one to specify, what they call “pseudo-priors”. Following their suggestion as well as that of Godsill (2001), here we use multivariate normal approximations (with posterior moments) of the joint posteriors of the parameters of the “other” model as pseudo-priors in their equation (2), together with equal prior probabilities for both the Weibull and log-normal models, denoted by $\pi (W)=\pi (L)=1/2$. Equation (1) of CC is same as sampling from the posteriors of the Weibull and log-normal model parameters, which can be done following the methods developed in Sects. 3, 4 and elsewhere.

We compute the nine BFs using this CC method, which we call CCBF henceforth, for all the nine priors mentioned above. Along with the CCBF for each of the nine priors, BF is also calculated (with $\pi (W)=\pi (L)=1/2$ for both Turn and Ground) using the Laplace approximation mentioned above. Both these BFs for log-normal versus Weibull for Turn and Ground are reported in Table 11.

Table 11 CCBF (Laplace approximated BF) for log-normal versus Weibull

Note that there is a wide discrepancy between the CCBF and the Laplace approximation of the corresponding BF. Though very different, even in terms of the direction of the evidence in most cases, none of these BFs actually even “positively” supports one model over the other in case of Turn. Here we use words like “positive” or “strong” in accordance to the second table in Section 3.2 of Kass and Raftery (1995). This interpretation of the BF values in case of Ground however leads one to two different conclusions. While according to the Laplace approximations, there isn’t any evidence “worth more than a bare mention”, in favor of Weibull over log-normal; the CCBFs say that there is “positive” to “strong” evidence in favor of log-normal over Weibull. Thus according to the Laplace approximations, there is no clear choice between the two models for either of the failure modes, while the CCBFs suggest the log-normal model for Ground. Hence for the purpose of illustration, we present Bayesian analyses for Turn and Ground under Weibull and log-normal model respectively.

5.2 Bayesian analyses

Through out this sub-section and the next, we work with normal priors for the stress coefficients of both the Weibull and log-normal models. The means and SDs of these normal priors are assumed to be respectively same as the MLE and SE of the corresponding parameters (i.e. the same prior as case (2,2) of Table 11). The corresponding priors for the Weibull-$\beta _j$ and log-normal-$\sigma _j^2$ are also assumed to be same as case (2,2) of Table 11. In the sequel, this prior is referred as prior-2 for both the Weibull and log-normal models. For the log-normal model, prior-1 is same as the non-informative prior given in (17), while for Weibull, prior-1 refers to $\pi (\theta _{11})\propto 1$, $\pi (\theta _{21})\propto 1$ and $\beta _1\sim \text {Gamma}(29.80,5.47)$.

Table 12 presents posterior mean, median, mode and Bayes’ estimates under the LINEX loss function for $\theta _{11}$, $\theta _{21}$ and $\beta _1$, the Weibull lifetime parameters for Turn. Table 12 also provides the posterior SDs and $95\,\%$ Highest Posterior Density Credible Sets (HPDCS). The posterior p.d.f.s of the model parameters are plotted in Fig. 1. Note that for both the priors, the Bayesian point estimates of the slope parameter $\theta _{21}$ is positive and their $95\,\%$ HPDCS exclude 0. This is suggestive of the fact that the mean log-lifetime of Turn reduces as the temperature increases.

Fig. 1

Density estimates of marginal posteriors of the lifetime parameters for turn

Table 12 Posterior summary measures for turn

Similarly the posterior p.d.f.s of the log-normal parameters $\theta _{12}$, $\theta _{22}$ and $\sigma _2$ for Ground are plotted in Fig. 2, and their posterior mean, median, mode, Bayes’ estimates under the LINEX loss function, SD and 95 % HPDCS are reported in Table 13. Note that here also, as expected,temperature seems to reduce the mean log-lifetime.

Fig. 2

Density estimates of marginal posteriors of the lifetime parameters for ground

Inferences on particular distributional parameters are meaningful if and only if the distribution is adequately supported by the data. In this case as seen in Sect. 5.1, neither the Weibull nor the log-normal model is “positively” supported by the data against each other for Turn. Though there is “positive” to “strong” evidence in favor of log-normal against Weibull for Ground, it will not be correct to behave as if one is “hundred percent certain” that it is so. That is, in either case there are uncertainties regarding the model—in case of Turn it is acute, much less for Ground. In such situations where there are model uncertainties, proper Bayesian inferences can still be drawn about different model-independent aspects of life distributions, which are indeed the quantities of actual interest in an ALT rather than the model parameters themselves, through Bayesian Model Averaging or BMA (see Hoeting et al. 1999, for example).

Table 13 Posterior summary measures for ground

5.3 Bayesian model averaging

In the context of ALT of series systems, where one is finally concerned with drawing inferences about reliability characteristics at usage stress, examples of such model-independent quantities of interest include component MTTF and component and system failure s.f. at usage stress. The component MTTFs for the jth component at usage stress are given by $e^{{\mu _j} (\theta _{1j},\theta _{2j},403.15)} \varGamma (1+1/\beta _j)$ and $e^{\mu _j(\theta _{1j},\theta _{2j},403.15)+\frac{1}{2}\sigma _j^2}$ for the Weibull and log-normal models respectively (where $\mu _j(\theta _{1j},\theta _{2j},403.15)$ is as in (18)). The expressions for component s.f. at usage stress in log-scale (for convenience of plotting) are similarly obtained from Table 1. Denoting these quantities by $\triangle (\varvec{\psi }_j,t)$ in Sect. 3.3, it was shown how to obtain a sample from the posterior distributions of such $\triangle (\varvec{\psi }_j,t)$s for a given fixed model, like Weibull (W) and log-normal (L). Now it will be convenient to denote them by $\triangle _W(t)$ and $\triangle _L(t)$ respectively. The uncertainties between W and L for drawing inference about $\triangle (t)$ are accounted through BMA as follows.

In the Bayesian paradigm, if one starts with prior model uncertainties given by $\pi (W)$ and $\pi (L)$ (here taken to be 1/2 each), in light of the observed data (and off course also the assumed priors on the individual model parameters), these uncertainties get naturally quantified by their respective posterior probabilities given by $\pi (W|{\mathscr {D}})$ and $\pi (L|{\mathscr {D}})$. The BFs reported in Table 11 are nothing but $\frac{\pi (L|{\mathscr {D}})/\pi (W|{\mathscr {D}})}{\pi (L)/\pi (W)}$ and thus here $\pi (L|{\mathscr {D}})=BF/(1+BF)$ and $\pi (W|{\mathscr {D}})=1-\pi (L|{\mathscr {D}})$. With model uncertainties thus quantified, it is now easy to see that this model-uncertainty-adjusted posterior of $\triangle (t)$ is just a mixture of posteriors of $\triangle _W(t)$ and $\triangle _L(t)$ with respective mixing proportions $\pi (W|{\mathscr {D}})$ and $\pi (L|{\mathscr {D}})$ (see, for example, equation (1) of Hoeting et al. (1999)). Thus a BMA sample of a $\triangle (t)$ (such as a component MTTF or s.f.) is easily obtained by first drawing a 0–1 valued random variate with $\text {Pr}(1)=\pi (W|{\mathscr {D}})$, and then drawing a sample from the posteriors of either $\triangle _W(t)$ or $\triangle _L(t)$, if it is 1 or 0 respectively. Such samples are needed for computation of a BMA HPDCS for $\triangle (t)$ for instance, but are not required if one is just interested in the first two BMA moments of $\triangle (t)$ (by using equations (18) and (19) of Kass and Raftery (1995), for example). For the later case it is enough to just have the value of $\pi (W|{\mathscr {D}})$ and samples from the posteriors of $\triangle _W(t)$ and $\triangle _L(t)$. The BMA mean, the Bayes’ estimate with respect to the squared error loss, is an important Bayesian estimate of $\triangle (t)$. For example, if $\triangle (t)$ denotes a component s.f. (or p.d.f. or c.d.f.), its BMA mean is same as its BMA predictive s.f. (or p.d.f. or c.d.f.).

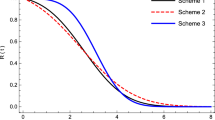
For the data set at hand, for illustrative purpose, we use the aforementioned prior-2 for both Weibull and log-normal. Recall that Gibbs samples from the respective posteriors of $\varvec{\psi }_j$s under this prior for both $j=1,2$ have already been obtained for computing the (2,2) entries of Table 11. At each of these sampled values we now compute $\triangle _W(t)$ and $\triangle _L(t)$ as in Sect. 3.3 to obtain samples from the posteriors of $\triangle _W(t)$ and $\triangle _L(t)$. Now the BMA sample generations and moment calculations, as explained above, are done using the (2,2) CCBFs of Table 11. The posterior densities of MTTF at usage stress for both Turn and Ground for both the models and their BMA counterparts are plotted in Fig. 3. The corresponding posterior summary measures are presented in Table 14. Figure 4 depicts the Weibull, log-normal and BMA predictive s.f. together with the BMA 95 % HPDCS band for the s.f. at usage stress for Turn and Ground.

Fig. 3

Posterior densities of MTTF at usage stress for Turn and Ground

Fig. 4

Predictive survival function at usage stress for Turn and Ground

Table 14 Posterior summary measures of MTTF at usage stress for Turn and Ground

We finish this section by estimating the system s.f. at usage stress. In this case, because of the assumed independence between the two failure modes, the BMA predictive system s.f. at usage stress is simply their product for each failure mode (which are already depicted in Fig. 4). A BMA sample of the system s.f. $\overline{F}_T(t)$ is generated by repeatedly, independently and randomly drawing one element each from the BMA samples of $\overline{F}_1(t)$ and $\overline{F}_2(t)$ and forming their product. This BMA sample on $\overline{F}_T(t)$ is then used to compute a BMA 95 % HPDCS band for $\overline{F}_T(t)$, which is plotted in Fig. 5, together with the BMA predictive system s.f. computed as explained above.

Fig. 5

Predictive survival function of motor at usage stress

6 Concluding remarks

This article presents full Bayesian analyses of fixed multi-stress ALT data of J-component series systems. It is assumed that the component log-lifetimes belong to independent arbitrary log-concave log-location-scale family of distributions. The location parameters of the component log-lifetimes are assumed to depend on the stress variables through a linear STF, which covers almost all the standard ones used in the engineering literature and practice, as special cases.

Next, a Bayesian methodology is developed for such generic log-concave log-location-scale family of component lifetime models. It is proved that the one-dimensional univariate conditional posteriors of each lifetime parameter given the rest is log-concave, provided the corresponding priors of these lifetime parameters are also log-concave. This fact is then utilized to carry out Bayesian analyses by drawing samples from the joint posterior of the model parameters via the ubiquitous Gibbs sampling. It is shown how the sample generated from the joint posterior of the lifetime parameters can be used for predictive inferences on the component and system reliability metrics at the usage stress, given fixed assumed models for component lifetimes.

Later this article focuses on the special case of log-normally distributed component lifetime, for its importance as a theoretical lifetime model, especially in the context of ALT. It is observed that for the log-normal model one can avoid computationally intensive log-concave sampling by adopting a data-augmentation scheme. A detailed simulation of the log-normal model reveal that there is hardly any difference in the performances of the posterior mean, median and mode of the stress coefficients and MTTF, provided the prior means are correctly specified. However if the prior means are misspecified, the Bayes’ estimates under LINEX loss may be a better choice. Furthermore it is also found that, in case of the SDs of the component log-lifetimes, the posterior modes perform poorly compared to other Bayesian point estimators, and the LINEX loss does not seem to exhibit the same expected (or otherwise) influence like in case of the location parameters.

Next the developed methodology is illustrated by analyzing a real data set pertaining to the electrical insulation system of a motor with two failure modes. First as is tacit in the rest of the article, an effort is made to choose a “correct” model for the two failure mode lifetimes based on the BFs. After not being able to conclusively arrive at such a “correct” model for at least one of the failure-modes (while for the other failure mode, curiously enough arriving at the log-normal model, having a special section in this article), subsequent Bayesian analyses of quantities of interest from a series system ALT are carried out using Bayesian model averaging.

Thus this article now provides methods of performing Bayesian analyses of fixed multi-stress series system ALT data, with standard models that are expected to be encountered in practice. However there are still issues such as objective criteria, utilization of prior information etc. for optimally planning or designing such fixed multi-stress ALTs. There are both design and analyses issues with other types of ALTs which are not fixed stress such as the step-stress ALT (Nelson 1980). These are a few future directions, research towards which will be fruitful and appreciated by reliability practitioners, apart from off course theoretical developments with dependent component lives or more complex systems.

Appendices

Appendix 1: Proof of Theorem 1

It is enough to show that $\log L_j\left( \varvec{\psi }_j|{\mathscr {D}}\right)$ ($=\ell _j\left( \varvec{\psi }_j|{\mathscr {D}}\right)$, say) is a concave function of $\theta _{kj}$ and $\tau _j$. From Eq. (8), one gets

$$ \begin{aligned} \ell _j\left( \varvec{\psi }_j|{\mathscr {D}}\right)= & {} n_j \log \tau _j + \displaystyle \sum _{\begin{array}{c} 1 \le i \le n\\ \& I^i=j \end{array}} \log f_j\left( {\tau _j}\left( t^{i}-{\mathbf s_j^i}'\varvec{\theta }_{j}\right) \right) \\&+ \displaystyle \sum _{\begin{array}{c} 1 \le i \le n\\ \& I^i \ne j \end{array}}\log \overline{F}_j\left( {\tau _{j}}\left( t^i-{\mathbf s_j^i}'\varvec{\theta }_j\right) \right) \\&+ \sum _{i=n+1}^N \log \overline{F}_j\left( {\tau _{j}}\left( t^i-{\mathbf s_j^i}'\varvec{\theta }_j\right) \right) , \end{aligned}$$

which implies

$$ \begin{aligned} \frac{\partial ^{2} \ell _j\left( \varvec{\psi }_j|{\mathscr {D}}\right) }{\partial \theta _{kj}^2}= & {} \displaystyle \sum _{\begin{array}{c} 1 \le i \le n\\ \& I^i=j \end{array}} \left( -\tau _j s_{kj}^i\right) ^2 \,\,\frac{\partial ^{2} \log f_j(u_j^i)}{\partial {u_{j}^i}^2} + \displaystyle \sum _{\begin{array}{c} 1 \le i \le n\\ \& I^i \ne j \end{array}} \left( -\tau _j s_{kj}^i\right) ^2 \,\,\frac{\partial ^{2} \log \overline{F}_j(u_j^i)}{\partial {u_{j}^i}^2}\\&+ \sum _{i=n+1}^N \left( -\tau _j s_{kj}^i\right) ^2 \,\,\frac{\partial ^{2} \log \overline{F}_j(u_j^i)}{\partial {u_{j}^i}^2}, \end{aligned}$$

and

$$ \begin{aligned} \frac{\partial ^{2} \ell _j\left( \varvec{\psi }_j|{\mathscr {D}}\right) }{\partial \tau _j^2}= & {} -\frac{n_j}{\tau _j^2} + \displaystyle \sum _{\begin{array}{c} 1 \le i \le n\\ \& I^i=j \end{array}} \left( \frac{u_j^i}{\tau _j}\right) ^2 \,\,\frac{\partial ^{2} \log f_j(u_j^i)}{\partial {u_{j}^i}^2} + \displaystyle \sum _{\begin{array}{c} 1 \le i \le n\\ \& I^i \ne j \end{array}} \left( \frac{u_j^i}{\tau _j}\right) ^2 \,\,\frac{\partial ^{2} \log \overline{F}_j(u_j^i)}{\partial {u_{j}^i}^2} \\&+ \sum _{i=n+1}^N \left( \frac{u_j^i}{\tau _j}\right) ^2 \,\,\frac{\partial ^{2} \log \overline{F}_j(u_j^i)}{\partial {u_{j}^i}^2}, \end{aligned}$$

where $u_j^i=\tau _j\left( t^i-{\mathbf s_j^i}'\varvec{\theta }_j\right)$. Note that $\frac{\partial ^{2} \log f_j(u_j^i)}{\partial {u_{j}^i}^2}<0$, since $f_j(\cdot )$ is log-concave. Furthermore, the log-concavity of $f_j(\cdot )$ implies the same for $\overline{F}_j(\cdot )$ (see Basu et al. 2003). Thus, $\frac{\partial ^{2} \log \overline{F}_j(u_j^i)}{\partial {u_{j}^i}^2}<0$. Therefore, $\frac{\partial ^{2} \ell _j\left( \varvec{\psi }_j|{\mathscr {D}}\right) }{\partial \theta _{kj}^2}< 0$ and $\frac{\partial ^{2} \ell _j\left( \varvec{\psi }_j|{\mathscr {D}}\right) }{\partial \tau _j^2}<0$, which completes the proof.

Appendix 2: Acronyms and notations

BF:

Bayes’ factor

BMA:

Bayesian Model Averaging

h.r.:

Hazard rate

MCMC:

Markov Chain Monte Carlo

MLE:

Maximum likelihood estimate

MTTF:

Mean time to failure

p.d.f.:

Probability density function

SD:

Standard deviation

SE:

Standard error

s.f.:

Survival function

J, j :

Number of components in series system and dummy in $\{1,\ldots ,J\}$

K, k :

Number of stress variables and and dummy in $\{1,\ldots ,K\}$

N, i :

Number of systems put on an ALT and dummy in $\{1,\ldots ,N (n)\}$

n :

Number of failed systems in an ALT

$X_j$, $Y_j$ :

Lifetime and log-lifetime of the jth component

T, I :

System log-lifetime and cause of failure

${\mathbf Z}=(Z_1,\ldots ,Z_K)'$ :

$K\times 1$ vector of stress variables

U, u :

A variable U and its observed value with or without an i in the super-script (like $U^i$ or $u^i$) for the ith system

$f(\cdot |\cdot )$, $\overline{F}\left( \cdot |\cdot \right)$, $h\left( \cdot |\cdot \right)$ :

p.d.f., s.f., and h.r. of random variables

$g_{kj}(\cdot )$ :

Known transformation of the kth stress variable acting on the jth component of the system

${\mathbf s_j}=(s_{1j},\ldots ,s_{Kj})'\, \text {with}\,\, s_{kj}=g_{kj}(z_k)$ :

$K\times 1$ vector of transformed stress variables for the jth component

$\mathbf S_j={[\mathbf s_j^1,\ldots ,\mathbf s_j^N]}'$ :

$N \times K$ stress matrix corresponding to component j

$\phi (\cdot )$, $\overline{\varPhi }(\cdot )$ :

p.d.f. and s.f. of the standard normal distribution

$\varvec{\theta }_j=(\theta _{1j},\ldots ,\theta _{Kj})'$, $\varvec{\theta }=(\theta _1',\ldots ,\theta _J')'$ :

$K\times 1$ and $KJ\times 1$ vectors of STF parameters for the jth component and system

$\mu _{j}(\varvec{\theta }_{j}, \mathbf {z})$, $\tau _j$, $\sigma _j^2$ :

STF (location) and scale parameters of $Y_j$ and its variance when normal

$\varvec{\psi }_j=(\varvec{\theta }_j',\tau _j)'$, $\varvec{\psi }=(\varvec{\psi }_1',\ldots ,\varvec{\psi }_J')'$ :

$(K+1)\times 1$ and $(KJ+J)\times 1$ vectors of lifetime parameters for the jth component and system

$\triangle$ :

A model-independent quantity

${\mathscr {D}}$, $\mathscr {Y}_j$, ${\mathscr {Y}}$ :

Observed, augmented and complete data

$L_j\left( \varvec{\psi }_j|{\mathscr {D}}\right)$, $L_j(\varvec{\psi }_j|{\mathscr {Y}})$, $L\left( \varvec{\psi }|{\mathscr {D}}\right)$ :

Likelihood function of $\varvec{\psi }_j$ and $\varvec{\psi }$ given ${\mathscr {D}}$ or ${\mathscr {Y}}$

$\pi (\cdot ), \pi (\cdot |{\mathscr {D}}), \pi (\cdot |{\mathscr {Y}})$ :

Prior and posterior of relevant quantities usually clear from the context