1 Introduction

Tolerances are the most important information in product design, manufacturing, and verification; and they play responsible and decisive key roles in product development [1]. Tolerance allocation is an important link in design engineering, which is closely related to product structural design and parameter design. In general, after the structural design of a product is completed, the assembly tolerances need to be determined based on the functionality and assemblability requirements of the product, and then, these required assembly tolerances need to be reasonably allocated to the design and process tolerances. The traditional tolerance allocation process is divided into two relatively independent stages: product design tolerance allocation and part process tolerance allocation [2]. In the former stage, assembly tolerances are allocated to the design dimensions of relevant parts according to the given design criteria (such as the minimum manufacturing cost criterion). In the later stage, the part design tolerances are assigned to the relevant process dimensions according to the process planning and design criteria of the parts. This serial tolerance allocation mode will prolong product design and production cycles, lead to the irrationality of product design and the possibility of cross-stage rework, and cause the increase of product manufacturing costs and the decline of market competitiveness. Instead of the serial tolerance allocation mode, the concurrent tolerance allocation mode is the integration of upstream design tolerance allocation and downstream process tolerance allocation. This mode can improve product design efficiency, shorten product development cycles, and reduce product manufacturing costs.

A looser tolerance means that it is less difficult to machine and test the part, which will reduce the manufacturing cost of the machined part, but it can lead to poor product quality and low customer satisfaction, while a tighter tolerance will bring higher product quality and better customer satisfaction, but the tighter tolerance makes it necessary for the part to require more sophisticated production equipment and testing instruments, which will lead to higher production and testing cost [3]. Instead of just considering the looser tolerance settings to reduce production and testing cost, the best policy is to consolidate manufacturing cost and quality loss in the same optimization objective to obtain the most excellent balance between product satisfaction and manufacturing cost [4, 5]. Early studies on concurrent tolerancing scarcely considered the influence of quality loss caused by product quality degradation. The quality loss function proposed by Taguchi quantitatively evaluates the quality loss caused by product quality characteristics deviating from its design target [6]. And it has become an important design philosophy to integrate Taguchi’s quality loss function into the total cost model of concurrent tolerance design [7]. Jeang [8,9,10] proposed a tolerance optimization model in which the combined manufacturing costs, quality loss, rework costs, and waste costs are minimized, and the constraints of functionality, product quality requirements, and process capability limits are considered. Subsequently, a lot of research has been carried out on the concurrent optimization tolerance allocation problem, which takes the minimization of manufacturing cost and quality loss as the objective function, and various optimization methods are adopted to obtain the optimal design and process tolerances. Al-Ansary and Deiab [11] presented a procedure to concurrently allocate both design and machining tolerances based on minimum total machining cost using the genetic algorithms method. Singh et al. [12] also reported an optimization approach using genetic algorithms and applying the penalty function approach for concurrently selecting design and manufacturing tolerances. Rout and Mittal [13] introduced a differential evolution optimization algorithm to simultaneously determine optimal parameters and tolerances, and the comparative test results show that the differential evolution algorithm converges faster compared to the genetic algorithm. Sivakumar et al. [14] proposed a method of using the NSGA-II (elitist non-dominated sorting genetic algorithm) and MOPSO (multi-objective particle swarm optimization) algorithms to achieve the simultaneous optimal allocation of design and manufacturing tolerances and alternative process selection. Lu et al. [15] investigated a game theory approach for concurrent tolerance design that simultaneously achieves lower manufacturing costs and good product assemblability. Previous studies on concurrent tolerance allocation mostly focused on minimizing manufacturing cost, quality loss, or a combination of both and paid scarce attention to the sequence of product operations. With this in mind, Geetha et al. [16] developed a genetic algorithm-based method for simultaneously allocating the component’s tolerance and determining the best product sequence of the scheduling. Kumar et al. [17] developed the bat algorithm to achieve the concurrent optimal tolerance design based on a concurrent objective to minimize the manufacturing cost, quality loss, and present worth of expected quality loss.

Although geometric tolerances have a significant impact on the functional requirement, fit quality, interchangeability, and other aspects of parts, studies on geometric tolerance allocation are rarely reported in the literature due to the complexity of their applications and the diversity of their items [18]. Along with the further perfection of the geometric tolerance specifications in the new generation of GPS and the more and more extensive application of geometric tolerances, it is necessary to consider both dimensional tolerances and geometric tolerances in concurrent tolerance allocation to ensure the functional requirements of the product. It has become a critical issue in computer-aided tolerancing for how to achieve tolerance allocation involving geometric tolerances, and some related studies have been carried out. Saravanan et al. [19] introduced a geometric tolerance framework based on assembly function requirement and sensitive factor and illustrated the application of the proposed framework for optimal geometric tolerance design through a case study. Andolfatto et al. [20] proposed a methodology for selecting assembly techniques and allocating part geometric tolerances by minimizing a cost indicator and maximizing a quality indicator. Huang and Zhong [21] investigated a concurrent tolerance optimization method for assigning the assembly functional tolerances to the process dimensional and geometrical tolerances by maximizing the summation of weight process tolerances of related operations. Some studies involved the application of material conditions associated with dimensional and geometrical tolerances. Wu [22] introduced a correlational design method for the dimension tolerance and geometric tolerance of the feature of size when applying the material conditions. Peng and Chang [23] presented a new approach to statistical geometrical tolerance analysis when applying the material conditions based on the combination of the unified Jacobian-Torsor model and Monte Carlo simulation.

It can be seen that most studies in literature mainly focus on the concurrent optimal allocation of dimensional tolerances, without taking geometric tolerances into account; some studies have involved geometric tolerances, but ignored the balance between product manufacturing cost and customer satisfaction. The main purpose of this study is to extend the concurrent tolerance allocation model to achieve concurrent hybrid tolerance allocation of dimensional tolerances and geometrical tolerances. Firstly, Sect. 2 discusses how to convert geometric tolerances with dimensional tolerance attributes into equivalent linear dimensions and tolerances when dimensional tolerances and geometrical tolerances are independent of each other. Then, on the basis of studying the function relationship between product manufacturing cost and process tolerances, expected quality loss, and process tolerances, a concurrent tolerance allocation model is established. Finally, the nonlinear programming technique encapsulated in MATLAB R2014b is employed to solve this optimization model to obtain the optimized design and process tolerances, achieving concurrent hybrid tolerance allocation of dimensional tolerances and geometrical tolerances.

2 Conversion of geometrical tolerance

According to ISO1101 [24], the commonly used geometrical tolerances are classified into five types: form, profile, orientation, position, and run-out. Different kinds of geometric feature characteristics are limited by different geometric tolerances, and the form tolerance can only limit the shape characteristics of the feature; the orientation tolerance can limit both the orientation and shape characteristics of the feature, whereas position tolerance can simultaneously limit the position characteristics, direction characteristics, and shape characteristics of the feature.

Not all geometrical tolerances have equivalent dimensions and tolerances. The geometrics for form and orientation specify only local characteristics and can only be modeled as additional tolerance constraints, whereas the geometrical tolerance terms that prescribe the location of the exact dimension can be converted to equivalent external tolerances [25].

2.1 Profile tolerance

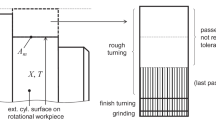
The profile tolerance is employed to limit the variations of any line/surface. The profile tolerance zone of any surface is limited by two surfaces enveloping spheres of diameter Tpr, the centers of which are situated on the surface having the true geometrical form.

As shown in Fig. 1, the profile tolerance Tpr can be converted into equivalent linear dimensions and tolerances; it is expressed as:

$$X\pm {T}_{pr}/2$$
(1)

where X is the theoretically exact dimension.

Fig. 1
figure 1

Conversion of profile tolerance

Full size image

2.2 Coaxiality tolerance

The coaxiality tolerance is used to limit the concentric variations of the actual feature relative to the datum feature. The coaxiality tolerance zone for a point is limited by a circle of diameter TC, the center of which coincides with the datum point; the coaxiality tolerance zone for an axis is limited by a cylinder of diameter TC, the axis of which coincides with the datum axis.

As shown in Fig. 2, the coaxiality tolerance can be converted into equivalent linear dimensions and tolerances on two mutually perpendicular coordinate axes. If TC is the coaxiality tolerance and \({\sum }_{i}^{p}{T}_{ji}\) is the accumulated process tolerances, then \({\sum }_{i}^{p}{T}_{ji}\) must be less than or equal to coaxiality tolerance TC. That is:

$$\sum_{i}^{p}{T}_{ji}\le {T}_{C}$$
(2)

where Tji is the process tolerance of process size xji related to the coaxiality tolerance, and p is the number of relevant production processes.

Fig. 2
figure 2

Conversion of coaxiality tolerance

Full size image

2.3 Symmetry tolerance

The symmetry tolerance is a location tolerance used to limit the symmetry variations of the actual measured feature with respect to the datum median feature. The tolerance zone is limited by two parallel planes a distance Tsy apart and disposed symmetrically to the median plane with respect to the datum axis or datum plane.

As shown in Fig. 3, if Tsy is the symmetry tolerance, the accumulated tolerances \({\sum }_{i}^{p}{T}_{ji}\) must be less than or equal to the specified symmetry tolerances. It is expressed as:

$$\sum_{i}^{p}{T}_{ji}\le \frac{{T}_{sy}}{2}$$
(3)

where Tji is the process tolerance of process size xji related to the symmetry tolerance, and p is the number of relevant production processes.

Fig. 3
figure 3

Conversion of symmetry tolerance

Full size image

2.4 Positional tolerance

The positional tolerance is employed to limit the location variations of actual (extracted) feature relative to the ideal feature with a theoretically exact position; the position of ideal feature is determined by the datums and the theoretically exact dimensions. The positional tolerance zone is a symmetric region centered on the theoretically exact position. The positional tolerance zone of a point is the inner region of a sphere with a diameter of tolerance Tpo, the center of which is determined by the theoretically exact dimensions relative to the datums. The positional tolerance zone of a line is limited by a cylinder of diameter Tpo, the axis position of which is determined by the datum planes and the theoretically exact dimensions. The positional tolerance zone of a flat surface is limited by two parallel planes a distance Tpo apart and disposed symmetrically with respect to the theoretically exact position which is determined by the datum plane, datum axis, and the theoretically exact dimensions.

Since positional tolerance is related to locations, it can be converted to equivalent linear dimensions and tolerances [26]. Figure 4 shows how positional tolerance can be converted into equivalent dimension tolerance that can be integrated into the dimensional tolerance chain. As shown in Fig. 4, the positional tolerance of the hole with respect to datums A and B is Tpo; the equivalent linear dimensional tolerances in two mutually perpendicular directions are Tpo·cos45° and Tpo·sin45°, respectively. Therefore, the conversion model of positional tolerance can be expressed as:

$$X\pm \frac{{T}_{po}}{2\sqrt{2}}$$
(4)

where X is the basic dimension, and Tpo is positional tolerance.

Fig. 4
figure 4

Conversion of positional tolerance

Full size image

2.5 Remaining geometrical tolerances

The remaining geometrical tolerances (such as run-out tolerances, form tolerances, and orientation tolerances) can be integrated into the concurrent tolerancing model as additional constraints. Specifically, these geometric tolerances should be less than or equal to the pertinent process tolerances:

$${T}_{g}\le {T}_{ji}$$
(5)

where Tg denotes geometric tolerance; Tji denotes bilateral tolerance of process dimension xji associated with the geometric tolerance.

According to the above discussions, only four geometrical tolerances, namely profile tolerance, coaxiality tolerance, symmetry tolerance, and positional tolerance directly affect the process tolerance chains and should be converted into equivalent dimensional tolerances; the remaining geometric tolerances can be modeled as additional machining constraints.

3 Machining cost-process tolerance model

The tolerances directly affect the functionalities of a product and the production cost of the machined parts. The literature research shows that tremendous studies on the mathematical modeling of cost-tolerance relations have already been done in the past. Different cost-tolerance models have been developed based on empirical production cost-tolerance data from commonly used machining processes [27]. Several widely used cost-tolerance models are the Exponential Model, the Reciprocal Squared Model, the Reciprocal Powers Model, the Combined Reciprocal Powers and Exponential Model, the Reciprocal Powers and Exponential Hybrid Model, the Reciprocal Model, the Discrete Cost-Tolerance Model, the Improved Exponential Model, the Combined Linear and Exponential Model, the Cubic Polynomial Model, Fourth Order Polynomial Model, etc.

Assuming that the machining cost of obtaining process tolerance Tji in the ith machining operation for the jth part feature is:

$${c}_{ji}=C({T}_{ji})$$
(6)

So, the total manufacturing cost is the sum of the machining costs of all machining processes:

$$\begin{array}{cc}MC\left({T}_{ji}\right)=\sum_{j=1}^{q}\sum_{i=1}^{p}C({T}_{ji})& \begin{array}{cc}i=\text{1,2},\cdots ,p;& j=\text{1,2},\cdots ,q\end{array}\end{array}$$
(7)

where C(Tji) is the function relation formula between machining cost and process tolerance Tji; q is the number of part features; p is the number of machining operations of the jth part feature.

For example, the widely used reciprocal powers and exponential hybrid model recommended by Dong et al. [27], is expressed as follows:

$$C\left({T}_{ji}\right)={a}_{0}+{a}_{1}{T}_{ji}^{-{a}_{2}}+{a}_{3}{e}^{-{a}_{4}{T}_{ji}}$$
(8)

where a0, a1, a2, a3, and a4 can be determined using the least squares approximation method based on the empirical cost-tolerance data of common machining processes.

The one for face milling:

$$C\left({T}_{ji}\right)=0.00001+0.00001{T}_{ji}^{-1.836}+455.3{e}^{-18.24{T}_{ji}}$$
(9)

The one for drilling and hole machining:

$$C\left({T}_{ji}\right)=0.00001+\text{5.326}{T}_{ji}^{-0.4475}+6.652{e}^{-11.72{T}_{ji}}$$
(10)

The one for turning on lathe:

$$C\left({T}_{ji}\right)=0.005228+0.36{T}_{ji}^{-0.9044}+63.39{e}^{-2.531{T}_{ji}}$$
(11)

The one for rotary surface grinding:

$$C\left({T}_{ji}\right)=39.03+17.90{T}_{ji}^{-0.00001}+30.84{e}^{-63.47{T}_{ji}}$$
(12)

In addition, Hu and Xiong [28] proposed the following practical production cost-tolerance models based on the empirical cost-tolerance data frequently used in machining processes.

The model for position tolerance of cylindrical feature:

$$C\left({T}_{ji}\right)=8.052+0.00001{T}_{ji}+30.87{e}^{-12.09{T}_{ji}}$$
(13)

The model for perpendicularity tolerance:

$$C\left({T}_{ji}\right)=5.425+0.00001{T}_{ji}+12.43{e}^{-10.82{T}_{ji}}$$
(14)

4 Quality loss–process tolerances relation

Generally, the functional requirements of a product are often determined by several assembly functional parameters. Assuming that the kth assembly functional parameter zk (k = 1, 2, …, r) can be expressed as a function of q part design parameters, that is:

$${z}_{k}={g}_{k}({y}_{i},{y}_{2},\cdots ,{y}_{q})$$
(15)

where yj (j = 1, 2, …, q) is the jth part design parameter.

By expanding Eq. (15) using the Taylor series and omitting second-order and higher-order terms, the deviation value of assembly feature parameter zk can be expressed as:

$${\delta }_{{z}_{k}}={z}_{k}-{m}_{k}=\sum_{j=1}^{q}\left(\frac{{\partial g}_{k}}{{\partial y}_{j}}\right){\delta }_{{y}_{j}}$$
(16)

where mk is the target value of feature parameter zk, \({m}_{k}={g}_{k}(\overline{y })\); δyj denotes the deviation of parameter yj from its mean value \({\overline{y} }_{j}\), that is \({\delta }_{{y}_{j}}={y}_{j}-{\overline{y} }_{j}\).

Lee and Tang [29] extended Taguchi’s quality loss function and recommended a general format for evaluating the quality loss of products with multiple correlated characteristics as follows:

$$L\left({z}_{k}\right)=\sum_{k=1}^{r}\sum_{l=1}^{k}{B}_{kl}({z}_{k}-{m}_{k})({z}_{l}-{m}_{l})$$
(17)

where Bkl is the quality loss constant. The expected quality loss for batch products can be written as [4]:

$$QL\left({z}_{k}\right)=\sum_{k=1}^{r}{B}_{kk}\left[{\sigma }_{{z}_{k}}^{2}+{\delta }_{{z}_{k}}^{2}\right]+\sum_{k=2}^{r}\sum_{l=1}^{k-1}{B}_{kl}\left[{\sigma }_{{z}_{k}{z}_{l}}^{2}+{\delta }_{{z}_{k}}{\delta }_{{z}_{l}}\right]$$
(18)

where \({\sigma }_{{z}_{k}}^{2}\) is the variance of parameter zk; \({\sigma }_{{z}_{k}{z}_{l}}^{2}\) is the covariance between parameters zk and zl.

In the product design stage, it is assumed that both the product assembly parameter variations and the part design parameter variations follow normal distribution. The variance and covariance of product assembly parameters can be expressed by using the statistical theory as follows:

$${\sigma }_{{z}_{k}}^{2}=\sum_{j=1}^{q}{\left(\frac{{\partial g}_{k}}{{\partial y}_{j}}\right)}^{2}{\sigma }_{{y}_{j}}^{2}$$
(19)
$${\sigma }_{{z}_{k}{z}_{l}}^{2}=\sum_{j=1}^{q}\left(\frac{{\partial g}_{k}}{{\partial y}_{j}}\right)\left(\frac{{\partial g}_{l}}{{\partial y}_{l}}\right){\sigma }_{{y}_{j}}^{2}$$
(20)

where \({\sigma }_{{y}_{j}}^{2}\) is the variance of parameter yj.

Under normal production conditions, it can be assumed that the variation of the machined dimension exhibits a symmetrical normal distribution with respect to its mean value. The tolerance zone of the machined dimension lies within the interval [− 3σ, + 3σ] around the mean value (σ is the standard deviation), the corresponding part has a qualified rate of 99.73% [30], and then we have:

$${\sigma }_{{y}_{j}}^{2}={\left(\frac{{T}_{j}}{3}\right)}^{2}$$
(21)

where Tj is the bilateral tolerance of yj.

In the part processing stage, the part design parameter yj can also be expressed as a function of the process dimension xji (i = 1, 2, …, p), as follows:

$${y}_{j}={f}_{j}({x}_{j1},{x}_{j2},\cdots ,{x}_{jp})$$
(22)

where xji is the ith process dimension of yj, including the geometric tolerance terms with nominal process dimensions of zero; p is the number of production processes of part design parameter yj.

Under stable machining conditions, assume that all machined dimensions xji are normally distributed, similarly:

$${\sigma }_{{y}_{j}}^{2}=\sum_{i=1}^{p}{\left(\frac{{\partial f}_{i}}{{\partial x}_{ji}}\right)}^{2}{\sigma }_{{x}_{ji}}^{2}$$
(23)
$${\delta }_{{y}_{j}}=\sum_{i=1}^{p}{\left(\frac{{\partial f}_{i}}{{\partial x}_{ji}}\right)}^{2}{\delta }_{{x}_{ji}}$$
(24)

where \({\sigma }_{{x}_{ji}}^{2}\) is the variance of process dimension xji; \({\delta }_{{x}_{ji}}\) denotes the deviation of process dimension xji from its mean value \({\overline{x} }_{ji}\).

Substituting Eqs. (23) and (24) into Eqs. (19), (20), and (16), we get:

$${\sigma }_{{z}_{k}}^{2}=\sum_{j=1}^{q}{\left(\frac{{\partial g}_{k}}{{\partial y}_{j}}\right)}^{2}\sum_{i=1}^{p}{\left(\frac{{\partial f}_{j}}{{\partial x}_{ji}}\right)}^{2}{\sigma }_{{x}_{ji}}^{2}$$
(25)
$${\sigma }_{{z}_{k}{z}_{l}}^{2}=\sum_{j=1}^{q}\left(\frac{{\partial g}_{k}}{{\partial y}_{j}}\right)\left(\frac{{\partial g}_{l}}{{\partial y}_{j}}\right)\sum_{i=1}^{p}{\left(\frac{{\partial f}_{j}}{{\partial x}_{ji}}\right)}^{2}{\sigma }_{{x}_{ji}}^{2}$$
(26)
$${\delta }_{{z}_{k}}=\sum_{j=1}^{q}\left(\frac{{\partial g}_{k}}{{\partial y}_{j}}\right)\sum_{i=1}^{p}\left(\frac{{\partial f}_{i}}{{\partial x}_{ji}}\right){\delta }_{{x}_{ji}}$$
(27)

imilar to Eq. (21), we have:

$${\sigma }_{{c}_{ji}}^{2}={\left(\frac{{T}_{ji}}{3}\right)}^{2}$$
(28)

where Tji is the bilateral tolerance of process dimension xji.

Substituting Eqs. (21) and (28) into Eq. (23) yields the functional relationship equation between design tolerance and process tolerances as follows:

$${T}_{j}^{2}=\sum_{i=1}^{p}{\left(\frac{{\partial f}_{j}}{{\partial x}_{ji}}\right)}^{2}{T}_{ji}^{2}$$
(29)

Substituting Eq. (28) into Eqs. (25) and (26) yields the variance and covariance expressions of product functional parameters expressed as the functions of process tolerance Tji as follows:

$${\sigma }_{{z}_{k}}^{2}=\sum_{j=1}^{q}{\left(\frac{{\partial g}_{k}}{{\partial y}_{j}}\right)}^{2}\sum_{i=1}^{p}{\left(\frac{{\partial f}_{j}}{{\partial x}_{ji}}\right)}^{2}{\left(\frac{{T}_{ji}}{3}\right)}^{2}$$
(30)
$${\sigma }_{{z}_{k}{z}_{l}}^{2}=\sum_{j=1}^{q}\left(\frac{{\partial g}_{k}}{{\partial y}_{j}}\right)\left(\frac{{\partial g}_{l}}{{\partial y}_{j}}\right)\sum_{i=1}^{p}{\left(\frac{{\partial f}_{j}}{{\partial x}_{ji}}\right)}^{2}{\left(\frac{{T}_{ji}}{3}\right)}^{2}$$
(31)

By substituting Eqs. (30) and (31) into Eq. (18), the expected quality loss equation expressed as the function relationship of process tolerance Tji can be obtained.

5 Concurrent tolerance optimization model

In this section, the existing concurrent tolerance allocation model is extended to achieve concurrent hybrid tolerance allocation of dimensional tolerances and geometrical tolerances. In the extended model, the objective function is to minimize the total cost of the product (including the manufacturing cost and the expected quality loss), which is the function of pertinent process tolerances. The constraint conditions include the product function constraints, geometric tolerance constraints, and the economical process tolerance range constraints.

5.1 Objective function

The objective function of the optimization model is to minimize the sum of expected quality loss and manufacturing cost:

$$\mathit{min}\{QL\left({\text{T}}_{\text{ji}}\right)+MC({\text{T}}_{\text{ji}})\}$$
(32)

where QL(Tji) and MC(Tji) are the expected quality loss and manufacturing cost of the product, respectively, both of which can be formulated as the functions of pertinent process tolerances.

5.2 Constraint conditions

  • (1) Product function constraints

    The concurrent tolerance stack-up constraints based on the WC (worst-case) model:

    $$\sum_{j=1}^{q}\sum_{i=1}^{p}{\left|\frac{{\partial g}_{k}}{{\partial y}_{j}}\right|}_{\overline{y} }\left.\cdot {\left.\frac{{\partial f}_{j}}{{\partial x}_{ji}}\right|}_{\overline{x} }\right|{T}_{ji}\le {T}_{{z}_{k}}$$
    (33)

    where \({T}_{{z}_{k}}\) is the upper tolerance limit of product functional parameter zk.

  • (2) Geometrical tolerance constraints

    As mentioned in the previous section, only profile tolerance, coaxiality tolerance, symmetry tolerance, and positional tolerance can be directly converted into equivalent dimensional tolerances. The remaining geometrical tolerances, such as flatness, straightness, roundness, perpendicularity, and parallelism, can be regarded as additional machining constraints, that is, the geometrical tolerances should not be greater than the related process tolerances.

  • (3) Economical process tolerance range constraints

    $${T}_{ji}^{-}\le {T}_{ji}\le {T}_{ji}^{+}(j=\text{1,2},\cdots ,q,i=\text{1,2},\cdots ,p)$$
    (34)

    where \({T}_{ji}^{-}\) and \({T}_{ji}^{+}\) are the lower and upper tolerance limits of process tolerance Tji, respectively.

6 Illustrative example

As shown in Fig. 5, the concurrent tolerance allocation of a bevel gear assembly is taken as an example to illustrate the application of the proposed model and verify its effectiveness. This bevel gear assembly consists of housing 1, bearing-end covers 2 and 8, bearings 3 and 7, shaft 4, bevel gear 5, bushing 6 and adjusting gaskets, etc.

Fig. 5
figure 5

The bevel gear assembly

Full size image

The nominal design dimensions of this assembly have been assigned (unit, mm), and two critical assembly function parameters should be satisfied to guarantee the product function requirements (reliability, sealing, etc.). The critical gap z1 between housing 1 and cover 2 must be not less than 0.15 mm and not more than 0.65 mm to maintain the axial preload between bearing 3 and cover 2. The axial deviation z2 of the cone tops of two bevel gears must be located in the interval [− 0.036, + 0.036] to ensure the correct engaging position of the two bevel gears. In the bilateral tolerance system, two critical assembly function parameters will be z1 = 0.4 ± 0.25 mm and z2 = 0 ± 0.036 mm, respectively. The following work is to optimally allocate the critical tolerances of z1 and z2 determined by these two assembly function requirements to the related process tolerances. Assume that when critical parameters z1 and z2 deviate from their nominal vectors with values \(\underline{\boldsymbol D}^{(1)}=\lbrack\begin{array}{cc}\underline D_1^{\left(1\right)}&0\end{array}\rbrack^T=\lbrack{\begin{array}{cc}0.25&0\end{array}\rbrack}^T\), \(\underline{\boldsymbol D}^{(2)}=\lbrack{\begin{array}{cc}0&\underline D_2^{\left(2\right)}\end{array}\rbrack}^T=\lbrack{\begin{array}{cc}0&0.036\end{array}\rbrack}^T\) and \(\underline{\boldsymbol D}^{(3)}=\lbrack{\begin{array}{cc}\underline D_1^{\left(3\right)}&\underline D_2^{\left(3\right)}\end{array}\rbrack}^T=\lbrack{\begin{array}{cc}0.15&0.025\end{array}\rbrack}^T\) will cause product failure and result in a quality loss of $200. The quality loss constants can be calculated using the method proposed by Peng [4].

$${{\varvec{B}}}_{11}=\frac{{{\varvec{Q}}}^{(1)}}{{\left({\underset{\_}{{\varvec{D}}}}_{1}^{(1)}\right)}^{2}}=\frac{200}{{0.25}^{2}}=3200$$
$${{\varvec{B}}}_{22}=\frac{{{\varvec{Q}}}^{(2)}}{{\left({\underset{\_}{{\varvec{D}}}}_{2}^{(2)}\right)}^{2}}=\frac{200}{0.{036}^{2}}=154321$$
$$\begin{array}{c}{{\varvec{B}}}_{12}={{\varvec{B}}}_{21}=\frac{{{\varvec{Q}}}^{(3)}-{{\varvec{Q}}}^{(1)}{\left({\underset{\_}{{\varvec{D}}}}_{1}^{(3)}\right)}^{2}/{\left({\underset{\_}{{\varvec{D}}}}_{1}^{(1)}\right)}^{2}-{{\varvec{Q}}}^{(2)}{\left({\underset{\_}{{\varvec{D}}}}_{2}^{(3)}\right)}^{2}/{\left({\underset{\_}{{\varvec{D}}}}_{2}^{(2)}\right)}^{2}}{2\cdot {\underset{\_}{{\varvec{D}}}}_{1}^{(3)}\cdot {\underset{\_}{{\varvec{D}}}}_{2}^{(3)}}\\ =\frac{200-200\times {0.15}^{2}/{0.25}^{2}-200\times {0.025}^{2}/{0.036}^{2}}{2\times 0.15\times 0.025}\\ =4206.37\end{array}$$

6.1 The expected quality loss

Since z1 and z2 are two important characteristics to guarantee this assembly performance, it is not difficult to identify two critical assembly dimension chains, whose equations formulated as the functions of part design dimensions are as follows:

$${z}_{1}={g}_{1}\left({y}_{j}\right)=-{0.5y}_{1}+{y}_{2}+0.5\left({y}_{3}+{y}_{4}+{y}_{5}+{y}_{6}+{y}_{7}\right)$$
$${z}_{2}={g}_{2}\left({y}_{j}\right)={y}_{8}-{0.5y}_{1}$$

where y3 and y7 are the widths of bearing 3 and bearing 7, respectively, the tolerance effects of which are not considered in the following analysis.

According to Eq. (16), the deviation equations of these two critical assembly function parameters will be:

$${\delta }_{{z}_{1}}=-0.5{\delta }_{{y}_{1}}+{\delta }_{{y}_{2}}+0.5({\delta }_{{y}_{4}}+{\delta }_{{y}_{5}}+{\delta }_{{y}_{6}})$$
$${\delta }_{{z}_{2}}=-0.5{\delta }_{{y}_{1}}+{\delta }_{{y}_{8}}$$

Assuming that all part parameter variations follow a normal distribution, according to Eqs. (19) and (20), the variances and covariance of z1 and z2 will be:

$${\sigma }_{{z}_{1}}^{2}=0.25{\sigma }_{{y}_{1}}^{2}+{\sigma }_{{y}_{2}}^{2}+0.25({\sigma }_{{y}_{4}}^{2}+{\sigma }_{{y}_{5}}^{2}+{\sigma }_{{y}_{6}}^{2})$$
$${\sigma }_{{z}_{2}}^{2}=0.25{\sigma }_{{y}_{1}}^{2}+{\sigma }_{{y}_{8}}^{2}$$
$${\sigma }_{{z}_{1}{z}_{2}}^{2}=0.25{\sigma }_{{y}_{1}}^{2}$$

Figures 6, 7, 8, 9, and 10 show the related structures, critical dimensions, and machining datums for each machined part. The corresponding machining processes and economical process tolerance bounds for each machined part are listed in Table 1.

Fig. 6
figure 6

Critical dimensions and machining datums of housing 1

Full size image
Fig. 7
figure 7

Critical dimensions and machining datums of cover 2

Full size image
Fig. 8
figure 8

Critical dimensions and machining datums of shaft 4

Full size image
Fig. 9
figure 9

Critical dimensions and machining datums of bevel gear 5

Full size image
Fig. 10
figure 10

Critical dimension and machining datums of bushing 6

Full size image
Table 1 Machining processes of parts
Full size table

According to the given machining processes of parts, six machining equations can be written as:

$${y}_{1}={f}_{1}\left({x}_{1i}\right)={x}_{12}+{x}_{pe1}-{x}_{13}+{x}_{pe2}$$
$${y}_{2}={f}_{2}\left({x}_{2i}\right)={x}_{pe3}+{x}_{23}+{x}_{pe4}$$
$${y}_{4}={f}_{4}\left({x}_{4i}\right)=-{x}_{42}+{x}_{r1}+{x}_{43}-{x}_{44}+{x}_{r2}$$
$${y}_{5}={f}_{5}\left({x}_{5i}\right)={x}_{52}+{x}_{r3}-{x}_{53}+{x}_{r4}$$
$${y}_{6}={f}_{6}\left({x}_{6i}\right)={x}_{62}+{x}_{r5}-{x}_{63}+{x}_{r6}$$
$${y}_{8}={f}_{8}\left({x}_{8i}\right)={x}_{14}$$

where x14 is a theoretically exact dimension with no tolerance; T14 is converted from positional tolerance Tpo.

So using Eq. (23), one has:

$${\sigma }_{{y}_{1}}^{2}={\sigma }_{{x}_{12}}^{2}+{{\sigma }_{{x}_{pe 1}}^{2}+\sigma }_{{x}_{13}}^{2}+{\sigma }_{{x}_{pe 2}}^{2}$$
$${\sigma }_{{y}_{2}}^{2}={\sigma }_{{x}_{pe 3}}^{2}+{\sigma }_{{x}_{23}}^{2}+{\sigma }_{{x}_{pe 4}}^{2}$$
$${\sigma }_{{y}_{4}}^{2}={\sigma }_{{x}_{42}}^{2}+{\sigma }_{{x}_{r1}}^{2}+{\sigma }_{{x}_{43}}^{2}+{\sigma }_{{x}_{44}}^{2}+{\sigma }_{{x}_{r2}}^{2}$$
$${\sigma }_{{y}_{5}}^{2}={\sigma }_{{x}_{52}}^{2}+{\sigma }_{{x}_{r3}}^{2}+{\sigma }_{{x}_{53}}^{2}+{\sigma }_{{x}_{r4}}^{2}$$
$${\sigma }_{{y}_{6}}^{2}={\sigma }_{{x}_{62}}^{2}+{\sigma }_{{x}_{r5}}^{2}+{\sigma }_{{x}_{63}}^{2}+{\sigma }_{{x}_{r6}}^{2}$$
$${\sigma }_{{y}_{8}}^{2}={\sigma }_{{x}_{14}}^{2}$$

And the functional relationship between the variance of part design parameter yj and its related process tolerances can be established by combining Eqs. (23) and (28).

$${\sigma }_{{y}_{1}}^{2}=\frac{1}{9}({T}_{{x}_{12}}^{2}+{T}_{{x}_{pe 1}}^{2}+{T}_{{x}_{13}}^{2}+{T}_{{x}_{pe 2}}^{2})$$
$${\sigma }_{{y}_{2}}^{2}=\frac{1}{9}({T}_{{x}_{pe3}}^{2}+{T}_{{x}_{23}}^{2}+{T}_{{x}_{pe4}}^{2})$$
$${\sigma }_{{y}_{4}}^{2}=\frac{1}{9}({T}_{{x}_{42}}^{2}+{T}_{{x}_{r1}}^{2}+{T}_{{x}_{43}}^{2}+{T}_{{x}_{44}}^{2}+{T}_{{x}_{r2}}^{2})$$
$${\sigma }_{{y}_{5}}^{2}=\frac{1}{9}({T}_{{x}_{52}}^{2}+{T}_{{x}_{r3}}^{2}+{T}_{{x}_{53}}^{2}+{T}_{{x}_{r4}}^{2})$$
$${\sigma }_{{y}_{6}}^{2}=\frac{1}{9}({T}_{{x}_{62}}^{2}+{T}_{{x}_{r5}}^{2}+{T}_{{x}_{63}}^{2}+{T}_{{x}_{r6}}^{2})$$
$${\sigma }_{{y}_{8}}^{2}=\frac{1}{9}{T}_{{x}_{14}}^{2}$$

Under the stable manufacturing condition, each process dimension variation will obey normal distribution, assuming that the distribution center of each process dimension is just equal to its nominal value. Thus, the variance and covariance of the assembly functional parameters can be formulated as the functions of the related process tolerances using Eqs. (19) and (20).

$$\begin{array}{c}{\sigma }_{{z}_{1}}^{2}=\frac{1}{36}({T}_{{x}_{12}}^{2}+{T}_{{x}_{pe1}}^{2}+{T}_{{x}_{13}}^{2}+{T}_{{x}_{pe2}}^{2})+\frac{1}{9}({T}_{{x}_{pe3}}^{2}+{T}_{{x}_{23}}^{2}+{T}_{{x}_{pe4}}^{2})\\ +\frac{1}{36}({T}_{{x}_{42}}^{2}+{T}_{{x}_{r1}}^{2}+{T}_{{x}_{43}}^{2}+{T}_{{x}_{44}}^{2}+{T}_{{x}_{r2}}^{2}+{T}_{{x}_{52}}^{2}+{T}_{{x}_{r3}}^{2})\\ +\frac{1}{36}({T}_{{x}_{53}}^{2}+{T}_{{x}_{r4}}^{2}+{T}_{{x}_{62}}^{2}+{T}_{{x}_{r5}}^{2}+{T}_{{x}_{63}}^{2}+{T}_{{x}_{r6}}^{2})\end{array}$$
$${\sigma }_{{z}_{2}}^{2}=\frac{1}{36}({T}_{{x}_{12}}^{2}+{T}_{{x}_{pe1}}^{2}+{T}_{{x}_{13}}^{2}+{T}_{{x}_{pe2}}^{2})+\frac{1}{9}{T}_{{x}_{14}}^{2}$$
$${\sigma }_{{z}_{1}{z}_{2}}^{2}=\frac{1}{36}({T}_{{x}_{12}}^{2}+{T}_{{x}_{pe1}}^{2}+{T}_{{x}_{13}}^{2}+{T}_{{x}_{pe2}}^{2})$$

By substituting the above three equations into Eq. (18), the expected quality loss will be:

$$\begin{array}{c}QL\text{(}{T}_{ji}\text{)}=4609.29({T}_{12}^{2}+{T}_{pe1}^{2}+{T}_{13}^{2}+{T}_{pe2}^{2})+17146.78{T}_{14}^{2}+355.56({T}_{23}^{2}+{T}_{pe3}^{2}+{T}_{pe4}^{2})\\ +88.89({T}_{42}^{2}+{T}_{r1}^{2}+{T}_{43}^{2}+{T}_{r2}^{2}+{T}_{44}^{2}+{T}_{52}^{2}+{T}_{r3}^{2}+{T}_{53}^{2}+{T}_{r4}^{2}+{T}_{62}^{2}+{T}_{r5}^{2}+{T}_{63}^{2}+{T}_{r6}^{2})\end{array}$$

6.2 The manufacturing cost

It should be noted that only the expected quality losses caused by variations of the machining characteristics interrelated with assembly functional requirements were considered in this example. Other machining characteristics were assigned the most economical tolerance values, the variations of which did not contribute to quality loss. The same considerations were appropriate for manufacturing costs. The summation of manufacturing costs of these considered machining characteristics is:

$$\begin{array}{c}MC({T}_{ji})=C({T}_{12})+C({T}_{pe1})+C({T}_{13})+C({T}_{pe2})+C({T}_{14})+C({T}_{po})\\ +C({T}_{21})+C({T}_{pe3})+C({T}_{23})+C({T}_{pe4})+C({T}_{42})\\ \begin{array}{c}+C({T}_{r1})+C({T}_{43})+C({T}_{r2})+C({T}_{44})+C({T}_{52})+C({T}_{r3})+C({T}_{53})\\ +C({T}_{r4})+C({T}_{62})+C({T}_{r5})+C({T}_{63})+C({T}_{r6})\end{array}\end{array}$$

where the cost function relation formulas C(T12) and C(T13) both adopt the cost-tolerance model of Eq. (9); C(T14) adopts the model of Eq. (10); C(T21), C(T42), C(T43), C(T44), C(T52), and C(T53) all adopt the model of Eq. (11); C(T23), C(T62), and C(T63) all adopt the model of Eq. (12); C(Tpo) adopts the model of Eq. (13); the remaining terms all adopt the model of Eq. (14).

6.3 The concurrent tolerance optimization model

Finally, the entire concurrent tolerance allocation problem of the bevel gear assembly will be formulated by the analyses above as:

$$\begin{array}{c}\text{min}\{\left[0.00002+0.00001\left({T}_{12}^{-1.836}+{T}_{13}^{-1.836}\right)+455.3\left({e}^{-18.24{T}_{12}}+{e}^{-18.24{T}_{13}}\right)\right]+\left[0.00001+5.326{T}_{14}^{-0.4475}+{6.652}^{-11.72{T}_{14}}\right]+[0.005228\times 6\\ +0.36\left({T}_{21}^{-0.9044}+{T}_{42}^{-0.9044}+{T}_{43}^{-0.9044}+{T}_{44}^{-0.9044}+{T}_{52}^{-0.9044}+{T}_{53}^{-0.9044}\right)+63.39({e}^{-2.531{T}_{21}}+{e}^{-2.531{T}_{42}}+{e}^{-2.531{T}_{43}}+{e}^{-2.531{T}_{44}}+{e}^{-2.531{T}_{52}}+{e}^{-2.531{T}_{53}})]\\ \begin{array}{c}+\left[39.03\times 3+17.90\left({T}_{23}^{-0.00001}+{T}_{62}^{-0.00001}+{T}_{63}^{-0.00001}\right)+30.84\left({e}^{-63.47{T}_{23}}+{e}^{-63.47{T}_{62}}+{e}^{-63.47{T}_{63}}\right)\right]+[8.052+0.00001{T}_{po}+30.87{e}^{-12.09{T}_{po}}]\\ +[5.425\times 10+0.00001\left({T}_{pe1}+{T}_{pe2}+{T}_{pe3}+{T}_{pe4}+{T}_{r1}+{T}_{r2}+{T}_{r3}+{T}_{r4}+{T}_{r6}\right)+4609.29\left({T}_{12}^{2}+{T}_{pe1}^{2}+{T}_{13}^{2}+{T}_{pe2}^{2}\right)+17146.78{T}_{14}^{2}\\ \begin{array}{c}+12.43({e}^{-10.82{T}_{pe1}}+{e}^{-10.82{T}_{pe2}}+{e}^{-10.82{T}_{pe3}}+{e}^{-10.82{T}_{pe4}}+{e}^{-10.82{T}_{r1}}+{e}^{-10.82{T}_{r2}}+{e}^{-10.82{T}_{r3}}+{e}^{-10.82{T}_{r4}}+{e}^{-10.82{T}_{r5}}+{e}^{-10.82{T}_{r6}})]\\ +355.56\left({T}_{23}^{2}+{T}_{pe3}^{2}+{T}_{pe4}^{2}\right)+88.89({T}_{42}^{2}+{T}_{r1}^{2}+{T}_{43}^{2}+{T}_{r2}^{2}+{T}_{44}^{2}+{T}_{52}^{2}+{T}_{r3}^{2}+{T}_{53}^{2}+{T}_{r4}^{2}+{T}_{62}^{2}+{T}_{r5}^{2}+{T}_{63}^{2}+{T}_{r6}^{2})\}\end{array}\end{array}\end{array}$$

Subjected to:

  • (1) Product function constraints

    The product functional constraints ensure that the process tolerance variations are within the range of product assembly functional requirements. Based on the worst-case model, we have the following tolerance Fstack-up constraints:

    $$0\le 0.5\left({T}_{12}+{T}_{pe1}+{T}_{13}+{T}_{pe2}\right)+{T}_{pe3}+ {T}_{23} +{T}_{pe4}+ 0.5\cdot ({T}_{42} +{T}_{r1}+ {T}_{43}+ {T}_{44}+{T}_{r2}+ {T}_{52}+{T}_{r3}+ {T}_{53}+{T}_{r4}+ {T}_{62}+{T}_{r5}+ {T}_{63}+{T}_{r6}) \le 0.50$$
    $$0\le 0.5({T}_{12} +{T}_{pe1} + {T}_{13} +{T}_{pe2})+ {T}_{14} \le 0.072$$

  • (2) Geometrical tolerance constraints:

    Based on the analysis in the previous section, we get the following geometric tolerance constraints, in which tolerance T14 of the theoretically exact dimension x14 is converted from the position tolerance Tpo.

    $$\begin{array}{cc}{T}_{pe 1}\le {T}_{12}& {T}_{r3}\le {T}_{52}\end{array}$$
    $$\begin{array}{cc}{T}_{pe2}\le {T}_{13}& {{\varvec{T}}}_{{\varvec{r}}4}\le {{\varvec{T}}}_{53}\end{array}$$
    $$\begin{array}{cc}{T}_{pe3}\le {T}_{21}& {T}_{r5}\le {T}_{62}\end{array}$$
    $$\begin{array}{cc}{T}_{pe4}\le {T}_{23}& {T}_{r6}\le {T}_{63}\end{array}$$
    $$\begin{array}{cc}{T}_{r1}\le {T}_{42}& {T}_{po}/\sqrt{2}={T}_{14}\end{array}$$
    $${T}_{r2}\le {T}_{44}$$

  • (3) Economical process tolerance range constraints

    For each machining process, the following economical process tolerance ranges should be met:

    $$\begin{array}{cc}0.019 \le {T}_{12} \le 0.048& 0.027 \le {T}_{43} \le 0.070\end{array}$$
    $$\begin{array}{cc}0.010 \le {T}_{pe1} \le 0.030& 0.010 \le {T}_{r2} \le 0.025\end{array}$$
    $$\begin{array}{cc}0.019 \le {T}_{13} \le 0.048& 0.016 \le {T}_{44} \le 0.042\end{array}$$
    $$\begin{array}{cc}0.010 \le {T}_{pe2} \le 0.030& 0.016 \le {T}_{52} \le 0.042\end{array}$$
    $$\begin{array}{cc}0.015 \le {T}_{po} \le 0.040& 0.010 \le {T}_{r3} \le 0.025\end{array}$$
    $$\begin{array}{cc}0.019 \le {T}_{21} \le 0.048& 0.016 \le {T}_{53} \le 0.042\end{array}$$
    $$\begin{array}{cc}0.012 \le {T}_{pe3} \le 0.030& 0.010 \le {T}_{r4} \le 0.025\end{array}$$
    $$\begin{array}{cc}0.015 \le {T}_{23} \le 0.040& 0.011 \le {T}_{62} \le 0.030\end{array}$$
    $$\begin{array}{cc}0.010 \le {T}_{pe4} \le 0.020& 0.008 \le {T}_{r5} \le 0.020\end{array}$$
    $$\begin{array}{cc}0.016 \le {T}_{42} \le 0.042& 0.011 \le {T}_{63} \le 0.030\end{array}$$
    $$\begin{array}{cc}0.010 \le {T}_{r1} \le 0.025& 0.008 \le {T}_{r6} \le 0.020\end{array}$$

6.4 Solution and result

A program based on the proposed model has been developed in MATLAB R2014b to solve this nonlinear programming optimization problem, and the optimized process tolerances are listed in the middle column of Table 2. As a comparison, the optimized process tolerances from the model of Peng et al. [2] that did not consider geometric tolerances are listed in the last column of Table 2. By comparing the results, it indicates that the optimized process tolerances based on the proposed model are usually smaller than those based on the model without considering geometric tolerances, which is an inevitable result of considering the influence of geometric tolerances in concurrent tolerance allocation.

Table 2 Comparison of optimized process tolerances (mm)
Full size table

From Eq. (29), we get:

$${T}_{1}^{2}={T}_{12}^{2}+{T}_{pe1}^{2}+{T}_{13}^{2}+{T}_{pe2}^{2}$$
$${T}_{2}^{2}={T}_{pe3}^{2}+{T}_{23}^{2}+{T}_{pe4}^{2}$$
$${T}_{4}^{2}={T}_{42}^{2}+{T}_{r1}^{2}+{T}_{43}^{2}+{T}_{44}^{2}+{T}_{r2}^{2}$$
$${T}_{5}^{2}={T}_{52}^{2}+{T}_{r3}^{2}+{T}_{53}^{2}+{T}_{r4}^{2}$$
$${T}_{6}^{2}={T}_{62}^{2}+{T}_{r5}^{2}+{T}_{63}^{2}+{T}_{r6}^{2}$$
$${T}_{8}^{2}={T}_{14}^{2}$$

According to the above relation formulas, the optimized design tolerances of this bevel gear assembly are listed in the middle column of Table 3. For comparison, the optimized design tolerances from the model of Peng et al. [2] are listed in the last column of Table 3; without any doubt, the optimized design tolerance values based on the proposed model are not greater than those based on the model without considering geometric tolerances.

Table 3 Comparison of optimized design tolerances (mm)
Full size table

The example also indicates that the proposed model can achieve concurrent hybrid tolerance allocation of dimensional tolerances and geometrical tolerances.

7 Conclusions

The concurrent tolerance allocation model integrates the product design stage with the part machining stage to realize the simultaneous allocation of the process tolerances and the design tolerances of the part. Based on the mathematical expression of geometric tolerances, this study further extends this concurrent tolerance allocation model to consider geometric tolerance requirements. More specifically, geometrical tolerances associated with positional characteristics can be converted into equivalent dimensional tolerances. Other geometrical tolerances associated with shape or orientation characteristics are treated as additional geometrical constraints, and then equivalent dimensional tolerances and additional geometric constraints are integrated into the concurrent tolerancing model to achieve concurrent allocation of design and process tolerances containing geometrical tolerances. Finally, nonlinear optimization techniques are employed to minimize the summation of expected quality loss and manufacturing cost, and then, the optimized design and process tolerances are obtained.

Further research will be conducted on this model to address the concurrent tolerance allocation including the tolerancing principle associated with the dimensional and geometrical tolerances.