1 Introduction

Concurrent design attempts to organize the product realization process so as to increase the amount of information about a product's life cycle available at all stages of the design process. Sometimes, this is also referred to as Design for X, where X stands for the customer, manufacturing, quality, and so on. Tolerance is a bridge between design, manufacturing, and quality engineers, and as such it plays a key role in concurrent engineering. Ideally, one can imagine that the best technique for tolerance synthesis takes into account the coupling between design, manufacturing, and quality, for the sake of achieving a minimal total cost and reducing lead-time. However, in existing work on tolerance synthesis, this has not been the case.

Conventionally, tolerance synthesis is carried out in two stages: design and process planning. However, design engineers allocating design tolerances are often unaware of manufacturing processes and their production capabilities. This may be due to either a lack of communication between design engineers and process engineers, or a lack of knowledge of the manufacturing processes by the design engineers. The resulting process plans often cannot be executed effectively, or can only be executed at undesirably high manufacturing cost. When this happens, process engineers must modify the design tolerances.

Furthermore, manufacturing engineers who allocate processes must typically work within the tolerance limits set by design engineers; to do otherwise requires cycling through the design/process-planning loop and results in longer lead times. But in accepting tolerances set by design engineers, the process planners also limit the range within which they can set process tolerances. This, in turn, leads to tight process tolerances and higher manufacturing cost.

One well-used method for measuring quality is quality loss as introduced by Taguchi [16]. He proposed that performance degradation can be measured as a deviation from some target value, and asserted that the degradation can be related to a loss in value to the consumer called a quality loss. Taguchi emphasized that the level of a product's quality is not the same as the number of defective products; rather, it refers to the magnitude of societal losses. Even if a product is well within its specifications, it has a quality loss if its quality characteristic value is not at the ideal performance target. This loss is defined in monetary terms so that it can be compared to the product's manufacturing cost.

Tight tolerances are preferred to ensure product performance, which degrades as parts deviate from nominal values. However, tight tolerances imply higher manufacturing cost, so loose tolerances are preferred from a manufacturing perspective. This conflicting relation between the effect of tolerances on quality loss and on manufacturing cost make it very difficult to establish near-optimal tolerance specifications.

Unfortunately, all existing methods for tolerance synthesis of which the authors are aware either fail to consider quality loss (e.g. methods of tolerance synthesis for manufacturing) or are not concurrent engineering methods (e.g. quality-based methods). The purpose of the authors' work is to develop a new tolerance synthesis method, simultaneous tolerance synthesis for manufacturing and quality (STS), to achieve near-optimal tolerance allocation for dimensional tolerances (so far).

2 Literature review

A review of the recent literature suggests that existing techniques for tolerance synthesis can be grouped into three categories: traditional methods, methods focusing on manufacturing, and methods focusing on quality.

2.1 Traditional tolerance synthesis methods

Traditional tolerance synthesis methods are implemented separately in the design and the process planning stages. Some typical examples of these methods are found in [2, 9, 13, 15, 19]. All these models allocate tolerances in the design stage without considering manufacturing processes. Process planners are thus constrained to work with smaller ranges of possible process tolerance values, which lead to higher manufacturing costs. Wu et al. [20] compared the above models and concluded that models that defined cost as a combined (exponential/reciprocal power) function of tolerances (such as [9]) were the most accurate, followed by models based on exponential relations (such as [13]), and by models based on reciprocal relations (e.g. [14]).

2.2 Tolerance synthesis for manufacturing

In order to lower manufacturing cost, tolerances are assigned based on the particular sequencing of machining processes. Optimal tolerance allocation over multiple process alternatives has been treated by various researchers.

Ostwald and Huang [11] first formulated a technique for optimal tolerance allocation choosing one of possible many process alternatives. It used linear 0–1 integer programming, with cost as the objective function and design requirements as constraints. This technique is suitable where sequences and tolerances of operations are fixed. A similar model is that of Lee and Woo [8], in that tolerances are treated as process-specific, but this model uses a simplified stack-up condition and a more efficient branch-and-bound algorithm. As a result, its applicability was improved. Chase et al. [3] present three methods—exhaustive search, univariate search, and sequential quadratic programming—to solve the models originally proposed by Ostwald and Huang. The advantages and disadvantages of each approach are discussed. Nagarwala et al. [10] proposed a new slope-based method that took into account process selection. This method eliminates component-wise process selection, hence eliminating the generation of process combinations and improving efficiency.

All these models assume each component dimension is produced by only one process. The tolerance obtained from the process has a single fixed value. A cost is associated with each tolerance value. This assumption limits the model, however, because it rarely holds in practice.

Zhang and Wang [23] reported an analytical model for simultaneously allocating design and machining tolerances based on a criterion of least manufacturing cost. In their model, tolerance allocation is formulated as a nonlinear optimization problem based on cost-tolerance relationships. A simulated annealing algorithm is used to solve the optimization problem. Al-Ansary and Deiab [1] solved the same model using genetic algorithms; they found that genetic algorithms performed better than simulated annealing algorithms for solving nonlinear programming problems.

The model of Zhang and Wang is more practical than those previously mentioned because it allows single dimensions to be produced by multiple processes, and because the cost-tolerance function is treated as continuous rather than discrete. Because the model allows tolerances to be loosened—compared to the other models—it has been considered quite successful. However, it also fails to consider product quality, which degrades when tolerances are loosened.

2.3 Quality-based methods of tolerance synthesis

Taguchi [16] proposed that quality loss should be treated as a cost along with manufacturing cost. This quality loss measure represents the loss to society that occurs when a product deviates from the optimum set of design parameters. The deviations are controlled by tolerances. The quality loss function transforms the degradation into a cost to society that can then be included in an objective function along with manufacturing costs.

Kapur et al. [6] presented a general optimization model in terms of costs associated with variances of the components and losses associated with the variability from the quality characteristic target. They also derived formulae to calculate quality loss as a deviation from a norm.

Cook and DeVor [4] proposed a means of computing the quality loss function from their S-model of manufacturing. The model of Vasseur et al. [18] allocates tolerances based on profit maximization. The quality loss function is used to determine the reduction in value due to an off-target product, which is then balanced against reductions in manufacturing cost. Optimal profit occurred when the derivatives of the quality loss and manufacturing cost functions were equal, but only with respect to design tolerances and not manufacturing processes. Again, this introduces the likelihood that the manufacturing tolerances will be too tight as a result.

Soderberg [12] developed a quality loss function based on component lifetime. Total component lifetime represents the customer's objective, and a function is developed from physical relations between critical dimensions and lifetime. The total loss function for the customer is then determined by including component price.

Jeang [5] developed a few general mathematical models to determine product tolerances minimizing the combined manufacturing costs and quality losses (but not manufacturing processes), using quadratic and geometrical decay functions. The models were also formulated with multiple variables, which represented the set of characteristics of a part.

Krishnaswami and Mayne [7] presented a procedure to incorporate quality loss concepts into the optimal tolerance allocation process. Manufacturing cost and estimated quality loss were considered simultaneously.

Xue et al. [21] developed a method that uses functional performance rather than quality loss. They provided a method to jointly evaluate and optimize the combined effects. However, establishing a usable and accurate representation of the functional performance is difficult and requires further study.

Thornton [17] proposed a method of decision making that balances the cost of reducing variation against the cost of reworking parts. The cost of variation reduction is similar to Taguchi's quality loss function curve. The cost of rework is a traditional pass/fail measure. The method focuses on decision making rather than tolerance synthesis.

From this overview, it appears that models based on quality loss treat the design tolerance allocation problem without considering manufacturing processes and process tolerance allocation. The manufacturing cost function is based, in all the reviewed work, on a generic model in which the cost is a function of design tolerance. In that they do not consider manufacturing processes and process tolerance allocation, these tolerance allocation methods are not concurrent, but rather use a traditional sequential, iterative method.

Quality loss is used to limit the loosening of design tolerances. These models tend to allocate tight design tolerances to each component dimension in order to minimize quality loss. Their major drawback is that they cannot share the allocation of tolerances with downstream process-planning stages because they do not consider both manufacturing processes and process tolerance allocation in allocating design tolerances. If overly tight tolerances are assigned during design as a result, the manufacturing engineer will be forced to request changes that will increase product development lead time as well as increase the chance of error by complicating the overall design process.

3 STS method development

The literature review indicates that both traditional tolerance synthesis methods and methods based on quality loss tend to allocate tight tolerances, leading to higher manufacturing costs as a result of a lack of concurrency or a lack of consideration of both manufacturing processes and process tolerance allocation. Some methods (e.g. [23]) allow for loosening of process tolerances, but with the result of a relatively uncontrolled quality loss. A new method is needed that can simultaneously allocate tolerances to balance manufacturing cost and quality loss and thus optimize cost over the product's life.

In order to develop the simultaneous tolerance synthesis (STS) method, the following assumptions are adopted. These assumptions are consistent with assumptions made in papers surveyed in Sect. 2.

  1. 1.

    The design function can be retrieved and formulated from an assembly context. This function defines a relationship between a set of deviations in a dimension chain and a product performance characteristic. In this paper design function is assumed one-dimensional.

  2. 2.

    The resultant tolerance of a dimension chain is given. This is the functional tolerance, which comes from functional or customer requirements and is available from the outset of a design project.

  3. 3.

    A process plan for each dimension is given. In a concurrent engineering environment, it is commonplace to find manufacturing engineers developing process plans while designers are still detailing the product. Even with incomplete or unreliable information, a manufacturing engineer can estimate a process plan.

  4. 4.

    Each process has a normal distribution and is under statistical control. This allows six-sigma theory to be applied.

  5. 5.

    The dimensions in a dimension chain and the processes for each dimension are independent.

  6. 6.

    Only dimensional tolerances are treated.

These assumptions are made for two reasons. First, they simplify the implementation of the STS. At this time, our concern is to carry out a "proof-of-concept" implementation of simultaneous tolerance synthesis. These assumptions let us focus on the main point without having to also cope with the many other issues that would arise in their absence. Second, these assumptions are typical of those made in the other research surveyed in the preceding section and, as is indicated in that research, are not particularly onerous. Applications such as stamping dies, gear boxes, actuators, vehicle suspension systems, and so on can all be toleranced under these assumptions. Since STS has the same assumptions as other tolerance synthesis methods, their results are more directly comparable. This is a matter of some importance to the authors at this time: we must be able to demonstrate the relative merits of STS with respect to other methods. Maintaining the same set of assumptions as the other methods helps us to do just that. Indeed, we show that STS can provide significant cost savings over the lifetime of a product compared to a number of existing methods.

A special note is warranted with respect to assumption 3. Clearly, some iteration is needed between the designer and the manufacturing engineer to converge on an acceptable solution. In sequential design environments (i.e. where a concurrent method such as STS is not used), iteration arises from the mathematical requirements of the problem and from workflow inefficiencies due to ineffective information exchange between design and manufacturing engineers. In a concurrent environment (i.e. where a concurrent method like STS is used), there is at least an opportunity to eliminate completely the workflow inefficiencies. So while iteration can still be expected, the concurrency provided by STS will lower the expected number of iterations required to reach a solution.

3.1 Overview of STS method

The first step in developing the STS method is to identify those shortcomings in existing models that it should overcome. Traditional tolerance synthesis and quality loss-based tolerance synthesis are carried out in two stages. At the design stage, design tolerances are optimized with manufacturing cost as a constraint. Then, at the process planning stage, design tolerances are distributed to each operation, again constrained to minimum manufacturing cost. These methods have the following shortcomings:

  1. 1.

    Optimal design tolerances cannot be obtained at the design stage because realistic information about manufacturing cost is generally unavailable.

  2. 2.

    The actual manufacturing cost depends on the process(es) chosen, information about which the design engineer lacks during the design stage, unless the design engineer interacts with a manufacturing engineer. Even so, multiple iterations will generally be required before both stakeholders are satisfied.

  3. 3.

    There is no direct relation between the deviation of a product specification and its process tolerances, so design tolerances cannot be directly allocated to processes. Indirect relations, though usable in principle, tend to be very complex and prone to error, and thus difficult to use and manage.

  4. 4.

    Lead time is increased because of the serial and iterative nature of the methods.

The methods of tolerance synthesis for manufacturing, such as Zhang's method, allocate tolerances as loose as possible in order to lower manufacturing costs. These methods can cause large quality losses.

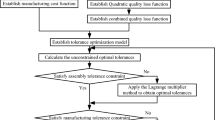
The STS method integrates the two steps of tolerance synthesis, providing a vehicle to implement concurrent engineering practice at the level of tolerance design. Through this parallelization, the STS method obviates the need for intermediate design tolerances, can significantly reduce lead-time, and achieves a balance between design function tolerances and process tolerances.

Tolerance synthesis can be formulated as an optimization problem. In order to implement this new method, an optimization model must be developed. In the model, the objective function is chosen as a combination of manufacturing cost and quality loss. By combining the two measures, the method seeks to balance them and achieve an overall minimum total cost over the product's lifetime. Design tolerance and process tolerance are taken as the decision variables in the model; manufacturing cost is a function of process tolerances, and quality loss is a function of design tolerances.

3.2 The optimization model

An explanation follows the mathematical statement of the model. The goal of the model is to minimize the total cost, written as

$$ C_{\rm{T}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^{p_i } {W_1 C\left( {tp_{ij} } \right) + W_2 k\sigma _y^2 ,} } $$
(1)

subject to the following constraints. The design function constraint in the statistical case is

$$ \sum\limits_{i = 1}^n {\left| {{{\partial f} \over {\partial x_i }}} \right|^2 t_{id}^2 \le T_{\rm{f}}^2 } , $$
(2)

and in the worst case is

$$ \sum\limits_{i = 1}^n {\left| {{{\partial f} \over {\partial x_i }}} \right|t_{id} \le T_{\rm{f}} } . $$
(3)

The operational constraint is

$$ \forall i,j\;\;tp_{ij} + tp_{ij - 1} \le Tp_{ij} . $$
(4)

The process capability constraint is

$$ tp_{ij}^{{\rm{min}}} \le tp_{ij} \le tp_{ij}^{{\rm{max}}} . $$
(5)

The relationship between design tolerance and manufacturing tolerance is given by

$$ tp_{ip_i } = t_{id} , $$
(6)

where

$$ \sigma _y^2 = \sum\limits_{i = 1}^n {\left( {{{\partial f} \over {\partial x_i }}} \right)^2 \left( {{{t_{id} } \over {3C_{pi} }}} \right)^2 ,} $$
(7)
$$ C_m (tp_{ij} ) = A_{ij} {\rm{e}}^{ - B_{ij} \left( {tp_{ij} - C_{ij} } \right)} + D_{ij} , $$
(8)
$$ k = {A \over {T_{\rm{f}}^2 }}. $$
(9)

3.2.1 Explanation of the objective function

The objective function minimizes the total cost of the simultaneous manufacturing cost and quality loss. The weights W 1 and W 2 are introduced to represent the relative importance of the two components of the objective function.

In manufacturing, tighter tolerances mean higher machining costs. Previous research in tolerance synthesis focused on cost–design tolerance models, wherein several manufacturing processes are combined to relate total machining cost and design tolerance. But since a single design tolerance is usually obtained through a series of machining operations, this simple combination may be insufficient to capture the actual cost-tolerance relationship with sufficient accuracy.

Developing more accurate models, however, can be very difficult. The models are design-dependent: each feature–tolerance combination can have a different model. Also, different manufacturing processes are needed to produce features with different tolerances. A good cost–tolerance model must reflect all the related production operations. Without prior knowledge of the manufacturing process of the part, it is not feasible to form an accurate cost–accuracy model at the design stage determined by the downstream production operations. The availability of cost–design tolerance models is a severe obstacle to the practical application of tolerance synthesis. At the manufacturing stage, however, very accurate cost–process tolerance models can be constructed because abundant empirical data exists for commonly used machining operations.

In the STS method, a cost–process tolerance function is adopted as the manufacturing cost component of the objective function. This avoids the inaccuracies of cost–design tolerance models, and permits direct distribution of functional tolerances to each process tolerance. The total manufacturing cost is then the sum of the manufacturing costs of each machining process of each component's dimension

$$ C_m \left( {tp_{ij} } \right)=\sum\limits_i^n {\sum\limits_{j = 1}^{p_i } C } \left( {tp_{ij} } \right), $$
(10)

where n is the number of dimensions in the dimension chain, p i is the number of processes to produce dimension i, and C(tp ij ) is the cost–tolerance function of the machining process. In this research, an exponential function is used to model cost–process tolerances, in keeping with best practice as discussed in the literature survey. For a particular manufacturing process, we have

$$ C_m \left( {tp_{ij} } \right) = A_{ij} {\rm{e}}^{ - B_{ij} \left( {tp_{ij} - C_{ij} } \right)} + D_{ij} . $$
(11)

Quality loss is quantified, per Taguchi, as a quadratic expression relating the loss to the variation of a product characteristic

$$ L(Y) = k(y - m)^2 , $$
(12)

where k=A/T f, A is the cost of replacement or repair if the dimension does not meet the tolerance requirements, T f is the functional tolerance requirement, m is the target value of the functional dimension, and y is the design characteristic.

We assume the functional dimension has a normal distribution and a mean at the target value. The quality loss can then be represented by the standard deviation of the functional dimension. Then, the expected value of the loss function can be written as

$$ QL = E\left( {L\left( Y \right)} \right) = k\left( {\left( {\mu - m} \right)^2 + \sigma _y^2 } \right), $$
(13)

where µ and σ 2 y are the mean and the variance of Y, respectively. The equation combines linearly the variance of Y and distance of the mean of Y , that is, µ, from the target value m. To lower the quality loss (and hence its associated cost), a quality engineer adjusts µ during parameter design. These adjustments do not affect the value of process variability σ y . From this point of view, then, the quality loss can be written

$$ QL = E\left( {L\left( Y \right)} \right) = k\sigma _y^2 . $$
(14)

Based on the design function, the resultant overall quality characteristic can be estimated from the set of individual quality characteristics in the design function. These approximation functions can be found by using Taylor series expansions. The resultant variance can then be expressed in terms of the variances, σ 2 xi , of the individual quality characteristics

$$ \sigma _y^2 = \sum\limits_{i = 1}^n {\left( {{{\partial f} \over {\partial x_i }}} \right)^2 \sigma _{xi}^2 .} $$
(15)

Tolerances are always related to manufacturing processes, and they must be designed in conjunction with the application of a specific manufacturing process. If a tolerance is determined without considering a specific process, one risks creating a mismatch between the required tolerance and the capability of a given process. One way to express this relationship is with a process capability index C p , which is the ratio of design tolerance boundaries to the measured variability of the output response of the manufacturing process. The process capability index C p is a measure of the ability of a process to manufacture a product that meets its specification, and is defined by

$$ C_p = {{t_d } \over {3\sigma }}. $$
(16)

We can now write

$$ \sigma _{xi} = {{t_{id} } \over {3C_{pi} }}. $$
(17)

Substituting into Eq. (15) gives

$$ \sigma _y^2 = \sum\limits_{i = 1}^n {\left( {{{\partial f} \over {\partial x_i }}} \right)^2 \left( {{{t_{id} } \over {3C_p }}} \right)^2 ,} $$
(18)

and the total quality loss is

$$ QL\left( {t_d } \right) = k\sigma _y^2 . $$
(19)

Traditionally, cost has been considered of paramount importance. However, since the 1980s, and especially as a result of Japanese efforts, quality in the broadest sense has become at least as important. Indeed, although cost and quality sometimes contradict one another, they are the two most important effects for an industrial company. Still, it is not easy to rank their importance with respect to each other, even on a per-application basis. For example, in modern automotive markets, strong competition forces companies to improve product quality constantly, and quality can vary between different parts in the same product. This suggests that quality should be ranked as more important than cost, but only to a point. Thus, determining appropriate weighting factors for cost and quality should be integrated into a company's management system and strategic planning.

3.2.2 Constraints

Design function is always used as a constraint to guarantee that assembly tolerances will not exceed function tolerance: the resultant design function tolerances must be less than or equal to the assembly functional tolerance limits. To quantify this, we begin by considering that different dimensions contribute differently to the assembly tolerance. For a worst case, we have

$$ \sum\limits_{i = 1}^n {\left| {{{\partial f} \over {\partial x_i }}} \right|t_{id} w_{ij} \le T_{\rm{f}} } , $$
(20)

where T f is the assembly functional tolerance limit. For the statistical case

$$ \sum\limits_{i = 1}^n {\left| {{{\partial f} \over {\partial x_i }}} \right|^2 t_{id}^2 w_{ij} \le T_{\rm{f}}^2 } . $$
(21)

In allocating machining tolerances, consideration should be given not only to process capability, but also to the amount of machining allowance for each operation. The machining allowance is the size of the layer of material that is to be removed from the surface of a workpiece in order to obtain the required accuracy and surface quality. It influences greatly the quality and production efficiency of the machined part. Excessive machining allowance increases the consumption of material, machining time, tools, and power, thereby increasing manufacturing cost. On the other hand, insufficient machining allowance fails to remove any roughness or surface defects of a previous operation, thus lowering part quality.

The amount of machining allowance is the difference between the machining dimension obtained from the preceding operation and that in the current operation. Because of operation errors, the actual amount of material removed varies within some range; this variation is a cumulative sum of manufacturing tolerances. In practice, typical levels of material removal are set on a per-process basis and are defined in various handbooks. We can represent this as

$$ \forall i,j:tp_{ij} + tp_{ij - 1} \le Tp_{ij} . $$
(22)

Each process operation has its own accuracy (again, usually available from reference handbooks) and must be performed within its process capability. Thus

$$ tp_{ij}^{\min } \le tp_{ij} \le tp_{ij}^{\max } . $$
(23)

In the STS model, manufacturing cost is a function of process tolerances, while quality loss is a function of design tolerances, acting in combination. Since the intermediate process tolerances are not final tolerances on a manufactured dimension, they affect neither functional performance nor quality, so no quality loss is associated with them. It is instead the tolerances of last processes (i.e. design tolerances) that constitute the final tolerances for a manufactured dimension. Quality loss is associated with design tolerances, which are the tolerances of the last processes. That the last process tolerances equal the design tolerances links the manufacturing cost and the quality loss; that is,

$$ tp_{ip_i } = t_{id} . $$
(24)

This concludes the explanation of the mathematics of the STS model.

4 An example

This section presents an example (originally used in [23, 1]) and compares the performance of the STS model to those in the cited works. The reader is referred to Fig. 1. The clearance X between the piston and the cylinder is the critical dimension. The given diameter of the piston is 50.8 mm, the cylinder bore diameter is 50.856 mm, and the clearance is 0.056±0.025 mm. The quality loss coefficient A is set at $100 (from [16]). Data for the process plans and capabilities, machining allowance, and coefficients of manufacturing cost–tolerance function for each process are given in the Appendix and are taken from [1].

Fig. 1.
figure 1

Assembly schematic of an automobile piston/cylinder, with relevant dimensions and tolerances indicated

Full size image

In the piston–cylinder bore assembly, there is only one resultant dimension (the clearance between the two parts) and two dimensions that form the chain (the diameters of the piston and cylinder bore). So, the design function is

$$ X = D_{\rm{p}} - D_{\rm{c}} . $$
(25)

Since we are only interested in determining the near-optimal tolerances for these parts with respect to the clearance between them, the tolerance stack-up function can be written as four equations, representing four possible cases:

$$ {\rm{W}}_{\rm{1}} {\rm{ = W}}_{\rm{2}} {\rm{ = 1,}}\;{\rm{C}}_{p{\rm{1}}} {\rm{ = C}}_{p{\rm{2}}} {\rm{ = 1;}} $$
(26a)
$$ {\rm{W}}_{\rm{1}} {\rm{ = W}}_{\rm{2}} {\rm{ = 2,}}\;{\rm{C}}_{p1} {\rm{ = C}}_{p2} {\rm{ = 1;}} $$
(26b)
$$ {\rm{W}}_{\rm{1}} {\rm{ = W}}_{\rm{2}} {\rm{ = 1,}}\;{\rm{C}}_{p1} {\rm{ = C}}_{p2} {\rm{ = 0}}{\rm{.5;}} $$
(26c)
$$ {\rm{W}}_{\rm{1}} {\rm{ = W}}_{\rm{2}} {\rm{ = 1,}}\;{\rm{C}}_{p1} {\rm{ = C}}_{p2} {\rm{ = 1}}{\rm{.5}}{\rm{.}} $$
(26d)

The LINGO software package (LINDO Systems, USA) was used to solve this model.

In the first case, manufacturing cost and quality loss have the same weight—that is, they are equally important—and C p =1 in accordance with typical North American practice for quality standards. The results for this case (Table 7) show that the STS method saves 3.4% compared to Zhang's method, and 36.4% compared to the traditional method (as that of Al-Ansary and Deiab).

The traditional method allocates tolerances in two steps, resulting in tight process tolerances (refer to Tables 5 and 6), thus incurring the highest manufacturing costs and lowest quality losses among the three methods. Zhang's method, on the other hand, lowers manufacturing cost by loosening tolerances, but at the expense of higher quality losses. The STS method balances these two aspects of the tolerance allocation problem: though one of either Zhang's method or the traditional method outperforms STS with respect to either manufacturing cost or quality loss, STS achieves the best total performance.

In the second case, quality loss is considered twice as important as manufacturing cost. Here, STS outperforms the other models by 8.6% (for Zhang's method) and 34% (for the traditional method), as shown in Table 8. This suggests that STS is useful in situations where high quality is required.

In the third case, quality is set at a low level. STS again outperforms the other methods, which suggests that the proposed method can create substantial cost savings (between 18% and 30%, per Table 9) in low-quality situations.

Finally, in the fourth case, quality is set at a high level. Even though in this case little quality loss is expected, STS still performs better than the other methods (between 0.9% and 39%, per Table 10). In situations of mass production, even a savings of less than 1% per unit can amount to very substantial savings over an entire product run.

Our use of weights W i allows us to separate determining the relative importance of quality loss and manufacturing cost on the one hand from modeling the quality loss and manufacturing cost themselves. The weights may be thought of as capturing the preferences of the members of a concurrent engineering team. Clearly, as the weights are coupled, all stakeholders in the design should approve the weights that are selected. Indeed, the weights serve as a strong reminder to the designers about the coupling between quality loss and manufacturing cost, and the importance of engineering products in a collaborative way.

Alternatively, one may consider the weights as aggregate values of experience, derived from analysis of past designs. That is, a company may choose to adopt a system such as STS and then track changes in the weights over time within single projects and over multiple projects. One may expect that, over time, patterns in the allocation of the weights for designs that were "successful" could emerge. Clearly, there is a risk here: there is no guarantee that useful patterns will emerge, and the cost required to collect, analyze, and maintain the database of past experience can be considerable. Nonetheless, it remains a possibility, especially in environments where ubiquitous computing is encouraged by corporate culture.

Various other examples were conducted, comparing STS to various other models. In no case did the STS model perform worse than the competing models; in many cases, STS far exceeded the competing models. Details on the other methods and examples are available in [22].

5 Implementing STS in industrial environments

In this section, the authors sketch a procedure for implementing the proposed STS method in industrial settings, and identify key issues that must be treated if the implementation is to be successful. The specifics of any implementation will depend to a large extend on the corporate structure of the company and the resources and design infrastructure in place at the time of implementation. However, the list of issues outlined below would have to be treated, one way or the other, in any implementation.

Step 1: Machine tool database

Data used in this article were taken from machining handbooks. In practical applications, a database would have to be constructed containing process capabilities, cost–process tolerance functions, process capability indices, and maximum machining allowances for each available machine tool. All these data can be determined by experiment and data analysis. In some cases, it may be purchased from equipment vendors. It could also be shared with other companies through consortia and so-called information "brokers".

Step 2: System and parameter design

System design establishes an architecture for product performance so as to satisfy functional requirements. Such architectures are typically parametric. Some of the parameters are distinguished for their importance in minimizing the functional deviations of the product. From the values established for these parameters, specification of the functional tolerances can be derived.

Step 3: Identification of functional dimension trains

From the system design, a geometric description of the product can be developed. Combined with functional tolerance specifications, the product drawings can be analyzed to extract functional dimension chains.

Step 4: Process planning

Design tolerances are estimated using an averaging method. This is acceptable because the design tolerances are only interim results. From these tolerances, an appropriate manufacturing process is selected. The design tolerances can then be discarded.

Step 5: Sensitivity analysis

Using sensitivity analysis, the impact of each component dimension on the functional tolerance can be established.

Step 6: Development of optimization model

Using the STS method and the information gathered in the preceding steps, an optimization model for the product is developed.

Step 7: Solution of optimization model

The optimization model is solved using conventional software packages, such as LINDO, MatLab, etc. The solution of the model results in near-optimal design and process tolerances.

It is evident that the process sketched above involves substantial "manual" work. Clearly, many aspects of the various steps could be implemented in a computer-based environment, which in turn would increase both the speed and the efficiency with which the process would occur. It is a matter of ongoing research to develop the appropriate computational infrastructure to support this process in a semiautomated manner.

6 Conclusions

A new method of synthesizing tolerances simultaneously for both manufacturing cost and quality has been presented. The method, called simultaneous tolerance synthesis (STS), has been shown to at least match other existing tolerance synthesis models and, in many cases, exceed them substantially. The best results were attained in cases where quality was either a high concern or was deliberately set at low levels. The method is then well-suited to engineering environments where either high quality or low-cost products are designed and manufactured.

Criteria for evaluating STS with respect to other models involve trading off near-term manufacturing costs against the losses in quality that adversely affect the long-term operational life of the product. Arguably, this criterion is more realistic than others focusing only on either manufacturing costs or quality losses. As such, the STS method is inherently suited for use in concurrent engineering environments. Weights built into the method allow product- and enterprise-specific factors to be taken into account.

The STS method is comparatively simple. It eliminates the need for various intermediate results (e.g. cost–design tolerance functions), thus improving computability and making the model easier to understand by design and manufacturing engineers.

Some directions for future work on STS include:

  • relaxing at least some of the assumptions made in Section 3:

    • clarifying how STS can be integrated into concurrent design environments to facilitate development of process plans;

    • extending STS to cover more than just normal distributions for processes; and

    • identifying the relationships between each dimension in a chain and the chain itself, and extending STS to take those relationships into account.

  • extending STS to handle geometric tolerances;

  • developing methods to help designers select the best possible weights for the STS model, either through theoretical considerations or through empirical analysis of past experiences;

  • studying the impact of robust design methods on the setting of the STS weighting factors; and

  • providing a means within STS to select machine tools on a per-process basis.

The STS method is new, and requires much more work before it is ready for deployment in an arbitrary design environment. However, the authors believe the results presented here indicate the relative merits of the method as compared to others, particularly as a concurrent design method for tolerance synthesis that accounts for losses throughout a product's life.