1 Introduction

The VH-CATT gear is a novel gear type featuring a circular arc tooth profile. Except for the involute profile of the middle section, the profiles of other sections are envelopes of a family of hyperbolic curves, endowing the VH-CATT gear with distinctive geometric characteristics [1]. Compared with helical gears, the VH-CATT gear generates no axial force, is less sensitive to coaxiality errors during installation, and exhibits lower noise and more stable performance than spur gears. These features make VH-CATT gears promising for high-speed and heavy-load transmission in aerospace and other applications [2,3,4,5]. However, due to the absence of specialized processing equipment, currently only CNC multi-axis milling machines can be used for processing, which is both inefficient and costly. Moreover, the theory and manufacturing systems for VH-CATT gear processing remain incomplete.

To achieve this, scholars have conducted research on the design of specialized machine tools. Wu proposed a simplified model of the machine tool and analyzed the influence of the machine tool structure on the gear blank [6, 7]. Liang analyzed the structural parameters of the machine tool and established the optimal machining parameters [8, 9]. To further improve the surface accuracy of the gear teeth, it is necessary to explore the influence of the machine tool error sources on the accuracy of the gear teeth, in order to provide a starting point for compensation. Tseng et al. proposed a processing method for cylindrical gears with arc tooth lines, and discussed the influence of different tooth line radius on the deviation of tooth surface [10]. Dai et al. proposed a method for continuous machining of circular-arc-toothed cylindrical gears, and deduced the digital model of gears according to this method [11]. Chen deduced the error transfer model of bevel gear machine tool with multi-body system theory and D-H method, and verified the correctness of bevel gear error surface model by experiment [12]. To accurately and efficiently measure the error of the rotating shaft in the five-axis machine tool, Li et al. proposed an error measurement method based on the double-ball measurement technique, which overcomes the uncertainties and limitations of the existing measurement method [13, 14]. Xing et al. utilized spatial errors to characterize the precision of machine tools and proposed a spatial error detection system. By analyzing spatial error data, it enables improved monitoring of the accuracy of five-axis machine tools [15]. Xiang et al. established a spatial error model of a six-axis CNC grinding machine using forward and inverse kinematics. They also established an error compensation mechanism based on this model, resulting in a significant improvement in the accuracy of processed gears after compensation [16]. Wu et al. proposed a general machine tool error compensation method based on multi-body theory and coordinate transformation. This method obtains the orientation vector of the tool end and then compensates for errors by adjusting the relationship between the CNC command and the actual tool trajectory, resulting in improved machining accuracy [17].

The research on machine tools for VH-CATT gear in the literature above is still in its early stages, or it has only been applied to helical gear machine tools and other standard machine tools. There is currently no literature available on the geometric error of VH-CATT gear special machine tools. Therefore, this paper aims to establish a machine tool error model consisting of 40 error sources, including the cutter head error, based on the general machine tool error model, taking into account the unique structure of the customized cutter head in the special machine tool. Based on machine topology and multi-body theory, the error transfer matrix of the machine tool is established using the D-H method, and the tool trajectory equation with error is derived. The error tooth surface of the VH-CATT gear is fitted using the second-order approximate surface, and the impact of different machine tool error sources on the tooth surface error is analyzed according to the difference surface. Finally, a trial cutting test of the special machine tool is conducted to verify the accuracy of the error surface.

2 System model of special machine tool for VH-CATT gear

2.1 Structural features of VH-CATT gears

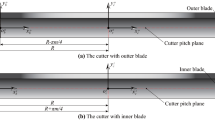
Currently, the processing method for VH-CATT gears generally involves milling using multi-axis machine tools or a translational mechanism, which is not only inefficient but also costly. In contrast to other common circular arc tooth trace cylindrical gears, VH-CATT gears are characterized by the same radial section of the cutter head, as shown in Fig. 1. It can be observed from the figure that the gear teeth are symmetrical along the middle section, thereby allowing axial forces to cancel each other out, reducing the likelihood of tooth breakage due to eccentric load, and generating no additional thrust on the bearing. The fixed arc radius characteristic of VH-CATT gear provides a prerequisite for industrial processing and mass production.

Fig. 1
figure 1

Structure of VH-CATT gear. (a) Digital model; (b) Experimental prototype

Full size image

2.2 Special machine tool structure of VH-CATT gear

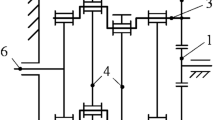
A special machine tool is designed in accordance with the characteristics of the VH-CATT gear structure, with reference to the Gleason machine. The special machine tool consists of three moving axes (X-axis, Y-axis and Z-axis) and two rotary axes (A-axis and C-axis), as shown in Fig. 2. Due to the large radius of the cutter head, the mass and rotational inertia of the VH-CATT gear are significantly larger than those of conventional cutter heads. To ensure cutting stability, the machine tool spindle is fixed to the bed through the base, thereby improving the stiffness of the system. The column moves along the Y-axis on base of the machine tool, and the movement of the Z-axis is realized by two slide rails in contact with the column. The movement of the X-axis is mainly used to achieve the centering adjustment of the gear blank and is not included in the composite movement of the machining process. The A-axis motion is achieved by the indexing mechanism.

Fig. 2
figure 2

VH-CATT gear special machine tool structure diagram. 1-Machine tool body 2-Cutter head 3-Cutting tool 4-Z-axis 5-.X-axis 6-Gear blank 7-Indexing mechanism 8-Y-axis. (a) Axial drawing of structure, (b) Prototype physical diagram

Full size image

To facilitate the description, the coordinate system of the machine tool is established, and the specific structure is shown in Fig. 3.

Fig. 3
figure 3

VH-CATT gear special machine tool coordinate system

Full size image

The bed coordinate system OM-xMyMzM was established based on the bed, and the C-axis coordinate system OC-xCyCzC was established based on the center of the rotary cutter head. The origin OC of the C-axis coordinate system OC-xCyCzC was set in the positive direction of the zM axis of the origin OM of the bed coordinate system OM-xMyMzM. On the basis of the C-axis coordinate system OC-xCyCzC, the cutter head coordinate system OH-xHyHzH is established, and its origin OT is rotated around the zC axis in the N plane of the C-axis coordinate system OC-xCyCzC and the angle is θ. The origin of the cutter coordinate system OT-xTyTzT is in the OH-xHyH plane of the cutter coordinate system OH-xHyHzH, and the distance between the origin OH and OT is the cutter radius Rt. Similarly, the Y-axis coordinate system OY-xYyYzY carried by the column mechanism is established in the yM direction of the bed coordinate system OM-xMyMzM. Based on OY, the zY axis coordinate system OZ-xZyZzZ is established along the direction, and the X-axis coordinate system and A-axis coordinate system are further established along the xZ axis. Among them, the angle between A-axis coordinate system and X-axis coordinate system is φ, and the column mechanism will be linked along yM in the machining process.

2.3 The machining principle of cutter head

The VH-CATT gear is manufactured using a rotary milling process, which involves the use of a special machine tool. The machining principle is depicted in Fig. 4. To simplify the explanation of the evolution movement during the machining process, the decomposition movement of each component is introduced from the fixed axis.The cutter head rotates around the C-axis at a constant speed that is predetermined in the manufacturing process, and it does not participate in the multi-axes synchronous formation process. The X-axis, Y-axis and Z-axis slides move to the predetermined point. Subsequently, the X-axis and Z-axis maintain a fixed posture on the machine tool column, and the Y-axis further translates with the tooth blank towards the cutter until the tooth blank moves to the point of tool alignment.

Fig. 4
figure 4

Structure of cutter head-spindle system

Full size image

Similar to the machining principle used for involute spur gears with a straight rack, the indexing mechanism and the tooth blank start to link up with the Y-axis. The cutter and the tooth blank then roll without sliding along the Y-axis direction, resulting in a tight spreading motion. The complete machining process involves the tool moving from the start point to the exit point, milling according to the above motion. Finally, each guide rail slides back to the standby position, and the indexing mechanism returns to the origin around the A-axis and zeroes the cumulative error. It then turns to the angle of the next tooth slot processing and prepares the next tooth slot processing. This movement is repeated until the entire gear processing is completed.

3 Multi-system description of the special machine tool

3.1 Description of topology

According to the Houston lower numbered body array method proposed by, the relationship between machine parts can be summarized directly. Figure 5 illustrates the simplified multi-body system of the machine tool in this paper, with each component in the diagram defined according to the lower sequence arrangement method. The geodetic coordinate system R is designated as object 0 (denoted as B0), while the machine bed is denoted as 1. Moving away from 1, each component is calibrated according to the growth sequence, from one branch of the system to another, until all components are calibrated. It can be seen from Fig. 5 that each component has an adjacent lower-order object. For any typical body K, J serves as its adjacent lower-order object, and L(K) is defined as the lower-order object array.

Fig. 5
figure 5

Topology structure of special machine tool

Full size image
$$L\left(K\right)=J$$
(1)

L(K) possesses the following properties

$$\left\{\begin{array}{c}{L}^{n}\left(K\right)=L\left({L}^{n-1}\left(K\right)\right)\\ {L}^{0}\left(K\right)=K\\ L\left(0\right)=0\end{array}\right.$$
(2)

The machine tool components are arranged in the following order: Earth B0, Machine bed B1, C-axis component B2, Cutter head B3, Cutter B4, Y-axis component B5, Z-axis component B6, X-axis component B7, A-axis component B8. According to the machine tool system structure model in Fig. 2, the machine tool system can be divided into two branches.

  • Branch 1: Machine bed B1, C-axis component B2, Cutter head B3, Cutter B4.

  • Branch 2: Machine bed B1, Y-axis component B5, Z-axis component B6, X-axis component B7, A-axis component B8.

The topology of a multi-body system is described by a low-order object array L(K) that is established according to the rules, and this array relationship between the components in the system is revealed. The components that do not appear in L1(K) are called the end-body of the multi-body system(e.g. B4 and B8 in Fig. 5), while the components that are repeated in L1(K) are called the branching body(e.g. B1). All other components, except the end-bodies and branching bodies, are referred to as intermediates. Each component in the system belongs to a branch, and each branch contains a terminal body with the highest serial number and a branch with a lower serial number. For instance, B3 belongs to branch B1-B2-B3-B4, where B4 is the terminal body with the highest serial number and B1 is the branch with a lower serial number. By using L(K), it is possible to determine the branch of a typical body K, along with the serial numbers of all components that are part of that branch. (Table 1).

Table 1 Lower numbered body array of the special machine tool
Full size table

3.2 Description of Multi-body motion

Multi-body motion typically involves multiple adjacent components moving in coordination with one another. Figure 6 illustrates the relative coordinate relationship between a typical component Bk and the adjacent lower sequence component Bj.

Fig. 6
figure 6

Relation of adjacent lower order objects

Full size image

The coordinate system R(o0-x0y0z0) is fixed with the inertial body B0 to describe the absolute motion of the components of the multi-body system. On the other hand, the coordinate system Rk(ok-xkykzk) is a reference coordinate system fixed with the typical Bk, whose right-handed orthogonal basis vector group is \({\left({n}_{k1},{n}_{k2},{n}_{k3}\right)}^{T}\). The coordinate system Rj(oj-xjyjzj) is a reference coordinate system fixed with the typical body Bj, whose right-handed orthogonal basis vector group is \({\left({n}_{j1},{n}_{j2},{n}_{j3}\right)}^{T}\).

The point M is connected to Bk on the typical body Bj, and vector mk is the position vector of point M in the coordinate system Rj. The vector sk represents the displacement vector of the origin Ok of the Rk coordinate system relative to mk, which can be understood as point M in the coordinate system Rk. Additionally, vector n0 represents the position vector of point N on the typical body Bk in coordinate system Rk. vector nj represents the position vector of N point in coordinate system Rj. vector nk represents the position vector of point N in coordinate system Rk.

3.3 Multi-body transformation matrix of the special machine tool

Based on the above transfer relationships, it is relatively straightforward to establish a transformation matrix between adjacent structures, in combination with the machine tool coordinate system shown in Fig. 3. To do so, the ideal coordinate transformation between components should be established first, without taking errors into account. There are several methods for doing this, including the D-H method [18] and screw theory [19].

For the purposes of this paper, the D-H method has been chosen for coordinate transformation. The conversion matrices for each component can be obtained as follows.

A12: from C-axis B2 to bed B1

$${A}_{12}=\left[\begin{array}{c}\begin{array}{ccc}1& 0& \begin{array}{cc}0& 0\end{array}\end{array}\\ \begin{array}{ccc}0& 1& \begin{array}{cc}0& 0\end{array}\end{array}\\ \begin{array}{c}\begin{array}{ccc}0& 0& \begin{array}{cc}1& {z}_{H}\end{array}\end{array}\\ \begin{array}{ccc}0& 0& \begin{array}{cc}0& 1\end{array}\end{array}\end{array}\end{array}\right]$$
(3)

A23: from cutter head B3 to C-axis B2

$${A}_{23}=\left[\begin{array}{ccc}\begin{array}{c}\mathrm{cos\varphi }\\ \mathrm{sin\varphi }\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}-\mathrm{sin\varphi }\\ \mathrm{cos\varphi }\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\\ \begin{array}{c}1\\ 0\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ 1\end{array}\end{array}\end{array}\end{array}\right]$$
(4)

A34: from cutter head B4 to cutter head B3.

$${A}_{34}=\left[\begin{array}{ccc}\begin{array}{c}1\\ 0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}0\\ 1\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\\ \begin{array}{c}1\\ 0\end{array}\end{array}& \begin{array}{c}0\\ R\\ \begin{array}{c}0\\ 1\end{array}\end{array}\end{array}\end{array}\right]$$
(5)

where zH is the Z-coordinates of the cutter head and R is the radius of the cutter head, so the ideal conversion matrix from the tool to the bed is A14 = A12A23A34. The conversion matrices for each component can be obtained as follows.

A15: from Y-axis B5 to bed B1

$${A}_{15}=\left[\begin{array}{ccc}\begin{array}{c}1\\ 0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}0\\ 1\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\\ \begin{array}{c}1\\ 0\end{array}\end{array}& \begin{array}{c}0\\ {y}_{V}+{y}_{s}\\ \begin{array}{c}0\\ 1\end{array}\end{array}\end{array}\end{array}\right]$$
(6)

A56: from Z-axis B6 to Y-axis B5

$${A}_{56}=\left[\begin{array}{ccc}\begin{array}{c}1\\ 0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}0\\ 1\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\\ \begin{array}{c}1\\ 0\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}{z}_{W}\\ 1\end{array}\end{array}\end{array}\end{array}\right]$$
(7)

A67: from X-axis B7 to Z-axis B6

$${A}_{67}=\left[\begin{array}{ccc}\begin{array}{c}1\\ 0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}0\\ 1\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\\ \begin{array}{c}1\\ 0\end{array}\end{array}& \begin{array}{c}0\\ -{y}_{W}\\ \begin{array}{c}0\\ 1\end{array}\end{array}\end{array}\end{array}\right]$$
(8)

A78: from A-axis B8 to X-axis B7

$${A}_{78}=\left[\begin{array}{ccc}\begin{array}{c}1\\ 0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}0\\ \mathrm{cos}\theta \\ \begin{array}{c}\mathrm{sin}\theta \\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ -\mathrm{sin}\theta \\ \begin{array}{c}\mathrm{cos}\theta \\ 0\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ 1\end{array}\end{array}\end{array}\end{array}\right]$$
(9)

Among them, yV represents the y-coordinate from the Z-axis to the origin of the machine tool coordinate system, ys represents the y-coordinate of the column feed during gear machining, zW represents the z coordinate from Z-axis to Y-axis, yW represents the y coordinate from X-axis to Z-axis. Similarly, the transformation matrix from tool to bed can be obtained as, A18 = A15A56A67A78.

4 Error derivation analysis of VH-CATT gear

4.1 Geometric error sourcesof machine tool system

Given the complexity of the machine tool system and the composite motion of several parts involved in the gear machining process, it is challenging to establish a linear relationship between single error and accuracy [20]. To overcome this challenge, a coordinate transformation approach can be adopted to transfer all errors to the tooth blank and tool. By analyzing the relative trajectory deviation value of the cutter and the tooth blank after accumulating various errors, the mechanism of error on the tooth surface can be explored.

The VH-CATT gear special machine tool is characterized by a complex system with multiple sources of errors. These include six errors arising from the three moving and two rotating axes, as well as inaccuracies associated with the cutter head. The impact of these errors on the system’s accuracy is further complicated by considerations such as the perpendicularity between components and flatness of motion, as illustrated in Fig. 7 and Fig. 8. Furthermore, tool radius error, pressure angle error, and height error represent additional sources of potential deviation from ideal performance, as illustrated in Fig. 9 and Fig. 10.

Fig. 7
figure 7

Error source of moving shaft

Full size image
Fig. 8
figure 8

Error source of rotating shaft

Full size image
Fig. 9
figure 9

Error source of tool radius and pressure angle

Full size image
Fig. 10
figure 10

Error source of height

Full size image

The diagram in Fig. 7 illustrates that the Y-axis of the VH-CATT cylindrical gear special machine tool is affected by three types of displacement errors, namely the straightness errors in the X-axis, Y-axis, and Z-axis directions (referred to as errors \({\delta }_{x\left(Y\right)}\), and \({\delta }_{z\left(Y\right)}\), respectively), as well as three types of rotational errors, namely the rolling error around the three axes (error \({\varepsilon }_{x\left(Y\right)}\)), the pitch error (error \({\varepsilon }_{y\left(Y\right)}\)), and the yaw error (error \({\varepsilon }_{z\left(Y\right)}\)). To account for these errors, a transformation matrix is used to describe the error propagation between each consecutive transmission in the system.

$$E=\left[\begin{array}{ccc}\begin{array}{c}1\\ {\delta }_{z}\\ \begin{array}{c}-{\delta }_{y}\\ 0\end{array}\end{array}& \begin{array}{c}-{\delta }_{z}\\ 1\\ \begin{array}{c}{\delta }_{x}\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}{\delta }_{y}\\ -{\delta }_{x}\\ \begin{array}{c}1\\ 0\end{array}\end{array}& \begin{array}{c}{\varepsilon }_{x}\\ {\varepsilon }_{y}\\ \begin{array}{c}{\varepsilon }_{z}\\ 1\end{array}\end{array}\end{array}\end{array}\right]$$
(10)

The error analysis of the machine tool is conducted based on the detection report of the specialized machine tool and the small error theory. The error components are identified and quantified, as presented in Table 2.

Table 2 Error source of the VH-CATT gear special machine tool
Full size table

4.2 Derivation of ideal tooth surface equation

The working section of the tool can be deduced from Fig. 4:

$$r_c=\begin{bmatrix}0\\-\left(R_t\mp\frac\pi4\pm u\;\mathrm s\mathrm i\mathrm n\;\alpha\right)\\\begin{array}{c}u\;\cos\;\alpha\\1\end{array}\end{bmatrix}$$
(11)

where m represents the modulus of the tooth blank to be machined, u is the distance from the tool to the reference axis xt along the generatrix direction, and the positive direction is defined as along the positive Zt half axis. Rt is the nominal radius of the cutter head in the ideal state, that is, the distance from the symmetric line of the trapezoidal tool to the axis of the cutter head. α is the pressure angle of the gear. The symbol “ ± ” denotes the internal and external edges of the tool respectively. In this paper, the internal edge is unified to take upper part of the symbols, and the external edge is unified to take bottom part of the symbols.

The rotation of the tool section around C-axis forms the tool rotation surface, and the motion trajectory of B4 in the coordinate system OC-XCYCZC can be obtained as follows

$${r}_{c}=\left[\begin{array}{c}-\left({R}_{t}\mathrm{m}\frac{\pi }{4}m\pm u\;\mathrm{sin\;}\alpha \right)\mathrm{sin}\;\theta \\ -\left({R}_{t}\mathrm{m}\frac{\pi }{4}m\pm u \mathrm\;{sin }\;\alpha \right)\mathrm{cos}\;\theta \\ \begin{array}{c}u\;cos\;\alpha \\ 1\end{array}\end{array}\right]$$
(12)

In the Eq. (12), θ represents the rotation angle (in degrees) of the tool from the tooth blank section to the end face, which is the position angle of the tooth profile. Correspondingly, the normal vector of the tool can be represented as

$${{\varvec{n}}}_{t4}=\left[\begin{array}{c}\mathrm{cos}\;\alpha\;\mathrm{sin}\;\theta \\ \mathrm{cos}\;\alpha\;\mathrm{cos}\;\theta \\ \begin{array}{c}\pm \mathrm{sin}\;\alpha \\ 0\end{array}\end{array}\right]$$
(13)

The position vector of point Pg on the tooth surface and point Pt on the cutter rotary surface in the machine tool coordinate system OM-XMYMZM are identical based on the gear meshing principle. Furthermore, at the contact point, the relative velocity vgt of the tooth surface and the cutter rotary surface is perpendicular to the normal line nt of the cutter rotary surface [21]. To correctly express the gear meshing equation, the aforementioned relative motion must be transformed into a unified coordinate system using transformation matrices. Hence, the tool trajectory can be represented in the A-axis coordinate system OA-XAYAZA as follows

$${{\varvec{r}}}_{t8}={M}_{18}^{-1}{M}_{14}{{\varvec{r}}}_{t4}$$
(14)

To transform the tool trajectory into the coordinate system OM-XMYMZM and then differentiate it, the velocity of point Pt is given by

$${{\varvec{v}}}_{t1}={\dot{M}}_{14}{{\varvec{r}}}_{t4}$$
(15)

Similarly, the speed of the point Pg is expressed as

$${{\varvec{v}}}_{g1}={\dot{M}}_{18}{{\varvec{r}}}_{t8}$$
(16)

The normal vector in machine tool coordinate system OM-XMYMZM is:

$${{\varvec{n}}}_{t1}={M}_{14}{{\varvec{n}}}_{t4}$$
(17)

The meshing equation of VH-CATT gear can be obtained by combining Eq. (11) and (17):

$$f\left(\varphi ,\theta \right)={{\varvec{n}}}_{t1}{{\varvec{v}}}_{gt1}={{\varvec{n}}}_{t1}\left({{\varvec{v}}}_{g1}-{{\varvec{v}}}_{t1}\right)=0$$
(18)

4.3 Derivation of tooth surface equation with error

To account for various forms of errors in the transmission of motion on each axis during actual machining, the tool trajectory with errors in the A-axis coordinate system OA-XAYAZA can be expressed similarly to the previous section

$${{\varvec{r}}}_{t4}*=\left[\begin{array}{c}-\left({R}_{t}^{*}\mathrm{m}\frac{\pi }{4}m\pm u\mathrm\;{sin}\;{\alpha }^{*}\right)\mathrm{sin}\;\theta \\ -\left({R}_{t}^{*}\mathrm{m}\frac{\pi }{4}m\pm u\mathrm\;{sin}\;{\alpha }^{*}\right)\mathrm{cos}\;\theta \\ \begin{array}{c}u\mathrm\;{cos}\;\alpha \\ 1\end{array}\end{array}\right]$$
(19)

Here, \({R}_{t}^{*}={R}_{t}+{\Delta R}_{t}\), \({\alpha }^{*}=\alpha +\Delta \alpha\). The normal vector of the tool with errors can be represented as

$${{{\varvec{n}}}_{t4}}^{*}=\left[\begin{array}{c}\mathrm{cos}\;{\alpha }^{*} \mathrm{sin}\;\theta \\ \mathrm{cos}\;{\alpha }^{*} \mathrm{cos}\;\theta \\ \begin{array}{c}\pm \mathrm{sin}\;{\alpha }^{*} \\ 0\end{array}\end{array}\right]$$
(20)

The tool trajectory in the A-axis coordinate system OA-XAYAZA is

$${{\varvec{r}}}_{r8}^{*}={T}_{18}^{-1}{T}_{14}{{\varvec{r}}}_{t4}^{*}$$
(21)

Converting tool moving path into coordinate system OM-XMYMZM, the velocity of point Pt is

$${{\varvec{v}}}_{r8}^{*}={\dot{T}}_{14}{{\varvec{r}}}_{r4}^{*}$$
(22)

Similarly, the speed of the point Pg in coordinate system OM-XMYMZM is

$${{\varvec{v}}}_{g1}^{*}={\dot{T}}_{18}{{\varvec{r}}}_{t8}^{*}$$
(23)

The expression of normal vector in system OM-XMYMZM is:

$${{\varvec{v}}}_{t1}^{*}={T}_{14}{{\varvec{n}}}_{t4}^{*}$$
(24)

The engagement equation of VH-CATT gear can be obtained by combining Eq. (23) and (24):

$${f}^{*}\left(\varphi ,\theta \right)={{\varvec{n}}}_{t1}^{*}\left({{\varvec{v}}}_{g1}^{*}-{{\varvec{v}}}_{t1}^{*}\right)={{\varvec{n}}}_{t1}^{*}{{\varvec{v}}}_{g1}^{*}=0$$
(25)

Because in Eq. (22), \({\dot{T}}_{18}=0\). The tooth surface equation of VH-CATT gear with error can be obtained by combining the equations.

5 Error surface for VH-CATT gear

5.1 Definition of gear error surface

Assuming that both the ideal surface and actual surface of the gear can be expressed by the spatial surface, defined by \({\sum }_{i}\) and \({\sum }_{a}\) respectively, then \({\sum }_{i}\) can be expressed as:

$${r}_{i}\left(u,v\right)\in {C}^{k}\left(k\ge 2\right)$$
(26)
$${{\varvec{n}}}_{i}\left(u,v\right)$$
(27)
$$\frac{\partial {r}_{i}}{\partial u}\times \frac{\partial {r}_{i}}{\partial v}\ne 0$$
(28)

In this equation, \({r}_{i}\) and \({{\varvec{n}}}_{i}\) respectively denote the position vector and unit normal vector of the ideal tooth surface, while \(\left(u,v\right)\) represents the Gauss coordinate or curve coordinate of the surface.

Similarly, the actual tooth surface \({\sum }_{\alpha }\) can be expressed as

$${{\varvec{r}}}_{a}\left(u,v\right)={{\varvec{r}}}_{i}\left(u,v\right)+{F{\varvec{n}}}_{i}\left(u,v\right)$$
(29)

F represents the deviation between the actual point and the theoretical point. Combined with Eq. (25) and (28), we can obtain:

$$F=\left({{\varvec{r}}}_{a}-{{\varvec{r}}}_{i}\right)\bullet {{\varvec{n}}}_{i}=\Delta r\bullet {{\varvec{n}}}_{i}$$
(30)

During the actual measurement and analysis of gear errors, the relative positions of \({\sum }_{i}\) and \({\sum }_{\alpha }\) are fixed, meaning that \({{\varvec{r}}}_{i}\) and \({{\varvec{n}}}_{i}\) remain constant. Thus, the difference between the corresponding points of the two surfaces, \(\Delta r\), is a constant value, and their dot product is also a geometric invariant. The deviation of the two surfaces along the \({{\varvec{n}}}_{i}\) direction is also geometrically invariant. Therefore, using the deviation surface can accurately reflect the machining error of the tooth surface.

5.2 Error surface characterization of VH-CATT gear

Due to the VH-CATT gear tooth surface being a complex spatial curve, the position vector of the ideal tooth surface ri and the unit normal vector ni of the ideal tooth surface can be deduced. However, the workload of measuring the tooth surface coordinates and fitting ra the surface is enormous. Therefore, it is difficult to directly solve the error surface and a series of preprocessing is required. Referring to the Gleason gear error analysis method, the error is discretized and analyzed. In the tooth width and tooth height directions, 45 points are taken on the tooth surface rotation projection plane based on the principle of 9 × 5 ordered points [22]. Considering the gear fillet, chamfer, and root cut, the range of the discretized error surface is smaller than the actual tooth surface, as shown in Fig. 11.

Fig. 11
figure 11

Error surface mesh planning

Full size image

The grid division of the error surface on the gear surface rotation projection plane o-zr is shown in Fig. 12, and the upper and lower limits of the discrete points in the radial direction are shown in Eqs. (33) and (34), respectively.

Fig. 12
figure 12

Mesh division of error surface

Full size image
$${r}_{1}=\frac{m\left(z-2\right)}{2}+0.1m$$
(31)
$${r}_{2}=\frac{m\left(z+2\right)}{2}-0.1m$$
(32)

From Fig. 12, the coordinates of any point Pij on the grid node in the o-zr plane can be obtained as shown in Eq. (33).

$$\left\{\begin{array}{l}\begin{array}{l}{r}_{ij}={r}_{1}+\left(i-1\right)\frac{\left({r}_{2}-{r}_{1}\right)}{4}\\ \left(i=\mathrm{1,2},\cdots ,5;j=\mathrm{1,2},\cdots ,9\right)\end{array}\\ {z}_{ij}=-0.45b+\frac{\left(j-1\right)b}{10}\end{array}\right.$$
(33)

The coordinates \(\left({x}_{g},{y}_{g},{z}_{g}\right)\) of the point on the tooth surface corresponding to the grid node should meet Eq. (34).

$$\left\{\begin{array}{c}\sqrt{{x}_{g}^{2}+{y}_{g}^{2}={r}_{ij}}\\ {z}_{g}={z}_{ij}\end{array}\right.$$
(34)

Equation (33) is a nonlinear system of equations that includes two unknowns \(\varphi\) and \(\theta\). The number of equations is equal to the number of unknowns, which can be solved iteratively using numerical methods. Combining Eq. (33) and (34), the tooth surface parameters corresponding to each grid node can be solved. By substituting \(\left({\varphi }_{ij}, {\theta }_{ij}\right)\) and machine errors into Eq. (31), the discretized gear error surface can be obtained.

5.3 Characteristic parameters of error surface

By observing the absolute value of the discrete tooth surface error, the local error near a certain observation point can be directly obtained. To analyze the overall influence of machine tool errors on tooth surface errors, a reference value needs to be set. The average value of the absolute value of the discretized gear surface error and the ratio of machine tool errors are often used to define the ratio as the coefficient of influence of the average gear surface error.

$${W}_{k}=\frac{\sum \left|{}^{\left({\Delta }_{k}\right)}{F}_{ij}\right|}{{\Delta }_{k}}$$
(35)

Here, \({\Delta }_{k}\) is the kth machine tool error and \({}^{\left({\Delta }_{k}\right)}{F}_{ij}\) is the normal error of tooth surface at Pij caused by \({\Delta }_{k}\).

The 45 coordinate points of the tooth surface obtained by Eq. (33) can represent the error trend of the tooth surface, but the specific expression of the error surface cannot be directly written out. Based on the obtained discrete points, an equation that is infinitely close to the actual tooth surface is fitted. The equation of the error surface can be represented using a set of bases in the surface space.

$$F={a}_{0}+{a}_{1}z+{a}_{2}r+{a}_{3}{z}^{2}+{a}_{4}{r}^{2}+{a}_{5}zr+\mathrm{L}$$
(36)

Here, \(\left(z,r\right)\in G\), G represents the domain in the o-zr plane.

Typically, a second-order surface can achieve high precision fitting, and higher-order coefficients can be directly ignored [22]. The coefficients of each polynomial have different geometric meanings. By analyzing the machine tool error with the coefficients of the quadratic surface, the orientation and quantitative analysis of the influence of the tooth surface can be achieved. Because the second-order surface includes normal deviation error, pressure angle error, helix angle error, profile drum-type error, tooth line drum-type error, and tooth surface runout error, the quadratic surface expression is given by

$$F={a}_{0}+{a}_{1}z+{a}_{2}r+{a}_{3}{z}^{2}+{a}_{4}{r}^{2}+{a}_{5}zr$$
(37)

In the equation, a0 is the zero-order coefficient, which causes the deviation error of the tooth surface in the normal direction. a1 is the first-order coefficient in the tooth line direction, which causes the helix angle error, that is, it leads to the theoretical contact area deviating towards one end face along the tooth line direction. a2 is the first-order coefficient in the tooth height direction, which causes the pressure angle error, that is, it leads to the contact area shifting along the tooth height direction. a3 is the second-order coefficient in the tooth line direction, which causes the change in the major axis of the contact area to cause tooth profile error. a4 is the second-order coefficient in the tooth height direction, which causes the change in the minor axis of the contact area to cause tooth profile crowning error. a5 is the comprehensive first-order coefficient in the tooth length and height directions, which causes the diagonal error of the tooth surface.

6 Error analysis

As the processing principle for concave and convex tooth surfaces of VH-CATT gears is the same, the influence of machine tool error on both surfaces is similar. Therefore, this paper focuses on analyzing the influence of machine tool errors on the concave tooth surface error only. The errors of machine are shown in Table 3. Table 4 presents the machining parameters of the VH-CATT gear. The following steps analyze the influence of machine tool errors on the tooth surface. Equations (33) and (34) are used to transform the coordinate system of the gear from OA-XAYAZA to O-rz, based on the machining parameters. This transformation yields the parameters of the ideal concave tooth surface mesh node. By using the trajectory equation and meshing equation of the cutting tool, the coordinate values and unit normal vectors of the concave tooth surface mesh nodes can be solved under ideal conditions. Similarly, the actual coordinate values of concave tooth surface mesh nodes can be obtained by using the coordinate transformation matrix with error. The normal tooth surface error of each mesh node can be calculated by applying Eq. (36) to the ideal coordinate value, unit normal vector, and coordinate value with error. This process generates the discrete error surface corresponding to each machine tool error.

Table 3 The value of error source
Full size table
Table 4 The key machining parameters
Full size table

To analyze the influence of different errors on the tooth surface, we conducted 40 groups of single-factor test simulations. We then selected several groups of factors that resulted in the largest tooth surface errors for further analysis. Firstly, the maximum error was found to be associated with the Y-axis of the moving axis. This is because the Y-axis has the largest movement trajectory and plays a significant role in the linkage during the gear development process. This is illustrated in Fig. 13. that the errors resulting in the normal offset caused by the zero-order coefficient include \({\delta }_{x\left(Y\right)}\), \({\delta }_{z\left(Y\right)}\)\({\varepsilon }_{x\left(Y\right)}\), \({\varepsilon }_{y\left(Y\right)}\)\({\varepsilon }_{z\left(Y\right)}\). Out of all the errors, \({\varepsilon }_{y\left(Y\right)}\) has the greatest impact on the tooth surface error, with an error peak near the gear tooth top of -11.145 μm. \({\delta }_{x\left(Y\right)}\) follows closely behind, while the impact of \({\delta }_{z\left(Y\right)}\), \({\varepsilon }_{x\left(Y\right)}\) and \({\varepsilon }_{z\left(Y\right)}\) can be negligible. The machine tool error factors that cause helix angle errors include \({\delta }_{y\left(Y\right)}\), \({\delta }_{z\left(Y\right)}\), \({\varepsilon }_{x\left(Y\right)}\), and \({\delta }_{z\left(Y\right)}\). Among them, \({\varepsilon }_{z\left(Y\right)}\) causes a deviation of 13.731 μm near the left tooth top. The order of the impact trend of each factor on the tooth surface error from the largest to the smallest is \({\varepsilon }_{z\left(Y\right)}\), \({\varepsilon }_{x\left(Y\right)}\), \({\delta }_{z\left(Y\right)}\), and \({\delta }_{z\left(Y\right)}\), and all error factors cannot be ignored. The machine tool error factors that cause pressure angle errors include \({\delta }_{x\left(Y\right)}\), \({\delta }_{y\left(Y\right)}\), \({\varepsilon }_{x\left(Y\right)}\), \({\varepsilon }_{y\left(Y\right)}\), and \({\varepsilon }_{z\left(Y\right)}\). Among them, \({\varepsilon }_{z\left(Y\right)}\) has the greatest impact, resulting in inconsistent deviation of the tooth top and root on both end faces and the middle cross-section. The impact of ex follows closely behind, while the effects of \({\delta }_{x\left(Y\right)}\), \({\delta }_{y\left(Y\right)}\), and \({\varepsilon }_{y\left(Y\right)}\) are relatively small and can be ignored.

Fig. 13
figure 13

Influence of Y-axis component errors on tooth surface (a) \({\delta }_{x\left(Y\right)}\) (b) \({\delta }_{y\left(Y\right)}\) (c) \({\delta }_{z\left(Y\right)}\) (d) \({\varepsilon }_{x\left(Y\right)}\) (e) \({\varepsilon }_{y\left(Y\right)}\) (f) \({\varepsilon }_{z\left(Y\right)}\) 

Full size image

The machine tool error factors that cause tooth profile crowning error include \({\delta }_{z\left(Y\right)}\) and \({\varepsilon }_{x\left(Y\right)}\), both of which are very small and can be ignored. The machine tool error factor that causes tooth surface crowning error is only \({\varepsilon }_{x\left(Y\right)}\), which can also be ignored. The machine tool error factors that cause tooth helix error include \({\varepsilon }_{x\left(Y\right)}\) and \({\varepsilon }_{z\left(Y\right)}\), both of which can be ignored.

Then, the same method was used to analyze the influence of errors on the rotating shaft. The error with a relatively large effect on the rotating shaft is the A-axis, as the A-axis not only needs to complete the indexing of a single tooth but also participates in the linkage during the forming process.

From Fig. 14, it can be seen that the errors causing the normal deviation due to the zero-order coefficients include \({\delta }_{x\left(A\right)}\), \({\delta }_{y\left(A\right)}\), \({\varepsilon }_{\alpha \left(A\right)}\), \({\varepsilon }_{\beta \left(A\right)}\) and \({\varepsilon }_{\gamma \left(A\right)}\). Among them, \({\varepsilon }_{\gamma \left(A\right)}\) shows the largest impact on the tooth surface error, causing a deviation of -18.109 μm near the tooth top. The deviation caused by \({\delta }_{x\left(A\right)}\) and \({\delta }_{y\left(A\right)}\) decreases, while the impact of \({\varepsilon }_{\alpha \left(A\right)}\) and \({\varepsilon }_{\beta \left(A\right)}\) can be negligible. The error factors that cause helix angle error include \({\delta }_{z\left(A\right)}\), \({\varepsilon }_{\alpha \left(A\right)}\) and \({\varepsilon }_{\beta \left(A\right)}\). The trend of the influence of each factor on tooth surface error is arranged in descending order as \({\varepsilon }_{\beta \left(A\right)}\), \({\varepsilon }_{\alpha \left(A\right)}\) and \({\delta }_{z\left(A\right)}\), and all error factors cannot be ignored. The factors that cause pressure angle error include \({\delta }_{x\left(A\right)}\), \({\delta }_{y\left(A\right)}\), \({\delta }_{z\left(A\right)}\), \({\varepsilon }_{\alpha \left(A\right)}\), \({\varepsilon }_{\beta \left(A\right)}\) and \({\varepsilon }_{\gamma \left(A\right)}\), where the largest influences are the deviation amounts of \({\delta }_{y\left(A\right)}\). Then, \({\varepsilon }_{\alpha \left(A\right)}\), \({\delta }_{x\left(A\right)}\), \({\delta }_{z\left(A\right)}\) and \({\varepsilon }_{\beta \left(A\right)}\) are in decreasing order, while the influences of \({\delta }_{z\left(A\right)}\) and \({\varepsilon }_{\gamma \left(A\right)}\) are relatively small and can be ignored.The machine tool error factors that cause tooth axial runout error include \({\delta }_{x\left(A\right)}\) and \({\delta }_{y\left(A\right)}\), with \({\delta }_{x\left(A\right)}\) being very small and negligible. The machine tool error factor that causes tooth profile runout error is only \({\varepsilon }_{\alpha \left(A\right)}\) and can also be ignored. The machine tool error factors that cause tooth surface diagonal error are \({\varepsilon }_{\alpha \left(A\right)}\) and \({\varepsilon }_{\beta \left(A\right)}\), and among them, the offset caused by \({\varepsilon }_{\alpha \left(A\right)}\) is more significant.

Fig. 14
figure 14

Influence of A-axis component errors on tooth surface (a) \({\delta }_{x\left(A\right)}\) (b) \({\delta }_{y\left(A\right)}\) (c) \({\delta }_{z\left(A\right)}\) (d) \({\varepsilon }_{\alpha \left(A\right)}\) (e) \({\varepsilon }_{\beta \left(A\right)}\) (f) \({\varepsilon }_{\gamma \left(A\right)}\) 

Full size image

In addition to the A-axis and C-axis, other rotating and moving axes also have similar effects on tooth surface errors, which will not be discussed in detail here. In addition, errors in each axis’s flatness, perpendicularity, and tool disk can also have different effects on the tooth surface.

By combining the parameters of Fig. 15 and data of key points, the influence of flatness error on tooth surface accuracy can be seen. The zero-order normal deviation error of 10−4 μm is induced with \({\varphi }_{y\left(A\right)}\), and the absolute value deviation of the helix angle error of the addendum reaches 9.589 μm. In contrast, the pressure angle error is smaller, and the tooth line drum-shaped error, tooth profile drum-shaped error and tooth face angle error are small to be ignored. The flatness error \({\varphi }_{z\left(A\right)}\) has the greatest influence on the normal deviation, and the peak value of the four vertices reaches -18.091 μm. In addition, tooth direction drum-shaped error and tooth profile drum-shaped error caused by \({\varphi }_{z\left(A\right)}\) can be ignored. The normal deviation error of \({\varphi }_{x\left(C\right)}\) is 10−24 μm level, which can be ignored. The normal deviation error of \({\varphi }_{y\left(C\right)}\) is second after \({\varphi }_{z\left(A\right)}\), and the pressure angle error, and the pressure angle error and the tooth profile drum-shaped error induced by \({\varphi }_{y\left(C\right)}\) are relatively the largest.

Fig. 15
figure 15

Influence of flatness errors on tooth surface (a) \({\phi }_{y\left(A\right)}\) (b) \({\phi }_{z\left(A\right)}\) (c) \({\phi }_{x\left(C\right)}\) (d) \({\phi }_{y\left(C\right)}\) 

Full size image

Compared with the flatness error, the influence of the verticality error on the tooth surface is relatively smaller. The effects of SXY and SYZ are similar, both of which contain obvious helix angle error, negligible normal offset error, pressure angle error, tooth drum-shaped error and tooth profile drum type error. As can be seen from Fig. 16, the biggest difference between the two factors is that the helix angle error of SXY is larger, while the tooth face angle error of SYZ can not be ignored. SYZ causes a peak value of -11.147 μm normal deviation error, and contains a small pressure angle error and the tooth to drum-shaped error can be ignored.

Fig. 16
figure 16

Influence of perpendicularity errors on tooth surface (a) SXY (b) SYZ (c) SZX

Full size image

As can be seen from Fig. 17, the influence of \({\Delta R}_{t}\) and \(\Delta h\) in the cutter head error is relatively single, which causes the normal deviation error of -14.104 μm and -6.841 μm respectively, and does not induce other errors. The error caused by \(\Delta \alpha\) is more complex, including the normal deviation error of 0.566 μm, the pressure angle error near the addendum also reaches 16.358 μm, and the larger tooth profile drum-shaped error and smaller tooth direction drum-shaped error are also included.

Fig. 17
figure 17

Influence of cutter head errors on tooth surface (a) \(\Delta \alpha\) (b) \({\Delta R}_{t}\) (c) \(\Delta h\)  

Full size image

The actual gear surface error is formed by the combined action of all errors, so the value in Table 3 can be brought in to obtain the theoretical maximum error surface. The influence of the comprehensive error on the tooth surface is shown in Fig. 18. It can be seen that the maximum deviations near the addendum and the root are − 316.597 μm, − 248.304 μm and − 297.124 μm, − 238.867 μm, respectively.

Fig. 18
figure 18

Influence of the comprehensive error

Full size image

To further analyze the influence of the comprehensive error on the tooth surface, the deviation value at the origin P35 of the tooth surface is − 278.697 μm by observing the shape of the tooth surface and viewing the data. The coordinate points of the tooth surface change continuously along the z-axis and r-axis, indicating that there are both spiral angle error and pressure angle error. At the same time, it is not difficult to see that the cumulative tooth profile drum-shaped error and tooth line drum-shaped error, as well as the tooth face angle error. To quantify the influence of each error factor on the tooth surface, 45 points of the tooth surface are fitted by Eq. (32), and the fitting error surface and coefficients are shown in Fig. 19 and Table 5 respectively.

Fig. 19
figure 19

Second-order surface fitting error tooth surface

Full size image
Table 5 Quadratic surface fitting coefficient
Full size table

The maximum error surface obtained above is that the extreme deviation value between the actual tooth surface and the ideal tooth surface, which is the upper limit of the tooth surface error. To verify the correctness of the tooth surface error, the gear is detected and the parameters of 37 teeth are obtained, as shown in Fig. 20.

Fig. 20
figure 20

Detection of gear surface data

Full size image

Firstly, the gear is placed flat on the measuring table, and shaft hole surface data obtained by scanning the surface of a gear shaft hole with a probe. Then the data is processed by software to obtain the center of the shaft hole. Therefore, the center of the shaft hole of the VH-CATT gear is taken as the z-axis, and the upward direction is set as the positive direction. Then, the data coordinates are obtained by scanning the probe on the both end surfaces of the gear as shown in the Fig. 20, and then the the data of upper and lower surfaces of the gear can be obtained. Also, The middle section can also be calculated by calculation, that is, the xoy plane. The concave and convex tooth surface of the No.1 tooth is scanned by the probe to obtain the coordinate data, and calculation and comparison with the numerical model. If the tooth profile data of the concave and convex tooth surface is asymmetric at the middle section, it is necessary to scan and measure until it is symmetrical. Then, the symmetrical surface of the tooth profile at the middle section of the concave and convex tooth surface of the No.1 tooth is taken as the xoz plane, so that the x-axis of the measurement coordinate system is determined by the xoy plane and the xoz plane, and it is assumed to be positive to the outer side of the gear. The intersection of the x-axis and z-axis is the coordinate origin of the measurement coordinate system. Finally, the gear measurement coordinate system is uniquely determined by the x-axis, z-axis and coordinate origin. All the detection data are measured based on the coordinate system.

The exhaustive method for complete tooth surface detection is extremely time-consuming and costly. Refer to the Gleason gear error to the middle section of the benchmark, nine tooth profiles are selected for each tooth surface, with an interval of 7 mm between two adjacent profiles. Each tooth profile selects 100 sampling points, and then the sampling points are fitted into a curve and compared with the theoretical tooth profile. Then, 37 concave tooth surfaces are screened to determine the tooth surfaces with maximum error and minimum error. Select the most representative of the mid-section tooth profile curve and pitch circle plane curve, the maximum and minimum values are shown in Fig. 21, 22, 23 and 24.

Fig. 21
figure 21

Maximum error of middle section

Full size image
Fig. 22
figure 22

Minimum error of middle section

Full size image
Fig. 23
figure 23

Maximum error of tooth line

Full size image
Fig. 24
figure 24

Minimum error of tooth line

Full size image

As can be seen from the Fig. 24, in the 37 tooth surfaces, the maximum and minimum values of the tooth profile error of the middle section are 0.0192 mm and 0.0085 mm respectively, while the maximum and minimum values of the tooth line error of the pitch circle plane are 0.0208 mm and 0.0077 mm respectively. Each error is within the maximum comprehensive error surface, which verifies the correctness of the influence law of the comprehensive error on the tooth surface, and also shows that the actual value of each error factor is in the reasonable range.

7 Conclusion

According to the machining principle of VH-CATT gear, the digital model of special machine tool is constructed and the prototype is built. The influence of error sources of special machine tools on tooth surface accuracy is explored, and the design and calculation method of VH-CATT gear surface error is proposed. The gear machining experiment of the special machine tool was carried out, and the surface data of the machined gear was tested to verify the correctness of the numerical simulation results of the tooth surface error analysis.

  • Based on the kinematics of multi-body system, the topology of special machine tool is derived, and the lower numbered body array of gear machine tool is derived and the machine tool coordinate system is established. According to the motion relationship of each relative component, the ideal motion transfer matrix and the tooth surface equation without error are derived.

  • Based on the small error theory, 40 machine tool error sources are summarized and tested to obtain specific error values. Then the motion transfer matrix with error is derived, and the tooth surface equation with error is obtained according to the meshing principle. The design and calculation method of error surface is proposed, and the influence of error on tooth surface is described by the method of second-order approximate surface. The influence of single error factor and multiple error factors on the tooth surface is analyzed, and the range of the influence of the maximum comprehensive error on the tooth surface is solved.

  • The error sources of the machine tool cause the tooth surface to produce normal deviation error, helix angle error, pressure angle error, tooth line drum-shaped error, tooth profile drum-shaped error and tooth surface angle error. The single error factor analysis shows that the moving axis error sources cause greater zero-order and first-order errors, and the rotating axis error sources cause greater second-order errors. Comparing the multi-error factor test results with the gear detection data, the errors in the tooth profile direction and the tooth direction are less than the upper limit of the comprehensive error. The experimental results verify the correctness of the error law proposed in this paper.