1 Introduction

In typical 3-axis machining, to ensure the geometric dimension accuracy of the machined workpiece, computer-aided manufacturing (CAM) systems generally use linear lines instead of curves to discretize the tool-paths into a large number of G01 line segments [1]. To realize high-speed continuous motion, computer numerical control (CNC) systems usually adopt the corner smoothing algorithm based on pre-planning [2]. However, given the existence of multiple buffers, the real-time performance of the system is not strong, and spline interpolation has computational efficiency and accuracy issues. Thus, this study presents a novel real-time smooth trajectory generation technology for accurate interpolation of 3-axis machining.

The G-code generated by CAM is a linear tool-path of point-to-point (P2P) and only has position continuity; thus, it must be completely stopped at the segment transfer, resulting in an extended processing time [3, 4]. To ensure the smoothness of the machining path and the high-order continuity of speed, CNC usually adopts “local blending/smoothing” or “global blending/smoothing” algorithms to improve the geometric continuity of the path and then carries out speed planning and interpolation. In related research, by inserting a line segment, arc, B-spline, and Bezier curve at the adjacent tool-path [5, 6], the smooth transition at the corner is realized and the speed continuity of the path corner is improved. The local smoothing has a good local property and can effectively control the contour error at the corner [6]. Compared with the local smoothing method, the global smoothing method adopts the fitting or interpolation to fit a large number of continuous short linear segments into one or more smooth spline curves under the contour error constraint; commonly used splines include Bezier, B-spline, and NURBS curves [7,8,9]. However, most algorithms adopt iterative calculation or even offline mode, which may affect the real-time performance of the system [2]. The tool-path is often complex and mixed with long and short segments in actual machining. Therefore, local smoothing and global smoothing algorithms must be used in segments according to the track type, and some tracks at the junction of the two fairing algorithms need to be repeatedly faired. The algorithm structure is complex, and the contour accuracy is not easy to control.

After the trajectory is smoothed, the CNC system needs to perform speed planning based on the kinematic constraints of the machine tool, the geometric constraints of the machining path, and the contour errors. The acceleration of S-shaped velocity is continuous, the vibration of the machine tool is reduced, and the surface quality of the workpiece is improved; thus, it is widely used in practical applications [10,11,12]. Furthermore, algorithms with continuous acceleration and even continuous jerk have also been proposed [13,14,15]. As the order of velocity continuity increases, the amount of calculation also increases geometrically.

Finite impulse response (FIR) technology has the characteristics of good smoothness, simple calculation, and no spline fitting. Song [16] proved that the velocity curve after FIR filtering is equivalent to the polynomial velocity curve. Thus, some scholars proposed to use the FIR filters to realize the trajectory control process of the CNC system in one step. The algorithm has a simple structure and is conducive to real-time calculation. For the long segment tool-paths, Sencer [17] and Liu [18] proposed a path-smoothing algorithm based on FIR filtering for adjacent corners. The dwell time is deduced according to the given contour error to adjust the overlapping speed area of the adjacent segments and realize the precise contouring control while meeting the requirements of vibration avoidance, high precision, and short machining time. Bearee [19] realized the maximum utilization of acceleration and shortened the processing time by changing the time constant of the filter. Furthermore, in order to realize jerk continuity, Li [20] further deduced the model of constant velocity sequence passing through the third filter and obtained the third-order continuous velocity curve, satisfying the contour error constraint. Another scheme of contour error control is adjusting the adjacent speed within the delay time, also called the velocity-controlled blending algorithm [21], which can further reduce velocity fluctuation at the corner.

The above studies only considered two adjacent trajectories at the corner but did not give continuous micro-segment processing methods. Hayasaka [22] proposed a block-splitting method to adjust the speed within the delay time and realized the machining of continuous micro-segments based on FIR filtering. Sencer [23, 24] proposed a highly computationally efficient global smoothing interpolation method and determined the final velocity proportion coefficient by solving the influence of each corner on multi-stage speed. In the algorithm, trapezoidal shaped velocity (acceleration limited) is used to solve the contour error, but S-shaped velocity (jerk limited) is commonly used in processing.

This study proposes a universal algorithm of acceleration continuity based on FIR filtering for complex path machining of CNC systems. Using second-order FIR filters, the interpolation smoothing trajectory with continuous acceleration can be generated by adjusting the velocity proportion coefficient. Firstly, a non-stop velocity proportion compression algorithm for continuous long linear segments is proposed, and the adjustment coefficients of the speed of the front and rear segments are calculated according to the contour errors at the corners. On this basis, a blending velocity proportion compression algorithm for continuous micro-segments is proposed. Considering the influence of multiple trajectories before and after a single corner, the final velocity proportion compression coefficient is calculated, so that the generated trajectory satisfies the contour of each corner. Finally, a pre-discrete velocity proportion compression algorithm for blending tool-paths is proposed, which is suitable for complex trajectories in practical machining. Thus, the paper is organized as follows. Section 2 introduces the generation of acceleration continuous jerk-bounded tool-paths based on FIR filters. Section 3 presents the continuous trajectory generation that satisfies the contour error constraint. Section 4 verifies the effectiveness of the algorithm through simulation and actual machining experiments.

2 Jerk-bounded trajectory generation based on FIR filtering

2.1 FIR filter principle

The commonly used velocity acceleration curve of the numerical control system is S-shaped velocity; that is, the acceleration is continuous, and the jerk is bounded, which can be easily obtained by passing through two cascaded FIR filters through the equivalent speed sequence. The transfer function (TF) of the first-order FIR filter under Laplace(s) domain is as follows:

$${H}_{i}(s)=\frac{1}{{T}_{i}}\frac{1-{e}^{-s{T}_{i}}}{s},i=1\dots N$$
(1)

where \({T}_{i}\) is the time duration for the \(i\) th FIR filter. The transfer function consists of an integrator \(\frac{1}{s}\) and a pure delay element \({e}^{-{sT}_{i}}\). The impulse response is obtained by inverse Laplace transform:

$${h}_{i}(t)={L}^{-1}({H}_{i}(s))=\frac{u(t)-u(t-{T}_{i})}{{T}_{i}}\text{ where }u(t)=\{\begin{array}{c}1,t\ge 0\\ 0,t<0\end{array}$$
(2)

\({h}_{i}\left(t\right)\) is a rectangular pulse of unit area, as shown in Fig. 1, revealing that the final position of the trajectory will not change after passing through the FIR filter, which is the “position invariance” of the FIR filter [18].

Fig. 1
figure 1

Impulse response of FIR filter

Full size image

2.2 Generation of S-shaped velocity curve

In 3-axis machining, for each line of G-code, the start position coordinate \({P}_{s}\left({X}_{s},{Y}_{s},{Z}_{s}\right)\), end position coordinate \({P}_{E}\left({X}_{E},{Y}_{E},{Z}_{E}\right)\) and feed rate \(F\) can be obtained by compiling and analyzing. The speed planning of the rectangular-frame is obtained from the segment length \(L\) and the feed rate \(F\):

$$L=\Arrowvert P_E-P_S\Arrowvert\;\mathrm{and}\;T_v=\frac LF$$
(3)

where \({T}_{v}\) represents the duration of the rectangular frame speed pulse. When the velocity curve of the rectangular-frame is convolved with an FIR filter with a time constant of \({T}_{1}\) and then convoluted with an FIR filter with a time constant of \({T}_{2}\), the S-shaped velocity curve commonly used in CNC system can be obtained [16]. To get a seven-segmented S-shaped velocity curve, that is, the acceleration curve of the system is a trapezoid and its jerk is bounded; it must also be ensured that \({T}_{v}>{T}_{1}+{T}_{2}\) and \({T}_{2}<{T}_{1}\). At this time, the maximum acceleration and jerk of the system are calculated as:

$$a_{\max}=\frac F{T_1}\;\mathrm{and}\;j_{\max}=\frac F{T_1T_2}$$
(4)

After the filtering effect of these two cascaded FIR filters, the obtained speed is as follows:

$${v}^{^{\prime}}\left(t\right)=v\left(t\right)*{h}_{1}\left(t\right)*{h}_{2}\left(t\right)=\left\{\begin{array}{c}\begin{array}{cc}\frac{1}{2}\frac{F}{{T}_{1}{T}_{2}}{t}^{2}& {0}\le t\text{<}{T}_{2}\end{array}\\ \begin{array}{cc}\frac{1}{2}\frac{F{T}_{2}}{{T}_{1}}+\frac{F}{{T}_{1}}(t-{T}_{2})& {T}_{2}\le t<{T}_{1}\end{array}\\ \begin{array}{c}\begin{array}{cc}F-\frac{1}{2}\frac{F}{{T}_{1}{T}_{2}}{\left(\left({T}_{1}+{T}_{2}\right)-t\right)}^{2}& {T}_{1}\le t<{T}_{1}+{T}_{2}\end{array}\\ \begin{array}{cc}F& {T}_{1}+{T}_{2}\le t<{T}_{v}\end{array}\\ \begin{array}{c}\begin{array}{cc}F-\frac{1}{2}\frac{F}{{T}_{1}{T}_{2}}{\left(t-{T}_{v}\right)}^{2}& {T}_{v}\le t<{T}_{v}+{T}_{2}\end{array}\\ \begin{array}{cc}F-\frac{1}{2}\frac{F{T}_{2}}{{T}_{1}}-\frac{F}{{T}_{1}}(t-({T}_{v}+{T}_{2}))& {T}_{v}+{T}_{2}\le t<{T}_{v}+{T}_{1}\end{array}\\ \begin{array}{c}\begin{array}{cc}{\frac{1}{2}\frac{F}{{T}_{1}{T}_{2}}\left(\left({T}_{v}+{T}_{1}+{T}_{2}\right)-t\right)}^{2}& {T}_{v}+{T}_{1}\le t<{T}_{v}+{T}_{1}\text{+}{T}_{2}\end{array}\\ \begin{array}{cc}0& t\ge {T}_{v}+{T}_{1}+{T}_{2}\end{array}\end{array}\end{array}\end{array}\end{array}\right.$$
(5)

The acceleration and position can be obtained by differentiating and integrating the velocity. The whole process is shown in Fig. 2.

Fig. 2
figure 2

S-shaped speed curve generation by FIR filtering

Full size image

The total processing time of the system is calculated as:

$$\begin{array}{ccc}T={T}_{v}+{T}_{d}={T}_{v}+{T}_{1}+{T}_{2},& \mathrm{where}& {T}_{d}\text{=}{T}_{1}+{T}_{2}\end{array}$$
(6)

where \({T}_{d}\) is the delay time brought by the introduction of the filter. If the system introduces an nth order FIR filter, theoretically, the speed curve can achieve nth order continuity [17, 25], and the delay time \({T}_{d}\) is calculated as:

$${T}_{d}={T}_{1}+\cdots \cdots +{T}_{n}$$
(7)

3 Continuous trajectory generation under contour error constraints

It has been introduced that a single-segment S-shaped velocity curve with continuous acceleration can be generated based on FIR filtering. Thus, this chapter will further introduce the trajectory generation method for continuous tool-paths following contour control. Section 3.1 first solves the velocity proportion coefficients of the two front and rear trajectories under the constraint of contour error at a single corner for long segments. The velocity proportion coefficient is used to adjust the speed of each track segment on the premise that the track segment length remains unchanged, so as to meet the contour accuracy at the track corner. Section 3.2 extends this idea to the case of continuous micro-segments, solves the influence of multiple trajectories at a single corner under the constraint of contour error one by one, and obtains the velocity proportion coefficient of each micro-segment by synthesizing the results at multiple corners. Section 3.3 adopts pre-discretization to scatter the complex trajectory into continuous micro-segments to satisfy the application of the algorithm in Sect. 3.2 and realize a universal continuous trajectory generation method based on FIR filtering.

3.1 Non-stop velocity proportion compression for long segments

As described in Section 2, the premise of obtaining the S-shaped curve of the maximum feed speed \(F\) is to ensure \({T}_{v}>{T}_{1}>{T}_{2}\) and \({T}_{v}\ge {T}_{d}={T}_{1}+{T}_{2}\). Then, for continuous trajectory, by carrying out rectangular-frame speed planning (RSP), a series of rectangular-frame speeds can be obtained. If the dwell time between adjacent rectangular-frame is greater than or equal to the delay time, a full-stop and an exact P2P motion can be obtained; that is, the system will continue to run the next track after each track has completely stopped, as shown in Fig. 3. At this time, the system shows no contour error, but this movement will seriously affect the machining efficiency of the system and greatly increase the machining time. Therefore, Ref. [21] proposed two methods: non-stop dwell-time control path blending (NS-DCB) and non-stop velocity-controlled blending (NS-VCB). By adjusting the dwell time between adjacent rectangular-frame (corresponding to NS-DCB) or the mixing velocity between adjacent rectangular-frame (corresponding to NS-VCB), the system can shorten the processing time to satisfy the contour error constraint. However, as pointed out in the literature, both methods are only suitable for long segments, which require \({T}_{v}\ge {T}_{d}\).

Fig. 3
figure 3

P2P mode by FIR filtering

Full size image

To suggest a general trajectory control algorithm based on FIR filtering for long segments, this paper proposes a non-stop velocity proportion compression algorithm (NS-VPC), which makes the system dwell time Tdwell = 0 and the mixing time Tmix = Td − Tdwell = Td at the corner. At this time, the system starts to perform the trajectory interpolation of the second segment when the first segment of the trajectory has not reached the end position, resulting in mixed corner and contour errors, as shown in Fig. 4.

Fig. 4
figure 4

Blending error under long segments

Full size image

Line \(\mathrm{N}1\) corresponds to the starting point \({P}_{1}\left({X}_{1},{Y}_{1},{Z}_{1}\right)\), line \(\mathrm{N}2\) corresponds to the intermediate point \({P}_{2}\left({X}_{2},{Y}_{2},{Z}_{2}\right)\), and line \(\mathrm{N}3\) corresponds to the ending point \({P}_{3}\left({X}_{3},{Y}_{3},{Z}_{3}\right)\). The unit vector of the \({N}_{1}{N}_{2}\) track segment is \(\overrightarrow{{O}_{1}}\), the unit vector of the \({N}_{2}{N}_{3}\) track segment is \(\overrightarrow{{O}_{2}}\), and it is assumed that the feed rate of the two tracks is the same, that is, \({F}_{1}={F}_{2}=F\). The maximum contour error of the system occurs at the angle bisector of \(\angle {P}_{1}{P}_{2}{P}_{3}\) [21], the corresponding time is set to \({T}_{b}\), and the maximum contour error is set to \(\varepsilon\).

Where

$$\left\{\begin{array}{c}{T}_{b}={T}_{v1}+\frac{1}{2}{T}_{d}\\ \varepsilon =\parallel \overrightarrow{{P}_{2}{P}_{b}}\parallel =\parallel \overrightarrow{{l}_{2}}-\overrightarrow{{l}_{1}}\parallel \end{array}\right.$$
(8)

\(\overrightarrow{{l}_{1}}\) corresponds to the vector of the post-influence area \({s}_{1}\) at the maximum contour error of the first track, and \(\overrightarrow{{l}_{2}}\) corresponds to the vector of the pre-influence area \({s}_{2}\) at the maximum contour error of the second track.

From Eq. (5),

$${s}_{1}={s}_{2}=\underset{0}{\overset{t=\frac{{T}_{d}}{2}}{\int }}{v}^{^{\prime}}(t)dt=\left\{\begin{array}{c}\begin{array}{cc}\frac{1}{6}\frac{{FT}_{2}^{2}}{{T}_{1}}\text{+}\frac{1}{2}\frac{F{T}_{2}}{{T}_{1}}\text{(}{T}_{1}-{T}_{2})+\frac{1}{2}\frac{F}{{T}_{1}}{(t-{T}_{2})}^{2}& {T}_{d}<2{T}_{1}\end{array}\\ \begin{array}{cc}\frac{1}{6}\frac{{FT}_{2}^{2}}{{T}_{1}}\text{+}\frac{1}{2}\frac{F{T}_{2}}{{T}_{1}}\text{(}{T}_{1}-{T}_{2})+\frac{1}{2}\frac{F}{{T}_{1}}{\left({T}_{1}-{T}_{2}\right)}^{2}-\frac{1}{6}\frac{F}{{T}_{1}{T}_{2}}{\left(t-{T}_{1}\right)}^{3}+\frac{1}{2}\frac{F}{{T}_{1}}{\left(t-{T}_{1}\right)}^{2}+\frac{1}{2}\frac{F(2{T}_{1}-{T}_{2})}{{T}_{1}}\left(t-{T}_{1}\right)& {T}_{d}\ge 2{T}_{1}\end{array}\end{array}\right.$$
(9)

Therefore,

$$\left\{\begin{array}{c}\overrightarrow{{l}_{1}}={s}_{1}\cdot \overrightarrow{{O}_{1}}\\ \overrightarrow{{l}_{2}}={s}_{2}\cdot \overrightarrow{{O}_{2}}\end{array}\right.$$
(10)

where

$$\left\{\begin{array}{c}\overrightarrow{{O}_{1}}=\frac{({X}_{2}-{X}_{1},{Y}_{2}-{Y}_{1},{Z}_{2}-{Z}_{1})}{{L}_{1}}=({x}_{1},{y}_{1},{z}_{1})\\ \overrightarrow{{O}_{2}}=\frac{({X}_{3}-{X}_{2},{Y}_{3}-{Y}_{2},{Z}_{3}-{Z}_{2})}{{L}_{2}}=({x}_{2},{y}_{2},{z}_{2})\end{array}\right.$$
(11)

Thus, by plugging Eqs. (9)–(12) into Eq. (8), \(\varepsilon\) is calculated as:

$$\varepsilon =\parallel ({s}_{2}{x}_{2}-{s}_{1}{x}_{1},{s}_{2}{y}_{2}-{s}_{1}{y}_{1},{s}_{2}{z}_{2}-{s}_{1}{z}_{1})\parallel$$
(12)

Assuming that the allowable error given by the numerical control system is εallow, the velocity proportion coefficient \({k}_{v}\) should be calculated as:

$${k}_{v}=\frac{{\varepsilon }_{allow}}{\varepsilon }$$
(13)

To satisfy the contour error of the system, the velocity of the \({N}_{1}{N}_{2}\) trajectory segment and the \({N}_{2}{N}_{3}\) trajectory segment should be adjusted is calculated as:

$$\left\{\begin{array}{c}{v}_{1}^{^{\prime}}={k}_{v}\cdot {F}_{1}\\ {v}_{2}^{^{\prime}}={k}_{v}\cdot {F}_{2}\end{array}\right.$$
(14)

To ensure that the length of the track segment remains unchanged, the time of these two segments should also be adjusted accordingly.

$$\left\{\begin{array}{c}{T}_{v,1}^{^{\prime}}=\frac{{L}_{1}}{{v}_{1}^{^{\prime}}}\\ {T}_{v,2}^{^{\prime}}=\frac{{L}_{2}}{{v}_{2}^{^{\prime}}}\end{array}\right.$$
(15)

It should be noted that the above derivation is based on \({F}_{1}={F}_{2}\). If \({F}_{1}\ne {F}_{2}\), the maximum contour error at the corner is not at the angle bisector of \(\angle {P}_{1}{P}_{2}{P}_{3}\), but the actual contour error is greater than the calculated value of Eq. (12), and the above algorithm can still meet the contour error constraint of the system [21].

3.2 Multi-stage mixing velocity proportion compression for micro-segments

In CNC machining, CAM usually breaks up the spline into a large number of continuous tiny linear segments. Then, because of \({T}_{v}<{T}_{2}<{T}_{1}\), the NS-VPC algorithm is no longer applicable. Therefore, based on the NS-VPC algorithm in Section 3.1, this section proposes a multi-stage mixing velocity proportion compression (MM-VPC) algorithm for continuous micro-segments, which can effectively ensure that the system meets the contours. Under the premise of error constraints, a smooth transition of the angular velocity is achieved.

Given \({T}_{v}<{T}_{2}<{T}_{1}\), the maximum speed and acceleration that the system can reach at this time is calculated as:

$$\left\{\begin{array}{c}{v}_{\mathrm{max}}=\frac{{\text{FT}}_{v}}{{T}_{1}}\\ {a}_{\mathrm{max}}=\frac{{\text{FT}}_{v}}{{T}_{1}{T}_{2}}\end{array}\right.$$
(16)

The jerk is the same as that in the case of the long segment, which is still \({j}_{\mathrm{max}}=\frac{F}{{T}_{1}{T}_{2}}\). Then, after the rectangular-frame speed passes through the second-order FIR filter, the S-shaped speed curve is shown in Fig. 5.

Fig. 5
figure 5

S-shaped velocity curve

Full size image

Its speed formula is calculated as:

$${v}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(t\right)=v\left(t\right)*{h}_{1}^{\mathrm{^{\prime}}}\left(t\right)*{h}_{2}^{\mathrm{^{\prime}}}\left(t\right)=\left\{\begin{array}{c}\begin{array}{cc}\frac{1}{2}\frac{F}{{T}_{1}{T}_{2}}{t}^{2}& 0\le t<{T}_{v}\end{array}\\ \begin{array}{cc}\frac{1}{2}\frac{{FT}_{v}^{2}}{{T}_{1}{T}_{2}}+\frac{{FT}_{v}}{{T}_{1}{T}_{2}}\left(t-{T}_{v}\right)& {T}_{v}\le t<{T}_{2}\end{array}\\ \begin{array}{c}\begin{array}{cc}\frac{{FT}_{v}}{{T}_{1}}-\frac{1}{2}\frac{F}{{T}_{1}{T}_{2}}{\left(\left({T}_{v}+{T}_{2}\right)-\right)}^{2}& {T}_{2}\le t<{T}_{v}+{T}_{2}\end{array}\\ \begin{array}{cc}\frac{{FT}_{v}}{{T}_{1}}& {T}_{v}+{T}_{2}\le t<{T}_{1}\end{array}\\ \begin{array}{c}\begin{array}{cc}\frac{{FT}_{v}}{{T}_{1}}-\frac{1}{2}\frac{F}{{T}_{1}{T}_{2}}{\left(t-{T}_{1}\right)}^{2}& {T}_{1}\le t<{T}_{v}+{T}_{1}\end{array}\\ \begin{array}{cc}\frac{{FT}_{v}}{{T}_{1}}-\frac{1}{2}\frac{{FT}_{v}^{2}}{{T}_{1}{T}_{2}}-\frac{{FT}_{v}}{{T}_{1}{T}_{2}}\left(t-\left({T}_{v}+{T}_{1}\right)\right)& {T}_{v}+{T}_{1}\le t<{T}_{1}+{T}_{2}\end{array}\\ \begin{array}{c}\begin{array}{cc}\frac{1}{2}\frac{F}{{T}_{1}{T}_{2}}{\left(\left({T}_{v}+{T}_{1}+{T}_{2}\right)-t\right)}^{2}& {T}_{1}+{T}_{2}\le t<{T}_{v}+{T}_{1}+{T}_{2}\end{array}\\ \begin{array}{cc}0& t\ge {T}_{v}+{T}_{1}+{T}_{2}\end{array}\end{array}\end{array}\end{array}\end{array}\right.$$
(17)

For a continuous micro-segment trajectory, the maximum value of the contour error at the kth contour point is generated in \({T}_{b,k}\), and the maximum contour error \({\varepsilon }_{k}\) is affected by the displacement vector of the rear area of the front \(m\) rectangular-frames and the front area displacement of the rear \(n\) rectangular-frames, as shown in Fig. 6.

Fig. 6
figure 6

Blending error under micro-segments

Full size image

Where,

$$\left\{\begin{array}{c}{T}_{b,k}={T}_{k}+\frac{{T}_{d}}{2}\\ {\varepsilon }_{k}=\Vert \sum_{i=0}^{n-1}\overrightarrow{{l}_{k+i}}-\sum_{j=0}^{m-1}\overrightarrow{{l}_{k-j-1}}\Vert \end{array}\right.$$
(18)

where \({T}_{k}\) represents the starting time of the kth rectangular-frame. Then, the key of the algorithm is to solve the displacement vectors \(\overrightarrow{{l}_{k+i}}\) and \(\overrightarrow{{l}_{k-j-1}}\).

$$\left\{\begin{array}{c}\overrightarrow{{l}_{k+i}}=\left({\int }_{0}^{{t}_{k+i}}{v}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(t\right)\right)\bullet \overrightarrow{{O}_{k+i}},i=0,\dots ,n-1\\ \overrightarrow{{l}_{k-j-1}}=\left({L}_{k-j-1}-{\int }_{0}^{{t}_{k-j-1}}{v}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(t\right)\right)\bullet \overrightarrow{{O}_{k-j-1}},j=0,\dots ,m-1\end{array}\right.$$
(19)

where \({L}_{k-j-1}\) represents the length corresponding to the (\(k-j-1\))th rectangular-frame, \({t}_{k+i}\) represents the influence time of each rectangular-frame in the previous \(m\) rectangular-frames on the contour error point and \(\overrightarrow{{O}_{k+i}}\) is its direction vector. \({t}_{k-j-1}\) represents the influence time of each of the following \(n\) rectangular-frames on the contour error point, and \(\overrightarrow{{O}_{k-j-1}}\) is its direction vector.

$$\left\{\begin{array}{c}{t}_{k+i}={T}_{b,k}-{T}_{k+i},i=0,...,n-1\\ {t}_{k-j-1}={T}_{k-j-1}+{T}_{v,k-j-1}+{T}_{d}-{T}_{b,k},j=0,...,m-1\end{array}\right.$$
(20)

By substituting Eqs. (19) and (20) into Eq. (18), the contour error \({\varepsilon }_{k}\) of the system at the \(k\) th contour point can be obtained, and the velocity proportion coefficient \({k}_{v,k}\) is calculated as:

$${k}_{v,k}=\frac{{\varepsilon }_{{\text{allow}},k}}{{\varepsilon }_{k}}$$
(21)

Therefore, the velocity scale coefficient of the \(m+n\) rectangular-frames at the kth contour point is \({k}_{v,k}\). Given that each rectangular-frame may affect more than one corner, it may have multiple speed scale factors. The minimum value is taken as the final velocity proportion coefficient among the multiple velocity proportion coefficients of each rectangular-frame to ensure that the contour error of each contour point meets the constraint.

$${k}_{v}^{^{\prime}}=\mathrm{min}\left\{{k}_{v,0},\cdots ,{k}_{v,k},\cdots ,{k}_{v,n}\right\}$$
(22)

Its speed and duration are also adjusted accordingly as:

$$\left\{\begin{array}{c}{F}^{^{\prime}}={k}_{v}^{^{\prime}}\bullet F\\ {T}_{v}^{^{\prime}}=\frac{L}{{F}^{^{\prime}}}\end{array}\right.$$
(23)

3.3 Pre-discrete velocity proportion compression algorithm for blending tool-paths

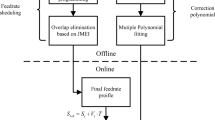
In actual processing, most G-codes are mixed paths with long segments and micro-segments. In this case, neither the NS-VPC nor MM-VPC algorithms are applicable anymore. Thus, this section proposes a pre-discrete velocity proportion compression algorithm (PD-VPC) for mixed paths, which can meet the needs of various machining paths and improve machining efficiency by effectively ensuring contour error constraints.

The key to the PD-VPC algorithm is to pre-discretize in advance, break the long G-codes into micro-segments based on certain rules, and then put the broken G-code into the MM-VPC algorithm to realize speed adjustment and interpolation. The algorithm flow is shown in Fig. 7.

Fig. 7
figure 7

PD-VPC algorithm process

Full size image

The premise of the MM-VPC algorithm is to satisfy \({T}_{v}<{T}_{2}<{T}_{1}\), the critical condition \({T}_{v}={T}_{2}\), and the system acceleration reaching the maximum value at this time. Thus, the minimum time for segmentation is Tdiv,min = T2. Firstly, the entire G-code is read in advance, the speed planning of the rectangular-frame is carried out, the line segment Tv ≥ Tdiv,min is marked as a long segment, and linear interpolation is performed on the long segment and discretize into micro-segments. To break up the long segment into a certain number of micro-segments, a discrete coefficient \({k}_{s}\) is introduced, and the duration of each micro-segment is denoted as \({T}_{v,s}\),

$${T}_{v,s}={k}_{s}\cdot {T}_{2},{k}_{s}\in \left(0,1\right)$$
(24)

It should be noted that the value of \({k}_{s}\) will not affect the actual running time and velocity acceleration trend of G-code trajectory but only break the long segment into micro-segments for application to the MM-VPC algorithm. However, the value of \({k}_{s}\) will directly affect the number of broken segments, thus affecting the operational efficiency of the algorithm.

Assuming that the running time of a long segment of G-code is denoted as \({T}_{i}\), the coordinates of the starting point are \({P}_{i-1}\left({X}_{i-1},{Y}_{i-1},{Z}_{i-1}\right)\), and the coordinates of the end point are \({P}_{i}\left({X}_{i},{Y}_{i},{Z}_{i}\right)\). Then, the number of short segments that will be broken up into the following:

$$N={\text{ceil}}\left(\frac{{T}_{i}}{{T}_{v,s}}\right),N\in {N}^{*}\text{and }N\ge 2$$
(25)

The ceil function means rounding up. Through linear interpolation, the newly added intermediate position G-code point \({P}_{n}=\left({X}_{n},{Y}_{n},{Z}_{n}\right)\) can be obtained. The coordinates of each axis are solved as follows where \(n=\mathrm{1,2},\dots ,N-1\).

$$\begin{array}{c}{X}_{n}={X}_{i-1}+({X}_{i}-{X}_{i-1})*\frac{n}{N}\\ {Y}_{n}={Y}_{i-1}+({Y}_{i}-{Y}_{i-1})*\frac{n}{N}\\ {Z}_{n}={Z}_{i-1}+({Z}_{i}-{Z}_{i-1})*\frac{n}{N}\end{array}$$
(26)

4 Experimental results

This study uses an actual 5-axis machine tool for practical verification in combination with the interpolation point data generated by the simulation experiment. The experimental machine tool is shown in Fig. 8. The machine tool adopts five-axis full closed-loop control and supports locking the rotating axes. The maximum feed speed of the linear axis is 48,000 [mm/min], and the control resolution is 0.001 [mm]. In this section, the rotating axes are locked in the whole experiment, and the closed-loop sampling period of the servo control system is set to 1 [kHz].

Fig. 8
figure 8

Experimental machine tool

Full size image

The Mercedes-Benz mold testing sample is the standard test sample of 3-axis milling in the industry [2]. It is recognized by many countries in Europe and the USA and is widely used to evaluate NC machine tools’ machining efficiency and accuracy. The specimen’s surface contains various complex tool-path features such as lines, curves and surfaces, as shown in Fig. 9a. By importing the G-code of the Mercedes Benz mold testing sample into the PD-VPC algorithm proposed in this paper, given the FIR filter parameters and contour error (the specific parameters are the same as below), the interpolation points that meet the actual processing requirements can be obtained. The speed expressed by the coloring method is shown in Fig. 9b. The dark red represents the maximum speed of 3000 [mm/min], and the dark blue represents the speed approaching 0. It can be seen from the figure that the speed trend conforms to the track characteristics of the Mercedes Benz sample. There are different degrees of deceleration at each corner, and the maximum speed is basically obtained at long segments and small curvature.

Fig. 9
figure 9

The Mercedes Benz pattern

Full size image

As the Mercedes Benz sample is composed of several regions, and the number of G-code points for finish machining exceeds 620 thousand, this study needs to select a representative path for specific comparison. The G-code tool-paths in the red dotted box in Fig. 9 has a large curvature change, and the complexity of the track segment length is the largest. Thus, this study uses a section of the line-cutting path as the processing path, as shown in Fig. 10, to verify the feasibility and effectiveness of the algorithm. The red point represents the command position of G-code, and the blue line is the tool-path formed by the command position. The tool-path is composed of long segments and continuous micro-segments, and the trajectory contour includes lines, curves, sharp corners, and rounded corners. This multi-feature complex tool-path is representative of practical NC machining.

Fig. 10
figure 10

The line-cutting of Benz pattern

Full size image

The line-cutting trajectory includes 233 linear segments, of which the shortest path length is 0.021 [mm], the longest path length is 29.078 [mm], the total path length is 221.849 [mm], and the average length is 0.952 [mm]. The given feed rate during machining is 3000 [mm/min], and the set contour error is 10 [μm]. To make a fair and comprehensive comparison, this study uses the following FIR filter interpolation algorithms for the line-cutting trajectory: (1) the P2P mode, where the dwell time is equal to the delay time; (2) the NS-DCB algorithm proposed in Ref. [21], which controls the dwell time according to the contour error; (3) the proposed PD-VPC algorithm; (4) velocity directly blending mode, whose dwell time is zero and hereinafter referred to as VDB mode. It is worth mentioning that the NS-VCB algorithm proposed in Ref. [21] is only applicable to long segments; thus, it does not participate in the comparative experiment.

For the above three algorithms, the same filter constant must be used. In this study, T1 = 20 [ms] and T2 = 10 [ms] are set. The PD-VPC algorithm needs to discretize the G-code points in advance. Through the simulation of the line-cutting trajectory, the running time Trun of the algorithm and the total interpolation time Tinterp of G-code under different \({k}_{s}\) are obtained, as shown in Fig. 11.

Fig. 11
figure 11

The influence law of discrete coefficient

Full size image

It can be seen from the figure that when \({k}_{s}\) is close to 1, the running time of the algorithm Trun is short. Due to the number of discrete segments of the system is small, the speed of some regions is depressed and the duration time is long, so the total interpolation time of G-code Tinterp is long. When \({k}_{s}\) is close to 0.67, the total interpolation time Tinterp is significantly shorter, but the running time Trun is slightly increased because of too many discrete segments of the system. Later, as \({k}_{s}\) exceeds 0.5 and approaches 0.1, the total interpolation time Tinterp basically remains unchanged, while the running time Trun increases exponentially. Thus, the running time of the algorithm and the total interpolation time of G-code are usually appropriate when \({k}_{s}\in \left[0.5,0.75\right]\) is usually taken. In this study, the local optimal solution \({k}_{s}=0.5\) is chosen.

The G-code track before and after discretization is shown in the Fig. 12. The blue point is the original G-code point, and the orange point is the discrete G-code point. It is obvious that long segments are regularly broken into short segments, while the micro-segments remain unchanged. After discretization, the number of track segments is 799, and the length of the shortest segment remains unchanged because this segment is not discretized. The longest segment length is 0.503 [mm], and the duration of its rectangular-frame speed can be calculated to be 10.12 [ms], which is approximately equal to the delay time of the second-order filter. As shown in the red dotted line box in the figure, on the one hand, in the area of rapid curvature change, such as corner [1], the track segments are micro-segments and will not be discrete. On the other hand, the micro-segment on a path close to a straight line, such as corner [2], also remains unchanged. Discretization realizes consistent processing of trajectory characteristics, making the processed trajectory meet the input requirements of the MM-VPC algorithm.

Fig. 12
figure 12

G-code pre-discretization

Full size image

Figure 13a shows the distribution of trajectory velocity on the interpolation contour obtained by the PD-VPC algorithm. RGB, three primary colors, are selected to represent the speed. Red color represents high speed, and light colors represent low speed. There are 13 obviously light colored areas, corresponding to the deceleration part in Fig. 13b. For large corners, that is, close to a straight line, such as corners [2, 4, 12], the speed will drop slightly, and then quickly return to the maximum speed. However, for areas with large curvature changes, such as corners [3, 7, 11], the corresponding deceleration time is longer, and there are multiple speed extreme points. Consequently, the result of velocity planning conforms to the geometric characteristics of the trajectory.

Fig. 13
figure 13

Velocity distribution on the contour and profiles

Full size image

Figure 14 shows the machining contour calculated by interpolation with four algorithms, in which the blue point represents the G-code point of the Benz sample. The 3-axis contouring performance for the interpolation schemes are measured in Fig. 15. As can be seen from the figures, the P2P mode performs point-to-point precise motion. It completely coincides with the G-code point trajectory. Thus, no contour errors are observed. The VDB mode directly mixes the speed without considering the contour error constraint. So out-of-tolerance is evident at the corner. The proposed PD-VPC algorithm complies with the set contour error requirement of 10 [μm] in all processing areas, whereas the NS-DCB algorithm has an out-of-tolerance phenomenon in local areas. The corners [1,2,3,4,5,6] in the Fig. 14 show that the contour error of the PD-VPC algorithm is smaller than that of the NS-DCB algorithm at various corners. Figure 15 also shows that the contour error of the PD-VPC algorithm is smaller than NS-DCB algorithm in most areas of the whole trajectory. Summarily, the PD-VPC algorithm can effectively and accurately control contour error.

Fig. 14
figure 14

Interpolation point track of line-cutting

Full size image
Fig. 15
figure 15

Experimental contouring errors

Full size image

The composite velocity, acceleration, and jerk of the four algorithms are shown in Fig. 16. No dwell time is observed in VDB mode. Thus, the processing time is the shortest, only 4.47 [s]. In P2P mode, given frequent acceleration and deceleration, the processing time is the longest, which is 11.43 [s]. Although the processing time of the PD-VPC algorithm is slightly longer than that of the NS-DCB algorithm, Fig. 16b and c show that the PD-VPC algorithm effectively reduces the acceleration and jerk amplitude of the system. The performance of acceleration on CNC machine tools is force. Decreasing the acceleration and jerk means that the amplitude and change rate of the force on the system become smaller. Therefore, system vibration will be reduced, and the surface quality will be improved. Given the starting and ending of the profiles correspond to the feed section and withdrawal section of the machining, it is not considered when comparing the acceleration and jerk amplitude.

Fig. 16
figure 16

Interpolated kinematic profiles along line-cutting

Full size image

Figure 17 shows the single-axis kinematics parameters for the X-axis and Z-axis of the system. Figure 17b and c show that the motion trajectory acceleration generated by the PD-VPC algorithm is continuous, the jerk is bounded, and the amplitude of acceleration and jerk is greatly reduced. Thus, the interpolation point trajectory generated by PD-VPC algorithm is smooth and second-order continuous. The PD-VPC algorithm can effectively reduce the uniaxial vibration of the system. Given the trajectory characteristics of the Benz tool-path, the performance on each axis is also different. The acceleration amplitude of X-axis is reduced by 18%, and the jerk amplitude is reduced by 73%. The acceleration amplitude of Z-axis is reduced by 51%, and the jerk amplitude is reduced by 82%. Conclusively, the acceleration amplitude of each axis is reduced to a certain extent, and the jerk amplitude is greatly reduced.

Fig. 17
figure 17

X-axis and Z-axis interpolated kinematic profiles

Full size image

5 Conclusions

This paper presents a universal algorithm for blending tool-paths machining of CNC system based on FIR filtering. The results show that the algorithm can control the contour error effectively, reduce system vibration, and improve machining quality. The existing algorithms mainly focus on smooth trajectory generation for long segments. Few studies for continuous micro-segments adopt the trapezoidal shaped velocity scheme when calculating the corner contour error. This study proposes a general algorithm for generating continuous acceleration trajectory based on FIR filtering, which can be applied to the blending tool-paths with long segments and micro-segments and effectively control the contour error. Experimental results show that the overall processing time can be reduced up to 50% compared to the P2P mode. On the other hand, the acceleration amplitudes of the single axis can be reduced up to 10–50%, and the jerk amplitude can be reduced up to 70–80%. Thus, the algorithm can effectively suppress the vibration in the processing process and improve machining surface quality. In the future, the PD-VPC algorithm will also be applied to the research of 5-axis trajectory planning, and the core problem is to solve the model of tool orientation vector contour error.