1 Introduction

It is tough and time-consuming to design defect detection methods for complex real-world industrial operations [1]. Numerous manufacturing cells execute a variety of assembly activities as well as functional tests in modern computer-based manufacturing systems. Computer software supervises a specific production process, many of which are custom created, and the cells are controlled by it. One of the most significant duties for computers assigned to manufacturing plant supervision is to detect as well as diagnose product problems. Obtaining data required for process analysis is the initial stage in this task. Only a few data-generating mechanisms and sensing devices were used in first inspection systems. As a result, engineers could only analyze a limited amount of data for fault diagnosis method, and a more method based on structured data analysis was needed [2]. Limit checking is still the only method of fault detection utilized in numerous manufacturing plants today [3]. In this example, for a given characteristic in production process for a product, maximal and minimum values are known as thresholds. When value of a feature is within these defined boundaries, it is said to be in a normal functioning state. Although simple, resilient, and trustworthy, this technique is sluggish to respond to deviations in a particular data characteristic as well as fails to detect complicated failures, which are detected by examining feature correlations. Another issue with this method is difficulty in defining threshold values for each attribute.

In terms of data analysis, industrial applications with heavy machinery, in particular, might advantage from a deeper understanding of underlying methods as well as equipment state to modify their maintenance plans [4]. These components are used in the machine’s rotating mechanics. These bearing parts deteriorate over time as a result of friction as the machine rotates. Traditionally, condition of a rolling bearing element was estimated using breakdown data from the past. Nowadays, state of a bearing element is determined by installing vibration sensors on certain sections of machines or detecting the motor currents of electrical engine that drives these elements. Vibrations, in particular, have proven to be beneficial in revealing underlying status of bearings. Raw signals must be denoised as well as pre-processed before analysis, utilizing complicated and time-consuming signal processing methods to obtain useful data, which is a vital requirement for an effective analysis. As a result, the emphasis has switched to deep learning algorithms that can analyze raw data and create features automatically by recognizing patterns in input data. This automated approach saves time, is less prone to human error, and may need a specialized domain expert with less subject experience [5].

FDD (fault detection and diagnosis) is a vital control technique for achieving this task among numerous process supervision techniques because many industries seek to enhance their process performance by increasing their FDD capability. FDD’s primary functions are categorized into 2 sections: (1) monitoring process behavior and (2) disclosing presence, characteristics, and root causes of errors. To preserve high process output as well as throughput in industrial processes, rapid, significant detection tools for process or equipment failures that may affect whole system’s performance are needed [4,5,6]. The FDD for many different processes has gained a lot of attention from many industrial sectors and academia over the years due to the many significant benefits that may be obtained from lowering process or product-related costs, improving quality and productivity. FDD has played a key role in a variety of industrial engineering methods, including semiconductor production and chemical and software engineering to name a few. As a result, there is an enhancing requirement for effective detection as well as diagnosis of suspicious defects to avert process deterioration, which could ultimately result in a decrease in product yield or process throughput. In general, the FDD work is conducted based on multiple processes as well as equipment data measured by instruments as a key way for process supervision [6].

Research contribution is as follows:

  • To collect historical data from soft sensors in designing fault detection systems for monitoring and controlling with optimization

  • To pre-process the collected data in removing null values and missing data

  • To detect and diagnose the faults of processed data using probabilistic multi-layer Fourier transform perceptron (PMLFTP)

  • To optimize and control the data of soft sensors using auto-regression-based ant colony optimization (AR_ACO)

The experimental analysis has been carried out in terms of computational rate, quality of service (QoS), root mean square error (RMSE), fault detection rate, control optimization for various fault scenarios.

2 Related works

The value of foreign direct investment (FDI) was originally recognized in high-risk fields such as flight control, railways, medicine, nuclear power plants, and many others. Due to the growing use of computational intelligence for data analysis done by real-time methods, the necessity for problem detection has become even more pressing. This is particularly true in real-time energy-efficient management of distributed resources [7], real-time control as well as mobile crowd sensing [8], and protection of sensitive data collected by wearable sensors [9]. Regular inspections of sensor validation, measurement device calibration, software configuration, and preventative maintenance are required to ensure error-free operation. [10]. According to [11], maintenance costs might be anything from 15 to 60% of the entire cost of manufacturing items. Within these margins, almost 33% of maintenance costs are directly related to redundant as well as inappropriate equipment maintenance. As a result, enhancing equipment efficiency while lowering the costs of costly maintenance could result in a significant reduction in overall production costs [12]. According to [13], equipment maintenance can be divided into three categories: (1) modification maintenance entails upgrading components to boost machine productivity as well as performance, (2) preventive maintenance entails replacing a component just before it fails, and (3) breakdown corrective maintenance is when a part fails and needs to be replaced, resulting in machine downtime. Focus on preventive maintenance in this paper, which is divided into 2 types: UBM (usage-based maintenance) and condition-based maintenance (CBM) are two types of maintenance. Time-domain analysis and frequency-domain analysis are two traditional methods for identifying representative characteristics to categorize signals [14, 15]. The large number of features derived from various domains results in an HD dataset, as one could expect. As a result, features are chosen [16] and methods like PCA (principal component analysis) [17] or LDA (linear discriminant analysis) [18] are typically employed to reduce dimensionality of these features. In addition, [19], for example, used data entropy to preprocess raw time series data. RPCA (recursive PCA) [20], DPCA (dynamic PCA) [21], and KPCA (kernel PCA) [22] are used to monitor a variety of industrial processes, including adaptive, dynamic, and nonlinear processes [23]. Two RPCA algorithms were published in [24] to adapt for regular process changes in semiconductor production operations. They did this by iteratively updating the correlation matrix [25].

3 System model

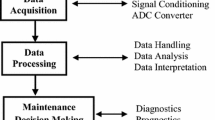
This section discusses the fault detection in automation industry based on soft sensors in monitoring and controlling with optimization. The data has been collected from soft sensors in which the fault has to be detected. This collected data has been pre-processed for removal of samples containing null values. For this processed data, the detection and diagnosis have been carried out using probabilistic multi-layer Fourier transform perceptron (PMLFTP). Then, controlling of data in soft sensors has been optimized using auto-regression-based ant colony optimization (AR_ACO) which has effect in increasing the production of industry automatically. The overall proposed architecture is shown in Fig. 1.

Fig.
figure 1

Overall proposed architecture

Full size image

3.1 Fault detection and diagnosis using probabilistic multi-layer Fourier transform perceptron (PMLFTP)

Input variables of model under study are given by N-dimensional vector x =  × 1, × 2,…,xN, and response variable is represented by g (x). As stated in Eq. (1), the answer g(x) is a hierarchical correlated function expansion of input variables:

$$\begin{array}{ll}g(\mathbf x)=&g_0+\sum\nolimits_{i=1}^Ng_i\left(x_i\right)+\sum\nolimits_{1\leq i_1<i_2\leq N}g_{i_1i_2}\left(x_{i_1},x_{i_2}\right)+\cdots\\&+\sum\nolimits_{1\leq i_1<\cdots<i_1\leq N}g_{i_1i_2\dots i_i}\left(x_{i_1},x_{i_2},\dots,x_{i_i}\right)+\cdots+g_{12\dots N}\left(x_1,x_2,\dots,x_N\right)\end{array}$$
(1)

where g0 denotes the 0th order component function or mean response of g(x). Function gi1i2 (xi1, xi2) is a 2nd-order that defines how variables xi1 and xi2 work together to produce output g(x). Last one g12,…, N (× 1, × 2,…, xN) comprises any residual dependency of all input variables linked together cooperatively to impact output g(x). For component functions in Eq. (2), this approach reduces to the following relationship.

$$\begin{array}{rl}{g}_0&={g}\left(\mathbf c\right),\\{g}_i\left(x_i\right)&={g}\left(x_i,\mathbf c^i\right)-{g}_0\\\left.{{g}_{i_1i_2}\left(x_{i_1},\right.x}_{i_2}\right)&={g}\left(x_{i_1},x_{i_2},\mathbf c^{i_1i_2}\right)-{g}_{i_1}\left(x_{i_1}\right)-{g}_{i_2}\left(x_{i_2}\right)-{g}_0\end{array}$$
(2)
$$\begin{array}{cl}{g}\left(\mathbf x\right)&{={g}}_0+\sum\nolimits_{i=1}^N{g}_i\left(x_i\right)+{\mathcal R}_2\\{g}\left(\mathbf x\right)&{=\sum}_{i=1}^N{g}\left(c_1,\dots,c_{i-1},x_i,c_{i+1},\dots,c_N\right)-(N-1){g}(\mathbf c)+{\mathcal R}_2\end{array}$$
(3)

Now consider the 1st order of g(x) given by Eqs. (3) and (4):

$$\grave{g}(\mathbf x)={g}\left(x_1,x_2,\dots,x_N\right)=\sum\nolimits_{i=1}^N{g}\left(c_1,\dots,c_{i-1},x_i,c_{i+1},\dots,c_N\right)-(N-1){g}(\mathbf c)$$
(4)

Fourier transform pairs formulation is given by Eqs. (5) and (6):

$${M}_{Y}(\theta )={\int }_{-\infty }^{\infty } {p}_{Y}(y){e}^{2\pi \theta iy}dy$$
(5)
$${p}_{Y}(y)={\int }_{-\infty }^{\infty } {M}_{Y}(\theta ){e}^{2\pi \theta iy}d\theta$$
(6)

The marginal density and features function of Y are pY(y) and MY (θ) indicates imaginary number given as i = √ − 1 given by Eq. (7):

$$\begin{array}{l}f_p^{(m)}(t)\equiv f_F^{(m)}(t)\\=C_0^{(m)}+\sum\nolimits_{n=1}C_k^{(m)}\cos\;k\left(t-t^{(m)}\right)+S_k^{(m)}\sin k\left(t-t^{(m)}\right)k=\frac{2\pi n}{h^{(m)}};\\n=0,\pm1,\pm2,\dots;\;t\in\left(t^{(m)};\;t^{(m)}+h^{(m)}\right);\end{array}$$
(7)
$${S}_{k}^{(m)}=\frac{2}{{h}^{(m)}}{\int }_{\left.{t}^{m}\right)}^{(m)} f(t)\mathrm{sin}\;k\left(t-{t}^{(m)}\right)d\theta$$

Since the function \({f}_{p}(t)\) in points \(t={t}^{(m)}\) and \(t={t}^{(m)}+{h}^{(m)}\) has discontinuities, for Fourier series following relations are valid by Eq. (8):

$$f_F\left(t^{(m)}\right)=f_F\left(t^{(m)}+h^{(m)}\right)=f\left(t^{(m)}\right)+\frac12\left\{f\left(t^{(m)}+h^{(m)}\right)-f\left(t^{(m)}\right)\right\}==f_l^{(m)}+\frac12\Delta f_l^{(m)}=C_0^{(m)}+\sum\nolimits_{k=1}^\infty C_k^{(m)}$$
(8)

The following integral is local Fourier transform given by Eqs. (9) and (10):

$$F\left\{f\left(t\right)\right\}=F\left(m,k\right)=\frac{2}{{h}^{\left(m\right)}}{\int }_{{t}^{\mathrm{^{\prime}}=1}}^{t\left(x\right)} f\left(t\right){e}^{-\beta \left(t\right)}\left(t-{t}^{\left(*\right)}\right)dt,$$
(9)

where \(k=\frac{2\pi n}{{h}^{(m)}}={\omega }^{(m)}n;n=0,\pm 1,\pm 2,\dots ;\;m=\mathrm{1,2},\dots .\)

$$\begin{array}{cl}f\left(t^{(m)}\right)&=\frac12\sum\nolimits_{n=-\infty}^\infty F(m,k)-\frac12\Delta f\left(t^{(m)}\right)\\&=\frac12F(m,0)+\sum\nolimits_{n=1}^\infty C_k^{(m)}-\frac12\Delta f\left(t^{(m)}\right)\end{array}$$
(10)

Steps in proposed technique for fault probability evaluation are as follows:

  1. 1.

    If \(\mathrm{u}={\left\{{u}_{1},{u}_{2},\dots ,{u}_{N}\right\}}^{T}\in {\mathfrak{R}}^{N}\) is standard Gaussian variable, let \({\mathrm{u}}^{*}={\left\{{u}_{1}^{*},{u}_{2}^{*},\dots ,{u}_{N}^{*}\right\}}^{T}\) be MPP or design point. Create an orthogonal matrix \(\mathrm{R}\in {\mathfrak{R}}^{N\times N}\) whose N − th column is\({\alpha }^{*}={\mathrm{u}}^{*}/{\beta }_{HL}\), i.e., \(\mathrm{R}=\left[{\mathrm{R}}_{1}\mid {\alpha }^{*}\right]\) where \({\mathrm{R}}_{1}\in {\mathfrak{R}}^{N\times N-1}\) satisfies \({\alpha }^{*T}{\mathrm{R}}_{1}=0\in {\mathfrak{R}}^{1\times N-1}\). MPP has a distance βHL, which is commonly mentioned as Hasofer-Lind reliability index [1–3]. For an orthogonal transformation u = Rv. Let \(\mathrm{v}={\left\{{v}_{1},{v}_{2},\dots ,{v}_{N}\right\}}^{T}\in {\mathfrak{R}}^{N}\) indicates rotated Gaussian space with MPP \({\mathrm{v}}^{*}={\left\{{v}_{1}^{*},{v}_{2}^{*},\dots ,{v}_{N}^{*}\right\}}^{T}\). Gaussian space v with \(={\left\{{v}_{1}^{*},{v}_{2}^{*},\dots ,{v}_{N}^{*}\right\}}^{T}\) as reference point as Eq. (11):

    $$\begin{array}{c}\grave{g}(\mathbf{v})\equiv g\left({v}_{1},{v}_{2},\dots ,{v}_{N}\right)\\ =\sum\nolimits_{i=1}^{N} g\left({v}_{1}^{*},\dots ,{v}_{i-1}^{*},{v}_{i},{v}_{i+1}^{*},\dots ,{v}_{N}^{*}\right)-(N-1)g\left({\mathbf{v}}^{*}\right)\\ \sum\nolimits_{n=-\infty }^{\infty } F(m,k)=-j\pi \sum\nolimits_{i=1}^{I} {A}_{i}(m){\sum }_{s=1}^{S} {b}_{si}\mathrm{ctg}\left(j\pi {a}_{si}\right)\end{array}$$
    (11)

Furthermore, MPP is selected as reference point. Terms \(g\left({v}_{1}^{*},\dots ,{v}_{i-1}^{*},{v}_{i},{v}_{i+1}^{*},\dots ,{v}_{N}^{*}\right)\) are individual component functions which are independent of each other as shown by Eq. (12).

$$\begin{array}{l}{\grave{g}}(\mathbf v)=a+\sum\nolimits_{i=1}^N{g}\left(v_i,\mathbf v^{\ast i}\right)\\f\left(t^{(m)}\right)=\frac{-j\pi}2\sum\nolimits_{i=1}^lA_i(m)\sum\nolimits_{s=1}^Sb_{si}\mathrm{ctg}\left(j\pi a_{si}\right)-\frac12\Delta f\left(t^{(m)}\right)\end{array}$$
(12)

The Park-Goreva equations for synchronous machine are stated utilizing the relative unit method given by Eq. (13).

$$\begin{array}{l}-{u}_{d}=r{i}_{d}+\frac{d}{d\theta }\left({x}_{d}{i}_{d}+{x}_{ad}{i}_{f}+{x}_{ad}{i}_{1d}\right)+{x}_{q}{i}_{q}+{x}_{aq}{i}_{1q}\\ -{u}_{q}=r{i}_{q}+\frac{d}{d\theta }\left({x}_{q}{i}_{q}+{x}_{aq}{i}_{1q}\right)-\left({x}_{d}{i}_{d}+{x}_{ad}{i}_{f}+{x}_{ad}{i}_{1d}\right)\\ \begin{array}{c}{u}_{f}={r}_{f}{i}_{f}+\frac{d}{d\theta }\left({x}_{ad}{i}_{d}+{x}_{f}{i}_{f}+{x}_{ad}{i}_{1d}\right)\\ 0={r}_{1d}{i}_{1d}+\frac{d}{d\theta }\left({x}_{ad}{i}_{d}+{x}_{ad}{i}_{f}+{x}_{1d}{i}_{1d}\right)\end{array}\end{array}$$
(13)

New intermediate variables are given as Eq. (14)

$${z}_{i}=g\left({v}_{i},{\mathbf{v}}^{*i}\right)$$
(14)

These new variables are used to convert approximation function into the following form using Eq. (15).

$$\grave{g}(\mathbf{v})=a+{z}_{1}+{z}_{2}+\cdots +{z}_{N}$$
(15)

In system of walking coordinates given by Eq. (16), the following equation is obtained in mth local interval of recurrence of converter within the duration of commutation of stages γ related to valve switching:

$${u}_{f}^{(m)}=\sqrt{3}E\mathrm{cos}(\theta -\pi /3)-2{r}_{c}{i}_{f}^{(m)}-2{x}_{c}\frac{d{i}_{f}^{(m)}}{d\theta }+{r}_{c}{i}_{\gamma }^{(m)}+{x}_{c}\frac{d{i}_{\gamma }^{(m)}}{d\theta }$$
(16)

where \(\theta =\omega t,\theta \in [\alpha ;\;\alpha +\gamma ];\;{i}_{\gamma }^{(m)}-\) exciter current stage, ending switching and \({i}_{\gamma }^{(m)}(\alpha )={i}_{f}^{(m)}(\alpha ),{i}_{\gamma }^{(m)}(\alpha +\gamma )=0\).

The index l corresponds to value of variable at switching point, i.e., when controlling signal is submitted to next thyristor of converter, as demonstrated by following formula, Eq. (17):

$$\Delta {I}_{fl}^{(m)}={i}_{f}^{(m)}(\alpha +\pi /3)-{i}_{f}^{(m)}(\alpha )={I}_{fl}^{(m+1)}-{I}_{fl}^{(m)}$$
(17)

Consider above-mentioned synchronous generator has outputs coupled to active and inductive loads \({r}_{W},{x}_{W}\), as given in Eq. (18):

$$\left.\begin{array}{c}\\ {u}_{d}={r}_{w}{i}_{d}+{x}_{w}\frac{d{i}_{d}}{d\theta }+{x}_{w}{i}_{q},\\ {u}_{q}={r}_{w}{i}_{q}+{x}_{w}\frac{d{i}_{q}}{d\theta }-{x}_{w}{i}_{d}\cdot \end{array}\right\}$$
(18)

After applying LFT to Eqs. (19), (20), and (21) in the field, obtain the synchronous generator’s equations as well as its activator.

$$\begin{array}{l}\left({r}_{s}+jk{x}_{ds}\right){\grave{I}}_{d}(m,k)+jk{x}_{ad}{\grave{I}}_{f}(m,k)+jk{x}_{ad}{\grave{I}}_{1d}(m,k)+{x}_{qs}{\grave{I}}_{q}(m,k)+\\ +{x}_{aq}{\grave{I}}_{1q}(m,k)=-\frac{6}{\pi }{x}_{ds}\Delta {I}_{d}^{(m)}-\frac{6}{\pi }{x}_{ad}\Delta {I}_{f}^{(m)}-\frac{6}{\pi }{x}_{ad}\Delta {I}_{1d}^{(m)},\\ -{x}_{ds}{\grave{I}}_{d}(m,k)-{x}_{ad}{\grave{I}}_{f}(m,k)-{x}_{ad}{\grave{I}}_{1d}(m,k)+\left({r}_{s}+jk{x}_{qs}\right){\grave{I}}_{q}(m,k)+\\ +jk{x}_{aq}{\grave{I}}_{1q}(m,k)=-\frac{6}{\pi }{x}_{qs}\Delta {I}_{q}^{(m)}-\frac{6}{\pi }{x}_{aq}\Delta {I}_{1q}^{(m)},\\ jk{x}_{ad}{\grave{I}}_{d}(m,k)+\left({r}_{fs}+jk{x}_{fs}\right){\grave{I}}_{f}(m,k)+jk{x}_{ad}{\grave{I}}_{1d}(m,k)=-\frac{6}{\pi }{x}_{c}{I}_{f}^{(m)}+\end{array}$$
(19)
$$+\grave{B}\left(m,k\right)\left(r_c+jkx_c\right)I_f^{\left(m\right)}-\frac{6\sqrt3}\pi E\frac{\cos\left(\alpha-\frac\pi6\right)+\mathrm{jksin}\left(\alpha-\frac\pi6\right)}{k^2-1}--\frac6\pi x_{ad}\Delta I_d^{\left(m\right)}-\frac6\pi x_{fs}\Delta I_f^{\left(m\right)}-\frac6\pi x_{ad}\Delta I_{1d}^{\left(m\right)},$$
(20)
$$\begin{array}{c}jk{x}_{ad}{\grave{I}}_{d}(m,k)+jk{x}_{ad}{\grave{I}}_{f}(m,k)+\left({r}_{1d}+jk{x}_{1d}\right){\grave{I}}_{1d}(m,k)==-\frac{6}{\pi }{x}_{ad}\Delta {I}_{d}^{(m)}-\frac{6}{\pi }{x}_{ad}\Delta {I}_{f}^{(m)}-\frac{6}{\pi }{x}_{1d}\Delta {I}_{1d}^{(m)}\\ jk{x}_{aq}{\grave{I}}_{q}(m,k)+\left({r}_{1q}+jk{x}_{1q}\right){\grave{I}}_{1q}(m,k)=-\frac{6}{\pi }{x}_{aq}\Delta {I}_{q}^{(m)}-\frac{6}{\pi }{x}_{1q}\Delta {I}_{1q}^{(m)}\end{array}$$
(21)

In this context, it is generally known that the equation gives MLPNN state space formulation with one hidden layer (22).

$$\begin{array}{c}\mathbf{z}(n)={\mathbf{A}}^{T}(n)\left[\begin{array}{c}\mathbf{x}(n)\\ 1\end{array}\right]\mathbf{u}(n)=\mathbf{f}(\mathbf{z}(n))={\left[f\left({z}_{0}(n)\right)\cdots ,f\left({z}_{I-1}(n)\right)\right]}^{T}y(z)={\mathbf{b}}^{T}(n)\left[\begin{array}{c}\mathbf{u}(n)\\ 1\end{array}\right]\\ \mathbf{x}(n)=\left[x(n)\cdots {x}_{i}(n)\right)=\mathrm{tanh}\left({z}_{i}(n)\right),i=1,\dots ,I\end{array}$$
(22)

where \(\mathbf{x}(n)={\left[\begin{array}{llll}x(n)& \cdots & x(n-K+1)& 1\end{array}\right]}^{T}\) is (K + 1) × 1 input vector, which is constituted by elements of perceptual feature vector and bias of MLPNN; z(n) = \({\left[\begin{array}{ccc}{z}_{0}(n)& \cdots & {z}_{l-1}(n)\end{array}\right]}^{T}\) is neuron output vector in hidden layer.

$$\begin{array}{l}{\mathbb{w}}(n)={\left[{\mathbf{a}}^{T}(n){\mathbf{b}}^{T}(n)\right]}^{T}\\ {E}_{T}(\mathbf{w}(n))=\sum e(n)=\sum \frac{1}{2}{\left(y(n)-{y}_{d}(n)\right)}^{2}\\ \nabla {\mathbf{E}}_{T}(n)=\nabla {\mathbf{E}}_{T}(\mathbf{w}(n))={\left[\nabla {\mathbf{E}}_{\mathbf{a}}^{T}(n)\nabla {\mathbf{E}}_{\mathrm{b}}^{T}(n)\right]}^{T}\end{array}$$
(23)

The desired output is yd(n), output error is e(n), and the error measure’s gradients concerning a(n) and b(n) are ∇Ea(n) and ∇Eb(n). From Eq. (24) concept of error measures, in the least-squares sense, it is observed that MLPNN seeks to make its output as near to subjective measure yd(n) as possible.

$$\begin{array}{l}\nabla{\mathbf E}_{\mathbf A}(n)=\frac{\partial e(n)}{\partial\mathbf A(n)}=\begin{bmatrix}\overline{\partial e}(n)&\cdots&\partial e(n)\\\overset\leftharpoonup\partial a_{1,1}(n)&&\partial a_{1,I}(n)\\\vdots&\ddots&\vdots\\{\overline{\partial e}}_{(K),1}\overset-{(n)}&\cdots&{\overline{\partial a}}_{(K+1),I}(n)\end{bmatrix}\nabla{\mathbf E}_A(n)=\begin{bmatrix}\mathbf x(n)\\1\end{bmatrix}\frac{\partial e(n)^T}{\partial\mathbf z(n)}\frac{\partial e(n)}{\partial\mathbf z(n)}=\left[\begin{array}{lcc}\frac{\partial e(n)}{\partial z_1(n)}&\cdots&\frac{\partial e(n)}{\partial z_I(n)}\end{array}\right]^T\\\frac{\partial\mathbf f(n)}{\partial\mathbf s(n)}=\grave{\mathbf f}(n)=\left[\frac{\partial f_1(n)}{\partial s_1(n)}\cdots\frac{\partial f_I(n)}{\partial s_I(n)}\right]^T\frac{\partial e(n)}{\partial\mathbf z(n)}=(\mathbf b(n)\cdot\grave{\mathbf f}(n))e(n)\end{array}$$
(24)

Let the differential operator be expressed by Eq. (25),

$${\left.{R}_{\mathrm{d}}\{g(w(n))\}\equiv \frac{\partial }{\partial \alpha }g(w(n)+\alpha d(n))\right|}_{\alpha =0}$$
(25)

Then, H(w(n))d(n) is given by Eq. (26)

$$\mathrm{H}(\mathrm{w}(n))\mathrm{d}(n)=\mathfrak{R}\left\{\nabla {\mathrm{E}}_{\mathrm{T}}(\mathrm{w}(\mathbf{n}))\right\}$$
(26)

During training and tests were calculated based on correlation, ρ, and variance of error \({\sigma }_{e}^{2}\), given by Eqs. (27) and (28):

$$\rho=\frac{\sum_{i=0}^{N-1}\left(x_i(n)-{\displaystyle\overset\leftharpoonup x}(n)\right)\left(y_i(n)-\overset\leftharpoonup y(n)\right)}{\sqrt{\sum_{i=0}^{N-1}\left(x_i(n)-\overset\leftharpoonup x(n)\right)^2\sum_{i=0}^{N-1}\left(y_i(n)-\overset\leftharpoonup y(n)\right)^2}}$$
(27)
$$\sigma_e^2=\frac1N\sum\nolimits_{i=1}^N\left[\left(x_i(n)-y_i(n)\right)-(\overset\leftharpoonup x(n)-\overset\leftharpoonup y(n))\right]^2$$
(28)

3.2 Data controlling and optimization using auto-regression-based ant colony optimization (AR_ACO)

The autoregressive model AR(p) uses a linear combination of the p last values by Eq. (29) to determine the value of a process at an arbitrary time step t.

$${y}_{t}={\phi }_{1}\cdot {y}_{t-1}+{\phi }_{2}\cdot {y}_{t-2}+\dots +{\phi }_{p}\cdot {y}_{t-p}+{\varepsilon }_{t}$$
(29)

The order of the AR model is denoted by the number p. The model parameters are the weights φi of the linear combination. They are thought to be constant. Furthermore, an AR model requires that this process is superimposed by white noise. εt are regarded uncorrelated in time and identically distributed, with a zero expected value and finite variance. AR(p) is the abbreviation for this model.

The AR(p) model is used to characterize a given time series, as shown in Eq. (30):

$${y}_{t-3},{y}_{t-2},{y}_{t-1},{y}_{t},{y}_{t+1},{y}_{t+2},{y}_{t+3},\dots$$
(30)

This calculation assumes a one-unit change over time. In general, the time step can be of any unit, and it can be substituted by ∆t by altering the unit of time, and the equation can be rewritten as Eq. (31):

$$\frac{{y}_{t}-{y}_{t-\Delta t}}{\Delta t}={\phi }_{0}+\left({\phi }_{1}-1\right){y}_{t-\Delta t}$$
(31)

The AR(p) model can be thought of as a linear operator that is applied to an initial vector of time series data. In this view, the definition’s equation is expressed as a matrix equation by Eqs. (32) and (33):

$$\begin{array}{ccc}\underbrace{\begin{pmatrix}y_t\\y_{t-1}\\\vdots\\y_{t-p+1}\end{pmatrix}}&=&A_p\cdot\begin{pmatrix}y_{t-1}\\y_{t-2}\\\vdots\\y_{t-p}\end{pmatrix}\end{array}$$
(32)

with a matrix

$${\mathrm{A}}_{p}=\left(\begin{array}{ccccccc}{\phi }_{1}& {\phi }_{2}& {\phi }_{3}& \dots & {\phi }_{p-2}& {\phi }_{p-1}& {\phi }_{p}\\ 1& 0& 0& \dots & 0& 0& 0\\ 0& 1& 0& \dots & 0& 0& 0\\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & \vdots \\ 0& \dots & 0& 1& 0& 0& 0\\ 0& \dots & 0& 0& 1& 0& 0\\ 0& \dots & 0& 0& 0& 1& 0\end{array}\right)$$
(33)

The attribute graph’s nodes are arranged in the same order as the composite vector’s boundary values. There are N edges eik, k1::N between two consecutive nodes vi and viz1 when N binary BCs are combined. Each edge, eik in E, shows a couple of conditional probabilities (i.e., \(p\left(\left[{v}_{i},{v}_{i+1}\right]\mid {c}_{1}\right),p\left(\left[{v}_{i},{v}_{i+1}\right]\mid \overline{{c }_{2}}\right)\) integrated with attribute interval \(\left[{v}_{i},{v}_{i+1}\right]\). Conditional probability distribution of original instance of attribute from kth BC is used to calculate these probabilities. Conditional probabilities labelling edge \({e}_{11}=\left[{v}_{1},{v}_{2}\right]\) are evaluated in the following way by Eq. (34):

$$p\left(\left[{v}_{1},{v}_{2}\right]\mid {c}_{1}\right)=\frac{p\left(\left[{v}_{1}^{1},{v}_{2}^{1}\right]\mid {c}_{1}\right)*\left({v}_{2}-{v}_{1}\right)}{\left({v}_{2}^{1}-{v}_{1}^{1}\right)}$$
(34)

The characteristic polynomial of Ap is \({\chi }_{p}(\lambda )=(-1{)}^{p}\cdot \left({\lambda }^{p}-{\phi }_{1}{\lambda }^{p-1}-\dots -{\phi }_{p-1}\lambda -{\phi }_{p}\right)\)

The case p = 1 with Eq. (35)

$$\mathrm{det}\left({\mathbf{A}}_{1}-\lambda \mathbf{I}\right)=\mathrm{det}\left({\phi }_{1}-\lambda \right)={\phi }_{1}-\lambda =-1\cdot \left(\lambda -{\phi }_{1}\right)={\chi }_{1}\left(\lambda \right).$$
(35)

Induction step starts with Eq. (36):

$$\mathrm{det}\left({\mathbf{A}}_{p}-\lambda \mathbf{I}\right)=\mathrm{det}\left(\begin{array}{ccccccc}{\phi }_{1}-\lambda & {\phi }_{2}& {\phi }_{3}& \cdots & {\phi }_{p-2}& {\phi }_{p-1}& {\phi }_{p}\\ 1& -\lambda & 0& \cdots & 0& 0& 0\\ 0& 1& -\lambda & \cdots & 0& 0& 0\\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & \vdots \\ 0& \cdots & 0& 1& -\lambda & 0& 0\\ 0& \cdots & 0& 0& 1& -\lambda & 0\\ 0& \cdots & 0& 0& 0& 1& -\lambda \end{array}\right)$$
(36)

As indicated in Eq. (37), the determinant of this matrix will be determined by utilizing the Laplace expansion along the last column.

$$\mathrm{det}\left({\mathbf{A}}_{p}-\lambda \mathbf{I}\right)=-(-1{)}^{p}\cdot {\phi }_{p}\cdot \mathrm{det}\left(\begin{array}{cccc}1& -\lambda & 0& \dots \\ 0& 1& -\lambda & \dots \\ \vdots & \ddots & \ddots & \ddots \\ 0& \dots & 0& 1\end{array}\right)+(-\lambda )\cdot \mathrm{det}\left({\mathbf{A}}_{p-1}-\lambda \mathbf{I}\right)$$
(37)

The Laplace expansion reduces the p × p matrix (Ap − λI) into two matrices. The first matrix’s determinate is one since its structure has a lower triangular matrix of zeros, and the diagonal’s product is one. The induction hypothesis is met by the second matrix, which is given by Eq. (38):

$$\mathrm{det}\left({\mathbf{A}}_{p}-\lambda \mathbf{I}\right)=(-1{)}^{p}\cdot \left(-{\phi }_{p}\right)-\lambda \cdot \mathrm{det}\left({\mathbf{A}}_{p-1}-\lambda \mathbf{I}\right)=(-1{)}^{p}\cdot \left(-{\phi }_{p}\right)-\lambda .\left[(-1{)}^{p-1}\cdot \left({\lambda }^{p-1}-{\phi }_{1}{\lambda }^{p-2}-\dots -{\phi }_{p-2}\lambda -{\phi }_{p-1}\right)\right]$$
(38)

characteristic polynomial of \({\mathbf{A}}_{p}\) is \({\chi }_{p}(\lambda )\)

k-fold application of linear operator Ap is represented by Eq. (39):

$$\boldsymbol A_p^k=\left(\mathbf{TDT}^{-1}\right)^k=\mathrm{TD}\;\begin{array}{cc}\underbrace{\mathrm T^{-1}\cdot\mathrm T\;}_{=1}&\mathrm{DT}^{-1}\dots.\end{array}\mathrm{TDT}^{-1}=\mathrm{TD}^k\mathrm T^{-1}$$
(39)

Using corresponding eigenvectors, matrix A2 is decomposed into \({\mathbf{A}}_{2}=\mathbf{T}\cdot \mathbf{D}\cdot {\mathbf{T}}^{-1}\) shown in Eq. (40):

$$\mathrm T=\begin{pmatrix}\frac12-\frac{\sqrt5}{10}&\frac12+\frac{\sqrt5}{10}\\-\frac{\sqrt5}5&\frac{\sqrt3}5\end{pmatrix}\mathrm{and}\;\mathrm D=\begin{pmatrix}\frac12-\frac12\sqrt5&0\\0&\frac12+\frac12\sqrt5\end{pmatrix}$$
(40)

closed form of this AR(2)-model is represented by Eq. (41):

$$\left(\begin{array}{c}{y}_{k+1}\\ {y}_{k}\end{array}\right)={\mathbf{A}}_{2}^{k}\cdot \left(\begin{array}{l}{y}_{1}\\ {y}_{0}\end{array}\right)=\mathbf{T}\cdot \left(\begin{array}{cc}{\left(\frac{1}{2}-\frac{1}{2}\sqrt{5}\right)}^{k}& 0\\ 0& {\left(\frac{1}{2}+\frac{1}{2}\sqrt{5}\right)}^{k}\end{array}\right)\cdot {\mathbf{T}}^{-1}\cdot \left(\begin{array}{l}{y}_{1}\\ {y}_{0}\end{array}\right){y}_{k+1}=\left(\frac{1}{2}-\frac{3}{10}\sqrt{5}\right)\cdot {\left(\frac{1}{2}-\frac{1}{2}\sqrt{5}\right)}^{k}+\left(\frac{1}{2}+\frac{3}{10}\sqrt{5}\right)\cdot {\left(\frac{1}{2}+\frac{1}{2}\sqrt{5}\right)}^{k}$$
(41)

The key principle behind understanding a differential equation as an AR model is that it is symmetric; not only can the difference equation be understood as an AR model, but it can also be reversed. Furthermore, higher-order AR models relate to differential equations of increasing degree. Aside from the following difference quotients, namely, forward difference by Eq. (42):

$$\frac{\Delta y}{\Delta t}=\frac{{y}_{t+\Delta t}-yt}{\Delta t}\frac{\Delta y}{\Delta t}=\frac{{y}_{t}-{y}_{t-\Delta t}}{\Delta t}\frac{\Delta y}{\Delta t}=\frac{{y}_{t+\Delta t}-{y}_{t-\Delta t}}{2\Delta t}$$
(42)

There are also difference quotients for the numerical calculation of higher derivatives to approach the first-order derivative. Equation (43) provides a recursive definition of higher-order central difference quotients:

$$\frac{{\Delta }^{n}y}{\Delta {t}^{n}}=\frac{1}{\Delta {t}^{n}}\cdot {\sum }_{k=0}^{n} (-1{)}^{k}\left(\begin{array}{l}n\\ \Box\end{array}\right){y}_{t+k-n/2}$$
(43)

for even degrees of n, and by Eq. (44):

$$\frac{{\Delta }^{n}y}{\Delta {t}^{n}}=\frac{1}{2\Delta {t}^{n}}\cdot {\sum }_{k=0}^{n-1} (-1{)}^{k}\left(\begin{array}{c}n-1\\ k\end{array}\right)\cdot \left({y}_{t+k+1-(n-1)/2}-{y}_{t+k-1-(n-1)/2}\right){a}_{n}{y}^{(n)}+{a}_{n-1}{y}^{(n-1)}+\dots +{a}_{2}{y}^{\prime\prime}+{a}_{1}{y}^{\prime}+{a}_{0}y=f(x){y}^{(n)}+{a}_{n-1}{y}^{(n-1)}+\dots +{a}_{2}{y}^{\prime\prime}+{a}_{1}{y}^{\prime}+{a}_{0}y=f(x).$$
(44)

by substituting k-th derivative by \({\lambda }^{k}\) in Eq. (45):

$$\chi (\lambda )={\lambda }^{n}+{a}_{n-1}{\lambda }^{(n-1)}+\dots +{a}_{2}{\lambda }^{2}+{a}_{1}\lambda +{a}_{0}$$
(45)

The roots are real or occur in conjugate pairs if all coefficients ai are real. The rules for solving higher-order differential equations with constant coefficients can then be used to find the required n linearly independent solutions: If r is a real root that appears k times, then Eq. (46) represents the solutions:

$$y={e}^{vt},y=t\cdot {e}^{r-t},y={t}^{2}\cdot {e}^{r\cdot t},\cdots ,y={t}^{k-1}\cdot {e}^{r-t}$$
(46)

If r = α ± βi are complex conjugate roots appearing k times, then results are given by Eq. (47):

$${e}^{\Delta -t}\mathrm{cos}(\beta \cdot t),{e}^{\Delta \cdot t}\mathrm{sin}(\beta \cdot t)t\cdot {e}^{a-t}\mathrm{cos}(\beta \cdot t),t\cdot {e}^{\Delta t}\mathrm{sin}(\beta \cdot t){t}^{2}\cdot {e}^{(-t}\mathrm{cos}(\beta \cdot t),{t}^{2}\cdot {e}^{a\cdot t}\mathrm{sin}(\beta \cdot t),{\mathbf{U}}^{(t)}=\left[\begin{array}{ccc}{u}_{11}^{(l)}& \cdots & {u}_{1N}^{(l)}\\ \vdots & \ddots & \vdots \\ {u}_{c1}^{(l)}& \cdots & {u}_{eN}^{(l)}\end{array}\right]$$
(47)
$${t}^{k-1}\cdot {e}^{a-t}\mathrm{cos}(\beta \cdot t),{t}^{k-1}\cdot {e}^{a-t}\mathrm{sin}(\beta \cdot t)$$

The proposed optimization algorithm is discussed below (Fig. 2).

  • Stage 1: Assign number of clusters to c = 2 and cmax, and use formula to obtain the right number of clusters (8). Set settings for ACO technique, initialize solution Si, I = 1,…, T, and replace Si with 2i = Si in fitness function (5).

  • Stage 2: Sort answers by fitness function and then organize them in ascending order. Probability value for renewing results as Si I = 1,…, T) using (9) and (10).

  • Stage 3: Evaluate mean µ utilizing probability value produced by Step 2 and roulette technique and set SD σ i v utilizing (11). If condition \(\left|{f}^{(l+1)}\left({\mu }^{i}\right)-{f}^{(l+1)}\left({S}_{i}\right)\right|<0\) is satisfied, then set Si = µ i; otherwise, keep original Si.

  • Stage 4: If condition \(\left|{f}^{(l+1)}\left({S}_{i}\right)-{f}^{(t)}\left({S}_{i}\right)\right|<\delta\) is satisfied, then define Si ≡ 2i; otherwise set l = l + 1 and return to Step 2.

  • Stage 5: Examine for less fitness value utilizing (5) until condition \(\Vert {\mathbf{U}}_{n-1}^{(d+1)}-{\mathbf{U}}^{(l)}\Vert <\varepsilon\) is satisfied, where \({\mathbf{U}}^{(t)}=\left[\begin{array}{ccc}{u}_{11}^{(l)}& \cdots & {u}_{1N}^{(l)}\\ \vdots & \ddots & \vdots \\ {u}_{c1}^{(l)}& \cdots & {u}_{eN}^{(l)}\end{array}\right]\)

Fig. 2
figure 2

Optimization algorithm

Full size image

The center of bell-shaped MF α i q and SD of bell-shaped MF \({\beta }_{q}^{i}\) is given by following formulas given by Eqs. (48) and (49):

$${\alpha }_{q}^{i}=\frac{{\sum }_{k=1}^{n} {u}_{ik}{x}_{Q}}{{\sum }_{k=1}^{n} {u}_{ik}}$$
(48)
$${\beta }_{q}^{i}=\sqrt{\frac{2{\sum }_{k=1}^{n} {u}_{ik}{\left({x}_{q}-{\alpha }_{q}^{i}\right)}^{2}}{{\sum }_{k=1}^{n} {u}_{ik}}}$$
(49)

The grade of MF \({A}_{g}^{i}\left({x}_{q}(k)\right)\) is given by (3) weight wi(k) and output yˆ is given as \({w}_{i}(k)={\prod }_{q=1}^{n} {A}_{q}^{i}\left({x}_{q}(k)\right)\), and \(\grave{y}(k)=\frac{{\sum }_{i=1}^{\sum } {m}_{i}(k){y}^{\mathrm{^{\prime}}}(k)}{{\sum }_{i=1}^{\sum } {m}_{i}(k)}\)

  • Stage 6: Replace input–output data and yˆ(k) by Eq. (50).

$$\mathbf y=\overset\leftharpoonup{\mathrm\Phi}\grave\Theta^T+\mathbf e$$
(50)

where \(\mathbf{e}=\mathbf{y}-\grave{\mathbf{y}},\) real model \(\mathbf{y}={\left[\begin{array}{lll}y(1)& \dots & y(N)\end{array}\right]}^{T}\) the established model \(\grave{\mathbf{y}}={\left[\begin{array}{lll}\grave{y}(1)& \dots & \grave{y}(N)\end{array}\right]}^{T},\Phi\) is shown in Eq. (51)

$$\Phi =\left[\begin{array}{c}\Phi (1)\\ \vdots \\\Phi (N)\end{array}\right]={\left[\begin{array}{c}{x}_{1}^{T}\\ \vdots \\ {x}_{r}^{T}\end{array}\right]}^{T}=\left[\begin{array}{ccccccccc}{\Phi }_{1}& {\Phi }_{1}{x}_{1}(1)& \cdots & {\Phi }_{1}{x}_{n}(1)& \cdots & {\Phi }_{c}& {\Phi }_{c}{x}_{1}(1)& \cdots & {\Phi }_{c}{x}_{n}(1)\\ {\Phi }_{1}& {\Phi }_{1}{x}_{1}(2)& \cdots & {\Phi }_{1}{x}_{n}(2)& \cdots & {\Phi }_{c}& {\Phi }_{c}{x}_{1}(2)& \cdots & {\Phi }_{e}{x}_{n}(2)\\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ {\Phi }_{1}& {\Phi }_{1}{x}_{n}(N)& \cdots & {\Phi }_{1},{x}_{n}(N)& \cdots & {\Phi }_{c}& {\Phi }_{c}{x}_{1}(N)& \cdots & {\Phi }_{e}{x}_{n}(N)\end{array}\right]$$
(51)
$${\Phi }_{i}={w}_{i}/{\sum }_{i=1}^{c} {w}_{i},\grave{\Theta }=\left[\begin{array}{lll}{\Theta }_{1}& \cdots & {\Theta }_{c}\end{array}\right]=\left[\begin{array}{lllllll}{a}_{0}^{1}& \cdots & {a}_{n}^{1}\mid & \cdots & \mid {a}_{0}^{c}& \cdots & {a}_{n}^{c}\end{array}\right]$$

  • Step 7: Convert set χi, where i = 1,...,r, produced from Step 6 as orthogonal basis vectors, utilizing subsequent process:

  1. 1.

    \(\mathrm{Set}\;\overset\leftharpoonup m=1\)  

  2. 2.

    \({\Gamma }_{1}={\chi }_{1}\) and \({q}_{1}=\frac{\langle {\Gamma }_{1}\cdot {y}_{2}\rangle }{\langle {\Gamma }_{1}\cdot {\Gamma }_{1}\rangle }\).

  3. 3.

    For \(\overset\leftharpoonup m=2\) to \(r\)

    $$\gamma_{\mathrm{iin}}=\frac{\langle\Gamma_{1,xa\rangle}}{\langle\Gamma_{i,\Gamma}\rangle},1\leq i<\overset\leftharpoonup m$$

\({q}_{i}=\frac{\langle {\Gamma }_{i}y\rangle }{\langle {\Gamma }_{i},{\Gamma }_{i}\rangle }\) 3) Figure out \(\grave{\Theta }\) by subsequent equation:

$$\mathbf{A}{\Theta }^{T}=\mathbf{q}$$

where

$$\begin{array}{cc}\mathrm{A}& =\left[\begin{array}{cccccc}1& {\gamma }_{12}& {\gamma }_{13}& \cdots & \cdots & {\gamma }_{1r}\\ 0& 1& {\gamma }_{23}& \cdots & \cdots & {\gamma }_{2r}\\ 0& 0& 1& \cdots & \cdots & {\gamma }_{3r}\\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots \\ 0& 0& 0& \cdots & 1& {\gamma }_{(r-1)r}\\ 0& 0& 0& \cdots & 0& 1\end{array}\right]\\ \mathrm{q}& =\left[\begin{array}{llll}{q}_{1}& {q}_{2}& \cdots & {q}_{r}\end{array}\right].\end{array}$$

4 Results and discussion

The Python programming language was used to implement the strategy. The proposed solution is implemented using the The ano library, which features dynamic C code generation, robust and rapid optimization techniques, and integration with mathematical NumPy library. A learning method plus a real-time module make up implementation. Learning method learns the parameters for both spatial pooling as well as temporal inference continuously and saves them in a database that is shared with real-time module. Real-time method uses parameters contained in shared database to execute real-time FDI. Module is simply concerned with execution of technique with already learned parameters and does not perform any learning. This operation of separating the learning and execution processes is required to provide real-time functioning, which would otherwise be impossible to achieve. The learning method is executed on a dedicated server, and deployed method is made available as a service. System begins by obtaining multiple data samples from an SPC database. Database stores a lot of signals created by manufacturing methods as they occur throughout time. This information is recorded in a database as textual data as well as imported into computer memory by learning method as a list of string objects.

Table 1 shows the parametric comparison for fault situation 1, fault situation 2, and fault situation 3. The parameters considered are computational rate, QoS, RMSE, fault detection rate, and control optimization. The techniques compared are PCA and LDA with proposed technique. The graph for above comparison table is given below.

Table 1 Comparative analysis for various fault situations between proposed and existing technique
Full size table

Figures 3, 4, and 5 show parametric analysis in terms of computational rate, QoS, RMSE, fault detection rate, control optimization. The proposed technique has been compared with existing PCA and LDA. In terms of computational rate of 50%, QoS of 80%, RMSE of 57%, fault detection rate of 89%, and control optimization of 92% for fault situation 1 by proposed technique. Computational rate of 52%, QoS of 79.9%, RMSE of 50%, fault detection rate of 89.9%, and control optimization of 92% for fault situation 2 calculated based on fault detection. Based on this comparison, proposed technique obtained higher QoS and fault detection rate in fault location. In terms of computational rate of 40%, QoS of 78%, RMSE of 45%, fault detection rate of 90%, and control optimization of 93% for fault situation 3 by proposed technique.

Fig. 3
figure 3

Analysis of fault situation 1 in terms of a computational rate, b QoS, c RMSE, d fault detection rate, e control optimization

Full size image
Fig. 4
figure 4

Analysis of fault situation 2 in terms of a computational rate, b QoS, c RMSE, d fault detection rate, e control optimization

Full size image
Fig. 5
figure 5

Analysis of fault situation 3 in terms of a computational rate, b QoS, c RMSE, d fault detection rate, e control optimization

Full size image

More crucially, an inferential model like this might be used to forecast paperboard qualities like flat crush strength and compression strength directly. Controlling the refining parameters directly based on feedback from the finished product (board or paper) quality could be a modern control method for refining. Overall, the findings of this study showed that machine learning–based solutions have a lot of promise in the pulp and paper industry, as long as the constraints of data-driven solutions are understood and significant process expertise is used when constructing predictive models.

5 Conclusion

This research proposed novel design in monitoring and control optimization of soft sensors in automation industry for fault detection. The aim is to collect the historical data from soft sensors in designing fault detection systems for monitoring and controlling with optimization. Then, to pre-process the collected data in removing null values and missing data. For detection and diagnosis of the faults of processed data using probabilistic multi-layer Fourier transform perceptron (PMLFTP). Then, optimization and control of the data of soft sensors have been done using auto-regression-based ant colony optimization (AR_ACO) which has effect in increasing the production of industry automatically. The experimental results have been carried out in terms of computational rate of 40%, QoS of 78%, RMSE of 45%, fault detection rate of 90%, and control optimization of 93% which been obtained for various historical data–based evaluations.