1 Introduction

In the aerospace field, there is an urgent need for a large number of thin-walled parts with high machining accuracies, such as aero-engine impellers and blades. Milling is one of the most widely used mechanical techniques for producing thin-walled parts. However, due to the poor stiffness of thin-walled parts and the unreasonable selection of machining parameters, chatter often exists in the whole machining process. Chatter is a crucial factor affecting surface quality, machining efficiency, and tool life. To avoid the impact of chatter on the production process, literature [1,2,3] established a physical model of milling machining, drew a stable lobe diagram (SLD), and selected reasonable machining parameters. However, due to the complex milling environment and the influence of the dynamic characteristics of the system, the accuracy of the SLD is insufficient. Therefore, real-time detection of chatter vibration is of great significance to improve the machining efficiency and quality of parts.

Real-time chatter detection can avoid the establishment of complex physical models, mainly including signal preprocessing, feature extraction, and processing state identification. Various sensors are used in chatter detection, such as accelerometers [4, 5], force sensors [6, 7], sound sensors [4, 8], and current sensors [9, 10]et al. When chatter occurs, the vibration energy of the cutting system increases. FU et al. [11] used the acceleration sensor to collect the vibration signal of the spindle and analyzed the milling processing states online. Wang et al. [5] applied acceleration sensors to collect vibration signals in robotic milling, and their experimental results showed that the signals were robust. When chatter occurs, the amplitude of the sound signal in the time domain will be significantly higher than that of the stable processing, so using a microphone to collect the sound signal can also detect the chattering. Gao et al. [12]. pointed out that the sound signal contains more time domain and frequency domain information and considered that the sound signal during processing is the best choice for the chatter detecting signal. Using a microphone to collect sound signals is not only cheap, simple and convenient to install, and will not affect the stiffness of the system, but it is particularly sensitive to noise in the process of signal acquisition, which increases the workload of later signal processing. Force sensors are often bulky and expensive and have limitations in where they can be installed, but it is the preferred signal in chatter detecting. Tlusty et al. [13] found that force signal is more sensitive to chatter characteristics than other signals, because cutting force is a necessary factor to cause tool and workpiece vibration. Liu et al. [14] applied fast kurtosis and frequency band power to analyze the force signal of milling process to detect milling chatter. Experiments show that the force signal has good sensitivity to chatter. Therefore, this paper will use the force sensor to collect the milling processing signal.

In chatter detection, after selecting a suitable signal, methods in the time domain, frequency domain, and time–frequency domain are usually used to extract sensitive features related to chatter. Time-domain analysis also known as waveform analysis directly analyzes the original sequence of the signal. YE et al. [15] calculated the root mean square of the time-domain sampling sequence and used the ratio of the standard deviation and the mean of the root mean square sequence as the coefficient of variation to identify chatter. Although the time domain analysis method is simple and intuitive, in actual processing, the dynamic characteristics of the tool and the workpiece will lead to nonlinear and non-stationary signals, which are easily disturbed by external signals, resulting in misjudgment of the milling processing state. Frequency domain analysis is also known as spectrum analysis. When chatter occurs, the amplitude of the signal will change drastically, and the frequency of the chatter will approach the natural frequency of the processing system. F. Rumusanu et al. [16] transformed the cutting force signal from the time domain to the frequency domain through the fast Fourier transform (FFT), then calculated the ratio of the maximum amplitude value to the average value of the cutting force signal in the given frequency domain, and used this value to assess processing system stability. Tang et al. [17] used the power spectral density (PSD) of the cutting force signal for chatter detection during cutting. However, the traditional spectrum analysis based on FFT is only suitable for stationary signal analysis, because the chatter signal is often nonlinear and unstable, resulting in its poor robustness. To solve the above problems, some adaptive signal decomposition methods are used in chatter detection, such as empirical mode decomposition (EMD) [18], ensemble empirical mode decomposition (EEMD) [11, 19, 20], wavelet transform (WT) and its improved algorithm [18, 21, 22], and variational mode decomposition (VMD) [23, 24]. When EMD processes the signal, there is a problem of loss of part of the time scale, resulting in mode aliasing, which makes the IMF components lose the physical meaning of decomposition. Although EEMD can solve the modal aliasing problem of EMD, there are still some problems: the amplitude of white noise added to the signal must be selected appropriately. The problem of the rapid increase in quantity, the possibility of non-standard IMF, and the problem of mode splitting will occur when the signal is decomposed. Among them, VMD is a non-recursive adaptive analysis method, which has a solid theoretical foundation and is efficient in decomposing signals. However, it is necessary to set the optimal penalty coefficient and the number of decomposition modes in advance. Optimizing VMD parameters is time-consuming, which seriously affects the performance of VMD applications in chatter detection. Based on this question, Kai Yang et al. [25] optimized the VMD penalty factor and the number of decomposed modes globally based on the simulated annealing algorithm (SA). Compared with EMD, it was found that the optimized VMD was robust and could accurately identify chatter. Liu et al. [7] proposed to automatically select the method of VMD’s parameters based on kurtosis. VMD is widely used as an emerging chatter detection method, but how to choose the best combination of decomposition layers and penalty factors still needs in-depth research.

To detect the occurrence of chatter vibration in the actual machining process, an appropriate feature must be selected as the standard for the detection of chatter vibration. Liu et al. [18] proposed an effective chatter detection indicator, based on the Hilbert-Huang spectrum, to calculate the mean and standard deviation of its instantaneous frequency, and set the thresholds of its characteristics to 710 Hz and 0.02, respectively. However, under different cutting conditions, the threshold value of this method will also change, and the generality is not strong. Currently, the selection of chatter features mainly focuses on some features derived from the concept of entropy, such as permutation entropy [23] (PE), energy entropy [26] (EE), sample entropy [19, 20] (SE), and power spectrum entropy(PSD) [19]. These features are sensitive to chatter and are suitable for different processing conditions. However, when a single feature indicator faces complex processing conditions, it is easy to misjudge or miss the processing state. Therefore, many scholars apply the multi-feature fusion method to detect the chatter in real-time to increase the robustness of the method. Wang et al. [27] analyzed and processed the acceleration signal, sound signal, and bending moment signal based on the data-driven method and fused the three features of kurtosis, root mean square, and fractal dimension to judge the occurrence of chatter. Li Kai et al. [23] extracted multi-scale permutation entropy (MPE) and multi-scale power spectral entropy (MPSE) based on VMD to detect chatter in real time and used the Laplace scoring algorithm to obtain the most apparent scale for processing state features. In order to solve the problem that it is difficult to detect the machining chatter state during the machining process, Liu et al. [28] proposed a chatter feature extraction method based on optimized variational mode decomposition (OVMD) and multi-scale permutation entropy (MPE). Multiscale permutation entropy (MPE) and multiscale fuzzy entropy (MFE) are two types of entropy features that are applicable to feature metrics for complex signals. In this study, based on the above two characteristic indicators, a method for online detection of chatter is proposed. The effectiveness of the way is confirmed by simulation signals and experimental results. Compared with the literatures [23, 28], the noise part of the raw signal is processed, the VMD decomposition parameters are determined by a more scientific parameter optimization algorithm (GWO), and the study uses two different multi-scale entropy, which greatly shortens the calculation time.

To sum up, in this paper, the comb filter and EMD are combined to preprocess the signal for the first time, and the purpose is to remove the periodic part and the noise part in the original signal. To eliminate the influence of EMD mode aliasing, the Pearson correlation coefficient is used to reconstruct the signal with the rich information extracted from the IMF. The selected IMFs are strongly correlated with the raw signal, and the mean, variance, and standard deviation of the reconstructed signal and the raw signal are compared and analyzed subsequently. Considering that when chatter occurs, the energy of the chatter frequency band increases sharply, and the energy entropy of the chatter frequency band also increases. Therefore, with the maximum energy entropy as the fitness function, this paper proposes to apply the GWO optimization algorithm to the global VMD parameters. Based on the optimized VMD decomposition, to accurately identify the chatter frequency band, the energy entropy is applied to reconstruct the signal. This paper introduces the concept of multi-scale. The chatter feature rises from single dimension to multi-dimensional, forming a trend curve, which is more convincing for judging the processing state. The PE and FE at each scale are calculated, respectively, and the multi-feature and multi-dimensional fusion is realized to evaluate the processing state. Both the PE and the FE are indicators for evaluating the degree of confusion of time series and have strong robustness for processing nonlinear signals.

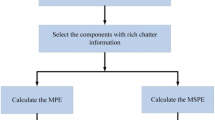
The remainder of the article is organized as follows: In Sect. 2, the basic principles of online chatter detection are introduced. In Sect. 3, a simulation signal containing chatter information is constructed, and the simulation signal is used to verify the effectiveness of the proposed chatter detection method. In Sect. 4, the experimental setup and process are briefly introduced, and the experimental results are analyzed and discussed. In Sect. 5, the full text is summarized, as shown in Fig. 1.

Fig. 1
figure 1

Flow chart of extracting chatter features by combining EMD and O-VMD

Full size image

2 Basic principles of online chatter detection

2.1 Principles of EMD and VMD

According to the literature [29], a real signal \(z\left(t\right)\) corresponding to the analytical signal \(z\left(t\right)\) is defined:

$$z\left(t\right)=x\left(t\right)+jy\left(t\right)=\sqrt{{x}^{2}\left(t\right)+{y}^{2}\left(t\right){e}^{j\theta \left(t\right)}}$$
(1)

The instantaneous phase is:

$$\theta \left(t\right)=\mathrm{arctan}\frac{y\left(t\right)}{x\left(t\right)}$$
(2)

The instantaneous frequency can be obtained by taking the derivative of the instantaneous phase:

$$\widetilde{\omega }=\frac{d\left(\mathrm{arctan}\frac{y\left(t\right)}{x\left(t\right)}\right)}{dt}$$
(3)

The purpose of EMD is to obtain the instantaneous frequency. \(z\left(t\right)\) can be expressed as a sum of components of IMF, and a residual term.

$$x\left(t\right)={\sum }_{j-=1}^{n}{C}_{j}\left(t\right)+{r}_{n}\left(t\right)$$
(4)

where \({r}_{n}\left(t\right)\) is the residual, which represents the average trend; each segment contains different frequency components given by each IMF components \({C}_{j}\left(t\right)\); the distribution of other frequency components varies with the signal itself.

Variational mode decomposition theory is an adaptive decomposition algorithm. Some of the algorithm’s characteristics, such as quasi-orthogonality, good noise robustness, and energy conservation, make it widely used in signal processing.

The VMD algorithm uses a non-recursive method for the input signal \(f\), decomposing a signal into sub-signals with quasi-orthogonal and sparse properties, modal \({u}_{k}\) [25]. The VMD decomposition process can be regarded as a constrained optimization problem. It minimizes the sum of estimated modal \({u}_{k}\) bandwidths. The constraint model is as follows:

$$\underset{\left\{{u}_{k}\right\},\left\{{\omega }_{k}\right\}}{\mathrm{min}}\left\{\sum_{k}{\Vert {\partial }_{t}\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)*{u}_{k}\left(t\right)\right]{e}^{-j{\omega }_{k}t}\Vert }_{2}^{2}\right\}\text{\hspace{1em}}s.t.\sum_{k}{u}_{k}=f$$
(5)

where \({u}_{k}=\left\{{u}_{1},{u}_{2},\cdots {u}_{k}\right\}\) and k represent the raw signal \(f\) decomposed into k IMF components and corresponding center frequencies, respectively. \(\delta\) represents the Dirac distribution, \(*\) represents the convolution operator.

Penalty factors α and Lagrange multipliers \(\lambda \left(t\right)\) are introduced. The transformation from constrained problem to unconstrained problem is realized. In summary, the Lagrange multiplier expression is as follows [30]:

$$\begin{array}{c}L\left(\left\{{u}_{k}\right\},\left\{{\omega }_{k}\right\},\lambda \right)=\alpha \sum_{k}{\Vert {\partial }_{t}\left[\left(\delta (t)+\frac{j}{\pi t}\right)*{u}_{k}\left(t\right)\right]{e}^{-j{\omega }_{k}t}\Vert }_{2}^{2}\\ +{\Vert f\left(t\right)-\sum_{k}{u}_{k}\left(t\right)\Vert }_{2}^{2}+\langle \lambda \left(t\right),f\left(t\right)-\sum_{k}{u}_{k}\left(t\right)\rangle \end{array}$$
(6)

In the presence of Gaussian noise, \(\alpha\) guaranteed reconstruction accuracy, and \(\lambda \left(t\right)\) guaranteed strictness of constraints. The VMD algorithm solves the constraint problem shown in the above formula, using the alternating direction multiplier method (ADMM) to solve the “saddle point.” The update for the mode \({u}_{k}\) is equivalent to solving the minimization problem as follows:

$${u}_{k}^{n+1}=\underset{{u}_{k\in X}}{arg\mathrm{min}}\left\{\alpha {\Vert {\partial }_{t}\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)*{u}_{k}\left(t\right)\right]{e}^{-j{\omega }_{k}t}\Vert }_{2}^{2}+{\Vert f\left(t\right)-\sum_{t}{u}_{i}\left(t\right)+\frac{\lambda \left(t\right)}{2}\Vert }_{2}^{2}\right\}$$
(7)

Transform the above equation to the frequency domain using the Parseval/Plancher Fourier equidistant transform in the norm \({L}_{2}\):

$${\widehat{u}}_{k}^{n+1}=\underset{{\widehat{u}}_{k},{u}_{k}\in X}{arg\mathrm{min}}\left\{\alpha {\Vert j\omega \left[\left(1+\mathrm{sgn}\left(\omega +{\omega }_{k}\right)\right){\widehat{u}}_{k}\left(\omega +{\omega }_{k}\right)\right]\Vert }_{2}^{2}+{\Vert f\left(\omega \right)-\sum_{i}{\widehat{u}}_{i}\left(\omega \right)+\frac{\widehat{\lambda }\left(\omega \right)}{2}\Vert }_{2}^{2}\right\}$$
(8)

Replace the \(\omega\) in the first term of the above formula with \(\left(\omega -{\omega }_{k}\right)\), according to the Hermitian symmetry property; the above procedure can be written in integral form:

$${\widehat{u}}_{k}^{n+1}\left(\omega \right)=\frac{\widehat{f}\left(\omega \right)-{\sum }_{i\ne k}{\widehat{u}}_{i}\left(\omega \right)+\frac{\widehat{\lambda }\left(\omega \right)}{2}}{1+2\alpha {\left(\omega -{\omega }_{k}\right)}^{2}}$$
(9)

By similar reasoning, the center frequency \({\omega }_{k}^{n+1}\) can be obtained as:

$${\omega }_{k}^{n+1}=\frac{{\int }_{0}^{\infty }\omega {\left|{\widehat{u}}_{k}^{n+1}\left(\omega \right)\right|}^{2}d\omega }{{\int }_{0}^{\infty }{\left|{\widehat{u}}_{k}^{n+1}\left(\omega \right)\right|}^{2}d\omega }$$
(10)

2.2 Mathematical model of Comb filter

The milling processing signals are collected by the sensor including periodic signals (domain frequency and its multiplier), noise signals, and chatter signals. To more accurately extract sub-signals containing rich chatter information, it is necessary to preprocess it. The primary function of the comb filter is to filter out the periodic signals in the raw signal. The biggest feature of the comb filter is that it is suitable for filtering rotating mechanical frequencies and has good stability for filtering periodic frequency signals. The comb filter is introduced to delete the spindle frequency and its harmonics. It is designed according to the reference [14]:

$${G}_{c}=\frac{\beta \left(1-{Z}^{-b}\right)}{1-\alpha {Z}^{-b}}$$
(11)

where α and β are the bandwidth coefficients of the comb filter. The filter coefficients are designed as follows:

$$\gamma =\sqrt{\frac{1-{\left|{G}_{c}\right|}^{2}}{\left|{G}_{c}\right|}}\mathrm{tan}\frac{d{w}_{b}}{4},\alpha =\frac{2}{1+\gamma }-1,\beta =\frac{1}{1+\gamma }$$
(12)

where wb is the desired normalized bandwidth with a quality factor of Q;

$${w}_{b}=\frac{2\pi \left(\frac{{w}_{n}}{{f}_{s}}\right)}{Q}$$
(13)

2.3 Mathematical model of Pearson correlation coefficient and energy entropy (EE)

To achieve the effect of noise reduction, EMD decomposition is used based on the filtered signal. Still, to the complexity of thin-walled parts processing and the defects of EMD decomposition itself, an indicator is needed to extract IMFs that can fully represent the raw signal information. Therefore, the Pearson correlation coefficient is used in this paper. Pearson correlation coefficient is suitable for correlation analysis of time series, with a solid theoretical foundation, high efficiency, and obvious effect. The Pearson correlation coefficient is defined as:

$$\rho \left(X,Y\right)=\frac{1}{N-1}\sum_{i=1}^{N}\left(\frac{{X}_{i}-\overline{X}}{{\sigma }_{X}}\right)\left(\frac{{Y}_{i}-\overline{Y}}{{\sigma }_{Y}}\right)$$
(14)

where \(\frac{{X}_{i}-\overline{X}}{{\sigma }_{X}},\overline{X },{\sigma }_{x}\) are the standard score, sample mean, and sample standard deviation of the sample \({X}_{i}\), respectively.

The correlation coefficient matrix for two sets of time series is the correlation coefficient matrix for each combination of time series.

$$R=\left(\begin{array}{cc}\rho \left(X,X\right)& \rho \left(X,Y\right)\\ \rho \left(Y,X\right)& \rho \left(Y,Y\right)\end{array}\right)$$
(15)

Since X and Y are always directly related to themselves, the diagonal elements are both 1.

$$R=\left(\begin{array}{cc}1& \rho \left(X,Y\right)\\ \rho \left(Y,X\right)& 1\end{array}\right)$$
(16)

According to the relevant literature, during the milling process, the energy changes with the change in the milling state. In the stable state, the energy is mainly concentrated on the domain frequency and its multiplier. In the chatter state, the amplitude of the chatter frequency increases sharply, meaning that the energy is focused on the frequency band containing the chatter frequency.

\({u}_{1}\left(t\right),{u}_{2}\left(t\right),\cdots {u}_{n}\left(t\right)\) represents the IMFs after EMD decomposition, so the energy \({R}_{i}\) of each order IMF is expressed as:

$${R}_{i}={\int }_{-\infty }^{+\infty }{\left|{u}_{i}\left(t\right)\right|}^{2}dt\text{\hspace{1em}}i=\mathrm{1,2}\cdots n$$
(17)

Energy entropy is the expansion of energy in the entropy field, which indicates the degree of disorder of energy in a time series. Since IMFs are orthogonal and anisotropic, then the EE of IMFs is expressed as:

$${E}_{i}=\sum_{i=1}^{n}{T}_{i}\mathrm{log}{T}_{i}$$
(18)

where \({T}_{i}={R}_{i}/R\) represents the energy of the IMF as a percentage of the total energy R of the entire signal.

2.4 Automatic selection method of VMD’s parameters based on GWO

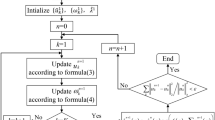
In VMD decomposition, the penalty factor α and the number of decomposition layers K will have a crucial impact on the decomposition result. To extract chatter features with high efficiency and high precision, it is urgent to find the optimal parameter combination. Therefore, in this paper, the gray wolf algorithm (GWO) is applied to find the global optimal parameter combination. The basic steps of GWO are as follows [31]:

  1. (1)

    Initialize the parameters and determine the maximum energy entropy as the fitness function

  2. (2)

    Initialize the gray wolf position

  3. (3)

    Calculate the fitness function value at different positions

  4. (4)

    Compare the size of the fitness value to update the gray wolf position

  5. (5)

    Determine whether the best fitness value or the maximum iteration is reached

  6. (6)

    Output the best parameter combination

2.5 Mathematical model of MPE and MFE

Permutation entropy (PE) measures the randomness of time series and detects dynamic changes in time series. Multi-scale permutation entropy (MPE) is defined as the set of PE values of time series at different scales, and its calculation method is as follows [32]:

  1. (1)

    The time series \(\left\{x\left(i\right),\right\}i=\mathrm{1,2},\cdots ,N\) is “coarse-grained” and each coarse-grained time series is calculated according to the following formula \({y}_{j}^{\left(\tau \right)}\):

    $${y}_{j}^{\left(\tau \right)}=\frac{1}{\tau }\sum_{i=\left(j-1\right)\tau +1}^{j\tau }{x}_{i},j=\mathrm{1,2},\cdots N/\tau$$
    (19)

    where \({y}_{j}^{\left(\tau \right)}\) represents a scale factor, the length of the time series after coarse-graining is \(N/\tau\).

  2. (2)

    After the raw time series is coarse-grained with different scale factors, the PE of the corresponding scale factors is calculated. This process is MPE analysis. However, to study its dynamic characteristics, the signal can be embedded into a high-dimensional space using the delayed embedding method. In the multi-scale application of this paper, the delay time is 10 and the embedding dimension is 4.

Fuzzy entropy (FE) measures the probability of the emergence of new patterns in time series, which is similar to the physical meaning of approximate entropy and sample entropy. Scale fuzzy entropy (MFE) is defined as the set of FE values of time series without time scale entropy, and its calculation method is as follows:

  1. (1)

    The coarse-graining process of its time series is the same as that of MPE

  2. (2)

    Calculate the fuzzy entropy (FE)

For a given N-dimensional time series \(\left[u\left(1\right),u\left(2\right),\cdots u\left(N\right)\right]\), define the phase space dimension \(m\left(m\le N-2\right)\) and the similarity tolerance r, reconstructed phase space:

$$X\left(i\right)=\left[u\left(i\right),u\left(i+1\right),\cdots ,u\left(i+m-1\right)\right]-{u}_{0}\left(i\right),i=\mathrm{1,2},\cdots ,N-m+1$$
(20)

where \(u\left(i\right)=\frac{1}{m}\sum_{j=0}^{m-1}u\left(i+j\right)\)

Introduce fuzzy membership function

$$A\left(x\right)=\left\{\begin{array}{cc}1& x=0\\ \mathrm{exp}\left[-\mathrm{ln}\left(2\right){\left(\frac{x}{r}\right)}^{2}\right]& x>0\end{array}\right.$$
(21)

where r represents the similarity tolerance.

For \(i=\mathrm{1,2},\cdots ,N-m+1\), calculate

$${A}_{ij}^{m}=\mathrm{exp}\left[-\mathrm{ln}\left(2\right)\cdot {\left({d}_{ij}^{m}/r\right)}^{2}\right],j=\mathrm{1,2},\cdots N-M+1,and\text{\hspace{0.17em}}j\ne i$$
(22)

where \({d}_{ij}^{m}=d\left[X\left(i\right),X\left(j\right)\right]=\begin{array}{c}max\\ p=\mathrm{1,2},\cdots ,m\end{array}\left(\left|u\left(i+p-1\right)-{u}_{o}\left(i\right)\right|-\left|u\left(j+p-1\right)-{u}_{o}\left(j\right)\right|\right)\) is the maximum absolute distance between the window vectors \(X\left(i\right)\) and \(X\left(j\right)\).

Defined:

$${\Phi }^{m}\left(r\right)=\frac{1}{N-m+1}\sum_{i=1}^{N-m+1}{C}_{i}^{m}\left(r\right)$$
(23)

where \({C}_{i}^{m}\left(r\right)=\frac{1}{N-m}\sum_{j=1, j\ne i}^{N-m+1}{A}_{ij}^{m}\).

Therefore, the fuzzy entropy of the raw time series is:

$$\underset{N\to \infty }{\mathrm{lim}}\left[\mathrm{ln}{\Phi }^{m}\left(r\right)-\mathrm{ln}{\Phi }^{m+1}\left(r\right)\right]$$
(24)

3 Chatter feature extraction of simulated signal

3.1 Simulated signal filtering and reconstruction

The effectiveness of the proposed method is proved by simulating the milling signal, setting the spindle speed to 1500r/min, the spindle speed frequency \({f}_{SP}\) is 25 Hz and the amplitudes of the first three harmonic components are assigned the values of 5, 3, and 2, respectively. The chatter frequency \({f}_{CH}\) is 133 Hz. Its sampling frequency is set to 1000 Hz. Based on the dynamic analysis of the milling process and the character analysis of the chatter signal, the following expressions are constructed [33]:

$$\begin{array}{c}{s}_{1}=5sin\left({f}_{SP}\cdot 2\pi t\right)+3sin\left(2{f}_{SP}\cdot 2\pi t\right)+2sin\left(3{f}_{SP}\cdot 2\pi t\right),0<t\le 1\\ {s}_{2}=\left(\frac{50}{1+{e}^{-15\left(t-1\right)}}-25\right)\cdot cos\left({f}_{CH}\cdot 2\pi t+0.5\mathrm{sin}\left({f}_{SP}\cdot 2\pi t\right)\right),0<t\le 1.5\\ {s}_{3}=25cos\left({f}_{CH}\cdot 2\pi t+0.5\mathrm{sin}\left({f}_{SP}\cdot 2\pi t\right)\right),1.5<t\le 2.5\end{array}$$
(25)

where period part \({s}_{1}\) contains the spindle rotational frequency and its harmonics, \({s}_{2}\) represents the transition part, and \({s}_{3}\) represents the chatter part.

The simulation signal is as follows:

$$s\left(t\right)=\left\{\begin{array}{c}{s}_{1},0<t\le 1\\ {s}_{1}+{s}_{2},1<t\le 1.5\\ {s}_{1}+{s}_{3},1.5<t\le 2.5\end{array}\right.$$
(26)

Figure 2 shows the time-domain waveform diagrams and corresponding spectrum distribution diagrams of the periodic part, the transition part, and the chatter part. As can be seen from Fig. 2, the frequency in the periodic signal only includes the spindle rotation frequency and its multiplier. The transition signal contains three chatter frequencies, but their amplitudes are much smaller than those of the chatter part. The distribution of these frequencies corresponds to different cutting states, so during milling, the final time-domain simulation signal can be seen as a combination of these parts.

Fig. 2
figure 2

a The time-domain signal; b the corresponding FFT spectrums

Full size image

In actual machining, in the stable milling state, the waveform of the time domain signal is smooth and the amplitude is small. When the machining state changes from stable to chatter, the amplitude of the signal increases with the severity of the chatter. When the chatter occurs entirely, the waveform of the time domain signal tends to be smooth again, and the amplitude is stable. The variation trend of the simulated milling signal is very similar to the time domain signal obtained experimentally in the literature[34].

The raw contains periodic signals (domain frequency and its multiplier), noise signals, and chatter signals. To make the tremor characteristics more sensitive, it is necessary to filter the cyclical signal and noise signal. Therefore, this article uses a comb filter and EMD decomposition to pre-process the above interference signals. The comb filter is implemented by MATLAB software, and the specific setting parameters are as follows. Q is set to 10, the sampling frequency fs is 1000Hz, and the periodic signal frequency ω is 25Hz.

In the stable processing state, the periodic signal dominates the raw signal, as shown in Fig. 3a. When the milling process is in a transition state, as shown in Fig. 3b, the amplitude of the time-domain signal suddenly increases. After filtering out periodic signals, rich chatter information is preserved. Finally, as shown in Fig. 3c, when the milling process is in the chattering state, the chatter part dominates. Furthermore, the amplitude of the chatter is significantly higher than that of the transition-state chatter. The comb filter is applied to filter the raw time domain signal, which can accurately remove the periodic part and preserve the chatter part. Perform EMD on the filtered signal to obtain IMFs. To select IMFs that can fully represent the primary information of the raw signal for signal reconstruction, the Pearson correlation coefficients of IMFs are analyzed in Table 1. After comparative analysis, it can be seen that the Pearson correlation coefficient of IMF1 is relatively high. According to the definition of Pearson’s correlation coefficient, its correlation strength is extremely strong and contains rich raw signal information, so IMF1 is selected as the reconstructed signal. Furthermore, this method avoids the modal aliasing effects of EMD decomposition and preserves valuable signals.

Fig. 3
figure 3

Time-domain and frequency domain waveforms: a stable state; b transition state; c chatter state

Full size image
Table 1 Pearson correlation coefficient between IMFs and raw signal
Full size table

To verify the accuracy of the reconstructed signal, the statistical characteristics including the mean–variance and standard deviation are researched which is shown in Table 2. Table 2 shows statistical traits, which include meaning, variance, and standard deviation. It shows that the reconstructed signal can represent many raw signal information.

Table 2 Mathematical statistics of two signals
Full size table

3.2 Influence analysis of essential parameters of VMD decomposition

The quality of the VMD decomposition result is restricted by several essential parameters: number of decomposition modes K, penalty factor α, discriminant accuracy e, and fidelity \(\tau\). Among them, the selection of discrimination accuracy and adherence usually takes the default values. Two other critical influencing parameters have a crucial impact on the VMD decomposition results.

3.2.1 Number of decomposition modes K

VMD decomposition needs to set the number of decomposition modes in advance K. The size of the K value mainly has the following effects on the quality of the decomposition result: (1) If the value of K is too large, it is prone to an over-decomposition phenomenon, and a specific component appears in multiple modes, which waste time; (2) if the value of K is too tiny, mode aliasing is prone to occur, and multiple components are aliased in the same model, and the model is lost. The following briefly introduces the influence of the decomposition model number K on the decomposition effect through the simulation signal. On the contrary, when K = 3, it is easy to find modal aliasing by observing its spectrum, and multiple components are aliased in the same model. When K = 5, the spectral distribution of the spectrum is over-decomposed, as shown in Fig. 4. In addition, the value of K will restrict the decomposition efficiency of VMD, and the decomposition time of VMD will increase with the increase of K value, as shown in Table 3.

Fig. 4
figure 4

K = 3, K = 5, VMD results and spectral distribution of different IMFs

Full size image
Table 3 Influence of K value on VMD decomposition efficiency
Full size table

3.2.2 Penalty factor α

Another critical parameter that VMD decomposition needs to set in advance is α. Its function is mainly to transform the solution of the constrained variational problem into an unconstrained variational problem. The size of the value of α will have the following effects on the decomposition result:(1) If α a is too large, modal aliasing will occur, and redundant frequency bands will appear; (2) if α is too small, it will cause modal aliasing and center frequency aliasing, and the frequency band amplitude will be too large. Analyze the simulated signal, take K = 4, α = 500, α = 2500, α = 4500, and α = 6500 compare the calculation results, as shown in Fig. 5. When α = 500, the residual periodic signal is mainly decomposed in the first-order IMF. Comparative analysis shows that if the penalty factor is too small, the amplitude of the signal will increase, thus affecting the accuracy of the decomposition; when α = 6500, 108 Hz appears in all IMFs components, modal aliasing occurs, which leads to the failure of VMD decomposition, and in the fourth-order IMF, there is also an over-decomposition phenomenon. This frequency band has a small amplitude and is neither a chatter frequency nor a period. The frequency of the signal makes this order of IMFs meaningless.

Fig. 5
figure 5

Effect of penalty factor changes on the spectral distribution

Full size image

3.3 Parameter optimization VMD

For the selection of the two essential parameters mentioned in the previous section, to accurately extract the chatter characteristics under the best parameter combination, this paper proposes a parameter optimization method based on the maximum energy entropy criterion combined with the gray wolf optimization (GWO) algorithm. When using GWO to optimize the combination of two parameters of VMD, it is assumed that in a two-dimensional space, the position coordinate of the gray wolf is (K, α). The update of the wolf position is achieved by comparing the magnitude of the fitness function.

In this paper, the principle of the maximum energy entropy of the fitness function is adopted, and the optimal first three parameter combinations are assigned to the α, β, δ wolves in turn by comparing the fitness function values of the gray wolves. The specific implementation steps of parameter optimization are shown in Fig. 6.To verify the effectiveness of the above parameter optimization method, the simulation signal of Eq. (25) is used for analysis.

Fig. 6
figure 6

Parameter optimization theory flow chart

Full size image

First, the VMD parameter combination (K, α) is optimized by GWO with the maximum energy entropy as the fitness function, then perform VMD and calculate the energy entropy values of different IMFs, and compare them with the spectrograms of IMFs. After parameter optimization calculation, the optimal parameter combination of the simulated signal is obtained as (4.3500). For this parameter combination, the results of VMD decomposition are shown in Fig. 7. The energy entropy corresponding to each order of IMFs is shown in Table 4. After analysis, it is found that the parameter combination after GWO optimization can make the VMD decomposition more accurate, the spectrum distribution is more precise, and the energy entropy characteristics corresponding to the chatter frequency band are pronounced.

Fig. 7
figure 7

Spectrum distribution of IMFs

Full size image
Table 4 Energy entropy of IMFs
Full size table

To make the parameter optimization scheme convincing, the time efficiency of GWO is analyzed. The time efficiency is mainly limited by the number of wolves, the maximum number of iterations, and the kind of fitness function. In this paper, the fitness function is energy entropy, and the effects of the number of wolves and the maximum number of iterations are analyzed, as shown in Table 5. Program operating environment, Processor: 11th Gen Intel(R) Core (TM) i7-11800H @ 2.30 GHz, operating system: Windows 11, software and version number: MatlabR2019a.

Table 5 GWO time efficiency analysis
Full size table

After the above analysis, it can be seen that the time efficiency of GWO parameter optimization is related to the product of the number of wolves and the maximum number of iterations. The larger the product, the higher the time cost, and the smaller the product, the lower the time cost. It has nothing to do with the number of single factors in it.

3.4 Chatter characteristic analysis

To eliminate the influence of EMD mode aliasing and obtain richer chatter frequency information, GWO-VMD is used to extract the chatter frequency. The frequency bands of the IMFs will be further subdivided by GWO-VMD, and the modal aliasing will be separated. It can be seen from the simulation signal that the chatter frequencies in the transition state and chatter state are 108 Hz, 133 Hz, and 158 Hz, respectively. It can be seen from Table 4 that the EE of the IMFs corresponding to the chatter frequency is higher, which proves that it is IMFs that the energy level of chaos is also higher. In addition, it can also be seen from Table 4 that the third-order IMFs with a higher EE are IMF2, IMF3, and IMF4, respectively. Therefore, IMF2, IMF3, and IMF4 are used as the second reconstruction signal, and the reconstructed signal is shown in Fig. 8. As shown in Fig. 8, the reconstructed signal contains rich chatter information. In addition, by analyzing the Hilbert spectrum, it is found that comb filters and EMD decomposition have filtered out periodic signals and useless information.

Fig. 8
figure 8

Time-domain and frequency-domain diagrams of the second reconstructed signal

Full size image

In this paper, two detection indicators, MPE and MFE, are applied to online chatter detection. The above simulation signal is divided into three parts, the stabilization stage, the transition stage, and the chatter state. The time-domain waveform of the simulation signal is shown in Fig. 9.

Fig. 9
figure 9

Three states of simulating signal

Full size image

The MPE and MFE of the above three parts are calculated, respectively, as shown in Fig. 10. As can be seen from Fig. 10, the two feature indicators can well distinguish the three processing states of stability, transition, and chatter. By introducing multi-scale, the features are more evident in different dimensions. However, according to the concept of coarse-grain, if the sample points of the time series are minor, larger coarse-graining will make the length of the raw sequence too small, resulting in the value of the sample points of the new sequence being too large or too small, making the calculated features inaccurate, thus affecting the identification of the machining state. It can be seen in the blue dashed box in Fig. 10 that in MPE, the scale starts from 5, and the distinction between the transition state and chatter state is not apparent. When the scale is 7 or 9, the PE values of the three states overlap, which leads to the failure of the feature to discriminate the processing state. In MFE, at scale 4, it is difficult to identify the machining state accurately, and at scale 7 or 8, the situation reappears.

Fig. 10
figure 10

MPE and MFE of simulated signals: a MPE; b MFE

Full size image

Table 6 verifies the growth rates of the feature in the three processing states at the best scale in Fig. 10. It can be seen from Table 6 that the growth rate of the feature from the stable state to the transitional state is significantly greater than that from the transitional state to the chatter state.

Table 6 Growth rate of feature at the best scale
Full size table

After the above analysis, it can be seen that although MPE and MFE can distinguish the processing state, when applying the multi-scale concept, the appropriate scale should be determined according to the size of the raw time series sample points to coarse-grain the sequence, and the optimal scale eigenvalue should be selected to carry out discrimination of processing state.

4 Experimental verification

4.1 Experimental setup

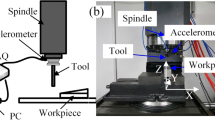
To prove the effectiveness and reliability of the proposed chatter detection method, milling experiments under different dry-cutting conditions are conducted on DMC635V vertical machining center. The machining center adopts Siemens operating system, with a total of X, Y, Z, and four machining axes. The experimental setup is shown in Fig. 11.The cutter is GM4ED10, which is a flat-end milling tool with 4 teeth. The experimental workpiece is an aluminum alloy Al6061 with a size of 100 mm × 100 mm × 50 mm. Its detailed geometric parameters are shown in Table 7. During the milling process, the milling force signal is obtained by the dynamometer Kistler9257B. The entire milling process is in a dry milling state. The dynamometer is fixed on the workbench and the workpiece is clamped by jaw vice, as shown in Fig. 11. The sampling frequency is set to 7000 Hz. The milling parameters are listed in Table 8.

Fig. 11
figure 11

The experimental setup

Full size image
Table 7 Tool parameters and material properties of Al6061
Full size table
Table 8 Cutting parameters for the milling experiments
Full size table

4.2 Result and discussion

4.2.1 Raw signal filtering and reconstruction

The proposed chatter detection scheme is validated. Considering that the cutting force signal in the y-direction is more suitable than the x and z directions in actual industrial production, this scheme adopts the cutting force signal in the y-direction. According to different spindle speeds, the periodic signal in the raw signal is processed by the comb filter. The result of the comb filter is mainly limited by the setting of the quality factor, and the comb filter can only perform integer multiple periodic filtering. FFT spectra filtered with different quality factors are shown in Fig. 12. It can be seen from Fig. 12 that when the Q value is not selected properly, the filtering result is not satisfactory.

Fig. 12
figure 12

Comparison of comb filter characteristics under different quality factors

Full size image

Using a comb filter, the periodic component signal can be well differentiated from the measured vibration signal, where the quality factor Q is 8, and the sampling frequency fs is 7000 Hz, as shown in Fig. 13. In Fig. 13a and b, it can be seen that the periodic signal part in the raw signal is filtered out. From the frequency domain waveform, it can be found that the amplitude of the periodic signal becomes extremely small, and the rest is the amplitude of the noise signal. It can be found in Fig. 13c and d that after filtering out the periodic component from the measurement signal, the signal of the chatter part is obtained, and the amplitude of the chatter part in its FFT spectrum is not significantly reduced.

Fig. 13
figure 13

Separation of the periodic and chatter components on Test 1 and Test 3

Full size image

In actual industrial production, the signal collected by the sensor contains a lot of useless information (noise signal), resulting in inaccurate detection results. According to the Pearson correlation coefficient, the IMF components with rich raw signal information can be selected more accurately. Therefore, the EMD decomposition algorithm is used to obtain the components of each order IMFs. The appropriate IMFs are chosen to reconstruct the signal. The y-direction cutting force signal in experiment 3 is selected for signal reconstruction. The purpose of EMD decomposition is to eliminate the influence of noise in the raw signal, and to extract sub-signals with rich raw signal information for reconstruction. This scheme calculates the Pearson correlation coefficient of each order IMFs respectively, as shown in Table 9. It can be seen from Table 9 that the Pearson correlation coefficient in IMF1 is much larger than that of other IMF components; the correlation degree is extremely strong, and a lot of raw signal information is preserved.

Table 9 Pearson correlation coefficient between IMFs and raw signal
Full size table

In addition, to verify the noise reduction function of the EMD decomposition algorithm, the filtered signal and the reconstructed signal are compared and analyzed, as shown in Fig. 14a and b. In Fig. 14a, the persistence spectrum is composed of two frequency sections, the noise part, and the chatter part. At the 0–600 Hz, the power of the signal fluctuates sharply, so it is judged that this part is the noise part, the peaks of other frequency sections, and the fluctuation is the chatter part. Combined with time–frequency domain images, the noise part always exists in the whole process. Since the next step is to optimize the VMD parameters with energy entropy as the fitness function, the energy entropy of the noise part may lead to the failure of the optimization results, so EMD is used to reduce noise. It can be seen from the persistence spectrum in Fig. 14b that the peak of 0–600 Hz disappears and becomes a relatively gentle frequency band, the chatter part is not affected by the EMD decomposition, and the chatter part in the raw signal is retained information. In the time–frequency domain, the noise from 0 to 6 s disappears, and the coincidence of the noise frequencies from 6 to 10 s is significantly reduced.

Fig. 14
figure 14

Time–frequency domain analysis of Raw and reconstructed signal: a raw signal; b reconstructed signal

Full size image

To verify the accuracy of the reconstructed signal, the statistical characteristics including the mean–variance and standard deviation are researched which is shown in Table 10. Table 10 shows statistical traits, which include meaning, variance, and standard deviation. It shows that the reconstructed signal can represent many raw signal information. Through comparative analysis, the IMF1 extracted according to the Pearson correlation coefficient not only retains a lot of raw signal information but also realizes the noise reduction of the signal.

Table 10 Mathematical statistics of two signals
Full size table

4.2.2 GWO optimization of VMD parameters

In the VMD decomposition, the penalty factor and the number of decomposition layers always restrict the efficiency and accuracy of the decomposition. Therefore, this paper proposes to use the GWO algorithm to globally optimize the optimal parameter combination of VMD. Take the four-stage processing signals of 2–4 s, 8–10 s in Test 2 and 1–3 s, 7–9 s in Test 4 for GWO optimization, as shown in Fig. 15. The lengths of the above four-segment signals are all 14,000 sample points, and GWO parameters are optimized. The initialization parameters of GWO parameter optimization are shown in Table 11.

Fig. 15
figure 15

Time-domain processing signals of Test 2 and Test 4: a Test 2; b Test 4

Full size image
Table 11 GWO Parameter Initialization
Full size table

where M indicates the size of the wolf pack, Gmax is the maximum number of iterations, Dim is the search dimension, and L1 and L2 are the search ranges of VMD parameters K and α, respectively.

It can be found from the above table that GWO optimization randomly performs 600 VMD decompositions under different combinations of decomposition levels and penalty factors. After each parameter optimization, the parameter combination corresponding to the maximum energy entropy is output. The parameter combinations corresponding to the maximum energy entropy of the above four-state signals are shown in Fig. 16. It can be seen from Fig. 16a that when K = 5 and α = 1235, the maximum energy entropy is 0.36788; it can be seen from Fig. 16b that when K = 8 and α = 4979, the maximum energy entropy is 0.36764; it can be seen from Fig. 16c that when K = 11 and α = 1536 for the third segment of the signal, the maximum energy entropy is 0.36788; it can be seen from Fig. 16d that when K = 12 and α = 2698 for the fourth segment signal, the maximum energy entropy is 0.36788. Take the parameter combination in Fig. 16c to perform VMD decomposition on this signal. To judge whether the 11 IMFs obtained by decomposition are correct, we performed the FFT analysis on each IMF as shown in Fig. 17.

Fig. 16
figure 16

Three-dimensional diagram of energy entropy of cutting signal under all groups of K and α

Full size image
Fig. 17
figure 17

IMFs frequency distribution

Full size image

According to related literature [30], the chatter frequency is not equal to the primary frequency and its multiplier frequency, but the frequency with a larger amplitude. It can be seen from Fig. 18 that the frequency distribution of each order IMF is clear, and the chatter frequency band can be seen. The amplitudes of IMF3, IMF5, IMF6, and IMF10 are much larger than other IMFs, and the peak frequency is not equal to the domain frequency and its multiplier. Therefore, it can be judged that the VMD decomposition under this parameter combination can well retain rich chatter information. To further verify the accuracy of the optimization of the GWO algorithm, Hilbert-Hang (HHT) spectrum analysis is used for processing, as shown in Fig. 18.

Fig. 18
figure 18

HHT analysis of IMFs of various orders

Full size image

4.2.3 Second signal reconstruction

After the above analysis, the reliability of GWO to optimize VMD parameters is verified. The amplitude of the chatter frequency band is significantly higher than that of the domain frequency and its multiplier or other frequency bands. To further extract chatter features, this paper uses the energy entropy feature to extract IMF components with rich chatter information after GWO-VMD decomposition. In previous articles, the energy entropy feature can be directly used as an indicator for judging the machining state, but when milling thin-walled parts, the dynamic characteristics of the system change nonlinearly, resulting in fluctuations in the energy entropy feature value. Setting the threshold here may lead to the machining state misjudgment. Therefore, this scheme applies the energy entropy value as the feature of the second reconstructed signal to extract sub-signals with rich chatter information. According to the four-group signal optimized by the above-mentioned four-group GWO, the energy entropy characteristics are calculated respectively. The second signal reconstruction is performed, as shown in Table 12. Test 2 and Test 4 are the stable state and the chatter state, respectively. It can be seen from Table 12 that in the stable state, the energy entropy is larger at the first three IMFs, while in the chatter state, the energy entropy is more significant at IMF4, IMF5, and IMF6. According to the previous analysis of the article, just in the chatter frequency band. Therefore, in this paper, IMF components with energy entropy greater than 0.3 are selected for signal reconstruction.

Table 12 Four-state signal IMF energy entropy of each order
Full size table

4.2.4 MPE and MFE chatter feature analysis

Based on the second reconstructed signal, this paper proposes to apply multi-scale permutation entropy and multi-scale fuzzy entropy as features for detection chatter. In Test 3 and Test 4, three cutting force signals were intercepted, as shown in Fig. 19.

Fig. 19
figure 19

Cutting force signal of two groups of tests: a Test 3; b Test 4

Full size image

The multi-scale entropy characteristics of the six groups of cutting force signals above are calculated respectively. The machining state is divided into a stable state, slight chatter state, and severe chatter state, as shown in Fig. 20. Figure 20a and c are multi-scale permutation entropy; Fig. 20b and d are multi-scale fuzzy entropy. In Fig. 20a and c, at different scales, the permutation entropy distinguishes processing states more clearly. Still, individual scales, the numerical value of permutation entropy is not precise enough; for example, in Fig. 20a, when the scale is 5, the entropy values of slight chatter and severe chatter are sharply close, and the entropy value of slight chatter reaches 0.896; in Fig. 20c, the tremendous entropy values also appear at scales 3, 5, and 7; the entropy values are almost equal for slight chatter and severe chatter. When the scale is 9, the permutation entropy of slight chatter is greater than that of severe chatter. Although the multi-scale permutation entropy can observe the changing trend of entropy features at multiple time scales, selecting the optimal scale is also an urgent problem to be solved. As shown in Fig. 20b and d, the multi-scale fuzzy entropy has the same issues as the multi-scale permutation entropy, which leads to the failure of each scale. Although the multi-scale entropy has the above problems in judging the processing state, at the best scale, the distinction between the processing states is more prominent, as shown in the dotted line in Fig. 20. In general, the multi-scale permutation entropy and multi-scale fuzzy entropy applied in this paper can distinguish the milling processing state well and are not affected by the processing parameters. The entropy value of the feature discriminates the processing state.

Fig. 20
figure 20

MPE and MFE of cutting force signal: a MPE of Test 3; b MFE of Test 3; c MPE of Test 4; d MFE of Test 4

Full size image

The multi-scale permutation entropy and multi-scale fuzzy entropy of Test 1 and Test 2 are at the best scale, and the values of each processing state are shown in Table 13. To verify the sensitivity of the proposed two feature indicators to chatter. From the stable cutting to slight chatter in Test 3, the growth rates of MPE are 162.9%. And from the slight chatter to severe chatter, the growth rates of MPE are 25.1%. From the stable cutting to the slight chatter in Test 4, the growth rates of MPE are 204.9%. From slight chatter to severe chatter, the growth rates of MPE are 16.3%. From the stable cutting to the slight chatter in Test 3, the growth rates of MFE are 47.7%. And from slight chatter to severe chatter, the growth rates of MFE are 48.33%. From the stable cutting to the slight chatter in Test 4, the growth rates of MFE are 27.7%. From slight chatter to severe chatter, the growth rates of MFE are 32.7%. It can be seen that the growth rate of MPE and MFE from stable state to slight chatter is significantly higher than that from slight to severe chatter. The above growth rates of features under different processing conditions are in line with the actual situation. Based on the above analysis, if chatter occurs, the chatter detection scheme proposed in this paper can effectively identify it.

Table 13 MPE and MFE in Test 1and Test 2
Full size table

4.3 Performance comparison

To demonstrate the effectiveness of the method, the MPE of the original signal was extracted and compared. Using the same method, the MPE values at different scales are extracted, and the results are shown in Fig. 21. Figure 21 shows the comparison between the proposed scheme and the other two methods. The milling signal under severe chatter is selected. The other two schemes are that the periodic signal and noise signal of the raw signal are not processed and the VMD decomposition parameters are not optimized. It can be seen from the figure that the permutation entropy extracted by the proposed scheme is significantly higher than the other two schemes at most scales under a severe chatter state. The results show that periodic signals and noise signals in the raw signal can interfere with the chatter characteristics and cause it to be insensitive. Unoptimized VMD is not as effective as O-VMD in chatter detection, and this conclusion is also verified in Sect. 3.3, and it is found that K and α have a great impact on the performance of VMD.

Fig. 21
figure 21

Comparison with existing chatter detection solutions

Full size image

5 Conclusions

To more accurately extract the chatter frequency band and calculate the chatter features, this paper proposes a combination of EMD and optimized VMD to extract multi-dimensional and multi-entropy features as indicators for judging the processing state. The periodic signal and noise parts are filtered out by comb filter and EMD decomposition respectively, and the first signal reconstruction is carried out using Pearson correlation coefficient. The energy entropy is used as the fitness function to optimize the GWO parameters of the reconstructed signal. The second signal reconstruction is based on O-VMD decomposition, calculates the energy entropy characteristics of IMFs of each order, and selects IMF components whose entropy value is more significant than 0.3. Calculate the MFE and MPE of the second reconstructed signal.

  1. (1)

    The comb filter and EMD decomposition can effectively separate the periodic signal and noise parts. The Pearson correlation coefficient proposed in this paper is used to reconstruct the signal, and the mean, variance, and standard deviation characteristics of the raw signal are compared. The results show that the reconstructed signal contains rich information from the raw signal; the correlation strength is extremely strong, and noise reduction is achieved.

  2. (2)

    To optimize the VMD decomposition, this paper proposes a GWO optimization algorithm with the maximum energy entropy as the fitness function. It can be seen from Figs. 17 and 18 that the VMD decomposition after GWO optimization not only has apparent distribution in each frequency band but also maximizes the energy entropy of the chatter frequency band.

  3. (3)

    The MPE and MFE proposed in this paper can detect the processing state from multiple dimensions at the optimal scale. The three processing states (stable, slight chatter, severe chatter) are differentiated. In Test 3, the MPE characteristics of each processing state increased by 162.9% and 25.1%, respectively, and the MFE characteristics increased by 47.7% and 48.33%. In Test 4, the MPE characteristics of each processing state increased by 204.9% and 16.3%, respectively, and the MFE characteristics increased by 27.7% and 32.7%. Based on the above analysis of the growth rate, if chatter occurs, the chatter detection scheme can effectively identify the milling process state.