1 Introduction

Through the accurate prediction of cutting force, the tool and machining parameters can be reasonably selected to improve cutting performance. Many researchers around the world have also done a lot of research on oblique cutting, because the majority of metal machining is non-free oblique cutting. At present, although most of the research is focused on the cutting force prediction of orthogonal free cutting, in which the cutting direction is performed along one straight cutting edge, non-free cutting, in which both primary and minor cutting edges are involved, is most widely used such as cylindrical turning in practice. The cutting conditions, the nose radius, and the main cutting edge angle also affect the cutting force in turning; therefore, comprehensive consideration of these factors is essential to accurately predict cutting forces. Besides, the dead metal zone also has major effect on cutting force and cutting performance in micro-machining [1, 2].

Cylindrical turning, one of the commonest processes in manufacturing components, is widely used in automotive, aerospace, and so on. It is a typical non-free cutting operation whose chip deformation process is very complex. The calculation of cutting forces in turning is roughly divided into three methods: empirical, analytical, and numerical models. Parakkal et al. [3] developed a relatively simple mechanistic model to predict cutting forces for grooved tool in oblique cutting, which considered the effect of the tool edge radius. This model was used to investigate the effects of cutting conditions and grooved parameters on the cutting forces. Kone et al. [4]. identified empirical cutting force equations; the chip flow angle of groove coated tool cutting 304L austenitic steel under dry cutting condition is deduced. Venkatarao [5, 6] proposed a power consumption optimization-base strategy couple with 3D FEM simulation to reduce power consumption in micro-machining, the optimal value of process parameters is obtained for minimum cutting force, and a power consumption model was developed in terms of cutting force directions in ultrasonic vibration helical milling. Colwell [7] proposed the equivalent cutting edge that is used to replace the real cutting edge with an imaginary straight line in the tool rake face and assumed that the equivalent cutting edge is perpendicular to the chip flow direction. However, the chip flow direction defined above is not suited for cylindrical turning due to the nose radius. Hu et al. [8] extended Colwell’s concept of equivalent cutting edge to the case of non-zero inclination angle. Kushima and Minato [9] divided the cutting edge into many small units and supposed that the component chip flow direction of each unit is perpendicular to the component cutting edge, and then the resultant chip flow direction is obtained by vectorial sum of the component chip flow directions. Young et al. [10] regarded the chip as many independent chip units and assumed that the thickness and direction of undeformed chip part of each unit are variable. The equivalent cutting edge is a straight line perpendicular to the direction of friction and can be obtained by calculating the resultant force per unit friction. Similarly, Wang et al. [11]. extended Young’s method to the tool nose with non-zero rake and inclination angle and evaluated cutting force through numerical integration. Endres et al. [12]. introduced a nonlinear relationship among the unit friction, cutting force, and the chip thickness by considering the size effect of rounded edge on the tool nose. Khlifi et al. [13]. applied an equivalent tool geometry method to induce the same cutting force components as the real tool while taking into account the radius of the tool nose and edge. In addition to estimating the tool flank and crater wear, this method can also predict cutting force components in turning.

In the primary shear zone, Merchant [14] proposed a single shear plane analytical model. The shear angle was obtained by the minimum energy theory; many analytical models were then proposed for the modeling of orthogonal cutting process, such as the classical parallel-sided shear zone theory proposed by Oxley [15], which supposed that the primary shear zone is equally divided by the primary shear plane. However, Li et al. [16] established the unequal division shear zone theory by observing the strain rate distribution in the primary shear zone is inconsistent, the analytical results showed that the unequal division shear zone theory has acceptable accuracy. In subsequent research, this model is widely used to predict the cutting force and chip flow direction and to identify material constitutive equation. In addition, the existence of the rounded nose and the main cutting edge angle makes the cutting mechanism more complicated. Simultaneously, they have a significant influence on the geometry of the undeformed chip area, cutting forces, chip geometry, heat generation, and tool wear during turning. Redetzky et al. [17] divided the cutting edge into many trapezoidal units that are perpendicular to the component edge and calculated the cutting force of each discrete unit through unit cutting force, unit edge force, and unit lateral force. Hagiwara et al. [18] developed the hybrid model by Redetzky et al. [17] to predict the chip side-flow angle for complex grooved tool inserts in contour turning operations by applying the effective cutting conditions and tool geometry. Armarego et al. [19]. put forward to the generalized cutting edge concept to replace the rounded edge of tool nose. Storch et al. [20] investigated the unit force distribution on the rounded edge for free cutting and found that both the tool nose and the main cutting edge affect the machined surface quality and chip formation process. Fang [21] developed an improved oblique cutting model different from traditional model by considering the two cases where the tool main cutting edge angle is not equal to 90° and the influence of the tool feed velocity on the resultant cutting velocity is not ignored. Molinari et al. [22] established a new thermo-mechanical model of oblique cutting to take into account the real cutting edge geometry; the rounded nose is discretized into a set of cutting edge units to obtain the component cutting force and temperature distribution along the rake face, but their oblique model is based on the inertia item, mainly suitable for adiabatic shear process in high-speech machining. Budak et al. [23] proposed a thermo-mechanical model that considered both the sticking and sliding contact on rake face, and applied this model to obtained the local forces acting on each element by dividing the nose of the turning into small elements. Abdellaoui et al. [24] also analysed the effects of tool nose radius and established a thermo-mechanical model, which allows predicting cutting force components and thermo-mechanical parameters.

In conclusion, the existing turning force prediction model mainly apply the single shear plane theory and the parallel shear zone theory in the primary shear zone. In such case, these models cannot accurately describe the real plastic deformation state and stress–strain relationship of the primary shear zone. In this paper, a novel turning force prediction model based on unequal shear theory is presented for cylindrical turning, considering the influence of the tool nose radius and the main cutting edge angle on cutting force.

In this present work, the oblique cutting theory based on the unequal division shear zone theory investigated by Li et al. [16, 25], and combined with the tool discretization approach of Molinari and Moufki [22], is developed to predict the cutting forces in turning of 304 stainless steel. This paper is organized as follows. Section 2 presents the analytical modeling of non-free oblique cutting with geometrical characterization and governing equations. The unequal shear theory and material constitutive equation are described in Sect. 3. In Sect. 4, the discretization of the tool cutting edge and the component geometry of each cutting edge unit are described. The component and resultant cutting force calculation are detailed in Sect. 5. The turning experiments for 304 stainless steel were conducted, and the effect of cutting parameters on cutting force is also discussed in Sect. 6. Finally, some conclusions are provided in Sect. 7.

2 Characteristics of the improved oblique cutting

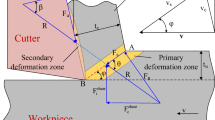
To study the turning process, an analytical model of oblique cutting of the unequal division shear zone theory is developed for the case that the tool cutting edge angle relative to the main cutting edge is not equal to 90°, namely, the feed rate fr is not equal to the undeformed chip thickness t. In view of this, Fang [21] also proposed an improved method for the oblique cutting model and applied it to chip control experiment. Figure 1 illustrates the process of improved oblique cutting.

Fig. 1
figure 1

The improved oblique cutting process

Full size image

In this model, where t, aw, and φr are undeformed chip thickness, cutting width, and lead angle (complementary angle of the main cutting edge angle κr), respectively. The cutting depth ap, feed rate fr, cutting velocity V, normal rake angle γn, and inclination angle λs are known, and the geometric relations of these parameters are shown in Fig. 2. Some planes that can be used to determine the location of the cutting edges, rake face, and flank face are defined.

  • The reference plane Pr

  • The working plane Pf

  • The back plane Pp

  • The cutting plane Ps

  • The orthogonal plane Po

  • The normal plane Pn

  • The shear plane Psh

  • The equivalent plane Pe

Fig. 2
figure 2

The geometrical relationship of oblique cutting

Full size image

As shown in Figs. 1 and 2, to calculate the relationships of geometry, motion, and force in the improved oblique cutting model, a series of coordinate systems are defined.

  • Frame (xa, ya, za), xa is parallel to the cutting velocity direction, za is parallel to the feed direction, (xa, ya) is the back plane Pp, (ya, za) is the reference plane Pr, (xa, za) is the working plane Pf.

  • Frame (xo, yo, zo)

  • Frame (xn, yn, zn)

  • Frame (xr, yr, zr)

  • Frame (x, y, z)

  • Frame (xc, yc, zc)

  • Frame (xs, ys, zs)

  • Frame (xe, ye, ze)

The eight frames can be related by rotation transformation, as shown in Fig. 3. Take for example, (xo, yo, zo) is obtained by the rotation of angle -φr of the frame (xa, ya, za) around the xa axis. It can be expressed as the following form:

Fig. 3
figure 3

The rotation transformation relationships between the coordinate systems

Full size image
$$(\mathbf{x}_\mathrm{a},\mathbf{y}_\mathrm{a},\mathbf{z}_\mathrm{a})\stackrel{\mathbf{R}({x}_{a},-{\varphi }_{r})} {\longrightarrow}(\mathbf{x}_{\mathrm{o}},\mathbf{y}_{\mathrm{o}},\mathbf{z}_{\mathrm{o}})$$

The rest of the frames can also be given by the above method; Φn is the normal shear angle, ηc is the chip flow angle, ηs is the shear flow angle, and ηe is the equivalent plane angle. To locate the equivalent plane of each discrete edge unit, of which k is used to represent the number, the shear flow angle and the equivalent plane angle are taken by the following expression [22].

$$tan\;\eta_e^k=\frac{\tan\;\eta_c^k\cos\;\eta_s^k+\sin(\phi_n^k-\gamma_n^k)\sin\;\eta_s^k}{\cos(\phi_n^k-\gamma_n^k)}$$
(1)
$$tan\;\eta_s^k=\frac{\tan\;\lambda_s^k\cos(\phi_n^k-\gamma_n^k)-\tan\;\eta_c^k\sin\;\phi_n^k}{\cos\gamma_n^k}$$
(2)

Since the chip flow angle is affected by the non-free chip in turning, the chip flow angle ηc formula of free oblique cutting which was proposed by Moufki and Molinari [26] or others no longer suitable for no-free oblique cutting. The chip velocity can be calculated as:

$$V_c^k=\frac{V\cos\;\lambda_s^k\sin\phi_n^k}{\cos\;\eta_c^k\cos(\phi_n^k-\gamma_n^k)}$$
(3)

The normal shear angle can be calculated with the Merchants formula [14].

$${\phi }_{n}^{k}=\frac{\pi }{4}-\frac{{\beta }_{k}}{2}+\frac{{\gamma }_{n}^{k}}{2}$$
(4)

The mean friction angle βk can be defined by mean friction coefficient, and the mean friction coefficient may be a power function of the chip velocity, as shown in Fig. 4. The friction coefficient is given by:

$$f={f}_{0}{V}_{c}^{p}$$
(5)

where f0 is constant, f is mean friction coefficient, while p < 0. The coefficients f0 and p can be identified by the experimental data in orthogonal cutting.

Fig. 4
figure 4

The fitting curve of mean friction coefficient f with chip velocity Vc

Full size image

3 Governing equations of the primary shear zone

Johnson–Cook model is used as flow stress model of workpiece material [27].

$${\tau }^{k}=\frac{1}{\sqrt{3}}[A+B{(\frac{{\gamma }^{k}}{\sqrt{3}})}^{n}][1+C\mathrm{ln}(\frac{{\dot{\gamma }}^{k}}{{\dot{\gamma }}_{0}})][1-{(\frac{{T}^{k}-{T}_{r}}{{T}_{m}-{T}_{r}})}^{m}]$$
(6)

where, \({\tau}^{k}\), \(\gamma^k\), \({\dot{\gamma }}^{k}\), and \({T}^{k}\) are the shear stress, the shear strain, the shear strain rate, and the instantaneous temperature of the workpiece, respectively. \({\dot{\gamma }}_{0}\) is reference plastic strain rate, Tm is melting temperature of the workpiece material, and Tr is room temperature or initial workpiece temperature. A, B, C, m, and n is the material constants which can be identified through split Hopkinson bar (SPHB), the material coefficients of Johnson–Cook model are listed in Table 1.

Table 1 Johnson–Cook parameters of 304 stainless steel
Full size table

The unequal division shear zone theory is used to predict the turning forces, as shown in Fig. 5. In this model, the strain, strain rate, and the temperature of discrete chip are calculated as follows [25]:

$${\dot{\gamma }}^{k}=\left\{\begin{array}{l}\frac{{\dot{\gamma }}_{m}^{k}}{{({k}_{u}^{k}h)}^{q}}{({z}_{e}^{k})}^{q}\;\;\;\;\;{z}_{e}^{k}\in [0,{k}_{u}^{k}h]\\ \frac{{\dot{\gamma }}_{m}^{k}}{{(1-{k}_{u}^{k})}^{q}{h}^{q}}{(h-{z}_{e}^{k})}^{q}\;\;\;\;\;{z}_{e}^{k}\in [{k}_{u}^{k}h,h]\end{array}\right.$$
(7)
$$\gamma^k=\left\{\begin{array}{l}\frac{\dot\gamma_m^k\cos\;\eta_e^k}{(q+1)V\cos\;\lambda_s^k\sin\;\phi_n^k{(k_u^kh)}^q}{(z_e^k)}^{q+1}\;\;\;\;\;z_e^k\in\lbrack0,k_u^kh\rbrack\\-\frac{\dot\gamma_m^k\cos\;\eta_e^k}{(q+1)V\cos\;\lambda_s^k\sin\;\phi_n^k{(1-k_u^k)}^qh^q}{(h-z_e^k)}^{q+1}+\frac{\cos\;\gamma_n^k\cos\;\eta_e^k}{\cos(\phi_n^k-\gamma_n^k)\cos\;\eta_s^k\sin\;\phi_n^k}\;\;\;\;\;z_e^k\in\lbrack k_u^kh,h\rbrack\end{array}\right.$$
(8)

where \({\dot{\gamma }}_{m}^{k}\) is the maximum strain rate, \({k}_{u}^{k}\) is unequal division ratio, q is a parameter to characterize the non-uniform distribution of the tangential velocity in the primary shear zone, and h is the thickness of the primary shear zone; 0.025 mm is an acceptable approximation of h in reference by observing Shaw’s research [28]. Besides, the boundary of the primary shear zone can be considered adiabatic so that the heat transfer equation can be expressed in the following form, and the chip temperature at the entry boundary is equal to the initial workpiece temperature.

$${k}_u^k=\frac{\cos \left({\phi}_n^k-{\gamma}_n^k\right)\cos {\eta}_s^k\left(\cos {\phi}_n^k\cos {\eta}_s^k+\tan {\lambda}_s^k\sin {\eta}_s^k\right)}{\cos {\gamma}_n^k}$$
(9)
$${\dot{\gamma}}_m^k=\frac{\left(q+1\right)V\cos {\lambda}_s^k\cos\ {\gamma}_n^k}{h\cos\ {\eta}_s^k\cos \left({\phi}_n^k-{\gamma}_n^k\right)}$$
(10)
$$\frac{dT^k}{dz_e^k}=\frac{\cos {\eta}_e^k}{\rho cV\ \sin {\phi}_n^k\cos {\lambda}_s^k}{\mu \tau}^k{\dot{\gamma}}^k$$
(11)
$${\left.T\right|}_{z_e^k=0}={T}_w$$
(12)
Fig. 5
figure 5

The unequal division shear zone model

Full size image

 Where ρ, c, and μ represent material density, heat capacity, and Taylor-Quinney coefficient, respectively. These values of 304 stainless steel are ρ=7900kg/m3, c=400J/(kg·K) and μ=0.85, respectively. The material behavior and thermo-mechanical evolution in the primary shear zone are governed by Eqs. (6), (7), (8) and (11). Using the boundary conditions (12), the shear stress \({\tau }_{s}^{k}\) on the main shear plane can be calculated.

4 Cylindrical turning geometry and the cutting edge discretization

Considering the complexity of chip formation in turning, the majority of current research is based on the equivalent cutting edge method, i.e., a fictitious straight cutting edge is used to replace the real cutting edge, as shown in Fig. 6. When some studies need to know the local information about stress and temperature on the rake face, this method is very disadvantageous to the study of tool design and tool wear. Therefore, in order to obtain the component state of real cutting edge during chip formation, the cutting edge needs to be discretized.

Fig. 6
figure 6

The equivalent cutting edge method

Full size image

In cylindrical turning, the modeling process is more complicated than the traditional oblique cutting with a single cutting edge on account for the existence of the tool rounded nose. In this paper, the discretization method of the cutting edge proposed by Molinnari and Moufki [22] is used to model the cylindrical turning process. The rounded edge is divided into finite straight cutting edge units. For each component edge unit, the expressions of component normal rake angle and inclination angle are derived by using geometric relationships. For the case of cylindrical turning, as shown in Fig. 7. The cutting conditions to be given are cutting velocity V, feed rate fr, cutting depth ap, and tool geometric parameters (the main cutting edge angle κr, inclination angle λs, normal rake angle γn and nose radius rn); the tool geometry is defined by six planes (Pr, Ps, Pn, Po, Pf, and Pp) to determine the spatial position of the cutting edge. Figure 8 illustrates the discrete process of tool nose in cylindrical turning.

Fig. 7
figure 7

The Geometric model of cylindrical turning

Full size image
Fig. 8
figure 8

The cutting edge discretization of the engaged part in the rake face

Full size image

On the reference plane Pr, the cutting edge can be discretized into K + 2 parts of the straight cutting edge section by the index k (\(0\le k\le \text{K}+1\)). The tool nose is discretized into K + 1 straight cutting edge units, and the chip thickness corresponding to each component edge unit is variable as shown in Fig. 8. In the turning process, the rounded edge in contact with the workpiece can be divided into two parts by the angles ϕs and ϕa respectively. ϕst and ϕex are the entry and exit angles in the first part (see Fig. 8). The first part (for the interval angle of ϕs) can be subdivided into K cutting edge units which are identified as k (1 ≤ k ≤ K), and Δϕ is taken as the increment angle. The second part is also considered as a single unit with the index k = K + 1. Figure 8 shows an example of discretization for K = 3, which corresponds to the projection of a discrete cutting edge on the reference plane. According to the geometric relationship, the following equations of these angles can be obtained:

$${\phi }_{st}=\left\{\begin{array}{l}\mathrm{arcsin}(({r}_{n}-{a}_{p})/{r}_{n})\qquad\qquad{a}_{p}<{r}_{n}(1-\mathrm{cos}\;{\kappa }_{r})\\ \pi /2-{\kappa }_{r}\qquad\qquad\qquad{a}_{p}\ge {r}_{n}(1-\mathrm{cos}\;{\kappa }_{r})\end{array}\right.$$
(13)
$${\phi }_{ex}=\pi /2-\mathrm{arcsin}(0.5f_{r}/{r}_{n})$$
(14)
$${\phi }_{s}={\phi }_{ex}-{\phi }_{st}$$
(15)
$$\Delta \phi ={\phi }_{s}/\text{K}$$
(16)
$${\phi }_{a}=2\mathrm{arcsin}(0.5f_{r}/{r}_{n})$$
(17)

For the rounded edge, the geometric description of the discrete cutting edge is mainly defined by the planes \({P}_{r}\),\({P}_{s}^{0}\),\({P}_{n}^{0}\),\({P}_{s}^{k}\), and \({P}_{n}^{k}\), as shown in Fig. 8. \({P}_{s}^{0}\) and \({P}_{n}^{0}\) correspond to the cutting plane and normal plane of the main cutting edge (k = 0). \(P_{s}^{k}\) is defined as containing the kth component edge and being perpendicular to Pr. \({P}_{n}^{k}\) is normal to the kth component edge. \({\theta }_{r}^{k}\) is the angle between the planes \({P}_{s}^{0}\) and \(P_{s}^{k}\) measured in the plane Pr, \({\theta }_{a}^{k}\) is the angle between the main cutting edge (k = 0) and the kth component edge (1 ≤ k ≤ K) measured in the tool rake face (see Fig. 8). As shown in Fig. 9, the component parameters \({\phi }_{k}\),\({\kappa }_{r}^{k}\),\({\varphi }_{r}^{k}\),\({\theta }_{r}^{k}\),\({a}_{w}^{k}\), and \({t}_{k}\) in the reference plane Pr can be obtained as below:

$${\phi }_{k}={\phi }_{st}+(k-1)\Delta \phi$$
(18)
$${\kappa }_{r}^{k}=\pi \text{/2}-{\phi }_{k}-\Delta \phi /2$$
(19)
$${\varphi }_{r}^{k}=\pi \text{/2}-{\kappa }_{r}^{k}$$
(20)
$${\theta }_{r}^{k}={\kappa }_{r}-{\kappa }_{r}^{k}={\phi }_{k}-\pi \text{/2}+{\kappa }_{r}+\Delta \phi /2$$
(21)
$${a}_{w}^{k}=2{r}_{n}\mathrm{sin}(\Delta \phi /2)$$
(22)
$${t}_{k}={f}_{r}\mathrm{sin}({\kappa }_{r}^{k})$$
(23)

where \({\phi }_{k}\), \({\kappa }_{r}^{k}\), \({\varphi }_{r}^{k}\), \({a}_{w}^{k}\), and \({t}_{k}\) represent, respectively, the angular position, the component cutting edge angle, the component lead angle, the component cutting width, and the component cutting thickness corresponding to the kth component cutting edge. The following relations can be obtained for the main cutting edge (k = 0):

Fig. 9
figure 9

Projection of discrete cutting edge on reference plane

Full size image
$$\left\{\begin{array}{lc}\theta_r^0=0&\\a_w^0=\left\{\begin{array}{l}0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;a_p\;<r_n\;(1-\cos\;\kappa_r)\\(a_p-r_n(1-\cos\;\kappa_r^0))/\sin\;\kappa_r^0\;\;\;\;\;\;\;\;a_p\geq r_n\;(1-\cos\;\kappa_r)\;\;\;\;\;\;\;\;\;\;\;\;k=0\end{array}\right.&\\t_0=f_r\;\sin(\kappa_r^0)&\end{array}\right.$$
(24)

The chip load Ak of the kth (0 ≤ k ≤ K) component edge is defined as the undeformed chip area. For the chip load AK+1 of the k = K + 1 component edge, the following relationship can be obtained.

$$A^k=a_w^kt_k\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\leq k<\text{K}$$
(25)
$${A}^{\text{K}+1}={r}_{n}^{2}\mathrm{arcsin}(0.5f_r/{r}_{n})-0.5f_{r}\sqrt{{r}_{n}^{2}-{(f_{r})}^{2}/4}$$
(26)

The relationship between the discrete cutting edge on the rake face and its projection on Pr is processed by coordinate transformation. The component cutting conditions corresponding to each component cutting edge, that is, the component cutting angles (cutting edge angle, inclination angle, normal rake angle) and the component undeformed chip area, are also determined. In the rake face. The projection of \({y}_{r}^{k}\) on the reference plane Pr is oriented by the unit vector \({y}_{o}^{k}\); \({y}_{r}^{k}\) is the vector along the kth component edge and is contained in the \({P}_{s}^{k}\) as shown in Fig. 9. To calculate the angles \({\theta }_{a}^{k}\), \({\lambda }_{s}^{k}\), and \({\gamma }_{n}^{k}\), a set of frames is introduced. These frames can be related by rotation transformation, as shown in Fig. 10. Based on the relationship of the coordinate systems shown in Fig. 10, the following expression can be obtained:

Fig. 10
figure 10

Coordinate transformation relationship in the discrete process of turning tool

Full size image
$$\mathbf{R}({x}_{r}^{0},-{\theta }_{a}^{k})\cdot \mathbf{R}({y}_{n}^{0},{\gamma }_{n}^{0})\cdot \mathbf{R}({z}_{o}^{0},{\lambda }_{s}^{0})=\mathbf{R}({y}_{n}^{k},{\gamma }_{n}^{k})\cdot \mathbf{R}({z}_{o}^{k},{\lambda }_{s}^{k})\cdot \mathbf{R}({x}_{o}^{0},-{\theta }_{r}^{k})$$
(27)

Therefore, by considering Eq. (27) and after some algebraic manipulation, \({\theta }_{r}^{k}\) corresponding to the projection of \({\theta }_{a}^{k}\) in the reference plane Pr is obtained:

$$\tan\;\theta_a^k=\frac{\cos\;\lambda_s^0\tan\;\theta_r^k}{\cos\;\gamma_n^0-\tan\;\theta_r^k\sin\;\gamma_n^0\sin\;\lambda_s^0}$$
(28)

The component inclination angle \({\lambda }_{s}^{k}\) and the component normal rake angle \({\gamma }_{n}^{k}\) for the kth component edge are measured in \({P}_{s}^{k}\) and \({P}_{n}^{k}\), respectively. For the main cutting edge (k = 0), the cutting angles are given by \({\lambda }_{s}^{0}={\lambda }_{s}\) and \({\gamma }_{n}^{0}={\gamma }_{n}\). The angles \({\lambda }_{s}^{k}\) and \({\gamma }_{n}^{k}\), for 1 ≤ k ≤ K + 1, are determined from the following relationships by Eq. (27).

$$\sin\;\lambda_s^k=\cos\;\theta_a^k\sin\;\lambda_s^0-\sin\;\theta_a^k\sin\;\gamma_n^0\cos\;\lambda_s^0$$
(29)
$$\sin\;\gamma_n^k=\cos\;\theta_r^k\sin\;\gamma_n^0+\sin\;\theta_r^k\sin\;\lambda_s^0\cos\;\gamma_n^0$$
(30)

The component cutting edge geometry can be characterized by these angles \({\kappa}_{r}^{k}\), \({\gamma }_{n}^{k}\), \({\lambda }_{s}^{k}\), \({\theta }_{r}^{k}\), and \({\theta }_{a}^{k}\).

5 Cutting forces model of cylindrical turning

5.1 Component equilibrium of the discrete chip unit

For the improved oblique cutting model, the shear force \({F}_{s}^{k}\) and normal force \({F}_{ns}^{k}\) exerted by the workpiece on the kth chip unit can be expressed as:

$$\mathbf{F}_{k}=-{F}_{s}^{k}{\mathbf{x}}_{s}^{k}+{F}_{ns}^{k}{\mathbf{z}}_{s}^{k}$$
(31)

The component force balance acting on the kth chip unit can be expressed in the form of a vector:

$$- F_{s}^{k} {\mathbf{x}}_{s}^{k} + F_{ns}^{k} {\mathbf{z}}_{s}^{k} + F_{nc}^{k} {\mathbf{x}}_{c} - F_{fc}^{k} {\mathbf{z}}_{c} + F_{mc}^{k} {\mathbf{y}}_{c} = 0$$
(32)

Equation (32) can be transformed into the component equations in the coordinate system (xk, yk, zk). The following expressions were deduced by Moufki and Molinari [26].

$$\left\{\begin{array}{l}{F}_{nc}^{k}(cos({\phi }_{n}^{k}-{\gamma }_{n}^{k})-tan{\beta }_{k}sin({\phi }_{n}^{k}-{\gamma }_{n}^{k})cos{\eta }_{c}^{k})-{F}_{mc}^{k}sin({\phi }_{n}^{k}-{\gamma }_{n}^{k})sin{\eta }_{c}^{k}-{F}_{s}^{k}cos{\eta }_{s}^{k}=0\\ {F}_{nc}^{k}tan{\beta }_{k}sin{\eta }_{c}^{k}-{F}_{mc}^{k}cos{\eta }_{c}^{k}-{F}_{s}^{k}sin{\eta }_{s}^{k}=0\\ {F}_{nc}^{k}(sin({\phi }_{n}^{k}-{\gamma }_{n}^{k})+tan{\beta }_{k}cos({\phi }_{n}^{k}-{\gamma }_{n}^{k})cos{\eta }_{c}^{k})+{F}_{mc}^{k}cos({\phi }_{n}^{k}-{\gamma }_{n}^{k})sin{\eta }_{c}^{k}-{F}_{ns}^{k}=0\end{array}\right.$$
(33)

Equation (33) is an algebraic equation which can be solved by combing with \({F}_{s}^{k}\). Meanwhile, the unknown forces \({F}_{nc}^{k}\), \({F}_{mc}^{k}\), and \({F}_{ns}^{k}\) can be determined. The shearing force \({F}_{s}^{k}\) is given by:

$$F_s^k=\frac{\tau_s^k}{\cos\;\lambda_s^k\sin\;\phi_n^k}A_k$$
(34)

where \({\tau }_{s}^{k}\) is the shear stress on the main shear plane of the primary shear zone; it can be obtained from the unequal division shear zone theory.

5.2 Resultant chip equilibrium and cutting forces.

In order to determine the value of the main chip flow angle \({\eta }_{c}^{0}\), the resultant force balance equation acting on the entire chip can be simplified as:

$$\sum_{k= \text{0} }^{{\text{K}}+1}(-{F}_{s}^{k}{\mathbf{x}}_{s}^{k}+{F}_{ns}^{k}{\mathbf{z}}_{s}^{k}+{F}_{nc}^{k}{\mathbf{x}}_{c}-{F}_{fc}^{k}{\mathbf{z}}_{c})=0$$
(35)

Through combining Eqs. (32) and (35), the implicit Eq. (36) can be obtained, and the main chip flow angle can be obtained by Eqs. (36) and (32). In the resultant chip balance, the sum of \({F}_{mc}^{k}\) is equal to zero for the interaction force \({F}_{mc}^{k}\) between discrete chip units.

$$\sum_{k=0}^{\text{K}+ \text{1} }{F}_{mc}^{k}=0$$
(36)

Because the variables \({\eta }_{e}^{k}\), \({\eta }_{s}^{k}\), \({\phi }_{n}^{k}\), \({\beta }_{k}\), and \({F}_{mc}^{k}\) all depend on the main chip flow angle \({\eta }_{c}^{0}\), numerical iteration is applied to obtain their values. The main chip flow angle \({\eta }_{c}^{0}\) is determined by Eq. (36), it considers the influence of material properties of workpiece, tool geometry, and cutting parameters. Adibi-Sedeh et al. [29] considered the effects of the nose-rounded radius and the cutting angle on the chip flow direction when the main cutting edge angle is not equal to zero for the traditionally defined equivalent cutting edge.

For the improved oblique cutting model of the kth component edge, in Fig. 3, the resultant force Fk is expressed as the (\(\mathbf{x}_{\text{o}}^{k}\), \(\mathbf{y}_{\text{o}}^{k}\),\(\mathbf{z}_{\text{o}}^{k}\)) components of \({F}_{c}^{k}\) (cutting force), \({F}_{d}^{k}\) (back force), and \({F}_{f}^{k}\) (feed force).

$$\mathbf{F}_{k}\text{=}-{F}_{c}^{k}\mathbf{x}_{\text{o}}^{k}-{F}_{d}^{k}\mathbf{y}_{\text{o}}^{k}\text{+}{F}_{f}^{k}\mathbf{z}_{\text{o}}^{k}$$
(37)
$$\begin{pmatrix}F_c^k\\F_d^k\\F_f^k\end{pmatrix}=\left(\begin{array}{c}cos\eta_s^k\;cos\phi_n^k\;cos\lambda_s^k+sin\eta_s^k\;sin\lambda_s^k\\cos\eta_s^k\;cos\phi_n^k\;sin\lambda_s^k-sin\eta_s^k\;cos\lambda_s^k\\-cos\eta_s^ksin\phi_n^k\end{array}\begin{array}{c}sin\phi_n^k\;cos\lambda_s^k\\sin\phi_n^k\;sin\lambda_s^k\\cos\phi_n^k\end{array}\right)\begin{pmatrix}F_s^k\\F_{ns}^k\end{pmatrix}$$
(38)

These force components can then be transformed to the frame (xa, ya, za) by:

$$\left(\begin{array}{c}{F}_{x}^{k}\\ {F}_{y}^{k}\\ {F}_{z}^{k}\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& -\mathrm{cos}{\varphi }_{r}^{k}& \mathrm{sin}{\varphi }_{r}^{k}\\ 0& \mathrm{sin}{\varphi }_{r}^{k}& \mathrm{cos}{\varphi }_{r}^{k}\end{array}\right)\left(\begin{array}{c}{F}_{c}^{k}\\ {F}_{d}^{k}\\ {F}_{f}^{k}\end{array}\right)$$
(39)

where \({F}_{x}^{k}\) is the tangential force, \({F}_{y}^{k}\) is radial force, and \({F}_{z}^{k}\) is the longitudinal force as shown in Fig. 2. The algorithm to calculate cutting forces for cylindrical turning is as follows in Fig. 11.

Fig. 11
figure 11

Flow chart for the improved oblique cutting model applied to cylindrical turning

Full size image

At the beginning, the component cutting angles can be calculated by giving an initial value of \({\eta }_{c}^{0}\), These output parameters such as strain, strain rate, stress, and temperature distributions in the primary shear zone for each chip unit can be computed by numerical iterative method. If \(\sum \limits_{k=0}^{\text{K}+ \text{1} }{F}_{mc}^{k}\) is not equal to zero, a new estimated value of \({\eta }_{c}^{0}\) will be obtained by adding an increment \(\Delta \eta\). The computation will stop until the iteration requirement is satisfied. Conclusively, the component cutting force (\({F}_{x}^{k}\), \({F}_{y}^{k}\), \({F}_{z}^{k}\)) of the kth cutting edge unit is deduced by Eqs. (38) and (39); Fmc can be determined by Eq. (36). All steps of calculations were performed programmatically by MATLAB software.

6 Experimental validation and analysis

In order to validate the proposed method above, a series of turning experiments for 304 stainless steel were conducted without cutting fluid in Mazak lathe. The cutting forces were measured by Kisler Dynamometer (6275A); the force signals that pass through the charge amplifier (5070A) was addressed by the Dynoware software, as shown in Fig. 12. The experiment was carried out in three cases:

  • The influence of cutting depth ap, feed rate fr, and cutting velocity V on turning forces was analysed with different cutting parameters.

  • The influence of the tool nose radius rn on turning forces was analysed with different tool insert.

  • The influence of the main cutting edge angle κr on turning forces was analysed with different toolholder.

Fig. 12
figure 12

The experiments of cutting forces in cylindrical turning of 304 stainless steel

Full size image

6.1 Effects of cutting conditions

The experiment used SNMG120408-MR2025 insert and DSBNR2525M12 holder of Sandvik to study the influence of cutting parameters on turning forces of 304 stainless steel. The geometry parameters of the insert and the cutting conditions are shown in Tables 2 and 3, respectively. Specifically, there were three procedures in the experiment to obtain the reliable results, namely, the experiment with the same cutting parameters was repeated twice; the measurement interval time of the cutting process is more than 10 s, and the insert was replaced by a new one after each cutting test with the same cutting parameters.

Table 2 Geometry parameters of tool insert
Full size table
Table 3 Cylindrical turning conditions of 304 stainless steel
Full size table

In Fig. 13, it can be seen that the cutting force increases approximately linearly with the increase of cutting depth. When the cutting depth is very small, the change of cutting force shows obvious nonlinearity. The reason is that the straight main cutting edge plays a leading role in the cutting process when the cutting width aw (aw = ap/sin(κr)) increases in a positive proportion with the cutting depth increases. Furthermore, when the cutting depth is close to the nose radius, the influence of the nose radius on the cutting force must be considered. At this time, the nonlinear variation can only be measured in a more stable environment with precise equipment.

Fig. 13
figure 13

The effect of cutting depth ap on turning forces

Full size image

As shown in Fig. 14, the cutting force also shows a linear trend with increasing feed rate, which is different from the effect of cutting depth on cutting force. This is because the chip thickness t (t = frsin(κr)) has been increasing in a positive proportion with the increase of feed rate. However, with the increase of feed speed, the increase of temperature will lead to the decrease of friction coefficient and cutting force in the turning process. Considering the positive and negative effects, the influence of feed rate on cutting force should be nonlinear. At the same time, it can be found from Figs. 14a and b that the cutting force increase is slow with the increase in feed rate when the cutting velocity is very high.

Fig. 14
figure 14

The effect of feed rate fr on turning force

Full size image

For the 304 stainless steels, the nonlinear effect of cutting velocity on turning force is shown in Fig. 15. It can be seen that the cutting force decreases with the increase of cutting velocity in Fig. 15; the variation trend of cutting forces is consistent with the experimental results of Young et al. [10]. and Arsecularate et al. [30]. This is due to the fact that the deformation coefficient and friction coefficient decrease with the cutting velocity increases. It should be noted that the tool-chip friction is mainly caused by high temperature, high pressure, and high chip velocity. In cylindrical turning, the friction coefficient of each discrete chip unit will change, the average tool-chip temperature decreases with the cutting velocity increases, which will lead to the decrease of average tool-chip friction coefficient and cutting force. Meanwhile, it can be seen in Fig. 15 that the changing ratio of cutting force is obviously slow when cutting velocity is very low.

Fig. 15
figure 15

The effect of cutting speed V on turning force

Full size image

6.2 Effects of the main cutting edge angle

The cutting experiments of 304 stainless steel with three kinds of the main cutting edge angle were carried out. Table 4 illustrates the geometric parameters of the tool, and normal rake angle γn is approximately regarded as 0°, inclination angle λs is − 6°, and nose radius rn is 0.8 mm. The predicted values of the proposed model and the experimental results are shown in Fig. 16; the main cutting edge angle κr is investigated in the range of 30° to 90°. It can be found from Fig. 16 that the influence of the main cutting edge angle is approximately linear. As the main cutting edge angle increases, Fx and Fz are increasing, Fy is decreasing, and this trend is consistent with the experimental results of Young et al. [10]. However, Fx basically remains constant with the increase of the main cutting edge angle. Although the incensement of the main cutting edge angle will result in a decrease in the engaged length in cutting, the area A (A = frap) of the undeformed chip which mainly determines the cutting force not depend on the tool main cutting edge angle. It can be seen in Fig. 16 that Fx is increased significantly when the main cutting edge angle increases to the range between 60 and 90°. It can generally be considered that the main cutting edge angle mainly affects the cutting force through the cutting thickness. With the increase of κr, the contact length of the tool rounded edge will also increase (at this time, the non-free cutting effect will be more significant). When the cutting area is constant, the cutting thickness increases with the increase of the main cutting edge angle. As a result, the deformation of chip formation will become large, which will lead to the increase of Fx. Nevertheless, the cutting thicknesses of the discrete chip units for tool nose part decreases in order as shown in Fig. 16, and they are smaller than the cutting thickness of the main cutting edge. When the cutting area is constant and the main cutting edge angle is increased, the cutting thickness will increase. The influence of the main cutting edge angle on Fz and Fy is mainly through the projection components of the resultant cutting force in the Z and Y directions. Therefore, Fz will decrease and Fy will increase as the main cutting edge angle increases.

Table 4 The tool geometric parameters
Full size table
Fig. 16
figure 16

The effect of the main cutting edge angle κr on turning force

Full size image

6.3 Effects of the tool nose radius

The effect of four kinds of the tool nose radius on turning force of 304 stainless steel was studied. The rounded edge parameters are presented in Table 5. Figure 17 illustrates the predicted variation of turning force with the nose radius and the experimental results. In the experiments, the main cutting edge is not involved in cutting process (ap < rn(1-cos(κr)). It can be seen in Fig. 17a that Fx is basically a constant, which may be because the total undeformed chip area A is nearly independent of the nose radius and only related to feed rate and cutting depth. The predicted curve in Fig. 17 shows an increase of Fy and a decrease of Fz with the increase of the nose radius. The experimental results of 304 stainless steel are also basically consistent with the predicted law, which is also consistent with the experimental results of Young [10] and Arsecularatne et al. [30]. According to the previous discussion, Fz will increase with the increase of the main cutting edge angle and decrease with the increase of \(\eta_{c}^{0}\); the change law of Fy is opposite. However, when the main cutting edge is involved in cutting (ap > rn(1-cos(κr)), as shown in Fig. 17b and c. When the cutting depth ap and feed rate fr are constant, the tool nose radius length and cutting width increase with the increase of the main cutting edge angle. Conversely, the cutting thickness and the tool component cutting edge angle of the discrete edge units will decrease; these lead to the increase of cutting deformation and cutting force. It has a greater influence on Fy than on Fx as shown in Fig. 17.

Table 5 The tool rounded edge parameters
Full size table
Fig. 17
figure 17

The effect of tool nose radius rn on turning force

Full size image

7 Conclusion

This paper extended the previous work for the traditional oblique cutting model to non-free turning with a rounded edge. The main conclusions can be summarized as follows:

  • The improved oblique cutting model considers the condition that the main cutting edge angle is unequal to be 90° and the tool nose has a rounded edge.

  • Through applying the coordinate transformation method, the geometry relations for the non-free turning are analysed. The unequal division shear zone theory in orthogonal cutting is used in oblique cutting modeling.

  • The tool rounded edge was discretized into small oblique cutting edges characterized by component cutting angles. For every engaged cutting chip unit, the cutting forces in different directions are obtained during oblique cutting. The effects of tool geometrical parameters and workpiece material properties on the cutting force are considered as their coupling interaction.

A MATLAB-based program has been given to facilitate the application of the analytical model for cutting forces. The experiments with three types of cutting conditions have been conducted to validate the prediction model and the deviation between the predicted results and experiment data is within an acceptable range. The proposed models have also been used to investigate the effects of cutting conditions and tool angles on the cutting forces. This quantitative information is helpful in selecting the appropriate cutting parameters and optimization of cutting edge geometry. It should be noted that the above description law of the influence of the machining parameters on the turning forces has appeared in many literatures, but most are obtained by curve fitting from the experimental results. The significance of this paper lies in proposing a new analytical model to predict the trend, and these methods are mutually verified.