An investigation into the effect of pre-bending on the tube hydro-forging technology

Abstract

THFG is an advanced technology to manufacture tubular components with complex cross-sections. Meanwhile, curved axis often exists in such components, which is formed by pre-bending steps before THFG. However, the effect of pre-bending on the subsequent THFG, especially on the critical internal pressure required to inhibit wrinkling, has not been clarified yet. Considering the difference in the cold work-hardening and the thickness distribution caused by pre-bending, the change rule between the critical internal pressure and the hoop strain was re-established based on the energy method. It is found that the cold work-hardening has a great influence on the change rule. Subsequently, by solving the three-dimensional mechanics condition of single and double curvature differential segments respectively, the distribution of hoop strain after THFG was obtained by combining pre-bending. Pointing out that the initial thickness has an obvious effect on the hoop strain distribution, while the cold work-hardening is almost negligible. The maximum hoop strain was brought into the change rule between critical internal pressure and hoop strain, then, a new analytical model between the critical internal pressure and the punch stroke considering pre-bending was built. The critical internal pressure considering pre-bending is determined by that of outer straight wall, and its value is always greater than the critical internal pressure without considering pre-bending under the same punch stroke. With the reduction of bending radius, the critical internal pressure distinction between considering and not considering pre-bending will be greater. Moreover, the smaller the friction coefficient also will lead the distinction to be more prominent. In this work, our proposed new prediction model of critical internal pressure is meticulously demonstrated, which can improve the accuracy by 74% at least when existing the pre-bending.

1 Introduction

A complex cross-sectional tubular component is one of the important ways to realize the lightweight technology, which has been widely used in the automotive and aerospace industry. Particularly, with the wide application of lightweight materials (such as the high-strength steel and the aluminum alloy), the weight reduction effect of such components is more and more obvious.

To date, a series of methods have been developed to fabricate the cross-sectional shape. Here, high-pressure tube hydroforming (HPTH) has been the most popular technology [1]. However, due to the expansion deformation, HPTH will cause the excessive thinning of the formed part and the cracking. In addition, as the strength of the material increases, the required forming internal pressure is growing explosively. For this reason, Nikhare et al. [2] proposed the low-pressure tube hydroforming (LPTH) to replace the HPTH process. In contrast to HPTH, LPTH avoids the expansion deformation by introducing the action of die movement, so it can control the occurrence of cracking defects successfully. Meanwhile, LPTH can reduce the required internal pressure (about 5 to 15% of HPTH) and the tonnage of the equipment greatly [3]. Unfortunately, LPTH is only suitable to form the component with a constant perimeter along the axial direction [4]. Besides, the bending moment is introduced during LPTH; hence, the cross-sectional spring back is inevitable [5]. In recent years, Chu et al. [6] first proposed tube hydro-forging technology (THFG) to form the tubular components with complex cross-sections. In THFG, under sufficient internal pressure, the cross-section can be compressed by the upper die movement to obtain the required shape. It is because the material has always born the compression state in three directions, which can effectively avoid the occurrence of thickness thinning and cracking [7]. The cross-section with variable perimeter along the axial direction can be produced by setting different punch strokes simultaneously. Moreover, this technology relies on the clamping force as the driving force. In other words, the internal pressure only plays the function of supporting, thereby diminishing the demand for high-pressure equipment.

As we all know, in order to meet the needs of space assembly, those tubular components always have a curved axis [8]. The initial tube needs preforming operations like pre-bending to obtain the same or similar shape of the axis of the product. However, the pre-bending will lead to a series of changes, such as the thinning of the outer layer and thickening of the inner layer, the cold work-hardening, the axis springback, and the cross-sectional distortion [9]. Consequently, analyzing the influence of pre-bending on the subsequent cross-section forming process has gathered significant interest among researchers.

For example, compared with the straight tube, the outer layer of pre-bending tube is more easily to lead the thinning and the cracking during HPTH [10]. Besides, because of a curved axis, the material is difficult to achieve the feeding along the axial direction, which makes the cracking defect more obvious. Prabhu et al. [11] pointed out that the process parameter of pre-bending has an important effect on HPTH and found that the formability of HPTH could be degenerated with the reduction of bending radius. Gao and Strano [12] proposed that the increase of friction coefficient can aggravate the degree of thickness thinning during pre-bending, which also promotes the generation of fracture defects after HPTH. In order to overcome the above problems, Han et al. [13] put forward a method to adjust the contact sequence of tube and die surface to solve the inhomogeneous deformation problem in hydroforming of a bending tube, effectively controlling the cracking defect. Moreover, a higher internal pressure is needed during HPTH because of the cold working-hardening caused by pre-bending. For LPTH, the cross-sectional distortion caused by pre-bending also will lead to the unequal perimeter along the bending axis, what further increases its difficulty in forming complex cross-sections.

As can be seen from the above, the pre-bending step has an important bearing on the final quality of the product. Although THFG has many advantages in forming complex cross-sectional tubular components, but because of the compression, the straight wall is prone to wrinkling when the internal pressure is insufficient [14], which also exists in the LPTH process [15]. Fortunately, Chu et al. [6] emphasized that excessive hoop strain is the ultimate reason and there is a critical internal pressure (the minimum forming internal pressure to inhibit wrinkling). Through the energy method combined with finite element (FE) simulation, the critical internal pressure can be obtained. However, when studying the wrinkling behavior and the critical mechanics condition, it is necessary to focus on the influence of material properties, thickness, geometry of parts, etc. Under double side constraint, Cao and Wang [16, 17] established a more accurate analytical model to predict the critical pressure required to suppress wrinkling in sheet drawing. Thereafter, considering the thickness variation, a revised model for the sheet drawing wrinkling was proposed in the recent research [18]. Because of different geometric shapes, when solving the sidewall wrinkling model for Tee-joint hydroforming, the effects of stress ratio (ratio of hoop stress to axial stress) must be comprehensively analyzed [19]. Meanwhile, the influence of thickness and cold work-hardening on the forming limit of Tee-joint was studied and found that the thicker the thickness, the stronger the resistance to wrinkling [20, 21]. As a new forming method, the existing theoretical result has not considered the effect of pre-bending on THFG, especially on the critical internal pressure. Therefore, by combining the energy method and the classical plastic theory, this paper will establish a new mathematical model for the critical internal pressure when considering the pre-bending in order to improve prediction precision.

2 Tube hydro-forging

2.1 Process principle

Figure 1 shows the schematic diagram of THFG combined with pre-bending. At first, the performing part with the desired curved axis is obtained through the pre-bending process. During THFG, the internal pressure plays a supporting role, and then the upper die moves ∆ to compress the cross-section. If the internal pressure is enough, the material at the inner/outer straight wall will be compressed and the perimeter of the cross-section will be reduced by 2∆, but when the internal pressure is insufficient, the wrinkling will occur at the inner/outer straight wall instead of stable compression deformation, as shown in Fig. 1. It is a typical compression instability defect caused by excessive hoop compression strain. The reasonable loading path between the critical internal pressure $p_{{{\text{cri}}}}$ with the punch stroke ∆ is the key to control wrinkling during THFG.

Fig. 1

Schematic diagram of tube hydro-forging combined with pre-bending

2.2 Critical internal pressure

As shown in Fig. 2, it is a traditional solution process of the critical internal pressure for a straight tube, which is mainly composed of three steps [6]: in step 1, the energy method is used to solve the change rule between the critical internal pressure $p_{{{\text{cri}}}}$ and the hoop strain $\varepsilon_{\varphi }^{{{\text{th}}}}$ during THFG; next, in step 2, the hoop strain distribution on the cross-section under the certain punch stroke ∆ is determined according to FE method; in step 3, by substituting the maximum hoop strain on the cross-section into the change rule, the critical internal pressure $p_{{{\text{cri}}}}$ can be obtained under the certain punch stroke ∆ at last.

Fig. 2

Traditional solution process of critical internal pressure

For the straight tube, the initial state of each differential segment on the cross-section is the same, but for the pre-bending tube, the thickness and work-hardening degree of each differential segment is different. In addition, due to the existence of a curved axis, the mechanics conditions of wrinkling must be different from that of a straight tube during THFG. These changes not only affect the change rule but also decide the specific distribution of the hoop strain on the cross-section. Therefore, the above factors inevitably lead to the critical internal pressure difference between considering and not considering pre-bending. Consequently, the state of each differential segment after pre-bending should be determined at first. Then, on the basis of pre-bending, through analyzing the mechanics conditions of pre-bending, the change rule and the hoop strain distribution should be solved. Substituting the maximum hoop strain into the change rule, the critical internal pressure considering pre-bending can be obtained finally.

3 Theoretical model

Before theoretical derivation, reasonable simplification can not only ensure the calculation accuracy but also improve its efficiency:

• 1. The Hollomon hardening law is taken to describe the stress–strain relationship of the material:

  $$\overline{\sigma } { = }K\overline{\varepsilon }^{n}$$

  (1)

  where K is the strength coefficient and n is the strain-hardening exponent, both can be obtained from the uniaxial tensile test.

• 2. According to the Von Mises yield criterion for isotropic material, the equivalent stress $\overline{\sigma }$ and the equivalent strain $\overline{\varepsilon }$ can be obtained respectively:

  $$\overline{\sigma } = \frac{1}{\sqrt 2 }\sqrt {\left( {\sigma_{\varphi } - \sigma_{\theta } } \right)^{2} + \left( {\sigma_{\theta } - \sigma_{t} } \right)^{2} + \left( {\sigma_{t} - \sigma_{\varphi } } \right)^{2} }$$

  (2)
  $$\overline{\varepsilon } = \frac{\sqrt 2 }{3}\sqrt {\left( {\varepsilon_{\varphi } - \varepsilon_{\theta } } \right)^{2} + \left( {\varepsilon_{\theta } - \varepsilon_{t} } \right)^{2} + \left( {\varepsilon_{t} - \varepsilon_{\varphi } } \right)^{2} }$$

  (3)

• 3. The pre-bending process is assumed to be plane strain and plane stress [22]; that is, the normal stress $\sigma_{t}^{{{\text{bd}}}}$ and the hoop strain $\varepsilon_{\varphi }^{{{\text{bd}}}}$ can be ignored, what can be expressed by Eq. (4):

  $$\left\{ \begin{gathered} \sigma_{t}^{{{\text{bd}}}} = 0 \hfill \\ \varepsilon_{\varphi }^{{{\text{bd}}}} = 0 \hfill \\ \end{gathered} \right.$$

  (4)

• 4. The arbitrary cross-section of the tube remains plane before and after pre-bending.

• 5. A plane strain state along the axial direction can be also assumed during THFG:

  $$\varepsilon_{\theta }^{{{\text{th}}}} = 0$$

  (5)

• 6. The distribution of stress–strain state and thickness at each differential segment are continuous after pre-bending and before THFG.

3.1 Results of pre-bending

As previously mentioned, the state of each differential segment after pre-bending should be solved firstly, and its specific solution process is shown in Appendix 1. The distribution of thickness after pre-bending t^bd can be acquired, as shown in Eq. (6):

$$t^{{{\text{bd}}}} = \begin{cases}{} \frac{{\rho_{{\text{u}}} t_{0} }}{R}\begin{array}{*{20}c} {} & {} & {} & {\begin{array}{*{20}c} {} & {} & {} & {\begin{array}{*{20}c} {} & {} & {\begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} } & {\varphi = \frac{\pi }{2}} \\ \end{array} } \\ \end{array} } \\ \end{array} \hfill \\ \frac{{ - \left( {R + r\cos \varphi } \right) + \sqrt {\left( {R + r\cos \varphi } \right)^{2} + 4\cos \varphi t_{0} \rho_{{\text{u}}} } }}{2\cos \varphi }\begin{array}{*{20}c} {} & {\varphi \ne \frac{\pi }{2}} \\ \end{array} \hfill \\ \end{cases}$$

(6)

Simultaneously, due to the cold work-hardening, the distribution of flow stress $\overline{\sigma }^{{{\text{bd}}}}$ and equivalent strain $\overline{\varepsilon }^{{{\text{bd}}}}$ is also solved:

$$\overline{\sigma }^{{{\text{bd}}}} = K\left[ {\beta \ln \frac{{R + \left( {r + t^{{{\text{bd}}}} } \right)\cos \varphi }}{{\rho_{{\text{u}}} }}} \right]^{n} \begin{array}{*{20}c} {} & {} & {0 \le \varphi \le \pi } \\ \end{array}$$

(7)

$$\overline{\varepsilon }^{{{\text{bd}}}} = \beta \ln \frac{{R + \left( {r + t^{{{\text{bd}}}} } \right)\cos \varphi }}{{\rho_{{\text{u}}} }}\begin{array}{*{20}c} {} & {} & {0 \le \varphi \le \pi } \\ \end{array}$$

(8)

Meanwhile, we can notice that the thickness and flow stress of each differential segment at the inner or outer straight-wall are the same. Next, based on the above pre-bending results, the new mathematical model of the critical internal pressure will be established during THFG.

3.2 Change rule

Compared with a straight tube, it is necessary to consider the cold work-hardening and thickness variation when calculating the change rule between the critical internal pressure $p_{{{\text{cri}}}}$ and the hoop compression strain $\varepsilon_{\varphi }^{{{\text{th}}}}$ for pre-bending tube. Through Appendix 2, the change rule considering pre-bending can be obtained:

$$\begin{aligned} p_{{{\text{cri}}}}^{{{\text{bd}}}} & = \left[ {\left( {\beta \varepsilon_{\varphi }^{{{\text{th}}}} + \overline{\varepsilon }^{{{\text{bd}}}} } \right)^{n + 1} - \left( {\overline{\varepsilon }^{{{\text{bd}}}} } \right)^{n + 1} } \right]\frac{{3Kt^{{{\text{bd}}}} }}{{2\delta \left( {n + 1} \right)}} \\ & - \left[ {\left( {\frac{{\beta t^{{{\text{bd}}}} }}{2} + \overline{\varepsilon }^{{{\text{bd}}}} \left( {\frac{2}{{m^{2} \delta }} + \frac{{t^{{{\text{bd}}}} }}{2}} \right)} \right)^{n + 1} - \left( {\overline{\varepsilon }^{{{\text{bd}}}} \left( {\frac{2}{{m^{2} \delta }} + \frac{{t^{{{\text{bd}}}} }}{2}} \right)} \right)^{n + 1} } \right]\frac{{3Kt^{{{\text{bd}}}} \left( {\frac{2}{{m^{2} \delta }} + \frac{{t^{{{\text{bd}}}} }}{2}} \right)^{ - n} }}{{L\delta \left( {n + 1} \right)}}\tan^{ - 1} \left( {\sqrt {e^{{{ - \varepsilon_{\varphi }{{\text{th}}}} }} - 1} } \right) \end{aligned}$$

(9)

3.3 Hoop strain distribution

After obtaining the change rule, the following will solve the hoop strain $\varepsilon_{\varphi }^{{{\text{th}}}}$ distribution after THFG. It can be seen from Sect. 3.1 that the degree of work-hardening on each differential segment is different. According to the plastic theory, only when the equivalent stress of each differential segment reaches and exceeds its corresponding flow stress, the subsequent yield will occur, which results in the generation of hoop strain $\varepsilon_{\varphi }^{{{\text{th}}}}$ afterwards. In this case, whether the subsequent yield occurs can be judged by comparing the equivalent stress $\overline{\sigma }^{{{\text{th}}}}$ and its flow stress $\overline{\sigma }^{{{\text{bd}}}}$. Here, the equivalent stress $\overline{\sigma }^{{{\text{th}}}}$ can be obtained under the simultaneous action of a hoop stress $\sigma_{\varphi }^{{{\text{th}}}}$ and a normal stress $\sigma_{t}^{{{\text{th}}}}$:

$$\overline{\sigma }^{{{\text{th}}}} { = }\frac{1}{\sqrt 2 }\sqrt {\left( { - \sigma_{\varphi }^{{{\text{th}}}} - 0} \right)^{2} + \left( {0 - - \sigma_{t}^{{{\text{th}}}} } \right)^{2} + \left( { - \sigma_{t}^{{{\text{th}}}} - - \sigma_{\varphi }^{{{\text{th}}}} } \right)^{2} }$$

(10)

If $\overline{\sigma }^{{{\text{th}}}} \succ \overline{\sigma }^{{{\text{bd}}}}$, the subsequent yield will occur; otherwise, the subsequent yield will not occur. The hoop stress $\sigma_{\varphi }^{{{\text{th}}}}$ is related to the hoop force F and the thickness t^bd:

$$\sigma_{\varphi }^{{{\text{th}}}} = \frac{F}{{t^{{{\text{bd}}}} }}$$

(11)

Once the pre-bending radius R is fixed, the flow stress $\overline{\sigma }^{{{\text{bd}}}}$ and thickness t^bd can be determined. Therefore, whether the subsequent yield occurs only depends on its hoop force F, so the distribution of hoop force F during THFG will be analyzed below.

3.3.1 Hoop force distribution

As shown in Fig. 3, due to the existence of a curved axis, the differential segments on the cross-section can be divided into two categories: the double-curvature differential segment and the single-curvature differential segment. Owing to the different mechanics conditions, the distribution of hoop force at these two kinds of differential segments will be solved individually.

• 1. The double-curvature differential segment

Fig. 3

Static stress equilibrium model: a double-curvature differential segment, b single-curvature differential segment

The hoop force distribution is caused by friction force. When the friction coefficient μ is fixed, the friction force f is only determined by the normal contact pressure p'. According to Fig. 3a, we first establish the static stress equilibrium model along the normal direction on the double-curvature differential segment:

$$\begin{aligned} \sigma_{\varphi }^{{{\text{th}}}} & \left[ {R + r\cos \left( \varphi \right)} \right]d\theta \cdot t^{{{\text{bd}}}} \sin \left( {{{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) + \left( {\sigma_{\varphi }^{{{\text{th}}}} - d\sigma_{\varphi }^{{{\text{th}}}} } \right)\left[ {R + r\cos \left( \varphi \right)} \right]d\theta \cdot t^{{{\text{bd}}}} \sin \left( {{{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \hfill \\ & + 2\sigma_{\theta }^{{{\text{th}}}} rd\varphi \cdot t^{{{\text{bd}}}} \sin \left( {{{d\theta } \mathord{\left/ {\vphantom {{d\theta } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) + prd\varphi \cdot \left( {R + r\cos \varphi } \right)d\theta = p^{\prime}rd\varphi \left( {R + r\cos \varphi } \right)d\theta \hfill \\ \end{aligned}$$

(12)

Among them, $d\sigma_{\varphi }^{{{\text{th}}}}$ also can be solved by building the static stress equilibrium model along the hoop direction:

$$\begin{aligned} \sigma_{\varphi }^{{{\text{th}}}} & \left[ {R + r\cos \left( \varphi \right)} \right]d\theta \cdot t^{{{\text{bd}}}} \cos \left( {{{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) - \left( {\sigma_{\varphi }^{{{\text{th}}}} - d\sigma_{\varphi }^{{{\text{th}}}} } \right)\left[ {R + r\cos \left( \varphi \right)} \right]d\theta \cdot t^{{{\text{bd}}}} \cos \left( {{{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \hfill \\ & = \mu p^{\prime}\left[ {R + r\cos \left( \varphi \right)} \right]d\theta \cdot rd\varphi \hfill \\ \end{aligned}$$

(13)

Equation (13) can be simplified:

$$d\sigma_{\varphi }^{{{\text{th}}}} = \frac{p^{\prime}\mu rd\varphi }{{t^{{{\text{bd}}}} \cos \left( {{{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}$$

(14)

According to Eq. (5), when the subsequent yield occurs, the axial stress $\sigma_{\theta }^{{{\text{th}}}}$ meets the condition: $\sigma_{\theta }^{{{\text{th}}}} = {{\left( {\sigma_{\varphi }^{{{\text{th}}}} + \sigma_{t}^{{{\text{th}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{\varphi }^{{{\text{th}}}} + \sigma_{t}^{{{\text{th}}}} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}$, and the normal stress $\sigma_{t}^{{{\text{th}}}}$ can be expressed as: $\sigma_{t}^{{{\text{th}}}} = {{\left( {p + p^{\prime}} \right)} \mathord{\left/ {\vphantom {{\left( {p + p^{\prime}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}$. Consequently, the relationship between the hoop stress $\sigma_{\varphi }^{{{\text{th}}}}$ and the axial stress $\sigma_{\theta }^{{{\text{th}}}}$ is obtained as follows:

$$\sigma_{\theta }^{{{\text{th}}}} = \frac{{\sigma_{\varphi }^{{{\text{th}}}} }}{2} + \frac{p}{4} + \frac{p^{\prime}}{4}$$

(15)

Substituting Eqs. (14) and (15) into Eq. (12), after simplification, we can get:

$$\sigma_{\varphi }^{{{\text{th}}}} t^{{{\text{bd}}}} \left[ {\frac{r}{2} + \left( {R + r\cos \varphi } \right)} \right] + pr\left[ {\frac{{t^{{{\text{bd}}}} }}{4} + \left( {R + r\cos \varphi } \right)} \right] = p^{\prime}r\left[ {\left( {R + r\cos \varphi } \right) - \frac{{t^{{{\text{bd}}}} }}{4}} \right]$$

(16)

Further arrangement, the normal contact pressure p' can be expressed:

$$p^{\prime} = \frac{{\sigma_{\varphi }^{{{\text{th}}}} t^{{{\text{bd}}}} \left[ {\frac{r}{2} + \left( {R + r\cos \varphi } \right)} \right] + pr\left( {R + r\cos \varphi } \right)}}{{r\left( {R + r\cos \varphi } \right)}}$$

(17)

Assuming the double-curvature differential segment along the curved axis is the unit length, so the contact pressure p' at the double-curvature differential segment can be described as:

$$p^{\prime} = \frac{{F\left[ {\frac{r}{2} + \left( {R + r\cos \varphi } \right)} \right] + pr\left( {R + r\cos \varphi } \right)}}{{r\left( {R + r\cos \varphi } \right)}}{ = }\lambda F + p$$

(18)

Here, we can define $\lambda = {{\left[ {{r \mathord{\left/ {\vphantom {r 2}} \right. \kern-\nulldelimiterspace} 2} + \left( {R + r\cos \varphi } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {{r \mathord{\left/ {\vphantom {r 2}} \right. \kern-\nulldelimiterspace} 2} + \left( {R + r\cos \varphi } \right)} \right]} {\left[ {r\left( {R + r\cos \varphi } \right)} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {r\left( {R + r\cos \varphi } \right)} \right]}}$, especially, which can be further simplified as $\lambda \approx {1 \mathord{\left/ {\vphantom {1 r}} \right. \kern-\nulldelimiterspace} r} + {1 \mathord{\left/ {\vphantom {1 {2R}}} \right. \kern-\nulldelimiterspace} {2R}}$ when R > 2r.

However, for the differential segment that does not enter into the subsequent yield, its axial stress $\sigma_{\theta }^{{{\text{th}}}}$ remains in the stress state at the end of pre-bending:

$$\sigma_{\theta }^{{{\text{th}}}} = \sigma_{\theta }^{{{\text{bd}}}}$$

(19)

Similarly, if the subsequent yield does not occur, by substituting Eq. (19) into Eq. (12) and simplifying, we can get the following result:

$$p^{\prime} = \frac{F}{r} + p + \frac{{\sigma_{\theta }^{{{\text{bd}}}} t^{{{\text{bd}}}} }}{R + r\cos \varphi } \approx \frac{F}{r} + p + \frac{{\sigma_{\theta }^{{{\text{bd}}}} t^{{{\text{bd}}}} }}{R}$$

(20)

After the contact pressure p' is obtained, the hoop force F distribution on the cross-section can be calculated. In this paper, BB' is the parting surface, so the direction of material flow during THFG is shown in Fig. 4. According to the flow law of material, there must have two fixed differential segments A (A') and D (D') which are relative to the die; hence, the cross-section can be divided into two parts: ABCD segment and A'B'C'D' segment. When the punch stroke is ∆, the perimeter of ABCD and A'B'C'D' will be compressed by ∆ simultaneously. For convenience, we can assume that the angle of AB segment is φ₁₁, the length of BC segment is l₁₁, the angle of CD segment is φ₁₂, likewise, the angle of A'B' segment is φ₂₁, the length of B'C' segment is l₂₁, and the angle of C'D' segment is φ₂₂. Meanwhile, according to the geometric relationship, there are following expressions: φ₁₁ + φ₂₁ = π, φ₁₂ + φ₂₂ = π, l₁₁ = l₂₁.

Fig. 4

Hoop force distribution during tube hydro-forging

Therefore, according to Fig. 4, the force balance formula on the double-curvature differential segment can be established as shown in Eq. (21):

$$F_{1} { = }F_{0} - f = F_{0} - \mu \frac{\varphi }{n}p^{\prime}r$$

(21)

Substituting Eq. (18) into Eq. (21), we can get

$$F_{1} { = }\left( {1 - \mu \lambda \frac{\varphi }{n}r} \right)F_{0} - \mu \frac{\varphi }{n}pr$$

(22)

In the same way:

$$F_{2} { = }\left( {1 - \mu \lambda \frac{\varphi }{n}r} \right)^{2} F_{0} - \mu \frac{\varphi }{n}pr\left[ {1 + \left( {1 - \mu \lambda \frac{\varphi }{n}r} \right)} \right]$$

(23)

According to the analogy method, it can be concluded that:

$$F_{n} { = }\left( {1 - \mu \lambda \frac{\varphi }{n}r} \right)^{n} F_{0} - \mu \frac{\varphi }{n}pr\left[ {1 + \left( {1 - \mu \lambda \frac{\varphi }{n}r} \right) + \ldots + \left( {1 - \mu \lambda \frac{\varphi }{n}r} \right)^{n - 1} } \right]$$

(24)

When $n \to \infty$, the limit of F_n can be taken as:

$$F_{n} = e^{ - \mu \lambda r\varphi } \left( {F_{0} + \frac{p}{\lambda }} \right) - \frac{p}{\lambda }$$

(25)

In the same way, if the differential segment has not entered into the subsequent yield, by using Eq. (20), we can obtain its hoop force distribution:

$$F_{n} = e^{ - \mu \varphi } \left( {F_{0} + pr + \frac{{\sigma_{\theta }^{{{\text{bd}}}} t^{{{\text{bd}}}} r}}{R}} \right) - pr - \frac{{\sigma_{\theta }^{{{\text{bd}}}} t^{{{\text{bd}}}} r}}{R}$$

(26)

• 2. The single-curvature differential segment

Through the above analysis, the hoop force distribution on the double-curvature differential segment has been solved. Moreover, the hoop force distribution on the single-curvature differential segment also can be derived using the same method. As shown in Fig. 3b, the static stress equilibrium model on the single-curvature differential segment can be built at first:

$$2\sigma_{\theta }^{{{\text{th}}}} dl \cdot t^{{{\text{bd}}}} \sin \left( {\frac{d\theta }{2}} \right) + pdl \cdot Rd\theta = p^{\prime}dl \cdot Rd\theta$$

(27)

By simplifying, the contact pressure p' on the single-curvature differential segment which has entered into the subsequent yield can be calculated as follows:

$$p^{\prime} = \frac{F}{2R} + p$$

(28)

In the same measure, when $n \to \infty$, it can assume the limit of F_n:

$$F_{n} {\text{ = e}}^{{ - \frac{\mu l}{{2R}}}} \left( {F_{0} + 2Rp} \right) - 2Rp$$

(29)

For the single-curvature differential segment that has not entered into the subsequent yield, substituting Eq. (19) into Eq. (27), and then we can get:

$$p^{\prime}{ = }\frac{{\sigma_{\theta }^{{{\text{bd}}}} t^{{{\text{bd}}}} }}{R} + p$$

(30)

Next, for the differential segment without entering into subsequent yield, it can be obtained by an analogous method:

$$F_{n} { = }F_{0} - \mu \left( {\frac{{\sigma_{\theta }^{{{\text{bd}}}} t^{{{\text{bd}}}} }}{R} + p} \right)l$$

(31)

• 3. Hoop force distribution on the whole cross-section

Through the above efforts, the hoop force distribution on the whole cross-section has been obtained. For example, if all differential segments have entered into the subsequent yield, the hoop force distribution can be obtained in turn:

For the ABCD segment, if the hoop force at the differential segment A is F_A, we can get the hoop force F_B at the differential segment B:

$$F_{{\text{B}}} = e^{{\mu \lambda r\varphi_{11} }} \left( {F_{{\text{A}}} + \frac{p}{\lambda }} \right) - \frac{p}{\lambda }$$

(32)

The hoop force F_C at the differential segment C:

$$F_{{\text{C}}} = e^{{ - \frac{{\mu rl_{11} }}{2R}}} \left( {F_{{\text{B}}} + 2Rp} \right) - 2Rp$$

(33)

The hoop force F_D at the differential segment D:

$$F_{{\text{D}}} = e^{{ - \mu \lambda \varphi_{12} }} \left( {F_{{\text{C}}} + \frac{p}{\lambda }} \right) - \frac{p}{\lambda }$$

(34)

Similarly, for the A'B'C'D' segment, if the hoop force of the differential segment A' is F_A', we can also get the hoop force F_B' at the differential segment B':

$$F_{{\mathrm{B}{^{\prime}} }} = e^{{\mu \lambda \varphi_{21} }} \left( {F_{\mathrm{A{^{\prime}} }} + \frac{p}{\lambda }} \right) - \frac{p}{\lambda }$$

(35)

The hoop force F_C' at the differential segment C':

$$F_{\mathrm{C{^{\prime}} }} = e^{{ - \frac{{\mu l_{21} }}{2R}}} \left( {F_{\mathrm{B{^{\prime}} }} + 2Rp} \right) - 2Rp$$

(36)

The hoop force F_D' at the differential segment D':

$$F_{\mathrm{D{^{\prime}} }} = e^{{ - \mu \lambda \varphi_{22} }} \left( {F_{\mathrm{C{^{\prime}} }} + \frac{p}{\lambda }} \right) - \frac{p}{\lambda }$$

(37)

In which, F_A' is equal to F_A, so it can be found that the hoop force at any differential segment on the cross-section can be solved by the hoop force F_A, such as:

$$F_\mathrm{C} = e^{{ - \frac{{\mu l_{11} }}{2R}}} \left[ {e^{{\mu a\varphi_{11} }} \left( {F_\mathrm{A} + \frac{p}{\lambda }} \right) - \frac{p}{\lambda } + 2Rp} \right] - 2Rp$$

(38)

If the differential segment has not entered into the subsequent yield, it just needs to substitute Eqs. (26) and (31) into the above analysis.

3.3.2 Stress–strain corresponding relationship

The hoop force distribution on the cross-section is obtained, and then by combining with Eq. (11), the hoop stress distribution also can be acquired. In order to get the distribution of hoop strain on the cross-section, it is necessary to solve the stress–strain corresponding relationship (Fig. 5).

Fig. 5

Stress/strain state at differential segment

At first, when the hoop stress does not satisfy the subsequent yield condition, there is no plastic deformation on the corresponding differential segment:

$$\varepsilon_{\varphi }^{{{\text{th}}}} = 0$$

(39)

However, if the hoop stress $\sigma_{\varphi }^{{{\text{th}}}}$ reaches the subsequent yield, the corresponding differential segment will undergo plastic deformation, and the hoop strain $\varepsilon_{\varphi }^{{{\text{th}}}}$ will generate. Considering that THFG satisfies the plane strain ($\varepsilon_{\theta }^{{{\text{th}}}} = 0$), so it can be obtained by combining the Eqs. (2)–(3):

$$\overline{\sigma }^{{{\text{th}}}} = \frac{\sqrt 3 }{2}\left| {\sigma_{\varphi }^{{{\text{th}}}} - \sigma_{t}^{{{\text{th}}}} } \right|$$

(40)

$$\overline{\varepsilon }^{{{\text{th}}}} = \frac{2}{\sqrt 3 }\left| {\varepsilon_{\varphi }^{{{\text{th}}}} } \right|$$

(41)

According to Appendix 1, there is $\beta { = }2/\sqrt 3$.

Substituting Eqs. (40) and (41) into the Hollomon hardening law, it can be got:

$$\frac{1}{\beta }\left| {\sigma_{\varphi }^{{{\text{th}}}} - \sigma_{t}^{{{\text{th}}}} } \right| = K\left| {\beta \varepsilon_{\varphi }^{{{\text{th}}}} } \right|^{n}$$

(42)

The hoop stress $\sigma_{\varphi }^{{{\text{th}}}}$ can be got by simplifying Eq. (42):

$$\sigma_{\varphi }^{{{\text{th}}}} { = }K\beta^{n + 1} \varepsilon_{\varphi }^{{{\text{th}{n}}}} + \sigma_{t}^{{{\text{th}}}}$$

(43)

Consequently, the hoop force F can be described:

$$F = \sigma_{\varphi }^{{{\text{th}}}} t^{{{\text{th}}}} = \left( {K\beta^{n + 1} \varepsilon_{\varphi }^{n} + \sigma_{t}^{{{\text{th}}}} } \right)t^{{{\text{th}}}}$$

(44)

Because of $\varepsilon_{\varphi }^{{{\text{th}}}} { = - }\varepsilon_{t}^{{{\text{th}}}}$, so the thickness after THFG t^th can be expressed by $\varepsilon_{\varphi }^{{{\text{th}}}}$:

$$t^{{{\text{th}}}} = t^{{{\text{bd}}}} \left( {1 + \varepsilon_{\varphi }^{{{\text{th}}}} } \right)$$

(45)

By combining Eqs. (44) and (45) and neglecting the high order item $\sigma_{t}^{{{\text{th}}}} \varepsilon_{\varphi }^{{{\text{th}}}}$, we get:

$$\frac{{F - \sigma_{t}^{{{\text{th}}}} t^{{{\text{bd}}}} }}{{t^{{{\text{bd}}}} K\beta^{n + 1} }} = \varepsilon_{\varphi }^{{{\text{th}{n}}}} + \varepsilon_{\varphi }^{{\text{th}{n + 1}}}$$

(46)

Subsequently, we can establish the mathematical expression of hoop strain $\varepsilon_{\varphi }^{{{\text{th}}}}$:

$$\varepsilon_{\varphi }^{{{\text{th}}}} = \frac{1}{2}\sqrt {n^{2} + 4n\left( {\frac{{F - \sigma_{t}^{{{\text{th}}}} t^{{{\text{bd}}}} }}{{Kt^{{{\text{bd}}}} \beta^{n + 1} }}} \right)^{1/n} } - \frac{n}{2}$$

(47)

Section 3.3.1 has obtained the hoop force F distribution on the cross-section. Substituting it into Eq. (47), the hoop strain $\varepsilon_{\varphi }^{{{\text{th}}}}$ distribution on the cross-section can be obtained, and then the maximum hoop strain on the cross-section also can be got.

3.3.3 Relationship between maximum hoop strain and punch stroke

According to the analysis in Sects. 3.3.1 and 3.3.2, in order to establish the distribution model of hoop force and hoop strain when considering the pre-bending, three unknowns need to be solved, namely F_A, φ₁₁, and φ₂₁. And for any punch stroke ∆_i, we can get the following three expressions:

• 1. The integral of the whole hoop strain of ABCD segment is equal to the punch stroke ∆_i:

  $$\int_{0}^{{\varphi_{11} }} {\varepsilon_{\varphi }^{{{\text{th}}}} d\varphi } + \int_{0}^{{l_{11} }} {\varepsilon_{\varphi }^{{{\text{th}}}} dl} + \int_{0}^{{\varphi_{12} }} {\varepsilon_{\varphi }^{{{\text{th}}}} d\varphi } = \Delta_{{\text{i}}}$$

  (48)

• 2. The integral of the whole hoop strain of A'B'C'D' segment is also equal to the punch stroke ∆_i:

  $$\int_{0}^{{\varphi_{21} }} {\varepsilon_{\varphi }^{{{\text{th}}}} d\varphi } + \int_{0}^{{l_{21} }} {\varepsilon_{\varphi }^{{{\text{th}}}} dl} + \int_{0}^{{\varphi_{22} }} {\varepsilon_{\varphi }^{{{\text{th}}}} d\varphi } = \Delta_{{\text{i}}}$$

  (49)

• 3. The values of hoop force F_D and F_D' are the same:

  $$e^{{ - \mu \lambda \varphi_{12} }} \left( {F_{C} + \frac{p}{\lambda }} \right) - \frac{p}{\lambda } = e^{{ - \mu \lambda \varphi_{22} }} \left( {F_{C^{\prime}} + \frac{p}{\lambda }} \right) - \frac{p}{\lambda }$$

  (50)

Through solving Eqs. (48)–(50), the three unknowns under any punch stroke ∆_i can be obtained. Substituting these three unknowns into the above theoretical derivation, the distribution of hoop force and hoop strain under any punch stroke ∆_i will be obtained, and then the maximum hoop strain under this punch stroke ∆_i also can be got.

3.4 Calculation process

Figure 6 lists the specific calculation process for the critical internal pressure when considering the pre-bending. In order to obtain the critical internal pressure under any punch stroke ∆_i, there needs a cycle calculation. At first, it is necessary to give an initial value of internal pressure p₀. Subsequently, the corresponding maximum hoop strain on the cross-section can be solved. By substituting it into the change rule, we can get the temporary value of critical internal pressure $\overline{p}_{{\text{cri,i}}}$. If it meets the condition:$\left| {p_{0} /\overline{p}_{{\text{cri,i}}} - 1} \right| \le 1{\text{\% }}$, the critical internal pressure $p_{{{\text{cri}},{\text{i}}}}^{{{\text{bd}}}}$ of pre-bending tube is $\overline{p}_{{\text{cri,i}}}$ ($p_{{{\text{cri}},{\text{i}}}}^{{{\text{bd}}}}$ = $\overline{p}_{{\text{cri,i}}}$). Otherwise, let p₀ = $\overline{p}_{{\text{cri,i}}}$ and re-substitute p₀ into the cycle calculation until the condition is met. Finally, by iterating ∆_i+1 = ∆_i + d∆, the loading path between the critical internal pressure and the punch stroke can be built for when considering pre-bending.

Fig. 6

Specific calculation process

4 Experiment and FE simulation

4.1 Materials and experiment

The material used in this paper is the DP800 tube. The strip-shaped specimens were cut from the tube along the axial direction. Through the uniaxial tensile test, the true stress–strain curve of the material was obtained and corresponding mechanical parameters are shown in Table 1. Besides, its cross-sectional shape parameters also are shown in Fig. 7.

Table 1 Material mechanical parameters for DP800

Fig. 7

True stress–strain curve for DP800

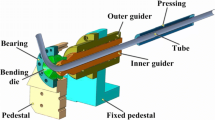
In practical production, there are many methods to realize the pre-bending process, such as rotary draw bending (RDB), press bending, pushing bending, etc. RDB which is combined with computer numerical control (CNC) can obtain the required bending radius and angle stably. And through the application of mandrel, the bending wrinkling, and the cross-sectional distortion both can be controlled. In addition, the cross-sectional characteristics of the pre-bending tube formed by RDB are more consistent along the axis, which is also conducive to the following theoretical analysis. As shown in Fig. 8a, the experiment device of RDB included a pressure die, clamping die, mandrel, and bending die. The radius of the bending die was set as 100, 150, 200, and 250 mm respectively to study the influence of different bending radius R on the critical internal pressure.

Fig. 8

Experiment device: a rotary draw bending machine, b special hydro-forging machine

THFG needs a special experimental device: hydro-forging machine which could control the loading path between the internal pressure and the punch stroke accurately. The machine was mainly composed of three parts: experiment setup, computer control system, and pressurization system, as shown in Fig. 8b. Additionally, the experiment setup included an upper die, lower die, and sealing means. All the digital signals were collected into the computer control system, thus the experimental data could be output in real time. For the effect of friction coefficient, two kinds of experimental conditions were set up [23]: dry friction and MoS₂. Their corresponding friction coefficients are shown in Table 2. In order to reduce the experimental error, each group of the experiment was repeated three times, and finally, the average value was taken as the experimental result.

Table 2 Friction coefficients of different lubricants [23]

4.2 FE method

According to the experiment requirement, the RDB simulation model and the THFG simulation model were established respectively, as shown in Fig. 9. The RDB model also consisted of five parts: ① pressure die, ② clamp die, ③ mandrel, ④ tube, and ⑤ bending die. The dies were all defined as a rigid body, while the tube was set as a deformable body with the isotropic material model. Meanwhile, the tube was discretized by the element type of C3D8R. In order to guarantee the accuracy of FE simulation, the element sizes were 2 mm and 5 mm along the hoop and axial direction respectively, and the thickness direction was defined 5 elements. The radius of the bending die was selected as 100, 150, 200, and 250 mm respectively. The THFG model adopted restart analysis, and the model mainly included three parts: ① upper die, ② tube (imported by pre-bending step), and ③ lower die. Here, since the performing tube in this step was imported from the pre-bending step, its settings were the same as before. According to Table 2, the friction coefficient μ between the die and the tube was set to 0.09 and 0.018 respectively, and the Coulomb friction criterion was used in FE simulation.

Fig. 9

FE simulation: a rotary draw bending model: ① pressure die, ② clamp die, ③ mandrel, ④ tube, ⑤ bending die; b hydro-forging model: ① upper die, ② tube (imported from pre-bending step), ③ lower die

5 Results and discussion

5.1 Experiment results

Some of the experiment results are shown in Fig. 10. When the punch stroke was 3 mm, different wrinkling situations could be obtained by applying different internal pressure. For the straight tube, according to the previous mathematical model deduced by Chu et al. [6], its critical internal pressure $p_{{{\text{cri}}}}^{{{\text{str}}}}$ was 46 MPa. However, for the pre-bending tube, when the provided internal pressure $p_{{{\text{pro}}}}$ was 46 MPa, wrinkling only occurred at the outer straight wall, but not at the inner straight wall. When $p_{{{\text{pro}}}}$ reduced to 30 MPa, wrinkling occurred at both inner and outer straight-wall; otherwise, the wrinkling could be restrained entirely until the $p_{{{\text{pro}}}}$ expanded to 80 MPa. From the experiment results, we can conclude that under the same punch stroke ∆, the difference in critical internal pressure exists not only in the pre-bending tube and the straight tube but also in the inner and outer straight wall of pre-bending tube. It can be seen that if the influence of pre-bending on THFG is not considered, the calculation reliability of its critical internal pressure will be dropped considerably.

Fig. 10

Wrinkling situations of pre-bending tubes under different internal pressure

5.2 Analysis of the pre-bending effect

The distribution of flow stress and thickness on the cross-section after pre-bending is studied at first, as shown in Fig. 11. When the R = 150 mm, the thickness reduction at the B'C' segment (outer straight-wall) is the most serious, and the thickness increase at the BC segment (inner straight-wall) is the most prominent. Similarly, due to the cold work-hardening, the flow stress at each differential segment all improves to different degrees. The flow stress distribution on the cross-section is approximately concave, and the cold work-hardening degree of BC and B'C' segment is the most serious, while the cold work-hardening degree of the neutral layer is the least. It can be found that the initial state of the differential segment at the inner/outer straight-wall is different due to the effect of pre-bending.

Fig. 11

Distribution of flow stress and thickness after pre-bending

According to Sect. 3.2, we can obtain the change rule between the critical internal pressure and the hoop strain for the pre-bending tube. In Fig. 12, when pre-bending is considered, it can be clearly seen that the change rules on the inner/outer straight wall are basically the same. When the R is 150 mm, for the inner/outer straight-wall, their thickness after pre-bending is 1.29 mm and 1.76 mm respectively, and their flow stress is 875 MPa and 878 MPa individually. A conclusion can be drawn by comparing the change rule of the inner/outer straight-wall: the difference in thickness has little effect on the change rule, while cold work-hardening has a significant effect on that. Especially if the hoop strain is fixed, the critical internal pressure required for the pre-bending tube is always greater than that required for the straight tube. With the increase of hoop strain, the change rule difference between pre-bending tube and straight tube also increases.

Fig. 12

Influence of pre-bending on the change rule

After obtaining the change rule between critical internal pressure and hoop strain, it is necessary to analyze the hoop strain $\varepsilon_{\varphi }^{{{\text{th}}}}$ distribution. For comparative purposes, the critical internal pressure for the straight tube $p_{{{\text{cri}}}}^{{{\text{str}}}}$ is applied to the pre-bending tube and the straight tube concurrently; that is, let $p_{{{\text{pro}}}} { = }p_{{{\text{cri}}}}^{{{\text{str}}}}$, as shown in Fig. 13, where the punch strokes ∆ are taken as 0.5, 1, 2, and 3 mm respectively. It can be seen from the figure that the fixed differential segments A (A') and D (D') on the pre-bending tube will move with the increase in ∆, but for the straight tube, the above-fixed differential segments always remain at the midpoint of the arc. The different initial after pre-bending leads to the asymmetry of plastic deformation at ABCD and A'B'C'D' segment during subsequent THFG.

Fig. 13

Hoop strain distribution under different punch stroke: a ∆ = 0.5 mm, b ∆ = 1 mm, c ∆ = 2 mm, d ∆ = 3 mm

More importantly, for ABCD and A'B'C'D' segment, the hoop strain $\varepsilon_{\varphi }^{{{\text{th}}}}$ at the straight-wall is always greater than that at the arc under any punch stroke, when the pre-bending is considered. This is because the differential segments B and B' are the parting surface, where the hoop force is the largest. And under the action of friction, the hoop force diminishes along both sides of the parting surface and reaches its minimum value at fixed differential segments A (A') and D (D') respectively. According to Eq. (47), the hoop strain is proportional to the hoop force, so the hoop strain at the arc is always smaller than that at the straight wall. In addition, it also can be found that when ∆ is 0.5 mm, the hoop strain does not occur at some differential segments. Due to the cold work-hardening caused by pre-bending, the hoop force F does not reach the subsequent yield condition of these differential segments.

From the above analysis, it can be known that the hoop strain at the straight wall is always greater than that at the arc, and reaches its maximum value at differential segments B and B' respectively, when the pre-bending is considered. Wrinkling is most likely to occur at the maximum hoop strain, so the following will study the effect of pre-bending on the strain at differential segments B and B'. Obviously, under the same ∆ and $p_{{{\text{pro}}}}$, the hoop strain at B' differential segment of pre-bending tube is larger than that at the same position of straight tube, while the hoop strain at differential segment B of pre-bending tube is smaller than that at the same position of straight tube, as shown in Fig. 13. This is because when the R is 150 mm, the thickness t^bd at B' differential segment reduces to 1.29 mm after pre-bending. On the one hand, the decrease of thickness results in the larger hoop stress under the same hoop force, which leads the differential segment B' being easier to enter into the subsequent yield firstly according to Eq. (10). On the other hand, based on Eq. (47), the thinner the thickness is, the greater the hoop strain will be under the same punch stroke at the differential segment B’. In addition, the thickness at differential segment B increases to 1.76 mm, which causes the opposite result compared with differential segment B’. The thickness of a straight tube is between the above two differential segments, so its hoop strain is also between the above two differential segments. Meanwhile, according to the analysis of the change rule, although the provided internal pressure $p_{{{\text{pro}}}}$ can inhibit the wrinkling of a straight tube, it is not enough for pre-bending tube. Therefore, the wrinkling of the pre-bending tube will occur in this case.

To complement the theory, the FEM results allow us to intuitively observe the effect of pre-bending on the distribution of hoop strain on the differential segments B' and B as shown in Fig. 14. When considering the effect of pre-bending, the hoop strain on the differential segment B' is always greater than that on the differential segment B under any punch stroke. However, for a straight tube, the value of hoop strain on the differential segments B' and B is equal, and the value is just between that at the inner/outer straight wall of pre-bending tube. The reason has been explained above. In addition, with the increase of punch stroke, the hoop strain difference between differential segments B' and B also increases. Here, it can be seen that the error between the analytical and numerical results is relatively small, which preliminarily verifies the correctness of the previous analytical derivation.

Fig. 14

Hoop strain at the differential segments B and B' under the critical internal pressure

According to the specific calculation process shown in Fig. 6, the critical internal pressure required for the inner/outer straight-wall to suppress wrinkling can be obtained respectively, as shown in Fig. 15. The FE simulation cannot accurately reflect the wrinkling of tubes, so the loading path between critical internal pressure and punch stroke is mainly verified by experiments [19]. When the different internal pressure is applied, there are three different results:

• 1. When the provided internal pressure $p_{{{\text{pro}}}}$ is greater than the critical internal pressure $p_{{{\text{req}}}}^{{{\text{out}}}}$ of the outer straight wall ($p_{{{\text{pro}}}} \succ p_{{{\text{cri}}}}^{{{\text{out}}}}$), the wrinkling can be completely inhibited.

• 2. However, when the provided internal pressure $p_{{{\text{pro}}}}$ is smaller than the critical internal pressure $p_{{{\text{req}}}}^{{{\text{in}}}}$ of the inner straight-wall ($p_{{{\text{pro}}}} \prec p_{{{\text{cri}}}}^{{{\text{in}}}}$), wrinkling occurs on the outer/inner straight-wall simultaneously.

• 3. Besides, when $p_{{{\text{cri}}}}^{{{\text{out}}}} \succ p_{{{\text{pro}}}} \succ p_{{{\text{cri}}}}^{{{\text{in}}}}$ is applied, the wrinkling only occurs at the outer straight wall, but not at the inner straight wall.

Fig. 15

Loading path for outer/inner straight wall when the R is 150 mm

Consequently, the experimental results in Sect. 5.1 can be reasonably explained. The third result needs relatively high internal pressure, so its wrinkling height is less than that of the second result. Meanwhile, it can be seen that the critical internal pressure $p_{{{\text{cri}}}}^{{{\text{str}}}}$ of the straight tube is just between $p_{{{\text{cri}}}}^{{{\text{out}}}}$ and $p_{{{\text{cri}}}}^{{{\text{in}}}}$. It can be found that the agreement between the analytical and experimental results is good.

In conclusion, the critical internal pressure $p_{{{\text{cri}}}}^{{{\text{out}}}}$ of the outer straight wall is the minimum internal pressure required to inhibit the wrinkling of pre-bending tube entirely. Therefore, the $p_{{{\text{req}}}}^{{{\text{out}}}}$ can be defined as the critical internal pressure $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ of the pre-bending tube. And the $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ is always greater than the $p_{{{\text{cri}}}}^{{{\text{str}}}}$ under the same punch stroke ∆. Besides, with the increase of punch stroke, the effect of pre-bending is more significant. On the one hand, the growth of punch stroke leads to amplifying the hoop strain difference between the pre-bending tube and the straight tube; on the other hand, according to Fig. 12, the greater the hoop strain difference, the greater the change rule difference between the pre-bending tube and the straight tube. Therefore, the difference in the critical internal pressure enlarges with the increase of punch stroke.

5.3 Different pre-bending radius

The following will mainly study the influence of different pre-bending radius R on the $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ through the combination of experiment and theory. Here, the bending radii of 100, 150, 200, and 250 mm are selected respectively.

For the pre-bending tube, the $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ is determined by its outer straight wall. Figure 16 shows the influence of different R values on the change rule between hoop strain and critical internal pressure for the outer straight wall. Under the same hoop strain $\varepsilon_{\varphi }^{{{\text{th}}}}$, the critical internal pressure $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ increases slightly with the decrease of radius. According to the analysis in Sect. 5.2, the cold work-hardening caused by pre-bending is the main reason for the difference between the pre-bending tube and straight tube. The smaller the R, the more severe the cold work-hardening on the outer straight-wall, which in turn leads to the greater the critical internal pressure required.

Fig. 16

Influence of pre-bending radius on the change rule

It can be seen from the above that the maximum hoop strain of pre-bending tube is located at the differential segment B', and the effect of pre-bending radius on the maximum hoop strain is shown in Fig. 17 where the line is the theoretical result and the scatter point is the FEM result. Apparently, when the punch stroke is fixed, the maximum hoop strain difference at the differential segment B' between pre-bending tube and straight tube decreases with the increase of pre-bending radius. The thickness reduction of the outer straight wall is the main cause of the hoop strain difference. According to Eqs. (6) and (7), as the bending radius increases, the effect of pre-bending on the thickness reduction is weakened, which leads to the decrease of maximum hoop strain difference.

Fig. 17

Influence of pre-bending radius on hoop strain at differential segment B'

Then, by substituting the hoop strain at the differential segment B' into the change rule, the influence of the R on the critical internal pressure $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ can be obtained, as shown in Fig. 18 where the line is the theoretical result and the scatter point is the experimental result. On the one hand, according to the change rule shown in Fig. 16, the smaller the R is, the higher the critical internal pressure $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ is under the fixed hoop strain; On the other hand, with the decrease of R, the maximum hoop strain difference between pre-bending tube and straight tube increases. Therefore, combining the above reasons, there is an important conclusion that with the decrease of the R, the critical internal pressure difference between $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ and $p_{{{\text{cri}}}}^{{{\text{str}}}}$ increases under the same punch stroke. For example, if the punch stroke ∆ is 4 mm (shown in Fig. 18d), the minimum value of the difference $\delta p_{\min }^{\Delta = 4}$ is 24.2 MPa when the R is 250 mm, and the difference reaches its maximum value $\delta p_{\max }^{\Delta = 4}$ = 52.9 MPa when the R reduces to 100 mm, which cannot be ignored in actual production. On the contrary, with the decrease of punch stroke, the difference of critical internal pressure between $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ and $p_{{{\text{cri}}}}^{{{\text{str}}}}$ also decreases. When the R is 100 mm, if the punch stroke decreases to 2 mm, the maximum value $\delta p_{\max }^{\Delta = 2}$ will reduce to 23.4 MPa. The experimental results are consistent with the theoretical results what proves the correctness of the theoretical derivation.

Fig. 18

Effect of pre-bending radius on critical internal pressure $p_{{{\text{cri}}}}^{{{\text{bd}}}}$: a ∆ = 1 mm, b ∆ = 2 mm, c ∆ = 3 mm, d ∆ = 4 mm

5.4 Friction coefficient

Through the above theoretical analysis, it is found that friction is one of the important factors affecting the hoop force distribution. Therefore, in this paper, two lubrication conditions (dry friction and MoS₂) are selected to study the influence of friction on the critical internal pressure $p_{{{\text{cri}}}}^{{{\text{bd}}}}$, and the specific friction coefficient values are shown in Table 1. From Fig. 19, whether the pre-bending is considered, the increase of μ value will lead to the increase of the critical internal pressure under the same punch stroke. The reason is that according to the theoretical analysis in Sect. 3.3, in order to produce the same punch stroke, the larger the μ value will increase the hoop force and the hoop strain required at differential segment B', and then the critical internal pressure required also will be enlarged. In addition, with the decrease of μ, the effect of pre-bending becomes more pronounced, that is, the critical internal pressure difference between $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ and $p_{{{\text{cri}}}}^{{{\text{str}}}}$ increases with the reduction of friction coefficient. Therefore, the smaller the friction coefficient, the more important it is to consider the influence of pre-bending.

Fig. 19

Effect of friction coefficient on critical internal pressure: a △ = 3 mm, b △ = 4 mm

5.5 Practical application

The automobile longeron is a typical complex cross-sectional tubular component with a curved axis, as shown in Fig. 20. There are two difficulties in forming this part: (1) because of 3D curved axis, the axis springback after pre-bending is large and difficult to control (springback was 10 mm) (2) The cross-sectional shape is complex, and the perimeter difference between the maximum cross-section and the minimum cross-section can reach 15%. THFG combined with pre-bending is very suitable to manufacture this kind of component. According to the model of this paper, the critical internal pressure required for THFG when considering the pre-bending is 54 MPa. Finally, not only the axis springback can be controlled (dropped almost to zero) [24], but also the variable cross-section along the axis can be obtained without wrinkling.

Fig. 20

Automobile longeron formed by THFG combining with pre-bending

6 Conclusion

By combining the energy method with mechanics analysis, the influence of pre-bending on the subsequent THFG, especially on the critical internal pressure required to inhibit wrinkling, was clarified in this research. The main following conclusions were obtained:

• 1. Through the energy method, the change rule of the critical internal pressure with the hoop strain can be obtained first when existing the pre-bending. Because of cold work-hardening, the critical internal pressure of pre-bending tube is higher than that of a straight tube under the same hoop strain, and their difference becomes more obvious with the decrease of bending radius. On the contrary, the variation of thickness caused by pre-bending has little effect on this change rule.

• 2. Based on the mechanics analysis, the hoop strain distribution and the maximum hoop strain considering pre-bending both can be determined. For the pre-bending tube, mainly due to the thickness variation, the maximum hoop strain of the outer straight wall is greater than that of the inner straight wall. And the decrease of R value leads to the increase of the maximum hoop strain difference between the pre-bending tube and straight tube.

• 3. After substituting the maximum hoop strain at the inner/outer straight-wall of pre-bending tube into the change rule, the mathematical model of the corresponding critical internal pressure $p_{{{\text{cri}}}}^{{{\text{out}}}}$ and $p_{{{\text{cri}}}}^{{{\text{in}}}}$ can be obtained respectively. When the provided internal pressure $p_{{{\text{pro}}}} \prec p_{{{\text{cri}}}}^{{{\text{in}}}}$, wrinkling occurs at both the outer/inner straight-wall, while $p_{{{\text{cri}}}}^{{{\text{out}}}} \succ p_{{{\text{pro}}}} \succ p_{{{\text{cri}}}}^{{{\text{in}}}}$, wrinkling only occurs at the outer straight-wall, and only under $p_{{{\text{pro}}}} \succ p_{{{\text{cri}}}}^{{{\text{out}}}}$, wrinkling can be suppressed entirely. Therefore, $p_{{{\text{cri}}}}^{{{\text{out}}}}$ is defined as the critical internal pressure $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ of the pre-bending tube.

• 4. The critical internal pressure $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ of the pre-bending tube is always greater than that $p_{{{\text{cri}}}}^{{{\text{str}}}}$ of a straight tube under the same punch stroke. Moreover, with the decrease of bending radius, the difference between $p_{{{\text{cri}}}}^{{{\text{bd}}}}$ and $p_{{{\text{cri}}}}^{{{\text{str}}}}$ will increase. If the punch stroke is 4 mm, the critical internal pressure difference is 33% when the R is 250 mm, while the R decreases to 100 mm, the critical internal pressure difference enlarges to 74%. Besides, the bigger the punch stroke, the more significant the pre-bending effect.

• 5. Whether pre-bending is considered, the smaller the friction coefficient is, the smaller the critical internal pressure requires. But the smaller the friction coefficient will lead the influence of pre-bending to be more prominent.

The above results were verified by experiment and FE simulation. In conclusion, this work provided a new prediction model of critical internal pressure which can improve the accuracy by 74% at least when existing the pre-bending.

Appendices

Appendix 1. Mathematical model for pre-bending

Fig. 21

Parameter diagram of any cross-section during bending

According to Eq. (4), the expression $\sigma_{\varphi }^{{{\text{bd}}}} { = }{{\sigma_{\theta }^{{{\text{bd}}}} } \mathord{\left/ {\vphantom {{\sigma_{\theta }^{{{\text{bd}}}} } 2}} \right. \kern-\nulldelimiterspace} 2}$ can be satisfied. Subsequently, by combining with Eqs. (2) and (3), the equivalent stress $\overline{\sigma }^{{{\text{bd}}}}$ and the equivalent strain $\overline{\varepsilon }^{{{\text{bd}}}}$ after pre-bending can be reduced to:

$$\overline{\sigma }^{{{\text{bd}}}} { = }\frac{\sqrt 3 }{2}\left| {\sigma_{\theta }^{{{\text{bd}}}} } \right|$$

(51)

$$\overline{\varepsilon }^{{{\text{bd}}}} = \frac{2}{\sqrt 3 }\left| {\varepsilon_{\theta }^{{{\text{bd}}}} } \right|$$

(52)

Here, let $\beta = \frac{2}{\sqrt 3 }$.

On the basis of the previous study [25], the radius of neutral layer ρ_u after pre-bending can be determined as follows, as shown in Fig. 21:

$$\rho_{{\text{u}}} = r\sqrt {\left( \frac{R}{r} \right)^{2} - 1}$$

(53)

The normal strain $\varepsilon_{t}^{{{\text{bd}}}}$ and the axial strain $\varepsilon_{\theta }^{{{\text{bd}}}}$ can be expressed as:

$$\varepsilon_{t}^{{{\text{bd}}}} = \ln \frac{{t^{{{\text{bd}}}} }}{{t_{0} }}$$

(54)

$$\varepsilon_{\theta }^{{{\text{bd}}}} { = }\ln \frac{{R + \left( {r + t^{{{\text{bd}}}} } \right)\cos \varphi }}{{\rho_{{\text{u}}} }}$$

(55)

Here, t₀ is the initial thickness and t^bd is the thickness after pre-bending.

In case of $\varepsilon_{t}^{{{\text{bd}}}} { = } - \varepsilon_{\theta }^{{{\text{bd}}}}$, the distribution of thickness t^bd and equivalent strain $\overline{\varepsilon }^{{{\text{bd}}}}$ after pre-bending can be achieved by combining Eqs. (54) and (55):

$$t^{bd} = \begin{cases} \frac{{\rho_{u} t_{0} }}{R}\begin{array}{*{20}c} {} & {} & {} & {\begin{array}{*{20}c} {} & {} & {} & {\begin{array}{*{20}c} {} & {} & {\begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} } & {\varphi = \frac{\pi }{2}} \\ \end{array} } \\ \end{array} } \\ \end{array} \hfill \\ \frac{{ - \left( {R + r\cos \varphi } \right) + \sqrt {\left( {R + r\cos \varphi } \right)^{2} + 4\cos \varphi t_{0} \rho_{u} } }}{2\cos \varphi }\begin{array}{*{20}c} {} & {\varphi \ne \frac{\pi }{2}} \\ \end{array} \hfill \\ \end{cases}$$

(56)

$$\overline{\varepsilon }^{{{\text{bd}}}} = \beta \ln \frac{{R + \left( {r + t^{{{\text{bd}}}} } \right)\cos \varphi }}{{\rho_{{\text{u}}} }}\begin{array}{*{20}c} {} & {} & {0 \le \varphi \le \pi } \\ \end{array}$$

(57)

By substituting the Eq. (57) into the Hollomon hardening law, the flow stress distribution $\overline{\sigma }^{{{\text{bd}}}}$ after pre-bending can be obtained:

$$\overline{\sigma }^{{{\text{bd}}}} = K\left[ {\beta \ln \frac{{R + \left( {r + t^{{{\text{bd}}}} } \right)\cos \varphi }}{{\rho_{{\text{u}}} }}} \right]^{n} \begin{array}{*{20}c} {} & {} & {0 \le \varphi \le \pi } \\ \end{array}$$

(58)

Appendix 2. Solution of the critical internal pressure by energy method

Fig. 22

Schematic of the wrinkling plate being suppressed: (a) perfect plate, (b) wrinkling plate

As shown in Fig. 22 of the Appendix, if there is a small edge displacement u_φ/2 and the internal pressure p is enough, the wrinkling will not produce and still remain the perfect plate, which needs the plastic strain energy in a perfect plate E0. However, when the internal pressure p is insufficient, wrinkling will occur, and the bending energy in a wrinkling plate is E_w. According to the energy method [16], if the wrinkling can be suppressed by internal pressure p exactly, the difference between E₀ and E_w is the minimum external work W_p which is executed by the internal pressure p and can be expressed as:

$$W_{p} = E_{0} - E_{{\text{w}}}$$

(59)

First, we can assume that the mode shape of the wrinkling plate is a cosine wave:

$$y = \frac{\delta }{2}\left( {1 - \cos mx} \right)$$

(60)

In which, L denotes the wrinkling wavelength and δ is the maximum wrinkling amplitude. Besides, m is the frequency of the cosine mode, which can be expressed as:

$$m = \frac{2\pi }{{L - u_{\varphi } }}$$

(61)

For a perfect plate, if a certain edge displacement u_φ/2 is applied, the hoop compression strain $\varepsilon_{\varphi }^{{{\text{th}}}}$ can be determined as:

$$\varepsilon_{\varphi }^{{{\text{th}}}} = \ln \left( {1 - \frac{{u_{\varphi } }}{L}} \right)$$

(62)

Therefore, the m also can be expressed as:

$$m = \frac{2\pi }{{Le^{{{\varepsilon_{\varphi }{}} }} }}$$

Assuming that the length of the plate before and after wrinkling is equal, both are L. Therefore, according to the arc length integral criterion, we can get:

$$L{ = }\int_{0}^{{L - u_{\varphi } }} {\sqrt {1 + y^{{\prime}{2}} } d\varphi } \approx \int_{0}^{{L - u_{\varphi } }} {1 + \frac{1}{2}y^{{\prime}{2}} d\varphi }$$

(63)

Through Taylor expansion, the maximum wrinkling amplitude δ can be calculated by the hoop compression strain $\varepsilon_{\varphi }^{{{\text{th}}}}$:

$$\delta { = }\frac{2}{\pi }\sqrt {u_{\varphi } \left( {L - u_{\varphi } } \right)} = \frac{2L}{\pi }\sqrt {e^{{{\varepsilon_{\varphi }{{\text{th}}}} }} - e^{{{2\varepsilon_{\varphi }{{\text{th}}}} }} }$$

(64)

In addition, Cao and Wang [16] take the wrinkling in a deep-drawing operation as the research object and assume that the external force F satisfies $F{ = }F_{\max } - F_{\max } \left( {y/\delta - 1} \right)^{2}$, so the critical internal pressure p_cri can be described:

$$p_{{{\text{cri}}}} = \frac{{3\left( {E_{0} - E_{w} } \right)}}{2\delta L}$$

(65)

According to Eq. (5), a plane strain state along the axial direction is assumed, thus the equivalent strain can be expressed as:

$$\overline{\varepsilon }^{{{\text{th}}}} { = }\beta \varepsilon_{\varphi }^{{{\text{th}}}}$$

(66)

Substituting Eq. (66) into the Hollomon hardening law to solve the equivalent stress:

$$\overline{\sigma }^{{{\text{th}}}} { = }K\left( {\beta \varepsilon_{\varphi }^{{{\text{th}}}} } \right)^{n}$$

(67)

For the pre-bending tube, compared with a straight tube, it is necessary to consider the effect of thickness variation and work-hardening when calculating E₀ and E_W. Therefore, based on the result in Sect. 3.1, E₀ and E_w can be expressed as follows respectively [6]:

$$E_{0} = \iint {\overline{\sigma }^{{{\text{th}}}} d\overline{\varepsilon }^{{{\text{th}}}} dV} = \frac{{KLt^{{{\text{bd}}}} }}{n + 1}\left[ {\left( {\beta \varepsilon_{\varphi }^{{{\text{th}}}} + \overline{\varepsilon }^{{{\text{bd}}}} } \right)^{n + 1} - \left( {\overline{\varepsilon }^{{{\text{bd}}}} } \right)^{n + 1} } \right]$$

(68)

$$E_{{\text{w}}} = \frac{{2Kt^{{{\text{bd}}}} }}{n + 1}\left[ \begin{gathered} \left( {\frac{{\beta t^{{{\text{bd}}}} }}{2} + \overline{\varepsilon }^{{{\text{bd}}}} \left( {\frac{2}{{m^{2} \delta }} + \frac{{t^{{{\text{bd}}}} }}{2}} \right)} \right)^{n + 1} \hfill \\ - \left( {\overline{\varepsilon }^{{{\text{bd}}}} \left( {\frac{2}{{m^{2} \delta }} + \frac{{t^{{{\text{bd}}}} }}{2}} \right)} \right)^{n + 1} \hfill \\ \end{gathered} \right]\left( {\frac{2}{{m^{2} \delta }} + \frac{{t^{{{\text{bd}}}} }}{2}} \right)^{ - n} \tan^{ - 1} \left( {\frac{m\delta }{2}} \right)$$

(69)

By substituting Eqs. (68) and (69) into Eq. (65), the change rule between the critical internal pressure and the hoop compression strain under pre-bending conditions can be obtained:

$$\begin{aligned} p_{cr} & = \left[ {\left( {\beta \varepsilon_{\varphi }^{{{\text{th}}}} + \overline{\varepsilon }^{{{\text{bd}}}} } \right)^{n + 1} - \left( {\overline{\varepsilon }^{{{\text{bd}}}} } \right)^{n + 1} } \right]\frac{{3Kt^{{{\text{bd}}}} }}{{2\delta \left( {n + 1} \right)}} \\ & - \left[ {\left( {\frac{{\beta t^{{{\text{bd}}}} }}{2} + \overline{\varepsilon }^{{{\text{bd}}}} \left( {\frac{2}{{m^{2} \delta }} + \frac{{t^{{{\text{bd}}}} }}{2}} \right)} \right)^{n + 1} - \left( {\overline{\varepsilon }^{{{\text{bd}}}} \left( {\frac{2}{{m^{2} \delta }} + \frac{{t^{{{\text{bd}}}} }}{2}} \right)} \right)^{n + 1} } \right]\frac{{3Kt^{{{\text{bd}}}} \left( {\frac{2}{{m^{2} \delta }} + \frac{{t^{{{\text{bd}}}} }}{2}} \right)^{ - n} }}{{L\delta \left( {n + 1} \right)}}\tan^{ - 1} \left( {\sqrt {e^{{{ - \varepsilon_{\varphi }{{\text{th}}}} }} - 1} } \right) \end{aligned}$$

(70)

According to the Cao’s mathematical model [17], for two certain wrinkling lengths L₁ and L₂, there is a corresponding transition strain $\varepsilon_{\varphi }^{{{\text{th}}}}$; thus, the following relationship can be built as:

$$p_{1} \left( {L_{1} ,\varepsilon_{\varphi }^{{{\text{th}}}} } \right) = p_{2} \left( {L_{2} ,\varepsilon_{\varphi }^{{{\text{th}}}} } \right)$$

(71)

Eventually, we can use computer software to obtain the $\varepsilon_{\varphi }^{{{\text{th}}}}$ with different wrinkling lengths L, and then substitute it into Eq. (70) to build the change rule between the hoop compression strain $\varepsilon_{\varphi }^{{{\text{th}}}}$ and the critical internal pressure $p_{{{\text{cri}}}}$:

$$p_{{{\text{cri}}}} { = }f\left( {\varepsilon_{\varphi }^{{{\text{th}}}} } \right)$$

(72)