1 Introduction

Grinding machine is a finishing-machined machine tool, and the final accuracy of any part is directly related to the grinding machine processing accuracy. As a result, machining accuracy is one of the performance indicators for grinding machine tool, and its improvement is critical for machine tool design research [1, 2]. Geometric error, thermal error, and system dynamic error are elements that result in machine tool error; geometric error has the greatest effect of all of them [3, 4].

To improve the precision of machine tool, geometric error compensation techniques are generally employed by scholars [5]. It encompasses modeling, identification, and detection, as well as compensation [6,7,8]. At present, the most widely used compensation model for machine tool geometric error is based on multi-body system theory. Denavit and Hartenberg proposed this theory based on mechanism kinematics, and two examples of application to space mechanisms are given [9]. Liu et al. developed and validated three-axis machining center error compensation model based on it [10]. Su and Li carried out the geometric error compensation model for five-axis machine tool and estimated the machining accuracy [11]. However, the modeling process requires the establishment of complex multi-coordinate system, and the number of second-order and higher-order terms in the model has little influence on the total error, which can only be eliminated manually. In addition, the comprehensive error model is limited in describing the effect of a single moving part on a tool.

To compensate for geometric errors, various methods have been developed, which can be classified generally into two categories. The first way is to improve the precision of mechanical parts and the overall assembly precision of machine tool, which is the hardware method; the second method is to build error model based on multi-body system theory and use iterative method for error compensation, namely, the software method [12,13,14]. Yang et al. constructed the geometric error model of CNC forming grinding wheel grinding machine and used function compensation to reduce the errors of gears, laying the groundwork for increasing the machine tool accuracy [15]. Zhang examined the positioning accuracy of a CNC turntable equipped with the HNC-818B system and corrected based on the hardware method for the CNC turntable pitch error [16]. While the hardware and software approaches are practical, both have limitations. The former is too expensive for small businesses and is constrained by the level of machine assembly and manufacture. The latter is predicated on the complicated multi-body system theory, and once the coordinate system mistake is established, subsequent compensation is invalid. Additionally, the iterative correcting procedure is sophisticated and difficult to comprehend.

Literature review shows that geometric error analysis serves as the foundation for compensation technology, and changes of the error value affect the comprehensive error. However, little research has been done on relation between error term and machining instruction, such as the unclear relationship between motion error and z in Fig. 6. To describe this relation in a mathematical sense, a mathematical model of this relation is obtained. Then, combining the model with the comprehensive error model, the comprehensive error model about the machining instruction is obtained.

Aiming at the limitations of previous study, this study proposes an error compensation method based on the differential theory. Then, the proposed compensation method is verified by CNC precision cylindrical grinding machining experiments. Section 2 describes the geometric error modeling of grinding machine based on differential matrix. Section 3 provides a detailed description of the mathematical function model for basic geometric error terms (BGETs) based on MATLAB curve fitting tool. Section 4 describes the error compensation method based on Jacobian matrix. Section 5 certifies the feasibility of the aforementioned methods through workpiece machining experiments. Section 6 is the conclusion.

2 Geometric error modeling of CNC precision cylindrical grinding machine based on differential motion matrix

2.1 Differential motion relation between coordinate systems of CNC precision cylindrical grinding machine

2.1.1 Description of differential motion between coordinate systems

The differential motion matrix is a six-dimensional matrix that describes the relationship between two coordinate systems in terms of differential motion. The minor error of a machine tool axis can be thought of as a small motion, which is typically stated mathematically as a differential. This little movement can be transferred to the tool coordinate system using differential motion theory to reflect the influence on the tool. Thus, the differential motion relation between coordinate systems can be used to express the meaning of errors.

2.1.2 Differential motion between coordinate systems of grinding machine

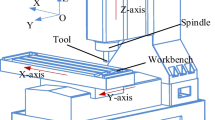
Taking B2-K3032 CNC precision cylindrical grinding machine as an example, as shown in Fig. 1, it is equipped with HNC-818B CNC system, HVS-180 servo drive, and X, Z, B, C-axis. The geometric error modeling and compensation method based on differential motion relations will be studied. As shown in Fig. 2, this grinding machine is composed of bed, tool, working table, sliding seat, spindle, and other components. The Z-direction slide seat drives the workpiece clamped between the headstock and tailstock along the Z-direction guide rail, while the X-direction slide seat drives the tool along the X-direction guide rail. The spindle turns the workpiece around the Z-axis, while the turntable turns the tool around the Y-axis.

Fig. 1
figure 1

B2-K3032 CNC precision cylindrical grinding machine

Full size image
Fig. 2
figure 2

Schematic diagram of moving parts of CNC precision cylindrical grinding machine

Full size image

To construct the error model, it is important to define the coordinate system of each moving part in order to characterize its indirect influence on the tool coordinate system, thus allowing for the construction of a thorough geometric error model on the tool coordinate system. According to the traditional machine tool coordinate system determination method, the coordinate system of B2-K3032 CNC precision cylindrical grinding machine is shown in Fig. 3. \(S_{i} (i = 1,2,3,4)\) represents constants related to the structure of the grinding machine, and \(O_{i} (i = O,X,Z,B,C)\) represents the coordinate system of each moving part of the grinding machine [17].

Fig. 3
figure 3

B2-K3032 CNC grinding machine coordinate system

Full size image

Along with the coordinate system specification, it is required to explain the location and posture of the CNC machine tool motion axis. The motion axis pose is defined by the position of its own coordinate system in the machine tool coordinate system. Let \({\varvec{n}}\), \({\varvec{o}}\), and \({\varvec{a}}\), respectively, represent the unit vectors in the X, Y, and Z directions of the coordinate system of axis. For example, there are two coordinate systems A and B, and the differential motion of the coordinate system A relative to B is expressed in the form of homogeneous coordinates:

$${\varvec{M}}_{{\varvec{B}}}^{{\varvec{A}}} = \left[ {\begin{array}{*{20}c} {\varvec{n}} & {\varvec{o}} & {\varvec{a}} & {\varvec{p}} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {n_{x} } & {o_{x} } & {a_{x} } & {p_{x} } \\ {n_{y} } & {o_{y} } & {a_{y} } & {p_{y} } \\ {n_{z} } & {o_{z} } & {a_{z} } & {p_{z} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {n_{x} } & {o_{x} } & {a_{x} } & 0 \\ {n_{y} } & {o_{y} } & {a_{y} } & 0 \\ {n_{z} } & {o_{z} } & {a_{z} } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {p_{x} } \\ 0 & 1 & 0 & {p_{y} } \\ 0 & 0 & 1 & {p_{z} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(1)

In Eq. (1), \({\varvec{p}}\) is unlimited; (\({\varvec{a\;o\;n}}\)) must satisfy \(\user2{n = o} \times {\varvec{a}}\). On the contrary, the differential motion of B relative to A can be expressed in homogeneous coordinate form as:

$${\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{B}}}^{{\varvec{A}}} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {{\varvec{n}}^{{\varvec{T}}} } \\ {{\varvec{o}}^{{\varvec{T}}} } \\ {{\varvec{a}}^{{\varvec{T}}} } \\ \end{array} } \right]} & { - \left[ {\begin{array}{*{20}c} {{\varvec{n}}^{{\varvec{T}}} } \\ {{\varvec{o}}^{{\varvec{T}}} } \\ {{\varvec{a}}^{{\varvec{T}}} } \\ \end{array} } \right] \times \user2{S(p)}} \\ {{\varvec{0}}^{{\varvec{T}}} } & {\left[ {\begin{array}{*{20}c} {{\varvec{n}}^{{\varvec{T}}} } \\ {{\varvec{o}}^{{\varvec{T}}} } \\ {{\varvec{a}}^{{\varvec{T}}} } \\ \end{array} } \right]} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {n_{x} } & {n_{y} } & {n_{z} } & { - n_{y} p_{z} + n_{z} p_{y} } & {n_{x} p_{z} - n_{z} p_{x} } & { - n_{x} p_{y} + n_{y} p_{x} } \\ {o_{x} } & {o_{y} } & {o_{z} } & { - o_{y} p_{z} + o_{z} p_{y} } & {o_{x} p_{z} - o_{z} p_{x} } & { - o_{x} p_{y} + o_{y} p_{x} } \\ {a_{x} } & {a_{y} } & {a_{z} } & { - a_{y} p_{z} + a_{z} p_{y} } & {a_{x} p_{z} - a_{z} p_{x} } & { - a_{x} p_{y} + a_{y} p_{x} } \\ 0 & 0 & 0 & {n_{x} } & {n_{y} } & {n_{z} } \\ 0 & 0 & 0 & {o_{x} } & {o_{y} } & {o_{z} } \\ 0 & 0 & 0 & {a_{x} } & {a_{y} } & {a_{z} } \\ \end{array} } \right]$$
(2)

The differential motion vector in the A is expressed as Eq. (3), and the differential matrix then expresses the differential motion vector in B as Eq. (4).

$${\varvec{D}} = \left[ {\begin{array}{*{20}c} {d_{x} } & {d_{y} } & {d_{z} } & {q_{x} } & {q_{y} } & {q_{z} } \\ \end{array} } \right]^{T}$$
(3)
$${\varvec{D}^{\varvec'}} = {\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{B}}}^{{\varvec{A}}} } \right] \times {\varvec{D}}$$
(4)

where \({\varvec{D}}\) is the differential motion vector in the A; \({\varvec{D}^{\varvec'}}\) is the differential motion vector expression in the B; \({\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{B}}}^{{\varvec{A}}} } \right]\) is the differential motion matrix of A with respect to B. From the perspective of error, \({\varvec{D}}\) and \({\varvec{D}^{\varvec'}}\) are the comprehensive errors in the A and B, respectively.

2.2 Forward motion topology structure and modeling of CNC precision cylindrical grinding machine

For a robot, forward kinematics is from the joint parameters to the end effector. Similarly, it is the movement from table to the tool on a grinding machine. According to the multi-body system theory, the tool and workpiece branches were established, and the bed of the CNC precision cylindrical grinding machine was defined as O body, the Z-slide carriage as Z body, and so on, as shown in Fig. 4. When combined with the forward kinematics theory of the robot and the multi-body system theory, the differential theory-based forward motion topological structure of the grinding machine can be constructed, as illustrated in Fig. 5.

Fig. 4
figure 4

Topological structure based on multi-body system theory

Full size image
Fig. 5
figure 5

Forward motion topology of CNC precision cylindrical grinding machine

Full size image

After the theory of differential motion is coupled with the topology of forward motion, the effect of the tool motion axis is determined. Then superimposing these influence components, the tool total influence is obtained. The detail steps to establish the comprehensive geometric error model of grinding machine are as follows:

  1. 1.

    Homogeneous transformation matrix between adjacent bodies

In an ideal working environment, the homogeneous transformation matrices between adjacent bodies are, respectively, \({\varvec{M}}_{{\varvec{c}}}^{{\varvec{w}}}\), \({\varvec{M}}_{{\varvec{z}}}^{{\varvec{c}}}\), \({\varvec{M}}_{{\varvec{o}}}^{{\varvec{z}}}\), \({\varvec{M}}_{{\varvec{o}}}^{{\varvec{x}}}\), \({\varvec{M}}_{{\varvec{x}}}^{{\varvec{b}}}\), and \({\varvec{M}}_{{\varvec{b}}}^{{\varvec{t}}}\). Since the workpiece is fixed on the C axis and the tool is fixed on the B-turntable, \({\varvec{M}}_{{\varvec{c}}}^{{\varvec{w}}}\) and \({\varvec{M}}_{{\varvec{b}}}^{{\varvec{t}}}\) are the unit matrix \({\varvec{E}}_{{\varvec{4}}}\). Assume that the rotation angles of C axis and B-turntable are, respectively, c and b, and the movement distances of the X/Z-slide carriage are, respectively, x and z. Based on the forward motion topological structure and differential theory of grinding machine, the homogeneous transformation matrix between adjacent bodies is obtained. \({\varvec{M}}_{{\varvec{c}}}^{{\varvec{w}}}\) of workpiece relative to C axis is transformed into the \({\varvec{M}}_{{\varvec{w}}}^{{\varvec{z}}}\) of C axis relative to workpiece. Similarly, other matrices are shown in the Table 1.

Table 1 Homogeneous transformation matrix between adjacent bodies of grinding machine
Full size table
  1. 2.

    Homogeneous transformation matrix of tool in each axis coordinate system

According to the topological structure in Fig. 5, the homogeneous transformation matrix of the tool of grinding machine relative to the workpiece is:

$${\varvec{M}}_{{\varvec{w}}}^{{\varvec{t}}} = {\varvec{M}}_{{\varvec{w}}}^{{\varvec{c}}} \times {\varvec{M}}_{{\varvec{c}}}^{{\varvec{z}}} \times {\varvec{M}}_{{\varvec{z}}}^{{\varvec{o}}} \times {\varvec{M}}_{{\varvec{o}}}^{{\varvec{x}}} \times {\varvec{M}}_{{\varvec{x}}}^{{\varvec{b}}} \times {\varvec{M}}_{{\varvec{b}}}^{{\varvec{t}}}$$
(5)

Equation (5) is also known as the forward kinematics equation of grinding machine. Accordingly, the matrix of the tool relative to other bodies is respectively expressed in Eqs. (6)–(11):

$$\begin{aligned} {\varvec{M}}_{{\varvec{w}}}^{{\varvec{t}}} & = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {\cos (c)} & { - \sin (c)} & 0 & 0 \\ {\sin (c)} & {\cos (c)} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]^{ - 1} \times \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]^{ - 1} \\ & \times \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & x \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {\cos (b)} & 0 & {\sin (b)} & 0 \\ 0 & 1 & 0 & 0 \\ { - \sin (b)} & 0 & {\cos (b)} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {cos(b)*cos(c)} & {sin(c)} & {cos(c)*sin(b)} & {x*cos(c)} \\ { - cos(b)*sin(c)} & {cos(c)} & { - sin(b)*sin(c)} & { - x*sin(c)} \\ { - sin(b)} & 0 & {cos{\text{(b)}}} & { - z} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ \end{aligned}$$
(6)
$${\varvec{M}}_{c}^{{\varvec{t}}} = {\varvec{M}}_{{\varvec{c}}}^{{\varvec{z}}} \times {\varvec{M}}_{{\varvec{z}}}^{{\varvec{o}}} \times {\varvec{M}}_{{\varvec{o}}}^{{\varvec{x}}} \times {\varvec{M}}_{{\varvec{x}}}^{{\varvec{b}}} \times {\varvec{M}}_{{\varvec{b}}}^{{\varvec{t}}} = \left[ {\begin{array}{*{20}c} {cos(b)*cos(c)} & {sin(c)} & {cos(c)*sin(b)} & {x*cos(c)} \\ { - cos(b)*sin(c)} & {cos(c)} & { - sin(b)*sin(c)} & { - x*sin(c)} \\ { - sin(b)} & 0 & {cos{\text{(b)}}} & { - z} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(7)
$${\varvec{M}}_{z}^{{\varvec{t}}} = {\varvec{M}}_{{\varvec{z}}}^{{\varvec{o}}} \times {\varvec{M}}_{{\varvec{o}}}^{{\varvec{x}}} \times {\varvec{M}}_{{\varvec{x}}}^{{\varvec{b}}} \times {\varvec{M}}_{{\varvec{b}}}^{{\varvec{t}}} = \left[ {\begin{array}{*{20}c} {\cos (b)} & 0 & {\sin (b)} & x \\ 0 & 1 & 0 & 0 \\ { - \sin (b)} & 0 & {\cos (b)} & { - z} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(8)
$${\varvec{M}}_{o}^{{\varvec{t}}} = {\varvec{M}}_{{\varvec{o}}}^{{\varvec{x}}} \times {\varvec{M}}_{{\varvec{x}}}^{{\varvec{b}}} \times {\varvec{M}}_{{\varvec{b}}}^{{\varvec{t}}} = \left[ {\begin{array}{*{20}c} {\cos (b)} & 0 & {\sin (b)} & x \\ 0 & 1 & 0 & 0 \\ { - \sin (b)} & 0 & {\cos (b)} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(9)
$${\varvec{M}}_{x}^{{\varvec{t}}} = {\varvec{M}}_{{\varvec{x}}}^{{\varvec{b}}} \times {\varvec{M}}_{{\varvec{b}}}^{{\varvec{t}}} = \left[ {\begin{array}{*{20}c} {\cos (b)} & 0 & {\sin (b)} & 0 \\ 0 & 1 & 0 & 0 \\ { - \sin (b)} & 0 & {\cos (b)} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(10)
$${\varvec{M}}_{b}^{{\varvec{t}}} = {\varvec{M}}_{{\varvec{b}}}^{{\varvec{t}}} = {\varvec{E}}_{{\varvec{4}}}$$
(11)
  1. 3.

    The differential motion vector of the geometric error of each axis of motion

Assuming the axis is a rigid body, it has six degrees of freedom. Due to assembly and manufacturing reasons, errors in the direction of six degrees of freedom exist, which are referred to as geometric errors. Geometric error can be classified into motion error and position error based on how it varies with axis movement. [18].

The motion error is affected by processing instruction; here we call them the basic geometric error terms and shorthand for BGETs. Such as Fig. 6, BGETs with respect to z are \(\delta_{x} (z),\delta_{y} (z),\delta_{z} (z),\varepsilon_{x} (z),\varepsilon_{y} (z),\varepsilon_{z} (z)\). The position error is continuous and independent of the processing instruction, and it is comprised of the squareness error and position deviation. The squareness error is the difference between the real and ideal position of an axis, and its magnitude is the deviation between the angle of the two axes and 90 degrees. The rotation axis position deviation is defined as the difference between the real and ideal axes [19,20,21]. Take B axis as an example, as shown in Fig. 7.

Fig. 6
figure 6

Diagram of Z-axis motion

Full size image
Fig. 7
figure 7

Position deviation of B axis

Full size image

The micro translation motion and rotation angle of each axis of grinding machine are respectively three linear displacement errors and three angular displacement errors, as shown in Fig. 6. The position error is defined as the recombination of the reference axis (Y axis) and the mechanical coordinate system Y axis, then there is no squareness error in Y axis, and the actual plane between X axis and Y axis is the X–Y reference plane, so there is only one squareness error \(v_{xz} (\mu rad)\) of X axis in the Z direction. The position deviations of C axis and B axis are \(p_{cx} ,p_{bx} ,p_{bz} (\mu m)\), respectively. According to Eq. (3), the differential motion vectors of the BGETs of each axis are known, as shown in Eq. (12). The first 3 terms represent the linear displacement errors in the direction of \(i(\mathrm{X,\,Z,\,B,\,C})\) axis, and the others represent the angular displacement errors. The differential motion vector of squareness error is expressed by Eq. (13), and the differential motion vector of position deviation of rotation B axis and C can be respectively expressed by Eq. (14):

$$\user2{Berror\_i} = \left[ {\begin{array}{*{20}c} {\delta_{x} (i)} & {\delta_{y} (i)} & {\delta_{z} (i)} & {\varepsilon_{x} (i)} & {\varepsilon_{y} (i)} & {\varepsilon_{z} (i)} \\ \end{array} } \right]^{T} \begin{array}{*{20}c} {} \\ \end{array} i(\mathrm{X,\,Z,\,B,\,C})$$
(12)
$$\user2{Verror\_z} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & {v_{xz} } & 0 \\ \end{array} } \right]^{T}$$
(13)
$$\left\{ {\begin{array}{*{20}l} {\user2{Perror\_b} = \left[ {\begin{array}{*{20}c} {p_{bx} } & 0 & {p_{bz} } & 0 & 0 & 0 \\ \end{array} } \right]^{T} } \hfill \\ {\user2{Perror\_c} = \left[ {\begin{array}{*{20}c} {p_{cx} } & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{T} } \hfill \\ \end{array} } \right.$$
(14)
  1. 4.

    The differential motion matrix of each axis in the tool coordinate system

Combined with the above differential motion vectors of the geometric errors of each axis, the differential motion vectors of the parts are obtained respectively (Eq. (15)).

$$\left\{ {\begin{array}{*{20}l} {\user2{error\_x} = \user2{Berror\_x} = \left[ {\begin{array}{*{20}c} {\delta_{x} (x)} & {\delta_{y} (x)} & {\delta_{z} (x)} & {\varepsilon_{x} (x)} & {\varepsilon_{y} (x)} & {\varepsilon_{z} (x)} \\ \end{array} } \right]^{T} } \hfill \\ {\user2{error\_z} = B\user2{error\_z} + \user2{Verror\_z} = \left[ {\begin{array}{*{20}c} {\delta_{x} (z)} & {\delta_{y} (z)} & {\delta_{z} (z)} & {\varepsilon_{x} (z)} & {\varepsilon_{y} (z) + v_{xz} } & {\varepsilon_{z} (z)} \\ \end{array} } \right]^{T} } \hfill \\ {\user2{error\_c} = B\user2{error\_B} + \user2{Perror\_B} = \left[ {\begin{array}{*{20}c} {\delta_{x} (b) + p_{bx} } & {\delta_{y} (b)} & {\delta_{z} (b) + p_{bz} } & {\varepsilon_{x} (b)} & {\varepsilon_{y} (b)} & {\varepsilon_{z} (b)} \\ \end{array} } \right]^{T} } \hfill \\ {\user2{error\_c} = \user2{Berror\_c} + \user2{Perror\_c} = \left[ {\begin{array}{*{20}c} {\delta_{x} (c) + p_{cx} } & {\delta_{y} (c)} & {\delta_{z} (c)} & {\varepsilon_{x} (c)} & {\varepsilon_{y} (c)} & {\varepsilon_{z} (c)} \\ \end{array} } \right]^{T} } \hfill \\ \end{array} } \right.$$
(15)

Combined with the homogeneous transformation matrix of the tool in the coordinate system of each part, the calculation of this process reflects the influence of each part on the machining precision of grinding machine. Equations (16)–(21) are the differential motion matrices of each part in the tool.

$${\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{w}}}^{{\varvec{t}}} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{M}}_{{{\varvec{11}}}} } & {{\varvec{M}}_{{{\varvec{12}}}} } \\ {{\varvec{M}}_{{{\varvec{21}}}} } & {{\varvec{M}}_{{{\varvec{22}}}} } \\ \end{array} } \right]$$
(16)
$${\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{c}}}^{{\varvec{t}}} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{T}}_{{{\varvec{11}}}} } & {{\varvec{T}}_{{{\varvec{12}}}} } \\ {{\varvec{T}}_{{{\varvec{21}}}} } & {{\varvec{T}}_{{{\varvec{22}}}} } \\ \end{array} } \right]$$
(17)
$${\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{z}}}^{{\varvec{t}}} } \right] = \left[ {\begin{array}{*{20}c} {\cos (b)} & 0 & { - \sin (b)} & 0 & {x*\sin (b) - z*\cos (b)} & 0 \\ 0 & 1 & 0 & z & 0 & x \\ {\sin (b)} & 0 & {\cos (b)} & 0 & { - x*\cos (b) - z*\sin (b)} & 0 \\ 0 & 0 & 0 & {\cos (b)} & 0 & { - \sin (b)} \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & {\sin (b)} & 0 & {\cos (b)} \\ \end{array} } \right]$$
(18)
$${\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{o}}}^{{\varvec{t}}} } \right] = \left[ {\begin{array}{*{20}c} {\cos (b)} & 0 & { - \sin (b)} & 0 & {x*\sin (b)} & 0 \\ 0 & 1 & 0 & z & 0 & x \\ {\sin (b)} & 0 & {\cos (b)} & 0 & { - x*\cos (b)} & 0 \\ 0 & 0 & 0 & {\cos (b)} & 0 & { - \sin (b)} \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & {\sin (b)} & 0 & {\cos (b)} \\ \end{array} } \right]$$
(19)
$${\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{x}}}^{{\varvec{t}}} } \right] = \left[ {\begin{array}{*{20}c} {\cos (b)} & 0 & { - \sin (b)} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ {\sin (b)} & 0 & {\cos (b)} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\cos (b)} & 0 & { - \sin (b)} \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & {\sin (b)} & 0 & {\cos (b)} \\ \end{array} } \right]$$
(20)
$${\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{b}}}^{{\varvec{t}}} } \right] = {\varvec{E}}_{{\varvec{6}}}$$
(21)
  1. 5.

    The comprehensive geometric error in the tool coordinate system

By superpositioning the differential motion vectors of each axis geometric error terms and the differential motion matrices of each part relative to the tool, the comprehensive geometric error is produced. By combining Eqs. (15) and (16)–(21), the vector form of the geometric error terms of the axes X, Z, B and C, and the other is shown in Eq. (22). Equation (23) is the comprehensive geometric error.

$$\left\{ {\begin{array}{*{20}c} {\varvec{error\_x}^{\varvec{^{\prime}}} = {\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{x}}}^{{\varvec{t}}} } \right] \times \varvec{error\_x}} \\ {\varvec{error\_z}^{\varvec{^{\prime}}} = {\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{z}}}^{{\varvec{t}}} } \right] \times \varvec{error\_z}} \\ {\varvec{error\_b}^{\varvec{^{\prime}}} = {\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{b}}}^{{\varvec{t}}} } \right] \times \varvec{error\_b}} \\ {\varvec{error\_c^{\prime}} = {\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{c}}}^{{\varvec{t}}} } \right] \times \varvec{error\_c}} \\ {\varvec{error\_o}^{\varvec{^{\prime}}} = {\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{o}}}^{{\varvec{t}}} } \right] \times \varvec{error\_o}} \\ {\varvec{error\_w}^{\varvec{^{\prime}}} = {\varvec{TW}}\left[ {{\varvec{M}}_{{\varvec{w}}}^{{\varvec{t}}} } \right] \times \varvec{error\_w}} \\ \end{array} } \right.$$
(22)
$$\begin{aligned} {\varvec{error}}^{\varvec{^{\prime}}} & = \varvec{error\_w}^{\varvec{^{\prime}}} + \varvec{error\_x}^{\varvec{^{\prime}}} + \varvec{error\_z}^{\varvec{^{\prime}}} + \varvec{error\_o}^{\varvec{^{\prime}}} + \varvec{error\_c}^{\varvec{^{\prime}}} + \varvec{error\_b}^{\varvec{^{\prime}}} \\ & = \left[ {\begin{array}{*{20}l} {\left( \begin{array}{l} \cos (b)*\cos (c)*(\delta_{x} (c) + P_{cx} ) - \cos (b)*\sin (c)*\delta_{y} (c) + \delta_{x} (b) \hfill \\ - \sin (b)*\delta_{z} (x) + x*\sin (b)*\sin (c) - z*\cos (b)*\sin (c)*\varepsilon_{x} (c) \hfill \\ - \sin (b)*\delta_{z} (z) + x*\cos (c)*\sin (b)*\varepsilon_{y} (c) + \cos (b)*\delta_{x} (z) + P_{bx} \hfill \\ + (x*\sin (b) - z*\cos (b))*(\varepsilon_{y} (z) + v_{xz} ) + \cos (b)*\delta_{x} (x) - \sin (b)*\delta_{z} (x) \hfill \\ \end{array} \right)} \hfill \\ {\left( \begin{array}{l} \sin (c)*\delta_{x} (c) + \cos (c)*\delta_{y} (c) + z*\cos (c)*\varepsilon_{x} (c) \hfill \\ - z*\sin (c)*\varepsilon_{y} (c) + x*\varepsilon_{z} (c) + \delta_{y} (z) + \hfill \\ z*\varepsilon_{x} (z) + x*\varepsilon_{z} (z) + \delta_{y} (x) + \delta_{y} (b) \hfill \\ \end{array} \right)} \hfill \\ {\left( \begin{array}{l} \cos (c)*\sin (b)*\delta_{x} (c) + \cos (b)*\delta_{z} (c) \hfill \\ - (x*\cos (b)*\sin (c) + z*\sin (b)*\sin (c))*\varepsilon_{x} (c) \hfill \\ - x*\cos (b)*\sin (c)*\varepsilon_{y} (c) + \sin (b)*\delta_{x} (x) + \sin (b)*\delta_{x} (z) \hfill \\ + \cos (b)*\delta_{z} (z) - (x*\cos (b) + z*\sin (b))*(\varepsilon_{y} (z) + v_{xz} ) \hfill \\ + \cos (b)*\delta_{z} (x) + \delta_{z} (b) + P_{bz} - \sin (b)*\sin (c)*\delta_{y} (c) \hfill \\ \end{array} \right)} \hfill \\ {\left( \begin{array}{l} \cos (b)*\cos (c)*\varepsilon_{x} (c) - \cos (b)*\sin (c)*\delta_{y} (c) - \hfill \\ \sin (b)*\delta_{z} (c) + \cos (b)*\varepsilon_{x} (z) - \sin (b)*\varepsilon_{z} (z) + \hfill \\ \cos (b)*\varepsilon_{x} (x) - \sin (b)*\varepsilon_{z} (x) + \varepsilon_{x} (b) \hfill \\ \end{array} \right)} \hfill \\ {\left( {\sin (c)*\varepsilon_{x} (c) + \cos (c)*\delta_{y} (c) + \varepsilon_{y} (z) + v_{xz} + \varepsilon_{y} (x) + \varepsilon_{y} (b)} \right)} \hfill \\ {\left( \begin{array}{l} \cos (c)*\sin (b)*\varepsilon_{x} (c) - \sin (b)*\sin (c)*\varepsilon_{y} (c) + \hfill \\ \cos (b)*\varepsilon_{z} (c) + \sin (b)*\varepsilon_{x} (z) + \cos (b)*\varepsilon_{z} (z) + \hfill \\ \sin (b)*\varepsilon_{x} (x) + \cos (b)*\varepsilon_{z} (x) + \varepsilon_{z} (b) \hfill \\ \end{array} \right)} \hfill \\ \end{array} } \right] \\ \end{aligned}$$
(23)

3 The mathematical function of BGETs based on MATLAB curving fitting tool

3.1 Measurement and identification of geometric errors

Laser interferometers have been widely employed in high-end equipment such as machine tool and trilinear coordinate measuring instrument as a representation of current precision measuring instruments [22].

The SJ6000 laser interferometer was used to measure the B2-K3032 grinding machine. Twenty evenly distributed mark points with a stroke of 0–365 mm on the X-guide rail were selected for error measurement; twenty evenly distributed mark points with a stroke of 0–1500 mm on the Z-guide rail were selected; ten evenly distributed mark points with a stroke of 0–1500 mm on the C-principal axis were selected; ten evenly distributed mark points with a stroke of 0–360° on the B-grinding wheel turntable were selected. Due to the project secrecy, the measurement process is only shown in the form of schematic diagram in this study; the linear measurement, rotation axis error, straightness, and diagram of squareness error measurement are depicted in Figs. 8, 9, 10 and 11.

Fig. 8
figure 8

Schematic diagram of linear measurement

Full size image
Fig. 9
figure 9

Rotation axis error measurement

Full size image
Fig. 10
figure 10

Schematic diagram of straightness measurement

Full size image
Fig. 11
figure 11

Diagram of perpendicularity measurement

Full size image
Fig. 12
figure 12

The Sum of sine fitting curve of the geometric error of the displacement of each axis of motion a) X axis, b) Z axis, c) B axis, d) C axis

Full size image
Fig. 13
figure 13

The Sum of sine fitting curve of geometric error of angular displacement of each axis a) X axis, b) Z axis, c) B axis, d) C axis

Full size image

The error values for the X, Z, B, and C axes after measurement with the laser interferometer are shown in Figs. 12 and 13. Due to the fact that the position error is unrelated to the processing instruction, the squareness error \(v_{xz}\) is 8.9883 \(\mu rad\), the position deviation \(p_{cx}\) is − 6.74 \(\mu m\), and the position deviations \(p_{bx} ,p_{bz}\) are 21.451 \(\mu m\) and 14.042 \(\mu m\) using the nine-line identification method.

3.2 The mathematical fitting function model of BGETs

Curve fitting is a critical technique in data analysis since it involves selecting the proper curve type to match the given data and analyzing the relationship between variables using the fitted curve equation. The most often used data analysis software includes MATLAB, Origin, and Maple [23, 24]. BGETs and x, z, b, and c have no known relationship, and the error changes with the distance and angle of the axis motion. To explore the relation further, the curving fitting tool is utilized to fit BGETs and identify its functional relationship.

There are four indexes to evaluate the fitting effect. SSE (the sum of squares due to error) is called the square sum of the residuals. The closer SSE is to 0, the better the fitting degree is. R-square measures the success of the fitting in explaining the changes in the data. The closer the value is to 1, the more complete the interpretation model is. RMSE (root mean square error) is the root mean square error between the fitting data and the input data. The closer RMSE is to 0, the better the fitting degree is. Adjusted R-square can accept any value less than or equal to 1, and a value closer to 1 is a better fit.

By comprehensive comparison, the fitting results show that the sum of sine fitting have good fitting effects, as shown in Figs. 12 and 13 and Tables 2, 3, 4 and 5. Fig. 12 is the Sum of sine fitting diagram of 12 term displacement errors of four motion axes. Fig. 13 is the fitting diagram of 12 term angular errors. The sum of sine fitting functions of the BGETs of this fitting are shown in Eqs. (24)–(27):

$$\left\{ {\begin{array}{*{20}l} {\delta_{x} (x) = 3.145\sin (1.784x + 0.3403) + 1.638\sin (3.492x + 1.196) + 1.055\sin (12.57x - 2.129)} \hfill \\ {\delta_{y} (x) = 0.4953\sin (0.7338x + 1.359) + 0.0938\sin (3.726x - 0.995) + 0.2046\sin (4.545x + 0.8417)} \hfill \\ {\delta_{z} (x) = 5.2545\sin (0.868x - 1.011) + 5.121\sin (0.8957x + 2.222)} \hfill \\ {\varepsilon_{x} (x) = 0.118\sin (1.16x + 1.848) + 0.0623\sin (3.585x + 2.246)} \hfill \\ {\varepsilon_{y} (x) = 0.05469\sin (01.9425x - 1.825)} \hfill \\ {\varepsilon_{z} (x) = 0.088\sin (1.361x - 1.383)} \hfill \\ \end{array} } \right.$$
(24)
$$\left\{ {\begin{array}{*{20}l} {\delta_{x} (z) = 3.145\sin (1.784z + .03403) + 1.638\sin (3.492z + 1.196) + 1.055\sin (12.57z - 2.129)} \hfill \\ {\delta_{y} (z) = 15.69\sin (1.604z - 1.873) + 23.29\sin (1.781z + 1.359) + 2.193\sin (6.359z + 1.47)} \hfill \\ {\delta_{z} (z) = 2293\sin (6.391z + 1.925) + 2293\sin (6.932z - 1.216)} \hfill \\ {\varepsilon_{x} (z) = 135.2\sin (0.7929z - 2.955) + 132.3\sin (0.8188z + 0.1923)} \hfill \\ {\varepsilon_{y} (z) = 0.5075\sin (1.298z + 1.943) + 0.3481\sin (3.914z + 2.479)} \hfill \\ {\varepsilon_{z} (z) = 14.99\sin (0.7591z - 0.4776) + 14.51\sin (0.7865z + 2.695)} \hfill \\ \end{array} } \right.$$
(25)
$$\left\{ {\begin{array}{*{20}l} {\delta_{x} (b) = 2.312\sin (4.45b + 1.369) + 3.555\sin (2.399b + 0.1697)} \hfill \\ {\delta_{y} (b) = 34.08\sin (1.555b - 2.194) + 33.47\sin (1.687b + 1.013)} \hfill \\ {\delta_{z} (b) = 533.5\sin (6.551b + 1.826) + 533.3\sin (6.554b - 1.314)} \hfill \\ {\varepsilon_{x} (b) = 8.7775\sin (1.429b - 1.858) + 8.499\sin (1.494b + 1.264)} \hfill \\ {\varepsilon_{y} (b) = 1.268\sin (1.344b - 2.825) + 24.23\sin (0.02485b - 0.0068)} \hfill \\ {\varepsilon_{z} (b) = 0.02897\sin (1.225b + 1.672)} \hfill \\ \end{array} } \right.$$
(26)
$$\left\{ {\begin{array}{*{20}l} {\delta_{x} (c) = 32.9\sin (0.9583c + 1.052) + 27.53\sin (1.058c - 2.063)} \hfill \\ {\delta_{y} (c) = 47.455\sin (0.8169c + 0.3983) + 45.24\sin (0.84117c - 2.768)} \hfill \\ {\delta_{z} (c) = 6.521\sin (0.573c + 1.048) + 2.296\sin (3.101c - 2.063)} \hfill \\ {\varepsilon_{x} (c) = 0.4898\sin (0.567c + 1.229) + 0.081\sin (4.021c - 5.115) + 0.127\sin (6.002c - 0.382)} \hfill \\ {\varepsilon_{y} (c) = 0.6802\sin (0.9289c - 1.666)} \hfill \\ {\varepsilon_{z} (c) = 0.6925\sin (1.094c - 1.471) + 0.1694\sin (3.675c - 1.865)} \hfill \\ \end{array} } \right.$$
(27)
Table 2 Sum of sine fitting evaluation parameters of X-axis BGETs
Full size table
Table 3 Sum of sine fitting evaluation parameters of Z-axis BGETs
Full size table
Table 4 Sum of sine fitting evaluation parameters of B axis BGETs
Full size table
Table 5 Sum of sine fitting evaluation parameters of C axis BGETs
Full size table

4 Geometric error compensation of grinding machine based on Jacobian matrix

4.1 Overview of the Jacobian matrix and the generalized inverse matrix

In vector calculus, the Jacobian matrix is formed of first partial derivatives and is structured in a certain way. It is essentially the best linear approximation to a given point of a differentiable equation. If m functions exist: \(y_{{1}} (x_{1} ,x_{2} , \cdots ,x_{n} )\), \(y_{2} (x_{1} ,x_{2} , \cdots ,x_{n} )\),…, \(y_{m} (x_{1} ,x_{2} , \cdots ,x_{n} )\); then the partial derivatives of these functions can form a matrix with m rows and n columns, namely, the Jacobian matrix, as shown in Eq. (28):

$${\varvec{J}}_{{{\varvec{m}} \times {\varvec{n}}}} = \left[ {\begin{array}{*{20}c} {\frac{{\delta y_{{1}} }}{{\delta x_{{1}} }}} & \cdots & {\frac{{\delta y_{1} }}{{\delta x_{n} }}} \\ \vdots & \ddots & \vdots \\ {\frac{{\delta y_{m} }}{{\delta x_{{1}} }}} & \cdots & {\frac{{\delta y_{m} }}{{\delta x_{n} }}} \\ \end{array} } \right]$$
(28)

If \(y_{i} (i = 1, \cdots ,m)\) is differentiable at point P, then the optimal linear approximation of \(y_{i}\) near point P can be expressed as Eq. (29), and the expression of differentiation is shown in Eq. (30):

$${\varvec{y}}_{{\varvec{i}}} \user2{(x)} = {\varvec{y}}_{{\varvec{i}}} \user2{(p)} + {\varvec{J}}_{{{\varvec{m}} \times {\varvec{n}}}} \cdot (x - p) + o^{2} (x - p)$$
(29)
$${\varvec{dy}} = {\varvec{J}}_{{{\varvec{m}} \times {\varvec{n}}}} \times {\varvec{dx}}$$
(30)

In Eq. (30), \({\varvec{dy}} = \left[ {\begin{array}{*{20}c} {dy_{1} } & {dy_{2} } & \cdots & {dy_{m} } \\ \end{array} } \right]^{T}\), \({\varvec{dx}} = \left[ {\begin{array}{*{20}c} {dx_{1} } & {dx_{2} } & \cdots & {dx_{n} } \\ \end{array} } \right]^{T}\).

In linear algebra, since there is no inverse matrix for non-square matrices, there is no inverse matrix, and the inverse of a non-square matrix is a generalized inverse. The numbers of equations and unknown number are m and n, respectively, if \(m > n\); Eq. (31) has no solution. However, the generalized inverse matrix \(\user2{G(x)}^{\user2{ + }}\) is used to get the answer in the least squares sense, as shown in Eq. (32).

$$\left\{ \begin{gathered} g_{1} (x_{1} ,x_{2} ,x_{3} , \cdots ,x_{n} ) = 0 \hfill \\ g_{2} (x_{1} ,x_{2} ,x_{3} , \cdots ,x_{n} ) = 0 \hfill \\ g_{3} (x_{1} ,x_{2} ,x_{3} , \cdots ,x_{n} ) = 0 \hfill \\ \vdots \hfill \\ g_{m} (x_{1} ,x_{2} ,x_{3} , \cdots ,x_{n} ) = 0 \hfill \\ \end{gathered} \right.$$
(31)
$$\user2{G(x)}^{\user2{ + }} = \left( {\user2{G(x)}^{{\varvec{T}}} \user2{G(x)}} \right)^{ - 1} \user2{G(x)}^{{\varvec{T}}}$$
(32)

4.2 Geometric error compensation method based on Jacobian matrix

The grinding machine four-axis linkage results in a total error, and the minuscule motion of each axis is represented by \((\begin{array}{*{20}c} {dx} & {dz} & {db} & {dc} \\ \end{array} )\). The Jacobian matrix is constructed in accordance with the differential motion matrix, which is capable of correcting the entire geometric error [25]. This process is described by Eq. (33). Equation (34) is a thorough statement in which the left matrix represents the comprehensive geometric error, and the right second matrix represents the minor geometric error on each axis; the first matrix represents the Jacobian matrix. Then, using the sum of sine function models of the 24 BGETs acquired in Sect. 3 (Eqs. (24)–(27)) as well as the identified squareness error and position deviation, we can compensate for the grinding machine comprehensive error. Where, \({\varvec{J}}_{{\varvec{e}}}^{\user2{ + }} = \left( {{\varvec{J}}_{{\varvec{e}}}^{{\varvec{T}}} {\varvec{J}}_{{\varvec{e}}} } \right)^{ - 1} {\varvec{J}}_{{\varvec{e}}}^{{\varvec{T}}}\) is the generalized inverse of the Jacobian matrix; \(\left[ {\begin{array}{*{20}c} {dx} & {dz} & {db} & {dc} \\ \end{array} } \right]^{T}\) is the compensation dosage.

$$\varvec{error^{\prime}}{ = }{\varvec{J}}_{{\varvec{e}}} \times \left[ {\begin{array}{*{20}c} {dx} & {dz} & {db} & {dc} \\ \end{array} } \right]^{T}$$
(33)
$$\left[ {\begin{array}{*{20}c} {e1} \\ \vdots \\ {e6} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{\delta e1}{{\delta x}}} & \cdots & {\frac{\delta e1}{{\delta c}}} \\ \vdots & \ddots & \vdots \\ {\frac{\delta e6}{{\delta x}}} & \cdots & {\frac{\delta e6}{{\delta c}}} \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {dx} \\ {dz} \\ {db} \\ {dc} \\ \end{array} } \right]$$
(34)
$$\left[ {\begin{array}{*{20}c} {dx} & {dz} & {db} & {dc} \\ \end{array} } \right]^{T} = {\varvec{J}}_{{\varvec{e}}}^{\user2{ + }} \times \left[ {\begin{array}{*{20}c} {e1} & {e2} & {e3} & {e4} & {e5} & {e6} \\ \end{array} } \right]^{T}$$
(35)

5 Experiment

To verify the proposed modeling method based on differential theory, the mathematical model of BGETs based on MATLAB curving fitting tool, and the compensation method based on the Jacobian matrix in the grinding machine, a stepped shaft experiment will be conducted to demonstrate the feasibility of theoretical method.

5.1 Description of experimental workpiece and measurement items

B2-k3032 CNC precision cylindrical grinder produces primarily BT30\BT40 and the material for 40Cr spindles, so this experiment uses a 40Cr stepped shaft. There are five axial segments, as shown in Fig. 14. Each shaft segment is distinct in length and diameter, totaling 500 mm in length and a maximum diameter of 40 mm.

Fig. 14
figure 14

Schematic diagram of experimental processing stepped shaft

Full size image

Geometric tolerances should be chosen in accordance with the part structure and requirements. When achieving functional requirements, easier-to-measure items should be chosen instead of difficult-to-measure [26, 27]. Therefore, the radial circular run-out error is chosen to reflect the grinding machine machining precision.

5.2 Experimental process and results

Firstly, two identical workpiece were processed by B2-K3032 CNC precision cylindrical grinding machine, as shown in Fig. 15. The workpiece had five axial segments with different lengths; hence, each segment had two, three, seven, two, and four measuring points. Then, using the RA1000 series roundness instrument from WALE Company, the radial circle run-out errors of 18 measuring points on the two workpieces were determined, and each measuring point was measured five times. Finally, taking the average value after the improvement rate was calculated. Figure 16 is the comparison of the parts before and after compensation and theoretical processing. Table 6 shows the average machining accuracy improvement rate of measuring points for each segment. According to Table 6, the improvement rates of machining accuracy of five shaft segments are, respectively, 17.54%, 15.22%, 15.71%, 18.4%, and 12.87%; and the average machining accuracy is improved by 15.948%. Therefore, the geometric error modeling method and the error compensation method based on the differential theory and Jacobian matrix are effective and applicable to improve the machining accuracy of the CNC precision cylindrical grinding machine.

Fig. 15
figure 15

Machining site drawing of B2-K3032 grinding machine

Full size image
Fig. 16
figure 16

Comparison of theoretical machining trajectories of each shaft segment with those before and after modification

Full size image
Table 6 Machining accuracy improvement rate of each shaft segment
Full size table

6 Conclusions

This paper presented a geometric error modeling and compensation method based on differential theory and Jacobian matrix to improve machining accuracy of CNC precision cylindrical grinding machine. Firstly, the advantages of the modeling method based on differential motion theory are as follows: (1) simple calculation process; (2) the differential matrix can clearly reflect the influence of each component on the tool; (3) in-depth study of this method in the field of CNC grinding machine. Then, the functional relationship between BGETs and processing instructions is studied, and 24 sinusoidal fitting functions are obtained in this paper. Finally, an error compensation method based on Jacobian matrix is proposed. In addition, the experimental results demonstrated that the modeling, fitting, and compensation methods suggested in this study are viable and useful for grinding machine applications. It can be used to correct geometric errors in CNC grinding machines and serves as a reference for machine tool design and scientific research firms.

Although progress had been made in the field of geometric error compensation of CNC grinding machine in this paper, this error modeling method was not widely used in CNC machine tool and not certain whether it is applicable to other high-end CNC equipment. Furthermore, the oscillation of the fitting function may have an effect on the model. Therefore, a model is needed to better express the functional relationship between errors and processing instructions.