1 Introduction

Machine tools and their components are sensitive to temperature change that could exert an influence on mechanical structure deformation thereby inducing thermal error of motion drive systems [1]. Studies have shown that, for high-speed and high-precision machine tools, processing and manufacturing errors caused by thermal deformation account for about 40% to 70% of the total manufacturing errors [2]. Therefore, the research of machine tool thermal error has become an important research direction.

Of all factors that contribute to the thermal error of a machine tool, thermal error of ball screw system plays a very important role [1]. In order to investigate the thermal error of the ball screw, the finite element models are frequently performed [3]. Week uses the finite element method-possibilities and limitations to compute the thermal of machine tools [4]. Xu et al. [5] used the finite element method to estimate the thermal error of the ball screw system and effectiveness of the air cooling system. Ming and Jiang [6] developed an integrated thermal model by the aid of the finite-element method to analyze the temperature distribution of a ball screw feed drive system, considering the thermal contact resistance between the bearing and its housing. Li et al. [7] provides a comprehensive error compensation method for the time-varying positioning error of machine tools based on simulation and experimental analysis. Oyanguren et al. [8] presents a numerical modelling strategy to predict the preload variation due to temperature increase using a thermo-mechanical 3D finite element method based model for double nut-ball screw drives. Huang et al. [9] studies further the relationship between thermal deformation and heat quantity through modeling the thermal deformations of stretching bar and bending beam using heat quantity as the independent variable, and the stretching model is verified based on finite element method. Li et al. [10] develops an adaptive real-time model for predicting the thermal characteristics of the ball screw drive system on line with a finite element method integrated with the Monte Carlo method. Nevertheless, few researchers focused on how to get the analytical solution of the thermal model through theoretical methods.

A good thermal error model with high accuracy and robustness is the key factor for error compensation [11,12,13,14,15]. Lee et al. [16] presents a thermal error model using a fuzzy logic strategy, which does not require any complex procedure such as multiregression or information about the characteristics of the plant. But the error model parameters are only calculated mathematically. Ma et al. [17] proposes the predictive model for thermal contact conductance based on the micro morphology description of rough surfaces and the contact load distribution of solid joints. Then, the dynamic thermal-structure model of the ball screw feed drive system was established. Han et al. [18] presents a new approach for building an effective mathematic thermal error for machine tools which is capable of improving the accuracy of the machine tool effectively. Wu et al. [19] introduced a comprehensive multiple regression method to study the relationship between temperature variation and thermal error for a ball screw system. Wang et al. [20] proposed a compound error model for the geometric and thermal errors of a milling center based on Newton interpolation. Most of the work done above focused on studying the relationship between thermal error and the temperature of the key heat source. However, under changing thermal conditions, the temperature field of the ball screw is usually inconsistent with the temperature of the key heat source.

There are also some researchers who focus on the measurement of temperature changes during the operation of machine tools. Wu et al. [21] proposes a thermal error model based on the five key temperature points by using genetic algorithm-based back propagation neural network, which improves the accuracy and reduces computational cost for the prediction of thermal deformation in the turning center. Xu et al. [22, 23] introduced an improved ball screw feed drive thermal error compensation system. Based on this system, the stroke input was calculated and modified by the controller of control unit, and then the compensation was completed. Zhang et al. [24] presents different prediction models for positioning error of ball screw feed drive system based on the mounting condition. And the coefficients in the model are identified using the multiple linear regression method. Wei et al. [25] leads to the proposal of a comprehensive temperature-feature extraction method that uses feature extraction algorithm and weight optimization to construct linear temperature-sensitive points. Experimental facilities verified the feasibility of its proposal. Sun et al. [26] presented a precision testing method called seven-sensor configuration method to measure the thermal errors of a horizontal machining center with linear optical grating scale. Li et al. [27] tests the temperatures and positional deviations of the ball screw feed drive system and the linear motor feed drive system equipped with linear scales and analyzes the factors that affect the positioning error. Then, the temperatures and positioning coordinates were used as inputs to build the thermally induced positional deviation model of full closed-loop feed drive system.

In this paper, based on the thermal boundary obtained from the experiment, we get the analytical solution of the thermal model of the ball screw feed system. Based on the definition of thermal expansion, the axial thermal elongation of the ball screw is calculated, and the temperature of the ball screw at different positions is measured experimentally, and the correctness of the model is verified by comparison with theoretical data. Finally, the influence of system parameters on the temperature field of the ball screw feed system is discussed.

2 Thermal error model of BSFS

2.1 Heat generation and thermal boundary conditions

The generation of heat is the root cause of the temperature rise and thermal deformation of the ball screw feed system. When the BSFS produces thermal deformation, thermal errors occur, too. Before discussing the thermal expansion and deformation of the BSFS, it is assumed that the ball screw is a solid cylindrical rod, and the temperature distribution in the radial direction is uniform.

2.1.1 Main heat source and heat generation

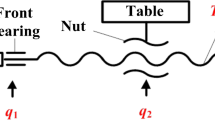
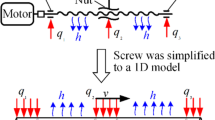
When the BSFS is in the transmission work, the heat is generated from friction heat, and the friction heat is mainly caused by the friction between the ball and the raceway or groove during the working process of the bearing and nut. Therefore, the main heat sources include the front and rear bearings and nut pairs, and the heat generation principle diagram is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of heat generation of ball screw feed system

Full size image

During the working of the ball screw, friction and heat are generated between the bearing balls and the inner and outer rings of the bearing. The friction loss of the bearing is almost entirely converted into heat inside the bearing, which causes the temperature of the bearing to rise. The calorific value of the bearing can be calculated by the following empirical formula [28]:

$$Q_{b} = 1.047 \times 10^{ - 4} nM_{1}$$
(1)

where Qb is the calorific value of the bearing; n is the speed of the ball screw; and M1 is the total friction torque of the bearing.

The preload of the ball screw nut pair will cause friction and heat generation of the nut pair. During the movement of the nut pair on the ball screw, the ball, the nut, and the groove of the ball screw will rub against each other, producing frictional heat, and the heat will be transferred to the ball screw. It causes the temperature of the ball screw to rise. According to the empirical formula, the friction heat of the nut pair can be obtained by the following formula [29, 30]:

$$Q_{n} = 0.12\pi nf_{0} v_{0} M_{2}$$
(2)

where Qn is the calorific value of the nut; f0 is the coefficient related to the nut type and lubrication method; ν0 is the kinematic viscosity of the lubricating fluid; M2 is the total friction torque of the nut.

According to the law of conservation of energy, it can be known that part of the heat generated by the bearing and nut is transferred to the screw, and the other part is lost to the air. The heat lost to the air includes two parts: heat convection heat dissipation and heat radiation heat dissipation. Since the heat radiation loss is relatively small, it can be ignored. Therefore, we have

$$\left\{ {\begin{array}{*{20}c} {Q = Q_{sc} + Q_{sT} + Q_{c} } \\ {Q_{sc} = c_{s} m_{s} \left( {T - T_{0} } \right)} \\ {Q_{sT} = h_{s} A_{{\text{s}}} \left( {T - T_{0} } \right)} \\ {Q_{c} = h_{c} A_{c} \left( {T_{n} - T_{0} } \right)} \\ \end{array} } \right.$$
(3)

where Q is the heat generated by the bearing or nut; Qsc is the heat that causes the temperature of the ball screw to rise; QsT is the heat lost by the heat convection of the screw; and Qc is the heat lost to the air by the nut heat convection. c2 is the specific heat capacity of the ball screw; m2 is the mass of the ball screw; hc is the convective heat transfer coefficient of the nut; Ac is the surface area of the nut component; Tn is the temperature function of the nut; T0 is the temperature of the air adjacent to the surface; As is the surface area of the ball screw; hs is the convective heat transfer coefficient of the ball screw.

Heat dissipates from the ball screw shaft into the ambient air through forced convective heat transfer. The calculation of the heat transfer coefficient for convection follows a series of steps. First, the mean velocity of the fluid with respect to the solid surface is determined. When the parameter is known, the Reynolds number is determined. For the ball screw shaft rotating at an angular velocity of δ, the Reynolds number is written as

$$R_{e} = \frac{{\delta d^{2} }}{{2\nu_{l} }}$$
(4)

where νl is the kinematic viscosity of the air and d is the diameter of the screw shaft.

Second, the Nusselt number is determined by

$$N_{u} = 0.133R_{e}^{2/3} P_{r}^{1/3}$$
(5)

where the Prandtl number Pr is a material parameter of the fluid and calculated as [31]

$$P_{r} = \frac{{C_{l} u_{l} }}{{\gamma_{l} }}$$
(6)

where Cl is the specific heat capacitance of the air, μl is the dynamic viscosity of the air, and γl is the thermal conductivity of the ambient air.

Then, the heat transfer coefficient is expressed as

$$h = \frac{{N_{u} \gamma_{l} }}{d}$$
(7)

2.2 Heat conduction equation of ball screw

The frictional heat of the bearing and the nut will cause the temperature rise of the ball screw, as its thermal behavior directly makes a great impact on the positioning error of the feed drive system. In order to obtain the thermal deformation of the ball screw, we established the heat conduction equation of the ball screw as follows [32]:

$$\frac{{\partial^{2} T\left( {x,t} \right)}}{{\partial x^{2} }} = \frac{\rho c}{\lambda }\frac{{\partial T\left( {x,t} \right)}}{\partial t}$$
(8)

where λ is the thermal conductivity, ρ is the density, and c is the heat capacity.

At the start time, the initial temperature can be regarded as room temperature T0. As for the heat boundary conditions of Eq. (8), there are mainly divided into two types [33]:

  1. i.

    At both ends of the screw shaft, it is supported by bearings, so the temperature at both ends is equal to the temperature of the bearing. Therefore, we have

    $$\left. {T\left( {x,t} \right)} \right|_{x = 0,l} = T_{b}$$
    (9)

    where Tb is the bearing temperature; it can be obtained by polynomial fitting of experimental data.

  2. ii.

    Assuming that the heat generated by the nut due to friction is uniformly applied to the ball screw [34], the temperature function of the nut can be obtained according to Eq. (3).

As shown in Fig. 1, three typical heat sources are contributing to the ball screw temperature rise. Because Eq. (8) is a linear differential equation, the temperature change of ball screw should be equal to the sum of temperature change responding to every single heat source. So we have

$$T\left( {x,t} \right) = \sum\limits_{i = 1}^{3} {T_{i} } \left( {x,t} \right)$$
(10)

2.2.1 Determination of boundary conditions

The test was completed on the Yingtai CJK6130 CNC machine tool, as shown in Fig. 2. Before the test, the ambient temperature T0 was measured, and the measured initial ambient temperature was 17 °C. Then an infrared thermal imager is used to take pictures of the front and rear bearings and nut every 10 min during the working process of the machine tool, and the real-time temperature data are obtained as shown in Table 1.

Fig. 2
figure 2

CNC machine tool fittings

Full size image
Table 1 Temperature of front and rear bearings and nut at different times
Full size table

The temperature curve of the bearing can be obtained by polynomial fitting as shown in Figs. 3 and 4. The temperature function of the bearing can be obtained in Eqs. (11) and (12):

$$T_{b1} \left( t \right) = 25.6303 - 8.506e^{ - 0.0718t}$$
(11)
$$T_{b2} \left( t \right) = 28.4766 - 11.3821e^{ - 0.0338t}$$
(12)
Fig. 3
figure 3

The change curve of the temperature of the front bearing with time

Full size image
Fig. 4
figure 4

The change curve of the temperature of the rear bearing with time

Full size image

Similarly, the temperature curve of the nut bearing can be obtained by polynomial fitting, as shown in Fig. 5, and the temperature function of the nut can be obtained in Eq. (13):

$$T_{{\text{n}}} \left( t \right) = 30.6726 - 13.933e^{ - 0.0697t}$$
(13)
Fig. 5
figure 5

The change curve of the temperature of the nut with time

Full size image

2.2.2 Solution of the heat conduction equation

Based on the experimental data, the temperature function of the boundary conditions is obtained by fitting. But the method of separating variables is only suitable for the case where the differential equations and boundary conditions are both homogeneous, so we need to homogenize the non-homogeneous boundary conditions. The temperature function is expressed as the following form:

$$T\left( {x,t} \right) = u\left( {x,t} \right) + w\left( {x,t} \right)$$
(14)

where w(x,t) is the selected known function and satisfies the Eqs. (11) and (12). The simplest selection method is the linear function of x as follows:

$$w\left( {x,t} \right){ = }A\left( t \right)x + B\left( t \right)$$
(15)

Substituting the boundary conditions into Eq. (15), the following equation can be obtained:

$$\left\{ {\begin{array}{*{20}c} {A\left( t \right) = \frac{{T_{b2} \left( t \right) - T_{b1} \left( t \right)}}{L}} \\ \quad \quad {B\left( t \right){ = }T_{b1} \left( t \right)} \\ \end{array} } \right.$$
(16)

where L is the length of the ball screw.

Substituting the Eq. (16) into the Eq. (15), so the w(x,t) can be expressed as

$$w\left( {x,t} \right){ = }\frac{{T_{b2} \left( t \right) - T_{b1} \left( t \right)}}{L}x + T_{b1} \left( t \right)$$
(17)

Substituting Eqs. (14) and (15) into Eq. (8), the following equation can be obtained:

$$\frac{{\partial^{2} u\left( {x,t} \right)}}{{\partial x^{2} }} - \frac{{\partial u\left( {x,t} \right)}}{\partial t} = \frac{\rho c}{\lambda }\frac{{\partial w\left( {x,t} \right)}}{\partial t}$$
(18)

As for Eq. (18), it is a non-homogeneous differential equation under homogeneous boundary conditions. So we need to solve the homogeneous analytical solution of the equation. We solve the homogeneous analytical solution of Eq. (19), and the Eq. (19) can be obtained as follows:

$$u\left( {x,t} \right){ = }u_{1} \left( {x,t} \right) + u_{2} \left( {x,t} \right)$$
(19)

where u1(x, t) is the solutions of homogeneous partial differential equations under homogeneous boundary conditions. u2(x, t) is the solutions of non-homogeneous partial differential equations under homogeneous boundary conditions.

$$\left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} u_{1} \left( {x,t} \right)}}{{\partial x^{2} }} - \frac{{\partial u_{1} \left( {x,t} \right)}}{\partial t} = 0} \\ {u_{1} \left( {0,t} \right) = 0} \\ {u_{1} \left( {L,t} \right) = 0} \\ {u_{1} \left( {x,0} \right) = T_{0} - w\left( {x,0} \right)} \\ \end{array} } \right.$$
(20)
$$\left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} u_{2} \left( {x,t} \right)}}{{\partial x^{2} }} - \frac{{\partial u_{2} \left( {x,t} \right)}}{\partial t} = \frac{\rho c}{\lambda }\frac{{\partial w\left( {x,t} \right)}}{\partial t}} \\ {u_{2} \left( {0,t} \right) = 0} \\ {u_{2} \left( {L,t} \right) = 0} \\ {u_{2} \left( {x,0} \right) = 0} \\ \end{array} } \right.$$
(21)

First, we solve the relatively simple homogeneous partial differential equations. Suppose u1(x,t) = Y1(x) F1(t), then Eq. (20) can be expressed by the method of separating variables as follows [35]:

$$\frac{1}{{Y_{1} \left( x \right)}} \cdot \frac{{d^{2} Y_{1} \left( x \right)}}{{dx^{2} }} = a\frac{1}{{F_{1} \left( t \right)}} \cdot \frac{{dF_{1} \left( t \right)}}{dt}$$
(22)

where a represents ρc/λ.

If the above equation is true, then both sides must be equal to the same constant (-ω2); then the following equation can be obtained:

$$\frac{1}{{Y_{1} \left( x \right)}} \cdot \frac{{d^{2} Y_{1} \left( x \right)}}{{dx^{2} }} = a\frac{1}{{F_{1} \left( t \right)}} \cdot \frac{{dF_{1} \left( t \right)}}{dt}{ = } - \omega^{2}$$
(23)

Therefore, we can get two differential equations from Eq. (23) as follows:

$$\left\{ {\begin{array}{*{20}c} {\frac{{d^{2} Y_{1} \left( x \right)}}{{dx^{2} }} + \omega^{2} Y_{1} \left( x \right) = 0} \\ {a\frac{{dF_{1} \left( t \right)}}{dt} + \omega^{2} F_{1} \left( t \right){ = }0} \\ \end{array} } \right.$$
(24)

Solving the two differential equations in Eq. (24), then the solution result can be obtained:

$$\left\{ {\begin{array}{*{20}c} {Y_{r} \left( x \right) = \sin \frac{r\pi }{L}x,r = 1,2,3...} \\ {F_{1} \left( t \right){ = }Ce^{{ - \frac{1}{a}\left( {\frac{\pi r}{L}} \right)^{2} t}} } \\ \end{array} } \right.$$
(25)

where C is the integral constant, which can be obtained by the boundary conditions.

Therefore, substituting the Eq. (25) into u1(x,t) = Y1(x)F1(t), So the solution of u1(x,t) can be expressed as

$$u_{1} \left( {x,t} \right) = \sum\limits_{r = 1}^{\infty } {Ce^{{ - \frac{{\omega^{2} t}}{a}}} } \sin \frac{r\pi }{L}x,r = 1,2,3...$$
(26)

Then we solve the non-homogeneous partial equations under the homogeneous boundary by Fourier series expansion method [36]. Taking the solution of Eq. (20) as the eigenfunction which is sin(πrx /L), so the Fourier series of the result and the inhomogeneous term at the right end are expanded as follows:

$$u_{2} \left( {x,t} \right) = \sum\limits_{r = 1}^{\infty } {q_{r} } \left( t \right)\sin \frac{\pi r}{L}x$$
(27)
$$\left\{ {\begin{array}{*{20}c} {f\left( {x,t} \right) = \sum\limits_{r = 1}^{\infty } {f_{r} \left( t \right)} \sin \frac{\pi r}{L}x} \\ {f_{r} \left( t \right) = \frac{2}{L}\int_{0}^{L} {f\left( {x,t} \right)\sin \frac{\pi r}{L}xdx} ,r = 1,2,3...} \\ \end{array} } \right.$$
(28)

Then substituting Eqs. (27) and (28) into Eq. (21), the following equation can be obtained:

$$\sum\limits_{r = 1}^{\infty } {\left[ { - \left( {\frac{\pi r}{L}} \right)^{2} q_{r} \left( t \right)\sin \frac{\pi r}{L}x} \right]} - \sum\limits_{r = 1}^{\infty } a q_{r}^{\prime } \left( t \right)\sin \frac{\pi r}{L}x = \sum\limits_{r = 1}^{\infty } {f_{n} \left( t \right)} \sin \frac{\pi r}{L}x$$
(29)

By simplifying the Eq. (29), the following formula can be obtained:

$$q_{r}^{\prime } \left( t \right) + \frac{{\pi^{2} r^{2} }}{{aL^{2} }}q_{r} \left( t \right) - \frac{{f_{r} \left( t \right)}}{a} = 0,r = 1,2,3...$$
(30)

First, by solving the homogeneous solution of the differential equation corresponding to Eq. (30) and the Eq. (31), it can be obtained as follows:

$$q_{r} \left( t \right) = C_{1} \cdot e^{{ - \frac{{\pi^{2} r^{2} }}{{aL^{2} }}t}}$$
(31)

Then we use the constant variation method to solve the special solution of Eq. (30). Supposed C1 = h(t), then Eq. (31) can be expressed as follows:

$$q_{r} \left( t \right) = h\left( t \right) \cdot e^{{ - \frac{{\pi^{2} r^{2} }}{{aL^{2} }}t}} ,r = 1,2,3...$$
(32)

Substituting Eq. (32) and its derivative result into Eq. (32), the following formula can be obtained:

$$h^{\prime}\left( t \right) \cdot e^{{ - \frac{{\pi^{2} r^{2} }}{{aL^{2} }}t}} - h\left( t \right) \cdot \frac{{\pi^{2} r^{2} }}{{aL^{2} }}e^{{ - \frac{{\pi^{2} r^{2} }}{{aL^{2} }}t}} + h\left( t \right)\frac{{\pi^{2} r^{2} }}{{aL^{2} }}e^{{ - \frac{{\pi^{2} r^{2} }}{{aL^{2} }}t}} - \frac{{f_{r} \left( t \right)}}{a} = 0,r = 1,2,3...$$
(33)

The solution results of h(t) are as follows:

$$h\left( t \right) = \int {\frac{{f_{r} \left( t \right)}}{a}e^{{\frac{{\pi^{2} r^{2} }}{{aL^{2} }}t}} } dt,r = 1,2,3...$$
(34)

So the solution of qr(t) can be obtained as follows:

$$q_{r} \left( t \right) = \left( {\int {\frac{{f_{r} \left( t \right)}}{a}e^{{^{{\frac{{\pi^{2} r^{2} }}{{aL^{2} }}t}} }} dt} } \right) \cdot e^{{^{{ - \, \frac{{\pi^{2} r^{2} }}{{aL^{2} }}t}} }} ,r = 1,2,3...$$
(35)

So the solution of the u2(x, t) can be obtained as follows:

$$u_{2} \left( {x,t} \right) = \sum\limits_{r = 1}^{\infty } {\left( {\int {\frac{{f_{r} \left( t \right)}}{a}e^{{^{{\frac{{\pi^{2} r^{2} }}{{aL^{2} }}t}} }} dt} } \right) \cdot e^{{^{{ - \, \frac{{\pi^{2} r^{2} }}{{aL^{2} }}t}} }} } \cdot \sin \frac{\pi rx}{L}$$
(36)

Substituting Eqs. (17), (26) and (36) into Eq. (14), under considering the influence of bearing heat source, the temperature rise of the lead screw can be obtained:

$$\begin{aligned}T\left( {x,t} \right) & = \left[ {\frac{{T_{b2} \left( t \right) - T_{b1} \left( t \right)}}{L}x + T_{b1} \left( t \right)} \right] \\ & + \sum\limits_{r = 1}^{\infty } {\left( {C + \int {\frac{{\lambda f_{r} \left( t \right)}}{\rho c}e^{{^{{\frac{\lambda }{\rho c}\frac{{\pi^{2} r^{2} }}{{L^{2} }}t}} }} dt} } \right) \cdot e^{{^{{ - \frac{\lambda }{\rho c}\frac{{\pi^{2} r^{2} }}{{L^{2} }}t}} }} \cdot } \sin \frac{r\pi x}{L}\end{aligned}$$
(37)

Then, considering the influence of the uniform thermal boundary of the nut on the temperature rise of the ball screw, Eq. (13) is substituted into Eq. (3), and through the law of conservation of energy, Eq. (38) can be obtained as follows:

$$\begin{aligned}\frac{{0.12\pi nL_{b} \left[ {F_{a} \left( {1 - \eta^{2} } \right) + F_{p} \left( {1 - \eta } \right)} \right]t}}{2\pi \eta }& = \left( {c_{2} m_{2} + h_{s} A_{s} t} \right)\left( {T - T_{0} } \right)\\& + h_{c} A_{c} \left( {T_{nut} - T_{{^{0} }} } \right)t\end{aligned}t$$
(38)

After simplifying and separating Eq. (38), the temperature rise of the ball screw can be obtained:

$$\Delta T = \frac{{0.12\pi nL_{b} \left[ {F_{a} \left( {1 - \eta^{2} } \right) + F_{p} \left( {1 - \eta } \right)} \right] \times t/2\pi \eta - h_{c} A_{c} \left( {T_{nut} - T_{{^{0} }} } \right)t}}{{c_{2} m_{2} + h_{s} A_{s} t}}$$
(39)

where c2 is the specific heat capacity of the ball screw; m2 is the mass of the ball screw; hc [37] is the convective heat transfer coefficient of the nut; Ac is the surface area of the nut assembly; Fp is the preload of the nut pair of the ball screw; Lb is the lead of the ball screw; η is the efficiency of the ball screw pair; Fa is the axial load; As is the surface area of the ball screw; and hs is the convective heat transfer coefficient of the ball screw.

$$\begin{aligned} T\left( {x,t} \right) & = \left[ {\frac{{T_{b2} \left( t \right) - T_{b1} \left( t \right)}}{L}x + T_{b1} \left( t \right)} \right] + \sum\limits_{r = 1}^{\infty } {\left( {C + \int {\frac{{\lambda f_{r} \left( t \right)}}{\rho c}e^{{^{{\frac{\lambda }{\rho c}\frac{{\pi^{2} r^{2} }}{{L^{2} }}t}} }} dt} } \right) \cdot e^{{^{{ - \frac{\lambda }{\rho c}\frac{{\pi^{2} r^{2} }}{{L^{2} }}t}} }} \cdot } \sin \frac{r\pi x}{L} \\ & + \frac{{0.12\pi nL_{b} \left[ {F_{a} \left( {1 - \eta^{2} } \right) + F_{p} \left( {1 - \eta } \right)} \right] \times t/2\pi \eta - h_{c} A_{c} \left( {T_{nut} - T_{{^{0} }} } \right)t}}{{c_{2} m_{2} + h_{s} A_{s} t}} \\ \end{aligned}$$
(40)

In summary, the temperature rise of the lead screw caused by the two types of heat sources is added together, and the temperature of the lead screw can be expressed as Eq. (40), and the change curve of the temperature of the ball screw with time and position is shown as Fig. 6.

Fig. 6
figure 6

The change curve of the temperature of the ball screw with time and position

Full size image

2.3 Thermal deformation analysis

From a macro perspective, the thermal effect of the ball screw shaft of the ball screw feed system is axial elongation. For the screw shaft, the principle can be shown in Fig. 7.

Fig. 7
figure 7

Schematic diagram of thermal expansion analysis of ball screw

Full size image
Fig. 8
figure 8

Distribution of measured points for the ball screw

Full size image

Consider a very small part of ΔL0 for analysis (ΔL0 is small enough) (Fig. 8). At time t, the temperature increases from T0 to T(x, t), the length extends to ΔL(x), and the point x moves to x(t). The axial deformation at position x can be obtained by Eq. (41) [38]:

$$x\left( t \right) - x = \int\limits_{0}^{x} {\alpha \left( {T\left( {x,t} \right) - T_{0} } \right)d} \delta$$
(41)

where α is the thermal expansion coefficient.

So the thermal expansion deformation of a ball screw with a length of L can be expressed as

$$\Delta L = L\left( t \right) - L = \int\limits_{0}^{L} {\alpha \left( {T\left( {x,t} \right) - T_{0} } \right)d} x$$
(42)

Substituting Eq. (40) into Eq. (42), the following equation can be obtained:

$$\Delta L = \int\limits_{0}^{L} {\alpha \left( \begin{array}{l} \left[ {\frac{{T_{b2} \left( t \right) - T_{b1} \left( t \right)}}{L}x + T_{b1} \left( t \right)} \right] + \sum\limits_{r = 1}^{\infty } {\left( {C + \int {\frac{{\lambda f_{r} \left( t \right)}}{\rho c}e^{{^{{\frac{\lambda }{\rho c}\frac{{\pi^{2} r^{2} }}{{L^{2} }}t}} }} dt} } \right) \cdot e^{{^{{ - \frac{\lambda }{\rho c}\frac{{\pi^{2} r^{2} }}{{L^{2} }}t}} }} \cdot } \sin \frac{r\pi x}{L} \\ + \frac{{0.12\pi nL_{b} \left[ {F_{a} \left( {1 - \eta^{2} } \right) + F_{p} \left( {1 - \eta } \right)} \right] \times t/2\pi \eta - h_{c} A_{c} \left( {T_{nut} - T_{{^{0} }} } \right)t}}{{c_{2} m_{2} + h_{s} A_{s} t}} - T_{0} \end{array} \right)d} x$$
(43)

3 Experimental verification of BSFS thermal error model

In the previous section, the temperature field model of the ball screw feed system has been established and solved analytically, and the temperature of the ball screw is obtained as a function of time and position. In order to verify the correctness of the model and the solution results, experiments are required verification. The correctness of the solution is verified by comparing the experimentally measured data with the theoretically calculated temperature. First, before the machine tool is started, measure the room temperature and record the initial temperature, and then select 3 points at 100 mm, 200 mm, and 400 mm on the lead screw as the test objects as shown in Figs. 2 and 7. Use an infrared thermal imager to measure the temperature of selected some points on the ball screw every 10 min and record it in Table 2.

Table 2 The temperature of the screw shaft at different positions
Full size table

Figure 9 shows the test measurement data at the 100-mm position of the ball screw and the theoretical simulation temperature versus time curve. Through calculation, it can be seen that the relative error between the test and the theoretical temperature is 10.38%, which is within the allowable tolerance within range.

Fig. 9
figure 9

Comparison of test and theoretical temperature of ball screw at 100 mm

Full size image

Figure 10 shows the experimental measurement data at the 200-mm position of the ball screw and the theoretical simulation temperature variation curve with time. Through calculation, it can be seen that the relative error between the experimental and theoretical temperature is 9.58%, which is within the allowable tolerance within range.

Fig. 10
figure 10

Comparison of test and theoretical temperature of ball screw at 200 mm

Full size image

Figure 11 shows the experimental measurement data at the 400-mm position of the ball screw and the theoretical simulation temperature change curve. Through calculation, it can be seen that the relative error between the experimental and theoretical temperature is 12.2%, which is within the allowable error within range.

Fig. 11
figure 11

Comparison of test and theoretical temperature of ball screw at 400 mm

Full size image

In summary, the relative errors between the experimental data and theoretical simulation data at three locations at 100 mm, 200 mm, and 400 mm that we selected are all less than 15%, which is within the allowable range of error, verifying the theoretical model and solution results.

4 Influencing factors of BSFS

In this section, the nut is taken as the research object, and its influence on the temperature field change and thermal deformation of the system is studied by changing some basic parameters [39]. It can be found from Eq. (23) that the parameters that affect the temperature rise of the system include speed, initial preload, lead, and axial load.

4.1 The influence of rotational speed

As shown in Fig. 10, the temperature rise of the ball screw varies with the speed. Here, three different speeds of 1000 r/min, 2000 r/min, and 3000 r/min are selected to study the speed of the ball screw feed system and its temperature impact of the field. It can be seen that as the rotation speed increases, the temperature of the ball screw gradually increases. It can also be found that the faster the rotation speed, the shorter the time to reach thermal equilibrium. Therefore, when the machine is preheated, a higher speed is used for preheating, and the thermal equilibrium is reached faster to improve the processing accuracy.

In Fig. 12, the maximum temperature rise of the lead screw during thermal equilibrium can be obtained. According to the thermal deformation Eq. (26), the thermal deformation of the lead screw can be calculated as shown in Table 3. It can be found that as the temperature increases, the thermal deformation gradually becomes larger.

Fig. 12
figure 12

The temperature rising and thermal deformation of the lead screw changes with the speed

Full size image
Table 3 Temperature rise and thermal deformation of the system at different speeds
Full size table

4.2 The influence of preload

Figure 13 shows the curve of the temperature rise of the ball screw with the initial preload. Three different initial preloads of 1000 N, 2000 N, and 3000 N are selected to study the preload of the ball screw feed system. The influence of its temperature field is as shown in Fig. 13. It can be seen that as the pre-tightening force increases, the temperature of the ball screw gradually increases.

Fig. 13
figure 13

The temperature rising and thermal deformation of the lead screw changes with the preload

Full size image

Table 4 shows the maximum temperature and the thermal deformation of different preload. It can be found that as the temperature increases, the thermal deformation gradually becomes larger. The influence of preload on the temperature rise and thermal deformation of the ball screw is greater than the influence of the speed.

Table 4 Temperature rise and thermal deformation of the system at different preload
Full size table

4.3 The influence of lead

Figure 14 shows that the lead of BSFS affects the temperature variation of the nut. Three different leads of 10 mm, 12 mm, and 15 mm are selected to study the lead of the ball screw feed system. As the lead of the ball screw increases, the temperature of the ball screw increases in general.

Fig. 14
figure 14

The temperature rising and thermal deformation of the lead screw changes with the lead

Full size image

Table 5 shows the maximum temperature and thermal deformation of different lead. It can be found that as the temperature increases, the thermal deformation gradually becomes larger. There is an approximately linear increase between the change in temperature rise and thermal deformation and the lead.

Table 5 Temperature rise and thermal deformation of the system at different preload
Full size table

4.4 The influence of Convection heat transfer coefficient

Figure 15 shows that the convection heat transfer coefficient of ball screw affects the temperature variation of the nut. Three different convection heat transfer coefficients of 100 W/(m2·℃), 250 W/(m2·℃), and 400 W/(m2·℃) are selected to study the convection heat transfer coefficient of the ball screw feed system. As the convection heat transfer coefficient of the ball screw increases, the temperature of the ball screw reduces in general.

Fig. 15
figure 15

The temperature rising and thermal deformation of the lead screw changes with the lead

Full size image

Table 6 shows the maximum temperature and thermal deformation of different convection heat transfer coefficient. It can be found that as the temperature increases, the thermal deformation gradually becomes smaller. There is an approximately linear reduce between the change in temperature rise and thermal deformation and the lead. Therefore, in order to reduce the influence of thermal deformation, the convection heat transfer coefficient should be increased as much as possible.

Table 6 Temperature rise and thermal deformation of the system at different convection heat transfer coefficient
Full size table

4.5 Experimental verification

In order to further verify the correctness of the model, we experimented to record the axial thermal deformation of the ball screw at different speeds and preloads and recorded them. Because the nut has been installed and fixed, it will no longer be experimentally verified. As shown in Fig. 16, we use the laser displacement sensor to measure the deformation of the end of the ball screw and recorded the data in Tables 7 and 8.

Fig. 16
figure 16

Experimental site

Full size image
Table 7 Comparison of test and theoretical value of influence of different rotation speed on thermal deformation of ball screw
Full size table
Table 8 Comparison of test and theoretical value of influence of different preload on thermal deformation of ball screw
Full size table

Through calculation, it can be found that the relative errors between the experimental measured value and the theoretical calculated value of the thermal deformation of the ball screw at different speeds and different preloads are within the allowable error within range; this shows that our simulation is reliable.

5 Conclusion

This paper solves the thermal error model of the ball screw by using the Fourier series expansion method and investigates the relationship between the temperature rise and thermal deformation of the ball screw. We got the temperature field model of the BSFS. Based on the results and analysis, some conclusions can be drawn as follows:

  1. 1.

    As time increases, the temperature of the lead screw gradually rises and finally reaches a thermal equilibrium state; as the length of the lead screw increases, the thermal elongation of the axis will increase.

  2. 2.

    As the speed, preload and lead increase, the temperature and thermal deformation of the ball screw gradually increase. The influence of preload on the temperature rising and thermal deformation of the ball screw is greater than the influence of the speed on it.