1 Introduction

For the sake of adapting to the ongoing shift from mass production to mass customization of products, manufacturing enterprises have to keep evolving their assembly lines to handle more product variation, shorter product life cycles, and smaller batch sizes [1,2,3], i.e., developing flexible assembly lines. Current industrial robots are notoriously difficult to program, leading to high change-over time and expert labor consumption. To make robotic assembly applicable to low-volume high-mix production, one approach is to make the programming of assembly tasks so intuitive that can be accomplished by workers without traditional robot programming skills [4, 5]. Learning from demonstration (LfD) [6], or programming by demonstration, is a paradigm that aims to transfer human’s skills to robots by human demonstration instead of the unintuitive and tedious robot programming by expert robot users [7]. The strength of LfD pays in industrial assembly applications as some assembly processes are such complicate that can be neither easily scripted nor easily defined as an optimization problem, but can be easily demonstrated [8]. With LfD, one or more assembly policies can be learned from the demonstration data which can also generate robots’ actions under new conditions, i.e., enable robots’ adaptive behavior [9].

The robotic assembly processes, as exhibited in Fig. 1, can be divided into two consecutive phases based on the density feature of the demonstration data and variance of the demonstration trajectories. When the human operator performs an assembly demonstration, he/she may guide the end-effector from anywhere convenient to approach the fixed part as soon as possible. As a result, demonstration data in this process feature low density. Moreover, since the initial pose is random, profiles of the demonstrated trajectories deviate significantly from each other in this process. Afterwards, the human operator carefully adjusts the pose of the part in hand to a specific pose that is convenient for assembling the two parts. Then, the human operator assembles the part by delicately moving the end-effector. As a result, density of the data after the specific pose is relatively high. In this process, there are only small deviations among trajectories because they are constrained by the design of the two parts. Therefore, the two phases exhibit quite different data densities and trajectory variances. By taking the pose of the end-effector where the gripped part starts contacting with the fixed part as the cutting point, the assembly process before it is defined as the approaching phase and that after it is defined as the assembling phase. The cutting point is called the pre-assembly pose, as shown in Fig. 1. During the approaching phase, end-effector of the robot moves to the pre-assembly pose after picking up one part from some vessel, and the robot assembles one part to the other that is fixed somewhere in the assembling phase.

In the literature, one formulation of LfD-based parts assembly tasks is the peg-in-hole problem [10,11,12] which regards the assembly process as inserting a peg into a hole and the clearance between them is tight. In those works, the pegs (the gripped parts in Fig. 1) are always assumed to have been placed in contact with the holes (the fixed parts in Fig. 1). Those works focus on compensation of the motion error and relate to the assembly process in the assembling phase. Reinforcement Learning-based methods are widely applied to learn a decision making policy that maps states to actions through trial-and-error [13,14,15,16]. However, assembly motion during the assembling phase of skillful assembly tasks [8] may not be just inserting movement. Some LfD studies upon assembly applications regard the assembly tasks as the robot taking one part from somewhere and moving to some given goal pose [10, 17, 18]. A pre-structured policy [6] is learned through supervised [10] or unsupervised [17, 18] machine learning algorithm. Given novel initial and goal pose of the part, the policy generates smooth robot assembly motion trajectories or real-time control input to drive the robot to the goal pose. This formulation reduces the assembly tasks to a pick-and-place problem and can be deemed as a process in the approaching phase. To the best knowledge of the authors, no studies tried to provide an overall solution for the WHOLE assembly process, consisting of the consecutively approaching and assembling phases. The fundamental difficulty lies in how to formulate the two distinct phases by a single unified framework.

Fig. 1
figure 1

The whole assembly process consisting of the approaching and the assembling phases

Full size image

In this work, we focus on the small part assembly tasks and regard the robot LfD problem as a policy learning problem given multiple demonstrated robot assembly motion trajectories of one object. To accomplish such assembly tasks with robots, two constraints must be taken into account, namely the environment constraint and the object constraint. In the industrial fields, the environment constraint is introduced by the deployment of industrial agents such as placement of robots, sensors, and conveyors. It varies from line to line, or even from day to day in re-configurable assembly lines [2] and allows of large variation in the assembly motion of robots. Hence, the generalization ability of the learned policy matters in the approaching phase. The object constraint includes the assembly motion (position and orientation trajectories) required and the corresponding force and torque pattern throughout the assembly process. It is totally defined by the design of product. Therefore, generalization ability of the learned policy in the assembling phase is not so important as that in the approaching phase. By improving the task-parameterized Gaussian mixture model (TP-GMM) and task-parameterized Gaussian mixture regression (TP-GMR) algorithm, a unified robot LfD framework is tailored for skillful small parts assembly in this work. Two cascaded policies in Cartesian space are learned from separated demonstration data for the approaching and assembling phases, respectively. Contributions of this work go as follows. By taking the two constraints into account, a novel unified LfD framework for assembly applications that governs an assembly task as two assembly phases is developed with two cascaded policies that coupled position, orientation and force-torque (wrench) are learned separately to avoid the under-fitting problem. A switch strategy between the two policies is also applied to avoid unexpected jump between the trajectories generated by the two polices. The assembly policies are designed to couple the orientation and wrench information with the generated position trajectories which enjoys more robustness over the unique query variable trick and enables online trajectory adaptation.

Remained content of this article is organized follows. Section 2 expounds the proposed robot LfD assembly framework from system overview (Section 2.1) to policy learning (Section 2.2). Experiment verification of it lies in Section 3. Section 4 concludes this article.

Fig. 2
figure 2

Work flow of the robot LfD assembly framework

Full size image

2 Methodology

2.1 Framework overview

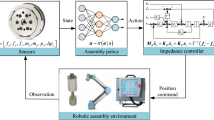
Work flow of the proposed robot LfD assembly framework is exhibited in Fig. 2. A typical LfD framework always contains three work steps, namely demonstration, policy learning and policy execution (under strange environments), that is, the first decision to be made when designing a LfD system is which demonstration technique is used given specific applications [6]. Here the kinesthetic teaching technique is selected for the sake of its usability for non-expert robot users. During demonstration, the operator successively performs the approaching motion and assembling motion. Afterwards, two assembly policies \(P_{app/ass}\) are learned given the separated demonstration data \(D_{app/ass}\). During the policy execution process, the learned polices serve to generate both position \(\hat{\xi }\) and orientation \(\hat{q}\) motion trajectories and the force/torque profile given new task parameters \(\{A,b\}\). As for robots’ execution of the policies given the initial, pre-assembly and goal pose, a Cartesian impedance controller, which takes the joint torque \(\tau\) as control input, serves to enact those policies.

2.2 Assembly policy

By an assembly policy, what we mean here is an assembly skill model that takes the initial pose, goal pose as inputs while generates a suitable robot motion trajectory as output. In assembly tasks, both position and orientation play important roles while the force and torque information (wrench) also matters. Policies related to position, orientation and wrench are separately learned but coupled in this work.

2.2.1 Position policy

Three elements ought to be considered to pre-structure the policy for assembly skill learning. First, as for modeling the assembly skills, the location primitives [18] are preferable to the trajectory primitives. This is because the robot ought to try to imitate the position/orientation pattern of the assembly demonstration data rather than the velocity pattern. Second, the stochastic models [6] instead of deterministic models are essential because there are always variances among each demonstration trajectories. And last but not least, the generalization capability [19] of the model is necessary since the task parameters may vary during both the policy learning and policy execution process. On accounting of these elements, the task-parameterized Gaussian mixture model (TP-GMM) [20] is taken to pre-structure the assembly policies and task-parameterized Gaussian mixture regression (TP-GMR) algorithm is used to generate the motion trajectories. Unfortunately, given the assembly tasks in Fig. 1 the classical TP-GMM together with TP-GMR algorithm exhibits poor performance owing to the two distinct phases. As shown in Fig. 8 GMM-based policies encapsulate the demonstration trajectories with multiple Gaussian distributions. Once there are small number of Gaussian distributions (\(K=8\) in the comparison experiment), the policy may fail to generate applicable trajectories. This is because there are not enough distributions to encapsulate the delicate motion in the assembling phase. In this case the policy is unreliable, let alone capable of generalization. However, the larger the number of Gaussian distribution is, the more redundant motion will be generated. In this case, the policy is inefficient and will lead to extra wearing of the robot. In summary, it is difficult to balance the efficiency and reliability of the classical TP-GMM-based policy.

Hence, in this work two parametric policies pre-structured by TP-GMM are learned respectively to model the two phases of the demonstrated assembly skill and generate the assembly motion trajectory by \(\alpha\)TP-GMR [19]. With TP-GMM, the position trajectory distribution \(P(\xi )\) of the assembly skill in the j-th task frame is modeled by

$$\begin{aligned} P\left( \xi ^{(j)}\right) =\sum _{k=1}^{K}\pi _{k}\mathcal {N}\left( \left. \xi ^{(j)} \right| \mu _{\xi ,k}^{(j)},\Sigma _{\xi ,k}^{(j)} \right) \end{aligned}$$

where \(\xi ^{(j)}\triangleq [t,x^{(j)},y^{(j)},z^{(j)}]^{\top }\) is the position in the j-th task frame at time/phase t, \(\pi _{k}\) is the prior of the k-th multivariate Gaussian distribution with \(\sum _{k=1}^{K}\pi _{k}=1\), \(\mu _{\xi ,k}^{(j)}\in \mathbb {R}^{4}\) and \(\Sigma _{\xi ,k}^{(j)}\in \mathbb {R}^{4\times 4}\) as centers and co-variances. The parameters of TP-GMM are summarized as

$$\begin{aligned} \left\{ \pi _{k}, \left\{ \mu _{\xi ,k}^{(j)}, \Sigma _{\xi ,k}^{(j)} \right\} _{j=1}^{J} \right\} _{k=1}^{K} \end{aligned}$$
(1)

The so-called task frames, or task parameters, are given by the J task frames \(\{A_{j}, b_{j}\}_{j=1}^{J}\) that are time-invariant in this work and practical industrial assembly tasks,

$$\begin{aligned} A_{j} = \begin{pmatrix} 1 &{} \mathbf {0} \\ \mathbf {0} &{} R_{j} \end{pmatrix},\quad b_{j} = \begin{pmatrix} 0 \\ p_{j} \end{pmatrix} \end{aligned}$$
(2)

in which \(R_{j} \in SO(3)\) and \(p_{j} \in \mathbb {R}^{3}\) are rotation matrix and translation vector of frame j with respect to the world frame. Given the demonstration data \(D: \{\xi _{n}\}_{n=1}^{N}\) in the world frame, rather than directly used to estimate the parameters, it is transformed to J task frames firstly through

$$\begin{aligned} \xi _{n}^{(j)} = A_{j}^{-1}(\xi _{n} - b_{j}) \end{aligned}$$

Parameters in (1) are estimated in each frame individually by Expectation-Maximization algorithm in which the joint distribution of data in J task frames are used to compute the expectation (E-Step) but parameters are estimated only with the data in the corresponding frame (M-Step).

By taking time/phase variable t as query variable, given the task frames (2), a retrieved or generalized assembly motion trajectory will be computed through TP-GMR algorithm [20]. Anyway, generalization (interpolation and extrapolation) capability of the approaching policy counts for much more than that of the precise assembly policy. In order to further boost the generalization capability of the approaching policy \(P_{app}\), i.e. to preserve the local structure of demonstration data around the approaching frame, the frame-weighted TP-GMR algorithm (\(\alpha\)TP-GMR) [19] is utilized here instead of the typical one. In the j-th frame, the Gaussian center \(\mu\) and covariance \(\Sigma\) can be partitioned as

$$\begin{aligned} \mu _{\xi ,k}^{(j)} = \begin{pmatrix} \mu _{t,k}^{(j)} \\ \mu _{\xi _{\mathcal {O},k}}^{(j)} \end{pmatrix}, \quad \Sigma _{\xi ,k}^{(j)} = \begin{pmatrix} \Sigma _{t,k}^{(j)} &{} \Sigma _{t\xi _{\mathcal {O}},k}^{(j)} \\ \Sigma _{\xi _{\mathcal {O}}t,k}^{(j)} &{} \Sigma _{\xi _{\mathcal {O},k}}^{(j)} \end{pmatrix} \end{aligned}$$

and the trajectory distribution in the jth frame generated by GMR is given by

$$\begin{aligned} \begin{aligned} P\left( \widehat{\xi }_{\mathcal {O},n}^{(j)} \vert t_{n} \right)&= \mathcal {N} \left( \sum _{k=1}^{K}\phi _{k}(t_{n}) \widehat{\xi }_{\mathcal {O},k,n}^{(j)}, \right. \\&\qquad \qquad \qquad \left. \sum _{k=1}^{K}\phi _{k}^{2}(t_{n})\widehat{\Sigma }_{\xi _{\mathcal {O}},k,n}^{(j)} \right) \end{aligned} \end{aligned}$$
(3)

where

$$\begin{aligned} \begin{aligned} \widehat{\xi }_{\mathcal {O},k,n}^{(j)}&= \mu _{\xi _{\mathcal {O}},k}^{(j)} + \Sigma _{\xi _{\mathcal {O}}t,k}^{(j)}\left( \Sigma _{t,k}^{(j)}\right) ^{-1}\left( t_{n}-\mu _{t,k}^{(j)}\right) \\ \widehat{\Sigma }_{\xi _{\mathcal {O}},k,n}^{(j)}&= \Sigma _{\xi _{\mathcal {O}},k}^{(j)}-\Sigma _{\xi _{\mathcal {O}}t,k}^{(j)}\left( \Sigma _{t,k}^{(j)}\right) ^{-1}\Sigma _{t\xi _{\mathcal {O}},k}^{(j)} \\ \phi _{k}(t_{n})&= \frac{\pi _{k}\mathcal {N}\left( t_{n} | \mu _{t,k},\Sigma _{t,k} \right) }{\sum _{l=1}^{K}\pi _{k}\mathcal {N}\left( t_{n} | \mu _{t,l},\Sigma _{t,l}\right) } \end{aligned} \end{aligned}$$

Then the generated trajectory distribution in the world frame is estimated by

$$\begin{aligned} \begin{aligned} \mathcal {N}\left( \widehat{\xi }_{\mathcal {O},n},\widehat{\Sigma }_{\xi _{\mathcal {O}},n}\right) \propto&\prod _{j=1}^{J}\mathcal {N}\left( R_{j}\widehat{\xi }_{\mathcal {O},n}^{(j)}+p_{j}, \right. \\&\qquad \qquad \qquad \left. \frac{1}{\alpha _{n}^{(j)}}R_{j}\widehat{\Sigma }_{\xi _{\mathcal {O}},n}^{(j)}R_{j}^{T} \right) \end{aligned} \end{aligned}$$

in which \(\widehat{\xi }_{\mathcal {O}}\) and \(\widehat{\xi }_{\mathcal {O}}^{(j)}\) are queried variable by GMR in world frame and the j-th task frame respectively (\([x,y,z]^{T}\) in this work), and \(\widehat{\Sigma }_{\xi _{\mathcal {O}}}\) stands for the corresponding co-variance. \(\alpha _{n}^{(j)}\) indicates the weight of the j-th task frame at step n,

$$\begin{aligned} \alpha _{n}^{(j)} = \frac{\left\| \left( \tilde{\Sigma }_{n}^{(j)}\right) ^{-1} \right\| }{\sum _{l=1}^{J}\left\| \left( \tilde{\Sigma }_{n}^{(l)}\right) ^{-1} \right\| } \end{aligned}$$
(4)

\(\tilde{\Sigma }_{n}^{(j)}\) in (4) is the covariance of demonstration data in the j-th task frame at time step n, computation of which costs additional effort but only required once after demonstration. As for the assembling policy \(P_{ass}\), typical TP-GMR algorithm (\(\alpha _{n}^{(j)} = 1\)) will work well since there is little variation in the profile of position trajectories in the assembling phase.

Anyway, generating the trajectories with two polices does not means simply performing the TP-GMR algorithm one by one. As indicated in Fig. 2, the pre-assembly frame \(\left\{ A_{pre}, b_{pre}\right\}\) is given in advance but destination of the motion generated by the approaching policy will not exactly be the pre-assembly pose. There may exist unexpected gap between the motion trajectories between the two phases which leads to redundant motion. To deal with this issue, a switch strategy between the two policies is proposed. To begin with, the last pose of the trajectories generated by the approaching policy is taken as the dummy pre-assembly frame utilized for the assembling policy. After generation of the trajectory of the whole assembly process, we calculate two cutting points by

$$\begin{aligned} \begin{aligned} \widehat{\xi }_{\mathcal {O},\tilde{n}_{app}}&= P_{app}\left( \arg \max _{k}\mu _{t,k}^{(j)}\right) \\ \widehat{\xi }_{\mathcal {O},\tilde{n}_{ass}}&= P_{ass}\left( \arg \min _{k}\mu _{t,k}^{(j)}\right) \end{aligned} \end{aligned}$$

where \(\mu _{t,k}^{(j)}\) refers to the first entry of the center \(\mu _{k}^{(j)}\) of the TP-GMM (1). That is to say, the center \(\mu _{k}^{(j)}\) of the temporally last Gaussian distribution of the approaching policy and that of the temporally first Gaussian distribution of the assembling policy are taken as the cutting points. Note that the first entry of the Gaussian center \(\mu _{\xi ,k}^{(j)}\) is the time/phase variable that are identical in each task frame. Then we interpolate \(\tilde{n}_{ass}\) positions between the two cutting points while get rid of the trajectories temporally after \(\widehat{\xi }_{\mathcal {O},\tilde{n}_{app}}\) and those before \(\widehat{\xi }_{\mathcal {O},\tilde{n}_{ass}}\).

2.2.2 Orientation policy

As one of the key aspects, it is inevitable to take the orientation trajectories required in many assembly tasks. In the literature, unit quaternion \(q \triangleq [q_{w}, q_{x}, q_{y}, q_{z}]^{\top }\) is a popular representation of orientation in LfD studies [10, 18, 21], which is a kind of non-minimal representation defined on an unit sphere manifold \(\mathcal {S}^{3}\) whose tangent space \(\mathcal {T}_{q}\mathcal {S}^{3}\) locally linearizes the manifold and behaves like Euclidean space \(\mathbb {R}^{3}\) [22]. Compared with minimal representations of orientation such as Euler angle, it benefits from no singularity. By taking the orientation of the pre-assembly or goal pose as auxiliary quaternion \(q_{a}\) [21], the demonstrated orientation data q can be transformed to the tangent space of \(q_{a}\) through the logarithmic map \(\mathcal {S}^{3} \rightarrow \mathcal {T}_{q_{a}}\mathcal {S}^{3}\)

$$\begin{aligned} \eta \triangleq \log (\tilde{q}) = \left\{ \begin{aligned}&\arccos (\tilde{q}_{w})\frac{\tilde{\mathbf {u}}}{\Vert \tilde{\mathbf {u}}\Vert },&\Vert \tilde{\mathbf {u}} \Vert \ne \mathbf {0} \\&[0,0,0]^{\top },&\text {otherwise} \end{aligned}\right. \end{aligned}$$
(5)

where \(\tilde{q} = q*\bar{q}_{a} \triangleq \left[ \tilde{q}_{w}, \tilde{\mathbf {u}}^{\top } \right] ^{\top }\) with \(\tilde{\mathbf {u}} \triangleq [\tilde{q}_{x}, \tilde{q}_{y}, \tilde{q}_{z}]^{\top }\) is the vector part of unit quaternion. \(\bar{q}_{a}\) denotes the quaternion conjugation of \(q_{a}\). \(*\) represents the quaternion multiplication operation [23]. \(\eta \in \mathcal {T}_{q_{a}}\mathcal {S}^{3} \subset \mathbb {R}^{3}\) is the projection of q in the tangent space of \(q_{a}\).

Fig. 3
figure 3

Graphic representation of the relationship between q and \(\eta\)

Full size image

Afterwards, policy learning (EM algorithm) and trajectory generation (GMR) processes are carried out on \(\mathcal {T}_{q_{a}}\mathcal {S}^{3}\) with Euclidean distance \(dist(\eta _{1}, \eta _{2}) = \Vert \eta _{1} - \eta _{2} \Vert\). Finally, orientation trajectories generated by the GMR ought to be projected back to the unit sphere manifold \(S^{3}\) via the exponential map \(\mathcal {T}_{q_{a}}\mathcal {S}^{3} \rightarrow \mathcal {S}^{3}\)

$$\begin{aligned} \tilde{q} = \exp (\eta ) = \left\{ \begin{aligned}&\cos \left( \left\| \eta \right\| \right) + \sin \left( \left\| \eta \right\| \right) \frac{\eta }{\left\| \eta \right\| }, \quad \eta \ne 0 \\&[1,0,0,0]^{T}, \qquad \qquad \text {otherwise} \end{aligned} \right. \end{aligned}$$
(6)

Figure 3 exhibits the relationship between q and \(\eta\). Note that both (5) and (6) are defined with respect to the same auxiliary unit quaternion \(q_{a}\).

Fig. 4
figure 4

Structure of the approaching policy

Full size image
Fig. 5
figure 5

Structure of the assembling policy

Full size image

In many assembly tasks, the coupling of position and orientation must be taken into consideration. In \(\mathcal {S}^{3}\) manifold, it is also feasible to make use of TP-GMM for generalization to new goal orientation [24]. By doing so, translation and rotation movements are coupled by the unique query variable. However, it is evident that during the approaching phase, orientation of the end-effector does not matter in the early phase but does matter around the vicinity of pre-assembly pose. Therefore, in this work the positions with respect to the pre-assembly and goal frame act as query for retrieving or generalizing the trajectories of orientation, i.e. rotation and translation movements are coupled by the covariance of multi-variate Gaussian distributions. Compared with coupling by the unique query variable, strength of the proposed coupling strategy lie in the fact that the robot may not exactly follow the generated assembly trajectories owing to the performance of controller, noise of sensors and perturbation, which makes online adaptation of orientation plays a valuable role. By doing so, we estimate the end-effector’s orientation given the current position rather than current time/phase. Figures 4 and 5 indicate the proposed coupling technique and describe the structure of the approaching policy and assembling policy respectively. Taking the output of (3) in pre-assembly frame or goal frame as query variable, state of the GMM is defined as \(\varphi \triangleq \left[ \xi _{\mathcal {O}}, \eta \right] ^{T}\), i.e. parameters of the GMM are \(\left\{ \pi _{\varphi ,k},\mu _{\varphi ,k},\Sigma _{\varphi ,k} \right\} _{k=1}^{K}\). Similar to (3), the orientation trajectory distribution generated by GMR turns out to be

$$\begin{aligned} \begin{aligned} P\left( \widehat{\eta }_{n} \left| \widehat{\xi }_{\mathcal {O},n}\right. \right)&= \mathcal {N}\left( \sum _{k=1}^{K}\phi _{k}\left( \widehat{\xi }_{\mathcal {O},n} \right) \widehat{\eta }_{k,n},\right. \\&\qquad \qquad \left. \sum _{k=1}^{K}\phi _{k}\left( \widehat{\xi }_{\mathcal {O},n} \right) ^{2}\widehat{\Sigma }_{\eta ,k,n} \right) \\ \widehat{q}_{n}&= \exp (\widehat{\eta }_{n})*q_{a} \end{aligned} \end{aligned}$$
(7)

where \(\widehat{\eta }_{n}\), \(\widehat{\Sigma }_{\eta ,k,n}\), \(\phi _{k}(\cdot )\) are counterparts of those in (3) and the number of Gaussian distributions K may not be the same as that in (1).

2.2.3 Wrench policy in the assembling phase

A typical assembly operation requires the knowledge of not only position and orientation trajectories but also the accompanying wrench profiles for successful assembly [10]. There is no probabilistic model in terms of the wrench w in the approaching policy since the end-effector of the robot is moving through the air as indicated by Fig. 1. In the assembling phase, the wrench pattern is modeled by GMM. As shown in Fig. 5, the wrench policy also takes position with respect to the goal frame as query variable. Wrench trajectory distribution generated by GMR shares the similar policy structure and coupling strategy as (7) just by replacing \(\widehat{\eta }\) by \(\widehat{w}\)

$$\begin{aligned} \begin{aligned} P\left( \widehat{w}_{n} \left| \widehat{\xi }_{\mathcal {O},n}\right. \right)&= \mathcal {N}\left( \sum _{k=1}^{K}\phi _{k}\left( \widehat{\xi }_{\mathcal {O},n} \right) \widehat{w}_{k,n},\right. \\&\qquad \qquad \left. \sum _{k=1}^{K}\phi _{k}\left( \widehat{\xi }_{\mathcal {O},n} \right) ^{2}\widehat{\Sigma }_{w,k,n} \right) \end{aligned} \end{aligned}$$
(8)

Anyway, there is no need to exactly follow the generated wrench trajectory during assembly processes [10]. In this work, the queried wrench trajectory distribution (8) plays two roles. First and foremost, it provides a reference wrench pattern for successful execution of the task since the parts require enough wrench to be assembled. Secondly, it also serves as an indicator of possible damaging of the parts. Variability of the demonstrations is encapsulated in the covariance matrices of the trajectory distribution which can be exploited to detect if the robot reaches an unexpected pose [25]. By eigenvalue decomposition of covariance matrix \(\widehat{\Sigma }_{w,n} = V\Lambda _{w,n} V^{-1}\), each eigenvalue \(\lambda _{i,t}\) corresponds to the allowable variability of the force/torque term at time/phase \(t_{n}\). In the experiment, we stop motion of the robot once any one dimension of the current external wrench \(w_{i,t}\) exceeds the limit

$$\begin{aligned} \left[ \hat{w}_{i,t}-\beta |\lambda _{i,t}|, \hat{w}_{i,t}+\beta |\lambda _{i,t}|\right] , \beta > 1 \end{aligned}$$

3 Experiment verification

3.1 Experiment setup

Fig. 6
figure 6

The PCB and bottom case of a cursor mouse

Full size image
Fig. 7
figure 7

Kinesthetic guiding demonstration process

Full size image

In this section, a printed circuit board (PCB) [26] assembly task is selected to demonstrate the work flow of the proposed robot LfD assembly framework and validate its effectiveness. As shown in Fig. 6, to successfully assemble the PCB to its bottom case, after plugging it through the scroll wheel holder the robot ought to carry out an insertion motion and then fit the PCB to the locating pins while pressing it to make it fastened by the resilient fasteners. The tolerance between the PCB and the bottom case is \(0.5\pm 0.1\)mm in the assembly process. A torque-controlled Franka Emika 7-DoF robot, whose position repeatability is \(\pm 0.1\)mm, serves as the policy executor. A structured light camera works to acquire the goal frame \(\{A_{goal},b_{goal}\}\) in the experiment, as exhibited by Fig. 7. The structured light camera is capable of obtaining 6-D pose of the bottom case. The initial pose of the PCB is obtained by forward kinematics of the robot. Figure 7 also demonstrates the kinesthetic teaching process. To begin with, the operator guides the robot with gravity compensation by the pilot on the robot’s 7th joint from arbitrary initial pose to the pre-assembly pose (the approaching phase). Afterwards, through carefully adjusting the pose of the end-effector to guarantee safety, the operator performs the PCB assembly task (the assembling phase).

In both the approaching and the assembling phases, the number of task frames \(J = 2\) in (1) as indicated by Fig. 2. The goal frame can be estimated via observing the pose of the bottom case with the 3D camera while the pre-assembly frame \(\{A_{pre},b_{pre}\}\) is calculated with the constant transformation from the goal frame to it. Let \(\{p_{pre}^{(m)},q_{pre}^{(m)}\}_{m=1}^{M}\) and \(\{p_{goal}^{(m)}, q_{goal}^{(m)}\}_{m=1}^{M}\) represent the M demonstrated pre-assembly and goal poses respectively. To estimate the transformation between the two poses, we take the average of both poses first. The average positions \(\bar{p}_{pre}\) and \(\bar{p}_{goal}\) can be simply calculated by

$$\begin{aligned} \bar{p}_{pre} = \frac{1}{M}\sum _{m=1}^{M}p_{pre}^{(m)}, \quad \bar{p}_{goal} = \frac{1}{M}\sum _{m=1}^{M}p_{goal}^{(m)} \end{aligned}$$

However, with regards to the average orientations (unit quaternions) we follow the method [27] and calculate

$$\begin{aligned} Q_{pre} = \sum _{m=1}^{M}q_{pre}^{(m)} \cdot {q_{pre}^{(m)}}^{\top },\quad Q_{goal} = \sum _{m=1}^{M}q_{goal}^{(m)} \cdot {q_{goal}^{(m)}}^{\top } \end{aligned}$$
(9)

Note that the multiplication operator “\(\cdot\)” in (9) represents quaternion dot product [23] (Euclidean inner product for vectors in \(\mathbb {R}^{4}\)) rather than quaternion multiplication. Afterwards, by applying principal component analysis (PCA) upon \(Q\in \mathbb {R}^{4\times 4}\) the normalized eigenvector corresponding to the largest eigenvalue is taken as the average quaternion which can be converted into rotation matrix \(\bar{R}\). Then given the estimated goal frame \(\{A_{goal},b_{goal}\}\) and recall the definition (2), we can calculate the pre-assembly frame through

$$\begin{aligned} \begin{aligned} A_{pre}&= A_{goal}\begin{pmatrix} 1 &{} \mathbf {0} \\ \mathbf {0} &{} \bar{R}_{goal}^{\top } \end{pmatrix} \begin{pmatrix} 1 &{} \mathbf {0} \\ \mathbf {0} &{} \bar{R}_{pre} \end{pmatrix}, \\ b_{pre}&= A_{goal}\begin{pmatrix} 0 \\ \bar{R}_{goal}^{\top }\bar{p}_{pre} - \bar{R}_{goal}^{\top }\bar{p}_{goal} \end{pmatrix} + b_{goal} \end{aligned} \end{aligned}$$

Since human operators can never perform one task multiple times within the same period, it is necessary to temporally align the demonstration data before policy learning. Dynamic time wrapping (DTW) is a populous temporal alignment method in LfD studies [18, 28, 29] including this work. With kinesthetic teaching, the human operator corrupts the wrench profile estimated by joints torques [10] in the assembling phase. To attenuate this effect, in this experiment the robot plays back the demonstrated motion in the assembling phase to obtain clean wrench demonstration data. Moreover, separation of demonstration data is performed manually, nonetheless, automatic separation is also possible by analyzing velocity and acceleration feature of it [8, 28].

Fig. 8
figure 8

The learned assembly policy for the approaching phase in the initial frame (a) and pre-assembly frame (b), and assembly policy for assembling phase in the pre-assembly frame (c) and goal frame (d). Each ellipsoid represents a Gaussian distribution \(\mathcal {N}(\mu _{\xi _{\mathcal {O}},k}^{(j)},\Sigma _{\xi _{\mathcal {O}},k}^{(j)})\). Coordinates of the centers are the means \(\mu _{\xi _{\mathcal {O}},k}^{(j)},k=1,2,\dots ,K\). Each ellipsoid has three semi-axes whose directions are along the eigenvectors of the co-variance matrix \(\Sigma _{\xi _{\mathcal {O}},k}^{(j)}\) and lengths equal to square roots of the corresponding eigenvalues. The grey curves are demonstration data within the approaching phase (a)-(b) and assembling phase (c)-(d). These ellipsoids are drawn in different color to be distinguishable from each other

Full size image
Fig. 9
figure 9

Demonstrated (grey) and retrieved (colored) position trajectories of the whole assembly process (left) and the assembling phase (right) in which “\(*\)” denotes the starting positions and “\(\circ\)” denotes the end positions of the retrieved trajectories. The frames indicate the given initial and goal frames

Full size image
Table 1 Lengths of the generated position trajectories in the demonstration retrieval experiment. The “Fail” indicates that end-effector of the robot collided with something in the environment unexpectedly when tracked the trajectory. (Unit: m)
Full size table
Fig. 10
figure 10

Demonstrated (grey), retrieved (blue) and recorded (orange) orientation profiles in the approaching phase

Full size image
Fig. 11
figure 11

Demonstrated (grey) and retrieved (blue) wrench profiles in the assembling phase. The recorded wrench profiles are not plotted since the wrench profile is not required to be tracked by the robot

Full size image

3.2 Cartesian impedance controller

In order to drive the robot tracking the assembly motion trajectories \(\left\{ \widehat{\xi }_{\mathcal {O}}, \widehat{q}\right\}\), the Cartesian impedance controller [9] is utilized in the experiment. With joint torque \(\tau\) as input, the controller turns out to be

$$\begin{aligned} \tau = \mathbf {J}^{T}\left( \mathbf {K} \begin{bmatrix} \widehat{\xi }_{\mathcal {O}} - \xi _{\mathcal {O}} \\ \log \left( \widehat{q} * \bar{q} \right) \end{bmatrix} - \mathbf {D} \begin{bmatrix} v \\ \omega \end{bmatrix} \right) - \mathbf {J}^{T}\hat{w} + h(\theta ,\dot{\theta }) \end{aligned}$$
(10)

where

$$\begin{aligned} \mathbf {K} = \begin{pmatrix} \mathbf {K}^{pos} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {K}^{ori} \end{pmatrix}, \quad \mathbf {D} = \begin{pmatrix} \mathbf {D}^{pos} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {D}^{ori} \end{pmatrix} \end{aligned}$$

are semi-positive definite matrices of impedance parameters. \(\mathbf {J}\) in (10) is the Jacobian and \(h(\cdot )\) represents dynamic model of the robot that allows for compensation of gravity, Coriolis force and friction. v and \(\omega\) stand for linear and angular velocities of the robot’s end-effector. \(\mathbf {J}^{T}\widehat{w}\) serves as a feed forward term. In the experiment, both \(\mathbf {K}\) and \(\mathbf {D}\) are set to be diagonal matrices, i.e.

$$\begin{aligned} K^{pos/ori} = \gamma ^{pos/ori}I,\quad D^{pos/ori} = \beta ^{pos/ori}I \end{aligned}$$

where \(\gamma ^{pos/ori} > 0\) and \(\beta ^{pos/ori}>0\). The control input \(\tau\) is fed to the robot controller at 1kHz. In the approaching phase, compared with compliance what makes greater sense for the controller is driving the robot to the approaching pose as soon as possible, that is, efficiency dominates. Hence, in this phase, high stiffness (\(\gamma ^{pos} = 6000\) and \(\gamma ^{ori} = \sqrt{\gamma ^{pos}}\)) is assigned to the controller and there is no feed forward term in the controller (10). The assembling phase puts an requirement on the compliance of the robot’s end-effector due to unavoidable position or orientation error and tight tolerances between the parts. During the assembling phase, stiff execution may not be safe for robots and objects in interaction [30]. Therefore, low stiffness (\(\gamma ^{pos} = 3000\) and \(\gamma ^{ori} = \sqrt{\gamma ^{pos}}\)) is assigned to the controller in operation to perform compliant assembly which is robust against motion inaccuracy and disturbance [31, 32]. In addition, the damping coefficients are \(\beta ^{pos} = 100, \beta ^{ori} = \sqrt{\beta ^{pos}}\) for both assembly phases in the experiment.

Fig. 12
figure 12

Demonstrated (grey) and generalized (colored) position data of the whole assembly process (left) and the assembling phase (right) where the blue one is generated by the proposed method, the orange one is generated by \(\alpha\)TP-GMR with \(K=8\), and the green one is generated by \(\alpha\)TP-GMR with \(K=13\). “\(*\)” denotes the starting positions and “\(\circ\)” denotes the goal positions of the assembly motion trajectories. The frames indicate the given initial and goal frames

Full size image

The n-th reference pose \(\left\{ \widehat{\xi }_{\mathcal {O},n}, \widehat{q}_{n}\right\}\) is fed to the robot controller constantly until the position tracking error \(\Vert \widehat{\xi }_{\mathcal {O}} - \xi _{\mathcal {O}}\Vert\) converges to a given threshold which is 0.0002m in the experiments. Data point in the generated assembly motion trajectory \(\left\{ \widehat{\xi }_{\mathcal {O},n}, \widehat{q}_{n}\right\} _{n=1}^{N}\) are tracked one by one. The impedance parameters of the controller are changed online without halting the motion of the robot.

3.3 Experiment results & discussion

Demonstrations are performed from randomly selected initial pose to an unique pre-assembly and goal pose. In this experiment, rather than absolute time a phase variable \(t\in [0,1]\) is selected as query variable for position data generation. Figure 8 exhibits the TP-GMM learned from the demonstration data via EM algorithm. The assembly polices for the approaching and assembling phases are learned separately and we assign \(K = 8\) in (1) for the former one and \(K=5\) for the latter one. The number of Gaussian distributions K is the only hyper-parameter of TP-GMM (1). In this experiment, the hyper-parameters of the assembly policies in the approaching and assembling phase are optimally and individually selected based the Bayesian information criterion (BIC) [33]. Moreover, the demonstrated motion in the assembling phase is much smaller than that in the approaching phase. This partially accounts for the necessity of separating the demonstration and learn two specific assembly policies. Some key motion in the assembling phase may be deemed to be noise once only one policy is learned to model the whole assembly process.

Table 2 Lengths of the generated position trajectories in the initial pose generalization experiment. (Unit: m)
Full size table
Fig. 13
figure 13

Orientation trajectories generated by the orientation policy (blue) and the recorded orientation trajectories (orange) during the approaching phase

Full size image

Figure 9 shows both the demonstrated and retrieved position trajectories of the whole assembly process (left) and assembling phase (right). Retrieval means generating the trajectories by the learned assembly policies given the same task frames (2) as the demonstrated ones [20]. Figure 9 (a) exhibits that position trajectories are retrieved by the proposed method. For comparison purposes, two TP-GMM [20] based assembly polices, whose \(K = 8\) and \(K = 13\) respectively, are exploited in the experiment as proposed in [17, 18]. The success rate and length of the generated position trajectory are taken as the performance indices to validate the reliability and efficiency of the proposed LfD method. For the sake of fairness, the orientation and wrench trajectories are also generated through the proposed orientation and wrench policy. And \(\alpha\)TP-GMR is also utilized for position trajectories generation, which is different from [17, 18]. Moreover, the K-means algorithm is used to initialize the parameters of the proposed policy and the policies for comparison. As shown by the orange curves in Fig. 9(b), some motion trajectories generated by typical \(\alpha\)TP-GMR with \(K=8\) fail to be feasible because some segments of them around the goal pose are outside the demonstration data. In the experiment, the PCB may contact with the bottom case in an undesired relative pose once follows those trajectories, which leads to assembly failure or even part damage. Though it has the same number of Gaussian distributions as the proposed approaching policy in the experiment, key positions of the demonstrated assembly are not encapsulated by it. However, when \(K = 13\), which equals to sum of that of our approach and assembling policy, TP-GMM with large number of Gaussian distributions can encapsulate not only key positions but also redundant motions in the demonstration data. The redundant motion represents the unnecessary movement of the PCB to be assembled to the bottom case. As indicated by the green curves in Fig. 9(c), there are more redundant motions generated by \(\alpha\)TP-GMR with \(K=13\) compared with the blue curves in Fig. 9(a). In the right figures of both Fig. 9(b) and (c), there are jagged curves around the beginning of the assembling phase. This is because the demonstration trajectories are jagged caused by the human operator’s repeatedly aligning pose of the PCB to the pre-assembly pose during the demonstration process. Lots of redundant demonstration motion are collected and then used to learn the TP-GMM-based policy. On the contrary, with the proposed LfD method those redundant motions are reduced. Table 1 presents the lengths of the retrieved position trajectories to quantitatively indicates the greater reliability and higher efficiency of the proposed LfD method compared with \(\alpha\)TP-GMR with \(K=8\) and \(K=13\). The success rate of \(\alpha\)TP-GMR with \(K=8\) is the lowest (\(<44.45\%\)), which is referred to as the under-fitting problem. Compared with lengths of the trajectories retrieved by \(\alpha\)TP-GMR with \(K=13\), those retrieved by the proposed method are shorter in each experiment episode. High efficiency is achieved by the proposed method, which leads to higher productivity in the robotic assembly applications. Note that it is not fair to compare the time consumption of these methods. This is because two impedance controllers of different parameters are used in the proposed method but cannot be used in the two comparison experiments since there is no pre-assembly pose defined therein. In Fig. 9 each initial position generated by \(\alpha\)TP-GMR does not coincides with the corresponding initial frame and so does the end position, as a result of which extra control periods are required for the end-effector of the robot to move to the initial pose.

Figure 10 exhibits the demonstrated, retrieved and recorded orientation trajectories in the approaching phase. As queried by the z-axis position in the pre-assembly frame, those trajectories converge to the orientation \([1,0,0,0]^{T}\) in the pre-assembly frame. Due to the same reason, the retrieved orientation trajectories (blue curves) overlap each other. As shown in Fig. 4, the orientation trajectories are retrieved in advance in this experiment. However, with the proposed coupling strategy, reference orientation can also be queried at any time step given current Cartesian position. This online adaptation technique can deal with unexpected perturbation during the assembly process. Figure 11 exhibits the demonstrated and retrieved wrench profiles in the assembling phase. Only one retrieved wrench profile is exhibited because the parts to be assembled do not vary among the experiment scenarios. As discussed in Section 2.2, we do not drive the robot tracking the wrench trajectory as it only serves as a feed forward term and safety indicator.

To verify the generalization capability of our proposed method, 4 novel initial poses are selected in the experiment. By generalization what we mean is to generate the trajectories by the learned policy given the task frames (2) outside the demonstration ones [20]. Here only the initial frames are changed in each experiment episode since the initial pose of the gripped part (PCB) may vary but the goal pose is kept fixed in the robotic assembly tasks as exhibited by Fig. 1. Figure 12 shows the position trajectories generated by the proposed LfD method (blue), \(\alpha\)TP-GMR with \(K=8\) (orange) and \(\alpha\)TP-GMR with \(K=13\) (green). The position trajectories generated by the proposed method contain less redundant motions than those generated by the other two policies in each experiment episode. Table 2 presents lengths of generalized trajectories, among which the ones generated by the proposed policy are the shortest in each experiment episode. Some segments of the orange curves in Fig. 12 are also outside the demonstration data around the pre-assembly pose. Figure 13 presents the generalized orientation trajectories (blue curves) via GMR and the recorded orientation trajectories during assembly process (orange curves). In contrast to Fig. 10, orientation data in Fig. 13 are plotted along the time sequence in the approaching phase due to the fact that variable z is not monotonously varying in these cases but the orientation policy (7) still works. In Figs. 10 and 13, it can be seen that during the approaching phase the recorded orientation trajectories quickly converge to the retrieved/generalized ones almost before the motion of position. This is mainly because the absolute value of the initial orientation error \(\log (\widehat{q}(0)*\bar{q}(0))\) in (10) is numerically much larger than that of position.

In the generalization experiment, only the initial frame varies. We can also change the goal frame by moving the mouse bottom case to another pose which will be estimated by the 3D camera as shown in Fig. 7. Anyway, the demonstration data within the approaching phase can only provide limited information about the environment, which means that unexpected collision with some objects, such as the holder of the 3D camera, may occur during the approaching phase. With TP-GMM-based policy, this problem can be solved by extra demonstration or correction demonstration from the human operator to adjust the parameters of the policy [33].

4 Conclusion

To enable robots quickly acquire new assembly skills in assembly lines, the learning from demonstration paradigm provides a flexible solution to transfer workers’ assembly skills to robots. A robot LfD framework is developed in this article for skillful industrial assembly applications. In this framework, the assembly task is divided into approaching and assembling phases, which is the key to avoid the potential under-fitting problem introduced by the large difference in variability of demonstration data between the two assembly phases. By exploiting the stochastic nature and generalization capability of TP-GMM, the demonstrated position data are modeled and retrieved through \(\alpha\)TP-GMR. The corresponding orientation and wrench are also queried by the position via GMM, which turns out to be an effective coupling strategy that enables online adaptation of orientation and wrench. A PCB assembly experiment is taken as illustration for the proposed robot LfD assembly framework. It indicates that the learned policies can generate feasible and efficient assembly position and orientation trajectories in both phases.