An energy-concentrated synchrosqueezing transform using a reassignment operator for the analysis of nonstationary signals

Abstract

The synchrosqueezing transform (SST) is a novel promising time–frequency analysis (TFA) method that has drawn increasing attention in the signal processing field. Compared with classical TFA methods, SST can provide a higher TF resolution and achieve the decomposition of intrinsic mode function more precisely, which can also benefit various engineering applications, e.g., fault diagnosis of machinery, mechanical intelligent manufacturing, and condition monitoring of machines. However, with the gradual understanding of SST, some drawbacks are recognized. One drawback is that when dealing with strongly frequency-modulated (FM) signals, the SST results smear heavily, which will lead to poor TF resolution and low-accuracy mode decomposition. To solve this problem, we propose a novel method combining the advantages of the SST and reassignment (RS) methods. First, we explore the theory of SST and RS from a geometric perspective and then propose a novel squeezing operator to enhance the TF resolution of SST results based on geometric relationships. Compared with SST, the theoretical analysis shows that the proposed method can provide a more energy-concentrated TF representation and achieve a higher TF resolution. Compared with RS, our proposed method can allow for signal reconstruction and mode decomposition. Numerical and real-world signals are employed to validate the effectiveness of the proposed method, such as bat echo signals, gravitational wave signals, and mechanical vibration signals.

1 Introduction

Rotating machinery, e.g., gas compressors, wind turbines, and aero-engines, occupies an important place in industrial fields. How to prevent severe breakdowns of these machinery has been a hot topic in industrial engineering [1, 2]. Bearing faults are one of the most common failures in rotating machinery [3]. Vibration signal-based processing is an effective method for bearing fault diagnosis [4, 5]. In practical engineering, the vibration signal recorded from rotating machinery under time-varying speed conditions usually tends to be strongly time-varying [6,7,8]. In the past few decades, time–frequency (TF) analysis (TFA) methods have drawn considerable attention for dealing with such a signal since TFA methods can characterize essential TF features closely related to the instantaneous operation of machinery [9, 10]. Conventional methods, e.g., short-time Fourier transform (STFT), wavelet transform (WT), and Wigner-Ville distribution (WVD), show powerful capabilities in dealing with the signals measured in industrial fields [11, 12]. However, restricted by the Heisenberg uncertainty principle or unexpected cross-terms, the TF results generated via conventional methods are often blurry, and it is impossible to provide a precise TF description for a time-varying signal [13]. Therefore, one challenging task of bearing fault diagnosis based on TFA methods is how to achieve highly concentrated results for time-varying signals. This is because a more concentrated method can help us to more precisely extract the bearing fault features.

The TFA method is an effective tool to analyze time-varying signals and draws considerable attention, as it can expand one-dimensional time series into a two-dimensional time–frequency plane. From this time–frequency plane, we can observe the time-varying features and achieve the decomposition of different components. Recently, the synchrosqueezing transform (SST) has become a promising TFA method for such purposes. The SST can greatly enhance the TF resolution of the classical TFA method and allow precise mode decomposition or signal reconstruction [6,7,8,9,10]. SST, as a popular TFA method, has been applied in many fields [11,12,13,14,15,16,17,18,19,20]. However, with the increasing understanding of SST, some drawbacks are recognized. One drawback of SST is that when dealing with strongly frequency-demodulated signals, the energy of TF representation generated by SST will smear heavily. To solve this problem, many energy-concentrated SST methods have been proposed in recent decades [8, 9, 14,15,16,17,18, 21,22,23,24,25]. In [8, 9], the authors proposed a two-step SST method, which first computes the demodulated version of time-varying signals and then uses SST technology to enhance the TF resolution of the first-step results. In [21, 22], an iteratively demodulated procedure is proposed so that the energy of TF representation can be concentrated step by step. In [23,24,25], based on the second-order model of a nonstationary signal, a one-step method was provided in the analysis of chirp-like signals.

Recently, some researchers proposed a novel TFA method called the synchroextracting transform (SET), which is able to achieve significant improvement in concentrating TF energy [26]. In theory, the SET is proposed as a postprocessing tool of the STFT. In many studies, it has been shown that the STFT can be regarded as a first-order TFA method, which means that the considered signal should be piecewise stationary in a short time [27]. Therefore, the SET method only works well in dealing with weakly time-varying signals. However, in industrial fields, practical signals often tend to be strongly time-varying and cannot meet the applied requirements of SET. Therefore, the TF results of strongly time-varying signals generated by the SET method may suffer from some heavy problems, e.g., blurry TF energy. SET employs an extracting operator to retain only the TF coefficients in the IF trajectory. Thus, an energy-concentrated representation can then be created from this postprocessing procedure. It is known that the SET can be regarded as a ridge detection result of the STFT. The ridge in the STFT cannot allow for perfect reconstruction for nonstationary signals. Therefore, the reconstruction of the SET only approximates the original signal instead of obtaining perfect recovery. Some new TFA methods employing a postprocessing procedure have been proposed, e.g., multisynchrosqueezing transform (MSST). MSST employs an iterative procedure to squeeze the STFT result, which intends to gradually enhance the energy concentration. However, the MSST uses the first-order IF estimator that offers an accurate estimate for purely harmonic signals. Hence, the MSST cannot be used for highly nonstationary signals. When signals recorded in the real world cannot meet the requirement of the purely harmonic assumption, the MSST fails to produce a satisfactory result for such signals.

To generate a concentrated representation for strongly time-varying signals, it is necessary to guarantee that the preprocessing TFA method is relatively concentrated. In many studies, it has been shown that the demodulated technique is an effective way to address strongly time-varying signals. The classical demodulated techniques include chirplet transform (CT) [28, 29], local polynomial transform (LPT) [30,31,32], general parameterized transform (GPT) [33], and matching demodulated transform (MDT) [34, 35].

Faced with complex real-world situations, it is found that most real-world signals cannot be suitably described by polynomial models, e.g., vibration signals of rotating machinery under unknown time-varying speeds [18,19,20]. To address more highly nonlinear signals, GPT, and MDT techniques suggest introducing more complex mathematical models to design the basis function, e.g., spline models and Fourier series models. These two demodulated techniques provide much more flexible solutions for characterizing a time-varying signal, which should be the best choice as the preprocessing method of the SET.

The reassignment (RS) method is a TFA method sharing a similar postprocessing manner with SST [5]. Although RS can generate a more energy-concentrated TF result than SST, it cannot allow signal reconstruction and mode decomposition. In this paper, inspired by RS technology, we propose a novel TFA method, termed energy-concentrated SST (ESST), which combines the advantages of SST and RS. First, we provide geometric explanations for SST and RS, which can help us to understand the postprocessing manner of SST and RS more clearly. Then, based on the geometric relationship, the ESST is proposed in the study.

2 The theory of the proposed method

2.1 STFT method

We start this study from the framework of STFT. The STFT of a function ${s}\in {L}^{2}(\mathbb{R})$ with respect to the real and even window ${g}\in {L}^{2}(\mathbb{R})$ is defined by

$${V}_{s}\left(t,\omega \right)={\int }_{-\infty }^{+\infty }g\left(u-t\right)\cdot s(u)\cdot {e}^{-i\omega (u-t)}du$$

(1)

where ${V}_{s}(t,\omega )$ is defined as the spectrogram of STFT. A multicomponent signal with amplitude-modulated (AM) and frequency-modulated (FM) laws can be modeled as

$$s\left(t\right)=\sum\limits_{k=1}^{n}{A}_{k}(t)\cdot {e}^{{i\varphi }_{k}(t)}$$

(2)

where ${A}_{\kappa }(t)$ and ${{\varphi }^{^{\prime}}}_{\kappa }(t)$ are assumed to be positive and slow-varying, respectively. ${A}_{\kappa }(t)$ and ${{\varphi }^{^{\prime}}}_{\kappa }(t)$ are called the instantaneous amplitude (IA) and instantaneous frequency (IF), respectively. IA and IF are two key features to understand the time-varying behaviors of the multicomponent signal. However, just from the time-series data, the instantaneous feature of a multicomponent signal cannot be characterized. The STFT expands a one-dimensional time-series signal into a two-dimensional time–frequency plane so that we can observe and extract the IA and IF information of the signal.

Another important application of the STFT is to reconstruct the monocomponent signal from a multicomponent signal. For Eq. (1), we calculate the integration with respect to frequency variable $\omega$; then, we obtain

$$\begin{array}{c}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_{-\infty}^{+\infty}V_s\left(t,\omega\right)d\omega=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g\left(u-t\right)\cdot s\left(u\right)\cdot e^{-i\omega(u-t)}dud\omega\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=2\pi\cdot\int_{-\infty}^{+\infty}g\left(u-t\right)\cdot s\left(u\right)\cdot\delta(u-t)du\\\;\;\;=2\pi g\left(0\right)\cdot s(t)\cdot\end{array}$$

(3)

Thus, the original signal s(t) can be reconstructed by

$${s\left(t\right)=(2\pi g(0))}^{-1}\cdot\int_{-\infty}^{+\infty}V_s(t,\omega)d\omega$$

(4)

According to [8], the STFT of a multicomponent signal s(t) can be approximately represented as

$${V}_{s}(t,\omega )\approx \sum\limits_{k=1}^{n}{A}_{k}\left(t\right){e}^{{i\varphi }_{k}\left(t\right)}\cdot\hat{g}(\omega -{\varphi}{^{\mathrm{{\prime}}}}_{k}(t))$$

(5)

where $\widehat{g}$ denotes the Fourier transform of the window. We take the spectrogram of ${V}_{s}(t,\omega )$, and (5) can be written as

$$\left|V_s\left(t,\omega\right)\right|\approx\sum_{k=1}^nA_k\left(t\right)\cdot\hat g\left(\omega-\varphi^{\mathrm{\prime}}_k\left(t\right)\right)$$

(6)

The STFT separation condition of signal s(t) is written as

$${{\varphi }^{\mathrm{{\prime}}}}_{k+1}\left(t\right)-{{\varphi }^{\mathrm{{\prime}}}}_{k}\left(t\right)>2\Delta$$

(7)

where $k\in \left\{1,\dots ,n-1\right\}$, and $\Delta$ denotes the frequency support of window $g$. Because $\widehat{g}$ is compact in the frequency domain, if the separation condition is satisfied, the different components can occupy distinct TF domains in the TF plane. Therefore, each component can be reconstructed by integrating the TF coefficients ${V}_{s}(t,\omega )$ around its IF ${{\varphi }^{^{\prime}}}_{\kappa }(t)$ in the frequency direction, i.e.,

$${{s}_{k}\left(t\right)=(2\pi g(0))}^{-1}\cdot{\int }_{\left|{{\omega -\varphi }^{\mathrm{{\prime}}}}_{k}(t)\right|\le \Delta }{V}_{s}(t,\omega )d\omega$$

(8)

2.2 RS method

However, the TF energy of the STFT spectrogram smears heavily, which will lead to a low TF resolution. To observe the time-varying TF features more precisely, RS technology is designed to improve the readability of TF representation. The RS expression is usually written as

$$Rm\left(v,\eta\right)=\int_{-\infty}^{+\infty}\left|V_s(t,\omega)\right|\cdot\delta\left(v-\widehat\omega\left(t,\omega\right)\right)\cdot\delta(\eta-\widehat t(t,\omega))dtd\omega$$

(9)

where $\delta$ denotes the Dirac distribution, and the reassignment operators $\widehat{\omega }(t,\omega )$ and $\widehat{t}(t,\omega )$ can be calculated as

$$\widehat{\omega }\left(t,\omega \right)=\omega -\mathrm{Im}\left(\frac{{V}_{s}^{{g}^{\mathrm{{\prime}}}}(t,\omega )}{{V}_{s}(t,\omega )}\right)$$

(10)

$$\widehat{t}\left(t,\omega \right)=t+\mathrm{Re}\left(\frac{{V}_{s}^{\mathrm{tg}}(t,\omega )}{{V}_{s}(t,\omega )}\right)$$

(11)

where ${V}_{s}^{{g}^{{\prime}}}(t,\omega )$ and ${V}_{s}^{tg}(t,\omega )$ can be regarded as the STFT using alternative windows, ${g}^{{\prime}}$denotes the derivative of $g(t)$ with respect to time, and $tg=t\cdot g(t)$. RS considers spectrogram $\left|{V}_{s}(t,\omega )\right|$ reassignment, so the RS result cannot be used to reconstruct the signals.

In Fig. 1, we give the STFT result and RS result of a linear FM signal. The spectrogram of the STFT suffers a low TF resolution, and the RS representation shows a high TF resolution. According to the findings of Professor Auger [5], RS has the ability to reassign the spectrogram energy into the IF trajectory of a linear FM signal so that the RS result can achieve an ideal TF location for a linear FM signal. Based on the reassignment manner of RS, we can build the corresponding geometric relationship, as shown in Fig. 2.

Fig. 1

(a) STFT result, (b) magnified STFT result, (c) RS result, and (d) magnified RS result

As shown in Fig. 2, we assume that $(t,\omega )$ is an arbitrary point in the TF plane and that $(\widehat{t}\left(t,\omega ),\widehat{\omega }\left(t,\omega \right)\right)$ is the corresponding reassignment operator and should be located in the IF trajectory. From a geometric perspective, RS reassigns the STFT spectrogram $\left|{V}_{s}(t,\omega )\right|$ into the TF position $(\widehat{t}\left(t,\omega ),\widehat{\omega }\left(t,\omega \right)\right)$ from a two-dimensional TF direction. Therefore, for a linear FM signal, RS can provide an ideal TF representation. Herein, we define the time-reassignment distance Dt and frequency reassignment distance $D\omega$ as Eq. (12), which will be used in the next subsection.

$$Dt=\widehat{t}\left(t,\omega \right)-t, D\omega =\widehat{\omega }\left(t,\omega \right)-\omega$$

(12)

2.3 SST

According to [6, 7], the SST expression is written as

$$St\left(t,\eta\right)=\int_{-\infty}^{+\infty}V_s\left(t,\omega\right)\cdot\delta(\eta-\omega_0(t,\omega))d\omega$$

(13)

Where

$${\omega }_{0}\left(t,\omega \right)=-i\cdot\frac{{\partial }_{t}{V}_{s}(t,\upomega )}{V(\mathrm{t},\upomega )}$$

(14)

Considering ${\mathrm{V}}_{\mathrm{s}}(\mathrm{t},\upomega )$ being written as Eq. (1), ${\partial }_{t}{V}_{s}(t,\upomega )$ can also be calculated by

$$\begin{array}{c}{\partial }_{t}{V}_{s}\left(t,\omega \right)={\partial }_{t}\left({\int }_{-\infty }^{+\infty }g\left(u-t\right)\cdot s\left(u\right) {e}^{-i\omega (u-t)}du\right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; =-{\int }_{-\infty }^{+\infty }{g}^{\mathrm{{\prime}}}\left(u-t\right)\cdot s\left(u\right) {e}^{-i\omega (u-t)}du\\ \begin{array}{c}\;\;\;\;\;\;\;\;\;\;\;\;+i\omega {\int }_{-\infty }^{+\infty }g\left(u-t\right)\cdot s\left(u\right) {e}^{-i\omega (u-t)}du\\ =-{V}_{s}^{{g}^{\mathrm{{\prime}}}}\left(t,\omega \right)+i\omega {V}_{s}(t,\omega )\end{array}\end{array}$$

(15)

Hence, ${\omega }_{0}(t,\omega )$ can be rewritten as

$${\omega }_{0}\left(t,\omega \right)=\omega +i \cdot\frac{{V}_{s}^{g\mathrm{^{\prime}}}(t,\omega )}{{V}_{s}(t,\omega )}$$

(16)

In practical calculation, it is necessary to take the real part of ${\omega }_{0}(t,\omega )$ so that it can be rewritten as

$${\omega }_{0}\left(t,\omega \right)=\omega -\mathrm{Im}\left(\frac{{V}_{s}^{{g}^{\mathrm{{\prime}}}}\left(t,\omega \right)}{{V}_{s}\left(t,\omega \right)}\right)$$

(17)

From expressions (10) and (17), ${\omega }_{0}\left(t,\omega \right)$ is equal to $\widehat{\omega }(t,\omega )$, which means that the SST can be regarded as a special case of RS because the SST only considers the reassignment in the frequency direction, i.e., $(t,\omega )\to (t,\widehat{\omega }(t,\omega ))$. The reassignment manner of SST can also be understood more clearly, as shown in Fig. 3. For a linear FM signal, the reassignment ability of SST is not enough to squeeze all TF coefficients into the IF region. In Fig. 5a, b, the SST result of a linear FM signal is displayed. The TF resolution of the SST result is higher than that of the STFT result but lower than that of the RS result.

Fig. 2

The reassignment manner of RS

A fundamental difference between SST and RS is that SST squeezes the TF coefficients ${V}_{s}(t,\omega )$ along the frequency direction whereas RS reassigns the TF spectrogram $\left|{\mathrm{V}}_{\mathrm{s}}(\mathrm{t},\upomega )\right|$ along the two-dimensional TF direction. According to expression (8), one can reconstruct the signal by integrating the TF coefficients ${\mathrm{V}}_{\mathrm{s}}(\mathrm{t},\upomega )$ around its IF ${{\varphi }^{{\prime}}}_{k}(t)$ in the frequency direction. The SST is a technology that only considers frequency reassignment so that we can reconstruct the signal using an expression similar to Eq. (8), as follows:

$${s}_{k}\left(t\right){=(2\pi g(0))}^{-1} \cdot{\int }_{\left|{{\omega -\varphi }^{\mathrm{{\prime}}}}_{k}(t)\right|\le \mathrm{ds}}St(t,\omega )d\omega$$

(18)

where ds denotes the bandwidth of SST. Due to the ability of signal reconstruction, the SST can be used in the applications of signal denoising, data compression, and intrinsic mode decomposition. This point is a superior aspect of SST over that of RS because the RS result cannot be used to recover the time-series signal.

2.4 Energy-concentrated SST

Although the SST allows for reconstructing original signals, it has to suffer a low-TF resolution because it only considers frequency reassignment. Herein, a question arises as to why we cannot utilize the reassignment operator of the RS method to enhance the SST result and why the signal reconstruction ability can be reserved simultaneously. Before achieving this goal, we need to identify two key distinctions between RS and SST, i.e. the issue of TF resolution and the issue of signal reconstruction. RS can generate a high-resolution TF result because it employs a two-dimensional reassignment operator applied to the spectrogram $\left|{\mathrm{V}}_{\mathrm{s}}(\mathrm{t},\upomega )\right|$. However, the spectrogram-based RS result cannot be used to recover the time-series signal because no signal reconstruction expression of the STFT is available based on the spectrogram result. According to reconstruction expression (4) of the STFT, if we want to reconstruct the monocomponent modes contained in a signal, we need to calculate the integration of the STFT result along the frequency direction. For the STFT-based postprocessing reassignment technology, the way to possess the ability of signal reconstruction is to only consider the frequency reassignment, which should be the most important significance to propose SST as indicated by Professor Daubechies et al. [6]. Therefore, the SST can be understood as follows: as a similar method to RS, the SST sacrifices the TF resolution to reobtain the ability of signal reconstruction so that the monocomponent mode can be decomposed out to achieve a similar goal as the empirical mode decomposition method. Now, we reconsider the question of how to utilize the reassignment operator of RS to enhance the SST result. To resolve this question, we first rebuild a new geometric relationship, as shown in Fig. 4.

Fig. 3

The reassignment manner of SST

Figure 4 demonstrates the reassignment manner of RS $\left(t,\omega \right)\to (\widehat{t}\left(t,\omega \right),\widehat{\omega }(t,\omega ))$ and SST $(t,\omega )\to (t,\widehat{\omega }(t,\omega ))$. Because the operator $(\widehat{t}\left(t,\omega \right),\widehat{\omega }(t,\omega ))$ is located in the IF trajectory, RS can generate a more energy-concentrated TF result than SST, which only considers the frequency reassignment. The geometric relationship in Fig. 4 inspires us to utilize the time-reassignment distance $\mathrm{ Dt}$ of RS to extend the frequency reassignment distance $\mathrm{ D\omega }$ of SST. The extended frequency distance is denoted as $\mathrm{dx}$, and we assume that the TF point $(t,\widehat{\omega }\left(t,\omega \right)+dx)$ can be located in the IF trajectory. Thus, we obtain the following equation:

$$dx=\tan\;\alpha\cdot Dt$$

(19)

Now, an essential question is how to calculate the value of $\mathrm{tan}\alpha$. Actually, the angle $\alpha$ denotes the IF slope of the linear FM signal. For a linear FM signal, the operator $(\widehat{t}\left(t,\omega \right),\widehat{\omega }(t,\omega ))$ can be located in the IF trajectory, and an adjacent operator $(\widehat{t}\left(t,\omega +\Delta \omega \right),\widehat{\omega }(t,\omega +\Delta \omega ))$ should also be located in the IF trajectory. According to this geometric relationship, $\mathrm{tan}\alpha$ can be calculated by

$$\tan\;\alpha=\frac{\widehat\omega\left(t,\omega+\Delta\omega\right)-\widehat\omega(t,\omega)}{\widehat t\left(t,\omega+\Delta\omega\right)-\widehat t(t,\omega)}$$

(20)

Therefore, to make the original SST result more energy-concentrated, we use the new squeezing operator $\widehat{\omega }\left(t,\omega \right)+\mathrm{tan}\alpha \cdot Dt$ to substitute the original squeezing operator $\widehat{\omega }(t,\omega )$, and the novel SST method can be written as

$$RTs\left(t,\eta \right)={\int }_{-\infty }^{+\infty }{V}_{s}\left(t,\omega \right) \cdot\delta (\eta -(\widehat{\omega }\left(t,\omega \right)+\mathrm{tan\;\alpha }\cdot Dt))d\omega$$

(21)

This novel method is named energy-concentrated SST (ESST). In Fig. 5c–d, we give the ESST result of the abovementioned linear FM signal. The TF representation is more concentrated than the SST result. Because the ESST only considers the reassignment of TF coefficients in the frequency direction, it allows signal reconstruction by

$${s}_{k}\left(t\right){=(2\pi g(0))}^{-1}\cdot{\int }_{\left|{{\omega -\varphi }^{\mathrm{^{\prime}}}}_{k}(t)\right|\le dr}RTs(t,\omega )d\omega$$

(22)

For the signal reconstruction expressions (8), (18) and (22), the regions $\omega \in [{{\varphi }^{{\prime}}}_{k}\left(t\right)-\Delta ,{{\varphi }^{{\prime}}}_{k}\left(t\right)+\Delta ]$, $\omega \in [{{\varphi }^{{\prime}}}_{k}\left(t\right)-ds,{{\varphi }^{{\prime}}}_{k}\left(t\right)+ds]$ and $\omega \in [{{\varphi }^{{\prime}}}_{k}\left(t\right)-dr,{{\varphi }^{{\prime}}}_{k}\left(t\right)+dr]$ are called the reconstruction regions of the STFT, SST, and ESST, respectively. ESST can generate the most energy-concentrated TF representation, such that the corresponding reconstruction region should be the most compact, which can also be understood as $dr\le ds\le \Delta$.

To estimate the ridges of the TFR, the following procedure is employed in this study. In most studies on SST, the ridge detection method has been accepted as an effective tool to detect IF trajectories, that is,

$$E\left(\phi \right)=-{\int }_{-\infty }^{+\infty }{\left|TFR\left(t,{\phi }_{k}\left(t\right)\right)\right|}^{2} dt+{\int }_{-\infty }^{+\infty }{(\lambda \cdot {\phi }_{k}^{\mathrm{{\prime}}}(t)}^{2}+\beta \cdot {{\phi }_{k}\left(t\right)}^{2})dt$$

(23)

where $(t,{\phi }_{k}(t))$ is the estimation of the IF trajectories in the TF plane, and $\lambda$ and $\beta$ are two parameters to adjust the level of regularization. According to Eq. (23), the IF of the mode with the largest energy is first detected. After one IF trajectory is estimated, the corresponding TF coefficients are set to zero. Then, the retained TF representation is substituted into Eq. (23). By this iterative procedure, the IF trajectories of all active modes can be estimated one by one. In summary, the whole procedure of the adaptive mode decomposition method based on the proposed ESST can be summarized as follows.

3 Numerical validation

In this subsection, we utilize several numerical signals to compare the performance of STFT, SST, RS, and ESST in energy concentration and signal reconstruction.

3.1 The first case

The first numerical signal is considered a summation of three components with distinct linear FM laws and the same AM trend.

$$\begin{array}{c}\;\;C_1\left(t\right)=\sin(2\pi(4t))\\\;\;\;\;\;\;\;\;\;\;\;\;C_2(t)=\sin(2\pi(7t+2.5t^2))\\\;\;\;\;\;\;\;\;\;\;\;C_3(t)=\sin(2\pi(11t+5t^2))\end{array}$$

(24)

From Eq. (23), we know that signal C1 is a harmonic component $(IF=4 Hz)$, the FM law of signal C2 is stronger $(IF=7+5t Hz)$, and signal C3 has the strongest FM law $(IF=11+10t Hz)$. The TF representations generated by STFT, SST, RS, and ESST are displayed in Fig. 6. The energy of the STFT result (see Fig. 6a) smears around the IF with poor TF resolution. For the SST result (see Fig. 6b), the weak FM component (C1) looks more energy-concentrated than the strong FM component (C3). With increasing FM law, the SST result smears more heavily, which means that the SST cannot deal with a strong FM signal effectively. For the RS result and ESST result (see Fig. 6c–d), all the components are energy-concentrated. For quantitative comparison, the Rényi entropy is employed to evaluate the performance of different methods. It is well known that a lower value of Rényi entropy denotes a more energy-concentrated TF representation. The corresponding Rényi entropy values are listed in Table 1. It is shown that compared with the STFT, the SST can greatly improve the energy concentration. However, to ensure that different modes can be decomposed out, the SST only considers frequency reassignment, which leads to the TF representation of the strong FM component being very blurred. This means that for a strong FM signal, the one-dimensional reassignment of SST is not enough to work well. RS technology is based on two-dimensional TF reassignment, so the corresponding TF result can concentrate on the IF more highly. However, the reassignment manner of RS has to lose the ability of signal reconstruction. From the Rényi entropy, we can see that our proposed method can provide an energy-concentrated TF result similar to the RS result; furthermore, the TF representation can be used to decompose each monocomponent mode. Moreover, the computational time of various methods is proposed in Table 2. The proposed ESST has a very low-computational burden.

Table 1 The Rényi entropy of different TFA results

Table 2 Required computation time

Herein, we test the reconstructed performance of SST and ESST. The SST and ESST are intended to reassign all TF coefficients into the IF trajectory. Therefore, for reconstruction Eqs. (18) and (22), we first let $\mathrm{dr}=\mathrm{ds}=0$, i.e., just using the TF coefficient in the IF trajectory to reconstruct each monocomponent. The IF trajectory can be estimated using the ridge detection method [1]. The reconstructed results of SST and ESST are shown in Fig. 7a, b, respectively (the black solid line is the original component, and the red dotted line denotes the recovered component). For the harmonic component (C1), both of these methods can provide a satisfactory reconstructed result. However, for the time-varying component (C2 and C3), the reconstructed result by ESST is much closer to the original signal than that by SST.

Fig. 4

The reassignment manner of the proposed method

In Fig. 7, using only the TF coefficient in the IF trajectory to recover the components, the ESST can do a better job than the SST. This is because for strong FM signals, the ESST can reassign more TF coefficients into the IF trajectory than the SST. Herein, we consider a larger reconstruction region to recover the components, where the corresponding reconstruction region is shown in Fig. 8. To recover these three components, we just need to integrate the TF coefficients in the reconstruction region along the frequency direction. In addition, the reconstruction results are shown in Fig. 9. The SST results are much closer to the original signal than just using the TF coefficient in the IF trajectory. However, the ESST results are similar to the results obtained using only the TF coefficient in the IF trajectory. This result indicates that because the SST results smear heavily, to recover the components precisely, a larger reconstruction region is needed than ESST.

Fig. 5

(a) SST result, (b) magnified SST result, (c) ESST result, and (d) magnified ESST result

Fig. 6

(a) STFT result, (b) SST result, (c) RS result, and (d) ESST result

3.2 The second case

For SST processing, the time-varying components with different FM rates lead to distinct energy-concentration TF results. The distinct integral regions yield different reconstruction results. However, the ESST is not sensitive to the signal FM rate. Herein, a series of signals with uniformly changing FM rates are employed to compare the proposed method with other TFA methods, including STFT, SST, and RS. The signal is modeled as $s\left(t\right)=\mathrm{sin}(2\pi (7t+FM\cdot {t}^{2}))$, where $FM=0.2, 0.4\dots 5$.

3.3 Case two

The second numerical signal is considered a summation of two components with crossed IF.

$$\begin{array}{c}C_1\left(t\right)=\cdot sin\left(0.78t\right)\sin(2\pi(25t))\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;C_2\left(t\right)=\sin\left(0.78t\right)\cdot sin(2\pi(25t+10\sin(1.5t)))\end{array}$$

(25)

The TF representations by the four methods are shown in Fig. 10, and the corresponding Rényi entropy and computational cost are listed in Tables 3 and 4. The ESST result is the most energy-concentrated. To recover the two components, the reconstruction regions are considered, as shown in Fig. 11. In addition, the reconstructed results are shown in Fig. 12. For the harmonic component, the SST and ESST give similar reconstructed results. However, for the time-varying component, the ESST can provide a more precise reconstructed result.

Table 3 The Rényi entropy of different TFA results

Table 4 Required computation time

Fig. 7

The reconstructed results by (a) SST and (b) ESST (the black solid line is the original component, and the red dotted line denotes the recovered component)

Fig. 8

The reconstruction regions corresponding to three components

4 Experimental validation

4.1 The first case

A popular bat signal recorded by Rice University is employed to validate the proposed method [9]. By producing the frequency-modulated and sweeping-downward signal and collecting the echo-delay signal, bats can identify objects successfully in a complex environment. This signal is sampled at 400 points, and its sampling frequency is 14 kHz. The TF results generated by the STFT, SST, RS, and ESST are shown in Fig. 13. The corresponding Rényi entropy values are listed in Table 5, which shows that the ESST result is the most energy-concentrated.

Table 5 The Rényi entropy of different TFA results

To validate the invertible ability of ESST, we utilize the ESST result to reconstruct the monocomponents contained in the bat signal. The decomposed results are shown in Fig. 14a–d. Four monocomponents are decomposed out. Figure 14e displays the summation of these four components (the black solid line is the original bat signal and the red dotted line denotes the summation of recovered components). The error between the summation and original bat signal is plotted in Fig. 14f. It can be seen that the error is small compared to the original signal, which denotes that the ESST can achieve the decomposition of the monocomponents and recover the original signal to a highly precise degree.

4.2 The second case

The focus of the second experiment is on analyzing a gravitational-wave (GW) signal generated in the procedure of merging a pair of black holes, which is recorded by the laser interferometer GW observatory (LIGO) [25]. It is well known that the successful detection of the GW signal brought the 2017 Nobel Prize to the inventors of the LIGO. The merger of two black holes is a time-varying procedure, which leads to the GW signal being also strongly varying in a short time. Therefore, extracting more information from the time-varying GW signal is a challenging task.

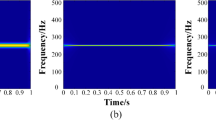
The waveform of the GW signal of event GW150914 is shown in Fig. 15a. Over 0.2 s, this signal increases in frequency and amplitude in approximately eight cycles, where the amplitude reaches a maximum. The varying frequency is closely related to the initial mass of two black holes and the mass of the eventual black hole. In Pham and Meignen [25], the frequency information is extracted by the WT method. However, the WT belongs to the linear TFA method, which must be restricted by the Heisenberg uncertainty principle. It is impossible to precisely characterize the time-varying frequency with concentrated energy by the WT technique. To generate the concentrated TF representations, we select the STFT, SST, and ESST to deal with this signal. The TF representations are displayed in Fig. 15b–d, and the local TF features are shown on the right. It is obvious that the SST result smears heavily. Although the high-order SST results increase the energy concentration, the TF energy is still somewhat blurry. In Fig. 15d, it can be observed that the ESST provides a significantly concentrated TF result for the GW signal.

Furthermore, we extract the time-varying IF trajectory from the MSST, which can also be used for recovering the noise-reduced signal. Meanwhile, the reconstructed signal is displayed in Fig. 16, which is plotted together with the numerical GW signal calculated by general relativity. The reconstructed signal is highly consistent with the numerical GW signal. Moreover, we calculate the SNRs of the measured signal and reconstructed signal with respect to the numerical signal, which are 5.7367 dB and 7.0121 dB, respectively. It can be concluded that the ESST can effectively improve the TF energy concentration and the SNR of the recovered signal.

Fig. 9

The reconstructed results by (a) SST and (b) ESST (the black solid line is the original component, and the red dotted line denotes the recovered component)

4.3 The third case

In engineering applications, vibration signal processing is usually applied in condition monitoring, fault diagnosis, etc., because vibration signals can contain the currently essential information about the analyzed machine. In nonstationary cases, the collected vibration signals will show some time-varying behaviors, so TFA methods are the most commonly employed methods to address them [36, 37]. In this subsection, we utilize the proposed method to analyze the vibration signal recorded in a start-up procedure from 800 to 2400 rpm of a tractor [38,39,40,41,42,43,44,45,46]. The instantaneous speed (IS) is shown in Fig. 17a, and the recorded vibration signal is displayed in Fig. 17b. Figure 17c shows the frequency spectrum.

From the waveform and spectrum of the signal, we cannot obtain the time-varying information about the tractor [47]. The TF representations generated by SST and ESST are shown in Fig. 18. The vibration components related to instantaneous speed are characterized, which include the first-order (1 ×) component of the rotating frequency and its high-order components (2 × , 3 × , 4″…). From the SST result (Fig. 18a), the 1 × component is characterized clearly. However, because the high-order components have stronger FM laws, the corresponding TF energy smears heavily. It is well known that a larger TF energy denotes a larger vibration level, which can provide essential information about the running status of machines. According to the smeared SST result, we cannot obtain accurate information about the different vibration components.

From the ESST results (see Fig. 18b), each component is well characterized and energy concentrated. The 1 × , 3 × , and 4 × components are the most obvious, which denotes that these three components are closely related components that cause the vibration of the tractor. To observe the time-varying features of these components more clearly, we reconstruct them using the ESST result, as shown in Fig. 19. Each component is decomposed into mono-modes, and the time-varying waveform is characterized clearly, which can be used to guide the control of tractor vibration effectively. Combining the IS information, we find that the amplitude of these three components will reach a maximum at approximately 2300 rpm, and the corresponding frequencies are 38 Hz, 115 Hz, and 153 Hz. These three frequencies have a close relationship to the intrinsic mode of the tractor and should be the main factor considered to be reduced.

Fig. 10

(a) STFT result, (b) SST result, (c) RS result, and (d) ESST result

Fig. 11

The reconstruction regions corresponding to two components

Fig. 12

The reconstructed results by (a) SST and (b) ESST (the black solid line is the original component, and the red dotted line denotes the recovered component)

Fig. 13

(a) STFT result, (b) SST result, (c) RS result, and (d) ESST result

Fig. 14

(a–d) Four decomposed components, (e) summation of four components (red) and the original signal (black), and (f) reconstruction errors between the summation and original signal

Fig. 15

(a) Waveform of the measured GW signal, (b) STFT result, (c) SST result, and (d) ESST result

Fig. 16

Reconstructed GW signal from the ESST result

Fig. 17

(a) Instantaneous speed of the tractor, (b) time-domain waveform, and (c) frequency spectrum

Fig. 18

(a) SST result and (b) ESST result

Fig. 19

The decomposed monocomponent signals

5 Conclusion

The SST, RS, and the proposed ESST are the postprocessing methods based on the STFT. The STFT can expand a one-dimensional time-series signal into a two-dimensional TF plane. Because the phase information of the original signal is retained, we can reconstruct the signal precisely by integrating the TF coefficients related to different components along the frequency direction. SST considers only the reassignment of TF coefficients in the frequency direction, so it allows signal reconstruction and has a reconstruction expression similar to that of the STFT. The distinct point is that SST is intended to provide a more energy-concentrated TF representation, which can help us to understand the time-varying feature of signals more precisely. RS is an interesting method that can provide a more energy-concentrated TF result than SST, but it loses the ability to reconstruct signals. Our proposed ESST is a novel method combining the advantages of SST and RS, and the effectiveness is validated by numerical and real-world signals. Compared with SST, ESST can provide a more energy-concentrated TF representation and achieve a higher TF resolution. Compared with RS, the ESST can allow for signal reconstruction and mode decomposition.

In the feature, more theoretical works can be done from the framework of the proposed method, e.g., synchroextracing transform and multisynchrosqueezing transform. Furthermore, the proposed method can be applied in various real applications, e.g., mechanical engineering fault diagnosis, operating condition monitoring, and so on.