1 Introduction

It is critical and of paramount importance that industrial and manufacturing systems operate at their full potential, producing products with the highest achievable quality. To reach this goal, tremendous efforts have been devoted to both quality and maintenance concepts to ensure that the industrial processes move smoothly during the production run with minimum waste. In this regard, control charts are powerful graphical tools in Statistical Process Control (SPC) providing significant operational cost reduction. Control charts are commonly used to monitor the process over time to ensure the stability of the process and to promptly detect any quality shift in the process. In brief, there are two states associated with a process, i.e., the “in-control” or the “out-of-control” states. When an assignable cause happens, the process is said to be in the “out-of-control” state and before such an event, the process is assumed to be in the “in-control” state [1]. In cases that a process enters the “out-of-control” state, it is required to perform corrective actions for repairing the systems and bring it back to the healthy (in-control) state.

Within the SPC context, control charts are developed to achieve different objectives among which the commonly used design measures are the economic and economic-statistical design. Advancements and developments of the economic and economic-statistical designs of control charts [2,3,4,5] have attracted considerable attention due to their potentials to significantly improve the overall performance of the underlying systems. The application of control charts has not been limited to manufacturing, and they have also been applied successfully in various other application domains such as maintenance planning and optimization [6, 7]. In particular, a close relationship is established between equipment maintenance and product quality [8]. The equipment used in manufacturing processes is subject to degradation due to daily usage and age. Maintenance actions such as preventive and corrective maintenance are, therefore, commonly performed with a direct effect on the performance and reliability of the equipment. It is expected that improving equipment’s performance would consequently increase the product’s quality. In addition, when the equipment fails during the production run, the process is stopped, which leads to a considerable loss in the process, delays in delivery, and customer dissatisfaction. It is, therefore, vital and of great practical importance and theoretical significance to develop integrated models of SPC and MP, which is the target area of this paper.

Generally speaking, integrated MP and SPC models can be classified into two main categories:

  1. (i)

    The first group of researchers [9,10,11,12,13] focused on the development of SPC control charts to monitor a process, which is subject to instantaneous shift. This particular type of shift can be attributed to an equipment failure, and;

  2. (ii)

    The second group of researchers [14, 15] has considered the similarity between on-line quality control and Condition Monitoring (CM) for maintenance purposes. The goal is to design SPC charts for direct monitoring of equipment’s health condition.

The main difference between the two categories is that the former deals with process monitoring such that a sample of size n is collected from the process. Furthermore, the process is usually assumed to be in one of the two unobservable states, namely in-control or out-of-control states. Then, quality-related statistics are plotted on a control chart and as soon as a point falls above or below the control limits, the process is stopped and investigation is triggered. Then, proper maintenance actions are performed on the equipment/system. The common assumption in the first category is that failure of the system/equipment causes this shift in the process. In the second group, on the other hand, the focus is on direct system/equipment monitoring, which is subject to stochastic degradation leading to potential failures. The system is usually assumed to be in one of the three states, two operational states, and one observable failure state. The CM data are collected from the system and plotted on the control chart. If the control chart signals, the system is stopped and inspection is performed followed possibly by preventive maintenance.

In this paper, based on the intuitively appealing concept of Opportunistic Maintenance (OM), we propose a novel integrated SPC and MP model referred to as the Opportunistic Maintenance Integrated Model (OMIM) for a two-stage dependent process. In particular, the concept of OM policy is taken into considerations in the MP phase. It is worth mentioning that the OM policy is widely discussed in maintenance literature as well as integrated SPC and MP models while the main focus was on equipment/system monitoring, i.e., Category (ii) [16]. On the contrary, in this paper, we consider the application of the OM policy in the integrated models while the special focus is on process monitoring, i.e., Category (i), which is a new development in this line of research. In addition, to evaluate the effectiveness of the proposed framework, another integrated model is developed, referred to as the Non-Opportunistic Maintenance Integrated Model (NOMIM). Both models are then compared with a conventional stand-alone maintenance model.

The remainder of the paper is organized as follow: The literature review is presented in Section 2. Section 3 describes the research methodology. Section 4 deals with problem description and industrial context. In Section 5, process evolution in one production cycle is discussed. In Section 6, the proposed integrated SPC and MP model considering OM policy is discussed. Section 7 deals with the optimization procedure for the OMIM. The integrated model of SPC and MP without considering OM policy is discussed in Section 8. Section 9 continues with the presentation of the optimization procedure for the NOMIM. Section 10 presents the numerical example, and finally, Section 11 concludes the paper.

2 Literature review

Different types of control charts have been used for the development of integrated models of MP and SPC ranging from traditional charts such as \(\bar{X}\), chi-square, and Multivariate Exponentially Moving Average (MEWMA) to multivariate Bayesian control charts. Table 1 summarizes the literature on integrated models of MP and SPC. Different inspection policies are, typically, used including periodic monitoring, variable monitoring, and constant-hazard policies. Furthermore, different failure/deterioration mechanisms are considered to model the underlying system ranging from an exponential distribution, Weibull distribution, to general continuous/discreet distributions. Finally, in some integrated models, the maintenance impact on the system is supposed to be perfect, meaning that maintenance action renews the system to the as-good-as-new condition. Imperfect maintenance is also taken into the consideration, which brings the system to a state between a perfect and a failure state. The authors in [13] proposed a model for two-stage dependent processes, where it is assumed that the system failure follows an exponential distribution, and a fixed sampling interval is used as the inspection policy. Furthermore, two stand-alone models, i.e., maintenance and SPC models, are developed to evaluate the effectiveness of the proposed integrated model. The results showed that the integrated model considerably outperforms the two stand-alone models in terms of cost reduction. Next, we provide a detailed comparison between multi-stage integrated models and single-stage models to better illustrate the existing research gap in this domain and justify the need to address the identified gaps.

Multi-stage integrated models vs. single-stage models

In the practical application of SPC within manufacturing and industrial sectors, most of the systems and processes consist of more than one unit/stage. Maintenance and control models for a single unit system/process cannot be applied to such multi-stage systems/processes when there is a dependency between stages, as the optimal maintenance policy for one is not necessarily optimal for the whole system/process [21]. Therefore, it is imperative to develop domain-specific maintenance models for multi-stage processes. Among different methods for maintenance decision-making in this context, integrated models have attracted considerable attention recently. Studies in the area of integrated models for maintenance planning, however, have focused mainly on single-stage processes or single-unit systems.

There are a few researches devoted to multi-stage processes due to the unique and complex characteristics of multi-stage processes [22, 23]. In particular, in multi-stage processes, different quality characteristics may need to be monitored in each stage. Generally speaking, multi-stage processes can be classified into: (a) multi-stage dependent processes, and; (b) multi-stage independent processes. In a multi-stage dependent process, which is the focus of this paper, the quality characteristics of a downstream stage are affected by the ones in the upstream stage. This property of multi-stage dependent processes is commonly known as the “Cascade Property” [24]. Alternatively, in a multi-stage independent process (Category (b)), the quality characteristics of different stages are independent of each other. It is widely discussed in the literature that due to the cascade property, the control charts applied for monitoring multi-stage independent processes may be inappropriate for monitoring the multi-stage dependent processes [25,26,27]. Alternatively, cause-selecting control charts and Hotelling’s \(T^2\) control charts have been proposed by researchers to monitor multi-stage dependent processes [25, 26]. The superiority of cause-selecting control charts over Hotelling’s \(T^2\) control chart has been broadly discussed in this context. Accordingly, in this research, to monitor the second stage of the process, cause-selecting control charts are employed, while the first stage is monitored using Shewhart-type control charts.

3 Research methodology

In this section, research objectives and research questions are explained together with the adopted research strategy, the inference approach, and the utilized data analysis.

Research objective

The development of integrated models of MP and SPC for multi-stage dependent processes is overlooked in the literature due to the demanding and challenging nature of such problems. In other words, while integrated SPC and MP models for a single-stage process have been widely studied in the quality control literature, the development of integrated models for a multi-stage process is still in its infancy [17,18,19]. Based on the above mentioned observation, we follow an inductive inference approach to develop a novel integrated model for a multi-stage dependent process. The main objective of this research work is to address this gap, i.e., to jointly optimize the integrated SPC and MP model for a two-stage dependent process in order to minimize the long-run expected average cost per unit time. Along this objective, two distinguished integrated models of SPC and MP are developed for a two-stage dependent process. The quality characteristic of the second stage is affected by the one in the first stage because of the cascade property. The first stage is monitored using a Shewhart type control chart, while the second stage is monitored using a cause-selecting control chart. The simultaneous effect of changes in the mean and variance of the process is investigated under different maintenance policies.

Research questions

Towards achieving the aforementioned objective, in this research work, we aim to answer the following three questions:

  1. 1.

    How significant is the impact of conducting an opportunistic maintenance policy for decreasing the expected total cost of a two-stage dependent process?

  2. 2.

    For a multi-stage process, how much does the integration of maintenance and quality control decisions reduce the total expected cost of the process compared to stand-alone models?

  3. 3.

    What are the effects of the process parameters on the expected total cost and decision variables in an integrated model of maintenance and quality?

The methodology of the paper to address the above-mentioned questions is based on development of mathematical models. More specifically, the problem is formulated based on the renewal theory and Genetic Algorithm (GA) is applied to find the optimal values of the decision variables to minimize the long-run expected average cost per unit time. The effects of the process parameters on the decision variables and cost are analyzed using the Design of Experiments (DOE) approach.

Research strategy

To answer the targeted questions and develop new models towards achieving our objective, it is assumed that the process has the cascade property. More specifically, the quality characteristic of a downstream stage is affected by the one in the upstream stage. This cascade property (inter-related stages) is modeled based on a regression formula. We further assume that two types of assignable causes denoted by AC1 and AC2 can occur, which are attributed to equipment degradation and failure. The AC1 affects the first stage, while AC2 is associated with the second stage. Each type of the two assignable causes affects both the mean and variance of the process. The failure of the equipment/system for each stage is a general continuous random variable. Four control charts, namely \(\bar{X}-S^2\), and \(\bar{e} - S_e^2\) are designed to monitor the first and second stages of the process, respectively.

Employing and comparing different maintenance policies to coordinate the decisions of MP and SPC for a two-stage dependent process are the main contributions of the paper. To this end, two main integrated models are developed. The proposed models have the following key advantages compared to the existing integrated models of SPC and maintenance for multi-stage processes:

  • The simultaneous effect of change on both the mean and variance of the process is considered.

  • Applicability to deferent types of inspection policies.

  • In addition to the multi-stage dependent process, the proposed models can be applied for a multi-stage independent process.

  • Unlike the excising integrated models in the literature, no restrictive assumptions are made regarding the process failure mechanism.

Regarding the inspection policies, it should be noted that, in developing the proposed integrated models, the time points of sampling inspection are considered as the decision variables. The proposed model, therefore, is capable of adapting to different inspection policy types. We should point out that in designing an integrated model, three inspection policies have been investigated, namely: (i) Fixed inspection using periodic interval; (ii) Constant hazard policy, and; (iii) Variable inspection interval. The former inspection policy, i.e., the fixed inspection interval, is the most widely used in practice within manufacturing and industrial sectors because it is easy to implement, especially when it comes to multi-stage/unit processes. Therefore, most of the recently proposed integrated models are developed based on fixed inspection policy as can be seen in Table 1. Although the analysis of Section 10 is conducted assuming the fixed inspection interval policy, other inspection policies can be applied. One of the advantages and contributions of the proposed model is that no restrictive assumptions are made regarding the process failure mechanism. In other words, the proposed model can be applied considering different failure mechanisms including but not limited to Weibull, exponential, Gamma, and Lognormal distributions. As Weibull is a widely used distribution in maintenance literature due to its versatility and flexibility, we have performed our analysis based on Weibull distribution in Section 10.

Data analysis

To validate the developed models, we consider a practical application, i.e., cotton yarn manufacturing process. In this context, root-cause analysis is performed to determine the main factors affecting failure of each underlying system/equipment. Based on such analysis, process prediction is performed based on the historical data where the failure distributions of the failure root causing system/equipment are determined. By incorporating the failure probability, and by considering occurrence of different scenarios within an inspection interval, the probability of conducting different maintenance policies is computed to minimize the long-run expected average cost of the process. A regression model is then established to predict the quality characteristic of the second stage from the quality characteristic of the first stage using historical data while the process is in the in-control state. It is worth mentioning that within the targeted application, availability of modern testing devices such as Uster Advanced Information System (AFIS) and High Volume Instrument (HVI) [20] makes it possible to collect the parameters regarding the quality of cotton fiber relatively quickly. These devices are suitable for obtaining large quantity of data allowing the quality and process engineers to develop and compute statistics and regression models to predict yarn properties from cotton fiber property parameter.

Table 1 Classification of different studies on integrated SPC and MP models
Full size table

4 Industrial context and problem description

Within manufacturing and industrial sectors, typically, one deals with applications consisting of more than one unit/stage, where dependencies exist between the underlying stages. In this section, description of the problem at hand is provided before which potential industrial applications are discussed in Sub-section 4.1.

4.1 Industrial context

There are various examples of multi-stage dependent (and particularly two-stage dependent) manufacturing processes (such as brazing process) in different industries including but not limited to tool industry, textile industry, and automobile industry. For the first category, according to [53], the gold concentration (X) in the first process step had the greatest impact on the thickness of the thin golden films (Y) in the second process step. The thickness variation increases as the concentration increased. Another example is the cotton yarn factory within textile industry that manufactures cotton yarn in two processes, as explained in [13]. The quality variable Y, which is produced in the current process, denotes the skein strength of the cotton yarn. The most essential single indicator of spinning quality is yarn strength. Good yarn strength indicates good spinning and weaving performance as well as increasing the range of usefulness of given cotton. The fiber length of the cotton yarn is denoted by the quality variable X, which is produced in the first process. The skein strength can be determined using fiber length, and the relationship between the two quality variables can be discovered by studying historical data.

Another example is the automobile crankshaft machining process includes two stages, an automobile body assembly that has multiples elements assembled in a couple of stations, and print circuit board manufacturing that contain exposure to black oxide, lay-up, hot press, cutting, drilling, and inspection [41]. Reference [30] discussed an interrelation among the stages of a multi-stage manufacturing process known as quality-dependent failure. It means the failure of downstream levels caused by the defective product manufactured in the upstream stages. For example, in the automotive industry, the car body assembly line includes several serial stations that typically collect a 150 to 250 sheet metallic elements. A meeting station can fail because of catastrophic tooling failures as a result of defective products. Certainly, big dimensional errors associated with the locating holes of one sheet metal part may also lead to locating tool failures such as locating pin being broken during the part loading process, a part being stuck at pins, or a part being unable to be correctly positioned by the locators. Reference [34] presented examples from automated paint shops where vehicles need to go through the phosphate, sanding, sealing, and multiple cleaning and coating operations. Multiple inspections are carried out after these operations.

4.2 Problem description

Fig. 1
figure 1

A two-stage series production process

Full size image

Consider a production process producing items in two successive stages as shown in Figure 1. The following general regression model is utilized to represent this relation:

$$\begin{aligned} Y_{ij} \mid X_{ij} = f(X_{ij}) + \xi _{ij}, \quad \text {for}\ i= 1,2,\ldots ,m-1, \text { and};\ j= 1,2,...,n \end{aligned}$$
(1)

where subscripts i and j represent the sampling epoch and item number in a sample, respectively. Term \(\xi _{ij}\) is a random error, which follows a Gaussian distribution, i.e., \(\xi _{ij}\sim N(0, \sigma _{\xi }^2)\). As stated previously, process monitoring is conducted using four control charts at the same time. Specifically, the \(\bar{X}-S^2\) control charts are jointly used to monitor the mean and variance of the process in Stage 1, while the \(\bar{e} - S^2_e\) control charts are jointly used to monitor the process in Stage 2. The \(\bar{X}-S^2\) control charts are Shewhart control charts that are set up based on the \(\bar{X}\) and \(S^2\) statistics. The \(\bar{e} - S^2_e\) charts are Cause-Selecting Control Charts (CSCC) that are set up based on the mean and the variance of cause-selecting values.

A sample of size n is collected from Stage 2 at time \(t_1, t_2, \ldots , t_{m-1}\). Therefore, the observation pair \((X_{i1},Y_{i1}), (X_{i2},Y_{i2}), \ldots , (X_{in},Y_{in})\) is available at sampling time \(t_i\). Based on the collected observations, the statistics \(\bar{X_i}, S^2_i, \bar{e_i}\), and \(S^2_{e_i}\) are calculated as follows:

$$\begin{aligned} \bar{X_i}=\frac{\sum _{j=1}^{n} X_{ij}}{n}; \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \bar{e_i} = \frac{\sum _{j=1}^{n} e_{ij}}{n};\qquad \qquad \nonumber \\ {S_i^2} = \frac{\sum _{j=1}^{n} (X_{ij}-\bar{X}_{ij})^2}{n-1}; \ \ \ \ \ \ \ \ {S_{e_i}^2} = \frac{\sum _{j=1}^{n} (e_{ij}-\bar{e}_{ij})^2}{n-1}, \end{aligned}$$
(2)

where \(e_{ij} = Y_{ij}\mid X_{ij} - \hat{Y}_{ij}\mid X_{ij}\) and \(\hat{Y}_{ij}\mid X_{ij}\) is the fitted value of \(Y_{ij}\mid X_{ij}\). The values of \((\bar{X_i}, {S_i^2})\) and \((\bar{e_i}, {S_{e_i}^2} )\) are plotted on \(\bar{X}-S^2\) and \(\bar{e} - S^2_e\) control charts such that the control limits of \(\bar{X}-S^2\) are given by:

$$\begin{aligned} LCL_{\bar{X}}= & {} \mu -\frac{k_1\sigma _x}{\sqrt{n}}, \nonumber \\ UCL_{\bar{X}}= & {} \mu +\frac{k_1\sigma _x}{\sqrt{n}}, \nonumber \\ UCL_{S^2}= & {} k_2 \sigma ^2_x. \end{aligned}$$
(3)

The control limits of \(\bar{e} - S^2_e\) are given by:

$$\begin{aligned} LCL_{\bar{e}}= & {} -\frac{k_3\sigma _\xi }{\sqrt{n}}, \nonumber \\ UCL_{\bar{e}}= & {} \frac{k_3\sigma _\xi }{\sqrt{n}}, \nonumber \\ UCL_{S^2_e}= & {} k_4 \sigma ^2_\xi . \end{aligned}$$
(4)

When an assignable cause happens, the process is said to be in the “out-of-control” state and before such an event the process is assumed to be in the “in-control” state. Here, it is assumed that the process can be affected by two assignable causes, namely, AC1 and AC2. The AC1 affects the mean and variance of the process in Stage 1 such that the distribution of \(\bar{X}\) changes from \(\bar{X}\!\sim \!N(\mu , \frac{\sigma _X^2}{n})\) to \(\bar{X}\!\sim \! N(\mu +\frac{\delta _1\sigma _X}{\sqrt{n}}, \frac{\delta _2^2\sigma _X^2}{n})\). Similarly, AC2 affects the process in the second stage such that the distribution of \(\bar{e}\) shifts from \(\bar{e}\!\sim \!N(0, \frac{\sigma ^2_\xi }{n})\) to \(\bar{e}\!\sim \!N(\frac{\delta _3 \sigma _\xi }{\sqrt{n}}, \frac{\delta _4^2 \sigma ^2_\xi }{n})\) such that \(\delta _1, \delta _3> 0\) and \(\delta _2, \delta _4 >1\).

The probabilities associated with Type I (\(\alpha\)) and Type II (\(\beta\)) errors are computed using the following equations [53]:

$$\begin{aligned} \alpha _{\bar{X}}= & {} 2 \phi (-k_1) \nonumber \\ \alpha _{S^2}= & {} 1- F_{X^2}\big ((n-1)k_2\big ), \nonumber \\ \alpha _{\bar{e}}= & {} 2 \phi (-k_3),\nonumber \\ \alpha _{S^2_e}= & {} 1- F_{X^2}\big ((n-1)k_4\big ), \nonumber \\ \end{aligned}$$
(5)

and

$$\begin{aligned} \beta _{\bar{X}}= & {} \phi (\frac{k_1}{\delta _2} -\frac{\delta _1}{\delta _2}) - \phi (-\frac{k_1}{\delta _2} -\frac{\delta _1}{\delta _2}),\nonumber \\ \beta _{S^2}= & {} F_{X^2}\big (\frac{(n-1)k_2}{\delta _2^2}\big ), \nonumber \\ \beta _{\bar{e}}= & {} \phi (\frac{k_3}{\delta _4} -\frac{\delta _3}{\delta _4}) - \phi (-\frac{k_3}{\delta _4} -\frac{\delta _3}{\delta _4}),\nonumber \\ \beta _{S^2_e}= & {} F_{X^2}\big (\frac{(n-1)k_4}{\delta _4^2}\big ), \end{aligned}$$
(6)

where \(\phi (\cdot )\) and \(F_{x^2} (\cdot )\) indicate the Cumulative Density Function (CDF) of a standard Gaussian distribution and a Chi-square distribution with \(n-1\) degrees of freedom, respectively. Next, different maintenance actions during process evaluation in a production cycle are discussed.

5 Maintenance actions during a production cycle in the OMIM

According to the observations obtained in the sampling time point \(t_i~(i = 1, 2, \ldots , m-1)\), Eq. (2) computes the corresponding statistics of each control chart. If at time point \(t_i\), at least one of the control charts signals, according to the OM policy, both stages of the process will be investigated, which takes \(T_I\) time units with the cost of \(C_I\). If the investigation result indicates the true alarm, corrective maintenance will be performed; otherwise, if it is a false alarm, the process will be continued. Similarly, if none of the control charts issue a signal, the process continues its operation.

For the two-stage manufacturing process and based on the above-mentioned discussion, the state-space is defined by pair \((u,\nu )\), for (\(u,\nu =\{0,1\}\)), such that the first component indicates the state of the process in Stage 1, and the second component indicates the state of the process in Stage 2. The process in each stage can be either in the “in-control” state, denoted by 0, or in the “out-of-control” state denoted by 1. Therefore, the process is characterized by the following states:

  • State (0,0): In this state, the process is not affected by ACs, and both stages are in the in-control state. No maintenance action is required, and the production cycle continues. In this state, indeed, the control charts may issue false alarms due to Type I error.

  • State (1,0): In this state, Stage 1 is affected by AC1 while the distribution of \(\bar{e}\) remains unchanged. In this state, a Reactive Maintenance (RM) action denoted by RM(1, 0) is conducted, which renews the process, and the cycle is terminated.

  • State (0,1): In this state, Stage 2 is affected by AC2 while the distribution of \(\bar{X}\) remains unchanged. In this state, a corrective maintenance action denoted by RM(0, 1) is conducted, which renews the process and the cycle is terminated.

  • State (1,1): In this state, both stages are affected by AC1 and AC2 where corrective maintenance denoted by RM(1, 1) is conducted, which renews the process, and the cycle is terminated.

Preventive/Planned Maintenance (PM) is applied at \(t_m\) if the process is not affected by the RMs in the previous inspection intervals. This terminates the production cycle and renews the process. Based on the above description, each production cycle starts in the in-control state with zero age and terminates due to the effect of one type of RM or PM.

The main objective is to jointly optimize the integrated SPC and MP model for a two-stage dependent process in order to minimize the long-run expected average cost per unit time. The computational algorithm is formulated based on the renewal theory, and the optimal control chart parameters, namely the sample size, sampling intervals, and control limits, are obtained. This completes the model description. In the next section, details of the computation procedure will be discussed.

6 OMIM: Integrated SPC and MP model considering the OM policy

In this section, we proceed to develop the main proposed integrated SPC and MP model, referred to as the OMIM. Let E(CL) and E(TC) be the expected cycle length and the expected total cost incurred in one cycle, respectively. From the renewal theory, for any stationary policy \(\eta\) determined by \(t_1,t_2, \ldots ,t_{m}, k_1,k_2,k_3,k_4,n,m\), the long-run Expected average Cost per unit time (ECC) can be computed as follows:

$$\begin{aligned} ECC_{OMIM}(\eta ) =\frac{E_\eta (TC)}{E_\eta (CL)}, \end{aligned}$$
(7)

where the expected total cost is computed as follows:

$$\begin{aligned} E(TC)= & {} \sum _{\nu =0,1}\sum _{u=0,1} C_{QC}^{u,\nu } E(T_{u,\nu }) + \underset{u+\nu \ne 0}{\sum _{\nu =0,1}\sum _{u=0,1}} C_{RM}^{u,\nu } P_{RM}^{u,\nu } + C_{PM} P_{PM} \nonumber \!\!\!\!\!\!\!\!\!\!\!\!\\+ & {} C_{Q} E (QC) + C_I E(\alpha ) +C_I (1-P_{PM}). \end{aligned}$$
(8)

Terms on the Right Hands Side (RHS) of Eq. (8) represent the expected total quality cost, corrective maintenance cost, preventive maintenance cost, sampling cost, and inspection cost, respectively. It is worth mentioning that as stated in the previous section, at time \(t_m\) if the process is renewed due to the PM action, the investigation will not be performed; therefore, the last term in Eq. (8) is added. Similarly, the expected cycle length is calculated as follows:

$$\begin{aligned} E(CL)= & {} \sum _{\nu =0,1}\sum _{u=0,1} E (T_{u,\nu }) + \underset{u+\nu \ne 0}{\sum _{\nu =0,1}\sum _{u=0,1}} T_{RM}^{u,\nu } P_{RM}^{u,\nu } + T_{PM} P_{PM} \nonumber \\+ & {} T_I E (\alpha ) + T_I (1-P_{PM}). \end{aligned}$$
(9)

Terms on the RHS of Eq. (9) represent the expected in-control and out-of-control times in each production cycle, expected time to perform corrective and preventive maintenance, and expected time to perform investigation. To be able to calculate Eqs. (8)-(9), we need to compute \(E(T_{u,\nu })\), \(P_{RM}^{u,\nu }\), \(P_{PM}\), E(QC) and \(E(\alpha )\). Before proceeding with calculations of the required components, different scenarios that may occur during an inspection interval should be investigated. These scenarios are discussed in the next subsection followed by a detailed calculation of each required component.

6.1 Possible scenarios within an interval

Fig. 2
figure 2

(a,b) Possible scenarios during a sampling inspection interval

Full size image

During each inspection interval, e.g., \((t_{i-1},t_i)\) for \(i=0, 1, \ldots , m\), ten different scenarios may occur. Figure 2 illustrates these scenarios along with their corresponding details. It is assumed that the number of sampling periods, m, is larger than 1.

The probability of occurrence of each scenario is denoted by \(P(Ss_{t_{i-1}})\), for \(s \in \{1,2, \ldots ,10\}\). For example, \(P(S1_{t_{i-1}})\) is the probability that both stages are in the in-control state at the beginning of the sampling inspection, i.e., \(t_{i-1}\), and remain in this state until \(t_i\). Let \(T_1\) and \(T_2\) denote the time of the quality shift of Stages 1 and 2, respectively. Furthermore, let \((u,\nu )_{t_{i-1}}\) represent the state of the process at time \(t_{i-1}\). The probability of occurrence for Scenario 1 can be written as follows:

$$\begin{aligned} P(S1_{t_{i-1}}) = P \Big (T_1> t_i, T_2 > t_i \mid (u,\nu )_{t_{i-1}} = (0,0) \Big )= \frac{\bar{F_1} (t_i)}{\bar{F_1} (t_{i-1})} \frac{\bar{F_2} (t_i)}{\bar{F_2} (t_{i-1})}. \end{aligned}$$
(10)

[26] provides the derivation of all the above-mentioned probabilities. This completes our discussion on the process evolution within a single interval. Next, we need to compute the process’s state at the beginning of an interval.

6.2 State of the process at the start of a sampling period

In this subsection, we compute the probability that the process operates in a special State \((u,\nu ); u,\nu \in \{0,1\}\) at the start of an inspection period. Let \(P_{t_i}^{u,\nu }\) denote the probability of being in State \((u,\nu )\) immediately after an inspection performed at \(t_i\). The required probabilities are computed as follows:

$$\begin{aligned} P_{t_i}^{0,0}= & {} \bar{F_1} (t_i) \bar{F_2} (t_i), \quad \text {for}\quad i \in \{1, 2, \ldots , m\}, \end{aligned}$$
(11)

and for \(i \in \{1, 2, \ldots , m-1\}\)

$$\begin{aligned} P_{t_i}^{1,0}= & {} \beta _{\bar{X}} \beta _{S^2} (1-\alpha _{\bar{e}}) (1-\alpha _{S_e^2}) \big [ P_{t_{i-1}}^{0,0} \times P(S2_{t_{i-1}}) + P_{t_{i-1}}^{1,0} \times P(S8_{t_{i-1}}) \big ],\end{aligned}$$
(12)
$$\begin{aligned} P_{t_i}^{0,1}= & {} \beta _{\bar{e}} \beta _{S^2_e} (1-\alpha _{\bar{X}}) (1-\alpha _{S^2}) \big [ P_{t_{i-1}}^{0,0} \times P(S3_{t_{i-1}}) + P_{t_{i-1}}^{0,1} \times P(S6_{t_{i-1}}) \big ], \end{aligned}$$
(13)
$$\begin{aligned} P_{t_i}^{1,1}= & {} \beta _{\bar{X}} \beta _{S^2} \beta _{\bar{e}} \beta _{S^2_e} \big [ P_{t_{i-1}}^{0,0} \times P(S4_{t_{i-1}}) + P_{t_{i-1}}^{0,0} \times P(S5_{t_{i-1}}) \nonumber \\+ & {} P_{t_{i-1}}^{0,1} \times P(S7_{t_{i-1}}) + P_{t_{i-1}}^{1,0} \times P(S9_{t_{i-1}}) + P_{t_{i-1}}^{1,1} \times 1\big ]. \end{aligned}$$
(14)

Equation (11) indicates that the process will be in State (0,0) at time \(t_i\) if the occurrence times of both types of ACs are greater than \(t_i\). The term inside the bracket on the RHS of Eq. (12) indicates the probability of being in State (1,0) just before the inspection time \(t_i\). These two terms are obtained based on Scenarios 2 and 8. The first term on the RHS of Eq. (12) is the probability that no alarm is triggered by the control charts after inspection time \(t_i\) given that the process is in State (1,0). Similarly, Eqs. (13) and (14) represent the probability of being in States (0,1) and (1,1) at time \(t_i\), respectively. Computation of expected in-control and out-of-control times will be discussed next.

6.3 Computation of \(E(T_{u,\nu })\)

In this subsection, we derive the required expressions to compute the expected in-control and out-of-control times, i.e., \(E(T_{u,\nu })\), in one production cycle. Let \(T^{i}_{u,\nu }\) be the expected time length in interval \((t_{i-1}, t_i)\), while the process operates in State \((u,\nu )\). Therefore, \(E(T_{u,\nu })\) can be computed as follows:

$$\begin{aligned} E(T_{u,\nu }) = \sum _{i=1}^{m} T^{i}_{u,\nu }, \quad \text {for} \ u,\nu \in \{0,1\}, \end{aligned}$$
(15)

where

$$\begin{aligned} T^i_{0,0}&= P_{t_{i-1}}^{0,0} \Big [\frac{\bar{F_1} (t_i)}{\bar{F_1} (t_{i-1})} \frac{\bar{F_2} (t_i)}{\bar{F_2} (t_{i-1})}(t_i-t_{i-1}) + \frac{\bar{F_2} (t_i)}{\bar{F_2} (t_{i-1})} \int _{t_{i-1}}^{t_i} \frac{f_1(t)}{\bar{F_1}(t_{i-1})} (t-t_{i-1}) dt\nonumber \\&+ \frac{\bar{F_1} (t_i)}{\bar{F_1} (t_{i-1})} \int _{t_{i-1}}^{t_i} \frac{f_2(t)}{\bar{F_2}(t_{i-1})} (t-t_{i-1}) dt \qquad \qquad \qquad \qquad \qquad \ \ \nonumber \\&+ \int _{t_{i-1}}^{t_i} \frac{f_1(t)}{\bar{F_1}(t_{i-1})} \int _{t}^{t_i} \frac{f_2(t^{\prime })}{\bar{F_2}(t)} (t-t_{i-1}) dt^{\prime } dt \qquad \qquad \qquad \qquad \ \ \nonumber \\&+ \int _{t_{i-1}}^{t_i} \frac{f_2(t)}{\bar{F_2}(t_{i-1})} \int _{t}^{t_i} \frac{f_1(t^{\prime })}{\bar{F_1}(t)} (t-t_{i-1}) dt^{\prime } dt \Big ], \text {for} \ i =1,2, \ldots ,m. \end{aligned}$$
(16)

Equation (16) is obtained based on Scenarios S1 to S5 where the process starts in the in-control state at time \(t_{i-1}\). More specifically, if Scenario S1 occurs, the process operates in State (0,0) during the whole interval of \((t_{i-1},t_i)\). We note that although a simpler equation can be derived for \(T^{i}_{0,0}\), to be consistent with other equations, instead, Eq. (16) is considered. On the other hand, if S2, S3, S4 or S5 occurs, the system operates in State (0,0) for a duration within \(t-t_{i-1}\). Similarly, the remaining expected times are computed as follows:

$$\begin{aligned} T^i_{0,1}= & {} P_{t_{i-1}}^{0,0} \Big [ \frac{\bar{F_1} (t_i)}{\bar{F_1} (t_{i-1})} \int _{t_{i-1}}^{t_i} \frac{f_2(t)}{\bar{F_2}(t_{i-1})} (t_{i}-t) dt + \int _{t_{i-1}}^{t_i} \frac{f_2(t)}{\bar{F_2}(t_{i-1})} \int _{t}^{t_i} (t^{\prime }-t) \frac{f_1(t^{\prime })}{\bar{F_1}(t)} dt^{\prime } dt \Big ] \nonumber \\+ & {} P_{t_{i-1}}^{0,1} \Big [ \frac{\bar{F_1} (t_i)}{\bar{F_1} (t_{i-1})} (t_i-t_{i-1}) + \int _{t_{i-1}}^{t_i} \frac{f_1(t)}{\bar{F_1}(t_{i-1})} (t-t_{i-1}) dt \Big ], \quad \text {for} \ i =1,2,...,m.\!\!\!\!\! \end{aligned}$$
(17)
$$\begin{aligned} T^i_{1,0}= & {} P_{t_{i-1}}^{0,0} \Big [ \frac{\bar{F_2} (t_i)}{\bar{F_2} (t_{i-1})} \int _{t_{i-1}}^{t_i} \frac{f_1(t)}{\bar{F_1}(t_i-1)} (t_i-t) dt + \int _{t_{i-1}}^{t_i} \frac{f_1(t)}{\bar{F_1}(t_{i-1})} \int _{t}^{t_i} (t^{\prime }-t) \frac{f_2(t^{\prime })}{\bar{F_2}(t)} dt^{\prime } dt \Big ] \nonumber \\+ & {} P_{t_{i-1}}^{1,0} \Big [ \frac{\bar{F_2} (t_i)}{\bar{F_2} (t_{i-1})} (t_i-t_{i-1}) + \int _{t_{i-1}}^{t_i} \frac{f_2(t)}{\bar{F_2}(t_{i-1})} (t-t_{i-1}) dt \Big ], \quad \text {for} \ i =1,2,...,m. \end{aligned}$$
(18)
$$\begin{aligned} T^i_{1,1}= & {} P_{t_{i-1}}^{1,1} \times (t_i-t_{i-1}) + P_{t_{i-1}}^{0,0} \Big [ \int _{t_{i-1}}^{t_i} \frac{f_1(t)}{\bar{F_1}(t_{i-1})} \int _{t}^{t_i} (t_i-t^{\prime }) \frac{f_2(t^{\prime })}{\bar{F_2}(t)} dt^{\prime } dt \nonumber \\+ & {} \int _{t_{i-1}}^{t_i} \frac{f_2(t)}{\bar{F_2}(t_{i-1})} \int _{t}^{t_i} (t_i-t^{\prime }) \frac{f_1(t^{\prime })}{\bar{F_1}(t)} dt^{\prime } dt \Big ] + P_{t_{i-1}}^{1,0} \int _{t_{i-1}}^{t_i} \frac{f_2(t)}{\bar{F_2}(t_{i-1})} (t_{i}-t) dt \nonumber \\+ & {} P_{t_{i-1}}^{0,1} \int _{t_{i-1}}^{t_i} \frac{f_1(t)}{\bar{F_1}(t_{i-1})} (t_i-t) dt. \quad \text {for} \ i =1,2, \ldots ,m. \end{aligned}$$
(19)

This completes the calculations required for Eq. (15). Next, derivations for computation of the required components in Eqs. (8) and (9) are presented.

6.4 Computation of E(QC)

Let \(P^i_{QC}\) be the probability of performing a sampling inspection at \(t_i\). Therefore, E(QC) is calculated as follows:

$$\begin{aligned} E(QC) = \sum _{i=1}^{m-1} P^{i}_{QC} = \sum _{i=1}^{m-1} P^{0,0}_{t_{i-1}} + P^{1,0}_{t_{i-1}} + P^{0,1}_{t_{i-1}}+ P^{1,1}_{t_{i-1}}. \end{aligned}$$
(20)

6.5 Computation of \(E(\alpha )\)

At a given sampling time, a false alarm is issued from the control charts if both stages are in the in-control state and at least one of the control charts issues a false alarm. Therefore, the expected number of false alarms during a production cycle can be calculated as follows:

$$\begin{aligned} E(\alpha ) = \sum _{i=1}^{m-1} P^{i}_{\alpha }= \sum _{i=1}^{m-1} \bar{F_1} (t_i) \bar{F_2} (t_i) \alpha . \end{aligned}$$
(21)

where \(P^{i}_{\alpha }\) indicates the probability of issuing a false alarm at time \(t_i\). The probability that at least one of the control charts issues a false alarm, i.e., \(\alpha\), is computed as follows:

$$\begin{aligned} \alpha = 1- (1-\alpha _{\bar{X}}) (1-\alpha _{S^2}) (1-\alpha _{\bar{e}}) (1-\alpha _{S^2_e}). \end{aligned}$$
(22)

6.6 Computation of \(P_{RM}^{u,\nu }\) and \(P_{PM}\)

For \(u,\nu \in \{0,1\} , u+\nu \ne 0\), the probabilities of conducting PM and RM actions for a production cycle are as follows:

$$\begin{aligned} P_{RM}^{u,\nu }= & {} \sum _{i=1}^{m-1} P^i_{RM(u,\nu )},\nonumber \\ P_{PM}= & {} 1- \sum _{\nu =0,1} \sum _{u=0,1} P^i_{RM(u,\nu )}, \end{aligned}$$
(23)

where \(P^i_{RM(u,\nu )}\) is the probability of conducting RM in State (u, v) after performing the inspection at time \(t_i\). For each possible state and, for \(1\le i\le m-1\), Term \(P^i_{RM(u,\nu )}\) can be calculated as follows:

$$\begin{aligned} P^i_{RM(1,0)} =& \underbrace{\Big [ 1-\beta _{\bar{X}} \beta _{S^2} (1-\alpha _{\bar{e}}) (1-\alpha _{S^2_e}) \Big ]}_{\textit{Term I}}\qquad \qquad \qquad \qquad \nonumber \\ &\times \underbrace{\Big [ P^{0,0}_{t_{i-1}} \times P(S2_{t_{i-1}}) + P^{1,0}_{t_{i-1}}\times P(S8_{t_{i-1}}) \Big ]}_{\textit{Term II}}.\!\!\!\!\!\!\! \end{aligned}$$
(24)

Term I on the RHS of Eq. (24) is the probability that at least one of the control charts releases an alarm when the process operates in State (1,0) just after the inspection at \(t_i\). Term II on the RHS of Eq. (24) is the probability of the process operating in State (1,0) just before the inspection time \(t_i\), which is achieved based on Scenarios 2 and 8. Similarly, for \(1\le i\le m-1\), we have:

$$\begin{aligned} P^i_{RM(0,1)} =&\Big [ 1-\beta _{\bar{e}} \beta _{S^2_e} (1-\alpha _{\bar{X}}) (1-\alpha _{S^2}) \Big ] \qquad \qquad \qquad \qquad \nonumber \\ &\times \Big [ P^{0,0}_{t_{i-1}}\times P(S3_{t_{i-1}}) + P^{0,1}_{t_{i-1}} \times P(S6_{t_{i-1}}) \Big ], \!\!\!\!\!\!\! \end{aligned}$$
(25)
$$\begin{aligned} P^i_{RM(1,1)} = \Big [ 1-\beta _{\bar{X}} \beta _{S^2_e} \beta _{\bar{e}} \beta _{S^2} \Big ] \Big [ P^{0,0}_{t_{i-1}}\times P(S4_{t_{i-1}}) + P^{0,0}_{t_{i-1}} \times P(S5_{t_{i-1}}) \qquad \nonumber \\+ P^{0,1}_{t_{i-1}}\times P(S7_{t_{i-1}}) + P^{1,0}_{t_{i-1}} \times P(S9_{t_{i-1}}) + P^{1,1}_{t_{i-1}} \times P(S10_{t_{i-1}})\Big ].\ \ \end{aligned}$$
(26)

This completes all the calculations required for computing the long-run expected average cost per unit time defined in Eq. (7). Next, we present the optimization problem for the proposed model.

7 Optimization procedure for OMIM

In the above sections, the expected cycle length and cycle cost are calculated. The optimization problem for the proposed OMIM can be formulated as follows:

$$\begin{aligned} \textit{Minimize} \ ECC_{OMIM}(\eta )= & {} \frac{E_\eta (TC)}{E_\eta (CL)},\nonumber \\ \textit{Subject to} \ ARL_0< & {} \frac{1}{\alpha }\nonumber \\ ARL_1> & {} \frac{1}{1- \beta _{\bar{X}} \beta _{S^2} }\nonumber \\ ARL_1> & {} \frac{1}{1- \beta _{\bar{e}} \beta _{S^2_e} }\nonumber \\ t_m> & {} t_{min}. \end{aligned}$$
(27)

Terms E(TC) and E(CL) are calculated based on Eqs. (8) and (9). The first three constraints guarantee existence of suitable statistical characteristics for the control charts in the in-control and out-of-control states. The last constraint is added to avoid very short planned maintenance interval. The optimal policy \(\eta ^*\) is obtained, which is characterized by the optimal values of inspection times \((t_1,t_2, \ldots ,t_{m-1})\), time of performing PM actions, control limit parameters \(k_1,k_2,k_3,k_4\), sample size n, and finally, the maximum number of inspection periods m.

This completes our discussion of the proposed computational algorithm. Next, we present the second integrated model by considering the policy that only one stage of the process is stopped for investigation.

8 NOMIM: Integrated model of SPC and MP without considering OM policy

In this section, another integrated model referred to as the NOMIM is presented. The core of this policy is that sampling inspection is conducted similarly to that of the OMIM policy; however, if the control chart associated with one of the stages signals an alarm, that particular stage is investigated to verify the correctness of the signal with the cost of \(C^\prime _I\) taking \(T^\prime _I\) time units. The result of the investigation will be either a true or a false alarm. In a sampling time point, one of the following four scenarios may happen:

  • None of the control charts signals an out-of-control condition. In this case, the process continues its operation without any interruption.

  • At least one of the control charts associated with Stage 1 signals an out-of-control condition while there is no alarm produced by the control charts corresponding to Stage 2. In this case, Stage 1 is investigated to verify the correctness of the received signal. If a false alarm is investigated, the production cycle continues; otherwise, a minimal maintenance action denoted by \(MM^1\) is conducted with the cost of \(C_{MM^1}\), which takes \(T_{MM^1}\) time unit bringing the first stage of the process to the in-control state.

  • At least one of the control charts associated with Stage 2 signals an out-of-control condition while there is no alarm produced by the control charts corresponding to Stage 1. In this case, Stage 2 is investigated to verify the correctness of the received signal. If a false alarm is investigated, the production cycle continues; otherwise, a minimal maintenance action denoted by \(MM^2\) will be conducted with the cost of \(C_{MM^2}\), which takes \(T_{MM^2}\) time units bringing the second stage of the process to the in-control state.

  • In both stages, at least one of the control charts releases a signal. In this case, both stages are investigated. If there is a false alarm in both stages, the production cycle continues. If the signal of the first stage indicates the true alarm and the signal of the second stage indicates the false alarm, \({MM}^1\) is conducted, which brings the first stage to the in-control state. Conversely, if the signal associated with the first stage indicates the false alarm and the signal corresponding to the second stage indicates true alarm, \({MM}^2\), is conducted, which brings Stage 2 to the in-control state. Finally, if the signals indicate true alarms, it means that both ACs affect the process and the state of the process is (1, 1). Corrective maintenance action should be performed to bring back the whole process to the in-control state.

  • If the process is not renewed during the previous inspection epochs due to the performance of RM actions, PM is conducted at time point \(t_m\).

It is worth mentioning that, in this policy, conducting RM or PM terminates the production cycle and renews the process, while minimal maintenance actions just bring back the corresponding stage to the in-control state and does not terminate the production cycle. Thus, during a production cycle, \({MM}^1\) or \({MM}^2\) may be performed more than once. Similar to the previous policy, let E(CL) and E(TC) be the expected cycle length and the expected total cost incurred in one cycle, respectively. From renewal theory, for any stationary policy \(\eta\) determined by \(t_1,t_2,\ldots ,t_{m}, k_1,k_2,k_3,k_4,n,m\), the long-run expected average cost per unit time for this integrated model represented by \(ECC_{NOMIM}\) can be computed as follows:

$$\begin{aligned} ECC_{NOMIM}(\eta ) =\frac{E_\eta (TC)}{E_\eta (CL)}, \end{aligned}$$
(28)

where the expected total cost and cycle length for this policy are computed as follows:

$$\begin{aligned} E(TC)= & {} \sum _{\nu ,u=0,1} C_{QC}^{u,\nu } E (T_{u,\nu }) + C_{RM} P_{RM} + C^\prime _I \Big [ E({MM^1}) + E({MM^2}) + E(\alpha ) \Big ]\nonumber \\ &+ {} C_{PM} P_{PM} + C_I P_{RM}+ C_{Q} E(QC) + C_{MM^1} E({MM^1}) + C_{MM^2} E({MM^2}).\nonumber \\&\end{aligned}$$
(29)
$$\begin{aligned} E(CL)= & {} \sum _{\nu ,u=0,1} E (T_{u,\nu }) + T_{RM} P_{RM}+ T^\prime _I \Big [ E({MM^1}) + E({MM^2}) + E(\alpha ) \Big ] \nonumber \\ &+ {} T_{PM} P_{PM} + T_I P_{RM} + T_{MM^1} E({MM^1}) + T_{MM^2} E({MM^2}). \end{aligned}$$
(30)

Similar to the previous developments, in order to calculate Eqs. (29)-(30), first we need to compute the closed-form expressions for each component, which are presented in the following subsections.

8.1 Different scenarios within an interval in the NOMIM

The possible scenarios in a sampling period are the same as those of the OMIM approach presented in Section 6. Thus, different scenarios for the evolution can be derived from Fig. 2.

8.2 Process state at the start of the sampling period

Term \(\hat{P}^{u,\nu }_{t_i}\) is defined as the probability of operating the process in State \((u,\nu )\) just before performing an inspection at \(t_i\). Therefore, the probabilities of being in a particular state at the beginning of the sampling inspection interval are given by the following recursive formulas:

$$\begin{aligned} P_{t_i}^{0,0}= & {} \hat{P}_{t_i}^{0,0} \quad \text {for} \ 1\le i \le m \end{aligned}$$
(31)
$$\begin{aligned} P_{t_i}^{0,0}= & {} \bar{F_1} (t_i) \bar{F_2} (t_i), \quad \text {for} \ 1\le i \le m \end{aligned}$$
(32)
$$\begin{aligned} \hat{P}_{t_i}^{1,0}= & {} P_{t_{i-1}}^{0,0} \times P(S2_{t_{i-1}}) + P_{t_{i-1}}^{1,0} \times P(S8_{t_{i-1}}), \quad \text {for} \ 1\le i \le m-1 \end{aligned}$$
(33)
$$\begin{aligned} {P}_{t_i}^{1,0}= & {} \beta _{\bar{X}} \beta _{S^2} \times \hat{P}_{t_i}^{1,0} + \beta _{\bar{X}} \beta _{S^2} (1- \beta _{\bar{e}} \beta _{S^2_e}) \times \hat{P}_{t_i}^{1,1}. \quad \text {for} \ 1\le i \le m-1 \end{aligned}$$
(34)

Equation (33) is obtained based on Scenarios 2 and 8. Derivation of Eq. (34) is based on the following two possible cases: (i) The process operates in State (1,0) before performing an inspection at \(t_i\), and the control charts of Stage 1 cannot detect the shift in the process, and; (ii) The process operates in State (1,1) before the inspection at \(t_i\), while the control charts of Stage 2 release a signal and detect the shift in Stage 2. The control charts of Stage 1 cannot detect the shift of Stage 1. Similarly, for \(1\le i \le m-1\), the remaining probabilities are given by:

$$\begin{aligned} \hat{P}_{t_i}^{0,1}= & {} P_{t_{i-1}}^{0,0} \times P(S3_{t_{i-1}}) + P_{t_{i-1}}^{0,1} \times P(S6_{t_{i-1}}), \end{aligned}$$
(35)
$$\begin{aligned} {P}_{t_i}^{0,1}= & {} \beta _{\bar{e}} \beta _{S^2_e} \times \hat{P}_{t_i}^{0,1} + \beta _{\bar{e}} \beta _{S^2_e} (1- \beta _{\bar{X}} \beta _{S^2}) \times \hat{P}_{t_i}^{1,1}. \end{aligned}$$
(36)
$$\begin{aligned} \hat{P}_{t_i}^{1,1}= & {} P_{t_{i-1}}^{0,0} \times P(S4_{t_{i-1}}) + P_{t_{i-1}}^{0,0} \times P(S5_{t_{i-1}}) +P_{t_{i-1}}^{0,1} \times P(S7_{t_{i-1}}) \nonumber \\+ & {} P_{t_{i-1}}^{1,0} \times P(S9_{t_{i-1}})+ P_{t_{i-1}}^{1,1} \times P(S10_{t_{i-1}}), \end{aligned}$$
(37)
$$\begin{aligned} {P}_{t_i}^{1,1}= & {} \beta _{\bar{X}} \beta _{S^2} \beta _{\bar{e}} \beta _{S^2_e} \times \hat{P}_{t_i}^{1,1}. \end{aligned}$$
(38)

8.3 Computation of \(E(T_{u,\nu })\)

Expected in-control and out-of-control time durations in each production cycle can be computed using equations presented in Subsection 6.3.

8.4 Computation of E(QC)

The expected number of sampling periods in each production cycle can be calculated similarly to those presented in Subsection 6.4.

8.5 Computation of \(E(\alpha )\)

The expected number of false alarms in each production cycle is derived as follows:

$$\begin{aligned} E(\alpha ) =& \sum _{i=1}^{m-1} P^{i}_{\alpha }= {} \sum _{i=1}^{m-1} \Big [ 1- (1-\alpha _{\bar{X}}) (1-\alpha _{S^2}) (1-\alpha _{\bar{e}}) (1-\alpha _{S^2_e}) \Big ] \times \hat{P}_{t_i}^{0,0} \nonumber \\ &+\Big [ 1- (1-\alpha _{\bar{e}}) (1-\alpha _{S^2_e}) \Big ] \times \hat{P}_{t_i}^{1,0} + \Big [ 1- (1-\alpha _{\bar{X}}) (1-\alpha _{S^2}) \Big ] \times \hat{P}_{t_i}^{0,1}.\nonumber \\ \end{aligned}$$
(39)

The first, second, and third terms on the RHS of Eq. (39) represent the probability of issuing a false alarm while the process is in State (0,0), (1,0), and (0,1), respectively.

8.6 Computation of E(MM)

In this subsection, a closed-form expression for the expected number of minimal maintenance actions in a production cycle is derived, which is given by:

$$\begin{aligned} E(MM^1)= \sum _{i=1}^{m-1} P^i_{MM^1}= & {} \sum _{i=1}^{m-1} (1-\beta _{\bar{X}} \beta _{S^2}) \times \hat{P}_{t_i}^{1,0} + \beta _{\bar{e}} \beta _{S^2_e} (1-\beta _{\bar{X}} \beta _{S^2}) \times \hat{P}_{t_i}^{1,1},\nonumber \!\!\!\!\!\!\\&\end{aligned}$$
(40)
$$\begin{aligned} E(MM^2)= \sum _{i=1}^{m-1} P^i_{MM^2}= & {} \sum _{i=1}^{m-1} (1-\beta _{\bar{e}} \beta _{S^2_e}) \times \hat{P}_{t_i}^{0,1} + \beta _{\bar{X}} \beta _{S^2} (1-\beta _{\bar{e}} \beta _{S^2_e}) \times \hat{P}_{t_i}^{1,1},\nonumber \!\!\!\!\!\!\\&\end{aligned}$$
(41)

where \(P^i_{MM^1}\) and \(P^i_{MM^2}\) denote the probabilities of performing minimal maintenance of Type 1 and Type 2, respectively, after inspection at time \(t_i\). Next, we calculate the final term required for computation of Eq. (28).

8.7 Probability of Conducting PM or RM

As mentioned previously, the process will be renewed when either PM or RM is performed. Thus, the cycle ends with the following probabilities:

$$\begin{aligned} P_{PM}= & {} {P}_{t_{m-1}}^{0,0} + {P}_{t_{m-1}}^{1,0} +{P}_{t_{m-1}}^{0,1}+{P}_{t_{m-1}}^{1,1},\nonumber \\ P_{RM}= & {} 1-P_{PM}. \end{aligned}$$
(42)

At this point, all the required components for the calculation of the long-run expected average cost per unit time are derived. Next, the NOMIM optimization model will be presented.

9 Optimization procedure for NOMIM

The NOMIM optimization can be presented as follows:

$$\begin{aligned} \textit{Minimize} \ ECC_{NOMIM}(\eta )= & {} \frac{E_\eta (TC)}{E_\eta (CL)},\nonumber \\ \textit{Subject to} \ ARL_0< & {} \frac{1}{1-(1-\alpha _{\bar{X}}) (1-\alpha _{S^2})}\nonumber \\ ARL_0< & {} \frac{1}{1-(1-\alpha _{\bar{e}}) (1-\alpha _{S^2_e})}\nonumber \\ ARL_1> & {} \frac{1}{1- \beta _{\bar{e}} \beta _{S^2_e} }\nonumber \\ ARL_1> & {} \frac{1}{1- \beta _{\bar{X}} \beta _{S^2} }\nonumber \\ t_m> & {} t_{min}. \end{aligned}$$
(43)

This completes the derivation of the proposed integrated models. In the next section, we provide numerical examples to evaluate the performance of the proposed OMIM and NOMIM integrated models.

10 Numerical examples

In this section, we present different numerical examples to evaluate the proposed methodologies and illustrate their innovative aspects. It should be noted that although the proposed models have the versatility to conform with different inspection processes and different failure mechanisms, for illustration purposes, some assumptions regarding inspection scheme and failure mechanism are considered in the numerical examples.

10.1 Numerical illustration of the proposed integrated models

To emphasize the application of the proposed integrated models, a real example from the textile industry is considered.

Cotton yarn manufacturing process consists of different systems and equipment including but not limited to woolen mill machines, thread winding machines, and spinning machine. Each system is subject to degradation and failure due to different factors, where root-cause analysis can be performed to determine the main factors affecting each failure. For example, one of the factors that influence the spinning machine failure is bearing degradation/failure, which consequently leads to poor quality of the manufactured product and process stoppage. Therefore, accurate bearing degradation process prediction is key to effectively implement preventive maintenance and can prevent unexpected failures in the process and minimize the overall maintenance costs. In the proposed model, the failure distributions of the failure root causing system/equipment are determined based on the historical data. In the case study, it is observed that the failure root causing system follows Weibull distribution. By incorporating the failure probability, and by considering occurrence of different scenarios within an inspection interval, the probability of conducting different maintenance policies is computed in order to minimize the long-run expected average cost of process. More specifically, Cotton yarn factory produces cotton yarn in the two-stage dependent process. The quality characteristic of the first stage X is the fiber length of the cotton yarn, while the quality characteristic of the second stage Y is the skein strength of the cotton yarn, which is affected by fiber length [13]. Samples are taken at the end of the second stage, and observations are measured on the same item of the production. According to the historical data of the process in the in-control state, variables X and Y follow normal distributions with the following parameters: \(X \sim N(77.05,4.8^2)\), and \(Y \sim N(95.755,8^2)\). The relationship between them is \(Y=11+1.1X+\varepsilon\). Failure mechanism associated with the equipment in each stage follows the Weibull distribution with the following cumulative distribution function:

$$\begin{aligned} F(t) = 1- e^{-(\lambda t)^{\gamma }}, \end{aligned}$$
(44)

where \(\gamma\) and \(\lambda\) are the shape and scale parameters of the Weibull distribution, respectively. We consider periodic sampling inspection policy such that samples are collected at time epochs \(t_i= i \times t_1\), for (\(1 \le i \le m-1\)). The costs of conducting different maintenance actions are reported in Table 2 in dollars. The duration of the time to conduct maintenance actions as well as other parameters related to time is reported in hour in Table 2. For example, the cost of conducting reactive maintenance while both stages of the process are in the out-of-control state is $5, 000 and it takes 4 hours.

Table 2 Input Parameters
Full size table

In order to find the optimum values for the proposed models, at first and as an exact method, a full enumeration algorithm coded in MATLAB software is employed. As the run time of the full enumeration algorithm is long, in the next step, the Genetic Algorithm (GA) is applied. GA is a well-established metaheuristic method to optimize complex mathematical models. It has broadly been employed to optimize the integrated models of maintenance and quality [18, 55]. The parameters of the GA, e.g., mutation rate and crossover rate, are determined based on the full enumeration algorithm. Several simulations are conducted with different parameters, where the performance of the GA was compared with that of the exact full enumeration algorithm. The result of the comparison for the example of Table 2 is provided in Table 3.

The GA is applied based on the following steps:

  • Step 1. Initialization: 20 solutions are randomly generated. The following constraints are considered in producing the population: \(1\le k_i \le 5\) for \(i= \{1,2,3,4\}\); \(2\le n\le 30\) ; \(2\le m\le 100\).

  • Step 2. Fitness Function Computation: The value of the ECC is considered as the fitness function.

  • Step 3. Parent Chromosome Selection: A solution with a better fitness function has a greater chance to be selected as a parent chromosome. We used a roulette rule to select a chromosome.

  • Step 4. Crossover: The crossover rate is considered as 0.4; therefore, \(20.4=8\) chromosomes are used for crossover operation, and cross position is randomly selected.

  • Step 5. Mutation: The mutation rate is considered as 0.1, and the mutation position is randomly selected.

  • Step 6. Children Replacement in the Population: In this step, a roulette rule is applied to replace the children in the population.

  • Step 7. Repeat step 2 to 6 until a termination criterion is satisfied. The termination criterion is considered as 100 iterations of Steps 2 to 6.

Table 3 The Results of Optimization
Full size table

The results are reported in Table 3. As the results of Table 3 show, under the OM policy, the values of ECC for the GA and the full enumeration algorithm are 110 and 105.68, respectively, which have a little difference. The long-run expected average cost without considering the OM policy is considerably higher than that of the NOMIM. The time to perform PM based on the NOMIM model is considerably lower than the time to perform PM based on the OM policy, i.e., \(118.4< 176\). The cost reduction achieved by the OMIM is 26%. More specifically, based on Table 3, for the OMIM policy, at equal time intervals of 4.4, a sample with the size of 16 is taken from the second stage of the system. For each item in the sample, a paired observation is obtained as (x, y), i.e., observations \((x_{i1},y_{i1}), \ldots , (x_{i16},y_{i16})\) are collected at sampling time \(t_i\). The values of four statistics including \(\bar{x}_i, S_i^2, \bar{e}_i\), and \(S_{e_i}^2\) are computed based on the developments of Subsection 3.2 and plotted on the corresponding control charts. Then, Eqs. 3 and 4 are used to compute the upper and lower control limits of the corresponding charts. At a given sampling time point, if at least one of the control charts releases an alarm, according to the opportunistic maintenance policy, both stages of the process are investigated. This inspection may be followed by RMs, which renew the process. The maximum number of inspection periods is 40. In other words, if the process is not renewed due to the performance of RMs in the previous 39 inspection periods, PM is implemented at the time point of 176. Based on Table 3, for the OMIM policy, the control limit parameters of \(\bar{X}, S^2, \bar{e}\), and \(S_{e_i}^2\) are 3.63, 3.58, 4.29, and 2.52, respectively. Applying this policy minimizes the long-run ECC, which equals \(ECC = 110\). For the NOMIM policy, at equal time intervals of 1.48, a sample with the size of 10 is taken from the second stage of the system. In this scenario, the control limit parameters of \(\bar{X}, S^2, \bar{e}\), and \(S_{e_i}^2\) are 3.58, 2.75, 3.45, and 4.45, respectively. The minimized long-term ECC under the NOMIM policy is 148.25.

10.2 Comparison with the no-sampling inspection policy

In this subsection, we compare the performance of our proposed maintenance policies with the no-sampling inspection policy, which does not take into account sampling information, i.e., a stand-alone conventional maintenance policy. In the stand-alone maintenance model, it is assumed that no control charts and no sampling inspections are employed to monitor the state of the process. In other words, in each production cycle, the process starts its operation at zero-age (in the as-good-as-new state), while both stages of the process are in the in-control states. After a specific point of time, which is denoted by \(t_m\), i.e., decision variable of the model, the process is stopped and preventive/planned maintenance is conducted on the process. In the stand-alone maintenance model, therefore, the process is only renewed based on PM actions. Here, we consider the conventional maintenance policy where regardless of the state of the process, PM actions are performed at time \(t_m\). From renewal theory, the expected average cost per unit time for this policy is given by:

$$\begin{aligned} ECC(t_m) = \frac{\sum _{\nu =0,1}\sum _{u=0,1} C_{QC}^{u,\nu }E (T_{u,\nu }) +C_{PM}}{t_m+T_{PM}}. \end{aligned}$$
(45)

The optimal time to perform PM action for this policy is achieved, which is equal to 47.2 with a total cost of 166.30. As it is observed, the cost of the no-sampling inspection policy is considerably higher than the cost of the two proposed models.

10.3 Designed experiment

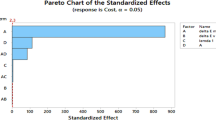
In this subsection, we perform a Designed Experiment (DE) to investigate which input parameters have significant effects on the model outputs considering the OM policy. For this purpose, a fractional factorial design with 11 factors and 32 runs is employed. More specifically, a \(2^{11-6}\) factorial design with resolution IV is conducted. For this experiment, we have selected input parameters at two levels in the DE, which are shown in Tables 4-6. The design is generated in MINITAB according to the parameters of each experiment, and the GA code of the models is implemented in MATLAB software for 32 runs. The results of the runs are analyzed in MINITAB, and the main findings are reported in Table 5 as well as Fig. 3. The main findings of the DE are reported here, and details of each run, which are not included here to save on space, are available upon request.

Table 4 The high and low levels of each factor in the DE
Full size table
Table 5 The results of the DE
Full size table

The “+” and “-” signs in each cell indicate the effect of each factor on response variables. For example, plus sign indicates a positive correlation between factors and response variables. A blank cell means that the corresponding response variable is insensitive to the factor. According to the results of the DE, for example, the values related to the magnitude of the shift of variance of both stages, i.e., \(\delta _2, \delta _4\) and the values that characterize the failure mechanism of the equipment, i.e., the shape and mean parameter of Weibull distribution, have a negative effect on the value of the ECC. On the other hand, the value of the cost of the process operating in the in-control and out-of-control states, the cost of sampling, and the cost of maintenance actions have an increasing effect on the value of the ECC. The results obtained from the factorial design are intuitive to some extent, e.g., as the results indicate, it is expected that increasing the value of the mean of failure mechanism leads to a decrease in the value of the ECC.

Fig. 3
figure 3

Normal probability plot associated with different effects on the \(t_m\)

Full size image

Table 5 summarizes the result of DE using Minitab software illustrating the effects of each factor on the response variables. Additionally, a normal probability plot associated with each effect on \(t_m\) is obtained as shown in Fig. 3, which is conducted to determine significant effects. The cut-off point of p-value is set to 0.05 to determine the significant factors. From the normal probability plot, it can be observed that the square points, which are colored in red, are significant factors as they appear far from the noise line. The points close to the noise line indicate the nonsignificant factors. According to Fig. 3, \(\delta _2,\delta _4\) and \(\mu _1,\mu _2\) have positive effects on \(t_m\), while costs associated with quality have negative effects on \(t_m\). Figure 4 illustrates the effects of change in the shape parameter \(\gamma\) of the Weibull distribution and the mean of Probability Failure Mechanism (PFM) \(\mu\) on the ECC for three maintenance models, i.e., OMIM, NOMIM, and stand-alone policy. In this analysis, without loss of generality, the same value is used for the mean of the PFM for both stages. In summary, the following conclusions are obtained:

  • As Fig. 4(a) indicates, increasing the value of \(\gamma\) leads to a decrease in the value of ECC for all three policies. In other words, the shape parameter of the Weibull distribution has a negative effect on ECC. This result is well-aligned with the results of DE summarized in Table 5.

  • As Fig. 4(a) indicates, increasing the value of \(\gamma\) decreases the differences between ECC of OMIM and NOMIM policies. In other words, the shape parameter has a negative effect on IF. This is an expected observation as the result of DE in Table 5 indicates the same behavior.

  • As can be observed in Fig. 4(b), increasing the mean, significantly decreases the ECC for all three policies. This means that \(\mu _1\) and \(\mu _2\) have a negative effect on ECC, which is also observable from the results of the DE. The reason for this behavior is that when the value of \(\mu\) is small, the meantime which the process is in control becomes smaller indicating a less stable process. Furthermore, it means that the time duration that the process spends in the in-control state is short. As such in the long run, the process spends more time in the out-of-control state, which eventually increases the long-run expected average cost. On the other hand, when \(\mu\) is large, the process is more stable; therefore, the low cost will be incurred.

  • The results also show that the proposed OMIM policy has a superior performance in terms of cost reduction in comparison with its counterparts.

Fig. 4
figure 4

(a) Effect of shape parameter on the total cost. (b) Effect of mean on total cost

Full size image

10.4 Comparison of the OMIM and the NOMIM

In this subsection, we compare the two proposed integrated models based on the Improvement Factor (IF), which is defined as follows:

$$\begin{aligned} IF = \Big (1- \frac{ECC_{OMIM}(\eta )}{ECC_{NOMIM}(\eta )}\Big ) \times 100. \end{aligned}$$
(46)

The value of the IF indicates the reduction in the operational cost due to the performance of the opportunistic policy. The DE is again employed for the NOMIM, and the value of the \(ECC_{NOMIM} (\eta )\) is computed in each run. Note that in order to perform the DE for the NOMIM model, the following additional factors introduced in Table 6 are considered:

Table 6 The high and low levels associated with each factor in the DE for the NOMIM model
Full size table

Using Eq. (46), the values of the IF can be obtained for 32 runs considering both the OMIM and the NOMIM models. The results are summarized in Table 5. According to the results, the following factors have significant effects on the value of the IF: (i) The values related to the shape and the mean of the Weibull distribution, and; (ii) The value of the process operation cost in the in-control state. These factors have a negative effect on the IF, meaning that for the smaller values of the process operational cost in the in-control state, the OM policy leads to more improvement with respect to the NOMIM policy. Also, utilization of the OM policy for the equipment that has a larger failure rate is more effective. Furthermore, the result of 32 runs of the DE shows that the OM policy leads to an average decrease of \(15\%\) in the expected total cost. Although in some cases, a \(35\%\) reduction in the operational cost is observed. From the analyses of this section, three main findings can be summarized as follows:

  • Conducting OM policy significantly decreases the operational costs of the system. As the failure rate of the system increases, more savings can be expected from the implementation of OM.

  • The effectiveness of the OM policy in reducing operational costs of the system increases as the variation in the failure mechanism of the system increases.

  • Coordination of the decision of maintenance and quality control in multi-stage manufacturing systems noticeably decreases the cost of the system in comparison with standalone models.

11 Conclusion

Most of advanced manufacturing systems, such as the process assembly of automobile bodies, involve several stages where operations are sequentially conducted to manufacture the final product. Such dependent multi-stage manufacturing processes heavily rely on the operation of their constituent technical components and systems, which are subject to degradation and unexpected failures. In this context, we considered a two-stage dependent process and have developed two innovative integrated SPC and MP models to minimize the long-run expected average cost per unit time. The proposed models can be applied to a wide range of industries within manufacturing such as tool industry, textile industry, and automobile industry to name but a few, and other sectors such as healthcare and transportation with some modifications. Developments of the paper are, therefore, of practical importance for industrial practitioners who aim to jointly incorporate proper maintenance and control strategies to achieve cost minimization. More specifically, we assumed the presence of two types of assignable causes each associated with one of the two stages of the underlying process, which affect both the mean and the variance of the process. Four control charts, \(\bar{X}-S^2\), \(\bar{e} - S^2_e\) are simultaneously designed and applied for process monitoring. Two main integrated SPC and MP models namely the OMIM and NOMIM are developed such that the former is developed based on the OM concept. On the other hand, to see the effectiveness of the OM policy within an integrated model, the NOMIM is also developed considering no opportunistic maintenance. Besides, the proposed models are compared with a no-sampling inspection policy. The proposed models are formulated in the renewal theory framework, and GA is applied to obtain the optimal values of decision variables minimizing the long-run expected average cost per unit time. The models are developed based on recursive equations and considering different scenarios in an inspection interval rather than different scenarios in a production cycle, which strengthens the proposed models.

The results of 32 runs of the DE show that the OM policy leads to an average decrease of 15% in the expected total cost, although in some cases, a 35% reduction in the operational cost is observed. It is concluded that utilization of the OM policy for the equipment that has a larger failure rate is more effective. Furthermore, for the production process with Weibull distributed failure mechanism, as the shape parameter of the distribution decreases and approaches to an exponential distribution, more savings can be expected by employing the OM policy. Finally, integration of the decisions of the maintenance and quality yields a noticeable decrease in the total expected cost of multi-stage production systems. These results illustrate the superior performance of the newly developed OMIM model, which can be considered as a major step forward contribution within the context of integrated SPC and MP modeling.