A novel sensitivity analysis of translational axis operation considering key component tolerances

Abstract

At present, it is difficult to predict the operation accuracy of machine tools in the preliminary design stage. How to quantitatively reflect the contribution of tolerance on the position error of machine tool has a significant guidance for machine tool design stage. Thus, this paper presents a sensitivity analysis method based on components tolerance, which can clearly give the machine tool designer key the tolerances. Firstly, taking the translational axis as the research object, the operation accuracy model of Y-axis is established based on the homogeneous transform matrix (HTM) and multi-body system (MBS) theory. Meanwhile, the relationship between tolerances and geometric errors has been mapped by the Fourier expansion and the model of parameters have been identified by self-design simulation. As a basis, the tolerance sensitivity analysis (TSA) method based on the single-factor partial derivation is constructed to acquire the key tolerance parameters. Finally, the result of the experiment shows that the assembly tolerance of the Y-Z plane of the base, the manufacturing tolerance of the lead screw and the assembly tolerance of the X-Y plane of the carriage contribute a great deal to the position error, which needs to be strictly controlled in the future design to improve the accuracy of the machine tool.

1 Introduction

Many factors affect the machining accuracy of the machine tools, such as geometric errors, thermal errors, cutting-force induced errors, and tool wear errors. In these errors, the geometric error, which is caused by inaccuracies built-in components and assembly errors, forms one of the biggest sources of inaccuracy [1]. In order to improve the machining accuracy of machine tools, the geometric errors of machine tools have been studied deeply in the past decades. At present, there are two main methods of position error modeling : (1) Establishment of position error model based on multi-body system theory (MBS) and homogeneous transformation coordinate transformation (HTM) [2]. (2) The spinor method introduce by the principle of robot motion [3]. In the modeling of machine tool position error, the translational axis is generally at the low end of the machine tool kinematic chain, which means that the accumulation of its geometric errors has a negative effect on the position error. Therefore, it is of great significance to promote the machining accuracy in the whole machine by improving the running accuracy of translational axis. However, in the machine tool design stage, it is impossible for the designer to obtain the position error of the machine tool in advance, which means that the tolerance value of machine tool components can only be set by experience. Obviously, it is enough to flexibly adjust the relationship between the accuracy of machine tool and other factors, such as customer demand, cost, etc., according to the empirical design method, which greatly limits the development of machine tool. Thus, it is an important method to improve the machining accuracy to establish the relationship between the assembly and manufacturing tolerance and the position error of the translational axis. In this paper, the translational axis is selected as the research object, and the assembly error of its key components is studied.

In addition, most of them focused on the study of guide surface morphology error, which reveals the relationship between error source parameters and tolerance by establishing the mathematical model of guide surface morphology. In one of the earliest studies, Bryan [4]. Tani et al. [5] measured the granite surface geometric straightness errors of a coordinate measuring machine with an air bearing slider and compared the directly measured joint kinematic straightness with the indirectly determined one through joint kinematic angular error integration. Hwang et al. [6] proposed a three-probe system for measuring the parallelism and straightness of a pair of rails for ultra-precision guideways. They performed a numerical analysis of the measurement algorithm and validated it with a pair of function defined rails. Ekinci et al. [7] carried out an experiment in researching relationship between SaA errors. The author firstly gave a systematic error classification about different error definitions, and a simulation between guideway and errors was introduced. Zha et al. [8] presented an approach to model and compensate the vertical straightness error of gantry type open hydrostatic guideways. Tang et al. [9] introduced a systematic method to calculate the straightness and angle error based on the measurement of guideway surface and fitting curve. Through accurate measurement, he selected more accurate trigonometric function and polynomial fitting method to replace the traditional Fourier fitting method. Until 2017, Fan et al. [10] introduced the concept of guide tolerance for the first time and used truncated Fourier expansion to reveal the internal relationship between the error source parameters and guide tolerance, which means a further step in the design of the quantitative precision of the guide tolerance. As can be observed abovementioned researches, the above models were insufficient to clearly reveal the mapping rules of geometric errors and surface morphology of the guideways to predict the geometric error of translational axis. However, the assembly error of key components of the translational axis was not considered. It is also essential that the error relationship in the assembly process should be paid more attention. Besides, it is apparent that in the design stage of machine tools, only the information of key components’ tolerance can be acquired in advance. The geometric errors are unknown, since geometric error is a parameter generated after assembly of translational axis. Thus, a new error model of translational axis based on tolerance is urgently needed for the identification of crucial tolerance parameters to improve the accuracy of translational axis.

On the basis of the established error model, the sensitivity of model parameters is usually quantified by the sensitivity analysis (SA). the SA is more suitable for the position error, which has componenticular error ranges and the intercoupling and random characteristics. Fan et al. [11] performed a sensitivity analysis of the 3-PRS parallel kinematic spindle platform by using the componential differential method based on the error transformation vectors and found the critical parameters to the accuracy. Pott et al. [12] analyzed the sensitivity of the kinematic sensitivity of parallel mechanism by means of a simplified sagittal force; the correctness of the method was verified by analyzing the 6-DOF parallel mechanism. Cheng et al. [13] took the stochastic characteristic of geometric errors into consideration and used the Sobol method to identify key geometric errors of machine tool, which is helpful to improve the machining accuracy of multi-axis machine tool. Fan et al. [14] proposed kinematics of a multi-body system theory (MBS) by adding movement and positioning error terms. This approach allowed development of a generalized kinematic model, applicable to the NC machine tools. Through strict geometric error sensitivity analysis (SA), the most critical geometric errors can be identified and strictly controlled, which significantly improved the machining accuracy of CNC machine tools [15]. In view of the above, it should be noted that SA is a direct and effective method to solve the problem of high coupling of multiple factors, which is expressed by the contribution of a certain factor to the total system. However, these SA methods are aimed to find the key geometric error parameters that are sensitive to position error, which is difficult to give instructional advice at the stage of machine tool design. It is obvious that there is lack of a complete theoretical analysis method in quantitative analysis the tolerance and position error of translational axis at present.

To overcome the drawbacks of above problems, this paper proposed a novel tolerance sensitivity analysis (TSA) method combing for identify the key tolerance parameters. It means that the position error of translational axis is firstly established to present the mapping rules between geometric errors and tolerance based on truncated Fourier. Then, the tolerance sensitivity analysis (TSA) model of translational axis, which result possesses useful information to help machine tool designers, is built to quantify tolerance sensitivity for the determination of the key tolerance and sensitive components.

The remains of the paper are organized as follow. The position error model of the translational axis is established by homogeneous transform matrix (HTM) and multi-body system (MBS) theory in Section 2. In Section 3, the TSA method of translational axis is modeled. In Section 4, the simulation for the parameters of TSA is performed to identify the key tolerance parameters and component. At last, the conclusions are drawn in Section 5.

2 Geometric errors of the translational axis

The geometric errors of the translational axis are predominantly caused by the assembly deviations and manufacturing defects of the motion axes. In order to study the geometric error that influence the accuracy of the translational axis, the each geometric error of component will be explored in the error model. It is essential to determine the assembly relationship of components for modeling the position error of translational axis. On the basis, the HTM and MBS theory are used to establish the position error model of translational axis. The position error represents the overall position errors of the base relative to the carriage in a translational axis combining all the axis kinematic errors and link geometric errors such as the squareness errors between axes. The basic structure of the translational axis is analyzed, and its structure diagram is shown in Fig. 1. It is mainly composed of base, guideway, slider, lead screw, support unit, carriage and driving component. In the basic structure of translational axis, the guideway is fastened on the base by bolts, which the side is pressed with a wedge block. The sliders and the guideway are usually in contact with the ball in the slider. The carriage is fixedly connected with the four sliders on the guideway by bolts. This paper mainly considers the geometric error of the single axis movement, ignoring the influence of the motor drive and servo matching of the lead screw component.

Fig. 1

Structure drawing of translational axis

2.1 Position error model of translational axis

In the analysis of the structural relationship between the components of the single axis, the transmission process of geometric error is the transmission chain from the base to the carriage. The assembly error of the base will cause two major squareness errors. Similarly, when the guideway and slide block are installed on the base, there are also two main squareness errors. However, due to the relative motion of the guideway and the slider, there will generate five geometric errors except positioning error caused by manufacturing errors, including two straightness errors and three angle errors. The position error of sliders is mainly caused by the imperfection of ball screw pair or the servo drive of the motor. Since carriage and the four sliders are fastened by bolts, there will occur two squareness errors in X-Y and Y-Z plane. Thus, there are 12 geometric errors of translational axis shown in Table 1.

Table 1 The geometric error of translational axis

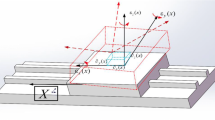
Taking Y-axis as an example, the structure of the axis is divided into four components: base, guideway, slider, and carriage. Based on the above analysis of the errors of each component of the translational axis, it is necessary to establish the characteristic transfer matrix among each component. According to the above four components of the single axis, the base, the guideway slider and the carriage, the coordinate system of the translational axis is established, as shown in Fig. 2. The coordinate system 1 is established on the upper surface of the base, whose the center point is taken as the origin of the coordinate system. The coordinate system 2 and the coordinate system 3 are established for the guideway and sliders respectively, whose the origin of the coordinate system is at the initial position of the upper surface of the guideway. The origin of coordinate system 4 is the place where the center points of the four sliders coincide with the carriage The four sliders are marked as 1, 2, 3, and 4 respectively. The error characteristic matrix of different components in different coordinate systems is established respectively, and then the position error model of single axis is established according to the transmission chain from base to carriage.

Fig. 2

Schematic diagram of coordinate

Based on HTM, it can be used to represent the transformation matrix of the base relative to the reference coordinate system at a small displacement. The actual transformation matrix of one axis is regarded as consisting of four matrices: position matrix, position error matrix, motion matrix, and motion error matrix [16, 17]. The assembly error and manufacturing error of translation axis are established as position error matrix and motion error matrix respectively. They have been commonly used in the geometric error modeling, which is the basis of quantitative error to calculation.

The ideal transformation matrix and the error transformation matrix are as follow respectively.

$$ \left\{\begin{array}{c}{T}_1^p=\left[\begin{array}{cccc}1& 0& 0& {x}_1\\ {}0& 1& 0& {y}_1\\ {}0& 0& 1& {z}_1\\ {}0& 0& 0& 1\end{array}\right],{T}_1^{pe}=\left[\begin{array}{cccc}1& -{\varepsilon}_{1 yz}& 0& 0\\ {}{\varepsilon}_{1 yz}& 1& -{\varepsilon}_{1 xy}& 0\\ {}0& {\varepsilon}_{1 xy}& 1& 0\\ {}0& 0& 0& 1\end{array}\right]\\ {}{T}_1^s=E=\left|\begin{array}{cccc}1& 0& 0& 0\\ {}0& 1& 0& 0\\ {}0& 0& 1& 0\\ {}0& 0& 0& 1\end{array}\right|,{T}_1^{se}=E\end{array}\right. $$

(1)

where T_jp,T_jpe T_js,T_jserepresent the j-th body of position matrix, position error matrix, motion matrix and motion error matrix, respectively. E represents the forth order unit matrix.

Based on the coordinate transformation theory, the error characteristic matrix of the guideway is given. On this basis, the ideal and error transformation matrices and are given respectively.

$$ \left\{\begin{array}{c}{T}_2^p=\left[\begin{array}{cccc}1& 0& 0& {x}_2\\ {}0& 1& 0& {y}_2\\ {}0& 0& 1& {z}_2\\ {}0& 0& 0& 1\end{array}\right],{T}_2^{pe}=\left[\begin{array}{cccc}1& -{\varepsilon}_{2 yz}& 0& 0\\ {}{\varepsilon}_{2 yz}& 1& -{\varepsilon}_{2 xy}& 0\\ {}0& {\varepsilon}_{2 xy}& 1& 0\\ {}0& 0& 0& 1\end{array}\right]\\ {}{T}_2^s=\left[\begin{array}{cccc}1& 0& 0& 0\\ {}0& 1& 0& y\\ {}0& 0& 1& 0\\ {}0& 0& 0& 1\end{array}\right],{T}_2^{se}=\left[\begin{array}{cccc}1& -{\varepsilon}_{2z}(y)& {\varepsilon}_{2y}(y)& {\delta}_{2x}(y)\\ {}{\varepsilon}_{2z}(y)& 1& -{\varepsilon}_{2x}(y)& {\delta}_{2y}(y)\\ {}-{\varepsilon}_{2y}(y)& {\varepsilon}_{2x}(y)& 1& {\delta}_{2z}(y)\\ {}0& 0& 0& 1\end{array}\right]\end{array}\right. $$

(2)

To give more clarifications to Eq. (2), it is assumed that the center of the four sliders is the bottom rotation center point of the carriage fixed on the four sliders. Because of the need to calculate the geometric errors of the four sliders, the error characteristic matrix is established for the geometric errors of the four sliders. The ideal transformation matrix and error transformation matrix of the four sliders are as follow respectively.

$$ \left\{\begin{array}{c}{T}_{2a}^p=\left[\begin{array}{cccc}1& 0& 0& {x}_{2a}\\ {}0& 1& 0& {y}_{2a}\\ {}0& 0& 1& {z}_{2a}\\ {}0& 0& 0& 1\end{array}\right]{T}_{2a}^{se}=\left[\begin{array}{cccc}1& -{\varepsilon}_z(y)& {\varepsilon}_y(y)& {\delta}_x(y)\\ {}{\varepsilon}_z(y)& 1& -{\varepsilon}_x(y)& {\delta}_y(y)\\ {}-{\varepsilon}_y(y)& {\varepsilon}_x(y)& 1& {\delta}_z(y)\\ {}0& 0& 0& 1\end{array}\right]\\ {}{T}_{2b}^p=\left[\begin{array}{cccc}1& 0& 0& {x}_{2a}+{D}_x\\ {}0& 1& 0& {y}_{2a}\\ {}0& 0& 1& {z}_{2a}\\ {}0& 0& 0& 1\end{array}\right]{T}_{2b}^{se}=\left[\begin{array}{cccc}1& -{\varepsilon}_z(y)& {\varepsilon}_y(y)& {\delta}_x(y)\\ {}{\varepsilon}_z(y)& 1& -{\varepsilon}_x(y)& {\delta}_y(y)\\ {}-{\varepsilon}_y(y)& {\varepsilon}_x(y)& 1& {D}_x\ast {\varepsilon}_{2 xz}+{\delta}_z(y)\\ {}0& 0& 0& 1\end{array}\right]\\ {}{T}_{2c}^p=\left[\begin{array}{cccc}1& 0& 0& {x}_{2a}\\ {}0& 1& 0& {y}_{2a}-{D}_y\\ {}0& 0& 1& {z}_{2a}\\ {}0& 0& 0& 1\end{array}\right]{T}_{2c}^{se}=\left[\begin{array}{cccc}1& -{\varepsilon}_z(y)& {\varepsilon}_y(y)& -{D}_y\ast {\varepsilon}_{2 xy}+{\delta}_x(y)\\ {}{\varepsilon}_z(y)& 1& -{\varepsilon}_x(y)& {D}_x\ast {\varepsilon}_{2y\mathrm{z}}+{\delta}_y(y)\\ {}-{\varepsilon}_y(y)& {\varepsilon}_x(y)& 1& {\delta}_z(y)\\ {}0& 0& 0& 1\end{array}\right]\\ {}{T}_{2d}^p=\left[\begin{array}{cccc}1& 0& 0& {x}_{2a}+{D}_x\\ {}0& 1& 0& {y}_{2a}-{D}_y\\ {}0& 0& 1& {z}_{2a}\\ {}0& 0& 0& 1\end{array}\right]{T}_{2d}^{se}=\left[\begin{array}{cccc}1& -{\varepsilon}_z(y)& {\varepsilon}_y(y)& -{D}_y\ast {\varepsilon}_{2 xy}+{\delta}_x(y)\\ {}{\varepsilon}_z(y)& 1& -{\varepsilon}_x(y)& {D}_x\ast {\varepsilon}_{2 yz}+{\delta}_y(y)\\ {}-{\varepsilon}_y(y)& {\varepsilon}_x(y)& 1& {D}_x\ast {\varepsilon}_{2 xz}+{\delta}_z(y)\\ {}0& 0& 0& 1\end{array}\right]\end{array}\right. $$

(3)

Since the slider and carriage are fixed by bolts, the geometric errors of the four slider centers can be calculated to get the geometric errors of the slider. The linear errors in the X, Y and Z directions can be obtained from the average errors of the four sliders. The angle error can be obtained by calculating the angle error of the center line of the carriage. The yaw angle around the Y axis and the pitch angle around the X axis can be obtained by calculating the inclination angle of the median line of the carriage, and the inclination angle around the Z axis can be obtained by calculating the X, y translational vectors and the length of the diagonal line of the carriage. According to Eq. (3), the position vectors of the center points of the four sliders are calculated as follows.

$$ \left\{\begin{array}{c}{\delta}_{2x}(y)=\frac{\delta_x(y)+{\delta}_x(y)-{D}_x\ast {\varepsilon}_{2 xy}+{\delta}_x(y)-{D}_y\ast {\varepsilon}_{2 xy}+{\delta}_x(y)}{4}={\delta}_x(y)-\frac{D_y\ast {\varepsilon}_{2 xy}}{2}\\ {}{\delta}_{2y}(y)=\frac{\delta_y(y)+{\delta}_y(y)+{D}_z\ast {\varepsilon}_{2y\mathrm{z}}+{\delta}_y(y)+{D}_z\ast {\varepsilon}_{2y\mathrm{z}}+{\delta}_y(y)}{4}={\delta}_y(y)+\frac{D_z\ast {\varepsilon}_{2 yz}}{2}\\ {}{\delta}_{2y}(y)=\frac{\delta_y(y)+{\delta}_y(y)+{D}_z\ast {\varepsilon}_{2y\mathrm{z}}+{\delta}_y(y)+{D}_z\ast {\varepsilon}_{2y\mathrm{z}}+{\delta}_y(y)}{4}={\delta}_y(y)+\frac{D_z\ast {\varepsilon}_{2 yz}}{2}\\ {}\begin{array}{c}{\varepsilon}_{2x}(y)=\frac{\frac{\varepsilon_{2 ax}(y)+{\varepsilon}_{2 cx}(y)}{2}-\frac{\varepsilon_{2 bx}(y)+{\varepsilon}_{2 dx}(y)}{2}}{D_x}\\ {}{\varepsilon}_{2y}(y)=\frac{\frac{\varepsilon_{2 ay}(y)+{\varepsilon}_{2 by}(y)}{2}-\frac{\varepsilon_{2 cy}(y)+{\varepsilon}_{2 dy}(y)}{2}}{D_y}\\ {}{\varepsilon}_{2z}(y)=\frac{\sqrt{{\left[{\delta}_{2x}(y)\right]}^2+{\left[{\delta}_{2y}(y)\right]}^2}}{\sqrt{\frac{D_x^2+{D}_y^2}{2}}}\end{array}\end{array}\right. $$

(4)

Unfortunately, Eq. 4 is overdetermined equations which needs to be solved by minimizing the total square deviation. In fact, there are other factors, such as small unexpected deviations caused by temperature changes and stress deformation. Thus, the correct geometric errors will minimize the total square deviation. It is assumed that there is always a deviation ∆ n between the actual position of the center point under the sliding plate and the position of the point obtained according to the transfer matrix. It is assumed that there is always a deviation between the actual position of the center point under the slide plate and the position of the point obtained according to the transfer matrix.

$$ \Delta n={\left|\overrightarrow{n_{2a3}}-\overrightarrow{n_{2a}}\right|}^2+{\left|\overrightarrow{n_{2b3}}-\overrightarrow{n_{2b}}\right|}^2+{\left|\overrightarrow{n_{2c3}}-\overrightarrow{n_{2c}}\right|}^2+{\left|\overrightarrow{n_{2d3}}-\overrightarrow{n_{2d}}\right|}^2 $$

(5)

In order to get the minimum deviation, the minimum value is obtained by solving these equation where the total square deviation Δn has no intrinsic connection with assembly error ɛij (i,j=x,y,z).

$$ \frac{\mathrm{\partial \Delta }n}{\partial {\varepsilon}_{2 xy}}=0,\frac{\mathrm{\partial \Delta }n}{\partial {\varepsilon}_{2 xz}}=0,\frac{\mathrm{\partial \Delta }n}{\partial {\varepsilon}_{2 yz}}=0 $$

(6)

In the assembly process of guideway, the error transfer relationship model has been obtained. This method has a deeper understanding of the error relationship between sliders and guideway in the assembly process.

The geometric error of the carriage is mainly affected by the assembly error between the carriage and the sliders.

$$ \left\{\begin{array}{c}{T}_3^p=\left[\begin{array}{cccc}1& 0& 0& {x}_3\\ {}0& 1& 0& {y}_3\\ {}0& 0& 1& {z}_3\\ {}0& 0& 0& 1\end{array}\right],{T}_3^{pe}=\left[\begin{array}{cccc}1& -{\varepsilon}_{3 yz}& 0& 0\\ {}{\varepsilon}_{3 yz}& 1& {\varepsilon}_{3 xy}& 0\\ {}0& -{\varepsilon}_{3 xy}& 1& 0\\ {}0& 0& 0& 1\end{array}\right]\\ {}{T}_3^s=E,{T}_3^{se}=E\end{array}\right. $$

(7)

Assuming that the measured point of the carriage is r=(0,0,d,1) in the coordinate of carriage, the position error of Y-axis can be calculated.

$$ \overrightarrow{\Delta E}={\left(\Delta {E}_x,\Delta {E}_x,\Delta {E}_x,0\right)}^T=\overrightarrow{T_a}-{\overrightarrow{T}}_i=\sum \limits_{j=1}^3\left({T}_j^p{T}_j^{pe}{T}_j^s{T}_j^{se}-{T}_j^p{T}_j^s\right)\overrightarrow{\gamma} $$

(8)

By simplifying and removing the higher-order terms, the position error of the Y-axis can be calculated

$$ {\displaystyle \begin{array}{l}\Delta {E}_x=\hbox{-} d\ast {\varepsilon}_y(y)\hbox{-} {\varepsilon}_{1 yz}\ast {y}_2\hbox{-} {x}_3+{z}_3\ast {\varepsilon}_y(y)\hbox{-} \mathrm{Y}\ast \left({\varepsilon}_{1 yz}+{\varepsilon}_{2 yz}\ \right)+{\delta}_x(y)\\ {}\Delta {E}_y={x}_3\ast {\varepsilon}_z(y)-{\mathrm{y}}_3-{\varepsilon}_{1 xy}\ast {z}_2+{y}_3-{z}_3\ast \left({\varepsilon}_{1 xy}+{\varepsilon}_{2 xy}+{\varepsilon}_x(y)\right)+{\delta}_y\left(\mathrm{y}\right)\\ {}-d\ast \left({\varepsilon}_{3 xy}+{\varepsilon}_{2 xy}+{\varepsilon}_{1 xy}+{\varepsilon}_x(y)\right)+{\varepsilon}_{1 yz}\ast {x}_2\\ {}\Delta {E}_z={\varepsilon}_{1 xy}\ast {y}_2-d-{\mathrm{z}}_3-{x}_3\ast {\varepsilon}_y(y)+{\varepsilon}_{3 xy}\ast d+Y\ast \left({\varepsilon}_{1 xy}+{\varepsilon}_{2 xy}\right)\\ {}+{y}_3\ast \left({\varepsilon}_{1 xy}+{\varepsilon}_{2 xy}+{\varepsilon}_x(y)\ \right)+{z}_3+{\delta}_z(y)\end{array}} $$

(9)

3 TSA of key components of translational axis

In the stage of machine tool design, it is available for the designer of machine tool possess the information about the tolerance of components instead of the assembly and manufacturing error source parameters. Therefore, it is significant to identify the key tolerance parameters for improving the accuracy of machine tools. In this paper, the position error of Y-axis is selected as the total system output and the tolerance is selected as the system input parameter which are used to establish a single factor sensitivity analysis model. It is more intuitive and effective to reflect the contribution of each tolerance parameter to the position error of Y-axis. However, there are two steps to analyze the tolerance sensitivity of Y-axis components. Firstly, the internal relationship between the geometric error parameters and the corresponding tolerance parameters needs to be mapped, which is the key for tolerance quantitative analysis. Secondly, on this basis, the tolerance sensitivity analysis (TSA) model is derived to evaluate the key tolerance parameters of component.

3.1 Describe the relationship between tolerance and geometric error

In the past research, the tolerance modeling of guideway has been deeply studied, such as trigonometric series [9], Fourier expansion method [3], polynomial method [18], and truncated Fourier expansion method [10], where the geometric error parameters are fitted by the related tolerance using the function relations. The assembly and manufacturing errors of key components of translational axis are the main cause for geometric errors, which are confined within the tolerance zone. There are several different surface error forms of Y-axis components due to different machining processes. Since these geometric errors of Y-axis fulfill Dirichlet boundary conditions, the geometric error can be fitted by the corresponding tolerance. Taking Y-axis as an example, the geometric error can be deserved as

$$ G=d\sin \lambda y $$

(10)

where G represents the geometric error parameter, d represent the corresponding tolerance, and λ represents the tolerance model parameter.

The straightness errors and angle errors [19] of the guideway can be estimated by the corresponding tolerance parameters. As is known to us, the straightness errors and angle errors of guideway can be described by the corresponding tolerance parameters, respectively.

$$ \left\{\begin{array}{c}{\delta}_x(y)={d}_{sx}\sin {\lambda}_1y,{\delta}_{\mathrm{z}}(y)={d}_{sz}\sin {\lambda}_1y\\ {}{\varepsilon}_x(y)=\frac{\delta_z(y)}{D_y},{\varepsilon}_y(y)={d}_{2 hxz}\frac{\sin {\lambda}_1y}{D_x}\\ {}{\varepsilon}_z(y)=\frac{\delta_x(y)}{D_y}\end{array}\right. $$

(11)

Since these geometric error parameters are all caused by manufacturing error of the guideway, the fitting parameter λ₁ is the same. The positioning error of the guideway is mainly caused by the accumulated error of the lead screw and the tolerance of the lead screw. Its error parameters can be expressed by a first-order linear function and a first-order truncated Fourier. Thus, the positioning error can be expressed as

$$ {\delta}_y(y)= ay+{d}_{sy}\sin {\lambda}_2y $$

(12)

where a is the constant coefficient, and the fitting parameter λ₂ is related to the tolerance of the lead screw.

However, the squareness errors are considered as fixed values according to Ref [10], ignoring the influence of assembly errors on the total system errors. It will undeniably lead to an error increment of 1 in sensitivity analysis, which will greatly distort the error analysis results. In the actual assembly process, the shape variable of the bolt connection between the two contact surfaces caused by the different preloading force will lead to the assembly error of each position on the guideway is not unique [2]. Therefore, this paper takes symmetrical slider as an example to build the relationship between squareness errors and tolerance. As can be seen from Fig. 3, the squareness error ε_xy of sliders in the X-Y plane can be fitting by tolerance d_hxy. Since it is assumed that all components of the Y axis have the same assembly mode, the fitting parameter λ₃ is the same in the assembly error.

Fig. 3

Relationship diagram of assembly error and tolerance

$$ \left\{\begin{array}{c}{\varepsilon}_{xy}={d}_{hxy}\frac{\sin {\lambda}_3y}{f_y}\\ {}{\varepsilon}_{yz}={d}_{hyz}\frac{\sin {\lambda}_3y}{f_y}\end{array}\right. $$

(13)

where d_sx, d_sy, d_szrepresent straightness tolerance in X, y and Z directions respectively. d_hrepresents the parallelism tolerance between two identical bodies, L represents the distance between two identical bodies, and f_y represents the length of each key component of Y-axis in the Y direction. The fitting parameter λ₃ is related to the assembly tolerance of each key component.

By substituting the tolerance and error model into the position error model of Y-axis, the position error model based on tolerances can be obtained

$$ {\displaystyle \begin{array}{l}\Delta {E}_x=\hbox{-} d\ast {d}_{2 hxz}\sin \left({\lambda}_1\mathrm{y}\right)/{\mathrm{D}}_y\hbox{-} {\mathrm{d}}_{1 hyz}\ast \sin \left({\lambda}_3\mathrm{y}\right)\ast {y}_2/{\mathrm{D}}_y\hbox{-} {x}_3+{z}_3\ast {d}_{2 hxz}\sin \left({\lambda}_1\mathrm{y}\right)/{\mathrm{D}}_x\ \\ {}\hbox{-} \mathrm{Y}\ast \left({\mathrm{d}}_{1 hyz}/\mathrm{L}+{\mathrm{d}}_{2 hyz}/{\mathrm{D}}_{\mathrm{y}}\right)\ast \sin \left({\lambda}_3\mathrm{y}\right)+{d}_{2 sz}\sin \left({\lambda}_1\mathrm{y}\right)\\ {}\Delta {E}_y={x}_3\ast {d}_{2 sz}\sin \left({\lambda}_1\mathrm{y}\right)/{\mathrm{D}}_y-{\mathrm{y}}_3-{d}_{1 hxy}\ast \sin \left({\lambda}_3\mathrm{y}\right)\ast {z}_2+{y}_3-{z}_3\ast \left[{d}_{1 hxy}\ast \sin \left({\lambda}_3\mathrm{y}\right)+{d}_{2 hxy}\ast \sin \left({\lambda}_3\mathrm{y}\right)+{\varepsilon}_x(y)\right]\\ {}+{d}_n\sin {\lambda}_2y+ ay-d\ast \left({d}_{3 hxy}/L+{d}_{2 hxy}/{\mathrm{D}}_{\mathrm{y}}+{d}_{1 hxy}/L\right)\sin \left({\lambda}_3\mathrm{y}\right)+\mathrm{d}\ast {d}_{2 sx}\sin \left({\lambda}_1\mathrm{y}\right)/{\mathrm{D}}_y+{d}_{1 hyz}\ast \sin \left({\lambda}_3\mathrm{y}\right)\ast {x}_2\\ {}\Delta {E}_z={d}_{1 hxy}\ast \sin \left({\lambda}_3\mathrm{y}\right)\ast {y}_2/L-d-{\mathrm{z}}_3-{x}_3\ast {d}_{2 hxz}\sin \left({\lambda}_1\mathrm{y}\right)/{\mathrm{D}}_x+{d}_{3 hxy}\ast \sin \left({\lambda}_3\mathrm{y}\right)\ast d/L\\ {}+Y\ast \left({d}_{1 hxy}/L+{d}_{2 hxy}/{\mathrm{D}}_{\mathrm{y}}\right)\ast \sin \left({\lambda}_3\mathrm{y}\right)+{y}_3\ast \left({d}_{1 hxy}/\mathrm{L}+{\mathrm{d}}_{2 hxy}/{\mathrm{D}}_{\mathrm{y}}\right)\ast \sin \left({\lambda}_3\mathrm{y}\right)\\ {}+{y}_3\ast {d}_{2 sz}\sin \left({\lambda}_1\mathrm{y}\right)/{\mathrm{D}}_y\ \Big)+{z}_3+{d}_{2 sz}\sin \left({\lambda}_1\mathrm{y}\right)\end{array}} $$

(14)

For the convenience of expression, let λ=(λ₁,λ₂,λ₃) represent a collection of parameters. It should be noted that

• (1) Elastic deformation of components is not taken in consideration, and all components are rigid bodies by default.

• (2) The processing technology of each same component is exactly the same.

3.2 Define of TSA

In order to speed up the identification of the key tolerance parameters, it is necessary to analyze the sensitivity of position error. Sensitivity analysis is a method to study the quantitative description of mathematical model. The common methods of sensitivity calculation are direct method, first-order function method and higher-order function method. The direct solution method needs a lot of calculation, and the process is more complex, and the feasibility is poor. the sensitivity function method widely spread and applied in all fields at present, which has great advantages in the amount of calculation and practicability. The higher-order sensitivity function method is difficult to solve and its application scope is small. Therefore, the single-factor partial derivative method is applied to solve the sensitivity index of each tolerance. For a system with N input parameters, the response function is F(x). Assuming that F(x) = [x₁, x₂…x_n]is differentiable and X_j represents the parameter of the function, the first-order sensitivity of the i-th input parameter to F(x) can be deserved as

$$ {S}_j=\left|\frac{\partial F(x)}{\partial {x}_j}\right|,j=1,2\dots n $$

(15)

In practice, each system function may contain multiple subfunctions, and the weight of each parameter in the subfunction may be different. It is necessary to carry out sensitivity analysis on each subfunction, and then calculate the weight in the whole system. If y_i=[x₁,x₂...x_n] is the component function of F(y)=[y₁,y₂...y_m], the sensitivity of the jth input parameter to the ith subsystem will be obtained as

$$ {S}_{x_j}^{{\mathrm{y}}_i}=\left|\frac{\partial {\mathrm{y}}_i}{\partial {x}_j}\right|,i=1,2\dots n,j=1,2\dots m $$

(16)

In the tolerance sensitivity analysis, it should be noted that the tolerance parameters represent the impact factor, the geometric errors are regard as an intermediate system, and the position error is the output of total system. Therefore, by calculating the sensitivity coefficient of each tolerance parameter, each sensitivity index can be acquired and the key tolerance parameters can be identified. The sensitivity of input tolerance parameter e in the k (k=x,y,z) direction can be expressed as

$$ {S}_{ke}=\left[\begin{array}{c}{S}_{xe}\\ {}{S}_{ye}\\ {}{S}_{ze}\end{array}\right]=\frac{\mathrm{\partial \Delta }E}{\partial {T}_e}=\frac{\mathrm{\partial \Delta }E}{\partial G}\ast \frac{\partial G}{\partial {T}_e} $$

(17)

However, what is really meaningful in precision design is the maximum value of each error sensitivity index in the whole range. It reveals that only when the tolerance range of each geometric error source is allocated according to the maximum sensitivity, the position error of translational axis can meet the requirements of design index in the whole range. Thus, the maximum sensitivity of the input parameter △E to the position error model can be calculated from the total error model of translational axis in Eq. (13)

$$ \Delta {S}_e=\max \sqrt{{\left(\frac{\mathrm{\partial \Delta }{E}_x}{\partial G}\ast \frac{\partial G}{\partial {T}_e}\right)}^2+{\left(\frac{\mathrm{\partial \Delta }{E}_y}{\partial G}\ast \frac{\partial G}{\partial {T}_e}\right)}^2+{\left(\frac{\mathrm{\partial \Delta }{E}_z}{\partial G}\ast \frac{\partial G}{\partial {T}_e}\right)}^2} $$

(18)

According to the position error model of the translational axis and the relationship between the tolerance of its components and the parameters of the error source, the parameters are substituted into Eq. (18), and the sensitivity coefficients of the tolerance parameters are calculated. In order to express more accurately and intuitively, the sensitivity index of single tolerance parameters is normalized.

$$ {SV}_i=\frac{\left|\Delta {S}_i\right|}{\sum \left|\Delta {S}_i\right|} $$

(19)

4 Simulation and experiment

4.1 Verification method and conditions

Five-axis gantry milling machine is selected as the experimental object as shown in Fig. 4. The characteristic of its stroke length is more obvious to verify the tolerance model. Dimensional parameters of the machine are shown in Table 1. By referring to the machine tool design manual, the key component tolerance parameters can be found in Table 2. Since the parameters λ in the model have not been determined, the following simulation needs to be designed.

Fig. 4

Geometric error parameter detection scene

Table 2 Tolerance parameters of Y-axis

Based on the TSA model given in Eq. (18), confirmation of key tolerance of Y axis is transformed into confirmation of model parameter λ. The geometric errors of the components of the Y-axis assembly need to be measured to verify the correctness of relationship between assembly error and the corresponding parallelism tolerance. In this paper, the laser interferometer and dial indicator are selected to identify the squareness errors and kinematic errors of Y-axis, respectively.

The measurement of squareness error needs the cooperation of high-precision ruler, L-type measuring fixture and dial indicator. First of all, adjust the level ruler to be parallel to the left guide rail, and place the level ruler on the bed. At the same time, the dial indicator is adsorbed on the sliding block, whose needle contacts with the upper surface and the side of the ruler, respectively. The measurement form is to measure two adjacent and vertical planes S1 and S2 on the components, and measure the coordinate positions of at least three points on each plane. The straightness errors and angle errors of Y-axis can be measured with nine-line method. Laser interferometer, as shown in Fig. 5, can measure linear positioning error, straightness error and angle error in the process of linear axis movement. Its essence is through the interference principle of light wave, that is, two trains of waves with the same frequency, own to the phase difference between them. In the process of superposition, the light intensity will redistribute. The interferometer can measure the optical path difference of two waves by detecting the light intensity distribution of the sensor, and then calculate the error in the process of object movement. By identifying the discrete point values of the geometric error parameters, the MATLAB toolbox was used to fit the curve to determine the value of parameter λ.

Fig. 5

Schematic diagram of laser interferometer XL-80

In the course of the experiment, the NC machine tool needs to be preheated in advance to reduce the interference of thermal error. Meanwhile, the room temperature was kept at about 20±2 °C during the measurement. Moreover, it is of importance that the experiment was repeated five times and the result select the average value ultimately to avoid random errors.

4.2 Confirmation of model parameters

Although the TSA model in the previous section has been established, it is urgent to determine the value of parameter λ in the model. Therefore, this section will introduce a self-developed simulation method. The confirmation of model parameters has periodic action rules between the tolerance parameters of machine tools and the movement travel of components, while there are some uncertain factors. In order to obtain the parameters of the model accurately, the nonlinear regression analysis which follows the least square method is cited and verified ultimately.

When input data points (y, z), the estimated value $\overset{\Lambda}{\lambda }$ of regression coefficient λ is solved, so that the residual of regression model f (λ, y) satisfies the minimum value.

$$ \min {\left\Vert {z}_i-f\left(\lambda, {y}_i\right)\right\Vert}^2 $$

(22)

In order to verify the accuracy of prediction model, R² model is used to estimate the fitting effect of discrete point.

$$ F(c)\underset{c}{=}\mathit{\min}{\left\Vert y-f\left(\lambda, {z}_i\right)\right\Vert}_2^2 $$

(23)

It can be noticed that when the value of R² gets closer to 1, the fitting accuracy of the model is higher.

The simulation steps are implemented as follows

• 1. Set a parameter λ and the number of twenty measurement points for fitting the error source.

• 2. A set of geometric errors G is given for simulation. The least square method is used to fit the measured error data identified by laser interferometer. Meanwhile the fitting curves are taken as the initial assumed error for simulation

• 3. By mapping the relationship between the position error by laser interferometer and the geometric error parameters, the three direction error increments corresponding to each measuring point on the measuring track are calculated, and the position error of Y-axis vector ∆ E can be obtained.

• 4. Other simulation factors affect the input error ∆ n

• 5. When the tolerance parameter values are substituted into the simulation model, R² test was used to test the fitting effect, whether the parameters meet the requirements or not.

• 6. Finally, the fitting parameters λ are estimated. Otherwise it needs to re-enter the loop.

In this model, it is evident that the relationship between the undetermined coefficient and the position error is nonlinear. The Gauss-Newton method can be used to calculate the regression dilution iteratively to minimize the sum for squares of the residual errors of the estimation points (Fig. 6). Through the above simulation process, parameters λ is ultimately confirmed, as can be seen from Table 3. In order to save space, three types of geometric error parameters (kinematic error, positioning error and squareness error) fitting graphs are selected, which represent the error fitting of different parameter λ shown in Figs. 7, 8, and 9. The fitting values R² of simulation result can be obtained as 0.972, 0.961 and 0.967 respectively, which results are in coincidence with the measured result. Furthermore, the average residuals of all the fitting error parameters are controlled within ±5um. In addition, the maximum residuals error of the three geometric errors are 4.4um (ε_z(y)), 3.7um (δ_y(y)) and 5.7um (ε_1xy). Compared with the geometric error measurement results, the residual error is quite small and can be ignored. It indicates that the fitting curves basically meet the curves of the actual measured points.

Fig. 6

Fitting function optimization flow chart

Table 3 Related parameters of machine tool

Fig. 7

Simulation results of manufacturing errors (ε_z(y))

Fig. 8

Simulation results of positioning error(δ_y(y))

Fig. 9

Simulation results of assembly errors (ε_1xy)

5 Result of TSA

Since a single tolerance may affect one or more geometric error parameters, it is obvious that the tolerance parameter terms are less than the geometric error parameter terms. Therefore, the TSA method can avoid the highly nonlinear problem of the error parameters in the position error deftly. For the convenience of TSA, the tolerance parameters are numbered as shown in Table 4. The TSA results show that the contribution of each tolerance to the position error of Y-axis. All the assembly error parameters studied have a significant impact on the position error, but they have a relatively small impact on the position error in the Y direction, as shown in Fig. 10. As can be seen from Fig. 10(a), it can be safely concluded that the TSA values of d1hxy, dn, d3hxy are bigger than others when the Y-axis move in the test stroke. The sum TSA value of d1xyand d3xy have reached 49%, it indicates that Assembly tolerance has a great influence on the X-direction deviation. Therefore,d1hxy, dn, d3hxyare considered to be prominent tolerance parameters in the X direction. Similarly, the message conveyed in Fig. 10(b) that the TSA values of d1hyz, d2sz, dn are largest among all tolerances. It is obvious that tolerance parameter dn have great impact in the Y direction, which value of TSA have achieved to 43% lonely. Thus, these tolerance parameters are regarded as the significant tolerances in the Y direction. According to the Fig 10(c), there is no doubt that d1hyz, d2sx, d2sz andd3hyhave been paid more contributions to the Z-direction deviation. Especially, the tolerance parameter of dszhas more positive effect in the Z direction. Simultaneously, it can be seen from Fig. 10 (d) that the key tolerance parameters of d1hyz, d2szanddn have been identified in all workspace, which TSA index reach 68% totally. To improve the accuracy of machine tools, the three tolerance parameters need to be strictly controlled as long as the cost permits. Based on the result of tolerance sensitivity analysis above, it can be known that the key tolerance parameters (d1hyz, dszanddn) has made the main contribution in the position error of Y-axis. In addition, manufacturing tolerances are more sensitive to position error than assembly tolerances. It can be seen from Fig. 11 that the tolerance of base is more sensitive in the X direction, which value gets to 0.367. However, in other directions, the tolerance of guideway is the most sensitive in position error of Y-axis. In general, the tolerances of guideway affect the running accuracy more which can be controlled in the future design.

Table 4 The results of simulation parameters

Fig. 10

a Contribution of each tolerance parameter on the X-direction deviation b Contribution of each tolerance parameter on the Y-direction deviation c Contribution of each tolerance parameter in the Z-direction deviation d Contribution of each tolerance parameter on the position error

Fig. 11

a Contribution of each component in the X-direction deviation b Contribution of each component in the Y -direction deviation c Contribution of each component in the Z-direction deviation d Contribution of each component on the position error

It should be noted these points based on the TSA results. (1) It can be found that the sensitivity of assembly tolerance is higher than that of manufacturing tolerance. Assembly tolerance has a greater impact on position error, which should be paid attention to in the future machine tool design. (2) The assembly tolerance sensitivity of the base is relatively large, which may be caused by the bottom of the transfer error matrix. Thus, it is necessary to adjust the key tolerance items based on TSA result to reduce systems error. (3) Although the tolerance parameter d_n plays an important role in position error, it contributes very small in the X and Z directions (Table 5).

Table 5 Tolerance number of Y-axis

6 Conclusion

In this paper, a tolerance sensitivity analysis method is proposed to eliminate the contribution of tolerance parameters to the position error. For the sake of the effective implementation of the method, the position error of Y-axis considering assembly errors and manufacturing errors is established by the assembly process of various components. Then, the geometric error parameters are fitted by first-order Fourier expansion with the corresponding tolerance and the fitting parameters are confirmed. Finally, the TSA method is deduced to identify the key tolerance parameters, which have an important effect on the volume. It should be noted that the position error of machine tool is the result of highly nonlinear coupling of error parameters, which makes error compensation difficult to achieve the desired effect. This paper reveals the position error of translational axis from the angle of tolerance. By analzying the assembly process of the key components of the translational axis, the tolerance sensitivity model is established, and the key tolerance parameters are identified, which provides a scientific and effective reference for the machine tool design stage.

In addition, compared with previous methods, the major contributions of the paper are as follows

• (1) Based on HTM and MBS theory, the accurate error vectors caused by the assembly error and manufacturing error of Y-axis are established, instead of treating geometric errors as constant angle error or linear error. It comprehensively analyzes the geometric error parameters of the components manufacturing and assembly process of the translational axis and gives the position error model of the single axis ultimately.

• (2) When fitting the relationship between geometric error parameters and tolerance parameters of Y-axis, an improved simulation process is proposed to determine the fitting parameters. The quantitative relationship between tolerance and geometric error parameters is established ultimately.

• (3) The TSA model of was established to express the contributions of tolerance parameters on the position error. The real contributions of tolerance are evaluated and the vital tolerance parameters are realized, which can be given directly to the machine tool designers to help them for improving the machining accuracy of the machine tool.

In the future work, cutting force error, thermal error, servo error, and other factors need to be taken into account.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article.