Multi-objective optimization and finite element method combined with optimization via Monte Carlo simulation in a stamping process under uncertainty

Abstract

The response surface methodology (RSM), which uses a quadratic empirical function as an approximation to the original function and allows the identification of relationships between independent variables x_i and dependent variables y_s associated with multiple responses, stands out. The main contribution of the present study is to propose an innovative procedure for the optimization of experimental problems with multiple responses, which considers the insertion of uncertainties in the coefficients of the obtained empirical functions in order to adequately represent real situations. This new procedure, which combines RSM with the finite element (FE) method and the Monte Carlo simulation optimization (OvMCS), was applied to a real stamping process of a Brazilian multinational automotive company. For RSM with multiple responses, were compared the results obtained using the agglutination methods: compromise programming, desirability function (DF), and the modified desirability function (MDF). The functions were optimized by applying the generalized reduced gradient (GRG) algorithm, which is a classic procedure widely adopted in this type of experimental problem, without the uncertainty in the coefficients of independent factors. The advantages offered by this innovative procedure are presented and discussed, as well as the statistical validation of its results. It can be highlighted, for example, that the proposed procedure reduces, and sometimes eliminates, the need for additional confirmation experiments, as well as a better adjustment of factor values and response variable values when comparing to the results of RSM with classic multiple responses. The new proposed procedure added relevant and useful information to the managers responsible for the studied stamping process. Moreover, the proposed procedure facilitates the improvement of the process, with lower associated costs.

1 Introduction

1.1 Research background

In today’s intricate industrial environment, it is essential that organisations continuously improve their business processes, to sustain their competitive advantage [1].The field of industrial statistics and optimization has introduced a range of statistical and optimization methods for managing and improving processes in diverse industries [2,3,4].

In response surface methodology—RSM, an important DOE technique, linear or quadratic polynomial functions are employed to describe the problem studied, and to explore experimental conditions to obtain its optimization [5, 6].

In the field of operations research, Optimization via Monte Carlo Simulation (OvSMC) is suitable for problem solving with many local optimal solutions, including objective functions, complex restrictions, and continuous or discrete variables, as pointed out by Conway and [7] .

Monte Carlo simulation (MCS) provides decision-makers with a scenario analysis, with a range of possible outcomes and related probability distributions, besides also offering graphical results and sensitivity analysis [8]. MCS is based on the use of random numbers (sampling) and probability statistics to investigate problems in many areas, such as material science, economics, chemical and biophysics, statistical physics, nuclear physics and traffic flow [9]. Furthermore, MCS can be used to solve complex engineering problems because it can deal with a large number of random variables, various distribution types, and highly nonlinear engineering models [10].

The development of this study was primarily motivated by demands presented by companies in Brazil, in different sectors, which use DOE, mainly RSM, to improve their manufacturing processes and services. The problem observed by managers, in practice, was that, although the adopted RSM models could be statistically significant with respect to the modeled real situation, the adjustment of the optimized factors (or decision variables, x_i), as recommended by RSM, sometimes had generated very different response variables values (y_s) if compared to those observed in the real process. These situations have ended up creating difficulties to the managers regarding the adjustments that needed to be made in the company’s processes to improve performance, because they lost the confidence that the optimized values of the factors suggested by the RSM were, in fact, appropriate for implementation, since the investments in these changes can be high, as commented by [2].

In this context, a particular and important problem was presented by managers of a Brazilian multinational automotive industry and it is related to how to reduce the weight of stamping parts that, in recent years, has consumed great efforts of the engineers to get an adequate solution [11, 12]. It should be noted that it is not a simple problem, involving many relevant aspects for vehicle manufacturing, because that most of the energy absorbing members in vehicle body are fabricated by stamping process which can result in non-uniform thickness, substantial residual strains/stresses especially for high strength steel or advanced high strength steels, etc. [13, 14].

Besides these previous concerns, maybe it is not a good option to chose independent factors values, related to stamping process, by using a deterministic optimization procedure, because this could result in unreliable or unstable designs with respect to crashworthiness [15]. In fact, the occurrence of uncertainties about material properties, stamping process and geometry usually propagate from manufacturing phase to operational phase, and these can generate problems to the vehicle, for example, associated to crashworthiness [13].

There are two types of sheet metal forming methods: one is the incremental method based on flow theory, and the other is the total deformation theory of plasticity [16]. The former provides high precision, but it is time-consuming, and the latter is somewhat less accurate, but the simulation is rapid; i.e. it is suitable for the simulation of sheet metalstamping in the early design stages [16].

In order to mitigate the effects of uncertainty in stamping processes, since the early 1990s, there has been a significant increase in the use of simulations by finite element (FE) methods to sheet conformation in industry [17,18,19]. For example, FE simulations are useful for reducing lead time in the design and tool development stage, as pointed out by [20].

Pimental et al. [17] stated that problems involving new materials and new technologies constantly require the need to develop more robust, efficient, reliable and accurate FE analysis and simulation tools. These authors analyzed three FE software, AUTOFORM^TM, PAM-STAMP ^TM and DD3IMP^TM, and found that their accuracy was roughly the same. Thus, beyond the fundamentals differences in their FE formulation, Autoform^TM and Pam-Stamp^TM showed very similar numerical results, which was in good adherence with the real results. Similarly, [21] used simulations by finite element (FE) methods associated with RSM and ANOVA [4] to perform the optimization of multi-point forming process parameters.

In this study, an innovative procedure that include the application of optimization via Monte Carlo simulation—OvMCS [2] combined with response surface methodology—RSM [22] and finite element methods—FE [22] is proposed to analyze the impact of uncertainty occurrences in two objective functions (compression and traction) associated with stamping process parameters.

The main difference of this research when compared with the study developed by [2] is that, besides being a multi-objective problem involving multiple responses, the compression and traction functions are optimized through three agglutination methods: compromise programming—CP [23], desirability function [24] and modified desirability function [25]. Thus, the best option for a stamping process of a Brazilian multinational automotive company is proposed.

1.2 Contributions of this study

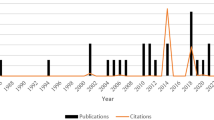
To verify the importance and to identify research opportunities in the area of experiment planning, a literature search was conducted, and the results are presented in Fig. 1. By using combinations of the keywords “Response Surface Methodology”, “Uncertainty” and “Monte Carlo Simulation” in the Scopus database, filtering results from 1989 to 2019, a total of 47 documents were identified, being 38 documents published between 2010 and 2021, which evidences the contemporaneity of the field.

Fig. 1

Number of publications (article) with keywords “Response Surface Methodology”, “Uncertainty” and “Monte Carlo Simulation”. Source: Scopus

Silva et al. [2] chronologically discussed the scope of these articles. Thus, it is possible to identify the innovative character of the new procedure described here, which propose an experimental design method incorporating uncertainty influences to the parameters.

Herein, the results of the literature survey are further explored by combining the following keywords: “Response Surface Methodology”, “Uncertainty” and “Monte Carlo Simulation”. Figure 2 shows a cluster map constructed using VOSViewer [26], in which the keywords that occurred with a frequency greater than or equal to five in these articles are highlighted.

Fig. 2

Clusters Map for keywords “Response Surface Methodology”, “Uncertainty” and “Monte Carlo Simulation”. Source: VOSViewer software and Scopus data base

An analysis of Fig. 2 reveals the formation of several clusters associated with representative keywords, and it can be inferred that there are researchers who combined RSM, FE, uncertainty and MCS, or RSM, as well as uncertainty and optimization. These results show the scientific and practical interest in combining these techniques. However, revealing the originality of our approach, none of the 51 articles published related to the cited keywords has adopted the same procedure proposed herein, i.e. the combination of the RMS, FE, MCS, and optimization for a multiple response problem related to a stamping process, considering uncertainty occurrence on the factors.

Finally, Table 1 presents the results of a search carried out in the Scopus database up to 2019, with the keywords “Design of Experiments”, “Response Surface Methodology”, “Polynomial Function”, “Uncertainty”, “Optimization”, “Monte Carlo Simulation” and “Optimization via Monte Carlo Simulation”. The filters used in this search were “Articles” and “Proceedings Papers”, in which keywords were cited in titles or abstracts.

Table 1 Number of publications and citations with keywords—“Design of Experiments”, “Response Surface Methodology”, “Polynomial Function”, “Optimization” and “Monte Carlo Simulation”. Source: Scopus

It should be observed that only 74 publications included the keywords “DOE”, “Uncertainty” and “RSM” together, which indicates that there is still a good opportunity for research involving these subjects. Besides that, it should be pointed out that, when it was included the keyword “Optimization via Monte Carlo Simulation”, along with the three previous keywords, with the filters used, no papers were found in the consulted database.

Therefore, it should be highlighted that the present study provides an interesting academic and practical contribution to the field, since there is a need for new knowledge about experimental problems considering uncertainty. In this context, a proposal of an innovative approach for DOE, involving RSM, OvMCS and uncertainty is included, which was statistically validated by a real stamping process application.

1.3 Research questions and objectives

After the presented contextualization, this paper looked for answer the following research questions:

• 1. What is a suitable procedure to incorporate uncertainties in the parameters of RSM problems with multiple responses?

• 2. For a stamping process, for each agglutination method, how to choose weights values (w_s) in the optimizations of the response variables?

• 3. For a stamping process, what is the best agglutination method, with respect to traction and compression, that would provide a feasible solution to be implemented?

To answer these questions, the general objective of this study was to develop a new procedure, considering the uncertainty occurrences in the coefficients of the objective functions of experimental multi responses problems modeled by RSM. As previously mentioned, the method selected to insert uncertainty in the coefficients of the objective functions was Optimization via Monte Carlo Simulation (OvMCS). The specific objectives included applying the proposed procedure to a stamping process in a Brazilian multinational automotive company, aiming:

• To identify the advantages of the proposed procedure compared to the traditional multiple response RSM, which adopts deterministic optimization.

• To statistically validate the proposed procedure.

This paper is organized as follows. Section 2 presents definitions and concepts related to RMS and OvMCS. Section 3 describes agglutination methods for processes with multiple responses. Section 4 describes the method and materials and outlines the steps for the application of the proposed procedure. The results of the proposed procedure when applied to a real stamping process, and a comparison among different agglutination methods are in Section 5. Finally, Section 6 presents the conclusions and suggestions for further research.

2 Background of response surface methodology and optimization via Monte Carlo simulation

In this section, it is shown the features of two techniques that were used in the proposed procedure to deal with problems with multiple responses by the response surface methodology (RMS), considering the occurrence of uncertainties in the factors of the studied process. As highlighted by [27]), in process optimization problems, it is of fundamental importance to develop adequate models that mathematically describe the relationship between independent variables x_i and response variables y_s. The models can be classified in two broad classes [28]: phenomenological models and empirical models. Phenomenological models are based on a prior knowledge of the physical and chemical processes that are in some way associated to the studied systems [27]. On the other hand, empirical models are built from a statistical analysis of experimental observations, using regression [29] and design of experiments (DOE) techniques.

DOE is adopted to identify the important variables (or factors) in a process, and what their values (or conditions) should be to optimize the performance of the studied process. For each factor, based on the results of the experiments, limit values are selected, and, in general, two levels are tested for each factor. Therefore, the total number of experiments for a complete factorial design is given by 2ⁿ, with n being the number of studied factors. In this complete factorial experimental scheme, when the number of factors increases, the number of experiments increases exponentially, and it can become infeasible to use it when there are many factors to be considered [4].

An important and very useful DOE technique is RSM, which substitutes a complex optimization problem with a sequence of simpler problems, with objective functions approximated by response surfaces (usually a second degree polynomial), and enabling a faster resolution of large real problems [2, 5, 30]. As explained by [2], there are two traditional ways to model problems in RSM: central composite designs—CCD [4] and Box-Behnken designs—BBD [31]. In general, a response variable of interest y is related to the factors (variables) x_i of a process and can be expressed by Eq. (1):

$$ y=f{(x_{1},x_{2},...,x_{n})}+\epsilon $$

(1)

where 𝜖 is a random error, which includes the variations of the response variable y that are not explained by the factors x₁,x₂,…,x_n.

Since, in the majority of practical problems, addressed by RSM, the function (1) is not known, it is adopted an approximation of the real function in the form of a second-order polynomial function [4] and [32], as given by Eq. (2):

$$ y=\beta_{0}+\sum\limits_{i=1}^{n}\beta_{i} x_{i}+ \sum\limits_{i=1}^{n}\beta_{ii} {x_{i}^{2}}+\sum\limits_{i=1}^{n}{\sum}_{j=i+1}^{n}\beta_{ij}x_{i}x_{j}+\epsilon $$

(2)

where y is the (dependent) response variable, x_i is the i th independent variable, x_j is the j th independent variable, β₀ is the offset term, β_i is the linear effect and β_ii is the squared effect, β_ij is the interaction effect, and 𝜖 is a random error.

Due to the use of experimental data to estimate the parameters of the empirical function (2), it is necessary to construct Confidence Intervals (CI) for them using (3) [33]:

$$ \begin{array}{@{}rcl@{}} CI (\beta, 1-\alpha) = [ \hat{\beta} \pm z_{1-\frac{\alpha}{2}} \times \text{SD} (\hat{\beta})] \end{array} $$

(3)

where $\hat {\beta }$ is an estimated value for parameter β, SD is the associated standard deviation, and $z_{1-\frac {\alpha }{2}}$ is obtained on a normal distribution table associated with the value of a significance level α.

An operations research (OR) technique utilized in the procedure proposed herein is Monte Carlo simulation—MCS, which is the common name for a wide variety of probability techniques, and it is a powerful statistical analysis tool. It is based on the use of random numbers (sampling) and probability statistics to investigate problems in fields as diverse as material science, economics, chemistry and biophysics, statistical physics, nuclear physics, flow of traffic flow and many others [9].

MCS is commonly used for solving complex engineering problems, since it can deal with a large number of random variables, various distribution types, and highly nonlinear engineering models [10, 34, 35]. Besides that, MCS is useful to help the manager in industrial-related problems, because of the need to optimize systems or processes that are frequently influenced by uncertainties, for example, in the coefficients of the objective function and in the coefficients in the restrictions [36]. As pointed out by [37], the MCS is an adequate way to evaluate the possible consequences of uncertainties in the optimization problems [38].

Sahinidis [39] pointed out that stochastic optimization is applied in several areas of knowledge, such as in production planning, natural resource management, and finance. One of its advantages is the possibility of extracting a set of relevant information related to the problem in question, and thus, enabling the analysis of different scenarios. In this sense, Optimization via Monte Carlo Simulation (OvMCS), which aims to find the best values for simulation model input parameters in the search of one or more desired outputs, has been shown to be relevant to deal with stochastic optimization problems [40].

According to [41], an OvMCS problem can be formulated as being:

$$ max {g(x)=E_{P}[G(x,\omega)]}, x \in X $$

(4)

where G: $\mathbb {R}^{n} \times {\Omega } \to \mathbb {R}$ and the expectation is taken with respect to probability P, defined in a sample space (Ω,F) and X⊂ $\mathbb {R}^{n}$.

It should be noted that, in practical problems, the search of an adequate solution does not necessarily imply the determination of optimal operating conditions, since it is practically impossible to establish the optimum point, due to the unlimited number of variables that impact an industrial process [27]. In this way, local optimum solution within a feasible search subspace [42] and using Heuristics or Metaheuristics Methods [43] can be performed for process improvement.

For [44], simultaneous optimization of multiple responses has been a priority in many industries, and much of the effort has been directed to researching alternative methods for the efficient determination of process adjustments that achieve predetermined goals. Moreover, multiple-response optimization problems often involve conflicting objectives [45], such as in manufacturing processes related to the minimization of production time versus equipment cost.

According to [46], there is still a gap between theory and practice in the optimization using multiple responses, and it is common to use agglutinated functions of multiple responses to obtain a single objective function to be optimized. Since there are a wide variety of agglutination methods, a comparative study of these methods is necessary to determine their individual efficiency [27]. The most used process optimization method in scientific studies is the joint use of the desirability function with the generalized reduced gradient (GRG) method [25]. In the next section, three agglutination methods are presented, which were tested in the procedure proposed in the present study for optimization with RSM, in the occurrence of uncertainties.

3 Agglutination methods for processes with multiple response

3.1 Compromise programming

Compromise programming (CP) was firstly presented by [47]. This method is characterized by the attempt to identify solutions that might be closer to an “ideal” solution, considering the distance between a given solution and the ideal solution [23]. This ideal (or target) solution is only a point of reference for the decision maker (DM). Thus, CP assumes that any DM seeks a solution as close as possible to an ideal point, and to achieve this closeness, a distance function is introduced into the analysis. It should be noted that the concept of distance is not used in its geometric sense, but as a proxy measure for human preferences [48].

When seeking the minimization of a given function f_s(x), CP can be obtained from Eq. (5) and (6):

$$ \text{Min} CP= \left( \sum\limits_{s=1}^{p}w_{s} [f_{s}({x}) - T_{s}]^{t}\right)^{\frac{1}{t}} $$

(5)

$$ \sum\limits_{s=1}^{p}w_{s} = 1 $$

(6)

where, for f_s(x), T_s is the ideal value and w_s is its weight, usually it is adopted t = 2.

Since the units used to measure various objectives are different, they must be normalized in order to avoid a meaningless summation [49].

3.2 Desirability function

One of the most commonly used techniques to simultaneously optimize multiple responses is to transform the equations that model each of these (answers) responses into individual utility functions [27]. The next step is optimize a global utility function known as total desirability function (DF), given in terms of the individual utility functions [4]. [24] present individual utility functions (d) for nominal-the-best (NTB), larger-the-better s and maller-the-better (STB) answers, as described below:

- When the target value (T) of an answer ($\hat {y})$ is between a maximum value (U) and a minimum value (L), the response is said to be of the NTB type. The utility function (d) is defined in Eq. (7):

$$ \begin{array}{@{}rcl@{}} d= \begin{cases} \left[\frac{\hat{y}-L}{T-L} \right]^{S} ~~L \leq \hat{y} \leq T \\ \left[\frac{\hat{y}-U}{T-U} \right]^{R} T \leq \hat{y} \leq U \\ ~~~~~~~~~~0 ~~~~~~~~\hat{y} \leq L \text{or} \hat{y} \geq U \end{cases} \end{array} $$

(7)

where R and S are weighting factors, which may assume values greater than 1 when it is desired to prioritize the maximization, or the minimization, of the response [27, 50].

- When the target value (T) of an answer ($\hat {y})$ must reach the minimum value of the function, the response is said of STB type. The utility function (d) is defined in Eq. (8):

$$ \begin{array}{@{}rcl@{}} d= \begin{cases} 0 ~~~~~~~~~~~~~~~~~~\hat{y} > U \\ \left[\frac{\hat{y}-U}{L-U} \right]^{R} L \leq \hat{y} \leq U \\ 1 ~~~~~~~~~~~~~~~~~~\hat{y} < L \end{cases} \end{array} $$

(8)

- When the target value (T) of an answer ($\hat {y})$ must reach the maximum value of the function, the response is said to be of LTB type. The utility function (d) is defined in Eq. (9):

$$ \begin{array}{@{}rcl@{}} d= \begin{cases} 0 ~~~~~~~~~~~~~~~~~~\hat{y} < L \\ \left[\frac{\hat{y}-L}{U-L} \right]^{R} L \leq \hat{y} \leq U \\ 1 ~~~~~~~~~~~~~~~~~~\hat{y} > U \end{cases} \end{array} $$

(9)

According to [4], the agglutination of the multiple responses involved in a problem can be performed by maximizing a global utility function given by Eq. (10):

$$ \text{Max} D= \left( d_{1} \times d_{2} \times d_{3} \times {\dots} \times d_{s} \right)^{\frac{1}{s}} $$

(10)

where s is the number of responses to be optimized.

Moreover, it is possible to use Eq. (11) instead of Eq. (10) to determine the value of the global utility function, which allows assigning weights (w_s) to each utility function (d_s), as presented by [27]:

$$ \text{Max} D= \left( d_{1}^{w_{1}} \times d_{2}^{w_{2}} \times d_{3}^{w_{3}} \times {\dots} \times d_{s}^{w_{s}} \right)^{1/\scriptstyle\sum w_{s}} $$

(11)

3.3 The modified desirability function

Chng et al. [25] propose that the global utility function calculated by Eq. (11) could be modified as an arithmetic mean to avoid obtaining false optimal values. The proposed modifications can be seen in Fig. 3, where $\hat {y_{s}}$ is the studied response s, $d_{s}(\hat {y_{s}})$ is the utility function value for the response s, U is an upper limit for response $\hat {y_{s}}$, L is a lower limit for response $\hat {y_{s}}$.

Fig. 3

Modified desirability function. Source: [25]

As presented and discussed by [25], the utility function d_s can be calculated by Eq. (12), and there are three cases to be considered for the (ideal) target value (T_s) and the associated utility function d_s value, expressed by Eq. (13), (14) and (15):

$$ d_{s}(\hat{y_{s}})= \frac{2\hat{y_{s}}-(U+L)}{U-L} + 1 $$

(12)

$$ \text{If} L < T < (L + U)/2, \text{then} 0 < d_{s}(T_{s}) < 1, $$

(13)

$$ \text{If} T= (L+U)/2, \text{then} d_{s}(T_{s})=1, $$

(14)

$$ \text{If} (L+U)/2 < T < U, \text{then} 1 < d_{s}(T_{s}) < 2. $$

(15)

Therefore, according to [25], a new global utility function, named by modified desirability function—MDF, can be calculated by Eq. (16):

$$ \text{Min} \textrm{MDF} = \frac{\sum\limits_{s=1}^{p}w_{s}|d_{s}(\hat{y_{s}})-d_{s}(T_{s})|}{p} $$

(16)

where $d_{s}(\hat {y_{s}})$ and d_s(T_s) are, respectively, function and target values associated to the estimated response $\hat {y_{s}}, s$ is the total number of responses that were agglutinated by the function D and w_s is the weight assigned to $d_{s}(\hat {y_{s}})$, with $\sum \limits _{s=1}^{p} w_{s}=1$.

The following section presents the classification of this study and materials and methods. Moreover, it is described the proposed procedure for optimizing experimental problems under uncertainty, using RSM and OvMCS..

4 Materials and methods

The research described in this study can be classified as being applied in its nature, presenting normative empirical objectives based on a quantitative approach. The technical procedures included the realization of experiments and the use of modeling and simulation [29]. Figure 4 presents a flowchart with the steps for applying the new proposal to optimize an experiment with multiple responses, with uncertainty occurrences, including the combination of RSM, finite element method and OvMCS.

Fig. 4

Proposed procedure flowchart. Source: Adapted from [2]

The techniques used to apply of the proposed procedure (see Fig. 4) were:

• – Step 2 - Generation of the empirical functions representing the objective functions of RSM was performed with the ordinary least squares (OLS) algorithm [4].

• – Step 3 - The traditional (deterministic) optimization was performed with the generalized reduced gradient—GRG algorithm, available in Solver from Ms-Excel^TM.

• – Step 5 - OptQuest optimizer from the Crystal-Ball^TM Trial Version software [51] towas used to complete the optimizations in three stages (Fig. 5). OptQuest incorporates metaheuristics to guide its search algorithm towards better solutions [52].

Fig. 5

OptQuest Flow. Source: [52]

The eight steps of the general procedure proposed, as shown in Fig. 5, are described as follows:

Step 1 - To identify the experimental problem to be addressed by RSM, finite element method and OvMCS. This involves understanding the context in which the manufacturing process or services will be studied and the identification of the response variables of interest and the independent variables that influence this process. Data are collected to obtain the experimental matrix with the values of the response variables and the associated independent variables considered in the process. The experimental matrix was coded according to the RSM technique by adopting: central composite designs (considering two levels for each factor) or Box-Behnken designs (considering more than two levels for each factor).

Step 2 –To generate empirical functions associated with the objective functions of RSM, which represent the response variables (y_s) as a consequence of the independent variables considered in the process to be studied.

The encoded experimental matrix associated with the process studied, obtained in step 1, it is used to generate the empirical functions and the confidence intervals (CI), of 95% and 99%, for all the coefficients of the independent variables. Based on the results from the F and t-Student statistical tests [4], in Eq. (2), the terms that are not significant with α = 5% are disregarded. Observe that, in Eq. (2), if the terms of the interaction effects, β₁₁x₁x₂,…,β_nx_n− 1x_n are significant, it is recommended to keep the terms from the linear effects, β₁x₁,β₂x₂,…,β_nx_n, even if they are not significant.

The justification for the choice of these confidence values for the CI that 95% is the standard used in experimental problems addressed by RSM and 99% represents the greatest range of variation of the coefficients of the empirical function in relation to the value estimated by the regression analysis.

Step 3 -To optimize the empirical functions y_s, obtained in step 2, by agglutination methods, without considering the occurrence of uncertainties. The GRG algorithm can be used to solve the two optimization problems, it is available in the Solver of MS-Excel^TM [53].

Step 4 - To enter the occurrence of uncertainties in the coefficients (β) of the empirical function, obtained in step 2. For this purpose, based on [4], continuous uniform distribution in the [a, b] interval was chosen, which represents the situation in which any value, among the limits considered, has the same probability of occurring. The values of the lower (a) and upper (b) limits should be tested, associated with the CI of 95% and 99%, for each coefficient of the empirical function, considerando a probability density function (PDF) as shown in Fig. 6:

$$ \begin{array}{@{}rcl@{}} PDF(\beta)= \begin{cases} \frac{1}{b-a} \ \ \text{if} & a \leq \beta \leq b \\ 0 & \text{Otherwise} \end{cases} \end{array} $$

(17)

Fig. 6

Continuous uniform distribution. Source: [4]

In this context, [54] pointed out that based on the quantitative approach, the evaluation measures are calculated as the probabilities of occurrence of the main events and the reliability or insecurity of the main events.

Step 5 - To optimize the empirical functions with the occurrence of uncertainties, obtained in step 4, where the decision variables are the factors x_i and the response variables are y_s. OvMCS is applied with support from the Crystal Ball ^TM software and the OptQuest^TM optimizer.

Step 6 - To analyze the results from the traditional approach (step 3 - deterministic optimization) with the results of the optimization under uncertainty (step 5 - with OvMCS - CI - 95% and OvMCS - CI - 99% This will be done by comparing the optimized values of the factors (x_i) and the final value of the optimized objectives functions (y_s), observing similarities and differences.

Step 7 - To analyze the behavior of the response variable from the experimental problem optimized by OvMCS and statistical validation. The statistical validation will be done through a confirmation experiment, relating it to the behavior of the objective functions and to the factors optimized by OvMCS.

Step 8- Recommendations.

After statistical validation, it will be possible to use different configurations in the experiment and to accurately predict the confidence interval of the investigated response variables, carrying out more realistic experiments for different experimental configurations, without the need to carry out the confirmation experiment, which is often time-consuming and costly.

For the purposes of illustration and validation of the proposed general procedure, including the occurrence of uncertainties in the coefficients of the objective functions of experimental problems modeled by RSM, a real case involving a stamping process in a Brazilian multinational automotive company was used. The studied instance has five factors, and the response variables were y₁ (traction) and y₂ (compression), RSM with Box-Behnken design was used to illustrate how to statistically validate the proposed procedure.

To solve the example, we used an Intel Core i7-9750H coffee lake refresh, 12MB cache, GHZ processor 2.6 to 4.5 turbo Boost, with 32 GB RAM, and Windows operational system, with Video car NVIDIA^TM GeForce^TM RTX 2070 GPU (8GB GDDR6) MAX-Q design. The computational time for performing optimization by GRG algorithm was about two seconds, and the simulation stop rule was used to perform OvMCS by optimizer Optquest of the Crystal Ball^TM software. There were a total of 1000 simulations runs with 1000 replications each, and the computational time was about twenty minutes. In the next Section, the proposed procedure application for this studied real problem is presented in details.

5 A stamping problem solved by the proposed procedure

In the sequence, considering a real stamping problem, the results obtained in each step (see Fig. 8) of the proposed procedure are presented.

Step 1 - To identify the experimental problem

The object of study was a Brazilian multinational automotive company, with 31 units in 14 countries and about 15 thousand employees. It is a manufacturer of steel wheels and stamped automotive components, including chassis of small and heavy vehicles. The studied product was a transmission cross member, with thickness of 6.8 mm, using LNE 380 steel. The products of stamping supports are manufactured using raw material supplied by steel mills in coils or flat sheets. The products obtained with this manufacturing process are made of structural steels with mechanical strengths from 260 to 600 (MPa), thicknesses ranging from 2 to 10 (mm) and lengths from 100 to 2200 (mm), with weights between 0.1 and 20 (kg). The stamping tool is the device by which the most varied stamping components are obtained. The upper part of the device is fixed in the movable part of the press, which is called “hammer”, and in the lower part is called “lower table”, as shown in Fig. 7.

Fig. 7

Stamping tool. Source: Rhinoceros^TM software

The actuation of the press causes the displacement of the hammer and the upper part of the tool, which provides the mechanical action of the upper part of the tool against the lower part that is fixed in the lower base of the press. With this action, the tool geometry is transferred to the plate, obtaining the product in the desired shape by plastic deformation of the material. The product obtained in the stamping operation might or might not undergo other press operations, such as drilling, cutting, and calibration, among others. Then, it is ready for the final painting operation. Thickness reduction in the critical region of the embossed crosspiece, subjected to tensile stresses during the embossing process, and increased compression thickness in the critical region of the embossed crosspiece might cause cracks to occur during the stamping operation, increasing the risk of product breakage when running into field in the same stretching and compression region. Figure 8 shows the bottom of the tool, currently used by the company, with no compensation in the lower stamp.

Fig. 8

The stamping tool under study. Source: A internal file of the studied company

The major problem identified by stamping professionals is the lack of parameters to define the compensations in the tool design phase, which undermines the decisions made by the company’s engineers and specialists regarding the geometry to be adopted for the tools.

At this stage, it is common to use specific finite element method simulation software (such as Autoform^TM Software). Nevertheless, even with all the experience that engineers have acquired over time, this is a slow process and should be repeated several times. Inadequate decisions are often made, leading to additional costs as well as additional stamping operations.

As an example of this procedure, para o produto estudado, Fig. 9 was constructed with the Autoform^TM Software, which plots the stress-strain curve, which is an important tool to evaluate the fracture strength of a material. In fact, in the stamping industry, finite element simulation is a critical step to optimize of the sheet metal forming processes [55], and an indispensable input to the finite element model is the flow stress curve of the sheet material, also known as the true stress-strain curve [55].

Fig. 9

Critical region in the analysis. Source: Autoform^TM Software

Therefore, the studied company has to solve a complex problem associated with the occurrence of cracks in stamped parts, as highlighted in red in Fig. 9, which shows the reduction of the thickness of the crossbeam, from 6.8 mm to 4.857 mm, obtained with the current configuration of the mold during the stamping process. In summary, the problems detected by the engineers were:

• – Reduction of thickness in the critical region (traction) of the stamped components during the forming process.

• – Increase of thickness in the critical (compression) region of the stamped components during the forming process.

• – Incidence of cracks during the forming operation and possibility of cracks during use of the product.

• – Lack of parameters to define compensations, in the tool project planning phase.

  The following text describes the application of the proposed procedure when dealing with this practical situation.

Step 1 - Identification of the experimental problem to be solved by RMS and FE and OvMCS

The practical situation involves choosing the number of inserts and their position in the mold in the stamping process to mitigate the effects of Traction (response variable y₁) and Compression (response variable y₂) on the studied product. As presented in [2], the company’s engineers suggested to placing inserts of different heights along the mold to decrease the appearance of cracks. As an experiment in planning strategy, before using the Box-Behnken design, a Plackett-Burman design [4] was used, since initially there were many (in a total of 23) x_i factors (positioning the inserts in the mold) to be investigated (see Fig. 10).

Fig. 10

Geometry of the mold of the stamped product without and with the inserts. Source: [2]

Therefore, in a similar way like it was made and described in details in [2] for one response variable, from the practical experience of the company’s engineers, and based on the Pareto chart built by the Minitab^TM software [4], it was possible to reduce the number of x_i factors from 23 to 15, and a Plackett-Burman design N16 experiment was performed for an one-response variable, now considering two response variables y₁ and y₂.

After using the Plackett-Burman design N16, the number of factors was reduced to five, which was the number used in the application of the RSM with Box-Behnken design, as shown in Table 2.

Table 2 Experimental matrix of the stamping process example. Source: [2]

Figure 11 shows the adjustments of the inserts made in the mold for the execution of the RSM with Box - Behnken design experiment. Appendix A presents all the 243 = 3⁵ possible combinations used in this experiment. As an illustration, a small part of it is reproduced in Table 3.

Fig. 11

Positioning the inserts for the RSM and Box-Behnken design. Source: Adapted from [2]

Table 3 Natural factor values for each experiment and the associated values for the two responses variables, obtained by finite element simulation (In Appendix A is the whole database)

Step 2 - Generate empirical functions for the two responses variables by RSM

By applying the OLS algorithm, with the data from Table 3, the empirical quadratic function (18)–(19) and the constraints (20)–(22), for y₁ (traction) were obtained:

$$ \begin{array}{@{}rcl@{}} \hat{y_{1}}= \beta_{1}x_{1}&+&\beta_{2}x_{2}+\beta_{3}x_{3}+\beta_{4}x_{4}+\beta_{5}x_{5}+\beta_{6}{x_{2}^{2}} \\ &+&\beta_{7}{x_{4}^{2}} +\beta_{8}{x_{5}^{2}}+\beta_{9}x_{1}x_{4}+\beta_{10}x_{2}x_{4} \end{array} $$

(18)

$$ \begin{array}{@{}rcl@{}} \hat{y_{1}}= &-&0.01049784x_{1}+-0.012858642x_{2}\\ &-&0.002599383x_{3}+0.192685194 \\ &+&0.174519113x_{5}+ 0.000268939{x_{2}^{2}} \\ &-&0.002288908{x_{4}^{2}}-0.006298995{x_{5}^{2}} \\ &+&0.000170417x_{1}x_{4}+0.000253935x_{2}x_{4} \end{array} $$

(19)

subject to:

$$ -20 \leq x_{i} \leq 20, i \in = \left\{1,2,3\right\}. $$

(20)

$$ 30 \leq x_{4} \leq 50 \\ $$

(21)

$$ 10 \leq x_{5} \leq 20 $$

(22)

By applying the OLS algorithm, with the data from Table 3, the empirical quadratic function (23)–(24) and the constraints (25)–(27), for y₂ (compression) were obtained:

$$ \begin{array}{@{}rcl@{}} \hat{y_{2}}&=& \beta_{1}x_{2}+\beta_{2}x_{2}+\beta_{3}x_{3}+\beta_{4}x_{4}+\beta_{5}x_{5}+\beta_{5}{x_{3}^{2}}\\ &&+ \beta_{6}{x_{4}^{2}}+\beta_{7}{x_{5}^{2}}+\beta_{8}x_{3}x_{4}+\\ &&+ \beta_{9}x_{3}x_{5}+\beta_{10}x_{2}x_{2}+\beta_{11}x_{4}x_{5} \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} \hat{y_{2}}= &-&0.00306419x_{2}-0.00918935x_{3}+ 0.28553739x_{4}\\ &+& 0.323947771x_{5} +\\ &+&0.174519113x_{5}+ 0.00138346{x_{3}^{2}} - 0.0029276{x_{4}^{2}}-0.0065740{x_{5}^{2}} \\ &+&0.00092564x_{3}x_{4} - 0.00086694x_{3}x_{5}+0.00019976x_{2}x_{3}\\ &-& 0.0032292x_{4}x_{5} \end{array} $$

(24)

subject to:

$$ -20 \leq x_{i} \leq 20, i \in = \left\{1,2,3\right\}. $$

(25)

$$ 30 \leq x_{4} \leq 50 \\ $$

(26)

$$ 10 \leq x_{5} \leq 20 $$

(27)

Step 3 - Optimizing the empirical functions without uncertainty

In this step, without considering the occurrence of uncertainty in the coefficients of the empirical functions, three agglutination methods were tested for both response variables: compromise programming (CP), desirability function (DF) and modified desirability function (MDF). The generalized reduced gradient (GRG) method was applied to optimize (19)–(22) and (24)–(27).

Tables 4, 5 and 6 present the results obtained by the GRG algorithm for each agglutination method, highlighting the best-fit values. Appendix B presents the FE simulations for these best fits.

Table 4 Optimization by GRG, without occurrence of uncertainty, using compromise programming—CP

Table 5 Optimization by GRG, without occurrence of uncertainty, using desirability function—DF

Table 6 Optimization by GRG, without occurrence of uncertainty, using modified desirability function—MDF

The weight values for each optimization scenario were calculated using a mixture design [4]. Additionally, for the application of the Desirability function, with the support of the company engineers, the values of the parameters U and L, were established, respectively, for $\hat {y_{1}}$ and $\hat {y_{2}}$: U= 6.8 and L= 4.857, L= 6.8 and U= 9.193. Finally, to apply the modified desirability function, also with the support of the company’s engineers, the values of the parameters U and L, were established, respectively, for $\hat {y_{1}}$ and $\hat {y_{2}}$: U= 6.8 and L= 4.857, L= 6.8 and U= 9.193. In addition, as a suggestion of the consulted engineers, it was adopted T = (L + U)/2 and by using Eq. (14) resulted in d_s(T_s) = 1.

Step 4 - Insert the occurrence of uncertainty in the coefficients of empirical functions

Equation (28) presents the new coefficients of the empirical function $\hat {y_{1}}$ (associated to response variable Traction), with the insertion of uncertainty, as is in Table 7, for CI - 95% and CI - 99%:

$$ \begin{array}{@{}rcl@{}} \hat{y_{1}}&=& \tilde{\beta_{1}}x_{1}+ \tilde{\beta_{2}}x_{2}+ \tilde{\beta_{3}}x_{3}+ \tilde{\beta_{4}}x_{4}+ \tilde{\beta_{5}}x_{5}\\ &&+ \tilde{\beta_{6}}{x_{2}^{2}} + \tilde{\beta_{7}}{x_{4}^{2}} + \tilde{\beta_{8}}{x_{5}^{2}}+ \tilde{\beta_{9}}x_{1}x_{4}+ \tilde{\beta}_{10}x_{2}x_{4} \end{array} $$

(28)

Table 7 Coefficients in the empirical function $\hat {y_{1}}$ with occurrence of uncertainty. Source: [2]

Table 7 shows for $\hat {y_{1}}$ the CI - 95% and the CI - 99%, as is in [2].

Equation (29) presents the new coefficients of the empirical function $\hat {y_{2}}$ (associated to response variable Compression), with the insertion of uncertainty, as is in Table 8, for CI - 95% and CI - 99%:

$$ \begin{array}{@{}rcl@{}} \hat{y_{2}}&=& \tilde{\beta_{1}}x_{2}+ \tilde{\beta_{2}}x_{3}+ \tilde{\beta_{3}}x_{4}+ \tilde{\beta_{4}}x_{5}+ \tilde{\beta_{5}}{x_{3}^{2}}+ \tilde{\beta_{6}}{x_{4}^{2}} \\ &&+ \tilde{\beta_{7}}{x_{5}^{2}} + \tilde{\beta_{8}}x_{3}x_{4} + \tilde{\beta_{9}}x_{3}x_{5} + \tilde{\beta}_{10}x_{2}x_{3} +\tilde{\beta_{11}}x_{4}x_{5} \end{array} $$

(29)

Table 8 Coefficients in the empirical function with occurrence of uncertainty

Step 5 - Optimize empirical functions with uncertainty

For both studied response variables, Tables 9 and 10, show, respectively, the results of OvMCS - CI - 95% and OvMCS - CI - 99%, using Crystal Ball^TM software with its OptQuest^TM optimizer, with the compromise programming—CP function.

Table 9 Results with the occurrence of uncertainty using CP and OvMCS - CI- 95%

Table 10 Results with the occurrence of uncertainty using CP and OvMCS - CI - 99%

For both studied response variables, Tables 11 and 12 show, respectively, the results of OvMCS - CI - 95% and OvMCS - CI - 99%, using Crystal Ball^TM software with its OptQuest^TM optimizer, with the desirability function—DF function.

Table 11 Results with the occurrence of uncertainty using DF and OvMCS - CI - 95%

Table 12 Results with the occurrence of uncertainty using DF and OvMCS - CI - 99%

For both studied response variables, Tables 13 and 14 show, respectively, the results of OvMCS - CI - 95% and OvMCS - CI -99%, using Crystal Ball^TM software with its OptQuest^TM optimizer using the modified desirability function—MDF.

Table 13 Results with the occurrence of uncertainty using MDF and OvMCS - CI - 95%

Table 14 Results of the uncertainty using MDF and OvMCS - CI - 99%

Step 6 - Analyzing the results of traditional multiple-response optimization with RSM (obtained in step 3), and with RSM and FE and OvMCS (obtained in step 5)

The engineers of the studied company considered that a 20% thickness increase or decrease is acceptable for the studied stamping process, and the best fit should meet the following criteria

• - $\hat {y_{1}}_{\min \limits }$ = 5.440 (mm).

• - $\hat {y_{2}}_{\max \limits }$ = 8,160 (mm).

• - keeping the lowest value for the ratio: $\frac {\hat {y_{2}}}{\hat {y_{1}}}$.

From the 45 scenarios generated by optimization (See Tables 4, 5, 6, 9, 10, 11, 12, 13 and 14), only 5 scenarios met the established criteria:

• – Solution by OvMCS - CI - 95%, with weights w₁= 0.75 and w₂ = 0.25, using CP - Found at the last line of Table 9 .

• – Solution by OvMCS - CI - 95%, with weights w₁= 0.75 and w₂ = 0.25, using DF - Found at the last line of Table 11.

• – Solution by OvMCS - CI - 99%, with weights w₁= 0.75 and w₂ = 0.25, using DF - Found at the last line of Table 12 .

• – Solution by GRG algorithm, with weights w₁= 0.75 and w₂ = 0.25, using CP - Found at the last line of Table 4.

• – Solution by GRG algorithm, with weights w₁= 0.75 and w₂ = 0.25, using DF - Found at the last line of Table 5.

Using the information in Appendix B for illustration, Figs. 12 and 13, show the EF simulation of the best optimization settings for the CP function without the uncertainties (Table 4 in step 3) with the uncertainties (Table 9 in step 5), respectively.

Fig. 12

FE simulation of best fit without uncertainty for Compromise Programming: weights w₁ = 0.75 and w₂ = 0.25

Fig. 13

EF simulation of best fit without uncertainty for Compromise Programming with OvMCS - CI - 95%: w₁ = 0.75 and w₂ = 0.25

With these results, the engineers of the company under study were asked which solution (without uncertainty - step 3 or with uncertainty - step 5) would provide the best practical effect on the studied stamping process. The answer was that the best performance setting would be that obtained for CP, with weights w₁ = 0.75 and w₂ = 0.25, using OvMCS - CI - 95% (Fig. 13). This adjustment better met all three criteria already discussed, and thus would provide the best practical tool configuration, resulting in increased quality and reliability of the stamping process.

Step 7 - Analyze the behavior of the response variables from RSM and FE and OvMCS. Validate the results

Model validation of uncertain structures is a challenging research focus because of uncertainties involved in modeling, manufacturing processes, and measurement systems [56].

In order to validate the proposed procedure, graphical analysis was used, as shown in Figs. 14 and 15, respectively, to evaluate the behaviors of both response variables $\hat {y_{1}}$ and $\hat {y_{2}}$, associated with the adjustment chosen as being the most appropriate in step 6, which was the solution by OvMCS - CI - 95%, with weights w₁ = 0.75 and w₂ = 0.25, using CP.

Fig. 14

Frequency chart for $\hat {y_{1}}$ for OvMCS - CI - 95% applied to compromise programming function, with w₁ = 0.75 and w₂ = 0.25. Source: Crystal Ball^TM

Fig. 15

Frequency chart for $\hat {y_{2}}$ for OvMCS - CI - 95% applied to Compromise Programming function, with w₁ = 0.75 and w₂ = 0.25. Source: Crystal Ball^TM

Considering this solution, Figs. 14 and 15 were obtained by performing 10⁶ simulation runs in Crystal-Ball^TM Trial Version software, using the OptQuest optimizer, according to the flowchart in Fig. 5, for the response variables y₁ and y₂, respectively. In this simulation, random values were generated for the coefficients of the empirical functions (19) and (24), according to continuous uniform distributions for the factor coefficients, which are shown in the second column of Table 7, associated with the CI - 95% interval.

Figure 16, also considering the CP agglutination method, with w₁ = 0.75 and w₂ = 0.25 shows the behavior of the solutions obtained by OvMCS - CI - 95% for each of the 10⁶ simulation runs for the CP function. All the solutions were viable, with the Best Solutions arranged parallel to the abscissa axis (number of simulations), drawn at the bottom of Fig. 16. There was only one last best solution, which is highlighted with a green rhombus symbol.

Fig. 16

Performance chart for solutions obtained by OvMCS - CI - 95% applied to compromise programming function, with w₁ = 0.75 and w₂ = 0.25. Source: Crystal Ball^TM

As verified by the simulation with the finite element method, the obtained solution presented good quality in the understanding of the company engineers. Thus, the proposed procedure can be considered validated. Finally, it should be noted that the procedure was very promising, presenting advantages when compared with the traditional methods of optimization of experimental multi-response problems, commonly adopted in companies.

Step 8 - Recommendations

Therefore, at the end of the application of the proposed procedure, it was recommended to the engineers of the company the use the solution obtained for CP, with weights w₁ = 0.75 and w₂ = 0.25, using OvMCS - CI - 95% (Fig. 13) for the studied stamping process.

6 Conclusions and suggestions for future research

Therefore, with the conduction of the present study, all research questions were answered and the established objectives were achieved. Based on the tests performed for a stamping problem at a Brazilian multinational automotive company, an innovative procedure that combines RSM and FE with OvMCS was described. This procedure proved to be adequate to introduce the occurrence of uncertainties in the objective function coefficients of experimental multi-response problems, adopting the continuous uniform distribution. Furthermore, it was statistically validated by the studied stamping problem.

For the studied real problem, regarding the tested multiple response methods, it was possible to identify the best choices for the weight values for the optimizations, calculated by a mixture design methodology, which would be w₁ = 0.75 and w₂ = 0.25, met the criteria set by the company’s engineers. Finally, it was evidenced that the best option would be to use OvMCS - CI - 95% with the compromise programming function and the weight values mentioned above.

RSM and FE combined with OvMCS surpasses the use of the procedures that are usually adopted in companies, which is the (deterministic) optimization for experimental problems with multiple responses, using the GRG algorithm and the desirability function. The use of different agglutination methods with different weights was interesting because it allowed the generation of 15 scenarios without considering uncertainties (see Tables 4, 5 and 6) and 30 scenarios for optimization considering uncertainties (see Tables 9, 10, 11, 12, 13 and 14). Thus, it allowed the development of a sensitivity analysis that generated more knowledge about the studied stamping process.

This system provided engineers with useful information that will facilitate their work when seeking improvements to the process. In fact, the application of OvMCS - CI - 95%, with the continuous uniform distribution used to insert the occurrence of uncertainties in the objective function coefficients presented interesting options to the managers. Moreover, it also proposed a higher quality solution than the one generated by the GRG algorithm and the Desirability function.

For future study, it is intended to test the new procedure proposed here in other types of application, such as service companies, inserting the occurrence of uncertainties, which is an important research gap for both the academic as well as the practical point of view.