1 Introduction

Closed hoisting ropes are multilayer single helical strand ropes. They are used as a traction element in lifting and transport machines and mechanisms, for example, pump rods for oil production from deviated wells [1, 2]. Such ropes must have high strength and sufficient flexibility, so they consist of a large number of small round and shaped wires.

According to the Russian State Standard (GOST) 10505-76, the first three layers of round wires of a closed hoisting rope are twisted around the central wire; according to the principle of linear tangency, subsequent layers of wires of round and shaped cross-sections are twisted according to the principle of point tangency. The direction of the lay of the wires in the two upper adjacent layers should alternate.

An algorithm for scientifically grounded design of ropes for reliable and safe operation requires the development of reliable methods for determining the stress-strain state (SSS). These methods must be both highly accurate and wide range of applications. In work [3] directions of approaches to the theory of calculation of ropes are outlined. These areas are based on:

  1. a)

    The discrete model, in which the rope is represented as a statically indeterminate rod system. Calculation of stresses in this system is possible using the methods of structural mechanics [4].

  2. b)

    The theory of a fiber composites and the solution of the Saint-Venant problem for a cylinder with helical anisotropy [5].

Determination of the force factors in the cross-section of the rope elements at joint tension and torsion occurs in the process of solving the static equation [4]:

$$ P=A\cdotp \varepsilon +C\cdotp \theta \kern0.5em \mathrm{and}\ M=C\cdotp \varepsilon +B\cdotp \theta $$
(1)

where P is the axial force; M is torque; ε and θ are relative elongation and relative torsion angle; and A, B, and C are generalized stiffness coefficients.

The values of the generalized coefficients are determined by the equations:

According to the model of M.F. Glushko [4]:

$$ {\displaystyle \begin{array}{c}A={\sum}_{i=1}^n{A}_i={\sum}_{i=1}^n\left[E{F}_i{\mathit{\cos}}^3{\alpha}_i\right]+E{I}_i\frac{{\mathit{\sin}}^4{\alpha}_i}{r_i^2}{\mathit{\cos}}^3{\alpha}_i+G{I_{\rho}}_i\frac{{\mathit{\sin}}^6{\alpha}_i}{r_i^2}{\mathit{\cos}}^2{\alpha}_i;\\ {}C={\sum}_{i=1}^n{C}_i={\sum}_{i=1}^n\Big[E{F}_i{r}_i{\mathit{\cos}}^2{\alpha}_i\mathit{\sin}{\alpha}_i+G{I}_{\rho i}\frac{{\mathit{\cos}}^4{\alpha}_i}{r_i}{\mathit{\sin}}^3{\alpha}_i-\\ {}\begin{array}{c}E{I}_i\left(1+{\mathit{\cos}}^2{\alpha}_i\right)\frac{{\mathit{\cos}}^2{\alpha}_i}{r_i}{\mathit{\sin}}^3{\alpha}_i\Big];\\ {}B={\sum}_{i=1}^n{B}_i={\sum}_{i=1}^n\Big[E{F}_i{r}_i^2\mathit{\cos}{\alpha}_i{\mathit{\sin}}^2{\alpha}_i+G{I}_{\rho i}{\mathit{\cos}}^7{\alpha}_i+\\ {}E{I}_i{\left(1+{\mathit{\cos}}^2{\alpha}_i\right)}^2{\mathit{\sin}}^2{\alpha}_i\mathit{\cos}{\alpha}_i\Big].\end{array}\end{array}} $$
(2)

where E and G are the elastic and shear modulus of the wire material; Fi is the cross-sectional area of the wires of the i-th layer; Ii is the axial inertia moment of the i-th layer section of wires relative to the axis of the rope; Ipi is polar inertia moment of the i-th layer section of wires relative to the center of the rope; αi is the i-th layer wire lay angle; and ri is the average radius of the i-th layer.

According to the model of I.P. Getman and Yu.A. Ustinov [5]:

$$ {\displaystyle \begin{array}{c}A=\pi {k}_1{a}^2E\left[1-\left(1+\frac{\nu }{2}\right){\mathit{\sin}}^2\alpha \right];\\ {}C=\pi {k}_1{a}^3E\cdotp tg\alpha \frac{\left[1-\left(\frac{4}{3}+\nu \right){\mathit{\sin}}^2\alpha \right]}{2};\\ {}B=\pi {k}_1{a}^4E\cdotp t{g}^2\alpha \frac{\left[1-\left(\frac{3}{2}+\frac{3\nu }{4}\right){\mathit{\sin}}^2\alpha \right]}{3}\end{array}} $$
(3)

where k1 is the ratio of the total cross-sectional area of the wires ΣFi to the cross-sectional area of the rope as a round cylinder FК; a is radius of the rope as a round cylinder; ν is Poisson’s ratio of the wire material; and α is the outer layer wire lay angle.

Solutions of equations (1) with respect to deformations ε and θ are presented in the form [4]:

$$ \varepsilon =\frac{B}{\varDelta }P-\frac{C}{\varDelta}\cdotp M\kern0.5em \mathrm{and}\ \theta =-\frac{C}{\varDelta}\cdotp P+\frac{A}{\varDelta }M $$
(4)

where Δ = A · B − C2.

The considered approaches do not take into account the frictional forces and contact interaction between the rope elements, which reduces the reliability of determining the stress-strain state of the rope. An effective tool for ensuring the operability of multilayer ropes during operation is computer finite element modeling of the stress-strain state of ropes using various software packages [6] [7] [8] [9] [10] [11] [12] [13]. Computer finite element modeling is not inferior in reliability to experimental and analytical methods. The number of works on the computer simulation of the SSS of closed ropes is limited [14].

The purpose of the work is to study the effectiveness of using the method of computer simulation of the stress-strain state of a closed rope during tension and torsion to predict service properties.

2 Materials and methods

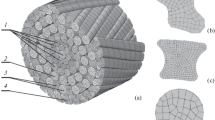
The analysis of the SSS of the closed rope elements during axial tension and torsion was carried out by the finite element method using the licensed SIMULIA/Abaqus software package. The SIMULIA/Abaqus software package allows obtaining results with the required accuracy and productivity [15]. The cross-section of the closed rope and its elements (outer layer 6 of Z-profile wires, subsurface layer 5 of alternating round and H-profile wires, layer 4 and a core of the structure 1 + 7 + 7/7 + 14 of round wires) are shown in Fig. 1.

Fig. 1
figure 1

Cross-section of the closed rope a (part of the outer layer is conditionally removed) and its elements with the finite element mesh: b Z-profile; c H-profile; d round profile; (1) core (round wires); (2) 4th layer (round wires); 3–5th layer (round/H-profile wires); 4–6th layer (Z-profile wires)

Full size image

The core of the 1 + 7 + 7/7 + 14 structure is a single-strand wire rope of a round profile with axes in the form of helical lines. The wires are twisted with the same pitch in several layers around the central straight wire (Fig. 1). Laying of the core is carried out in one technological operation according to the principle of linear tangency: the wires of the layer above are placed in the recesses formed by the wires of the lower layer. The contact between the layers of wires occurs along the lines.

Laying of subsequent layers of the rope is carried out by separate technological operations. At each operation, the direction of the wire lay in the layers is changed. The direction of the lay of 4th layer from wires of a circular profile and 6th layer from wires of Z-profile was taken for the right and 5th layer of alternating wires of round and H-profile and the core for the left. With different directions of lay, the contact of the layers of round wires occurs at points. The contact of layers of shaped profile wires can be considered as linear [4].

The C3D8R cells type was used for all elements of the rope – continuous three-dimensional eight-node elements with reduced integration. The elongation of the cells along the axis of the wires of all profiles was 1.5 mm, and in the cross-section, 0.1 mm for the H-profile, 0.2 mm for the Z-profile, and 0.26–0.3 mm for round profile of the wires. The choice of the cells size was determined by the degree of curvature of the individual elements of the profile. The helical elements of the rope were obtained by the method of extrusion (solid extrude) with a turn with a predetermined pitch of the cross-section of the wires, which also led to a helical “torsion” of the finite element mesh. The appearance of the finite element mesh at the end of the wires is shown in Fig. 1b, c, and d.

The length of the simulated rope sample is l0 = 130 mm, the elastic modulus of the wire material is E = 2·105 MPa, and the friction coefficient is μ = 0.1. The wire rope material was set to isotropic. An increase in local plastic deformation leads to an increase in the resistance to deformation σs according to the known dependences for wires of the used strength groups. For the material of the wires of round profile, steel with the initial value of the yield point σso = 1280 MPa was used and for the shaped profile σso = 1120 MPa [16].

To determine the loads and torques taken by the layers of the rope during tension or torsion, the ends of the layers wires at the rear end of the simulated rope before stretching were firmly connected to the end surface of the movable hard disk of the rig, and on the front – with coaxially located fixed rigid inner disk (core 1 + 7 + 7/7 + 14) and rings (layers 4–6) [16]. The deformation of the rope sample under tension was carried out due to the axial movement of the movable hard disk and the subsequent torsion – due to the turns of the movable hard disk at the achieved axial load (with the possibility of axial movement during the torsion). Internal forces and torques in each of the layers were determined from the time-varying reactions of the supports on the fixed inner disk and rings at the front end, which are fixed at each step of the simulation.

The determination of the characteristics of the SSS of the rope elements in tension and torsion was carried out for two loading options.

In 1st simulation version, at the first stage, the ends of the rope sample, fixed in devices that exclude their rotation, were moved apart at a speed of 4 mm/s to the value of the axial force P ~ 120 kN. This force takes into account the passport carrying capacity of 80 kN and the weight of the rope with a length of 1500 m. The torsion of the rope sample by the external M torque was carried out at the second stage. The direction of torsion led to the unwinding of the outer layer of the Z-profile wires.

According to 2nd simulation version, at the first stage, the sample was stretched similarly to the first stage of 1st simulation version, and at the second stage, the external M torque carried out the twisting of the rope sample in the opposite direction to 1st simulation version. This caused the outer layer of the Z-profile wires to twist.

The torsion of the rope sample at the second stage of the 1st and 2nd simulation version was carried out at a speed of 36 deg/s for 0.55 s (angle of rotation φ≈20°). During the torsion process, the external load P, reached at the first stage, remained unchanged. The direction of the external torque M in the direction of torsion of the outer layer of the rope sample was taken to be positive. The loading scheme at the first stage (pure tension: θ = 0, ε ≠ 0) was a model of longitudinal force transfer, and at the second stage (torsion under load: θ ≠ 0, ε ≠ 0), it was a model of rotational motion from a surface drive to a downhole pump [16].

3 Results

The scheme of analytical calculation of the SSS of a helical rope according to traditional approaches [4] [5] consists of the following steps. For a given external load on the rope in the form of an axial force P and the torque M, the generalized coefficients of the rigidity of the rope are determined by equations (2) and (3), and then, the deformation coefficients ε and θ are found from equations (4). Next, the distribution of power and moment loads over the rope layers and internal forces in the cross-sections of the wires are calculated.

The axial and polar moments of inertia of the rope layers in equations (2) were determined as for ring sections. The direction of laying the wires of the outer layer was taken to be positive. The difference in the directions of the lay of the wires’ layers of the closed rope affects the value of the coefficient C, since the sine of the lay angle enters into an odd power in equation (2) to determine it. One of the main reasons for stratification may be the “untwisting” effect, the magnitude of which, in addition to technological reasons, depends on the value of the stiffness coefficient C.

The values of the generalized stiffness coefficients of the investigated rope calculated according to equations (2) and (3) are given in Table 1.

Table 1 The results of calculating the generalized coefficients by analytical methods and according to computer finite element modeling
Full size table

The results of the analytical calculation of the SSS of a helical rope using traditional approaches were compared with those obtained in the course of computer finite element modeling. The resulting values of the forces and moments in the rope, obtained by summing the internal forces and moments in each of the layers of the rope during tension and subsequent torsion [16], are shown in Fig. 2.

Fig. 2
figure 2

Distribution of axial force (a) and torques (b) in the rope during tension (stage 1) and torsion (stage 2): (1) untwisting the rope; (2) twisting the rope

Full size image

Modeling makes it possible to determine the values of the axial force P, torque M, relative elongation ε, and relative torsion angle θ = φ/lo of the rope sample at given values of axial displacement (the first stage) and the torsion angle of the cross-section (the second stage). Further, it is possible to solve the inverse problem – to determine the generalized stiffness coefficients using equation (1). This avoids time-consuming analytical calculations.

The first stage

Pure tension of the rope.

This type of loading causes elongation of the rope sample in the direction of the force action (ε ≠ 0), accompanied by its untwisting. The ends of the rope sample are secured against rotation (θ = 0).

Under pure tension, from equations (1) are obtained equations:

$$ \varepsilon =P/A; $$
$$ M=C\cdotp \varepsilon =C\cdotp P/A. $$
(5)

From the results of modeling, it follows that with the force of P ~ 120 kN, the elongation of the rope sample, achieved in a time of ~ 0.2 s, is ε = 0.563%, the tensile stiffness coefficient (Fig. 2a):

А = Р/ε = 213,1·10 5 N

The elastic modulus of the rope E = A/F≈0.8· 105 MPa obtained from the simulation results is significantly lower than the usually given values E = (1.3 − 1.5)·105 MPa for helical ropes at the first loading [17]. The residual structural elongation εres associated with the running-in of twisted wires at the first loading is 0.24% [16]. The exclusion of the residual structural elongation from the total deformation gives the value of the elastic elongation of the rope sample ε = 0.563 − 0.24 = 0.323%. In this case, the elastic modulus of the rope is E = 1.38·105 MPa, corresponding to the traditionally used one, and the stiffness coefficient is A = 371.5·105 N (Table 1).

The results of modeling the deformation of the rope under tension [16] are confirmed by the experimental data obtained by stretching a rope sample on a test universal hydraulic horizontal machine LabTest 6.2000N.7 (Czech Republic). From the tension diagram in Fig. 3, it follows that with the exclusion of the initial structural elongation of the sample εres = 0.26% from the total deformation; the elastic elongation of the rope sample at P ~ 120 kN is ε = 0.318%. The experimentally determined value of the elastic modulus of the rope is E = 1.37·105 MPa. The difference between the values of the elastic modulus obtained during modeling and the experimental data is ≈ 1.5%.

Fig. 3
figure 3

Diagram of stretching of the rope sample on a test universal hydraulic horizontal machine LabTest 6.2000N.7: (1) section of constructional elongation; (2) section of elastic elongation

Full size image

Under the action of a tensile force, the torque Mk arises in the rope layers. It is directed in the direction opposite to the direction of the wire lay in the layer. The resulting torque, counterbalanced by the torque in the fastening, is equal to the algebraic sum of the torques in the layers of the rope [16], and by the end of the first stage, it takes the value M = 68.4 N·m (Fig. 2b). From equations (5), the value of the influence coefficient is C = A/ε = 121.5·105 N·mm, and in the case of excluding residual elongation, from the total deformation C = 211.8·105 N·mm (Table 1).

The value of elongation ε obtained in the simulation of the stage of tension at a force of P ~ 120 kN exceeds the values of elongations obtained by analytical calculation by the methods [4] [5] (Table 2). This discrepancy is associated with a large difference in the values of the stiffness coefficients A (Table 1). An increase in the tensile stiffness of the rope is usually achieved by preliminary stretching of the rope (the elastic modulus increases by an average of 20% [18]).

Table 2 Comparison of the values of elongation and torsion angle obtained by analytical methods and according to computer simulation data
Full size table

The calculated values of the torques obtained by the methods [4, 5] are M = 87.8 N·m and M = 210.1 N·m, respectively. The discrepancy between the values is explained by the difference in the values of the influence coefficient C (see Table 1), associated with taking into account the direction of the layering of the layers when calculating according to equations (2). The value of the torque M = 68.4 N·m obtained during the simulation (Fig. 2b) is close to the result obtained by the method of M.F. Glushko.

Thus, the results of modeling the pure tension of the rope are consistent with equations (5) and correlate well with the results of calculation by the method of M.F. Glushko, which more accurately takes into account the real construction of the ropes.

The second stage

Torsion of the rope with a constant longitudinal tensile force P = 120 kN (ε ≠ 0, θ ≠ 0).

When modeling a complex loading, a given relative angle of untwisting (twisting) of a rope sample θ = φ/l = ± 2.66 rad/mm is achieved when the rope sample is twisted by an external torque M = − 252.4 N·m (untwisting) and M = 573, 3 N·m (twisting). These values of the torques correspond to the final values of the torque on curves 1 and 2 (Fig. 2b).

The elongation achieved at the first stage (tension) can decrease or increase during torsion, depending on the sign of the external torque. The untwisting torque tends to lengthen the top layer of the rope, while the twisting moment tends to compress it. The simulation results under the given loads show that by the end of the second stage the relative elongation of the rope during the untwisting of the outer layer decreases by the value Δε = 0.06% and remains unchanged during twisting (Table 2).

In contrast to computer modeling, the results of the analytical calculation of elongation according to the methods [4, 5] when untwisting the rope indicate an increase, and when twisting, a decrease in the relative elongation in comparison with the first stage (Table 2). This is most clearly manifested for the method [5]. The differences are associated with the low value of the torsional stiffness coefficient B = 1780.7·105 N·mm2 (Table 1).

With various models of calculation, the angle of torsion θ of the section of the rope sample during untwisting takes negative values and during twisting, positive values (Table 2). The θ values obtained by the methods [4, 5] differ several times from the simulation results.

The static equations (1) are valid for a rope, for which deformations ε and θ are the same for all rope elements. At the second stage, this condition is not met due to the difference in the directions of layering.

Thus, the results of computer simulation of the complex loading of the closed rope differ from the results of the calculation according to equations (1), which is associated with the peculiarities of the distribution of internal forces and torques over the layers of the rope with different directions of wire lay [16].

It is known [19] that in the case of tight twisting of wires, an inconsistent transverse narrowing of the layers under tension during operation or even during preliminary stretching leads to the appearance of radial gaps between the layers. Radial gaps can lead during the operation of the rope to a violation of the structural integrity and failure with multiple reiterations of the load-unload cycle.

A coordinated transverse narrowing of adjacent layers of a closed rope is possible if there are gaps between the shaped wires in the rope layers. According to GOST 10505-76, a gap is allowed between the shaped wires that does not violate the rope lock. The criteria for choosing the size of the gap can be the degree of residual structural elongation of the rope, the tolerance for the size of the wire, as well as the magnitude of the contact stresses between the rope elements when they come into contact [20]. Computer simulation of the SSS of closed rope elements allows determining the contact stresses between shaped wires in layers and between layers (Fig. 4).

Fig. 4
figure 4

Change in contact stresses between the wires in the cross section of the closed rope during tension (initial tangential gaps between the wires of the outer layer Δ = 0.035 mm (a) and Δ = 0.13 mm (b)): (1 and 2) tangential stresses between the wires in the outer and subsurface layers, respectively, (3) radial stresses σr between the outer and subsurface layers

Full size image

From Fig. 4a, it follows that under conditions of stretching the rope with initial gaps Δ = 0.035 mm, the tangential contact stresses between the wires of the outer layer reach σc = 300–400 MPa (curve 1). The contact stresses between the layers (curve 3) and the wires of the subsurface layer (curve 2) are insignificant. This indicates that the narrowing of the outer layer lags behind the subsurface layer, which contributes to the formation of a radial gap between these layers, leading to an unstable position of the wires. As already mentioned, the occurrence of a radial clearance can cause a possible violation of the structural integrity of the outer layer with repeated reiterations of the load-unloading cycle during the operation of the rope.

When the rope is stretched with initial gaps Δ = 0.13 mm (Fig. 4b), the values of the tangential contact stresses between the wires of the outer layer (curve 1) decrease in comparison with those shown in Fig. 4a; at the same time, the stresses σc between the wires of the subsurface layer increase (curve 2). In this case, the contact radial stresses between the wires of the outer and subsurface layers increase significantly and reach the value of σr = 900–1100 MPa (curve 3). This indicates that the outer layer becomes self-tightening, overloaded, which increases the chance of breakages and reduced service life.

Thus, the computer simulation of the SS of the rope elements of a closed structure makes it possible to assess the consistency of the narrowing of the layers during axial tension by analyzing the contact stresses between adjacent wires in the cross-section of the rope.

In this work [16], it was shown that the twisting of the rope causes an increase in the equivalent stresses σeq in the elements of the twisted layers, in comparison with tension. This should affect the reliability of the rope during operation; therefore, it is proposed to determine the safety factor of the rope layers in relation to the ratio of permissible stress values in accordance with the wire-marking group to the average stress values σeq over the wire cross-section.

A distinctive feature of the used method of computer modeling is the ability to determine the distribution of force factors over the volume of each rope element. The example shows the distribution of equivalent stresses σeq in the cross-sections of the elements of the layers in the radial direction with the adopted parameters of external loading (Fig. 5). The distribution of equivalent stresses along the diameter of the round wires of the core layer 3 and the intermediate layer 4 of the closed rope, as well as the profiled wires of the 5th and 6th layers, is indicated.

Fig. 5
figure 5

Curves of intensity distribution of equivalent stresses in the radial direction under tension (ε≈0.6%, curve 1)and torsion (φ≈20°; curve 2, untwisting; curve 3, twisting)

Full size image

When stretching (stage 1), the rope elongates in the direction of the force action, accompanied by untwisting. The intensity of the stresses generally increases towards the center of the rope. The excess of the values of σeq in the outer layer in comparison with the subsurface layer 5 is associated with a smaller gap between the wires along the lower flange of the Z-profile [21]. In the middle part of layer 3 of the core, a minimum is observed, and at the contact with the wires of adjacent layers 2 and 4 – maxima of stress intensity values.

The distribution of stress intensity over the layers is nonuniform during the untwisting and twisting of the rope (stage 2). The scatter of the average values of σeq over the layers is characteristic, which is explained by the difference in the directions of layering of layers. The maximum values of σeq, evenly distributed over the cross-section of the wires, significantly exceeding the values of σeq under tension, are observed in the twisted layers. The untwisted layers are characterized by an increase in the stress intensity in the contact regions of the adjacent rolled layers. Thus, the stress intensity in the cross-section of the wires of the untwisted layer 5 increases in the zone of contact interaction with the wires of the twisted outer layer.

Thus, the distribution of the intensity of equivalent stresses in the elements of the rope makes a significant contribution to ensuring the durability and reliability of closed ropes during operation.

4 Conclusions

  1. 1.

    The results of computer simulation of the SSS of the closed rope elements in tension correlate well with the results of the analytical calculation of deformations and efforts according to the equations of statics.

  2. 2.

    Finite element modeling of the SSS of closed rope elements allows at the design stage: it is justified to approach the choice of the size of the gaps between the shaped wires in the layers of the rope based on the analysis of the change in contact stresses between the elements of the rope during tension. Optimization of the gap ensures the compatibility of the layers in the radial direction and the preservation of the structural integrity of the rope during operation, and by the distribution of equivalent stresses in the cross-sections of the rope elements during joint tension and torsion, it predicts the durability and reliability of closed ropes during operation.