A general identification method for position-dependent geometric errors of rotary axis with single-axis driven

Abstract

Position-dependent geometric errors (PDGEs) of rotary axis affect the accuracy of the multi-axis machine tool. However, many PDGE identification methods were not general enough and not applicable when the structure of the machine tool was limited or changed. In this paper, a general PDGE identification method with single-axis driven was proposed. Firstly, the comprehensive length change model of the double-ball bar (DBB) was established. The simplification was conducted through the constraint condition to obtain the identification matrix. Then, the effect of the installation errors of the DBB was analyzed and eliminated. Simulations were carried out to validate the correctness of the proposed method when considering the installation errors. Next 10 measurement patterns were determined according to the structure limitation of the small-size 5-axis machine tool. Totally 364 combinations with full rank identification matrix are available. Finally, the prediction experiments and analysis for standard deviation were conducted to further validate the effectiveness of the proposed method. It turned out that the small condition number of the identification matrix can more likely achieve high accuracy. And an improved combination using 5 patterns was proposed with the same accuracy achieved compared to that using a total of 10 patterns.

1 Introduction

1.1 Background

The rotary axis is an important part of the 5-axis machine tools, and the accuracy of the rotary axis affects the machining quality to a great extent. The geometric errors are considered as one of the most important evaluation indicators of accuracy [1, 2]. Compared with the linear axis, the geometric errors of rotary axis are much more difficult to detect [3, 4]. According to the ISO standards [5, 6] and previous research [7, 8], the geometric errors of rotary axis are divided into the position-dependent geometric errors (PDGEs) and position-independent geometric errors (PIGEs). The PIGEs were mainly caused by the imperfect assembling process while the PDGEs were mainly caused by defects in the manufacturing process [9, 10].

The double-ball bar (DBB) was first designed and developed to test the linkage performance of machine tools, which has already been used widely [11, 12]. In recent years, the DBB was also used to identify the geometric errors of rotary axis. Tsutsumi and Saito [13] proposed an identification method for the geometric errors with three measurements in the radius, tangential, and axial directions carried out. This method had been used and improved by many other researchers. Based on that, Xiang et al. identified 10 PDGEs [10] and 8 PIGEs [14] for the 5-axis machine tools. Fu et al. [15] proposed 6-circle methods with 6 installations of the DBB in the tests. Zhong et al. [16] evaluated and quantitated the comprehensive accuracy of the 5-axis machine tools with 9 times measurement using the DBB. In addition, the ISO standard provides a recommended method to obtain the geometric errors [5]. However, the linear axes must be linked to moving in the measurement. In this way, the geometric errors of the linear axes needed to be measured and compensated in advance. For simplification, these methods with multi-axis moved were named as multi-axis-driven method (MADM). Using the MADM, geometric errors of the rotary axis in 6 degrees of freedom are identified.

Compared to MADM, the measurement patterns of the single-axis-driven method (SADM) is much simpler. Only the rotary axis to be tested moved in the whole process. The extra effect of the geometric errors of the linear axis can be avoided. Lee and Yang used SADM to identify the PDGEs [17] and PIGEs [18], respectively. Ding et al. [19] studied and identified the PDGEs of the rotary axis with 6 measurement patterns used based on SADM. Zargarbashi et al. [20, 21] proposed an identification method for a swing axis. The outstanding characteristic is that only 1 time installation of the DBB is needed. Different from the MADM, it is a problem for SADM to obtain the angular positioning error of rotary axis. However, with the maturity of commercial products like XR20, the angular positioning error of the rotary axis is available (https://www.renishaw.com/en/xr20-w-rotary-axis-calibrator%2D%2D15763) [22]. The MADM is no longer attractive as before. The SADM is an optional choice when identifying the error of a single rotary axis.

1.2 Existing problems

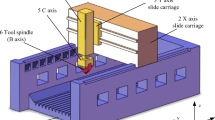
Overall, the identification and compensation of PIGEs are much more mature than those of PDGEs, and some CNC systems even provide simple calibration and compensation functions for PIGEs (http://www.huazhongcnc.com/portal/list/index/cid/20.html). To further improve the accuracy of rotary axis, the identification of PDGEs is necessary. Using the DBB to obtain the PDGEs of the rotary axis is feasible and many researches had proved that. And the main route of the existing method is measurement pattern-identification model. The measurement patterns were firstly designed, and then, the identification model will be established based on the measurement patterns. With different lengths and installations of the DBB, different identification methods were proposed. These methods were practical for the PDGE identification for a special rotary axis of the machine tools. However, when the structure of the rotary axis changed, some of the methods may not be able to be adopted. For example, the identification method in Ref. [20, 21] cannot be used for the turntable. In addition, for some small-size 5-axis machine tools, the travel of X-axis or Y-axis is less than 200 mm as shown in Fig. 1a, the methods in Ref. [10, 19] would not be suitable. For the rotary axis of gear machine tools, the workpiece ball cannot be directly installed on the center axis line as shown in Fig. 1b, then the methods in Ref. [15, 17] would not be suitable. Besides, the installation of the DBB would be difficult due to the structure limitation. These rotary axes with the structure limitation greatly decrease the applicability of these identification methods. Some scholars have proposed some general kinematic and compensation models of machine tools with different structures [23, 24], but there are few studies focused on the general models for error identification. Different models were used for those machine tools with different structures.

Fig. 1

a, b Rotary axis of special machine tools with structure limitation

On the other hand, some problems were habitually ignored in the measurement and identification process like the influence of the installation errors of the DBB. When identifying the PDGEs, the installation errors would be an important factor that affects the results; thus, some scholars proposed different methods to deal with the installation errors. Lee and Yang [18] and Chen et al. [25] developed a homemade device to adjust the installation errors. And these devices mainly focus on the installation error of the ball connected with the tool cup. As for the installation error on the center mount side, Lee and Yang [26] used a dial indicator to measure the installation error for the workpiece ball. The problem is that much attention and micro-adjustment were needed to guarantee no installation error, and very skillful operations would be needed.

Among these researches about the installation errors, an agreement is reached that the installation error does directly affect the measurement results [2, 20]. Reducing installation times became a trend for identification methods. However, the effects of the installation error to the two kinds of errors, PDGEs and PIGEs, are not exactly the same, which were necessary to analyze the difference.

In the paper, a general PDGE identification method was proposed with only one axis driven, which can evolve into different kinds of methods, according to the detailed structure of the machine tool and specific measurement environment. In addition, the effect of the installation errors on the PDGEs was analyzed and eliminated. This paper is arranged as follows: in Section 2, the comprehensive length change model of the DBB is established, and the constraint condition of the DBB is used to simplify the model and obtain the identification matrix. In Section 3, the installation errors and the effect on the identified results were analyzed. Series simulations were carried out to validate the methods when considering the installation errors. In Section 4, experiments were conducted to identify the PDGEs and further verify the proposed method. In Section 5, some conclusions are obtained finally.

2 General identification model for rotary axis

2.1 Definition of position-dependent geometric errors

According to the degree of freedom of the rigid body in space, 6 geometric errors including 3 translational errors and 3 angular errors [27, 28] are enough for describing the difference between the theoretical and actual movement of the rotary axis. To further reflect the characteristics of geometric errors, the standard defined two kinds of geometric errors of rotary axis, error motions of axis rotation and location error of axis average line [5, 6]. These two kinds of errors can be also equivalent to PDGEs and the PIGEs according to whether they are related to the position of the axis of motion [29]. The definitions of the PIGEs in the previous researches are almost the same representing the deviation between the axis average line and the theoretical axis line [6]. However, some different understandings exist about the PDGEs. In Ref. [29], the PIGEs were considered as constant terms of the PDGEs, and the PIGEs were even no longer paid attention to and distinguish sometimes [27]. While in Ref. [30, 31], the PDGEs and PIGEs were independent. A simple diagram can show the differences between these definitions as shown in Fig. 2. The two definitions can both work for error identification. In this work, it is a precondition that the PIGEs and PDGEs are independent.

Fig. 2

Difference between the definitions of PDGEs

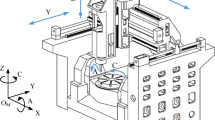
Taking a turntable as the example in Fig. 3, 6 PDGEs of the rotary axis are defined relative to the fixed coordinate P-XYZ. 3 translational errors along X-, Y-, and Z-axis are denoted as E_XC, E_YC, and E_ZC, while the 3 angular errors around X-, Y-, and Z-axis are denoted as E_AC, E_BC, and E_CC as shown in Fig. 3.

Fig. 3

Definition of PDGEs [6, 32]

The PIGEs of the rotary axis are defined relative to another fixed coordinate O-XYZ, and the Z-axis line is the theoretical axis line of rotary axis as shown in Fig. 4. As the ISO defined, the axis average line is determined by calculating the center of least-square circle of radial error motion. It is assumed that P and P_H represent two centers of the least-square circles in XY plane at height of O and O_H. In this way, the straight line PP_H would be the axis average line. It is well recognized that the location errors of axis average line are directly considered and calculated as the eccentricities of the DBB trajectories [33, 34] in each plane. Thus, the 4 PIGEs including 2 translational errors, E_XOC and E_YOC, and 2 angular errors E_AOC and E_BOC are easily obtained.

Fig. 4

Axis average line and PIGEs [34, 35]

Due to the independence of the PIGEs and PDGEs, the comprehensive geometric errors, the DBB trajectories, and the length change of the DBB can also be divided into two parts, caused by the PIGEs and PDGEs [30]. After determining the PIGEs, the rest parts of the DBB trajectories and the length change of DBB are entirely caused by the PDGEs.

2.2 Length changing model with single-axis driven

In the measurement of DBB, the workpiece ball center is denoted as P₀(x_w,y_w,z_w) while the tool ball center is denoted as Q(x_t,y_t,z_t). The theoretical and actual motion transformation matrix of the rotary axis T_i and T are expressed as Eq. (1) and Eq. (2).

$$ {T}_i=\left[\begin{array}{cccc}\cos (c)& -\sin (c)& 0& 0\\ {}\sin (c)& \cos (c)& 0& 0\\ {}0& 0& 1& 0\\ {}0& 0& 0& 1\end{array}\right] $$

(1)

$$ T=\left[\begin{array}{cccc}1& -{E}_{CC}& {E}_{BC}& {E}_{XC}\\ {}{E}_{CC}& 1& -{E}_{AC}& {E}_{YC}\\ {}-{E}_{BC}& {E}_{AC}& 1& {E}_{ZC}\\ {}0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}\cos (c)& -\sin (c)& 0& 0\\ {}\sin (c)& \cos (c)& 0& 0\\ {}0& 0& 1& 0\\ {}0& 0& 0& 1\end{array}\right] $$

(2)

Then, the theoretical and actual centers of the workpiece ball in the moving process are denoted as P_i(x_i,y_i,z_i) and P(x,y,z), respectively, which are calculated as Eq. (3).

$$ \left\{\begin{array}{c}{P}_i={T}_i\cdot {\left[{P}_0\kern0.5em 1\right]}^T\\ {}P=T\cdot {\left[{P}_0\kern0.5em 1\right]}^T\end{array}\right. $$

(3)

The deviation ΔP is expressed as Eq. (4) and Eq. (5), where Δx, Δy, and Δz represent the deviation components in X-, Y-, and Z-direction.

$$ \varDelta P=\left[\varDelta x\kern0.5em \varDelta y\kern0.5em \varDelta z\kern0.5em 1\right]=P-{P}_i $$

(4)

$$ \left[\begin{array}{c}\Delta x\\ {}\Delta y\\ {}\Delta z\end{array}\right]=\left[\begin{array}{c}{E}_{XC}+{z}_0{E}_{BC}-{y}_0\cos (c){E}_{CC}-{x}_0\sin (c){E}_{CC}\\ {}{E}_{YC}+{z}_0{E}_{AC}-{x}_0\cos (c){E}_{CC}-{y}_0\sin (c){E}_{CC}\\ {}{E}_{ZC}-{x}_0\left[\cos (c){E}_{BC}-\sin (c){E}_{AC}\right]+{y}_0\left[\cos (c){E}_{AC}+\sin (c){E}_{BC}\right]\end{array}\right] $$

(5)

Then, the length change of the DBB Δr is obtained as Eq. (6).

$$ {\displaystyle \begin{array}{c}\varDelta r=\left| PQ\right|-\left|{P}_iQ\right|=\sqrt{{\left(x-{x}_t\right)}^2+{\left(y-{y}_t\right)}^2+{\left(z-{z}_t\right)}^2}-r\\ {}=\sqrt{{\left({x}_i+\varDelta x-{x}_t\right)}^2+{\left({y}_i+\varDelta y-{y}_t\right)}^2+{\left({z}_i+\varDelta z-{z}_t\right)}^2}-r\end{array}} $$

(6)

Ignoring the high order of the errors, Eq. (7) can be considered as a simplified expression of the length change of the DBB.

$$ \varDelta r=\frac{1}{r}\left[\left({x}_i-{x}_t\right)\varDelta x+\left({y}_i-{y}_t\right)\varDelta y+\left({z}_i-{z}_t\right)\varDelta z\right] $$

(7)

Substitute Eq. (3) and Eq. (5) into Eq. (7), and the relationship between the length change Δr and the PDGEs are obtained in Eq. (8).

$$ {\displaystyle \begin{array}{c} r\varDelta r=\left[{x}_w\cos (c)-{y}_w\sin (c)-{x}_t\right]{E}_{XC}+\left[{x}_w\sin (c)+{y}_w\cos (c)-{y}_t\right]{E}_{YC}+\left[{z}_w-{z}_t\right]{E}_{ZC}\\ {}+\left[{y}_t{z}_w-{y}_w{z}_t\cos (c)-{x}_w{z}_t\sin (c)\right]{E}_{AC}+\left[{x}_w{z}_t\cos (c)-{y}_w{z}_t\sin (c)-{x}_t{z}_w\right]{E}_{BC}\\ {}+\left[{x}_t{y}_w\cos (c)-{x}_w{y}_t\cos (c)+{x}_w{x}_t\sin (c)+{y}_w{y}_t\sin (c)\right]{E}_{CC}\end{array}} $$

(8)

2.3 Constraint condition

In every test trajectory, the theoretical length of the DBB should be always equal to the standard radius r, which is considered as the constraint condition expressed as Eq. (9) as the expanded form.

$$ {\displaystyle \begin{array}{c}{r}^2=\left({}^{x_i}+\right({}^{y_i}+\Big({}^{z_i}={x}_w^2-2{z}_w{z}_t+{y}_w^2+{x}_t^2+{y}_t^2+{z}_w^2+{z}_t^2\\ {}-2{x}_w{x}_t\cos (c)-2{y}_w{y}_t\cos (c)-2{x}_w{y}_t\sin (c)+2{x}_t{y}_w\sin (c)\end{array}} $$

(9)

In the circular test for rotary axis, Eq. (9) should always hold when c changes from 0 to 360 degree. (x_w, y_w, z_w) and (x_t, y_t, z_t) are the initial positions of the workpiece ball and the tool ball, which are constant values as well as the standard radius r of the DBB. In this way, the following part of the equation should be constant.

$$ -2{x}_w{x}_t\cos (c)-2{y}_w{y}_t\cos (c)-2{x}_w{y}_t\sin (c)+2{x}_t{y}_w\sin (c)= cons $$

(10)

Change Eq. (10) into Eq. (11).

$$ \sqrt{{\left({x}_w{x}_t+{y}_w{y}_t\right)}^2+{\left({x}_w{y}_t-{x}_t{y}_w\right)}^2}\sin \left(c+\arctan \frac{x_w{x}_t+{y}_w{y}_t}{x_w{y}_t-{x}_t{y}_w}\right)= cons $$

(11)

To make Eq. (11) hold, the requirement should be met as shown in Eq. (12).

$$ {\left({x}_w{x}_t+{y}_w{y}_t\right)}^2+{\left({x}_w{y}_t-{x}_t{y}_w\right)}^2=0 $$

(12)

And then we can conclude Eq. (13).

$$ \left\{\begin{array}{c}{x}_w{x}_t+{y}_w{y}_t=0\\ {}{x}_w{y}_t-{x}_t{y}_w=0\end{array}\right. $$

(13)

Back to Eq. (8), k_CC denotes the coefficient of the angular positioning error E_CC. And the coefficient k_CC can be simplified to 0 as shown in Eq. (14).

$$ {\displaystyle \begin{array}{c}{k}_{CC}={x}_t{y}_w\cos (c)-{x}_w{y}_t\cos (c)+{x}_w{x}_t\sin (c)+{y}_w{y}_t\sin (c)\\ {}=\left({x}_t{y}_w-{x}_w{y}_t\right)\cos (c)+\left({x}_w{x}_t+{y}_w{y}_t\right)\sin (c)=0\end{array}} $$

(14)

In this way, there is no relation between the length change of the DBB and the angular positioning error E_CC, which means that the angular positioning error E_CC can never be solved with the SADM.

2.4 Identification matrix

With the standard configuration of the DBB, several radii are optional in the measurement including 100 mm and 150 mm [36]. Therefore, more measurement patterns are available. For different test radius and positions of the workpiece ball and the tool ball, Eq. (8) can be written as a matrix form as shown in Eq. (15). E, K, and Δr represent the PDGEs matrix, identification matrix, and the length changes matrix of the DBB, respectively. The subscripts represent the sizes of these matrixes. In detail, m represents the measurement times, and n represents the total number of measured points in the travel of rotary axis.

$$ {\mathrm{E}}_{5\times n}={\left[{\mathrm{K}}_{m\times 5}^T{\mathrm{K}}_{m\times 5}\right]}^{-1}{\mathrm{K}}_{m\times 5}^T\varDelta {\mathrm{r}}_{m\times n} $$

(15)

All variables are calculated in matrix form in Eq. (15). The error matrix E can be expressed as the combination of 5 PDGEs vectors including E_XC, E_YC, E_ZC, E_AC, and E_BC. The length change matrix Δr is expressed as the combination of m times length change vectors of the DBB including Δr₁, Δr₂, Δr₃, ……, Δr_m. The identification matrix K is expressed as the combination of 5 vectors. These variables were expressed as shown in Eq. (16). In addition, x_w, y_w, z_w, x_t, y_t, and z_t are the coordinate vectors of the workpiece ball and tool ball in the m times measurements. r is the vectors of test radius.

$$ {\mathrm{E}}_{5\times n}=\left[\begin{array}{c}{\mathrm{E}}_{XC\left(1\times n\right)}\\ {}{\mathrm{E}}_{YC\left(1\times n\right)}\\ {}{\mathrm{E}}_{ZC\left(1\times n\right)}\\ {}{\mathrm{E}}_{AC\left(1\times n\right)}\\ {}{\mathrm{E}}_{BC\left(1\times n\right)}\end{array}\right],\kern0.5em \varDelta {\mathrm{r}}_{m\times n}=\left[\begin{array}{c}\varDelta {\mathrm{r}}_{1\left(1\times n\right)}\\ {}\varDelta {\mathrm{r}}_{2\left(1\times n\right)}\\ {}\varDelta {\mathrm{r}}_{3\left(1\times n\right)}\\ {}\vdots \\ {}\varDelta {\mathrm{r}}_{m\left(1\times n\right)}\end{array}\right],\kern0.5em \mathrm{K}={\left[\begin{array}{c}{\mathrm{K}}_{XC\left(1\times m\right)}\\ {}{\mathrm{K}}_{YC\left(1\times m\right)}\\ {}{\mathrm{K}}_{ZC\left(1\times m\right)}\\ {}{\mathrm{K}}_{AC\left(1\times m\right)}\\ {}{\mathrm{K}}_{BC\left(1\times m\right)}\end{array}\right]}^T=\frac{1}{\mathrm{r}}{\left[\begin{array}{c}{\mathrm{x}}_w\cos (c)-{\mathrm{y}}_w\sin (c)-{\mathrm{x}}_t\\ {}{\mathrm{x}}_w\sin (c)+{\mathrm{y}}_w\cos (c)-{\mathrm{y}}_t\\ {}{\mathrm{z}}_w-{\mathrm{z}}_t\\ {}{\mathrm{y}}_t{\mathrm{z}}_w-{\mathrm{y}}_w{\mathrm{z}}_t\cos (c)-{\mathrm{x}}_w{\mathrm{z}}_t\sin (c)\\ {}{\mathrm{x}}_w{\mathrm{z}}_t\cos (c)-{\mathrm{y}}_w{\mathrm{z}}_t\sin (c)-{\mathrm{x}}_t{\mathrm{z}}_w\end{array}\right]}^T $$

(16)

It is necessary to point out that the number of measurements m can be greater than 5. In addition, the matrix must be full of ranks. That is because that even though we can install the DBB and use different test radius as many times as possible, parts of the tests could be actually useless in some specific patterns. Some common measurement patterns are listed in Table 1. K_i represents the coefficients vector of the PDGEs in the ith measurement pattern.

Table 1 Some common measurement patterns

In the above measurement patterns, the workpiece ball and the tool ball are installed in some special locations. Nevertheless, many other patterns are available. Here, we just take these 15 patterns as an example. Ideally, all the 5 PDGEs can be identified with 5 measurement patterns. Since some measurement patterns make the same contributions to the PDGE identification, some of the combinations could be useless. It is a simple principle to judge while the combination is feasible by calculating the rank of the identification matrix. The number of the whole combinations in these 15 patterns can be easily obtained as 3003 (C 5 15 = 15!/(5! × 10!)) when using 5 measurement patterns. The rank of each combination can be calculated. In detail, 619 combinations in these patterns cannot be applied to PDGE identification of rotary axis since the rank is smaller than 5 (as shown in Fig. 5).

Fig. 5

Combinations of the measurement patterns

By combining different measurement patterns, different identification methods are obtained. Some typical methods in previous researches are listed in Table 2. These methods can be composed of the measurement patterns in Table 1. The symbol (−) represents the symmetrical pattern.

Table 2 Typical identification in reference

3 Analysis and removal of the installation error and PIGEs

In any situation using the DBB, the installation errors will be the major factor that leads to the length change, even more than the geometric errors sometimes. In the previous researches on PIGE identification, many methods were proposed like adjusting the tool ball with a dial indicator and developing special devices [18, 25]. In general, the installation errors were reduced or eliminated through hardware in most cases. The main reason is that the installation errors had a similar effect on the length change as the translational errors of the PIGEs. They both kept constant during the circular test. Therefore, it is almost impossible to avoid the installation errors through a soft method for the PIGE identification. However, the situation is different when it came to the PDGE identification. And that provides the possibility of using a soft method to eliminate installation errors. Actually, simulations in Ref. [20] had demonstrated that the installation errors cause eccentricities and radius changes of the circular trajectories. Based on that, the analytical relationship between the length change and the PIGEs, PDGEs, and installation errors is further deduced in this section.

3.1 Effect of the installation error and PIGEs

Due to the imperfect installation, the installation errors will exist on both sides of the DBB. In this work, (δ_xt, δ_yt, δ_zt) and (δ_xw, δ_yw, δ_zw) denote the installation errors of tool ball and workpiece ball, respectively. For the test for a turntable, the tool cup and the center mount are connected with the setting ball through magnetism in the alignment process in a vertical plane. Therefore, the installation errors in Z-direction can be directly ignored. And then centers of workpiece ball and tool ball are re-expressed as P₀(x_w + δ_xw, y_w + δ_yw, z_w) and Q₀(x_t + δ_xt, y_t + δ_yt, z_t). Meanwhile, considering the PIGEs, then Eq. (2) is repressed as Eq. (17). Correspondingly, the deviation components in X-, Y-, and Z-direction can be modified as Eq. (18).

$$ T=\left[\begin{array}{cccc}1& -{E}_{CC}& {E}_{BC}+{E}_{BOC}& {E}_{XC}+{E}_{XOC}\\ {}{E}_{CC}& 1& -{E}_{AC}-{E}_{AOC}& {E}_{YC}+{E}_{YOC}\\ {}-{E}_{BC}-{E}_{BOC}& {E}_{AC}+{E}_{AOC}& 1& 0\\ {}0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}\cos (c)& -\sin (c)& 0& 0\\ {}\sin (c)& \cos (c)& 0& 0\\ {}0& 0& 1& 0\\ {}0& 0& 0& 1\end{array}\right] $$

(17)

$$ {\displaystyle \begin{array}{c}\left[\begin{array}{c}\Delta x\\ {}\Delta y\\ {}\Delta z\end{array}\right]=\left[\begin{array}{c}{E}_{XC}+{z}_w{E}_{BC}-{y}_w\mathit{\cos}(c){E}_{CC}-{x}_w\mathit{\sin}(c){E}_{CC}\\ {}{E}_{YC}-{z}_w{E}_{AC}+{x}_w\mathit{\cos}(c){E}_{CC}-{y}_w\mathit{\sin}(c){E}_{CC}\\ {}{E}_{ZC}+{x}_w\left[\mathit{\sin}(c){E}_{AC}-\mathit{\cos}(c){E}_{BC}\right]+{y}_w\left[\mathit{\cos}(c){E}_{AC}+\mathit{\sin}(c){E}_{BC}\right]\end{array}\right]\\ {}+\left[\begin{array}{c}{E}_{XOC}+{E}_{BOC}{z}_w\\ {}{E}_{YOC}-{E}_{AOC}{z}_W\\ {}{x}_w\left[\mathit{\sin}(c){E}_{AC}-\mathit{\cos}(c){E}_{BOC}\right]+{y}_w\left[\mathit{\cos}(c){E}_{AOC}+\mathit{\sin}(c){E}_{BoC}\right]\end{array}\right]\end{array}} $$

(18)

Then, the length change of the DBB ΔR considering the installation error of tool ball is obtained as Eq. (19).

$$ {\displaystyle \begin{array}{c}\Delta R=\left| PQ\right|-\left|{P}_iQ\right|=\sqrt{{\left({x}_i+\Delta x-{x}_t-{\delta}_{xt}\right)}^2+{\left({y}_i+\Delta y-{y}_t-{\delta}_{yt}\right)}^2+{\left({z}_i+\Delta z-{z}_t\right)}^2}-r\\ {}=\frac{1}{r}\left[\left({x}_i-{x}_t\right)\left(\Delta x-{\delta}_{xt}\right)+\left({y}_i-{y}_t\right)\left(\Delta y-{\delta}_{yt}\right)+\left({z}_i-{z}_t\right)\Delta z\right]\end{array}} $$

(19)

Substitute Eq. (18) into Eq. (19), and the relationship between the length change ΔR and the PDGEs is obtained in Eq. (20).

$$ {\displaystyle \begin{array}{c} r\varDelta R=\left[{x}_w\cos (c)-{y}_w\sin (c)-{x}_t\right]\left({E}_{XC}+{E}_{XOC}-{\delta}_{xt}\right)\\ {}+\left[{x}_w\sin (c)+{y}_w\cos (c)-{y}_t\right]\left({E}_{YC}+{E}_{YOC}-{\delta}_{yt}\right)\\ {}+\left[{z}_w-{z}_t\right]{E}_{ZC}\\ {}+\left[{y}_t{z}_w-{y}_w{z}_t\cos (c)-{x}_w{z}_t\sin (c)\right]\left({E}_{AC}+{E}_{AOC}\right)\\ {}+\left[{x}_w{z}_t\cos (c)-{y}_w{z}_t\sin (c)-{x}_t{z}_w\right]\left({E}_{BC}+{E}_{BOC}\right)\\ {}+\left[{x}_t{y}_w\cos (c)-{x}_w{y}_t\cos (c)+{x}_w{x}_t\sin (c)+{y}_w{y}_t\sin (c)\right]{E}_{CC}\\ {}+\left[{x}_w-{x}_t\cos (c)-{y}_t\sin (c)\right]{\delta}_{xw}+\left[{y}_w+{x}_t\sin (c)-{y}_t\cos (c)\right]{\delta}_{yw}\end{array}} $$

(20)

Combining the expression of the length change of DBB Δr caused by the PDGEs, the Eq. (20) was simplified as Eq. (21).

$$ \left\{\begin{array}{c} r\varDelta R= r\varDelta r+{\delta}_0+{\delta}_c\cos (c)+{\delta}_s\sin (c)\\ {}{\delta}_0={\delta}_{xw}{x}_w+{\delta}_{yw}{y}_w+{\delta}_{xt}{x}_t+{\delta}_{yt}{y}_t-{E}_{XOC}{x}_t-{E}_{YOC}{y}_t+{E}_{AOC}{y}_t{z}_w-{E}_{BOC}{x}_t{z}_w\\ {}{\delta}_c=-{\delta}_{xw}{x}_t-{\delta}_{yw}{y}_t-{\delta}_{xt}{x}_w-{\delta}_{yt}{y}_w+{E}_{XOC}{x}_w+{E}_{YOC}{y}_w-{E}_{AOC}{y}_w{z}_t+{E}_{BOC}{x}_w{z}_t\\ {}{\delta}_s=-{\delta}_{xw}{y}_t+{\delta}_{yw}{x}_t+{\delta}_{xt}{y}_w-{\delta}_{yt}{x}_w-{E}_{XOC}{y}_w+{E}_{XOC}{x}_w-{E}_{AOC}{x}_w{z}_t-{E}_{BOC}{y}_w{z}_t\end{array}\right. $$

(21)

For a full circle, the following relationship exists as Eq. (22).

$$ \left\{\begin{array}{c}{\int}_0^{2\pi}\sin \theta \cos \theta d\theta ={\int}_0^{2\pi}\sin \theta d\theta ={\int}_0^{2\pi}\cos \theta d\theta \\ {}{\int}_0^{2\pi }{\sin}^2\theta d\theta ={\int}_0^{2\pi }{\cos}^2\theta d\theta =\pi \end{array}\right. $$

(22)

In Section 2.1, we defined the axis average line and the PIGEs. It was recognized that the PIGEs lead to the eccentricities of the DBB trajectories [33, 34]. When removing the least-square circle caused by the PIGEs, the PDGEs were the rest part of the geometric errors, also described as the oscillation in Ref. [30]. Therefore, it can be considered that the PDGEs do not contribute to the eccentricities and the radius change of the least-square circle as expressed in Eq. (23).

$$ {\int}_0^{2\pi}\varDelta r dc={\int}_0^{2\pi}\varDelta r\cos (c) dc={\int}_0^{2\pi}\varDelta r\sin (c) dc=0 $$

(23)

Therefore, Eq. (24) is obtained.

$$ \left\{\begin{array}{c}\frac{1}{\pi }{\int}_0^{2\pi}\varDelta R\cos cdc=\frac{1}{\pi }{\int}_0^{2\pi}\left[\varDelta r+\frac{1}{r}{\delta}_0+\frac{1}{r}{\delta}_c\cos (c)+\frac{1}{r}{\delta}_s\sin (c)\right]\cos cdc=\frac{1}{r}{\delta}_c\\ {}\frac{1}{\pi }{\int}_0^{2\pi}\varDelta R\sin cdc=\frac{1}{\pi }{\int}_0^{2\pi}\left[\varDelta r+\frac{1}{r}{\delta}_0+\frac{1}{r}{\delta}_c\cos (c)+\frac{1}{r}{\delta}_s\sin (c)\right]\sin cdc=\frac{1}{r}{\delta}_s\\ {}\frac{1}{2\pi }{\int}_0^{2\pi}\varDelta R dc=\frac{1}{2\pi }{\int}_0^{2\pi}\left[\varDelta r+\frac{1}{r}{\delta}_0+\frac{1}{r}{\delta}_c\cos (c)+\frac{1}{r}{\delta}_s\sin (c)\right] dc\kern0.5em =\frac{1}{r}{\delta}_0\end{array}\right. $$

(24)

Then, the length change caused by the PDGEs is obtained as Eq. (25).

$$ \varDelta r=\varDelta R-\frac{\cos c}{\pi }{\int}_0^{2\pi}\varDelta R\cos cdc-\frac{\sin c}{\pi }{\int}_0^{2\pi}\varDelta R\sin cdc-\frac{1}{2\pi }{\int}_0^{2\pi}\varDelta R dc $$

(25)

It is a superior characteristic that the effects of the installation errors and PIGEs on the PDGE identification can be removed through Eq. (25). This will greatly reduce the difficulty of identification process, especially for those machine tools whose structures are different from the standard machine center, like the gear grinding machine. There are no tool holders in these machine tools, which are used for installing the tool cup of the DBB. And Eq. (25) allows that the magnet base can be used for the installation of the tool cup with ignoring the theoretical center axis of the rotary axis.

3.2 Simulation

To verify the proposed method when considering the installation errors, a series of simulations were carried out. The PDGEs, PIGEs, and the installation errors were previously set to some values, and then, the length change of the DBB was obtained through Eq. (25). In detail, we used three types of forms to describe the PDGEs, random form, polynomial form, and Fourier series form. According to the definition of the PDGEs and PIGEs, the modification was needed for the PDGEs to guarantee that the PDGEs would not lead to the change of the eccentricities and the radius of the least-square circle. For convenience, we can directly use the following Eq. (26) to ensure that. E(pre) represents the pre-set PDGEs with the random form, the form, and Fourier series form, while E(set) represents the PDGEs processed by Eq. (26), and E(cal) represents the PDGEs calculated with the proposed method.

$$ E(set)=E(pre)-\frac{\cos c}{\pi }{\int}_0^{2\pi }E(pre)\cos cdc-\frac{\sin c}{\pi }{\int}_0^{2\pi }E(pre)\sin cdc-\frac{1}{2\pi }{\int}_0^{2\pi }E(pre) dc $$

(26)

The measurement patterns 1–5 were used in the simulation. The 4 PIGEs, E_XOC, E_YOC, E_AOC, and E_BOC, were set 15 μm, 12 μm, 80 μrad, and − 90 μrad. To be more general, we assume that the installation errors are different in every measurement pattern as shown in Table 3, even though the installation times can be less than 5 in actual operation [10, 17] [20]. Moreover, the amplitudes of the random noises were set as 5% of the amplitudes of the length change Δr and ΔR. The flow chart and results of the simulation were presented in Figs. 6, 7, 8, and 9. The S₁, C₁, S₂, C₂, S₃, and C₃ represent sin(c), cos(c), sin(2c), cos(2c), sin(3c), and cos(3c), respectively, where c denotes the position of the rotary axis.

Table 3 Installation errors set in simulation (μm)

Fig. 6

Flow chart of simulation

Fig. 7

Simulation results of PDGEs with random values, a E_XC, b E_YC, c E_ZC, d E_AC, and e E_BC

Fig. 8

Simulation results of PDGEs with polynomial values, a E_XC, b E_YC, c E_ZC, d E_AC, and e E_BC

Fig. 9

Simulation results of PDGEs with Fourier values, a E_XC, b E_YC, c E_ZC, d E_AC, and e E_BC

Even though different forms of the PDGEs were set in the simulation, the proposed method can always achieve high accuracy. However, when comparing the identified PDGEs with the pre-set PDGEs, the deviation was very distinct. In addition, these deviations were different in the three simulations. In the first simulation, PDGEs were random values and the trend of all the identified PDGEs coincided with the pre-set PDGEs. When the mean value of the pre-set PDGEs was close to 0, the identified PDGEs can even coincide with pre-set PDGEs very well. In the second and third simulations, the PDGEs with polynomial form and Fourier series form and the trend of the identified PDGEs were obviously different from the pre-set PDGEs as well as the absolute values. For the reason of these differences in the three simulations, it is that some of the ingredients were removed from the pre-set PDGE due to the definition of the PDGEs. There was no component with a period of 2π in the PDGEs with random form, and it equaled to that the pre-set PDGEs did not lead to the eccentricities of the DBB trajectories. Therefore, the process as Eq. (26) did have no effect on the trend of the PDGE curve but only the absolute value. As a result, the set PDGE curve was only translated relative to pre-set PDGE curve. When the mean value of the pre-set PDGEs was close to 0, the pre-set PDGEs would be exactly equivalent to the PDGEs, which were evenly distributed on both sides of 0 on the whole.

To sum up, the series simulations indicated that the proposed methods could identify the PDGEs with high accuracy when considering the installation errors. It greatly decreased the requirement of the installation of the DBB.

4 Case study

4.1 Measurement patterns and identification of PDGEs

According to the general model, there are many combinations of measurement patterns which can be used for the PDGE identification. In this work, we take the turntable of a small-size 5-axis machine tool as the research object to perform the error identification. The installation of DBB is limited because the diameter of the turntable is small. The workpiece ball cannot be installed at a distance of standard length of the DBB from the center axis line. Even if the magnet base is used to extend the area of the turntable, there would be an interference problem as shown in Fig. 10. On the other hand, it is necessary to minimize the number of installations as many as possible to save time. For convenience, we chose to install the workpiece ball on the center axis for the PDGE identification.

Fig. 10

Structure limitation of the rotary axis

For the turntable, the 5 PDGEs can be identified with 5 times measurements through twice installations. However, to compare the results of different combinations, another 5 tests were further carried out as the supplements. The detailed patterns were listed in Table 4. The schematic diagrams of these measurement patterns were presented in Fig. 11.

Table 4 Total of 10 measurement patterns with 3 times installation

Fig. 11

10 measurement patterns for the rotary axis

It is necessary to point out that origin coordinate in Table 4 is not the actual absolute origin of C-axis coordinate system but a relative one. In fact, to obtain the absolute coordinate system of C-axis is not easy. Even though the CNC system provides the simple and relatively automated calibration and compensation function for the PIGEs as shown in Fig. 12, it is tough work to accurately install the DBB in special positions. This work focuses on the identification of PDGEs. In Section 3, it has been proved that effect of the PIGEs and the installation errors can be reduced to a very small extent. In addition, for the identification and evaluation of PDGEs, it does not make much difference as long as all the work is carried out in this relative coordinate system throughout. Therefore, we used a relative C-axis coordinate system for the identification and evaluation of PDGEs instead. However, when it comes to the compensation for all the geometric errors including the PIGEs and PDGEs, the absolute coordinate system is necessarily needed.

Fig. 12

Calibration and compensation function for PIGEs in CNC system (http://www.huazhongcnc.com/portal/list/index/cid/20.html)

Before the test, the warming up process was conducted for the machine tool. The DBB was installed carefully with the proposed method. In order to adapt different types of machine tools especially for those without tool holders, we used the center mount to install the tool ball instead of the tool holder and tool cup and used a magnet base and a tool cup to install the workpiece ball. Although it has been proved that subsequent processing as Eq. (23) can eliminate the effect of the installation errors, too large installation errors will lead to the length change out of the measurement range of the DBB. In this experiment, we developed a simple software, which can display the length change of the dial indicator and calculate the eccentricity of the whole circular trajectory. It can help adjust the position of the workpiece ball as shown in Fig. 13a, b. Then, move the center mount above the workpiece ball and connect the setting ball and the center mount with magnetism. Finally, the center mount is fixed (as shown in Fig. 13c). It should be emphasized that this step is not enough to remove the installation errors, but to reduce the installation errors to make the length change of DBB within its measurement range, from − 1 to 1 mm (Renishaw QC20-W).

Fig. 13

Installation of the workpiece ball and the tool ball

The 10 measurements were carried out with 3 times installations. In the first installation, measurement patterns 1, 2, and 3 were performed as shown in Fig. 14a–c. The length changes were denoted as Δr₁, Δr₂, and Δr₃.

Fig. 14

Measurement patterns 1, 2, and 3 in the first installation

In the second installation, measurement patterns 4, 5, 6, and 7 were performed as shown in Fig. 15a–d. The length changes were denoted as Δr₄, Δr₅, Δr₆, and Δr₇.

Fig. 15

Measurement patterns 4, 5, 6, and 7 in the second installation

In the third installation, measurement patterns 8, 9, and 10 were performed as shown in Fig. 16a–c. The length changes were denoted as Δr₈, Δr₉, and Δr₁₀.

Fig. 16

Measurement patterns 8, 9, and 10 in the third installation

Using these 10 measurement patterns, in total 364 (364 = 80 + 130 + 100 + 43 + 11) combinations are available for the PDGE identification with the rank of the identification matrix equals to 5 as shown in Table 5. As the number of the patterns used increases, the proportion of matrix with full rank gets bigger. It is widely recognized that the more measured data used, the more accuracy will be achieved. In the work, the PDGEs were directly identified with a total of 10 measurement patterns used. The identified PDGEs including E_XC, E_YC, E_ZC, E_AC, and E_BC were shown in Fig. 17. As previously defined, the identified PDGEs are uniformly distributed around 0 overall.

Table 5 Numbers of combinations with different ranks of the 10 measurement patterns

Fig. 17

Identified PDGEs using a total of 10 measurement patterns

4.2 Prediction experiments

As we mentioned early, there would be a solution if the rank of the identification matrix were 5, instead of considering how many the measurement patterns were used. It would also work theoretically if we used parts of the patterns as long as the rank of the identification matrix is 5. However, the accuracies of these identified results were different. The full rank of the matrix can only guarantee the existence of solutions, but it cannot guarantee the accuracy or correctness of solutions since the matrix could be ill-conditioned. To verify the correctness of the identified results, it is available to predict the length change of DBB.

Generally, the 10 measurement patterns can be divided in three types according to the installations or the heights of the workpiece ball. Therefore, 3 prediction experiments were performed, using the PDGEs from two installations to predict the length change from the third installation. For example, the PDGEs from installations #1 and #2 were used to predict the length change of the DBB from installation #3. In addition, the translational error E_ZC is very small according to the previous identified results, so the length changes in patterns 3 and 10 were not used for comparison. In detail, the three prediction experiments were set as shown in Table 6. As a result, three prediction results were shown in Figs. 18, 19 and 20.

Table 6 Prediction experiments setting

Fig. 18

Prediction results of length change, a Δr₈ and b Δr₉

Fig. 19

Prediction results of length change, a Δr₄, b Δr₅, c Δr₆, and d Δr₇

In general, the length change trend can be predicted in each prediction experiment, while the prediction accuracy is quite different. Among the three groups of the prediction experiments, it is obvious that the second group can achieve a better accuracy to predict the length change, Δr₄, Δr₅, Δr₆, and Δr₇, when compared with the others. The maximum residual error is almost less than 1 μm. While in the other prediction experiments, the maximum residual error can achieve 2 μm in Figs. 18a and 20a. It is large enough considering that the maximum length change is less than 4 μm, even though these large residuals do not occur many times in the whole test. For the reason, it is that the second prediction experiment has some advantages compared to the other two. Intuitively, the second prediction experiment is using data from two sides to predict the data in the middle, while the first and third prediction experiment are using data from one side to predict data on the other side. Figure 21 briefly shows the difference between these three prediction experiments.

Fig. 20

Prediction results of length change, a Δr₁ and b Δr₂

Fig. 21

Different among the three prediction experiments

In addition, it was noticed that these large residuals are more likely to appear at the inflection of the length change curve such as 90 degrees, 180 degrees, and 270 degrees. The main reason is the identification matrix is ill-conditioned even though the rank is full. The ill-conditioned matrix is sensitive in the calculation process, which would lead to a big change of output even with a little change of the input. At these inflection positions, the theoretical coordinates of the workpiece ball changed obviously, from positive to negative or from negative to positive, which would lead to the fluctuations of the identified results.

4.3 Improvement based on condition number

With these 10 measurement patterns, there were 364 combinations, which can be used for the identification process. Different combinations will lead to different identification results. In particular, the ill-conditioned matrix may directly lead to large deviations of the identified PDGEs. For simplification, we mainly focused on the combination containing 5 patterns.

As shown in Table 5, 80 combinations are available using 5 measurement patterns. The identification matrix of these combinations all satisfied the full rank condition. Use each combination to identify the PDGEs, and 80 groups of the PDGEs can be obtained. Taking one PDGEs, E_XC as an example, the distribution interval was shown in Fig. 22. In addition, the identified PDGEs with a total of 10 measurement patterns were considered as the standard reference value shown in Fig. 22.

Fig. 22

Distribution intervals of identified PDGEs with 5 patterns

The distribution diagram was intuitive to show the possible values of the identified PDGEs using these 80 combinations. The distribution interval reflects the trend of the standard value overall. However, the width of the distribution intervals was very large. That means a large residual error would appear if the improper combination with ill-conditioned matrix was used for the PDGE identification.

To evaluate the degree of the ill-conditioned matrix, the condition number was used. Normally, the bigger the condition number is, the more ill-conditioned the matrix is. However, there is no clear boundary between the ill-conditioned matrix and the well-conditioned matrix. Besides, the ill-conditioned matrix is relative. There is no guarantee that higher accuracy can be always achieved when the identification matrix is used with a smaller condition number. To show the relationship between condition number and identification accuracy, the standard deviation of the PDGEs is used as an indicator.

There are 80 practicable combinations with 5 patterns. The standard deviations of identified PDGEs of these 80 combinations, σ(E_XC), σ(E_YC), σ(E_ZC), σ(E_AC), and σ(E_BC), were calculated and shown in Fig. 23a. And the detailed principle of the standard deviations calculated can be expressed as follows, where E(cal) denotes the PDGEs calculated with current combination, and E(ref) denotes the referenced PDGEs calculated with the combination containing total 10 measurement patterns, and N denotes the sampling numbers of the whole circle, which is set as 360 in this work.

$$ \sigma =\sqrt{\frac{1}{N}\sum \limits_{i=1}^N{\left[E(cal)-E(ref)\right]}^2} $$

(27)

Fig. 23

Error variation trend of the PDGEs with the condition number increasing

It should be pointed out that the condition number distributed on the abscissa from small to large, and the abscissa only represents the sample number instead of the detailed value of the condition number. As a result, it is more likely that a small standard deviation can be achieved when the condition number is small, but not absolutely. On one hand, using the identification matrix with a big condition number can also get high accuracy. On the other hand, using the identification matrix with a small condition number can also get a low accuracy sometimes, especially for the translational error E_ZC. In essence, the accuracy of the solution is not only affected by the identification matrix, but also affected by the input, that is, the length change of the DBB. The length change in Z-direction is much smaller than those in other directions. This increased the instability of the solution. The translational E_ZC is much related to the length change in Z-direction and more easily affected than other PDGEs in the identification process.

To further show the relationship between the condition number and the identification accuracy, the standard deviations of PDGEs in other combinations using 6, 7, and 8 patterns were also shown in Fig. 23b–d. The same rules are shown in these results. Smaller condition numbers are more likely to correspond to smaller standard deviations. In addition, as the number of measurement patterns increases, the probability of obtaining a smaller standard deviation increases. On one hand, with the increase of the number of measurement patterns used, the identification condition is closer to the reference identification condition (using 10 measurement patterns). On the other hand, the condition number of the identification matrix in these kinds of combinations decreased overall. In detail, the mean values of the condition numbers were 94.8, 92.7, 87.9, and 80.7, respectively. The identification matrix was more and more well-conditioned overall.

From the analysis of the above results, we can conclude that it is optional to improve the identification accuracy by increasing the number of measurement patterns. Meanwhile, the pattern combination with a small condition number is more practical. In this way, when using 5 measurement patterns, we can choose the combinations with the smallest condition number, which is actually patterns 1, 2, 3, 8, and 9 in this work. Then, the PDGEs are obtained. In addition, the comparison with the referred PDGEs is shown in Fig. 24. The identified PDGEs using the improved combination are very close to the referred identified PDGEs using a total of 10 measurement patterns. That means only 5 measurement patterns would be enough to achieve a high identification accuracy.

Fig. 24

Comparison between the identified PDGEs using improved 5 patterns and the referred PDGEs

In Section 4, 10 measurement patterns were used for the identification of a small-size rotary axis. Three hundred sixty-four combinations using different patterns can be available to obtain a solution as long as the rank of the identification matrix is 5. However, the correctness and accuracy of the solution cannot be guaranteed. The prediction experiments indicated that the identification accuracy of those combinations is quite different. Generally, it is more likely to achieve high accuracy when the condition number of identification matrix is small. However, this rule is not absolute, and an acceptable accuracy would also be achieved by using the identification matrix with a big condition number. In general, a small number of conditions mean a higher probability to obtain a high identification accuracy. Therefore, an improved method was proposed by choosing the combination with a small condition number. In this way, the least measurement patterns would be enough to achieve a relatively high identification accuracy.

In addition, for further improving the identification and prediction accuracy for the PDGEs, some researchers identified the angular errors and translational errors separately [30]. This method can avoid the big condition number problem dramatically which means high accuracy is more likely to be achieved. However, this actually limits some measurement patterns. For example, when only identifying the translational PDGEs, the angular PDGEs should not be involved in the length change of DBB. As the simplest combinations, measurement patterns 1, 2, and 3 in Table 1 were necessarily needed to realize the identification for translational PDGEs. It is also an option to eliminate the effect of angular PDGEs by combining similar measurement patterns like using patterns 6 and 8 in Table 1 to eliminate the angular error E_BC. It is undeniable that a separate identification method can improve the identification accuracy, but in this method, special measurement patterns are necessarily needed, which limits the generality. Considering the prediction accuracy of the proposed method is acceptable as shown in Fig. 24, the separate identification method was no longer used and compared in this work. When higher accuracy is needed, the separate identification method can be considered.

5 Conclusion

In this work, a general identification method for the PDGEs of the rotary axis with one axis driven was proposed, which can evolve into different identification methods according to the special structure of the machine tool.

• (1) The comprehensive error model considering the PDGEs was established and simplified through the constraint condition. Being different from common measurement pattern-identification model principle, the measurement patterns in the proposed method were determined according to special structure of the rotary axis and the installation condition, which makes the identification method more general.

• (2) The effect of the installation error was analyzed and removed completely. A series of the simulations were carried out with 3 types of input PDGEs, and the results indicated that the proposed method can achieve a high identification accuracy when the installation errors exist.

• (3) According to the structure of a small-size turntable, 10 measurement patterns were designed for the PDGE identification. In total, 364 combinations with a full rank can be available. The combination containing 10 measurement patterns was used for the PDGE identification.

• (4) It is more likely that the identification matrix with a small condition number can achieve a high identification accuracy. Based on that, an improved method was proposed with only 5 measurement patterns by choosing the identification matrix with the smallest condition number. The results show that the selected 5 patterns can achieve the same performance as a total of 10 patterns.