1 Introduction

In the manufacturing process, as in several processes in which large material deformations occur, a large amount of heat is generated. The generation of heat due to the friction between materials and tool contact has a strong influence on the performance of these processes. The performance of tools is fundamental to the success of any manufacturing process, both from the point of view of the quality of the finished material and from the economic point of view in the production chain. The temperature of a cutting tool has a direct influence on its useful life, and better control of the machining parameters, such as the feed and cutting speed, yields an increase in productivity and lower production costs.

The technological evolution of tool production has led to the development and application of coatings on tools, facilitating friction cutting through the performance of tribological mechanisms. In industry, cutting tools are almost all coated with thin layers of titanium carbide (TiC), titanium carbonitrides (TiCN), cobalt (Co), titanium nitride (TiN), and aluminum oxide (Al2O3), which provide less wear, with thermal insulation characteristics [1].

According to Zhao and Liua [2], the role and influence mechanism of coatings on the thermal shock resistance and thermal barrier performance of cutting tools are unclear. In this work, the effects of the Ti0.41Al0.59N coating on the temperature distribution within the rake face area during the cutting process are quantitatively analyzed using the proposed one-dimensional transient and steady-state models. The thermophysical properties of the coating and substrate with the temperature are considered to vary with the tool rake face temperature.

According to Caselle and Barimani [3], more than 40% of all cutting tools are coated in modern industry today, and they are used to perform over 80% of all machining tasks. According to a report on chip control [4], thermal effects caused by coatings have an important influence on the behavior of the tribocontact between a cutting tool and a chip. First, the amount of thermal energy that is transferred into the chip body depends on the thermal conductivity of the outer limb deposited on the cutting tool insert. Second, there is a direct correlation between the tool-chip contact length and the properties of the cutting tool and the performance of the cutting process. Grzesik [5] shows the necessity to design efficient tool inserts, and the cutting conditions require the chip-tool contact length to be known. In addition, Grzesik [5] notes that a more comprehensive investigation of possible relationships between the coating system structure and the thermoelectric emfs signals must be conducted. He shows a systematic investigation of the influence of the coating system structure, starting from a onefold (TiC), through a twofold (TiC/TiN), to a threefold (TiC/Al2O3/TiN) coating, on the tool-chip contact behavior and the average interface temperature, which was carried out by a tool-workpiece thermocouple method. However, it must be mentioned that the use of the tool-workpiece thermocouple is limited to tools that can conduct electricity. In addition, the thermocouple does not measure the temperature at a specific point but an average temperature at the heat-affected zone between the tool and the workpiece. Direct measurements of the temperatures at the tool-chip-workpiece interfaces are very difficult due to the cutting movement and the small contact areas involved.

Behera et al. [6] present interesting work that deals with cutting insert (uncoated and coated carbide) on cutting force, tool-tip temperature, and chip morphology during dry machining of Inconel 825. The performance of the coated tool is compared to the uncoated insert. The authors concluded that the higher tool-tip temperature of the coated insert caused higher chip curling. The shear band microhardness of the chip (obtained using the coated tool) appears higher than that of the uncoated insert. These results are also obtained by Gonzalez et al. [7]. Considering the tribological aspect, they also concluded that machined workpieces using coated tools presented an ultrafine-grained (UFG) layer up to twice as thick as the machined workpieces using uncoated tools and that dislocation density of the workpieces increased up to 50 times after machining. These two cited works deals with experimental verification. The question is as follows: How can the coated act as a thermal barrier if the chip-tool-piece interface is higher? In this case, the interesting point is that although the interface temperature is higher, the relatively small thermal conductivity at high temperatures will provide more effective thermal protection to the substrate, varying the process temperature distribution (González et al [7]). Does it mean the temperature of the substrate is lower if compared to the uncoated tool interface? Few works in literature deal with this issue as treated in Oliveira et al. [8] and Rech et al. [9] . However, these works, beyond considering the 1D model, assume the heat flux imposed on the coated and uncoated tool be the same.

Unfortunately, in real machining processes, the heat flux generated at the chip-tool interface is unknown and strongly dependent on the cutting condition and on the types of workpiece and cutting tool used. Without heat flux input knowledge, the temperature cannot be estimated. Based on these aspects, the use of inverse heat conduction techniques represents a good alternative since this technique takes into account temperatures measured from accessible positions, e.g., away from the rake surface of the tool [2]. There are some works in the literature that address heat flux estimation during the cutting process [10,11,12,13].

Carvalho et al. [10] obtained the thermal model by a numerical solution of the transient three-dimensional heat diffusion equation that considers both the tool and the tool holder assembly. To determine the solution equation, the finite volume method was used. Several cutting tests using cemented carbide tools were performed to check the model and to verify the influence of the cutting parameters on the temperature field.

Kryzhanivskyy et al. [11] presented a proof of the time dependency of the heat flux that is transferred into a tool body. An approach based on the inverse heat conduction technique was used. A special experimental setup was designed and manufactured to minimize the temperature measurement inaccuracy because this approach is very sensitive to measurement errors.

Battaglia and Batsale [12] designed a special experimental setup and manufactured it to implement the inverse method. A series of dry machining experiments were conducted with high-speed steel and cemented carbide tooling. The heat flux and the temperature at the tip of a tool used in the turning process were estimated from temperature measurements at an interior point of the tool insert. Instead of using a classical direct model of the transient thermal behavior of the tool, two models that express the heat flux and the temperature at the tip of the insert according to the interior temperature were identified.

Norouzifard and Hanmedi [13] studied the thermal contact phenomena in the tool-chip contact area. To estimate the heat flux, an inverse procedure was developed based on the sequential function specification (SFS) method. Thermocouples inserted into specific locations of the cutting tool provided the inverse solver input data during the machining tests performed on AISI 1045 and AISI 304 steels. The temperature distribution in the tool was computed by performing transient thermal analysis using a 3D finite element model of the cutting tool.

All these works that address inverse heat flux estimation during the cutting process have a common characteristic. The thermal analysis of the cutting process is performed with uncoated tools. One of the difficulties in the thermal analysis of the effect of coatings is due to the large difference in dimensions: the coating thickness varies from 1 to 20 μ m and the tool thickness is on the order of 3 mm [14, 15]. The numerical treatment of the very thin coating is the major challenge in the use of numerical methods. This problem is due to the transition necessary for the construction of the numerical mesh. As the refining of the mesh in the coating region should be smaller than the layer (micrometers), an appropriate mesh results in millions of nodes, making the numerical technique very costly. An alternative is to use analytical solutions. The great strength is that the solutions are valid for any domain (coating or substrate) and can be exact or approximate.

This work tries to solve a literature gap due to these two main difficulties: obtaining the heat flux at a piece-chip-tool interface and the temperature field in a coated tool during an orthogonal cutting process.

The heat flux generated in the piece-chip-tool interface is obtained using the inverse TFBGF [16] technique. Since the heat flux is obtained, a 3D transient analytical model based on Green’s functions calculates the coated tool’s temperature field after the heat flux estimation.

Four sections organize this work. Section 2 presents the fundamentals and the formulation of the problem. It describes the chip formation mechanism during machining and the coated tool’s thermal modeling. In this section, the inverse technique used to estimate the heat flux generated at the piece-chip-tool interface is also presented. Section 3 presents and discusses the results. The temperatures at the cutting interface and the substrate (metal base) are compared. Section 4 presents the relevant conclusions of this work, observing the coating thermal barrier effect. Appendix 1 shows all the detailed equations and the solution intrinsic computational verification.

2 Coated tool thermal modeling

2.1 Chip formation mechanisms

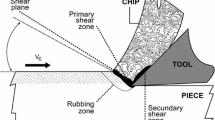
Studies of the mechanism of chip formation in a machining process consider that the process occurs in different stages, cyclically and at very high speeds and deformations. The stages can be described by considering the movement of the workpiece material in relation to the tool cutting edge [17], i.e., lifting of the material, plastic deformation, and rupture of the material. At the start of the cutting process, the workpiece material approaches the tool and is pressed against the cutting edge, undergoing compression at the contact area. The continued motion of the workpiece causes plastic deformation of the material that comes in contact with the tool rake face. The plastic deformation increases progressively until the formation of a stress state in the material ahead of the cutting edge, which promotes the initiation and propagation of a crack in the deformed material, causing it to rupture. The region where the rupture occurs is referred to as the primary shear zone. Figure 1 shows the location of the primary shear zone and the projection of the shear plane.

Fig. 1
figure 1

Chip formation during machining according to [18]

Full size image

In Fig. 1, the shear plane is perpendicular to the page and the direction of its projection relative to the cutting direction is given by the shear angle. According to [18], most of the heat generated by friction between the workpiece and tool goes to the chip. The temperatures in the interface are extremely high, and depending on the cutting conditions, the tool and the machined material can reach values above 700 K.

Figure 1 shows in detail the tool holder and the insert. In this scheme, the heat generated at the interface is represented by q(t) applied at the contact surface between the workpiece and the insert. The tool holder and the insert are exposed to an environment. The solution to this problem is presented below.

2.2 3D transient two-layer thermal model

An equivalent thermal model for the description of the heat conduction problem caused by a machining process using a coated tool of defined geometry is depicted in Fig. 2, where layer 1 represents the coating and layer 2 is the tool (substrate). The cutting tool is analyzed as a body of rectangular geometry that is subjected to a superficial heat flux.

Fig. 2
figure 2

X33Y 2C12Z33 Thermal problem [20]

Full size image

The problem shown in Fig. 2 is a heat conduction problem whose faces, except the region where heat flux occurs, are subject to a convection heat exchange. In an orthogonal cutting machining process, it is possible to identify that the lateral and upper surfaces are, in fact, exposed to a medium at room temperature.

The thermal problem given by Fig. 2 is described mathematically by the heat diffusion equation in region 1 as:

$$ \frac{\partial^{2}\theta_{1}}{\partial x^{2}} + \frac{\partial^{2}\theta_{1}}{\partial y^{2}} + \frac{\partial^{2}\theta_{1}}{\partial z^{2}} + \frac{g(x,W,z,t)}{k_{1}} = \frac{1}{\alpha_{1}} \frac{\partial{\theta_{1}}}{\partial{t}} $$
(1a)

and in region 2 as:

$$ \frac{\partial^{2}\theta_{2}}{\partial x^{2}} + \frac{\partial^{2}\theta_{2}}{\partial y^{2}} + \frac{\partial^{2}\theta_{2}}{\partial z^{2}}= \frac{1}{\alpha_{2}} \frac{\partial{\theta_{2}}}{\partial{t}} $$
(1b)

subjected to the boundary conditions on direction x:

$$ \left.-k_{1}\frac{\partial{\theta_{1}}}{\partial{x}}\right|_{x=0} = -h_{1}\theta_{1}; \qquad \left.-k_{1}\frac{\partial{\theta_{1}}}{\partial{x}}\right|_{x=L}= h_{2}\theta_{1} $$
(1c)

on direction y:

$$ \left.-k_{1}\frac{\partial{\theta_{1}}}{\partial{y}}\right|_{y=0} = -h_{3}\theta_{1}; \qquad \left.-k_{2}\frac{\partial{\theta_{2}}}{\partial{y}}\right|_{y=W} - h_{4} \theta_{2} = 0 $$
(1d)

on direction z:

$$ \left.-k_{1}\frac{\partial{\theta_{1}}}{\partial{z}}\right|_{z=0} = -h_{5}\theta_{1}; \qquad \left.-k_{1}\frac{\partial{\theta_{1}}}{\partial{z}}\right|_{z=R}= h_{6}\theta_{1} $$
(1e)

and to the continuity conditions:

$$ \left.\theta_{1}\right|_{y=b} = \left.\theta_{2}\right|_{y=b}; \qquad \left.-k_{1}\frac{\partial{\theta_{1}}}{\partial{y}}\right|_{y=b} = \left.-k_{2}\frac{\partial{\theta_{2}}}{\partial{y}}\right|_{y=b} $$
(1f)

and to the initial condition:

$$ \theta_{1}(x,y,z,0)= \theta_{2}(x,y,z,0)= F(x,y,z) - T_{\infty}=\theta_{0} $$
(1g)

The integral heat solution equation for multilayers based on Green’s fucntion can be written for each region i as [19]:

$$ \begin{array}{@{}rcl@{}} \theta_{1}(x,y,z,t) \!\!&=&\! \frac{4}{N_{y}} \theta_{0} \sum\limits_{p=1}^{\infty}\sum\limits_{m=1}^{\infty}\sum\limits_{n=1}^{\infty} e^{- \left( \frac{{\alpha^{2}_{m}}}{L^{2}} + {\lambda^{2}_{n}} + \frac{{\gamma^{2}_{p}}}{R^{2}}\right) \alpha(t)}\\ &&\times \frac{\left[ \alpha_{m} cos \left( \frac{\alpha_{m} x}{L}\right) + B_{1} sen \left( \frac{\alpha_{m} x}{L} \right) \right]}{({\alpha^{2}_{m}} + {B_{1}^{2}}) \left[ 1 + \frac{B_{2}}{{\alpha^{2}_{m}} + {B_{2}^{2}}} \right] + B_{1}} \\ && \times \left( cos(\phi y) + \frac{h_{3}}{k_{1} \phi} sen(\phi y) \right) \\ &&\times \frac{\left[ \gamma_{p} cos \left( \frac{\gamma_{p} z}{R}\right) + B_{5} sen \left( \frac{\gamma_{p} z}{R} \right) \right]}{({\gamma^{2}_{p}} + {B_{5}^{2}}) \left[ 1 + \frac{B_{6}}{{\gamma^{2}_{p}} + {B_{6}^{2}}} \right] + B_{5}} \\ &&\times \frac{1}{\alpha_{m}\gamma_{p}} [\alpha_{m} sen \alpha_{m} - B_{1}(cos \alpha_{m} - 1)]\!\!\\ &&\times \left[ \frac{sen(\phi b)}{\phi} + \frac{h_{3}}{k_{1} \phi^{2}}(\phi - cos(\phi b)) \right]\\ && \times [\gamma_{p} sen \gamma_{p} - B_{5}(cos \gamma_{p} - 1)] \\ \\ && + \frac{4}{N_{y}} \theta_{0} \sum\limits_{p=1}^{\infty}\sum\limits_{m=1}^{\infty}\sum\limits_{n=1}^{\infty} e^{- \left( \frac{{\alpha^{2}_{m}}}{L^{2}} + {\lambda^{2}_{n}} + \frac{{\gamma^{2}_{p}}}{R^{2}}\right) \alpha(t)}\\ &&\times \frac{\left[ \alpha_{m} cos \left( \frac{\alpha_{m} x}{L}\right) + B_{1} sen \left( \frac{\alpha_{m} x}{L} \right) \right]}{({\alpha^{2}_{m}} + {B_{1}^{2}}) \left[ 1 + \frac{B_{2}}{{\alpha^{2}_{m}} + {B_{2}^{2}}} \right] + B_{1}} \\ && \times \left( cos(\phi y) + \frac{h_{3}}{k_{1} \phi} sen(\phi y) \right)\\ &&\times \frac{\left[ \gamma_{p} cos \left( \frac{\gamma_{p} z}{R}\right) + B_{5} sen \left( \frac{\gamma_{p} z}{R} \right) \right]}{({\gamma^{2}_{p}} + {B_{5}^{2}}) \left[ 1 + \frac{B_{6}}{{\gamma^{2}_{p}} + {B_{6}^{2}}} \right] + B_{5}}\\ && \times \frac{1}{\alpha_{m}\gamma_{p}} [\alpha_{m} sen \alpha_{m} - B_{1}(cos \alpha_{m} - 1)]\\ && \times\! \left[\!\frac{-C sen(\eta b) + D cos(\eta b) + C sen(\eta W) - \! D cos(\eta W)}{\eta}\!\right]\!\!\\ &&\times [\gamma_{p} sen \gamma_{p} - B_{5}(cos \gamma_{p} - 1)] \\ \\ & &+ \frac{\alpha_{2}}{k_{2}} \frac{4}{N_{y}} \sum\limits_{p=1}^{\infty}\sum\limits_{m=1}^{\infty}\sum\limits_{n=1}^{\infty} e^{- \left( \frac{{\alpha^{2}_{m}}}{L^{2}} + {\lambda^{2}_{n}} + \frac{{\gamma^{2}_{p}}}{R^{2}}\right) \alpha(t - \tau)}\\ && \times \frac{\left[ \alpha_{m} cos \left( \frac{\alpha_{m} x^{\prime}}{L}\right) + B_{1} sen \left( \frac{\alpha_{m} x^{\prime}}{L} \right) \right]}{({\alpha^{2}_{m}} + {B_{1}^{2}}) \left[ 1 + \frac{B_{2}}{{\alpha^{2}_{m}} + {B_{2}^{2}}} \right] + B_{1}} \\ &&\times \left( cos(\phi y) + \frac{h_{3}}{k_{1} \phi} sen(\phi y) \right) \\ &&\times \left( cos(\phi W) + \frac{h_{3}}{k_{1} \phi} sen(\phi W) \right) \\ &&\times \frac{\left[ \gamma_{p} cos \left( \frac{\gamma_{p} z^{\prime}}{R}\right) + B_{5} sen \left( \frac{\gamma_{p} z^{\prime}}{R} \right) \right]}{({\gamma^{2}_{p}} + {B_{5}^{2}}) \left[ 1 + \frac{B_{6}}{{\gamma^{2}_{p}} + {B_{6}^{2}}} \right] + B_{5}}\\ &&\times \left[ L \left[sen \left( \frac{\alpha_{m} L_{2}}{L}\right) - sen \left( \frac{\alpha_{m} L_{1}}{L}\right)\right] \right.\\ &&\left.- \frac{B_{1} L}{\alpha_{m}} \left[ cos \left( \frac{\alpha_{m} L_{2}}{L}\right) - cos \left( \frac{\alpha_{m} L_{1}}{L}\right) \right]\right]\\ && \times \left[ R \left[sen \left( \frac{\gamma_{p} R_{2}}{R}\right) - sen \left( \frac{\gamma_{p} R_{1}}{R}\right)\right] \right. \end{array} $$
(2)
$$ \begin{array}{@{}rcl@{}} &&\left.- \frac{B_{5} R}{\gamma_{p}} \left[ cos \left( \frac{\gamma_{p} R_{2}}{R}\right) - cos \left( \frac{\gamma_{p} R_{1}}{R}\right) \right]\right] \end{array} $$
$$ \begin{array}{@{}rcl@{}} && \times {{\int}_{0}^{t}} \left[ q(\tau) e^{\left( \frac{{\alpha^{2}_{m}}}{L^{2}} + {\lambda^{2}_{n}} + \frac{{\gamma^{2}_{p}}}{R^{2}}\right) \alpha(t)} \right]d\tau \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \end{array} $$
$$ \begin{array}{ll} \theta_{2}(x,y,z,t) &= \\ & \frac{4}{N_{y}}\theta_{0} \sum\limits_{p=1}^{\infty}\sum\limits_{m=1}^{\infty}\sum\limits_{n=1}^{\infty} e^{- \left( \frac{{\alpha^{2}_{m}}}{L^{2}} + {\lambda^{2}_{n}} + \frac{{\gamma^{2}_{p}}}{R^{2}}\right) \alpha(t)}\times \frac{\left[ \alpha_{m} cos \left( \frac{\alpha_{m} x}{L}\right) + B_{1} sen \left( \frac{\alpha_{m} x}{L} \right) \right]}{({\alpha^{2}_{m}} + {B_{1}^{2}}) \left[ 1 + \frac{B_{2}}{{\alpha^{2}_{m}} + {B_{2}^{2}}} \right] + B_{1}} \\ & \times [C cos(\eta y) + D sen(\eta y)] \times \frac{\left[ \gamma_{p} cos \left( \frac{\gamma_{p} z}{R}\right) + B_{5} sen \left( \frac{\gamma_{p} z}{R} \right) \right]}{({\gamma^{2}_{p}} + {B_{5}^{2}}) \left[ 1 + \frac{B_{6}}{{\gamma^{2}_{p}} + {B_{6}^{2}}} \right] + B_{5}}\\ & \times \frac{1}{\alpha_{m}\gamma_{p}} [\alpha_{m} sen \alpha_{m} - B_{1}(cos \alpha_{m} - 1)]\times \left[ \frac{sen(\phi b)}{\phi} + \frac{h_{3}}{k_{1} \phi^{2}}(\phi - cos(\phi b)) \right]\\ & \times [\gamma_{p} sen \gamma_{p} - B_{5}(cos \gamma_{p} - 1)] \\ \\ & + \frac{4}{N_{y}} \theta_{0} \sum\limits_{p=1}^{\infty}\sum\limits_{m=1}^{\infty}\sum\limits_{n=1}^{\infty} e^{- \left( \frac{{\alpha^{2}_{m}}}{L^{2}} + {\lambda^{2}_{n}} + \frac{{\gamma^{2}_{p}}}{R^{2}}\right) \alpha(t)} \times \frac{\left[ \alpha_{m} cos \left( \frac{\alpha_{m} x}{L}\right) + B_{1} sen \left( \frac{\alpha_{m} x}{L} \right) \right]}{({\alpha^{2}_{m}} + {B_{1}^{2}}) \left[ 1 + \frac{B_{2}}{{\alpha^{2}_{m}} + {B_{2}^{2}}} \right] + B_{1}} \\ & \times [C cos(\eta y) + D sen(\eta y)]\times \frac{\left[ \gamma_{p} cos \left( \frac{\gamma_{p} z}{R}\right) + B_{5} sen \left( \frac{\gamma_{p} z}{R} \right) \right]}{({\gamma^{2}_{p}} + {B_{5}^{2}}) \left[ 1 + \frac{B_{6}}{{\gamma^{2}_{p}} + {B_{6}^{2}}} \right] + B_{5}}\\ & \times \frac{1}{\alpha_{m}\gamma_{p}} [\alpha_{m} sen \alpha_{m} - B_{1}(cos \alpha_{m} - 1)]\\ & \times \left[\frac{-C sen(\eta b) + D cos(\eta b) + C sen(\eta W) - D cos(\eta W)}{\eta}\right]\\ & \times [\gamma_{p} sen \gamma_{p} - B_{5}(cos \gamma_{p} - 1)] \\ \\ & + \frac{\alpha_{2}}{k_{2}}q_{2}(x,z,t) \frac{4}{LR} \frac{1}{N_{y}} \sum\limits_{p=1}^{\infty}\sum\limits_{m=1}^{\infty}\sum\limits_{n=1}^{\infty} e^{- \left( \frac{{\alpha^{2}_{m}}}{L^{2}} + {\lambda^{2}_{n}} + \frac{{\gamma^{2}_{p}}}{R^{2}}\right) \alpha(t - \tau)}\\ &\times \frac{\left[ \alpha_{m} cos \left( \frac{\alpha_{m} x}{L}\right) + B_{1} sen \left( \frac{\alpha_{m} x}{L} \right) \right]}{({\alpha^{2}_{m}} + {B_{1}^{2}}) \left[ 1 + \frac{B_{2}}{{\alpha^{2}_{m}} + {B_{2}^{2}}} \right] + B_{1}} \times [C cos(\eta y) + D sen(\eta y)] \\ &\times \left( cos(\phi W) + \frac{h_{3}}{k_{1} \phi} sen(\phi W) \right) \times \frac{\left[ \gamma_{p} cos \left( \frac{\gamma_{p} z}{R}\right) + B_{5} sen \left( \frac{\gamma_{p} z}{R} \right) \right]}{({\gamma^{2}_{p}} + {B_{5}^{2}}) \left[ 1 + \frac{B_{6}}{{\gamma^{2}_{p}} + {B_{6}^{2}}} \right] + B_{5}}\\ & \times \left[ L \left[sen \left( \frac{\alpha_{m} L_{2}}{L}\right) - sen \left( \frac{\alpha_{m} L_{1}}{L}\right)\right] - \frac{B_{1} L}{\alpha_{m}} \left[ cos \left( \frac{\alpha_{m} L_{2}}{L}\right) - cos \left( \frac{\alpha_{m} L_{1}}{L}\right) \right]\right]\\ & \times \left[ R \left[sen \left( \frac{\gamma_{p} R_{2}}{R}\right) - sen \left( \frac{\gamma_{p} R_{1}}{R}\right)\right] - \frac{B_{5} R}{\gamma_{p}} \left[ cos \left( \frac{\gamma_{p} R_{2}}{R}\right) - cos \left( \frac{\gamma_{p} R_{1}}{R}\right) \right]\right]\\ & \times {{\int}_{0}^{t}} \left[ q(\tau) e^{\left( \frac{{\alpha^{2}_{m}}}{L^{2}} + {\lambda^{2}_{n}} + \frac{{\gamma^{2}_{p}}}{R^{2}}\right) \alpha(t)} \right] d\tau \end{array} $$
(3)

where λn are the eigenvalues obtained from transcendental (4):

$$ \begin{array}{@{}rcl@{}} &&\frac{[\eta(b - W)] tan[\eta(b - W)] - \frac{h_{4}(b - W)}{k_{2}}}{\frac{h_{4}(b - W)}{k_{2}} tan[\eta(b - W)] + [\eta(b - W)]} \\&&= -K \frac{\phi b tan(\phi b) - \frac{h_{3} b}{k_{1}}}{\frac{h_{3} b}{k_{1}}tan(\phi b) + \phi b} \end{array} $$
(4)

2.3 Heat transfer function

As mentioned before, the inverse procedure used here is based on the transfer function based on Green’s function (TFBGF) method [16] adapted for the two-layer domain. This procedure is described in the following.

The methodology for identification of the analytical impulse response is based on the theory of dynamical systems of one input and one output.

Transfer functions are used to characterize the relationship between the input and output of a dynamic system, represented by x(t) and y(t), respectively, in Fig. 3. There is an equivalence between dynamic systems and problems of heat conduction, since both are described by a set of differential equations. Thus, the heat flux is treated as the input of the system, and the temperature field is treated as the response.

Fig. 3
figure 3

Single input/output dynamic system

Full size image

The analysis of dynamic systems is facilitated by the use of the Laplace transform, because it provides the mathematical relationship between the input and output of the dynamic system. It is known that for a linear dynamic system, as in Fig. 3, the relation between the input and output in the complex variable s domain is given by the multiplication shown in:

$$ Y(s) = H(s) \cdot X(s) $$
(5)

Applying the convolution theorem to Eq. 1, the output of the system, y(t), is given by the convolution between h(t) and x(t), represented symbolically by the operator (∗). That is, the convolution integral provides the relationship between the input and output in the time domain, and is given by:

$$ \begin{array}{@{}rcl@{}} y(t) &=& {{\int}_{0}^{t}} h(t - \tau)x(\tau)d \tau \Rightarrow \mathcal{L}^{-1}[Y(s)] \\&=& \mathcal{L}^{-1} [H(s) \cdot X(s)] = h(t) \ast x(t) \end{array} $$
(6)

Equation 6 can be written for regions 1 and 2 as:

$$ T_{1}(x,t) = h_{1}(x,t) \ast q(t) = {{\int}_{0}^{t}} h_{1}(x, t - \tau) q(\tau) d \tau $$
(7)
$$ T_{2}(x,t) = h_{2}(x,t) \ast q(t) = {{\int}_{0}^{t}} h_{2}(x, t - \tau) q(\tau) d \tau $$
(8)

As the transfer function is independent of the input/output pair, the Dirac Delta function, q(t) = δ(t), is proposed as the input signal (heat flux), that is:

$$ T_{1}(x,t) = h_{1}(x,t) \ast \delta (t) = {{\int}_{0}^{t}} h_{1}(x, t - \tau) \delta (\tau) d \tau = h_{1}(x,t) $$
(9)
$$ T_{2}(x,t) = h_{2}(x,t) \ast \delta(t) = {{\int}_{0}^{t}} h_{2}(x, t - \tau) \delta(\tau) d \tau = h_{2}(x,t) $$
(10)

Since h ∗ δ(t) = h(t), the impulse response is obtained without the need to evaluate the integral. In this sense, these equations can be solved if the transfer function given by Green’s function is known, which means that:

$$ \begin{array}{@{}rcl@{}} h_{1}(x,y,z,t)& =& \frac{\alpha_{1}}{k_{1}} {\int}_{L_{1}}^{L_{2}}{\int}_{R_{1}}^{R_{2}} G_{11}\\&&(x,y,z,t|x^{\prime},W,z^{\prime},\tau)dx^{\prime}dz^{\prime} \end{array} $$
(11)
$$ \begin{array}{@{}rcl@{}} h_{2}(x,y,z,t)& =& \frac{\alpha_{1}}{k_{1}} {\int}_{L_{1}}^{L_{2}}{\int}_{R_{1}}^{R_{2}} G_{21}\\&&(x,y,z,t|x^{\prime},W,z^{\prime},\tau)dx^{\prime}dz^{\prime} \end{array} $$
(12)

Appendix 1 shows all the detailed equations and the solution intrinsic computational verification.

2.4 Inverse problem procedure: TFBGF

For any dynamic system, see Fig. 3, the relation between the input and output in the complex variables s domain is given by the:

$$ \mathcal{L}[T_{1}(t)] = \mathcal{L}[h_{1}(t) \ast q(t)] \Rightarrow T_{1}(s) = H_{1}(s) \cdot q(s) $$
(13)

and

$$ \mathcal{L}[T_{2}(t)] = \mathcal{L}[h_{2}(t) \ast q(t)] \Rightarrow T_{2}(s) = H_{2}(s) \cdot q(s) $$
(14)

Or, we can write (13)–(14) as:

$$ q(s) = \frac{1}{H_{1}(s) } \cdot T_{1}(s) $$
(15)

or

$$ q(s) = \frac{1}{H_{2}(s) } \cdot T_{2}(s) $$
(16)

Equations 15 and 16 in the time domain are equivalent to the deconvolution:

$$ \begin{array}{@{}rcl@{}} \mathcal{L}^{-1}[q(s)] &=& \mathcal{L}^{-1} \left[ \frac{1}{H(x,s) \cdot T(x,s)}\right] \Rightarrow q(t) \\&=& \frac{1}{h_{1}(x,t)} \ast T_{1}(x,t) \end{array} $$
(17)

and

$$ \begin{array}{@{}rcl@{}} \mathcal{L}^{-1}[q(s)] &=& \mathcal{L}^{-1} \left[ \frac{1}{H(x,s) \cdot T(x,s)}\right] \Rightarrow q(t) \\&=& \frac{1}{h_{2}(x,t)} \ast T_{2}(x,t) \end{array} $$
(18)

Therefore, observing (17) and (18), an inversion occurred between the input/output pair. That is, the solution of the problem is the estimation of the system response, which is the heat flux, the output of which is the experimental temperature and the transfer function can be given by 1/H1(t) or 1/H2(t), as shown in Fig. 3. The position of the experimental temperature will determine which transfer function will be used. The heat flux is then obtained through the analytical identification of the impulse response and from knowledge of the temperature distribution (experimental or hypothetical) by performing the computational instructions: deconvolution (deconv) or Fourier transform fft and inverse Fourier transform ifft, which are functions of MATLAB and equivalent to the mathematical procedures described by Eqs. 17 and 18. More details regarding this technique can be found in ref [16].

The TFBGF inverse procedure algorithm can be summarized as follows:

  1. 1.

    Obtain the Green’s function related to the direct problem given by Eq. 21. Equation 24 defines Green’s function for each layer.

  2. 2.

    Obtain the transfer functions for both layer using Eqs. 12. Discretize and calculate 1/H1(t) and 1/H2(t).

  3. 3.

    Estimate the discret heat flux, qi. These heat flux are obtained by performing the computational instructions: deconvolution (deconv) or Fourier transform fft and inverse Fourier transform ifft, which are functions of MATLAB and equivalent to the mathematical procedures described by Eqs. 17 and 18. T1(x,t) or T2(x,t) represent the experimental temperature (or simulated temperature) at position of interest.

2.5 Temperature simulated data

Considering a typical known heat flux evolution, q(t), that appears in the orthogonal cutting process, temperature simulated data evolutions for the direct problem are generated using the solutions to Eqs. 2 and 3. Random errors are then added to these temperatures. The temperatures with error are then used in the inverse algorithm to reconstruct the imposed heat flux. The simulated temperatures are calculated from the following equation:

$$ y_{a}(t) = T_{a}(x,y,w,t) + \epsilon_{j} \sigma $$
(19)

where 𝜖j is a random number and σ the standard deviation. 𝜖j assumes values of 0, and within ± 1K.

This synthetic temperature calculation is a procedure that permits the analysis of the potential of a reverse procedure to deal with temperature signals that suffer from disturbance due to experimental errors. Usually, a small perturbation in the experimental data can be amplified in inverse procedures.

A composite sample of a cobalt coating with a thickness of b = 4 m, carbide substrate ISO K 10 as the base material, convection coefficients hi = 20 W/m2 K and, length L = W = 10− 2 m, R = 10− 2 m, a contact area of 2 × 0.210− 6 m2 (0.4 mm2, compatible with the geometry of a machining tool [10], T0 = 298K(25 ∘C), \( T_{\infty } = 303 K(30~^{\circ }\)C); dt = 1s and duration time tf = 200 s was simulated (Fig. 4).

Fig. 4
figure 4

X33Y 3C13Z33 problem with partial heating

Full size image

The heat flux imposed is then, assumed to be acting in the square area bounded by 0 < x < L/5 and 0 < z < R/50, in y = W. The temperatures at positions Ta1 = (L/5,W,4R/50), Ta2 = (4L/5,W,4R/50), and Ta3 = (0,W/2,R/50) are then calculated and added to random noise according to Eq. 19.

With the synthetic temperatures (with added noise) (Fig. 5) calculated for each position and the impulse response of the system calculated using Eqs. 35 and 35, we obtain estimations of the imposed heat flux using Eqs. 17 or 18. The eigenvalues αm, γn, and λp are obtained by solving the transcendental equation in each direction, where the indices m = 1,..M, n = 1,...N, and p = 1,..P define the number of eigenvalues required for the convergence of the series, given the truncation error, Δ = 10− 4, desired.

Fig. 5
figure 5

Sintetic temperautre evolution at 1, 2, and 3 positions

Full size image

3 Results and discussion

The temperature evolution at the respective positions of interest is shown in Fig. 5. Transfer functions are calculated at each position. These functions are shown in Fig. 6.

Fig. 6
figure 6

Heat transfer function at positions 1,2, and 3

Full size image

It is observed that for the position Ta3, the temperatures are higher when compared to the other positions, this is due to Ta3 being positioned at 4 μ m from the heat source.

It is observed that for the position Ta3, the temperatures are higher than those at other positions because Ta3 is positioned 4 μ m from the heat source.

From the pairs of the temperature and transfer function vectors, {Ta1, Ha1}, {Ta2, Ha2}, and {Ta3, Ha3}, one can estimate the heat flux using the TFBGF technique. Figures 7, 8, and 9 show a comparison between heat flux estimated (q1, q2, q3) using the data for each position and heat fux q imposed, respectively. It can be observed an excellent agreement between the heat flux obtaining deviations less than 4%, 1.5%, and 1% respectively for the positions Ta1, Ta2, and Ta3.

Fig. 7
figure 7

Comparison between estimated and imposed partial heat flux at position 1

Full size image
Fig. 8
figure 8

Comparison between estimated and imposed partial heat flux at position 2

Full size image
Fig. 9
figure 9

Comparison between estimated and imposed partial heat flux at position 3

Full size image

From the pairs of temperature and transfer function vectors, i.e., {Ta1, Ha1}, {Ta2, Ha2}, and {Ta3, Ha3}, one can estimate the heat flux using the TFBGF technique. Figures 7, 8, and 9 show a comparison between heat fluxes estimated (q1, q2, q3) using the data for each position and the heat flux q imposed, respectively. Excellent agreement can be observed between the heat flux obtaining deviations less than 4%, 1.5%, and 1% for positions Ta1, Ta2, and Ta3, respectively.

Since the heat flux is estimated, the temperature field can be obtained, solving the problem directly for any position in the domain. Figures 10, 11, and 12 show the temperature field on three sides, i.e., in the XZ plane with y = W, top view; in the XY plane with z = 0, front view; and in the YX plane with x = 0, side view, respectively, with a time of 60 s, which allows a better physical understanding of the problem.

Fig. 10
figure 10

Temperature field in XZ plane with y = W, superior view

Full size image
Fig. 11
figure 11

Temperature field in XY plane with z = 0, frontal view

Full size image
Fig. 12
figure 12

Temperature field in YZ plane with x = 0, lateral view

Full size image

The temperature fields are generated using the estimated heat flux q3 applied to the direct 3D double-layer problem. This is possible due to the thermal model allowing a temperature calculation for any point of interest in the domain. For this calculus, a coating of 4 μ m was considered.

One of the main objectives of the machining experiment is to estimate the temperature of the chip-tool interface, where due to friction between the work-piece and the tool, it is not possible to use temperature sensors. Thus, since the heat flux generated in this region is estimated, one obtains the temperature of the tool-chip interface by calculating the temperature field by the direct model, i.e., (34).

It should be mentioned that in addition to the very thin thickness of the coating, difficulties arise due to the very small contact area. The use of analytical solutions does not pose any difficulty. For example, the spatial temperature distribution in the XY plane that is formed by the coating and substrate layers (Fig. 10) or in the XZ plane, top view, with y = W, where the contact zone can be viewed in detail in Fig. 11. However, the use of numerical solutions requires an extremely refined mesh with a consequently high computational cost and worse accuracy.

The results show the thermal barrier effect. A temperature gradient of approximately 180 K can be observed in the contact region. However, this gradient is drastically reduced in thickness, with values of 30 K on the substrate region.

4 Conclusions

This work proposes the analytical solution of a 3D transient thermal problem that can model an orthogonal cutting process carried out by a coated cutting tool. The temperature field is obtained by using an inverse solution technique that estimates the heat flux delivered to the tool due to friction at the tool-piece interface. The inverse problem is solved by combining the analytical solution of the thermal model with the application of the TFBGF inverse technique.

The complexity of a transient three-dimensional thermal model with two layers with sizes on the order of centimeters and micrometers was addressed.

The heat flux was obtained by applying the TFBGF method to the substrate material. Once the heat flux was obtained, the direct problem could then be solved. This work shows the temperature field calculated in the region, including the contact zone in a cutting simulation.

The results demonstrate the thermal barrier effect produced by a 4 μ m of thickness of cobalt coating on an ISO K 10 carbide substrate. A temperature gradient of approximately 180 K can be observed in the contact region. However, this gradient is drastically reduced in thickness, with values of 30 K on the substrate.

This technique is an excellent mathematical tool for further investigation of the behavior of physical processes during a real cutting run. It can be used, for example, to estimate the influence of the thickness or thermal properties of different tool coatings. It can also be applied in the investigation of the heat flux delivered to the coated tool in a real cutting process with a coated tool. These works are in progress.