In-process measurement of springback in tube rotary draw bending

Abstract

Rotary draw bending of tubes allows repeatable and accurate manufacturing with narrow bending radii and high production rates, thanks to modern CNC controlled electrical machines. However, springback still represents one the main issues especially in small production batches or when the geometrical and mechanical properties of the raw profiles are not constant within the batch. In-process inertial measurements may allow the close-loop process control of the bending angle and, potentially, offer the possibility to compensate the springback by a real-time tuning of the bending. The paper focuses on a newly developed in-process measurement technique and presents an assessment of in-process inertial springback measurements. The springback of bent tubes is investigated as a function of the measurement gauge position and of the cross-section strain distribution along the bend.

1 Introduction

Bent tubes are used in a wide variety of applications ranging from static (i.e. structural and connecting elements) to dynamic applications (i.e. aerospace and automotive), thanks to their excellent combination of stiffness [1] and lightness [2]. The wide variety of applications, geometries, and dimensions has determined the development of different tube bending technologies that can be basically distinguished on the basis of the geometrical accuracy and the production rate that they allow to obtain [3]. Among these, rotary draw bending (RDB) presents the highest accuracy and repeatability even with bends having narrow bending radii [4], and, in the last decade, has seen significant innovations of the machines, fostering the transition from traditional hydraulic actuators to faster and more accurate electrical motors, with augmented competitiveness in terms of productivity and efficiency [5]. However, similar to all bending processes, it may be dramatically affected by the springback, which represents one of the main factors that limits the process accuracy and repeatability.

Such phenomenon appears strictly related to both material parameters and tube cross-section geometry. Springback was analytically described in Al-Qureshi [6] as function of the strain distribution in the tube cross-section and the material elastic deformation range given by the Young modulus and yield strength. Further investigations regarded the role of the work hardening exponent [7], and the strain distribution in the tube cross-section [8] which appear to be strictly dependent on geometrical parameters, namely the outer diameter and the wall thickness. The latter was investigated in Zhan et al. [9] with focus on the effects of the bend geometry (i.e. the bending radius and bending angle), and the process parameters (like the die geometries and the machine kinematic parameters), showing that it has the largest impact on the springback angle.

Concerning the process modelling, a review of the scientific literature shows the availability of both analytical and numerical approaches to predict the springback angle. Initially, analytical approaches have been proposed to predict the springback angle under pure bending conditions: the elastic-perfectly plastic formulation initially used in Al-Qureshi [6] was later extended using a strain hardening material formulation [10, 11]. Since in RDB the tools superpose a tensile stress state to the pure bending, the neutral layer shifts from the mid-layer and a non-symmetrical distribution of the fibres’ strains over the cross-section is realized [12]. In addition, all these models are affected by uncertain and non-uniform boundary conditions typical of the real processes, which intrinsically influence their accuracy, and, consequently, limit their use to academic or didactical pursues. To overcome these drawbacks, numerical simulations mainly based on finite element method (FEM) formulations have been proposed: some relevant findings are reported in Tang et al. [13] in which the influence of the booster system was evaluated in the case of thin walled copper tubes and in Gu et al. [14] with focus on the role that the mandrel kinematics has in the reduction of wrinkling and cross-section roundness. More recently, the emphasis of researches has been on the tuning of the process parameters, such as tools friction in RDB of Ti-alloys tubes [11], or the optimization of the process parameters in bending of rectangular cross-section tubes [15, 16]. Attractive as they seem, all the actual numerical methods can be used to support the initial set-up of the process parameters [17], but they show all their limits in the case of scattered material properties or geometrical tolerances, typical of batch productions as highlighted in Polyblank et al. [18].

Alternatively, a paradigm shift is emerging in recent years, with the scientists’ interest switching from the attempts of predicting the optimal process parameters to the application of adaptive techniques to compensate the scatter of boundary conditions. Allwood et al. showed how the accuracy and repeatability of metal forming processes can be enhanced through the application of sensors and monitoring system to evaluate and control the properties of the workpiece in real time [19]. Despite the rapid evolution of the measuring sensors, at now there are only a few available systems developed to monitor in-line the geometry in tube bending: in Pan et al. [20] a system to measure the tube final curvature after a cyclic bending operation by means of two touching probes was proposed, while the use of contact probes applied to the three-roll push bending process was shown in Chatti et al. [21]. But, only a few attempts to develop in-process monitoring system specifically developed for the tube RDB are reported in literature. The in-process available solutions are based on optical techniques involving one [22] or more laser systems [23], or CCD camera to measure the orientation of the straight part of the tube after the bending zone, with respect to the undeformed tube. However, both solutions are not applicable to complex bending due to the problem of dead angles [24], making the measuring area impossible to reach.

To overcome this gap, the paper presents a new approach to carry out in-line measurements of the tube bend in RDB operations. The system, originally developed for the three-roll push bending (TRPB) of tubes in Ghiotti et al. [25], was used also to detect the occurrence of wrinkles in tubes manufactured by TRPB [26] and RDB [27, 28], has been optimized for the springback and curvature measurement in tube RDB. An inertial measurement unit (IMU) is used to measure the orientation of the mandrel inside the bent tube, and the final springback is predicted by the analysis of the strain distribution along the bend. A mixed analytical and numerical approach has been developed to provide within the process cycle: (i) the actual bending angle applied to the tube and (ii) the springback at the end of the process before the tube discharging. The approach was validated on the RDB of AISI 304L round tubes.

2 Application case

2.1 Process description

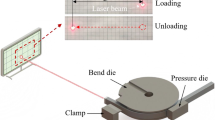
Figure 1 shows the RDB tools and kinematics. The straight tube is initially loaded on the machine, gripped by the push-carriage, and axially positioned with respect of the tools, before being closed between the clamp and the bend dies. Subsequently, this is bent by their rotation, while being constrained by the pressure die at the extrados, and the wiper die at the intrados to avoid the generation of wrinkles as in that zone the material is subjected to high compression stresses. While applying a normal load (in the Y direction shown in Fig. 1), the pressure die moves in the X direction (see Fig. 1) to limit the friction forces at the interface with the tube. An inner mandrel, made of a shank linked to one or more ball segments, supports the tube from collapsing, and it is kept in a fixed axial position during the process by means of a tie rod (see Fig. 4). After the bending stage, the clamp and the pressure dies are released, and the tube unloaded from the machine. The RDB allows to manufacture bends with different angles, but with a fixed curvature radius R_m that typically ranges from 0.5 to 10 times the outer diameter OD of the tube, and a maximum bending angle around 180°.

Fig. 1

Rotary draw bending machine: main tools and kinematics

2.2 Reference case

The industrial reference case is the bending of welded stainless-steel tubes, by means of a BLM Elect 52 electrical CNC bending machine with 10 working axes. The workpieces are round-section tubes made in AISI 304L with an outer diameter OD of 42(± 0.1) mm and a thickness t equal to 1.6(± 0.05) mm. The nominal inner radius, R_i, of the bend die is equal to 59 mm allowing to obtain bends with a nominal mean bending radius R_m of 80 mm, which corresponds to a ratio of R_m/OD equal to 1.9. To limit the flattening effect and the possible occurrence of wrinkles, a three-ball segment mandrel was used.

The experimental plan consisted in manufacturing 5 bent tubes, having a bending angle respectively of 15, 30, 45, 60, and 90°. All the bends were repeated 10 times with a constant nominal bending rate of 90 °/s, for a total number of 50 bends. Table 1 summarizes the main process parameters and the experimental plan.

Table 1 Process parameters for the application case

The bend die and the clamp die are made in 40NiCrMo7 steel, while the pressure die, the wiper die, and the mandrel elements are made in a bronze-aluminium alloy (BZ.Ampco 21) to limit both the friction forces and the tool wear. Table 2 reports the contact conditions between the tools and the tube. The chemical composition of the tube material is shown in Table 3. Dog-bone samples with a width of 10 mm and a gauge length of 50 mm were laser-cut from the tube and tested using an MTS 322 hydraulic dynamometer to assess the tube mechanical properties. Images of the tensile tests were acquired using a high-speed camera and processed using the DIC software GOM Aramis^TM to calculate the true strain and stress values. Figure 2 shows the tube flow stress curves obtained at room temperature with a constant strain rate of 0.1 s⁻¹. Such value of strain rate was chosen in accordance to the mean strain rate reached in typical draw bending operations. A repeatability equal to three was adopted for the tests. The tested material has a Young modulus of 196 GPa with a yield strength σ_Y of 372 MPa and a UTS value of 713 MPa. The material behaviour is well fitted by an elastic, linearly strain-hardening model (Eq. 10), as shown by the red-dashed lines overlapped with the experimental data in the chart (Fig. 2), with a maximum percentage deviation lower than 7%.

Table 2 Interface conditions between the tools and the tube

Table 3 Nominal chemical composition of AISI 304L tubes

Fig. 2

AISI304L flow stress behaviour

3 Measurement approach

The springback measurements are realized by a specifically developed mandrel that embeds an inertial measurement unit. The real-time control is fed by a twofold source: the mandrel that returns the tube spatial movement and the CNC bending machine engines that give the engine position during the process. The details of the hardware architecture and the measurement algorithms are reported in the following sections.

3.1 Bending mandrel

Figure 3 shows the device used in the experiments and the sketch of the meridian section with the details of the assembled parts. A standard 3-ball segment mandrel was modified to embed the IMU on the last segment, inside a hard cover to prevent any mechanical contact and interaction with the process lubricants. For the sake of comparison, the characteristics of the IMU used in the experiments are the same previously reported in Simonetto et al. [27]. The sensor is used to measure three accelerations and three angular velocities in the space, for a total of six degrees of freedom. For each measuring axis an analog-to-digital (AD) converter embedded in the sensor converts the analog measure in a 16-bit signal and the measuring ranges were set to be ± 250 dps for the gyroscopes and at ± 2 g for the accelerometers. The acquisition frequency was equal to 350 Hz when sampling all the six axes, while it increases up to 600 Hz in the case of acquisition of only the signals from the gyroscopes. Each sensor was calibrated according to the procedure presented in Simonetto et al. [28].

Fig. 3

Bending mandrel and sketch of the meridian section with details of the assembled parts

3.2 Measurement algorithm

During the bending stage each tube section is subjected to different rotations speed, namely ${\dot{\theta}}_{xi}$, ${\dot{\theta}}_{yi}$, and ${\dot{\theta}}_{zi}$. As reported in Fig. 4a, the local coordinate system Ox₁y₁z₁, aligned with the last ball segment, undergoes the rotation speed ${\dot{\theta}}_{\mathrm{x}1}$, ${\dot{\theta}}_{y1}$, and ${\dot{\theta}}_{z1}$. By measuring these angular rates, the angle θ_ji around the j-axis for the ith tube cross-section is calculated as

Fig. 4

Tool positions for three different bends at a 15°, b 30°, and c 90°

$$ {\theta}_{ji}=\int {\dot{\theta}}_{ji} dt $$

(1)

Therefore, the orientation of the ith cross-section, referred to the fixed reference system Oxyz, can be computed on the basis of the Eulerian angles according to

$$ \left(\begin{array}{c}{\boldsymbol{x}}_{\mathbf{1}}\\ {}{\boldsymbol{y}}_{\mathbf{1}}\\ {}{\boldsymbol{z}}_{\mathbf{1}}\end{array}\right)=\left[{R}_{\theta_{x1}}\right]\left[{R}_{\theta_{y1}}\right]\left[{R}_{\theta_{z1}}\right]\left(\begin{array}{c}\boldsymbol{x}\\ {}\boldsymbol{y}\\ {}\boldsymbol{z}\end{array}\right) $$

(2)

where [R_θx1], [R_θy1], and [R_θz1] are the rotation matrices of the Ox₁y₁z₁ around the three axes Oxyz respectively:

$$ \left[{R}_{\theta_{x1}}\right]=\left[\begin{array}{ccc}1& 0& 0\\ {}0& \cos {\theta}_{x1}& -\sin {\theta}_{x1}\\ {}0& \sin {\theta}_{x1}& \cos {\theta}_{x1}\end{array}\right] $$

(3)

$$ \left[{R}_{\theta_{y1}}\right]=\left[\begin{array}{ccc}\cos {\theta}_{y1}& 0& \sin {\theta}_{y1}\\ {}0& 1& 0\\ {}-\sin {\theta}_{y1}& 0& \cos {\theta}_{y1}\end{array}\right] $$

(4)

$$ \left[{R}_{\theta_{z1}}\right]=\left[\begin{array}{ccc}\cos {\theta}_{z1}& \sin {\theta}_{z1}& 0\\ {}-\sin {\theta}_{z1}& \cos {\theta}_{z1}& 0\\ {}0& 0& 1\end{array}\right] $$

(5)

The IMU fixed to the mandrel embeds three orthogonal gyroscopes to measure the three angular rates around the sensor axes. At each k-sample time the gyroscopes measure the angular rate along their own j-axis, θ_jk with a sampling rate f, and a period ΔT. Therefore, as the end ball segment is aligned with the tube and its axial distance from the bending end is defined by the mandrel length l_m (see Figs. 3 and 4), the relative orientation between the two coordinate systems Ox₁y₁z₁ and Oxyz can be determined at each kth sampling time allowing the computation of the angles along the j-axis θ_jik, namely θ_x1k, θ_y1k, and θ_z1k.

Since the RDB is typically performed in the horizontal plane Oxy, $\left[{R}_{\theta_{x1}}\right]$ and $\left[{R}_{\theta_{y1}}\right]$ of Eq. (2) become identity matrices, and the rotation angle ${\theta}_{zi_k}$ at the kth sampling time, on the i-point along the tube axis, can be computed using Eq. (6) as

$$ {\theta}_{zi_k}={\theta}_{zi_{\left(k-1\right)}}+{\dot{\theta}}_{zi_k}\cdotp \left(\Delta T\right) $$

(6)

where ΔT is the period between two subsequent k-samples. As the rotation angle is computed from the measured angular rates, it is worth to notice how it has not any limitation in terms of maximum measurable value.

Figure 4 shows the position of the inner mandrel inside the bent tube, at the end of the bending stage for three different angles respectively 15° (Fig. 4a), 30° (Fig. 4b), and 90° (Fig. 4c). Figure 4 also shows in the charts the evolution of the bending angle φ_k imposed by the machine during the bending stage and the corresponding ${\theta}_{z{1}_k}$ angle measured by the smart mandrel. In the case of a nominal bending angle φ of 15° bend, Fig. 4a shows the position of the local reference system Ox₁y₁z_1, aligned with the end ball segment that lies still inside the straight part of the tube just after the bent section. In this case l_m is longer than the bending length l_b, and the angle ${\theta}_{z{1}_k}$ between the local and fixed reference systems at the end of the bending stage can be considered equal to the nominal bending angle φ. Conversely, Fig. 4c shows the tools position at the end of a 90° bent where the local reference system Ox₁y₁z₁ lies inside the bend as l_m is shorter than the bending length l_b. In this configuration, at the end of the bending stage, the angle between the local and fixed reference systems ${\theta}_{z{1}_k}$ is lower than the total nominal bending angle φ. So, the limit bending angle that can be measured by using such approach is given by the condition l_m equal to l_b (see Fig. 4b), for which the measured angle ${\theta}_{z{1}_k}$ still remains equal to the nominal bending angle φ. If l_m is equal to l_b, ${\theta}_{z{1}_{\mathrm{lim}}}$ can be also calculated as the ratio l_m/R_m, where l_m is the mandrel length and R_m is the mean bending radius of the bend. Such approach was experimentally validated by comparing the actual angle ${\theta}_{Z{1}_k}$, measured by the sensor during the process, with the one measured by the machine motor φ_k, proving that ${\theta}_{z{1}_{\mathrm{lim}}}$ depends only on the geometrical characteristics of the tube bend and the number of ball segments in the mandrel.

In the reference case investigated in this work, with l_m equal to 42 mm and the mean bending radius R_m equal to 80 mm, the limit angle ${\theta}_{z{1}_{lim}}$ that can be directly measured by the sensor is about 30 deg as shown by Fig 4b.

Figure 5a plots both the signals from the sensing mandrel and from the electrical motors of the bending machines in the case of a 90° bend. The linear position signals, X_M and Y_Cd, represent respectively the axial positions of the mandrel shank and the clamp die: the former keeps its axial position unchanged over the process (signal X_M constant), while the latter moves applying a counter pressure to the outer surface of the tube at the bend extrados. After their closure, the bend and clamp dies start rotating and the sampled bend die angle signal, φ_k, increases up to the target value (90 deg in the case represented in the plot). At the end of the bending stage, when the clamp die is still closed, the angle φ is larger than ${\theta}_{z{1}_{\mathrm{lim}}}$ due to the reduced length of the mandrel (l_m < l_b), see Fig. 4c. At the end of the dwell time, the springback phenomenon takes place, being detected as a negative peak of the angular rate (see Fig. 5b), and the angle measured by the sensing mandrel decreases due to the springback from ${\theta}_{z{1}_b}$ to the final value after the springback ${\theta}_{z{1}_{fin}}$. Their difference returns the measure of the tube springback angle α_m.

Fig. 5

a CNC kinematics and sensors signals during a 90° bend. b Detail of the springback stage

3.3 Geometrical-based extension

A simple extension of the previously described model to evaluate the bending angles larger than ${\theta}_{z{1}_{\mathrm{lim}}}$ can be obtained through analytical considerations based on the bend geometry. Given the mandrel position inside the tube l_m, the bending length l_bk at the kth sampling time, the mean bending radius R_m and the bending angle from the motor φ_k at the kth sampling time, the relation between the measured angle ${\theta}_{zi_k}$, and the real bending angle following the linear geometrical equation:

$$ \left\{\begin{array}{ll}{\theta}_{zi_k}={\theta}_{zi_{\left(k-1\right)}}+{\dot{\theta}}_{z{i}_k}\cdotp \left(\Delta T\right)& {\theta}_{zi_k}\le {\theta}_{zi_{lim}}\\ {}\frac{\theta_{z{i}_k}}{\varphi_k}=\frac{l_m}{{l_b}_k}=\frac{l_m\ 180}{R_m{\varphi}_{k\ \pi }}& {\theta}_{zi_k}>{\theta}_{zi_{lim}}\end{array}\right. $$

(7)

With regard to the reference case described in Sect. 2.2, the final springback obtained by the so-called geometrical-based extension angle α_GB can be computed according to Eq. (8):

$$ \left\{\begin{array}{c}{\alpha}_{\mathrm{GB}}={\alpha}_m\kern10.25em {\theta}_{z{1}_b}\le {\theta}_{z{1}_{\mathrm{lim}}}\\ {}{\alpha}_{\mathrm{GB}}=\frac{{l_b}_k}{l_m}{\alpha}_m=\frac{R_m\ {\varphi}_{k\ \pi }}{l_m180}{\alpha}_m\kern3.25em {\theta}_{z{1}_b}>{\theta}_{z{1}_{\mathrm{lim}}}\end{array}\right. $$

(8)

Thus, the springback factor ${K}_{s_{GB}}$ obtained by the geometrical-based extended model is given by

$$ {K}_{s_{GB}}=\frac{\varphi -{\alpha}_{GB}\ }{\varphi } $$

(9)

where the numerator is the final angle after the springback and the denominator is the bending angle imposed by the machine motors.

4 Extended model

The limit of using simple linear correlations to predict the springback based on the bending angle was already investigated in Kinnel et al. [24]. In fact, in the axial strains in RDB are not limited to the bend length, but they comprise the tube zones under the clamp and pressure dies [29]. Due to that, the model provided in Sect. 3.3 has been extended by using FE simulations ad detailed in the following sections.

4.1 FE model

The numerical model of the reference RDB process was developed in LS-DYNA™ environment by using the explicit formulation. Figure 6 shows the tools at the beginning (a) and at the end (b) of a 90° bending process, in which the idle balls of the inner mandrel tilt due to the tube deformation.

Fig. 6

a FE model of the tube rotary draw bending and b effective plastic strain distributions for different bending angles

The tools and the tube were both modelled using fully-integrated quadrangular shell elements, with and 8 integration points. The formers were modelled as rigid parts without any elastic deformation; the latter was modelled according to the elastic, linearly strain hardening formulation, reported in Eq. (10):

$$ \left\{\begin{array}{c}\sigma = E\varepsilon \\ {}\sigma ={\sigma}_Y+{E}_p\left(\varepsilon -\frac{\sigma_Y}{E}\right)\end{array}\right.\kern6.75em {\displaystyle \begin{array}{c}\sigma <{\sigma}_Y\\ {}\sigma \ge {\sigma}_Y\end{array}} $$

(10)

where E is elastic modulus, σ_Y is the material yield strength, and E_p is the plastic modulus. Since the process is carried out at room temperature and the bending speed is limited, the effects of the temperature and strain rate were assumed negligible. The yield strength and the elastic modulus used to describe the material model are reported in Sect. 2.2, while the plastic modulus is equal to 1896 MPa. The fitting of the material model vs. the experimental date is showed in Fig. 2, and the maximum percentage difference between the two series is lower than 7%. The chosen elastic linearly strain hardening formulation not only shows a good fitting with the real material behaviour but can also be easily calibrated by means of cost-effective tensile tests on dog bone samples cut along the tube axial direction, easily performed also in the industrial production floor. Other rheological models were exploited in literature to predict the final springback, such as isotropic-hardening [30], mixed hardening, and Yoshida–Uemori two-surface hardening [31], and non-linear kinematic hardening [32] also combined with anisotropic yield criteria [33]. However, this requires complex, expensive, and time-consuming calibrations tests. All the tools and workpiece geometries and kinematics were modelled according to the data reported in Sect. 2.2 and Table 1. The links in the three-ball segment mandrel were modelled by means of spherical joints. An average mesh size of 1 mm was used for the tube, the bend die, and the mandrel segments, while an average mesh size of the 2 mm was used for the other tools in order to contain the total number of the model elements, keeping at the same time a good geometrical accuracy. The contacts between the tools and the tube were modelled by using the Coulomb model, described by Eq. (11):

$$ \tau =\mu \sigma $$

(11)

where τ and σ are respectively the tangential and the normal stress at the contact interfaces and μ is the coefficient of friction whose values for the different tribo-pairs are reported in Table 4. Two different friction coefficients were assigned to the bend die, as the straight part that grips the tube together with the clamp die is manufactured with a rougher surface, if compared with the curved parts, to prevent the tube from slipping.

Table 4 Friction coefficients between tube and dies

The springback angle depends on the fibre deformation that interest not only the bend length but also the gripping areas of the tube, theoretically undeformed respectively upstream and downstream of the bend die. Figure 6b shows the plastic strains computed for the tested bending angles before releasing the clamp die constrain, as well as the length of the bending length along the intrados (${l}_{bi_{\varphi }}$) and extrados side (${l}_{be_{\varphi }}$) for a bending angle φ. It is worth to notice that a so-called transition zone, in which plastic strains were detected, interests the axial fibres out of the bend length as shown by the plastic strain fields in Fig. 6b and the entity of these transition zones are not directly proportional to bending angle.

The plastic strains computed at the intrados and extrados for the tested bending angles are plotted in Fig. 7 respectively at the extrados in (a) and intrados in (b). For both the cases, the results of the FE analyses show that the strained fibres are always longer than the contact lengths in all the tested conditions; in particular, the smaller the bend angle, the larger the difference is between the strained fibres and the bend length. With regard to the reference case, the bend lengths at the extrados for a 15° and a 90° bends are respectively equal to 24.4 mm and 158.6 mm, while the length of the strained fibres for the same angles amounts to 86.7 mm and 210.5 mm, with a ratio between the strained and bending lengths respectively of 3.55 and 1.32. Similarly, at the intrados, the same ratios are equal to 4.1 and 1.4. The larger lengths of the transition zones at lower bend angles explain why the springback in tube rotary draw bending is greater for smaller bending angles.

Fig. 7

Plastic strain of the bending zone at the extrados (a) and the intrados (b) for different imposed bending angles

Figure 8 shows the strain distribution in the cross-section A-A represented in Fig. 6b for the 90° bend. As expected, the neutral layer (NL) shifts from the tube middle layer and this returns an asymmetric distribution of the strains over the cross section. This is due to the tensile axial force superposed by the wiper and the pressure dies that constrain the tube while the bend and the clamp die rotate. For this reason, the length of the deformed fibres at the intrados and the extrados are not exactly proportional to the inner and outer bending radii and must be numerically investigated case by case.

Fig. 8

Strain distribution along the tube cross section

4.2 Strain-based extension

The strain-based extended model postulates that the axial extension of the cross-section fibres deformed during RDB is larger than the arc of contact with the bend die. So, being α_m the springback angle measured by the sensing mandrel, the springback angle α_SB can be computed according to Eq. (12):

$$ \left\{\begin{array}{c}{\alpha}_{\mathrm{SB}}={\alpha}_m\kern15.25em {\theta}_{z{1}_b}\le {\theta}_{z{1}_{\mathrm{lim}}}\\ {}{\alpha}_{\mathrm{SB}}={\alpha}_m\frac{\left({l}_{\operatorname{ext},\varphi }+{l}_{\operatorname{int},\varphi}\right)/2}{\left({l}_{\mathit{\operatorname{ext}},{\theta}_{z{1}_{\mathrm{lim}}.}}+{l}_{\mathit{\operatorname{int}},{\theta}_{z{1}_{\mathrm{lim}}}}\right)/2}={\alpha}_m\frac{L_{\varphi }}{L_{\theta_{z{1}_{\mathrm{lim}}}}}\kern1.25em {\theta}_{z{1}_b}>{\theta}_{z{1}_{\mathrm{lim}}}\end{array}\right. $$

(12)

where:

l_{ext, φ}:

is the length of the deformed fibres at the tube extrados for the bending angle φ;

l_{int, φ}:

is the lengths of the deformed fibres at the tube intrados for the bending angle φ;

${l}_{\operatorname{ext},{\theta}_{z{1}_{\mathrm{lim}}}}$:

is the length of the deformed fibres at the tube extrados for the limit angle, ${\theta}_{z{1}_{\mathrm{lim}}}$, that can be directly measured by the mandrel (see Fig. 7 for the reference case, ${l}_{\operatorname{ext},{\theta}_{z{1}_{\mathrm{lim}}}}={l}_{\operatorname{ext},30{}^{\circ}}$ );

${l}_{\operatorname{int},{\theta}_{z{1}_{\mathrm{lim}}}}$:

is the length of the deformed fibres at the tube intrados for the limit angle, ${\theta}_{z{1}_{\mathrm{lim}}}$, that can be measured by the mandrel (see Fig. 7 for the reference case, ${l}_{\operatorname{int},{\theta}_{z{1}_{\mathrm{lim}}}}={l}_{\operatorname{int},30{}^{\circ}}$ );

L_φ:

is the mean length of the deformed fibres for the bending angle φ;

${L}_{\theta_{z{1}_{\mathrm{lim}}}}$:

are the mean length of the deformed fibres for the limit angle, ${\theta}_{z{1}_{\mathrm{lim}}}$.

Furthermore, by using Eq. (13) it is possible to compute the springback factor ${K}_{s_{SB}}$ using the angle α_SB given by Eq. (12):

$$ {K}_{s_{SB}}=\frac{\varphi -{\alpha}_{SB}\ }{\varphi } $$

(13)

Figure 9 shows the flow chart of the developed algorithm to monitor in-line the springback angle. The approach is divided in two parts: first, the FE analysis of the bending has to be run before the test in order to estimate the real length of the fibres interested by the deformation, and, then, the real-time measurements can be performed in-line with the sensing mandrel. During the process, the angle measured by the sensing mandrel θ_jik is recorded, and, if the mandrel length l_m is larger than l_b, α_GB is directly computed as the difference between the orientation before, ${\theta}_{ji_b}$, and after the dies unloading, ${\theta}_{ji_{\mathrm{fin}}}$, otherwise it is calculated according to Eq. (12).

Fig. 9

Flow chart of the measurement approach

4.3 Sensitivity analysis

Since the FE model is used to estimate the plastic zones at the intrados and extrados, its sensitivity in predicting the lengths of the strained fibres was assessed with respect to the main process parameters. The main conditions considered in the analysis were as follows: (i) the friction conditions between the tube and the dies, due do different amount of lubricants or to different closure forces exerted by the dies; (ii) the material properties, due to the scatter of the components composition for example between different batches of the same material; and (iii) the bent geometry, due to the variation of the imposed mean bending radius.

The first point was evaluated by varying the reference friction conditions reported in Table 4 by ± 20% with steps of 10%. The results expressed in terms of ratio ${L}_{\varphi }/{L}_{\theta_{z{1}_{\mathrm{lim}}}}$ are shown in Fig. 10. It was seen that the variation of the friction coefficient has a little influence on the results, with a maximum deviation equal to 4% for a 90° bend. Lower bending angles present minor deviations that were considered negligible.

Fig. 10

Deformed length ratios, as a function of the friction coefficients

Similarly, Fig. 11 shows that variations of the material yield strength σ_Y by ± 20% with steps of 10% have little influence on the ${L}_{\varphi }/{L}_{\theta_{z{1}_{\mathrm{lim}}}}$, with maximum deviation around 4.1% in the case of a bending angle of 60°.

Fig. 11

Deformed length ratios, as a function of the material yield strength

Figure 12 shows the results for different values of the mean bending radius R_m, which appears having a great influence on the model results. Geometries having a ratio R_m/OD equal to 1.67, 1.90, 2.12, 2.50, 3.00, and 4.00 were modelled, whereas the RDB process is ordinarily used to manufacture bends with R_m/OD ranging from 1.5 to 8. The maximum ratio that was used in the FE simulations was equal to 4, as larger values typically require different mandrel geometries. Figure 12, which shows the ratio ${L}_{\varphi }/{L}_{\theta_{z{1}_{\mathrm{lim}}}}$ for different bending angles and R_m/OD values, highlights that the bent geometry greatly affects the results, making it necessary to run a new numerical model whenever a new geometry is manufactured to assess the right coefficients necessary for the extrapolation model.

Fig. 12

Deformed length ratios, as a function of the mean bending radius

5 Validation

The approaches discussed in Sects. 3 and 4 were applied to the reference case described in Sect. 2 and validated by comparing the results with off-line measurements carried out on a coordinate measuring machine (CMM).

The springback was measured off-line by a Zeiss Prismo Vast 7 Contact Measurement Machine (CMM) as the result of

$$ {\alpha}_{{\mathrm{CMM}}_{\varphi }}={\varphi}_f-\varphi $$

(14)

where φ_f is the tube final angle, measured with the CMM after the springback, as shown by Fig. 13. To this aim, the CMM was equipped with a disc probe for the detection of the cylinders inscribed in the two straight extremities of the bent tube following and helical path (see Fig. 13), whose axes were derived and used for the evaluation of the final springback.

Fig. 13

CMM measurement procedure

Figure 14 shows the results obtained by using the two models normalized with respect to the value of ${\theta}_{z{1}_{\mathrm{lim}}}$. It was seen that the ratio between the mean length of the deformed fibres ${L}_{\varphi }/{L}_{\theta_{z{1}_{\mathrm{lim}}}}$ (defined in Eq. (12)) is in good agreement with the CMM measurements given by the ratio ${\alpha}_{{\mathrm{CMM}}_{\varphi }}/{\alpha}_{{\mathrm{CMM}}_{\theta_{z{1}_{\mathrm{lim}}}}}$ between the angle measured by the CMM ${\alpha}_{{\mathrm{CMM}}_{\varphi }}$ for a bending angle φ and the angle ${\alpha}_{{\mathrm{CMM}}_{\theta_{z{1}_{\mathrm{lim}}}}}$ measured by the CMM in correspondence of ${\theta}_{z{1}_{\mathrm{lim}}}$ (30° in the reference case). On the contrary, the direct measurements performed by using the sensing mandrel, given by the ratio l_b/l_m, overestimate the measurements. These results suggest that the strain-based extended model can better evaluate the deformation bending angles since it considers the strain distribution in the bent zone that is larger than the nominal curvature of the tube.

Fig. 14

Normalized parameters vs. the bending angle

Figures 15 and 16 show the comparison of the different models when applied respectively to the bending step and the springback evaluation. In the former, it is shown that before the tube unloading the direct measurement of the bending angle made by using the sensing mandrel, ${\theta}_{z{1}_b}$ (see Fig. 5), agrees with the value returned by the encoders of the electrical motors, φ, until the value of 30°; larger angles cannot be covered with a direct measurement since the mandrel is shorter than the bending length and it is not sensitive to the deformation. Although its simplicity, the correction of the measurement based on the geometrical extension model (Eq. (7)) demonstrates its effectiveness returning values very closed to the signals from the machine motors, with a maximum deviation of 2%. Conversely, the correction algorithm based on the strain computation did not return acceptable values, showing again an underestimation of the measurement compared with the actual value. This behaviour is explained by the fact that before the tube unloading, the relationship between the measured and the imposed bending angle is only a function of the mandrel position inside the bent section and not of the total mean deformed length.

Fig. 15

Measured bending angle vs nominal bending angle

Fig. 16

Springback angle vs. bending angle measured with the CMM and corrected with the geometrical and the strain-based model

The results of the comparison are completely different in the case of springback evaluation as shown in Fig. 16 where the results of the measurements carried out by using the sensing mandrel are compared with the off-line measurements carried out with the CMM. Again, the deviation of the springback measured by the mandrel α_m becomes relevant for bending angles larger than ${\theta}_{z{1}_{lim}}$, due to reduced mandrel length that affects the sensitivity of the sensor. The correction based on the geometrical extension in this case fails since the springback is more sensitive to the deformation of the bent fibres’ length than the geometrical length of the bend. The results of the experimental tests showed a deviation 38% for a 45° bend and more than 57% for a 60° bend, see Fig. 16. The correction based on the evaluation of the strains were in good agreement with the CMM measured results, with a mean difference of 4.4% corresponding to an angle of 0.1 deg, while the maximum deviation was measured equal to 0.3° for a 90° bend.

The results are plotted in terms of springback factors in Fig. 17. The reference values ${K}_{s_{\mathrm{CMM}}}$ obtained from the measures carried out with the CMM are compared with the ones obtained with the data measured by the sensing mandrel ${K}_{s_m}$. These values are consistent only for bending angles lower than ${\theta}_{z{1}_{\mathrm{lim}}}$, while for greater values the percentage difference between them increases up to 1.75%. The chart reports also the springback factors computed by applying the geometric based model ${K}_{s_{\mathrm{GB}}}$ according to Eq. (9) and the strain-based model ${K}_{s_{\mathrm{SB}}}$ according to Eq. (13). The former shows a maximum deviation from ${K}_{s_{\mathrm{CMM}}}$ over 4.16 %, while the correction based on the strain-extension model shows a maximum deviation of 0.36% and a mean one of 0.16%. The results given by the strain-based model, compared with the reference values obtained from CMM, point out also in this case how the springback angle is more sensitive to the strained length compared with the geometrical length of the bend.

Fig. 17

Springback factor vs. bending angle measured with: the CMM ${K}_{s_{\mathrm{CMM}}}$, the mandrel ${K}_{s_m}$and corrected with the geometrical-based model ${K}_{s_{\mathrm{GB}}}$ and the strain-based model ${K}_{s_{\mathrm{SB}}}$

6 Conclusions

The paper describes a new approach for the in-line evaluation of the springback angle in the tube rotary draw bending. This is based on the use of a newly developed sensing mandrel that embeds an IMU to measure the orientation of the bent tube, and the final springback is predicted by the analysis of the strain distribution along the curved area of the tube. A mixed analytical and numerical approach has been developed to provide within the process cycle: (i) the actual bending angle applied to the tube and (ii) the springback at the end of the process. The approach was validated on the RDB of AISI 304L round tubes.

The results show that springback angle is more sensitive to the length of the strained zones compared with the geometrical length of the bend. Based on such analysis, a strain-based correction algorithm has been proposed to overcome the above-mentioned limitation, in order to extrapolate the total springback angle. A good agreement with the springback angles measured by using a CMM was found, with a mean deviation of 4.4% equal to 0.1° and a maximum mean deviation of 7.7%. The results are consistent also in terms of springback factor, with a mean difference of 0.16% and a maximum one of 0.36%. The numerical model was used also to evaluate the sensitivity of the developed strain-based approach to variations of the most common process boundary conditions, showing that the approach is only slightly influenced by variations of the friction conditions or by the scatter of the material properties that are also one of the process main source of uncertainty, while it is more influenced by changes of the bending geometrical parameters which are usually know. The presented approach has proved to be reliable for the in-line monitoring of tube RDB, while the use of numerical models can be limited only to the initial estimation of the length of the deformed fibres. Thus, it has been demonstrated promising for applications oriented to the real-time process control.