1 Introduction

Assembly of the manufactured parts is based on the production precision of different connected pieces. The main concern in industry to assemble the parts is their dimensions after their manufacturing. Tubes and shafts are ones of the most used pieces that should be prepared for assemblies as they are very sensitive because of springback phenomena. Thick walled tubes are used in several industries and for their manufacturing bending or bending-torsion are widely used. Several bending processes have been invented and used in the production of three-dimensional tubes including rotary bending, compression bending, roll bending, etc. [1].

In nearly all of the forming and especially cold forming process and sheet forming the dimensions and angles of the products change after unloading. The main reason of this dimension changes, which is named springback, is the elastic unloading. Springback is mainly dependent on the elastic strain which is also dependent on the stress values and variations. Stress distribution during manufacturing process depends on the in-elastic deformation of the materials. Therefore, mechanical behaviour of the used material is essential in springback modeling [2,3,4].

Springback analysis of thin-walled tubes has been investigated to predict the bending angles by theoretical and numerical studies. Al-Qureshi presented a theoretical analysis model for predicting bending springback of two-dimensional tubes made of different metals [5]. Effect of strength coefficient and hardening exponent on the springback angles of bended tubes were studied by Zhan et al. [6]. Mandrel effect in springback reduction was modeled by FEM by [7]. They concluded that the springback angle diminished about 107%. Da-Xin et al. [8] investigated the effect of plastic modulus, hardening exponent and Young modulus effects on the springback of the bended tubes. They showed by finite element analysis that with decreasing the plastic modulus springback also decreased. They also showed that the springback angle increased with increasing the bending curvature but its relation with the tube thickness is vice versa.

Li et al. [9] showed that the thickness to radius ratio of the tubes in bending had the most influence in springback. In 2014 and 2016, Xue and Liao developed a new numerical model based on an integrated hemispherical and kinematic hardening model, as well as considering the effect of Bauschinger’s study on the return stress of two-dimensional tubes under torsion. The results showed that the developed elemental model with level-based hinged can offer more accuracy and also the friction between the two sides has a major impact on the return of the surface. The results also show that the return angle is considered to be very sensitive to the hardening model, while the springback due to the curvature is more sensitive to the yield level [7, 10].

Effects of different hardening models including isotropic hardening model, Mroz, nonlinear kinematic hardening models on the prediction of springback of tubes of Ti-3Al2.5 V alloy in a rotary draw bending has been investigated by Nayebi and Shahabi [11]. Also, Mandrel’s impact on the quality of the finished product and the damage to the tube, such as wall thickness, cross-sectional deformation, has also been considered.

Recently, Nayebi and Shahabi studied the effect of damage mechanics on the prediction of springback in metal forming processes. In this study, the effect of material properties changes due to the continuum damage mechanism was considered in finite element simulation to predict the springback of sheets that are under the V-shaped bending process. Hollomon’s isotropic hardening rules and Ziegler’s linear kinematic stiffening are considered to describe the behavior of materials. The results showed that considering the changes in the Young’s modulus due to plastic deformation is an effective strategy for simulating the processes of metal deformation. The continuum damage mechanics model of Lemaitre improved the precision of the springback results by using finite element simulations [12]. Leu [13] incorporated mechanical and geometrical properties in a simple model and the springback–radius in V-die bending was predicted which was in good comparison with the experimental results.

However, majority of the theoretical models have been developed to analyze bending of the tubes, but limited studies were carried out on the three-dimensional forming of the tubes. Springback problem is one of the main concerns about three-dimensional forming of tubes. Gantner proposed a finite element model that defined the shaping parameters for the springback prediction in 3D bending of tubes [14, 15]. Hudovernik et al. [16, 17] carried out the numerical simulations of the bending and torsion of the pipes. Their results lead to better understanding of the springback and cross-sectional deformation of square tubes.

Zhang et al. [18] presented a numerical model to determine the bending curvature ratio in loading and unloading. However, the shear stress is ignored. Later, Zhang et al. [19] characterized the springback of the tubes under bending and torsion by using perfect plastic properties. Wu et al. [20] investigated the springback rate of three-dimensional tubes based on isotropic hardening. However, their model cannot predict the reverse plastic flow which occurs usually in unloading of the thick tubes. In this study, the nonlinear kinematic hardening and Bauschinger’s effect are considered to predict springback of the tubes under combined bending and torsion. Different combinations of bending and torsion and their sequences are studied. Return mapping algorithm relations are developed. The numerical results are compared with experimental results. The developed method is applied for different tubes.

2 Theoretical model development

2.1 Three-dimensional bending and Torsion

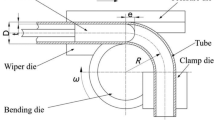
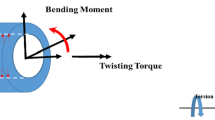
Deformation and springback of the thick-walled tubes are studied in this research. The deformation process is considered as a combination of bending and rotation (Fig. 1a). Therefore, the bending is considered as curvature, ρ, decreasing from the yield curvature and the section rotation is carried out by applying the torsion angle, ϕ. Both loadings are applied incrementally. The application of the rotation angle and the bending curvature can be followed according to Eq. 1:

Fig. 1
figure 1

a Schematic representation of the combined loading and b variation of bending curvature as a function of the twist angle

Full size image
$$\frac{\rho }{{\rho _{f} }} = f\left( {\frac{\phi }{{\phi _{f} }}} \right)$$
(1)

where ρf and ϕf are final bending curvature and torsion angle, respectively. In some of loading the relation between ρ and ϕ are power rule or it can also be sequential. It means that bending is applied and then the torsion is completely applied. Power law is used for the function of Eq. 1 and presented schematically in Fig. 1b.

$$f\left( x \right) = x^{n} ,\,\left( {n = \frac{1}{2},1,\,2} \right)$$
(2)

Application of bending and torsion simultaneously, can lead to different plastic zone evolution during loading. With application of bending the plastic onset starts from the top point and then the plastic zone spreads through the tube section. Several situations can happen: yield and plastic zone in the perimeter and its growth towards the inner radius or the plastic zone starts from the top point and then it spreads toward the neutral axis. Based on the bending curvature and torsion angle, different situations happen.

2.2 Theoretical background of the numerical method

Springback phenomenon is strongly dependent on the elastic and plastic behavior of the deformed material. In this study nonlinear kinematic hardening and Bauschinger’s effect are assumed. Therefore, the effect of reverse plastic which can occur in bending and torsion of thick-walled tube is considered. Thickness of the tube is constant and the distortion of the tube surface is neglected. The yield criteria is the von-Mises yield function (Eq. 3). Radial stress is neglected. Armstrong-Frederick model is supposed for the back-stress evolution as:

$$F = \left( {S_{ij} - x_{ij} } \right)\left( {S_{ij} - x_{ij} } \right) - \frac{2}{3}\sigma_{y}$$
(3)
$$d\varvec{x} = \frac{2}{3}Cd\varvec{\varepsilon}^{p} - \gamma \varvec{x}d\varvec{\varepsilon}_{e}^{p}$$
(4)

C and γ are the material constants which can be obtained from monotonic and cyclic uniaxial tests [21]. \(d\varvec{\varepsilon}_{e}^{p}\) is equivalent plastic strain component which can be obtained from Eq. 5. It was considered that the total strain increment (dε) is the sum of the elastic (dεe) and plastic (dεp) strains increments. Elastic strain follows the Hooke’s law (Eq. 6) and the plastic strain is obtained from the normality rule (Eq. 7).

$$d\varvec{\varepsilon}_{e}^{p} = \sqrt {\frac{2}{3}d\varvec{\varepsilon}^{p} :d\varvec{\varepsilon}^{p} }$$
(5)
$$d\varepsilon_{ij}^{e} = \frac{1}{2G}\left( {d\sigma_{ij} - \frac{\nu }{1 + \nu }d\sigma_{kk} } \right)$$
(6)
$$d\varepsilon_{ij}^{p} = d\lambda \frac{\partial F}{{\partial \sigma_{ij} }} = d\lambda \left( {S_{ij} - x_{ij} } \right)$$
(7)

where dλ is the plastic modulus increment and it can be obtained from the consistency condition (Eq. 8):

$$dF = \left( {S_{ij} - x_{ij} } \right)\left( {dS_{ij} - dx_{ij} } \right) = 0$$
(8)

2.3 Application of the numerical method of return mapping algorithm

The problem is considered as a displacement control. Bending curvature and torsion angle are applied incrementally and then the plastic strain, back stress and stresses are calculated by using return mapping algorithm. The tube section is divided into elements in radial and tangential directions and the numerical method is used for every element where plastic flow occurs.

Return mapping consists of two steps of elastic prediction and plastic correction. The loading is divided into several small increments. It is supposed that all parameters are known in the previous increment and then the loading increased by an increment. It is supposed that the response of the tube is elastic and then the new values of the variables are determined which are called trial variables (Eq. 9).

$$\left\{ {\begin{array}{*{20}c} {\varvec{\varepsilon}_{n + 1}^{p, Trial} =\varvec{\varepsilon}_{n}^{p} } \\ {\varvec{\varepsilon}_{n + 1}^{e, Trial} =\varvec{\varepsilon}_{n + 1} -\varvec{\varepsilon}_{n}^{p} } \\ {\varvec{x}_{Trial}^{n + 1} = \varvec{x}^{n} } \\ {\varvec{\sigma}_{Trial}^{n + 1} = C:\varvec{\varepsilon}_{n + 1}^{e, Trail} = C:\left( {\varvec{\varepsilon}_{n + 1} -\varvec{\varepsilon}_{n + 1}^{p, Trial} } \right)} \\ \end{array} } \right.$$
(9)

The yield function is verified according to the trial variables. If it is negative the trial solution is correct \(\left( {f_{t}^{n + 1} \left( {\varvec{\sigma}_{t}^{n + 1} ,\varvec{x}_{t}^{n + 1} } \right) \le 0} \right)\). Otherwise \(\left( {f_{t}^{n + 1} \left( {\varvec{\sigma}_{t}^{n + 1} ,\varvec{x}_{t}^{n + 1} } \right) > 0} \right)\), it means that the elastic solution needs a correction (Eq. 10-1 to 10-3). The yield function is solved by Newton–Raphson iterative method (Eq. 10-4).

$$\left\{ {\begin{array}{*{20}c} {\varvec{\varepsilon}_{n + 1}^{p} =\varvec{\varepsilon}_{n}^{p} + d\lambda}{\mathbf n} \\ {\varvec{x}^{n + 1} = \varvec{x}^{n} + \frac{2}{3}Cd\varvec{\varepsilon}_{p} - \gamma {\mathbf x^{n + 1}} dp} \\ {\varvec{\sigma}^{n + 1} = {\varvec{C}}:\left( {\varvec{\varepsilon}^{n + 1} -\varvec{\varepsilon}_{p}^{n + 1} } \right)} \\ {f\left( {\varvec{\sigma}^{n + 1} ,\varvec{x}^{n + 1} } \right) = 0} \\ \end{array} } \right.$$
(10)

where \(\varvec{n} = \frac{{\frac{{\partial f\left( {\varvec{\sigma},\varvec{x}} \right)}}{\partial \sigma }}}{{\left| {\frac{{\partial f\left( {\varvec{\sigma},\varvec{x}} \right)}}{{\partial\varvec{\sigma}}}} \right|}}\) and p is the accumulated plastic strain increment. The return mapping algorithm is summarized in Fig. 2.

Fig. 2
figure 2

Numerical flow chart

Full size image

3 FEM modeling

In order to compare and validate the used model, the combined bending and torsion (loading and unloading) of the thick tube is modeled by finite element method and springback of the tube is obtained. After mesh convergence study, 8521 elements of type C3D8 are used to model the combined loading. The mechanical properties of the used materials and tube, are given in Table 1. Outer and inner radius are 15 and 10 mm, respectively. One end of the tube is considered to be fixed in longitudinal and tangential direction. The loading consists of combined bending and torsion of the other tube end. Nonlinear kinematic hardening model is considered. Small deformation is considered and so the effect of the changing geometry is ignored.

Table 1 Used properties in numerical modeling by the present study and FEM simulations
Full size table

4 Results and discussion

4.1 Validation of the numerical method

In the first part, the loading consists of simultaneous bending and torsion of the tube. The mechanical properties in both methods are given in Table 1. The bending radius after full loading is 0.57 m and the torsion angle is 77°. Bending and torsion are applied according to Eqs. 1, 2 where n equals one. The equivalent von-Mises stress and plastic strain distribution in loading, obtained by the proposed numerical method, are illustrated Fig. 3a and b, respectively. These distributions after unloading are given in Fig. 4. Springback angles of bending and torsion is obtained by the present method and the FEM simulations. As it is shown in Fig. 5a and b, the numerical results of the present simple method are well compared with the FEM results. The difference between the FEM and the present model results are less than 4%.

Fig. 3
figure 3

a Equivalent stress and b plastic strain distribution after loading

Full size image
Fig. 4
figure 4

a Equivalent stress and b plastic strain distribution after unloading

Full size image
Fig. 5
figure 5

a Bending and b torsion springback angle as a function of bending radius

Full size image

The results of the simple numerical method are also compared with the experimental results of Wu et al. [20] in which the combined bending and torsion was carried out. They have measured the curvature during loading, ρ, and after unloading, ρf. The present model gives acceptable prediction of the curvature after unloading with respect to the results of Wu et al. [20]. They used isotropic hardening model (Fig. 6). The present numerical method ignores the radial stress during bending and torsion in contrast to the FEM simulations. As it can be seen in Fig. 6, this assumption leads to a good comparison of the present numerical method with respect to the FEM results (Fig. 5) experimental results of [20] (Fig. 6).

Fig. 6
figure 6

Comparison of the curvature before and after loading obtained by [20] and the present model

Full size image

4.2 Geometry effects on the combined loading springback

Geometry effect on the combined bending and torsion loading is also investigated. The thickness is considered to be constant and the outside diameter is varied from 30 to 38 mm. Figure 7 shows the variation of the springback angles as a function of the outside diameter. Increasing the outside diameter leads to the decrease of the bending and torsion springback angles.

Fig. 7
figure 7

Bending and torsion springback angles versus the outside diameter of the tube

Full size image

The effect of the thickness on the bending and torsion springback angles, is also studied. The thickness is varied from 4 to 8 mm by considering that the mean diameter constant as 25 mm. Both springback angles decrease with increasing the thickness of the tube.

4.3 Effect of loading application sequences

Combination of bending and torsion is carried out according to Eqs. 1 and 2. The plastic zone evolution is dependent on the exponent n. When the exponent is less than one and when it is greater than one, different evolution of the plastic zone happens. Two different exponents of ½ and 2 are considered.

This section examines the plasticity of the pipe section. Due to the different loading rates [the difference in the value of n in relation (2)], the plasticity of the tube section can occur in two ways. Below these two faces, the bounce back angle will be compared in each case. The first mode: the twist angle rate is greater than the bending curvature rate (n = 1/2). This mode is shown in Figs. 8, 9. The plasticity flow occurs at the outer radius and the plastic zone spreads toward the inner radius unsymmetrically because of the applied bending. When n increases to two, the bending is dominant and the plastic flow onsets from the top point. The plastic zone increases toward the horizontal axis when the applied bending and torsion increases. This mode is depicted in Fig. 10. These loading manners, influences the springback. Figure 11 compares the occurred springback after unloading. When n in Eq. 2 increases, bending becomes more important than torsion which causes that bending springback angles reduces. The behavior inverses for the torsion springback when n increases.

Fig. 8
figure 8

Variation of the springback angles of bending and torsion as a function of tube thickness

Full size image
Fig. 9
figure 9

Plastic zone and axial plastic strains evolution during combined loading when n = 1/2: a M/My = 0.227 and T/Ty = 1.06, b M/My = 0.262 and T/Ty = 1.117, c M/My = 0.313 and T/Ty = 1.163 and d M/My = 0.345 and T/Ty = 1.167

Full size image
Fig. 10
figure 10

Plastic zone and axial plastic strains evolution during combined loading when n = 2: a M/My = 1.208 and T/Ty = 0.04, b M/My = 1.461 and T/Ty = 0.09, c M/My = 1.721 and T/Ty = 0.316 and d M/My = 1.862 and T/Ty = 0.571

Full size image
Fig. 11
figure 11

a Bending and b torsion spring back angle variations for different loading conditions

Full size image

5 Conclusions

Return Mapping method was used to study the springback of thick-walled tubes under simultaneous loading of bending and twisting. Non-linear kinematic hardening model of Armstrong-Frederick has considered been used for previous studies. The bending and twist springback angels were calculated. Effect of the bending and torsion combination on the plastic flow and its distribution is discussed. It was shown that by changing the sequence and type of loading, plastic flow in the pipe changes and consequently, the bending and torsion springback angles vary. Springback angles under different loading paths are obtained and compared.

Even though, the present numerical method which is simple and ignores radial stress and anisotropy, gives acceptable prediction of the springback angles of bending and torsion. In our future research the effect of the anisotropy will be considered in the numerical model to better improve the springback predictions.