1 Introduction

NC machining simulation, which simulates and evaluates the actual NC machining process via computer graphics, has become an important step in modern manufacturing. By simulating the machining process prior to the actual cutting operation, inefficiency and errors in the tool path can be reduced and corrected at the programming stage. NC machining simulation technology contains two aspects: material removal process simulation and NC machining verification. The material removal process simulation realized via consecutive Boolean subtractions between the updated workpiece and the cutter swept volume is used to detect collisions and predict the final workpiece shape. NC machining verification algorithms are used to compare the geometrical differences between the simulated workpiece and the nominal part and to estimate whether the difference is within the allowable tolerance zone. NC machining simulation methods can be categorized into four major approaches according to the workpiece representation model, including the solid-based approach, object space-based approach, image space-based approach, and hybrid approach.

In the solid-based approach, the workpiece is represented by a constructive solid geometry (CSG) [1] or boundary representation (B-rep) model [2]. The material removal process is simulated by an explicit Boolean subtraction operation between the workpiece model and cutter swept volume [3], and verification is achieved by calculating the Boolean differences between the workpiece model and the nominal part. The solid-based approach can provide a precise and detailed geometric representation but requires heavy computational efforts[4], as the computation cost is reported to be O(n4) in the worst case using CSG and estimated to be O(n1.5) using the B-rep, where n is the number of cutter movements [2].

In the object space-based approach, the workpiece is approximately represented by a collection of basic geometric elements within the given accuracy. The object space-based approach can be further classified into the Z-map-based [5], vector-based [6], and voxel-based [7] approaches, where the workpiece is represented by three-dimensional (3D) histograms, surface points with vectors, and cubic cells, respectively. The object space-based approach suffers from the conflict between simulation accuracy and efficiency because the accuracy enhancement is inevitably accompanied by drastically increased computation time and memory consumption [8].

In the image space-based approach, the workpiece and cutter swept volume are represented by the depth pixel (called dexel) model. The material removal process simulation is performed in one-dimensional (1D) space by comparing the depth value of the pixels. Wang and Wang [9] were the first to apply the dexel model to real-time NC machining simulation. More recently, Sun et al. [10] applied the triple-dexel model, which contains the dexel information in the X, Y, and Z directions, to verify the effectiveness of the tool path in a 5-axis hybrid additive-subtractive manufacturing simulation. Since Boolean operations are performed in 1D space by comparing the depth value of the pixels, the image space-based approach is the fastest among all the simulation approaches. However, a true solid model of the updated workpiece is not directly available.

To take advantage of different workpiece representations, some studies adopted hybrid representations. Karunakaran and Shringi implemented an algorithm for converting the octree into B-rep [11] and applied the algorithm in their NC simulation system [12], where the workpiece is always stored as an octree model and the user can convert it into a B-rep for visual and dimensional verification. Yau and Tsou [13] used an octree-based voxel representation to save a significant amount of memory and constructed a triangular mesh from the voxel data to provide high-resolution and smooth displays. Lee and Nestler [14] adopted the triple-dexel model to represent the workpiece and then reconstructed a triangular mesh from the sampled data by recognizing the feature-sensitive geometries. In any case, those systems only provide approximate results for performance optimization.

The authors of this paper proposed an efficient STL model-based NC machining simulation approach [15], where both the workpiece and cutter swept volume are represented by STL models and the cutting process is simulated by performing consecutive Boolean subtractions between the two STL models. The STL model-based approach can generate an exact workpiece model, and the efficiency was improved by applying two spatial decomposition methods: workpiece division and background grid. In this work, the authors extended their previous work to investigate the NC machining verification approach by comparing the STL models of the machined workpiece and the nominal part, both of which are represented by a triangular mesh.

The rest of the paper is organized as follows. Some related work is briefly reviewed in Section 2. The details of the proposed algorithm for NC machining verification are described in Section 3. The experimental results of the algorithm accuracy and efficiency are discussed in Section 4. Finally, the conclusion is given in Section 5.

2 Related work

The core of NC machining verification is computing a distance measure between two geometric models, which is an important problem in diverse fields, including computer graphics, virtual environment, and geometric modeling. Various types of distance measures have been extensively investigated, and efficient algorithms have been proposed over the past two decades [16].

Metro [17] and MESH [18] are the earliest methods applied to evaluate the distance between two triangular meshes of similar shape by sampling each triangle of one mesh and computing the distance between each sample and the other mesh. However, no sampling analysis is provided, and triangles that have an area smaller than the sampling step are not sampled; thus, relevant details in the models’ shape are missed.

Tang et al. [16] presented a fast and simple algorithm to compute the Hausdorff distance between complicated polygonal models at interactive rates, and the computed distance is an approximation within a user-specified error bound. The algorithm was implemented by calculating tight upper and lower bounds for the exact Hausdorff distance value and then refining these bounds through polygon subdivision until the error bound was obtained. The algorithm is sensitive to the relative configuration of the objects, and its space complexity tends to infinity as the Hausdorff distance decreases.

Bartoň et al. [19] presented an exact algorithm for computing the precise Hausdorff distance between triangular meshes. The bisectors of the pairs of primitives (i.e., vertex, edge, or face) are analytically constructed and intersected with the other mesh, yielding a set of conic segments. For each conic segment, the distance functions to all of the primitives are constructed, and the maximum value of their low envelope function may correspond to a candidate point for the Hausdorff distance. Due to the high complexity, the worst-case time complexity was O (n4 log n) with a complete implementation.

Kang et al. presented an algorithm that computes the one-sided Hausdorff distance from a triangle mesh to a quad mesh using what is called “matching” and “upper bounding” of the candidate pieces [20]. Then, they completed the algorithm by computing the one-sided Hausdorff distance in the opposite direction: from the quad mesh to the triangle mesh [21]. Combining the two one-sided computational algorithms, the two-sided Hausdorff distance between the two meshes can be computed and used to evaluate a quad mesh approximation for a triangle mesh.

To realize the verification algorithm in the STL model-based NC machining, where both the machined workpiece and the nominal part are represented by a triangular mesh, we adopt some ideas used in Metro [17] and MESH [18] and make some improvements. First, the definition of the signed distance introduced in Metro [17] is adopted in this work because it can be used to evaluate whether the workpiece is undercut or overcut. Second, the sampling lattice used in MESH [18] is also adopted since it leads to significantly simpler computations of integrals over a surface. In addition, to avoid the loss of detail features, the three vertices of a triangle whose area is very small are treated as the sample points, so that each triangle in the STL model will be sampled and the computed distance will be more accurate.

3 The algorithm

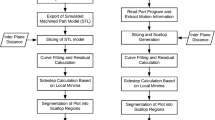
The overall algorithm for NC machining verification, as shown in Fig. 1, consists of three steps as follows:

  1. Step 1

    : Each triangle of the machined workpiece model is sampled under a user-defined sampling step.

  2. Step 2

    : The signed distance between each sample and the nominal part is computed, and thus, the maximal error, minimal error, and mean error between the two STL models are evaluated.

  3. Step 3

    : A 3D background grid is constructed to quickly search for the triangle closest to the sampling point, and therefore, the algorithm efficiency is improved.

Fig. 1
figure 1

The overall scheme of the NC machining verification algorithm

Full size image

3.1 Surface sampling

The first step of the algorithm is to sample each triangle of the machined workpiece model, which is achieved in the following way: two sides of the triangle are considered as the directions for the sampling lattice, as shown in Fig. 2. According to a given sampling step δ, each side is sampled with n points, and the number of samples in each triangle is n(n + 1)/2. The smaller the sampling step, the greater the number of sampling points there are in each triangle, so the algorithm results will be more accurate, but the algorithm efficiency will be lower.

Fig. 2
figure 2

Illustration of a sampling performed on triangles for n = 6

Full size image

Here, the sampling step δ is an important parameter that will affect the efficiency and accuracy of the algorithm. The relationships between efficiency and accuracy will be discussed in Section 4. Given the sampling step δ, n′ is defined as:

$$ n^{\prime }=\sqrt{\frac{1}{4}+\frac{2\left|{T}_1\right|}{\delta^2}}-\frac{1}{2} $$
(1)

where |T1| is the area of the triangle. In general, n′ is not an integer. The number n of samples on each triangle side is obtained by rounding n′ to an integer. If δ is relatively large and |T1| is relatively small, the computed n will be 0 or 1, which means that the triangle will not be sampled. For models with a large number of triangles, the proportion of these unsampled triangles is non-negligible, and thus, the accuracy of the algorithm results will be affected. Especially in the machined workpiece model, tiny triangles accumulate at the cusps between the tool paths, as shown in Fig. 3. If these tiny triangles are not sampled, the results of the NC machining verification algorithm are not accurate. To obtain accurate results, n will be set to 2 if the computed n is less than 2, which means that the three vertices of the triangle are taken as the samples when the triangle is too small to be sampled under the current sampling step δ.

Fig. 3
figure 3

An example of the cusp at the machined workpiece model

Full size image

The coordinates of the samples on each triangle are defined as:

$$ P\left(i,j\right)={P}_A+i\overset{\rightharpoonup }{e_1}+j\overset{\rightharpoonup }{e_2} $$
(2)

where 0 ≤ i ≤ n − 1, 0 ≤ j ≤ n − 1 − i, \( \overset{\rightharpoonup }{e_1}=\left({P}_B-{P}_A\right)/\left(n-1\right) \), and \( \overset{\rightharpoonup }{e_2}=\left({P}_C-{P}_A\right)/\left(n-1\right) \).

3.2 Error evaluation

After the triangles of the machined workpiece model are sampled, the signed distance between each sample and the nominal part can be defined as follows.

Given sample p of machined workpiece model S1 and triangle T2 of nominal part S2, the signed distance d(p, T2) between p and T2 is defined as:

$$ \left|d\left(p,{T}_2\right)\right|={\left\Vert p-{p}_{\mathrm{min}}\right\Vert}_2 $$
(3)

where pmin is the closest point in T2 to p and ‖‖2 denotes the usual Euclidean norm. The sign of d(p, T2) is measured by the sign of Np ∗ (pmin − p). If sample p is outside S2, the sign is positive; otherwise, the sign is negative.

The signed distance d(p, S2) between p and S2 is defined as:

$$ \left|d\left(p,{S}_2\right)\right|=\underset{T_2\in {S}_2}{\min}\left|d\left(p,{T}_2\right)\right| $$
(4)

The sign of d(p, S2) is defined as mentioned above. d(p, S2) can be used to represent the error value associated with each sample.

The signed distance defined in (4) can be used to define maximal error dmax(S1, S2), minimal error dmin(S1, S2), and mean error dmean(S1, S2) as follows.

$$ {d}_{\mathrm{max}}\left({S}_1,{S}_2\right)=\underset{p\in {S}_1}{\max }d\left(p,{S}_2\right) $$
(5)
$$ {d}_{\mathrm{min}}\left({S}_1,{S}_2\right)=\underset{p\in {S}_1}{\min }d\left(p,{S}_2\right) $$
(6)
$$ {d}_{\mathrm{mean}}\left({S}_1,{S}_2\right)=\frac{1}{\left|{S}_1\right|}\underset{p\in {S}_1}{\iint }d\left(p,{S}_2\right) dS $$
(7)

where |S1| is the total surface area of S1. Here, dmax(S1, S2) and dmin(S1, S2) can be used to detect the undercut and overcut, respectively, if they fall out of the allowable tolerance zone.

The computation of the integral defined in (7) is not too difficult thanks to the sampling lattice, as shown in Fig. 2. The integral of error defined in (7) is computed approximately by linear interpolation. Three samples of T1 ∈ S1, which are denoted as xi, j, xi + 1, j, and xi, j + 1, constitute a smaller triangle Ti, j. The integral of the error over Ti, j is denoted as:

$$ \left|{T}_{i,j}\right|\times \frac{e_{i,j}+{e}_{i+1,j}+{e}_{i,j+1}}{3} $$
(8)

where ei, j, ei + 1, j, and ei, j + 1 are the error values associated with xi, j, xi + 1, j, and xi, j + 1, respectively. Therefore, the integral of the error defined in (7) can be obtained by the summation of the integrals of the error over all the smaller triangles.

3.3 Background grid

The evaluation of the signed distances between each sample and the nominal part is very time-consuming if all the triangles of the nominal part are transversed. The background grid technique [22] can be used to quickly search for the triangle closest to the sampling point.

The construction of the background grid begins with the axis-aligned joint bounding box of S1 and S2, which is then decomposed into cubic cells of uniform size. For each cell, the cell-triangle intersection test can be efficiently computed by using the separating axis theorem [23], and the list of triangles of S2 intersecting with the cell is recorded.

For each sampling point p, the cell in which p is located is denoted by C. Dm(C) represents the set of cells that are at a distance m ∗ ∆d from C along with one of the coordinate axes, where ∆d is the side length of the cubic cells and m is the layer number of cells around C, as shown in Fig. 4. First, the distances from p to all the triangles intersecting C are calculated, and the minimum distance dmin is retained. Then, the adjacent cells in Dm(C) are processed by increasing the value of m, and dmin is updated accordingly until dmin is smaller than m ∗ ∆d.

Fig. 4
figure 4

An example of a 3D uniform grid represented in two dimensions

Full size image

As shown in Fig. 5, the sample is located in cell C, and the minimum distance from the sample to the triangles intersecting with C is dis1, which is assigned to the current dmin. Then, the first layer of cells D1(C) around C is traversed, and the blue cell shown in Fig. 5 is a cell of D1(C). The minimum distance from the sample to the triangles intersecting with D1(C) is dis2. Since dis2 is smaller than dis1, the current dmin is updated as dis2. Furthermore, as the current dmin is smaller than 1 ∗ ∆d, the second layer of cells D2(C) around C does not need to be traversed. Therefore, the minimum distance from the sample to the nominal part is determined and equals dis2.

Fig. 5
figure 5

An example of the minimum distance update

Full size image

Here, ∆d is an important parameter for constructing the background grid to improve algorithm efficiency. It should be chosen carefully so that the increase in speed gained by using uniform cells is in equilibrium with the overhead of handling them. Empirically, the side length of an average triangle, which is an equilateral triangle that has an area equal to the average triangle area of S2, is a reasonable value in most cases.

4 Results and discussion

The proposed algorithm has been implemented in Unity 3D coded with C# as a verification module for the NC machining simulation system. The verification module runs on a personal computer with an Intel(R) Core(TM) i7-10710U CPU 1.10 GHz with 16.00-GB memory. In our previous work, the NC simulation of the core block of an injection mold was carried out for performance evaluation, and the resulting roughing model, semifinishing model, and finishing model are used here to evaluate the NC machining verification algorithm. The approximate accuracy of the nominal STL model is 0.08 mm.

The influence of different sampling schemes on the accuracy of the NC machining verification algorithm is investigated and compared. Sampling scheme I represents all the triangles that are sampled, while sampling scheme II represents the tiny triangles that are not sampled because of the given sampling step. The maximal error, minimal error, and mean error as functions of sampling step δ in sampling scheme I applied to the roughing model, semifinishing model, and finishing model, as shown in Figs. 6a, 7a, and 8a, respectively, remain stable, while they change with sampling step δ in sampling scheme II, as shown in Figs. 6b, 7b, and 8b. It can be concluded that in scheme II, the algorithm accuracy is sensitive to sampling step δ, whereas the scheme I is not. This means that in scheme II, a small sampling step δ should be selected to improve the algorithm accuracy, but the computation time will be increased.

Fig. 6
figure 6

Comparison of the error and time with respect to different sampling schemes of the roughing model. a Sampling scheme I. b Sampling scheme II

Full size image
Fig. 7
figure 7

Comparison of the error and time with respect to different sampling schemes of the semifinishing model. a Sampling scheme I. b Sampling scheme II

Full size image
Fig. 8
figure 8

Comparison of the error and time with respect to the different sampling schemes of the finishing model. a Sampling scheme I. b Sampling scheme II

Full size image

Although the maximal error and minimal error are the same in both sampling schemes I and II when sampling step δ is 0.1%, the differences in the mean error are approximately 2.39%, 14.04%, and 29.03% in the roughing model, semifinishing model, and finishing model, respectively, as the numbers of unsampled triangles in sampling scheme II are 108,385 (50.45% of total), 323,307 (68.71% of total), and 1,044,904 (84.31% of total), respectively, as shown in Table 1. It should be pointed out that the number of unsampled triangles will increase as sampling step δ increases in sampling scheme II, which results in an inaccurate maximal error, minimal error, and mean error. Therefore, it can be concluded that the maximal error, minimal error, and mean error computed by sampling scheme II are not as accurate as those of sampling scheme I under the same sampling step δ.

Table 1 Comparison of the sampling schemes I and II (δ = 0.1%)
Full size table

The influence of different sampling step δ on the efficiency of the NC machining verification algorithm is also investigated. The time needed to perform the algorithm first decreases remarkably as sampling step δ increases and then remains almost stable when δ is either 0.5% or 0.6% in sampling schemes I or II, as shown in Figs. 6, 7, and 8. It seems that both the accuracy and efficiency of the NC machining verification algorithm are optimal when sampling scheme I is adopted and the sampling step δ is set to 0.6% of the bounding box diagonal.

The error visualization is given by coloring the machined workpiece model according to the signed distance associated with each sample; therefore, the distribution of the error on the model can be observed clearly. The error visualization of the roughing model, semifinishing model, and finishing model in sampling scheme I with sampling step δ set to 0.1% are shown in Figs. 9, 10, and 11, respectively. In the error visualization, zero error, positive error, and negative error are represented by green, red, and blue, respectively. In other words, the machined workpiece has as much material as the nominal part in the green area, more material in the red area, and less material in the blue area. Therefore, the undercut and overcut areas can be easily detected in the sampling scheme I by error visualization if the error value falls out of the allowable tolerance zone. However, the undercut and overcut areas cannot be accurately detected in sampling scheme II because a non-negligible proportion of the very small triangles that accumulate at the cusps and gouges are not sampled.

Fig. 9
figure 9

Error visualization of the roughing model (sampling scheme I, δ = 0.1%)

Full size image
Fig. 10
figure 10

Error visualization of the semifinishing model (sampling scheme I, δ = 0.1%)

Full size image
Fig. 11
figure 11

Error visualization of the finishing model (sampling scheme I, δ = 0.1%)

Full size image

Based on the above analysis, sampling scheme I is superior to sampling scheme II for three reasons: (1) the algorithm accuracy of sampling scheme I is robust to the sampling step δ while that of sampling scheme II is sensitive; (2) the maximal error, minimal error, and mean error computed by sampling scheme II are not as accurate as those of sampling scheme I under the same sampling step; (3) the undercut and overcut areas can be accurately detected by error visualization in sampling scheme I, but they cannot be completely detected by error visualization in sampling scheme II. Therefore, the improvement we made based on MESH [18] to sample all the triangles, including the very small triangles, is necessary and reasonable.

The worst-case computational complexity of the proposed algorithm depends on the sample number ns of the machined model S1 and the triangle number nt of the nominal part S2, and the resulting complexity is O(ns ∗ nt). In sampling scheme I, when the sampling step δ is 0.1%, the number of triangles tested to compute the minimal distance for each sample is 17,062 without applying the background grid; otherwise, only a few dozen of triangles are tested, as shown in Table 2. The ratios of the tested triangle numbers in these two cases are 302, 310, and 199 for the roughing model, semifinishing model, and finishing model, respectively, which means that the number of calculations of the signed distance for each sample can be reduced hundreds of times by applying the background grid. Therefore, the efficiency of the proposed algorithm is improved significantly.

Table 2 Efficiency improvement by applying the background grid (sampling scheme I, δ = 0.1%)
Full size table

5 Conclusion

The existing algorithms for evaluating the difference between two triangular meshes of similar shape are improved and applied for STL model-based NC machining verification, which consists of three steps: surface sampling, error evaluation, and background grid construction. In the improved algorithm, all the triangles including those that are too small to be sampled under the current sampling step δ are sampled to improve the verification accuracy; the signed distances are used to detect the undercut and overcut of the machined workpiece; and the background grid is applied to reduce the number of calculations of the signed distance for each sample. The experimental results demonstrate the accuracy and efficiency of the proposed NC machining verification algorithm based on STL models.