1 Introduction

Organizations are increasingly interested in producing high-quality products that meet customers’ requirements. Defects generated during the production processes may significantly impact on the final product, both in terms of quality and cost. In this view, designing inspection strategies affordable and effective in detecting defects occurring in the different production phases has always been a challenging issue for manufactures [1,2,3,4,5]. A considerable amount of scientific literature has deeply focused on defects generated in assembly processes [6,7,8,9,10,11,12,13]. Existing research recognizes the critical role played by operators in causing defects during assembly processes [6, 9, 12, 14,15,16,17,18]. It has previously been observed that human-induced defects in assembly process can be predicted using assembly complexity. For instance, Hinckley [17, 18] correlated defects per unit (DPU) with a process-based complexity factor, which included the total assembly time and the number of assembly operations. Shibata [14, 19] detailed the model proposed by Hinckley by subdividing the product assembly process into a series of workstations and, besides, by introducing a design-based assembly complexity factor. In line with the research carried out by Hinckley and Shibata in the field of semiconductor products, Su et al. [12] developed a new mathematical model of defects generation to match the characteristics of copier assembly. Antani [20] successfully tested the hypothesis that manufacturing complexity, which incorporates variables driven by design, process and human-factors, could reliably predict product quality in mixed-model automotive assembly. Krugh et al. [6, 9] adapted the predictive model methodology proposed by Antani for use with automotive electromechanical connections in a large complex system. Falck et al. [10] proposed a method for predictive assessment of basic manual assembly complexity by developing a tool to predict and control operator-induced quality errors.

In recent studies, the aforementioned models for defect prediction have been exploited for obtaining reliable estimates of defect occurrence probabilities in single-unit and low-volume productions. The most distinctive characteristic of such productions, although they may also be long-term lasting, is the low production rate and the high level of complexity and customization. For that reason, traditional statistical process control (SPC) techniques are often not appropriate [1, 11, 21,22,23,24]. These probabilities, together with several parameters related to inspection effectiveness and cost, are combined into a probabilistic model. Accordingly, two indicators depicting the overall inspection effectiveness and cost are derived in order to select the most effective and economically convenient inspection strategies.

Despite the importance of the issues relating to quality control in manufacturing processes, few studies proposed suitable models to plan quality inspections under uncertainty (see e.g. [24,25,26]). More in detail, no previous study investigated the combined use of the models of defects generation and the quality inspection indicators with the related uncertainty to plan effective and affordable inspection strategies. This paper aims to extend the analysis carried out by the authors in previous works [1, 2, 11, 27] by proposing a methodology to evaluate the uncertainty of defectiveness predictions and costs in quality inspection of low-volume assembly manufacturing processes. The paper focuses the attention on the following two research questions:

  • RQ1: Considering a low-volume production, how can the uncertainty of models for defectiveness and cost predictions be assessed?

  • RQ2: How does this uncertainty affect the selection of the most effective and affordable inspection strategy?

Starting from previous models for defects and costs predictions in assembly processes for low-volume productions, this study introduces a new methodology to evaluate the uncertainty of each statistical model by applying the law of combination of variances [28, 29]. Accordingly, the uncertainty is propagated to two inspection indicators which depict the overall effectiveness and cost of an inspection strategy. In order to test the proposed methodology, a case study concerning the assembly of mechanical components in the manufacturing of hardness testing machines is analyzed. The method allows to compare, with the required level of confidence, alternative inspection strategies, basing on the residual defectiveness after quality controls and the relating overall cost.

The remainder of the paper is organized into four sections. Section 2 illustrates some models of defects generation and the concept of inspection effectiveness and related cost. Section 3 presents a methodology to estimate the variability of the parameters of the defect generation models and the inspection strategy. Section 4 proposes a structured case study, concerning the application of the methodology in the low-volume production of hardness testing machines. Section 5 summarizes the contributions of this research, including its possible limitations.

2 Defect generation and inspection models

2.1 Review of defect prediction models in assembly

In this section, a short review of the most diffused defect prediction models developed for assembly processes is presented. Such models, recently analyzed and compared in the study of Galetto et al. [27], have been successfully exploited in the scientific literature to design and manage assembly complexity (see e.g. [30,31,32]).

In the assembly of semiconductors, Hinckley showed that the occurrence of defects could be predicted using the complexity of the assembly process [17, 18]. Specifically, he found empirically that the defects per unit (DPU) were positively correlated with the total assembly time and negatively correlated with the number of assembly operations.

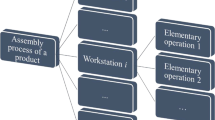
In later studies, Shibata [14, 19] applied Hinckley’s model to the assembly of Sony® home audio products, by introducing the decomposition of the product assembly process into a series of steps or workstations [12], in which a certain number of job elements (elementary operations) are performed. In order to predict the DPU in each workstation, he defined as predictors the process-based and the design-based complexity factors related to each workstation. The first predictor, similar to the complexity factor defined by Hinckley, is positively correlated with the workstation total assembly time and negatively correlated with the number of job elements in the workstation (see Eq. (2) [14]). The second predictor is based on the evaluation score from the Design for Assembly Cost-Effectiveness (DAC) method, developed by Sony Corporation [19, 33]. The two predictors were combined in a bivariate prediction model following a power-law relationship (see Eq. (1)).

According to the unsatisfactory result obtained by applying Shibata’s model to copier assembly, Su et al. [12] redesigned the approach to better adapt to the characteristics of copiers [12]. Specifically, a new process-based complexity factor was formulated by considering Fuji Xerox Standard Time instead of Sony Standard Time and by integrating the time variation [12]. The design-based complexity factor was redesigned by combining Ben-Arieh’s method [34] with the analytic hierarchy process (AHP) approach [35] (see Eq. (3)).

2.2 Model for defectiveness prediction

In this paper, the adopted defect generation model, reported in Eq. (1), is based on the abovementioned studies proposed by Shibata [14], Su et al. [12] and Galetto et al. [27].

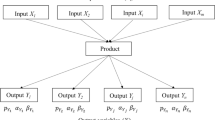
According to Shibata [14], the assembly process can be subdivided into a series (m) of manufacturing operations, later called “workstations” by Su et al. [12], defined through sheets of operation standard. Each workstation can be divided into a certain number (Na,i) of “job elements” [36], i.e. elementary operations, characterized by definite start and end points [14], as schematized in Fig. 1.

$$ DP{U}_i={k}_3\cdotp C{f}_{P,i}^{k_1}\cdotp C{f}_{D,i}^{k_2} $$
(1)
Fig. 1
figure 1

Schematic representation of the assembly process of a product, according to Shibata [14] and Su et al. [12]

Full size image

In Eq. (1), DPUi represents the defects per product unit occurring in each workstation i, which falls between 1 and m, i.e. the total number of workstations; CfP,i and CfD,i are the two predictors of the defect model, respectively the process-based complexity factor (see Eq. (2)) and the design-based complexity factor (see Eq. (3)) of a generic workstation i; k1, k2, and k3 are three regression coefficients that may be obtained by a power-law nonlinear regression [27].

The process-based complexity factor of a generic workstation i, CfP,i, is defined as follows [14]:

$$ C{f}_{P,i}=\sum \limits_{j=1}^{N{a}_i} SS{T}_{ij}-{t}_0\cdotp {N}_{a,i}= TA{T}_i-{t}_0\cdotp {N}_{a,i} $$
(2)

where Na,i is the number of job elements in the workstation i, SSTij is the time spent on job element j in the workstation i, TATi is the total assembly time relevant to the workstation i, and t0 is the threshold assembly time, i.e. the time required for performing the least complex assembly operation. Further information about the Sony Standard Time (SST) is provided by Shibata [14] and Aft [36].

The design-based complexity factor, CfD,i, was introduced by Su et al. [12] in addition to the previously mentioned CfP,i for predicting defects in each workstation. This factor is evaluated using specific geometrical and non-geometrical parameters, which are selected according to the characteristics of the products to be assembled [34]. For instance, the parameters used to describe the design complexity of an electromechanical product are, in detail, components shape, required forces, coupling directions, components alignment, components size, components geometry, ratio between components size and geometry, components play, worktable stability, equipment requirements and electrical disturbances. These parameters will also be used in the case study presented in Section 4. When dealing with electromechanical products, the design-based complexity factor may be defined as follows [11, 12]:

$$ C{f}_{D,i}=\sum \limits_{q=1}^l\left({w}_q\cdotp \frac{1}{e}\cdotp \sum \limits_{k=1}^e{A}_{kqi}\right) $$
(3)

where q falls between 1 and l, i.e. the total number of parameters selected as criteria for evaluating the design-based assembly complexity; wq is the weight of the parameter q allocated on a scale between 0 and 1 using the analytic hierarchy process (AHP) approach [37]; e is the number of evaluators involved in the comparison of the relative importance of each parameter to determine the difficulty of putting a part into a product; the degree of difficulty Akqi is the evaluation of the parameter q in the workstation i estimated by the evaluator k (it is a score between 0 and 10).

The probability of occurrence of at least one defect in each workstation i (pi) may be estimated as the fraction of nonconforming units in the workstation i [22]. Accordingly, pi may be calculated by exploiting the defect rates obtained using Eq. (1) and the number of job elements in the relative workstation, as shown in Eq. (4) [11]:

$$ {p}_i=1-{\left(1-\frac{DP{U}_i}{N_{a,i}}\right)}^{N_{a,i}} $$
(4)

It should be remarked that Eq. (4) is obtained under the assumptions that (i) each job element may introduce at most one defect, and (ii) for each workstation i, the probability of occurrence of a defect is the same for each job element [11, 17].

2.3 Modelling of inspection effectiveness and costs

The conformity of each workstation-output can be checked using different inspection strategies, depending on the type of defect to be detected. For instance, dimensional verification, visual check or comparison with reference exemplars may be adopted [3, 38, 39]. Accordingly, different inspection strategies may be defined [11, 40, 41].

Each ith workstation of the assembly process may be modelled by a Bernoulli distribution [22]. Accordingly, it can be described by the following three probabilities:

  • pi: probability of occurrence of a defective-workstation-output (which is estimated as the fraction of nonconforming units in the workstation i);

  • αi: probability of erroneously signalling a defective-workstation-output (i.e. type-I inspection error);

  • βi: probability of erroneously not signalling a defective-workstation-output (i.e. type-II inspection error)

where i=1, …, m, i.e. the total number of workstations.

The first probability, pi, concerns the defectiveness and, therefore, the quality of the ith workstation. It may be estimated, as a first approximation, by using Eq. (4). Inspection errors, αi and βi, concern the quality of the inspection and are strictly related to the characteristics of the inspection activity and the technical skills and experience of the inspector. They may be estimated based on prior experience, e.g. by using empirical values obtained in similar processes, or simulations [42,43,44,45].

According to previous studies, inspection effectiveness may be represented using a practical indicator defining the mean total number of defective-workstation-outputs which are erroneously not detected in the overall inspection strategy [1, 11]. According to Franceschini et al. [1], the inspection effectiveness indicator, D, is defined as follows:

$$ D=\sum \limits_{i=1}^mE\left({X}_i\right)=\sum \limits_{i=1}^m{p}_i\cdotp {\beta}_i $$
(5)

where Xi is a Bernoulli random variable equal to zero when either a defective-workstation-output is correctly signalled or no defect is present in the ith workstation, and equal to one when a defective-workstation-output is erroneously not signalled in the ith workstation.

It is worth remarking that the indicator D is obtained under both the following assumptions: the occurrence of defects and that of inspection errors are uncorrelated, and the parameters related to different workstations are uncorrelated.

In order to provide a more general overview of the inspection design, an inspection cost indicator aimed at evaluating the economic effects of inspection design should also be considered [3, 44, 46]. Franceschini et al. [1] proposed in a previous work an indicator depicting the total cost of the inspection strategy. It included the cost of the specific inspection activity, the necessary- and the unnecessary-repair costs, and the cost of undetected defects, as shown in Eq. (6):

$$ {C}_{tot}=\sum \limits_{i=1}^m{C}_{tot,i}=\sum \limits_{i=1}^m\left[{c}_i+ NR{C}_i\cdotp {p}_i\cdotp \left(1-{\beta}_i\right)+ UR{C}_i\cdotp \left(1-{p}_i\right)\cdotp {\alpha}_i+ ND{C}_i\cdotp {p}_i\cdotp {\beta}_i\right] $$
(6)

where:

  • ci is the cost of the ith inspection activity (e.g. manual or automatic inspection activities);

  • NRCi is the necessary-repair cost, i.e. the necessary cost for removing the defective-workstation-outputs;

  • URCi is the unnecessary-repair cost, i.e. the cost incurred when identifying false defective-workstation-outputs, e.g. despite there is no cost required for defective-workstation-outputs removal, the overall process can be slowed down, with a consequent extra cost.

  • NDCi is the cost of undetected defective-workstation-outputs, i.e. the cost related to the missing detection of defective-workstation-outputs.

Apart from the estimate of the probabilities pi, αi and βi, the calculation of the total cost requires the estimate of additional cost parameters. In general, ci and NRCi are known costs, URCi is likely to be relatively easy to estimate, while NDCi is difficult to estimate since it may depend on difficult-to-quantify factors, such as image loss and after-sales repair cost [23].

The indicator Ctot provides a preliminary indication of the total cost related to the inspection strategy in use. In this sense, it can be used as a proxy for economic convenience of an inspection strategy.

3 Uncertainty evaluation

In order to assess the reliability of the estimates of the defect probabilities, pi, and of the two indicators of inspection effectiveness and costs, D and Ctot, a quantitative indication of the variability of the prediction should be provided. To this aim, a procedure for characterizing the variability of predictions based on the evaluation of the uncertainty is proposed. The methodology proposed relies on the GUM (guide to the expression of uncertainty in measurement) [29], according to which the uncertainties of the model variables are obtained by applying the usual method for the combination of variances [28, 29].

3.1 Uncertainty evaluation of models for defectiveness prediction

The defects per unit in the ith workstation, DPUi, and the probability of occurrence of the ith defective-workstation-output, pi, are two random variables. Their mean values are estimated by Eqs. (1) and (4) reported in Section 2. In addition, being DPUi and pi statistical variables, their variability can be related to the variability of the other model parameters.

Let us assume that the uncertainty of the model parameters in terms of variance is known. Accordingly, the variances of both DPUi and pi may be estimated by applying the law of combination of variances [28].

As far as the variance of DPUi is concerned, it can be derived by combining the variances of the parameters k1, k2 and k3, for predefined values of CfP,i and CfD,i, as reported in matrix form in Eq. (7):

$$ VAR\left( DP{U}_i\right)\approx {\left[\begin{array}{c}\frac{\partial DP{U}_i}{\partial {k}_3}\\ {}\frac{\partial DP{U}_i}{\partial {k}_1}\\ {}\frac{\partial DP{U}_i}{\partial {k}_2}\end{array}\right]}^{\mathrm{T}}\cdotp \left[\begin{array}{ccc} VAR\left({k}_3\right)& \operatorname{cov}\left({k}_3,{k}_2\right)& \operatorname{cov}\left({k}_3,{k}_1\right)\\ {}\operatorname{cov}\left({k}_3,{k}_2\right)& VAR\left({k}_2\right)& \operatorname{cov}\left({k}_2,{k}_1\right)\\ {}\operatorname{cov}\left({k}_3,{k}_1\right)& \operatorname{cov}\left({k}_2,{k}_1\right)& VAR\left({k}_1\right)\end{array}\right]\cdotp \left[\begin{array}{c}\frac{\partial DP{U}_i}{\partial {k}_3}\\ {}\frac{\partial DP{U}_i}{\partial {k}_1}\\ {}\frac{\partial DP{U}_i}{\partial {k}_2}\end{array}\right] $$
(7)

The partial derivatives in Eq. (7) are evaluated at the mean values of the input parameters (i.e.\( {k}_1^{\ast } \), \( {k}_2^{\ast } \),\( {k}_3^{\ast } \)). Therefore, Eq. (7) becomes:

$$ VAR\left( DP{U}_i\right)\approx {\left[\begin{array}{c}C{f}_{P,i}^{k_1^{\ast }}\cdotp C{f}_{D,i}^{k_2^{\ast }}\\ {}{k}_3^{\ast}\cdotp C{f}_{D,i}^{k_2^{\ast }}\cdotp C{f}_{P,i}^{k_1^{\ast }}\ln \left(C{f}_{P,i}\right)\\ {}{k}_3^{\ast}\cdotp C{f}_{P,i}^{k_1^{\ast }}\cdotp C{f}_{D,i}^{k_2^{\ast }}\ln \left(C{f}_{D,i}\right)\end{array}\right]}^{\mathrm{T}}\cdotp \left[\begin{array}{ccc} VAR\left({k}_3\right)& \operatorname{cov}\left({k}_3,{k}_2\right)& \operatorname{cov}\left({k}_3,{k}_1\right)\\ {}\operatorname{cov}\left({k}_3,{k}_2\right)& VAR\left({k}_2\right)& \operatorname{cov}\left({k}_2,{k}_1\right)\\ {}\operatorname{cov}\left({k}_3,{k}_1\right)& \operatorname{cov}\left({k}_2,{k}_1\right)& VAR\left({k}_1\right)\end{array}\right]\cdotp \left[\begin{array}{c}C{f}_{P,i}^{k_1^{\ast }}\cdotp C{f}_{D,i}^{k_2^{\ast }}\\ {}{k}_3^{\ast}\cdotp C{f}_{D,i}^{k_2^{\ast }}\cdotp C{f}_{P,i}^{k_1^{\ast }}\ln \left(C{f}_{P,i}\right)\\ {}{k}_3^{\ast}\cdotp C{f}_{P,i}^{k_1^{\ast }}\cdotp C{f}_{D,i}^{k_2^{\ast }}\ln \left(C{f}_{D,i}\right)\end{array}\right] $$
(8)

The variance-covariance matrix reported in Eqs. (7) and (8) may be derived by applying Eq. (9) [47]:

$$ \left[\begin{array}{ccc} VAR\left({k}_3\right)& \operatorname{cov}\left({k}_3,{k}_2\right)& \operatorname{cov}\left({k}_3,{k}_1\right)\\ {}\operatorname{cov}\left({k}_3,{k}_2\right)& VAR\left({k}_2\right)& \operatorname{cov}\left({k}_2,{k}_1\right)\\ {}\operatorname{cov}\left({k}_3,{k}_1\right)& \operatorname{cov}\left({k}_2,{k}_1\right)& VAR\left({k}_1\right)\end{array}\right]=\left[\begin{array}{ccc} VAR\left({k}_3\right)& {\rho}_{k_3,{k}_2}\cdotp \sqrt{VAR\left({k}_3\right)\cdotp}\sqrt{VAR\left({k}_2\right)}& {\rho}_{k_3,{k}_1}\cdotp \sqrt{VAR\left({k}_3\right)\cdotp}\sqrt{VAR\left({k}_1\right)}\\ {}{\rho}_{k_3,{k}_2}\cdotp \sqrt{VAR\left({k}_3\right)\cdotp}\sqrt{VAR\left({k}_2\right)}& VAR\left({k}_2\right)& {\rho}_{k_2,{k}_1}\cdotp \sqrt{VAR\left({k}_2\right)\cdotp}\sqrt{VAR\left({k}_1\right)}\\ {}{\rho}_{k_3,{k}_1}\cdotp \sqrt{VAR\left({k}_3\right)\cdotp}\sqrt{VAR\left({k}_1\right)}& {\rho}_{k_2,{k}_1}\cdotp \sqrt{VAR\left({k}_2\right)\cdotp}\sqrt{VAR\left({k}_1\right)}& VAR\left({k}_1\right)\end{array}\right] $$
(9)

where \( {\rho}_{k_3,{k}_1} \) is the correlation coefficient between k3 and k1, \( {\rho}_{k_3,{k}_2} \) is the correlation coefficient between k3 and k2, and \( {\rho}_{k_2,{k}_1} \) is the correlation coefficient between k2 and k1.

Similarly, the variance of the probability of occurrence of the ith defective-workstation-output may be calculated by applying the law of combination of variances to Eq. (4), as follows [28]:

$$ VAR\left({p}_i\right)\approx {\left(\frac{\partial {p}_i}{\partial DP{U}_i}\right)}^2\cdotp VAR\left( DP{U}_i\right) $$
(10)

where the partial derivative, \( \frac{\partial {p}_i}{\partial DP{U}_i} \), is evaluated at the mean value of the input parameter \( \left( DP{U}_i^{\ast}\right) \). Therefore, it results:

$$ VAR\left({p}_i\right)\approx {\left(1-\frac{DP{U}_i^{\ast }}{N_{a,i}}\right)}^{2\cdotp \left({N}_{a,i}-1\right)}\cdotp VAR\left( DP{U}_i\right) $$
(11)

In Eq. (11), the variance of DPUi may be calculated using Eq. (8).

3.2 Uncertainty evaluation of inspection effectiveness and costs

Once the variance of pi is obtained, the same reasoning may be applied to the indicator of inspection effectiveness shown in Eq. (5). Specifically, in the hypothesis of the absence of correlations between defects originated in different workstations and between defects and inspection, as mentioned in Section 2.2, the variance of D may be derived as reported in Eq. (12).

$$ VAR(D)= VAR\left(\sum \limits_{i=1}^mE\left({X}_i\right)\right)=\sum \limits_{i=1}^m VAR\left[E\left({X}_i\right)\right]=\sum \limits_{i=1}^m VAR\left({p}_i\cdotp {\beta}_i\right) $$
(12)

As a result, Eq. (13) is obtained:

$$ VAR(D)\approx \sum \limits_{i=1}^m\left[{\left[\begin{array}{c}\frac{\partial E\left({X}_i\right)}{\partial {p}_i}\\ {}\frac{\partial E\left({X}_i\right)}{\partial {\beta}_i}\end{array}\right]}^{\mathrm{T}}\cdotp \left[\begin{array}{cc} VAR\left({p}_i\right)& 0\\ {}0& VAR\left({\beta}_i\right)\end{array}\right]\cdotp \left[\begin{array}{c}\frac{\partial E\left({X}_i\right)}{\partial {p}_i}\\ {}\frac{\partial E\left({X}_i\right)}{\partial {\beta}_i}\end{array}\right]\right] $$
(13)

The partial derivatives in Eq. (13), i.e. \( \frac{\partial E\left({X}_i\right)}{\partial {p}_i} \) and \( \frac{\partial E\left({X}_i\right)}{\partial {\beta}_i} \), are evaluated at the mean values of the input parameters (\( {p}_i^{\ast } \) and \( {\beta}_i^{\ast } \)). Accordingly, Eq. (14) is derived:

$$ VAR(D)\approx \sum \limits_{i=1}^m\left[{\beta}_i^{\ast 2}\cdotp VAR\left({p}_i\right)+{p}_i^{\ast 2}\cdotp VAR\left({\beta}_i\right)\right] $$
(14)

where the variance of pi may be calculated using Eq. (11).

As can be seen from Eq. (14), the variance of D is the sum of the variances of the parameters pi and βi, weighted respectively by the squares of \( {\beta}_i^{\ast } \) and \( {p}_i^{\ast } \). It should be noticed that the effect of relatively higher variances of pi can be compensated by relatively lower βi values, and vice versa.

With respect to Ctot (see Eq. (6)), the relevant variance may be expressed as:

$$ VAR\left({C}_{tot}\right)= VAR\left(\sum \limits_{i=1}^m VAR\left({C}_{tot,i}\right)\right) $$
(15)

again in the hypothesis of absence of correlations. From Eq. (15), it is possible to obtain:

$$ VAR\left({C}_{tot}\right)\approx \sum \limits_{i=1}^m{\left[\begin{array}{c}\frac{\partial {C}_{tot,i}}{\partial {p}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial {\alpha}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial {\beta}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial {c}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial NR{C}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial UR{C}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial ND{C}_i}\end{array}\right]}^{\mathrm{T}}\cdotp \left[\begin{array}{ccccccc} VAR\left({p}_i\right)& 0& 0& 0& 0& 0& 0\\ {}0& VAR\left({\alpha}_i\right)& 0& 0& 0& 0& 0\\ {}0& 0& VAR\left({\beta}_i\right)& 0& 0& 0& 0\\ {}0& 0& 0& VAR\left({c}_i\right)& 0& 0& 0\\ {}0& 0& 0& 0& VAR\left( NR{C}_i\right)& 0& 0\\ {}0& 0& 0& 0& 0& VAR\left( UR{C}_i\right)& 0\\ {}0& 0& 0& 0& 0& 0& VAR\left( ND{C}_i\right)\end{array}\right]\cdotp \left[\begin{array}{c}\frac{\partial {C}_{tot,i}}{\partial {p}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial {\alpha}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial {\beta}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial {c}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial NR{C}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial UR{C}_i}\\ {}\frac{\partial {C}_{tot,i}}{\partial ND{C}_i}\end{array}\right] $$
(16)

where the derivatives are once more evaluated at the mean values of the parameters. Therefore, it results:

$$ {\displaystyle \begin{array}{c} VAR\left({C}_{tot}\right)\approx \sum \limits_{i=1}^m\left[{\left( NR{C}_i- NR{C}_i\cdotp {\beta}_i- UR{C}_i\cdotp {\alpha}_i+ ND{C}_i\cdotp {\beta}_i\right)}^2\cdotp VAR\left({p}_i\right)+\right.\\ {}+{\left( UR{C}_i- UR{C}_i\cdotp {p}_i\right)}^2\cdotp VAR\left({\alpha}_i\right)+{\left(- NR{C}_i\cdotp {p}_i+ ND{C}_i\cdotp {p}_i\right)}^2\cdotp VAR\left({\beta}_i\right)+ VAR\left({c}_i\right)+\\ {}+{\left({p}_i-{p}_i\cdotp {\beta}_i\right)}^2\cdotp VAR\left( NR{C}_i\right)\left.+{\left({\alpha}_i-{p}_i\cdotp {\alpha}_i\right)}^2\cdotp VAR\left( UR{C}_i\right)+{\left({p}_i\cdotp {\beta}_i\right)}^2\cdotp VAR\left( ND{C}_i\right)\right]\end{array}} $$
(17)

where the variance of pi can be once more calculated using Eq. (11).

According to Eq. (17), the variance of Ctot is a sum of the variances of the input parameters, weighted by polynomial combinations of pi, αi, βi, NRCi, URCi and NDCi. It can be noticed that the weights of the variances of the probability parameters (pi, αi and βi) depend on both probability and cost parameters, while the weights of the variances of the cost parameters (ci, NRCi, URCi and NDCi) only depend on probability parameters.

4 Case study

4.1 Modelling of the assembly process of hardness testing machines

In this section, the proposed methodology aimed at evaluating the uncertainty of models for defectiveness prediction and inspection effectiveness and cost is applied to a case study concerning the assembly processes of a hardness testing machine, specifically AFFRI® LD 3000 AF. Since the production of these mechanical components is only of some tens per year, the examined manufacturing process may be considered a low-volume production. As far as the modelling of the production process is concerned, the overall assembly of hardness testers can be subdivided into nine phases. These are in detail (1) threaded shaft, (2) machine working axis, (3) axis movement mechanism, (4) machine head, (5) reference plan movement device, (6) measurement device unit, (7) machine processing unit, (8) machine electrical system, (9) final assembly.

This paper focuses on the overall assembly of the machine head, which corresponds to the first four assembly phases previously mentioned. Each of these four phases may be subdivided into different workstations, as represented in Fig. 2. Besides, the adopted inspection strategy requires each workstation-output to be inspected by performing a quality control activity. Different types of performed controls may be adopted, according to the specific type of defect to be detected. In particular, the inspections may be geometric, mechanical, dimensional or a combination of them (see Fig. 2).

Fig. 2
figure 2

Schematic representation of the workstations of the overall assembly of machine head, subdivided into four assembly phases, with the indication of the specific type of performed control

Full size image

4.2 Defectiveness prediction and variability estimation

For each of the 18 workstations of the machine head assembly, the defects per unit, DPUi, are calculated according to the defectiveness prediction model mentioned in Section 2.1. The adopted power-law regression model is reported in Eq. (18) and illustrated in Fig. 3. The estimates of the model parameters are obtained by applying a non-linear regression to the data of 30 workstations related to a similar process concerning the assembly of mechatronic devices [12, 14].

$$ DP{U}_i=3.04\cdotp {10}^{-5}\cdotp C{f}_{P,i}^{1.27}\cdotp C{f}_{D,i}^{1.49} $$
(18)
Fig. 3
figure 3

Surface plot of DPU against CfP and CfD: theoretical model and experimental points of 30 workstations concerning a similar assembly process for mechatronic devices

Full size image

The process-based complexity factor, CfP,i, and the design-based complexity factor, CfD,i, are calculated according to the model proposed by Shibata [14] and Su et al. [12]. Specifically, for each ith workstation, the CfP,i are obtained according to Eq. (2) by exploiting the total assembly time, TATi, and the number of job elements Na,i, which are reported in Table 1. The threshold assembly time, t0, is set to 0.5 min, i.e. the time required to perform the least complex job element. The design-based complexity factor, CfD,i, is evaluated, according to Eq. (3), by considering the eleven parameters reported in Table 2 and the relative weights. These parameters, concerning the complexity of the design of the assembly, are slightly modified with respect to those relevant to copiers chosen by Su et al. [12], in order to better match the characteristics of hardness testing machines. Table 1 reports the obtained process- and design-assembly complexity factors and the defectiveness predictions.

Table 1 Predictions of assembly complexity factors and defectiveness relevant to the workstations of the machine head assembly
Full size table
Table 2 Eleven parameters and relative weights used to evaluate the design-based assembly complexity factors of hardness testing machines
Full size table

The variances of the DPUi are estimated, according to Eq. (8), by exploiting the variance-covariance matrix of the regression parameters k1, k2 and k3. This matrix is derived, according to Eq. (9) and using the software Minitab®, by applying the QR decomposition produced by the Gauss-Newton method for the nonlinear regression applied to the model of Eq. (18) [47,48,49,50]. In particular, the obtained variances of the regression parameters and the Pearson correlation coefficients are listed in Table 3.

Table 3 Variances and correlation coefficients of the regression parameters k1, k2 and k3
Full size table

In addition to the variances, the relative 95% confidence interval and 95% prediction interval of each DPUi are calculated, according to Eqs. (19) and (20) respectively.

$$ \left({\mathrm{DPU}}_{\mathrm{i}}-2.052\sqrt{VAR\left( DP{U}_i\right)},{\mathrm{DPU}}_{\mathrm{i}}+2.052\sqrt{VAR\left( DP{U}_i\right)}\right) $$
(19)
$$ \left({\mathrm{DPU}}_{\mathrm{i}}-2.052\sqrt{VAR\left( DP{U}_i\right)+{S}^2}\kern0.66em ,\mathrm{DPUi}+2.052\sqrt{VAR\left( DP{U}_i\right)+{S}^2}\right) $$
(20)

In Eqs. (19) and (20), S is the standard error of the regression, also called the standard error of the estimate:

$$ S=\sqrt{\frac{RSS}{N-P}} $$
(21)

where RSS is the sum of the squared residuals, N is the number of observations and P is the number of free parameters. Specifically, S is equal to 3.49·10−4, and it is still obtained from the power-law nonlinear regression model of Eq. (18) using the software Minitab®.

The standard error used in Eq. (19) for the calculation of prediction intervals of DPUi is also the standard uncertainty of defects per unit that will be used to estimate the variability of pi (see Eq. (11)) and that of the inspection strategy indicators (see Eqs. (14) and (17)). Therefore, it will be denoted hereafter as u (DPUi):

$$ u\left( DP{U}_i\right)=\sqrt{VAR\left( DP{U}_i\right)+{S}^2} $$
(22)

In Table 4 the obtained variances and the square of the standard error of the prediction of defects per unit are reported, together with the relative 95% confidence intervals (CI) and the 95% prediction intervals (PI) of DPUs, separately for each workstation i.

Table 4 Defects per unit in each workstation i (DPUi), variance of DPUi (VAR (DPUi)), square of the standard error of the prediction of DPUi (u2(DPUi)), 95% confidence interval (CI) and 95% prediction interval (PI) of DPUi
Full size table

After the prediction of the defect rates, for each ith workstation the probability of occurrence of defective-workstation-output, pi, is derived from DPUi by applying Eq. (4). As can be observed in Table 5, the differences between DPUi and the relative value of pi are negligible for low values. In other words, pi values may be approximated by the corresponding DPUi values. This result can be demonstrated considering the first-order Maclaurin series expansion of pi with respect to DPUi obtained from Eq. (4) [11].

Table 5 Estimates of probabilities pi and relative variances, αi and βi relevant to each inspection activity of the workstation of machine head assembly
Full size table

The variances of pi are calculated according to Eq. (11) by exploiting the DPUi uncertainty (see Eq. (22)) and are reported in Table 5.

As mentioned in Section 4.1, the adopted inspection strategy requires each workstation to be inspected using quality controls shown in Fig. 2. Each inspection activity is affected by inspection errors, αi and βi. In this case study, the inspection errors αi and βi (see Table 5) are estimated by exploiting empirical values of similar assembly processes of mechatronic devices. As far as the standard deviation of each inspection error is concerned, it is assumed to be 5% of the relative value of the parameter itself.

The empirical validation of the proposed model of defectiveness prediction, and the associated uncertainty, is a critical issue. Indeed, the assembly of hardness testing machines may be considered a low-volume manufacturing process, and therefore, a real data collection would require too much time to be completed. In order to overcome this problem, a preliminary validation of the methodology can be provided, for some workstations, by collecting the data relevant to the assembly of different models of hardness testing machines and comparing the empirical values with those predicted. Empirical values of DPUi which have cumulated over the years for the various workstations confirm the results reported in Table 4. For the first four workstations, for example, DPUi values are as follows: 0.005 for the first and the second workstations, 0.0015 for the third workstation and 0.0020 for the fourth workstation. Accordingly, the corresponding empirical values of pi are consistent with those reported in Table 5 [11]. Empirical values of pi observed over the years are 0.54 for the first workstation, 0.50 for the second, 0.12 for the third and 0.20 for the fourth workstation.

4.3 Inspection effectiveness and costs

The inspection effectiveness indicator, D, may be obtained by applying Eq. (5) and using the estimates of the probabilities reported in Table 5. The resulting mean total number of defective-workstation-outputs which are erroneously not signalled in the overall inspection strategy is:

$$ D=\sum \limits_{i=1}^{18}{p}_i\cdotp {\beta}_i=1.70\cdotp {10}^{-4} $$
(23)

The obtained value indicates that, on average, in every ten thousand hardness testing machines assembled, 1.7 (about 2) are not detected by the adopted inspection strategy as defective, when they are actually not conforming.

The uncertainty associated with this value of inspection effectiveness may be calculated, according to Eq. (24), from the sum of the variances of the parameters pi and βi, weighted respectively by the squares of βi and pi, as follows:

$$ VAR(D)=\sum \limits_{i=1}^{18}\left[{\beta}_i^2\cdotp VAR\left({p}_i\right)+{p}_i^2\cdotp VAR\left({\beta}_i\right)\right]=7.95\cdotp {10}^{-11} $$
(24)

Once the uncertainty of D is obtained, the 95% confidence interval for D may be derived. Therefore, it results: (1.52·10−4; 1.88·10−4).

According to the obtained results, it can be concluded that the mean number of defective-workstation-outputs which are not detected by the adopted inspection strategy is, with a confidence level of 95%, of about 2 units, considering a production of ten thousand machine heads. As mentioned before, the production of the examined type of hardness testers is only of some tens per year. As a result, the amount of defective-workstation-outputs which are erroneously not identified by the inspection strategy may be considered negligible.

If the methodology is extended to the other five phases in which the assembly of hardness testing machines is decomposed, the indicator D becomes 3.8∙10−4, and the relative 95% confidence interval results (3.42·10−4; 4.22·10−4). Therefore, in the overall assembly of hardness testers, it can be affirmed with a confidence level of 95% that there are about 4 undetected defective-workstation outputs. These results are considered reasonable by the producer of hardness testing machines and are supported by the experience gained over the years in the field.

Furthermore, this methodology may be applied to separately analyze and compare the addends pi∙βi of the total inspection effectiveness D, which can be used to identify the most critical workstations in terms of residual defectiveness. For instance, according to the parameters’ estimates reported in Table 5, the workstations with the highest values of pi∙βi are the number 10 and the number 15. Therefore, the producer could design and adopt a more effective inspection activity in these two critical workstations.

Table 6 reports the estimates of the cost parameters for each workstation. These estimates were calculated considering the time required for identifying and repairing possible defective-workstation-outputs, and the labour cost of operators/inspectors.

Table 6 Estimates of cost parameters relevant to each workstation, in the overall assembly of the machine head
Full size table

The information contained in Table 6 may be exploited to derive the total cost for inspection and defective-workstation-outputs removal related to the overall production process (Ctot), according to Eq. (6):

$$ {C}_{tot}\sum \limits_{i=1}^m{C}_{tot\kern0.33em ,i}=7.35\ \text{\EUR} $$
(25)

Considering that the standard deviation of each cost parameter is assumed to be 5% of the relevant value of the parameter itself, the variance of Ctot can be obtained, according to Eq. (17):

$$ VAR\left({C}_{tot}\right)=0.02{\text{\EUR}}^2 $$
(26)

Finally, the 95% confidence interval for Ctot may be expressed as (7.06, 7.64) €.

By extending the analysis to the other five process phases, the indicator Ctot becomes 16.53 €, and the 95% CI becomes (15.88, 17.18) €. These results, considered reasonable by the producer of hardness testing machines, are a preliminary indication of the total cost related to the inspection strategy in use. In this sense, they can be used as a proxy for economic convenience of the inspection strategy and could be useful to compare the adopted inspection strategy with others, such as partial inspections in selected workstations, or strategies in which current control activities are modified or improved.

5 Conclusions

Defect prevention and elimination are increasingly being adopted in the manufacturing field, since the presence of defects may greatly affect the final quality and cost of products. Many works have been proposed in the literature in the field of defect generation models, especially for predicting operator-induced assembly defects. In more recent years, the focus has been on exploiting these models to obtain reliable predictions of the probability of occurrence of defects at each stage of the production, with the goal of designing quality control strategies for low-volume productions. In fact, because of the nature of these productions, which are characterized by small lots or batches, or even unique pieces, the traditional statistical process control methods are often not appropriate. However, the existing methodologies adopted to evaluate defectiveness and inspection effectiveness in low-volume productions do not include a robustness analysis, without which reliable results cannot be obtained.

A methodology for evaluating the uncertainty of the average outgoing defectiveness and total cost of inspection strategies in low-volume assembly manufacturing processes has been proposed in this paper. The uncertainties of the statistical variables of the model for defectiveness prediction (pi and DPUi) have been evaluated by applying the law of combination of variances. Accordingly, the uncertainty has been propagated to the inspection indicator which depicts the overall effectiveness of inspection strategies, D, and to the cost indicator which provides an indication of the total cost related to the inspection strategy in use, Ctot. The proposed approach has been tested on an industrial case study concerning the assembly of mechanical components in the manufacturing of hardness testing machines. The results show the potential of the method in providing reliable estimates of the inspection design parameters.

The main contribution of the proposed methodology lies in the quantitative evaluation of the uncertainty related to the models for defectiveness and inspection cost predictions. Indeed, through the estimates of the inspection design parameters and the relevant uncertainties, it is possible to compare alternative inspection strategies, in terms of outgoing defectiveness and overall cost, with the required level of confidence. Furthermore, this approach can be easily extended and applied to a wide range of different industrial contexts, involving low-volume and single-unit assembly production processes.

Although the mathematical modelling may appear complex and difficult to be implemented by production engineers in the Gemba, it can be easily automated and the whole process for data acquisition and defect prediction can be guided by specific software procedures, which draw information by historical databases and on-the-field acquisitions. A preliminary prototype of this software has already been tested in a production of components for the automotive industry.

Some limitations of the methodology arise from the simplifying assumptions of the absence of correlation between the occurrence of defects and inspection errors. These assumptions are usually acceptable for most of the applications, but in particular situations, they are not verified. This topic will be deepened in a future research.

Furthermore, the model requires the estimation of various not-so-easily-quantifiable parameters, but a deep knowledge of the process and the on-field experience of experts may contribute to overcome this issue.