Ensemble transfer learning for refining stability predictions in milling using experimental stability states

Abstract

A new approach for updating model-based stability chart predictions in milling based on experimental data is presented. The approach utilizes Deep Neural Networks (DNNs), which are pre-trained with simulated data that is generated by predicting machine dynamics through receptance coupling and evaluating stability through an analytical stability model. The weights in the DNN are fine-tuned by re-training the networks with a small experimental dataset containing only a few dozen samples. Target is to match network predictions with the experimentally observed stability states acquired under different cutting conditions. The presented approach avoids measurement or model-based estimation of cutting force coefficients as well as the measurement of tooltip dynamics or extensive model parameter identification, making it an attractive approach for industrial applications. In an experimental validation, where stability charts for various engagement conditions and different tool clamping lengths are predicted, a good match between predictions and experimental stability limits is achieved. It is shown that an ensemble learning method, where predictions of multiple networks are combined, can improve prediction accuracy. Furthermore, it is demonstrated that the new approach requires approximately five times fewer experimental samples than previously proposed model-free machine learning approaches to reach the same prediction accuracy on a test set.

1 Introduction

Up to today, chatter vibrations belong to the most critical phenomena limiting the productivity in milling. Typically, stability lobe diagrams are used to distinguish between stable and unstable cutting depths as a function of the spindle speed. Yet, it is often observed that the experimental stability limits differ from the theoretical ones. On the one hand, this is because the stability models yielding the theoretical stability limits are inaccurate. On the other hand, this is caused by the input parameters to these models, which may not be precisely known or changed during operation.

Besides information about the engagement conditions and tool geometry, the most critical parameters that are typically required for stability predictions are the cutting coefficients, which relate the uncut chip thickness with the resulting forces, and the dynamics at the Tool Center Point (TCP) of a cutting tool. Both of these inputs can either be obtained through models or experimental characterization. While modeling avoids the usage of expensive measurement equipment and time-consuming experiments, inaccuracies in the modeling stage can lead to significantly wrong predictions. On the other hand, experimental characterization may also be inaccurate if the boundary conditions of the actual process differ from the ones valid in the characterization stage.

Regarding the estimation of the cutting coefficients, two principal techniques have been established in the past. One possibility is to derive the coefficients from orthogonal turning experiments, where they are determined through an orthogonal-to-oblique transformation [1]. Another solution is mechanistic calibration, where average forces are recorded at various feed rates [2]. However, it must be taken into account that coefficients may change as a function of the spindle speed, as it was for example shown by Grossi [3], for different radial engagements and cutting strategies [4] and for different feed rates as investigated by Campatelli et al. [5].

Significant challenges also need to be overcome to achieve accurate model predictions or perform reliable measurements of the tooltip dynamics. A common model-based method for estimation of tooltip dynamics is the receptance coupling technique, which was introduced by Schmitz and Donalson [6] and Schmitz et al. [7]. In this approach, the tool and holder are segmented into Timoshenko beam elements and the dynamics of the tool-holder combination are analytically coupled with the dynamics of the machine and the spindle. This eliminates the need to measure each tool-holder combination. Several approaches have been proposed to identify the dynamics of the machine tool and spindle [8,9,10]. However, despite the advances in the precision of the models over the last years and decades, accurate prediction of the tooltip dynamics remains challenging due to several reasons. First, the precise modeling of the fluted section of a tool is very complex. Kops and Vo [11] suggested replacing the fluted portion of a tool with a cylinder having 80% of the nominal diameter. Özsahin and Altintas [12] sliced the fluted section of the tool and coupled the analytical predictions for each oriented slice to obtain tooltip frequency response function (FRF) predictions. This approach, however, requires the precise geometry of the tool, which is often not available to the machine user. Furthermore, contact parameters between tool and holder are very hard to estimate; yet, they can have a substantial influence on the resulting dynamics. The contact is typically modeled either by implementing a multi-point coupling along the contact length between holder and tool as it was for example proposed by Yang et al. [13], or by assuming a lumped spring-damper element between the holder and the outer portion of the tool as suggested by Schmitz and Donalson [6]. Experimental identification of the contact parameters can be performed in free-free boundary impact tests on the tool and holder, as proposed by Matthias et al. [14], or on the whole spindle-holder-tool assembly, as done by Özsahin et al. [15], but these procedures remain very time-consuming and require expensive equipment. Lastly, unless they are identified in extensive material identification tests, the material properties of a given tool and holder can only be estimated within an uncertainty range. All these points render precise model-based tooltip FRF predictions difficult.

If the tooltip dynamics of the whole machine-spindle-holder-tool assembly are characterized experimentally, the tooltip or the workpiece of interest is usually impacted with an instrumented impulse hammer and the response is measured by means of an accelerometer or non-contact sensor. Yet, the prediction accuracy may suffer since the dynamics of the system may change during operation of the machine. For example, Matsubara et al. [16] showed that thermal influences can lead to changes in the natural frequency of a spindle system. Among others, Cao and Altintas [17] showed that the centrifugal forces and gyroscopic moments at high spindle speeds can substantially influence the bearing and spindle shaft dynamics. Additionally, dynamics may change under different load conditions, as it was found by Jamil and Yusoff [18] and Postel et al. [19].

Due to previously described limitations, approaches that identify dynamics during operation have gained popularity over the last years. One possibility is the operational modal analysis (OMA) [20], where the response of the machine is measured with an accelerometer during regular cutting operation. This allows the estimation of the natural frequency and damping ratio, but the identification of the dynamic stiffness is not straightforward. Özsahin et al. [21] proposed an inverse identification approach that is based on experimentally determined limit axial depths of cut and chatter frequencies. Data for two slightly different spindle speeds are required for the inverse identification of the tooltip dynamics. Similar approaches were presented by Grossi and Campatelli [22] and Eynian [23]. These methods, however, require dedicated tests under defined conditions and are hence not suitable for shop floor environment.

Since both model-based and experimental methods usually demand intense preparation and analysis, in recent years, it was also tried to utilize machine learning techniques for the prediction of stability limits. Friedrich et al. [24] trained a classification neural network with simulated stable and unstable depths of cut for different radial engagements and spindle speeds. Their continuous learning algorithm was designed in a way that only more recent measurement points were taken into account, while old data points were deleted. Approximately 2500 simulated training points were necessary to replicate the stability chart with acceptable accuracy, but no validation of the method with experimental data was performed. Recently, Cherukuri et al. [25] presented a machine learning approach for turning stability prediction. The authors trained a multilayer neural network with simulated stability boundaries. For a training sample size of at least 600 samples, an acceptable match between predicted and analytical stability boundary was achieved.

It should be noted that the two previously listed approaches require a large number of samples to learn the shape of the stability lobes, which is also one of the reasons why only simulated data was used. Furthermore, the methods are limited to one specific tool-holder combination with one defined tool length and workpiece material, which means that all training points need to be acquired under these defined conditions.

The approach presented in this work can reduce the number of necessary experimental training points by approximately one order of magnitude while allowing the learning from and predictions for multiple dynamic configurations. This is achieved by utilizing transfer learning for deep neural networks (DNNs). A multi-layer classification network is trained with simulated stability data generated using a simple dynamic model of the tool and holder and an analytical stability model. This is done in order to make the network learn the general dependencies of the stability boundary on several influencing and easily measurable parameters. The pre-trained network is then fed with experimentally measured stability states and process conditions of arbitrary cuts to fine-tune the network with real data and allow for more accurate stability predictions in future processes. One of the main goals of the presented approach is to keep the measurement effort to a minimum, making it a promising approach for the industry. The required experimental data for fine-tuning can simply be gathered during regular cutting operations.

The remainder of this paper is organized as follows: In Chapter 2, the necessity to include feedback from actual chatter test results to obtain accurate stability predictions is motivated by showing the influence of modeling inaccuracies on the resulting stability boundary. Details about DNNs and the newly developed ensemble transfer learning approach are described in Chapter 3. Experimental validation of the method is given in Chapter 4 before the paper is concluded in Chapter 5.

2 Model-based stability predictions

In this section, the influence of modeling parameters on the resulting stability predictions is shown. The results motivate the need to include some feedback from actual cutting operations in order to obtain reliable stability predictions. For this purpose, the dynamics of a tool-holder combination are modeled analytically, and predicted tooltip dynamics are fed, together with process information, into an analytical stability model.

Such stability models usually require four different inputs: the dynamics in the tool-workpiece contact zone, process information such as the engagement conditions, information about the tool geometry, and the cutting coefficients, which relate the uncut chip thickness with the resulting forces. While the tool geometry and engagement conditions are usually known with sufficient precision, cutting coefficients and tooltip dynamics can be associated with high uncertainty. This is especially true when these parameters are modeled and not measured. To demonstrate the effect of modeling uncertainty on the predicted dynamics, the tool-holder combination shown in Fig. 1a) is considered for a full immersion cutting operation in aluminum. The specifications of the holder and tool are listed in Table 1.

Fig. 1

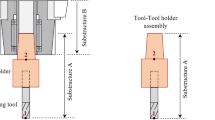
a Picture of a four fluted, 8-mm diameter solid carbide endmill clamped to an ER32 collet chuck with 40-mm clamping length. b Equivalent segmented beam model. K_ht is the lumped spring-damper matrix of the tool-holder contact and d_f is the outer diameter of the equivalent cylinder representing the fluted section of the tool. c Segmented model with 28-mm clamping length. Substructure B is indicated in Fig. 2

Table 1 Characteristics of the tool-holder combination used in the simulation and the experimental study

A commonly used approach to predict the required tooltip dynamics is the so-called receptance coupling substructure analysis (RCSA) technique, which is illustrated in Fig. 2 and was first proposed by Schmitz and Donalson [6]. The target is to avoid measurement of each new tool-holder combination and rather predict tooltip dynamics (Point 1) analytically. For this purpose, the tool and holder (substructure A) are modeled using Timoshenko beam elements and are then analytically coupled to the dynamics of the machine-spindle unit (substructure B) at the holder flange at Point 3 in Fig. 2. The dynamics of the machine tool up to the holder flange (Point 3) can be obtained through analytical modeling, finite element simulation or experimental identification and remain the same for all TCP FRF predictions. Figure 1b) shows an attempt to model the tool and holder by segmenting it into several beam elements. Compared to FE modeling, the analytical modeling has as advantage that the CAD files of the holder and tool are not required and that the model can quickly be adapted to new clamping lengths (see Fig. 1c).

Fig. 2

Concept of substructuring. Substructure B includes the machine tool and spindle up to the holder flange, substructure A the tool and holder from the holder flange on. Both substructures are coupled rigidly at Point 3. Point 2 is the elastic coupling point between tool and holder and Point 1 is the tooltip

The tooltip FRF can be evaluated as follows [26]:

$$ {\mathbf{H}}_{11}={\mathbf{H}}_{\mathrm{A},11}-{\mathbf{H}}_{\mathrm{A},13}{\left({\mathbf{H}}_{\mathrm{A},33}+{\mathbf{H}}_{\mathrm{B},33}\right)}^{-1}{\mathbf{H}}_{\mathrm{A},31,} $$

(1)

where all matrices include both translational (f) and rotational (M) receptances and their cross-terms):

$$ {\mathbf{H}}_{\mathrm{ij}}=\left[\begin{array}{cc}{h}_{ij, ff}& {h}_{ij, fM}\\ {}{h}_{ij, Mf}& {h}_{ij, MM}\end{array}\right],\kern1.25em i,j=1,2,3. $$

(2)

The tool and holder are elastically coupled with a connection matrix at the holder tip, which contains the contact stiffness and damping parameters between the cutting tool and the holder and has the following simplified form [14, 27, 28]:

$$ {\mathbf{K}}_{\mathrm{ht}}=\left[\begin{array}{cc}{k}_{xf}+ i\omega {c}_{xf}& 0\\ {}0& {k}_{\Theta M}+ i\omega {c}_{\Theta M}\end{array}\right] $$

(3)

In there, k_xf and k_ΘM are the translational and rotational stiffness terms and c_xf and c_ΘM the translational and rotational damping terms, respectively and ω is the frequency in rad/s.

H_B,33 is the identified direct receptance at the spindle flange and is identified experimentally by following the approach shown in the work by Namazi et al. [9]. For further details on the receptance coupling technique, the reader is referred to [26], for details on the modeling of the tool-holder contact to [14]. The top plot in Fig. 3 shows predicted tooltip FRFs in x-direction for the 8-mm diameter tool clamped to the collet chuck with various clamping lengths (see Fig. 1).

Fig. 3

Predicted tooltip FRFs in x-direction for different clamping lengths between 20 mm and 40 mm (top) and predicted stability limits for slotting operation (bottom). Reference values from Table 2 are assumed

In order to make model-based stability predictions, the zero order solution (ZOS) by Budak and Altintas [29] is used. In their analytical model, the critical limit axial depth of cut a_{p, lim} and the chatter frequency ω_c can be evaluated as a function of the FRFs in feed and normal direction and the tangential and radial cutting coefficients. The bottom plot in Fig. 3 shows predicted stability charts for a slotting operation when supplying the previously predicted, clamping length-dependent FRFs to the ZOS.

Cutting coefficients are assumed as K_tc=800 MPa and K_rc=300 MPa. These values were obtained in previous experiments with a 12-mm diameter, four-flute carbide endmill with 30° helix angle in Aluminum 7075 at 10000 rpm and serve as the reference values in this case study. It is important to note that the presented approach does not require precise values for the model parameters but will eventually correct erroneous model assumptions. For this reason, a rough estimate of the coefficients is sufficient at this stage.

Multiple challenges and uncertainties also exist when following an analytical substructuring approach for the tool and holder: First, for many segments that have features such as holes, threads, and grooves, it is not clear how the equivalent diameter of the cylindrical elements should be chosen. This is especially true for the fluted portion of the tool. Frequently, the assumption d_f=0.8·d_nom is made [11, 30, 31], where d_f is the equivalent outer diameter of the cylindrical element representing the fluted section and d_nom is the nominal outer diameter of the tool. Another issue is the contact between tool and holder, which is often either modeled as a lumped spring damper element or as distributed springs and dampers. Precise identification of these parameters is a challenge and many different approaches have been proposed over the years. Lastly, unless identified in material identification tests, the material properties, notably the Young’s modulus, Poisson’s ratio, and material loss factor of tool and holder material, can only be estimated within an uncertainty range. Table 2 lists all parameters that are assumed to be uncertain for the considered scenario, along with the respective reference values and the assumed standard deviations. The uncertainty of the equivalent diameter of the beam element representing the fluted section is considered, while all additional uncertainties of the geometric dimensions originating from features such as holes, threads, and chamfers are neglected. The reference values for the tool-holder contact are estimated based on previous contact parameter identifications, where the approach by Matthias et al. [14] was followed.

Table 2 List of all uncertain parameters along with the respective assumed reference values (mean) and standard deviations for the Gaussian distributions

Next, the clamping length is fixed at 28 mm, the uncertain parameters from Table 2 are varied according to their normal distributions, and tooltip FRF predictions are made in feed and normal direction. Subsequently, stability limits for a slotting operation are predicted using the ZOS. As stated before, rough estimates for the cutting coefficients are obtained from previous experiments but could, for example, also be derived from a database. They are also listed in Table 2. Figure 4 shows the resulting stability predictions, where all parameters were sampled 75 times from the respective distributions listed in Table 2. The prediction that is obtained with the reference values is also shown. It should be noted that many uncertainties are still not included in this simulation: Spindle dynamics may change during operation, identification of substructure B dynamics may be erroneous, and runout and tool wear may influence stability boundaries as well. Furthermore, the stability model may not be able to capture the full, possibly nonlinear, behavior of the system.

Fig. 4

Influence of the uncertainty of all parameters listed in Table 2 on the resulting stability boundary. All parameters were sampled 75 times from their respective normal distributions. “Reference” denotes the stability boundary that is obtained when assuming the reference values from Table 2

The observations show that precise model-based stability predictions without any feedback from actual cutting experiments or dynamic measurements are extremely challenging. Any effort to increase the accuracy of the model-based predictions leads to excessive measurement effort. In this work, the required feedback loop is closed by implementing a transfer learning approach, where the whole modeling stage is transformed into a DNN. Using this pre-trained DNN as a starting point, the weights in the network are then fine-tuned by making the network adapt its predictions to match the experimentally observed stability states. By following this approach, prediction inaccuracy originating from inaccurate model parameters and inaccurate modeling strategies can be compensated.

3 Ensemble transfer learning with DNNs

3.1 Deep neural networks

To compensate for the inaccuracies in the dynamic models and the stability model, in this work, deep neural networks (DNNs) are employed. The general structure of a DNN is shown in Fig. 5. It consists of one input layer having N_i input variables, one output layer with N_o output variables and L hidden layers in between the input and the output layer. Each hidden layer l has ${N}_n^{\left[l\right]}$ nodes, where each node j in layer l contains an activation function g^[l], which transforms the sum of each output of the previous layer ${a}_i^{\left[l-1\right]}$ multiplied with a weight ${w}_{j,i}^{\left[l\right]}$ and the bias term ${b}_j^{\left[l\right]}$ to obtain the output ${a}_j^{\left[l\right]}$ of this node,

$$ {\displaystyle \begin{array}{c}{a}_j^{\left[l\right]}={g}^{\left[l\right]}\left({\mathbf{W}}^{\left[l\right]},{a}^{\left[l-1\right]},{b}^{\left[l\right]}\right)\\ {}={g}^{\left[l\right]}\left(\sum \limits_{i=1}^{N_n^{\left[l-1\right]}}{w}_{j,i}^{\left[l\right]}\cdotp {a}_i^{\left[l-1\right]}+{b}_j^{\left[l\right]}\ \right)\end{array}} $$

(4)

where W^[l] is a matrix that contains all weights of the respective layer l,

$$ {\mathbf{W}}^{\left[l\right]}=\left[\begin{array}{ccc}{w}_{1,1}^{\left[l\right]}& \dots & {w}_{1,{N}_n^{\left[l-1\right]}}^{\left[l\right]}\\ {}\vdots & \ddots & \vdots \\ {}{w}_{N_n^{\left[l\right]},1}^{\left[l\right]}& \dots & {w}_{N_n^{\left[l\right]},{N}_n^{\left[l-1\right]}}^{\left[l\right]}\end{array}\right] $$

(5)

Fig. 5

Structure of a DNN with N_i inputs, L hidden layers, and N_o outputs. The bias terms that are added to each node of the hidden and the output layer are not shown

Here, the hyperbolic tangent, one of the most common activation functions for DNNs, is used as the activation function for the hidden layers,

$$ {g}^{\left[l\right]}(x)=\frac{\sinh (x)}{\cosh (x)}=\frac{e^{2x}-1}{e^{2x}+1}. $$

(6)

In the application case considered, the inputs to the network are the spindle speed n, the depth of cut a_p, the tool clamping length s_cl, as well as the entry angle φ_st and exit angle φ_ex, which are determined by the radial engagement of the tool. All these parameters are known with very high precision. Since a classification problem is considered, i.e., the process is stable or unstable, the output consists of two nodes, one of them representing stability and the other one instability. To obtain the probability for each of the two states, a softmax function is chosen as the output layer’s activation function. The softmax function normalizes the value of each output node by the sum of all outputs of the neural network. This makes the output of the respective output class correspond to the probability that sample s belongs to this output o,

$$ {p}_o=\frac{\exp \left(\sum \limits_{i=1}^{N_n^{\left[L\right]}}{w}_{o,i}^{\left[L+1\right]}\cdotp {a}_i^{\left[L\right]}+{b}_o^{\left[L+1\right]}\ \right)}{\sum_{j=1}^{N_o}\exp \left(\sum \limits_{i=1}^{N_n^{\left[L\right]}}{w}_{j,i}^{\left[L+1\right]}\cdotp {a}_i^{\left[L\right]}+{b}_j^{\left[L+1\right]}\ \right)}. $$

(7)

For this reason, it is especially well suited for a binary classification problem as it is considered here. In this special case, a typical loss function for the training of such a DNN is the binary cross-entropy loss [32], which is given by

$$ {L}_{CE}=-\frac{1}{N_s}\sum \limits_{s=1}^{N_s}\left[{y}_s\cdotp \log \left({\hat{y}}_s\right)+\left(1-{y}_s\right)\cdotp \log \left(1-{\hat{y}}_s\right)\right], $$

(8)

and is a particular case of the general cross-entropy loss. In there, y_s is the true class label for sample s (0 - stable or 1 - unstable) and ${\hat{y}}_s$ is the predicted probability for this sample being unstable. The total cross-entropy loss is obtained by summing all individual sample losses and dividing the sum by the number of samples N_s. Note that output node 1 corresponds to class 0 (stable) and the output of node 2 to class 1 (unstable). In this work, an Adam optimization algorithm is used for the training of the network. The mini-batch size is chosen as 16, and the learning rate as 0.001.

While such DNNs have been used in previous approaches for chatter prediction in milling and turning [25, 33], the methods required a very large amount of data samples for training. Here, a so-called transfer learning approach is used to decrease the number of necessary experimental training samples.

3.2 Optimized DNN structure

To perform efficient transfer learning, it is important to work with a neural network structure that is well suited for replication of the stability behavior.

For this task, a hyperparameter tuning for the network structure is performed by evaluating the performance on a simulated dataset. The reference values for each parameter from Table 2 are assumed.

The stickout length of the tool is varied, the Timoshenko beam model is updated to the respective clamping length, and tooltip FRF predictions are made through the receptance coupling theory. Additionally, the entry and exit angles are varied to make the network learn the influence of the radial engagement conditions.

The general network structure is hence as shown in Fig. 5, where the input parameters are

$$ I=\left[n,{a}_{sim},{\varphi}_{st},{\varphi}_{ex},{s}_{cl}\right], $$

(9)

and the categorical output classes are

$$ C=\left\{ stable, unstable\right\}. $$

(10)

In total, N_sim=14850 samples are generated, where for each sample, spindle speed, entry and exit angle and clamping length are sampled uniformly from the ranges [6000 rpm, 18,000 rpm], [0, 0.4π], [0.6π, π], and [20 mm, 40 mm], respectively. Artificial stable and unstable points are generated using the equation

$$ {a}_{sim}={a}_{ZOS}\cdotp \left(1+x\right), $$

(11)

where x is a random number between −0.3 and 0.3 and a_ZOS is the theoretical stability limit for sample s given by the zero order solution. The point is hence stable if the simulated depth of cut a_sim is lower than the theoretical stability limit a_ZOS, and unstable otherwise. While the ZOS is known to be inaccurate for some engagement conditions, for the application case here, it is important to generate general shapes of the stability limits such that the network can learn the idea of the lobes. The fine-tuning eventually happens with experimental data.

In order to find an appropriate network structure, the number of hidden layers and the number of nodes in each layer are set as hyperparameters. Additionally, the regularization λ, which penalizes large network weights and can avoid overfitting to the training data, is added as a hyperparameter as well. In this case, the cost function becomes a weighted sum of the cross-entropy loss from Eq. (8) and the sum of all weights

$$ L=\left(1-\lambda \right)\cdotp {L}_{CE}+\lambda \cdotp {w}_{ms}, $$

(12)

where w_ms is the mean of the sum of squares of all N_w network weights and biases,

$$ {w}_{ms}=\frac{1}{N_w}{\sum}_{i=1}^{N_w}{w}_i^2. $$

(13)

A genetic algorithm is employed to tune the hyperparameters. The simulated dataset is split into one training, one validation, and one test dataset containing 80%, 10%, and 10% of the data, respectively. The prediction accuracy of the validation set, i.e., the percentage of correctly predicted stable and unstable points is chosen as objective criteria for the hyperparameter tuning. The highest validation accuracy (93.5%) is obtained for a three-layer network containing 25, 12, and 27 nodes, respectively, and a regularization parameter λ=0.088. Its structure is shown in Fig. 6. Figure 7 shows one sample simulated analytical stability limit along with predictions made by the network, and a very good agreement can be observed.

Fig. 6

Structure of the optimized DNN. tanh stands for the hyperbolic tangent activation function

Fig. 7

Comparison of stability predictions using the optimized DNN and the prediction made by the analytical stability solution. Test conditons: 75% radial engagement up-milling, clamping length 28 mm

The optimized network structure is now kept for all the following operations.

3.3 Transfer learning for chatter prediction

Transfer learning describes a method where a model that has been trained on one problem is used as a starting point for a slightly different but related problem. In this application case, the original problem is to learn the idea of stability lobe diagrams from simulated data (pre-training), while the related, slightly different problem is to adapt the network weights such that the network’s predictions match with actual experimental observations (fine-tuning). Hereby, the required experimental dataset is several orders of magnitude smaller than the simulated one, which is used for pre-training. In this approach, the observation is exploited, that the general shape of the stability lobes is often comparatively well predicted with existing stability theories, but the lobes are shifted with respect to the spindle speed or the depth of cut.

While with the simulated data it is targeted to make the network aware of the general shape of stability lobes and its basic dependencies, the goal of the fine-tuning is to compensate four sources of errors, which were possibly present in the models and transferred to the pre-training stage:

• Inaccuracy in the modeling of TCP dynamics

• Uncertainty about the cutting coefficients

• Potential operational changes of dynamics and cutting coefficients (e.g., spindle speed dependency)

• Inaccuracies of the stability model used

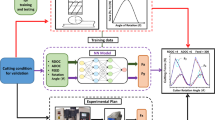
The concept is further explained with the help of Fig. 8. First, simulated data is generated by modeling the tooltip dynamics, assuming some cutting coefficients and feeding these inputs into an existing stability model. From the simulated stability charts, stable and unstable spindle speed/depth of cut combinations are derived. This simulated dataset is then used for training of the DNN. This step is called pre-training. The network is then aware of the main influences on the stability lobes and has also learnt the concept of stability pockets, which repeat with the spindle speed. Nevertheless, this network may have a poor performance when comparing its predictions with actual experimental stability states. This problem is tackled in the fine-tuning stage. A much smaller experimental dataset is now fed to the pre-trained network, whose initial weights are equal to the optimized network weights from the pre-training stage. The network weights will now adapt slightly to match the DNN predictions with the experimentally observed stability states. In the next step, this fine-tuned network can be used for stability predictions of new cutting scenarios and much more accurate stability predictions are possible.

Fig. 8

Concept of the transfer learning. First, a DNN is pre-trained with simulated data using existing models for dynamics and stability evaluation. Due to deficiencies in the models and inaccurate model parameters, this DNN will yield stability predictions that do not perfectly match the experimentally observed stability states. Still, it is already aware of the key dependencies of input parameters and stability states and knows the concept of lobes. The pre-trained network is then fine-tuned with experimental data, which makes the network adapt to the actual behavior of the system. This fine-tuned network can then be used to predict stability charts for new cutting operations

3.4 Ensemble transfer learning

For the generation of the simulated dataset it is not directly clear which values for the uncertain parameters from Table 2 should be assumed in the modeling stage. Here, an extension to the classic transfer learning idea is proposed, which takes the modeling uncertainty into account. It is based on the idea of ensemble learning, where multiple networks are trained and their individual estimates are combined to obtain a single prediction.

The concept is explained with the help of Fig. 9. All uncertain parameters are sampled N_net times from their distributions defined in Table 2 (Step 1). At the same time, N_sim artificial cutting samples are generated, where spindle speed, depth of cut, and entry and exit angles are sampled uniformly from defined ranges (Step 2). Also sampled is the clamping length, which is, together with the sampled uncertain parameters from Step 1, used for TCP FRF predictions through receptance coupling. Resulting FRFs, process conditions of the respective sample and sampled cutting coefficients are supplied to the stability model and stability is evaluated for each sample’s spindle speed/depth of cut combination (Step 3). The generated dataset consisting of the inputs spindle speed, depth of cut, and entry and exit angles as well as the clamping length and the outputs stable/unstable are used for pre-training of one network (Step 4). Steps 3 and 4 are repeated for each of the N_net networks.

Fig. 9

Ensemble transfer learning strategy with N_net networks. 1. All uncertain parameters are sampled N_net times from their respective distributions. 2. N_sim samples are generated with random clamping lengths, spindle speeds, and axial and radial engagements. 3. Theoretical tooltip dynamics and stabilty states of the respective samples are evaluated using receptance coupling theory and an analytical stability model. 4. The gathered inputs (clamping lengths, spindle speeds, axial and radial engagements) and outputs (stabilities of the simulated cuts) are used for pre-training of the networks. 5. These networks are then fine-tuned using experimental data. 6. For a new cutting scenario, the resulting stability predictions of the individual networks are averaged using the truncated mean approach from Eq. (14)

Each network is then fine-tuned using the same experimental dataset, which is typically one or more orders of magnitude smaller than the simulated dataset (Step 5).

When predicting a stability chart for new process conditions, each of the networks makes a prediction. Eventually, all network predictions are averaged using a truncated mean approach, where very high and very low predictions are excluded (Step 6),

$$ {a}_{pred}(n)=\frac{1}{N_{net}-2{k}_{excl}}{\sum}_{i={k}_{excl}+1}^{N_{net}-{k}_{excl}}{a}_n(i). $$

(14)

In there, a_n(i) is the i^th element of the vector a_n, which contains the sorted depth of cut predictions of all N_net networks at a specific spindle speed n. k_excl are the integer number of excluded lowest and highest predictions,

$$ {k}_{excl}=\mathit{\operatorname{int}}\left({p}_{excl}\cdotp {N}_{net}\right), $$

(15)

where, in this case, p_excl=0.25 is chosen to exclude the lowest and highest 25% of all predictions. To transform the classification prediction of a network at spindle speed n into a critical depth of cut a_n, for each network stability state predictions are made for incrementally increasing depths of cut, until the stability state changes from stable to unstable.

4 Experimental verification

4.1 Case study

Now, the tool-holder combination shown in Fig. 1a) is used for cutting operation in Aluminum 6082. The collet holder is clamped to a high-performance five-axis machining center and cuts are performed at various spindle speeds and radial and axial engagements, where the tool is clamped at different clamping lengths. In total, 90 cuts are recorded (56 stable, 34 unstable); a summary of the different cutting scenarios is given in Table 3. The feed rate is kept constant at f_t=0.05 mm/tooth with a feed in Y-direction. The specific cutting conditions (i.e., which case from Table 3 is chosen, the spindle speed, and the depth of cut) for the 90 cuts are sampled randomly using a MATLAB script. The experimental setup is shown in Fig. 10. The stability of each cut is evaluated through frequency analysis of the recorded sound using a waterproof microphone installed in the working chamber.

Table 3 Cutting cases and number of cuts (training samples) that were included in the fine-tuning in Sections 4.1–4.3 and Section 4.5

Fig. 10

Setup for the experimental case study

The previously described ensemble transfer learning approach is employed, and 200 individual networks are pre-trained. Each network is then fine-tuned using the experimental dataset.

Due to the high number of weights and bias terms in the network compared to the number of experimental training samples, each of the networks is able to reach 100% prediction accuracy for the training set after a couple of seconds of training. At this moment, the training process is stopped. Now, stability lobe predictions are made for all 18 cutting scenarios listed in Table 3, and the truncated mean prediction is calculated from Eq. (14). For each case, approximately 120 test cuts at different spindle speeds and depths of cut are performed. All cutting tests, along with the respective predictions, are shown in Fig. 11. The samples that are used in the training process are also indicated. For the test samples, a prediction accuracy (i.e., percentage of correctly predicted stability states) of 83.6% is achieved. Note that marginal cases are not included in the accuracy calculations.

Fig. 11

Comparison of experimental stability results and predictions made with the ensemble transfer learning approach (black continuous lines). Ninety samples were included in the fine-tuning stage (highlighted with black rectangles). Also plotted is the analytically predicted stability limit using receptance coupling and the zero order solution (dashed blue lines). For test conditions, see Table 3. Note the different y-scales. Marginal cuts are cuts that could not clearly be labeled as stable or unstable

Furthermore, the stability prediction that is obtained when using the dynamics predicted through receptance coupling, the estimated cutting coefficients and the ZOS is plotted in blue. For these model-based predictions, the reference values listed in Table 2 are used. The model approach yields a test accuracy of 59.4%. The ensemble transfer learning, hence, yields a relative improvement in accuracy of approximately 40% compared to the analytical model predictions.

4.2 Performance of ensemble learning

In this section, the performance of the ensemble approach is investigated. As described before, the resulting predictions for a new cutting scenario are averaged using a truncated mean approach, where the highest 25% and lowest 25% of the individual depth of cut predictions are excluded from the averaging. This is done to avoid the inclusion of heavily diverging predictions.

Figure 12 shows the individual predictions for three sample cases along with the truncated mean of all predictions. It can be seen that, while a significant number of individual predictions diverge strongly from the experimental stability boundary, the truncated mean yields a reasonable estimate of the actual stability boundary. However, it should be noted that the test accuracy was only slightly affected by the choice of p_excl. With an exclusion factor of p_excl=0.25, a relative improvement of 2.7% in test accuracy compared to the regular average of all network predictions (i.e., p_excl=0) could be achieved.

Fig. 12

Details on the ensemble prediction in three sample cases: Individual predictions of all 200 networks (dashed gray lines) and resulting ensemble predictions (black continuous lines). Also shown are the model predictions (dashed blue lines). Stable experimental cuts are indicated by green points, marginal ones by blue diamonds, and unstable ones by red points. For test conditions see Table 3

Figure 13 shows the influence of the number of individual networks that were included in the ensemble prediction method. It is clearly visible that the overall accuracy increases strongly at the beginning when more than one network is included in the ensemble prediction. From approximately 50 networks on, the test accuracy saturates around 83.6%. It is very interesting to note that the ensemble prediction is well above the mean prediction accuracy of all individual networks. It could be expected that the ensemble prediction is close to the mean or the median of the individual predictions, but it is significantly higher. In fact, only 18 out of the 200 networks achieve a higher test prediction accuracy than the one achieved by the ensemble method. However, since test data is not available during the training process, one cannot make any assumption about which of the networks would yield especially high accuracies. The ensemble method yields an approximately 4% higher test fitness than when a single arbitrary network is chosen (= median accuracy of the individual networks) and an improvement of approximately 8.3% compared to a single network which is pre-trained with the reference values from Table 2 (75.1% test accuracy).

Fig. 13

Comparison of test accuracies of the ensemble method and the individual networks as a function of the number of networks

4.3 Comparison against model-free machine learning approaches

It is furthermore interesting to compare the presented hybrid model/machine learning method against model-free machine learning approaches, as they have recently been proposed in the literature [24, 25].

In this case, the network from Fig. 6 is not pre-trained, but instead, the network weights are randomly initialized, and the network is trained directly with the training data. The same training set as it was used in Sections 4.1 and 4.2 (90 training samples) is used for training. The results of this approach, compared to the ensemble transfer learning approach, are shown in Fig. 14. Due to the small number of training samples, the algorithm fails to capture the concept of stability pockets. A test accuracy of 72.3% is obtained. To get a more complete picture of the performance of both approaches, with and without pre-training, the influence of training set size on the test accuracy is studied in the next section.

Fig. 14

Comparison of experimental stability results and predictions made with the ensemble transfer learning approach (black continuous lines). Ninety samples were included in the fine-tuning stage (highlighted with black rectangles). Also plotted is the stability limit obtained from the model-free approach, where a single DNN is trained with the experimental dataset (dashed black lines). For test conditons see Table 3. Note the different y-scales

4.4 Influence of the training set size

Now, the number of samples is incrementally increased from 10 to 475 for both the ensemble transfer learning approach and the model-free machine learning approach. Note that the samples were sampled randomly from all test cases. Figure 15 shows the development of the test set accuracy as a function of the training sample size. Three observations can be made:

• 1. For very small sample sizes, the ensemble transfer learning approach already starts with a higher accuracy compared to the model-free DNN approach.

• 2. The slope of the test accuracy is much higher in the low sample size range (~10–50 samples), which means that the shape of the experimental stability lobes is quickly captured by the ensemble transfer learning algorithm with the addition of further experimental points.

• 3. Over almost the whole range of investigated training set sizes, the model-free machine learning approach requires approximately five times more samples to reach the same test accuracy as it is obtained with the new proposed approach.

Fig. 15

Test set accuracy for the ensemble approach, the mean accuracy of all individual network predictions as well as the accuracy of the model-free DNN approach, i.e., when no pretraining is performed. The accuracy is the percentage of correctly predicted stable and unstable process conditions

4.5 Influence of the training sample distribution

Another interesting aspect is how the algorithm performs when the sample distribution of the training samples varies. This question is addressed in this section. It is assumed that only for some cases from Table 3 cuts have been recorded, while for other cases, no samples are available.

In particular, three additional scenarios to the reference scenario presented in Section 4.1 (90 tests from all cases) are investigated. They are listed in Table 4. The fine-tuning process described in Section 3 is run again for each of the three additional scenarios. Figure 16 shows an overview over the achieved test set accuracies for the reference scenario (Section 4.1) and the three additionally defined scenarios. The following observations can be made: If only cases with long clamping lengths (37.1−40 mm, Cases A−E) are supplied to the algorithm (Scenario 1), still very good prediction accuracies can be obtained for medium clamping lengths (27.9−34 mm, Cases G−L). On the other hand, the test accuracy deteriorates for very short clamping lengths (20−24.8 mm, Cases M−R). The resulting predictions for all cases are shown in Fig. 17. It is interesting to note that for cases M−R, the updated prediction is still relatively close to the model prediction (compared to, e.g., Cases A−J).

Table 4 Overview of which cases are included in the fine-tuning process for the different scenarios considered in this study: In the “Reference” scenario, as described in Section 4.1, all 90 samples are included. In scenarios 1–3, as defined in Section 4.5, only a subset of cases is used

Fig. 16

Test accuracies for the four scenarios listed in Table 4

Fig. 17

Comparison of experimental stability results and predictions made with the ensemble transfer learning approach (black continuous lines) for Scenario 1 from Table 4. The black rectangles are the samples that were included in the fine-tuning stage. Also plotted is the analytically predicted stability limit using receptance coupling and the zero order solution (dashed blue lines). For test conditions see Table 3. Note the different y-scales. Marginal cuts are cuts that could not clearly be labeled as stable or unstable

In both Scenario 2 and Scenario 3, four cases are excluded from the training. In these two scenarios, still very satisfying test accuracies can be obtained, see Fig. 16.

5 Conclusion

In this paper, a new hybrid approach for the refinement of stability limits in milling operations is presented. It combines knowledge about the general dynamic behavior of spindle-holder-tool assemblies and the resulting shapes of stability lobe diagrams under various cutting conditions with experimental data by employing ensemble transfer learning on deep neural networks. First, simulated stable and unstable points are generated using receptance coupling theory and an analytical stability model. These stability states deviate from the actual, experimentally observed stability states due to the imperfections of the models and uncertainties in the model input parameters. To be able to compensate for these deficiencies, the whole modeling strategy is transferred into a deep neural network by training it with the simulated data. The network is now aware of the general dependencies of the stability boundary on some easily measurable parameters and the concept of stability pockets. Few experimental samples are now used to fine-tune the network and adapt it to the real behavior of the system. The approach hence compensates uncertainties in the modeling stage regarding both uncertain input parameters as well as inaccuracies of the models used. It is further shown that the overall test performance is improved by employing an ensemble learning strategy, where the predictions of multiple networks are combined.

The presented method avoids any kind of measurement, except for one initial identification of machine tool and spindle dynamics, which could be done at the machine tool manufacturer when the machine leaves the assembly line. This makes it an attractive solution for industrial implementation.

For the future, it is targeted to also include simulated and measured chatter frequencies in the pre-training and fine-tuning stages, respectively. It is expected that this can further reduce the number of required training samples.