Accurate and efficient stability prediction for milling operations using the Legendre-Chebyshev-based method

Abstract

Stability prediction with both high computational accuracy and speed is still a challenging issue and has been attracting significant attention from the academia and industry. This study presents a Legendre-Chebyshev-based stability analysis method (LCM) for milling operations. According to the cutting state, it divides the system period of milling model into the free and the forced vibration time periods. By introducing appropriate transformation, the latter time interval is further discretized nonuniformly into the Chebyshev-Gauss-Lobatto points, which has explicit expression. Then, the state term over the discrete time points is approximated with the Legendre expansion, and its corresponding derivative is acquired via a novel and efficient algorithm. Thereafter, Floquet matrix within the system period of milling model can be determined for predicting the system stability via the known Floquet theory. Finally, we validate the effectiveness of the LCM by employing the single and two degrees of freedom (DOF) milling operations and making detailed comparisons with the recent representative algorithms, which indicates that the presented Legendre-Chebyshev-based method has both high prediction accuracy and speed.

1 Introduction

High-speed milling has made great progress in the modern manufacturing industry promoted by the ever-increasing demand for high-performance machining [1,2,3]. However, it has been greatly restricted because of the frequent occurrence of a kind of harmful and also unavoidable violent vibration, known as chatter [4]. Due to the relatively low mechanical impedance, it can appear in almost all machining processes and has detrimental impacts on both machining quality and efficiency [5,6,7,8]. As presented and validated in literature, it can be induced by four different mechanisms, and the regenerative mechanism can explain most of the milling instability behaviors. To avoid harmful effects of this nasty unstable vibration, scholars have attempted to model and predict or identify and control the milling instability behavior [3, 4, 9,10,11,12]. To achieve high-performance milling, accurate and efficient stability analysis for this undesirable instability and selecting proper machining parameters via stability boundaries are crucial for chatter avoidance and productivity improvement.

So far, researchers have proposed many methods to predict chatter stability. The first kind of methods, known as numerical methods, utilize numerical algorithms to solve the dynamic equation of the system, so as to acquire the stability characteristics by analyzing whether the amplitude is divergent [13,14,15,16,17,18]. For instance, a time-domain numerical simulation model considering both twist drill motion and torsional-axial coupling vibration was established in [18]. To obtain the time response of axial and torsional vibration, the authors adopted numerical algorithm to solve the dynamic equation of drilling operations. Although the numerical methods have strong versatility, their huge cost of calculation makes it difficult to meet the actual requirements. Fortunately, the latter two (analytical and semi-analytical ones) provide an alternative to obtaining the stability boundaries conveniently [19,20,21,22,23,24,25,26,27].

The analytic methods approximate the system periodic coefficient term by utilizing the Fourier series expansion, which transforms the delay differential equations into another domain representation. The famous zeroth-order approximation method based on Fourier transform was proposed in [19, 20], which was first employed in milling and has extremely high calculation speed. However, the zeroth-order approximation method cannot obtain high precision for stability problems under some conditions, such as milling stability prediction under small radial depth of cut conditions. Later, the research team from Altintas continued to make efforts to improve this method [21]. The semi-analytic methods are another kind of widely recognized algorithms, which obtain the Floquet matrix within the system period of milling model by numerically approximating the original delay differential equations. For instance, Butcher et al. [23, 24] proposed two stability analysis methods. Introduced in [25,26,27], the SDMs have good applicability for different machining conditions and low complexity of algorithm but suffer relatively low calculation speed. After that, these methods continue to develop with ever increasingly faster calculation speed and better convergence accuracy. To further improve the computational efficiency of SDM without accuracy loss, Dong et al. [28, 29] proposed a fast reconstructed prediction method. To efficiently and accurately predicting the milling stability, the 2nd SDM was recommended based on the Newton interpolation polynomials in [30]. From another point of view, the full-discretization method (FDM) was developed in [31]. FDMs achieve high calculation speed and do not sacrifice any numerical accuracy. Recently, enhanced FDMs were recommended by Sun [32], Ozoegwu [33, 34], Tang [35], and Yan [36], which employed higher interpolation or approximate methods. However, the computational speed decreases with the increase of algorithm complexity for these methods. With the aid of holistic-interpolation scheme, Qin et al. [37, 38] developed two holistic-discretization methods (HDM and PCHDM). It was shown that the PCHDM achieved higher both accuracy and efficiency than the updated FDMs of Tang [35] and Yan [36]. Olvera et al. [39] introduced the homotopy-based stability analysis algorithm. Also, the Chebyshev wavelets based method was recommended in [40]. The known numerical integration algorithm was proposed by Ding et al. [41, 42]. The complete discretization scheme (CDM) was recommended by [43], in which numerical method was utilized. To further increase the calculation efficiency and accuracy, Li et al. [44] developed an updated CDM. Ding et al. [45] proposed a semi-analytical wavelet-based method by utilizing compactly supported Daubechies scaling functions. As for the case of multiple time delays, Lu et al. [46] proposed the spline-based approach. From the point of view of numerical differentiation, two novel methods for the high-speed milling stability analysis were introduced in [47, 48]. Based on linear multistep methods, Qin et al. [49, 50] developed the Adams-Moulton-based methods (AMM and EAMM). Inspired by predictor-corrector scheme, Qin et al. [51] presented the ASM for improving calculation accuracy and speed. In depth analysis found that the ASM could save more computing time than the PCHDM, while its approximation order is similar with that of the PCHDM.

It can be seen from the above literature that the current semi-analytical methods are still difficult to balance the calculation accuracy and efficiency and researchers are still working to improve its convergence speed while reducing its computational cost. Inspired by the research on the optimal control problems [52], we propose a Legendre-Chebyshev-based algorithm for accurate and efficient stability prediction. To begin with, the forced vibration interval is discretized nonuniformly into Chebyshev-Gauss-Lobatto points by introducing appropriate variable transformation. The Chebyshev-Gauss-Lobatto points can be obtained analytically, which is quite beneficial to the calculation simplicity and efficiency. The Legendre expansion with spectral convergence accuracy is utilized for approximating the state term over discrete time points, and its corresponding derivative is obtained by a novel and fast algorithm. In the end, the Floquet matrix over the system period of milling model can be acquired to compute the stability boundaries. The rest of this study is organized as follows. Section 2 presents Legendre-Chebyshev-based algorithm (LCM). Section 3 validates the convergence rate and calculation speed of LCM, and Sect. 4 gives the conclusions of this work.

2 Milling model and Legendre-Chebyshev-based method

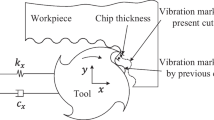
It is known that the milling dynamics model is a prerequisite for stability analysis. According to the Refs. [6, 9, 26], appearance of the most instability for milling processes behaviors can be attributed to the regenerative mechanism. Taking two DOF milling system as an example, it can be mathematically modeled by DDEs as follows:

$$ \mathbf{M}\overset{\cdotp \cdotp }{\boldsymbol{\Gamma} (t)}+\mathbf{C}\overset{\cdotp }{\boldsymbol{\Gamma} (t)}+\mathbf{K}\boldsymbol{\Gamma } (t)=\mathbf{F}(t)=-{a}_p\mathbf{G}(t)\left[\boldsymbol{\Gamma} (t)-\boldsymbol{\Gamma} \left(t-T\right)\right] $$

(1)

in which Γ(t) is the tool displacement vector, while M, C, and K are modal related matrices. T denotes system period of milling model. Define Ω as spindle speed (rpm) and N as the tool teeth number; then T is given by T = 60/(NΩ). Additionally, a_p represents the depth of cut, and G(t) represents coefficient matrix satisfying G(t) = G(t + T).

According to geometric relationship of cutting force, G(t) for the two DOF milling can be deduced as follows:

$$ \Big\{{\displaystyle \begin{array}{l}{g}_{xx}(t)=\sum \limits_{i=1}^N\left[{K}_t\cos \left({\phi}_i(t)\right)+{K}_n\sin \left({\phi}_i(t)\right)\right]g\left({\phi}_i(t)\right)\sin \left({\phi}_i(t)\right)\\ {}{g}_{xy}(t)=\sum \limits_{i=1}^N\left[{K}_t\cos \left({\phi}_i(t)\right)+{K}_n\sin \left({\phi}_i(t)\right)\right]g\left({\phi}_i(t)\right)\cos \left({\phi}_i(t)\right)\\ {}{g}_{xy}(t)=\sum \limits_{i=1}^N\left[-{K}_t\sin \left({\phi}_i(t)\right)+{K}_n\cos \left({\phi}_i(t)\right)\right]g\left({\phi}_j(t)\right)\sin \left({\phi}_i(t)\right)\\ {}{g}_{xy}(t)=\sum \limits_{i=1}^N\left[-{K}_t\sin \left({\phi}_i(t)\right)+{K}_n\cos \left({\phi}_i(t)\right)\right]g\left({\phi}_i(t)\right)\cos \left({\phi}_i(t)\right)\end{array}} $$

(2)

where K_n and K_t denote coefficients related to workpiece material and tool. According to the cutting state, the value of g(ϕ_i(t)) with input ϕ_i(t) = (2πΩ/60)t + 2π (i-1)/N equals to 1 or 0, namely,

$$ g\left({\phi}_i(t)\right)=\Big\{{\displaystyle \begin{array}{l}1,\kern0.5em {\phi}_{st}<{\phi}_i(t)<{\phi}_{ex}\ \\ {}0,\kern0.75em \mathrm{otherwise}\end{array}} $$

(3)

in which according to the type of milling operations and the value of radial immersion ratio a/D, start and exit immersion angles are calculated by

$$ \Big\{{\displaystyle \begin{array}{l}{\phi}_{st}=\operatorname{arccos}\left(2a/D-1\right),{\phi}_{ex}=\pi \kern0.5em \mathrm{down}-\mathrm{milling}\ \\ {}{\phi}_{st}=0,{\phi}_{ex}=\operatorname{arccos}\left(1-2a/D\right)\kern0.5em \mathrm{up}-\mathrm{milling}\end{array}} $$

(4)

To acquire Floquet matrix for stability analysis, we need to re-represent the milling dynamics model as the state-space form. Hence, matrix transformation is introduced by $\boldsymbol{\Theta} (t)=\mathbf{M}\overset{\cdotp }{\boldsymbol{\Gamma} (t)}+\mathbf{C}\boldsymbol{\Gamma } (t)/2$ andx(t) = [Γ(t), Θ(t)]^T. Specifically, by utilizing this transformation, the milling dynamics model, i.e., Eq. (1), is reformulated as follows:

$$ \overset{\cdotp }{\mathbf{x}(t)}=\left({\mathbf{S}}_c+\mathbf{S}(t)\right)\mathbf{x}(t)+\mathbf{R}(t)\mathbf{x}\left(t-T\right) $$

(5)

in which

$$ {\mathbf{S}}_c=\left(\begin{array}{cc}-{\mathbf{M}}^{-1}\mathbf{C}/2& {\mathbf{M}}^{-1}\\ {}\mathbf{C}{\mathbf{M}}^{-1}\mathbf{C}/4-\mathbf{K}& -\mathbf{C}{\mathbf{M}}^{-1}/2\end{array}\right),\kern0.36em \mathbf{S}(t)=-\mathbf{R}(t)=-{a}_p\left(\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ {}\mathbf{G}(t)& \mathbf{0}\end{array}\right) $$

(6)

In theory, since the matrices S(t) and R(t) in the above state-space equation are directly related to value of G(t), the dynamic process was determined whether experiences free or forced vibration by its elements. In terms of milling operations, if the milling tool is in cutting state, G(t) has nonzero variables. For such case, the milling operations experiences forced vibration according to the state equation. On the other hand, while the milling tool is not in cutting state, the time-periodic matrix G(t) degenerates into the zero matrix. Now, it will experience a simple form of vibration, namely, free vibration.

Taking above analysis into account, we divide Τ of G(t), i.e., the system period of milling model, into two subintervals. The first interval is corresponding to when milling cutter is out of cutting state, namely, the free vibration interval denoted by T_r, while another interval is corresponding to when milling cutter is just in cutting state, namely, the forced vibration interval denoted by T_o = T − T_r. To avoid the Runge effect in high-order interpolation and simplify the calculation process for high computational efficiency, the discrete time points employed to discretize the interval T_o are the Chebyshev-Gauss-Lobatto points that has explicit expression, namely,

$$ {t}_j=-\cos \left(j\frac{\pi }{m}\right),\kern0.5em j=0,\cdots, m $$

(7)

To transform the forced vibration time interval [T_r, T] into the standard interval [− 1, 1], we introduce the variable transformationη = [2t − (2T_r + T_o)]/T_o, η ∈ [−1, 1]. Then one can obtain$t=\frac{1}{2}{T}_o\eta +\frac{1}{2}\left(2{T}_r+{T}_o\right),t\in \left[{T}_r,T\right]$. Hence, Eq. (5) can be equivalently expressed as

$$ \frac{2}{T_o}\overset{\cdotp }{\mathbf{x}\left(\eta \right)}=\left({\mathbf{S}}_c+\mathbf{S}\left(\eta \right)\right)\mathbf{x}\left(\eta \right)+\mathbf{R}\left(\eta \right)\mathbf{x}\left(\eta -\frac{2T}{T_o}\right) $$

(8)

Then, to obtain high approximation accuracy, the state term x(t) over the discrete time points is approximated with the Legendre expansion of spectral convergence, and its corresponding derivative is acquired via a novel and fast algorithm. To begin with, the continuous state x(t) is accurately approximated by Legendre polynomials L_k(t), for k = 0,. .., m:

$$ x(t)\approx \sum \limits_{k=0}^m{a}_k{L}_k(t) $$

(9)

where a_k, for k = 0,. .., m, are Legendre coefficients to be determined.

To obtain these unknown coefficients a_k, for k = 0,. .., m, substitute the discrete time points into Eq. (9), and one can obtain

$$ \left(\begin{array}{c}{a}_0\\ {}{a}_1\\ {}\vdots \\ {}{a}_m\end{array}\right)={\left(\begin{array}{cccc}{L}_0\left({t}_0\right)& {L}_1\left({t}_0\right)& \cdots & {L}_m\left({t}_0\right)\\ {}{L}_0\left({t}_1\right)& {L}_1\left({t}_1\right)& \cdots & {L}_m\left({t}_1\right)\\ {}\vdots & \vdots & \ddots & \vdots \\ {}{L}_0\left({t}_m\right)& {L}_1\left({t}_m\right)& \cdots & {L}_m\left({t}_m\right)\end{array}\right)}^{-1}\left(\begin{array}{c}x\left({t}_0\right)\\ {}x\left({t}_1\right)\\ {}\vdots \\ {}x\left({t}_m\right)\end{array}\right)={\mathbf{L}}^{-1}\left(\begin{array}{c}x\left({t}_0\right)\\ {}x\left({t}_1\right)\\ {}\vdots \\ {}x\left({t}_m\right)\end{array}\right) $$

(10)

It is worth noting that the constant matrix L can be easily acquired by utilizing the following recursive formulas:

$$ \Big\{{\displaystyle \begin{array}{l}{L}_0(t)=1\\ {}{L}_1(t)=t\\ {}\left(n+1\right){L}_{n+1}(t)=\left(2n+1\right)t{L}_n(t)-n{L}_{n-1}(t),n=1,2,\cdots \end{array}} $$

(11)

On the other hand, to acquire the derivative term, i.e.,$\overset{\cdotp }{x(t)}$, we find the coefficients d_k that satisfy the following relationship.

$$ \overset{\cdotp }{x(t)}=\sum \limits_{k=0}^m{a}_k\overset{\cdotp }{L_k(t)}=\sum \limits_{k=0}^m{d}_k{L}_k(t) $$

(12)

Following the Ref. [53], the coefficients d_k can be obtained with the following transformation:

$$ \left(\begin{array}{c}{d}_0\\ {}{d}_1\\ {}\vdots \\ {}{d}_m\end{array}\right)=\mathbf{Q}\left(\begin{array}{c}{a}_0\\ {}{a}_1\\ {}\vdots \\ {}{a}_m\end{array}\right) $$

(13)

where Q can be deduced as

$$ \mathbf{Q}:= \left[{Q}_{hk}\right]:= \Big\{{\displaystyle \begin{array}{l}2h+1\ 0\le h,k\le m-1,k=h+1,h+3,h+5,\cdots \\ {}0\kern2.75em \mathrm{otherwise}\kern2.25em \end{array}} $$

(14)

On this basis, the derivative of x(t_j) can be obtained as

$$ \overset{\cdotp }{x\left({t}_j\right)}=\sum \limits_{k=0}^m{d}_k{L}_k\left({t}_j\right)=\left({L}_0\left({t}_j\right),{L}_1\left({t}_j\right),\cdots, {L}_m\left({t}_j\right)\right)\mathbf{Q}\left(\begin{array}{c}{a}_0\\ {}{a}_1\\ {}\vdots \\ {}{a}_m\end{array}\right) $$

(15)

Then, one can further obtain

$$ \left(\begin{array}{c}\overset{\cdotp }{x\left({t}_0\right)}\\ {}\overset{\cdotp }{x\left({t}_1\right)}\\ {}\vdots \\ {}\overset{\cdotp }{x\left({t}_m\right)}\end{array}\right)=\mathbf{LQ}\left(\begin{array}{c}{a}_0\\ {}{a}_1\\ {}\vdots \\ {}{a}_m\end{array}\right) $$

(16)

Substitute Eq. (10) into Eq. (16), and one can obtain

$$ \left(\begin{array}{c}\overset{\cdotp }{x\left({t}_0\right)}\\ {}\overset{\cdotp }{x\left({t}_1\right)}\\ {}\vdots \\ {}\overset{\cdotp }{x\left({t}_m\right)}\end{array}\right)=\mathbf{LQ}{\mathbf{L}}^{-1}\left(\begin{array}{c}x\left({t}_0\right)\\ {}x\left({t}_1\right)\\ {}\vdots \\ {}x\left({t}_m\right)\end{array}\right) $$

(17)

With the aid of Kronecker product, the vector form for Eq. (17) is deduced as

$$ \left(\begin{array}{c}\overset{\cdotp }{\mathbf{x}\left({t}_0\right)}\\ {}\overset{\cdotp }{\mathbf{x}\left({t}_1\right)}\\ {}\vdots \\ {}\overset{\cdotp }{\mathbf{x}\left({t}_m\right)}\end{array}\right)=\left(\mathbf{LQ}{\mathbf{L}}^{-1}\right)\otimes {\mathbf{I}}_{n\times n}\left(\begin{array}{c}\mathbf{x}\left({t}_0\right)\\ {}\mathbf{x}\left({t}_1\right)\\ {}\vdots \\ {}\mathbf{x}\left({t}_m\right)\end{array}\right)=\mathbf{H}\left(\begin{array}{c}\mathbf{x}\left({t}_0\right)\\ {}\mathbf{x}\left({t}_1\right)\\ {}\vdots \\ {}\mathbf{x}\left({t}_m\right)\end{array}\right) $$

(18)

where ⊗ represents the Kronecker product, while n denotes dimension for x(t).

On the other hand, over t_j, 0 ≤ j ≥ m, Eq. (8) needs to satisfy

$$ \frac{2}{T_o}\overset{\cdotp }{\mathbf{x}\left({t}_j\right)}=\left({\mathbf{S}}_c+\mathbf{S}\left({t}_j\right)\right)\mathbf{x}\left({t}_j\right)+\mathbf{R}\left({t}_j\right)\mathbf{x}\left({t}_j-\frac{2T}{T_o}\right) $$

(19)

However, over interval [0, T_r], the solution of milling dynamic equation has an explicit from. Therefore, x(t) at the first time point t₀ of the forced vibration time period can be obtained directly by

$$ \mathbf{x}\left({t}_0\right)={e}^{{\mathbf{S}}_c{T}_r}\mathbf{x}\left({t}_m-\frac{2T}{T_o}\right) $$

(20)

Utilizing [I_n × n, 0_n × n, …, 0_n × n] to replace first n rows of H, a new constant matrix H_s can be obtained. Combining Eqs. (18)~(20), one will acquire a discrete map as follows:

$$ \mathbf{U}\left(\begin{array}{c}\mathbf{x}\left({t}_0\right)\\ {}\mathbf{x}\left({t}_1\right)\\ {}\vdots \\ {}\mathbf{x}\left({t}_m\right)\end{array}\right)=\mathbf{W}\left(\begin{array}{c}\mathbf{x}\left({t}_0-\frac{2T}{T_o}\right)\\ {}\mathbf{x}\left({t}_1-\frac{2T}{T_o}\right)\\ {}\vdots \\ {}\mathbf{x}\left({t}_m-\frac{2T}{T_o}\right)\end{array}\right) $$

(21)

where

$$ \mathbf{U}=\frac{2}{T_o}{\mathbf{H}}_s+{a}_p\left(\begin{array}{cccc}\mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\\ {}\mathbf{0}& \mathbf{G}\left({t}_1\right)& \cdots & \mathbf{0}\\ {}\vdots & \vdots & \ddots & \vdots \\ {}\mathbf{0}& \mathbf{0}& \cdots & \mathbf{G}\left({t}_m\right)\end{array}\right)=\frac{2}{T_o}{\mathbf{H}}_s+{a}_p\mathbf{V} $$

(22)

$$ \mathbf{W}=\left(\begin{array}{cccc}\mathbf{0}& \mathbf{0}& \cdots & {e}^{{\mathbf{S}}_c{T}_r}\\ {}\mathbf{0}& \mathbf{R}\left({t}_1\right)& \cdots & \mathbf{0}\\ {}\vdots & \vdots & \ddots & \vdots \\ {}\mathbf{0}& \mathbf{0}& \cdots & \mathbf{R}\left({t}_m\right)\end{array}\right)={a}_p\mathbf{V}+\left(\begin{array}{cccc}\mathbf{0}& \mathbf{0}& \cdots & {e}^{{\mathbf{S}}_c{T}_r}\\ {}\mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\\ {}\vdots & \vdots & \ddots & \vdots \\ {}\mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\end{array}\right) $$

(23)

Then, the transition matrix Ψ via Chebyshev-Legendre-based algorithm is obtained by

$$ \boldsymbol{\Psi} ={\mathbf{U}}^{-1}\mathbf{W} $$

(24)

Eventually, by exploring the value of spectral radius of Ψ, i.e., κ(Ψ) = max (|λ(Ψ)|), one can gain stability characteristics via Floquet theory.

It should be noted that the matrix U can be easily obtained by multiplying the depth of cut a_p by a constant matrix V (i.e., a_pV) when sweeping the depth of cuts and multiplying the spindle speed related term 2/T₀ by a constant matrix H_s (i.e., 2/T₀H_s) when sweeping the spindle speeds. Consequently, W is acquired directly by simply employing [0, 0, …,${e}^{{\mathbf{S}}_c{T}_r}$] to replace first n rows of a_pV. Besides, Eq. (24) shows that constructing Ψ is fulfilled by simply one matrix multiplication. Therefore, benefiting from the explicit form of nonuniform discrete points and the way of constructing Ψ, the presented Chebyshev-Legendre-based algorithm should obtain high calculation speed.

3 Algorithm validation and milling stability prediction

In this section, algorithm validation of LCM is conducted with the same computational conditions and same program structure. Two milling models in Ref. [26] are employed when making comparisons with 2nd SDM and ASM. In general, conventional milling process and rough milling process adopt large radial immersions, in which the tool spends considerable large part of system period machining workpiece [6]. However, for highly interrupted milling operations (e.g., finish milling operations on flexible components), the radial immersion can be very low, in which milling cutter just takes a little part of system period to machine workpiece [13]. For such cases, it shows high intermittence in milling force, resulting in high-frequency components [9]. Hence, two different cases need to be explored and analyzed comprehensively for algorithm validation. Additionally, for completeness, the stability diagrams are predicted utilizing 2nd SDM, ASM, and LCM as well.

3.1 One DOF milling operation

As presented in Refs. [26, 51], the milling dynamic model of one DOF system is formulated as

$$ {m}_t\overset{\cdotp \cdotp }{x(t)}+2{m}_t\zeta {\omega}_n\overset{\cdotp }{x(t)}+{m}_t{\omega_n}^2x(t)=-{a}_p{g}_{xx}(t)\left[x(t)-x\left(t-T\right)\right] $$

(25)

in which g_xx(t) is deduced in Eq. (4) and equals to the coefficient matrix G(t). Meanwhile, m_t, ω_n, and ζ are the system modal parameters. With the aid of the transformation presented in previous part, the above equation could be re-expressed as

$$ \overset{\cdotp }{\mathbf{x}(t)}=\left({\mathbf{S}}_c+\mathbf{S}(t)\right)\mathbf{x}(t)+\mathbf{R}(t)\mathbf{x}\left(t-T\right) $$

(26)

with

$$ {\mathbf{S}}_c=\left(\begin{array}{cc}-\zeta {\omega}_n& 1/{m}_t\\ {}{m}_t{\zeta}^2{\omega_n}^2-{m}_t{\omega_n}^2& -\zeta {\omega}_n\end{array}\right),\kern0.36em \mathbf{S}(t)=-\mathbf{R}(t)=-{a}_p\left(\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ {}{g}_{xx}(t)& \mathbf{0}\end{array}\right) $$

(27)

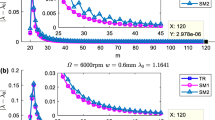
For ease of comparison, we use identical one DOF system parameters from [26] by: N = 2, K_n = 2 × 10⁸ N/m², K_t = 6 × 10⁸ N/m², m_t = 0.03993 kg, ω_n = 922 × 2π rad/s, ζ = 0.011, and down milling. As we all know, accuracy of semi-analytical algorithms could be presented intuitively through convergence rate curve. Accordingly, to validate proposed Chebyshev-Legendre-based algorithm, we will construct the diagrams of the convergence rate. It should be pointed out that the approximation order for ASM has been analyzed and proved to be greater than O(τ⁴), where τ denotes discrete step [51]. Simultaneously, the 2nd SDM is found to be O(τ³). Mathematically, the Legendre expansion is exponentially convergent, depending on the degree of the Legendre polynomials. Since time intervals m is consistent with the degree of the Legendre polynomials in the proposed method, it should gain better convergence rate than 2nd SDM and ASM. Figure 1 presents comparisons among 2nd SDM, ASM, and LCM with a/D = 1.0 and two different spindle speeds. The reference value calculated utilizing LCM with time intervals m = 600 is denoted as |λ₀| in Fig. 1. And the approximate ones written as |λ| are calculated utilizing 2nd SDM, ASM, and LCM. For completeness of comparison, various depths of cut a_p are adopted. Besides, we will employ logarithmic coordinates, which facilitates observation and comparison of results. As we can see, the approximate value |λ| predicted utilizing LCM converges to reference |λ₀| much faster than those predicted utilizing the other two algorithms. Consequently, the LCM obtains much higher accuracy than 2nd SDM and ASM.

Fig. 1

Comparisons among 2nd SDM, ASM, and LCM with a/D = 1.0 and spindle speed Ω = 7000 rpm, 9000 rpm

To avoid chatter and increase productivity, high-performance stability analysis and choosing appropriate cutting parameters are of vital importance. However, computational accuracy and calculation speed are generally limited to each other. Hence, for the completeness of algorithm verification, the stability lobes of these models are also constructed with 2nd SDM, ASM, and LCM. The domain of parameter combinations are selected as follows: a_p ∈ [0, 10]mm and the Ω ∈ [5, 25]krpm. Computing time for 2nd SDM, ASM, and LCM and stability lobes over a 250 × 150 sized grid with a/D = 1.0 are illustrated in Fig. 2. The reference stability limits with red line in Fig. 2 are calculated utilizing LCM with time intervals m = 600. Meanwhile, m for 2nd SDM, ASM, and LCM are selected as 30 and 40, respectively. Based on Fig. 2, the accuracy for lobes predicted utilizing LCM is better than those utilizing 2nd SDM and ASM with identical computing parameters. Hence, the results validate that the LCM achieves better computing accuracy than 2nd SDM and ASM. Simultaneously, LCM obtains faster calculation speed than 2nd SDM and ASM. Specifically, LCM could save computing time by almost 76~82% when comparing with 2nd SDM and by approximately 46~60% when comparing with ASM. Then, we select a/D as 0.6, and Fig. 3 presents the computing time of these methods and corresponding stability lobs. Now, m are set as 12 and 20. Figure 3 indicates that LCM obtains higher computing accuracy and speed than other two algorithms with a/D = 0.6. When comparing with 2nd SDM and ASM, LCM could save computing time by approximately 82~89% and 68~71%, respectively.

Fig. 2

Computing time for 2nd SDM, ASM, and LCM and stability lobes of the single-DOF milling with the a/D = 1.0 calculated by these algorithms

Fig. 3

Computing time for 2nd SDM, ASM, and LCM and stability lobes of the single-DOF milling with the a/D = 0.6 calculated by these algorithms

3.2 Two DOF milling operation

As presented in Refs. [26, 51], the milling model for two DOF case is formulated as

$$ {\displaystyle \begin{array}{l}\left[\begin{array}{cc}{m}_t& 0\\ {}0& {m}_t\end{array}\right]\left[\begin{array}{l}\overset{\cdotp \cdotp }{x(t)}\\ {}\overset{\cdotp \cdotp }{y(t)}\end{array}\right]+\left[\begin{array}{cc}2\zeta {\omega}_n{m}_t& 0\\ {}0& 2\zeta {\omega}_n{m}_t\end{array}\right]\left[\begin{array}{l}\overset{\cdotp }{x(t)}\\ {}\overset{\cdotp }{y(t)}\end{array}\right]+\left[\begin{array}{cc}{\omega_n}^2{m}_t& 0\\ {}0& {\omega_n}^2{m}_t\end{array}\right]\left[\begin{array}{l}x(t)\\ {}y(t)\end{array}\right]\\ {}\kern2.25em =-{a}_p\left[\begin{array}{cc}{g}_{xx}(t)& {g}_{xy}(t)\\ {}{g}_{yx}(t)& {g}_{yy}(t)\end{array}\right]\left(\left[\begin{array}{l}x(t)\\ {}y(t)\end{array}\right]-\left[\begin{array}{l}x\left(t-T\right)\\ {}y\left(t-T\right)\end{array}\right]\right)\end{array}} $$

(28)

By utilizing same matrix transformation, Eq. (28) could be re-expressed as

$$ \overset{\cdotp }{\mathbf{x}(t)}=\left({\mathbf{S}}_c+\mathbf{S}(t)\right)\mathbf{x}(t)+\mathbf{R}(t)\mathbf{x}\left(t-T\right) $$

(29)

in which

$$ {\mathbf{S}}_c=\left(\begin{array}{cccc}-\zeta {\omega}_n& 0& 1/{m}_t& 0\\ {}0& -\zeta {\omega}_n& 0& 1/{m}_t\\ {}\left({\zeta}^2-1\right){\omega_n}^2{m}_t& 0& -\zeta {\omega}_n& 0\\ {}0& \left({\zeta}^2-1\right){\omega_n}^2{m}_t& 0& -\zeta {\omega}_n\end{array}\right) $$

(30)

$$ \mathbf{S}(t)=-\mathbf{R}(t)=-{a}_p\left(\begin{array}{l}\kern0.75em 0\kern1.25em 0\kern1em 0\kern0.75em 0\\ {}\kern0.75em 0\kern1.25em 0\kern1em 0\kern0.75em 0\\ {}{g}_{xx}(t)\kern0.75em {g}_{xy}(t)\kern0.5em 0\kern0.75em 0\ \\ {}{g}_{yx}(t)\kern0.75em {g}_{yy}(t)\kern0.5em 0\kern0.75em 0\end{array}\right) $$

(31)

Figure 4 illustrates the computing time for 2nd SDM, ASM, and LCM and stability lobes of the two DOF milling with a/D = 1.0 and 0.6 calculated by these methods. The stability lobes are also draw on a 250 × 150 sized grid, while m is set as 30. Reference stability lobes with red line in Fig. 4 are gained utilizing LCM with time intervals m = 600 as well. For ease of comparison, we also adopt identical two DOF system parameters from [26]. Besides, the domain of cutting parameter combinations is set as follows: a_p ∈ [0, 10]mm and the Ω ∈ [5, 25]krpm. Based on Fig. 4, lobes predicted utilizing LCM reveal better agreement with reference lobes when comparing with 2nd SDM and ASM under same computational parameters. Consequently, it validates that LCM achieves better computing accuracy than 2nd SDM and ASM. Meanwhile, calculation speed for LCM is faster than 2nd SDM and ASM. Compared with 2nd SDM and ASM, it can save about 52~56% and 29% computational time, respectively. Then, we select a/D as 0.06, and select m as as 10 and 20, respectively. Results are shown in Fig. 5, which indicates that LCM obtains higher computing accuracy and faster computing speed than the other two algorithms with a/D = 0.06. When comparing with 2nd SDM and ASM, now it can save about 58~78% and 39~57% computational time, respectively.

Fig. 4

Computing time for 2nd SDM, ASM, and LCM and stability lobes for two DOF milling with a/D = 1.0 and 0.6 calculated by these algorithms

Fig. 5

Computing time for 2nd SDM, ASM, and LCM and stability lobes for two DOF milling with a/D = 0.06 calculated by these algorithms

4 Conclusion

In this study, it develops a Legendre-Chebyshev-based algorithm for improving accuracy of milling stability analysis and at the same time reducing the calculation time. The milling dynamics model, i.e., DDEs, is re-represented as the state-space equation utilizing specific transformation, and the period is divided into two subintervals based on cutting state of milling dynamic system. After that, we discretize forced vibration interval nonuniformly into the Chebyshev-Gauss-Lobatto points by introducing appropriate variable transformation. Finally, to acquire Floquet matrix over the system period of milling model, we employ the Legendre expansion with spectral accuracy to match the state term over nonuniform time points and obtain its corresponding derivative by a novel and fast algorithm.

To validate the convergence rate, calculation efficiency, and versatility of LCM, two benchmark models are employed, and comprehensive comparisons with recent 2nd SDM and ASM are conducted. It verifies that proposed LCM obtains higher computing accuracy and faster speed than 2nd SDM and ASM and can obtain accurate and fast stability lobes prediction. For the one and the two DOFs milling models, the computational time can be saved by almost 76~89% and 52~78% when compared with the 2nd SDM, respectively. Meanwhile, when comparing with ASM, LCM could save computing time by about 46~71% and 29~57% for the two benchmark milling examples, respectively. Consequently, it shows good application prospects in real manufacturing and can be used by engineers and technicians to determine optimal chatter-free milling parameters.