A model predictive path control algorithm of single-point incremental forming for non-convex shapes

Abstract

The geometrical error of the formed part is one of the most significant limitations that restricts the widespread application of incremental sheet forming (ISF) in aerospace industry. The geometry of ISF parts is dependent upon the tool path, so its correction can improve the part precision. Previous research has utilized model predictive control approach to achieve this, but the method was restricted to simple convex shapes. In this study, the tool path and the formed shape were parameterized and the analytical models of geometry responses relative to tool perturbations were proposed. Then, a model predictive control algorithm was developed, aiming at reducing the geometrical errors of the parts with complex non-convex shapes in the ISF process. Experimental validation of the developed control algorithm was carried out by forming a complex shape by single-point incremental forming. The results show that the developed control algorithm greatly reduced the geometrical error in the closed-loop process.

1 Introduction

Incremental sheet forming (ISF) is an emerging flexible manufacturing technology. A great advantage of ISF compared to traditional sheet forming methods, such as stamping, is that a part-specific die is not necessary, especially for the single-point ISF, leading to significant savings in cost and time for the die making [1]. In the ISF process, a flat sheet can be formed into a part with a specific shape through continued accumulation of localized deformation caused by the movement of a tool following a pre-designed path [1, 2]. The target shape of the part can be altered at any time by simply changing the tool path. This unique feature greatly increases the flexibility of sheet forming, which enables ISF to be a promising technology for rapid small-batch and customized production [3, 4].

Despite this advantage of ISF over conventional sheet manufacturing technologies, there are unfortunately several significant limitations which currently prevent the widespread industrial application of ISF [3, 5, 6]. The main reason is that standard implementations of ISF cannot meet the part geometrical accuracy requirements for aerospace manufacturing industries [1, 7, 8]. The geometrical error between the formed and the target shape of the part are primarily due to the sheet springback [9]. Springback refers to the shape change of the formed part when the tool is released or the part is unclamped, which is a significant problem for all sheet manufacturing technologies [1, 10]. Furthermore, the bulging of the sheet in the bottom area and the bending of the sheet at the edges are also noticeable sources of the geometrical error [10, 11].

Many researchers have contributed to the improvement of the geometrical precision of ISF parts. As the part geometry is to a large extent determined by the paths of the tool movement, in the previous researches, three paradigms have been used to modify the tool paths: (1) Experimental observations-based approaches. The geometric accuracy was improved by modification of the CAD model from which the tool path was planned [12], changing of tool path parameters such as step-depth and scallop height [13, 14], selecting the tool path parameters via multi-objective optimization [15], and proposing a quadratic spiral tool path generation strategy [16]. However, these ad hoc approaches are suitable only for simple shapes and difficult to be generalized to other shapes. (2) Iterative forming of the whole parts by experiment or simulation. The tool paths were optimized after each forming iteration to achieve better geometric precision based on the measurements of the geometric deviations of the formed parts and the CAD models of the target parts, and iterations are halted when the geometric accuracy met the pre-determined requirements. Multiple iterative tool path alteration approaches have been considered including direct error feedback [17], iterative learning control [18, 19], and fast Fourier and wavelet transform–based feedback [9]. These methods are more generic and systematic than the empirical approaches; however, a common limitation shared by these approaches is that multiple parts need to be formed until the optimized tool path is determined. (3) Online tool path adjustment based on in-process shape feedback. In this approach, process of forming the shape is split into the forming of a sequence of contours. Intermediate shapes are measured after each of the contours are formed. Based on these measurements, the remaining tool path can be adjusted during the ISF processes by several approaches such as proportional control [20], impulse response model–based optimal control [21], and model predictive control (MPC) [1, 7, 22]. This type of tool path correction approaches enables real-time reductions of geometrical errors due to inappropriate tool paths or possible system disturbances.

The model predictive control method has recently drawn the attention of researchers as a possible online ISF tool path control approach. In MPC, a prediction model is used to predict the system response under a specific system state and inputs, and the control sequence driving the system to a desired state can be computed online by solving mathematical optimization problems, satisfying the system and/or input constraints [23, 24]. MPC usually works in a receding horizon manner. More specifically, at each sampling step, the control sequence is only solved in a finite horizon and only the first action in the control sequence will be executed by the plant. At the next sampling step, the control sequence will be solved repeatedly with the current state feedback [23, 25]. Hao and Duncan [22] confirmed the feasibility of MPC in ISF tool path control for the first time. Prior to the closed-loop ISF process, an open-loop process of forming the same part was conducted to determine the impulse response of geometry to step-depth perturbation which was used to develop a geometry prediction model. Then, a MPC control framework was formulated and validated on forming a truncated cone and a truncated pyramid [22]. Instead of using the experiment-based prediction model, Lu et al. [1] proposed a geometry-based prediction model to predict the response of the geometry to step-depth, and thus the pre-forming process in the work of Hao and Duncan et al. [22] was no longer not required. The MPC control framework was established and utilized in correcting the step-depths in closed-loop processes of forming a truncated cone and a truncated pyramid. Later, Lu et al. [7] for the first time proposed a MPC control framework which contained two parallel MPC controllers, i.e., the vertical controller and the horizontal controller. The vertical controller was the same as that in their previous work [1], while the horizontal controller was newly built aiming at compensating the geometrical errors on the side walls of the part.

Although the existing MPC control framework showed effectiveness in the case studies with single-point ISF [7], it has significant limitations that narrows down its applicable cases to parts with simple convex shapes and makes its application in forming more complex non-convex parts difficult. Firstly, the tool path contour was parameterized in a polar coordinates system and the corrections were then restricted in radial directions for all the points. This parametrization approach is only valid for convex shapes with horizontal contours that are close to circles, as shown in Fig. 1a. However, when the tangent of the contour is away from perpendicular to the radial direction, this method becomes ineffective, as shown in Fig. 1b and c, since corrections in the radial direction (as opposed to normal direction) may end up being tangent to the contour (i.e., normal to the direction of the error). Therefore, aiming at forming more complex parts drives the demand for the development of a new contour parameterization method. Secondly, the measured geometry was sampled in a number of vertical sections passing the origin of the polar coordinates system. In the horizontal module, the scaling factors of the radial coordinates of the tool path points at each sampling section were optimized, and the scaling factors of the rest tool path points were calculated through linear interpolation based on nominal radial coordinates. The prerequisite of this radial-based interpolation method is that between each section, the nominal radial coordinates of the tool path points vary monotonically. This interpolation approach applied to simple convex shapes only and may have limited capability when applying to non-convex shapes. Additionally, in the existing MPC framework [7], the horizontal and vertical control modules are uncoupled and worked in parallel without sharing the optimization results. Actually, the step-depth and the step-over have coupled effects on the geometry, and the existing uncoupled control framework may result in poor performance when the part becomes complex. Thus, a new MPC framework that couples the two modules is expected to be proposed.

Fig. 1

The existing polar-based parameterization approach [7] is effective on a a convex part with circular horizontal contour, but ineffective on b a convex part with non-circular horizontal contour and c a non-convex part (representative figure, not to scale) because the radial direction differs from the error direction

In this work, the MPC control algorithm developed by Lu et al. [7] was improved and generalized to form complex parts by single-point ISF. Firstly, parameterization approaches of the tool path and the formed shape are presented. Furthermore, prediction models for horizontal and vertical geometry responses relative to tool perturbations are proposed. Then, an MPC control algorithm is developed with the horizontal and vertical modules coupled in a sequential manner. The optimizations are mapped to quadratic programming (QP) problems. To test the feasibility and performance of the developed control framework, a “dog bone”–shaped part which had a non-convex shape and varying curvatures is formed by single-point ISF.

2 Parameterization of the tool path and the formed shape

In this section, the parameterization of the tool path and the formed shape is presented, which will be applied in ISF process modeling (Section 3) and MPC control algorithm development (Section 4).

2.1 Parameterization of tool path

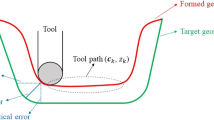
In most cases, as shown in Fig. 2, the ISF tool path is composed of a series of points in three-dimensional space, referred to as tool path points. In this work, when the controller is activated, the closed-loop tool path is parameterized by horizontal contours using periodic and parametric spline representation [26, 27] c and vertical depths z. With this parameterization, the initial tool path contour can be evenly sampled into m tool path points by spline interpolation. This ensures the uniform distribution of the tool path points and the corresponding tool path points in each contour share the same normal.

Fig. 2

Schematic diagram of single-point ISF processes

The ISF process performs effectively in discrete time, during which the tool usually moves clockwise or counterclockwise, following a tool path contour c_k in the horizontal plane with a fixed depth z_k to complete an intermediate step k and then steps down to an intermediate step k + 1, until the final step n, as is shown in Fig. 2. In this process, the geometry response relative to the tool perturbation is localized to the end of the tool. By the accumulation of the localized deformation, global deformation can be achieved. Since the movement of the machine tool used in this work is restricted into the vertical and horizontal directions only, between the two neighboring steps k and k + 1, the movement of the tool is decomposed into a vertical step-depth u_{v, k + 1} and a horizontal step-over u_{h, k + 1} respectively. The direction of the step-depth is fixed to the vertical direction, and thus u_{v, k + 1} is a vector of scalars. Whereas the directions of horizontal movement of all the tool path points are different, although they are in the same horizontal plane, u_{v, k + 1} is a vector of vectors. The two vectors are expressed as

$$ {\boldsymbol{u}}_{\mathrm{h},k+1}=\left[{\boldsymbol{u}}_{\mathrm{h},k+1,1}\kern0.5em {\boldsymbol{u}}_{\mathrm{h},k+1,2}\kern0.5em \mathbf{\cdots}\kern0.5em {\boldsymbol{u}}_{\mathrm{h},k+1,\mathrm{m}}\right] $$

(1)

$$ {\boldsymbol{u}}_{\mathrm{v},k+1}=\left[{u}_{\mathrm{v},k+1,1}\kern0.5em {u}_{\mathrm{v},k+1,2}\kern0.5em \mathbf{\cdots}\kern0.5em {u}_{\mathrm{v},k+1,\mathrm{m}}\right] $$

(2)

As is pointed out above, in each step of ISF process, the tool path contours are at fixed depths, and thus

$$ {u}_{\mathrm{v},k+1,1}={u}_{\mathrm{v},k+1,2}=\dots ={u}_{\mathrm{v},k+1,\mathrm{m}}:= {u}_{\mathrm{v},k+1} $$

(3)

Therefore, the relations of the tool path contours between the neighboring steps can be expressed as

$$ {\boldsymbol{c}}_{k+1}={\boldsymbol{c}}_k+{\boldsymbol{u}}_{\mathrm{h},k+1} $$

(4)

$$ {z}_{k+1}={z}_k+{u}_{\mathrm{v},k+1}. $$

(5)

2.2 Parameterization of the formed shape

The geometric error between the formed and the target shape of the part by single-point ISF is illustrated in Fig. 3. To facilitate further analyses, in this work, the target shape was virtually divided into four zones, i.e., edge, wall, conjunction, and base, as shown in Fig. 3. In Fig. 3, α is the wall angle, r is the radius of the tool, and w is the depth of the target shape. The edge zone is the area of the sheet near the edges of the target shape. Wang et al. [28] and Lu et al. [1] both reported that the geometrical error in the edge zone is mainly caused by sheet bending and for single-point ISF cannot be compensated through feedback control without support from underneath the sheet. For this reason, the shapes in the edge zones were not considered in their studies [1, 28] and this study. The base and the wall zones consist of the majority of the area of the part, and thus compensation for the error in the base and the wall zone is the focus of this research. The conjunction zone is the transient area between the wall and the base zone.

Fig. 3

Schematic diagram of the formed and the target shape (representative figure, not to scale)

For any point on the formed shape, the geometrical error is the distance to its nearest neighboring point on the target shape. As shown in Fig. 3, the geometrical error can be decoupled into the horizontal geometric error and the vertical geometric error. The horizontal geometric error is the major concern in the wall zone of which the geometry is mainly affected by the horizontal tool path contour c_k. The geometry of the base zone and the inside half of the conjunction zone is determined by the depth of the tool path contour z_k, and the vertical geometric error is the focus of this research. In the closed-loop ISF process, at each intermediate step, u_h and u_v can be optimized to reduce the horizontal and the vertical geometrical error respectively, leading to the improvement of final part precision. To this end, the formed shape is parameterized in the horizontal and vertical directions for the process modeling in the next section.

2.2.1 Horizontal parameterization

In the optimization of u_h, both the values and directions of step-overs for all the tool path points should be determined. In each contour, there are positive correlations between the number of tool path points and the size and the complexity of the target shape. Optimizing the values and directions of the step-overs for all the tool path points is practically infeasible, since the space of the possible step-overs is enormous [21]. To reduce the complexity of the optimization of u_h to meet the computational time requirement of the online MPC controller, Lu et al. [7] parameterized the tool path contour with polar coordinates system, and they set the directions of the step-overs of all the tool path points as their radial directions. In this way, the dimensionality of u_h was reduced to a vector of scalars, which make the on-line control of u_h feasible. However, as discussed in Section 1, this polar-based parameterization becomes less effective as the complexity of the target shape increases and is invalid for non-convex shapes. Therefore, a more generic contour-based parameterization approach is proposed in this work.

The unit normal vectors n_hfor all the closed-loop tool path points were calculated. In the optimization process of u_h, the direction of the optimized step-over was set as the normal direction of each tool path point. Thus,

$$ {\boldsymbol{u}}_{\mathrm{h},i}={u}_{\mathrm{h},i}{\boldsymbol{n}}_{\mathrm{h},i}\kern0.75em \forall i=1,2,\cdots, m $$

(6)

where the subscript i represents that the variable is related to ith tool path point in a tool path contour. Figure 4 shows the comparison between the directions of the optimized step-overs in the polar-based parameterization of [7] and the new contour-based parameterization approach. Therefore, for each tool path point, the optimization of the vector u_{h, i} was simplified to the optimization of the scalar u_{h, i}.

Fig. 4

Comparison between the directions of the optimized step-overs in the polar-based [7] and the new contour-based parameterization approach (representative data, not to scale)

An algorithm has been developed to detect the locations on the edge contour of the target shape, referred to as critical locations, where the curvature changes signs or is discontinuous. For the shape with constant slope, the algorithm only needs to be performed once, since the features of the horizontal contours of the shape at different depths are the same. The longitudinal section of the target shape at each critical location that passes its normal is referred to as a critical section. With the contour-based local coordinate systems taking the critical locations as the origins, the formed shapes of each intermediate step in each critical section are measured, and the step-overs in each critical section will be optimized. Figure 5 shows the critical locations on the edge of a “dog bone”–shaped part, and the comparison between the vertical sections at the critical locations in the polar-based [7] and the contour-based reference frame. Figure 6 shows the schematic diagram of a critical section.

Fig. 5

Critical locations on the edge of a “dog bone”–shaped part and the comparison between the vertical sections in the polar-based [7] and the contour-based reference frame

Fig. 6

Schematic diagram of a critical section

To meet the computational time requirement of the controller, the optimization of the step-overs is performed independently in these critical sections on the formed shape. In each critical section, one point on the wall, referred to as a horizontal geometry representation point, is chosen as a representative of the wall. As is shown in Fig. 6, in the contour-based local coordinate system, the intersection between the horizontal line with a depth of w_v + r(1 − cos α) and the measured shape is the horizontal geometry representation point. This point on the partially formed shape is identified in each intermediate step throughout the ISF process. The value of the geometry representation point on the n-axis, i.e., the horizontal distance from the geometry representation point to the edge, is the measured state of the geometry representation point y_h. The value of the target shape in the same critical section at the same depth is the reference state of the geometry representation point w_h. It is obvious that driving the horizontal geometry representation points in all the critical section to their references leads to the reduction of the horizontal geometrical errors over the entire shape.

However, there is no guarantee that for each critical section, there is a tool path point in it; thus, an approach to associate the calculation results in critical sections to the tool path points is proposed. As the tool path points are usually dense enough, the optimal values of step-overs calculated in each critical section are respectively assigned to the tool path points which are the nearest neighboring points to each of the corresponding critical locations on the edge of the shape. The step-overs of the unassigned tool path points can be approximated by linear interpolation based on the nominal spline length between the tool path points and two neighboring assigned tool path points. Since the initial tool path was evenly sampled, i.e., the distance between each pair of neighboring tool path points is constant, the interpolation process was performed based on the index of the tool path points, as illustrated in Fig. 7.

Fig. 7

Illustration of the association of the critical sections to tool path points (representative figure, not to scale)

2.2.2 Vertical parameterization

The formed and the target shape are registered into the same Cartesian frame of reference. An equally spaced grid representation in the horizontal plane is projected onto the surface of the formed shape. As the vertical geometric error is mainly seen in the surfaces of the part that are horizontal, i.e., the base zone and the inner half of the conjunction zone, the projection points on the formed shape in these zones are selected as the vertical geometry representation points. The measured state of each geometry representation point is its z coordinates, while the reference state is the target depth of the concerning step.

3 Modeling of ISF process

In the single-point ISF process, the part is formed from a flat sheet. In the initial period, i.e., first few steps, global deformation is dominating and the shape of the wall cannot be formed to the full extent [21, 29]. After the initial period, the response of the shape is localized to the end of the tool, and the development of an analytical model of the shape responses relative to the tool perturbation can become feasible [21]. Due to its high non-linearity, an ideal ISF prediction model ${\hat{y}}_{k+1}=f\left({y}_k,{c}_{k+1},{z}_{k+1}\right)$ is non-linear. To simplify the optimization problem, the model was decoupled as the horizontal prediction model ${\hat{y}}_{\mathrm{h},k+1}=h\left({y}_{\mathrm{h},k},{u}_{\mathrm{h}}\right)$ and the vertical prediction model ${\hat{y}}_{\mathrm{v},k+1}=v\left({y}_{\mathrm{v},k},{u}_{\mathrm{v}}\right)$. The horizontal model predicts the response of the horizontal geometry representation points relative to u_h, while the vertical model predicts the response of the vertical geometry representation points relative to u_v.

Allwood et al. [21] proposed that based on experience, it is very difficult to create a perfect non-linear geometry prediction model, and optimizing with the non-linear model is practically infeasible due to long computation time. Following [7, 22], to meet the computational time requirement of the MPC controller, the horizontal and vertical models are linearized to this general form

$$ {\hat{y}}_{d,k+1,\varTheta }={a}_{d,\varTheta }{y}_{d,k,\varTheta }+{b}_{d,\kern0.5em k+1,\varTheta }{u}_{d,k+1,\varTheta}\kern1.25em \forall k=\left[1,2,3,\cdots, n-1\right] $$

(7)

In Eq. (7), the subscript d represents the spatial direction which the equation is related to, and d can be h and v which represents for the horizontal and vertical directions respectively. The subscript Θ represents that the variable is related to the Θth geometry representation point in either horizontal or vertical direction. n is the number of total steps in the ISF process.

Assuming that the process is additive, i.e., the geometry change is independent on the previous geometry, in both horizontal and vertical models, a_{d, Θ} can be determined as 1. Thus, Eq. (7) can be further simplified as

$$ {\hat{y}}_{d,k+1,\varTheta }={y}_{d,k,\varTheta }+{b}_{d,\kern0.5em k+1,\varTheta }{u}_{d,k+1,\varTheta}\kern0.75em \forall k=\left[1,2,3,\cdots, n-1\right] $$

(8)

b_{d, k + 1, Θ} is the linear response of the geometry representation point relative to the spatial perturbation of the tool. This model assumes that the geometry of the formed part follows the tool path, and the springback of the sheet in the ISF process is handled through the feedback. Therefore, in the horizontal model, the linear response can be approximated by

$$ {b}_{\mathrm{h},\kern0.5em k+1,\tau }=\frac{{\hat{y}}_{\mathrm{h},k+1,\tau }-{y}_{\mathrm{h},k,\tau }}{u_{\mathrm{h},k+1,\tau }}\approx \frac{w_{\mathrm{h},k+1,\tau }-{w}_{\mathrm{h},k,\tau }}{{\overline{u}}_{\mathrm{h},\kern0.5em k+1,\tau }}=1\kern0.75em \forall k=\left[1,2,3,\cdots, n-1\right];\forall \tau =\left[1,2,3,\cdots, S\right] $$

(9)

where the subscript τ represents the variable is related to the τth horizontal geometry representation point; S is the total number of horizontal geometry representation points; ${\overline{u}}_{\mathrm{h}}$ represent for the nominal step-over; w_h is the reference state of the horizontal geometry representation points which can be obtained from the CAD model of the target shape. Similarly, in the vertical model, the linear response can be approximated as

$$ {b}_{\mathrm{v},\kern0.5em k+1,\eta }=\frac{{\hat{y}}_{\mathrm{v},k+1,\eta }-{y}_{\mathrm{v},k,\eta }}{u_{\mathrm{v},k+1}} \approx \frac{{\mathrm{w}}_{\mathrm{v},k+1,\eta }-{\mathrm{w}}_{\mathrm{v},k,\eta }}{{\overline{u}}_{\mathrm{v},k+1}}=1\kern0.75em \forall k=\left[1,2,3,\cdots, N-1\right];\forall \eta =\left[1,2,3,\cdots, G\right] $$

(10)

where the subscript η represents the variable is related to the ηth vertical geometry representation point; G is the total number of vertical geometry representation points; ${\overline{u}}_{\mathrm{v}}$ represent for the nominal step-depth; w_v is the reference state of the vertical geometry representation points.

For all the steps in the MPC prediction horizon, the above linear model can be built as the matrix equation

$$ {\hat{\boldsymbol{Y}}}_{k+1}={\boldsymbol{Y}}_k+\boldsymbol{B}{\boldsymbol{U}}_{k+1} $$

(11)

The detailed matrix building procedure can be found in [7].

4 Model predictive control algorithm

In an ISF process, the tool path contour is the input and the formed shape or partially formed shape is the output of the each forming step. Due to the computational complexity, the step-depth and step-over between each tool path contour and the positions of the geometry representation points are equivalently the input and output of this MPC control algorithm. MPC is performed after each step in a finite prediction horizon based on the feedback of the current shape. The goal of MPC is to minimize the difference, mathematically described by the ℓ₂-norm (‖·‖₂), between the predicted shape $\hat{\boldsymbol{Y}}$ and the reference shape W in the future steps.

As the prediction model is decoupled as the horizontal and the vertical model, in this MPC control algorithm, two control modules are developed, aiming at respectively optimizing step-over u_h and step-depth u_v. However, as the step-over u_h and step-depth u_v has coupled effects on the formed shape, to avoid possible opposing effects from two uncoupled modules and to achieve a better performance of the control algorithm, the two modules are coupled in a sequential manner in this work. More specifically, the horizontal module optimizes the step-over u_h first, and then the optimized step-over ${u}_{\mathrm{h}}^{\ast}$ are sent to the vertical module. This means, for the vertical module, the positions to step down are determined, and then the optimized step-depths ${u}_{\mathrm{v}}^{\ast}$ which match the optimized step-overs can be solved. Therefore, the optimal tool path of next step can be obtained

$$ {z}_{k+1}^{\ast }={z}_k+{u}_{\mathrm{v},k+1}^{\ast } $$

(12)

$$ {c}_{k+1,i}^{\ast }={c}_{k,i}+{u}_{\mathrm{h},k+1,i}^{\ast }{\boldsymbol{n}}_{\mathrm{h},i}\kern0.75em \forall i=1,2,\cdots, m $$

(13)

Figure 8 illustrates the block diagram of this control algorithm. The developments of the horizontal and vertical control module are presented respectively below.

Fig. 8

Block diagram of the developed control algorithm

In the horizontal control module, numerical optimization is performed to solve the optimal step-over in each critical section respectively. The optimization problem in the section τ can be mathematically expressed as

$$ {\displaystyle \begin{array}{c}\min {J}_{\mathrm{h},\tau }={\left\Vert {\hat{\boldsymbol{Y}}}_{\mathrm{h},k+\mathrm{p},\tau }-{\boldsymbol{W}}_{\mathrm{h},k+\mathrm{p},\tau}\right\Vert}_2+{\lambda}_{\mathrm{h}}{\left\Vert {\boldsymbol{U}}_{\mathrm{h},k+\mathrm{p},\tau }-{\overline{\boldsymbol{U}}}_{\mathrm{h},k+\mathrm{p},\tau}\right\Vert}_2\kern1.75em \\ {}\mathrm{subject}\ \mathrm{to}\kern0.75em {\Omega}_{\mathrm{h}1}\le {u}_{\mathrm{h},k+\rho, \tau }-{\overline{u}}_{\mathrm{h},k+\rho, \tau}\le {\Omega}_{\mathrm{h}2}\kern1.25em \forall \rho =1,2,\cdots, p\end{array}} $$

(14)

Similarly, the optimization problem of the vertical control module can be mathematically expressed as:

$$ {\displaystyle \begin{array}{c}\min {J}_{\mathrm{v}}={\left\Vert {\hat{\boldsymbol{Y}}}_{\mathrm{v},k+\mathrm{p}}-{\boldsymbol{W}}_{\mathrm{v},k+\mathrm{p}}\right\Vert}_2+{\lambda}_{\mathrm{v}}{\left\Vert {\boldsymbol{U}}_{\mathrm{v},k+\mathrm{p}}-{\overline{\boldsymbol{U}}}_{\mathrm{v},k+\mathrm{p}}\right\Vert}_2\kern2.5em \\ {}\mathrm{subject}\ \mathrm{to}\kern0.75em {\Omega}_{\mathrm{v}1}\le {u}_{\mathrm{v},k+\rho }-{\overline{u}}_{\mathrm{v},k+\rho}\le {\Omega}_{\mathrm{v}2}\kern1.25em \forall \rho =1,2,\cdots, p\kern1em \end{array}} $$

(15)

where λ_h and λ_v are non-negative weighting factors. In the cost functions, Eqs. (14) and (15), the first item quantifies the deviations between the predicted and target state and the second item represents the variations of the outputs from their nominal values. Following previous work [7], Eqs. (14) and (15) can be solved by mapping to quadratic programming (QP) problems.

5 Experimental verification

The performance of the control algorithm in forming the part with a non-convex shape by single-point ISF is assessed experimentally. A “dog bone”–shaped part, with non-convex horizontal contour and varying curvature, was selected as the benchmark in this work. The CAD model of the part is shown in Fig. 9 in which the forming areas on the sheet is marked in yellow. The detailed processing parameters are listed in Table 1. For comparison, the experiments were conducted with the existing control algorithm (MPC-0), the developed control algorithm in this work (MPC-1), and the control algorithm disabled (open-loop).

Fig. 9

The CAD model of the target shape

Table 1 Processing parameters

The experiments were conducted on an Amino computer-numerical-control (CNC) machine that can perform single-point and multi-point ISF processes. Z-level milling tool paths with constant step-depths were pre-generated by CAM with the surface milling module, and then the milling tool paths were further processed by an in-house program to be adapted to the single-point ISF process. To avoid the sheets being pushed to one side, for all the tests carried out in this work, the directions of the movement of the tool alternate between anticlockwise and clockwise. Backplates were placed under the sheets to provide additional supports to the non-forming areas of the sheets. Lubrication oil was used to decrease the friction between the end of the tool and the sheets. The geometry of the formed shapes and the intermediate shapes were measured by a Creaform HanyScan 300 3D scanner. The programming platform of the control algorithm was Python 3.6, and the package for solving the QP optimization was cvxopt [30]. The program was executed on a Windows 10 PC with a CPU of Intel Core i5-8400 and a RAM of 16GB.

In the open-loop experiments, all the intermediate steps were formed consecutively, and the final shapes were scanned. In the closed-loop experiments, due to the limitations of the equipment, the ISF process had to be temporarily paused at each intermediate step so that the measurement can by conducted by the 3D scanner. After the completion of one step, the tool was released, and the currently formed shape was scanned. Then, the tool moved back to the same position in which it was released for scanning to start the next step. The formed shapes of all the steps were scanned as clouds of points. The work coordinate system of CNC machine was set when planning the initial tool path with the CAD model of the target shape by CAM. For both the open-loop and the closed-loop experiments, all the scanned clouds of points were registered to the work coordinate system of CNC machine. The registration process consisted of two steps: (a) coarse registration—the cloud of points was manually registered to the CNC work coordinate system using the VXelements™ software [31]; (b) fine registration—the cloud of points was then registered to the CNC work coordinate system by an in-house plane-based Iterative Closest Points (ICP) algorithm [32, 33].

Following existing works [1, 7], in MPC-0, the vertical geometry representation points were selected from the origin to the top edge in a cross-section profile on the x-axis of the CNC work coordinate system. The horizontal geometry representation points were selected from the radial sampling sections at the same critical points on the edge as used in the newly developed algorithm, which is described in Section 2.1 and illustrated in Fig. 5. The prediction models in MPC-0 can be found in [1, 7].

As discussed in Section 3, the prediction model can only become valid after the first few steps in which the transition area is formed from the flat surface to the sloping wall and the shape of the wall cannot be formed to the full extent [21, 29]. Due to this limitation, in both closed-loop experiments, for steps 1–5, the ISF process was performed with the open-loop tool path. The controller was activated after the completion of step 5. In the following few steps from step 6, the vertical error on the base is large, which leads to large variance of the optimal step-depth to the nominal value. The vertical controller can reduce the vertical error rapidly, but it can cause large wall angle change. Hence, the horizontal controller was only enabled after the vertical error was significantly reduced. Therefore, the vertical module of the controller activated after step 5, while the horizontal controller activated after step 8. The control framework worked in the receding horizon manner. Considering the computational complexity, in both closed-loop experiments, the prediction horizon was 3 steps and was reduced when the final step was approaching. The other parameters of the control framework are list in Table 2.

Table 2 Parameters of the MPC

6 Results and discussions

Both the open-loop and closed-loop experiments were conducted for the assessment of the performance of the control algorithm. In the open-loop experiments, the initial tool path was executed by the CNC machine, with constant nominal step-depths and the step-overs. In the closed-loop experiment, after being activated, the vertical module and the horizontal module of developed algorithm responded quickly to take control of the step-depths and the step-overs. Figure 10 shows the output, i.e., the step-depths and the step-overs, of the control algorithm during the closed-loop process.

Fig. 10

Outputs of the control framework in the controlled steps of the ISF process: a step-depths of all tests, b step-overs of MPC-0 in section A, c step-overs of MPC-0 in section C, d step-overs of MPC-0 in section F, e step-overs of MPC-1 in section A, f step-overs of MPC-1 in section C, and g step-overs of MPC-1 in section F

Figures 11, 12, and 13 show the vertical sections of the part at the intermediate steps and the final step. The sections shown in Figs. 11, 12, and 13 pass three different critical locations shown in Fig. 5 and demonstrate the geometrical errors in the different areas on the part which represent different geometrical features of concave curve, convex curve, and the transition between the concave and the convex curves, respectively. The reduction of the geometrical error at different locations can be clearly observed in the section views, which was the contribution of the optimizations of the step-depths and the step-overs as shown in Fig. 10. As the vertical control module activated after step 5, the vertical geometrical error was reduced rapidly and tended to be stabilized after step 8. The horizontal control module was enabled after step 8, and in general, the horizontal geometrical error was reduced in the following steps.

Fig. 11

Comparisons of the target and the formed parts in normal vertical section A at the intermediate steps of a 5, b 8, and c 12 and the final step of d 15

Fig. 12

Comparisons of the target and the formed parts in normal vertical section C at the intermediate steps of a 5, b 8, and c 12 and the final step of d 15

Fig. 13

Comparisons of the target and the formed parts in normal vertical section F at the intermediate steps of a 5, b 8, and c 12 and the final step of d 15

To more clearly illustrate the geometrical error reduction achieved by the developed control algorithm, the global absolute error distribution maps of the parts formed by the open-loop and the closed-loop processes are presented in Fig. 14. In different zones on the part, i.e., edge, wall, conjunction, and base, statistical analyses of the global absolute error of the measured points were performed, and the results are listed in Tables 3, 4, 5, and 6 respectively. For the edge zone, there was no improvement of accuracy in both closed-loop processes. Hao and Duncan [28] and Lu et al. [1] both pointed out that due to lack of support from underneath, the geometric error cannot be reduced by closed-loop control approach in single-point ISF process, and the results in this work confirms their conclusions.

Fig. 14

Geometrical error distribution maps of the finally formed shapes with (a) controller disabled, (b) MPC-0, and (c) MPC-1

Table 3 Statistical analyses of the global absolute error in edge zone

Table 4 Statistical analyses of the global absolute error in wall zone

Table 5 Statistical analyses of the global absolute error in conjunction zone

Table 6 Statistical analyses of the global absolute error in base zone

In the base zone, the maximum errors were reduced from 1.84 mm (open-loop) to 0.50 mm (MPC-0) and 0.28 mm (MPC-1) respectively. Both algorithms greatly reduced the geometric error; however, the present MPC-1 algorithm achieved a lower maximum error by 44% compared to the previous MPC-0, which indicates that predictive model in MPC-1 can more accurately predict the geometric response relative to step-depth. In the wall zone, the maximum errors achieved in the tests were 1.73 mm (open-loop), 2.58 mm (MPC-0), and 1.03 mm (MPC-1), and the present MPC-1 had a lower maximum error by 60% compared to the previous MPC-0. In the conjunction zone, the maximum errors obtained in three tests were 1.65 mm (open-loop), 4.13 mm (MPC-0), and 1.06 mm (MPC-1), respectively, and the present MPC-1 achieved a lower maximum error by 74% compared to the previous MPC-0. It can be seen from Figs. 11 and 12 that in sections A and C, since the radial direction and the normal direction were identical, the measured profile of the part formed with the previous MPC-0 was similar to that with the present MPC-1. However, in sections where the radial direction is away from coincidence with the normal direction, such as section F, the difference between the measured profiles of the part formed by the previous and the present MPC algorithm became noticeable, as shown in Fig. 13. It can be noticed from Fig. 14 that with MPC-0, the geometric error of the formed part between sections B and C and sections C and D is higher than 2 mm. The reason was twofold. Firstly, the radial direction is not the direction of the springback on the wall of the part, and the springback cannot be effectively compensated by moving every tool path point along the radial direction. More importantly, the scaling factors of the tool path points lay between the sampled sections were calculated through radial-based interpolation method. This method become ineffective if the nominal radial coordinate of the unassigned point is out of the range of the radial coordinates of the two corresponding end points. For instance, the scaling factor of the 20th tool path point with a radial coordinate of 56.5624 was interpolated as 0.9857. As the springback on the wall was always toward inside, a scaling factor larger than 1.0 could enlarge the tool path contour to compensate the springback. However, a scaling factor smaller than 1.0 could shrink the contour. The experiment results demonstrate that although the existing control algorithm (MPC-0) performed effectively on forming simple shapes with single-point ISF in previous studies [7], it was not applicable to non-convex shapes. In contrast, the developed control algorithm (MPC-1) achieved a desired performance.

7 Conclusion

This work proposed and tested a general ISF tool path and geometry parameterization approach for non-convex shapes. With the step-depth and step-over between each forming step and the positions of the geometry representation points being the input and output, horizontal and vertical geometry prediction models were proposed, based on the assumption that the ISF process is additive and the geometry follows the tool path. An MPC control algorithm was developed with the geometry prediction model and quadratic programming optimizer, which includes the horizontal and the vertical modules that coupled in a sequential manner to optimize the tool paths, so as to achieve a lowest global geometrical error of the part.

To experimentally test the developed control algorithm, a “dog bone”–shaped part with non-convex horizontal contour and varying curvature was formed by single-point ISF. Both the open-loop process (with controller disabled) and the closed-loop process (with previous MPC-0 and present MPC-1) were conducted for comparison. The results show that in the base zone, the maximum errors were 1.84 mm (open-loop), 0.50 mm (MPC-0), and 0.28 mm (MPC-1) respectively; in the wall zone, the maximum errors were 1.73 mm (open-loop), 2.58 mm (MPC-0), and 1.03 mm (MPC-1) respectively; in the conjunction zone, the maximum errors were 1.65 mm (open-loop), 4.13 mm (MPC-0), and 1.06 mm (MPC-1) respectively. Compared to the previous MPC-0, the present MPC-1 reduced the maximum errors by 44%, 60%, and 74% in the base, wall, and conjunction zones respectively. This proved that the present control algorithm had a satisfactory performance in forming non-convex shapes, while the previous algorithm was not applicable.

The geometry response in the prediction model in this algorithm is approximated as constant for the entire shape. This may limit the performance of this algorithm when the target shape becomes more complex, since for different features on the part, such as flat surface, varying-sloped side wall, and constant-sloped side wall, the geometry response relative to tool perturbation may vary. Future work will focus on developing feature-based geometry prediction model to further adapt this MPC algorithm to processing more complex shapes by ISF.