Surfactant-induced retardation in lateral migration of droplets in a microfluidic confinement

Abstract

The present study deals with the effect of surfactants on the cross-stream migration of droplets in a confined fluidic environment, both experimentally and theoretically. Presence of an imposed flow induces droplet deformation and disturbs the equilibrium that results in subsequent surfactant redistribution along the interface. This further creates a gradient in surface tension, thus generating a Marangoni stress that significantly alters the droplet dynamics. On subsequent experimental investigation, it is found that presence of surfactants reduces the cross-stream migration velocity of the droplet. High-speed photography is utilized to visualize the transport of droplets in a microfluidic channel. It is shown that the channel confinement significantly enhances the surfactant-induced retardation of the droplet. In addition, a larger surfactant concentration is found to induce a greater reduction in cross-stream migration velocity of the droplet, the effect of which is reduced when the initial transverse position of the droplet is shifted closer to the channel centerline. To support our experimental results, an asymptotic approach is adopted to solve the flow field in the presence of bulk-insoluble surfactants and under the assumption of small shape deformation. A good match between our theoretical prediction and the experimental results is obtained. The present analysis provides us with a wide scope of application towards various droplet-based microfluidic as well as medical diagnostic devices where manipulation of droplet trajectory is a major issue.

1 Introduction

Manipulation of droplets and its dynamics within microchannels serves as a low-cost platform mimicking several operations found across fields as diverse as pharmaceutical to food industries. These encompass drug delivery, cell encapsulation, analyte detection, single cell analysis and even positioning of erythrocytes in blood flow through arteries (Stone et al. 2004; Di Carlo et al. 2007; Huebner et al. 2008; Teh et al. 2008; Baroud et al. 2010; Seemann et al. 2012; Zhu and Fang 2013). An important aspect of channel-based studies is the ability of isolation of droplets by a carrier phase brought about by the addition of surface active agents or surfactants. These enable compartmentalization of the droplets that can be employed as mini-reactors to study chemical reactions or to simply perform mixing of analytes. Thus, a fundamental understanding of such surfactant-laden flows can be of immense importance in stabilizing various emulsions (Puyvelde et al. 2001; Tucker III and; Moldenaers 2002; Fischer and Erni 2007), and separation of components in the domain of flow field fractionation (Giddings 1993; Yang et al. 1999) and flow cytometry (Bonner et al. 1972).

In view of the above applications, different experimental techniques used by various researchers for studying the motions of droplets in microchannels may be put into perspective. These techniques can be applied to precisely locate the position or even predict the trajectory of drops or cells in various microfluidic or medical diagnostic devices, respectively. Migration of droplets in the presence of a pressure-driven flow has been studied both theoretically and experimentally since a long time (Leal 1980; Stan et al. 2011; Chen et al. 2014). The different experimental techniques used can be broadly classified into two categories (Xuan et al. 2010): the first one involves the use of external sheath flows to locate a laminar stream containing particles and the second one uses hydrodynamic lift forces to drive particles in a cross-stream direction (which is normal to the direction of local flow velocity). In the present study, we resort to use the technique that falls under the latter category which is based on the balance between lift forces and traction generated due to non-uniform distribution of surfactants. These hydrodynamic lift forces can be produced through a variety of mechanisms (Young et al. 1959; Goldsmith and Mason 1962; Saffman 1965; Ho and Leal 1974; Chan and Leal 1979; Hanna and Vlahovska 2010). Amongst these, inertial lift forces are superior than their counterparts and they have been utilized to position particles in a microchannel (Di Carlo et al. 2007; Amini et al. 2014). In a recent study, Stan et al. (2011) studied experimentally the cross-stream migration of a droplet in a pressure driven microflow, where they took into consideration the effect of buoyancy and also the lift force induced due to droplet deformation and channel confinement. A number of previous studies can be found in the literature that deal with lift forces due to droplet deformation (Goldsmith and Mason 1962; Chan and Leal 1979) or due to hydrodynamic interaction between droplets or bubbles with channel walls (Magnaudet 2003; Takemura and Magnaudet 2003; Takemura et al. 2009; Sugiyama and Takemura 2010). Introduction of surfactants adds further nonlinearity to the physical system and it is imperative to outline the subsequent effect of surfactant addition on the resulting droplet dynamics. It is found that variation in the surfactant alters the interfacial tension, giving rise to Marangoni convection. The generated Marangoni stress is the major source of nonlinearity in such systems (Kim and Subramanian 1989; Leal 2007; Pak et al. 2014), which brings in interesting yet unexplored dynamics related to cross-stream migration of a droplet. The prime motivation of our present study is to delineate the underlying physics of surfactant-laden droplet migration in confined systems from an experimental stand point supported by complementary theoretical analysis.

It is pertinent to review the major theoretical propositions at this juncture. Hetsroni and Haber (1970) developed a three-dimensional theoretical model on the migration of an eccentrically placed droplet in an arbitrary flow field. They showed that a deformable droplet undergoes a cross-stream migration in the presence of an imposed Poiseuille flow. Later a deformable droplet in a pressure driven flow was shown to migrate towards the flow centerline for low viscosity ratio of the dispersed phase and the carrier phase (Chan and Leal 1979). Kim and Subramanian (1989), through analytical and numerical techniques, later proved that presence of surfactants results in the retardation of the thermocapillary migration of a droplet In a recent study, Pak et al. (2014) analytically showed that the presence of surfactants effectively reduces the cross-stream migration velocity of a non-deformable droplet in the limiting regime where the surfactant transport is dominated by surface diffusion. As the present study takes into account both the effect of droplet deformation and surfactant redistribution on its cross-stream migration, a subsequent temptation of application of linear superposition of the results of Pak et al. (2014) and Chan and Leal (1979) will be misleading due to unknown shape of the droplet. This challenge was tackled earlier in the work done by Das et al. (2017) and a similar approach is adopted for the present study as well, for the case of an imposed plane Poiseuille flow. Presence of droplet deformation brings in further nonlinearity into the system as the shape of the interface is not known as a priori. Hence, a trivial solution cannot be expected and an asymptotic approach is adopted to analytically investigate the present problem. Droplet deformation, although quite low due to presence of low viscous forces, plays an important role in dictating the droplet dynamics (Chan and Leal 1979). Chan and Leal (1979) showed that the cross-stream migration of an eccentrically placed surfactant-free droplet in an isothermal Poiseuille flow field takes place primarily due to its shape deformation. For the ideal scenario of a non-deformable spherical droplet, no cross-stream migration is present even if the droplet is eccentrically located with respect to the flow centerline.

In the current literature, although a significant number of studies have been reported on surfactant-induced Marangoni stress, nonetheless a comprehensive experimental analysis regarding the effect of surfactants on the lateral migration of droplets in a confined microfluidic environment is still lacking. In the present study, therefore, we focus on the effect of surfactant distribution on the lateral migration of a water droplet (dispersed phase) in presence of Triton X-100 (surfactant) suspended in an oil (sunflower oil) media. The experiments performed, which are primarily directed towards showcasing the effect of channel confinement ratio (ratio of the droplet radius to the channel height), surfactant concentration and initial position of the droplet on its cross-stream migration has opened up a wider scope for new strategies towards droplet manipulation which has not been explored earlier. It is observed that a larger confinement ratio enhances the retarding effect of surfactants. It is also found that even though a higher surfactant concentration increases the retardation in cross-stream migration of the droplet, the influence of the same significantly reduces if the initial transverse position of the droplet is shifted more close to the channel centerline. In addition, a three-dimensional theoretical model that can predict the cross-stream migration velocity of the droplet is also provided to support our experimental observations. It is seen that there is a fair match between our theoretical predictions and the outcomes from experiments performed for a microchannel with low confinement ratio and in the presence of a dilute surfactant concentration.

2 Theoretical modeling

2.1 Physical system

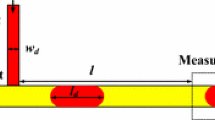
The physical system comprises of a neutrally buoyant surfactant-laden droplet of radius a, suspended in an unbounded plane Poiseuille flow field. A schematic of the physical system is provided in Fig. 1. All the quantities related to the droplet phase are indicated by a subscript ‘i’, whereas those belonging to the carrier phase are denoted by a subscript ‘e’. For instance, the droplet phase viscosity is denoted by μ_i while ${\mu _e}$ denotes the carrier phase viscosity. In the present problem, the droplet is initially placed at an off-center position with respect to the channel centerline. Hence, a three-dimensional spherical coordinate system $\left( {\bar {r},\theta ,\varphi } \right)$ is attached to the centroid of the droplet. However, as we are dealing with an imposed planar Poiseuille flow, a reference Cartesian coordinate system $(\bar {x},\bar {y})$ is attached at the bottom plate of the microchannel, as shown in Fig. 1. The model is developed based on a parallel plate configuration of the channel, with the length of both the plates along the z-direction being too large to have any influence on the flow field. For the purpose of an asymptotic analysis, the droplet radius is assumed to be much smaller in comparison to the channel height, $\bar {H}$, that is the confinement ratio, ${a \mathord{\left/ {\vphantom {a {\bar {H}}}} \right. \kern-0pt} {\bar {H}}} \ll 1$ which effectively signifies an unbounded flow field. The dashed lines representing the two walls or the region of zero imposed velocity are indications of the unbounded carrier phase. In Fig. 1, ${\bar {y}_{\text{d}}}$ represents the transverse position of the droplet measured with respect to the bottom channel wall or the x-axis. Surfactants, insoluble in either of the phases, are present at the interface of the droplet with a surface diffusivity of D_s. Presence of an imposed Poiseuille flow results in droplet deformation accompanied by surfactant redistribution that causes a variation in surface tension along the interface and hence generates Marangoni stress that plays an important role in the cross-stream droplet migration. The theoretical model derived can predict the temporal variation of the transverse position of a deformable droplet in the presence of surfactants.

Fig. 1

Schematic of a droplet of radius a suspended in a plane Poiseuille flow. The droplet is positioned eccentrically at distance of $({\bar {y}_{\text{d}}} - {{\bar {H}} \mathord{\left/ {\vphantom {{\bar {H}} 2}} \right. \kern-0pt} 2})$ from the flow centerline, where $\bar {H}$ is the total width of the flow field. The spherical coordinates $(\bar {r},\theta ,\varphi )$ are attached to droplet centroid, whereas the Cartesian coordinates $(\bar {x},\bar {y})$ is attached to the bottom plate. A different set of Cartesian coordinates $(\bar {X},\bar {Y},\bar {Z})$ are also shown attached to the droplet centroid

All the fluid properties for both the droplet and the carrier phase are assumed to be constant. The surface tension $(\bar {\sigma })$, however, is linearly dependent on the local surfactant concentration $(\bar {\Gamma })$ along the droplet surface through the equation of state given by Leal (2007):

$$\bar {\sigma }={\bar {\sigma }_{\text{c}}} - {R_{\text{g}}}{\bar {T}_{\text{o}}}\bar {\Gamma },$$

(1)

where ${R_{\text{g}}}$ denotes the universal gas constant and σ_c denotes the equilibrium surface tension for a surfactant-free droplet. Also ${\bar {\sigma }_{{\text{eq}}}}$ is taken to be the surface tension corresponding to an equilibrium surfactant concentration, ${\bar {\Gamma }_{{\text{eq}}}}$, on the droplet surface in an unperturbed flow and a reference temperature of ${\bar {T}_{\text{o}}}$. This linear dependence is obtained as a special case of the Langmuir isotherm under the assumption of a dilute surfactant concentration (Leal 2007).

Some of the basic assumptions, relevant to our experiments, are negligible fluid inertia, small droplet deformation, surface diffusion-dominated surfactant transport and a dilute surfactant concentration along the interface. The first assumption clearly indicates a low flow Reynolds number, Re = ${{\rho {{\bar {V}}_{\text{c}}}a} \mathord{\left/ {\vphantom {{\rho {{\bar {V}}_{\text{c}}}a} {{\mu _e}}}} \right. \kern-0pt} {{\mu _e}}}$ ≪ 1, where ρ and µ_e is the carrier phase density (918 kg/m³) and viscosity (0.04914 Pa s at 25 °C) and ${\bar {V}_{\text{c}}}$ is the centerline velocity of the imposed pressure driven flow. The next two assumptions indicate a low value of capillary number (Ca = ${{{\mu _e}{{\bar {V}}_{\text{c}}}} \mathord{\left/ {\vphantom {{{\mu _e}{{\bar {V}}_{\text{c}}}} {{\sigma _{{\text{eq}}}}}}} \right. \kern-0pt} {{\sigma _{{\text{eq}}}}}}$) and surface Péclet number (Pe_s = ${{{{\bar {V}}_{\text{c}}}a} \mathord{\left/ {\vphantom {{{{\bar {V}}_{\text{c}}}a} {{D_{\text{s}}}}}} \right. \kern-0pt} {{D_{\text{s}}}}}$) where D_s is the surface diffusivity of the surfactant used, which for the present scenario of Triton X-100 has magnitude that varies in between D_s ~ 10^− 7–10^− 6 m²/s. Based on the material properties, all of these assumptions are found relevant to the experiments performed in this study.

2.2 Governing equations and boundary conditions

Under the premise of the assumptions mentioned, the flow field is governed by the Stokes and the continuity equations, which for either of the phases can be expressed as

$$\left. \begin{gathered} - \bar {\nabla }{{\bar {p}}_i}+{\mu _i}{{\bar {\nabla }}^2}{{\bar {\mathbf{u}}}_i}={\mathbf{0}},\;\bar {\nabla } \cdot {{\bar {\mathbf{u}}}_i}=0, \hfill \\ - \bar {\nabla }{{\bar {p}}_e}+{\mu _e}{{\bar {\nabla }}^2}{{\bar {\mathbf{u}}}_e}={\mathbf{0}},\;\bar {\nabla } \cdot {{\bar {\mathbf{u}}}_e}=0. \hfill \\ \end{gathered} \right\}$$

(2)

It should be noted that henceforth all the quantities with an ‘overbar’ denotes dimensional quantities, whereas those without any ‘overbar’ indicate dimensionless quantities. The above governing equations for flow field are subjected to the following far-field conditions

$$\begin{gathered} {\text{as }}\bar {r} \to \infty ,\quad {{\bar {\mathbf{u}}}_e}={{{\mathbf{\bar {u}}}}_\infty }={{\bar {\mathbf{V}}}_\infty } - \bar {\mathbf{U}}, \hfill \\ {\text{as }}\bar {r} \to \infty ,\quad {{\bar {p}}_e}={{\bar {p}}_\infty }, \hfill \\ \end{gathered}$$

(3)

where ${\mathbf{\bar {U}}}$ is the droplet migration velocity, ${\bar {p}_\infty }$ is the pressure at the far-field and ${{\mathbf{\bar {V}}}_\infty }$ is the imposed Poiseuille flow field that can be expressed with respect to a Cartesian coordinate system $(\bar {X},\bar {Y},\bar {Z})$ attached to the centroid of the droplet in the following form:

$$\,\left. \begin{gathered} {{{\mathbf{\bar {V}}}}_\infty }={{\bar {V}}_{\text{c}}}\left\{ {{k_0}+{k_1}\bar {Y}+{k_2}{{\bar {Y}}^2}+{k_3}{{\bar {X}}^2}} \right\}{{{\mathbf{\hat {e}}}}_{\bar {X}}}, \hfill \\ {\text{where,}} \hfill \\ {k_0}=\frac{{4{{\bar {y}}_{\text{d}}}}}{{\bar {H}}}\left( {1 - \frac{{{{\bar {y}}_{\text{d}}}}}{{\bar {H}}}} \right),\;{k_1}=\frac{4}{{\bar {H}}}\left( {1 - \frac{{2{{\bar {y}}_{\text{d}}}}}{{\bar {H}}}} \right),\;{k_2}= - \frac{4}{{{{\bar {H}}^2}}},\;{k_3}=0. \hfill \\ \end{gathered} \right\}$$

(4)

The velocity and the pressure field inside the droplet $({{\mathbf{\bar {u}}}_i},{\bar {p}_i})$ is bounded at the droplet centroid $(\bar {r}=0)$. The boundary conditions at the droplet interface comprise the no-slip condition, the kinematic condition and the stress balance condition, all of which are presented below:

$$\left. \begin{gathered} {\text{at}}\;\bar {r}={{\bar {r}}_{\text{s}}},\;\;\;\;{{\bar {\mathbf{u}}}_i}={{\bar {\mathbf{u}}}_e}, \hfill \\ {\text{at}}\;\bar {r}={{\bar {r}}_{\text{s}}},\;\;\;\;{{\bar {\mathbf{u}}}_i} \cdot {\mathbf{n}}={{\bar {\mathbf{u}}}_e} \cdot {\mathbf{n}}=0, \hfill \\ {\text{at}}\;\bar {r}={{\bar {r}}_{\text{s}}},\;\;\;\;\;\left( {{{\bar {\varvec{\uptau}}}_e} \cdot {\mathbf{n}} - {{\bar {\varvec{\uptau}}}_i} \cdot {\mathbf{n}}} \right)= - {{\bar {\nabla }}_{\text{s}}}\bar {\sigma }+\bar {\sigma }\left( {\bar {\nabla } \cdot {\mathbf{n}}} \right){\mathbf{n}}, \hfill \\ \end{gathered} \right\}$$

(5)

where ${\bar {\nabla }_{\text{s}}}=\left( {{\mathbf{I}} - {\mathbf{nn}}} \right) \cdot \bar {\nabla }$ is the surface gradient operator, ${\bar {r}_{\text{s}}}$ denotes the radial position of the deformed droplet surface and ${\bar {\varvec{\uptau}}_{i,e}}= - {\bar {p}_{i,e}}\mathbf{I}+{\mu _{i,e}}\left[ {\bar {\nabla }{{\bar {\mathbf{u}}}_{i,e}}+{{\left( {\bar {\nabla }{{\bar {\mathbf{u}}}_{i,e}}} \right)}^{\text{T}}}} \right]$ represents the hydrodynamic stress tensors inside and outside the droplet. ${\mathbf{n}}$ in the above equations stands for the unit normal perpendicular to surface of the droplet and is given by

$${\mathbf{n}}=\frac{{\bar {\nabla }F}}{{\left| {\bar {\nabla }F} \right|}},$$

(6)

where $F=\bar {r} - {\bar {r}_{\text{s}}}=0$ is the equation of the surface of the droplet.

The local surfactant concentration is governed by a convection diffusion equation of the following form (Kim and Subramanian 1989):

$${\bar {\nabla }_{\text{s}}} \cdot \left( {{{\bar {\mathbf{u}}}_{\text{s}}}\bar {\Gamma }} \right)={D_{\text{s}}}\bar {\nabla }_{{\text{s}}}^{2}\bar {\Gamma },$$

(7)

where ${{\mathbf{\bar {u}}}_{\text{s}}}$ is the fluid flow velocity at the interface, ${\bar {\nabla }_{\text{s}}}$ is the surface gradient operator and $\bar {\Gamma }$ is the local surfactant concentration.

We now state the dimensionless set of governing equations and boundary conditions, that are derived with the aid of the following non-dimensional scheme: $r={{\bar {r}} \mathord{\left/ {\vphantom {{\bar {r}} a}} \right. \kern-0pt} a}$, ${\mathbf{u}}={{{\mathbf{\bar {u}}}} \mathord{\left/ {\vphantom {{{\mathbf{\bar {u}}}} {{{\bar {V}}_{\text{c}}}}}} \right. \kern-0pt} {{{\bar {V}}_{\text{c}}}}}$, $\Gamma ={{\bar {\Gamma }} \mathord{\left/ {\vphantom {{\bar {\Gamma }} {{{\bar {\Gamma }}_{{\text{eq}}}}}}} \right. \kern-0pt} {{{\bar {\Gamma }}_{{\text{eq}}}}}}$, $\sigma ={{\bar {\sigma }} \mathord{\left/ {\vphantom {{\bar {\sigma }} {{{\bar {\sigma }}_{\text{c}}}}}} \right. \kern-0pt} {{{\bar {\sigma }}_{\text{c}}}}}$, $p={{\bar {p}} \mathord{\left/ {\vphantom {{\bar {p}} {({{{\mu _e}{{\bar {V}}_{\text{c}}}} \mathord{\left/ {\vphantom {{{\mu _e}{{\bar {V}}_{\text{c}}}} a}} \right. \kern-0pt} a})}}} \right. \kern-0pt} {({{{\mu _e}{{\bar {V}}_{\text{c}}}} \mathord{\left/ {\vphantom {{{\mu _e}{{\bar {V}}_{\text{c}}}} a}} \right. \kern-0pt} a})}}$, and $\varvec{\tau }={{\varvec{\bar {\tau }}} \mathord{\left/ {\vphantom {{\varvec{\bar {\tau }}} {({{{\mu _e}{{\bar {V}}_{\text{c}}}} \mathord{\left/ {\vphantom {{{\mu _e}{{\bar {V}}_{\text{c}}}} a}} \right. \kern-0pt} a})}}} \right. \kern-0pt} {({{{\mu _e}{{\bar {V}}_{\text{c}}}} \mathord{\left/ {\vphantom {{{\mu _e}{{\bar {V}}_{\text{c}}}} a}} \right. \kern-0pt} a})}}$. The different ratios of the fluid properties as well as non-dimensional numbers encountered while deriving the same are (i) the viscosity ratio $\left( {\lambda ={{{\mu _i}} \mathord{\left/ {\vphantom {{{\mu _i}} {{\mu _e}}}} \right. \kern-0pt} {{\mu _e}}}} \right)$ that indicates the ratio of the droplet phase viscosity to that of the carrier phase viscosity; (ii) the elasticity parameter, $\beta ={{{{\bar {\Gamma }}_{{\text{eq}}}}{R_{\text{g}}}{T_{\text{o}}}} \mathord{\left/ {\vphantom {{{{\bar {\Gamma }}_{{\text{eq}}}}{R_{\text{g}}}{T_{\text{o}}}} {{{\bar {\sigma }}_{\text{c}}}}}} \right. \kern-0pt} {{{\bar {\sigma }}_{\text{c}}}}}$ that denotes the sensitivity of the surface tension to a change in the surfactant concentration along the droplet surface; (iii) the modified capillary number, $Ca={{{\mu _e}{{\bar {V}}_{\text{c}}}} \mathord{\left/ {\vphantom {{{\mu _e}{{\bar {V}}_{\text{c}}}} {{\sigma _{{\text{eq}}}}}}} \right. \kern-0pt} {{\sigma _{{\text{eq}}}}}}$ and (iv) the surface Péclet number, $P{e_{\text{s}}}={{{{\bar {V}}_{\text{c}}}a} \mathord{\left/ {\vphantom {{{{\bar {V}}_{\text{c}}}a} {{D_{\text{s}}}}}} \right. \kern-0pt} {{D_{\text{s}}}}}$, that signifies the relative importance of surfactant transport by surface convection to that by surface diffusion. It is evident from Eq. (1) that $\beta = - {{d({{\bar {\sigma }} \mathord{\left/ {\vphantom {{\bar {\sigma }} {{{\bar {\sigma }}_{\text{c}}}}}} \right. \kern-0pt} {{{\bar {\sigma }}_{\text{c}}}}})} \mathord{\left/ {\vphantom {{d({{\bar {\sigma }} \mathord{\left/ {\vphantom {{\bar {\sigma }} {{{\bar {\sigma }}_{\text{c}}}}}} \right. \kern-0pt} {{{\bar {\sigma }}_{\text{c}}}}})} {d\bar {\Gamma }}}} \right. \kern-0pt} {d\bar {\Gamma }}}$, which implies that the equilibrium surface tension for a surfactant-laden droplet can be expressed as σ_eq = σ_c(1 − β) corresponding to a uniform surfactant concentration of ${\bar {\Gamma }_{{\text{eq}}}}$. Hence the use of the capillary number based on surface tension of a droplet uniformly coated with surfactants is more mathematically convenient. The above relationship between the two types of surface tension also indicates that the value of β lies between 0 and 1.

The non-dimensional flow field governing equations, thus obtained, are next stated below

$$\left. \begin{gathered} - \nabla {p_i}+\lambda {\nabla ^2}{\mathbf{u}_i}={\mathbf{0}},\;\nabla \cdot {\mathbf{u}_i}=0, \hfill \\ - \nabla {p_e}+{\nabla ^2}{\mathbf{u}_e}={\mathbf{0}},\;\nabla \cdot {\mathbf{u}_e}=0, \hfill \\ \end{gathered} \right\}$$

(8)

which are subjected to the following set of boundary conditions:

$$\left. \begin{gathered} {\text{at}}\;r \to \infty ,\;\left( {{\mathbf{u}_e},{p_e}} \right)=\left( {{\mathbf{V}_\infty } - \mathbf{U},{p_\infty }} \right), \hfill \\ {\mathbf{u}_i}\,{\text{is bounded at }}r=0, \hfill \\ {\text{at}}\,r={r_{\text{s}}},\,{\mathbf{u}_i} \cdot {\mathbf{n}}={\mathbf{u}_e} \cdot {\mathbf{n}}=0, \hfill \\ {\text{at}}\,r={r_{\text{s}}},\,{\mathbf{u}_i}={\mathbf{u}_e}, \hfill \\ {\text{at}}\,r={r_{\text{s}}},\,\left( {{\varvec{\uptau}_e} \cdot {\mathbf{n}} - {\varvec{\uptau}_i} \cdot {\mathbf{n}}} \right)=\frac{\beta }{{\left( {1 - \beta } \right)Ca}}{\nabla _{\text{s}}}\Gamma +\frac{\sigma }{{Ca}}\left( {\nabla \cdot {\mathbf{n}}} \right){\mathbf{n}}. \hfill \\ \end{gathered} \right\}$$

(9)

The last equation, which is the stress balance condition is obtained with the help of the following non-dimensional equation of state (Kim and Subramanian 1989; Das et al. 2017; Mandal et al. 2017):

$$\sigma =1 - \beta \Gamma .$$

(10)

The dimensionless form of the surfactant transport equation is obtained as

$$P{e_{\text{s}}}{\nabla _{\text{s}}}\cdot\left( {{{\mathbf{u}}_{\text{s}}}\Gamma } \right)=\nabla _{{\text{s}}}^{2}\Gamma .$$

(11)

The flow field governing equations (Eq. 8) are subjected to kinematic and stress balance conditions at the interface as well as far-field conditions. As seen from Eqs. (8) and (11), the governing equations for flow field and the surfactant transport are coupled through the surface convection term in the convection–diffusion equation for surfactant concentration. In addition, presence of shape deformation brings in further nonlinearity into the system as the shape of the droplet is not known as a priori. As a result, an exact analytical solution for an arbitrary value of $P{e_{\text{s}}}$ is impossible. We thus utilize the asymptotic approach to solve for the flow field and surfactant concentration. A regular perturbation method is applied in the limiting case of surface diffusion-driven surfactant transport or Pe_s ≪ 1. Such a limiting case is close to a real scenario owing to low characteristic velocities [O(10^− 3) m/s] of flow in a microchannel. That is, under the present scenario with D_s ~ 10^− 7–10^− 6 m²/s and a droplet radius of 50 µm, the range of values of Pe_s lies between 0.1 and 0.005. The methodology adopted for the present study is similar to that used by Das et al. (2017), where the bulk flow was taken to be a circular Poiseuille flow. Hence the same is not repeated in this article.

The surfactant concentration in the above equation should also satisfy the mass conservation constraint that is provided below

$$\int\limits_{{\varphi =0}}^{{2\pi }} {\int\limits_{{\theta =0}}^{\pi } {\Gamma \left( {\theta ,\varphi } \right)r_{{\text{s}}}^{2}\sin \theta {\text{d}}\theta } {\text{d}}\varphi } =4\pi .$$

(12)

2.3 Asymptotic solution for Pe _s ≪ 1

As per the assumption of small droplet deformation and surface diffusion-induced surfactant transport, we can further assume that the surface Péclet number is of the same order as the capillary number, or the same can be expressed mathematically as (Li and Pozrikidis 1997):

$$P{e_{\text{s}}}\sim Ca \Rightarrow P{e_{\text{s}}}=kCa,$$

(13)

where $k={{a{{\bar {\sigma }}_{\text{c}}}(1 - \beta )} \mathord{\left/ {\vphantom {{a{{\bar {\sigma }}_{\text{c}}}(1 - \beta )} {{\mu _e}{D_{\text{s}}}}}} \right. \kern-0pt} {{\mu _e}{D_{\text{s}}}}}$ is dependent on the material properties solely and hence can be called as the property parameter. Since both Pe_s and Ca are of the same order of magnitude, hence k is finite and O(1). Since for any given value of β and k, the shape deformation is solely a function of Ca, hence the same is chosen as the perturbation parameter for the asymptotic analysis. Hence any flow variable, ψ, in the present analysis can be expanded in increasing powers of Ca as follows:

$$\psi ={\psi ^{(0)}}+{\psi ^{(Ca)}}Ca+O(C{a^2}),$$

(14)

where the first term on the RHS is the leading order term corresponding to no droplet deformation and the other terms to the right signify O(Ca) and O(Ca²) correction to the droplet shape. However, the local surfactant concentration, Γ, is expanded in the following form in order to satisfy the mass conservation constraint in Eq. (12) (Vlahovska et al. 2009)

$$\Gamma =1+{\Gamma ^{(0)}}Ca+{\Gamma ^{(Ca)}}C{a^2}+O\left( {C{a^3}} \right).$$

(15)

In order to obtain the droplet migration velocity, we follow the similar steps as was used by Das et al. (2017) and hence are not repeated here. However, we provide the expressions of the important results as obtained from this asymptotic analysis.

The leading order surfactant concentration, obtained by simultaneously solving the leading order flow field boundary conditions and the surfactant transport equation is provided below

$$\begin{gathered} {\Gamma ^{(0)}}=\Gamma _{{1,0}}^{{(0)}}{P_{1,0}}+\Gamma _{{2,1}}^{{(0)}}\cos \varphi {P_{2,1}}+\Gamma _{{3,0}}^{{(0)}}{P_{3,0}}+\Gamma _{{3,2}}^{{(0)}}\cos 2\varphi {P_{3,2}}, \hfill \\ {\text{where}} \hfill \\ \Gamma _{{1,0}}^{{(0)}}= - \frac{{4k\left( {1 - \beta } \right)}}{{{H^2}\left\{ {\left( {k - 3\lambda - 2} \right)\beta +3\lambda +2} \right\}}},\,\Gamma _{{3,0}}^{{(0)}}=\frac{7}{{3{H^2}}}\frac{{\left( {1 - \beta } \right)k}}{{\left\{ {\left( {k - 7 - 7\lambda } \right)\beta +7+7\lambda } \right\}}}, \hfill \\ \Gamma _{{2,1}}^{{(0)}}=\frac{{10}}{{3{H^2}}}\frac{{\left( {1 - \beta } \right)\left( {H - 2{y_d}} \right)k}}{{\left\{ {\left( {k - 5 - 5\lambda } \right)\beta +5+5\lambda } \right\}}},\,\Gamma _{{3,2}}^{{(0)}}=\frac{7}{{18{H^2}}}\frac{{\left( {1 - \beta } \right)k}}{{\left\{ {\left( {7+7\lambda - k} \right)\beta +7+7\lambda } \right\}}}, \hfill \\ \end{gathered}$$

(16)

where $H={{\bar {H}} \mathord{\left/ {\vphantom {{\bar {H}} a}} \right. \kern-0pt} a}$. The components of the leading order droplet migration velocity as obtained from the force-free condition $\mathbf{F}_{H}^{{\left( 0 \right)}}=4\pi \nabla \left( {{r^3}p_{{ - 2}}^{{(0)}}} \right)=0,$ are provided below

$$\begin{gathered} U_{x}^{{\left( 0 \right)}}= - \frac{4}{{{H^2}}}~y_{d}^{2}+\frac{4}{H}~{y_d} - \underbrace {{\frac{4}{{3{H^2}}}\frac{{\beta k+3~\lambda ~\left( {1 - \beta } \right)}}{{\left\{ {\beta k+\left( {3\lambda +2} \right)\left( {1 - \beta } \right)} \right\}}}}}_{{{\text{effect of surfactant distribution}}}},\, \hfill \\ U_{y}^{{\left( 0 \right)}}=U_{z}^{{\left( 0 \right)}}=0. \hfill \\ \end{gathered}$$

(17)

It should be noted that there is no cross-stream migration of the droplet for the leading order even though surfactants are present along the interface.

We next obtain the O(Ca) correction to the droplet shape with the help of the normal stress balance at the interface, which can be expressed as

$$\left( {{p_i} - {p_e}} \right){\mathbf{I}}+\left( {{{\mathbf{T}}_e} - {{\mathbf{T}}_i}} \right) \cdot {\mathbf{n}}=\frac{\sigma }{{Ca}}\left( {\nabla \cdot {\mathbf{n}}} \right),$$

(18)

where ${{\mathbf{T}}_i}$ and ${{\mathbf{T}}_e}$ are the traction vectors inside as well as outside the droplet, respectively. The deformed droplet shape can be expressed as

$$\begin{gathered} F=r - {r_{\text{s}}}, \hfill \\ {\text{where}} \hfill \\ r={r_{\text{s}}}=1+Ca{g^{(Ca)}}\left( {\theta ,\varphi } \right)+O\left( {C{a^2}} \right). \hfill \\ \end{gathered}$$

(19)

Here ${g^{(Ca)}}$ is the O(Ca) correction to the droplet shape. The expression of ${g^{(Ca)}}$ thus obtained from the leading order normal stress balance can be expressed as

$$\begin{gathered} {g^{(Ca)}}=L_{{2,1}}^{{(Ca)}}\cos \varphi {P_{2,1}}+L_{{3,2}}^{{(Ca)}}\cos 2\varphi {P_{3,2}}+L_{{3,0}}^{{(Ca)}}{P_{3,0}}, \hfill \\ {\text{where}} \hfill \\ \left. \begin{gathered} L_{{2,1}}^{{(Ca)}}=\frac{5}{{12{H^2}}}\left( {\frac{{19\lambda - 16bt - 19\lambda \beta +4k\beta +16}}{{5\beta +5\lambda \beta - 5\lambda - 5 - k\beta }}} \right){y_{\text{d}}}, \hfill \\ ~L_{{3.0}}^{{(Ca)}}= - \frac{7}{{60{H^2}}}\left( {\frac{{30 - 30\beta +33\lambda +5k\beta - 33\lambda \beta }}{{7\beta +7\lambda \beta - 7\lambda - 7 - k\beta }}} \right), \hfill \\ ~L_{{3,2}}^{{(Ca)}}=\frac{7}{{180{H^2}}}\left( {\frac{{30 - 33\lambda \beta +5k\beta - 30\beta +33\lambda }}{{7\beta +7\lambda \beta - 7\lambda - 7 - k\beta }}} \right). \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered}$$

(20)

The expression of O(Ca) surfactant concentration, next obtained on solving the O(Ca) flow field boundary conditions along with the O(Ca) surfactant transport equation, is provided below

$${\Gamma ^{(Ca)}}=\sum\limits_{{n=0}}^{4} {\sum\limits_{{m=0}}^{n} {\Gamma _{{n,m}}^{{(Ca)}}\cos (m\varphi ){P_{n,m}}(\cos \theta )} } ,$$

(21)

where the constant coefficients in the above expression, $\Gamma _{{n,m}}^{{(Ca)}}$ ≡ $f\left( {L_{{n,m}}^{{(Ca)}}} \right)$, are not presented here to preserve the conciseness of the text. Finally, the components of the O(Ca), migration velocity is next presented which is obtained with the help of the force-free condition

$$U_{y}^{{(Ca)}}=Ca\left[ {\,\left( {{c_1}{y_{\text{d}}}+{c_2}} \right)+\frac{{\sum\limits_{{i=1}}^{4} {\left( {\sum\limits_{{j=1}}^{4} {{c_{5 - ~i,5 - j}}~{k^{5 - j}}} } \right)~{\beta ^{5 - i}}} }}{{{c_3}}}} \right],\,U_{x}^{{(Ca)}}=U_{z}^{{(Ca)}}=0,$$

(22)

where the constant coefficients in the above expression are presented in Sect. 2 of the supplementary material. It has to be noted that even without the presence of surfactants (β = 0), there still exists a cross-stream component of the droplet migration velocity, whereas there is no presence of axial migration velocity for this order.

3 Experimental setup and methodology

We now discuss the experimental setup as well as the methodology adopted in the present study. All the experiments are performed in a controlled environment at 25 °C to prevent any influence of thermal fluctuations on fluid flow. In our experiments, commercially available sunflower oil is used as the carrier phase while water along with Triton X-100 is used as dispersed phase. Triton X-100 acts as the surfactant that alters the interfacial tension in presence of imposed pressure-driven flow which ultimately leads to the generation of Marangoni stress.

3.1 Microchannel fabrication

Microchannels are fabricated using photo-lithography and are replicated using soft lithography technique. Sylgard 184 is used as the raw material (polydimethylsiloxane, mixed in the base:cross-linker ratio 10:1) (Hongbin et al. 2009). The basal support for the fabricated channels is provided by a glass slide. Prior to this, the glass slides are subjected to rigorous cleaning procedure wherein they are subjected to piranha treatment (H₂O₂:H₂SO₄ = 1:1), and traces of the treatment are removed by rinsing in de-ionized (DI) water. To ensure complete moisture removal from the substrate, it is then dried by purging it with pure N₂ gas and oven-dried in a hot air oven at 95 °C for about 1 h. Then, the substrate is coated with SU8-2150 negative photoresist (Micro Chem Corp., USA) at 3000 rpm for about 25 s. Further, the photoresist-coated substrate is soft-baked at 65 and 95 °C for 7 and 40 min, respectively. Thereafter, the substrate is exposed to UV light (Hybralign 200 Mask aligner, OAI) through a chrome-coated quartz mask for about 25 s, followed by post-baking at 65 and 95 °C for 5 and 15 mi, respectively. Finally, the substrate is developed using SU8 developer for about 17 min to obtain the exposed pattern (or master pattern) on the top of the substrate.

To prepare the microchannel, polydi-methylsiloxane (PDMS), an elastomeric resin is prepared by mixing elastomeric base to cross-linker (Sylgard-184, Dow corning, USA) in 10:1 w/w ratio and allowed to be degassed in a vacuum desiccator to remove trapped air. The degassed mixture is thereafter poured over the master pattern and is allowed to cure overnight at 95 °C. Post-curing, the microchannels are peeled-off and bonded to plasma-treated hydrophilic cleaned glass surface.

3.2 Experimental setup

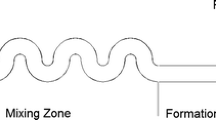
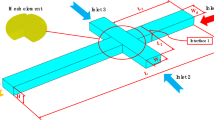
We now discuss on the experimental setup. A detailed schematic of the same is provided in Fig. 2. The setup includes an Olympus IX71 inverted fluorescent microscope which is fitted with a high-speed camera (Phantom V641) to capture the necessary images. The PDMS based microchannel, which is plasma-bonded on the glass slide, comprises three inlet and one outlet ports, all of which are fitted with Teflon tubes of identical diameters through connectors. The three inlet Teflon tubes consist of a primary inlet which causes the inflow of sunflower oil, a T-junction inlet that forces entry of water intermixed with Triton X-100 and finally the secondary inlet which also results in the entry of sunflower oil. Each of these three Teflon tubes is connected to a separate syringe pump (Harvard Apparatus PHD 2000: 0–100 ml min^− 1) that forces the respective fluid at a desired flow rate whereas the outlet is connected to a reservoir. The microchannel is placed on the observation platform of the inverted microscope such that the portion of the channel with enlarged width just past the secondary inlet lies above the 10× objective.

Fig. 2

A schematic of the experimental setup used for the present analysis. The Cartesian coordinate $(\bar {x},\bar {y},\bar {z})$ attached to the bottom plate of the microchannel is also shown in the figure above

3.3 Methodology

Unlike some of previous studies performed in this domain where a flow-focusing device was used for the purpose of droplet generation (Ward et al. 2005; Stan et al. 2011, 2013; Hatch et al. 2013), we have made use of a T-junction for the same purpose. The use of a T-junction significantly reduces the complexity in channel fabrication without any sacrifice in the level of accuracy. A priming test is performed with a test liquid (Milli-Q ultrapure water; Millipore India Pvt. Ltd) prior to performing real time experiments to check for any leakage in the channel. Subsequent inflow of sunflower oil from the primary inlet and water intermixed with Triton X-100 from the auxiliary inlet (T-junction) is initiated at flow rates of $120$ and $20$ μl/h, respectively, for a 200 µm channel. While fabricating the microchannel, we kept its height (in z-direction) significantly large (droplet radius ~ 0.30H) to ensure that the droplet, under no circumstances, collides with the channel walls while migrating in the cross-stream direction. This was possible due to the use of SU8-2150, as negative photoresist. The master pattern fabricated with this photoresist provided us a height of about 150 µm. However, in the experimental analysis the effect of bottom wall on the migration of the droplet was present, which was neglected in the 3D analytical model developed in the present study.

As soon as droplet generation starts, the flow of sunflower oil through the secondary inlet is also initiated at a rate of 15 μl/h in order to offset the position of the droplet with respect to the channel centerline. The above experiment is performed with Triton X-100 intermixed with DI water. Again, the experiment is repeated for different concentrations of Triton X-100 in the 200 micron channel. Subsequent experiments are also performed for different droplet radius in a 300-micron channel to study the effect of confinement ratio or bounding wall on the lateral migration of the droplet. In addition, by altering the secondary flow rate of sunflower oil, the offset position of the droplet was varied in microchannels of height 500 µm to investigate the influence of this initial offset position of the droplet on its trajectory. The entire trajectory of the droplet past the secondary inlet is recorded by means of a high-speed camera. For accurate visualization of the droplet migration in the flow field, images (image resolution: $600 \times 800$ pixels $\times 12$ bits) are captured at intervals of $\Delta t={10^{ - 3}}\,{\text{s}}$ at the rate of 1000 frames/s and at the same exposure. As the flow rates of the interacting fluids are less, there is no possibility of the occurrence of flow instability due to the vibration of syringe pump. At lower operating flow rate, several researchers (Garstecki et al. 2006; Fu et al. 2010; Carrier et al. 2014) have used mechanical syringe pump in production of droplet at T-junction. Furthermore, no recording of droplet migration in the microchannel was initiated until and unless (a) all the droplets passing the section at x₄ (refer to Fig. 4) were of the same size; (b) all the droplets were separated by the same distance (≥ two times the droplet diameter) while undergoing cross-stream migration and (c) all the droplets were flowing in a single stream with no oscillations. This ensured that flow is stable. Post-processing of the images captured is done with the help of an in-house image processing code in MATLAB. A schematic of the flow field in the microchannel is presented in Fig. 3. All the experiments in our setup are performed in a plane, orthogonal to the direction of gravitational force. As a result, there is no effect of buoyancy on the droplet dynamics irrespective of the difference in density of either of the phases.

Fig. 3

A schematic of the flow mechanism of a surfactant-laden droplet in the microchannel. The red box region, highlighted above, represents the T-junction responsible for droplet generation

Fig. 4

Plot of velocity profiles at different sections, x₁, x₂, x₃ and x₄ (measured from the secondary inlet) obtained by performing a numerical simulation of the flow field. The color bar indicates the magnitude of fluid flow velocity. a The velocity profiles when the secondary influx is Q_in = 5 µl/h, whereas in b the corresponding influx is increased to Q_in = 10 µl/h

It should be noted that our area of interest lies in the region past the secondary inlet and hence the transverse position of the droplet as result of this influx is taken as the initial position of the droplet trajectory. To be more precise, the initial position of the droplet is its location downstream the secondary inlet where the streamlines reach a steady state indicating a fully developed flow and all other disturbances alienate. A more clearer overview can be provided if we look into the velocity profiles at different sections (x₁, x₂, x₃, x₄) in this region as shown in Fig. 4, obtained after performing a numerical simulation of the flow field. The numerical simulations have been performed using finite element-based COMSOL multiphysics software to check for the region which encounters a fully developed flow. The distance of each section, shown in legends of the plots, is measured from the secondary inlet. It can be seen from Fig. 4a that the velocity profiles at sections x₂, x₃, x₄ overlap each other which suggests that the flow field becomes fully developed from x₂ = 30 µm when the secondary inflow rate is Q_in = 5 µl/h. On the other hand, Fig. 4b shows that the velocity profiles overlap only after x₃ = 80 µm, that is the flow is fully developed after x₃ = 80 µm when Q_in = 10 µl/h. It can thus be inferred that higher the secondary inflow rate, higher is the transverse initial position, which at the same time gets shifted further downstream. This axial distance of the initial position varies with change in channel height as well. Hence for each of the experiments, a corresponding numerical simulation is performed to acquire the axial distance of the droplet’s initial position, from which point all observations on droplet dynamics are recorded.

3.4 Materials

The carrier phase is commercially available sunflower oil, whose viscosity is 0.04914 Pa.s at 25 °C. The dispersed phase is de-ionized water, which has a viscosity of 8.9 × 10^− 4 Pa.s at the same temperature. The viscosities of the fluids are measured by stress controlled mechanism integrated in Rheometer (Anton Paar MCR 302). The values of the interfacial tension corresponding to different values of surfactant concentration, along the interface, are shown in a plot in Fig. 5. The interfacial tension has been measured using pendant drop method integrated in goniometer (250 G1, Rame̅hart, Germany).

Fig. 5

Variation of equilibrium interfacial tension with surfactant concentration at 25 °C temperature

Figure 5 shows variation of interfacial tension as a function of the local surfactant concentration, present in the bulk. Based on ranges of variation of ${\bar {\sigma }_{{\text{eq}}}}$ and ${\bar {V}_{\text{c}}}$, the capillary number is seen to vary between 0.002 and 0.01. It is seen that after reaching a certain critical concentration (C_s ≈ 400 ppm), the variation of surface tension significantly reduces. This is known as the critical micelle concentration (CMC). At CMC (here, CMC = 400 ppm), micelles start forming and the interface starts getting saturated with the surfactant molecules. However, even above the CMC, the Marangoni effect, although reduced, still exists which is evident from the experimental observations later. Due to low fluid flow velocity, the main mode of surfactant transport along the interface is taken to be that by surface diffusion, that is the surface Péclet number can be taken to be small enough. The theoretical model developed is based on this assumption. The cross-stream migration velocity of the droplets varies in the range of O(10⁻⁶) − O(10⁻⁵) m/s based on the incipient fluid flow velocity, which varies in between O(10⁻⁴) − O(10⁻³) m/s. Such low migration velocities ensure low convection mode of surfactant transport along the droplet interface as well as lower rate of adsorption (or desorption) of surfactants from (to) the bulk. To compare the experimental results with our theoretical model, a reasonably small concentration of surfactants (100 ppm < CMC) is premixed with the dispersed phase as well as the incipient fluid flow velocity is kept fairly high (~ 10⁻³ m/s) to ensure the surface diffusion time scale is significantly lower than the adsorption/desorption time scale. Both of these steps fairly approximate our assumption of bulk insolubility of the surfactants. However, for higher concentration of surfactants (above CMC) diffusion controlled adsorption and desorption sets in He et al. (2015). In the absence of any energy barriers for adsorption and desorption, the transport of surfactants along the interface due to diffusion is accompanied by the arrival and departure of surfactant molecules from the droplet surface, which changes the concentration of surfactants in the bulk instantaneously such that a balance (or an equilibrium) between the amount of surfactants along the interface and in the bulk is preserved. On the contrary, in the presence of high adsorption and desorption energy barriers, no instantaneous equilibrium of surfactant concentration between the interface and bulk is reached. In such a scenario, the kinetics of adsorption and desorption is governed by the Langmuir equation (He et al. 2015), which can be expressed as

$$\frac{{d\Gamma }}{{dt}}={k_{\text{a}}}C\left( {{\Gamma _\infty } - \Gamma } \right) - {k_{\text{d}}}\Gamma ,$$

(23)

where C is the concentration of surfactants in the bulk, Γ_∞ denotes the surfactant concentration at saturation state along the surface, k_a and k_d are adsorption and desorption constants, which can be expressed in terms of the adsorption and desorption energies in the following format:

$${k_{\text{a}}}=k_{{\text{a}}}^{{(0)}}\exp \left( {{{{E_{\text{a}}}} \mathord{\left/ {\vphantom {{{E_{\text{a}}}} {{k_{\text{B}}}T}}} \right. \kern-0pt} {{k_{\text{B}}}T}}} \right),\,{k_{\text{d}}}=k_{{\text{d}}}^{{(0)}}\exp \left( {{{{E_{\text{d}}}} \mathord{\left/ {\vphantom {{{E_{\text{d}}}} {{k_{\text{B}}}T}}} \right. \kern-0pt} {{k_{\text{B}}}T}}} \right).$$

(24)

Here, k_B is the Boltzmann’s constant and T is the ambient temperature. At equilibrium we can write dΓ/dt = 0. This in conjunction with Eq. (23) gives us

$$\frac{C}{{({{{k_{\text{d}}}} \mathord{\left/ {\vphantom {{{k_{\text{d}}}} {{k_{\text{a}}}}}} \right. \kern-0pt} {{k_{\text{a}}}}})}}=\frac{{{\Gamma \mathord{\left/ {\vphantom {\Gamma {{\Gamma _\infty }}}} \right. \kern-0pt} {{\Gamma _\infty }}}}}{{1 - {\Gamma \mathord{\left/ {\vphantom {\Gamma {{\Gamma _\infty }}}} \right. \kern-0pt} {{\Gamma _\infty }}}}},$$

(25)

which relates the surfactant concentration in the bulk and along the interface at equilibrium.

4 Results and discussion

In this section, we first demonstrate the role played by surfactants on the temporal variation of the transverse position of the droplet. The droplet, when suspended in an imposed flow field undergoes migration and at the same time due to interfacial fluid flow, the surfactants get redistributed. This leads to a non-uniform distribution of surfactants along the droplet surface resulting in an asymmetry in its concentration on either side of both the axial as well transverse planes. This non-uniform distribution of surfactants generates a gradient in surface tension along the interface and hence gives rise to a Marangoni stress. Towards showcasing the effect of surfactants on the cross-stream migration of a droplet, we first plot the temporal variation in the experimentally measured transverse position of the droplet centroid in a 500-µm microchannel and compare the same with the theoretical prediction for the case of an unbounded flow field (refer to Fig. 6b). In Fig. 6b, experimental data points for the lateral position of the droplet centroid are shown for the case of a clean droplet and a surfactant-laden droplet (C_s = 0.25 C_s, where C_s ≈ 400 ppm). The radius of the droplet for the present case is set at 50 µm by appropriately varying the flow rate of the dispersed phase (Q_d) from the auxiliary inlet for a constant inflow rate of the carrier phase (Q_c). The theoretical prediction for the transverse migration of the droplet as a function of time can be derived from the expression of the cross-stream migration velocity of the droplet which is given by

Fig. 6

a The trajectory of a surfactant-laden as well as a clean droplet in a 500-µm microchannel, recorded by a high-speed camera. b The variation of the transverse position of the droplet as function time elapsed, in the presence (100 ppm) as well in the absence of surfactants. The solid and dashed lines indicate the theoretical prediction with (β = 0.5, k = 1.35) and without (β = k = 0) the presence of surfactants. In the b, y_d is normalized by the droplet radius a, whereas t is made non-dimensional by the characteristic time, $a/{\bar {V}_{\text{c}}}$. The other parameters used for the theoretical plot are λ = 0.018 and Ca = 0.01. D_f denotes deformation parameter (Stan et al. 2011) defined as D_f = L_r/a_avg. L_r and a_avg denote the radius variation and average radius, respectively

$${U_y}=Ca\left[ {\underbrace {{\left( {{c_1}{y_{\text{d}}}+{c_2}} \right)}}_{\begin{subarray}{l} {\text{sole effect due to }} \\ {\text{shape deformation}} \end{subarray} }+\underbrace {{\frac{{\sum\limits_{{i=1}}^{4} {\left( {\sum\limits_{{j=1}}^{4} {{c_{5 - ~i,5 - j}}~{k^{5 - j}}} } \right)~{\beta ^{5 - i}}} }}{{{c_3}}}}}_{\begin{subarray}{l} {\text{combined effect of shape deformation }} \\ {\text{and surfactant redistribution}} \end{subarray} }} \right],$$

(26)

where the constant coefficients c₁, c₂, c₃ and c_p,q (p,q ϵ [1,4]) are provided in the Sect. 2 of the supplementary material. Here, β is the elasticity parameter that signifies the sensitivity in surface tension to a change in surfactant concentration along the droplet surface and k = Pe_s/Ca is the property parameter. The detailed expression of either of these parameters is provided in the supplementary material. The above expression clearly indicates the role of shape deformation as well as the imposed flow-induced surfactant redistribution on the cross-stream migration velocity of the droplet. The expression also indicates that cross-stream migration of the droplet takes place even without the presence of surfactants. The left-hand side of the above equation can be replaced by U_y = dy_d/dt, which provides us with an ordinary differential equation in y_d. The solution of Eq. (26) for y_d, thus obtained, is plotted in Fig. 6b with and without the presence of surfactants. The time, t, along the x-axis is normalized with respect to the characteristic time given by ${a \mathord{\left/ {\vphantom {a {{{\bar {V}}_{\text{c}}}}}} \right. \kern-0pt} {{{\bar {V}}_{\text{c}}}}}$.

As seen from Fig. 6, in the absence as well as in the presence of surfactants, our asymptotic theory succeeds in predicting the experimental results to a great extent. The values of the parameters used for the above plot are provided in the caption of Fig. 6. Both the values of β and k can be determined based on the values of the properties and characteristic length and velocities. For a reasonable value of equilibrium surfactant concentration, ${\bar {\Gamma }_{{\text{eq}}}}$ = 5 × 10^− 7 mol/m² (corresponding to 100 ppm of surfactant intermixed with the dispersed phase) and a interfacial tension (${\bar {\sigma }_{\text{c}}}$) of 23.91 × 10^− 3 N/m of the surfactant-free fluid–fluid interface between DI water and sunflower oil at an ambient temperature of 293 K, the value of β can be found out to be about 0.5. In a similar manner the range of values of k (= ${{a{{\bar {\sigma }}_{\text{c}}}(1 - \beta )} \mathord{\left/ {\vphantom {{a{{\bar {\sigma }}_{\text{c}}}(1 - \beta )} {{\mu _e}{D_{\text{s}}}}}} \right. \kern-0pt} {{\mu _e}{D_{\text{s}}}}}$) can be obtained as k ~ 1.2–12 from the following property values: viscosity of the carrier phase, µ_e = 0.04914 Pa.s at 25 °C, the diffusivity of Triton X-100 surfactant varied in between 10^− 7 − 10^− 6 m²/s and finally the radius of the droplet for experimental purposes can be used as 50 µm. Thus among other parameters, the viscosity ratio is calculated to be $\lambda =0.018$ and the property parameter, k (= 1.35) is used as a fitting parameter to obtain a good match between the theoretical and the experimental results. For the analytical plot in Fig. 6, the value of capillary number is taken as 0.01, which can be derived based on different material properties. It can be observed from Fig. 6b, that at larger times our exponential prediction deviates from the experimental observations. Although there is a good match between the trends in cross-stream migration of the droplet at lower times (t < 30), nonetheless our theoretical model predicts that the droplet would reach the channel centerline much earlier as compared to the experimental data. This is due to the assumption of negligible inertia and wall effect in our model, either of which generates a lift force that tends to drive the droplet away from the channel centerline and effectively retards its cross-stream migration.

It is evident from the experimental data points in Fig. 6b that the presence of surfactants retards the cross-stream migration of the droplet. The droplet traverses a much smaller distance in the cross-stream direction in the presence of surfactants for the same time elapsed. In other words, the cross-stream component of the droplet velocity reduces. Two different regimes of cross-stream migration of the droplet can be observed from Fig. 6b as well. That is, initially the cross-stream migration velocity of the droplet for either of the cases (β = 0 and β = 0.5) is high enough as compared to later times. Such a distinctive behavior can be explained as follows: initially the droplet is located far away from the channel centerline and hence the difference in the interfacial fluid flow velocity in between the upper and the lower hemisphere is significantly higher as compared to the case when the droplet is located closer to the channel centerline, at some later time. Thus the hydrodynamic stress driving the droplet is much higher for the former scenario which results in a higher droplet migration velocity. Figure 6a shows the snapshots of the droplet at different time frames as recorded with the help of a high-speed camera. Comparing the trajectories of both the surfactant-free as well as surfactant-laden droplet (in Fig. 6a), we infer that cross-stream migration velocity for the former is higher with respect to the later.

A proper physical explanation of the role of surfactants on the lateral migration of a droplet can be provided if we look into their distribution along the interface. The shape deformation makes it quite complicated to evaluate the surface divergence term in the surfactant transport Eq. (11). Representation of the variation of surfactant concentration along the deformed droplet surface also adds to further complexity. To tackle such a situation, the surfactant concentration is projected on an undeformed spherical surface from a deformed one with the use of the relationship $\tilde {\Gamma }=\Gamma \left( {{{r_{{\text{s}}}^{2}} \mathord{\left/ {\vphantom {{r_{{\text{s}}}^{2}} {{\mathbf{n}} \cdot {\mathbf{r}}}}} \right. \kern-0pt} {{\mathbf{n}} \cdot {\mathbf{r}}}}} \right)$ (Vlahovska et al. 2005). This is presented in Fig. 7a, which shows a contour plot for the distribution of surfactants projected along the undeformed droplet surface, as obtained from our theoretical prediction for the case of an unbounded flow. In our experiments as well as in our theoretical model, the droplet is positioned at an off-center location with respect to the flow centerline. For the experiments, a secondary inflow is used for the same purpose. Considering the case when the droplet is located at an off-center position above the centerline, it can be stated that the lower hemisphere of the droplet has a higher interfacial fluid flow velocity as compared to that of the above. In addition, due to axial migration of the droplet in the direction of the imposed flow, fluid flow along the surface occurs from the east pole (θ = 0) to the west pole (θ = π) of the droplet. Taking into account either of these factors the highest concentration of surfactant is expected near the north-west region of the droplet surface while the minimum surfactant concentration can be predicted to be near the north-east region. This is evident from Fig. 7a as well. The important thing to be noted from the same figure is the asymmetry in surfactant distribution along the droplet surface, both about the axial as well as the transverse plane. It should be kept in mind that this asymmetry in surfactant concentration is also a result of the imposed flow-induced shape deformation of the droplet. This asymmetric surfactant distribution gives rise to a gradient in surface tension. It is this asymmetry in surfactant concentration and hence the gradient in surface tension across the axial plane that affects the cross-stream migration of the droplet. To obtain a better insight, we have also shown the variation of the surface tension (σ = 1 − βΓ) along two axial planes (θ = π/4, 3π/4) on either side of the equator (θ = 0), corresponding to the parameter values provided in the caption of Fig. 7.

Fig. 7

a Contour plot showing the distribution of surfactants along the droplet surface. b The variation of surface tension along two different axial planes (θ = π/4, 3π/4) is shown as a function of the azimuthal angle, φ. c Variation of surface velocity with θ along a transverse plane, φ = π for different values of β. The different parameters involved for the above plots are H = 4, λ = 0.018, y_d = 2.8, Ca = 0.01, β = 0.5 and k = 1

Figure 7b clearly indicates the gradient in surface tension (|σ_max − σ_min|) across the axial plane of the droplet which results in the generation of Marangoni stress. In the presence of shape deformation, the streamlines in the vicinity of the droplet surface gets distorted as a result of which the fluid flow around the droplet gets affected. Since the shape deformation is not symmetric about either the axial or the transverse plane, this distortion in the streamlines are not uniform and a hydrodynamic force is generated which drives the droplet towards the flow centerline. Thus the asymmetry in surfactant distribution is further enhanced as a result of shape deformation. This is also evident since the O(Ca) surfactant concentration is dependent on the shape deformation of the droplet. The Marangoni stress thus generated acts against the hydrodynamic force due to the imposed flow induced shape deformation. This can also be seen from the contour plot in Fig. 7a, where the highest surfactant concentration is observed to be present in the north-west zone implying that the traction due to the Marangoni stress acts against the imposed hydrodynamic force. Figure 7c shows the variation of the interfacial fluid velocity (u_s,θ) with θ along the transverse plane φ = π. It can be seen that there is a stagnation point at θ = π/4 and θ = 3π/4 corresponding to β = 0.5, which supports the nature of surfactant distribution, as shown in Fig. 7a. The important point to be noted from the figure is that the interfacial fluid flow is reduced due to increase in β.

Figure 8a, b displays the variation in the theoretically obtained axial and cross-stream migration velocities as a function of the elasticity parameter, β, for different values of k. It can be seen that increase in either β or k results in a decrease in the magnitude of both the axial and the cross-stream migration velocity of the droplet. The negative sign in Fig. 8b indicates that the droplet migrates towards the centerline of flow. A possible explanation for such a behavior can be provided if we consider the significance of both β and k. For a higher value of β, there is a larger variation in the surface tension for the same gradient in surfactant concentration (|Γ_max − Γ_min|) along the interface. This indicates an increase in β is accompanied by an increase in the Marangoni stress acting along the droplet surface. Since the traction due to this Marangoni stress opposes the hydrodynamic force due to imposed flow that tries to drive the droplet towards the flow centerline, an increase in β ultimately leads to a decrease in the migration velocity of the droplet. This decrease in the migration velocity, in turn causes a reduction in the interfacial fluid flow, which can also be observed in Fig. 7c. Increase in k, on the other hand enhances the convection of surfactants along the interface, and thus increases the non-uniformity in surfactant concentration along the interface. This leads to a rise in Marangoni stress, which is accompanied by a corresponding decrease in the migration velocity of the droplet.

Fig. 8

Variation of the a axial and b the cross-stream migration velocity of the droplet as a function of β for different values of k (= 1,2.5,5). The different parameters involved for the above plots are H = 5, λ = 0.018, y_d = 2.8, Ca = 0.01, β = 0.5 and k = 1

It should be noted that in a previous study Chan and Leal (1979) theoretically investigated the cross-stream migration of a deformable surfactant-free droplet in a pressure driven flow, whereas in a recent work, Pak et al. (2014) did a similar analysis on a non-deformable surfactant-laden droplet suspended in an unbounded Poiseuille flow. Although it might seem quite intuitive to simply add the results of both of these studies to obtain the combined effect of shape deformation as well as Marangoni stress on the cross-stream migration of the droplet, nonetheless this approach is completely incorrect. This is due to the nonlinearity present due to the following two factors: first, the presence of convection of surfactants along the interface couples the flow field with the surfactant distribution, which can be seen from Eq. (7) of the main text and second, the shape of the droplet is not known as a priori due to presence of deformation of the droplet. We next discuss the effect of some of the pertinent parameters, frequently encountered in microfluidic devices, on the cross-stream migration of the droplet. These parameters include the confinement ratio of the channel, the surfactant concentration in the dispersed phase as well as the droplet initial position. For each of these cases experimental results are shown and proper reasoning is provided regarding the behavior of droplet.

4.1 Effect of channel confinement

In this section, we primarily focus on the effect of bounding walls on the surfactant-induced retardation in the cross-stream migration of the droplet. To vary the confinement ratio, $\,{a \mathord{\left/ {\vphantom {a {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}$, which is the ratio of the droplet radius to the channel height, we opt to alter the size of the droplet. This is possible by varying the inflow of the dispersed phase through the auxiliary channel (Q_d) for a constant inflow rate of the continuous phase (Q_c) in the T-junction. A larger inflow rate of the dispersed phase result in a larger volume of the same to pass through the auxiliary channel before the continuous phase cuts the auxiliary inflow at the T-junction. Hence a larger droplet size is attained by increasing the inflow ratio, Q_d/Q_c. We, thus, analyze the effect of channel wall on lateral migration of the droplet for three different values of $\,{a \mathord{\left/ {\vphantom {a {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}$ (0.295, 0.325, 0.36) corresponding to the T-junction inflow ratios (Q_d/Q_c) of 0.153, 0.23 and 0.35, respectively.

Figure 9a shows the microscopic images of droplets of varying sizes in a microchannel of height 300 µm. This in turn corresponds to different confinement ratios for the same channel height, ${a \mathord{\left/ {\vphantom {a {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}=0.36,0.325,0.295$. The variation of the transverse position of a clean droplet as a function of time elapsed for different values of ${a \mathord{\left/ {\vphantom {a {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}$ is shown in Fig. 9b. The time (t^*) used in this plot is normalized with respect to the characteristic time scale given by ${{\bar {H}} \mathord{\left/ {\vphantom {{\bar {H}} {{{\bar {V}}_{\text{c}}}}}} \right. \kern-0pt} {{{\bar {V}}_{\text{c}}}}}$, since the channel height, $\bar {H}$, is kept constant. It can be observed from the plot that decrement in the confinement ratio causes the droplet to traverse a smaller distance in the cross-stream direction for the same time elapsed. That is, for a constant channel height, a larger droplet possesses a higher cross-stream migration velocity. Similar observations can also be made from Fig. 9c where a surfactant-laden droplet of larger size is seen to traverse a greater distance in the same time interval as compared to a droplet of smaller size. The experimental observation, as shown in Fig. 9b for a clean droplet, are in direct agreement with the numerical and experimental results of Mortazavi and Tryggvason (2000) and Stan et al. (2011), where they showed that it is the larger droplet that reaches its steady state position (or the channel centerline) in the shortest span of time.

Fig. 9

a Experimentally recorded images of three different droplets of different size at t^* = 3, migrating in a microchannel of height 300 µm. b Temporal variation of normalized transverse position of a surfactant-free droplet for different confinement ratios. c Variation of transverse position of a surfactant-laden droplet (1200 ppm or 3 C_s) as a function of time for different values of confinement ratios (0.295, 0.325, 0.36). d Streamline of fluid flow circulation in and around a clean droplet

An interesting observation can also be made on comparison of Fig. 9b and c. It is seen that effect of surfactants in reducing the cross-stream migration velocity of a larger droplet or a droplet in a system with a higher confinement ratio, is more significant as compared to a droplet of smaller size. In other words, for a constant channel height and for the same amount of surfactants added to the dispersed phase (1200 ppm or 3 C_s), the decrease in the distance traversed in the transverse direction is significantly more for a larger droplet as compared to a smaller droplet for the time elapsed. If we look into Fig. 9b, the distance (${{{{\bar {y}}_{\text{d}}}} \mathord{\left/ {\vphantom {{{{\bar {y}}_{\text{d}}}} {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}$) traversed by a larger droplet (say ${a \mathord{\left/ {\vphantom {a {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}=0.36$) in the transverse direction in the absence of any surfactant is given by 0.05, whereas that traversed by a smaller droplet (say ${a \mathord{\left/ {\vphantom {a {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}=0.295$) is 0.027 for the same time elapsed (t* = 5). This agrees with our former observation. Now from Fig. 9c), it can be seen that due to presence of surfactants, the transverse distance traversed by the larger and the smaller droplet (${a \mathord{\left/ {\vphantom {a {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}=0.36,0.295$) reduces to 0.028 and 0.017, respectively, for the same time elapsed (t* = 5). Hence for the larger droplet, presence of surfactants reduces the transverse distance traversed by 0.022, whereas for the smaller droplet the decrease in the distance traversed in the cross-stream direction due to the presence of same amount of surfactants is 0.01 in the same time span (t* = 5). A proper physical explanation is now provided on the effect of confinement as discussed above. It can be noted that the hydrodynamic force due to shape deformation, which tends to drive the droplet towards the channel centerline, is greater for a droplet of larger size as compared to a smaller one. This explains the plot shown in Fig. 9b, where a surfactant-free droplet, larger in size, migrates in the cross-stream direction at a higher rate as compared to a smaller droplet. On the other hand, a larger droplet has a greater difference in interfacial fluid flow velocities between the upper and lower hemispheres as compared to a smaller droplet in the same microchannel. This results in a greater asymmetry in surfactant distribution for a larger droplet and hence a higher Marangoni stress is generated that opposes the hydrodynamic force due to the imposed flow induced shape deformation. Thus a fall in the net hydrodynamic force, acting on droplets of different sizes, is expected. In other words, the cross-stream migration of a clean droplet is affected more significantly in comparison to a surfactant-laden droplet for the same variation in its size. This can be observed from comparison of Fig. 9b and c and also has been discussed earlier. In the presence or in absence of surfactants, the larger droplet (or a higher channel confinement ratio) always possesses the highest cross-stream migration velocity. However, as a result of reduction in droplet size (for a constant channel height) by the same amount, the decrease in the cross-stream migration velocity is higher for a surfactant-free droplet as compared to a surfactant-laden droplet.

4.2 Effect of surfactant concentration

We next look into the effect of surfactant concentration on the cross-stream migration of the droplet for a constant confinement ratio. Towards this, we perform our experiments corresponding to three different amounts of surfactants (0.25 C_s, 2 C_s and 3 C_s) dissolved into the dispersed phase in a microchannel of height 200 µm. Figure 10a shows the time variation of transverse position of the droplet while Fig. 10b shows the droplet trajectory. It can be observed from the former that increase in the amount of surfactant concentration reduces the cross-stream migration velocity of the droplet, which will thus take a longer time to traverse the same distance in the cross-stream direction. On the other hand, Fig. 10b shows that the droplet with the highest concentration of surfactant traverses the least in the transverse direction for the same axial distance covered.

Fig. 10

a Experimentally observed variation of normalized lateral position of the droplet as a function of normalized time for different values of surfactant concentration (0.25 C_s, 2 C_s, 3 C_s). b Corresponding droplet trajectory along the length of the micro-channel of height 200 µm

A physical explanation regarding the above nature of droplet dynamics can be put forward if we look into the role played by the surfactants. For the same imposed flow, a droplet with a higher concentration of surfactants will have a greater asymmetry or a higher gradient in surfactant concentration (|Γ_max − Γ_min|) on either side of the axial plane. This will result in an increase in the surface tension gradient which in turn will lead to the generation of Marangoni stress of larger magnitude. Since the Marangoni stress generated opposes the hydrodynamic force due to the shape deformation, a droplet with a higher surfactant concentration will have a lower cross-stream migration velocity as compared to a droplet with lower surfactant concentration. In other words, a droplet with lower surfactant concentration will reach the channel centerline faster in comparison to a droplet with a higher surfactant concentration which also implies that the same will traverse a less axial distance. This is what can be observed from Fig. 10a, b.

4.3 Effect of droplet initial position

We next focus on the effect of droplet initial transverse position on the cross-stream migration of the droplet. How the surfactant-induced retardation of the droplet is affected by altering the droplet initial position, is also another aspect of this discussion. An accurate way to determine the transverse initial position of the droplet has been previously discussed. In order to vary the initial position, we alter the inflow rate of sunflower oil through the secondary inlet. A higher influx results in an initial position further away from the channel centerline. For the present scenario, we choose three inflow rates of 80, 100 and 130 µl/h to achieve the desired initial transverse positions of 275, 315 and 365 µm, respectively. A microchannel of height 500 µm is chosen for the experiments to be performed for this analysis.

Figure 11a shows the images of three initial transverse position of the droplets, ${{{{\bar {y}}_{{\text{d}},0}}} \mathord{\left/ {\vphantom {{{{\bar {y}}_{{\text{d}},0}}} {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}(=0.55,0.63,0.73)$, where ${\bar {y}_{{\text{d}},0}}={\bar {y}_{\text{d}}}(t=0)$. Figure 11b, on the other hand, shows effect of droplet initial position or the secondary influx on the surfactant-induced retardation of the cross-stream migration of the droplet. Interestingly, it can be observed that the closer the droplet is to the channel centerline, the lower is the effect of variation in surfactant concentration on its cross-stream migration. However, if the surfactant concentration of the droplet is fixed, then an increase in its initial transverse position merely increases the time required by it to reach the channel centerline with a subsequent decrease in the cross-stream migration velocity. This can be observed from Fig. 11c.

Fig. 11

a Images of droplet corresponding to three different secondary inflow rates that result in different transverse initial position of the droplet. b Variation of normalized transverse position of the droplet as a function normalized time elapsed for two different initial positions [${\bar {y}_{\text{d}}}$(t = 0)/$\bar {H}$ = 0.73, 0.63] and for different surfactant concentrations (0.25 C_s, 2 C_s, 3 C_s) for each of these cases. c Temporal variation of the lateral position of the droplet corresponding to different initial positions (0.55, 0.63, 0.73) and a total surfactant concentration of 800 ppm (2 C_s). d Variation of the cross-stream migration velocity with the time elapsed for different initial positions [${\bar {y}_{\text{d}}}$(t = 0)/$\bar {H}$ = 0.73, 0.55]

A proper reasoning regarding the above observations is now provided. For a droplet initially positioned at a point further away from the channel centerline $[{{{{\bar {y}}_{\text{d}}}(t=0)} \mathord{\left/ {\vphantom {{{{\bar {y}}_{\text{d}}}(t=0)} {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}=0.73]$, the difference in interfacial fluid flow velocity between its upper and lower hemispheres is larger as compared to a droplet situated near to the centerline $[{{{{\bar {y}}_{\text{d}}}(t=0)} \mathord{\left/ {\vphantom {{{{\bar {y}}_{\text{d}}}(t=0)} {\bar {H}}}} \right. \kern-0pt} {\bar {H}}}=0.63]$. This results in a larger asymmetry in surfactant distribution along the droplet surface on either side of the axial plane and hence a higher surface tension gradient for the former. A larger Marangoni stress is thus generated that opposes the hydrodynamic force due to droplet deformation. Thus increase in the total amount of surfactant along the droplet surface would result in an enhanced Marangoni stress for a droplet situated far away from the channel centerline. This supports our observation from Fig. 11b that for the same increase in surfactant concentration, reduction in the cross-stream migration velocity is larger for a droplet near the wall. For a fixed surfactant concentration, on the other hand, a higher Marangoni stress is generated for a droplet positioned furthest from the channel centerline which results in a lower cross-stream migration velocity. This can also be confirmed from Fig. 11d, which shows the variation of cross-stream migration velocity of the droplet as a function of the time elapsed. This variation of U_y is shown for two different initial positions of the droplet [${\bar {y}_{\text{d}}}$(t = 0)/$\bar {H}$ = 0.55, 0.73]. This explains the fact, as seen from Fig. 11c, that a droplet far from the channel centerline would require a larger time to traverse the same distance in the transverse direction as compared to a surfactant-free droplet.

5 Conclusions

In the present study, we experimentally show that presence of surfactants in the dispersed phase, suspended in a pressure driven flow, can bring about retardation in its cross-stream migration. Surfactants can be naturally present in a suspension (for example, contaminants) or may be artificially added to appropriately modulate the droplet dynamics. We also experimentally investigate the influence of some important parameters commonly encountered in various microfluidic applications, such as the confinement ratio, total concentration of surfactants as well as the initial transverse position of the droplet, on its migration characteristics. In addition, we develop a three-dimensional asymptotic theory in the limiting case of diffusion-dominated surfactant transport that takes into account the effect of shape deformation as well. Due to the coupled and non-linear nature of the governing equations for flow field and surfactant transport equation, a linear superposition of results does not serve the purpose. Instead a more strategic asymptotic approach has been adopted. Overall, our theoretical model is found to predict our experimentally obtained results with a decent accuracy. Some of the noteworthy outcomes of our study are presented below:

• 1. Irrespective of any change in parameters involved, the time required for a surfactant-laden droplet to reach the channel centerline is always larger as compared to a clean droplet. The trend of the temporal variation of the cross-stream migration of the droplet, which is obtained both from the theoretical model as well as from the experimental data, follows the same pattern, although there is not a significantly good match between the two at larger times. This can be observed for both a surfactant-free and a surfactant-laden droplet. The primary reason for this deviation is due to some of the major assumptions made while developing the theoretical model, for example, negligible wall effect and convection of surfactants as well as bulk insolubility of surfactants. As a result, our theoretical prediction is erroneous for any value of k larger than 1.

• 2. For a fixed channel height and for the same time elapsed, the cross-stream migration of a larger droplet is reduced to a greater extent as compared to a smaller droplet for the same amount of surfactants present.

• 3. A larger amount of surfactant in the dispersed phase is found to significantly reduce the cross-stream migration velocity.

• 4. The effect of surfactant concentration on the cross-stream migration of the droplet is found to be enhanced when the initial position is shifted further away from the channel centerline. However, for a constant amount of surfactant present in the dispersed phase, the droplet initially located near to the channel centerline has a higher cross-stream migration velocity.