1 Introduction

Recently, the applications of acoustic force as a flow control device have significantly increased and led to a science branch known as acoustofluidics. In this field, the effects of acoustics on the fluids were precisely investigated [1]. In some resources, the term “acoustofluidics” is limited to the application of the ultrasonic waves in microfluidic systems [2]. Acoustic streaming and acoustic radiation are the two main effects of these waves on the fluids. These phenomena are in various scientific and industrial applications such as pumping [3], heating, particle separation [4] and mixing [5]. Surface acoustic wave (SAW) can be generated by applying an electric field to a set of interdigital transducers on the surface of a piezoelectric substrate. When a traveling SAW contacts a liquid, the acoustic streaming is induced due to acoustic energy attenuation. The fluid motion highly depends on wave amplitude and wave frequency.

There are three main branches in this topic: analytical, experimental, and numerical. Most of the previous studies applied an experimental technique for their investigations. In analytical studies [6,7,8], a new term known as acoustic streaming force is introduced. In the references [9, 10], the development, operation and manufacturing of SAW-based systems are comprehensively studied. The application of SAW in mixing particles [11], active mixing [12], actuation of small drops along predetermined trajectories [13], jet of a drop [14], and the role of acoustic streaming in convection and fluidization in oscillatory flows [15] are some of empirical works that can be mentioned in this context. Brunet et al. [16] comprehensively focused on this topic and their empirical studies are the main resource for other scholars. The numerical works are mainly divided into three general sets: breaking down a total problem into several sub-problems [17,18,19,20], applying acoustic streaming as an external force [21,22,23,24,25,26], and applying oscillatory boundary conditions [27,28,29,30,31,32].

The contact line dynamics is a challenging item due to two primary reasons: the interplay of phenomena occurring over a wide range of length scales, from macro-size down to intermolecular distance and interactions among fluid and solid phases. In order to describe the contact line dynamics, computational methods are categorized into three major types: molecular dynamics (MD) [33], macroscopic hydrodynamic approaches, and lattice Boltzmann method (LBM) [34,35,36,37,38].

In a microscopic approach, intermolecular interactions determine the interface and dynamics of the contact line. Therefore, mesoscopic models such as LBM are more suitable for simulation of the complex dynamical behaviors [39]. LBM captures interfaces very straightforward and so, methods such as level set, front tracking, or guess of the interface shape are not used in this technique. Due to mesoscopic properties, this method can predict the motion of particles without applying slip boundary condition and hence, it can simulate the moving contact line. There are three major classes of interfacial multiphase LBM: color-gradient model (CGM) [40,41,42,43,44], pseudopotential model [Shan and Chen model (S-C)] [45, 46], and free energy model [47]. The focus of present paper is on CG model. CGM has been also widely used to study interfacial multiphase and multicomponent flows, so the interested readers can refer to references [6, 48,49,50].

However, some critical issues about the ability of CGM in dealing with high density ratio flows have been raised. Leclaire et al. [51,52,53] modified CGM, based on multi-relaxation time (MRT) collision operator, which enables their model to be capable of simulating flows with high density ratio. In order to recover the correct Navier–Stokes equations, Ba et al. [54] proposed a simple source term that could be added to the single-phase collision operator. They applied an equilibrium density distribution function derived from the third-order Hermite expansion of the Maxwellian distribution.

CGM is also used to study wetting phenomena [55, 56]. However, density ratio in these works is about unity. So, these models cannot be applied to practical problems. One goal of the present paper is to propose a geometrical boundary condition to simulate wetting phenomena and dynamical behavior of moving contact line in high density ratios. According to the model developed by Ba et al. [54], in order to study wetting problems in both steady and unsteady states, a new geometrical boundary condition is offered. The main difference between this work and similar research done by Liu et al. [56] is the higher density ratios.

The simulation of acoustofluidics based on LBM is the second innovation of this paper. In the previous work done by Alghane et al. [21], the computations are based on OpenFoam code and finite volume method, and consequently, in their study, the interface is considered constant and so, the simulations are limited to low frequencies. The behavior of interface affected by frequency and amplitude of SAW is the major novelty of our study. From the above-mentioned researches, a constant interface assumption is not considered just by Köster [18]. The interface was implemented as a boundary condition by Köster, whereas it is captured in our study. In addition, the interaction of hydrodynamics and acoustics is simulated more precisely in the present research by capturing the interface. Also, the effect of contact angle hysteresis is considered here and to our knowledge, this study has not been previously presented. Literature investigations on acoustic streaming are limited to qualitative description of the phenomena, and very few researchers have applied quantitative method. Thus, there is a need for accurate and general computations which help researchers to understand, optimize and scale up the actuators which operate based on these waves. The rest of the present paper is organized as follows: In Sect. 2, the governing equations and the numerical methods are described. A definition of the problem is presented in Sect. 3. For validation purposes, numerical results for benchmark problem are presented and then the simulation of acoustofluidics is investigated in the last section of paper and the results are described both qualitatively and quantitatively.

2 Numerical method

In the present model, two immiscible fluids are represented as red and blue fluids. The evolution of distribution function is expressed by the following LB equation:

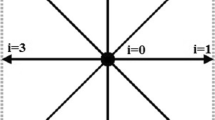
$$\begin{aligned} f_{i}^{k}\left( \vec {x}+\vec {c}_{i}\delta t,t+\delta t \right) =f_{i}^{k}\left( \vec {x},t \right) +\mathrm {\Omega }_{i}^{k}\left( f_{i}^{k}\left( \vec {x},t \right) \right) , \end{aligned}$$
(1)

where \(f_{i}^{k}( \vec {x},t )\) is the total distribution function in ith velocity direction at a position \(\vec {x}\) and time t subscript i, is lattice velocity direction (Fig. 1), superscript k represents the red and blue fluids (liquid or gas phases), \(\vec {c}_{i}\) is the lattice velocity in ith direction \(\delta t\) is time step, and \(\mathrm {\Omega }_{i}^{k}\) is collision operator. The particle velocity vector is as follows:

$$\begin{aligned} \vec {c}_{i}= & {} (0,0)\quad i=0, \end{aligned}$$
(2a)
$$\begin{aligned} \vec {c}_{i}= & {} \left( \cos \frac{\pi ( i-1)}{2},\sin \frac{\pi ( i-1 )}{2}\right) \quad i=1{-}4, \end{aligned}$$
(2b)
$$\begin{aligned} \vec {c}_{i}= & {} \sqrt{2} \left( \cos \frac{\pi \left( i-\frac{9}{2} \right) }{2},\sin \frac{\pi \left( i-\frac{9}{2} \right) }{2} \right) \quad i=5{-}8. \end{aligned}$$
(2c)
Fig. 1
figure 1

Particle distribution in D2Q9 model

Full size image

The collision operator \(\mathrm {\Omega }_{i}^{k}\) consists of three parts:

$$\begin{aligned} \mathrm {\Omega }_{i}^{k}=\left( \mathrm {\Omega }_{i}^{k} \right) ^{3}\left[ \left( \mathrm {\Omega }_{i}^{k} \right) ^{1}+\left( \mathrm {\Omega }_{i}^{k} \right) ^{2} \right] , \end{aligned}$$
(3)

where \(\left( \mathrm {\Omega }_{i}^{k} \right) ^{1}\) is a single-phase collision operator, \(\left( \mathrm {\Omega }_{i}^{k} \right) ^{2}\) is a perturbation operator which generates an interfacial tension, and \(\left( \mathrm {\Omega }_{i}^{k} \right) ^{3}\) is a recoloring operator which is used to produce phase segregation and maintain phase interface.

In LBM methods, MRT model is demonstrated to have better numerical stability than its Bhatnagar–Gross–Krook (BGK) counterpart, and in practical problems with a high density ratio, this property is absolutely vital. Using MRT collision model, the single-phase collision operator can be written as:

$$\begin{aligned} \left( \mathrm {\Omega }_{i}^{k} \right) ^{1}=-\left( M^{-1}S \right) \left( m_{i}^{k}-m_{i}^{keq} \right) +M^{-1}C_{i}^{k}. \end{aligned}$$
(4)

M and its inverse matrix are as follows:

$$\begin{aligned} M= & {} \left[ \begin{array}{lllllllll} 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1\\ -\,4 &{}\quad -\,1 &{}\quad -\,1 &{}\quad -\,1 &{}\quad -\,1 &{}\quad 2 &{}\quad 2 &{}\quad 2 &{}\quad 2\\ 4 &{}\quad -\,2 &{}\quad -\,2 &{}\quad -\,2 &{}\quad -\,2 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad -\,1 &{}\quad 0 &{}\quad 1 &{}\quad -\,1 &{}\quad -\,1 &{}\quad 1\\ 0 &{}\quad -\,2 &{}\quad 0 &{}\quad 2 &{}\quad 0 &{}\quad 1 &{}\quad -\,1 &{}\quad -\,1 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad -\,1 &{}\quad 1 &{}\quad 1 &{}\quad -\,1 &{}\quad -\,1\\ 0 &{}\quad 0 &{}\quad -\,2 &{}\quad 0 &{}\quad 2 &{}\quad 1 &{}\quad 1 &{}\quad -\,1 &{}\quad -\,1\\ 0 &{} \quad 1 &{}\quad -\,1 &{}\quad 1 &{}\quad -\,1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad -\,1 &{}\quad 1 &{}\quad -\,1\\ \end{array} \right] , \end{aligned}$$
(5)
$$\begin{aligned} M^{-1}= & {} \frac{1}{36}\left[ \begin{array}{lllllllll} 4 &{}\quad -\,4 &{}\quad 4 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 4 &{}\quad -\,1 &{}\quad -\,2 &{}\quad 6 &{}\quad -\,6 &{}\quad 0 &{}\quad 0 &{}\quad 9 &{}\quad 0\\ 4 &{}\quad -\,1 &{}\quad -\,2 &{}\quad 0 &{}\quad 0 &{}\quad 6 &{}\quad -\,6 &{}\quad -\,9 &{}\quad 0\\ 4 &{}\quad -\,1 &{}\quad -\,2 &{}\quad -\,6 &{}\quad 6 &{}\quad 0 &{}\quad 0 &{}\quad 9 &{}\quad 0\\ 4 &{}\quad -\,1 &{}\quad -\,2 &{}\quad 0 &{}\quad 0 &{}\quad -\,6 &{}\quad 6 &{}\quad -\,9 &{}\quad 0\\ 4 &{}\quad 2 &{}\quad 1 &{}\quad 6 &{}\quad 3 &{} \quad 6 &{} \quad 3 &{} \quad 0 &{} \quad 9\\ 4 &{}\quad 2 &{}\quad 1 &{}\quad -\,6 &{}\quad -\,3 &{}\quad 6 &{}\quad 3 &{}\quad 0 &{}\quad -\,9\\ 4 &{}\quad 2 &{}\quad 1 &{}\quad -\,6 &{}\quad -\,3 &{} \quad -\,6 &{}\quad -\,3 &{}\quad 0 &{}\quad 9\\ 4 &{}\quad 2 &{}\quad 1 &{}\quad 6 &{}\quad 3 &{}\quad -\,6 &{}\quad -\,3 &{}\quad 0 &{} \quad -\,9\\ \end{array} \right] . \end{aligned}$$
(6)

S is a diagonal matrix given by:

$$\begin{aligned} S=\text {diag}\left( s_{0},s_{1},s_{2},s_{3},s_{4},s_{5},s_{6},s_{7},s_{8} \right) =\text {diag}\left( 0,s_{e},s_{\zeta },0,s_{q},0,s_{q},s_{v},s_{v} \right) , \end{aligned}$$
(7)

where the element \(s_i\) represents the relaxation parameter. These parameters are chosen as \(s_e=\)1.25, \(s_{\zeta }=\)1.14, \(s_{q}=\)1.6 and, \(s_{v}\) is related to the dynamic viscosity of two fluids and is \(\frac{1}{\tau }\) where \(\tau \) is the relaxation time parameter. To consider unequal viscosity of two fluids and ensure the smoothness of the relaxation parameter \(s_{v}\) across the interface, \(\tau \) is calculated as:

$$\begin{aligned} \tau =\left\{ \begin{array}{lll} \tau ^{R} &{}\quad \rho ^{N}>\delta \\ g^{R}\left( \rho ^{N} \right) &{}\quad \delta \ge \rho ^{N}>0\\ g^{B}\left( \rho ^{N} \right) &{}\quad 0\ge \rho ^{N}>-\delta \\ \tau ^{B} &{}\quad \rho ^{N}<-\delta \\ \end{array} \right. , \end{aligned}$$
(8)

where \(\tau ^{k}\) is the relaxation parameter of the fluid k, that is related to kinematic viscosity by \(\nu ^{k}=\frac{1}{3}\left( \tau ^{k}-0.5 \right) \), and \(\delta \) is a free parameter associated with interface thickness which is taken as 0.98 in the present study. In the present model, phase-field \(\rho ^{N}\) is defined as follows:

$$\begin{aligned} \rho ^{N}=\left( \frac{\rho ^{R}}{\rho ^{R^{0}}}-\frac{\rho ^{B}}{\rho ^{B^{0}}} \right) \bigg / \left( \frac{\rho ^{R}}{\rho ^{R^{0}}}+\frac{\rho ^{B}}{\rho ^{B^{0}}} \right) , \end{aligned}$$
(9)

where \(\rho ^{R^{0}}\) and \(\rho ^{B^{0}}\) are the densities of the pure red and blue fluids; \(\rho ^{k}\) is the density of each fluid:

$$\begin{aligned} \rho ^{k}=\mathop {\sum }\limits _i f_{i}^{k}. \end{aligned}$$
(10)

The functions of \(g^{R}\) and \(g^{B}\) are as follows:

$$\begin{aligned} g^{R}= & {} \beta +\gamma \rho ^{N}+\varepsilon {\rho ^{N}}^{2}, \end{aligned}$$
(11)
$$\begin{aligned} g^{B}= & {} \beta +\eta \rho ^{N}+\zeta {\rho ^{N}}^{2}, \end{aligned}$$
(12)
$$\begin{aligned} \beta= & {} \frac{2\tau ^{R}\tau ^{B}}{\tau ^{R}+\tau ^{B}}, \end{aligned}$$
(13)
$$\begin{aligned} \gamma= & {} 2\frac{\tau ^{R}-\beta }{\delta }, \end{aligned}$$
(14)
$$\begin{aligned} \varepsilon= & {} -\frac{\gamma }{2\delta }, \end{aligned}$$
(15)
$$\begin{aligned} \eta= & {} 2\frac{\beta -\tau ^{B}}{\delta }, \end{aligned}$$
(16)
$$\begin{aligned} \zeta= & {} \frac{\eta }{2\delta }. \end{aligned}$$
(17)

The equilibrium distribution function in moment space \(m_{i}^{keq}\) is obtained by:

$$\begin{aligned} m^{keq}= & {} \rho ^{k}\left( 1,-3.6\alpha ^{k}-0.4+3\left| \vec {u} \right| ^{2},5.4\alpha ^{k}-1.4-3\left| \vec {u} \right| ^{2},u_{x},\right. \nonumber \\&\left. \left( -1.8\alpha ^{k}-0.2 \right) u_{x},u_{y},\left( -1.8\alpha ^{k}-0.2 \right) u_{y},u_{x}^{2}-u_{y}^{2},u_{x}u_{y} \right) ^{T}, \end{aligned}$$
(18)

where \(\vec {u}\) is flow velocity (\({u}_{x}\) and \({u}_{y}\) are x and y components, respectively) and it is obtained by:

$$\begin{aligned} \vec {u}=\sum \sum {f_{i}^{k}\vec {c}_{i}}. \end{aligned}$$
(19)

\(\alpha ^{k}\) is a free parameter and the stable interface assumption requires to satisfy the following relation:

$$\begin{aligned} \frac{\rho ^{R^{0}}}{\rho ^{B^{0}}}=\frac{1-\alpha ^{B}}{1-\alpha ^{R}} \end{aligned}$$
(20)

The constraint of \(0 \le \alpha ^{k} \le 1\) should be satisfied to avoid the unreal value of the speed of sound and negative value of fluid density.

The distribution function in moment space is obtained by \(m_{i}^{k}=\mathop {\sum }\nolimits _j {M_{ij}f_{j}^{k}} \). \(C_{i}^{k}\) is a source term added to the system of equations, in order to recover exact Navier–Stokes equations:

$$\begin{aligned} C^{k}=\left[ 0,C_{1}^{k},0,0,0,0,0,C_{7}^{k},0 \right] ^{T}, \end{aligned}$$
(21)

where

$$\begin{aligned} C_{1}^{k}= & {} 3\left( 1-\frac{s_{e}}{2} \right) \left( \frac{\partial Q_{x}}{\partial x}+\frac{\partial Q_{y}}{\partial y} \right) , \end{aligned}$$
(22a)
$$\begin{aligned} C_{7}^{k}= & {} 3\left( 1-\frac{s_{v}}{2} \right) \left( \frac{\partial Q_{x}}{\partial x}-\frac{\partial Q_{y}}{\partial y} \right) , \end{aligned}$$
(22b)
$$\begin{aligned} Q_{x}= & {} \left( 1.8\alpha ^{k}-0.8 \right) \rho ^{k}u_{x}, \end{aligned}$$
(22c)
$$\begin{aligned} Q_{y}= & {} \left( 1.8\alpha ^{k}-0.8 \right) \rho ^{k}u_{y}. \end{aligned}$$
(22d)

The second collision term is as follows:

$$\begin{aligned} \left( \mathrm {\Omega }_{i}^{k} \right) ^{2}=\frac{A_{k}}{2}\left| \vec {f} \right| \left[ w_{i}\frac{\left( \vec {c}_{i}\cdot \vec {f} \right) ^{2}}{\left| \vec {f} \right| ^{2}}-B_{i} \right] , \end{aligned}$$
(23)

where \(A_{k}\) is a parameter that affects the interfacial tension and \(\vec {f}\) is the color-gradient which is calculated as:

$$\begin{aligned} \vec {f}\left( \vec {x},t \right) =\sum \vec {c}_{i} \left[ \rho ^{R}\left( \vec {x}+\vec {c}_{i}\mathrm {\Delta }t,t \right) -\rho ^{B}\left( \vec {x}+\vec {c}_{i}\mathrm {\Delta }t,t \right) \right] . \end{aligned}$$
(24)

Also, \(B_{0} = -\frac{4}{27}\), \(B_{i} = \frac{2}{27}\) for \(i = 1, 2, 3, 4\) and \(B_{i} = \frac{5}{108}\), for \(i = 5, 6, 7, 8\). Using these parameters, the correct term due to interfacial tension in the Navier–Stokes equations can be recovered. Weighted constants \(w_{i}\) are calculated as:

$$\begin{aligned} w_{0}= & {} \frac{4}{9}, \end{aligned}$$
(25a)
$$\begin{aligned} w_{i}= & {} \frac{1}{9}\quad i=1,2,3,4, \end{aligned}$$
(25b)
$$\begin{aligned} w_{i}= & {} \frac{1}{36}\quad i=5,6,7,8. \end{aligned}$$
(25c)

The following equation gives the relationship between surface tension coefficient \(\sigma \) and the parameter \(A^{k}\):

$$\begin{aligned} \sigma =\frac{5\rho \left( A^{R}+A^{B} \right) }{6\tau }. \end{aligned}$$
(26)

To promote phase segregation and maintain a reasonable interface, the segregation operator proposed by Latva-Kokko and Rothman [57] is used, and it is given by:

$$\begin{aligned}&f_{i}^{R}\left( \vec {x},t \right) =\frac{\rho ^{R}}{\rho ^{R}+ \rho ^{B}}\left( {{f_{i}}^{\prime }}^{R}\left( \vec {x},t \right) +{{f_{i}}^{\prime }}^{B}\left( \vec {x},t \right) \right) +\beta \frac{{\rho ^{R}}{\rho ^{B}}}{\rho ^{R}+ \rho ^{B}}w_{i}\cos \varphi _{i}\left| \vec {c}_{i} \right| , \end{aligned}$$
(27a)
$$\begin{aligned}&f_{i}^{B}\left( \vec {x},t \right) =\frac{\rho ^{B}}{\rho ^{R}+\rho ^{B}}\left( {{f_{i}}^{\prime }}^{R}\left( \vec {x},t \right) +{{f_{i}}^{\prime }}^{B}\left( \vec {x},t \right) \right) -\beta \frac{\rho ^{R}\rho ^{B}}{\rho ^{R}+\rho ^{B}}w_{i}\cos \varphi _{i}\left| \vec {c}_{i} \right| , \end{aligned}$$
(27b)

where \({{f_{i}}^{\prime }}^{k}\) is the post-perturbation value of the distribution function, \(\varphi _{\mathrm {i}}\) is the angle between the \(\vec {\nabla }\rho ^{N}\) and the lattice direction \(c_{\mathrm {i}}\), and \(\beta \) is a parameter associated with the interface thickness which should take a value between zero and unity. In the literature, this step is called recoloring step.

In order to apply the effects of external body forces, the term \({\bar{F}}_{i}\) is added to Eq. (1):

$$\begin{aligned} {\bar{F}}=M^{-1}\left( I-\frac{1}{2}S \right) M{\tilde{F}}, \end{aligned}$$
(28)

where I is a \(9\times 9\) unit matrix and \({\tilde{F}}\) is as follows:

$$\begin{aligned} {\tilde{F}}_{i}=w_{i}\left[ 3\left( \vec {c}_{i}-\vec {u} \right) +9\left( \vec {c}_{i}\cdot \vec {u} \right) \vec {c}_{i} \right] \cdot \vec {F}, \end{aligned}$$
(29)

where \(\vec {F}\) is the body force.

In this paper, the displacement of a two-dimensional immiscible drop subjected to acoustic streaming force is studied. This force is represented as follows [14]:

$$\begin{aligned} \vec {F}_{ext}^{k}=-\rho \left( 1+\alpha _{1}^{2} \right) ^{\frac{3}{2}}A^{2}\omega ^{2}k_{i}exp2\left( k_{i}x+\alpha _{1}k_{i}y \right) . \end{aligned}$$
(30)

SAW excites the longitudinal wave transferred into the liquid with the Rayleigh (radiation) angle of \(\theta _{R}\) (respect to y-direction). This angle is related to the substrate and here, 23 degrees are assumed [21]. Also, \(\alpha _{1}\) is attenuation coefficient which is a function of frequency and substrate materials, A is SAW amplitude, \(\omega \) is angular frequency, and \(k_{i}\) is SAW energy dissipation after passing through the interface of the drop. For lithium niobate substrate, \(\alpha _1\) is 2.47 and \(k_i\) is \(-\,1340\) m\(^{-1}\) [21].

2.1 Boundary conditions

In a problem involving a partial differential equation, the solution of the problem relies heavily on the boundary data. In this study, periodic and no-slip boundary conditions are used. Indeed, the periodic boundary condition applies to the transformation step. For this purpose, the information that emits from the boundary is entered from the opposite one. No-slip boundary condition is applied at the solid wall by using simple bounce-back scheme [37].

The contact angle \(\theta \) is enforced at the wall through the geometrical formulation proposed by Ding and Spelt [58]:

$$\begin{aligned} {\rho _{i,1}^{N}}=\rho _{i,2}^{N}+\mathrm {\Theta }_{w}\left[ 1.5\frac{\partial \rho ^{N}}{\partial x}_{i,2}-0.5\frac{\partial \rho ^{N}}{\partial x}_{i,3} \right] , \end{aligned}$$
(31)

where i is a pointer in x-direction and \(\mathrm {\Theta }_{w}=\tan \left( \frac{\pi }{2}-\theta \right) \). Note that the sign of \(\mathrm {\Theta } _{w}\) is positive when \(\frac{\partial \rho ^{N}}{\partial x}>0\) and negative in \(\frac{\partial \rho ^{N}}{\partial x}<0\). After \(\rho _{i,1}^{N}\) is determined, the density can be obtained on the wall. For this, the value of \(\rho _{i,1}^{N}\) (surrounding fluid with lower density) is interpolated. Then, the value of \(\rho _{i,1}^{R}\) (wetting fluid with higher density) is computed by using Eq. (9). So, the density can be applied on the wall.

2.2 Contact angle hysteresis model

The contact angle hysteresis is known as a phenomenon in which the contact line (or the contact point in two-dimensional problems) remains fixed in a given position, provided that the local contact angle \(\theta \) lies within the window of \(\theta _{R}\le \theta \le \theta _{A}\), where \(\theta _{A}\) and \(\theta _{R}\) denote the advancing and receding contact angles, respectively.

At each time step, the values of \(\rho _{i,1}^{N}\) are taken from the previous time and an initial estimate of the local contact angle, \(\theta _0\) is obtained by Eq. (31). The value of \(\theta \) is gotten through the comparison between the value of \(\theta _0\) and those of \(\theta _{R}\) and \(\theta _{A}\). If \(\theta _0 < \theta _{R}\), the value of \(\theta \) is assigned as \(\theta = \theta _{R}\); and if \(\theta >_0 \theta _{A}\), the value of \(\theta \) is assigned as \(\theta =\theta _{A}\); else if \(\theta _R< \theta < \theta _{A}\), the value of \(\theta \) is assigned as \(\theta =\theta _0\). However, the newly assigned \(\theta \) is then used to compute the value of \(\rho _{i,1}^{N}\) in Eq. (31).

In this way, any wettability for fluids on a straight solid wall can achieve through inputting a specified window of contact angle hysteresis. Also, here the contact angle hysteresis is implemented with a given hysteresis window which is determined by the properties of the solid surface such as roughness.

To mention the relationship between the contact angle hysteresis model and the real physics (including real phenomena), we can illustrate that [59], if the contact angle is outside the hysteresis window (advancing or receding contact angle value), the contact line will move with the moving direction depending on the relative magnitude of \(\theta \), \(\theta _{A}\) and \(\theta _{R}\). Specifically, when \(\theta \ge \theta _{A}\), the contact line moves forward and when \(\theta \le \theta _{R}\), the contact line moves backwards.

3 Simulation setup

The drop with a certain diameter and contact angle is loaded on the path taken by SAW propagating through the substrate (Fig. 2). Density and viscosity ratios are 1000 and 15, respectively, and the surface tension coefficient is 0.072 N/m [16]. Moreover, the receding and advancing contact angles are \(95^{\circ }\) and \(105^{\circ }\), respectively, [16]. The no-slip boundary condition is implemented on the substrate and upper side. The periodic boundary condition is applied on other sides. The schematic of the problem is presented in Fig. 2.

Fig. 2
figure 2

Schematic of the problem

Full size image

4 Results and discussion

First, a drop attached on a non-ideal substrate subject to shear flow is investigated to test the hysteresis behavior of the contact angle. Then, the simulation of the drop dynamic behaviors, affected by SAW, is presented and is described both qualitatively and quantitatively.

4.1 Drop on a non-ideal substrate subject to a shear flow

The drop subjected to shear flow is considered here to test the hysteresis behavior of contact point. At first, a drop pinned on the solid surface due to a large hysteresis window is simulated and the obtained results are compared with the available numerical results. Then the influence of the hysteresis window on drop behavior is investigated at a fixed Capillary number (Ca).

The computational domain is a rectangle with 4L length and 2L width where \({L} = 0.5\) mm. The shear flows are driven by moving the upper wall at a constant velocity of \({v}_{w}\). The important non-dimensional parameter is Ca defined as:

$$\begin{aligned} \text {Ca}=\frac{\mu U}{\sigma }. \end{aligned}$$
(32)

The characteristic velocity U is taken as the flow velocity at the top of the drop and is defined as \(U=\frac{rv_{w}}{2L}\) with the 2L distance between the upper and the lower walls and r as the initial height of the drop. The density ratio and kinematic viscosity ratio are set to be 1 and a drop with a certain contact angle \(\theta \) is considered. The periodic condition is used for the lateral direction. The simple bounce-back is imposed on the bottom walls. The geometrical wetting boundary condition is used as explained in the previous section. The boundary condition with the known velocity of \({v}_{w}\) at the upper wall is implemented as follows [37]:

$$\begin{aligned} \rho _{N}= & {} \frac{1}{1+v_{w}}\left[ f_{0}+f_{1}+f_{3}+2\left( f_{2}+f_{6}+f_{5} \right) \right] , \end{aligned}$$
(33a)
$$\begin{aligned} f_{4}= & {} f_{2}, \end{aligned}$$
(33b)
$$\begin{aligned} f_{7}= & {} f_{5}+\frac{1}{2}\left( f_{1}-f_{3} \right) -\frac{1}{2}\rho _{N}v_{w}, \end{aligned}$$
(33c)
$$\begin{aligned} f_{8}= & {} f_{6}+\frac{1}{2}\left( f_{3}-f_{1} \right) +\frac{1}{2}\rho _{N}v_{w}. \end{aligned}$$
(33d)

Note that the values of \(f_{0}, f_{1}, f_{2}, f_{3}, f_{5}\), and \(f_{6}\) are obtained in the streaming step.

Initially, a drop with the contact angle \(\theta = 60^{\circ }\) is deposited on the bottom wall. Same as Ref. [56], a large hysteresis window (\(\theta _{R}\), \(\theta _{A}) = (5^{\circ }, 175^{\circ }\) ) is considered. Also, Ca is assumed 0.15. In this condition, the drop remains pinned on the bottom wall and this allows us to compare our results with those obtained by Liu et al [56]. After the grid convergence study, a \(401\times 201\) lattice configuration is used to perform simulations.

Figure 3 compares the simulated equilibrium shape of the drop with the numerical results of Liu et al [56]. In this figure, the simulated shape of the drop is represented by a solid line and the results of Liu et al. are shown by a dotted line. Also, x and y coordinates, relative to the center of the computational domain (\(x_0, y_0\)) are normalized by R which is the radius of the drop and is obtained from Eq. (34):

$$\begin{aligned} R=\frac{4H^{2}+L^{2}}{8H}, \end{aligned}$$
(34)

where H and L are the height and the base of the drop. It can be seen that the numerical results agree well with the results of Liu et al. and there is a good accuracy in the modified model for handling contact angle hysteresis.

Fig. 3
figure 3

Drop pinned on a non-ideal surface subject to shear flow

Full size image

Next, the effects of different contact angle hysteresis windows are investigated at a fixed Ca. A drop with the contact angle \(\theta =90^{\circ }\) is considered and the velocity of the moving wall is chosen in a way that \(\text {Ca}=0.32\). In addition, the hysteresis windows are \((\theta _{R},\theta _{A})=(0^{\circ }, 180^{\circ })\), \((0^{\circ }, 110^{\circ })\), \((70^{\circ }, 180^{\circ })\), and \((70^{\circ }, 110^{\circ })\). The time evolution of drop motion is illustrated in Fig. 4. For \((\theta _{R},\theta _{A}) = (0^{\circ },180^{\circ } )\), both the upstream and downstream contact angles cannot go outside the hysteresis window, so both contact points remain fixed. For \((\theta _{R},\theta _{A})=(0^{\circ }, 110^{\circ })\), the upstream contact angle is decreased, which is in the range of \((0^{\circ }, 110^{\circ })\), hence, the upstream contact point remains motionless. For the downstream contact point, it is pinned initially when the corresponding contact angle is less than \(110^{\circ }\) , and later it moves downstream so long as the contact angle becomes larger than \(110^{\circ }\). For \((\theta _{R},\theta _{A})=(70^{\circ }, 180^{\circ })\), the downstream contact angle increases continuously, but it stays in the range of hysteresis window at all times; consequently the downstream contact point is immobilized. For the upstream contact point, during the initial short time, it is pinned because the corresponding contact angle is larger than \(70^{\circ }\), and later it progresses downstream along the surface when the contact angle is less than \(70^{\circ }\). For \((\theta _{R},\theta _{A})=(70^{\circ }, 110^{\circ })\), the drop remains fixed and deforms continuously until the upstream and downstream contact angles reach their hysteresis limits and then starts to slip over the wall. These results are in qualitative agreements with the results of Liu et al. [56].

Fig. 4
figure 4

Temporal evolution of drop subject to shear flow. a Contact angle hysteresis window \((\theta _{R},\theta _{A})=(0^{\circ }, 180^{\circ })\), b Contact angle hysteresis window \((\theta _{R},\theta _{A})=(0^{\circ }, 110^{\circ })\), c Contact angle hysteresis window \((\theta _{R}, \theta _{A})=(70^{\circ }, 180^{\circ })\), d Contact angle hysteresis window \((\theta _{R}, \theta _{A})=(70^{\circ }, 110^{\circ })\)

Full size image

Based on these results, two different dynamical behaviors of the drop can be observed. In the first one which has occurred for \((\theta _{R},\theta _{A})=(0^{\circ }, 180^{\circ })\), the drop departs entirely from the wall. Otherwise, the drop breaks up into two separate parts, one moves in the carrier fluid and the other adheres to the solid wall. The size and shape of the pinched-off portion depend on the contact angle hysteresis window. For \((\theta _{R},\theta _{A})=(0^{\circ }, 180^{\circ })\) and \((0^{\circ }, 110^{\circ })\), the drop remains motionless, while for \((70^{\circ }, 110^{\circ })\), the drop slips over the surface.

4.2 Acoustofluidics

The surface acoustic waves are one of the flow control techniques. In this section, the interaction of SAW and the drop is comprehensively investigated through qualitative analysis. At first, the physical behavior of drop is presented according to experimental results. Then, the simulation results of the interaction of SAW and the drop are described.

As shown in Fig.  5 according to Ref. [60], when SAW is applied, acoustic streaming is induced due to leaky wave radiated into the drop. At low power, the drop vibrates at its position (Fig. 5a). Increasing the power makes acoustic streaming strong enough to result in a significant inertial force and drives the drop in the wave propagation direction (Fig. 5b). Further increase in the power makes acoustic streaming so violent that somehow the liquid is jetted into the air as shown in Fig. 5c. When the applied power is so high, strong capillary waves at the drop surface overcome capillary stress and lead to the atomization of drop (Fig. 5d).

Fig. 5
figure 5

Drop dynamics affected by SAW. a Streaming, b pumping, c jet, and d atomization [60]

Full size image

In this condition, two main phenomena occur. First, the energy absorbed by the drop is transformed into vibration energy. Second, the drop is deformed by acoustic pressure and begins to move. Three periodical steps can be seen in the process of drop distortion [61]. At first, the drop adopts a spherical shape on the surface. Then, the drop stands up and the solid/liquid interface decreases. In the third step, the top of drop bends to the side in the direction of SAW propagation. Finally, the three-phase contact line advances and the drop adopts a spherical shape again.

Now, the dynamical behavior of interface in three mentioned modes (streaming, pumping, and jetting) is presented and compared with the available experimental results. The fluid properties are similar to those of Sect. 3 and the computational grid is a \(801\times 401\) lattice configuration. Figure 6a presents the streaming mode. SAW has the amplitude and angular frequency of 0.5 nm and 20 MHz, respectively. It is important to notice that all quantities will be converted into lattice units. It is worthy to note that the wave propagates from left to right (x-direction). It is observed that the drop does not move after 6.6 s and it only bends to the radiation angle. Figure 6b clearly compares the drop shape in streaming mode [16], where the dotted line indicates the experimental result and the solid line represents the numerical simulation. Also, the same as the previous section, x and y coordinates relative to the center of the computational domain (\(x_0\)) are normalized by the radius of the drop. These significant effects such as drop mixing, drop heating, particle patterning, and particle concentration have been utilized in various applications.

Fig. 6
figure 6

Temporal evolution of drop in streaming state. a Numerical simulation and b comparison with experimental results [16]

Full size image

Secondly, SAW amplitude is increased to 1 nm. In this state, the drop moves as shown in Fig. 7a. The actuation of the drop has been used for pumping, sample collecting, and sample dispensing. Figure 7b compares the drop shape with the experimental results [16]. It is clear that the periodic behaviors of the drop are not observed in these results. In fact, the overall shape of the drop is similar to the experimental results.

Fig. 7
figure 7

Temporal evolution of drop in pumping state. a Numerical simulation and b comparison with experimental results [16]

Full size image

The variation of the advancing and receding contact angles as a function of time is presented in Fig. 8. During the initial time, both the upstream and downstream contact angles fluctuate around their hysteresis limits. After a short time, the receding contact angle reaches its hysteresis limit and the corresponding contact point moves downstream. The downstream contact point is pinned while the advancing contact angle is less than \(105^{\circ }\) , but after 1.15 s it moves downstream. The strength of retention force acting at the contact line of the substrate is related to \(\theta _{\mathrm {a}}-\theta _{\mathrm {r}}\) (where \(\theta _{\mathrm {a}}\) and \(\theta _{\mathrm {r}}\) are advancing and receding contact angle, respectively). When the \(\theta _{\mathrm {a}}\) and \(\theta _{\mathrm {r}}\) reach their hysteresis limits, the drop starts to slip over the wall.

Fig. 8
figure 8

Variation of dynamic contact angle, corresponding to the contact angle hysteresis window \((\theta _{R},\theta _{A})=(95^{\circ }, 105^{\circ })\)

Full size image

Figure 9 shows the temporal evolution of the dimensionless wetting length \(\frac{B}{2R}\) between the wall and the sliding drop. As shown in this figure, \(\frac{B}{2R}\) increases rapidly at first and then gradually decreases before it reaches a steady-state value. The drop minimizes its own interface with the solid and thus its movement is facilitated. The reduction of wetting length can be interpreted based on the contact angle hysteresis and the relative movement of contact points. When the advancing contact point is pinned on the surface, the rear contact angle reaches its hysteresis limit and the receding contact point starts to move. After about 1 s, the downstream contact point starts to move, but the upstream contact point is faster and thus the wetting length still diminishes. When the front contact point accelerates, the velocity of the rear point decreases and the drop subjected to acoustic force reaches its steady shape and continues to move.

Fig. 9
figure 9

Wetting length as a function of time

Full size image

In Fig. 10, the velocity of moving drop, obtained by varying the acoustic wave amplitude A at pumping mode, is compared with results of Brunet et al [16]. Also, the numerical results, with and without contact angle hysteresis, are compared to each other Note, \(\theta _{R}\) and \(\theta _{A}\) are set to be \(95^{\circ }\) and \(105^{\circ }\), respectively (based on data presented in Ref. [16]). As expected, the drop moves faster in large A. The velocity magnitudes in the numerical simulations are larger than those of the experimental data. Since a two-dimensional model is used for the simulations, it is reasonable to observe some discrepancy. Both numerical and experimental data show that the influence of A is strongly nonlinear and the drop velocity increases dramatically in large A. This figure shows that the numerical results are in good agreement with the experimental data. Also, the importance of modeling contact angle hysteresis phenomena can be seen in this figure. By applying contact angle hysteresis effects, the numerical results are improved about 20%.

Fig. 10
figure 10

Variation of drop velocity versus acoustic wave amplitude

Full size image

In the third state, the detachment of drop is observed. In Fig. 11 wave amplitude and angular frequency are 2 nm and 20 MHz, respectively. The height of the drop grows in this stage. After 0.32 s, the fluctuations are amplified and drop is detached from the wall finally Contrary to the previous observations, these results are not consistent with experimental data. Although the simulations show that the frequency and amplitude in which the jetting mode occurs are the same as the experimental data, the dynamical behavior of the drop is different.

Fig. 11
figure 11

Temporal evolution of drop in the jet state. a Numerical simulation and b comparison with experimental results [62]

Full size image

About Fig. 11, some discussions are necessary. Note that, there are two fundamental properties which have important roles in the interfacial phenomena. Surface tension is a main factor affecting the shape of fluid interfaces and controls their deformation. The contact angle and the wetting property are the second fundamental characteristics that strongly affect the multiphase flow physics. In this work, we use two-dimensional version of LBM and so our simulations are two-dimensional. Since the surface tension force for a three-dimensional object has one more curvature term than the two-dimensional object, the effects of the surface tension on the interface is noticeably smaller than the three-dimensional counterpart. The significant difference shown in Fig. 11 for the drop shape in the jet state may reflect the importance of modeling the interfacial force correctly as the contact angle started playing less important role during this stage due to a much smaller contact area comparing with the rest of the interfacial area.

Figure 12 summarizes the threshold amplitude that is required at different frequencies to induce the respective microfluidic phenomena under various SAW amplitudes and resonant frequencies. There are critical wave amplitude boundaries between various microfluidic phenomena of the liquid drops and these threshold values increase significantly by increasing f. At different frequencies, the minimum required wave amplitude considerably increases from streaming to pumping and pumping to jetting modes.

Fig. 12
figure 12

Relationship between SAW amplitude and frequency for identifying the boundaries of different phenomena

Full size image

In order to clearly demonstrate the coupled acoustic and hydrodynamic effects, the viscosity ratio is investigated here. Since the wave amplitude and frequency are 1 nm and 20 MHz, respectively, three viscosity ratios are considered: 1.31, 2.67, and 15. When the viscosity ratio is 1.31, the drop moves at a velocity of 27.8 mm/s; at 2.67, the drop velocity increases to 28.9 mm/s; and ultimately at the viscosity ratio of 15, the velocity is 44 mm/s. The increase in viscosity (decrease of viscosity ratio) reduces velocity as expected for moving drops. Indeed, viscosity is effective in dissipation rate in the vicinity of the contact line and hence, an equal driving force displaces viscous drops at a lower speed. The effect of viscosity in the dynamical behavior of jetting mode is illustrated in Fig. 13. For the fluid with high viscosity, the oscillations are very small, whereas the jet of fluid with low viscosity is unstable.

Fig. 13
figure 13

Dynamical behaviors of jet for two different viscosity ratios

Full size image

The effect of surface tension as another key parameter is also investigated in this work. The surface tension coefficient can be regarded as the surface energy per unit area of the interface. In similar conditions (i.e., \({A} = 1\) nm, \({f} = 20\) MHz, and \(\text {viscosity ratio} = 15\)), when the surface tension coefficient decreases from 0.072 to 0.066 N/m, the velocity of drop decreases from 44 to 24.5 mm/s. In fact, retention force is a function of surface tension coefficient and hence, this force also decreases. However, in higher surface tension coefficients, the drop detaches later from the surface as the SAW amplitude increases. This occurs due to the high resistance of drop against deformation.

The effect of the contact angle hysteresis window is investigated here. The analysis is divided into two parts: the pumping mode and the jetting mode. In the pumping mode, four contact angle hysteresis windows as \((\theta _{R},\theta _{A})=(0^{\circ }, 180^{\circ })\), \((0^{\circ }, 105^{\circ })\), \((95^{\circ }, 180^{\circ })\), and \((95^{\circ }, 105^{\circ })\) are considered. The wave amplitude and the wave frequency are 1 nm and 20 MHz, respectively.

Figure 14 compares the shape of the drop in the hysteresis windows and also shows the contact angles as a function of time. For the hysteresis window \((\theta _{R}, \theta _{A})=(95^{\circ },105^{\circ })\), the dynamic contact angle is presented in Fig. 8, which is not included in Fig. 14 to avoid repetition. The results show that for \((\theta _{R},\theta _{A})=(0^{\circ }, 180^{\circ })\), the drop is pinned on the substrate. Also, for the hysteresis window \((\theta _{R},\theta _{A})=(0^{\circ },105^{\circ })\), the drop moves at a very low speed of around 0.3 mm/s. For two another hysteresis windows \((\theta _{R},\theta _{A})=(95^{\circ },180^{\circ })\) and \((95^{\circ },105^{\circ })\), the drop moves more rapidly, but for \((\theta _{R},\theta _{A})=(95^{\circ }, 180^{\circ })\), this speed is about half the magnitude of velocity for \((\theta _{R},\theta _{A})=(95^{\circ }, 105^{\circ })\) and it is equal to 20 mm/s. As expected, these results indicate that on the surfaces with low roughness the drop moves faster, therefore, it is possible to pump the drop with less power consumption. Comparison between the dynamical behavior of contact angles in different hysteresis windows shows that the optimum condition for drop movement is \((\theta _{R},\theta _{A})=(95^{\circ }, 105^{\circ })\). In other windows, the advancing or receding contact angles or both are motionless and so the movement of the drop is disrupted.

Fig. 14
figure 14

Effects of contact angle hysteresis: pumping mode. a Shape of drop, b dynamic contact angle for hysteresis window \((\theta _{R},\theta _{A})=(0^{\circ }, 180^{\circ })\), c dynamic contact angle for hysteresis window \((\theta _{R},\theta _{A})=(0^{\circ }, 105^{\circ })\), and d dynamic contact angle for hysteresis window \((\theta _{R}, \theta _{A})=(95^{\circ }, 180^{\circ })\)

Full size image

Figure 15 illustrates the effect of the contact angle hysteresis windows on the jetting mode. The wave amplitude and the wave frequency are 2 nm and 20 MHz, respectively, and two contact angle hysteresis windows \((\theta _{R},\theta _{\mathrm {A}})=(0^{\circ }, 180^{\circ })\) and \((\theta _{R},\theta _{A})=(95^{\circ },105^{\circ })\) are investigated. It is observed that surface roughness has no effect on the drop shape in this mode and only increases the Weber number from 0.51 to 0.81, which indicates the instability of jet.

Fig. 15
figure 15

Effects of contact angle hysteresis: jetting mode

Full size image

5 Conclusion

In this paper, the displacement of a two-dimensional immiscible drop subjected to acoustic streaming forces has been simulated by MRT CGM LBM method and the contact angle hysteresis effects have been considered in the modeling. The acoustic streaming has been implemented as an external body force. The modified model is used to investigate the dynamical behavior of a drop on a non-ideal surface subject to a shear flow. It is shown that the numerical results obtained by the developed method are in good agreement with the available data

The dynamical behavior of drop affected by SAW is fully simulated in the three modes: streaming, pumping and jetting. The obtained results show a relatively good agreement with experimental data. Based on numerical results, the best condition for movement of the drop is when the contact angle hysteresis window is \((95^{\circ },105^{\circ })\). When the limitations of contact angle hysteresis are expanded, the drop is fixed on the surface. In the frequency ranges between 20 and 200 MHz, the minimum wave amplitude required to initiate pumping mode changes from 0.8 to about 1 nm. These variations in jetting mode are more significant when frequency varies from 20 to 200 MHz and the minimum wave amplitude is between about 2–4 nm. When the limits of contact angle hysteresis window are expanded to \((0^{\circ } ,180^{\circ })\), it is observed that the Weber number reaches 0.081, and consequently, the jet instabilities are amplified.

It is observed that the drop velocity increases when the SAW amplitude increases. The boundaries of microfluidic phenomena such as pumping and jetting increase when the frequency increases. The increase of viscosity is equal to the decrease in drop velocity because of dissipation phenomena. Accordingly, when the viscosity ratio varies from 1.31 to 15, the drop velocity changes from 27.8 to 44 mm/s. The resistance to deformation is amplified when the surface tension coefficient increases. Also, the effects of contact angle hysteresis are investigated. The results show that the contact angle hysteresis phenomenon has a significant effect on the flow dynamics and numerical results; hence, the contact angle hysteresis modeling can improve the results by up to 20%. When the surface roughness increases, the velocity of drop movement decreases in the pumping mode and the instabilities increase in the jetting mode.

This study is the first simulation of the acoustofluidics with contact angle hysteresis effects in a general form. But, there are some limitations which can be followed as future works. This simulation is two-dimensional, while some phenomena are three-dimensional. Three-dimensional effects are not adequately represented in this work, and some significant differences shown in results (specially in jetting mode) are for this reason. So, the three-dimensional formulation can improve the numerical results. Additionally, thermal effects are not considered. With respect to the limitations mentioned, the results are in relatively good agreement with the experimental results. By eliminating these limitations, acoustofluidics phenomenon can be simulated and SAW flow control systems can be optimized.