Numerical Analysis of Droplet Motion over a Flat Plate Due to Surface Acoustic Waves

Abstract

Micro-scale systems have gained considerable attention in recent years and a large amount of researches have been done in this field. In this study, the hydrodynamic interference of a droplet is comprehensively investigated under surface acoustic waves. This paper reveals the effects of some control parameters such as wave amplitude and wave frequency on the dynamical behavior of droplet. For these purposes, a two-dimensional multiple-relaxation-time color-gradient model lattice Boltzmann method is developed. This model is first validated by dynamical behaviors of a droplet subjected to shear flow. Moreover, displacement of a droplet affected by surface acoustic waves is comprehensively investigated. Our obtained simulations agree well with observations. According to our finding, the increase of frequency leads to the increment of required power to change the modes of the system from streaming to pumping or jetting states. Obtained results clearly show that hydrophobicity, reduction of viscosity, and increase of surface tension coefficient significantly influence on the flow control system and grow its sensitivity. Our results demonstrate that the minimum wave amplitude required to initiate pumping mode changes from 0.8 nm to about 1 nm when the frequency ranges are within 20 MHz to 200 MHz. The variations in jetting mode are also observed. Our findings clearly show that the minimum wave amplitude varies from about 2 nm to 4 nm when the frequency is changed from 20 MHz to 200 MHz. According to numerical analysis using lattice Boltzmann method, this work tried to capture the deformations of the fluid/fluid interface affected by surface acoustic waves and simulated the moving contact line in the high density ratio. These two main phenomena are recognized as significant parameter in our problem.

Introduction

Recently, the applications of acoustic force as a flow control device have significantly increased and led to a new scientific knowledge known as acoustofluidics. In this research topic, the effects of acoustics on the fluids were precisely investigated (Pedersen 2008). In some resources, the term “acoustofluidics” is limited to the application of the ultrasonic waves in microfluidic systems (Muller 2012). Acoustic streaming and acoustic radiation are two main effects of these waves on the fluids. These phenomena are applied in various scientific and industrial applications such as pumping (Yu and Kim 2002), heating, particle separation (Petersson et al. 2005) and mixing (Jang et al. 2007). In this field, one of the pioneer works is a nano-pump reported by Wixforth (Wixforth 2004). He described a novel way to actuate the droplets in a microarray by using surface acoustic waves (SAW).

Surface acoustic waves were defined by Lord Rayleigh in 1885. However, in recent decades, new researches have extensively focused in this topic. Surface acoustic wave can be generated by applying an electric field to a set of interdigital transducers on the surface of a piezoelectric substrate. When a traveling SAW contacts a liquid, the acoustic streaming is induced due to acoustic energy attenuation. It is clear that fluid motion highly depends on wave amplitude and wave frequency.

There are three main branches in this topic: 1. analytical, 2. experimental, and 3. numerical. Most of previous studies applied an experimental technique for their investigations. In analytical studies (Westervelt 1953; Nyborg 1953; Lighthill 1978), a new term known acoustic streaming force is introduced. Shiokawa et al. (Shiokawa et al. 1989) used the equations derived in mentioned studies and developed an expression to describe some aspects of these phenomena. In these two review papers (Yeo and Friend 2014; Ding et al. 2013), the development, operation, and manufacturing of SAW based systems are comprehensively studied. The application of SAW in mixing of particles (Shilton et al. 2014), active mixing (Sritharan et al. 2006), actuation of small droplets along predetermined trajectories (Wixforth et al. 2004), and the role of acoustic streaming in convection and fluidization in oscillatory flows (Valverde 2015) are some of empirical works that can be mentioned in this context. Brunet et al. comprehensively focused in this topic and their comprehensive empirical studies are the main resource for other scholars (Brunet et al. 2010).

The numerical works are mainly divided in three general sets: separation of scales (Tan et al. 2009a; Kӧster 2007; Frommelt et al. 2008a; Vanneste and Buhler 2011; Franke et al. 2013; Antil et al. 2009; Haydock and Yeomans 2003; Ovchinnikov et al. 2014; Riaud et al. 2017), applying acoustic streaming as an external force (Alghane et al. 2011; Frommelt et al. n.d.; Sankaranarayanan et al. 2008; Tang and Hu 2015; Moudjed et al. 2015; Gubaidullin and Yakovenko 2015), and applying oscillatory boundary conditions that often called direct numerical simulation (Sajjadi et al. 2015; Uemura et al. 2015). A reliable solution for full compressible Navier-Stokes equations, which govern the physics of fluid motion including the propagation of acoustic waves, is very difficult and sometime unreachable. In the first strategy, total problem is broken down into several sub-domains in which the fluid motions were separated into acoustic and streaming flows. The fluid and acoustic fields are coupled via theory of acoustic streaming. The acoustic streaming is not solved separately in the second method. Indeed, this is considered as a body force, and it is added to fluid equations system as an external force. On the other hand, this method is a particular case of perturbation analyses where, only the incident acoustic field is computed (acoustic propagation and reflections inside the droplet are neglected). In the third category, solid surface boundary conditions are applied in a manner that meets physical situations.

The contact line dynamics is a challenging item due to two primary reasons: interplay of phenomena occurring over a wide range of length scales, from macro size down to intermolecular distance and interactions among fluid and solid phases. In order to describe the contact line dynamics, computational methods are categorized into three major types: molecular dynamics (Satoh 2011), macroscopic hydrodynamic approaches, and lattice Boltzmann method (LBM) (He and Luo 1997; Lallemand and Luo 2000a; Sukop and Throne 2006; Mohamad 2011; Huang et al. 2015).

In microscopic approach, intermolecular interactions determine interface and dynamics of contact line. Therefore, mesoscopic models such as LBM are more suitable for simulation of the complex, dynamic behavior (Taeibi-Rahni et al. 2015). LBM capture interfaces very straightforward and so, methods such as level set, front tracking, or guess of the interface shape are not used in this technique. Due to mesoscopic properties, this method can predict the motion of particles without applying slip boundary condition and hence, moving contact line could be simulated in this method. There are three major classes of interfacial multiphase LBM: color-gradient model (CGM), pseudopotential model (Shan & Chen model) (Shan and Chen 1994; Shan 2006), and free energy model (Swift et al. 1996).

First multi-component multi-phase LBM model was presented by Gunstensen (Gunstensen et al. 1991) based on Rothman and Keller lattice gas model (1988) (Rothman and Keller 1988). Then, CGM was modified by Grunau et al. (Grunau et al. 1993) in 1993. Also, Leclaier et al. presented three-dimensional version of the modified model (Reis and Phillips 2007). One of the most important advantage of this model is sharp interfaces and also, by setting a single adjustable parameter, the surface tension is analytically calculated (Wu et al. 2008). Other characteristics of this model are as follow: complete immiscibility, stability for a broad range of viscosity ratios, ease of implementation, accuracy, and low spurious currents.

CGM have been also widely used to study some applicable problems such as direct computational acoustics (Tsutahara 2012; Nguyen and Wereley 2006), microfluidic flows (Montessori et al. 2018), and layered two-phase flows in two-dimensional channels (Huang et al. 2013). In order to simulate flows with high density ratios, Leclaire et al. (Leclaire et al. 2017a, b; Leclaire et al. 2016) modified CGM, based on multi-relaxation time (MRT) collision operator. For recovering the correct Navier-Stokes equations, a simple source term is proposed by Ba et al. (Ba et al. 2016), which could be added into the single-phase collision operator. They applied an equilibrium density distribution function that was derived from the third-order Hermite expansion of the Maxwellian distribution.

CGM is also used to study wetting phenomena (Ba et al. 2013; Liu et al. 2015). However, the issue of density-ratio in these works continues and so these models are not applicable in real practical problems. For solving this critical issue, according to model developed by Ba et al. (Ba et al. 2016), we proposed a geometrical boundary condition to simulate wetting phenomena and dynamical behavior of moving contact line in high density-ratios (Sheikholeslam Noori et al. 2019).

The simulation of acoustofluidics based on LBM is the second innovation of this paper. Haydock (Haydock and Yeomans 2003) has applied LBM to investigate a continuous flow in a channel with the oscillatory boundaries. In fact, fluid-fluid interface as an important subject is investigated in present paper. In previous work done by Alghane (Alghane et al. 2011), the computations are based on OpenFoam code and finite volume method. But, in this study, the interface is considered constant and so, the simulations are limited to low frequencies. The behavior of interface affected by frequency and amplitude of SAW is the major novelty of our study. From the above-mentioned researches, a constant interface assumption is not considered just by Köster (Kӧster 2007). Köster implemented the interface as a boundary condition, whereas interface is captured in our study. So, Kösterʼs model did not allow for droplet breakup.

Literature investigations on acoustic streaming are limited to qualitative description of the phenomena and very few researchers applied quantitative method. Thus, there is a need for accurate and general computations which help researchers to understand, optimize and scale up the actuators which operate based on these waves. The rest of the present paper is organized as follows: in section 2, the governing equations and the numerical methods are described. A definition of the problem is presented in section 3. For validation purposes, section 4 includes numerical results for dynamic droplet contact angle. The simulation of acoustofluidics is presented in the last section of paper and is described both qualitatively and quantitatively.

Numerical Method

In the present model, two immiscible fluids are represented as a red fluid and a blue fluid. The evolution of distribution function is expressed by following LB equation:

$$ {f_i}^k\left(\overrightarrow{x}+{\overrightarrow{c}}_i\delta t,t+\delta t\right)={f_i}^k\left(\overrightarrow{x},t\right)+{\Omega_i}^k\left({f_i}^k\left(\overrightarrow{x},t\right)\right), $$

(1)

where ${f_i}^k\left(\overrightarrow{x},t\right)$ is the total distribution function in ith velocity direction at position $\overrightarrow{x}$ and time t; subscript i is lattice velocity direction (Fig. 1); superscript k represents the red and blue fluids (liquid or gas phases); ${\overrightarrow{c}}_i$ is the lattice velocity in ith direction; δt is time step; and Ω_i^k is collision operator. In a D2Q9 LBM (two dimensions and nine moments), the particle velocity vector is as follow:

$$ \overrightarrow{c_i}=\left(0,0\right),i=0 $$

(2a)

$$ \overrightarrow{c_i}=\left(\cos \frac{\pi \left(i-1\right)}{2},\sin \frac{\pi \left(i-1\right)}{2}\right),i=1-4 $$

(2b)

$$ \overrightarrow{c_i}=\sqrt{2}\left(\cos \frac{\pi \left(i-\frac{9}{2}\right)}{2},\sin \frac{\pi \left(i-\frac{9}{2}\right)}{2}\right).i=5-8 $$

(2c)

Fig. 1

D2Q9 lattice representation

The collision operator Ω_i^k consists of three parts:

$$ {\Omega_i}^k={\left({\Omega_i}^k\right)}^3\left[{\left({\Omega_i}^k\right)}^1+{\left({\Omega_i}^k\right)}^2\right], $$

(3)

where (Ω_i^k)¹ is single phase collision operator, (Ω_i^k)² is perturbation operator which generates an interfacial tension, and (Ω_i^k)³ is recoloring operator which is used to produce phase segregation and maintain phase interface.

In LB methods, MRT model is demonstrated to have better numerical stability than its Bhatnagar-Gross-Krook (BGK) counterpart, and in practical problems with high density ratio, this property is absolutely vital. Using MRT collision model, the single phase collision operator can be written as:

$$ {\left({\Omega_i}^k\right)}^1=-\left({M}^{-1}S\right)\left({m_i}^k-{m_i}^{keq}\right)+{M}^{-1}{C_i}^k. $$

(4)

M and its inverse matrix are as follows:

$$ M=\left[\begin{array}{c}1\\ {}-4\\ {}\begin{array}{c}4\\ {}0\\ {}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}0\\ {}0\\ {}0\end{array}\end{array}\end{array}\end{array}\kern0.5em \begin{array}{c}1\\ {}-1\\ {}\begin{array}{c}-2\\ {}1\\ {}\begin{array}{c}-2\\ {}0\\ {}\begin{array}{c}0\\ {}1\\ {}0\end{array}\end{array}\end{array}\end{array}\kern0.5em \begin{array}{c}1\\ {}-1\\ {}\begin{array}{c}-2\\ {}0\\ {}\begin{array}{c}0\\ {}1\\ {}\begin{array}{c}-2\\ {}-1\\ {}0\end{array}\end{array}\end{array}\end{array}\kern0.5em \begin{array}{ccc}\begin{array}{c}1\\ {}-1\\ {}\begin{array}{c}-2\\ {}-1\\ {}\begin{array}{c}2\\ {}0\\ {}\begin{array}{c}0\\ {}1\\ {}0\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}1\\ {}-1\\ {}\begin{array}{c}-2\\ {}0\\ {}\begin{array}{c}0\\ {}-1\\ {}\begin{array}{c}2\\ {}-1\\ {}0\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}1\\ {}2\\ {}\begin{array}{c}1\\ {}1\\ {}\begin{array}{c}1\\ {}1\\ {}\begin{array}{c}1\\ {}0\\ {}1\end{array}\end{array}\end{array}\end{array}\end{array}\kern0.5em \begin{array}{ccc}\begin{array}{c}1\\ {}2\\ {}\begin{array}{c}1\\ {}-1\\ {}\begin{array}{c}-1\\ {}1\\ {}\begin{array}{c}1\\ {}0\\ {}-1\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}1\\ {}2\\ {}\begin{array}{c}1\\ {}-1\\ {}\begin{array}{c}-1\\ {}-1\\ {}\begin{array}{c}-1\\ {}0\\ {}1\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}1\\ {}2\\ {}\begin{array}{c}1\\ {}1\\ {}\begin{array}{c}1\\ {}-1\\ {}\begin{array}{c}-1\\ {}0\\ {}-1\end{array}\end{array}\end{array}\end{array}\end{array}\right], $$

(5)

$$ {M}^{-1}=\frac{1}{36}\left[\begin{array}{ccc}\begin{array}{c}4\\ {}4\\ {}\begin{array}{c}4\\ {}4\\ {}\begin{array}{c}4\\ {}4\\ {}\begin{array}{c}4\\ {}4\\ {}4\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}-4\\ {}-1\\ {}\begin{array}{c}-1\\ {}-1\\ {}\begin{array}{c}-1\\ {}2\\ {}\begin{array}{c}2\\ {}2\\ {}2\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}4\\ {}-2\\ {}\begin{array}{c}-2\\ {}-2\\ {}\begin{array}{c}-2\\ {}1\\ {}\begin{array}{c}1\\ {}1\\ {}1\end{array}\end{array}\end{array}\end{array}\end{array}\kern0.5em \begin{array}{ccc}\begin{array}{c}0\\ {}6\\ {}\begin{array}{c}0\\ {}-6\\ {}\begin{array}{c}0\\ {}6\\ {}\begin{array}{c}-6\\ {}-6\\ {}6\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0\\ {}-6\\ {}\begin{array}{c}0\\ {}6\\ {}\begin{array}{c}0\\ {}3\\ {}\begin{array}{c}-3\\ {}-3\\ {}3\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0\\ {}0\\ {}\begin{array}{c}6\\ {}0\\ {}\begin{array}{c}-6\\ {}6\\ {}\begin{array}{c}6\\ {}-6\\ {}-6\end{array}\end{array}\end{array}\end{array}\end{array}\kern0.5em \begin{array}{ccc}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}-6\\ {}0\\ {}\begin{array}{c}6\\ {}3\\ {}\begin{array}{c}3\\ {}-3\\ {}-3\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0\\ {}9\\ {}\begin{array}{c}-9\\ {}9\\ {}\begin{array}{c}-9\\ {}0\\ {}\begin{array}{c}0\\ {}0\\ {}0\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0\\ {}0\\ {}\begin{array}{c}0\\ {}0\\ {}\begin{array}{c}0\\ {}9\\ {}\begin{array}{c}-9\\ {}9\\ {}-9\end{array}\end{array}\end{array}\end{array}\end{array}\right]. $$

(6)

S is a diagonal matrix given by:

$$ S=\mathit{\operatorname{diag}}\left({s}_0,{s}_1,{s}_2,{s}_3,{s}_4,{s}_5,{s}_6,{s}_7,{s}_8\right)=\mathit{\operatorname{diag}}\left(0,{s}_e,{s}_{\zeta },0,{s}_q,0,{s}_q,{s}_v,{s}_v\right), $$

(7)

where the element s_i represents relaxation parameter. These parameters are chosen as s_e = 1.25, s_ζ = 1.14, s_q = 1.6 and, s_v is related to the dynamic viscosity of two fluids and is $\frac{1}{\tau }$ where τ is relaxation time parameter. To consider unequal viscosity of two fluids and ensure the smoothness of the relaxation parameter s_v across the interface, τ is calculated as:

$$ \tau =\left\{\begin{array}{c}{\tau}^R\\ {}\begin{array}{c}{g}^R\left({\rho}^N\right)\\ {}\begin{array}{c}{g}^B\left({\rho}^N\right)\\ {}{\tau}^B\end{array}\end{array}\end{array}\kern0.5em \begin{array}{c}{\rho}^N>\delta \\ {}\begin{array}{c}\delta \ge {\rho}^N>0\\ {}\begin{array}{c}0\ge {\rho}^N>-\delta \\ {}{\rho}^N<-\delta \end{array}\end{array}\end{array}\right., $$

(8)

where τ^k is the relaxation parameter of the fluid k, which is related to kinematics viscosity by ${\nu}^k=\frac{1}{3}\left({\tau}^k-0.5\right)$; δ is a free parameter associated with interface thickness and is taken as 0.98 in the present study. In the present model phase field ρ^N is defined as follows:

$$ {\rho}^N=\left(\frac{\rho^R}{\rho^{R^0}}-\frac{\rho^B}{\rho^{B^0}}\right)/\left(\frac{\rho^R}{\rho^{R^0}}+\frac{\rho^B}{\rho^{B^0}}\right), $$

(9)

where ${\rho}^{R^0}$ and ${\rho}^{B^0}$ are the densities of the pure red and blue fluids; ρ^k is the density of each fluids:

$$ {\rho}^k=\sum \limits_i{f_i}^k. $$

(10)

The functions g^R and g^B are as follows:

$$ {g}^R=\beta +\gamma {\rho}^N+\varepsilon {\rho^{N^2}}, $$

(11)

$$ {g}^B=\beta +\eta {\rho}^N+\zeta {\rho^{N^2}}, $$

(12)

$$ \beta =\frac{2{\tau}^R{\tau}^B}{\tau^R+{\tau}^B}, $$

(13)

$$ \gamma =2\frac{\tau^R-\beta }{\delta }, $$

(14)

$$ \varepsilon =-\frac{\gamma }{2\delta }, $$

(15)

$$ \eta =2\frac{\beta -{\tau}^B}{\delta }, $$

(16)

$$ \zeta =\frac{\eta }{2\delta }. $$

(17)

The equilibrium distribution function in the interaction mode space (a space spanned by the moments of the distribution functions (Lallemand and Luo 2000b)) m_i^keq is obtained by:

$$ {m}^{keq}={\rho}^k{\left(1,-3.6{\alpha}^k-0.4+3{\left|\overrightarrow{u}\right|}^2,5.4{\alpha}^k-1.4-3{\left|\overrightarrow{u}\right|}^2,{u}_x,\left(-1.8{\alpha}^k-0.2\right){u}_x,{u}_y,\left(-1.8{\alpha}^k-0.2\right){u}_y,{u_x}^2-{u_y}^2,{u}_x{u}_y\right)}^T, $$

(18)

where $\overrightarrow{u}$ is flow velocity (u_x and u_y are x and y components, respectively) and it is obtained by:

$$ \overrightarrow{u}=\sum \sum {f_i}^k{\overrightarrow{c}}_i. $$

(19)

α^k is a free parameter that the stable interface assumption requires to satisfy the following relation:

$$ \frac{\rho^{R^0}}{\rho^{B^0}}=\frac{1-{\alpha}^B}{1-{\alpha}^R} $$

(20)

Constraint of 0 ≤ α^k ≤ 1 should be satisfied to avoid the unreal value of speed of sound and negative value of fluid density.

The distribution function in the discrete velocity space is transformed into the interaction mode space by ${m_i}^k=\sum \limits_j{M}_{ij}{f_j}^k$. C_i^k is a source term added to system of equations, in order to be recovered exact NSEs:

$$ {C}^k={\left[0,{C_1}^k,0,0,0,0,0,{C_7}^k,0\right]}^T, $$

(21)

where

$$ {C_1}^k=3\left(1-\frac{s_e}{2}\right)\left(\frac{\partial {Q}_x}{\partial x}+\frac{\partial {Q}_y}{\partial y}\right), $$

(22a)

$$ {C_7}^k=3\left(1-\frac{s_v}{2}\right)\left(\frac{\partial {Q}_x}{\partial x}-\frac{\partial {Q}_y}{\partial y}\right), $$

(22b)

$$ {Q}_x=\left(1.8{\alpha}^k-0.8\right){\rho}^k{u}_x, $$

(22c)

$$ {Q}_y=\left(1.8{\alpha}^k-0.8\right){\rho}^k{u}_y. $$

(22d)

The second collision term is as follow:

$$ {\left({\Omega_i}^k\right)}^2=\frac{A_k}{2}\left|\overrightarrow{f}\right|\left[{w}_i\frac{{\left({\overrightarrow{c}}_i.\overrightarrow{f}\right)}^2}{{\left|\overrightarrow{f}\right|}^2}-{B}_i\right], $$

(23)

where A_k is a parameter that affects the interfacial tension and $\overrightarrow{f}$ is the color-gradient which is calculated as:

$$ \overrightarrow{f}\left(\overrightarrow{x},t\right)=\sum {\overrightarrow{c}}_i\left[{\rho}^R\left(\overrightarrow{x}+{\overrightarrow{c}}_i\Delta t,t\right)-{\rho}^B\left(\overrightarrow{x}+{\overrightarrow{c}}_i\Delta t,t\right)\right]. $$

(24)

Also, ${B}_0=-\frac{4}{27}$, ${B}_i=\frac{2}{27},$ for i = 1, 2, 3, 4 and ${B}_i=\frac{5}{108}$, for i = 5, 6, 7, 8. Using these parameters, the correct term due to interfacial tension in the Navier-Stokes equations can be recovered. Weighted constants w_i are calculated as:

$$ {w}_0=\frac{4}{9}, $$

(25a)

$$ {w}_i=\frac{1}{9},i=1,2,3,4 $$

(25b)

$$ {w}_i=\frac{1}{36},i=5,6,7,8 $$

(25c)

The following equation gives the relationship between surface tension coefficient σ and the parameter A^k:

$$ \sigma =\frac{5\rho \left({A}^R+{A}^B\right)}{6\tau }. $$

(26)

To promote phase segregation and maintain a reasonable interface, the segregation operator proposed by Latva-Kokko and Rothman (Latva-Kokko and Rothman 2005) is used, and it is given by:

$$ {f_i}^R\left(\overrightarrow{x},t\right)=\frac{\rho^R}{\rho^R+{\rho}^B}\left({{f_i}^{\prime}}^R\left(\overrightarrow{x},t\right)+{{f_i}^{\prime}}^B\left(\overrightarrow{x},t\right)\right)+\beta \frac{\rho^R{\rho}^B}{\rho^R+{\rho}^B}{w}_i\cos {\varphi}_i\left|{\overrightarrow{c}}_i\right|, $$

(27a)

$$ {f_i}^B\left(\overrightarrow{x},t\right)=\frac{\rho^B}{\rho^R+{\rho}^B}\left({{f_i}^{\prime}}^R\left(\overrightarrow{x},t\right)+{{f_i}^{\prime}}^B\left(\overrightarrow{x},t\right)\right)-\beta \frac{\rho^R{\rho}^B}{\rho^R+{\rho}^B}{w}_i\cos {\varphi}_i\left|{\overrightarrow{c}}_i\right|, $$

(27b)

where f_i^′k is the post-perturbation value of the distribution function; φ_i is the angle between the $\overrightarrow{\nabla}{\rho}^N$ and the lattice direction c_i; β is a parameter associated with the interface thickness and should take a value between zero and unity. In the literature, this step is called recoloring step.

In order to apply the effects of external body forces, the term ${\overline{F}}_i$ is added to Eq. (1):

$$ \overline{F}={M}^{-1}\left(I-\frac{1}{2}S\right)M\overset{\sim }{F}, $$

(28)

where I is a 9 × 9 unit matrix and $\overset{\sim }{F}$ is as follow (Ba et al. 2013):

$$ {\overset{\sim }{F}}_i={w}_i\left[3\left({\overrightarrow{c}}_i-\overrightarrow{u}\right)+9\left({\overrightarrow{c}}_i.\overrightarrow{u}\right){\overrightarrow{c}}_i\right].\overrightarrow{F}, $$

(29)

where $\overrightarrow{F}$ is the body force.

In this paper, the displacement of a 2-D immiscible droplet under the action of SAW is studied. The SAW has been modeled using a body force acting on the fluid volume. This force is represented as follows. Acoustic streaming and acoustic radiation are in the scale of ρA²ω², where A is SAW amplitude and ω is an angular frequency which related to SAW frequency, f, via ω = 2πf. The precise contribution of either acoustic streaming or acoustic radiation to the droplet movement is not still clear, so no exact expression will be used.

Most experiments report that in these conditions, the droplet deforms along the Rayleigh (radiation) angle direction, θ_R. Therefore, there is an empirical force which scales in ρA²ω² and is pointing in θ_R direction. When the force is considered homogeneous, the problem reduces to the droplet subject to gravitational forces. Hence, a simple inhomogeneous force is used instead. In a very crude approximation, the force density is scaled by the acoustic power density of the radiated SAW: exp2(k_ix + α₁k_iy).

Once SAW with frequency f and wavenumber k_R interacts with the liquid volume, its mode is changed to a leaky SAW with wavenumber k_L = k_r + ik_i, where the k_i is SAW dissipation under the liquid due to energy conservation (Vanneste and Buhler 2011). Indeed, as SAW propagates, it leaks some power in the liquid. Hence, according to the energy conservation principle, SAW power is decreased as the energy is lost in the liquid. The energy is lost mainly by momentum transfer (vibration).

The attenuation constant is ${\alpha}_1=\sqrt{1-{\left(\frac{V_L}{V_W}\right)}^2}$, where V_L and V_W are the leaky SAW and the sound velocities in the liquid, respectively. So, the external body force in this problem can be expressed as follows:

$$ {{\overrightarrow{F}}_{ext}}^k=-\rho {\left(1+{\alpha_1}^2\right)}^{\frac{3}{2}}{A}^2{\omega}^2{k}_i\mathit{\exp}2\left({k}_ix+{\alpha}_1{k}_iy\right)\left[\sin {\theta}_R\overrightarrow{i}+\cos {\theta}_R\overrightarrow{j}\right], $$

(30)

where, $\overrightarrow{i}$ and $\overrightarrow{j}$ are unit normal vectors in x and y directions, respectively. Note, this expression is very crude, that it is not acoustic streaming nor acoustic radiation pressure. So, many phenomena such as droplet mixing or droplet atomization cannot be explained with this model.

The eq. (30) is valid in the substrate adjacent to the liquid. So, we cannot apply this equation when α₁ = 0. The radiation angle is related to the substrate and it is assumed 23 degrees here (Riaud et al. 2017). Also, α₁ is a function of frequency and substrate materials, A is SAW amplitude, and ω is angular frequency. For Lithium Niobate substrate, α₁ is 2.47 and k_i is −1340 m⁻¹ (Riaud et al. 2017).

Boundary Conditions

In a problem involving a partial differential equation, the solution of the problem is highly relies on the boundary data. In this study, periodic and no-slip boundary conditions are used. Indeed, the periodic boundary condition applies to the transformation step. For this purpose, the particles that leave on one boundary are reintroduced on the opposite side of the simulation domain. No-slip boundary condition is applied at the solid wall by using simple bounce-back scheme (Mohamad 2011).

The contact angle θ is enforced at the wall through the geometrical formulation proposed by Ding and Spelt (Latva-Kokko and Rothman 2005). Schematic of the contact angle is presented in Fig. 2. In this figure, θ is contact angle, ${\overrightarrow{n}}_s$ is unit vector normal to the interface at contact point, ${\overrightarrow{n}}_w$ is unit vector normal to the wall, and ${\overrightarrow{t}}_w$ is tangential unit vector. Also, i and j are pointers in the x and y directions.

Fig. 2

Schematic of contact angle

We can write ${\overrightarrow{n}}_s$ based on gradient of the phase field as follows:

$$ {\overrightarrow{n}}_s=-\frac{\overrightarrow{\nabla}{\rho}^N}{\left|\overrightarrow{\nabla}{\rho}^N\right|}. $$

(31)

Also, with respect to Fig. 2, ${\overrightarrow{n}}_s$ can be written as:

$$ {\overrightarrow{n}}_s=\sin \theta {\overrightarrow{t}}_w+\cos \theta {\overrightarrow{n}}_w. $$

(32)

So, it can be shown that:

$$ \overrightarrow{\nabla}{\rho}^N.{\overrightarrow{n}}_w=-\left|\overrightarrow{\nabla}{\rho}^N.{\overrightarrow{t}}_w\right|\tan \left(\frac{\pi }{2}-\theta \right). $$

(33)

Now, based on gradient operator, $\overrightarrow{\nabla}{\rho}^N.{\overrightarrow{n}}_w=\frac{\partial {\rho}^N}{\partial y}$, and $\overrightarrow{\nabla}{\rho}^N.{\overrightarrow{t}}_w=\frac{\partial {\rho}^N}{\partial x}$. So, the equation of geometrical wetting boundary condition boundary condition is rewritten as follows:

$$ \frac{\partial {\rho}^N}{\partial y}=-\left|\overrightarrow{\nabla}{\rho}^N.{\overrightarrow{t}}_w\right|\tan \left(\frac{\pi }{2}-\theta \right). $$

(34)

For computation of $\frac{\partial {\rho}^N}{\partial x}$ at grid point (i,1), interpolation is used:

$$ \overrightarrow{\nabla}{\rho}^N.{\overrightarrow{t}}_w=1.5{\left(\frac{\partial {\rho}^N}{\partial x}\right)}_{i,2}-0.5{\left(\frac{\partial {\rho}^N}{\partial x}\right)}_{i,3}. $$

(35)

We used first order upwind scheme for discretization of $\frac{\partial {\rho}^N}{\partial y}$ and second order central scheme for to ${\left(\frac{\partial {\rho}^N}{\partial x}\right)}_{i,2}$ and ${\left(\frac{\partial {\rho}^N}{\partial x}\right)}_{i,3}$. Finally, the discretized form of the geometrical wetting boundary condition is obtained as follows:

$$ {\rho^N}_{i,1}={\rho^N}_{i,2}+\frac{1}{2}{\Theta}_w\left[1.5\left({\rho^N}_{i+1,2}-{\rho^N}_{i-1,2}\right)-0.5\left({\rho^N}_{i+1,3}-{\rho^N}_{i-1,3}\right)\right], $$

(36)

where ${\Theta}_w=\tan \left(\frac{\pi }{2}-\theta \right)$. It is most important to notice that the sign of Θ_w is positive when $\frac{\partial {\rho}^N}{\partial x}>0$ and Θ_w will be negative in $\frac{\partial {\rho}^N}{\partial x}<0$. After ρ_{i, 1}^Nis determined, the density can be obtained on the wall. For this, the value of ρ_{i, 1}^N (surrounding fluid with lower density) is interpolated. Then, the value of ρ_{i, 1}^R (wetting fluid with higher density) is computed by using Eq. (9). So, the density can be applied on the wall.

Simulation Setup

Droplet with certain diameter and contact angle is loaded on the path taken by a SAW propagating through the substrate (Fig. 3). Density and viscosity ratios are 1000 and 15, respectively, and surface tension coefficient is 0.072 N/m (Brunet et al. 2010). The no-slip boundary condition is implemented on the substrate and upper side. The periodic boundary condition is applied to other sides. The schematic of the problem is presented in Fig. 2.

Fig. 3

Schematic of the problem

Validation Results

In problems with moving contact lines, contact angle is a function of the slip velocity, and so, is called the dynamic contact angle θ_d (DCA). In order to validate the model, we focus on a droplet attached on an ideal substrate when it was subjected to a shear flow. The computational domain is a rectangle with length 4 L and width 2 L where L = 0.5 mm. The shear flows are driven by moving the upper wall at a constant velocity v_w.

The important non-dimensional parameter is capillary number (Ca) that is defined as:

$$ Ca=\frac{\mu U}{\sigma }. $$

(37)

The characteristic velocity U is taken as the flow velocity at the top of the droplet and is defined as $U=\frac{r{v}_w}{2L}$ with the distance between the upper and the lower walls 2 L and the initial height of the droplet r. The density ratio and kinematic viscosity ratio are set to be 1 and, a droplet with θ = 90 is considered. The periodic condition is used for the lateral direction. The simple bounce back is imposed at the bottom walls. The geometrical wetting boundary condition is used as explained in the previous section. The boundary condition with known velocity v_w at upper wall (velocity component driven shear flow) is implemented as follows (Mohamad 2011):

$$ {\rho}_N=\frac{1}{1+{v}_w}\left[{f}_0+{f}_1+{f}_3+2\left({f}_2+{f}_6+{f}_5\right)\right], $$

(38a)

$$ {f}_4={f}_2, $$

(38b)

$$ {f}_7={f}_5+\frac{1}{2}\left({f}_1-{f}_3\right)-\frac{1}{2}{\rho}_N{v}_w, $$

(38c)

$$ {f}_8={f}_6+\frac{1}{2}\left({f}_3-{f}_1\right)+\frac{1}{2}{\rho}_N{v}_w. $$

(38d)

It is important to note that the values of f₀, f₁, f₂, f₃, f₅, and f₆ are obtained in streaming step.

The dynamics of the droplet affected by shear flow can be classified into three modes. The first is the stationary mode where the droplet deforms, but its shape remains fix and stationary. The second is the slip mode where the droplet slips and steady states exist for the droplet shape and the droplet velocity. And the final is the break up mode where the droplet is divided into two pieces.

At first, a droplet with θ_s = 90; density ratio and kinematics viscosity ratio equal to 1; and Ca is considered 0.01. Figure 4-a shows the droplet shape after 1.5 s (stationary mode). Figure 4-b presents the slipping mode of droplet motion. The Ca is set to be 0.1. In this condition, the droplet velocity is equal to 0.1 cm/s. The dynamics of droplet in Ca = 0.5 is presented in Fig. 4-b. After about 1.25 s, the droplet breaks up. Note that, these three modes are compared with results of Kawasaki (Kawasaki et al. 2008). The left-side pictures are our present numerical results, and right side presents results of Ref. (Kawasaki et al. 2008).

Fig. 4

Comparison of numerical results (Sheikholeslam Noori et al. 2019) and Kawasaki (Kawasaki et al. 2008). a) Stationary mode, b) Slipping mode, and c) Break up mode

The dynamic contact angle is known as a function of contact line velocity. Latva-Kokko and Rothman proved that the dynamic contact angle always shows a universal behavior that is as follows (Latva-Kokko and Rothman 2007):

$$ F\left({\theta}_d\right)-F\left(\theta \right)=G(Ca), $$

(39)

where, F is scaling function and θ_d is the dynamic contact angle. For validation of the contact angle dependence on velocity, the well-known Cox-Voinov’s relationship (Snoeijer and Andreotti 2013) is used here. This model is as follow:

$$ {\theta_d}^3={\theta}^3+9\sigma Ca\ln \left(\frac{l}{l_m}\right), $$

(40)

where l is the characteristic length scale and l_m is microscopic length scale.

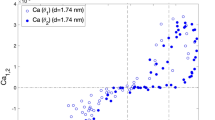
Figure 5 shows the advancing contact angle versus capillary number, because the Cox-Voinov’s relationship is valid for the advancing contact angle. Based on Gibbs energy for a liquid on a solid surface, the advancing contact angle is the highest metastable apparent contact angle that can be measured (Marmur et al. 2017). As expected (Eral and Oh 2013), the dynamic contact angle increases gradually and consequently, the numerical results agree well with the physical observations. Up to Ca = 0.2, the numerical results are in good agreements with the theoretical solutions. The transition of droplet dynamics from the slipping mode to the break up mode is a reason for the differences between the results. The theoretical relationship is valid when the droplet has a constant shape and its motion is steady. However in the break up mode, the deformation of interface is drastic and the Eq. (36) is not valid for Ca > 0.2.

Fig. 5

Dynamic contact angle as a function of Ca

Results and Discussions: Acoustofluidic

The surface acoustic waves are one of the flow control techniques. In this section, the interaction of SAW and droplet is comprehensively investigated by a qualitative analysis. At first, the physical behavior of droplet is presented according to experimental results. Then, the simulation results of interaction of SAW and droplet are described.

According to applied power through SAW to the droplet, four modes are observed: streaming, pumping, jetting, and atomization (which are illustrated in Fig. 6a-d, respectively). In this condition, two main phenomena occur. First, absorbed energy by the droplet is transformed to vibration energy. Second, the droplet is deformed by the pressure gradient caused by SAW energy and begins to move. Three periodical steps can be seen in the process of droplet distortion (Fig. 7).

Fig. 6

Droplet dynamics affected by SAW. a) Streaming, b) Pumping, c) Jet, and d) Atomization (Luong and Nguyen 2010)

Fig. 7

Periodical distortion of droplet (Beyssen et al. 2006)

Now, the dynamic behavior of interface in three modes (streaming, pumping, and jetting) are presented and compared with available experimental results. The flow quantities is approximately similar to that of section 3 and the computational grid is 801 × 401 lattice configuration. Figure 8-a presents the streaming mode. SAW has the amplitude and angular frequency of 0.5 nm and 20 MHz, respectively. It is important to notice that all quantities will be converted into lattice units. It is worthy to note that the wave, propagates from left to right (x-direction). For frequencies with order of magnitude of 20 MHz, wavelength of 0.2 mm is calculated, so compared to diameter of droplet, the plane waves in the droplet are possible. It is observed that the droplet doesn’t move after 6.6 s, and it only bends to the radiation angle. Figure 8-b clearly shows the droplet shape in streaming mode (Brunet et al. 2010), where the right-hand side picture is experimental result and left-hand side picture is numerical simulation. These significant effects such as droplet mixing, droplet heating, particle patterning, and particle concentration have been utilized in various applications.

Fig. 8

Temporal evolution of droplet in streaming state. a) Numerical simulation and b) Experimental results (Valverde 2015)

Secondly, the SAW amplitude is increased to 1 nm. In this state, the droplet moves as shown in Fig. 9-a. The actuation of droplet has been used for pumping, sample collecting, and sample dispensing. Figure 9-b compares the droplet shape with the experimental results (Brunet et al. 2010). It is clear that the periodic behaviors of droplet (reported in Ref. (Beyssen et al. 2006) by Beyssen et al.) are not observed in these results. In fact, the overall shape of the droplet is similar to experimental results.

Fig. 9

.Temporal evolution of droplet in pumping state. a) Numerical simulation and b) Experimental results (Brunet et al. 2010)

In the third state, the detachment of droplet is observed. In Fig. 10, the amplitude and angular frequency are 3 nm and 20 MHz, respectively. Numerical and experimental results of the temporal evolution of jet formation are shown in Fig. 10-a and b, respectively. So, the onset of jetting can be compared here. The height of the droplet grows in this stage. After 0.32 s, the fluctuations are amplified and finally, droplet is detached from the wall. As shown, it is observed that the dynamical behaviors of the droplet are approximately the same. The differences are due to two-dimensional simulation, disregarding the effects of gravity, and vibrations of the substrate which are not considered in these simulations. Also, computing the acoustic field in the droplet would probably yield more precise results.

Fig. 10

Temporal evolution of droplet in jet state. a) Numerical temporal evolution, b) Experimental temporal evolution (Tan et al. 2009b), and c) Experimental results (Guo et al. 2014)

In Fig. 11, the velocity of moving droplet, obtained by varying the acoustic amplitude A at pumping mode is compared with results of Brunet et al. (Brunet et al. 2010). As expected, the droplet moves faster in large A. The velocity magnitude in the numerical simulations are larger than that of the experimental data. Since two-dimensional model is used for the simulations, it is reasonable to observe some discrepancy. Both numerical and experimental data show that the influence of A is strongly non-linear and the droplet velocity increases dramatically in large A. However, the increase of velocity in the experimental data is lower than the numerical results. Also, the numerical results show that a velocity continuously increases. The main reason for these issues is the hysteresis phenomenon that has not been considered in this modeling due to simplification. In some conditions, the contact line doesn’t move not only at a certain contact angle but also in the interval around it. This phenomenon is called the contact angle hysteresis in which the static contact angle is not unique.

Fig. 11

Droplet velocity versus acoustic displacement

Figure 12 summarizes the threshold amplitude that is required at different frequencies to induce the respective microfluidic phenomena under various SAW amplitudes and resonant frequencies. There are critical amplitude boundaries between various microfluidic phenomena of the liquid droplets, and these threshold values increase by 25–50%, when f is increased. At different frequencies, the minimum required amplitude to achieve different acoustically induced microfluidic phenomena are dramatically different.

Fig. 12

Relationship between SAW amplitude and frequency identifying the boundaries of different phenomena

In order to clearly demonstrate the coupled acoustic and hydrodynamic effects, the viscosity ratio is investigated in Fig. 13. The increase of viscosity (decrease of viscosity ratio) decreases of the velocity as expected for moving droplets. Indeed, viscosity is effective in the dissipation rate in the vicinity of the contact-line and hence, an equal driving force displaces viscous droplets at lower speed.

Fig. 13

Droplet velocity versus SAW amplitude, for two different viscosity ratio

The viscous effects are applied by the single phase collision operator in LBM for the hydrodynamic motion. Therefore, the effects of viscosity are considered in simulation via the eq. (4). While, the wave amplitude and frequency are 1 nm and 20 MHz respectively, three different viscosity ratios are considered and the results are compared with experimental data (Brunet et al. 2010). The results are compared with reliable experimental data and noted that the related errors are almost the same. However, acoustic attenuation due to viscosity scales proportionally to ω², whereas SAW attenuation scales in ω. Hence, at low frequency, the SAW attenuation is highly essential, whereas at high frequency, the viscous attenuation is more important. This distinction is not accounted for by our model.

The effect of surface tension as another significant parameter is also investigated in this work. The surface tension coefficient can be regarded as the surface energy per unit area of the interface. In the same conditions (i.e. A = 1 nm, f = 20 MHz, and viscosity ratio = 15), when the surface tension coefficient decreases from 0.072 to 0.066 N/m, the velocity of droplet decreases. In fact, the retention force is a function of σ and hence, this force also decreases. However, in higher σ, the droplet detaches later from the surface as the SAW amplitude increases. This occurs due to high resistance of droplet to the deformation.

The hydrophobicity is the next parameter that can affect the dynamic behavior of contact line. In order to reveal the effect of this parameter in the coupled acoustic and hydrodynamic phenomena, a hydrophilic surface with SCA = 30 and a SAW with A = 1 nm and f = 20 MHz are considered. The other parameters remain constant. The temporal evolution of droplet is shown in Fig. 14-a. The droplet completely spreads over the substrate and moves slower than the condition with SCA = 90. The primary reason for low speed of movement is the high contact level. So, in order to move a droplet on a hydrophilic surface, a SAW with higher amplitude is required. The dynamics of interface in jetting state is not so different with SCA = 90. Figure 14-b shows the jetting of droplet, where A = 2.5 nm.

Fig. 14

Temporal evolution of droplet on a hydrophilic substrate. a) Pumping state and b) Jetting state

When the substrate is hydrophobic (for example SCA = 120), the contact level is low. So, the droplet moves fast in the pumping state. Also, in jetting state, droplet detaches easily. These phenomena are clearly observed in Fig. 15. In these two case studies, the frequency is 20 MHz and the SAW amplitudes are 1 nm and 2.5 nm in the pumping and jetting modes, respectively.

Fig. 15

Temporal evolution of droplet on a hydrophobic substrate. a) Pumping state and b) Jetting state

Korshak et al. (Korshak et al. 2005) observed four types of phenomena in the dynamical behavior of liquid droplet affected to SAW, which are: 1. progressive acoustic transport of a droplet, 2. vortex acoustic streaming inside a droplet, 3. the formation of quasi-stationary smoothed peak on the droplet surface under the action of counter-propagating SAW and its chaotic dynamics during evaporation, and 4. self-sustained oscillation of such a peak on the droplet surface in the case when the substrate has a slight slope with respect to the horizontal. The first two phenomena occur in traveling-wave mode, while the other two arise in standing-wave mode. In this work, we simulated traveling-SAW mode, in which the acoustic transport of droplet is investigated. Since however, the acoustic field is not simulated, the vortex acoustic inside the droplet has not been studied, here.

Conclusion

In this paper, the displacement of a two-dimensional immiscible droplet subjected to surface acoustic waves has been simulated by the MRT CGM LB method. Effects of SAW is modeled as an external body force acting on fluid volume. Some benchmark problems are computed to demonstrate the accuracy of the numerical method. It is shown that numerical results obtained by developed method are in good agreement with the analytical results.

The dynamical behavior of droplet affected by SAW is fully simulated in the three modes: streaming, pumping, and jetting. The obtained results show a good agreement with experimental data. It is observed that the droplet velocity increases when the SAW amplitude increases. The boundaries of microfluidic phenomena such as pumping and jetting increase when the frequency increases. The increase of viscosity is equal to decrease of droplet velocity because of dissipation phenomena. The resistance to deformation is amplified when the surface tension coefficient increases. On the hydrophobic surfaces, droplets subjected to SAW move easier than the hydrophilic surfaces. So, the sensitivity of flow control system is increased.

In the frequency ranges of 20 MHz–200 MHz, the minimum wave amplitude required to initiate pumping mode changes from 0.8 nm to about 1 nm. These variations in jetting mode is highly significant (about 50%). Since frequency is varied from 20 MHz to 200 MHz, the minimum wave amplitude changes from about 2 nm to 4 nm.

This study is the first investigation of droplet breakup due to acoustofluidic phenomena. But, there are some limitations that can follow as future work. In this study, contact angle hysteresis is not assumed. This simulation is two-dimensional, while some phenomena are three-dimensional. The thermal effects are not considered. Also, the expression applied for modeling the effects of SAW is very crude, that it is not acoustic streaming nor acoustic radiation pressure. So, it cannot explain many phenomena such as droplet mixing or droplet atomization. Even though, the current model gives visually pleasing results and quantitative predictions are possible if the acoustic field in the droplet is computed. With respect to limitations mentioned, the results are in good agreement with knowledge. By removing these aspects, it can simulate the acoustofluidic phenomenon and move to optimization the SAW flow control systems.