1 Introduction

The plane free shear layer (FSL) is composed of two parallel streams of fluid with different velocities or different densities. The comprehensive understanding of the physics of turbulence in FSL is essential for designing engineering systems, such as gas turbines, scramjet engines, and rocket exhausts. To predict the viability and efficiency of such systems, one must be able to estimate the turbulence in FSL accurately. In addition to traditional experimental approaches, numerical simulation is increasingly employed to study this flow. Below, we provide a review of previous studies on FSL.

1.1 Experimental studies

The experimental research on turbulent FSL dates back to the study by Liepmann and Laufer [49]. They measured the location of the transition from laminar to turbulent flow and observed the fully developed turbulent FSL in self-similar regions with a constant growth rate. Birch and Eggers [4] conducted an early study on the effect of compressibility. They first showed that an increase in Mach number could reduce the growth rate of the FSL. Later, Brown and Roshko [7] studied the turbulent FSL with different ratios of densities and velocities across the shear layer. The results showed that large coherent structures dominate the FSL and convect at almost constant speed downstream while growing. They also observed three-dimensional (3D) structures in the braid region between the large coherent structures. They suggested that the growth rate of a turbulent FSL is significantly affected by compressibility rather than density ratio.

Bernal [3] examined the successive frames in movies of planes normal to the streamwise and spanwise directions to study the structure of the secondary streamwise vortex and clarify the relation and interaction between the primary spanwise vortices and the secondary streamwise vortices. It was found that much of the growth of the primary vortices was due to the motions induced by the secondary vortices. Later studies [36, 50, 56] proposed that the FSL growth rate is proportional to the ratio of velocity in the high-speed side to that in the low-speed side. Papamoschou and Roshko [61] investigated the growth rate of the compressible, turbulent FSL experimentally with various free-stream Mach numbers. They found that the effect of compressibility on the turbulent FSL growth rate is much more complex than the effects of velocity and density ratios. They also observed that the reduction in the growth rate occurs in a range from subsonic to supersonic. They suggested that the compressibility effect only emerges before the appearance of any shock or expansion waves in the flow.

The role of compressibility in FSL is often studied in terms of the convective Mach number [5],

$$\begin{aligned} M_{\mathrm{c}} = \frac{U_1 - U_2}{c_1 + c_2}, \end{aligned}$$
(1)

where \(U_1\) and \(U_2\) are the velocities of the high- and low-speed streams, respectively, and \(c_1\) and \(c_2\) are the speeds of sound on the high- and low-speed sides of the FSL, respectively. Elliott and Samimy [10] and Hall et al. [22] proposed that the FSL growth rate decreases as the convective Mach number increases. Hall et al. [22] observed that the effects of incident shock and expansion waves on the growth rate of a turbulent FSL are negligible. Recently, laser Doppler velocimetry measurement was used by Barre and Bonnet [2] to extract velocity fluctuations in a compressible supersonic FSL. The authors proposed that the structure of the Reynolds stress tensor is nearly unaffected by increasing the convective Mach number; however, the values of all the components of the Reynolds stress tensor decrease.

1.2 Computational studies

In the early numerical studies, researchers mostly solved the full time-dependent Navier–Stokes equations numerically for a temporally developing FSL, due to the lower requirement of computational resources. Such studies [11, 57, 60, 71, 72, 76, 84] simulated the temporal development of the turbulent FSL in a computational domain with a fixed reference frame moving with the large structures while applying periodic boundary conditions in streamwise and spanwise directions. Moser and Rogers [57] were able to resolve the primary spanwise and secondary streamwise vortices. Sandham and Reynolds [72], Vreman et al. [84], and Pantano and Sarkar [60] studied the compressibility effects in great detail on the turbulent FSL. They observed a reduction in the growth rate with an increase in the convective Mach number. This finding is consistent with the results obtained by the use of linear stability analysis of compressible FSL [20, 28, 29, 55, 67, 71]. Karimi and Girimaji [37] investigated the compressibility effect on Kelvin–Helmholtz instability with a linear initial value problem. The authors found that the acoustic dynamics can lead to Kelvin–Helmholtz instability suppression.

Due to the drawbacks of the temporal simulation (for example, lack of ability to capture the effects of the velocity ratio across the FSL and the asymmetry of entrainment [70]) and the advances in computers, researchers turned their attention to spatially developing FSL. In a spatially developing FSL, the computational domain is in the same reference frame as that of the observer, with an inflow boundary at one end and an outflow boundary at the other. The outflow boundary often can allow all the structures to leave the computational domain with negligible effects on downstream. Rogers and Moser [58, 68, 69] carried out several 3D turbulent FSL simulations with different initial conditions. They found that the roll-up pairing restrains the growth of infinitesimal 3D disturbances and causes the transition to turbulence in highly 3D flows. They also showed that there are two kinds of coherent structures: one is spanwise structures, referred to as rollers; another is streamwise vortices, called rib vortices. These structures are present before the onset of the self-similar growth.

Lele [43, 47] simulated the two-dimensional (2D) spatial evolution of vortices and showed that the shear layer growth rate decreases as the convective Mach number increases. The study also demonstrated that an increase in the convective Mach number leads to a vorticity compression effect comparable with the advection effect. Sandham [70], and Sandham and Reynolds [71, 72] investigated the effect of Mach number on 2D and 3D FSL using direct numerical simulation (DNS). The authors found that the FSL growth rate decreases as the convective Mach number increases. Sandham and Reynolds [72] observed \(\lambda \) shape vortices at high convective Mach number cases. The study by Sarkar [74] proposed that dilatational dissipation and pressure-dilatation are responsible for the reduction in FSL growth. However, Sarkar [75] and Vreman et al. [84] later suggested that an increase in compressibility can lead to a decrease in turbulent production rather than dilatation terms. Also, Vreman et al. [84] presented a direct relationship between momentum thickness growth rate and turbulent production and showed that a decrease in pressure fluctuations through the pressure-strain term may lead to a reduction in turbulent production. Many review papers [15, 44, 79, 80] presented elaborated analyses for the FSL growth rate reduction in turbulent mixing layer.

The inflow condition plays a critical role in the spatial development of turbulent FSL. McMullan et al. [53] simulated the turbulent FSL with uniform density at a high Reynolds number to compare the effect of the hyperbolic tangent profile inflow and the boundary layer inflow conditions on turbulence transition. They observed that, with a boundary layer inflow condition, the turbulence transition occurs at a region further upstream than that with the hyperbolic tangent profile inflow condition. Their results also suggested that applying the hyperbolic tangent profile inflow condition to study the transition of turbulence in a FSL may produce unphysical DNS results. Many studies simulated the spatial mixing layer using a laminar mixing layer profile at the inlet with superposed small perturbations and the most unstable modes forcing [13, 48, 78, 86, 88, 89]. Studies by Fu and Li [13] and Li and Jaberi [48] investigated the compressible mixing layer with different convective Mach numbers. The authors were able to discover shocklets in the mixing layer at a convective Mach number of 1.2. Wang et al. [86] demonstrated that the interactions between large-scale rollers and rib vortices trigger the turbulence transition. Zhou et al. [89] and Zhang et al. [88] showed the complete instability evolution process in the mixing layer. However, a significant drawback of the forcing inflow conditions is that it yields an unrealistic initial shear layer development.

In order to obtain a high fidelity initial flow development, researchers turned to use an inflow condition consisting of a splitter plate and boundary layers [42, 64, 73, 77]. Sandham and Sandberg [73] investigated the early development of a turbulent mixing layer downstream of a splitter plate with zero thickness between a laminar and a turbulent boundary layer. The work of Laizet et al. [42] focused on the effect of the trailing edge shape on the flow field near the trailing edge in a spatially developing incompressible mixing layer. Pirozzoli et al. [64] studied the early evolution of the mixing layer spatially developing from two turbulent boundary layers at mild convective Mach number. A common research interest among the above-mentioned work is the flow field near the trailing edge of the splitter plate. They showed that the geometry of the splitter plate significantly influences the flow structures near the trailing edge and may affect the streamwise evolution of the flow as well. Sharma et al. [77] investigated three different inflow conditions in a spatially developing mixing layer by LES. They suggested that merging the laminar and turbulent boundary layers leads to the shorter distance to accomplish the self-similar average velocity profiles compared to merging two laminar boundary layers. The recent study by Wang et al. [85] investigated the passive scalar mixing in a supersonic mixing layer with different convective Mach numbers, density ratios, and velocity ratios. In addition to a reduction in the mixing layer growth rate with increasing convective Mach number, which is consistent with the previous studies, they found that the mixing efficiency increases as convective Mach number decreases, or density ratio decreases, or velocity ratio increases.

Based on this literature survey, experimental and numerical studies have been conducted on turbulent FSL. Experimental approaches have encountered difficulties in obtaining detailed information about the transition process and turbulent quantities, such as spanwise Reynolds stress and higher-order correlations in the Reynolds stress transport equations. DNS can generate all information in turbulent flows, which is impossible to accomplish in experiments. However, most of the early DNS studies were performed on temporally developing FSL. Such temporally evolving FSL cannot: (1) accurately account for the effects of divergent streamlines, (2) perceive the large-scale upstream influence, (3) produce the asymmetric entrainment, (4) generate the shift of the shear layer center to the low-speed side, (5) reproduce the interaction between FSL and shock waves at high convective Mach number [13, 25, 27, 51, 62]. The spatially developing approach is the closest realization of a transition experiment but is significantly more expensive than the temporally evolving method. Therefore, very few DNS studies on spatially developing, 3D FSL exist. In spatially developing turbulent FSL with naturally developing inflow condition, none of the previous studies examined the effects of compressibility on the location and length of the laminar–turbulence transition zone, the start of the self-similar region, single-point correlations, and budget of turbulence energy. In this context, a DNS study is presented here to investigate such effects. A high-order discontinuous spectral element method (DSEM) [33, 39, 40] is used to simulate such a flow. This method has previously been employed for DNS and large-eddy simulation (LES) of compressible flow in complex geometries [16, 17, 46]. The primary objectives of this work are: (1) to demonstrate an accurate and robust approach to perform DNS for a spatially developing turbulent FSL at high convective Mach number; (2) to provide useful DNS data for the design and calibration of the Reynolds-averaged Navier–Stokes (RANS) and large-eddy simulations (LES) models; (3) to identify the location of the turbulence transition zone by analyzing vorticities, Reynolds stresses, and the evolution of turbulent dissipation rate; (4) to investigate the effects of compressibility on the location and length of a laminar–turbulent transition and on the flow properties in the transition and self-similar regions. To the authors’ knowledge, this work presents the first DNS results for spatially developing, 3D compressible turbulent FSL with naturally developing inflow condition for different convective Mach numbers under identical simulation conditions. The remainder of this paper is organized as follows: First, we briefly describe the governing equations and the numerical methodology. Then, the problem setup and results of the simulations of the 3D turbulent FSL are presented and discussed. Finally, a summary of significant findings is presented.

2 Methodology

2.1 Governing equations

The governing equations for the compressible and viscous fluid flow are the full Navier–Stokes equations, which are solved in a conservative form. They are expressed in non-dimensional form with Cartesian vector notation as

$$\begin{aligned} \frac{\partial \mathbf {Q}}{{\partial t}} + \frac{\partial \mathbf {F}_{i}^a}{{\partial x_i}} - \frac{\partial \mathbf {F}_{i}^v}{{\partial x_i}} = 0, \end{aligned}$$
(2)

where

$$\begin{aligned} \mathbf {Q}= \left( \begin{array}{c} \rho \\ \rho u_1 \\ \rho u_2 \\ \rho u_3 \\ \rho e \\ \end{array} \right) ,\quad \mathbf {F}_{i}^a= \left( \begin{array}{c} \rho u_i\\ p\delta _{i1}+\rho u_1 u_i \\ p\delta _{i2}+\rho u_2 u_i \\ p\delta _{i3}+\rho u_3 u_i \\ u_i (\rho e+p) \\ \end{array} \right) ,\quad \mathbf {F}_{i}^v= \left( \begin{array}{c} 0\\ \sigma _{i1} \\ \sigma _{i2} \\ \sigma _{i3} \\ -q_i + u_k \sigma _{ik} \\ \end{array} \right) . \end{aligned}$$
(3)

Here, \(\mathbf {Q}\) is the solution vector, and \(\mathbf {F}_{i}^a\) and \(\mathbf {F}_{i}^v\) are the advective and viscous flux vectors, respectively. The total energy, viscous stress tensor, and heat flux vector are defined as

$$\begin{aligned} \rho e= & {} \frac{p}{{\gamma - 1}} + \frac{1}{2} \rho u_k u_k, \end{aligned}$$
(4)
$$\begin{aligned} \sigma _{ij}= & {} \frac{1}{\hbox {Re}_{f}} \left( \frac{\partial u_i}{{\partial {x_j}}} +\frac{\partial u_j}{{\partial {x_i}}}-\frac{2}{3}\frac{\partial u_k}{{\partial x_k}} \delta _{ij}\right) , \end{aligned}$$
(5)
$$\begin{aligned} q_j= & {} -\frac{1}{\left( \gamma -1\right) \hbox {Re}_{f}Pr_{f}M_{f}^2} \frac{\partial T}{\partial x_j}, \end{aligned}$$
(6)

respectively, where \(\delta _{ij}\) is the Kronecker delta. The reference Reynolds number, \(\hbox {Re}_{f} = \rho _{f}^* U_{f}^* L_{f}^*/\mu _{f}^*\), is defined based on the reference density, \(\rho _{f}^*\), reference velocity, \(U_{f}^*\), reference length, \(L_{f}^*\), and reference molecular viscosity, \(\mu _{f}^*\). The reference Prandtl number is defined as \(Pr_{f} = \mu _{f}^* C^*_{p}/k^*\), where \(C^*_p\) and \(k^*\) are the constant-pressure specific heat and thermal conductivity, respectively. The reference Mach number is defined as \(M_f = U_{f}^*/c_{f}^*\), with \(c_{f}^* = \sqrt{\gamma R T_{f}^*}\) denoting the reference speed of sound. R and \(T_{f}^*\) are the gas constant and reference temperature, respectively, and \(\gamma \) is the specific heat ratio. The superscript \(*\) indicates dimensional quantities. The equation of state closes the above equation system and is given by

$$\begin{aligned} p = \frac{\rho T}{{\gamma M_{f}^2}}. \end{aligned}$$
(7)

2.2 Numerical method

In this work, the DSEM code is used as the compressible flow solver [30, 32, 33]. The computational domain is partitioned into non-overlapping hexahedral elements. Each element is then mapped onto a unit hexahedron over the interval [0, 1] in each direction using isoparametric mapping. After the mapping, Eq. (2) reads

$$\begin{aligned} \frac{\partial {\widetilde{Q}}}{{\partial t}} + \frac{\partial {\widetilde{F}}_{i}^a}{{\partial X_i}} - \frac{\partial {\widetilde{F}}_{i}^v}{{\partial X_i}} = 0, \end{aligned}$$
(8)

where

$$\begin{aligned} {\widetilde{Q}}= J \mathbf {Q}, \quad {\widetilde{F}}_{i}^a= \frac{\partial X_i}{\partial x_j} \mathbf {F}_{j}^a, \quad {\widetilde{F}}_{i}^v= \frac{\partial X_i}{\partial x_j} \mathbf {F}_{j}^v. \end{aligned}$$
(9)

In the above equations, the solution vector \(\mathbf {Q}\) and flux vectors \(\mathbf {F}\) are on the physical grid, while \({\widetilde{Q}}\) and \({\widetilde{F}}\) are on the mapped grid. J denotes the determinant of the Jacobian matrix, which transforms the elements from the physical space to the mapped space [30]. The term \( \frac{\partial X_i}{\partial x_j}\) is the transformation matrix, where \(x_j\) and \(X_i\) are the coordinates of the physical and the mapped spaces, respectively.

In each element, the solution values, \({\widetilde{Q}}\), and the fluxes, \({\widetilde{F}}_{i}\), in Eq. (8) are approximated by a high-order Lagrange basis function on the Gauss quadrature points and Lobatto quadrature points, defined by

$$\begin{aligned} X_{j+1/2} = \frac{1}{2} \left\{ 1-\cos \left[ \frac{\left( 2j+1\right) \pi }{2N}\right] \right\} ,\quad j = 0, \ldots , N-1, \end{aligned}$$
(10)

and

$$\begin{aligned} X_{j} = \frac{1}{2} \left\{ 1-\cos \left[ \frac{\pi j}{N}\right] \right\} ,\quad j = 0, \ldots , N, \end{aligned}$$
(11)

respectively, within the interval [0, 1]. Here, \(N - 1\) is the polynomial order of the spectral element. The solution is approximated as

$$\begin{aligned} {\widetilde{Q}}\left( X,Y,Z\right) = \sum _{i=0}^{N-1}\sum _{j=0}^{N-1}\sum _{k=0}^{N-1} {\widetilde{Q}}_{i+1/2,j+1/2,k+1/2}h_{i+1/2}\left( X\right) h_{j+1/2}\left( Y\right) h_{k+1/2}\left( Z\right) , \end{aligned}$$
(12)

where X, Y, and Z are coordinates of the mapped space, while \(h_{j+1/2}\) is the Lagrange interpolating polynomial on the Gauss grid. After the viscous and inviscid fluxes are computed, a fourth-order low-storage Runge–Kutta scheme is employed for time integration.

Fig. 1
figure 1

Schematics of a the computational domain, b the real-scale buffer zone

Full size image

3 Problem setup

The inflow conditions shown in Fig. 1a, which are composed of two laminar boundary layers upstream evolving along the two sides of a zero thickness splitter plate, are used in this work for the spatially developing, 3D compressible turbulent FSL simulation. The extents in cross-stream and spanwise directions of the computational domain follow the DNS of Zhou et al. [89], while the streamwise length follows the study by Wang et al. [86]. Such computational domain size is carefully determined with the consideration that it allows the FSL to reach the self-similar turbulent state in the streamwise direction, to grow freely in the cross-stream direction, and to achieve a sufficient decorrelation in two-point correlations in the spanwise direction. The grid resolution of the computational domain follows the DNS study by Zhou et al. [89].

3.1 Simulation parameters

Necessary parameters are selected and used to analyze the compressibility effects on the turbulent FSL. It is widely accepted that the role of compressibility in the flow can be expressed in terms of the convective Mach number [5], \(M_{\mathrm{c}}\), which is defined in Eq. (1) for the flow of two streams with the same specific heat ratio. Three simulations are conducted with different convective Mach numbers and inflow Mach numbers. The inflow Mach numbers at the high- and low-speed sides are defined as \(M_1 = U_1/c_1\) and \(M_2 = U_2/c_2\), respectively. For the case with \(M_{\mathrm{c}} = 0.3\), the \(M_1\) and \(M_2\) are 0.8556 and 0.2556; with \(M_{\mathrm{c}} = 0.5\), the \(M_1\) and \(M_2\) are 1.4259 and 0.4259; finally, with \(M_{\mathrm{c}} = 0.7\), the \(M_1\) and \(M_2\) are 1.9963 and 0.5963 (see Table 1). The Reynolds number, \(\hbox {Re}_{\theta }\), based on the difference between the high- and low-speed streams, \(\Delta U = U_1 - U_2\), and the momentum thickness of the upper boundary layer (high-speed side) \(\delta _{\theta 1}\) evaluated just upstream of the trailing edge, is selected as 140, with the consideration that it is sufficiently large for a transition to turbulence and sufficiently small for resolving the flow. Here, the momentum thickness in a spatial compressible FSL is defined [35] as

$$\begin{aligned} \delta _{\theta } = \frac{1}{\rho _o} \int _{-\infty }^{+\infty } \langle \rho \rangle \frac{\lbrace u \rbrace -U_2}{\Delta U}\left( 1-\frac{\lbrace u \rbrace -U_2}{\Delta U}\right) \mathrm {d}y, \end{aligned}$$
(13)

where \(\rho _o\) is the initial inflow density, while \(\langle \rho \rangle \) and \(\lbrace u \rbrace \) are Reynolds-averaged density and Favre-averaged velocity, respectively. Hereafter, a pair of angled brackets, \(\langle \rangle \), indicates a Reynolds average, while a pair of curly brackets, \(\lbrace \rbrace \), denotes a density-weighted (Favre) average. Other parameters are the reference Prandtl number \(Pr_{f} = 0.7\) and the specific heat ratio \(\gamma = 1.4\). All dimensions are normalized by \(\delta _{\theta 1}\). The size of the computational domain for each case is set as \(L_x \times L_y \times L_z = 1982 \times 1600 \times 140 \). Here, \(L_x\), \(L_y\), and \(L_z\) denote the computational domain dimensions. The subscripts x, y, and z are the streamwise, cross-stream, and spanwise directions, respectively. The length of the splitter plate is set as \(L_s = 182\) such that the developed Blasius profiles at the end of the splitter plate are similar to the boundary layer inlet conditions used by Monkewitz and Heurre [54] and McMullan et al. [53]. The region of interest for all cases is bounded as \({-}\,182\le x \le 1300\) and \({-}\,100\le y \le 100\), which is devoted to studying the flow properties and the laminar–turbulent transition of the compressible FSL. The remainder of the domain is used as a buffer zone to prevent solution contamination from the boundaries, which is shown in Fig. 1. Figure 1b presents the real-scale buffer zone, where \(L_{x\hbox {-}\mathrm{str}} = 500\), \(L_{y\hbox {-}\mathrm{str}} = 700\), and \(L_{y\hbox {-}\mathrm{ins}} = 200\) are the lengths of grid stretching in the streamwise and cross-stream directions, and the length of the interest area in the cross-stream direction, respectively.

The computational domain is discretized according to the flow configuration. A non-uniform grid distribution is employed to achieve a finer grid in the FSL. For \( x \le 1300\), the grid in the x-direction achieves an average spacing \(\Delta x_{\mathrm{ave}} = 0.580\) with a minimum spacing \(\Delta x_{\mathrm{min}} = 0.057\), due to the nature of the Chebyshev grid used in this work. In the FSL region, the average vertical grid size is \(\Delta y_{\mathrm{ave}} = 0.668\), while the minimum vertical grid size is \(\Delta y_{\mathrm{min}} = 0.069\). The 2D baseline grid on the x–y plane is extruded uniformly in the spanwise, z, direction to construct a 3D mesh. The average spanwise grid size is \(\Delta z_{\mathrm{ave}} = 0.544\) and the minimum is \(\Delta z_{\mathrm{min}} = 0.055\) for a uniform grid in the z-direction. The grid consists of 1,368,260 elements. A polynomial order of \(p = 5\) is used in this study resulting in a total of 295,544,160 solution points.

3.2 Boundary and initial conditions

The computational domain is composed of inflow and outflow boundaries in the streamwise direction [31], non-reflecting boundaries in the cross-stream direction [31, 65, 81, 82], and periodic boundaries in the spanwise direction. A schematic of such a domain is shown in Fig. 1. In order to minimize the effect from the boundary conditions in the cross-stream direction, we have conducted extensive tests (not shown here) for a proper length in the cross-stream direction and an optimal grid stretching as a strong buffer zone. Therefore, combining the large cross-stream length (\(L_y = 1600\)) and the strong grid stretching (\(L_{y\hbox {-}\mathrm{str}} = 700\)) along the boundaries, the computational domain can be assumed as an open domain in the cross-stream direction [73]. Thus, flow can be freely entrained into the shear layer and the pressure gradient buildup along the streamwise direction can be minimized. Furthermore, the broad buffer zone along the boundaries functions as a damping-sponge, which is achieved by grid stretching, to damp any high wavenumber oscillations generated at the outlet boundary.

The inlet boundary layers thicknesses studied by Monkewitz and Heurre [54] are used in this work. Even if the convective Mach number is not identical for all cases, the inflow conditions are managed to be the same for all three cases. In this study, two laminar boundary layers, having a specified 99% thickness ratio \(\lambda = \delta _{2}/\delta _{1} = 1.6\) [53, 54] at the inflow section of the computational domain, evolve along both sides of the splitter plate. The subscripts 1 and 2 are used to denote the high- and low-speed sides, respectively. The two developed Blasius boundary layers pass the trailing edge of the splitter plate and merge into FSL downstream. The configuration of the splitter plate is shown in Fig. 1. The free-stream velocities at the high- and low-speed sides are specified to satisfy the velocity ratio \(R = (U_1 - U_2)/(U_1 + U_2) = 0.54\) for all simulations.

It is important to note that in the study by Laizet et al. [41], the authors employed two laminar streams to issue a mixing layer without any inflow perturbations. Consequently, they observed unrealistic flow dynamics which are similar to the results obtained from 2D simulations. The authors later concluded that the unrealistic results are due to the lack of perturbation to excite the 3D instabilities downstream of the trailing edge [42]. In light of these previous studies [41, 42] and our extensive tests for optimal level of instabilities, we superimpose a small perturbation on the upper boundary layer to allow a realistic initial development of disturbances, ensuring a naturally evolving destabilization in the boundary layer at the trailing edge [42]. The perturbation is generated by a stochastic model originally proposed by Gao and Mashayek [14]. The lower stream is laminar without perturbation [73]. Note especially that no forcing mechanism is used in both the inflow boundary layers [42, 64, 73, 77]. The Reynolds numbers on the two inlet boundary layers are \(\hbox {Re}_{\theta 1} = 200\) and \(\hbox {Re}_{\theta 2} = 60\) based on the corresponding free-stream velocities (\(U_1\) and \(U_2\)) and the momentum thicknesses (\(\delta _{\theta 1}\) and \(\delta _{\theta 2}\)) evaluated just upstream of the trailing edge. It is important to note that both Reynolds numbers are too small for a laminar boundary layer to develop any turbulence with this artificial generation of perturbation [42]. The developments of the boundary layers for each case are shown in Fig. 2 through the comparisons of the mean streamwise velocity profiles and the fluctuating kinetic energy profiles at \(x = {-}\,11.0 \delta _{\theta 1}\) and \(x = {-}\,1.0 \delta _{\theta 1}\), respectively. Note that the cross-stream extent presented in this figure is only 1.9% of the total length in the cross-stream direction. As we expect, the normalized streamwise velocity profiles are near identical for all three cases at the trailing edge. This is due to the fact that all cases use the same velocity ratio \(R = 0.54\). It can be seen that the normalized fluctuating kinetic energy imposed at the upper boundary layer has a maximum value of \(\approx \, 0.0017\), which is relatively small compared to that in the turbulent boundary layer. This confirms that the upper boundary layer at the trailing edge of the splitter plate is laminar. Temperature and density are uniformly initialized to \(\left( \Delta U / 2M_{\mathrm{c}}\right) ^2\) and 1.0, respectively. Note that when the self-similarity is achieved, the flow has forgotten the initial conditions [6].

Fig. 2
figure 2

Comparisons of the mean streamwise velocity profiles (a, b) and the fluctuating kinetic energy profiles (c, d) for the boundary layers on both sides of the splitter plate at \({-}\,11.0 \delta _{\theta 1}\) (a, c) and \({-}\,1.0 \delta _{\theta 1}\) (b, d), upstream of the trailing edge for \(M_{\mathrm{c}} = 0.3\), 0.5, and 0.7

Full size image

4 Validation and verification study

This section is devoted to validating the numerical methodology by comparing our results to published theoretical, experimental and DNS data. To obtain the necessary statistics, the simulation is initially run for five flow-through times to reach a quasi-stationary state. One flow-through time is defined as the time for the flow moving from the inlet to the outlet with the convective velocity, which is defined as

$$\begin{aligned} U_{\mathrm{c}} = \frac{c_{2}U_{1} + c_{1}U_{2}}{c_1 + c_2}. \end{aligned}$$
(14)

The first-order statistics are computed for another five flow-through times. Next, ten flow-through times are required to obtain sufficient information for the second-order statistics. Finally, post-processing for ensemble averages in the spanwise direction is implemented to enhance the accuracy of the statistics. Two types of averages are used in this study, Reynolds average and Favre average. Fluctuations from the Reynolds averages are denoted by superscript \(^{\prime }\). Fluctuations from Favre averages are indicated by superscript \(^{\prime \prime }\).

To ensure that the validation data are extracted from the self-similar turbulent region, the location of the laminar–turbulent transition region needs to be approximately outlined. Contours of the instantaneous spanwise vorticity after five flow-through times for \(M_{\mathrm{c}} = 0.3\), 0.5, and 0.7 are shown in Fig. 3. It can be seen that the large coherent vortices initiated from roll-up interact mutually and break down to small-scale structures within the computational domain. Thus, we approximate the area between the vortex roll-up and the emergence of the small-scale structures as the laminar–turbulent transition region, and the area downstream as the turbulence region [13, 86, 89]. This observation also preliminarily indicates that the longitudinal length of the computational domain is sufficiently large to develop self-similar turbulence.

Fig. 3
figure 3

Spanwise vorticity contours with \(M_{\mathrm{c}} = 0.3\), 0.5, and 0.7

Full size image

The adequacy of the domain width in the spanwise direction is examined via spanwise two-point correlation functions of all velocity components, which are shown in Fig. 4. The data used for computing the two-point correlation functions are extracted from a line along the spanwise direction (z-line) at \(x = 1297.1\) and \(y = {-}\,14.6\), located in the self-similar turbulent region. Although the two-point correlations do not show an absolute zero decorrelation at the end of the half domain, the absolute values of two-point correlations are smaller than 0.2 roughly behind one-quarter of the domain width (\(L_z = 140\)) for each case, ensuring that the spanwise length is sufficiently large for turbulence simulation [60, 89]. Figure 5 shows the one-dimensional spanwise energy spectra of the streamwise velocity in the self-similar turbulent region of the FSL for various convective Mach numbers. It can be observed that all three cases display the power-law behavior with the exponent of \({-}\,5/3\) in the inertial subrange, while the roll-off in the dissipation range compares well with the published studies [60, 66, 89], demonstrating that the grid resolution in the spanwise direction is adequate to resolve the finest scales in the turbulence.

Fig. 4
figure 4

Two-point correlation functions of velocity components at self-similar region with different convective Mach numbers

Full size image
Fig. 5
figure 5

One-dimensional spanwise energy spectra of the streamwise velocities for different convective Mach numbers

Full size image

The advantage of the spectral multidomain method is that it allows the spatial resolution to be adjusted at two levels. One level is to change the number of elements (h-refinement) to obtain a satisfying resolution. Another level is to modify the polynomial order within an element (p-refinement). It is well known that p-refinement gives an exponential convergence rate, whereas an algebraic convergence rate is provided by h-refinement [38]. Thus, p-convergence studies are conducted for the spatially developing FSL cases with \(M_{\mathrm{c}} = 0.3\), 0.5, and 0.7 for different polynomial orders. After a careful investigation on different grids, polynomial order \(p = 5\) is selected for the further simulations. The present DNS results are compared with theoretical, DNS, and experimental results.

Fig. 6
figure 6

Comparison of the streamwise mean velocity profiles for different locations and convective Mach numbers with classical erf function profile

Full size image
Fig. 7
figure 7

Normalized FSL growth rates with different convective Mach numbers

Full size image

To perform the comparison for the level of self-similarity, four profiles of the Favre-averaged streamwise velocity, \(\lbrace u \rbrace \), are extracted from four cross-stream lines (y-line). The lines are located in the self-similar turbulent region at \(x = 765\), 850, 950, and 1050 for the case with \(M_{\mathrm{c}} = 0.3\), at \(x = 900\), 1000, 1100, and 1200 for the case with \(M_{\mathrm{c}} = 0.5\), and at \(x = 1000\), 1100, 1200, and 1300 for the case with \(M_{\mathrm{c}} = 0.7\). Figure 6 shows the comparison with the classical erf function profile derived by Gortler [19]. Assuming constant viscosity and density across the shear layer, the Gortler erf profile can be defined as

$$\begin{aligned} \frac{\lbrace u \rbrace - U_2}{\Delta U}= \frac{1}{2}[1+\text {erf}(\eta )]. \end{aligned}$$
(15)

Here, \(\eta \) is the similarity variable, expressed as

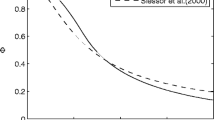
$$\begin{aligned} \eta = \sigma \frac{(y - y_{0.5})}{(x - x_0)}, \end{aligned}$$
(16)

where \(\sigma = \sigma _0/R \) and \(\sigma _0 = 11\) is usually used [87], while \(x_0\) and \(y_{0.5}\) are the origin of the FSL and the lateral position at which the streamwise velocity reaches the value of \(U_{\mathrm{c}}\) in the cross-stream direction, respectively. Figure 6 reveals the following: an excellent self-similar behavior is achieved; a good agreement between the present results and the classical erf function profile can be clearly observed; the difference between the normalized mean streamwise velocity profiles for different convective Mach numbers is small. The normalized momentum thickness growth rates for convective Mach numbers of 0.3, 0.5, and 0.7 in the self-similar region are compared with the published theoretical, experimental, and numerical results in Fig. 7. The normalized growth rate is \((\mathrm{d}\delta _{\theta }/\mathrm{d}x)/(\mathrm{d}\delta _{\theta 0}/\mathrm{d}x)\) and its values for \(M_{\mathrm{c}} = 0.3\), 0.5, and 0.7 are given in Table 1. Here, \( \mathrm{d}\delta _{\theta }/\mathrm{d}x \) and \( \mathrm{d}\delta _{\theta 0}/\mathrm{d}x \) are the momentum thickness growth rates of the present study and the corresponding incompressible FSL [4], respectively. Figure 7 shows the theoretical and numerical results from a linear stability analysis [9], temporal direct numerical simulation [60], and spatially developing direct numerical simulation [89]. For the experimental results in Fig. 7, three methods of shear layer thickness measurements are used, such as visual thickness [22], \(1\% \Delta U\) and \(10\% \Delta U\) thickness [4, 18], and shear layer pitot thickness [8, 61]. The present results fit well with the trend of the scattered experimental results. The scatter in the data is due to the following factors. First, experimental facilities, measurement techniques, and thickness definitions are not identical. Second, the shear layers do not achieve self-similarity fully. Finally, significant uncertainty exists in the estimation of the incompressible shear layer thickness [87]. The result obtained by Zhou et al. [89] may be one of the good examples of data scatter in this figure, which exhibits a much lower value than most of the results. This may be attributed to the extremely small Reynolds number that the authors used, requiring much longer streamwise domain length to achieve a fully self-similar turbulent flow. If not satisfying this condition, the shear growth rate is obtained in the transition region or even laminar region.

Table 1 The approximated values of some variables for the cases with \(M_{\mathrm{c}} = 0.3\), 0.5, and 0.7
Full size table

Comparisons of the Reynolds stress profiles in the self-similar region between the present results and experimental results are shown in Fig. 8. We can see that \(\lbrace u^{\prime \prime }u^{\prime \prime } \rbrace /(\Delta U)^2\) and \(\lbrace u^{\prime \prime }v^{\prime \prime } \rbrace /(\Delta U)^2\) of the present simulations agree very well with the experimental results from Goebel and Dutton [18] for \(M_{\mathrm{c}} = 0.46\) and 0.69, while \(\lbrace w^{\prime \prime }w^{\prime \prime } \rbrace /(\Delta U)^2\) shows good agreement with the experimental result by Gruber et al. [21], which is the only available source that we can obtain. \(\lbrace v^{\prime \prime }v^{\prime \prime } \rbrace /(\Delta U)^2\) falls between the results for \(M_{\mathrm{c}} = 0.2\) and 0.46 from Goebel and Dutton [18], and is higher than that by Gruber et al. [21] at \(M_{\mathrm{c}} = 0.8\). However, the \(\lbrace v^{\prime \prime }v^{\prime \prime } \rbrace /(\Delta U)^2\) at \(M_{\mathrm{c}} = 0.7\) of the present study agrees well with that by Goebel and Dutton [18] at \(M_{\mathrm{c}} = 0.46\). There are still some debates about the altering trends of the Reynolds stresses with changing \(M_{\mathrm{c}}\). Elliott and Samimy [10] found that all Reynolds stresses decrease considerably with increasing \(M_{\mathrm{c}}\), while Goebel and Dutton [18] and Gruber et al. [21] reported that the streamwise Reynolds stress remained relatively unaffected; additionally, Gruber et al. [21] observed a slight change in the spanwise Reynolds stress in their experimental study. These debates also exist in computational studies. Studies by Vreman et al. [84], Pantano and Sarkar [60], Fu and Li [13], and Foysi and Sarkar [11] showed that all Reynolds stresses decreased with increasing \(M_{\mathrm{c}}\), while the study by Freund et al. [12] found a relatively unaffected streamwise Reynolds stress. We speculate that these disagreements can be influenced easily by using different free-stream velocity ratios, density ratios, experimental facilities, and measurement techniques. This speculation may account for the controversies about Reynolds stresses obtained from both experimental and numerical studies. In the present study, the \(\lbrace u^{\prime \prime }u^{\prime \prime } \rbrace /(\Delta U)^2\) profiles for different convective Mach numbers are almost identical, meaning that the \(\lbrace u^{\prime \prime }u^{\prime \prime } \rbrace /(\Delta U)^2\) is not sensitive to the change of the convective Mach number [12]. However, the \(\lbrace v^{\prime \prime }v^{\prime \prime } \rbrace /(\Delta U)^2\) and \(\lbrace w^{\prime \prime }w^{\prime \prime } \rbrace /(\Delta U)^2\), as well as the \(\lbrace u^{\prime \prime }v^{\prime \prime } \rbrace /(\Delta U)^2\) show significant reductions as the convective Mach number increases [10, 13, 18, 21, 60, 83, 84].

Fig. 8
figure 8

Comparisons of the Reynolds stress profiles in self-similar turbulent region between the present results and experimental results, a streamwise, b cross-stream, c spanwise, d shear. Goebel1, Goebel2, and Goebel3 represent the results by Goebel and Dutton [18] for \(M_{\mathrm{c}} = 0.2\), 0.46, and 0.69, respectively. Gruber represents the results by Gruber et al. [21] for \(M_{\mathrm{c}} = 0.8\). Present1, Present2, and Present3 stand for the present results for \(M_{\mathrm{c}} = 0.3\), 0.5, and 0.7, respectively

Full size image

Following the work of Huang et al. [26], the turbulent kinetic energy (TKE) equation for a stationary flow is expressed as

$$\begin{aligned} -{\langle }\rho {\rangle }\{u_i^{\prime \prime }u_k^{\prime \prime }\} \frac{\partial \{u_i\}}{\partial x_k}= & {} \frac{\partial {\langle }\rho {\rangle }\{u_k\}\{k\}}{\partial x_k} +\frac{\partial {\langle }\rho {\rangle }\{u_k^{\prime \prime }k^{\prime \prime }\}}{\partial x_k} +\frac{\partial {\langle }p'u_k'{\rangle }}{\partial x_k} - \frac{\partial {\langle }\tau _{ik}' u_i'{\rangle }}{\partial x_k}\nonumber \\&+\left\langle \tau _{ik}'\frac{\partial u_i'}{\partial x_k}\right\rangle +{\langle }u_k^{\prime \prime }{\rangle }\frac{\partial {\langle }p{\rangle }}{\partial x_k} -{\langle }u_i^{\prime \prime }{\rangle }\frac{\partial {\langle }\tau _{ik}{\rangle }}{\partial x_k} -\left\langle p'\frac{\partial u_k'}{\partial x_k}\right\rangle . \end{aligned}$$
(17)

The term on the left-hand side (LHS) of Eq. (17) represents the turbulent production; the first term on the right-hand side (RHS) is turbulent convection; the second term is turbulent diffusion; the third term is diffusion due to velocity–pressure interaction; the fourth term is viscous diffusion; the fifth term is energy dissipation rate; and the last three terms are compressibility related terms with the pressure-dilatation correlation as the very last one. A large discrepancy between the term on the LHS and the sum of all the terms on the RHS would be the result of an unresolved turbulent flow due to a low grid resolution. In particular, an insufficient number of solution points results in inaccurate second-order statistics. Figure 9 compares profiles of the value of LHS and the sum of all terms on the RHS of the TKE equation for the cases with \(M_{\mathrm{c}} = 0.3\), 0.5, and 0.7, in the self-similar turbulent region. It can be seen from Fig. 9a–c that good agreements are achieved for all cases, meaning that the grid has sufficient solution points for resolving the turbulent FSL [52, 60, 89].

Fig. 9
figure 9

Comparisons of the TKE budgets on the LHS and the sum of the RHS of the TKE equation in the self-similar turbulence region for cases with a\(M_{\mathrm{c}} = 0.3\), b\(M_{\mathrm{c}} = 0.5\), c\(M_{\mathrm{c}} = 0.7\). All terms are normalized by \((\Delta U)^3\)

Full size image

5 Laminar–turbulent transition zone

The purpose of this section is to define the laminar–turbulent transition zone for turbulent FSL. The region of the laminar–turbulent transition is estimated by analyzing the vortex structures of the instantaneous flow and the normalized dissipation rate along the flow direction.

5.1 Instantaneous flow behavior

In Sect. 4, we briefly discussed a method to determine the approximate turbulence transition region by examining the contours of the spanwise vorticity shown in Fig. 3, based on the presence of small-scale structures [3, 43, 57,58,59, 66, 69, 86]. Since the spanwise vorticity contours are visualized in a 2D manner, the spanwise movements are not considered. However, the vortex stretching mechanism in the spanwise direction, such as the formation of secondary streamwise vortices and the breakdown of primary spanwise vortices, is responsible for the onset of turbulence transition [24, 43, 70]. In this context, we present a 3D representation of the turbulent structures via iso-surface of the second invariant of velocity gradient tensor in Fig. 10 for all the cases. In the cases with \(M_{\mathrm{c}} = 0.3\) and 0.5, the 2D primary spanwise coherent structures can be seen in the FSL [51, 86]. In the braid region, along with the 2D primary spanwise coherent structures, the 3D secondary streamwise vortex structures emerge and stretch the 2D primary spanwise coherent structures to break down to small-scale structures downstream. The interaction between the 2D and 3D instabilities facilitates the transition from laminar to turbulence in FSL and hence leading to a self-similar state [27, 51, 63, 72, 86]. This process is the main mechanism accounting for the formation of the fine vortex structures [70]. Therefore, the turbulence transition region can be approximated by measuring the emergence of the 2D primary spanwise coherent structures and the 3D secondary streamwise vortex structures. Based on the location of the first-formed 3D secondary streamwise vortex, the turbulence transition zone can be separated into two parts. The first part, mainly features the 2D primary spanwise vortices, while the second part shows the 3D secondary streamwise vortices interacting mutually with the 2D primary spanwise vortices. However, in the case with \(M_{\mathrm{c}} = 0.7\), only the elongated streamwise streaky structures can be observed in the transition region of the FSL [51], suggesting that the 3D secondary streamwise vortex structures become dominant in the transition region of the FSL. This is due to the fact that the elongated vortex structures in the FSL have less tendency to form spanwise vortices [45, 51, 71, 72]. Therefore, the approach of separating the transition region into two parts is not applicable for the FSL with \(M_{\mathrm{c}} = 0.7\). It should be noticed that as the convective Mach number increases from 0.3 to 0.7, the location where the FSL rolls into the transition zone significantly shifts downstream.

Fig. 10
figure 10

Iso-surface of the second invariant of velocity gradient tensor colored by streamwise velocity with convective Mach numbers of 0.3, 0.5, and 0.7

Full size image
Fig. 11
figure 11

a Cross-stream integrated dissipation rate, \(\varepsilon ^{I}\), normalized by \((\Delta U)^{3}\)b its first derivative with respect to x for \(M_{\mathrm{c}} = 0.7\)

Full size image

5.2 Turbulent dissipation rate

The turbulence transition region is approximated by the analysis of the evolution of the normalized cross-stream integrated turbulent dissipation rate. The turbulent dissipation rate, \(\varepsilon \equiv \frac{\partial {\langle }\tau _{ik}' u_i'{\rangle }}{\partial x_k}\), is the fifth term in the RHS of Eq. (17). The cross-stream integrated turbulent dissipation rate is defined as

$$\begin{aligned} \varepsilon ^{I} = \int _{-\infty }^{+\infty } \varepsilon \mathrm{d}y, \end{aligned}$$
(18)

where the superscript I represents the cross-stream (y-line) integration. This definition is also used to define the cross-stream integrated Reynolds stresses, TKE, turbulent production, and pressure-dilatation correlation. Figure 11a shows the evolution of the normalized cross-stream integrated turbulent dissipation rate along the flow direction for the case with \(M_{\mathrm{c}} = 0.7\). Initially, the dissipation rate is near-zero, until perturbations grow and increase the dissipation rate, reaching a peak during the turbulence transition, and eventually decaying smoothly. Self-similar behavior is evident due to the small variation in the profile. In boundary shear layer, researchers study the evolution of the wall shear stress along a surface to determine the laminar–turbulent transition region. Hirschel et al. [23] proposed that the profile of the evolution of the wall shear stress can be split into three branches based on its qualitative behavior: the laminar branch, the transition branch, and the turbulent branch. The authors also demonstrated a possible way to approximate the length of the transition region. The transition branch is defined as the area where the wall shear stress rises rapidly and reaches a maximum, while the turbulent branch is defined as the area where the wall shear stress decreases from a maximum and becomes approximately constant. This behavior, observed in boundary layer, is analogous to that observed in the FSL. Inspired by this, the qualitative behavior of the cross-stream integrated turbulent dissipation rate of a FSL can be analyzed in a manner consistent with the wall shear stress in a boundary layer. As such, for a FSL, we define the region upstream where the dissipation rate is relatively small as the laminar region. The region where the dissipation rate grows rapidly and reaches a peak is defined as the transition region. As the dissipation rate decays linearly downstream, the FSL becomes fully turbulent. This area is defined as the self-similar turbulent region.

To clearly identify the rate of change of \(\varepsilon ^{I}/(\Delta U)^3\) with respect to x, we compute the derivative, \(d(\varepsilon ^{I}/(\Delta U)^3)/\mathrm{d}x\), which is shown in Fig. 11b for \(M_{\mathrm{c}} = 0.7\). It can be seen that the value rapidly increases to a peak due to the fact that the growth of disturbances triggers the Kelvin–Helmholtz instability, and that the unstable vortex sheets emerge, roll up, pair, and finally convert into 3D secondary streamwise vortex structures, leading to an increase in the breakdown of the large-scale structures [45, 58, 68, 69]. Subsequently, the magnitude decays and maintains a roughly constant negative value, meaning that the flow evolves past the transition zone and turns into the self-similar turbulence region. By inspecting Fig. 11, we can estimate that the transition region starts at \(x \approx 230\) and completes at \(x \approx 670\). The analysis of the evolution of the cross-stream integrated turbulent dissipation rate may be a good alternative in the prediction of the turbulent transition region. Similar analyses for the cases with \(M_{\mathrm{c}} = 0.3\) and 0.5 are presented in Sect. 7.3, in which the compressibility effect on the dissipation rate is also discussed.

6 Compressibility effect on turbulent FSL

6.1 Autocorrelation and integral time scale

The effect of the convective Mach number is studied via the analyses of autocorrelation and integral time scale. The auto-covariance of the streamwise velocity, considered as the simplest multi-time statistics, is defined as [66]

$$\begin{aligned} R_u(s) = \langle u'(t)u'(t+s)\rangle , \end{aligned}$$
(19)

while its normalized form, the autocorrelation function of the streamwise velocity is

$$\begin{aligned} \rho _u(s) = \frac{\langle u'(t)u'(t+s)\rangle }{\langle u'^{2}(t)\rangle }, \end{aligned}$$
(20)

where \(u'\) and s are the streamwise velocity fluctuation and the time lag, respectively. Similarly, we can calculate \(\rho _v\) and \(\rho _w\), which are the autocorrelation functions of cross-stream and spanwise velocity components. Figure 12 presents the normalized autocorrelation functions of the streamwise, cross-stream, and spanwise velocities on the centerline of the FSL, where the momentum thicknesses are identical (\(x = 765.5\), 953.1, and 1299.5 for \(M_{\mathrm{c}} = 0.3\), 0.5, and 0.7, respectively), for different convective Mach numbers in the self-similar turbulent region. The correlations of all three velocity components exhibit a similar trend for the same convective Mach number. It is clear that the case with high convective Mach number, such as \(M_{\mathrm{c}} = 0.7\), has a steeper roll-off in the autocorrelation curve (faster drop to zero) than does the case with the low convective Mach number, such as \(M_{\mathrm{c}} = 0.3\) [11, 12, 60]. It has been known that a steep roll-off of the normalized autocorrelation curve represents high-frequency fluctuations, which are directly related to smallest-scale structures, and vice versa [66].

Fig. 12
figure 12

Autocorrelation functions of a streamwise velocity, b cross-stream velocity, c spanwise velocity, in the self-similar turbulent region

Full size image

To measure the longest connection in the turbulent behavior over time, the integral time scale,

$$\begin{aligned} \tau _u = \int _{0}^{\infty }\rho \left( s\right) \mathrm{d}s, \end{aligned}$$
(21)

is used, and similarly for \(\tau _v\) and \(\tau _w\). Here, \(\tau _u\), \(\tau _v\) and \(\tau _w\) are the integral time scales of u, v and w velocity fluctuations, respectively. The integral time scales for different convective Mach numbers are presented in Fig. 13 and Table 1. The results reveal that the integral time scale decreases as the convective Mach number increases [12, 60]. From this fact, it can be inferred that at any stationary turbulent FSL, an increase in the convective Mach number may cause a decrease in the size of largest-scale structure. This is also evident from the comparison of turbulence structures in Fig. 3.

Fig. 13
figure 13

Integral times-scales for convective Mach numbers of 0.3, 0.5, and 0.7

Full size image

6.2 Growth of the momentum thickness

The variation of the momentum thickness \(\delta _\theta (x)\) along the flow direction for different convective Mach numbers is shown in Fig. 14a. For better comparison, a linear trend-line is also included for the self-similar turbulent region for each case. The momentum thickness growth rates in the self-similar region are calculated as 0.0137, 0.0121, and 0.0106 for the corresponding convective Mach numbers of 0.3, 0.5, and 0.7 (see Table 1), meaning that the growth rate of the momentum thickness decreases as the convective Mach number increases [4, 8, 9, 11, 12, 18, 22, 34, 60, 61, 84, 85]. The momentum thickness growth primarily consists of three stages: the initial stage, the rapid evolving stage, and the self-similar stage, which are characterized by different growth rates. In the first stage, the fundamental mode of instability begins to develop, and the vortex starts to roll up at the end of this stage [70]. The growth of the FSL is slow but even slower with higher convective Mach number, which is shown in Fig. 14a in \(x < 400\) for \(M_{\mathrm{c}} = 0.7\). In the second stage, the adjacent vortices start to pair, and the growth rate reaches its peak. In high Mach number flow, the strong compressibility in the FSL stretches the roller from a nearly circular shape to a narrow ellipse shape [70]. This mechanism slows down the paring process. In the third stage, the self-similarity is achieved, and the flow has forgotten the initial conditions [6]. Figure 14b shows the position of the center of the FSL along the x-axis. As the shear flow evolves downstream, the center of the FSL shifts to the low-speed side due to the asymmetric entrainment to the high- and low-speed sides of the flow. This feature can be observed in experiments but not in the temporally developing numerical simulations of FSL [10, 13, 18, 21, 89]. This center shift is slightly affected by the change of convective Mach number.

Fig. 14
figure 14

a Evolution of the momentum thickness for convective Mach numbers of 0.3, 0.5, and 0.7, b center of the FSL along the x-axis

Full size image

7 Compressibility effect on turbulence transition

The results in the preceding section demonstrate that the numerical methodology used in this study can accurately capture the compressibility effect on the self-similar turbulent region. In this section, we investigate the effect of compressibility on the turbulence transition zone in terms of its location and length by analyzing the flow properties in the transition region, such as normal stress, TKE, and budgets of TKE.

7.1 Evolution of the normal stress and TKE

Evolutions of the normalized cross-stream integrated streamwise, cross-stream, and spanwise normal stresses, computed with different convective Mach numbers, are shown in Fig. 15. Comparison of Fig. 15a–c indicates that the streamwise normal stress, \(R_{11}^{I}\), is the largest component for all three cases. The evolution of the streamwise normal stress, in general, is similar to that of the other two components. All three stress components increase sharply from small values, followed by a reduction in the growth rate of stress for each case. This means that the FSL starts to reach a self-similar turbulent state. Eventually, the normal stresses show a small linear growth, especially for the cross-stream and spanwise normal stresses, \(R_{22}^{I}\) and \(R_{33}^{I}\), in the self-similar turbulent region. In addition, Fig. 15 reveals that there is a significant decrease in the magnitude of the stress with the increase in the convective Mach number for each stress component [1].

Fig. 15
figure 15

Cross-stream integrated, a streamwise normal stress, \(R_{11}^{I}\), b cross-stream normal stress, \(R_{22}^{I}\), c spanwise normal stress, \(R_{33}^{I}\), normalized by \((\Delta U)^{2}\) for different convective Mach numbers

Full size image

The TKE is composed of three normal stresses, i.e., streamwise normal stress, cross-stream normal stress, and spanwise normal stress. Figure 16 shows the evolution of the normalized TKE, \( \frac{k}{(\Delta U)^{2}}\), at the centerline of the FSL along streamwise direction for convective Mach numbers of 0.3, 0.5, and 0.7. The value of \( \frac{k}{(\Delta U)^{2}}\) of each case sharply increases and reaches a peak along streamwise direction. Both the growth rate and the peak are significantly lower as the convective Mach number increases [12, 76, 84]. Similar to the evolution of the cross-stream integrated dissipation rate in Fig. 11, the location of the peak of \( \frac{k}{(\Delta U)^{2}}\) shifts downstream with increasing \(M_{\mathrm{c}}\), implying that the position, where the FSL turns into self-similar turbulence, shifts downstream as well. As a complement to Fig. 16, Fig. 17a–c shows the cross-stream profiles of \( \frac{k}{(\Delta U)^{2}}\) at five carefully selected locations along the flow direction for all cases. The locations cover different areas including laminar, laminar–turbulent transition, and self-similar turbulent regions. Following the profiles of these five locations, i.e., \(x = 101\), 245, 430, 550, and 700, it can be seen that the location of the maximum \( \frac{k}{(\Delta U)^{2}}\) shifts toward downstream (from \(x = 245\)–430–550) as the convective Mach number increases. Another interesting observation is that the profiles at location \(x = 101\) for \(M_{\mathrm{c}} = 0.3\), at locations \(x = 101\) and 245 for \(M_{\mathrm{c}} = 0.5\), and at locations \(x = 101\), 245, and 430 for \(M_{\mathrm{c}} = 0.7\), shift toward the high-speed side of the FSL. We can refer to the evolution of the vortex structures to explain this phenomenon. At the positions not far from the trailing edge of the splitter plate, the roll-ups of lambda vortices and the formations of the hairpin vortices (see Fig. 10) originate on the high-speed side of the FSL. Thus, the velocity fluctuations become relatively stronger at the high-speed side than those at the low-speed side of the FSL before reaching the peak of \( \frac{k}{(\Delta U)^{2}}\). As the values of \( \frac{k}{(\Delta U)^{2}}\) reach its peaks, the locations of the peaks of the profiles are slightly tilted toward the low-speed side; the corresponding profile and the profiles downstream show similar shapes. This suggests that the location where the FSL turns into self-similar turbulent region is related to the peak of \( \frac{k}{(\Delta U)^{2}}\).

Fig. 16
figure 16

Evolution of the normalized TKE at the centerline of the FSL along streamwise direction for convective Mach numbers of 0.3, 0.5, and 0.7

Full size image
Fig. 17
figure 17

Cross-stream profiles of normalized TKE at five streamwise locations for a\(M_{\mathrm{c}} = 0.3\), b\(M_{\mathrm{c}} = 0.5\), c\(M_{\mathrm{c}} = 0.7\)

Full size image

The normalized cross-stream integrated TKE along the flow direction is plotted in Fig. 18a. The figure again underscores that the integrated TKE decreases with increasing convective Mach number. This is consistent with the previous discussion on normal stress and the TKE at the centerline of the FSL. Figure 18b shows the growth rate of the cross-stream integrated TKE, \(d(k^{I}/(\Delta U)^{2})/\mathrm{d}x\), along the flow direction for different convective Mach numbers. \(d(k^{I}/(\Delta U)^{2})/\mathrm{d}x\) starts with a low value and reaches its peak due to the Kelvin–Helmholtz instability. It is important to note that the locations of both the onset of instability and the peak of \(d(k^{I}/(\Delta U)^{2})/\mathrm{d}x\) move downstream for larger convective Mach numbers, implying that the transition starts with a delay at higher convective Mach numbers. Finally, \(d(k^{I}/(\Delta U)^{2})/\mathrm{d}x\) decays to an asymptotic value for each case. Note that the distance between the onset of \(d(k^{I}/(\Delta U)^{2})/\mathrm{d}x\) and the point where \(d(k^{I}/(\Delta U)^{2})/\mathrm{d}x\) reaches the asymptotic value is longer with increasing the convective Mach number. This implies that the length of the transition region increases as the convective Mach number increases.

Fig. 18
figure 18

Cross-stream integrated TKE normalized by \((\Delta U)^{2}\). a Evolution in flow direction, b its growth rate along the x-axis

Full size image

7.2 Evolution of the production of the TKE

We have shown that the growth rates of the momentum thickness and the TKE decrease with increasing the convective Mach number. These may be explained by analyzing the TKE budget. The production, \({-}\,{\langle }\rho {\rangle }\{u_i^{\prime \prime }u_k^{\prime \prime }\} \frac{\partial \{u_i\}}{\partial x_k}\), is the term on the LHS of Eq. (17). The cross-stream profiles of the normalized turbulent production at six streamwise locations are presented in Fig. 19. It can be seen in Fig. 19a that the production with the convective Mach number of 0.3 reaches its peak at \(x = 115\). The values in the other two cases remain very small compared to that of \(M_{\mathrm{c}} = 0.3\) at this location. In Fig. 19b, c, at \(x = 270\) and \(x = 380\), the productions of \(M_{\mathrm{c}} = 0.5\) rapidly increase and are greater than that of \(M_{\mathrm{c}} = 0.3\) and 0.7. The production of \(M_{\mathrm{c}} = 0.7\) is still relatively small compared to \(M_{\mathrm{c}} = 0.5\), while it is greater than that of \(M_{\mathrm{c}} = 0.3\). A monotonic increase in the production with the increase in Mach number is observed at \(x = 471\), and the production of \(M_{\mathrm{c}} = 0.7\) reaches its peak, shown in Fig. 19d. As the flow evolves downstream at \(x = 721\) and 996, in Fig. 19e, f, the differences, in terms of value and shape, between the three cases become smaller and smaller. In summary, Fig. 19 reveals that the location of the maximum production shifts downstream with increasing the convective Mach number.

Fig. 19
figure 19

Production of TKE at: a\(x = 115\), b\(x = 270\), c\(x = 380\), d\(x = 471\), e\(x = 721\), f\(x = 996\). The production is normalized by \((\Delta U)^{3}\) for each location

Full size image

More information pertaining to the production term can be obtained from its normalized cross-stream integrated profile along the flow direction. As approaching the end of the transition zone, the large-scale structures break down into smaller-scale structures, leading to a decrease in turbulence production. This is evident in Fig. 20a, which shows the streamwise evolution of the normalized cross-stream integrated turbulence production for different convective Mach numbers. It is clear that the cases with \(M_{\mathrm{c}} = 0.3\) and 0.5 have two peaks. This phenomenon can be explained by the following mechanisms. First, the FSL roll-up leads to the initial increase in turbulent production. Second, the vortex mutually interacts with the adjacent vortex, and the first pairing occurs, leading to a rapid increase in the turbulent production (first peak). After a short period of newly formed vortex rotation (the valley portion), the second pairing occurs and leads to the second peak of the production, where the self-similar FSL initiates. Note particularly that there is only one peak for the case with \(M_{\mathrm{c}} = 0.7\). This may be due to the fact that the 3D secondary streamwise vortex structures become dominant in the roll-up region of the FSL, which is demonstrated in Fig. 10 as well. Those elongated vortex structures have less tendency to roll and pair in the streamwise direction [45, 51, 72]. In addition, as the convective Mach number increases, the peak location shifts downstream. This trend is also evidenced by the production profiles in Fig. 19a–c. Therefore, it can be inferred that increasing the convective Mach number may lead to a delay in the onset of transition. This observation is consistent with that found from the analysis of the TKE in Sect. 7.1. Figure 20b shows the turbulent production at the centerline (x-line) of the FSL along the streamwise direction, normalized by \((\Delta U)^{3}\). In general, the shapes of the profiles in this figure for all three cases are somewhat similar to the corresponding ones in Fig. 18b. Also, the location of the peak of the production is similar to that of the growth rate of the integrated TKE for each case. A shoulder is observed in the profile right after the peak for cases with \(M_{\mathrm{c}} = 0.3\) and 0.5, which is similar to the second peak in the normalized cross-stream integrated profiles in Fig. 20a. In the self-similar region, the production (production at the centerline of the FSL) decays gradually to a small value and becomes relatively constant for each case.

Fig. 20
figure 20

a Cross-stream integrated turbulent production, \( P^{I} \), b the centerline values of the turbulent production along streamwise direction. All terms are normalized by \((\Delta U)^{3}\)

Full size image

7.3 Evolution of the dissipation rate of the TKE

The turbulent dissipation rate, \(\left\langle \tau _{ik}'\frac{\partial u_i'}{\partial x_k}\right\rangle \), is the fifth term on the RHS of Eq. (17). Recall that the increase in the convective Mach number leads to a reduction in the turbulent production, resulting in a decrease in the TKE and a lower growth rate of the momentum thickness. This could be in part related to the sink terms in the TKE budget. In this section, we investigate the possible compressibility effect on the laminar–turbulent transition via one of the sink terms in the TKE budget—viscous dissipation rate (the conversion of mechanical energy into internal energy). Figure 21a shows the normalized cross-stream integrated dissipation rate along the streamwise direction for different convective Mach numbers. The level of the dissipation rate increases along the streamwise direction before reaching a peak. This is due to the increase in the breakdown of the large-scale structures. However, the cases with lower convective Mach numbers show faster increases to their peaks than that with higher convective Mach numbers. A higher peak is also observed for the lower convective Mach number case [12, 76, 84]. Subsequently, the dissipation rate smoothly decays with a nearly constant rate for each case. Furthermore, both the onset and the peak of the dissipation rate shift downstream as the convective Mach number increases. This is also evident in Fig. 21b, which shows the first derivative of the normalized cross-stream integrated dissipation rate with respect to x. For convenience and clarity, \(x_{\mathrm{R}}\) is used to indicate the location where the roll-up of vortex sheet originates, while \(x_{\mathrm{E}}\) is the location where the transition ends. By inspecting Fig. 21b, \(x_{\mathrm{R}}\) and \(x_{\mathrm{E}}\) can be approximated for each case, and the results are tabulated in Table 1. For a better comparison, we label the horizontal axis as \(x-x_{\mathrm{R}}\) for each case, as shown in Fig. 21c. It is clear that the length of the transition zone increases as the convective Mach number increases.

Fig. 21
figure 21

Cross-stream integrated dissipation rate, \(\varepsilon ^{I}\), normalized by \((\Delta U)^{3}\). a Evolution in flow direction; b growth rate over x-axis; c same as b, but the x-axis is normalized by \(x_{\mathrm{R}}\), such as \(x-x_{\mathrm{R}}\)

Full size image

8 Summary and conclusions

The 3D spatially developing turbulent FSL has been studied using direct numerical simulations by employing a high-order discontinuous spectral element method. Two parallel streams, under naturally developing inflow condition, perturbed by relatively weak disturbances from a stochastic model, are separated by a splitter plate. The FSL originates at the trailing edge of the splitter plate and develops downstream. The Reynolds number, based on the initial momentum thickness and the difference between the two free-stream velocities across the FSL, is 140, for all three cases with convective Mach numbers of 0.3, 0.5, and 0.7. The numerical methodology is validated by comparing our results to the published numerical and experimental data. Good agreements are observed in the comparisons of the mean velocity, momentum thickness, normal stress, and the balance of the TKE equation, ensuring that the numerical methodology and the grid resolution adopted in our simulations are accurate and adequate.

Turbulence in the 3D compressible FSL is visualized via the iso-surface of the second invariant of the velocity gradient tensor. The location of the transition zone is identified and estimated by the following two approaches: analyzing the instantaneous flow structures and the evolution of the dissipation rate. For the first method, the transition zone is determined based on the emergence of small-scale structures. For the second method, the evolution of the normalized, cross-stream integrated dissipation rate along the flow direction, shows both the start and the completion of the turbulence transition. Hence, the lengths of the transition zones are approximated as 310, 380, and 440 for \(M_{\mathrm{c}} = 0.3\), 0.5, and 0.7, respectively.

The compressibility effects on the turbulent FSL are examined via the study of autocorrelation, integral time scale, momentum thickness growth rate, and Reynolds stresses for different convective Mach numbers. An increase in the convective Mach number causes a reduction in the sizes of largest-scale structures, leading to a decrease in turbulence production and the growth rate of the momentum thickness. The streamwise normal stress is the dominant stress among the three normal stresses and is almost unaffected by compressibility. However, the cross-stream and spanwise normal stresses, as well as the shear stress, show significant reductions with increasing compressibility.

To further determine the compressibility effect on the transition zone, all the terms in the TKE transport equation are computed and analyzed. The dominant term in the TKE budget is the production term, which decreases with increasing convective Mach number, resulting in a slower growth of the FSL. The evolution of the dissipation rate reveals that the transition starts with a delay and the length of the transition region is longer as the convective Mach number increases.

In the future, we plan to further investigate the compressibility effect on the energy budget of the turbulent FSL. Both the mean kinetic energy and mean internal energy (budget terms) will be examined in great detail. We will analyze the exchange between kinetic energy and internal energy. The compressibility effects on the mean kinetic energy, the mean internal energy, and the energy exchange between them will be studied.