1 Introduction

The crack problem in piezoelectric materials is strongly influenced by the phenomenon associated with intrinsic electromechanical coupling. This has stimulated great interest in this area and led to extensive investigations by several researchers (see, for example, [1,2,3,4,5,6,7]). In these discussions, the crack is regarded as an ideal slit resulting in an electroelastic field describing stresses, strains, electric displacements and electric fields which is singular at the crack tip. Although the elastic field for a blunt crack in an isotropic elastic material was first obtained by Creager and Paris [8] and most recently for a blunt crack in an anisotropic elastic material by Wang and Schiavone [9], to the best of our knowledge, the electroelastic field for a blunt crack in a generally anisotropic piezoelectric solid remains absent from the literature.

In this paper, we thus examine the electroelastic field for a blunt crack in an anisotropic piezoelectric material. The blunt crack is represented by a parabolic cavity with traction-free and charge-free boundary. A complete solution is derived by means of the Stroh octet formalism [4, 10,11,12]. Furthermore, explicit expressions for the stresses, electric displacements, displacements and electric potential are obtained by utilizing the inverse of a \(4\times 4\) Vandermonde matrix constructed from the four distinct Stroh eigenvalues [13] and by utilizing the identities developed as part of the Stroh octet formalism [10, 12]. Real form expressions for the stresses, strains, electric displacements, electric fields and rigid-body rotation at the vertex of the parabola (or at the tip of the blunt crack), which are valid for any mathematically degenerate materials, are derived.

2 The Stroh octet formalism

In a fixed rectangular coordinate system \(\left\{ {x_{i} } \right\} (i=1,2,3)\), the governing equations for an anisotropic piezoelectric solid are given by [4]

$$\begin{aligned} \begin{array}{l} \sigma _{ij} =C_{ijkl} u_{k,l} +e_{kij} \phi _{,k}, \quad D_{k} =e_{kij} u_{i,j} -\in _{kl} \phi _{,l} , \\ \sigma _{ij,j} =0, \quad D_{i,i} =0, \\ \end{array} \end{aligned}$$
(1)

in which we sum over repeated indices and an indicial comma represents differentiation; \(\sigma _{ij}\) and \(D_{i} \) are the stresses and electric displacements; \(u_{i} \) and \(\phi \) are the displacements and electric potential; \(C_{ijkl} \), \(e_{kij} \) and \(\in _{ij} \) are, respectively, the elastic, piezoelectric and dielectric constants.

In the case of two-dimensional problems in which all quantities depend only on \(x_{1} \) and \(x_{2} \), the general solution can be expressed as [4, 10,11,12]

$$\begin{aligned} \begin{array}{l} \mathbf{u }=\left[ {{\begin{array}{*{20}c} {u_{1} } &{} {u_{2} } &{} {u_{3} } &{} \phi \\ \end{array} }} \right] ^{\mathrm{T}}=\mathbf{Af }(z)+{{\bar{\mathbf{A }}}}\overline{\mathbf{f }(z)} , \\ {\varvec{\upvarphi }}=\left[ {{\begin{array}{*{20}c} {\varphi _{1} } &{} {\varphi _{2} } &{} {\varphi _{3} } &{} {\varphi _{4} } \\ \end{array} }} \right] ^{\mathrm{T}}=\mathbf{Bf }(z)+{{\bar{\mathbf{B }}}}\overline{\mathbf{f }(z)} , \\ \end{array} \end{aligned}$$
(2)

where

$$\begin{aligned} \begin{array}{l} \mathbf{A }=\left[ {{\begin{array}{*{20}c} {\mathbf{a }_{1} } &{} {\mathbf{a }_{2} } &{} {\mathbf{a }_{3} } &{} {\mathbf{a }_{4} } \\ \end{array} }} \right] ,\quad \mathbf{B }=\left[ {{\begin{array}{*{20}c} {\mathbf{b }_{1} } &{} {\mathbf{b }_{2} } &{} {\mathbf{b }_{3} } &{} {\mathbf{b }_{4} } \\ \end{array} }} \right] , \\ \mathbf{f }(z)=\left[ {{\begin{array}{*{20}c} {f_{1} (z_{1} )} &{} {f_{2} (z_{2} )} &{} {f_{3} (z_{3} )} &{} {f_{4} (z_{4} )} \\ \end{array} }} \right] ^{\mathrm{T}}, \\ z_{i} =x_{1} +p_{i} x_{2} ,\quad \text{ Im } \left\{ {p_{i} } \right\} >0, \;(i=1,2,3,4), \\ \end{array} \end{aligned}$$
(3)

with

$$\begin{aligned}&\mathbf{N }\left[ {{\begin{array}{*{20}c} {\mathbf{a }_{i} } \\ {\mathbf{b }_{i} } \\ \end{array} }} \right] =p_{i} \left[ {{\begin{array}{*{20}c} {\mathbf{a }_{i} } \\ {\mathbf{b }_{i} } \\ \end{array} }} \right] , \;(i=1,2,3,4) \end{aligned}$$
(4)
$$\begin{aligned}&\mathbf{N }=\left[ {{\begin{array}{*{20}c} {\mathbf{N }_{1} } &{} {\mathbf{N }_{2} } \\ {\mathbf{N }_{3} } &{} {\mathbf{N }_{1}^{\mathrm{T}} } \\ \end{array} }} \right] , \end{aligned}$$
(5)
$$\begin{aligned}&\mathbf{N }_{1} =-\mathbf{T }^{-1}\mathbf{R }^{\mathrm{T}},\mathbf{N }_{2} =\mathbf{T }^{-1},\mathbf{N }_{3} =\mathbf{RT }^{-1}\mathbf{R }^{\mathrm{T}}-\mathbf{Q }, \end{aligned}$$
(6)

and

$$\begin{aligned} \mathbf{Q }=\left[ {{\begin{array}{*{20}c} {\mathbf{Q }^{E}} &{} {\mathbf{e }_{11} } \\ {\mathbf{e }_{11}^{\mathrm{T}} } &{} {-\in _{11} } \\ \end{array} }} \right] ,\quad \mathbf{R }=\left[ {{\begin{array}{*{20}c} {\mathbf{R }^{E}} &{} {\mathbf{e }_{21} } \\ {\mathbf{e }_{12}^{\mathrm{T}} } &{} {-\in _{12} } \\ \end{array} }} \right] ,\quad \mathbf{T }=\left[ {{\begin{array}{*{20}c} {\mathbf{T }^{E}} &{} {\mathbf{e }_{22} } \\ {\mathbf{e }_{22}^{\mathrm{T}} } &{} {-\in _{22} } \\ \end{array} }} \right] , \end{aligned}$$
(7)
$$\begin{aligned} (\mathbf{Q }^{E})_{ik} =C_{i1k1} ,(\mathbf{R }^{E})_{ik} =C_{i1k2} , (\mathbf{T }^{E})_{ik} =C_{i2k2} , (\mathbf{e }_{ij} )_{m} =e_{ijm} . \end{aligned}$$
(8)

In addition, the extended stress function vector \({\varvec{\upvarphi }}\) is defined in terms of the stresses and electric displacements as follows

$$\begin{aligned} \begin{array}{l} \sigma _{i1} =-\varphi _{i,2} ,\quad \sigma _{i2} =\varphi _{i,1} ,\quad i=1,2,3; \\ D_{1} =-\varphi _{4,2} ,\quad D_{2} =\varphi _{4,1} . \\ \end{array} \end{aligned}$$
(9)

The two matrices A and B satisfy the following orthogonality relations

$$\begin{aligned} \begin{array}{l} \mathbf{B }^{\mathrm{T}}\mathbf{A }+\mathbf{A }^{\mathrm{T}}\mathbf{B }=\mathbf{I }={{\bar{\mathbf{B }}}}^{\mathrm{T}}{{\bar{\mathbf{A }}}}+{{\bar{\mathbf{A }}}}^{\mathrm{T}}{{\bar{\mathbf{B }}}}, \\ \mathbf{B }^{\mathrm{T}}{{\bar{\mathbf{A }}}}+\mathbf{A }^{\mathrm{T}}{{\bar{\mathbf{B }}}}=\mathbf{0 }={{\bar{\mathbf{B }}}}^{\mathrm{T}}\mathbf{A }+{{\bar{\mathbf{A }}}}^{\mathrm{T}}\mathbf{B }. \\ \end{array} \end{aligned}$$
(10)

Thus, we can introduce the following three \(4\times 4\) real generalized Barnett–Lothe tensors S, H and L [10, 12]

$$\begin{aligned} \mathbf{S }=\text{ i }(2\mathbf{AB }^{\mathrm{T}}-\mathbf{I }), \quad \mathbf{H }=2\text{ i }\mathbf{AA }^{\mathrm{T}},\quad \mathbf{L }=-2\text{ i }\mathbf{BB }^{\mathrm{T}}. \end{aligned}$$
(11)

Furthermore, the two matrices H and L are symmetric but no longer positive definite, while \(\mathbf{SH },\mathbf{LS },\mathbf{H }^{-1}\mathbf{S },\mathbf{SL }^{-1}\) are all skew-symmetric.

The following identities can be proved [10, 12]

$$\begin{aligned} \begin{array}{l} \mathbf{A }<p_{\beta }^{n}>\mathbf{B }^{-1}=\left( {\mathbf{N }_{2}^{(n)} -\mathbf{N }_{1}^{(n)} \mathbf{SL }^{-1}} \right) -\text{ i }\mathbf{N }_{1}^{(n)} \mathbf{L }^{-1}, \\ \mathbf{A }<p_{\beta }^{n}>\mathbf{A }^{-1}=\left( {\mathbf{N }_{1}^{(n)} +\mathbf{N }_{2}^{(n)} \mathbf{S }^{\mathrm{T}}\mathbf{H }^{-1}} \right) +\text{ i }\mathbf{N }_{2}^{(n)} \mathbf{H }^{-1}, \\ \mathbf{B }<p_{\beta }^{n}>\mathbf{B }^{-1}=\left( {(\mathbf{N }_{1}^{(n)} )^{\mathrm{T}}-\mathbf{N }_{3}^{(n)} \mathbf{SL }^{-1}} \right) -\text{ i }\mathbf{N }_{3}^{(n)} \mathbf{L }^{-1}, \\ \mathbf{B }<p_{\beta }^{n} >\mathbf{A }^{-1}=\left( {\mathbf{N }_{3}^{(n)} +(\mathbf{N }_{1}^{(n)} )^{\mathrm{T}}\mathbf{S }^{\mathrm{T}}\mathbf{H }^{-1}} \right) +\text{ i( }\mathbf{N }_{1}^{(n)} )^{\mathrm{T}}\mathbf{H }^{-1}, \\ \end{array} \end{aligned}$$
(12)

where \(< *>\) represents a \(4\times 4\) diagonal matrix in which each component is varied according to the Greek index \(\beta \) (from 1 to 4), n is an integer which can be positive or negative, and

$$\begin{aligned} \mathbf{N }^{n}=\left[ {{\begin{array}{*{20}c} {\mathbf{N }_{1}^{(n)} } &{}\quad {\mathbf{N }_{2}^{(n)} } \\ {\mathbf{N }_{3}^{(n)} } &{}\quad {\left( \mathbf{N }_{1}^{(n)} \right) ^{\mathrm{T}}} \\ \end{array} }} \right] , \end{aligned}$$
(13)

where

$$\begin{aligned} \mathbf{N }_{1}^{(n)} ,\mathbf{N }_{2}^{(n)} ,\mathbf{N }_{3}^{(n)} =\left\{ {{\begin{array}{*{20}l} \mathbf{N }_{1} ,\mathbf{N }_{2} ,\mathbf{N }_{3} &{}\text{ when }\, n=1, \\ \mathbf{I },\mathbf{0 },\mathbf{0 }&{} \text{ when }\,n=0. \\ \end{array} }} \right. \end{aligned}$$
(14)

3 The electroelastic field

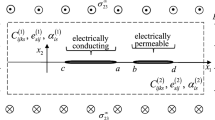
As shown in Fig. 1, we consider an anisotropic piezoelectric solid that occupies the region

$$\begin{aligned} x_{1} \ge -ax_{2}^{2} , a>0, \end{aligned}$$
(15)

the traction-free and charge-free boundary L of which is a parabola described by

$$\begin{aligned} L:x_{1} =-ax_{2}^{2} . \end{aligned}$$
(16)

Introduce the following mappings [9]:

$$\begin{aligned} \begin{array}{l} z_{\beta } =x_{1} +p_{\beta } x_{2} =\omega _{\beta } (\xi _{\beta } )=p_{\beta } \xi _{\beta } -a\xi _{\beta }^{2} , \\ \xi _{\beta } =\omega _{\beta }^{-1} (\xi _{\beta } )=\frac{p_{\beta } }{2a}\left( 1-\sqrt{1-{4az_{\beta } } \big / {p_{\beta }^{2} }} \right) ,\quad \beta =1,2,3,4, \\ \end{array} \end{aligned}$$
(17)

which map the region on the right of the parabola onto the lower half-plane in the \(\xi _{\beta } \)-plane. In addition, \(\xi _{1} =\xi _{2} =\xi _{3} =\xi _{4} =x_{2}\) for \(x_{1} +\text{ i }x_{2} \in L\).

Fig. 1
figure 1

An anisotropic piezoelectric material containing a parabolic cavity with a traction-free and charge-free boundary

Full size image

The traction-free and charge-free (or insulating) boundary conditions on the parabola L can be expressed in terms of the analytic vector function \(\mathbf{f }(z)\) as

$$\begin{aligned} \mathbf{Bf }(z)+{{\bar{\mathbf{B }}}}\overline{\mathbf{f }(z)} =\mathbf{h },x_{1} +\text{ i }x_{2} \in L, \end{aligned}$$
(18)

where h is an arbitrary constant real vector.

By enforcing the traction-free and charge-free conditions on L in Eq. (18) and using the mapping functions in Eq. (17), the analytic vector function \(\mathbf{f }(z)\) is found to take the following simple form:

$$\begin{aligned} \mathbf{f }(z)=-\frac{\text{ i }}{2\sqrt{2\pi a} }<p_{\beta } \sqrt{1-{4az_{\beta } } \big / {p_{\beta }^{2} }} >\mathbf{B }^{-1}\mathbf{k }, \end{aligned}$$
(19)

where

$$\begin{aligned} \mathbf{k }=\left[ {{\begin{array}{*{20}c} {K_{\text{ II }} } &{} {K_{\text{ I }} } &{} {K_{\text{ III }} } &{} {K_{\text{ IV }} } \\ \end{array} }} \right] ^{\mathrm{T}}, \end{aligned}$$
(20)

with \(K_{\text{ I }} ,K_{\text{ II }} ,K_{\text{ III }} \) denoting, respectively, the real-valued mode I, II and III stress intensity factors while \(K_{\text{ IV }} \) represents the real-valued electric displacement intensity factor.

By substituting Eq. (19) in Eq. (2) and making use of Eq. (9), the stresses, electric displacements, displacements and electric potential are distributed in the anisotropic piezoelectric solid with traction-free and charge-free parabolic boundary as follows

$$\begin{aligned} {\varvec{\upsigma }}_{1}= & {} -\frac{\text{1 }}{\sqrt{2\pi } }{\mathrm{Re}}\left\{ {\mathbf{B }<\frac{p_{\beta } }{\sqrt{z_{\beta } -\tfrac{1}{2}\rho p_{\beta }^{2} } }>\mathbf{B }^{-1}} \right\} \mathbf{k }, \end{aligned}$$
(21)
$$\begin{aligned} {\varvec{\upsigma }}_{2}= & {} \frac{\text{1 }}{\sqrt{2\pi } }{\mathrm{Re}}\left\{ {\mathbf{B }<\frac{1}{\sqrt{z_{\beta } -\tfrac{1}{2}\rho p_{\beta }^{2} } }>\mathbf{B }^{-1}} \right\} \mathbf{k }, \end{aligned}$$
(22)
$$\begin{aligned} \mathbf{u }= & {} \sqrt{\frac{2}{\pi }} {\mathrm{Re}}\left\{ {\mathbf{A }<\sqrt{z_{\beta } -\tfrac{1}{2}\rho p_{\beta }^{2} } >\mathbf{B }^{-1}} \right\} \mathbf{k }, \end{aligned}$$
(23)

where \(\rho =1 \big / {(2a)}\) is the radius of curvature at the vertex of the parabola, and

$$\begin{aligned} {\varvec{\upsigma }}_{1} =\left[ {{\begin{array}{*{20}c} {\sigma _{11} } &{} {\sigma _{21} } &{} {\sigma _{31} } &{} {D_{1} } \\ \end{array} }} \right] ^{\mathrm{T}},\quad {\varvec{\upsigma }}_{2} =\left[ {{\begin{array}{*{20}c} {\sigma _{12} } &{} {\sigma _{22} } &{} {\sigma _{32} } &{} {D_{2} } \\ \end{array} }} \right] ^{\mathrm{T}}. \end{aligned}$$
(24)

The \(4\times 4\) diagonal matrices \(<\frac{1}{\sqrt{z_{\beta } -\tfrac{1}{2}\rho p_{\beta }^{2} } }>\) and \(<\sqrt{z_{\beta } -\tfrac{1}{2}\rho p_{\beta }^{2} }>\) appearing in Eqs. (21)–(23) can be further expressed in the following form

$$\begin{aligned} \begin{aligned} \begin{array}{l}< \frac{1}{\sqrt{z_{\beta } -\tfrac{1}{2}\rho p_{\beta }^{2} } }> =< r_{\beta }^{-\tfrac{1}{2}} \text { e}^{-\tfrac{\text { i }\theta _{\beta } }{2}}> =\sum \limits _{n=1}^4 {< p_{\beta }^{n-1}> c_{n} } , \\< \sqrt{z_{\beta } -\tfrac{1}{2}\rho p_{\beta }^{2} }> =< r_{\beta }^{\tfrac{1}{2}} \text { e}^{\tfrac{\text { i }\theta _{\beta } }{2}}> =\sum \limits _{n=1}^4 {< p_{\beta }^{n-1} > d_{n} } , \\ \end{array} \end{aligned}\end{aligned}$$
(25)

where

$$\begin{aligned} r_{\beta }= & {} \left| {z_{\beta } -\tfrac{1}{2}\rho p_{\beta }^{2} } \right| ,\quad \theta _{\beta } =\text{ Arg }\left( z_{\beta } -\tfrac{1}{2}\rho p_{\beta }^{2} \right) , \end{aligned}$$
(26)
$$\begin{aligned} c_{n}= & {} \sum \limits _{m=1}^4 {h_{nm} r_{m}^{-\tfrac{1}{2}} \text{ e}^{-\tfrac{\text{ i }\theta _{m} }{2}}} ,\quad d_{n} =\sum \limits _{m=1}^4 {h_{nm} r_{m}^{\tfrac{1}{2}} \text{ e}^{\tfrac{\text{ i }\theta _{m} }{2}}} , \end{aligned}$$
(27)

with the complex constants \(h_{nm} \) determined by

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {h_{11} } &{} {h_{12} } &{} {h_{13} } &{} {h_{14} } \\ {h_{21} } &{} {h_{22} } &{} {h_{23} } &{} {h_{24} } \\ {h_{31} } &{} {h_{32} } &{} {h_{33} } &{} {h_{34} } \\ {h_{41} } &{} {h_{42} } &{} {h_{43} } &{} {h_{44} } \\ \end{array} }} \right] =\left[ {{\begin{array}{*{20}c} 1 &{} {p_{1} } &{} {p_{1}^{2} } &{} {p_{1}^{3} } \\ 1 &{} {p_{2} } &{} {p_{2}^{2} } &{} {p_{2}^{3} } \\ 1 &{} {p_{3} } &{} {p_{3}^{2} } &{} {p_{3}^{3} } \\ 1 &{} {p_{4} } &{} {p_{4}^{2} } &{} {p_{4}^{3} } \\ \end{array} }} \right] ^{-1}. \end{aligned}$$
(28)

Note that the right-hand side of Eq. (28), which is simply the inverse of a \(4\times 4\) Vandermonde matrix [13], exists when \(p_{1} \ne p_{2} \ne p_{3} \ne p_{4} \). Consequently, by substituting Eq. (25) in Eqs. (21)–(23) and applying the identities in Eq. (12), explicit expressions for the stresses, electric displacements, displacements and electric potential in the piezoelectric material with a parabolic cavity can be obtained as follows

$$\begin{aligned} {\varvec{\upsigma }}_{1}= & {} -\frac{\text{1 }}{\sqrt{2\pi } }\sum \limits _{m=1}^4 {\sum \limits _{n=1}^4 {r_{m}^{-\tfrac{1}{2}} \left[ {\begin{array}{l} \left[ {{h}'_{nm} \left( {(\mathbf{N }_{1}^{(n)} )^{\mathrm{T}}-\mathbf{N }_{3}^{(n)} \mathbf{SL }^{-1}} \right) +{h}''_{nm} \mathbf{N }_{3}^{(n)} \mathbf{L }^{-1}} \right] \mathbf{k }\cos \frac{\theta _{m} }{2} \\ +\left[ {{h}''_{nm} \left( {(\mathbf{N }_{1}^{(n)} )^{\mathrm{T}}-\mathbf{N }_{3}^{(n)} \mathbf{SL }^{-1}} \right) -{h}'_{nm} \mathbf{N }_{3}^{(n)} \mathbf{L }^{-1}} \right] \mathbf{k }\sin \frac{\theta _{m} }{2} \\ \end{array}} \right] } } , \end{aligned}$$
(29)
$$\begin{aligned} {\varvec{\upsigma }}_{2}= & {} \frac{\text{1 }}{\sqrt{2\pi } }\sum \limits _{m=1}^4 {\sum \limits _{n=1}^4 {r_{m}^{-\tfrac{1}{2}} \left[ {\begin{array}{l} \left[ {{h}'_{nm} \left( {(\mathbf{N }_{1}^{(n-1)} )^{\mathrm{T}}-\mathbf{N }_{3}^{(n-1)} \mathbf{SL }^{-1}} \right) +{h}''_{nm} \mathbf{N }_{3}^{(n-1)} \mathbf{L }^{-1}} \right] \mathbf{k }\cos \frac{\theta _{m} }{2} \\ +\left[ {{h}''_{nm} \left( {(\mathbf{N }_{1}^{(n-1)} )^{\mathrm{T}}-\mathbf{N }_{3}^{(n-1)} \mathbf{SL }^{-1}} \right) -{h}'_{nm} \mathbf{N }_{3}^{(n-1)} \mathbf{L }^{-1}} \right] \mathbf{k }\sin \frac{\theta _{m} }{2} \\ \end{array}} \right] } } , \end{aligned}$$
(30)
$$\begin{aligned} \mathbf{u }= & {} \sqrt{\frac{2}{\pi }} \sum \limits _{m=1}^4 {\sum \limits _{n=1}^4 {r_{m}^{\tfrac{1}{2}} \left[ {\begin{array}{l} \left[ {{h}'_{nm} \left( {\mathbf{N }_{2}^{(n-1)} -\mathbf{N }_{1}^{(n-1)} \mathbf{SL }^{-1}} \right) +{h}''_{nm} \mathbf{N }_{1}^{(n-1)} \mathbf{L }^{-1}} \right] \mathbf{k }\cos \frac{\theta _{m} }{2} \\ +\left[ {{h}'_{nm} \mathbf{N }_{1}^{(n-1)} \mathbf{L }^{-1}-{h}''_{nm} \left( {\mathbf{N }_{2}^{(n-1)} -\mathbf{N }_{1}^{(n-1)} \mathbf{SL }^{-1}} \right) } \right] \mathbf{k }\sin \frac{\theta _{m} }{2} \\ \end{array}} \right] } } , \end{aligned}$$
(31)

where \({h}'_{nm} \) and \({h}''_{nm} \) are, respectively, the real and imaginary parts of \(h_{nm} \). We can see from the above analysis that in order to obtain the full-field electroelastic field for a blunt crack, it is still necessary to determine the four distinct Stroh eigenvalues \(p_{1} ,p_{2} ,p_{3} ,p_{4} \) with positive imaginary parts by solving the eigenvalue problem in Eq. (4).

In particular, at the vertex of the parabola, we have the following real form expressions

$$\begin{aligned} {\varvec{\upsigma }}_{1} =\mathbf{0 },\quad {\varvec{\upsigma }}_{2} =\frac{1}{\sqrt{\pi \rho } }\mathbf{N }_{3}^{(-1)} \mathbf{L }^{-1}\mathbf{k },\quad {\varvec{\upvarepsilon }}_{1} =\frac{1}{\sqrt{\pi \rho } }\mathbf{N }_{1}^{(-1)} \mathbf{L }^{-1}\mathbf{k },\quad {\varvec{\upvarepsilon }}_{2} =\frac{1}{\sqrt{\pi \rho } }\mathbf{L }^{-1}\mathbf{k }, \end{aligned}$$
(32)

where

$$\begin{aligned} {\varvec{\upvarepsilon }}_{1} =\left[ {{\begin{array}{*{20}c} {\varepsilon _{11} }, &{} {\varepsilon _{12} +\varpi }, &{} {2\varepsilon _{31}}, &{} {-E_{1} } \\ \end{array} }} \right] ^{\mathrm{T}},\quad {\varvec{\upvarepsilon }}_{2} =\left[ {{\begin{array}{*{20}c} {\varepsilon _{12} -\varpi }, &{} {\varepsilon _{22} }, &{} {2\varepsilon _{32} }, &{} {-E_{2} } \\ \end{array} }} \right] ^{\mathrm{T}}, \end{aligned}$$
(33)

with \(\varepsilon _{ij} \) being the strains, \(E_{i} \) the electric fields and \(\varpi =\tfrac{1}{2}(u_{2,1} -u_{1,2} )\) the rigid-body rotation.

In Eq. (32), \(\mathbf{N }_{1}^{(-1)} \) and \(\mathbf{N }_{3}^{(-1)} \) can be expressed in terms of the reduced generalized compliances [14] while the generalized Barnett–Lothe tensor L can be computed directly from the electroelastic constants via an integral formalism without solving the eigenvalue problem in Eq. (4) [10]. Thus, Eq. (32) is valid for any mathematically degenerate materials. It is seen from Eq. (32) that the field intensity factors can be obtained once the electroelastic field at the vertex of the parabola is known.

4 Conclusions

We have derived full-field explicit expressions describing the electroelastic field in an anisotropic piezoelectric solid weakened by a blunt crack here described by a parabolic cavity with traction-free and charge-free boundary. These expressions are valid not only in the region very close to the tip of the blunt crack (as in [8] in the case of an isotropic elastic material) but, in fact, everywhere in the piezoelectric solid. A real form solution of the electroelastic field at the vertex of the parabola valid for mathematically degenerate materials is obtained in Eq. (32). Using a variation of the Stroh octet formalism [5, 10, 14], we can similarly derive the complete solution for an anisotropic piezoelectric solid with traction-free and conducting parabolic boundary.