1 Introduction

The Blended Wing Body (BWB) represents an innovative and unconventional aircraft layout. Its potential to revolutionize fuel consumption rate and aerodynamic efficiency positions BWB civil aircraft as the leading candidates to replace traditional tubular fuselage designs (Liebeck 2004; Chakraborty and Mavris 2017; Flansburg 2017; Arend, et al. 2017; Gern 2013; Min, et al. 2018; Corman et al. 2018; Mukhopadhyay et al. 2018; Kashiwagura and Shimoyama 2018). However, its non-circular sectional fuselage introduces unique challenges, particularly in handling the stress induced by cabin pressurization loads, exacerbated by bending moments from both the wing and fuselage (Mukhopadhyay 2012; Liebeck 2003). Faced with serious strength challenges, the National Aeronautics and Space Administration (NASA) and Boeing jointly proposed the Pultruded Rod Stitched Efficient Unitized Structure (PRSEUS). This initiative aims to leverage the mechanical properties of PRSEUS, such as high tensile and compressive strengths, significant stiffness and stability margins, and superior load-bearing efficiency (Wu et al. 2013). As illustrated in Fig. 1, the geometric structure of the PRSEUS panel consists of dry woven materials, pre-hardened rods, and foam core materials (Przekop 2012; Velicki and Jegley 2011; Papapetrou et al. 2016; Li and Velicki 2008).

Fig. 1
figure 1

PRSEUS structure

Full size image

Numerous studies have delved into the optimization of BWB aircraft. Qin et al. (2004) investigated the aerodynamic characteristics of the BWB layout based on existing models and completed the design optimization. Hansen and Horst (2008) proposed a two-stage optimization strategy for typical parts of the BWB aircraft fuselage structure. Meanwhile, they explored the design optimization of single-layer, double-layer, and sandwich structures under multiple load and constraint conditions. Mukhopadhyay (2014) analyzed finite element models to assess the effects of skin thickness, stringer spacing, and frame spacing on the fuselage deflection, stress distribution, and structural mass in BWB aircraft. Furthermore, Mukhopadhyay (2012) introduced six fuselage structural configurations in BWB aircraft to identify the lightest mid-fuselage configuration. Qian and Alonso (2018), utilizing high-precision optimization methods, reduced the ratio of the primary structural mass to the maximum takeoff mass. Subsequently, they incorporated buckling constraints into the optimization framework (Qian and Alonso 2021). Li (2015) applied a global–local calibration method to optimize the BWB entire aircraft structure, significantly reducing its mass. Zhu et al. (2019a) proposed a “global–local” structural optimization strategy for BWB airliners. Their case study revealed heightened optimization efficiency, particularly advantageous in the conceptual design stage. Xiao et al. (2019) established a comprehensive platform for analyzing and optimizing overall parameters of BWB civil aircrafts, investigated its overall design scheme through multi-disciplinary as well as single- and multi-objective approaches, resulting in valuable achievements. Quinlan and Gern (2016) used the BWB conceptual design and structural optimization program (HCDstruct) for structural optimization of medium-fidelity whole-machine with various BWB conceptual schemes, facilitating comprehensive mass assessment of conceptual schemes. Singh et al. (2016) applied topology optimization techniques to the layout design of BWB aircraft, yielding a rational structural layout for BWB airliners.

However, the aforementioned studies did not encompass vibration design constraints, and our literature review indicates a gap in research on the overall structural optimization of BWB civil aircraft that targets modal constraints. In the context of practical aircraft structural design, incorporating modal constraints in structural optimization is essential. It is crucial to recognize that optimal structural designs obtained without considering vibration may exhibit substantial discrepancies compared to designs that incorporate vibration considerations. Accordingly, this study proposed a dual-loop optimization strategy that considers the vibration impact on the BWB civil aircraft and balances both static mechanical and vibration performance. The optimization strategies proposed in this study can offer a reference for designers and researchers in related fields.

2 Finite element model analysis of BWB civil aircraft

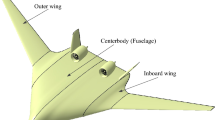
Northwestern Polytechnical University (NPU) proposed a BWB passenger aircraft scheme, known as NPU-330 (Chen et al. 2019). The aerodynamic shape of the BWB civil aircraft is depicted in Fig. 2, and its scaled-down model is illustrated in Fig. 3. Extensive high and low-speed tests were conducted in an industrial-grade wind tunnel, accompanied by thorough reviews and validations for both low- and high-speed designs. Taking the BWB civil aircraft as a case study, this study focuses on the structural design optimization. The maximum takeoff mass of the BWB civil aircraft is 210 tons, with a range of 13,000 km, as outlined in Table 1.

Fig. 2
figure 2

Aerodynamic shape of the BWB civil aircraft

Full size image
Fig. 3
figure 3

Scale-down model of the BWB civil aircraft

Full size image
Table 1 Key parameters of BWB civil aircraft
Full size table

The BWB aircraft employs specific methods for mass prediction (Zhu et al. 2019b), as displayed in Table 2.

Table 2 Mass prediction of BWB civil aircraft
Full size table

2.1 Mesh model

The aircraft structure was designed using CATIA V5R18, as given in Fig. 4. After that, BWB civil aircraft structure was divided into mesh (Tables 3, 4), with a mesh size of 50 mm and type as quads.

Fig. 4
figure 4

CATIA model of the BWB civil aircraft

Full size image
Table 3 Structural unit type for the BWB civil aircraft
Full size table
Table 4 Structural unit type for the PRSEUS
Full size table

Convergence study was conducted, specifically targeting the wing, the most load-bearing and deformation-prone region of the BWB civil aircraft structure. The analysis employed finite element models with mesh sizes of 40 mm, 50 mm, 60 mm, 70 mm, 80 mm, 120 mm, 130 mm, 140 mm, 160 mm, and 200 mm. The results, presented in the Table 5, reveal that while the wing's deformation remains largely unaffected by mesh size variation, its Mises equivalent stress and Tsai–Wu failure factor show considerable sensitivity to changes in mesh size.

Table 5 Finite element convergence study
Full size table

Figures 5, 6, 7, and 8 demonstrate the results of our finite element convergence study. The study shows that with an increasing number of elements, both the maximum Mises equivalent stress and the Tsai–Wu failure factor initially increase rapidly, then stabilize after reaching the convergence threshold. The converged mesh size was 120 mm, comprising 31,079 elements, and mesh sizes less than 120 mm satisfy the numerical accuracy criteria.

Fig. 5
figure 5

Convergence study using the Mises equivalent stress (elements number)

Full size image
Fig. 6
figure 6

Convergence study using the Mises equivalent stress (mesh size)

Full size image
Fig. 7
figure 7

Convergence study using the Tsai–Wu failure factor (elements number)

Full size image
Fig. 8
figure 8

Convergence study using the Tsai–Wu failure factor (mesh size)

Full size image

Figures 9 and 10 demonstrate the entire structure and the internal structure of the aircraft, respectively. The overall BWB aircraft structure primarily consists of skin, frames, stringers, partitions (the component separation surfaces between various fuselage sections and separation surfaces that subdivide the middle fuselage into distinct compartments), floors, wing ribs, and wing beams. The PRSEUS structure comprises straps, stacks, and pultruded rods. For the BWB aircraft, many parts, including upper and lower skin, component stacks, component flanges, component straps, floors, partitions, wing ribs, and wing beams, are composed of AS4 carbon fiber composite laminates (Wang et al. 2012). Among them, the 0° fibers of the stringer stacks, stringer flange, and stringer straps composite laminates are parallel to the direction of the stringer. In contrast, those of the skin, floor, frame stacks, frame flange, and frame straps composite laminates are parallel to the direction of the frames. In addition, the 0° fibers of the fuselage partition composite laminate exhibit parallel direction with the global coordinate system Y-axis. Besides, the 0° fibers of partition and wing rib composite laminate and those of wing beam composite laminate are parallel to the X-axis and Z-axis of the global coordinate system, respectively. The stringer pultruded rods are made of T800 carbon fiber and 3900-2B resin (Wang et al. 2012), and the foam core of the frames is fabricated of Rohacell foam (Wang et al. 2012). The composite material properties of the BWB aircraft are listed in Tables 6 and 7, respectively.

Fig. 9
figure 9

Mesh model of the BWB civil aircraft

Full size image
Fig. 10
figure 10

Internal structure of the mesh model for the BWB civil aircraft

Full size image
Table 6 Composite material properties
Full size table
Table 7 Material properties of pultruded rod and foam core
Full size table

The BWB civil aircraft PRSEUS structure is shown as in Fig. 11. The stringer is connected to the frames in a shared-node fashion. One-way carbon fiber pultruded rods are installed on top of the stringer. Since the pultruded rods are simplified as beam elements with circular cross-sections, it is not possible to simulate their composite material stack. We have determined the equivalent elastic modulus of the pultruded rods based on previous research (Yj et al. 2024). The flanges at bottom of the stingers, along with the straps, are stitched and connected to the skin. The frames are perpendicular to the stringers, consisting of a foam core and a composite stack. Similar to the stingers, flanges of the frames are also stitched with the straps to the skin, forming an out-of-plane reinforcement structure.

Fig. 11
figure 11

PRSEUS structure of the BWB civil aircraft

Full size image

Currently, some traditional metal materials still have certain market although the composite materials are increasingly applied in aircraft structures. In the BWB civil aircraft, the traditional metal materials are adopted in reinforcement frames of fuselage, the leading and trailing edge skins of the wings, and other areas with stress concentrations to enhance strength. Generally, 7075 aluminum alloy is employed in aircraft structures, and its primary parameters are provided in Table 8.

Table 8 Primary parameters of 7075 aluminum alloy
Full size table

The structural symmetry of a half-model finite element representation enables its application in mechanical analysis of the BWB civil aircraft, with a total of 1,076,039 nodes and 1,233,271 elements.

2.2 Structural analysis

The extreme loads for aircraft follow the provision in Airworthiness Standards for Transport Category Airplanes under the U.S. Federal Aviation Regulations FAR-25 (Federal Aviation Administration, FAA 2018). For BWB aircraft, over 80 load conditions are essential for evaluation and analysis to determine the specific load scenarios. In this study, the extreme load conditions under a 2.5 g overload in pitch maneuver with an added 1.5 times safety factor was selected for the aircraft to validate its performance under extreme situations. Meanwhile, this work checked the full aircraft strength and stiffness and optimize the structural design of the aircraft.

As shown in Fig. 12, to assess the impacts of external loads on the BWB civil aircraft structure, three translational degrees of freedom were constrained on the symmetry plane. This analysis necessitates the application of location-specific distributed loads on the structure. In this section, pressure distributions on the wing and tail, derived from fluid analysis, are mapped onto the airplane using coordinate systems. Aerodynamic loads on the fuselage are assigned to its structural mesh nodes and this is accomplished by automatically correlating the aerodynamic mesh nodes with the corresponding structural mesh nodes' numbers and coordinates.

Fig. 12
figure 12

Aerodynamic load

Full size image

The load includes not only the airplane's self-weight but also the fuel weight, which is segmented into three components: the left and right wing tanks, and the fuselage tank. As depicted in Fig. 13, the fuel volumes in the left and right wing tanks (A1 and A2) amount to 23 tons each, while the fuselage tank (B1) contains 30 tons. The total fuel volume reaches 76 tons. For the semi-modeled aircraft, the fuel volume is 38 tons. Additionally, a safety factor of 1.5 has been applied to all loads.

Fig. 13
figure 13

BWB civil aircraft fuel tank location

Full size image

A primary objective in aircraft design is the reduction of external atmospheric pressure's impact on cabin pressure. In this study, the pressurization load corresponds to a pressure differential of 0.0633 MPa between the interior and exterior of the fuselage at 2000 m altitude. As shown in Fig. 14, for the BWB civil aircraft's structural model, an internal pressure representing double this differential, 0.1266 MPa, is applied.

Fig. 14
figure 14

Pressurization load

Full size image
$$\Delta P={P}_{0}{-P}_{0}\times {\left(1-\frac{{H}_{\text{P}}}{\text{44,300}}\right)}^{5.256}=0.0633\,\text{MPa},$$
(1)
$$P=2\Delta P=0.1266\,\text{MPa}.$$
(2)

In the formula, \({P}_{0}\) represents the standard atmospheric pressure; \({H}_{\text{P}}\) denotes the flight altitude; \(\Delta P\) is the operational load; \(P\) is the design load used for analysis.

The Tsai–Wu failure criterion is a valuable tool for accounting for the difference in tensile and compressive performance of carbon fiber composites and its relationship with their failure strengths. As expressed in Eqs. 3 and 4, the Tsai–Wu failure criterion posits that the material failure occurs when the stress component in the primary laminate direction meets the failure criterion. In this study, the Tsai–Wu failure criterion was employed to check the static strength of the BWB civil aircraft structure, and the involved strength values of the composite materials are presented in Table 9.

Table 9 Strength values of composite materials (Velickia and Barajaj, damage arresting composite for shaped vehicle-final report1. 2009)
Full size table
$${F}_{1}{\sigma }_{1}+{F}_{2}{\sigma }_{2}+{F}_{11}{\sigma }_{1}^{2}+{F}_{22}{\sigma }_{2}^{2}+{F}_{66}{\sigma }_{6}^{2}+{2F}_{12}{\sigma }_{1}{\sigma }_{2}=1,$$
(3)
$$\left\{\begin{array}{c}{F}_{1}=\frac{1}{{X}_{\text{t}}}+\frac{1}{{X}_{\text{c}}},\\ {F}_{2}=\frac{1}{{Y}_{\text{t}}}+\frac{1}{{Y}_{\text{c}}},\\ {F}_{11}=-\frac{1}{{X}_{\text{t}}{X}_{\text{c}}},\\ {F}_{22}=-\frac{1}{{Y}_{\text{t}}{Y}_{\text{c}}},\\ {F}_{66}=\frac{1}{{S}_{12}^{2}},\\ {F}_{12}=-\frac{1}{2}\sqrt{{F}_{11}{F}_{22}.}\end{array}\right.$$
(4)

In the equations above, \({\sigma }_{1}\), \({\sigma }_{2}\), and \({\sigma }_{6}\) refer to the longitudinal, transverse, and shear stress, respectively; \({X}_{\text{t}}\) and \({Y}_{\text{t}}\) are the longitudinal and lateral tensile strength, respectively; \({X}_{\text{c}}\) and \({Y}_{\text{c}}\) denote the longitudinal and lateral compressive strength, respectively; and \({S}_{12}\) represents the in-plane shear strength.

Herein, the Tsai–Wu criterion was served as the structural strength failure criterion to assess the strength of the aircraft structure. The strength of the aluminum alloy was checked against allowable values. The numerical results in Fig. 15 demonstrate that the maximum displacement of the BWB aircraft occurs at the wingtip, with the largest displacement in the lift direction being 2884 mm. At this time, half-model of the BWB aircraft is 31,560 mm in wide, and the deformation in the lift direction accounts for approximately 9.14% of the width, meeting the stiffness requirements. Meanwhile, the half-model of the BWB aircraft weighs 32.68 tons, with a total mass of 65.36 tons, which is relatively heavy.

Fig. 15
figure 15

Pre-optimization displacement of the BWB civil aircraft

Full size image

Figure 16 displays the comprehensive stress distribution diagram, while Fig. 17 illustrates the Tsai–Wu failure criterion factor cloud diagram for the BWB civil aircraft structure. As mentioned earlier, the strength of the aluminum alloy is assessed against the strength limit of the alloy, while the evaluation of composite materials relies on the Tsai–Wu failure criterion. Upon examining the stress cloud diagram, it becomes apparent that the stress propagation is continuously distributed, with the central section of the wing leading edge being the primary concentration point of maximum stress. The maximum Mises equivalent stress is 377.4 MPa, which is less than 557.4 MPa, satisfying the strength requirements for the aluminum alloy. Besides, the cloud diagram unveils that the maximum Tsai–Wu failure factor reaches 0.9356, which is below the failure value of 1, thereby meeting the strength requirements of the composite materials. Notably, this maximum failure factor is also located at the wing skin. Consequently, both the evaluations of the metal and non-metal structure for the BWB aircraft point to the necessity for enhancing the strength of the wing section. The BWB aircraft compiles with the requirements for strength, providing significant optimization potential.

Fig. 16
figure 16

Pre-optimization equivalent displacement of the BWB civil aircraft

Full size image
Fig. 17
figure 17

Pre-optimization Tsai–Wu failure factor cloud diagram of the BWB civil aircraft

Full size image

3 Optimization of BWB civil aircraft ensemble of surrogate model

The integration of global optimization algorithms with finite element models is a common approach to address nonlinear engineering optimization. However, global optimization algorithms typically require multiple iterations, and a single finite element model exhibits quite extensive computation time, making the combined use of them computationally intensive. To alleviate this computational burden, the significant role of leveraging surrogate models based on the relationship between optimization indicators and design variables can't be ignored. Considering the inherent highly nonlinear nature of the entire BWB aircraft, the application of global optimization methods based on ensemble of surrogate models can enhance the optimization accuracy and efficiency. To circumvent the limitations of individual surrogate models, this study proposes an innovative design optimization approach for BWB aircraft structure based on the ensemble of surrogate models.

3.1 Sensitivity analysis

This study used a quasi-isotropic laminate, and employed the total thickness of components as the primary design variables. The total thickness represents the sum of the thicknesses of each ply. The finite element analysis results of the BWB aircraft structure mentioned earlier reveal that the strength values in most regions of the aircraft are comfortably distant from the material strength limits. This observation suggests significant strength margins in these areas, highlighting the potential for structural mass optimization. Based on strength values, the aircraft was divided into various regions based on structural characteristics, including sections like skin, frames, and stringers, yielding a total of 202 regions. Furthermore, the Latin Hypercube Sampling method was employed in this study. On one hand, it can ensure a uniform distribution of experimental points in the design space, enhancing the accuracy and realism of the fitting between factors and responses. On the other hand, it can identify the design parameters that significantly impact the overall aircraft structure mass by sampling the levels of 202 design variables and their response values, thus initiating sensitivity analysis of the model.

The upper and lower limits of the variables were defined as [− 50%, 50%]. A series of finite element simulation calculations were carried out with mass serving as the response parameter. By sampling 1000 sets of parameter combinations, the Pareto contribution values for each design variable were obtained, as represented in Fig. 18. It provides a visual depiction of the structural design parameters that significantly impact the aircraft mass (the top 46 based on their Pareto contribution values). Collectively, these top 46 influencing factors contribute to a cumulative Pareto value of 80.03%. Among them, MRFPARTR (the naming rule of the design variables is presented in “Appendix”) emerges as the most influential design parameter, with a Pareto contribution value of 14.03%. Although the impacts of other individual design parameters may not very pronounced, their combined effect on mass is obviously substantial and cannot be ignored. These design parameters will serve as the design variables for the subsequent phases of scheme optimization. In this way, the original 202 design variables were reduced to 46 areas, enhancing the optimization efficiency.

Fig. 18
figure 18

Tsai–Wu failure factor Pareto contribution values of the BWB civil aircraft

Full size image

3.2 Ensemble of surrogate model

Essentially, the surrogate models are to construct a mathematical model using interpolation or fitting techniques to serve as a substitute for complex engineering problems. In this study, the objective is to establish a surrogate model for the BWB aircraft structure that can replace the finite element model for calculations, ultimately enhancing optimization efficiency. The commonly used surrogate models encompass the Kriging model, the Radial Basis Function (RBF) model, and the Polynomial Response Surface (PRS) model. Both the global and local accuracy indicators are typically adopted to validate the accuracy of surrogate models.

Root Mean Square Error (\(\text{RMSE}\)), as a global accuracy indicator, is calculated using Eq. (5). A smaller \(\text{RMSE}\) indicates a higher prediction accuracy of the surrogate model.

$$\text{RMSE}=\sqrt{\frac{\sum_{j=1}^{n}{({a}_{i}-{\widehat{a}}_{i})}^{2}}{n}}.$$
(5)

In the equation above, \({a}_{i}\) is the actual response value of the sample point; \({\widehat{a}}_{i}\) is the predicted value from the surrogate model corresponding to the test sample point; and \(n\) refers to the number of test samples.

The local accuracy indicator is generally represented by the Maximum Absolute Error (\(\text{MAE}\)), as calculated with Eq. (6). The smaller the \(\text{MAE}\), the higher the prediction accuracy of the surrogate model.

$$\text{MAE}=\frac{\text{max}|{a}_{i}-{\widehat{a}}_{i}|}{\text{max}\left({a}_{i}\right)-\text{min}({a}_{i})}.$$
(6)

The ensemble of surrogate model, also known as the weighted average surrogate model, is unique due to utilization of various base functions for distinct types of surrogate models. However, it’s challenging to match a suitable surrogate model for unknown complex engineering problems. Fortunately, the ensemble of surrogate model technique can effectively address this issue. The prediction value \({\hat{y}}_{\text{e}}(x)\) of the ensemble of surrogate model can be expressed as follows:

$${\hat{y}}_{\text{e}}\left(x\right)=\sum_{i=1}^{M} {\omega }_{i}\left(x\right){\hat{y}}_{i}\left({\varvec{x}}\right),$$
(7)

where \({\hat{y}}_{i}(x)\) is the prediction value of the ith individual surrogate model; \({\omega }_{i}(x)\) refers to the weight coefficient of the \(i\)th surrogate model; and \({\sum }_{i=1}^{M} {\omega }_{i}(x)=1\).

To optimize the predictive accuracy of the ensemble of surrogate model, the assignment of weight factors is a critical consideration. Research (Viana et al. 2009) suggests that the selection of weight factors should meet the following two basic principles: (1) the weight factor should be proportional to the accuracy of the corresponding surrogate model; and (2) such selection could avoid poor performance of the approximation model in regions where samples are sparse. The Generalized Mean Square Error (\(\text{GMSE}\)) is often selected to evaluate the cross-validation. The closer the value of \(\text{GMSE}\) is to 0, the better the performance. This study investigated the weight factors based on \(\text{GMSE}\).

$$\text{GMSE}=\frac{1}{n}\sum_{i=1}^{n} {\left[y\left({{\varvec{x}}}_{i}\right)-{\hat{y}}^{\left(-i\right)}\left({x}_{i}\right)\right]}^{2},$$
(8)

where \(y\left({{\varvec{x}}}_{i}\right)\) is the actual response value at \({{\varvec{x}}}_{i}\); \({\hat{y}}^{(-i)}\left({{\varvec{x}}}_{i}\right)\) refers to the predicted response value of the surrogate model constructed using all training sample points except for \(\left({x}_{i},y\left({x}_{i}\right)\right)\); and \(n\) represents the number of training sample points.

The weight factor calculation methods based on GMSE adopted in this study included Inverse Proportional Average Method (Zerpa et al. 2005) (EZ), Heuristic Calculation Method (Goel et al. 2006) (EG), Mean Square Error Minimization Method (Acar and Rais-Rohani 2008) (EA), and Optimal Heuristic Calculation Method (Ye and Pan 2017) (ES).

3.2.1 EZ method

The EZ method stipulates that the weight factor of each surrogate model is inversely proportional to its prediction error, that is, there is a larger weight for the surrogate model with a smaller prediction error.

$${\omega }_{i}=\frac{\frac{1}{{E}_{i}}}{\sum_{j=1}^{M} \frac{1}{{E}_{j}}},$$
(9)
$${E}_{i}=\sqrt{{\text{GMSE}}_{i}}.$$

In the expressions above: \(M\) is the number of surrogate models; \({\text{GMSE}}_{i}\) denotes the \(\text{GMSE}\) value of the \(i\)th surrogate model; and \({E}_{i}\) stands for the square root of \({\text{GMSE}}_{i}\).

3.2.2 EG method

The EG method determines the corresponding weight factors by non-parametrically calculating the global errors of each surrogate model.

$${\omega }_{i}=\frac{{\left({E}_{i}+\alpha {bar{E}}\right)}^{\beta }}{\sum_{j=1}^{M} {\left({E}_{j}+\alpha {bar{E}}\right)}^{\beta }},$$
(10)
$${bar{E}}=\frac{1}{M}{\sum }_{i=1}^{M} {E}_{i}.$$

In the equation: \({bar{E}}\) is the average value of \({E}_{i}\) for all surrogate models; while \(\alpha\) and \(\beta\) represent the significance of \({bar{E}}\) and \({E}_{i}\), respectively, which are usually set as \(\alpha =0.05\) and \(\beta =-1\).

3.2.3 EA method

EA method transforms the calculation of the weight factor into an optimization process to determine the optimal combination of weight factors through iterative searching and optimization algorithms. Its ultimate goal is to assign the weight factors of each surrogate model by minimizing the mean squared error of the ensemble of surrogate model, thereby minimizing the prediction error.

$$\left\{\begin{array}{l}{\text{find}}\,{ \omega }_{i},i=1, 2,\dots ,M,\\ \text{min} {\text{GMSE}}_{\text{e}}=\frac{1}{n}\sum_{i=1}^{n} {\left[y\left({x}_{i}\right)-{\hat{y}}_{\text{e}}\left({\omega }_{i},{\hat{y}}^{(-i)}\left({x}_{i}\right)\right)\right]}^{2},\\ \text{s.t.} \, {\omega }_{i}\ge 0,\sum_{i=1}^{M} {\omega }_{i}=1,\end{array}\right.$$
(11)

In the equation above: \({\hat{y}}_{\text{e}}\left({\omega }_{i},{\hat{y}}^{(-i)}\left({x}_{i}\right)\right)\) is the predicted value of the ensemble of surrogate model constructed using all training sample points except \(\left({x}_{i},y\left({x}_{i}\right)\right)\).

3.2.4 ES method

The unknown parameters α and β for the EG method control the importance of the average and the individual surrogate model, respectively. Smaller values of α and more negative values of β result in higher weight factors assigned to the best surrogate model. The free ability to freely adjust α and β contributes to a higher flexibility of this weight factor calculation method, and reasonable parameter values will help to obtain a high-precision ensemble of surrogate model. In the EG method, the values of α and β are fixed as 0.05 and − 1, respectively. However, using fixed values of α and β may not be adapt to various characteristic engineering problems. Therefore, adjusting α and β becomes crucial for addressing different problems. To tackle this challenge, the ES method optimizes these two parameters as design variables to minimize the GMSE value of the constructed ensemble of surrogate model.

$$\left\{\begin{array}{l}\text{find }\alpha ,\beta ,\alpha <1, \beta <0,\\ \text{min} {\text{GMSE}}_{\text{e}}=\frac{1}{n}\sum_{i=1}^{n} {\left[y\left({x}_{i}\right)-{\hat{y}}_{\text{e}}\left({\omega }_{i},{\hat{y}}^{(-i)}\left({x}_{i}\right)\right)\right]}^{2},\\ \text{s.t.} \, \sum_{i=1}^{M} {\omega }_{i}=1,{E}_{i}+\alpha {bar{E}}>0.\end{array}\right.$$
(12)

After the weight factor of the individual surrogate model was determined, the ensemble of surrogate model was constructed using the following mathematical expression:

$${\hat{y}}_{\text{e}}={\omega }_{\text{Kriging}}\cdot {\hat{y}}_{\text{Kriging}}+{\omega }_{\text{RBF}}\cdot {\hat{y}}_{\text{RBF}}+{\omega }_{\text{PRS}}\cdot {\hat{y}}_{\text{PRS}}.$$
(13)

Both the EA and ES methods employ the Sequential Quadratic Programming (SQP) algorithm for optimization, with the specific parameters detailed in Table 10. Next, the prediction accuracy of three individual surrogate models (e.g., Kriging, RBF, PRS) was compared with that of the four ensemble of surrogate models (EZ, EG, EA, and ES).

Table 10 Input parameters of the SQP algorithm
Full size table

3.3 Comparison of surrogate model accuracy

In this section, the 46 structural partitions mentioned above were selected as design variables. The upper and lower limits for each design variable remain consistent with those specified in the previous section. The maximum Tsai–Wu failure factor from the static analysis of the BWB aircraft structure was served as the response quantity. Generally, collecting training data to construct a surrogate model requires a considerable amount of computational time and resources, as highlighted in prior research (Wang and Shan 2006; Joseph 2016). During the model construction, it aims to extract as much information as possible from limited sample points to improve the model precision. To mitigate the uncertainties in the experimental process and increase the generalizability of the experiment, the Latin Hypercube Sampling method was adopted in this section, generating a total of 1128 training sample points.

Individual surrogate models (Kriging, RBF, and PRS) are constructed using the generated training sample points along with their true objective function values. In the case of the Kriging model, the Gaussian function is determined as the correlation function. For the RBF model, the multi-quadratic function is adopted as the basis function. A quadratic polynomial response surface model is selected as the fundamental framework of the PRS model.

After construction of individual surrogate models, ensemble of surrogate models were trained using the three surrogate models as meta-models. Meanwhile, different weight factor calculation methods were employed to calculate the weight factors for each surrogate model. Table 11 presents the weight factors for the ensemble of surrogate models constructed using the EZ, EG, EA, and ES methods. Remarkably, the RBF model, distinguished by its prediction capability, received the largest weight factor in all four methods. In the EZ and EG methods, the weight factors were distributed according to their predictive capabilities, gradually increasing as the precision of the individual surrogate model improved. The EG method, with given constants \(\alpha = 0.05\) and \(\beta = -1\), constructed an ensemble of surrogate model similar in form to the EZ model, leading to closely aligned weight factors. In contrast, weight factors calculated by the EA method did not exhibit a strict linear relationship with model performance. In the ES method, after optimization, the optimal values for α and β are − 0.05 and − 4.21, respectively, showing varying degrees of reduction compared to the given values. The Kriging, RBF, and PRS ensemble of surrogate models constructed by the ES method possessed the weight factors of 0.035, 0.812, and 0.153, corresponding to the predictive capabilities of the individual surrogate models. The methods for constructing ensemble of surrogate models based on iterative optimization are assimilate toward the individual surrogate model with the best predictive capability, gradually reducing the weight factor of the individual model with poorer predictive accuracy.

Table 11 Weight factors of the ensemble of surrogate models
Full size table

After training, 112 randomly generated test sample points were based to verify the accuracy of the surrogate models. To minimize the random error of the experimental results, 10 repeated experiments were conducted, producing 10 sets of results. The number of training points and test points are based on the values mentioned in reference (Acar 2010). For the seven constructed surrogate models, the \(\text{MAE}\) and \(\text{RMSE}\) were calculated to evaluate the prediction accuracy of each surrogate model. The boxplots of these three indicators are illustrated in Figs. 19 and 20, respectively. The shorter the length of the rectangular box in the boxplot, the denser the data distribution, the less dependence on the experimental design, and the higher stability of the model.

Fig. 19
figure 19

Box plot for \(\text{MAE}\) of models

Full size image
Fig. 20
figure 20

Box plot for \(\text{RMSE}\) of models

Full size image

An examination of the length of the rectangular boxes and the median lines in the figures reveals that all ensemble of surrogate models outperform their individual surrogate models. This demonstrates that the ensemble of surrogate models generally exhibit higher prediction accuracy and greater stability in comparison to individual surrogate models. Among the ensemble of surrogate models, the EZ and EG models possessed very close accuracy, which aligns with the weight factor selection results discussed earlier. The introduction of the \(\overline{E }\) parameter in the EG model improves the optimization stability, resulting in slightly superior predictive accuracy when compared to the EZ model. However, the ES and EA surrogate models show significantly enhanced predictive capabilities than the EZ and EG models. Ensemble of surrogate models constructed through optimization methods consistently outshine their counterparts constructed with given parameters. Notably, the ES surrogate model is superior to all other ensemble of surrogate models. An analysis of the median lines of the rectangular boxes unveils that the ES model outperforms the other three models. Furthermore, an assessment of the lengths of the rectangular boxes indicates that the ES model boasts a relatively shorter box length, signifying the best stability.

The average of the experimental results serves as a valuable metric for characterizing the overall predictive capability of the surrogate model, while the optimal value reflects the highest predictive potential of the model. Table 12 presents the mean and optimal values of \(\text{MAE}\) and \(\text{RMSE}\). The table suggests that among the RBF surrogate model attains the highest prediction accuracy. Among the ensemble of surrogate models, the ES model exhibits the best accuracy. Notably, the error indicators for most ensemble of surrogate models are better in contrast those of their individual surrogate models. The ES model, in particular, achieves higher prediction accuracy in all indicators, and its average \(\text{MAE}\) and \(\text{RMSE}\) value is very close to the optimal value, reinforcing its performance.

Table 12 Mean and optimal values of \(\text{MAE}\) and \(\text{RMSE}\)
Full size table

3.4 Optimization using the ensemble of surrogate model

The optimization involves the 46 regions into which the BWB aircraft structure was divided, and the divided areas exhibit a higher Pareto contribution to the mass. As analyzed previously, the structural strength of the BWB aircraft is sufficient and the upper and lower limits of the design variables are [− 50%, 50%]. The objective function aims to minimize the total mass of the BWB aircraft. However, several constraints that must be satisfied during this process. The Mises equivalent stress within aluminum alloy structure of the BWB aircraft should not exceed 557.4 MPa; the Tsai–Wu failure factor should not surpass 1; and the displacement should not exceed 3156 mm. The mathematical model for the mass optimization of the BWB civil aircraft structure is defined as follows:

$$\left\{\begin{array}{c}\begin{array}{c}\text{Min}W\\ \text{ s.t. }{V}_{i}^{\text{min}}\le {V}_{i}\le {V}_{i}^{\text{max}}\\ {T}_{\text{max}}<1\\ {S}_{\text{max}}<557.4 \,\text{MPa}\end{array}\\ {U}_{\text{max}}<3 156 \,mm.\end{array}\right.$$
(14)

In the formula, \(W\) represents the mass of the BWB civil aircraft structure; \({V}_{i}^{\text{min}}\) and \({V}_{i}^{\text{max}}\) denote the lower and upper limits of the mass design parameters for the BWB civil aircraft structure, respectively set at − 50% and 50% of their initial design values; \({T}_{\text{max}}\) is the maximum Tsai–Wu failure factor of the BWB civil aircraft structure; \({S}_{\text{max}}\) is the maximum Mises equivalent stress of the BWB civil aircraft structure; and \({U}_{\text{max}}\) is the maximum displacement of the BWB civil aircraft structure.

Compared to traditional optimization methods, the Particle Swarm Optimization (PSO) algorithm is more likely to locate the global optima, ensuring greater population diversity and reducing the risk of falling into local optima. In theory, having more particles can expedite the algorithm’s ability to explore the solution space and converge to the global optimum faster.

Taking the maximum Tsai–Wu failure factor as an example, one of the constraints in the optimization of the BWB civil aircraft structure, Fig. 21 illustrates the impact of the MFLSKIN2 and MFUSKIN3 design parameters on the maximum Tsai–Wu failure factor of the BWB civil aircraft structure. The distribution map shows that areas with higher and lower maximum Tsai–Wu failure factors are spread throughout. This indicates that the maximum Tsai–Wu failure factor of the BWB civil aircraft structure does not linearly increase or decrease with changes in the sizes of the two selected design variables, but multiple maximum or minimum values may appear when the two variables reach certain sizes. In other words, the optimization problem of static strength for the BWB civil aircraft structure is a multi-peak and multi-valley problem with multiple optimal (or worst) solutions, and choosing the PSO algorithm helps to avoid results getting trapped in local optima.

Fig. 21
figure 21

Influence of MFUSKIN3 and MFLSKIN2 on the maximum Tsai–Wu failure factor

Full size image

The PSO algorithm was employed in this study to optimize the various components of the BWB aircraft structure after partitioning. The input parameters of this algorithm are provided in Table 13. To ensure a global distribution of particles, the number of particles is set as 1128, and the maximum number of iterations for each particle is the value of 50.

Table 13 Input parameters of the PSO algorithm
Full size table

The optimization results of the seven surrogate models are presented in Table 14. Judging from the actual predicted accuracy, it is evident that the relative errors of the individual surrogate models are above 10%, whereas those for the ensemble of surrogate models are below 10%. Specifically, the relative errors of the EA and ES models are above 5%, while those of the EZ and EG models are below 5%. Regarding the constraint conditions, all three individual surrogate models fail to satisfy the specified constraints. The maximum Tsai–Wu failure factors for all of them exceed the permissible value of 1. In contrast, the ensemble of surrogate models all satisfy the constraints.

Table 14 Optimization results of the severe models
Full size table

The optimization outcomes of the four ensemble of surrogate models reveal that the objective values of the EZ and ES models are 26.64 tons and 26.65 tons, respectively, showing the smallest values. In contrast, the EA model yields the largest objective value, reaching 27.15 tons. Comparison on the applications of various surrogate models in optimizing the BWB structure demonstrates that the ensemble of surrogate models possess the generally higher predictive capability. The weaker predictive capability of individual surrogate models results in their non-compliance with constraints. The EZ and ES models contribute more to achieving satisfactory optimal solutions than the EG and EA models.

In the ensemble of surrogate models, the weight factors for the EZ and EG models are not significantly different, which is reflected in the closely matched optimization results for both models. By leveraging iterative optimization methods to determine the weight factors, the relative errors of the EA and ES methods are small, measuring at 3.73% and 2.68%, respectively, and the ultimately yielded final objective values are 27.15 tons and 26.65 tons. Compared to the EA model, the ES model not only delivers better predictive accuracy but also promotes the search for the optimal solution. Consequently, it can be concluded that using the ES model as a substitute of the finite element model is suitable for the static mechanical optimization of the BWB structure.

The optimization results of the ES model are illustrated in below figures, with Figs. 22, 23, and 24 explicating the Mises equivalent stress, Tsai–Wu failure factor, and displacement after optimization, respectively. The optimization results of the design variables is presented in “Appendix”. After optimization, the aluminum alloy part of the BWB aircraft structure experiences the maximum Mises equivalent stress of 506.4 MPa, which is lower than the allowable stress of 557.4 MPa. Its maximum Tsai–Wu failure factor is 0.9458, which follows within the criteria of 1. Furthermore, BWB aircraft structure displays a maximum displacement of 3031 m, which is less than the constrained 3156 m. In addition, the optimized structure weights 26.65 tons, resulting in a reduction of 18.45% in comparison to the mass before optimization (32.68 tons).

Fig. 22
figure 22

Post-optimization Mises equivalent stress of ES model

Full size image
Fig. 23
figure 23

Post-optimization Tsai–Wu failure factor of ES model

Full size image
Fig. 24
figure 24

Post-optimization displacement of ES model

Full size image

4 Optimization of BWB civil aircraft considering vibration

Resonance presents a safety concern in civil aviation, as effects induced by resonance, such as flutter, can lead to the destruction of an aircraft and result in severe safety incidents. Additionally, resonance can impact passenger comfort during air travel, leading to considerable inconvenience throughout the journey. Modal analysis plays a crucial role in the overall aircraft analysis, as it unveils the inherent frequencies and vibration modes of the aircraft structure, enabling early structural improvements and thus avoiding resonance.

4.1 Surrogate model optimization considering vibration

An optimization model for the BWB civil aircraft considering vibration was established in this study. The first-order structural modal natural frequency of the BWB structure are displayed in Fig. 25. Compared with the literature (Li and Qin 2020), the first-order mode also occurs in the wing of BWB aircraft, with a natural frequency of 1.83 Hz, closely aligning with the results calculated in this study. Therefore, this structural model is used in the subsequent optimization efforts. With the first-order natural frequency as the response parameter, the vibration performance of the BWB civil aircraft was subjected to a sensitivity analysis. In this analysis, the top 45 modal design parameters with a Pareto contribution value totaling 80.12% were selected, as depicted in Fig. 26.

Fig. 25
figure 25

BWB civil aircraft pre-optimization first-order natural frequency

Full size image
Fig. 26
figure 26

Pareto contribution values for the first-order natural frequency of the BWB civil aircraft

Full size image

The optimization for improving vibration performance builds upon the static optimization results. After one round of optimization, the mass of the BWB aircraft structure is sufficiently reduced, but the first-order natural frequency still falls short of the allowable value. Therefore, the primary optimization objective is to maximize the first-order natural frequency of the BWB aircraft. The optimization considering vibration involves two types of design variables: one is associated with vibration performance, and the other pertains to static performance. The design variables for vibration performance comprise the aforementioned 45 partition variables, while those for static performance are the 11 partition variables that overlap between modal and static parameters. The upper and lower limits of the design variables are both set at [− 50%, 50%] to provide sufficient optimization flexibility. The structure must meet several critical constraints related to mass, material strength, deformation, and the first-order natural frequency. These constraints encompass the following. The total mass of the BWB civil aircraft is less than 26.65 tons, the Mises equivalent stress of aluminum alloy is below 557.4 MPa, and the Tsai–Wu failure factor should not exceed 1. In addition, the displacement is limited to less than 3 156 m, and the first-order natural frequency is greater than 1.83 Hz. Given that optimization problem involves a large number of design variables and constraints from different disciplines, this study a dual-loop optimization approach that integrates both vibration and statics considerations by referencing literature (Zhu et al. 2019a). The mathematical model for the modal optimization of the BWB civil aircraft structure is defined as follows:

$$\left\{\begin{array}{c}\begin{array}{c}\text{Min}{F}_{\text{a}}\\ \begin{array}{c}\text{s.t. }{N}_{i}^{\text{min}}\le {N}_{i}\le {N}_{i}^{\text{max}}\\ \text{W }<26.65\, \text{tons}\\ {T}_{\text{max}}<1\\ {S}_{\text{max}}<557.4 \,\text{MPa}\end{array}\\ {U}_{\text{max}}<3 156 \,mm\end{array}\\ {F}_{\text{a}}<1.83\, Hz.\end{array}\right.$$
(15)

In the formula, \({F}_{\text{a}}\) is the first-order natural frequency of the BWB civil aircraft structure; \({N}_{i}^{\text{min}}\) and \({N}_{i}^{\text{max}}\) respectively represent the lower and upper limits of the modal design parameters for the BWB civil aircraft structure, set at − 50% and 50% of their initial design values; \(W\) is the mass of the BWB civil aircraft structure; \({T}_{\text{max}}\) is the maximum Tsai–Wu failure factor of the BWB civil aircraft structure; \({S}_{\text{max}}\) is the maximum Mises equivalent stress of the BWB civil aircraft structure; and \({U}_{\text{max}}\) is the maximum displacement of the BWB civil aircraft structure.

4.2 Dual-loop optimization for vibration and statics

The newly introduced dual-loop strategy for the BWB aircraft structure primarily focuses on optimizing vibration performance. It employs modal and static optimization as its primary and secondary objectives, respectively. The proposed method is illustrated in Fig. 27 and comprises a primary loop and a secondary loop. The primary loop is to find the optimal values of design parameters that maximize the first-order natural frequency of the structure. The secondary loop inputs the optimal values obtained from the primary loop to calculate the Tsai–Wu failure factor, Mises equivalent stress, and displacement. It then feeds back into the primary loop, continuously iterating the design parameters until all response values are within the permissible range. In this manner, this dual-loop approach effectively transforms a complex an optimization problem with numerous variables into a primary and secondary loop optimization problem, effectively turning static strength stiffness issues and modal problems into a dual-loop issue. In the secondary loop, the static performance optimization variables were initially set as the optimal values from a previous round of optimization. The output results easily satisfy the constraint conditions and can be resolved with a relatively low computational cost. Given the minimal computational cost in the secondary loop, the vibration performance in the primary loop can be optimized within a reasonable computational budget.

Fig. 27
figure 27

BWB civil aircraft optimization process

Full size image

The dual-loop optimization strategy is illustrated in Fig. 28. The entire optimization process can be performed automatically. The primary loop focuses on optimizing the vibration performance of the aircraft. 45 Partition variables that significantly influence the first-order natural frequency were sampled, with their upper and lower limits set at [− 50%, 50%]. Furthermore, surrogate models for mass response and modal response were constructed using the Kriging, RBF, and PRS methods, respectively. Based on the results of the error analysis, the surrogate models built using the RBF method demonstrated good predictive capability for each response variable. Consequently, the RBF model was adopted for both mass response and modal response. The optimization objective in this case is to maximize the first-order structural natural frequency, while adhering to specific constraints. These constraints dictate that the total mass of the BWB aircraft structure should be less than 26.65 tons, and the first-order natural frequency should be greater than 1.83 Hz. The design variables of the secondary loop were selected from the 11 structural partitions that overlap between the modal parameters and the static mechanical parameters, with upper and lower limits set at [− 50%, 50%]. The ES ensemble of surrogate model is utilized for the Tsai–Wu failure factor response, stress response, and displacement responses. These design settings in the secondary loop are consistent with the optimized parameters detailed in Sect. 4.3.

Fig. 28
figure 28

Optimization framework

Full size image

The optimization algorithm employs the PSO algorithm. In this study, the number of particles was set to 1081, with other parameters set according to Table 13. The iterative process of optimization, as illustrated in Fig. 29, corresponds to the primary loop in the dual-loop optimization framework. In the figure, solid circles represent feasible solutions, indicating particles distributed throughout the space. Solid triangles symbolize local optimal solutions, signifying the best particles in the same region; while marked solid triangles are global optimal solutions, representing the best particles globally. In addition, solid circles tend to primarily concentrated in the lower left and upper right regions of the diagram, suggesting that feasible solutions gradually converge toward the global optimum as the optimization progresses. To visualize this convergence, local optimal solutions were extracted from the optimization results to plot the curves, with the fitting curve depicting the progression of the first-order natural frequency increasing with the number of iterations. The first-order natural frequency rapidly grows within the first 13 iterations, and experiences a slight fluctuation subsequently. The global optimum is achieved during the 23rd iteration.

Fig. 29
figure 29

Iteration progression of the first-order natural frequency

Full size image

The optimization results of the design variables is presented in “Appendix”. The optimization results after the dual-loop are shown in Figs. 30, 31, 32, and 33. These figures offer insights into displacement (Fig. 30), Mises equivalent stress (Fig. 31), Tsai–Wu failure factor (Fig. 32), and the first-order natural frequency (Fig. 33) of the optimized BWB aircraft structure. It is evident that the wing area bears a relatively large load, resulting in the most significant displacement deformation. Specifically, the wingtip displacement is 3093 m. Additionally, the maximum Mises equivalent stress in the aluminum alloy is 506.4 MPa, the maximum Tsai–Wu failure factor for composite materials is 0.943, and the first-order natural frequency reaches 2.0329 Hz. It is noteworthy that all these values meet the constraints for deformation, stress, Tsai–Wu failure factor, and modal frequency, indicating the successful achievement of design goals.

Fig. 30
figure 30

The post-optimization displacement of the dual-loop

Full size image
Fig. 31
figure 31

The Mises equivalent stress of the dual-loop after optimization

Full size image
Fig. 32
figure 32

Tsai–Wu failure factor of optimized dual-loop

Full size image
Fig. 33
figure 33

The first-order natural frequency of the optimized dual-loop

Full size image

As presented in Table 15, after the dual-loop optimization, the mass, Tsai–Wu failure factor, and stress level of the BWB aircraft structure experience minimal changes. However, the first-order natural frequency has increased to 2.0329 Hz, reflecting an improvement of 17.83%. Such result indicates that the dual-loop optimization for vibration and statics effectively enhance the first-order natural frequency without compromising strength and stiffness or adding mass. After the dual-loop optimization, the BWB civil aircraft structure weights 52.54 tons, with the aircraft structure accounting for 25.02%. Reference data from Chen et al. (2019) indicates that the structural weight factor in this study falls within a reasonable and acceptable range, confirming the accuracy and reliability of the overall optimization results.

Table 15 The optimization results of BWB civil aircraft
Full size table

4.3 Stability analysis

In the optimization process, only strength criteria were employed. However, as Fig. 32 unequivocally illustrates, the wing skin is subjected to substantial compressive loads, potentially resulting in buckling. This section employs a small-scale local model for stability analysis to ascertain whether the BWB civil aircraft structure is prone to buckling.

In static strength analysis, the wing skin is identified as the most critical area and is highly prone to buckling. Figure 34 illustrates that a section of the wing panel, specifically from the area exhibiting the highest Tsai–Wu failure factor, has been chosen to serve as a small-scale local model.

Fig. 34
figure 34

Selection of a small-scale local model

Full size image

Figure 35 displays a wing panel from the BWB civil aircraft structure, measuring 2300 mm in length and 770 mm in width. According to Table 17, the wing skin's minimum thickness post-optimization is 1.96 mm. Utilizing these dimensions, a small-scale local model known as the PRSEUS plate has been developed for buckling analysis. This analysis aims to evaluate whether the PRSEUS plate could experience buckling instability under extreme conditions at its minimal thickness. Additionally, Fig. 35 presents an in-plane displacement of 5.75 mm for the wing panel, which, as derived from the BWB civil aircraft structure’s validation data, will be used as the external load in designing the PRSEUS plate model.

Fig. 35
figure 35

Construction of a small-scale local model

Full size image

Figure 36 illustrates the load boundary conditions for the PRSEUS plate, which consist of: a fixed right boundary, a left boundary that restricts Y-direction translation and all rotational movements, and the application of an 8 mm X-direction displacement load on the left, marginally surpassing the wing panel's in-plane displacement of 5.75 mm. The top and bottom boundaries are constrained, limiting Y-direction translation, all rotational movements, and Z-direction rotational freedom.

Fig. 36
figure 36

Boundaries of a small-scale local model

Full size image

Figure 37 displays the nonlinear buckling response curve of the PRSEUS plate. Analysis of this curve suggests that despite a decrease in structural stiffness under the specified displacement load, there is no significant reduction that impacts the load-bearing performance. Consequently, it can be deduced that no failure has occurred. Additionally, the curve shows the in-plane displacement contour of the PRSEUS plate at an end shortening of 5.75 mm.

Fig. 37
figure 37

End shortening and load curve of PRSEUS plate

Full size image

5 Conclusion

This paper focuses on the design optimization strategies for the BWB civil aircraft. The main conclusions are summarized as follows:

  1. (1)

    Seven BWB civil aircraft structural surrogate models were developed using surrogate modeling techniques. Key considerations in constructing these ensemble of surrogate models are highlighted. The EG model, structurally similar to the EZ model, incorporates the \({bar{E}}\) parameter to enhance stability during its construction. This enhancement marginally improves the EG model's predictive capabilities over the EZ model. The EA and ES models, employing iterative optimization methods for weight factor determination, tend to converge toward or diverge from the single surrogate model with the highest or lowest accuracy, respectively. This study analyzes the primary factors influencing the predictive capacity of the ensemble of surrogate models and the principles governing the determination of their weight factors, informing the construction of ensemble of surrogate models in related domains.

  2. (2)

    A comparison of various surrogate models applied in optimizing the structure of BWB civil aircraft reveals that individual surrogate models generally exhibit poor predictive capabilities. In contrast, ensemble of surrogate models tend to show superior prediction accuracy, with the EA and ES models, developed using optimization methods, significantly outperforming the EZ and EG models, which are based on predefined parameters. Notably, the ES model has proven more effective in achieving satisfactory optimal solutions, particularly suitable for the lightweight design of BWB civil aircraft structures. Utilizing the ES model, the mass of the BWB civil aircraft structure was reduced by 18.45%, with a mass coefficient of 25.38%. The application of the ES model in this optimization context offers insights for the optimization of ensemble of surrogate models in related fields.

  3. (3)

    Based on the optimization results of the ES model, the influence of vibration effect on the BWB civil aircraft structure is considered, and a dual-loop optimization strategy that takes into account both vibration and static factors is proposed. In this approach, the primary loop focuses on optimizing modal design parameters, while the secondary loop adjusts static design parameters. Post-optimization, the first-order natural frequency of the BWB civil aircraft structure increased by 17.83%, with its mass constituting 25.02% of the maximum takeoff mass. This dual-loop optimization effectively enhances the first-order natural frequency without compromising the static strength and stiffness or adding to the mass, thereby offering insights for optimization in similar domains.

  4. (4)

    A small segment of the wing skin, identified as the most compressed area in the BWB civil aircraft structure following dual-loop optimization, was chosen as the small-scale local model known as the PRSEUS plate. The conducted stability analysis on this plate revealed that, despite a decrease in structural stiffness under the applied load, there was no significant diminution affecting the load-bearing capacity. Consequently, it is inferred that no damage occurred, thus maintaining the stability of the entire aircraft after optimization. Future studies aim to incorporate stability considerations into the optimization framework, focusing on the synergistic optimization of strength, stability, and modal characteristics.