1 Introduction

Thin-walled structures are often utilized as main load-bearing elements and are subjected to dynamic loads. Since these structures tend to be light and thin for the aim of high performance, serious vibration problems arise, affecting comfort and even bringing catastrophic consequences. One of the effective means of reducing structural vibration is using damping materials on the surface of the structure (Haciyev et al. 2018; Slifka and Whitton 2019; Cao and Zhang 2011). The schematic illustration of viscoelastic composite structure is presented in Fig. 1. Considering that additional damping materials increase the overall mass of the structure and also affect the dynamic performance, it is essential to optimize the design of damping materials for shell structures using topology optimization methods.

Fig. 1
figure 1

The schematic illustration of the viscoelastic composite structure

Full size image

For the sake of getting better structural performance, continuum topology optimization have been widely applied for the initial conceptual design of structures in the last two decades. Bendsøe (1988) studied the problem of optimal material distribution inside the structure. Subsequently, solid isotropic material with penaligation (SIMP) models (Bendsøe 1999; Lin and Yan 2001), bi-directional evolutionary structural optimization (Xie 1993; Huang 2007), independent continuous mapping (Yang and Liu 1999) and level set method (Wang and Wang 2003; Allaire and Jouve 2004) have been developed one after another. With the continuous maturity of optimization methods, the application of topology optimization of damping material in vibration control is researched extensively. Such studies are mainly divided into two categories: (1) dynamic properties purpose, aiming to obtain a large intrinsic/weighted modal loss factor (MLF) (Zheng et al. 2015; Moita and Soares 2013; Xu et al. 2017; Kim et al. 2013); (2) dynamic response purpose, the load form is generally harmonic excitation (Fang and Zheng 2015; Zheng et al. 2016; Takezawa et al. 2016; Zhang and Wang 2018), which can also be extended to transient excitation (Zhao 2016; Lee 2015; Yan and Cheng 2016; Zhang 2014; Yun 2018). In addition to planar plate and shell structures, damping material topology optimization for vibration reduction has also been applied in cylindrical shell structures (Yun 2018; Li et al. 2012).

The above studies mainly focus on the topology optimization of the damped structure subjected to the deterministic excitations. However, many random excitations exist in the real environment, such as earthquake, wind, wave and mechanical vibration disturbances. In order to solve such problems, Lin and Yan (2001) proposed the pseudo excitation method (PEM). In recent years, PEM have been widely applied for structural topology optimization under stationary random excitation with fruitful results. Lin et al. (2011) adopted PEM to optimize a piezoelectric energy device under stationary random vibration. Zhang and Liu (2015) proposed a response solution approach combining PEM and mode acceleration method (MAM) to achieve a better optimized configuration. Guided by the suggestion of calculating the random response of structures, Zhao et al. (2020) studied topology optimization by considering the constraints of dynamic stress responses under stationary random excitations. Meanwhile, Zhu et al. (2017) applied the topology design technology to frame structure subjected to random vibrations. Yang et al. (2017) further optimized the structures subjected to the excitation of random filtered white noise using the SIMP method. However, so far only limited work has focused on the optimal design of damping materials when subjected to random excitation. Fang and Hou (2018) discussed the optimal configuration of CLD treatment for attenuating the root mean square (RMS) of random response.

The aforementioned results are performed under the assumption of stationary random excitation. However, aircraft structures are often subject to non-stationary random excitations. For example, pressure fluctuations in the external turbulent boundary layer can lead to typical non-stationary random vibration. As a result, it is useful and practical to further study the optimal design of damped structures when subjected to non-stationary random excitation to reduce the vibration and noise. In recent years, many achievements have been introduced in the field of structural response and sensitivity analysis. Zhang et al. (2014) developed the PEM-based method to study non-stationary seismic problem. Li et al. (2016, 2017) analyzed the structural non-stationary random response by Karhunen–Loeve expansion. Bremner et al. (2019) reviewed transient statistical energy analysis models for non-stationary noise. Hu et al. (2016) propose a time-domain sensitivity expression of non-stationary random excitation. In addition, Li et al. (2020) developed a explicit method for solving non-stationary stochastic dynamic problems and applied it to the optimal design of damping structures under non-stationary stochastic excitation. Restricted by the computational cost and theoretical complexity, the structural optimization design using additional damping materials to reduce the vibration level under non-stationary random excitation is relatively rare. Especially considering the nonlinear properties of damping materials with frequency and temperature, the problem becomes more complicated. Many researchers (Oh 2008; Shu et al. 2014; Mokhtari et al. 2017) have pointed out that the frequency- and temperature-dependent properties of viscoelastic materials are remarkable for the study of dynamic response and optimal design of viscoelastic composite structures, but they have not received enough attention in the present study.

Inspired by these difficulties, this paper develops a topology design method of the damping material for planar shell structure under non-stationary random excitation, in which the dynamic properties of damping materials are characterized by the GHM model. No previous work has been reported to systematically address such problems. First, the governing equations of viscoelastic composite structures with frequency and temperature effects are established. Then, the PEM transforms the structural non-stationary random response into virtual transient response analysis under deterministic excitation. The HPD method is used to solve the virtual transient response. The average value of the displacement PSD in the specified frequency band and time interval is taken as the dynamic performance index. Sensitivity analysis is performed analytically to obtain gradient information. The optimization process is developed to obtain the optimal configuration of the damped structure to minimize the random response intensity.

The main contents are organized as follows. Section 2 introduces the GHM model to characterize the viscoelastic materials and establishes the governing equation of the three-layer composite structure. Section 3 develops a PEM-HPD-based method to analyze the composite structures under non-stationary random excitation. In Sect. 4, density-based optimization design problem is formulated and sensitivity analysis is performed. Section 5 presents several numerical examples and also further discusses the optimization results. Finally, the major conclusions are provided in Sect. 6.

2 System equation of viscoelastic composite structures

2.1 Finite element modeling

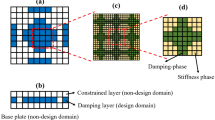
The damping composite structure is discretized by three-layer shell elements in Fig. 2, which respectively denote the base structure, viscoelastic layer and constrained layer. The structural dynamic model is established based on the first shear deformation theory (FSDT), which is well suited for thin and medium thickness plates, also has good predictive capacity and moderate computational times for larger-scale finite element models. An eight-node shell element with five degrees of freedom at each node, called the Serendip element (Zienkiewciz and Taylor 2000), is used in the finite element discretization process. The studies (Souhir et al. 2015) have proven that this element provides excellent performance for modeling constrained damping structures. The finite element nodes are located on the neutral plane of the laminated structure. The neutral axis can be assigned by force balance in the z-axis.

Fig. 2
figure 2

Schematic of the three-layer shell elements

Full size image

The elemental mass and stiffness matrices can be obtained as follows

$$\begin{aligned} \textbf{m}_{{i} }^{e}&=\int _{\Omega _{e} } \rho _{{i} } \textbf{N}^{\textrm{T} } \textbf{N} dV \end{aligned}$$
(1)
$$\begin{aligned} \textbf{k} _{i}^{e}&=\int _{\Omega _{e} } \left( \textbf{B}_{1i} ^\textrm{T} \textbf{D}_i \textbf{B}_{1i} +\textbf{B}_2^\textrm{T} \textbf{D}_i \textbf{B}_2 \right) dV \end{aligned}$$
(2)

where \(i=b,d,c\), respectively, denotes the base structure, viscoelastic layer and constrained layer; \(\textbf{N}\) represent the shape function matrix; \(\rho _i\) is corresponding material density. \({\textbf{D}}\) refers to elastic matrix and \({\textbf{B}}\) is the strain-displacement matrix. dV denotes the elementary volume. Then the composite elemental matrices can be obtained as \(\textbf{m}^e=\textbf{m}_{b}^e+\textbf{m}_{d}^e+\textbf{m}_{c}^e\) and \(\textbf{k}^e=\textbf{k}_{b}^e+\textbf{k}_{d}^e+\textbf{k}_{c}^e\).

Then the corresponding system equations for undamped three-layer structure are shown as

$$\begin{aligned} {\textbf{M}}\ddot{\textbf{y}}+{\textbf{K}}{\textbf{y}}={\textbf{Rf}(t)} \end{aligned}$$
(3)

where \({\textbf{M}}, {\textbf{K}} \in {{\textbf{R}}^{N \times N}}\) respectively denote the global mass and stiffness matrices; \(\textbf{y}\) is the displacements response; \(\textbf{R}\) represents the direction and position of the excitation, composed of 0 or 1; \({\textbf{f}}\in {{\textbf{R}}^{N \times 1}}\) indicates the external load vector.

2.2 GHM viscoelastic approach

The considered three-layer composite damping structure contains a viscoelastic layer in the middle of two elastic layers, thus the overall structure exhibits obvious viscoelastic behavior in addition to elastic behavior. Therefore, the global stiffness matrix can be divided into elastic matrix \({\textbf{K}}_{e}\) and viscoelastic matrix \({\textbf{K}}_{v}(s)\) as shown below.

$$\begin{aligned} {\textbf{K}}={\textbf{K}}_{e}+{\textbf{K}}_{v}(s) \end{aligned}$$
(4)

Then, the frequency-independent constant matrix can be separated from the \({\textbf{K}}_{v}(s)\), and the viscoelastic stiffness matrix is written as the multiplication of the constant matrix \(\overline{\textbf{K}}_{v}\) with the frequency-dependent modulus G(s), as follows

$$\begin{aligned} {\textbf{K}}_{v}(s)=G(s)\overline{\textbf{K}}_{v} \end{aligned}$$
(5)

Therefore, by Laplace transforms at both sides of Eq. (3) and substituting Eqs. (4) and (5), the system equation in Laplace domain can be obtained

$$\begin{aligned} \left( s^{2}\textbf{M} + \textbf{K}_e+sG\left( s \right) \overline{\textbf{K}} _v \right) \textbf{y} \left( s \right) =\textbf{Rf} \left( s \right) \end{aligned}$$
(6)

Golla (1985), Mctavish (1993) described the frequency-dependent modulus G(s) as:

$$\begin{aligned} G(s)=G_{0}\left( 1+\sum _{i=1}^{N_{G}} \alpha _{i} \frac{s^{2}+2 \zeta _{i} \omega _{i} s}{s^{2}+2 \zeta _{i} \omega _{i} s+\omega _{i}^{2}}\right) \end{aligned}$$
(7)

where the constant factor \({G_0}\) is the steady-state value, and the constants \({\alpha _i}\), \({\zeta _i}\) and \({\omega _i}\) are decided by the measurements of G(s). The \(N_G\) denotes the number of mini-oscillator terms.

Substitute Eqs. (7) into (6) and introduce dissipative coordinates

$$\begin{aligned} {\textbf{z}}\left( s \right) = \frac{{{{\omega }^2}}}{{{s^2} + 2 \zeta \omega s + {{\omega }^2}}}{\textbf{y}} (s) \end{aligned}$$
(8)

Then the time-domain governing equation of the damping composite structure can be obtained by Laplace inverse transformation

$$\begin{aligned} {\textbf{M}}_G\ddot{\textbf{Y}}+{\textbf{D}}_G\dot{\textbf{Y}}+{\textbf{K}}_G{\textbf{Y}}={\textbf{RF}}(t) \end{aligned}$$
(9)

with

$$\begin{aligned} \begin{aligned}&\textbf{M}_G =\begin{bmatrix} \textbf{M} &{} 0 \\ 0 &{} \frac{\alpha _{N_{G} } }{\omega ^{2} _{N_{G} } } \mathbf {\bar{K}} _{v} \end{bmatrix}, \quad \textbf{K}_G =\begin{bmatrix} \textbf{K}_e + (1+\alpha _{N_{G} })\mathbf {\bar{K}} _{v} &{} -\alpha _{N_{G} } \mathbf {\bar{K}} _{v} \\ -\alpha _{N_{G} } \mathbf {\bar{K}} _{v} &{} \alpha _{N_{G} } \mathbf {\bar{K}} _{v} \end{bmatrix}, \quad \\&\textbf{D}_G=\begin{bmatrix} 0 &{} 0 \\ 0 &{} \frac{2\alpha _{N_{G} } \zeta _{N_G} }{\omega _{N_{G} } } \mathbf {\bar{K}} _{v} \end{bmatrix}, \quad \textbf{Y}=\begin{Bmatrix} \textbf{y} \\ \textbf{z} \end{Bmatrix} , \quad \textbf{F}(t)=\begin{Bmatrix} \textbf{f}(t) \\ 0 \end{Bmatrix} \end{aligned} \end{aligned}$$
(10)

where \({\textbf{M}}_G\); \({\textbf{D}}_G\) and \({\textbf{K}}_G\) \(\in {\mathbf{{R}}^{n \times n}}\), with \(n=N(1+N_G)\), are the augmented mass, damping and stiffness matrices, respectively. Here only give the system matrices corresponding to the first-order micro-oscillator. The cases of multi-order micro-oscillators can be easily obtained by extension, so it is omitted here for brevity.

Obviously, the GHM model can accurately describe the dynamics characteristics of viscoelastic materials, and it is integrated with the traditional finite element method to establish the second-order linear system equation with constant coefficients.

3 Non-stationary random response analysis of the augmented system equation based on the PEM and HPD methods

In this section, the PEM-based random response of the three-layer viscoelastic structure when subjected to non-stationary random excitation is presented. Generally speaking, due to the complexity of the calculation of the structural random response under such excitation, the non-stationary vibration energy related to the frequency distribution in random vibration is often ignored, thus it can be simplified to uniformly modulated evolution random excitation, expressed as follows

$$\begin{aligned} \textbf{F} \left( t \right)&=\textbf{g} \left( t \right) \textbf{x} \left( t \right) \end{aligned}$$
(11)
$$\begin{aligned} \textbf{g} \left( t \right)&= \begin{bmatrix} g_{1} \left( t \right) &{} &{} &{} \\ &{} g_{2} \left( t \right) &{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} g_{r} \left( t \right) \end{bmatrix} , \textbf{x} \left( t \right) = \begin{bmatrix} x_{1}\left( t \right) \\ x_{2}\left( t \right) \\ \vdots \\ x_{r}\left( t \right) \end{bmatrix} \end{aligned}$$
(12)

where \(g \left( t \right)\) and \(\textbf{g} \left( t \right)\) denote the slowly varying modulation function and matrix; \(x \left( t \right)\) and \(\textbf{x} \left( t \right)\) represent the zero-mean stationary random process and matrix. The PSD matrix \({\textbf{S}}_{xx}(\omega )\) can be written as

$$\begin{aligned} \textbf{S}_{xx}(\omega )=\sum _{j=1}^{r} \kappa _{j} \mathbf {\varphi }^*_{j} \mathbf {\varphi }_{j}^{\textrm{T}}=\sum _{j=1}^{r} \mathbf {\gamma }^*_{j} \mathbf {\gamma }_{j}^{\textrm{T}} \end{aligned}$$
(13)

in which, r denotes the number of random excitations and \(\omega\) represents the excitation frequency. \(\kappa _{j}\) and \(\mathbf {\varphi }_{j}\) denote, respectively, the jth eigenvalue and eigenvector of \({\textbf{S}}_{xx}(\omega )\). The \(\mathbf {\gamma }_{j}\) is defined as \(\gamma _{j} \triangleq \sqrt{\kappa _{j}} \mathbf {\varphi }^*_{j}\).

Then construct the virtual excitation of the following form using eigenvalues and eigenvectors

$$\begin{aligned} \textbf{F} _{j} \left( t \right) =\sqrt{\kappa _{j} } \textbf{g} \left( t \right) \varphi _{j} \textrm{exp} \left( \textrm{i} \omega t \right) \quad j=1,2,\ldots ,r \end{aligned}$$
(14)

Replace Eq. (14) with the external load term of Eq. (9), and obtain

$$\begin{aligned} {\textbf{M}}_G\ddot{\textbf{Y}}_j+{\textbf{D}}_G\dot{\textbf{Y}}_j+{\textbf{K}}_G{\textbf{Y}}_j=\textbf{R}\sqrt{\kappa _{j} } \textbf{g} \left( t \right) \varphi _{j} \textrm{exp} \left( \textrm{i} \omega t \right) \end{aligned}$$
(15)

where \({\textbf{Y}}_j\) denotes the pseudo response corresponding to jth pseudo random excitation. The PEM converts the non-stationary random response analysis in Eq. (9) into the solution process of transient response under deterministic load in Eq. (15).

Considering the introduction of auxiliary dissipative coordinates in the established augmented system equation, the dimension of the system equation is significantly increased. Thus, a common method for reducing the computational cost is to transform the system matrices into the reduced-order modal space, in which the system response can be written as

$$\begin{aligned} \textbf{Y}_{j} =\mathbf \Phi \textbf{u} _{j} \end{aligned}$$
(16)

where \(\textbf{u} _{j}\) is the modal space coordinates. By premultiplicating both sides of Eq. (15) by \(\mathbf \Phi ^\mathrm T\) and substituting Eq. (16), the reduced-order governing equation is shown as follows

$$\begin{aligned} {\textbf{I}}\ddot{\textbf{u}}_j+\overline{\textbf{D}}\dot{\textbf{u}}_j+{\mathbf \Lambda }{\textbf{u}}_j=\mathbf \Phi ^\mathrm T\textbf{R}\sqrt{\kappa _{j} } \textbf{g} \left( t \right) \varphi _{j} \textrm{exp} \left( \textrm{i} \omega t \right) \end{aligned}$$
(17)

where \(\overline{\textbf{D}}=\mathbf \Phi ^\mathrm T \textbf{D}_G \mathbf \Phi\). The response vector \(\textbf{u} _{j}\) can be obtained by using the central difference method and newmark-\(\beta\), to solve Eq. (17).

To avoid the small enough time step required by the traditional algorithm, and further improve the efficiency and accuracy of solving the constructed pseudo transient response, the HPD is employed to obtain the pseudo transient response of Eq. (17).

The HPD integration method follows the introduction of dyadic variables in the Hamiltonian system and makes the associated matrix transformations, which allows the problem of solving the dynamics equations to be transformed into the process of solving differential equations. Therefore, suggested by Zhong and Williams (1994), Eq. (17) can be written as the general form as

$$\begin{aligned} \dot{\textbf{v}} =\textbf{Hv} +\textbf{r} \left( t \right) \end{aligned}$$
(18)

in which

$$\begin{aligned} \begin{aligned}&\textbf{H} = \begin{bmatrix} \textbf{A} &{} \textbf{I} \\ \textbf{B} &{} \textbf{A} \end{bmatrix} , \quad \textbf{v} = \begin{Bmatrix} \textbf{u} _{j} \\ \textbf{q} _{j} \end{Bmatrix} , \quad \textbf{r}\left( t \right) = \begin{Bmatrix} 0 \\ \mathbf {\Phi }^{\textrm{T} } \textbf{R}\sqrt{\kappa _{j} } \textbf{g} \left( t \right) \varphi _{j} \textrm{exp} \left( \textrm{i} \omega t \right) \end{Bmatrix} \\&\textbf{A} =-\mathbf {\overline{D} } /2, \quad \textbf{B} =-\left( \mathbf {\Lambda }-\mathbf {\overline{D} } {\mathbf {\overline{D} }} /4 \right) , \quad \textbf{q} _{j} =\dot{\textbf{u }} _{j}+ \mathbf {\overline{D} }\textbf{u }/2 \end{aligned} \end{aligned}$$
(19)

According to the theory, the general solution of Eq. (18) can be expressed as

$$\begin{aligned} \textbf{v} =\textrm{exp} \left( \textbf{H} t \right) \textbf{v}_{0} +\int _{0}^{t}\textrm{exp}\left( \textbf{H}\left( t-\tau \right) \right) \textbf{r}\left( \tau \right) \textrm{d} \tau \end{aligned}$$
(20)

The numerical discretization of Eq. (20) is carried out, and the time step is set as \(\bigtriangleup t=t_{k+1}-t_k\). One obtains

$$\begin{aligned} \begin{aligned} \textbf{v}_{k+1}&=\textrm{exp} \left( \textbf{H} t_{k+1} \right) \textbf{v}_{0} +\int _{0}^{t_{k+1}}\textrm{exp}\left( \textbf{H}\left( t_{k+1}-\tau \right) \right) \textbf{r}\left( \tau \right) \textrm{d} \tau \\&=\textrm{exp} \left( \textbf{H} {\bigtriangleup t} \right) \left( \textrm{exp} \left( \textbf{H} t_{k} \right) \textbf{v}_{0} +\int _{0}^{t_{k}}\textrm{exp}\left( \textbf{H}\left( t_{k}-\tau \right) \right) \textbf{r}\left( \tau \right) \textrm{d} \tau \right) \\&\quad +\int _{t_{k}}^{t_{k+1}}\textrm{exp}\left( \textbf{H}\left( t_{k+1}-\tau \right) \right) \textbf{r}\left( \tau \right) \textrm{d} \tau \\&=\textbf{T} \textbf{v} _k+ \int _{t_{k}}^{t_{k+1}}\textrm{exp}\left( \textbf{H}\left( t_{k+1}-\tau \right) \right) \textbf{r}\left( \tau \right) \textrm{d} \tau \end{aligned} \end{aligned}$$
(21)

where k denotes the iterations number.

The matrix \(\textbf{T}\) for the first term in Eq. (21) can be expanded by

$$\begin{aligned} \textbf{T} \left( \bigtriangleup t \right) =\textrm{exp} \left( \textbf{H} \times \bigtriangleup t \right) =\left[ \textrm{exp}\left( \textbf{H} \times \bigtriangleup t /b \right) \right] ^{b} = \left[ \textrm{exp}\left( \textbf{H} \times \tau \right) \right] ^{b} =\left[ \textrm{exp}\left( \textbf{H} \times \tau \right) \right] ^{2^{N} } \end{aligned}$$
(22)

When \(b=2^N\) is large enough, \(\tau\) is extremely small. Using the Taylor expansion, one obtain

$$\begin{aligned} \textrm{exp}\left( \textbf{H} \times \tau \right)&=\textbf{I} +\textbf{J} _{0} \approx \textbf{I} +\textbf{H} \times \tau +\left( \textbf{H} \times \tau \right) ^{2}/2!+\left( \textbf{H} \times \tau \right) ^{3}/3! \end{aligned}$$
(23)

substituting Eqs. (23) into (22), we obtain

$$\begin{aligned} \textbf{T}=\left( \textbf{I} +\textbf{J} _{0} \right) ^{2^{N} } =\left( \textbf{I} +\textbf{J} _{iter} \right) ^{2^{N-iter} } \end{aligned}$$
(24)

Since the element value of \(\textbf{J} _{iter}\) is very small relative to the identity matrix \(\textbf{I}\), in order to reduce the rounding error of the computer, the recursive operation of the following form is performed

$$\begin{aligned} for\left( iter=0;iter< N+1;iter++ \right) \textbf{J} _{iter}=2\times \textbf{J} _{iter-1} +\textbf{J} _{iter-1}\times \textbf{J} _{iter-1} \end{aligned}$$
(25)

With little loss of precision, Eq. (24) can be written

$$\begin{aligned} \textbf{T} =\textbf{I} +\textbf{J} _{N} \end{aligned}$$
(26)

The second term in Eq. (21) is a vector integral. Lin et al. (1995) and Shang et al. (2020) adopted the assumption of load linearization in time step to obtain numerical solutions. However, the inverse operation of matrix is inevitable, which is not only computationally expensive, but also has poor numerical stability, and may not exist inverse matrix. Therefore, Newton–Coates formula is utilized here to calculate the vector integral in Eq. (21) by numerical integration to avoid the matrix inversion of non-homogeneous equation.

$$\begin{aligned} \begin{aligned}&\int _{t_{k}}^{t_{k+1}}\textrm{exp}\left( \textbf{H}\left( t_{k+1}-\tau \right) \right) \textbf{r}\left( \tau \right) \textrm{d} \tau \\&=7\textrm{exp}\left( \textbf{H} {\bigtriangleup t} \right) \tau \left( t_{k} \right) + 32\textrm{exp}\left( \textbf{H}\cdot \frac{3}{4} {\bigtriangleup t} \right) \tau \left( t_{k} +\frac{1}{4} {\bigtriangleup t} \right) \\&\quad +12\textrm{exp}\left( \textbf{H}\cdot \frac{1}{2} {\bigtriangleup t} \right) \tau \left( t_{k} +\frac{1}{2} {\bigtriangleup t} \right) \\&\quad +32\textrm{exp}\left( \textbf{H}\cdot \frac{1}{4} {\bigtriangleup t} \right) \tau \left( t_{k} +\frac{3}{4} {\bigtriangleup t} \right) +7\tau \left( t_{k+1} \right) \end{aligned} \end{aligned}$$
(27)

The general solution can be obtained by combining Eqs. (26) and (27) and substituting them into Eq. (21). Then the displacement response of the original space can be obtained by Eq. (16).

4 Topology optimization scheme

In this paper, it is assumed that the base layer and the constrained layer are not involved in the optimization, and only the viscoelastic damping layer sandwiched in the middle is the designable domain. In this optimization model, the density of the core material is the optimization design variable. When the density of the core material is 1, it indicates that the region is covered with the solid core material, and when the density of the core material is 0, it indicates that there is no core material in the region. It should be noted that when the density of all materials in the viscoelastic layer is 0, the constrained layer damping structure is degraded to two elastic layers (i.e., only the base layer and the confining layer). The volume of the damping material is defined as the constraint condition. The topology optimization problem of considered viscoelastic structures under non-stationary random excitations is expressed as

$$\begin{aligned} \begin{aligned} find: \quad&x_{e}, \quad e=1,2, \ldots n \\ min: \quad&c \\ subject \quad to: \quad&{\textbf{M}}_G\ddot{\textbf{Y}}+{\textbf{D}}_G\dot{\textbf{Y}}+{\textbf{K}}_G{\textbf{Y}}={\textbf{RF}}(t) \\&\sum \limits _{e=1}^{n} {{x_e}V_e-{f_v}} \sum \limits _{e=1}^{n} {V_e^0 \le 0} \\&0\le {x_{\min }}\le {x_e}\le 1 \end{aligned} \end{aligned}$$
(28)

where \(x_e\) refers to design variable; n denotes the elements number; \({f_v}\) is the volume fraction; \(V_e^0\) is the eth element volume when \({x_e} = 1\); \({x_{\min }}\) is the minimum value of relative density, with a value of 0.1.

4.1 Objective function

Referring to the work of Shang et al. (2020), in order to be able to measure more comprehensively the vibration suppression performance of the layout scheme of the damping material for a given range of time and frequency, here the objective function c is chosen as the mean value of the displacement PSD of concerned DOFs in the given frequency band \(\left[ \omega _\alpha , \omega _\beta \right]\) and time interval \(\left[ 0 , T \right]\). The calculation formula is as follows:

$$\begin{aligned} c=\frac{1}{m}\frac{1}{T} \frac{1}{\omega _{\beta }- \omega _{\alpha }} \int _{\omega _{\alpha }}^{\omega _{\beta }}\int _{0}^{T}\sum _{i=1}^{m} S_{Y_{i}Y_{i}} \left( \omega ,t \right) \textrm{d} t\textrm{d} \omega \end{aligned}$$
(29)

where \(S_{{Y_i}{Y_i}}(\omega ,t )\) is the displacement PSD of ith DOF and m denotes the number of concerned DOFs. According to the PEM, the displacement PSD can be calculated as:

$$\begin{aligned} S_{{Y_i}{Y_i}}(\omega ,t )=\sum _{j=1}^{r} \left( {Y}_j\right) _i ^*\left( \omega ,t \right) \left( {Y}_j\right) _i ^\textrm{T}\left( \omega ,t \right) \end{aligned}$$
(30)

4.2 Material interpolation model

The well-known SIMP scheme performs well in static optimization of structure, but it has some limitations in configuration design under dynamic load. Since the punished stiffness is a high-order small quantity relative to the mass, local modal problem will be generated in the region with relative density less than 0.01, which is not conducive to the stable progress of optimization iteration. In order to eliminate this influence and obtain a clear design layout, polynomial interpolation scheme (PIS) (Zhu et al. 2010) is adopted as:

$$\begin{aligned} \begin{aligned}&\textbf{M}=\sum _{e=1}^{N_e} \left( \textbf{m}_{b}^e+\left( x_e \right) ^{q} \textbf{m}_{d}^e+\textbf{m}_{c}^e \right) \\&\textbf{K}_e=\sum _{e=1}^{N_e}\left( \textbf{k}_{b}^e+\frac{15\left( x_e \right) ^{p} +x_e }{16} \textbf{k}_{d}^e+\textbf{k}_{c}^e \right) \\&\mathbf {\bar{K}} _{v}=\sum _{e=1}^{N_e}\left( \frac{15\left( x_e \right) ^{p} +x_e }{16} \textbf{k}_{d}^e \right) \end{aligned} \end{aligned}$$
(31)

where \(N_e\) denotes the number of design variables; The penalty parameters p and q penalize the intermediate densities, with values of 3 and 1 respectively in this paper.

4.3 Non-stationary random sensitivity analysis of viscoelastic plate

The sensitivity analysis reflects the sensitivity of the objective function with respect to design variables and provides an efficient search path for structural dynamics optimization design. The time-domain sensitivity analyses of viscoelastic plate when subjected to non-stationary random excitation through direct differential method (DDM) and adjoint variable method (AVM) are derived respectively.

4.3.1 DDM-based sensitivity analysis

By solving the sensitivity of Eq. (29) with respect to the design variable \(x_e\), one obtain

$$\begin{aligned} \frac{\partial c}{\partial x_{e} } =\frac{1}{m}\frac{1}{T} \frac{1}{\omega _{\beta }- \omega _{\alpha }} \int _{\omega _{\alpha }}^{\omega _{\beta }}\int _{0}^{T}\sum _{i=1}^{m}\frac{\partial S_{Y_{i}Y_{i}} \left( \omega ,t \right) }{\partial x_{e} }\textrm{d} t\textrm{d} \omega \end{aligned}$$
(32)

in which \(\frac{\partial S_{Y_{i}Y_{i}} \left( \omega ,t \right) }{\partial x_{e} }\) can be solved by

$$\begin{aligned} \frac{\partial {S}_{{Y_i}{Y_i}}(\omega ,t)}{\partial x_e}=\sum _{j=1}^{r} \left( \frac{\partial \left( { Y}_j \right) _i^*\left( \omega ,t \right) }{\partial x_e} \left( { Y}_j \right) _i^\textrm{T}\left( \omega ,t \right) +\left( {Y}_j \right) _i^*\left( \omega ,t \right) \frac{\partial \left( { Y}_j \right) _i^\textrm{T}\left( \omega ,t \right) }{\partial x_e}\right) \end{aligned}$$
(33)

Thus, the Eq. (32) is equivalent to solve the sensitivity of pseudo transient response. The pseudo response sensitivities \(\frac{\partial \left( {Y}_j \right) _i}{\partial x_e}\) can be obtained

$$\begin{aligned} \frac{\partial \left( {Y}_j \right) _i}{\partial x_{e}}=\frac{\partial \left( \textbf{L}^{\textrm{T}} \textbf{Y}_{j}\right) }{\partial x_{e}}=\textbf{L}^{\textrm{T}} \frac{\partial \textbf{Y}_{j}}{\partial x_{e}} \end{aligned}$$
(34)

where \(\textbf{L}\) is the vector of all terms with 0 except ith DOF being 1.

Differencing Eq. (15) with respect to the design variables \(x_e\), one obtain

$$\begin{aligned} \textbf{M}_G \frac{\partial \ddot{\textbf{Y}}_j }{\partial x_e} + \textbf{D}_G \frac{\partial \dot{\textbf{Y}}_j }{\partial x_e} +\textbf{K}_G \frac{\partial {\textbf{Y}}_j }{\partial x_e}+\frac{\partial \textbf{M}_G }{\partial x_e} \ddot{\textbf{Y}}_j+ \frac{\partial \textbf{D}_G }{\partial x_e} \dot{\textbf{Y}}_j+\frac{\partial \textbf{K}_G }{\partial x_e} {\textbf{Y}}_j -\frac{\partial \textbf{RF}_j }{\partial x_e} =0 \end{aligned}$$
(35)

Considering \(\textbf{RF}_j\) are independent of design variables, so \(\frac{\partial \textbf{RF}_j }{\partial x_e} =0\).

therefore Eq. (35) can be rewritten as

$$\begin{aligned} \textbf{M}_G \ddot{\tilde{\textbf{Y}}}_j+ \textbf{D}_G \dot{\tilde{\textbf{Y}}}_j+\textbf{K}_G {\tilde{\textbf{Y}}}_j=\tilde{\textbf{F}}_j \end{aligned}$$
(36)

with

$$\begin{aligned} {\tilde{\textbf{Y}}}_j=\frac{\partial {\textbf{Y}}_j }{\partial x_e}, \dot{\tilde{\textbf{Y}}}_j=\frac{\partial \dot{\textbf{Y}}_j }{\partial x_e}, \ddot{\tilde{\textbf{Y}}}_j=\frac{\partial \ddot{\textbf{Y}}_j }{\partial x_e}, \tilde{\textbf{F}}_j=-\frac{\partial \textbf{M}_G }{\partial x_e} \ddot{\textbf{Y}}_j- \frac{\partial \textbf{D}_G }{\partial x_e} \dot{\textbf{Y}}_j-\frac{\partial \textbf{K}_G }{\partial x_e} {\textbf{Y}}_j \end{aligned}$$
(37)

Obviously, Eqs. (36) and (15) have exactly the same system matrices, except that the external excitation are different. The partial derivative \(\frac{\partial \textbf{M}_G }{\partial x_e}\), \(\frac{\partial \textbf{D}_G }{\partial x_e}\), \(\frac{\partial \textbf{K}_G }{\partial x_e}\) can be obtained at the element level on the basis of Eq. (31). Then, the same linear transformation can be applied to the reduced-order space for Eq. (36), and the proposed HPD method can be utilized to calculate it. Since Eq. (36) needs to be solved once for each design variable, the efficiency of DDM-based sensitivity analysis decreases sharply as the number of design variables increases.

4.3.2 AVM-based sensitivity analysis

For the topology optimization as the number of design variables is much larger than that of objective functions, a more effective method for sensitivity analysis is developed by constructing a series of adjoint equations.

The integral H from Eq. (29) is defined as follows

$$\begin{aligned} H=\int _{0 }^{T} S_{YY} \left( \omega ,t \right) \textrm{d} t \end{aligned}$$
(38)

By combining Eqs. (15) and (38), the adjoint vector \(\mathbf {\Xi } _{j}\left( j=1,2,\ldots r \right)\) in the time domain is introduced to construct the Lagrangian function L as

$$\begin{aligned} L\left( \textbf{Y} _{1},\ldots \textbf{Y} _{j},\ldots \textbf{Y} _{r} ,\xi _{1},\ldots \xi _{j},\ldots \xi _{r} \right) =H+\sum _{j=1}^{r}\tilde{L} _{j} +\sum _{j=1}^{r}\tilde{L} _{j}^{*} \end{aligned}$$
(39)

with

$$\begin{aligned} \tilde{L} _{j}=\int _{0}^{T} \xi _{j}^{\mathrm T}\left( {\textbf{M}}_G\ddot{\textbf{Y}}_j+{\textbf{D}}_G\dot{\textbf{Y}}_j+{\textbf{K}}_G{\textbf{Y}}_j-\textbf{R}\sqrt{\kappa _{j} } \textbf{g} \left( t \right) \varphi _{j} \textrm{exp} \left( \textrm{i} \omega t \right) \right) \textrm{d} t \end{aligned}$$
(40)

where \(\mathbf {\xi } _{j}\) denotes the corresponding adjoint vector of jth pseudo transient excitation and the superscript \((^{*})\) represents conjugate. Since Eq. (15) always holds at arbitrary time, H is equal to the Lagrange function L.

Differentiating Eq. (39) in regard to design variables \(x_e\) and considering the independence between pseudo transient excitation and design variables, one can be obtained

$$\begin{aligned} \frac{\partial L}{\partial x_{e} } =\sum _{j=1}^{r } \left( \left( D_{j} +D_{j} ^{*} \right) +\left( Q_{j} +\tilde{Q} _{j}\right) +\left( Q_{j} +\tilde{Q} _{j} \right) ^{*} \right) \end{aligned}$$
(41)

with

$$\begin{aligned} D_{j}=\int _{0}^{T}\frac{\partial S_{YY} }{\partial Y_{j} } \frac{\partial Y_{j} }{\partial x_{e} } \textrm{d} t \end{aligned}$$
(42)
$$\begin{aligned} Q_{j}&=\int _{0}^{T} \xi _{j}^{\textrm{T} } \left( \frac{\partial \textbf{M}_G }{\partial x_e} \ddot{\textbf{Y}}_j+ \frac{\partial \textbf{D}_G }{\partial x_e} \dot{\textbf{Y}}_j+\frac{\partial \textbf{K}_G }{\partial x_e} {\textbf{Y}}_j \right) \textrm{d} t \end{aligned}$$
(43)
$$\begin{aligned} \tilde{Q}_{j}&=\int _{0}^{T} \xi _{j}^{\textrm{T} }\left( \textbf{M}_G \frac{\partial \ddot{\textbf{Y}}_j }{\partial x_e} + \textbf{D}_G \frac{\partial \dot{\textbf{Y}}_j }{\partial x_e} +\textbf{K}_G \frac{\partial {\textbf{Y}}_j }{\partial x_e} \right) \textrm{d} t \end{aligned}$$
(44)

Here, integrating \(\tilde{Q}_{j}\) by parts and setting the initial condition to zero, then adding \(D_j\), we can get

$$\begin{aligned} \begin{aligned} D_{j}+\tilde{Q} _{j}= \int _{0}^{T}\left( \frac{\partial S_{YY}}{\partial \textbf{Y}_{j}}+\ddot{\xi }_{j}^{\textrm{T}} \textbf{M}_G-\dot{\xi }_{j}^{\textrm{T}} \textbf{D}_G+\xi _{j}^{\textrm{T}} \textbf{K}_G\right) \frac{\partial \textbf{Y}_{j}}{\partial x_{e}} \mathrm {~d} t-\cdots \\ \left( \dot{\xi }_{j}^{\textrm{T}}(T) \textbf{M}_G-\xi _{j}^{\textrm{T}}(T) \textbf{D}_G\right) \frac{\partial \textbf{Y}_{j}(T)}{\partial x_{e}}+\xi _{j}^{\textrm{T}}(T) \textbf{M}_G \frac{\partial \dot{\textbf{Y}}_{j}(T)}{\partial x_{e}} \end{aligned} \end{aligned}$$
(45)

The adjoint equation can be obtained by making Eq. (45) as zero to eliminate the \(\frac{\partial Y_{j} }{\partial x_{e} }\) term in Eq. (41). Using the variable substitution method, let \(\tau =T_{1} -t\) to transform the original terminal value problem into the initial value problem, as follows

$$\begin{aligned} \left\{ \begin{array}{l} \textbf{M}_G^{\textrm{T}} \frac{\textrm{d}^{2} \bar{\xi } _{j}}{\mathrm {~d} \tau ^{2}}+\textbf{D}_G^{\textrm{T}} \frac{\textrm{d} \bar{\xi }_{j}}{\mathrm {~d} \tau }+\textbf{K}_G^{\textrm{T}}\bar{\xi } _{j} = -\frac{\partial S_{YY}^{\textrm{T}}}{\partial \textbf{Y}_{j}} \\ \bar{\xi }_{j}(0) = 0, \quad \frac{\textrm{d} \bar{\xi } _{j}(0)}{\textrm{d} \tau } = 0 \end{array}\right. \end{aligned}$$
(46)

where \(\bar{\xi }_{j}(\tau )={\xi }_{j}(T-t)\). Clearly, Eq. (46) can be converted to the reduced-order modal space, and then HPD method is employed to solve such equation. Once the adjoint vector \(\mathbf {\Xi } _{j}\) is obtained, Eq. (41) can be simplified to \(\frac{\partial L}{\partial x_{e} } =\sum _{j=1}^{r } \left( Q_{j} + Q_{j} ^{*} \right)\).

Thus, the objective sensitivity is obtained as follows

$$\begin{aligned} \frac{\partial c}{\partial x_{e} } =\frac{1}{m}\frac{1}{T} \frac{1}{\omega _{\beta }- \omega _{\alpha }} \int _{\omega _{\alpha }}^{\omega _{\beta }}\sum _{i=1}^{m}\sum _{j=1}^{r}\left( Q_{j} + Q_{j} ^{*} \right) \textrm{d} \omega \end{aligned}$$
(47)

At discrete frequency and time points, the AVM-based sensitivity analysis depends only on the number of adjoint equations. As a result, sensitivity analysis based on AVM is significantly more efficient than that based on DDM.

Furthermore, regardless of whether the sensitivity analysis method is based on DDM or AVM, the calculation process does not involve calculating the sensitivity of the eigenvalues and eigenvectors of the structure with respect to the design variables, and also avoids the sensitivity solution problem of multiple eigenvalues. It has brought significant improvements in the accuracy and efficiency of sensitivity calculation.

4.4 Optimization flowchart

The sensitivity filtering technology (Sigmund and Petersson 1998) is used to address the checkerboard patterns and mesh dependence in topology optimization results. The filter radius is set to twice the element length. This filter modifies the design sensitivity of a specific element based on a weighted average of the element sensitivities in a fixed neighborhood, which is purely heuristic but produces results that are very similar to the local gradient constrained results and require almost no additional CPU time. The Heaviside projection method is then applied to obtain clear optimization results. The hyperbolic tangent function is selected by the Heaviside function, with a projection threshold of 0.5. The parameter \(\beta\) is initially set to 0.5 and is multiplied by 2 for each iteration until it reaches 20 and remains unchanged. The globally convergent method of moving asymptotes (GCMMA) algorithm (Svanberg 1995) is utilized as optimizer to update the design variables. The optimization process will cease when certain convergence criterion satisfies. The computations of all examples are implemented in MATLAB R2018a. Figure 3 presents the flowchart of optimization procedures.

Fig. 3
figure 3

Flowchart of the optimization procedures

Full size image

5 Numerical examples

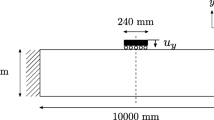
To eliminate the problems caused by geometric complexity, a three-layer planar shell structure is presented as the numerical example to verify the proposed design approach, as presented in Fig. 4. The model is a simply supported square plate, composed of two isotropic materials, with a downward vertical excitation at the center of the square plate. The material of the base structure and the restrained layer is aluminum, while the viscoelastic layer is made of 242F01. The material 242F01 is a kind of ultra-pure viscoelastic damping polymer and is manufactured by \(3\textrm{M}^\textrm{TM}\). The length L of the three layers is 200 mm, and the thickness is also consistent, with a value of 2 mm. The material properties are given in Table 1. The viscoelastic materials 242F01 are characterized by the GHM model, and the coefficients of the first-order micro-oscillator term at room temperature (25 °C) are obtained by the least square method, as shown in Table 2. Here, viscoelastic layer is considered as a design domain, while the other two elastic layers are non-design domains. The \(60 \times 60\) four-node quadrilateral shell elements is utilized to discretize the square plate to obtain the efficiently accurate optimization results and capture more topological details. In all cases, the integration steps of the frequency band and time interval are 0.01 Hz and 0.001 s, respectively.

Table 1 Materials properties of viscoelastic composite structure
Full size table
Table 2 Parameters of viscoelastic material
Full size table
Fig. 4
figure 4

Simply supported square plate subjected to the non-stationary random excitation

Full size image

5.1 Response and sensitivity analysis

The external load is a concentrated non-stationary random excitation, which is assumed to be modeled as the single modulation random excitation. The amplitude of PSD is 1 \(\mathrm {N^2/Hz}\), and the uniform modulation function is given as \(g\left( t \right) =12.21\left( e^{-0.4t}- e^{-0.5t} \right)\). Considering that the modes involved in the calculation should cover the range of excitation frequencies, the first 50 modes are used in the example while taking into account both accuracy and efficiency. Here, the damping layer is assumed to completely cover the base structure, with the preset relative density of 1. The frequency band and time interval of excitation are \(\left[ 100 \textrm{Hz} , 105 \textrm{Hz} \right]\) and \(\left[ 0.0 \textrm{s} , 0.2 \textrm{s} \right]\) respectively.

Fig. 5
figure 5

Comparison of non-stationary random response analysis: a Standard deviation of displacement response; b Computational time

Full size image
Fig. 6
figure 6

Performance at different time steps: a Standard deviation of displacement response; b Computational time

Full size image

To validate the correctness of the results, statistics-based Monte Carlo acheme is employed to illustrate the efficiency of PEM. Figure 5 represents the comparisons of the standard deviation curve of the displacement response at the specified location and the corresponding calculation time. It can be found that the results obtained by PEM and Monte Carlo method with 10,000 samples are highly consistent, which verifies the correctness of PEM results. On the contrary, due to the small number of samples, the error caused by Monte Carlo method based on 3000 samples is relatively large, indicating that the calculation accuracy of Monte Carlo method is greatly affected by the number of samples selected. In addition, in terms of calculation time, the PEM takes significantly less time than Monte Carlo acheme based on 3000 and 10,000 samples. Further, HPD and Newmark methods at different time steps are compared in terms of standard deviation of displacement response and calculation efficiency, as shown in Fig. 6. It can be observed that PEM-HPD gets almost the same result when \(\tau =0.001\) and \(\tau =0.004\), while PEM-Newmark shows the obvious difference at two different time steps. This means the sensitivity of time step to PEM-HPD is much lower than that of PEM-Newmark. Therefore, considering accuracy and efficiency, it is acceptable to choose a relatively rough time step \(\tau =0.004\).

Then, DDM-based and AVM-based sensitivity analysis are performed. For comparison, finite difference method (FDM) is also adopted as:

$$\begin{aligned} \frac{\partial c}{\partial x_{e} } \approx \frac{c\left( x_{e}+ \bigtriangleup x_{e} \right) -c\left( x_{e} \right) }{\bigtriangleup x_{e} } \end{aligned}$$
(48)

where \(\bigtriangleup x_{e}\) is a very small value, here, \(\bigtriangleup x_{e}=x_{e}/1000\).

Fig. 7
figure 7

Contour of objective function sensitivities: a DDM; b AVM; c FDM

Full size image
Fig. 8
figure 8

Contour of sensitivity error: a DDM and FDM; b DDM and AVM; c AVM and FDM

Full size image
Table 3 Calculation time of different sensitivity analysis methods
Full size table

Figure 7 presents the contour of objective sensitivities obtained by different methods. In order to make the more convincing comparison, the relative errors between the sensitivity results obtained by different methods are also calculated and the contour of the absolute values are shown in Fig. 8. Obviously, the DDM-based and AVM-based sensitivity results are basically the same except for differences near the loading point. The maximum of the relative error is about 2.73%, and the minimum is only 0.31%. These results strongly confirm the accuracy of the developed sensitivity analysis methods. The gap, however, is in calculation time listed in Table 3. The AVM-based method takes only 52 s, much lower than 197 s required for DDM-based method. For FDM-based method, the efficiency improvement is more obvious. Compared with the required 428 s, the calculation time of AVM-based sensitivity analysis is reduced by nearly 80%.

5.2 Optimization results

The same uniformly modulated excitation is adopted as the external load. The initial value of relative density is set as 0.5. The iterative history of the convergence process is illustrated in Fig. 9. The objective function converges stably to the optimal solution after 32 iterations, and the volume constraint also reaches the given value.

Fig. 9
figure 9

The iterative histories of the objective function and volume constraint

Full size image

The topological evolution of the iterative process is shown in Fig. 10, where the “blue” configuration represents the area covered with damping material, the “green” contour denotes the base structure, and the constrained layer is hidden. A “0-1” polarization distribution of the design variable can be observed. The damping material is symmetrically and partially attached around the loading points of the base structure to suppress vibrations effectively.

Fig. 10
figure 10

Topological configuration evolution of damped structures. a iteration=1; b iteration=2; c iteration=4; d iteration=8; e iteration=15; f iteration=30

Full size image

The time history curves of the standard deviation of the displacement response at the center of the plate are presented in Fig. 11. The “black” curve denotes the undamped plate, and the “red” and “blue” curves represent the plate covered with uniformly and optimized damping materials, respectively. The uniformly damped plate is completely covered by the damping material with half the thickness of the initial design for satisfying 50% volume constraint. Obviously, the proposed method effectively reduces the displacement vibration level. Compared with undamped plate and uniformly damped plate, the standard deviation of displacement response of the optimized plate is reduced by 73.17% and 43.22%, respectively. Figure 12 shows and compares the eigenfrequencies and eigenvectors of all the modes (in the sequence from 1 to 10) before and after optimization. The redistribution of damping material on the base structure changes the eigenfrequencies significantly, with the eigenfrequencies of some modes decreasing and the others increasing. In particular, the modal exchange between 2nd, 3rd and 5th, 6th modes can be observed clearly. The variations of the vibration shapes are extremely limited due to the unchanged geometry shape and mechanical properties of the viscoelastic plate. However, the 10th mode of the optimized structure is unique and fails to find a match in Fig. 12a, which is attributed to the change in the layout of the damping material that affects the vibration characteristics of the structure.

Fig. 11
figure 11

Standard deviation of displacement response at the center point of the plate

Full size image
Fig. 12
figure 12

Vibration shapes of viscoelastic structure. a before optimization; b after optimization

Full size image

Since the non-stationary random excitation is essentially a coupling of transient and steady-state processes, for the comparison purpose, the optimization results based on steady-state displacement response and stationary random excitation are also given here as shown in Fig. 13. Figure 13a is the optimized layout obtained subject to harmonic excitation and Fig. 13b is the optimized layout obtained by stationary random excitation. It should be emphasized that the model conditions and the optimization setup remain the same as the other cases, except for the excitation loads. It can be observed that the difference between the optimized layouts subjected to harmonic excitation and stationary random excitation and the optimized layout for the non-stationary random excitation in Fig. 10 is significant. Specifically, the design configuration obtained by harmonic excitation is relatively regular, with the area distribution roughly correlating with the vibration shapes of the adjacent modes; the design configuration of the stationary random excitation expands on this to include additional laying area for better suppression of the other modes that are being excited; and for the non-stationary random excitation, the damping layout is much more complex and detailed due to the combination of its frequency-domain and time-domain characteristics. These results fully confirm the influence of non-stationary random excitation on the optimization results of damping materials and its own uniqueness.

Fig. 13
figure 13

The optimized layouts of damping material by different excitation loads

Full size image

5.3 Discussions

On the basis of the optimization results in previous section, this section focuses on discussing the influence of several concerned parameters on the topological configuration of viscoelastic structure, including different viscoelastic material, frequency band and time interval of the random excitation, ambient temperature, and the multiple excitations.

5.3.1 Influence of different viscoelastic material

In this section, another different viscoelastic material is considered as the damping layer to compare the influence of different frequency-dependent modulus on the design solutions. The frequency band and time interval of excitation are set as \(\left[ 180 \textrm{Hz} , 185 \textrm{Hz} \right]\) and \(\left[ 0.0 \textrm{s} , 0.2 \textrm{s} \right]\), respectively. The ambient temperature is 25 °C. Here the GHM model is used to characterize the frequency-dependent properties of the viscoelastic material. One viscoelastic material is the previously mentioned 242F01, the other viscoelastic material is DYAD606. In order to compare clearly the differences in the frequency-dependent modulus of the two viscoelastic materials, the trend plots of the storage moduli and loss factors of the two materials with frequency are displayed in Fig.14. Obviously, the properties of the two viscoelastic materials are significantly different. 242F01 is relatively soft and has a large loss factor, While DYAD606 is relatively hard and has a small loss factor.

Fig. 14
figure 14

Frequency-dependent shear modulus for two different viscoelastic materials

Full size image

The optimized layout designs of the viscoelastic plate for two different viscoelastic material are given in Table 4, and the displacement standard deviation curves obtained before and after optimization are also shown for comparison. It can be seen that the two different frequency-dependent moduli have a significant effect on the layout design of the damping material. For 242F01, the material is relatively softer and has better damping performance, so it is mainly covered in the middle and the surrounding areas where the modal strain energy is larger; whereas for DYAD606, due to its relatively higher hardness, and poorer damping performance, the distribution area is relatively closer to the boundary in order to increase the stiffness at the boundary to achieve more energy dissipation. This is also supported by the displacement standard deviation curves, where the case of laying 242F01 has a greater overall decrease in the vibration intensity and better vibration suppression performance than the case of DYAD606. The results demonstrate that different viscoelastic materials can significantly change their optimal layout in the structure due to their different stiffness and loss factors.

Table 4 Optimization results of viscoelastic plate with different viscoelastic materials
Full size table

5.3.2 Influence of excitation frequency band

Here, \(\left[ 60 \textrm{Hz} , 65 \textrm{Hz} \right]\), \(\left[ 120 \textrm{Hz} , 125 \textrm{Hz} \right]\), \(\left[ 180 \textrm{Hz} , 185 \textrm{Hz} \right]\), and \(\left[ 240 \textrm{Hz} , 245 \textrm{Hz} \right]\) is selected as the different excitation frequency bands, while the excitation time interval is set as \(\left[ 0.0 \textrm{s} , 0.2 \textrm{s} \right]\) and the ambient temperature is 25 °C. The topological design configurations of the viscoelastic plate for different excitation bands are given in Table 5, and the displacement standard deviation curves obtained before and after optimization are also shown below the corresponding configurations. Obviously, the displacement response at the center of the plate decreases significantly in different excitation frequency bands, and the optimized damping layout can effectively suppress the vibration. However, the optimal layouts corresponding to different frequency bands are obviously disparate. In addition, design layouts obtained by higher frequency bands are more complex and localized than those obtained by lower frequency bands. This is because the excitation of higher frequency band can excite more higher-order modes, and the damping material always covers the region with larger modal strain energy to achieve the optimal performance of vibration suppression. It is confirmed that the excitation frequency bands have a notable effect on the optimal configuration of viscoelastic structures.

Table 5 Optimization results of viscoelastic plate under different excitation frequency bands
Full size table

5.3.3 Influence of time interval size

The comparison of topological configurations obtained in different time intervals is investigated. The common frequency band of excitation is \(\left[ 180 \textrm{Hz} , 185 \textrm{Hz} \right]\) and the ambient temperature is 25 °C. \(\left[ 0.0 \textrm{s} , 0.1 \textrm{s} \right]\), \(\left[ 0.0 \textrm{s} , 0.2 \textrm{s} \right]\), \(\left[ 0.0 \textrm{s} , 0.5 \textrm{s} \right]\), and \(\left[ 0.0 \textrm{s} , 1.0 \textrm{s} \right]\) are considered as the time intervals, respectively. Table 6 shows the optimized configurations and the corresponding displacement standard deviation curves for viscoelastic plates with different time interval sizes. The excellent vibration suppression performance confirms the effectiveness of the optimization method. It can be observed that the optimized layouts obtained for \(\left[ 0.0 \textrm{s} , 0.5 \textrm{s} \right]\) and \(\left[ 0.0 \textrm{s} , 1.0 \textrm{s} \right]\) are highly similar, but shows a large difference compared to the optimized configurations for \(\left[ 0.0 \textrm{s} , 0.1 \textrm{s} \right]\) and \(\left[ 0.0 \textrm{s} , 0.2 \textrm{s} \right]\). This indicates that the time interval size has a certain effect on the final optimized configuration. With the increase of time interval size, the final topology optimization results of damping materials tend to be stable, and closer to the optimization results with steady-state displacement response as the design objective. This is due to the increase of the time interval size, the free vibration of the structure determined by the initial conditions gradually attenuates due to the existence of damping materials, and the structural vibration also begins to stabilize. When the time interval is large enough, there is only the pure forced vibration caused by the external loads, of which amplitude and period are only related to the applied load and do not change with the increasing time.

Table 6 Optimization results of viscoelastic plate in the different time intervals
Full size table

5.3.4 Influence of ambient temperature

Here, the main purpose is to investigate the effect of the fluctuation of viscoelastic material properties caused by the change of ambient temperature on the structural design configuration. The frequency band and time interval of excitation are fixed as \(\left[ 150 \textrm{Hz} , 155 \textrm{Hz} \right]\) and \(\left[ 0.0 \textrm{s} , 0.2 \textrm{s} \right]\) respectively. Four different temperatures are considered, i.e. 10 °C, 25 °C, 40 °C and 50 °C, of which shear moduli are all represented by the GHM model, corresponding to the coefficients of the respective micro-oscillators. Figure 15 plots the variation curves of storage modulus and loss factor of viscoelastic materials at different temperatures in the frequency domain. Obviously, the energy storage and dissipation characteristics of damping materials are closely related to the ambient temperature. The optimized topology layout of the damping plate is shown in Table 7, and the variation curves of respective displacement standard deviation in the time domain are also given. Although the frequency band and time interval of excitation are consistent, it can still be seen that the topology of the damping plate shows some variation due to the significant difference in the viscoelastic properties of the damping material caused by the temperature changes. As the ambient temperature increases, the viscoelastic weight of the damping material changes, which is reflected in the performance index as the storage modulus decreases and the loss factor increases. We can conclude that the optimized layout of the damping material shows a better vibration suppression effect with increasing temperature. Generally, at lower temperatures, the optimal configuration is mainly concentrated in the center of the plate to achieve higher stiffness performance, while at higher temperatures, the damping materials are mainly distributed in the center and boundary of the plate to obtain maximum energy dissipation.

Fig. 15
figure 15

Shear modulus curves in frequency domain at different temperatures

Full size image
Table 7 Optimization results of viscoelastic plate at the different ambient temperatures
Full size table

5.3.5 Influence of the number of random excitations

The topology optimization problem of viscoelastic plates under multi-points non-stationary random excitations is studied. The cases of two-points and four-points random excitations are taken as examples. To avoid problems caused by asymmetry, assume that the position of excitation applied is symmetric, as shown in Fig. 16. The frequency band and time interval of excitation are set as performed \(\left[ 180 \textrm{Hz} , 185 \textrm{Hz} \right]\) and \(\left[ 0.0 \textrm{s} , 0.2 \textrm{s} \right]\) for more prominent comparison. Use the center of the plate as the reference point for the optimized design, and keep the other relevant settings consistent with the previous cases. For more convenient comparison, the configuration of single random excitation is also presented. The design layouts of multiple random excitations and obtained standard deviation curves are given in Table 8. The displacement responses at the central reference point of the viscoelastic plate are significantly suppressed under different numbers of random excitations, confirming the universality and scalability of the proposed method. One can be observed that the damping materials all exhibit aggregation near the loading point, and the others are mainly concentrated around the boundary to maximize the energy dissipation. The results demonstrate that the distribution characteristics of the optimal configuration of the damping materials are influenced by the location and the number of excitations.

Fig. 16
figure 16

Viscoelastic plates with different number of random excitations

Full size image
Table 8 Optimization results of viscoelastic plate under the different number of the random excitations
Full size table

6 Conclusions

This paper investigates the design optimization of a three-layer viscoelastic planar shell structure under non-stationary random excitation. The goal is to minimize the mean value of the displacement PSD within a specified frequency band and time interval. The GHM model is utilized to characterize the dynamic properties of viscoelastic materials. Additionally, an augmented dynamic equation is established by introducing the auxiliary dissipation coordinates. The study models non-stationary random excitations as uniformly modulated evolutionary random process, and analyzes the random response of the augmented system using the time-domain PEM-HPD approach. Non-stationary random sensitivity analysis is then performed based on the DDM and AVM methods, respectively. The validity and applicability of the proposed method are verified through several numerical examples. The precision and efficiency of the developed means for non-stationary random response and sensitivity analysis of the augmented system are compared. Numerical results demonstrate that this method can achieve a clear optimal solution, and significantly reduce the random vibration intensity of the structure without adding extra weight. In addition, this paper discusses the impact of frequency band and time interval of random excitation, ambient temperature and multiple excitations on optimization results. The paper presents a practical tool for the optimal design of viscoelastic structures under the non-stationary random excitation, and can also be extended to design configurations of cylindrical shell structures and hollow cylindrical shell structures.